Filamentous Network Mechanics and Active Contractility Determine Cell and Tissue Shape

Abstract

For both cells and tissues, shape is closely correlated with function presumably via geometry-dependent distribution of tension. In this study, we identify common shape determinants spanning cell and tissue scales. For cells whose sites of adhesion are restricted to small adhesive islands on a micropatterned substrate, shape resembles a sequence of inward-curved circular arcs. The same shape is observed for fibroblast-populated collagen gels that are pinned to a flat substrate. Quantitative image analysis reveals that, in both cases, arc radii increase with the spanning distance between the pinning points. Although the Laplace law for interfaces under tension predicts circular arcs, it cannot explain the observed dependence on the spanning distance. Computer simulations and theoretical modeling demonstrate that filamentous network mechanics and contractility give rise to a modified Laplace law that quantitatively explains our experimental findings on both cell and tissue scales. Our model in conjunction with actomyosin inhibition experiments further suggests that cell shape is regulated by two different control modes related to motor contractility and structural changes in the actin cytoskeleton.

INTRODUCTION

The relation of form and function is a long-standing issue in our understanding of biological systems. From an evolutionary viewpoint, form follows function. However, tissue cells adapt strongly to environmental cues; thus, cell shape is highly variable, with dramatic consequences for functionality. For example, it is well known that the geometric distribution of adhesive cues has a large impact on cellular function. Studies using microcontact printing techniques to control the spatial distribution of adhesive regions have shown that, for single endothelial cells, spreading area controls cellular response to mitogen stimulation, thus switching cell fate from proliferation to apoptosis (1). Later studies along these lines then showed that cell shape determines where lamellipodia were initiated (2) and where focal adhesions were assembled (3). Using micropatterned dots, it has been systematically analyzed over which ranges of dot sizes and distances cells spread when confronted with spatially separated sites of adhesion (4). Micropatterning techniques have also been used to demonstrate that the orientation of the mitotic spindle is determined by the geometry of the extracellular environment, which is mapped onto the cell by its adhesive structures (5). Cell adhesion is also strongly regulated by mechanical factors. Studies using soft elastic substrates have shown that cell organization, including the morphology and composition of adhesion sites and the structural state of the actin cytoskeleton, depend on extracellular stiffness (6). Elasticity of the extracellular environment seems to affect cellular organization mainly by regulating the level of internal tension in the actin cytoskeleton generated by myosin II motors (7).

Physical factors like geometry and mechanics are also crucial to understanding tissue function. It has been noticed earlier that fibroblast-like cells in collagen gels apply surprisingly large tension to their extracellular environment (8) and that this tension determines tissue shape (9). In these studies, mechanical factors emerged as important determinants of cellular structure formation in tissue contexts. Indeed, tension and mechanics are important regulators of tissue morphogenesis (10,11). Like for single cells, the relation between form and function is mutual. Recently it has been demonstrated with micropatterning techniques that the shape of tissue models can regulate their pattern of proliferation (12). Theoretical modeling suggests that cell proliferation in a tissue is regulated by an integral feedback loop operating on mechanical signals (13). Because cell organization in a tissue context is strongly influenced by mechanical cues, the mechanical conditions of the boundaries play an important role. For example, it has been found that cell orientation is different at free versus clamped tissue boundaries (14).

Although geometry, elasticity, and tension are emerging as common biological control elements spanning cell and tissue scales, our quantitative understanding of cell and tissue organization as a function of these physical determinants is still very limited. Advances along these lines would have far-reaching consequences for biomedical applications, including rational design of artificial tissues. In this study, we provide a quantitative perspective on universal shape determinants spanning cells and tissue scales. By combining adhesive patterning techniques and quantitative image analysis, we show that cell and tissue shapes are characterized by a surprising similarity. If pinned at discrete points of adhesion, both cell and tissue shapes resemble a sequence of inward-curved circular arcs. For cells, earlier studies have interpreted the arc-like shape features as indicating the validity of the Laplace law, which describes the shape of inanimate matter under tension (for example, soap bubbles). However, we find experimentally that, for both cells and tissues, radii increase with spanning distance between adhesion points. Such a relation cannot be explained from the local considerations resulting in the Laplace law and implies that the distribution of tension in cellular systems is more complex, including a dependence on boundary conditions. Yet and despite the underlying molecular complexity, the relation leads to surprisingly universal shapes both on cell and tissue levels. To explain our experimental findings, we use theoretical modeling and computer simulations to identify filamentous network mechanics and active contractility to be the unifying principles bridging cell and tissue scales. In particular, we derive a modified Laplace law that can explain our experimental findings in a quantitative manner. This novel type of Laplace law is first confirmed by computer simulations and then derived as a self-consistent equation for arc radius as a function of spanning distance. We show that our model implies two different control modes (tension versus elasticity control) that, for cells, correspond to two essential parts of Rho signaling to the cytoskeleton, namely reorganization of the actin cytoskeleton and activation of myosin II motors. Thus our deceptively simple mathematical results in fact allow us to dissect the opposing forces and regulatory systems underlying cell and tissue shape. We also discuss the relevance of our findings in the context of tissue organization and mention potential applications in tissue engineering.

MATERIALS AND METHODS

Substrate preparation

Micropatterned substrata were prepared using the microcontact printing technique as described elsewhere (4). Briefly, a silicon master was fabricated and used as a mold to produce a silicone stamp by the thin stamp technique. Using a gold-thiol chemistry, the structure of the stamp was transferred into a two-dimensional pattern consisting of several neighboring areas (size, 500 × 2000 μm), each of which contained a particular, uniform pattern of adhesive dots separated by various antiadhesive distances. The stamp was inked with a 1.5 mM solution of octadecylmercaptan (Sigma Aldrich, St. Louis, MO) in ethanol and pressed onto a gold-coated coverslip, forming self-assembled monolayers at the protruding parts of the stamp. Uncoated regions of the coverslip were blocked with a 1.5 mM solution of a tri(ethylene glycol)-terminated alkanethiol in ethanol. Solutions of human plasma fibronectin (10 μg/ml; Sigma-Aldrich, St. Louis, MO) in phosphate-buffered saline (PBS) were applied to the coverslips for 1 h at 4°C.

Cell culture

Mouse B16F1 melanoma cells (B16 cells) were kindly provided by G. Nicholson (Houston, TX) and buffalo rat liver (BRL) cells were from American Type Tissue Culture Collection (ATCC, Manassas, VA). Both cell types were grown in Dulbecco's modified Eagle's medium (DMEM, Invitrogen, Carlsbad, CA) supplemented with 10% bovine growth serum (BGS) (HyClone, South Logan, UT) under humidified atmosphere and 5% CO₂. Cells were washed twice with phosphate-buffered saline (PBS) (Ca²⁺- and Mg²⁺-free) and removed from tissue culture plates by treatment with Hank's Balanced Salt Solution (HBSS) containing 0.1% trypsin and 4 mM EDTA for 3 min. Dissociated cells were washed in DMEM without BGS, centrifuged, seeded on the patterned substrates in DMEM (1 × 10⁴ cells/cm²), and cultured for 1 h. To minimize secretion of the new matrix and to reduce cell migration, serum-free culture medium was used after replating (no BGS added).

Inhibition experiments

Cells were preincubated on patterned substrata for 1 h as described above. To reduce intracellular tension, the culture medium was replaced by serum-free medium containing either Y-27632 or blebbistatin. Y-27632 dihydrochloride (Tocris Bioscience, Ellisville, MO) was used to inhibit the Rho-kinase pathway and was applied at 50 μM for 20 min. Blebbistatin (Sigma) is a specific inhibitor of nonmuscle myosin II and was applied at 50 μM for 10 min.

Immunostaining

Cells were fixed for 10 min with 4% paraformaldehyde in PBS, washed three times for 5 min with PBS containing 0.1% Triton X-100 (PBS-Triton) and incubated for 1 h at room temperature or overnight at 4°C with primary antibodies (polyclonal antifibronectin (Sigma) to label the substrate pattern and either monoclonal antivinculin (Sigma) or monoclonal antipaxillin (BD Transduction Laboratories, Franklin Lakes, NJ) to label focal adhesions). Probes were washed three times for 5 min with PBS-Triton and incubated for 1 h at room temperature with a fluorescently coupled secondary antibody (goat antirabbit AMCA or goat antimouse Cy3) obtained from Dianova (Hamburg, Germany). To visualize the cell morphology, actin filaments were labeled with Alexa488-coupled phalloidin (Invitrogen, Carlsbad, CA). Slides were mounted in Mowiol (Hoechst, Frankfurt, Germany) containing 1% N-propyl gallate.

Tissue model

Collagen solutions of rat tail collagen type I were purchased from Sigma-Aldrich and dissolved in distilled water pH 3 and stirred overnight at 4°C. Collagen gels were mixed at 4°C using the following proportions: 5 parts collagen solution; 2 parts 5×F12 (Invitrogen) with HEPES, gentamicin (Sigma), and pen/strep (Invitrogen); 1 part serum (8% BGS gold/PAA and 2% chicken serum; Invitrogen); 1.5 parts PBS; and 0.5 parts 1 M NaOH. The final concentration of collagen in the gel was 1.5 mg/ml. Multiwell tissue culture plates (Greiner, Kremsmünster, Austria) were cast with a polydimethylsiloxane (PDMS) layer (Sylgard 184; Dow Corning, Midland, MI) and polymerized for 6 h at 60°C. Pinning points in the gel consisted of steel needles that were pushed into the PDMS. A basal layer of collagen was poured first and allowed to set at 37°C for 1 h; cells and additional collagen mixture were then poured over it. In all cultures, each well contained 1.5 ml of collagen solution and 5 × 10⁵ primary chicken fibroblast derived from the dermis of 8-day-old embryos. Collagen gels were cultured for 7 days, fixed with formaldehyde for 45 min, permeabilized with PBS-Triton for 24 h, and stained with phalloidin and DAPI (Hoechst) for 2 days. After removal of the steel needles, whole mounted collagen gels were imaged at a stereomicroscope (Zeiss Lumar.V12; Carl Zeiss, Oberkochen, Germany), or at an upright microscope (Axioplan; Carl Zeiss) using widefield fluorescence microscopy or an ApoTome (Carl Zeiss).

Microscopy and quantitative image analysis

Probes were analyzed with a laser scanning microscope (LSM 510; Zeiss) and all (3–5) z-slices projected onto one image. To quantitatively evaluate cell contour as a sequence of circular arcs, circles were fitted using a custom-made program (CellMicroPat) written in Matlab (Mathworks, Natick, MA). Routines based on the Matlab DIPimage toolbox (http://www.ph.tn.tudelft.nl/DIPlib/) were used for image processing, and the nonlinear least square fitting routine based on the Marquardt method from the Matlab immoptibox toolbox (http://www2.imm.dtu.dk/∼hbn/Software/) was used for fitting the arc radii. In CellMicroPat, arc endpoints are identified as focal adhesion from vinculin or paxillin staining, and their distance d is recorded. After supplying the two endpoints and four to five points along the cell contour by user clicks, CellMicroPat fits a preliminary circle to these points. It next generates 60 equally spaced radial actin intensity profiles across the arc and identifies the location of the intensity maxima along these rays. The final arc with radius R then follows by fitting a circle to these 60 points. Because it is hardly possible to measure the thickness of the peripheral stress fibers due to the limits of optical resolution, we defined arc strength S = (I_a − I_bg)/(I_c − I_bg) as obtained from three different actin intensities. I_a is the arc intensity, defined as the average of the maxima of the 60 intensity profiles used to determine the arc. I_bg is the background intensity of the overall image determined with the function background offset from DIPimage. I_c is the average actin intensity inside the cell obtained after thresholding the cell from the background. The normalization with respect to actin intensity both inside and outside the cell ensures that S is a good measure for fiber strength for experiments with different cells and different staining conditions.

Statistical data analysis

Statistical data analysis was performed using algorithms provided by the statistical toolbox in Matlab (Mathworks). Correlation coefficients C denote Pearson correlation coefficients. Bootstrapping was used for estimating confidence intervals for fitting parameters. A bootstrap analysis is based on data resampling and does not require any a priori hypothesis. In each case, it involved 100 to 1000 random sets sampled from the original data sets with repetition. Bootstrapping was also used to analyze the statistical significance of differences between experiments. In this context, statistical significance was assigned when the distribution for the parameters obtained from bootstrapping were not overlapping.

RESULTS

Cell and tissue shape for discrete sites of adhesion

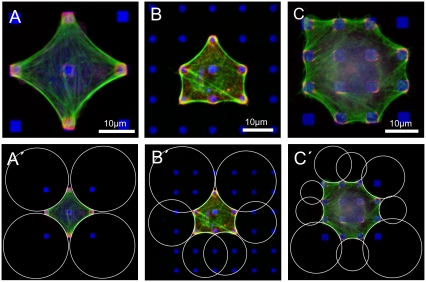
To study in a quantitative way how adhesion geometry affects cell shape, we used regular arrangements of micrometer-sized fibronectin dots produced by microcontact printing (4). By varying dot size and dot distance, we mimicked the spatial distribution of extracellular matrix ligands occurring in vivo. Buffalo rat liver (BRL) cells and a mouse melanoma cell line (B16) were cultured on patterned substrates for 1 h in serum-free medium and then fixed and stained for fibronectin, actin, and focal adhesion markers. Under these culture conditions, cell migration is largely reduced, and cell spreading is completed in such a way that the cells have established an almost stationary cell shape at the time of fixation (Fig. S1 in Supplementary Material, Data S1). In all cases, mature adhesion sites developed overlying the fibronectin dots and were connected by actin fibers, which mainly outline the cellular periphery in a sequence of inward-curved circular arcs (Fig. 1, A–C). Arc-like cell borders have also been observed for cells growing on homogeneously coated substrates (15,16) or on large adhesive islands with concave contours (17). For our dot patterns, we observed typical arc morphologies for a wide variety of dot sizes (0.5–3 μm) and lattice constants (5, 10, 15, 20, and 25 μm), and we thus conclude that it is a robust feature of cell adhesion on spatially separated ligand patches.

FIGURE 1.

Cell shape on micropatterned substrates. (A–C) Arc-like contours composed of actin fibers characterize the shape of BRL (A and B) and B16 cells (C) cultured on substrates of micropatterned fibronectin dots. Cultures were labeled for actin (green), paxillin (red), and fibronectin (blue). Scale bars 10 μm. (A′–C′) For all cases, arc-like contours fit well to circles determined by custom-made software. (B and C) The circles spanning diagonal distances show larger radii than the circles spanning the shorter distances between neighboring adhesions.

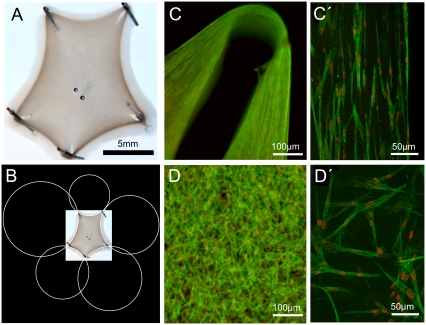
Strikingly, similar arc morphologies have been observed before in simple tissue models, namely for fibroblast-populated gels of collagen from bovine dermis (bd-collagen) (9). If embryonic fibroblasts are mixed with rat tail collagen (rt-collagen), it takes several days until the fluid mixture starts to condense into a gel-like structure. The shape of this structure is essentially determined by the spatial positioning of steel needles fixed to the bottom of the culture dish and indeed resembles a sequence of inward-curved circular arcs. The tissue model established after 1 week is shown in Fig. 2 A (full-time series illustrated in Fig. S2 in Data S1). As has been described previously (9), cellular traction is strong enough to lead to gel rupture next to the pinning needles, as can be seen from the inward-directed holes in the gel in Fig. 2 A.

FIGURE 2.

Simple tissue model. (A) Like for cells on micropatterned substrates, arc-like contours also mark the shape of a fibroblast-populated rat tail collagen gel pinned to the substrate at discrete sites by steel needles. Space bar is 5 mm. (B) The arcs are circular as revealed by automated fitting. (C) Detail of the upper right corner of the tissue model in (A) taken with widefield fluorescence microscopy (actin in green; nuclei in red). Note the circular hole where the steel needle has been removed and an elongated hole toward the gel center, which resulted from gel rupture close to the steel needles due to cellular contractility. (C′) Single optical section through the gel's rim taken with an ApoTome microscope (Carl Zeiss) reveals parallel-aligned cells in the periphery. (D and D′) In the bulk of the collagen gel, cells have a random orientation.

Quantitative image analysis of cell and tissue shape

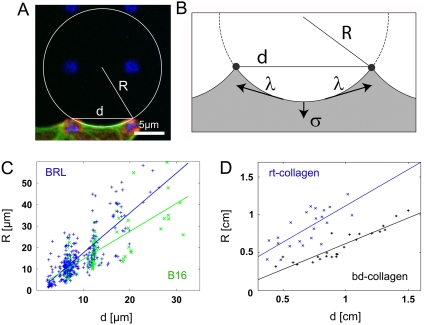
To quantitatively evaluate cell and tissue shape, we developed a computerized procedure to fit circular arcs to cell and tissue contours (Figs. 1, A′–C′, and 2 B). For each fit, we recorded arc radius R and spanning distance d (Fig. 3 A). We analyzed 91 BRL and 38 B16 cells on different dot patterns as well as fibroblast-populated collagen gels. The tissue models were made of collagen, either from rt-collagen (22 data points) or bd-collagen (24 data points). For both cell types, as well as for both types of tissue model, we found that radius R increases with spanning distance d in a statistically significant way (Fig. 3, C and D, correlation coefficients C_BRL = 0.80, C_B16 = 0.77, C_bd = 0.91). The differences between BRL and B16 are statistically not significant (Fig. S3 a in Data S1). The correlation between R and d also becomes evident by visual inspection of Figs. 1, A′–C′, and 2 B. In Fig. 1 B′, for example, the two circles at the two diagonal top sides are larger than the four circles at the other four sides.

FIGURE 3.

R-d relation. (A) For each arc, radius R and spanning distance d are recorded. (B) Simple tension model: Line tension λ straightens the contour between neighboring adhesions, whereas surface tension σ pulls the envelope inward toward the bulk. In mechanical equilibrium, the local radius of curvature is R = λ/σ and does not depend on the spanning distance d. (C) For both, BRL (blue) and B16 (green) cells, arc radius R increases with spanning distance d. (D) R and d also correlate for the simple tissue model based on rat tail (rt, blue crosses) and bovine dermis (bd, black pluses) collagen. The linear fits serve as guides to the eye.

Different kinds of tension

The formation of circular arcs seems to indicate the applicability of the Laplace law, a universal law that also determines the shape of inanimate matter such as soap bubbles in three dimensions. In this case, surface tension σ tries to decrease the bubble surface area, a tendency that is counteracted by the pressure difference p building up inside the bubble. Because this balance is locally achieved at every point on the bubble, it takes on the shape of a sphere with the radius R = 2σ/p. In the case of mature cell adhesion to a flat rigid substrate, one deals with an effectively two-dimensional situation. Similar to other modeling approaches in this field, we therefore used a reduced model that parameterizes cell shape by its two-dimensional contour (16,18,19). In the two-dimensional context, the forces drawing the cell inward correspond to a surface tension σ because they act geometrically to decrease the projected area of the cell. A counteracting force results from the resistance of the contour to an increase in length, which thus corresponds to a line tension λ. Surface tension σ and line tension λ locally balance each other at every point along the contour (Fig. 3 B). Mathematically, this finding implies that the radius of curvature obeys the relation R = λ/σ at every point along the contour (also compare with Data S1). For single adherent cells, these arguments based on the Laplace law have been used previously to explain the occurrence of circular arcs (16,17). Here the effective surface tension σ might include contributions from the actin cortex and the plasma membrane, which both tend to contract laterally and span the whole cell body. The contractile effects of the actin cortex and the plasma membrane at the cell edge enter into the effective line tension λ, which in addition includes the effect of the actin fibers lining the cell periphery. An additional active contribution could result from peripheral contractility, that is, from localization of myosin II motors to peripheral actin bundles. If one follows the Laplace law in assuming that both surface σ and line tension λ are local quantities, then one expects a constant radius R = λ/σ for all arcs, independent of the spanning distance d (simple tension model).

In marked contrast to this expectation, our quantitative analysis revealed that, for both cell types used in this study, larger spanning distances d correspond to larger radii R (Fig. 3 C). Even more surprisingly, we found a similarly increasing R-d correlation for the tissue model (Fig. 3 D). Indeed, there are many similarities between the two situations. Similar to the cell experiments, the tissue experiments also deal with an effectively two-dimensional situation; thus, one can again differ between surface and line effects. Surface tension σ and line tension λ are now determined by the spatial distribution of contractile cells throughout the collagen gel. Fig. 2 shows that cells accumulate and align in parallel at the boundary (Fig. 2, C and C′) but disperse isotropically in the bulk (Fig. 2, D and D′). Similar effects have been observed previously for other simple tissue models, although in a less controlled manner (8). Accumulation of cells and fibers at the rim effectively creates the line tension λ, whereas cell dispersion in the bulk leads to the isotropic tension σ.

Computer simulations

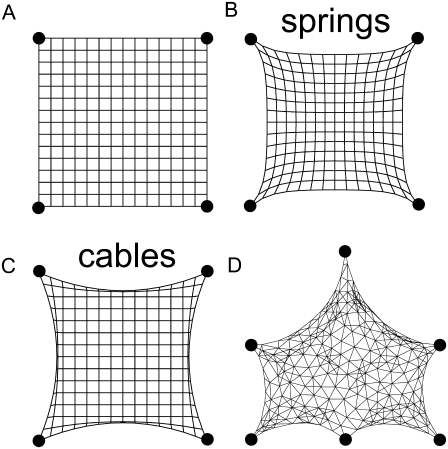
To understand the physical mechanism resulting in arc radii that depend on spanning distance, we conducted computer simulations accounting for the elastic effects missing in the simple tension model. For both cells and collagen gels, internal tension is generated by contractile elements embedded in a filamentous network (myosin II motors in the actin cytoskeleton (20) and fibroblasts in the collagen gel (21)). In contrast to the simple tension model, we now assume that the resistance to this contraction does not result from a simple line tension but from the elasticity of the filamentous network. We computationally simulated this situation as a mechanical network subject to isometric contraction. Fig. 4 A shows the tension-free state for a square contour pinned at four corners. Under isometric tension, the contour is drawn inward to an extent that is determined by the elastic resistance of the network. If the links between the nodes represent harmonic springs (a fully elastic network), the resulting arcs reveal a noncircular contour whose shape strongly depends on the global adhesion geometry (Fig. 4 B). In contrast, circular arcs result if links between the nodes act as cables rather than springs (Fig. 4 C). In a cable network, mechanical links respond like harmonic springs under tension, but they show no resistance to compression (22). Indeed, it is well known that the filaments building up the mechanical network (actin for the cytoskeleton and collagen for the tissue equivalent) buckle under compressive loading exerted by myosin motors (23) or contractile cells (24). For a cable network, our simulations resulted in circular contours, and this feature even persisted when the global adhesion geometry (squares, rectangles, etc.) or network topology (Fig. 4 D) was altered. Hence, the mechanics of actively contracting cable networks gives rise to the arc-like shape features observed experimentally.

FIGURE 4.

Computer simulations of mechanical networks under isometric tension. (A) Tension-free configuration of a regular network of mechanical links pinned to a square pattern. (B and C) In mechanical equilibrium with links simulated as harmonic springs (B) or cables (C), only cable networks show circular arcs. In contrast to harmonic springs, cables show no resistance to compression and so have an asymmetric force-extension relation. (D) In mechanical equilibrium for a disordered cable network, circular arcs form regardless of the details of the adhesion geometry and the network topology.

Tension-elasticity model

Because elastic effects depend on absolute distances, the computer simulations resulted in a correlation between arc radius R and spanning distance d. To facilitate the quantitative comparison between model predictions and the experimental data, we mapped our computer model to an effective contour model, which we call the “tension-elasticity model”. Similar to the simple tension model, the tension-elasticity model is based on the concepts of surface tension σ and line tension λ. Because cable networks do not propagate compression, we kept the notion of a nonelastic bulk surface tension σ. However, because for both cells and tissues a reinforcing and contractile contour exists, we introduced an elastically modified line tension λ = EA(L − L₀)/L₀ given by the product of the elastic rigidity of the contour EA and its relative deformation under force (strain, where L and L₀ are the strained contour length and its resting length, respectively). This equation can now be combined with the Laplace equation. Because L depends on arc radius R and spanning distance d through additional conditions set by the adhesion constraints, we arrived at the following implicit equation for R(d) (for a complete derivation and a more detailed discussion, see Data S1):

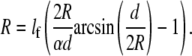Here, l_f = EA/σ is a length scale set by the ratio of rigidity and surface tension, and α = L₀/d is the rest-length parameter, which describes the relative length of the relaxed fiber with respect to the spanning distance. This equation predicts that arc radius R is a monotonously increasing function of spanning distance d, which is in agreement with our experimental observations (Fig. 3, C and D). In Fig. 5 A, we show that excellent agreement exists between the predictions of the tension-elasticity model (lines) and computer simulations of cable networks as shown in Fig. 4, C and D (circles).

FIGURE 5.

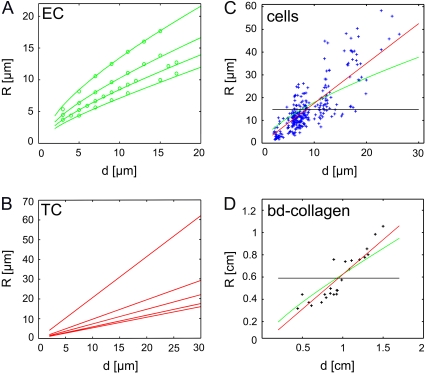
In contrast to the simple tension model, the tension-elasticity model predicts an R(d)-dependence due to the boundary conditions imposed by the adhesion constraints. (A) Elasticity control (EC): R(d) from the effective contour model with varying ratios of fiber rigidity and surface tension l_f = EA/σ (l_f = 500, 200, 100, 50 from top to bottom; rest-length parameter α = 1). The agreement with the computer simulations of cable networks, as shown in Fig. 4, C and D, (circles) is excellent. (B) Tension control (TC): R(d) from the effective contour model with varying rest-length parameter (α = 1.01, 1.05, 1.1, 1.2, and 1.3 from top to bottom, infinite l_f). (C and D) Fits of experimental data for BRL cells (C) and bd-collagen gels (D) to the EC model (green) and the TC model (red). A bootstrap analysis shows that both fits are statistically significant. The predictions of the simple tension model (average R without dependence d) are shown in black.

Tension and elasticity control

A detailed analysis of the tension-elasticity model (see Data S1) reveals that the two parameters l_f and α introduced in the above equation correspond to two fundamentally different control modes to λ, which in the following are discussed for the case of cells, but for which there exists a close analogy in tissue models. First, a structural reinforcement causes an increase in actin bundle thickness and so a change in bundle rigidity EA (elasticity control). This mode is controlled by the length l_f (Fig. 5 A). Second, an increased contractility in the actin bundles results in filament contraction and decreased bundle rest-length, thus increasing strain u (tension control). This mode is controlled by the rest-length parameter α (Fig. 5 B). A bootstrap analysis shows that each control mechanism alone can fit the experimental data in a statistically significant way, yielding a lower bound for l_f and an upper bound for α (Fig. 5 C: α = 1.01, l_f = 1.3 mm; the same result is found for the bd-gels, Fig. 5 D: α = 1.16, l_f = 4.0 mm). Hence, the tension-elasticity model explains the R-d relation in a quantitative way, although it is not capable of discriminating between tension and elasticity control.

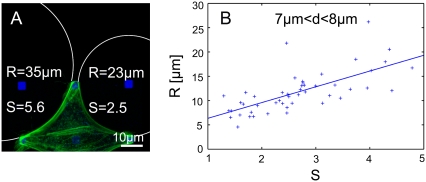
To clarify the relative contributions of tension and elasticity control, we studied the effect of rigidity variations on the arc radii. Because fiber thickness cannot be reliably measured due to limitations in optical resolution, we developed a dimensionless measure S for fiber strength, defined as the relative increase in the peripheral actin fluorescence intensity with respect to bulk levels. For each arc, S was determined in addition to R and d. For single cells, arc strength S varied considerably from arc to arc and might correlate with arc radius R, as suggested by Fig. 6 A. Although the spread of data is rather large, our data indeed show that, on average, a stronger arc (i.e., larger S) corresponds to a larger arc radius R at the same spanning distance d (Fig. 6 B: C = 0.70). We also checked that arc strength variation S does not correlate with spanning distance d (Fig. S4 in Data S1). Therefore, the large data spread in the cellular R(d) in Fig. 1 is in part due to arc strength variations, as confirmed by analyzing R(d) for S-homogenized subpopulations (Fig. S5 in Data S1). This observation suggests that cells use elasticity control to regulate the degree of line tension.

FIGURE 6.

Effect of arc strength. (A) BRL cell labeled for actin (green) and fibronectin (blue) indicates that arcs with stronger actin fluorescence (defined as arc strength S) might have a larger arc radius R than weak arcs. (B) Correlation between arc strength S and radius R for a fixed adhesion distance d between 7 and 8 μm. Despite the large data spread, the correlation is statistically significant.

Inhibition experiments

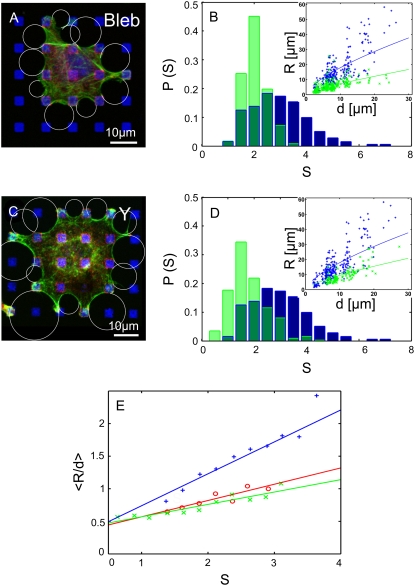
To study the role of actomyosin contractility, we treated BRL cells with two different inhibitors: Y-27632, a general inhibitor of the Rho-kinase pathway, and blebbistatin, a specific inhibitor of nonmuscle myosin II (Fig. 7, A and C). Both inhibition protocols caused smaller arc radii (Fig. 7, B and D, insets). This observation implies a strong reduction of λ accompanied by the presence of a residual σ in the system (for example, the plasma membrane tension). For both treatments, the distributions of fiber strength S shown in Fig. 7, B and D, shift to considerably smaller values (light green) compared to control cells (blue, with overlap in dark green). This structural weakening increases from blebbistatin to Y-27632 treatment and correlates significantly with the degree of arc radii reduction obtained from fitting the R(d) data shown as insets in Fig. 7, B and D, to the EC-model (control: 〈S〉 = 2.95, l_f = 1335 μm; blebbistatin: 〈S〉 = 2.04, l_f = 180 μm; Y-27632: 〈S〉 = 1.80, l_f = 70 μm). That inhibition of actomyosin contractility leads to structural weakening reflects that tension and elasticity are tightly coupled through mechanosensitive feedback systems.

FIGURE 7.

Effects of actomyosin contractility. (A) BRL cell labeled for actin (green), paxillin (red), and fibronectin (blue) treated with blebbistatin, a myosin II inhibitor. (B) Quantitative analysis revealed that blebbistatin treatment caused a shift in the probability distributions P of arc strength S to smaller values (light green) compared to control cells (blue, overlap in dark green). Inhibition of contractility also caused a reduction in arc radius R. (Inset: R(d) for inhibited cells (green) compared to control cells (blue). Lines are fits to the EC model). (C) BRL cell treated with Y-27632, an inhibitor of the Rho-kinase pathway. (D) Y-27632 treatment caused similar effects as blebbistatin. (E) Evidence for TC control: the average of R/d as a function of arc strength S for control (blue), blebbistatin-treated (red), and Y-27632-treated (green) cells. The two inhibition experiments are statistically identical and lead to smaller arc radii than predicted from variations of arc strength S alone.

To test whether actomyosin contractility affects cell shape only via elasticity control, the averaged values of R/d were plotted as a function of arc strength S for control and inhibited cells (Fig. 7 E). If the reduction of arc strength S was the only reason for decreased arc radii R, then 〈R/d〉 would be a universal function of S for all experimental conditions. Indeed, Y-27632- and blebbistatin-treated cells were statistically not different (Fig. S3 b in Data S1), indicating that force reduction is saturated and that arc strength has the same effect in both cases. Uninhibited cells, however, show considerably greater values for 〈R/d〉 at the same S. This finding suggests that contractility contributes to the line tension in a direct way, for example, by changing the effective rest-length as predicted by our model for tension control (Fig. S6 in Data S1). Thus, both elasticity and tension control are operative in cells.

DISCUSSION

In this study, we have identified and explained a surprising similarity between two well-established but rather different model systems for the culture of tissue cells. In both cases, we focused on the role of the attachment geometry. For single cells, attachment geometry was controlled by an adhesive dot pattern produced by microcontact printing. For the fibroblast-populated collagen gel, attachment geometry was controlled by discrete pinning needles stuck into the underlying PDMS layer. Our analysis showed that both cell and tissue shape were characterized by a sequence of circular arcs for which in average arc radius R increased with spanning distance d. Although micropatterning techniques have been used for a long time to study the effect of adhesion geometry on single cells (1–5,17), a quantitative analysis of cell shape as a function of the positions of the adhesion sites has not been presented before to our knowledge. The occurrence of circular arcs has been noted previously for cells on homogeneous substrates and interpreted in terms of a simple Laplace law (15–17). An elastic element of the line tension has been suggested previously from actin inhibition experiments (16). However, to our knowledge, the effect of the spanning distance d on arc radii R has not been considered before. Computer simulations indicate that the simplest possible theoretical concept capturing our experimental findings is a contracting cable network, which does not have compression modes in contrast to a purely elastic theory. By mapping the computer simulations onto the tension-elasticity model, we could derive a modified Laplace law and so explain both the occurrence of circular arcs and the R-d relation. Earlier models considered either elasticity (25) or tension (26) to be key determinants of cell shape. In this study, we have shown that it is essential to consider their combination with the twist of using the mechanics of fibrous networks rather than the mechanics of isotropic linear material. Our conclusion is strongly supported by our finding the same results on the tissue level. Indeed, filamentous network mechanics and active contractility are also essential elements on the tissue level. Thus our study, for the first time to our knowledge, provides a unifying perspective on shape in biological systems spanning both cell and tissue scales.

Our study has shown that the elastic response of filamentous networks under active contractility is an essential element determining cell and tissue shape. We have modeled filamentous networks as cable networks, which take into account the most basic properties of polymers: they respond elastically under tension but buckle under compression (22). Our analysis demonstrates that this asymmetry in the mechanical response prevents long-ranged propagation of compressive modes and results in the tension-elasticity model and the generalized Laplace law. This finding, however, does not imply that compression is irrelevant in general. Resistance to compression in cellular systems is usually attributed to microtubules (26). Recently it has been shown that microtubules are targeted into focal adhesions (27), and that they are immersed into the actin cytoskeleton (28). These findings suggest that microtubules might carry more compressive load than formerly appreciated. Moreover, in our experiments, actin is locally condensed into actin cables, which also can carry a more compressive load than single filaments (29). Our analysis suggests that in the setup studied here, tension dominates to such an extent that these effects are not relevant. This conclusion is in line with earlier studies showing that, in mature cell adhesion, most of the tensile load (∼86%) is balanced by the adhesions rather than by microtubules (30). This observation is in contrast to the situation with poorly spread cells, where a substantially larger part of the load (>50%) is carried by the microtubules (31).

The relevance of cable network mechanics is probably more apparent for the tissue model studied here. Other studies have demonstrated that collagen gels immersed in fluid without attachment to adhesion points are inherently unstable under active cellular traction, suggesting that the resistance to a compressive load is rather weak in this case (8,9). In vivo, the proteoglycans, probably missing in our assay, are usually implicated in conferring stability under compression. Moreover, collagen might be organized in superstructures conferring additional stability under tension. Future tissue experiments are required to clarify if these aspects are sufficient to override the arc-like shape response resulting from the asymmetric force extension relation of cable networks.

Our model suggests that two control modes exist for modulating cell and tissue shape, one by structurally reinforcing the boundary and another by actively contracting the cable contour and so reducing its rest-length. For cells, this finding agrees nicely with the molecular evidence that Rho-signaling to the cytoskeleton splits into two pathways, one responsible for reorganization of the actin structures (through the formin mDia) and one leading to myosin II motor activity (through Rho-associated kinase) (32,33). Using motor inhibition experiments, we took a first step to clarify the biophysical role of these two control modes in modulating cell shape and found evidence that cells use both tension and elasticity control. A difficulty in interpreting these experiments is that, in principle, motor inhibition should also affect surface tension. Thus, it is difficult a priori to predict whether arc radii should increase or decrease. The observed strong decrease of arc radii implies that the effects on line tension are much stronger than on surface tension. In addition, both control modes are intertwined by a biomechanical regulatory feedback loop, that is, a reduction in motor tension also causes a reduction in arc strength. To disentangle the effect of these different regulators, a model for contractile actin bundles combining mechanics and biochemistry is required (34). Potential experimental realizations to test these relations include laser cutting of stress fibers in cultured cells (35) or micromanipulation of extracted stress fibers (29).

As evidenced for example by the R-d correlation shown in Fig. 3 C and the R-S correlation shown in Fig. 6 B, there is a considerable spread of data in the cell experiments. There are many factors that might contribute to this data heterogeneity, including cell-spreading history, differences in substrate homogeneity, and intracellular differences and fluctuations, for example in signal transduction events. We expect that an in-depth analysis of the dynamics of cell spreading might help explain the data spread in more detail. It is important to note, however, that our data demonstrate statistically significant correlations for both cells and tissues and that a dynamical theory is not required to explain our experimental results.

For tissue models, is has been found previously that cellular contractility can lead to dramatic structural changes (8,9). Furthermore, active contraction of the extracellular matrix allows cells to sense the mechanical properties of their environment and adapt their internal organization to these physical cues (7). In this work, we have found that cells at the periphery of the tissue model align in parallel with the free boundary and in the direction of the mechanically fixed anchor points (14). This observation suggests that developmental processes also might be driven by similar large-scale arrangements determined by mechanical factors. In particular, our findings open up completely new perspectives for building tissue models in which cell growth can be directly controlled by adhesion geometry–dependent distribution of tension. For example, one can imagine controlling the positions of the pinning points by mechanical actuators. In this way, one could control online where cells grow in the model tissue, eventually paving the way to quantitative control of form and function of artificial tissue.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.