Abstract
Despite the spontaneity of some in vitro protein-folding reactions, native folding in vivo often requires the participation of barrel-shaped multimeric complexes known as chaperonins. Although it has long been known that chaperonin substrates fold upon sequestration inside the chaperonin barrel, the precise mechanism by which confinement within this space facilitates folding remains unknown. We examine the possibility that the chaperonin mediates a favorable reorganization of the solvent for the folding reaction. We discuss the effect of electrostatic charge on solvent-mediated hydrophobic forces in an aqueous environment. Based on these physical arguments, we construct a simple, phenomenological theory for the thermodynamics of density and hydrogen-bond order fluctuations in liquid water. Within the framework of this model, we investigate the effect of confinement inside a chaperonin-like cavity on the configurational free energy of water by calculating solvent free energies for cavities corresponding to the different conformational states in the ATP-driven catalytic cycle of the prokaryotic chaperonin GroEL. Our findings suggest that one function of chaperonins may involve trapping unfolded proteins and subsequently exposing them to a microenvironment in which the hydrophobic effect, a crucial thermodynamic driving force for folding, is enhanced.
INTRODUCTION
Efficient production of natively folded protein is an absolute requirement for cell survival. Although the amino-acid sequence of a small polypeptide generally suffices to specify the chain's native structure under conditions favorable to spontaneous folding in vitro, the protein-folding problem in vivo is more challenging in several respects. To begin with, the cell must somehow protect the delicate homeostasis of its proteome against various environmental stresses that wreak havoc with the thermodynamics and kinetics of folding. Moreover, folding reactions that occur in the highly crowded intracellular milieu may never proceed to completion because of the tendency of partially unfolded polypeptides to aggregate nonspecifically and irreversibly at high concentrations. Even under more dilute conditions, a large protein that circuitously explores many nonnative kinetic traps along the way to its native state may fold too slowly to be of any use in a biological context.
Proteins known as molecular chaperones enable the cell to overcome these obstacles (1,2). Chaperones are characterized by their ability to bind the exposed hydrophobic moieties of nonnative polypeptides, and guide these wayward chains back onto productive folding pathways. Perhaps the most intriguing type of chaperone is the chaperonin, a barrel-shaped, multimeric complex that engulfs and releases its substrates in an ATP-dependent manner (2–4). Chaperonins subdivide into groups I (eubacterial) and II (archaebacterial/eukaryotic). The group I tetradecamer Hsp60/GroEL from Escherichia coli is the most extensively studied model of chaperonin action. The open conformation of GroEL uses its largely hydrophobic inner surface to snare an unfolded substrate. Subsequent binding of ATP and the GroES cofactor induces a conformational change in GroEL, after which the substrate may attempt to fold inside a closed complex whose interior cavity surface displays many hydrophilic residues. Once ATP hydrolysis occurs, GroES dissociates from the complex and the barrel reopens, releasing the substrate into the surroundings and completing the reaction cycle.
For some of its substrates, GroEL mainly provides an isolated “Anfinsen cage” environment in which a protein may fold without risk of aggregation. For others, however, it was shown that confinement within the chaperonin barrel is accompanied by a marked increase in the rate of folding, even under conditions that preclude aggregation (5). The origins of this chaperonin foldase activity are largely unclear, but recent experiments have begun to shed some light on the question (6). Tang et al. (6) assayed the activity of a wide range of GroEL mutants, and found that the acceleration of folding achieved by a chaperonin mutant correlated with the net charge and hydrophilicity of its interior cavity surface. This intriguing result suggests that the hydrophilic walls of the cavity somehow modulate the folding-energy landscape of a confined protein to favor progression to the native state (4). The mechanism for this modulation remains mysterious, and an explanation of how it might come about would undoubtedly do much to improve our understanding of protein folding in vivo.
This study suggests one such explanation by considering the role of water in folding under confinement. Folding reactions take place in aqueous solvent, and it is the strong tendency of water molecules to hydrogen-bond with each other that generates the “hydrophobic effect” (7), a thermodynamic force that helps drive proteins to fold by causing nonpolar amino-acid residues to reduce their solvent-exposed surface area (8). Hydrogen-bond quality is sensitive to the relative orientations of molecules, and numerous studies documented substantial changes in the behavior of water once the liquid is confined in a small enough space that the organization of the hydrogen-bond network becomes significantly constrained (9–11). It is therefore reasonable to hypothesize that the high degree of confinement experienced by water that participates in folding reactions inside GroEL may substantially alter the solvent free energy, and therefore the folding landscape, relative to what it would be in the cytosol. This scenario is especially plausible in light of “in silico” and experimental studies demonstrating the modulation of hydrophobic forces in the presence of charges (12–19).
We investigate the capacity of a nanopore to modulate the free energy of water confined within it by undergoing shifts in surface chemistry that mimic the conformational changes in the catalytic cycle of GroEL. We discuss the physics behind simulations that explore the interplay between electrostatic and hydrophobic forces in water. Based on our physical arguments, we develop a simple phenomenological theory for the free energy of fluctuations in density and hydrogen-bond order in bulk water that captures the essential physics behind the previous results of simulations. Using the phenomenological model as an illustrative tool, we compute the effect of confinement in hydrophilic and hydrophobic cavities on the “folding landscape” of a simple model protein. Our findings raise the possibility that GroEL may preferentially bind unfolded substrates and allow them to fold in a microenvironment in which the hydrophobic effect is enhanced above cytosolic levels.
THEORY
Although it is widely acknowledged that both electrostatic and hydrophobic interactions play important roles in the stabilization of native protein structure, relatively few theoretical studies of protein-folding point out that these two types of interactions are intimately linked. From an electrostatic standpoint, it is relevant that water molecules possess molecular dipole moments that feel torques and net forces in the electric field gradient of a point charge. Thus, aqueous solvent in the vicinity of a strong enough charge will organize itself differently than in the bulk liquid, so as to interact most favorably with the ambient electrostatic field. In contrast, the hydrophobic effect originates from the tendency of water molecules to form hydrogen bonds with each other (and not with hydrophobic solutes), and the changes in solvent structure that occur during the solvation of a nonpolar group help minimize the unfavorableness of the liquid's interaction with the inert solute.
The exact nature of the solvent-restructuring that occurs next to a hydrophobic surface, however, depends subtly on how the surface is shaped (7,20). Small, nonpolar solutes such as methane can be accommodated by the aqueous medium without breakage of hydrogen bonds, leading to a largely entropic cost of solvation that scales approximately with the volume of the solute and is accompanied by a somewhat counterintuitive rise in average solvent density near the solute surface. As the solute size increases, however, the decreasing curvature of the solute's surface forces water molecules to form fewer hydrogen bonds near the solvent-solute interface. This enthalphic cost of solvation can lead to a local depletion of water density near the solute, known as dewetting, whose severity is determined by the strength of the van der Waals attraction between surface and solvent (21).
The key point here is that charged and hydrophobic surfaces make very different demands on the aqueous environment around them. Charged surfaces tend to increase liquid density in their vicinity and align molecules along electric field lines. Hydrophobic surfaces favor molecular orientations and liquid densities that optimize the local hydrogen-bond network. Thus, if hydrophobic and charged surfaces are brought close together in a bulk medium, one would expect the solvent to mediate a repulsive force between them: the farther apart the two surfaces are, the more freedom the solvent near each surface has to reorganize itself independently and lower the free energy of the system, without attempting (and failing) to satisfy the competing demands of both types of surface.
This phenomenon of repulsion between charged and hydrophobic groups is best known in the context of “salting-out” studies, in which the introduction of certain ionic salts to an aqueous solution causes increased aggregation of amphipathic or hydrophobic molecules (12–14). The same type of effect was also reported in studies of all-atom simulations of hydrophobic and charged solutes in water. Bulone et al. probed the solvent-mediated forces acting on nonpolar bodies in the vicinity of a charge, and observed a repulsion between the hydrophobic and charged groups (15,16). Dzubiella and Hansen (17,18) demonstrated that the hydrophobic attraction between inert spheres is eliminated when the spheres become charged and attract water to their surfaces. Thus, in light of the apparent importance of charged cavity resides to the proper functioning of GroEL (6), we analyzed the reaction cycle of GroEL, based on assumptions consistent with our physical understanding of the interplay between electrostatic and hydrophobic effects.
Phenomenological model
To examine the possible role of GroEL in remodeling the solvent of the folding reaction, we developed an analytical framework for describing the thermodynamics of confined water. We sought to construct a phenomenological theoretical model that would be simple and tractable, yet adequate for providing a demonstration of the impact that the physics discussed above may have on folding under confinement. Following previous work (22–24) that attempted to explain the anomalous bulk properties of water using a Landau-like statistical field theory, we posited that the effective free energy of a fluctuation in the configuration of bulk water at a given temperature 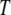 and chemical potential
and chemical potential 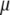 depends entirely on two order parameters: the local density of the fluid
depends entirely on two order parameters: the local density of the fluid 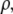 and the additive inverse of the local free energy density per molecule, which we call the “quality” of the hydrogen-bond network
and the additive inverse of the local free energy density per molecule, which we call the “quality” of the hydrogen-bond network 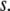 Defining
Defining 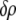 and
and 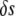 as the respective deviations of these quantities from their average values
as the respective deviations of these quantities from their average values 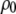 and
and 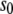 in the bulk, we can write the free energy of water for small configurational fluctuations in a volume
in the bulk, we can write the free energy of water for small configurational fluctuations in a volume 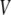 as
as
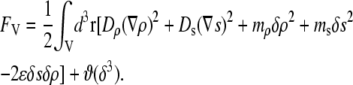 |
(1) |
The coefficients multiplying each term in the integral should, in principle, be functions of 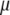 and
and 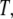 although we would expect the coupling between the density and hydrogen-bond order to equal approximately the strength of a hydrogen bond. The derivative terms simply ensure that both order parameters do not vary too rapidly over space, because they are only well-defined quantities on length scales larger than a water molecule. The squared terms ensure that larger deviations from bulk values of the order parameter carry higher free energetic costs, whereas the cross-term proportional to
although we would expect the coupling between the density and hydrogen-bond order to equal approximately the strength of a hydrogen bond. The derivative terms simply ensure that both order parameters do not vary too rapidly over space, because they are only well-defined quantities on length scales larger than a water molecule. The squared terms ensure that larger deviations from bulk values of the order parameter carry higher free energetic costs, whereas the cross-term proportional to 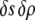 dictates that the formation of more hydrogen bonds lowers the energy of the system.
dictates that the formation of more hydrogen bonds lowers the energy of the system.
Because we did not include cubic and quartic terms in our free-energy functional, we would be unable to use it to capture the tradeoff between fluid density and hydrogen-bond network quality that leads to the anomalous decrease in the density of water as it cools to its freezing point. Moreover, without a quartic interaction, our model will be unable to capture first-order transitions such as capillary evaporation (25), where water undergoes a discontinuous decrease in density after confinement destabilizes the liquid phase relative to the vacuum. Our analysis, however, assumes that we are in a regime where the liquid phase remains stable, and thus expanding to second order about a single free-energy minimum is a reasonable approximation. We expect such a theory to do well at a qualitative level with systems that would not be expected to exhibit any sort of evacuation transition to a new free-energy minimum that was well-separated from the liquid phase by a barrier.
In a similar vein, we emphasize that the model considered here cannot capture the subtle length-scale dependence of hydrophobic solvation mentioned above (7,20). The scalar order parameters of particle density and hydrogen-bond network quality are inadequate for representing differences in how water organizes itself next to surfaces of low and high curvature. However, the model does succeed in demonstrating that the closer two locations are together in the aqueous medium, the stronger the preference becomes for the water at those locations to be organized in similar ways. Because this principle underlies the physics of “salting-out” discussed above, we can be confident that our model will be useful in addressing the questions of interest despite its limitations.
Thus far, we have presented a phenomenological theory of order fluctuations in bulk water. Before we can apply this theory to the study of confined water, we must augment it by introducing an additional contribution to the free-energy functional that comes from the interaction between the liquid and the surface that encloses it. Thus, let our system consist of water confined within a shell 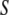 of thickness
of thickness 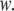 If
If 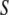 is perfectly nonpolar, it cannot participate in hydrogen bonds, and we must require that the contribution to the free energy due to hydrogen bonding that would be given approximately by
is perfectly nonpolar, it cannot participate in hydrogen bonds, and we must require that the contribution to the free energy due to hydrogen bonding that would be given approximately by 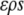 in the bulk must be zero in the shell. We may further introduce some potential
in the bulk must be zero in the shell. We may further introduce some potential 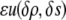 that accounts for any additional effects from the surface chemistry of
that accounts for any additional effects from the surface chemistry of 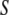 such as an attraction between water and charges on the surface. Thus, we obtain a new term in our functional:
such as an attraction between water and charges on the surface. Thus, we obtain a new term in our functional:
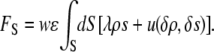 |
(2) |
Here, 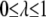 is a parameter that reflects the degree of hydrophobicity of the surface, with
is a parameter that reflects the degree of hydrophobicity of the surface, with 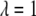 corresponding to a completely nonpolar surface.
corresponding to a completely nonpolar surface.
To find the equilibrium density and hydrogen-bond order, we minimize the total free energy 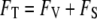 with respect to the order parameter fields by using the calculus of variations. This process of minimization determines the rearrangement that must occur in the solvent near the bounding surface as a result of interactions described in
with respect to the order parameter fields by using the calculus of variations. This process of minimization determines the rearrangement that must occur in the solvent near the bounding surface as a result of interactions described in 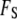 that occur directly at the surface. Thus, although the free energy is formally divided into the two terms
that occur directly at the surface. Thus, although the free energy is formally divided into the two terms 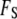 and
and 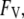 it is the quantity
it is the quantity 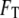 that describes the total free energy of the interface between the surface and the liquid. The minimized equilibrium fields
that describes the total free energy of the interface between the surface and the liquid. The minimized equilibrium fields 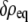 and
and 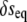 will obey a system of Helmholtz equations that may be decoupled by a change of basis. In the cases of spherically and planar symmetric systems, it is straightforward from there to obtain closed-form solutions whose integration constants must be set by plugging back into the functional and minimizing
will obey a system of Helmholtz equations that may be decoupled by a change of basis. In the cases of spherically and planar symmetric systems, it is straightforward from there to obtain closed-form solutions whose integration constants must be set by plugging back into the functional and minimizing 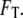 For arbitrary cavity geometries and surface chemistries, however, it is necessary to seek a numerical solution. We therefore restrict our attention to analytically tractable cases that are somewhat easier to deal with but that suffice as tools for examining the issues of interest in this study.
For arbitrary cavity geometries and surface chemistries, however, it is necessary to seek a numerical solution. We therefore restrict our attention to analytically tractable cases that are somewhat easier to deal with but that suffice as tools for examining the issues of interest in this study.
MATERIALS AND METHODS
For each choice of parameters and boundary conditions, the sum of Eqs. 1 and 2 was extremized using the calculus of variations, leading to an analytical solution with undetermined coefficients. The general solutions were plugged back into Eqs. 1 and 2, and the resulting expression for free energy was minimized with respect to the unknown coefficients, using Mathematica 5.1 software (Champaign, IL). All plots and free-energy changes were then generated in Mathematica for these choices of coefficients. The total run time for these calculations was negligible on a single G4 1GHz processor.
RESULTS
We modeled GroEL as a spherical pore of radius 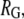 and the chaperonin substrate protein as a smaller sphere of radius
and the chaperonin substrate protein as a smaller sphere of radius 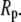 The chaperonin barrel was assumed to have two different states that reflected the open and closed conformations identified in structural studies of GroEL (26). In the open state, the inner surface of the chaperonin was treated as a largely nonpolar surface, meaning
The chaperonin barrel was assumed to have two different states that reflected the open and closed conformations identified in structural studies of GroEL (26). In the open state, the inner surface of the chaperonin was treated as a largely nonpolar surface, meaning 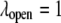 and
and 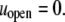 In the closed state, the chaperonin cavity was treated as highly hydrophilic because of its richness in charged and polar residues that participate in hydrogen bonds with (and electrostatically attract) water molecules. Thus, we set
In the closed state, the chaperonin cavity was treated as highly hydrophilic because of its richness in charged and polar residues that participate in hydrogen bonds with (and electrostatically attract) water molecules. Thus, we set 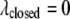 and
and 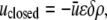 where
where 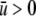 accounts for the net attraction of favorably oriented molecular electric dipole moments to the net charge of the cavity surface. The protein was also assumed to have two states, i.e., native and unfolded. The native conformation was assumed to have a hydrophilic surface chemistry described by
accounts for the net attraction of favorably oriented molecular electric dipole moments to the net charge of the cavity surface. The protein was also assumed to have two states, i.e., native and unfolded. The native conformation was assumed to have a hydrophilic surface chemistry described by 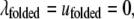 and the unfolded state was assumed to be partially hydrophobic, where
and the unfolded state was assumed to be partially hydrophobic, where 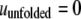 and
and 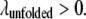
Our approach ignored a variety of factors that might complicate the story of chaperonin action in reality. Direct interactions between GroEL and its substrate, fluctuations in the substrate's radius of gyration, and expansion of the chaperonin cavity upon binding of GroES all have the potential to affect the forces experienced by a substrate as it searches the folding landscape. The calculation performed here also significantly oversimplifies the nature of the interaction between hydrophobic or charged surfaces and water. In real liquids, mean solvent density near a surface wobbles on the length scale of a few angstroms because of solvation layers, and this oscillation could lead to switching between attraction and repulsion at different distances in the scenario we have considered. Because our model does not account for the discreteness of individual molecules, it can only be expected to capture behavior at a more smeared, coarse-grained level. Although all of these effects should be included in a complete description of how GroEL functions, we see great value in focusing on the free energy of the confined solvent in a simplified model, so as to begin understanding what contribution it makes to the overall outcome.
The solutions to the resulting Helmholtz equations were linear combinations of terms of the form 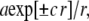 with coefficient
with coefficient 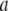 determined through minimization of the total free energy
determined through minimization of the total free energy 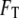 obtained by integrating the free-energy functional over the enclosed volume and bounding surface, and the correlation length scales
obtained by integrating the free-energy functional over the enclosed volume and bounding surface, and the correlation length scales 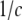 set by the parameters of the theory. These solutions were similar to those derived in earlier work by Marcelja and Radic (22) and Marcelja et al. (23), who used a single-order parameter Landau-Ginzburg mean field approach. To plot them, it was necessary to choose specific values for the parameters in the free-energy functional. We selected parameters such that the coupling
set by the parameters of the theory. These solutions were similar to those derived in earlier work by Marcelja and Radic (22) and Marcelja et al. (23), who used a single-order parameter Landau-Ginzburg mean field approach. To plot them, it was necessary to choose specific values for the parameters in the free-energy functional. We selected parameters such that the coupling 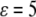 was approximately equal to the strength of a hydrogen bond (∼5 kcal/mol (27)), and the correlation length scales of the theory were both on the order of unity in angstroms. The protein was assumed to be ∼2 nm in diameter, consistent with the size of a substrate of GroEL that partially fills an approximately 6-nm-wide cavity. A charged surface was assumed to produce an attractive potential about as strong as a hydrogen bond (
was approximately equal to the strength of a hydrogen bond (∼5 kcal/mol (27)), and the correlation length scales of the theory were both on the order of unity in angstroms. The protein was assumed to be ∼2 nm in diameter, consistent with the size of a substrate of GroEL that partially fills an approximately 6-nm-wide cavity. A charged surface was assumed to produce an attractive potential about as strong as a hydrogen bond (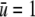 ) in its vicinity. The precise parameter set used for this study was somewhat arbitrary, and the quantitative results of the calculations are likely informative only at the order-of-magnitude level. We were, however, unable to observe any qualitative change in the results after varying the coefficients, so long as it was assured that bulk density and hydrogen bond order remained a free-energy minimum.
) in its vicinity. The precise parameter set used for this study was somewhat arbitrary, and the quantitative results of the calculations are likely informative only at the order-of-magnitude level. We were, however, unable to observe any qualitative change in the results after varying the coefficients, so long as it was assured that bulk density and hydrogen bond order remained a free-energy minimum.
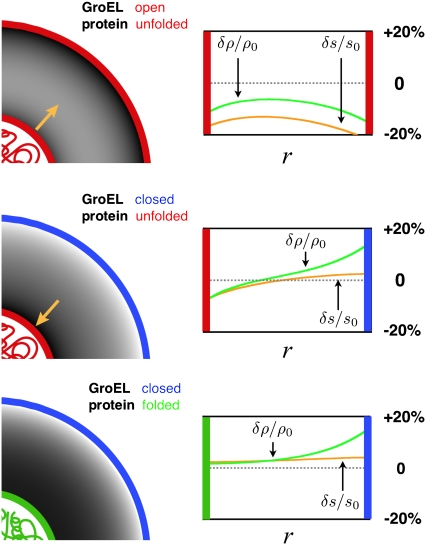
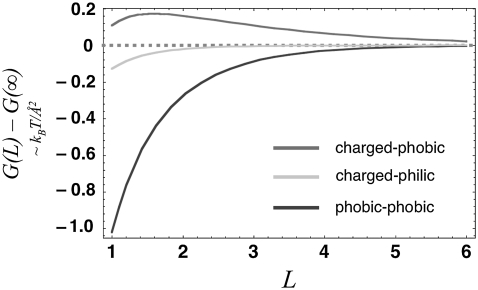
Fig. 1 displays the equilibrium liquid density and hydrogen-bond order profiles for the different states of GroEL and its substrate. For the case of a nonnative substrate inside an open GroEL complex, both surfaces confining the solvent are hydrophobic (Fig. 1, top). As a result of the loss of hydrogen bonding at these surfaces (more precisely, the reduction of quality of the hydrogen-bonding network, which could result from either an increase in enthalpy density or a decrease in entropy density), water withdraws from them and from the cavity as a whole, driving the average density below bulk levels. Moreover, it is apparent from a calculation of the free energy of solvent trapped between two planar surfaces of the same type that the force between the nonnative substrate and the chaperonin wall is attractive (Fig. 2, dark gray curve), and would favor binding. This result is consistent with our expectation of a solvent-mediated attractive force between two hydrophobic surfaces, although we should note that because we neglected quartic terms in our free-energy functional, we cannot capture the possibility of a dewetting transition that would bring about a sharper binding potential between the hydrophobic surfaces after they came within a certain range. After the chaperonin forms a closed complex and undergoes its conformational change, the projection of charged and polar side-chains into the barrel's interior causes the solvent order and resulting thermodynamic forces to change. With the inner surface of the barrel now highly hydrophilic, the solvent density is elevated near the chaperonin wall and depressed surrounding the unfolded protein (Fig. 1, middle). The result is a repulsive force between surfaces that pushes the substrate toward the center of the cavity, to drive solvent of elevated density away from a surface that cannot form hydrogen bonds (Fig. 2, gray curve). This force arises in the model from differences in how water becomes organized near charged and hydrophobic surfaces, and is analogous to the repulsion between hydrophobic and charged surfaces that was observed in atomistic simulations of charged and nonpolar objects in aqueous solution (12–16) (as mentioned above, however, the repulsion arises in realistic simulations from a more complex set of salting-out effects that only sometimes involve a depletion of density at hydrophobic surfaces). Finally, upon folding, the substrate surface becomes more hydrophilic, allowing the density of the nearby solvent to relax to bulk levels (Fig. 1, bottom), with the result that the force between chaperonin and substrate becomes very weak (Fig. 2, light gray curve).
FIGURE 1.
Equilibrium order parameters 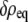 and
and 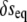 inside spherical shells were calculated using
inside spherical shells were calculated using 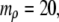
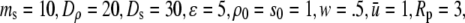 and
and 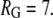 All data reported in this study use the same parameters for the free-energy functional. Units of length are set by ℓ, the size of a water molecule (∼4 Å). Order parameters are unitless, and are measured as a fraction of their bulk value, whereas
All data reported in this study use the same parameters for the free-energy functional. Units of length are set by ℓ, the size of a water molecule (∼4 Å). Order parameters are unitless, and are measured as a fraction of their bulk value, whereas 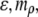 and
and 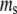 have units of kcal/mol/
have units of kcal/mol/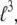 and
and 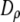 and
and 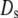 have units of kcal/mol/ℓ. (Left) Liquid density (darker shading corresponding to lesser density) is plotted in the space between the surface of the protein (red, unfolded; green, folded) and the cavity (red, hydrophobic; blue, hydrophilic) wall for an unfolded protein inside an “open” hydrophobic cavity (top), an unfolded protein inside a “closed” hydrophilic cavity (middle), and a folded protein in a closed cavity (bottom). Gold arrows indicate the direction of solvent-mediated force between the two surfaces (Fig. 2) (Right) Liquid density (green curves) and hydrogen-bond order (orange curves) are plotted as a fraction of their bulk values. At a hydrophobic surface, there is a loss of hydrogen bonding and a depletion of liquid density. In contrast, at a highly hydrophilic surface, there is an elevation in liquid density and a greater amount of hydrogen bonding.
have units of kcal/mol/ℓ. (Left) Liquid density (darker shading corresponding to lesser density) is plotted in the space between the surface of the protein (red, unfolded; green, folded) and the cavity (red, hydrophobic; blue, hydrophilic) wall for an unfolded protein inside an “open” hydrophobic cavity (top), an unfolded protein inside a “closed” hydrophilic cavity (middle), and a folded protein in a closed cavity (bottom). Gold arrows indicate the direction of solvent-mediated force between the two surfaces (Fig. 2) (Right) Liquid density (green curves) and hydrogen-bond order (orange curves) are plotted as a fraction of their bulk values. At a hydrophobic surface, there is a loss of hydrogen bonding and a depletion of liquid density. In contrast, at a highly hydrophilic surface, there is an elevation in liquid density and a greater amount of hydrogen bonding.
FIGURE 2.
Solvent free energy, estimated in 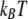 per unit area of surface, is plotted as a function of separation
per unit area of surface, is plotted as a function of separation 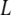 for pairs of horizontal plates. Distance is measured in units of the shorter correlation length of the Landau theory, about equivalent to the size of a few water molecules. Between two hydrophobic plates (dark gray curve), the solvent mediates an attractive force that grows stronger with proximity. Between a hydrophobic plate and a highly hydrophilic plate (gray curve), there is a weaker repulsive force. Between two hydrophilic plates, the force is essentially nonexistent (light gray curve).
for pairs of horizontal plates. Distance is measured in units of the shorter correlation length of the Landau theory, about equivalent to the size of a few water molecules. Between two hydrophobic plates (dark gray curve), the solvent mediates an attractive force that grows stronger with proximity. Between a hydrophobic plate and a highly hydrophilic plate (gray curve), there is a weaker repulsive force. Between two hydrophilic plates, the force is essentially nonexistent (light gray curve).
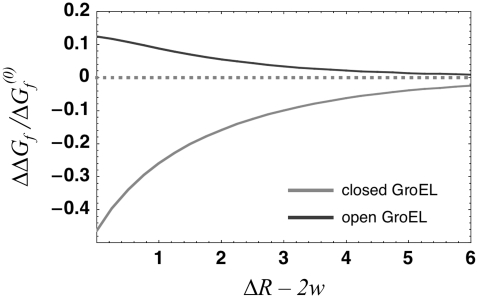
With equilibrium density and bond-order profiles in hand, we were able to compute the solvent free-energy changes for folding inside the different conformers of GroEL (Fig. 3) by plugging the profiles into the surface and volume free-energy functionals and integrating over the spherical shell between the chaperonin and protein surface. Within the framework of the model considered here, folding without the involvement of a chaperonin simply consists of a gradual reduction in hydrophobicity of the surface of a sphere of radius 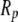 surrounded by aqueous solvent. In contrast, chaperonin-assisted folding divides into several stages. First, the hydrophobic interior of the barrel in its open conformation decreases its free energy by binding to hydrophobic moieties exposed by a partially unfolded substrate. After the nonnative protein is inside the cavity, the solvent free-energy change associated with folding is rendered less negative by the surrounding hydrophobic walls, and the chaperonin therefore provides a thermodynamic drive toward unfolding that increases as the radius of confinement becomes smaller (Fig. 3, dark gray curve). This effect occurs because the hydrophobic cavity walls deplete the amount of water in the cavity, making the solvent's tendency to hydrogen-bond with the protein surface lower than it is in bulk solution. (However, the attraction between hydrophobic parts of the protein and chaperonin wall are likely to drive unfolding by inducing binding and adsorption, a process our model could be incapable of describing because of its lack of quartic terms in its free-energy functional. Such terms would enable a treatment of dewetting phenomena, whose importance to the process of adsorption would depend on the strength of the van der Waals attraction between the hydrophobic surfaces and the ambient water (7,21)). After GroEL binds to GroES and ATP and undergoes its conformational change, the reverse is true: the solvent portion of the free energy of folding inside the cavity becomes more negative than that of folding in bulk solution, with the magnitude of the effect again increasing as the confinement becomes more severe (Fig. 3, light gray curve). This dramatic shift occurs because the charged inner surface of the chaperonin has elevated the density of water in the cavity, thereby raising the number of molecules that have difficulty finding a hydrogen-bonding partner when the hydrophobic substrate surface area is presented to the solvent. Thus, our model predicts that the conformational change in GroEL brings about a remodeling of the confined solvent that enhances the hydrophobic effect above its strength in bulk solvent, and helps drive the folding reaction to completion.
surrounded by aqueous solvent. In contrast, chaperonin-assisted folding divides into several stages. First, the hydrophobic interior of the barrel in its open conformation decreases its free energy by binding to hydrophobic moieties exposed by a partially unfolded substrate. After the nonnative protein is inside the cavity, the solvent free-energy change associated with folding is rendered less negative by the surrounding hydrophobic walls, and the chaperonin therefore provides a thermodynamic drive toward unfolding that increases as the radius of confinement becomes smaller (Fig. 3, dark gray curve). This effect occurs because the hydrophobic cavity walls deplete the amount of water in the cavity, making the solvent's tendency to hydrogen-bond with the protein surface lower than it is in bulk solution. (However, the attraction between hydrophobic parts of the protein and chaperonin wall are likely to drive unfolding by inducing binding and adsorption, a process our model could be incapable of describing because of its lack of quartic terms in its free-energy functional. Such terms would enable a treatment of dewetting phenomena, whose importance to the process of adsorption would depend on the strength of the van der Waals attraction between the hydrophobic surfaces and the ambient water (7,21)). After GroEL binds to GroES and ATP and undergoes its conformational change, the reverse is true: the solvent portion of the free energy of folding inside the cavity becomes more negative than that of folding in bulk solution, with the magnitude of the effect again increasing as the confinement becomes more severe (Fig. 3, light gray curve). This dramatic shift occurs because the charged inner surface of the chaperonin has elevated the density of water in the cavity, thereby raising the number of molecules that have difficulty finding a hydrogen-bonding partner when the hydrophobic substrate surface area is presented to the solvent. Thus, our model predicts that the conformational change in GroEL brings about a remodeling of the confined solvent that enhances the hydrophobic effect above its strength in bulk solvent, and helps drive the folding reaction to completion.
FIGURE 3.
The change in folding free energy 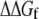 is defined as the difference between the free energy of folding under confinement
is defined as the difference between the free energy of folding under confinement 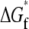 and the free energy of folding in bulk solution
and the free energy of folding in bulk solution 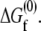 The fractional change in this solvent free energy of folding is plotted as a function of confinement radius
The fractional change in this solvent free energy of folding is plotted as a function of confinement radius 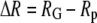 for
for 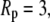 less the width
less the width 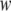 of the interaction shell at each surface. Length is measured in units of the shorter correlation length of the theory of solvent fluctuations described in Eq. 3. When the protein is confined in the largely hydrophobic open GroEL cavity (dark gray curve), the folded state is more destabilized as the degree of confinement increases. However, when confined in the closed, highly hydrophilic chaperonin cavity (light gray curve), stabilization of the folded state increases with degree of confinement.
of the interaction shell at each surface. Length is measured in units of the shorter correlation length of the theory of solvent fluctuations described in Eq. 3. When the protein is confined in the largely hydrophobic open GroEL cavity (dark gray curve), the folded state is more destabilized as the degree of confinement increases. However, when confined in the closed, highly hydrophilic chaperonin cavity (light gray curve), stabilization of the folded state increases with degree of confinement.
The results of the phenomenological model used here are suggestive, but qualitative. To complete the argument, it is necessary to quantify the forces involved and see whether they are strong enough to affect a folding protein whose marginal stability is on the order of 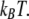 For the best estimate of the impact of electrostatics on hydrophobic forces, we examined the results of atomistic simulations performed by Dzubiella and Hansen, in which charges abrogated the hydrophobic attraction between nonpolar spheres with radii of 10 Å separated by a distance of several angstroms (17). The authors reported an electrostatic modulation of the solvent-mediated force on the order of several kBT per angstrom for spheres with a surface-charge density of 0.004 proton charges per square angstrom. Modeling the closed GroE complex as a cylinder 60 Å across and 80 Å in height, with a net charge of −42 (6), we obtained a surface-charge density of ∼0.003. Moreover, this modest net charge belies the total number of charged residues on the order of hundreds that would likely attract the solvent more strongly by electrostriction than would a uniformly charged surface. Thus, we conclude that the effective unfavorable water-mediated free energy of interaction between the hydrophilic wall and protein hydrophobes is significant enough in magnitude to affect protein-folding.
For the best estimate of the impact of electrostatics on hydrophobic forces, we examined the results of atomistic simulations performed by Dzubiella and Hansen, in which charges abrogated the hydrophobic attraction between nonpolar spheres with radii of 10 Å separated by a distance of several angstroms (17). The authors reported an electrostatic modulation of the solvent-mediated force on the order of several kBT per angstrom for spheres with a surface-charge density of 0.004 proton charges per square angstrom. Modeling the closed GroE complex as a cylinder 60 Å across and 80 Å in height, with a net charge of −42 (6), we obtained a surface-charge density of ∼0.003. Moreover, this modest net charge belies the total number of charged residues on the order of hundreds that would likely attract the solvent more strongly by electrostriction than would a uniformly charged surface. Thus, we conclude that the effective unfavorable water-mediated free energy of interaction between the hydrophilic wall and protein hydrophobes is significant enough in magnitude to affect protein-folding.
DISCUSSION
Previous attempts to explain the foldase activity of chaperonins pointed to a diverse list of possible causes. Whereas some researchers focused on evidence that GroEL may assist in the unfolding of kinetically trapped substrates (28,29), others saw a role for the barrel-shaped cavity in accelerating folding by reducing the conformational entropy of a protein's unfolded state (30), and still others proposed that interactions between the protein and side chains on the cavity wall might help smooth out some of the pitfalls in the protein's free-energy landscape (31,32). We examined a novel dimension of the chaperonin puzzle by studying the thermodynamics of the aqueous solvent in which the folding reaction takes place. By developing a theory of order fluctuations in confined water, we were able compute the free energy of water in cavities that mimicked the salient features of protein-folding inside GroEL. Our theory was adequate for describing two solvent-mediated forces that are likely to be important in understanding the function of chaperonins, i.e., the well-known attraction between two hydrophobic surfaces, and the less intuitive repulsion between hydrophobic and charged hydrophilic groups previously observed in simulations. Our findings highlight the potential importance of solvent effects in a complete description of how GroEL promotes folding.
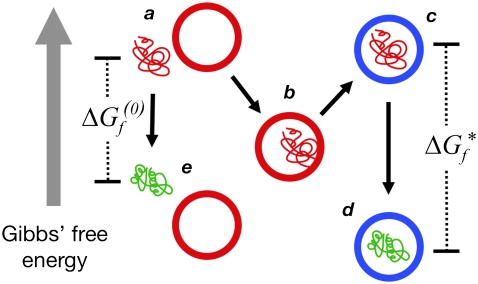
Fig. 4 summarizes the model of chaperonin action that emerges from our study. A nonnative protein that exposes hydrophobic groups to the bulk solvent will be engulfed by an open GroEL complex because of attractive hydrophobic forces mediated by the solvent. At this point, the substrate becomes bound to the wall of the chaperonin. After GroES and ATP bind, however, the solvent travels uphill in free energy, as a conformational change in GroEL presents charged residues to the barrel's interior. As a result, the substrate is forced away from the walls into the center of the cavity, a prediction that is consistent with experimentally measured increases in substrate fluorescence anisotropy after closing the complex (6). The subsequent folding reaction takes place inside a charged, hydrophilic chamber, and is therefore accompanied by a more drastic decrease in free energy of the surrounding solvent that results from the “salting-out” effect (12–14) of the charged residues in the cavity. In other words, the interior of GroEL may provide a microenvironment in which the hydrophobic effect is substantially stronger than in bulk solution.
FIGURE 4.
A model of chaperonin action. Hydrophobic forces cause an unfolded (red) protein to bind to the wall of the open (red) GroEL barrel (a → b). Upon formation of a closed (blue) complex containing GroES and ATP, rearrangements in the barrel present a hydrophilic surface to the interior that repels the substrate into the center of the cavity (b → c). Because of this repulsion, the free energy 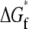 of folding to the native (green) conformation inside the cavity (c → d) is more negative than the folding free energy
of folding to the native (green) conformation inside the cavity (c → d) is more negative than the folding free energy 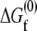 out in bulk solution (a → e). The hydrolysis of ATP therefore drives a local enhancement of the hydrophobic effect inside the chaperonin.
out in bulk solution (a → e). The hydrolysis of ATP therefore drives a local enhancement of the hydrophobic effect inside the chaperonin.
This finding leads us to propose a novel mechanism for the acceleration of folding by chaperonins. The hydrophobic effect is known to be a crucial contributor to the thermodynamic stability of natively folded proteins. However, several studies also documented the importance of hydrophobic forces to folding kinetics (33–35), in terms of bringing about nucleation through hydrophobic collapse (34), and through stabilization of the folding transition state (33). Others demonstrated that an effective moderate enhancement of the hydrophobic effect through the use of osmolite solvent additives (such as ethylene glycol) speeds the folding of some polypeptides through a solvent-driven collapse of the polymer; only when this enhancement is intensified and the collapse becomes more severe does one observe a retardation of the folding rate (36–38). It is therefore plausible that the stronger hydrophobic effects experienced by substrates inside closed GroEL complexes would hasten progression toward the native state. Thus, through its interaction with the confined solvent of the folding reaction, the chaperonin could reshape the free-energy landscape, to promote more rapid folding.
We expect that such an acceleration of folding could arise from confinement in at least two ways. First, the repulsion between the hydrophilic cavity walls and the hydrophobic parts of the protein (Fig. 2) should produce a drive to pack the confined protein into a smaller volume than it would explore when bounded by a nonrepulsive surface of the same shape and size (and because the strength of the interaction between cavity and substrate falls off with distance, this effect would act preferentially on more extended states that are likely to be in greater need of hydrophobic collapse). This notion is consistent with the results of our recent simulations to demonstrate a hydrophilic cavity's ability to drive the collapse of hydrophobes by effectively forcing them into a smaller volume, and therefore a higher local concentration (J. England, D. Lucent, and V. Pande, unpublished results). However, our model cannot describe the process of hydrophobic collapse itself (i.e., what happens to water that becomes trapped between hydrophobes as they condense into a ball) because it is based on a quadratic theory. Rather, the model describes the state of more moderately perturbed solvent around the boundary of the collapsing protein, and predicts a force that, in a model of hydrophobic collapse, could be considered an exogenous driving force toward nucleation.
However, confinement inside a hydrophilic cavity might also be expected to drive folding by “strengthening” the hydrophobic effect, i.e., by generating a stronger thermodynamic force in favor of rearranging the side chains and backbone of an already collapsed protein globule, to reduce further the hydrophobicity of the globule's surface. This process, which must be properly distinguished from the process of “hydrophobic collapse,” is represented in the reduction of protein-surface hydrophobicity depicted in Fig. 1 (middle to bottom) or in Fig. 4 (as stages a–e, and c–d). Because of the solvent-mediated repulsion between the cavity surface and hydrophobic patches on the protein surface, the native state and other low-hydrophobicity conformations are stabilized relative to the broad ensemble of collapsed conformations.
This hydrophobic enhancement model of chaperonin action provides a ready means for explaining the puzzling relationship between foldase activity and cavity hydrophilicity reported in recent experiments. Our model assumes that charged groups on the interior of GroEL draw water into the barrel chamber, and that this elevation of solvent density leads directly to an enhancement of hydrophobic effects. The model therefore predicts that the overall reduction in surface hydrophilicity brought about by replacement of amino-acid residues inside the GroEL complex should significantly reduce the chaperonin's foldase activity. In mutational studies by Tang et al. (6), a range of different alterations to the interior cavity surface was assayed for their affect on the foldase activity of the enzyme when it acts on a slow-folding mutant of maltose-binding protein. Because the wild-type cavity has a net negative charge, reducing the magnitude of this net charge by mutation would be expected to bring about a decrease in the folding rate relative to the wild type. The data seem consistent with this prediction, demonstrating a moderate correlation (−0.63) between surface charge and folding rate.
More strikingly, the deviations from this trend seem consistent with our model, in light of the fact that a surface with a net charge of zero can still be highly hydrophilic, so long as it has many residues of both positive and negative charge. One such mutant (termed “KKK1” by the authors of the Tang study) involved the substitution of 21 lysines for 14 glutamates and seven aspartates. Thus, the number of charged residues in the cavity was conserved, but the net charge was diminished from −42 to zero. This mutant exhibited foldase activity greater than or equal to the foldase activity of two charged-to-neutral mutants with more negative final surface charge each of which had 21 fewer charged residues. The KKK1 mutant also exhibited significantly higher foldase activity than another charged-to-neutral mutant with the same final surface charge but 42 fewer charged residues. Thus, a preliminary analysis of these data suggests that they are quite consistent with our proposed mechanism for GroEL action. Interestingly, the same study (6) also reported a negative correlation between foldase activity and the volume of the GroEL folding chamber. Although this result was interpreted as a product of the reduction in conformational entropy of the unfolded protein that confinement causes, it is worth noting that because hydrophobic enhancement rises with degree of confinement (Fig. 3), our model provides an alternative explanation for the outcomes of those experiments as well.
Further evidence pointing to charged surface residues as an important determinant of GroEL activity was provided by Wang et al. (39). According to them, GroEL-GroES was optimized through directed evolution to fold green fluorescent protein more rapidly. Green fluorescent protein is a small protein with an exceptionally well-buried hydrophobic core that would be likely to form more rapidly in response to an enhancement of hydrophobic effects. The authors found that a key mutation for accelerating the folding of green fluorescent protein involved the replacement of an aromatic tyrosine on the interior surface of GroES with either arginine or histidine, both charged residues. Following this lead, the authors tested six other point mutants of the tyrosine residue, and found that for all substitutions of charged or polar residues (E, K, Q, and D), the folding efficiency improved, but for substitutions of hydrophobic residues (L and F), it remained unchanged. These results are consistent with our proposal that hydrophilic-cavity residues accelerate folding by strengthening the hydrophobic effect.
However, the interior-surface chemistry of the GroE complex is assuredly more complex than as represented in our model in at least one respect, i.e., the bottom portion of the bacterial chaperonin is filled by flexible glycine-glycine-methionine repeats that do not appear in the crystal structure because they are disordered (26). Thus, a substantial portion of the GroE inner surface is hydrophobic, in contrast to the uniformly hydrophilic cavity modeled in this study. Because the effects we described in our model result from relatively local reorganizations of solvent, it is likely that a cavity surface of nonuniform composition that more accurately mimicked the GroE chamber would provide a mixed environment, in which much of the cavity experienced stronger hydrophobic effects, whereas one region provided an adsorbing surface for hydrophobic groups in the substrate protein. In light of previous work (31) on modeling GroEL that indicated the potential of such an adsorbing surface to help smooth out kinetic traps in the folding landscape, it is tempting to speculate that the glycine-glycine-methionine repeats, in combination with the barrel's charged surface residues, may help the chaperonin provide its substrate with the best of both worlds: a smoother landscape to traverse along the way to the folded state, and a stronger drive to get there.
The evidence consistent with the mechanism of chaperonin foldase activity proposed here is substantial, but too indirect to be compelling by itself. Fortunately, our model's most endearing quality is that it makes clear predictions that can easily be tested “in silico” and in the laboratory. At the most basic level, we would expect an all-atom simulation of water and hydrophobic solutes inside a sufficiently hydrophilic cavity to show that hydrophobic forces between solutes are enhanced by confinement. We also predict that a large-scale simulation of previously characterized mutants of charged residues on the interior of the closed GroE complex would show that solvent density along the cavity surface was correlated with the experimentally measured capacity for each mutant to refold substrates through a single round of encapsulation. Performing studies of this kind is particularly important because one can thus more adequately account for complicating effects not considered explicitly in the model here, such as screening from dissolved salts that might reduce the impact of charges on solvent organization (however, our assumption that the attraction between water and a charged surface is finite in range may already account for the presence of ions in a rough sense). We are conducting such full-atom simulations of GroEL, and the preliminary results support our prediction (J. England, D. Lucent, and V. Pande, unpublished results). Finally, and most conclusively, we are preparing to perform experiments that use Förster resonance energy transfer and other techniques to measure the strength of hydrophobic forces between solutes inside GroEL, with the model-driven hypothesis that closure of the barrel through the binding of GroES and ATP is necessary and sufficient to enhance the hydrophobic effect inside the cavity.
Acknowledgments
The authors thank E. Miller, D. Kaganovich, and D. Lucent for helpful comments.
J.L.E. thanks the Fannie and John Hertz Foundation for support. This work was supported by the National Institutes of Health National Institute of General Medical Sciences (grant R01 GM062868) and the National Institutes of Health Nanomedicine Center for Protein Folding Machinery (grant PN1EY016525).
Editor: Arup Chakraborty.
References
- 1.Frydman, J. 2001. Folding of newly translated proteins in vivo: the role of molecular chaperones. Annu. Rev. Biochem. 70:603–647. [DOI] [PubMed] [Google Scholar]
- 2.Hartl, F. U., and M. Hayer-Hartl. 2002. Molecular chaperones in the cytosol: from nascent chain to folded protein. Science. 295:1852–1858. [DOI] [PubMed] [Google Scholar]
- 3.Sigler, P. B., Z. Xu, H. S. Rye, S. G. Burston, W. Fenton, and A. L. Horwich. 1998. Structure and function in GroEL-mediated protein folding. Annu. Rev. Biochem. 67:581–608. [DOI] [PubMed] [Google Scholar]
- 4.Fenton, W. A., and A. L. Horwich. 2003. Chaperonin-mediated protein folding: fate of substrate polypeptide. Q. Rev. Biophys. 36:229–256. [DOI] [PubMed] [Google Scholar]
- 5.Brinker, A., G. Pfeifer, M. J. Kerner, D. J. Naylor, F. U. Hartl, and M. Hayer-Hartl. 2001. Dual function of protein confinement in chaperonin-assisted protein folding. Cell. 107:223–233. [DOI] [PubMed] [Google Scholar]
- 6.Tang, Y., H. Chang, A. Roeben, D. Wischnewski, N. Wischnewski, M. J. Kerner, F. U. Hartl, and M. Hayer-Hartl. 2006. Structural features of the GroEL-GroES nano-cage required for rapid folding of encapsulated protein. Cell. 125:903–914. [DOI] [PubMed] [Google Scholar]
- 7.Chandler, D. 2005. Interfaces and the driving force of hydrophobic assembly. Nature. 437:640–647. [DOI] [PubMed] [Google Scholar]
- 8.Spolar, R., J. Ha, and M. Record. 1989. Hydrophobic effect in protein folding and other noncovalent processes involving proteins. Proc. Natl. Acad. Sci. USA. 86:8382–8385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Raviv, U., P. Laurat, and J. Klein. 2001. Fluidity of water confined to subnanometre films. Nature. 413:51–54. [DOI] [PubMed] [Google Scholar]
- 10.Singh, S., J. Houston, F. v. Swol, and C. J. Brinker. 2006. Superhydrophobicity: drying transition of confined water. Nature. 442:526. [DOI] [PubMed] [Google Scholar]
- 11.Byl, O., J. Liu, Y. Wang, W. Yim, J. K. Johnson, and J. T. Yates. 2006. Unusual hydrogen bonding in water-filled carbon nanotubes. J. Am. Chem. Soc. 128:12090–12097. [DOI] [PubMed] [Google Scholar]
- 12.Kalra, A., N. Tugcu, S. M. Cramer, and S. Garde. 2001. Salting-in and salting-out of hydrophobic solutes in aqueous salt solutions. J. Phys. Chem. B. 105:6380–6386. [Google Scholar]
- 13.Ghosh, T., A. Kalra, and S. Garde. 2005. On the salt-induced stabilization of pair and many-body hydrophobic interactions. J. Phys. Chem. B. 109:642–651. [DOI] [PubMed] [Google Scholar]
- 14.Cacace, M. G., E. M. Landau, and J. J. Ramsden. 1997. The Hofmeister series: salt and solvent effects on interfacial phenomena. Q. Rev. Biophys. 30:241–277. [DOI] [PubMed] [Google Scholar]
- 15.Bulone, D., V. Martorana, P. L. San Biagio, and M. B. Palma–Vitorelli. 1997. Effects of electric charges on hydrophobic forces. I. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 56:R4939–R4942. [DOI] [PubMed] [Google Scholar]
- 16.Bulone, D., V. Martorana, P. L. San Biagio, and M. B. Palma–Vitorelli. 2000. Effects of electric charges on hydrophobic forces. II. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 62:6799–6809. [DOI] [PubMed] [Google Scholar]
- 17.Dzubiella, J., and J.-P. Hansen. 2003. Reduction of the hydrophobic attraction between charged solutes in water. J. Chem. Phys. 119:12049–12052. [Google Scholar]
- 18.Dzubiella, J., and J.-P. Hansen. 2004. Competition of hydrophobic and Coulombic interactions between nanosized solutes. J. Chem. Phys. 121:5514–5530. [DOI] [PubMed] [Google Scholar]
- 19.Vaitheeswaran, S., and D. Thirumalai. 2006. Hydrophobic and ionic interactions in nanosized water droplets. J. Am. Chem. Soc. 128:13490–13496. [DOI] [PubMed] [Google Scholar]
- 20.Rajamani, S., T. Truskett, and S. Garde. 2005. Hydrophobic hydration from small to large lengthscales: Understanding and manipulating the crossover. Proc. Natl. Acad. Sci. USA. 102:9475–9480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hummer, G., and S. Garde. 1998. Cavity expulsion and weak dewetting of hydrophobic solutes in water. Phys. Rev. Lett. 80:4193–4196. [Google Scholar]
- 22.Marcelja, S., and N. Radic. 1976. Repulsion of interfaces due to boundary water. Chem. Phys. Lett. 42:129–130. [Google Scholar]
- 23.Marcelja, S., D. J. Mitchell, B. W. Ninham, and M. J. Sculley. 1977. Role of solvent structure in solution theory. J. Chem. Soc., Faraday Trans. 2:630–648. [Google Scholar]
- 24.Tanaka, H. 1998. Simple physical explanation of the unusual thermodynamic behavior of liquid water. Phys. Rev. Lett. 80:5750–5753. [Google Scholar]
- 25.Lum, K., and A. Luzar. 1997. Pathway to surface-induced phase transition of a confined fluid. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 56:R6283–R6286. [Google Scholar]
- 26.Braig, K., Z. Otwinowski, R. Hegde, D. Boisvert, A. Joachmiak, A. L. Horwich, and P. B. Sigler. 1994. The crystal structure of the bacterial chaperonin GroEL at 2.8 A. Nature. 371:578–586. [DOI] [PubMed] [Google Scholar]
- 27.Suresh, S. J., and V. M. Naik. 2000. J. Chem. Phys. 113:9727–9732. [Google Scholar]
- 28.Cheung, M., and D. Thirumalai. 2006. Nanopore-protein interactions dramatically alter stability and yield of the native state in restricted spaces. J. Mol. Biol. 357:632–643. [DOI] [PubMed] [Google Scholar]
- 29.Betancourt, M., and D. Thirumalai. 1999. Exploring the kinetic requirements for enhancement of protein folding rates in the GroEL cavity. J. Mol. Biol. 287:627–644. [DOI] [PubMed] [Google Scholar]
- 30.Takagi, F., N. Koga, and S. Takada. 2003. How protein thermodynamics and folding mechanisms are altered by the chaperonin cage: molecular simulations. Proc. Natl. Acad. Sci. USA. 100:11367–11372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Baumketner, A., A. Jewett, and J. E. Shea. 2003. Effects of confinement in chaperonin assisted protein folding: rate enhancement by decreasing the roughness of the folding energy landscape. J. Mol. Biol. 332:701–713. [DOI] [PubMed] [Google Scholar]
- 32.Jewett, A. I., A. Baumketner, and J. E. Shea. 2004. Accelerated folding in the weak hydrophobic environment of a chaperonin cavity: creation of an alternate fast folding pathway. Proc. Natl. Acad. Sci. USA. 101:13192–13197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Viguera, A., C. Vega, and L. Serrano. 2002. Unspecific hydrophobic stabilization of folding transition states. Proc. Natl. Acad. Sci. USA. 99:5349–5354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Northey, J. G. B., A. Di Nardo, and A. R. Davidson. 2002. Hydrophobic core packing in the SH3 domain folding transition state. Nat. Struct. Biol. 9:126–130. [DOI] [PubMed] [Google Scholar]
- 35.Calloni, G., N. Taddei, K. Plaxco, G. Ramponi, M. Stefani, and F. Chiti. 2003. Comparison of the folding processes of distantly related proteins. Importance of hydrophobic content in folding. J. Mol. Biol. 330:577–591. [DOI] [PubMed] [Google Scholar]
- 36.Jacob, M., T. Schindler, J. Balbach, and F. X. Schmid. 1997. Diffusion control in an elementary protein folding reaction. Proc. Natl. Acad. Sci. USA. 94:5622–5627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Plaxco, K., and D. Baker. 1998. Limited internal friction in the rate-limiting step of a two-state protein folding reaction. Proc. Natl. Acad. Sci. USA. 95:13591–13596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Silow, M., and M. Oliveberg. 2003. High concentrations of viscogens decrease the protein folding rate constant by prematurely collapsing the coil. J. Mol. Biol. 326:263–271. [DOI] [PubMed] [Google Scholar]
- 39.Wang, J. D., C. Herman, K. A. Tipton, C. A. Gross, and J. S. Weissman. 2002. Directed evolution of substrate-optimized GroEL/S chaperonins. Cell. 111:1027–1039. [DOI] [PubMed] [Google Scholar]