Modeling Subunit Cooperativity in Opening of Tetrameric Ion Channels

Abstract

Most potassium channels are tetramers of four homologous polypeptides (subunits). During channel gating, each subunit undergoes several conformational changes independent of the state of other subunits before reaching a permissive state, from which the channel can open. However, transition from the permissive states to the open state involves a concerted movement of all subunits. This cooperative transition must be included in Markov models of channel gating. Previously, it was implemented by considering all possible combinations of four subunit states in a much larger expanded model of channel states (e.g., 27,405 channel states versus 64 subunit states), which complicates modeling and is computationally intense, especially when accurate modeling requires a large number of subunit states. To overcome these complexities and retain the tetrameric molecular structure, a modeling approach was developed to incorporate the cooperative transition directly from the subunit models. In this approach, the open state is separated from the subunit models and represented by the net flux between the open state and the permissive states. Dynamic variations of the probability of state residencies computed using this direct approach and the expanded model were identical. Implementation of the direct approach is simple and its computational time is orders-of-magnitude shorter than the equivalent expanded model.

INTRODUCTION

In recent years, major advancements have been made in our knowledge of ion-channel structure (1–3) and understanding of ion-channel gating (4–8). Incorporating properties of single ion channels into models of their electrophysiological function requires a Markovian formulation, which represents discrete kinetic states of the channel and their interactions (9). Unlike the macroscopic Hodgkin-Huxley type models of ionic currents through large ensembles of channels (10), single channel Markov models allow us to simulate state-specific channel properties and their alterations by mutations, disease, or drug binding. As Markov models simulate both single channel and macroscopic currents, they provide an implicit relationship between the single channel records and the macroscopic current. Explicit relations have been derived as well (11–15). In cardiac electrophysiology, Markov models of ion channels have been used to study channel function during the action potential (9,16,17), the cellular electrophysiological consequences of ion-channel mutations (17–21), and pharmacogenetics of anti-arrhythmic drug therapy (22). Most potassium channels, including cardiac channels, are tetramers consisting of four homologous polypeptides, termed subunits. Each subunit contains a voltage-sensing domain. It has been established experimentally that each of the voltage sensors undergoes several conformational changes before reaching a permissive (or activated) state, from which the channel can open (5,23,24). The process of a subunit reaching the permissive state is independent of the other subunits. The final transition from the subunits permissive states to the channel open state is a cooperative process that involves a concerted movement of all subunits (25–29). This situation, that is typical of potassium channels, causes dependency between state residencies of subunits. The dependency between subunits has been implemented in Markov models by considering channel states (rather than subunit states), with each channel state representing a possible combination of four subunit states (9,26,27,30). The number of channel states in such expanded models is much larger than the number of subunit states and increases drastically with the number of subunit states. Therefore, inclusion of more subunit states for more detailed modeling is limited with this approach. More detailed modeling may also be achieved by assuming time-dependent transition rates between channel states, which in turn complicates the simulation and calibration procedure (31). Obviously, a direct simulation approach that does not require transformation into the expanded model is highly desired, as it involves much smaller models and allows inclusion of many subunit states and therefore, development and calibration of Markov models based on the molecular structure of ion channels.

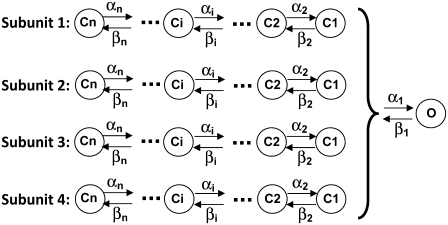
As stated above, the gating of a tetrameric ion channel can be simulated by modeling its four subunits with identical Markov structures. In this modeling approach, the transition of the channel to the open state may occur only if all the subunits are in the permissive preopening state. Fig. 1 is a schematic of a cooperative Markov model of a tetrameric ion channel. The model consists of four identical Markov structures representing the four subunits of the channel and a final cooperative transition to the open state. It should be noted that each subunit closed state may be modeled by any form of a Markov structure and is not restricted to a linear sequence of transitions to the permissive state. In this figure, Ci values are the subunit states and C1 is the subunit permissive state. Transition rate to the open state is α₁ if all the subunits are in C1. The channel transitions to the closed state (all subunits in C1) from the open state with a rate β₁. Conformational changes of each subunit are assumed independent of the other subunits. This implies that transitions between states of a subunit Markov model are independent of other subunits. Because of the cooperative transition to the open state, the Markov models of the subunits are coupled and computing the occupancy of Markov states in each subunit requires that this dependency be included.

FIGURE 1.

Schematic representation of a cooperative Markov model of a tetrameric ion channel. C1 is the permissive state. O is the open state. Ci (i = 2: n) are subunit closed states. The values α_i and β_i are transition rates.

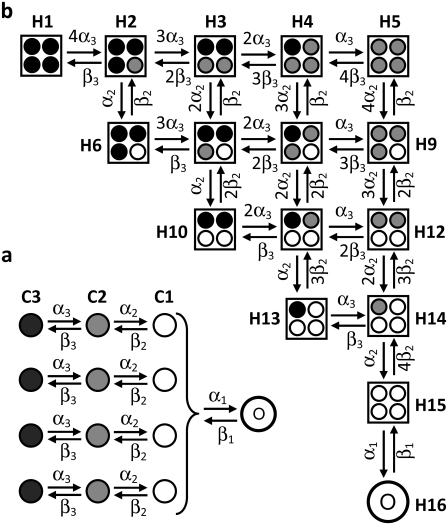
For small models of the subunits, this dependency will be automatically considered by deriving the expanded model of the ion channel in which the permissive state is one of the Markov states (9). Fig. 2 a shows a tetrameric model and Fig. 2 b shows its associated expanded model for an ion channel with three closed states in each subunit. The channel closed states in the expanded model have been determined by considering all the possible combinations of the closed states of its four subunits. The transition rates between channel states in the expanded model can be obtained from the transition rates within subunits in the tetrameric model by determining the possible subunit transitions that can cause a specific ion channel transition (9,16,25,27). There are 5 channel closed states for two subunit closed states and 15 channel closed states for three subunit closed states. The number of channel closed states, N_Ch, for n subunit closed states (n > 3) has been derived in Appendix A and is equal to

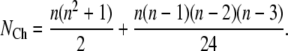(1)

Clearly, increasing the number of subunit states leads to a much greater increase in the number of channel states and a very large expanded Markov structure for the ion channel. Subunit Markov models that are developed and calibrated based on the molecular structure of an ion channel require many subunit states. Implementing the expanded Markov model of the ion channel for such cases is extremely difficult and computationally expensive. It is also less representative of the tetrameric structure of the channel. In this article, we derive a mathematical scheme for calculating the cooperative channel open probability and occupancy of subunit states directly from the tetrameric Markov model of the channel subunits, without using the expanded model of the channel.

FIGURE 2.

(a) A cooperative Markov model of a tetrameric ion channel. Each subunit has two closed states (C3, C2) and a permissive state (C1). (b) An equivalent expanded Markov model of the ion channel in panel a. Circles inside each square show the combination of four subunit states associated with each channel state. Transition rates of the expanded channel model are shown in terms of transition rates of the subunit states.

THEORETICAL ANALYSIS

Statistical characteristics and governing equations

In a cooperative Markov model (Fig. 1), all four or none of the subunits of the channel may be in the open state. This means that the probability of any subunit being in the open state is equal to the probability of the channel being in the open state:

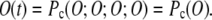(2)

We term the residency probability of the subunit states by the name of the states (Ci(t) and O(t)) and the probability of channel residency in any combination of subunit states by P_c(S1;S2;S3;S4), where Si represents the state of subunit i. Note that all the subunits are identical and so the probability of distribution of subunits among different states is the same for all four subunits. Transitions of a subunit between Ci states are independent of the other subunits. However, the probability of a subunit residing in a particular state is not independent of the state residency of other subunits:

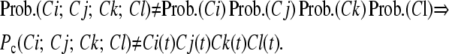(3)

Transitions of subunits to and from the open state cause this dependency, as these transitions occur to and from specific combinations of subunit states. For example, the probability that all the subunits reside in C1 increases by a net flux from the open state and decreases by a net flux to the open state.

To include this dependency in the model equations we first introduce the following two parameters.

• A: The probability that all subunits reside in C1 (the permissive state).

• F: The net flux (transition) from the open state to C1.

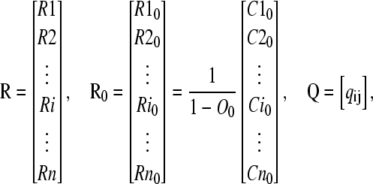
Assume that Q is the transition rate matrix (32) for the Markov structure of a subunit without the last transition to the open state (only Ci states), and C is the vector of all Ci states:

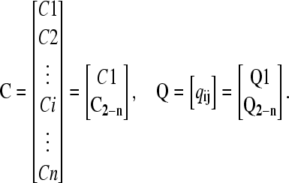(4)

Where C_2-n is a column vector of states C2 to Cn, Q₁ (1 by n) is the transition rate matrix representing the net transition to C1 from Ci states, and Q_2-n (n-1 by n) is the transition rate matrix representing net transitions to states C2, C3, …, Cn from Ci states. All the transitions to C_2-n states are from Ci states. For the C1 states, in addition to the net flux from the Ci states, there is a net flux from the O state. Therefore, the system equations can be written as

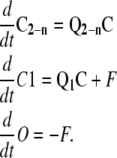(5)

The net flux from the open state to the permissive state can be calculated in terms of the probability of residency in the permissive state, A:

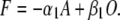(6)

To solve the system equations, we need to find A in terms of transition rates and state residencies. The state residency is the number of channels (or subunits) that occupy that state. However, as the total number of channels scales the state residencies, we define the normalized residency which is the number of channels (or subunits) in each state divided by the total number of channels (or subunits). This is the same as the probability of a state being occupied by a channel (or a subunit). Therefore, the sum of the normalized residencies in all states is one:

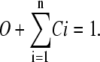(7)

In this article, we use normalized residency and probability of states interchangeably and refer to both as concentration of states.

Steady-state concentrations

As the first step for finding the concentration of states in a cooperative Markov model, we consider the equilibrium state (steady state) of the model. At steady state the system equations are

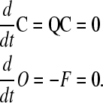(8)

We divide the subunits into two groups: subunits in the O state; and subunits in the Ci states. Therefore, if O_ss is the concentration of the open state at steady state, then 1-O_ss is the total concentration of all Ci states. For subunits in Ci states, the concentration of states at steady state is governed by the equation QC = 0. Elements on the diagonal of Q are minus the summation of all other elements in corresponding columns, therefore, the sum of all rows of the matrix is a zero vector indicating that the rows of Q are linearly dependent. As a consequence, the determinant of the Q matrix is zero, and this equation has a set of solutions for the C vector that are proportional to each other and to the steady-state concentration of states. We define C* as the normalized solution:

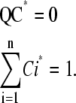(9)

The vector C* is the concentrations of Ci states among subunits of this group. The concentration of Ci states among all subunits, C_ss, is

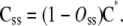(10)

As F is zero at steady state, from Eq. 6 we conclude that

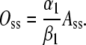(11)

At steady state, the net flux from the open state to the permissive state is zero, meaning that the transition to the open state does not have any effect on the distribution of subunits among Ci states and consequently, the probability of a subunit in Ci states is independent of other subunits. Therefore,

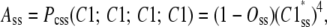(12)

where 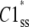is the steady-state probability of a subunit of Ci states residing in the C1 state; 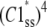is the probability that all four subunit reside the in C1 state (based on their independence). Combining Eqs. 11 and 12, the steady-state concentration of the open state is

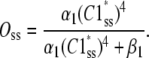(13)

Dynamic changes of state concentrations

At resting membrane potential, the concentrations of states have reached their steady-state values that can be determined using Eqs. 8, 9, and 12. Changing the membrane potential changes the transition rates between states and therefore the concentration of states is no longer equilibrated. Consequently, there will be net transitions (in general) between states toward new equilibrated concentrations associated with the new transition rates. As the net flux from the open state is nonzero during this transition, the concentrations of states in different subunits are not independent. In this case, the concentration of the permissive state, A, cannot be expressed in terms of (C1)⁴ and should be calculated considering this dependency.

Similar to steady-state derivation, we divide the ion channels to two groups: the ones that are initially in the open state with concentration O₀; and those that are initially in Ci states with a total concentration 1-O₀. The net flux from the open state, F, changes the concentration of open states accordingly to

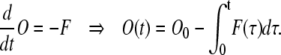(14)

The concentration of Ci states will change by redistribution according to the new transition rates and also by the subunits entering (or leaving) the Ci states with a net flux, F.

Positive flux

Assume that the net flux, F, is always positive (from O to C1) during the transition to new steady-state concentrations. We may divide the subunits in the Ci states into two subgroups: the first, termed E group, includes subunits that entered to the Ci states from the open state, and the second, termed R group, includes subunits that were initially in Ci states. The probability distribution within subunits of the R group is Ri. As (1-O₀) of subunits are in the R group, the concentration of Ci state in the R group is (1-O₀)Ri. Similarly, the initial concentrations of states in the R group, Ri₀, are the initial concentrations of Ci states, Ci₀, divided by (1-O₀). In the R group, there is no net flux from the open state and therefore the concentration of states in each subunit is independent of other subunits of the ion channel. Therefore, the dynamic changes of the concentration of states in the R group can be derived by solving the Markov model of one subunit:

(15)

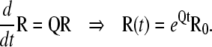(16)

Once the concentration of states is found, the concentration of the permissive state (in the R group) can be obtained based on the subunit independence property. In the R group, the probability that all four subunits reside in the C1 state (the permissive state) is

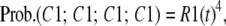(17)

and among all the subunits, it is

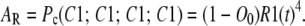(18)

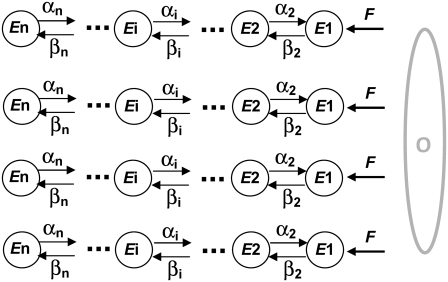
We call the equivalent of Ri for the E group Ei. Initially, the concentrations of states in group E are zero and they increase over time by the net influx from the open state. Similar to Eq. 15, the concentration of states in group E can be found by solving the differential equations of the Markov model of a subunit:

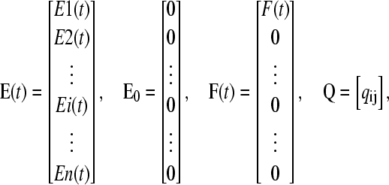(19)

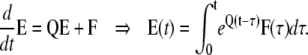(20)

In comparison to the R group, here the initial conditions are zero, but the equations have a nonzero input function, F(t). Note that the concentration of states in this group depends on F that is not known yet. To find the concentration of the permissive state for the subunits of this group (all four subunits in C1 state) we use a differential method. Fig. 3 shows a schematic of a tetrameric ion channel model for subunits in the E group. During a differential time interval between τ and τ +dτ, a differential amount of states equal to Fdτ enter the C1 state (note that the C1 state of this group is labeled by its concentration E1 in the figure). Although this differential amount of states is in C1 at timeτ, it will be distributed among other states as time progresses. The concentration of states in this group can be found by integrating the distribution of all the differential amounts that entered C1 over time. To find the distribution of a differential amount of influx to C1 among Ci states, we need to find the concentration of Ci states when all states are initially at C1. Assume U(t) is the response of the Markov model of a subunit (with no input) when all the subunits are initially at the C1 state, then

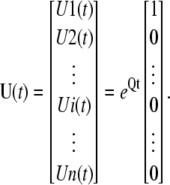(21)

As the system is a linear time invariant system, the distribution among Ci states of F(τ)dτ states, that are in C1 at time τ, will be F(τ)dτ Ui(t − τ) at a later time t. The concentration of states can be found by integrating these differential concentrations and is the same as Eq. 20. Using the differential method we can also determine concentrations of the permissive state for subunits in the E group. In this approach the subunits of group E are modeled with an infinite number of differential distributions. In each of these differential distributions there is no additional flux to C1 other than the differential amount added at timeτ. Therefore, the four subunits are independent and the probability that all four reside in C1 for each differential distribution is

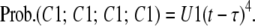(22)

FIGURE 3.

The ion channel model of subunits in the Ei group. These subunits are initially in the open O state and enter Ci states with a rate F.

This probability can be scaled by the number of subunits in each differential distribution to find the probability of the permissive state in that distribution within all subunits,

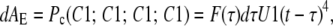(23)

and can be integrated over time to find the permissive state concentration in subunits of the E group (among all subunits),

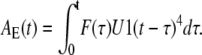(24)

The total concentration of Ci states, Ci, and total concentration of the permissive state, A, can be found by combining these concentrations for subunits of groups E and R:

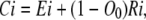(25)

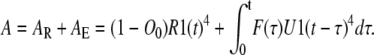(26)

Equations 6, 14, and 26 can be solved to find the three unknown functions: O(t), A(t), and F(t). Substituting for A from Eq. 26 and for O from Eq. 14 in Eq. 6 results in the following integral equation for F:

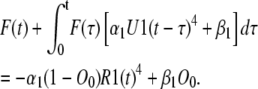(27)

Note that R1 and U1 are known functions.

Negative flux

In the previous section we assumed that during the transient response F is always positive, meaning that the net transition is always from the open state to the permissive state. However, the net flux, F, may be negative as well. Assume that during the time interval between τ and τ +dτ the net flux is negative and a differential amount of states |F|dτ exit the permissive state to the open state. If these states would have remained among Ci states, they would have been distributed according to |F|dτ Ui(t − τ). Therefore, we should subtract this distribution from the distribution of Ci states, or simply include F with a negative sign in the equations above and add the negative resultant concentration of Ci states in the E group to the concentration of Ci states in the R group.

SIMULATIONS AND RESULTS

A cooperative Markov model consisting of one open state and three linearly connected Ci states was chosen to test the new formulation for direct solution of the tetrameric model (Fig. 2 a). This Markov structure has been used to model various ion channels, including the Shaker potassium channel (27,30) and slow delayed rectifier potassium channels (I_Ks) (16). The dynamic changes of the concentrations of subunit states are simulated for a voltage-clamp test and compared with the prediction of the expanded model. This provides a validation test for the new direct formulation, as both methods are expected to predict identical dynamics for the ion channel. However, the direct solution of the tetrameric structure predicts the concentration of subunit states while the expanded model predicts the concentration of channel states. In the following, we first derive the relationship between the concentration of subunit states, Ci, and the concentration of channel states, Hi. We then compare the predictions of the two approaches for the steady-state values and dynamic variations of the concentrations of subunit states.

Relation between concentrations of subunit states and channel states

The concentration of each subunit state can be calculated by a weighted summation of the concentration of channel states where the weights are the repeats of that specific subunit state in the channel states. If the number of repeats of the subunit state Ci in the channel state Hj is k_ij, then the concentration of subunit states is

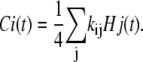(28)

The factor of one-fourth is required as there are four subunit states in each channel state. The concentration of a subunit open state and the channel open state is the same, as either all or none of the four subunits of a channel are in the open state. Therefore, O represents both the concentration of the channel and subunit open state. Table 1 lists the coefficients k_ij for the cooperative Markov model of Fig. 2. Eq. 28 is valid for steady-state conditions as well as during the dynamic changes of states.

TABLE 1.

k_ij, the number of repeats of the subunit state Ci in the channel state Hj

i/j	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1	0	0	0	0	0	1	1	1	1	2	2	2	3	3	4
2	0	1	2	3	4	0	1	2	3	0	1	2	0	1	0
3	4	3	2	1	0	3	2	1	0	2	1	0	1	0	0

To validate our direct approach for a tetrameric model of subunits against the expanded model of channel states, both models should start from equivalent initial concentrations of states. If the initial concentrations of channel states, H_j0, are given, then the initial concentrations of subunit states, C_i0, can be calculated using Eq. 28. However, it is possible to calculate H_i0 from C_i0 knowing that initially the ion channel is at the steady state associated with its resting potential. It can be shown that (Appendix B) if the channel state, Hj, consists of m repeats of C3, n repeats of C2, and p repeats of C1 then, at steady state, concentration of this channel state can be derived in terms of the concentrations of subunit states as

(29)

where

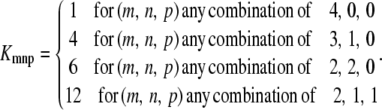(30)

Note that m, n, and p are 0, 1, 2, 3, or 4 and m + n + p = 4.

Steady-state concentrations

We first validate the direct method for steady-state conditions. In the simulation, the following transition rates were assigned to the model:

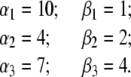(31)

Therefore, the Q matrix for the Ci states is

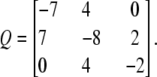(32)

Unit of transition rates is 1/ms. The normalized steady-state concentrations of these states is the Eigenvector associated to Eigenvalue 0 of the Q matrix:

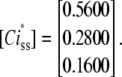(33)

O_SS can be calculated from Eq. 13,

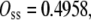(34)

and from Eq. 10, the steady-state concentrations of Ci states are

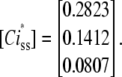(35)

The steady-state concentrations of channel states can be found similarly from the 16 × 16 transition rate matrix, Q_C, and are

(36)

H16 in the expanded model is the open state and its steady-state concentration, H16_ss, is the same as open state concentration, O_ss, derived using the new direct approach for the tetrameric model. In our direct solution of Ci subunit states we calculate the concentrations of all other channel states using Eq. 29 and the results match the concentrations of the expanded channel model in Eq. 36. Inversely, the subunit concentrations, Ci, can be calculated from the channel state concentrations in the expanded model using Eq. 28 and are the same as the subunit concentrations derived directly from the tetrameric model in Eq. 35. This provides validation for the direct approach under steady-state conditions.

Dynamic changes of the concentrations of states

We compare the solution of both methods for the dynamic changes of subunit states and channel states during an arbitrary voltage-clamp test. We assume that the channel is already at rest with an initial distribution of states and then subjected to a test potential for which the transition rates of the model are given in Eq. 31. The initial concentrations of subunit states at rest (associated to the transition rates at the resting potential) are chosen to be

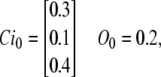(37)

and the initial concentrations of channel states, Hj₀, are calculated from these values using Eq. 29 to set both the expanded model and tetrameric model at equivalent initial conditions.

The channel state concentrations of the expanded model can be calculated as

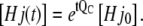(38)

H16 is the open state in the expanded model (Fig. 2 a) and so the open probability is H16(t). In the direct approach we first find the two auxiliary functions: the response of the Markov structure of one subunit (without an open state) to the normalized initial concentrations of states, R1(t), and its response when all the subunits are initially in the C1 state, U1(t). R1(t) and U1(t) are calculated according to Eqs. 16 and 21, and are shown in Fig. 4. Once these auxiliary functions are known, we can compute the net flux from the open state, F(t), using Eq. 27. This is a nonlinear integral equation that we solve numerically using a finite difference method. Substituting the integral with a summation of rectangular or trapezoidal approximations over small intervals enables finding an approximation for F at the n_th interval from its approximated values on previous n-1 intervals. The initial value of F is required for this finite difference method and can be derived from Eq. 27 by setting t = 0:

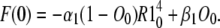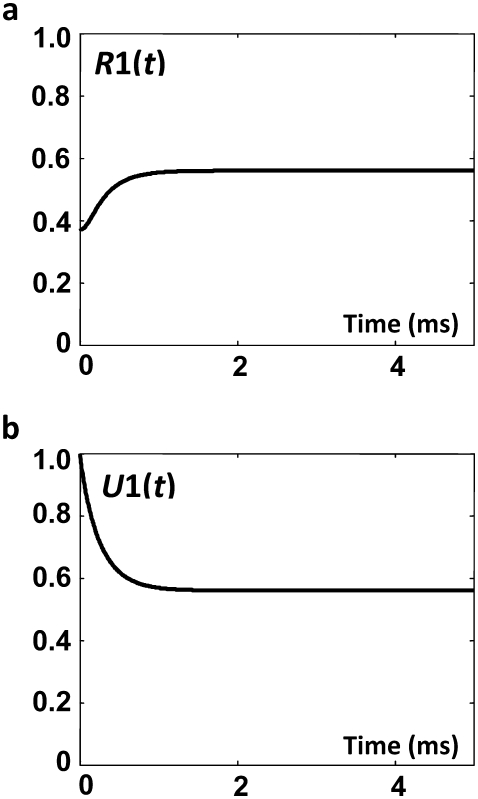
(39)

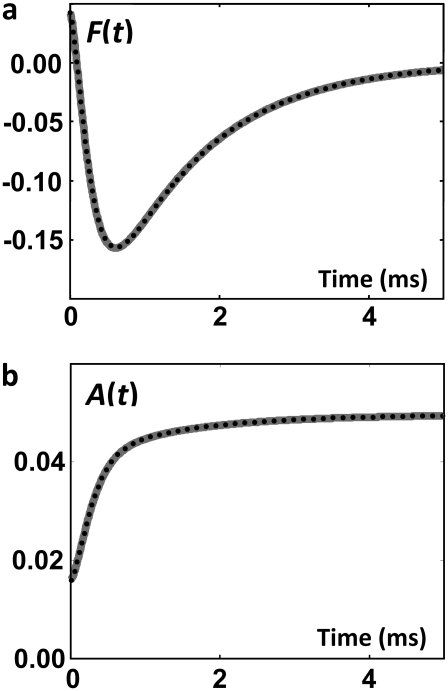
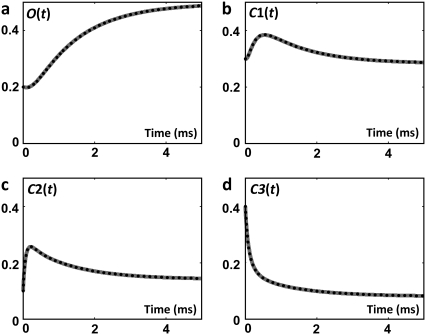
Once F is known, the concentration of the permissive state, A, is calculated using Eq. 26. The permissive state in the expanded model is H15 (Fig. 2) and its concentration is given by Eq. 38. Knowing the concentrations of the open state (O ≡ H16) and permissive state (A ≡ H15), we compute F in the expanded model through Eq. 6. Fig. 5 shows the net flux from the open state, F, and the concentration of the permissive state, A. As expected, the net flux from the open state and concentration of the permissive state calculated from the direct solution of the tetrameric model or from the expanded model are identical. Knowing F(t), the concentrations of subunits in the E group, Ei(t), in the R group, Ri(t), and in the open state, O(t), are calculated using Eqs. 20, 16, and 14, respectively. The concentrations of Ci subunit states, Ci(t), are calculated from Ei(t) and Ri(t) through Eq. 25 and from the expanded model through Eq. 28. These concentrations are shown in Fig. 6.

FIGURE 4.

The two auxiliary functions (a) R1(t) and (b) U1(t) calculated for the voltage-clamp test of the tetrameric model presented in this article.

FIGURE 5.

(a) Net flux from the open state, F(t), in the voltage-clamp test and (b) concentration of the permissive state, A(t). Dotted curves resulted from direct solution of the tetrameric model; shaded curves resulted from the expanded model of the ion channel. Note that the curves are superimposed, demonstrating complete equivalence of the direct and expanded methods.

FIGURE 6.

Concentrations of subunit states: (a) O, (b) C1, (c) C2, and (d) C3 as a function of time in the voltage-clamp test. Dotted curves resulted from direct solution of the tetrameric model; shaded curves from the expanded model of ion channel. The curves are superimposed.

The direct approach presented here is developed to find the concentrations of the open state, O, and subunit states Ci in the tetrameric model. However, if desired, the concentrations of channel states (any four combinations of subunit states) can be found as well. The approach is similar to that used for calculating the concentration of the permissive state, A. Note that the permissive state is a channel state with a (C1; C1; C1; C1) combination of subunit states. If the channel state, Hj, consists of m repeats of C3, n repeats of C2, and p repeats of C1, then the dynamic concentration of this channel state can be computed through the equation

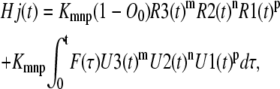(40)

where K_mnp is defined by Eq. 30.

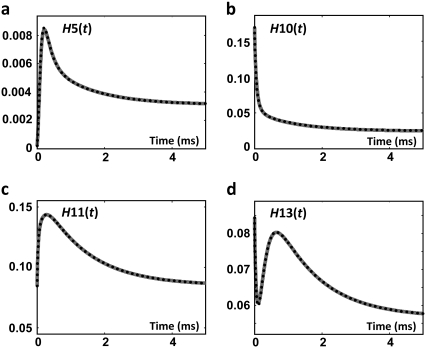
The ion-channel concentrations have been calculated using Eq. 40 and are compared with the solution of the expanded model in Fig. 7.

FIGURE 7.

Concentrations of channel states: (a) H5, (b) H10, (c) H11, and (d) H13 as a function of time in the voltage-clamp test. Dotted curves resulted from direct solution of the tetrameric model; shaded curves from the expanded model of ion channel. The curves are superimposed.

SUMMARY AND CONCLUSIONS

In this article, we present an algorithm for finding the probability distribution (concentrations) of states in a cooperative tetrameric model of an ion channel. Cooperative Markov models have been proposed to model ion channels based on their tetrameric structure that consists of four identical repeats of transmembrane segments. Such models can be used to relate the channel function to its molecular structure. As the transition of the channel to the open state requires a cooperative transition of all four subunits, the common approach for solving Markov models cannot be applied in this case. The equivalent expanded model of the entire channel can be used for obtaining the concentration of channel states. However, the number of states in expanded models is much larger than the number of subunit states, as the expanded model includes all possible combinations of the states of the four subunits. Therefore, in practice the application of expanded models has been limited to models that incorporate up to three states in each subunit. Conformational changes of subunits during channel gating involve several degrees of freedom. Representation of these changes requires several states per subunit. Implementing the expanded model for several subunit states is extremely difficult and computationally very expensive. In comparison, implementation of the algorithm presented in this article is simple and its computational time is orders-of-magnitude shorter than the equivalent expanded model. For example, if the conformational changes of an ion channel subunit during gating can be approximated by only three independent degrees of freedom and each degree of freedom is assigned only four Markov states, then each subunit has 64 Markov states. The size of the Q matrix in the direct approach is 64 × 64 = 4096, which can be implemented and solved on a personal computer in a reasonable time. The equivalent expanded model requires 27,405 Markov states and the size of the Q_ch matrix is 27,405 × 27,405 = 751,034,025, which is extremely difficult to implement and requires a supercomputer to solve.

Implementation for variable voltage tests

The direct approach can be generalized for variable voltage conditions, enabling the tetrameric models to be integrated into models of the action potential. For a variable voltage, we cannot find F(t) independently from R1(t) and U1(t) because the transition rates and so the Q matrix depends on the membrane potential and varies with time. In this case, the variations of state concentrations are calculated during the dt interval between t and t + dt in terms of the concentrations, transition rates, and net flux from the open state at time t and then integrated to find concentrations of subunit states at time t + dt. Knowing the concentrations of states and F at time t, the variations in the concentrations of states within dt are

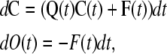(42)

where

(43)

Calculating F depends on the concentration of the permissive state, which can be computed in a similar way. Equation 26 can be rewritten as

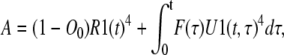(44)

where R1(t) is the concentration of the C1 state calculated using Eq. 42 by setting F = 0 and using the normalized concentrations of Ci states as initial conditions. U1(t,τ) is the concentration of the C1 state calculated using Eq. 42 by setting F = 0 and setting the initial concentrations of C1 to one and all other Ci states to zero at time t = τ. This provides the distribution of the differential amount of subunits that entered to C1 at time τ as a function of time, t. Unlike the voltage-clamp test, U1 here is a two-dimensional function, as the system characteristics defined by the transition rates vary with time (autonomous system). Clearly U1 is zero if t < τ. If the transition rates vary according to specific functions of time, the concentration of each subunit state approaches to a specific function of time (in comparison to a constant value when transition rates are constant) regardless of the initial concentration of states. Consequently, at any time t ≫ 0 the distributions of the subunit states that have been initially in Ci states and those that have entered C1 at times τ ≪ t will eventually be the same:

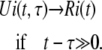(45)

Combining Eqs. 6, 14, and 44 results in the following equation for F(t):

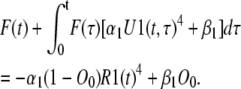(46)

This equation is the same as Eq. 27 for the voltage-clamp test, except that U1(t − τ) is replaced with U1(t,τ). However, unlike in the voltage-clamp test, U1(t,τ) should be computed simultaneously with F(t) as it depends on the variation of membrane potential which in turn is determined knowing F. Note that although U1 (or any Ui) is a two-dimensional function, we do not need to save all the values of the function. We only need the most current value at time t for all τ from 0 to t, which requires a one-dimensional function that is updated at each time step. Appendix C provides a pseudo code for implementing this approach in whole cell action potential.

Model with multiple open states or multiple permissive states

The model we presented here has one permissive state and one open state. The analysis can be generalized for multiple open states, multiple permissive states, or both. If there is one permissive state and multiple open states (and possibly inactivated states connected to the open states) with only one cooperative transition from the permissive state to an open state termed O1, then the approach is very similar to that presented here. In this case, the concentrations of open states will be calculated using the transition rate matrix of the Markov structure of open states considering the cooperative flux, F, as an input function. In Eq. 6, O should be replaced by O1 which, in turn, can be expressed in terms of F. Equation 26 still holds for the concentration of the permissive state, except that O₀ is the sum of all initial concentrations of open states. Substituting for A and O1 in terms of F in Eq. 6 results in an integral equation that can be solved to find F(t) and consequently the concentration of states.

For cases with multiple permissive states and one open state, there will be multiple cooperative transitions that should be modeled with more than one cooperative flux. For example, if channel states that are formed by any combinations of C1 and C2 states are considered as permissive states (five permissive states), then the approach requires considering two net fluxes from the open state: F1 and F2, which represent the average net flux from the open state to the C1 and C2 states, respectively. In this case, Eq. 6 will become two equations, let term, Eq. 6a for F1 and Eq. 6b for F2. These equations express F1 and F2 in terms of concentrations of the O state and all five permissive states A1–A5. Concentrations of the permissive states and O state can be calculated in terms of both F1 and F2 using the Markov model equations and can be substituted into Eqs. 6a and 6b to derive two coupled integral equations for F1 and F2. From F1 and F2 the concentrations of states can be computed.

APPENDIX A: NUMBER OF CHANNEL STATES IN EXPANDED MODELS

Assume a tetrameric Markov model consisting of n subunit closed states and one cooperative transition to the open state from the permissive state. The expanded model has one channel open state associated with all subunits in the open state and N_ch channel closed states associated with all combinations of closed states of the four subunits. Any combination of closed states of the four subunits fall in one of the following categories:

1. All of the subunits are in the same state.

2. Three of the subunits are in one state and the fourth is in a different state.

3. Two of subunits are in one state and the other two in another state.

4. Two of the subunits are in one state and the other two are in two different states.

5. Four subunits are in four different states.

Clearly there are n combinations in group 1 as there are n subunit closed states. In group 2, the three subunits in the same state can be in any of n states and the fourth subunit can be in any of the remaining n-1 states. Therefore there are n(n-1) or 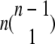combinations in this group. The number of combinations in other groups can be derived similarly and are 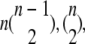and 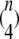for groups 3, 4, and 5, respectively. The total number of channel closed states is

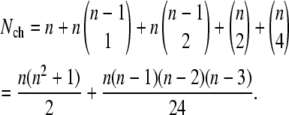(47)

APPENDIX B: STEADY-STATE CONCENTRATIONS OF CHANNEL STATES (EXPANDED MODEL) IN TERMS OF CONCENTRATIONS OF SUBUNIT STATES

Assume three subunit closed states C3, C2, and C1 and a channel closed state, Hj, consisting of m repeats of C3, n repeats of C2, and p repeats of C1 where m + n + p = 4. At steady state, there is no net flux from the open state and the concentrations of subunit states are independent of each other. We define K_mnp as the number of permutations of a channel state that includes m repeats of C3, n repeats of C2, and p repeats of C1. 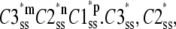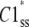Given the independence of subunit concentrations at steady state, the probability of each of these permutations among the closed states is and are the steady-state concentrations of subunit states C3, C2, and C1 among the closed states,

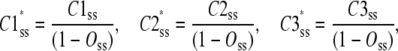(48)

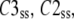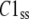where and are the steady-state concentrations of subunit states C3, C2, and C1. Therefore, the concentration of the Hj channel state at steady state is

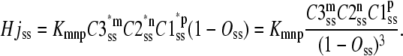(49)

There is one permutation when all four subunits are in the same state (C3, C2 or C1). There are four permutations when three of the subunits are in one state and one is in a different state as the one in the different state can be in any of the four subunits. When two of the four subunits are in one state, these two subunits can be selected in 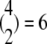different ways. For each of these choices, if the other two subunits are in different stats there are two ways for assigning the two states to the two remaining subunits. Therefore, the number of permutations of a channel state that includes two subunits in one state and two in another state is 6, and the number of permutations of a channel state that includes two subunits in one state and two in two different states is 12. The number of permutations of a channel state is summarized in the following:

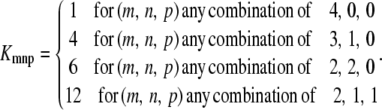(50)

Note that if there are three subunit closed states, in any channel state one subunit state has been repeated at least twice.

APPENDIX C: PSEUDO CODE TO IMPLEMENT DIRECT APPROACH IN WHOLE CELL AP MODEL

Oks	Probability that IKs channels are in the open state.
Iks	Current through IKs channels.
Ik	Sum of potassium currents.
INa	Sum of sodium currents.
ICa	Sum of calcium currents.
V	Potential across the membrane.
C	Membrane capacitance.
M	The number of time steps required to reach the steady-state condition (usually equivalent to a few seconds).
a1Func	Transition rate to open state as a function of V.
b1Func	Transition rate from open state as a function of V.
C10,
C20,	Initial probability of IKs subunit states.
C30,
Oks0
QMatrix	The transition rate matrix for subunit states:
	1 R = 1/(1-Oks0)*[C10C20C30]T
	2 U = [1 0 0]T
	3 Oks = Oks0
	4 S = 0
	5 F(1) = −α1*(1-Oks0)*R[1] ^ 4 + β1*Oks0
	6 for i = 1 to number of timesteps
	7 Oks = Oks-F(i)*dt
	8 Ik = Ikr + Iks + Ik1 + …
	9 Ik = Ikr + Iks
	10 Iion = INa + ICa + Ik
	11 V = V-1/C *Iion* dt
	12 Q = QMatrix(V)
	13 a1 = a1Func(V)
	14 b1 = b1Func(V)
	15 R = R + Q*R*dt
	16 U = [[U + Q*U*dt], [1 0 0]T]
	17 Ftemp = 0
	18 for k = 1 to Min{i,M}
	19 Ftemp = F(k)*(a1*U(1,k) ^ 4 + b1)*dt
	20 end
	21 Ftemp = −a1*(1-Oks + S)*R(1) ^ 4 + b1*(Oks-S) − Ftemp
	22 F(i + 1) = Ftemp/(1 + dt*(a1 + b1))
	23 if i > = M
	24 S = S + F(1)*dt
	25 F = F(2:M + 1)
	26 U = U(:,2:M + 1)
	27 end
	28 end