Double Bilayers and Transmembrane Gradients: A Molecular Dynamics Study of a Highly Charged Peptide

Abstract

The position and extent of movement of a charged peptide within a membrane bilayer provides much controversy. In our study, we have examined the nature of the highly charged helix-turn-helix motif (S3b and S4) to address how a highly charged peptide is stabilized within a bilayer in the presence of various transmembrane electrical potentials. Our double-bilayer simulation results show how the variation of the salt concentrations between the inner and outer bath establishes a transmembrane potential. Our results also show that important features of the peptide affected by changes in electrical potential are the center of mass depth, the swivel/kink degrees of conformation, and the hydrogen-bonding patterns. As the voltage gradient across the bilayer increased, the center of mass of the peptide shifted in a direction toward the outer bath. The peptide also has a higher percent helical content and the swivel/kink conformation is more rigid for nonpolarized systems where no voltage drop occurred between salt baths. Our results also provide some suggestions for how this domain may be affected by environmental changes as part of the voltage sensor in a K-channel.

INTRODUCTION

Membrane proteins with charged residues play important roles in the function and regulation of many biological processes. The role of charged residues is especially important in regard to charged peptides and ion channels. Previous studies for these peptides and proteins have focused on the ability of a membrane to accept the charged state of the protein (1–8), on the lipid headgroup dependence (9–15), on the structure itself (16–20), on the motions of the channel (21–31), and on the energetics and conductance (32–41) of the channel. However, the question of how charged side chains behave in response to a realistic potential based on the explicit variation of salt concentrations has not been examined.

Since the initial voltage-clamp experiments carried out by Hodgkin and Huxley (42), voltage-gated potassium channels (Kv) have become a prototype for understanding membrane proteins. K⁺ channels play a key role in maintaining ionic balance across the membrane (43). The channel undergoes a structural change to facilitate the passage of potassium ions across the cellular membrane that depends on the transmembrane voltage, a process called “gating” (43). It is clear that a change in potential moves the “gating charges” within the S4 region whose movement in turn is mechanically coupled to the “gate” in the pathway. The position and extent of movement of the domain has been the focus of much research due to its charged state (5–7,9–16,18,19,21–32,34,35,37,38,41). An intriguing question is what type of conformational changes of the S4 domain lead to the transition between the open and closed states of the channel when a transmembrane potential is applied.

Recent x-ray structures of this charged domain illustrate the difficulty in predicting how the charged S4 domain can be oriented within a bilayer under different environmental conditions (5,8,16,17,20). The KvAP and Kv1.2 structures generated several theories for how the S4 domain can be oriented and move within a bilayer environment due to the different behavior of the domain and its charged arginines (5,14,20,23). The theories behind the structures have sparked numerous studies concerning the orientation of the domain and movement of charged side chains within a lipid core environment (1–4,7,10,14,15,18,21,22,24–26,34,35,38). Several new experimental studies have been geared toward understanding how the charged domain interacts with its lipid environment (10,12). However, it is experimentally difficult to control the local environment of a heterogeneous protein-membrane environment. We believe that as of yet, these experiments cannot provide the level of atomic detail needed to fully understand the environment of charged side chains and lipids.

Molecular dynamics (MD) simulations can provide atomic information necessary to better understand details relating to charged side chains. A number of computational studies have been carried out illustrating atomic details of charged side chains within a membrane environment (2,6,11,13,27,28,35,38). Some of these studies quantitatively assess the thermodynamic stability and partitioning of charged side chains within a lipid core environment (1–4). They show that the thermodynamic cost of inserting a single arginine on a leucine-rich peptide into a bilayer is on the order of 70–73 kJ/mol (1–3). These thermodynamic studies were important to pave the way for us to consider how a highly charged peptide interacts with its environment when a voltage gradient is applied across a bilayer (1–4).

In this study, we investigate the environment of a highly charged peptide with a known sequence in the bilayer under varying transmembrane potentials. Due to its charged nature and ability to respond to a transmembrane potential, we chose to use the helix-turn-helix (HTH) motif from KvAP as our charged peptide. We established four one-dimensional potential of mean force (PMF) profiles to determine the initial peptide starting configurations for our transmembrane potential simulations. Whereas the PMF profiles were generated using a continuum method, the qualitative results from our profiles provide relevant transmembrane starting positions for the peptide.

The starting peptide positions within the bilayer for the atomic simulations were chosen based on the results from our potential of mean force calculations. The all-atom systems differ in both the starting position of the HTH motif relative to the bilayer and the strength of the potential gradient across the electrified bilayers. We show that different transmembrane potentials affect the orientation and position of the peptide as well as the environment of the solvent. In addition, we speculate how our all-atom explicit calculations explore environmental effects in a similar manner to that produced by a voltage gradient on a K⁺ channel.

METHODS

The voltage sensor domain functions as an independent gating domain of KvAP channels (5,7,9–11,14,18,19,21,22,25–28,32,34,37,38,41). The structure of the sensor domain was determined by crystallography (PDB ID: 1ORS) (16). The crystallographic structure abstracted to the HTH motif includes the S3b and S4 segments, which represents residues 99–151 of the entire KvAP channel. We reduced the structure to include only the HTH motif (sequence: PAGLALIEGLAGLGLFRLVRLRFLRILISRGSKFLSAIADADKLVPR) to maintain the charged nature of the motif within a bilayer. The titratable residues were simulated using their default charged state in the charmm27 force field parameters, where Arg and Lys had a charge of +1 and Glu and Asp had a charge of −1. The total net charge for a single HTH motif is +5.

Implicit bilayer calculations

Previous molecular dynamics studies of charged membrane peptides or the K⁺ channel have been based on all-atom models (1–4,6,9,15,18,19,22,26,29,34,36,37,41,44). In this article, we used implicit bilayer calculations to qualitatively determine several different starting positions for the peptide in a bilayer when running all-atom calculations. For our calculations, we use the implicit generalized Born simple switching model (GBSW) as well as the all-atom parameter PARAM22 using the CHARMM program (version c32b1) for the HTH paddle (45–50). This generalized Born continuum electrostatics theory includes the mean influence of both water and the biological membrane (45–48). We chose the GBSW method for ease of use and thorough literature documentation but other types of implicit models also exist (45–48,51,52).

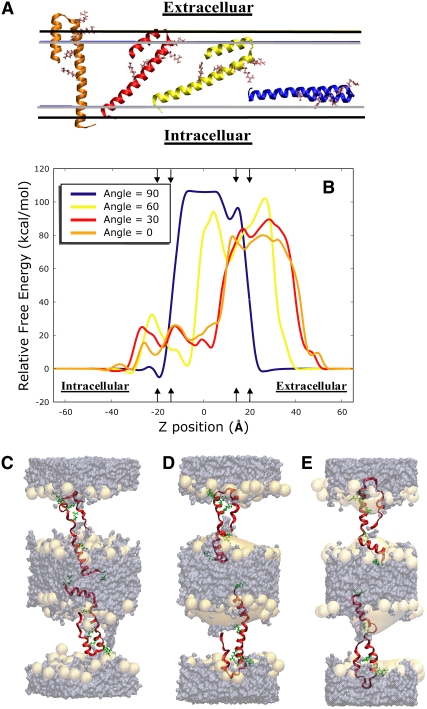
A series of simulations were setup varying the center of mass position of the sensor domain along the z axis. The HTH motif was oriented at four different angles (0°, 30°, 60°, 90°) relative to the bilayer normal (Fig. 1 A). The motif was sampled over peptide center of mass positions ranging from −65 Å to 65 Å relative to the center of the implicit bilayer (centered at 0 Å of the z axis). Umbrella sampling was used to constrain the peptide to the relative positions.

FIGURE 1.

(A) For the reaction coordinate, the center of mass of the peptide was translated along the z-axis at four orientations relative to the bilayer. The helix-turn-helix (HTH) motif is shown in an implicit bilayer where the boundaries are depicted by the gray and black horizontal lines. The gray lines indicate the boundary of the hydrophobic core and the black lines show the outer boundary of the interfacial regions. The helix-turn-helix (HTH) motif is represented with a ribbon backbone trace and the four gating side chains are shown as sticks. The orange motif is at 0° relative to the bilayer normal. The red motif is 30°, the yellow motif is 60°, and the blue motif is 90°. (B) The potential of mean force profiles for four angles along the z-distance from the bilayer normal. The center of mass of the peptide moved along the z-axis created an asymmetry between the two sides of the bilayer. Note that the angle of rotation to the bilayer was restrained with a harmonic potential function. Arrows indicate where the boundaries for the interfacial regions are located and help to show the intracellular and extracellular regions of the bulk solvent and the orientation of the peptide in relation to part A. (C–E) The HTH motif backbone is traced with the arginine side chains rendered as sticks. The orange surface shows the DOPC headgroup density and the purple surface shows the water/salt density over a simulation time of 10 ns. Note the water penetrating the headgroup region for each system. (C) The HTH motif at the −5.0 Å with a 30° orientation is placed in an all-atom double bilayer system. (D) The HTH motif at the 0 Å with a 30° orientation is placed in an all-atom double bilayer system. (E) The HTH motif at the 5.0 Å with a 30° orientation is placed in an all-atom double bilayer system.

The miscellaneous mean field potential (MMFP) algorithm was used to harmonically restrain the peptide relative to the bilayer. These constraints ensured that we accurately sample along our reaction coordinates. The harmonic restraints, one planar and two cylindrical, positioned the center of mass of the motif to keep it from moving too fast laterally through the bilayer and to maintain the orientation angle of the motif relative to the bilayer. MMFP force constant values ranged from 200 to 6600 kcal/(mol Ų), depending on the position of the motif within the bilayer. The data from these windows were directly used for umbrella sampling to obtain the average distribution function along our reaction coordinate. The use of higher force constants was necessary to sample at a particular point of the umbrella where the underlying free energy surface was steep and under sampled; however, this increase in force at points along the reaction coordinate does not affect the overall PMF because we later use WHAM to unbias our data.

Molecular dynamics simulations for all the HTH motif angles were carried out with a time step of 2 fs for a total simulation time of 10 ns at a temperature of 300 K for each simulation window along the z-direction. The GBSW membrane parameters used 30 Šfor the thickness of the membrane hydrophobic core, 5 Šfor each membrane interface, and a surface tension coefficient of 0.04 kcal/(mol Ų) to represent the nonpolar solvation energy. We chose to create a total membrane thickness of 40 Što best represent our explicit simulation lipid type, dioleoylphosphatidylcholine bilayer (DOPC).

The weighted histogram analysis method, WHAM, estimates the relative free energy surface along a reaction coordinate (53–56). In this study, we use WHAM to determine the initial starting positions for the HTH motif (S3b and S4). A converged PMF profile for four different angles relative to the bilayer normal helped determine our all-atom simulation starting points, significant orientations, and z-positions of the HTH motif within the bilayer. A series of 1D PMF profiles were constructed for each of the four orientations due to the time required to obtain convergence for these angles. Approximately 550 windows with a minimum bin size of 800 and a tolerance of 0.0001 were needed to obtain a converged PMF profile for each of the angles.

All-atom calculations

For this study, we wanted to understand how the environment of a highly charged transmembrane peptide is stabilized when a transmembrane potential is applied. From the 1D PMF profiles, three z-position points (−5.0 Å, 0 Å, and 5.0 Å) were chosen from the 30° profile. These z-positions were used for our double bilayer systems to determine how this highly charged transmembrane peptide responds to a transmembrane gradient within a DOPC bilayer environment.

We used a double bilayer system to establish a more realistic potential across the membrane (57). Previous simulations regarding a transmembrane voltage gradient have largely used an implicit applied potential to create a voltage drop across a single bilayer containing a protein (58). Our simulation setup allows us to create a voltage gradient that mimics biology in which the voltage is dependent solely on the charge concentrations felt across a bilayer. Through the use of a double bilayer system we maintain two independent bath charge concentrations and we create a potential drop based on the explicit variation of the salt concentrations between the two baths (Fig. 1, C–E). The potential difference between the inner and outer bath was calculated as described in Sachs et al. (57).

The three motif z-positions were used as starting points for several unconstrained double bilayer all-atom simulations under varying salt bath concentrations (Tables 1–3). It is important to note that the simulations had a constant total number of ions and that to create the different voltage gradients ions were exchanged between the two baths. Simulation potential conditions were defined as nonpolarized when the system transmembrane gradient was within physiological conditions (a voltage drop within 0 ± 10 mV between the inner and outer bath). The three different electrified systems (depolarized, hyperpolarized, and strongly-hyperpolarized) were created by the exchange of two ions located in opposite baths from a nonpolarized double bilayer system thus facilitating the creation of a transmembrane electrified potential. The depolarized systems describe a salt exchange where a net charge of −1 in the outer bath and a net charge of +1 is present in the inner bath is present thus simulating a positive voltage gradient across the bilayer. The hyperpolarized systems describe a salt exchange where a net charge of +1 in the outer bath and a net charge of −1 in the inner bath is present thus simulating a negative voltage gradient across the bilayer. The strongly-hyperpolarized systems describe a salt exchange where a net charge of +2 in the outer bath and a net charge of −2 in the inner bath is present thus simulating a strongly negative voltage gradient across the bilayer.

TABLE 1.

Bath charge concentrations of negative HTH motif position

Bath description	Outer bath	Inner bath	Peptide 1position	Peptide 2 position	Potential gradient
Strongly hyperpolarized	8 K+, 8 Cl− 8 Arg, 2 Glu	4 K+, 14 Cl− 4 Lys, 4 Arg, 4 Asp	−7 Å	−8.5 Å	−270 mV
Hyperpolarized	6 K+, 10 Cl− 8 Arg, 2 Glu	6 K+, 12 Cl− 4 Lys, 4 Arg, 4 Asp	−7 Å	−7 Å	−130 mV
Nonpolarized	5 K+, 11 Cl− 8 Arg, 2 Glu	7 K+, 11 Cl− 4 Lys, 4 Arg, 4 Asp	−2.2 Å	−5.9 Å	−100 mV
Depolarized	4 K+, 12 Cl− 8 Arg, 2 Glu	8 K+, 10 Cl− 4 Lys, 4 Arg, 4 Asp	−2.5 Å	−3 Å	+75 mV

TABLE 3.

Bath charge concentrations of positive HTH motif position

Bath description	Outer bath	Inner bath	Peptide 1position	Peptide 2 position	Potential gradient
Strongly hyperpolarized	5 K+,11 Cl− 10 Arg, 2 Lys, 2 Glu	7 K+, 11 Cl− 2 Lys, 2 Arg, 4 Asp	+4.5 Å	+4.9 Å	−180 mV
Hyperpolarized	4 K+, 12 Cl− 10 Arg, 2 Lys, 2 Glu	8 K+, 10 Cl− 2 Lys, 2 Arg, 4 Asp	+5.1 Å	+5.9 Å	−75 mV
Nonpolarized	3 K+, 13 Cl− 10 Arg, 2 Lys, 2 Glu	9 K+, 9 Cl− 2 Lys, 2 Arg, 4 Asp	+5.8 Å	+6.2 Å	+1 mV
Depolarized	2 K+, 14 Cl− 10 Arg, 2 Lys, 2 Glu	10 K+, 8 Cl− 2 Lys, 2 Arg, 4 Asp	+7.5 Å	+7.5 Å	+100 mV

TABLE 2.

Bath charge concentrations of zero HTH motif position

Bath description	Outer bath	Inner bath	Peptide 1position	Peptide 2 position	Potential gradient
Strongly hyperpolarized	6 K+, 10 Cl− 10 Arg, 2 Glu	6 K+, 12 Cl− 4 Lys, 2 Arg, 4 Asp	+1 Å	−1.7 Å	−150 mV
Hyperpolarized	5 K+,11 Cl− 10 Arg, 2 Glu	7 K+, 11 Cl− 4 Lys, 2 Arg, 4 Asp	+1 Å	+1.8 Å	−70 mV
Nonpolarized	4 K+, 12 Cl− 10 Arg, 2 Glu	8 K+, 10 Cl− 4 Lys, 2 Arg, 4 Asp	+3.3 Å	+1 Å	+10 mV
Depolarized	3 K+, 13 Cl− 10 Arg, 2 Glu	9 K+, 9 Cl− 4 Lys, 2 Arg, 4 Asp	+3.5 Å	+2 Å	+63 mV

All the simulations for the three peptide z-positions were carried out using the program LAMMPS with the charmm27 force field (59,60). All molecular dynamics simulations ran for a total simulation time of 10 ns using a Nose–Hoover thermostat/barostat that held the simulations at a temperature and pressure near 300 K and 1 atm. The analysis for the all-atom calculations was predominately completed using MDAnalysis scripts, an analysis library developed by Michaud-Agrawal (http://code.google.com/p/mdanalysis/). The cutoff and angle values used to assess our H-bond patterns were based on Gromacs' default H-bond settings (r_HB = 0.35 nm and α_HB = 60′) (61). To calculate the swivel/kink analysis for the peptide, we used Swink, a program developed by Cordes et al. (62). The interaction energy calculations for some supplementary figures were made using code developed by Michaud-Agrawal in the LAMMPS program (63). Each energy component was calculated by selecting the two groups of atoms indicated within the figures and then computing the nonbonded electrostatic and van der Waals energy between the groups, neglecting the energy within each group (see Fig. S3 in Supplementary Material, Data S1).

RESULTS

The response of the highly charged HTH motif to a series of transmembrane electrical potentials was measured based on its conformational and environmental stability within a double bilayer system (Fig. 1, C–E).

Implicit simulations

The choice to use the continuum GBSW method was based on the necessity to locate some qualitative initial peptide starting configurations for our electrical potential simulations (Fig. 1, A and B). Although this implicit method has limitations that do not allow for water penetration of the bilayer or bilayer deformation, characteristics seen in explicit simulations, it provided three qualitative starting orientations for our atomistic simulations.

We wanted to locate transmembrane z-positions within an approximate relative free energy with respect of each other from a specific orientation. The HTH motif translated as a rigid body for each orientation along the reaction coordinate and provided a series of one-dimensional PMF profiles. The one-dimensional PMF profiles displayed the relative free energy values associated with specific orientations and z-positions in an implicit bilayer. Although this method does not account for bilayer deformation or water penetration, the advantage to using this method versus running an implicit bilayer adiabatic/point energy calculation is it allows for the motif to fluctuate and stabilize while being harmonically restrained to specific location and orientation with the bilayer. Furthermore, because we were searching for starting positions relative to one another for our all-atom simulations, this method provided qualitative starting positions.

Our implicit PMF data showed the most stable transmembrane orientations were around z-dimensions of −19.1 Å at an angle of 90°, −7.0 Å for an orientation of 60°, and −5.0 Å and 5.0 Å at an angle of 30° relative to the bilayer. As seen in Fig. 1 B, the relative free energy profiles for 90° resembles a profile that would be expected of an ion passing through a bilayer because all the charged residues (a net charge of +5) are located within the same xy-plane. This orientation was used primarily as confirmation that we would see the expected result in a PMF profile for such a highly charged peptide using this implicit method.

The 60°, 30°, and 0° profiles have a high relative free energy barrier within the z-dimension of 15 Å to 40 Å. For this region of the PMF, the charged residues close to the C-terminal end of the HTH motif moving into the hydrophobic core region of the bilayer and the hydrophobic residues moving into the bulk solvent region despite the gating charges being located in bulk solvent region. This high relative free barrier results from partitioning the charged aspartic acids, charged arginines, and charged lysines within the hydrophobic core of a bilayer. The Born radii in our method reflect the high energetic barrier for partitioning a charged aspartic acid in the core of the bilayer that is on the order of 20 kJ mol⁻¹ more than partitioning an arginine or lysine (3). Thus, the fact that the gating charges were positioned outside the bilayer configurations within this region an inappropriate choice for our all-atom simulations. The lower energy barriers between z-positions −20 Å to 15 Å results from the fact that only one or two of the arginines are positions within the hydrophobic core whereas the other two to three arginines position themselves near the interfacial regions of the bilayer or the bulk solvent region. Because the gating charges had a transmembrane location and some distinct minima and maxima were observed, the selection for possible all-atom voltage simulation candidates were better.

From the PMF profiles, we chose a set of three different starting z-position configurations for the all-atom calculations (−5.0 Å, 0 Å, and +5.0 Å) from the 30° orientation PMF profile because they displayed a defined maximum or minimum (Fig. 1 B). Furthermore, these positions were within a relative free energy difference of ±8 kcal/mol of each other and ±7 Å from each other along our z-position reaction coordinate. All of these criteria made these positions more attractive candidates for our all-atom simulations. By choosing positions within close proximity energetically and positionally, we could explore environmental changes at different z-positions when varying the transmembrane potential. We wanted to understand if observed environmental fluctuations from varying the voltage gradient would be specific to the location of the peptide within the bilayer.

All-atom simulations

Potential profiles

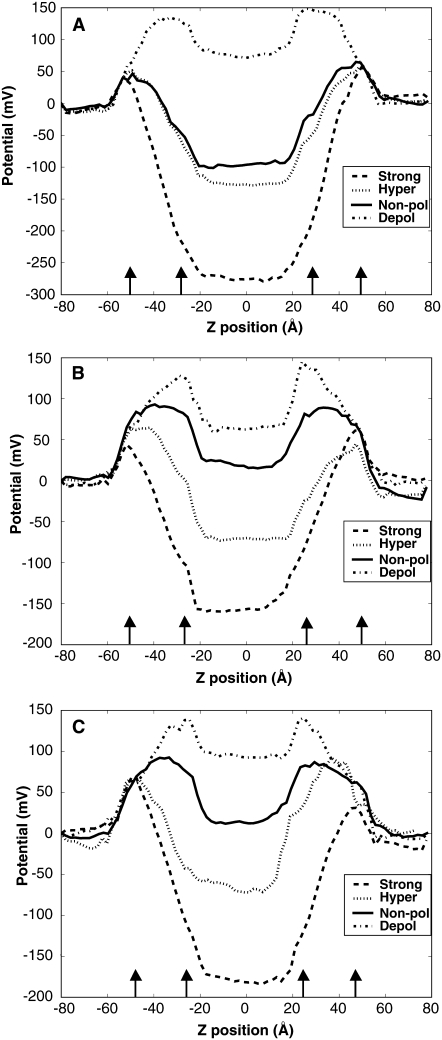
Our results show how varying the salt concentrations between the inner and outer bath establishes a voltage potential for each system thus creating a more realistic transmembrane potential. The electrostatic potential profiles from both the nonpolarized and electrified bilayer simulations are shown in Fig. 2. As seen in Tables 1–3, the voltage gradient for the systems varied ranging from drops of −270 mV to +100 mV. The shape of the profile in the electrified simulations differs from previous double bilayer simulations carried out by Sachs et al. (57) and Lee and Baker (64). This difference can be attributed to the heterogeneity of our system from placing peptides within the bilayers. The presence of the charges from the peptide changes the potential drop relative to a pure bilayer system—this is understood as a shift in the salt and water distribution to adjust to the presence of the peptide (Fig. 2 and Tables 1–3). It further reflects the changes on a molecular level that occur as the voltage changes and the peptide responds.

FIGURE 2.

Transmembrane potential profiles. The line style corresponds to the expected voltage gradient for each system: dot-dashed, strongly-hyperpolarized; dotted, hyperpolarized; solid, nonpolarized; dashed, depolarized. The arrows indicate the location of the average DOPC headgroup region. (A) The profile for HTH motif at the center of mass −5.0 Å from the nonpolarized and electrified simulations across the entire 160 Å system (B) The profile for HTH motif at the center of mass 0 Å from the nonpolarized and electrified simulations across the entire 160 Å system. (C) The profile for HTH motif at the center of mass 5.0 Å from the nonpolarized and electrified simulations across the entire 160 Å system.

The systems for the 0 Å and +5 Å starting z-positions show the initial types of potential profiles that might be expected to result based on the charge concentrations of the baths. They display a depolarized potential, a nonpolarized potential, and two different hyperpolarized potentials based on varying the salt concentrations between the inner and outer bath. However, the potential profiles for the −5 Å starting z-position systems show a different behavior. This difference in potential profile behavior can be attributed to the formation of salt-bridges necessary to stabilize the peptides at this particular z-location within the bilayers (see Figs. S4 and S5 in Data S1).

Peptide stability

The orientation of the peptides remained similar to the initial starting configuration 30° ± 2° for all systems (see Fig. S1 in Data S1). The small fluctuations in orientation are one indication that a highly charged peptide was able to remain stable. If larger fluctuations were observed in the angle the stability of the systems would be an important concern. On the timescale of 10 ns, the peptides adopt a minimal number of conformations that can be observed in parameters such as shifts in the center of mass and changes in helicity, swivel/kink angles, and hydrogen-bond patterns.

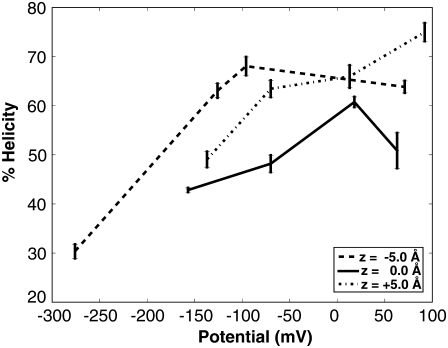
The peptide conformation remained stable in a bilayer environment over a time period of 10 ns as assessed by DSSP. The peptide maintains its overall helical nature for most of the nonpolarized systems and for the systems with a potential drop. The percentage helicity varied under different peptide positions and electrical potentials (Fig. 3). For the starting z-positions of −5.0 Å and 0 Å, the nonpolarized systems maintained a higher percent helical content than for polarized systems whereas the depolarized system had a higher helicity for the starting z-positions of +5.0 Å. Helical content differed between peptide positions due to occasional kinking around the central region of the S4 domain.

FIGURE 3.

The percent helical content as function of transmembrane potential. The line style corresponds to the initial starting position of the system (dotted, center of mass starting at −5.0 Å; solid, center of mass starting at 0 Å; dashed, center of mass starting at 5.0 Å). The error bars represent the standard deviation.

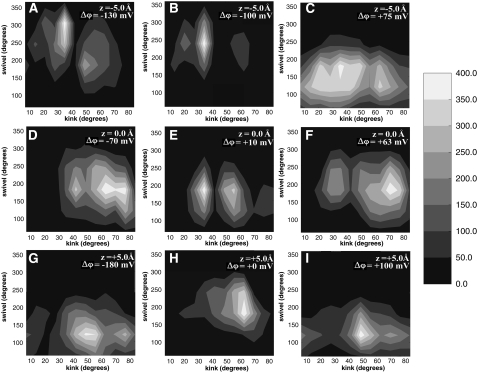
In some simulations, the S4 continuity of the helix is disrupted by the formation of a kink within the peptide. The hinge formation of the peptide was evaluated using Swink (62), which calculates two types of peptide rotations: a kink (magnitude θ) and a swivel (magnitude τ). The hinge was located between R133–K136 that is the approximate region where the S4 region bends as seen in x-ray structures (16,20). Fig. 4 shows that a kink and swivel is present for all peptide systems regardless of the presence of a potential and that for some systems the peptide swivel/kink conformation displays a two-state behavior. However, the degree of these rotations varies as a function of the voltage gradient.

FIGURE 4.

Selected swivel versus kink contour plots of the HTH motif. (A) HTH motif with a center of mass at −5.0 Å with negative applied electrical potential. (B) The peptide with a center of mass at −5.0 Å and nonpolarized potential. (C) HTH motif with a center of mass at −5.0 Å with positive applied electrical potential. (D) HTH motif with a center of mass at 0 Å with negative applied electrical potential. (E) The peptide with a center of mass at 0 Å and nonpolarized potential. (F) HTH motif with a center of mass at 0 Å with positive applied electrical potential. (G) HTH motif with a center of mass at 5.0 Å with negative applied electrical potential. (H) The peptide with a center of mass at 5.0 Å and nonpolarized potential. (I) HTH motif with its center of mass at 5.0 Å and a positive electrical potential.

In particular, our results show a trend in the nature of the swivel/kink conformation as a function of voltage gradient (Fig. 4). When no transmembrane potential is present, the swivel and kink angles have defined values and thus the peptide conformation is more rigid. However, when a transmembrane potential is applied then the peptide can be more flexible.

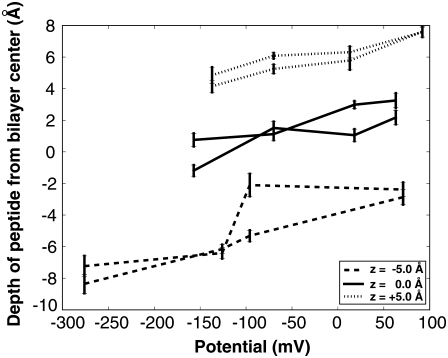
Fig. 5 shows a trend that for the nonpolarized potential system (systems within 0 ± 10 mV), the center of mass remained close to the starting position, ±1.0 Å, except for the system with the starting position of −5 Å. The reason for this nonpolarized system deviating from its starting position of −5 Å is due to salt-bridging stabilizing the peptide as explained in the potential profile section above. The position of the center of mass of the peptide shifts under differing electrical potentials (Fig. 5 and Tables 1–3). A slight trend was present in that for hyperpolarized potential systems the depth of the center of mass of the peptides decreases. As the voltage gradient increases the depth of the center of mass of the peptides increases.

FIGURE 5.

The electrical potential versus z-position for average center of mass of the peptide. The line style corresponds to the initial starting position of the system (dotted, center of mass starting at 5.0 Å; solid, center of mass starting at 0 Å; dashed, center of mass starting at −5.0 Å). The error bars show the standard deviation.

Bilayer deformation

Our double bilayer simulation results exhibit both bilayer thinning and water penetration within the bilayer (Fig. 1, C–E). The nonpolarized, hyperpolarized, strongly-hyperpolarized, and depolarized systems all exhibited these solvation characteristics due to the presence of the charged peptide in the bilayer. However, the extent of bilayer thinning and water penetration for each system was influenced by strength of the voltage gradient.

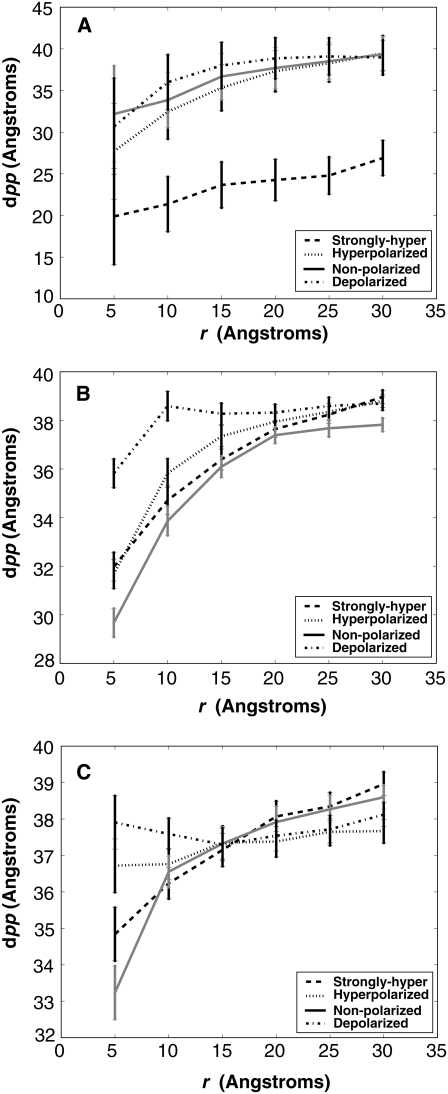
Although no unifying trend between the types of voltage potentials was present, one can see the extent of bilayer thinning was dependent on the position of the peptide within the bilayer as a result of the potential (Fig. 6). Our results show a deformation of the bilayer for both the nonpolarized and three electrified systems. The bilayer thickness was measured as the average distance between upper and lower phosphate atoms (d_PP) versus the distance of the atoms in the xy plane from the center of mass of the corresponding protein (r) over the last 10 ns of each simulation (Fig. 6). The d_PP vs. r curves are given for four different electrical potentials for each z-position. A distinctive difference in bilayer thinning was seen for the salt-bridging system at a starting z-position of −5.0 Å and can be attributed to the unique peptide hydrogen-bonding pattern. Although no trend between voltage gradient values was present, based on our simulation timescale, we can see that the bilayer thickness is affected by both peptide position and voltage potential.

FIGURE 6.

The local bilayer thickness measured as the average distance between upper and lower phosphate atoms (d_PP) versus the distance of the atoms in the xy plane from the center of mass of the corresponding protein (r). The different curves are representative of d_PP vs. r curves at different voltage potentials and the error bars represent the standard deviation. (A) Phosphate curves for the peptide at the negative center of mass position. (B) Phosphate curves for the peptide at the zero center of mass position. (C) Phosphate curves for the peptide at the positive center of mass position.

Hydrogen-bonding patterns and water penetration

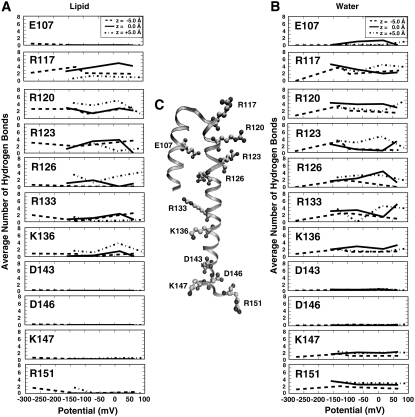
The thinning of the bilayer is due to the necessity to stabilize a highly charged peptide by forming hydrogen bonds with lipid headgroups and water molecules (Fig. 7). The side chains form hydrogen bonds with the lipid and water molecules occupying the region where charged side chains are located (Fig. 7 and see Fig. S2 in Data S1). Our results showed the strength of the voltage drop across the bilayer affected the overall number of lipid headgroups or water molecules hydrogen-bonding with the charged residues (Fig. 7).

FIGURE 7.

Hydrogen bonds formed by the HTH motif. (A) The average number of lipid hydrogen bonds for each charged residues and z-position as a function of the system electrical potential. (B) The distributions show average number of water hydrogen bonds for each charged residues and z-position as a function of the system electrical potential. (C) The S3b and S4 helices (represented as a ribbon) from the start of simulation. The charged residues are depicted in stick format, with cationic and anionic side chains. (The distribution of the number of hydrogen bonds is shown in Fig. S2 in Data S1.)

Negatively charged residues rarely formed hydrogen bonds with the DOPC bilayer (Fig. 7 A) whereas for a positively charged residue, we show an average lipid hydrogen-bond configuration that was 3 ± 2 DOPC for each system (Fig. 7 A and see Fig.S2 in Data S1). The residues with the greatest number of lipid hydrogen bonds were residues predominantly located within the bilayer and containing a positive charge. A unique hydrogen-bonding pattern was seen for the strongly-hyperpolarized system at a starting z-position of −5.0 Å. We believe this difference is attributed to instability of the charged arginines created by the change in salt concentration. The arginines formed more hydrogen bonds with the lipids closest in proximity to the turn region of the peptide (the upper bilayer leaflet) to compensate for the arginine depth and orientation within the bilayer. This change in number of hydrogen bonds in turn caused a large bilayer deformation.

The peptide was also stabilized due to hydrogen bonding with water present within the bilayer (Fig. 7 and see Fig. S2 in Data S1). Fig. 1, C–E illustrates how water penetration of the bilayer occupied regions near charged residues thus forming hydrogen bonds (see Fig. S2 in Data S1). Positively charged residues had between two to five waters hydrogen bonding. Negatively charged residues had one to two waters hydrogen bonding. The number of hydrogen bonds varies for the charged residues located within the bilayer when the electrical potential varies. The number of waters hydrogen bonding located outside the bilayer residues remained the same regardless of the potential.

An interesting trend from the hydrogen-bonding pattern data was seen. The transmembrane charged residues exhibited a reciprocal water-lipid hydrogen-bonding pattern (Fig. 7 and see Fig. S2 in Data S1). For example, if the number of lipid hydrogen bonds for a residue increases the number of water hydrogen bonds to that residue decreases. The total number of hydrogen bonds per charged transmembrane residue remained constant regardless of the transmembrane potential or the type of hydrogen bond. On average a negatively charged residue had one to two hydrogen bonds whereas a positively charged residue formed five to eight hydrogen bonds. However, under varying membrane potentials, the patterns showed compensation or shifts between the number of water hydrogen-bonds with the number of lipid hydrogen-bonds formed with a particular transmembrane residue.

DISCUSSION

Previous membrane bound protein and peptide simulations have examined numerous effects of solvent and lipid dependence (6,9–12,29,30,34). Current research has begun to focus on the charged nature of the residues for these proteins and peptides (1–4,9,11,34). The results of this work show how the fluctuations of the highly charged HTH motif respond to a series of transmembrane electrical potentials based on its conformational and environmental stability within a double bilayer system (Fig. 1 C). The observed differences include shifts in center of mass and hydrogen-bonding patterns and changes in helicity and swivel/kink angles.

Potential profiles

Previous transmembrane voltage gradient simulations have created a voltage drop across a single bilayer containing a protein through the use of an implicit applied potential (58). We chose to apply the voltage gradient method used by Sachs et al. (57) and Lee et al. (64) that established a voltage drop across a pure bilayer. The advantage of this type of double bilayer system is that we maintain two independent bath charge concentrations. The creation of two independent baths allows us to use an explicit variation of salt concentrations between the inner and outer bath to mimic a natural biological voltage gradient.

Our simulations show the role salt concentration plays in establishing an electric field when a highly charged peptide is located within the bilayer (Fig. 2). As the salt concentration between the baths differ, the voltage gradient across the bilayer varies thus creating differing forms for the transmembrane potential. Our results illustrate how the effects of adding a highly charged peptide to the bilayer creates a different profile shape than that of a pure bilayer profile (57,58).

A range of potential profiles was created for all three starting z-positions. The result from the 0 Å and +5 Å starting z-positions produced expected results of a standard nonpolarized potential and three different polarized potentials. However, the potential profiles for the −5 Å starting z-position system exhibits behavior different from what was expected based on the charge concentrations of the inner and outer bath. This difference is especially seen in the system containing equal charge concentrations between the inner and outer bath in that a potential drop occurred across the bilayers.

This change in the shape of the −5 Å, peptide profile was due to the salt effects and the concentrated nature of peptide to lipid ratio in our small systems. As the simulations were not constrained, the systems could allow for intrapeptide salt bridging to occur between residue E107 and R126 (Fig. 2 and see Figs. S4 and S5 in Data S1). The nature of salt-bridging was evaluated based on direct N-H → O hydrogen cutoff distance of 4 Å between Glu and Arg (see Fig. S5 in Data S1) and an interaction energy between these residues less than −20 kcal/mol (see Fig. S4 in Data S1). We speculate that the reason for salt-bridging for this system is due to the difficulty for enough water to penetrate the bilayer to fully stabilize all the arginines on this time scale. The formation of salt-bridging in this system changed the effects of the salt concentrations within the baths and thus affected the shape of the transmembrane potential.

Because the profiles exhibited changes in the voltage gradient, we wanted to determine if differences between the systems exhibited different energetic contributions when the transmembrane potential changes. The energetic contributions of different voltage potentials (see Fig. S3 in Data S1) did not show differences in the average interaction energies of the protein with the various molecular groups in its environment. As no dramatic change in interaction energy was seen between the varying potential for each z-position this illustrates the large degree of compensation that can occur in these systems.

Peptide stability and conformation

We suggest transmembrane voltage gradients across a bilayer cause a peptide to adopt a minimal number of conformations and affect the peptide flexibility (Figs. 3–5). The most significant aspects of peptide stability associated with changes in the electrical potential of our systems were the percent helicity (Fig. 3), the swivel/kink degrees of freedom of the peptide (Fig. 4) and the depth of the center of mass of the peptide (Fig. 5).

The swivel and kink figure shows that under nonpolar potential conditions the peptide conformation is more rigid whereas under applied potential conditions the peptide is more flexible. The position of our swivel/kink value is close to the hinge region (R133-K136) where the S4 region bends as seen in x-ray structures (16,20). These swivel/kink results may also account for why experimental results observe a kinking and “screw-like” motion for this peptide under certain environmental conditions (14). Moreover, our conformational analysis for the S3b-S4 motif suggest, similar to the concept suggested by Sands and Sansom (9), that under different environmental conditions this region can exhibit a degree of flexibility.

The peptide conformation was also influenced by how the solvent environment responded to these changes in salt concentration (Figs. 2, 6, and 7). The voltage gradient changes the salt concentrations for the baths and as a result the charged side chains compensate by interacting differently with a membrane environment. These environmental compensations include bilayer deformation (Fig. 6) and changes in hydrogen bonding patterns (Fig. 7) as a result of the charged nature of the peptide.

Bilayer deformation

Our data suggest that when a transmembrane electrical potential is applied the lipid environment stabilizes a highly charged peptide differently depending on the peptide's location within the bilayer (Figs. 6 and 7 A). We show charged residues coordinating differently with lipids depending on their positions within the bilayer and the strength of the applied potential (Fig. 7 A). Lipids coordinate with the peptide differently depending largely on peptide position within the bilayer (Fig. 7 A). The residues responsible for gating motion (R117, R120, R123, R126) exhibit different hydrogen-bonding patterns that lead to a correlation between the applied voltage potential and the effects of the lipid on the peptide.

Previous simulations have shown results comparable to ours in that bilayer thinning is necessary to stabilize a charged side chain within the bilayer (1–4,6,9,34). Furthermore, Dorairaj and Allen (1) and MacCallum et al. (3) suggest that there is a considerable energetic barrier for inserting a single arginine into the hydrophobic core of a bilayer. Hence, it is important to understand how this change in energy and bilayer fluidity may be associated when applying a transmembrane potential.

We believe that under varying voltage gradients the thickness of a bilayer will change based on both transmembrane potential and the location of charged side chains. Our data show a bilayer deformation of ∼10 Å at the center of the bilayer for our systems where no voltage drop is present (Fig. 6). However, the data show the presence of an applied transmembrane potential affects the magnitude of bilayer thinning differently depending on the position of the peptide within the bilayer. This result shows why it is increasingly important to examine systems under varying electrical potential conditions to determine if lipids coordinate differently with charged side chains.

Another important point of interest relates to how these lipid headgroups interact and coordinate with a charged side chain within a bilayer. Two recent studies have quantified how many lipids coordinate with a side chain in relation to the depth of the side chain within the bilayer (2,9). Li et al. (2) characterized the number of lipids coordinating a single charged arginine on a transmembrane peptide as a function of arginine position from the center of the bilayer. They showed that at the center of the bilayer one lipid was associated with the arginine and at the interface one to two lipids were associated with the arginine. Sands and Sansome (9) also carried out a study modeling the charged voltage sensor domain (S1-S4) of the KvAP channel showing the distance between monolayers of the bilayer varies as a function of lipid compositions. Sands and Sansome (9) also show that one to three lipids may be associated with the interfacial arginines in a PC environment and one to four lipids associated with interfacial arginines in a PC/PG environment. These results suggest the number of lipids coordinating with charged side chains may depend on the environment. The question then becomes does the deformation for these bilayers change under varying transmembrane potentials? Our data suggest there might be a difference in lipid-hydrogen-bonding when varying the transmembrane potential.

Water penetration

Our results show water penetration plays a role in the stability of our peptides within the bilayers when varying the depth of the peptide and voltage gradient. The depth of the peptide causes differences in the amount of water penetration when a similar voltage potential is applied. Fig. 1, C–E, illustrates this variation of water penetration as the peptide z-position changes with a similar voltage gradient of −150 mV ± 30 mV. Furthermore, because the amount of water penetration differs between the systems, the hydrogen-bonding pattern of the waters with the buried charged residues also changes.

We show that a combination of the strength of the electrical potential and peptide location within the bilayer affect the number of waters hydrogen bonding with the side chains. In Fig. 7, the residues not assumed to be responsible for channel gating motion have similar hydrogen-bonding patterns independent of the transmembrane potential. Similar to lipid hydrogen-bond patterns, the residues responsible for gating motion and occasionally E107 in the case of the 0 Å starting position exhibit different hydrogen-bonding patterns—clearly showing a relationship between transmembrane potential and the effects of water on the peptide (Fig. 7 B).

Numerous simulations have shown that when charged side chains are located or buried within the hydrophobic region of the bilayer, water penetrates the hydrophobic core to maintain the hydration of these charges (1–4,9,34). Li et al. (2) calculated the number of water molecules that coordinate a single charged arginine attached to an otherwise hydrophobic transmembrane peptide. Approximately four water molecules were associated with the arginine at the center of a lipid core environment and five to seven waters would associate with the arginine in the bulk solvent environment. Sands and Sansom (9) showed one to seven waters may be associated with the charged residues of the S4 domain in a DOPC environment. The distribution of the number of hydrogen bonds formed per residue varied depending on the residue location within a bilayer and lipid environment. Our results are comparable to that seen in previous research when using standard hydrogen bond cutoff and orientation values (r_HB = 0.35 nm and α_HB = 60′) (61). In Fig. 7, we observed an average of five to seven waters hydrogen bonding with positively charged residues and an average of one to two waters hydrogen bonding with negatively charged residues.

Extensions/limitations

Currently, it is computationally difficult to simulate a global potential similar to that observed in the Hodgkin and Huxley (42) voltage clamp experiments on a detailed atomistic level. Two current methods, the constant field assumption and the double bilayer method, both provide some connections to the effect of voltage on molecular systems. However, it is important to note that both methods make assumptions. The constant field method assumes the time and space averaging of the macroscopic voltage holds immediately on the microscopic level. In other words, a time and space averaged profile is assumed to hold throughout all time and space of a simulation cell. In contrast, the double bilayer method assumes that a microscopic level of voltage change can be used to illustrate the changes across an ensemble set of bilayer patches. With enough simulation time the microscopic double bilayer system could be enlarged to include more membrane, water, and salt and the effects of different initial distributions and the temporal response of the system more fully understood. Thus although the double bilayer does make assumptions on simulation time and length scales, the ability to view fluctuations of salt, water and peptide and to determine local charge interactions within separate baths makes the double bilayer method an attractive approach for studying specific interactions of membrane proteins.

Implications for gating

Based on our results, we speculate on the principles behind the effects of voltage on the S4 domain for the entire voltage sensor or channel function. Previous studies have emphasized the importance of protein/lipid interactions (6,9–12,29,30,34) in the absence of a voltage gradient whereas in this study we emphasize the importance of changes in peptide behavior under a varying voltage gradient. We suggest that the helix-turn-helix segment can “sense” a change in transmembrane potential because the results show consistent changes in fluctuations of parameters such as helicity, peptide rigidity, peptide center of mass, and hydrogen bonding partners with voltage. This concept would be consistent with the K-channel structures and mutagenesis work (7,14,16,20,22,23,27,41). The results also suggest that, the presence of a change in voltage would shift the energy balance of hydrogen bonding partners between the arginine residues and their local environment. As the voltage shifts, the frequency of hydrogen bonding to water or to lipid headgroups may also change (Fig. 7) and the free energy required for this change will vary depending on the HTH depth and orientation (Tables 1–3). We speculate with the full channel “pre-paying” for the orientation and depth of the HTH motif, the free energy necessary to change a particular orientation and depth of the HTH motif with a voltage gradient will be even smaller than what is calculated here. This is similar to the effects in drug binding between a floppy compound in solution and one with a restricted conformation in solution. In principle, the full set of relative free energies could be calculated. Although the hydrogen-bonding pattern itself may differ when including the full channel the overall principle behind these free energy changes should be similar to what is seen for the domain motion in this study.

CONCLUSION

Although more work will be required to understand the motion of charged membrane proteins as a function of transmembrane potential, our results provide a beginning for associating free energy values with specific positions of a charged motif within the bilayer under varying transmembrane potential conditions. We have shown how under varying voltage gradients several environmental components such as bilayer deformation, hydrogen-bonding interactions, and water penetration contribute to the stability of highly charged membrane proteins. These environmental components highlight the importance of using the explicit solvent to simulate membrane proteins and understand how membrane proteins adjust to transmembrane potentials. The study also serves to motivate further research for charged residues within an implicit bilayer and double bilayer transmembrane potential simulations.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.