Taxol Allosterically Alters the Dynamics of the Tubulin Dimer and Increases the Flexibility of Microtubules

Abstract

Taxol is a commonly used antitumor agent that hyperstabilizes microtubules and prevents cell division. The interaction of Taxol with tubulin and the microtubule has been studied through a wide array of experimental techniques; however, the exact molecular mechanism by which Taxol stabilizes microtubules has remained elusive. In this study, through the use of large-scale molecular simulations, we show that Taxol affects the interactions between the M and H1-S2 loops of adjacent tubulin dimers leading to more stable interprotofilament interactions. More importantly, we demonstrate that Taxol binding leads to a significant increase in the dynamics and flexibility of the portion of β-tubulin that surrounds the bound nucleotide and makes contact with the α-monomer of the next dimer in the protofilament. We conclude that this increase in flexibility allows the microtubule to counteract the conformational changes induced by nucleotide hydrolysis and keeps the protofilaments in a straight conformation, resulting in a stable microtubule.

INTRODUCTION

Microtubules are essential players in the function of eukaryotic cells. Together with actin filaments and intermediate filaments, they comprise the cytoskeleton, and this group of polymers is collectively responsible for providing most of the structure and spatial organization in the cell. Microtubules are hollow, cylindrical polymers formed from the self-association of α-β-tubulin heterodimers into linear protofilaments, with 13 of these protofilaments joining together laterally to form the closed tube. Apart from providing structure, microtubules also play critically important roles in transport, migration, and mitosis. Many of these functions require that microtubules dynamically assemble and disassemble, and this requirement is paramount during mitosis where microtubules segregate and separate the chromosomes. Compounds that alter the assembly or disassembly of microtubules can be used to interfere with mitosis and thereby control the fate of the dividing cell. Taxol is one such drug, and it is commonly used as an antitumor agent in a number of human cancers since it hyperstabilizes microtubules and halts entry into anaphase. Taxol binds stoichiometrically to the β-subunit of the tubulin dimer and results in microtubules that are stable against depolymerization induced by Ca²⁺, cold, and dilution (1).

Tubulin exists as a stable heterodimer of α- and β-tubulin. These two forms of tubulin have ∼40% sequence homology and their tertiary structures are highly similar (see Fig. 1). Each monomer of tubulin binds GTP and hydrolysis of the nucleotide in β-tubulin is thought to be linked to dynamic instability, an intrinsic property of microtubules where periods of slow microtubule growth are stochastically interrupted by rapid disassembly (2). The protofilaments in disassembling microtubules have been observed to curl away from the microtubule (3), suggesting that the loss of lateral contacts between the tubulin dimers results in instability. Models of the microtubule based on cryo-EM work find several points of interaction between adjacent tubulin dimers, the central elements being the M-loop and H1-S2 loop (4) (see Fig. 1). The cryo-EM structure of tubulin also clearly shows that Taxol binds behind the M-loop in the β-monomer (5,6). Based on this position within the microtubule lattice, it has been postulated that Taxol helps facilitate interactions between the M-loop of one β-monomer with the H1-S2 loop of the β-monomer in the adjacent protofilament (4). This increase in lateral interactions would logically result in an increase in the overall stability of the microtubule and hence explain the observed phenotype; however, some observations do not support this hypothesis of Taxol function. As discussed by Amos and Löwe, the ability of Taxol to stabilize open, Zn-induced tubulin sheets suggests some other mechanism may be at work (7). The protofilaments in a Zn-sheet are arranged in an alternating, antiparallel fashion, and this orientation eliminates the M/H1-S2 loop interactions that exist within the microtubule. Further support comes from the recent observation that Taxol can straighten individual protofilaments, suggesting that there must be intrinsic changes within the dimer or within the dimer-dimer interface of an individual protofilament (8). Here we present molecular details on the interaction between Taxol and the microtubule, and demonstrate the effects that Taxol binding has on the dynamics of the tubulin dimer and the microtubule as a whole.

FIGURE 1.

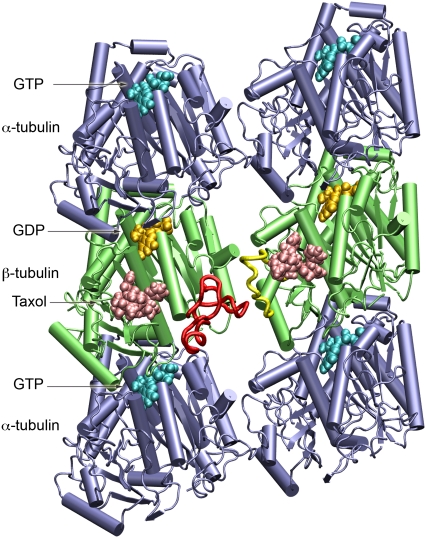
The protein system used in the molecular dynamics simulations. The microtubule fragment consists of two tubulin α/β heterodimers and two additional α-monomers to minimize potential end effects. GTP and GDP are shown in cyan and gold, respectively; Taxol is colored salmon; β-tubulin is green; and α-tubulin is blue. The β-monomer on the right is the main protein studied since it has Taxol at the interprotofilament site. The M-loop for this monomer is colored yellow and the interacting H1-S2 loop of the adjacent monomer is colored red. Note that this perspective corresponds to the view from inside the microtubule. This figure and all molecular graphics were produced using VMD (42).

MATERIALS AND METHODS

Preparation of the microtubule structure

Four bovine tubulin heterodimers (PDB id: 1JFF) docked into two adjacent protofilaments of a 13-protofilament, 3-start helix microtubule model (9) were used as a starting point. In the electron crystallographic structure of wild-type bovine tubulin (PDB id: 1JFF), the N-terminal H1-S2 loop of the α-subunit (Gln³⁵ to Lys⁶⁰), and the C-termini of both the α-subunit (Val⁴⁴⁰ to Tyr⁴⁵¹) and the β-subunit (Ala⁴²⁸ to Ala⁴⁴⁵), were not resolved (5). As the α- and β-subunits share high structural identity (6), the structure of β-tubulin was used as a template for homology modeling of the α-tubulin H1-S2 loop. The missing C-termini were not rebuilt since they were distal to the Taxol binding site, and their inclusion would have required increasing the water in the simulation box by ∼50%, making long timescale simulations even more prohibitive. Furthermore, subtilisin-treated tubulin, where the C-termini are cleaved, polymerizes and binds Taxol normally. The side chains of the H1-S2 loop of α-tubulin were modeled based on their sequences in PDB id: 1JFF, using WHAT-IF (10). Subsequently, the entire system was minimized using the OPLSAA force field in Tinker (http://dasher.wustl.edu/ponder; (11)) to correct for the bonds, angles, and torsions, where the missing loop was remodeled. The rebuilt tubulin dimer was has already been used in a series of molecular modeling studies (12,13) and has always appeared to be stable. In particular, the rebuilt H1-S2 loop in α-tubulin has performed well in drug-docking studies, suggesting that the molecular details are very reasonable (13,14).

Parameterization of Taxol

The molecular geometry of the T-Taxol structure from the PDB id: 1JFF was optimized with ab initio Hartree Fock calculations at the 6-31G* level using Gaussian 98 (15). The Merz-Singh-Kollman CHELPG style atom-centered point charges that best reproduce the electrostatic potential of the molecule were derived with the 6-31G* basis set using Gaussian 98 software (15). The bond-stretching, angle-bending, torsional, and Lennard-Jones force-field parameters for Taxol were either applied directly or adapted ensuring correct atom hybridization from the CHARMM22 force-field parameters for proteins and the CHARMM27 force-field parameters for lipids and nucleic acids (16–18). Energy minimization of the Taxol molecule in a box of TIP3P water was performed with the derived Coulombic charges and CHARMM27 force field using the molecular dynamics program NAMD 2.5 (19). The bond and angle parameters of the energy-minimized Taxol molecule computed at the molecular mechanics level using the CHARMM27 force-field libraries compared quite well with the corresponding parameters of the optimized structure computed using Hartree Fock calculations with the 6-31G* basis set.

Molecular dynamics simulations

To limit the computational work required to simulate our system while still capturing the essential parts of the microtubule, we removed the terminal β-subunits leaving a system of six tubulin monomers as shown in Fig. 1. The N-sites on the α-monomers were given GTP while the E-sites on β-tubulin were set to GDP, both with associated Mg²⁺ ions. The isolated α-tubulin subunit in each protofilament was included to account for any conformational changes that may occur in the β-tubulin subunit at the interdimer interface. The apo system consisted of 2610 amino-acid residues, three GTP molecules, three GDP molecules, four Mg²⁺ ions, 106 Na⁺ ions to neutralize the protein, and a 12 Å water shell surrounding the protein on each side, with a total of ∼180,000 atoms. In the holo system, in addition, two molecules of Taxol in the T-Taxol binding mode were included at the β-tubulin binding site in the two dimers. Using the parallelized MD program NAMD 2.5, simulations of the apo and holo systems were performed on BlueGene/L supercomputing resources in the user-friendly phase, using the NPT ensemble with CHARMM27 force field and TIP3P model for water. Interactions were evaluated based on a multiple-time stepping algorithm where bonded interactions (using the SHAKE algorithm) were computed every 2 fs, short-range nonbonded electrostatic and van der Waals interactions (10 Å cutoff with a smooth switching function beginning at 8.5 Å, and pair-list distance of 11.5 Å) every 2 fs, and long-range electrostatic interactions every 4 fs. Particle-mesh Ewald method was used to compute long-range electrostatics without cutoff with grid points at least 1/Å in all directions. Isothermal-adiabatic (NPT) simulations were performed at 1 atm using a Nosé-Hoover Langevin piston with a decay period of 200 fs and a damping timescale of 100 fs (for heating and equilibration phases) and 500 fs (for production phase), coupled with temperature control involving Langevin dynamics. The steps of the MD simulations included:

• Energy minimization until the gradient tolerance was <0.1 kJ/mol.

• Heating with Cα restrained to 300 K at intervals of 50 K.

• Equilibration with Cα restrained for 200 ps.

• Equilibration with no restraints for 1.6 ns followed by 29.5 ns of production run (of which the first 4.5 ns was the time required for the potential energy to stabilize, and is not included in the analysis).

• Structures were extracted every 25 ps from the 25 ns trajectory for subsequent analysis.

Bootstrap root mean-square fluctuations (RMSF) analysis

We applied bootstrap analysis to provide a statistical measure for any differences in the RMSF measurements between the apo- and Taxol-bound simulations. We first determined the number of independent points in our MD trajectories by looking at the autocorrelation of root mean-square deviations of the structures. From this analysis we found a correlation time of ∼1 ns, indicating that we have 25 independent structures in each of our 25 ns trajectories. To calculate the RMSF we therefore selected 25 random points, with replacement, from the trajectory and repeated this 200 times, giving us a mean RMSF value and a standard error of the mean for each amino acid in the protein. Using these values we applied a student's t-test to the data and identified contiguous regions of four or more amino acids that showed significant differences at a significance level of p < 0.005.

RESULTS

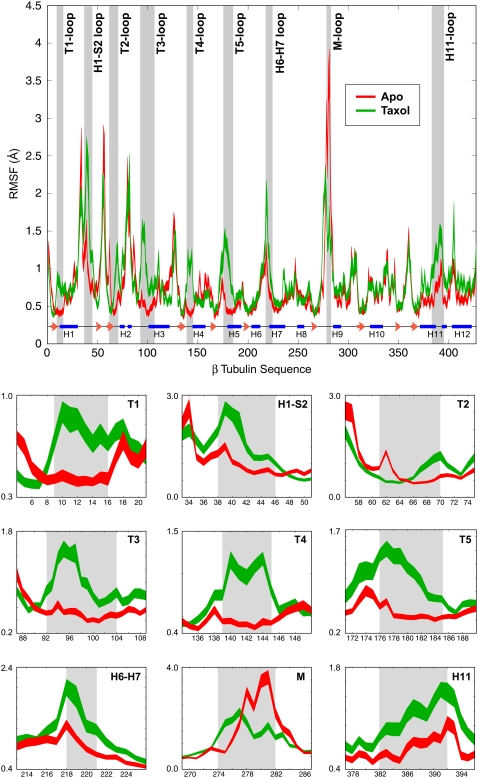
To assess the molecular mechanism of Taxol function, we performed two large-scale molecular dynamics simulations using a fragment of a microtubule in both the presence and absence of Taxol (see Fig. 1). There have been simulations of tubulin monomers and dimers in past studies (12–14,20), but to our knowledge these represent the first molecular simulations of tubulin within the microtubule lattice. By having two simulations we have a convenient control since we can directly relate the dynamics of the apo microtubule to the identical protein system with bound Taxol. Comparing such large molecular simulations is nontrivial since there are numerous degrees of freedom in the system. We have found that RMSF is one of the best methods of comparing dynamics and we use this measure throughout. This calculation finds the degree of movement of each C_α around its average position—i.e., parts of the protein that highly flexible will have a large RMSF value while portions that are constrained will result in a low RMSF (see Methods for more details). Taxol binds to the β-monomer at the interface between neighboring protofilaments (Fig. 1). As expected, we found that the β-monomers exhibited the largest change in dynamics, and we primarily studied the β-monomer with the Taxol at the interprotofilament site because it should most closely mimic the situation within the intact microtubule. Fig. 2 shows the RMSF plot for both the apo- and Taxol-bound forms of this β-monomer. The width of the line for each plot is the standard error of the mean determined from performing bootstrap analysis on each molecular dynamics trajectory. The regions that show a significant difference in dynamics, as determined by a student's t-test, are highlighted with gray bars and shown in detailed plots at the bottom of the figure. Overall we find nine individual regions that show a significant change when Taxol binds. Interestingly, these regions include portions of the protein that make direct contact with the bound drug as well as more distal portions of the protein.

FIGURE 2.

Root mean-square fluctuations for apo- and Taxol-bound β-tubulin. The RMSF plots for the apo- and Taxol-bound structures show very similar behavior over much of the protein; however, nine regions exhibited a statistically significant difference in dynamics when Taxol was bound. These areas are highlighted by the gray bars and are shown in more detailed plots at the bottom of the figure. The apo simulation is shown in red, the Taxol-bound simulation is in green, and the secondary structure of β-tubulin is illustrated at the bottom of the full RMSF plot.

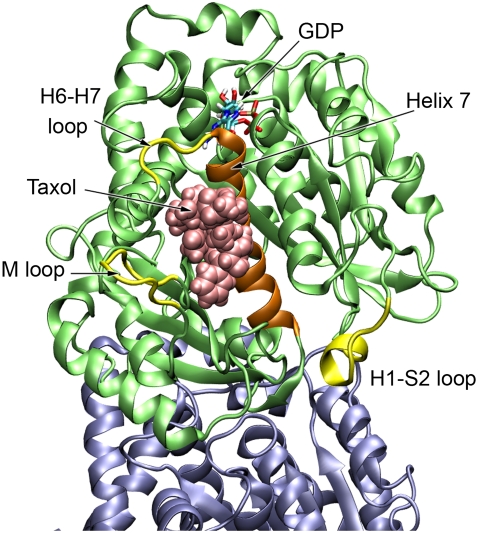
The regions of the protein that are close to the bound Taxol and show a change in dynamics include portions of the M-loop (residues 274–282), the H6-H7 loop (residues 218–221), and the H1-S2 loop (residues 38–46) that are at the opposite end of helix H7 (Fig. 3). From the RMSF measurements we see that the M-loop becomes less dynamic when Taxol is bound, due in large part to the drug sterically blocking the loop from exploring its full range of motion. Conversely, the H6-H7 loop and H1-S2 loop both exhibit an increase in dynamics. The increased movement of the H6-H7 loop is concomitant with a partial melting of the N-terminal portion of H7 (data not shown). This feature may be responsible for propagating changes induced by Taxol binding to other portions of the tubulin dimer, such as those discussed next.

FIGURE 3.

The regions in close proximity to the Taxol site that show significant change in dynamics. The M-loop becomes less dynamic since Taxol sterically blocks much of its motion, but both the H6-H7 loop and the H1-S2 loop show an increase in dynamics when Taxol binds. Helix H7 or the core helix is shown in orange.

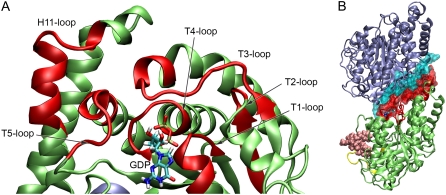
In addition to effects close to the Taxol binding site, Taxol also gives rise to long-range allosteric changes in the β-monomer. Six other regions of β-tubulin show a marked increase in dynamics upon Taxol binding—the T1–T5 loops and a portion of H11 (Fig. 4 A). All of these loops cluster around the exchangeable nucleotide site (E-site) and make contact with the bound GTP or GDP. These loops not only comprise the nucleotide binding site, but also constitute the binding interface with the next α-monomer along the protofilament (Fig. 4 B). The increased flexibility we observe in these loops has significant implications for the overall conformation and mechanics of the protofilament and the microtubule, and this point is further explored in the Discussion.

FIGURE 4.

Depiction of the regions distal to the Taxol binding site that show changes in dynamics when Taxol binds. (A) Colored in red are the T1–T5 loops as well as a portion of H11 that show a significant increase in dynamics when Taxol binds. These loops make up the nucleotide binding site in β-tubulin. (B) These same loops also form the binding interface for α-tubulin of the next dimer along the protofilament. The molecular surface corresponding to the T1–T5 and H11 loops are shown in red and the contact surface in α-tubulin is shown in cyan.

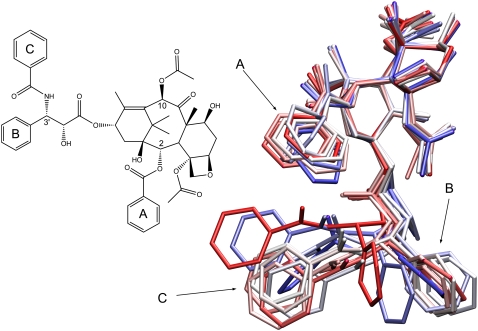
Finally we examined the dynamics of Taxol itself since there is significant ongoing effort to design and characterize novel taxane, paclitaxel, and epothilone analogs. Taxol was present in the refined structure of tubulin although several of the phenyl side chains were poorly resolved and had low electron densities (5). To assess the in situ dynamics of Taxol, we examined 25 structures at 1 ns intervals from our simulation. As is observed in Fig. 5, the core portion of the taxane ring remains quite rigid and displays relatively little movement, and most of the side groups appear to be well coordinated by the residues surrounding the Taxol binding site. The three phenyl rings show a fair degree of mobility and explore a relatively wide range of conformations, in good agreement with the structural results (5).

FIGURE 5.

Illustration of the dynamics of Taxol while bound to β-tubulin. This is an overlay of 25 structures taken at 1 ns intervals from the MD trajectory. The central taxane ring shows a small range of motion but the three phenyl groups exhibit a much higher degree of flexibility.

DISCUSSION

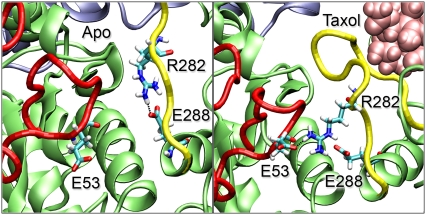
The primary function of Taxol has long been thought to be its ability to increase the strength and/or duration of lateral interactions between protofilaments (4,9). The atomic structure of tubulin revealed that the Taxol binding site was behind the M-loop, and structural models of the microtubule lattice predicted interactions between the M-loop of one β-monomer with the H1-S2 loop of the adjacent β-monomer (4). Although the system used in this study is relatively small, it has the essential features of the full microtubule, providing us unique insight into molecular level dynamics and interactions. Indeed, our atomic-level simulations reveal that Taxol induces significant changes in the dynamics and conformation of the M-loop as well as an increase in the lateral interactions between neighboring β-monomers. Taxol displaces the M-loop down and away from H6 in the β-monomer, and this action directly facilitates increased interactions with the neighboring H1-S2 loop, consistent with previous model structures of the microtubule (9). These two loops interact via van der Waals, electrostatic, and ionic interactions, and we observe a stable salt bridge formed between Glu⁵³ in the M-loop and Arg²⁸² in the neighboring H1-S2 loop when Taxol is bound (Fig. 6). These interactions make both the M-loop and H1-S2 loop less dynamic and the RMSF for each of these regions is sharply decreased. Without Taxol, this ionic bond between protofilaments is replaced with an intramonomer salt bridge between Arg²⁸² and Glu²⁸⁸. Both of these residues are in the M-loop and this bond changes the conformation of the M-loop, resulting in a slight opening of the Taxol binding site. This open conformation could play a role in the association or affinity of Taxol and notably the Arg²⁸²Gln mutation has been found to confer epothilone and taxane resistance (21).

FIGURE 6.

Interprotofilament interactions between the M-loop and H1-S2 loop. In the absence of Taxol (left) we see a salt bridge formed between Arg²⁸² and Glu²⁸⁸, both in the M-loop (yellow). When Taxol binds (right), the M-loop conformation is changed such that Arg²⁸² now forms a salt bridge with Glu⁵³ of the H1-S2 loop (red) in the neighboring protofilament.

There has been significant effort to identify the molecular basis of Taxol and epothilone resistance (for a recent review see (22)). As one might expect, a significant fraction of resistant mutations occur in the M-loop of β-tubulin (e.g., Phe²⁷⁰, The²⁷⁴, Arg²⁸²), but many are also found in the H6-H7 loop and Helix 7 (Leu²¹⁵, Leu²¹⁷, Leu²²⁸, Ala²³¹), in the T2 loop (Val⁶⁰), T5 loop (Pro¹⁷³) and in Helix 11 (Ala³⁶⁴) (23–29). Tubulin from Saccharomyces cerevisiae shares ∼75% sequence identity with vertebrate tubulin, but yeast microtubules are largely insensitive to Taxol (30). Gupta et al. found that a set of five amino acids could be mutated to produce Taxol binding in yeast (31). These mutations included residues close to the Taxol site, such as Tyr²⁷⁰ in the M-loop, but also included Ala¹⁹ in the T1-loop, Thr²³ and Gly²⁶ in Helix 1, and Asn²²⁷ in the H6-H7 loop. Together these sets of studies emphasize the fact that both proximal and distal amino acids can affect drug binding, and as found in our simulations, Taxol binding can likewise influence the dynamics of distal parts of tubulin.

A recent study used hydrogen/deuterium exchange to examine the protection of tubulin as a free dimer and in a GTP-microtubule both with and without Taxol (32). These authors found several regions of the tubulin dimer with altered protection upon the addition of Taxol, including portions of the protein both near and far from the Taxol binding site and the M-loop. Interestingly, the distal sites that are changed upon Taxol binding again include parts of the T2, T3, T4, and T5 loops of β-tubulin. It is not immediately obvious what effect changes in flexibility would have on hydrogen/deuterium exchange, but it is noteworthy that these sites correspond extremely well with the regions identified in our study.

Although strengthening the lateral interactions between the M and H1-S2 loops could certainly influence the overall stability of the microtubule, it is not obvious that this effect would be sufficient to stabilize a microtubule constructed from GDP-tubulin. Protofilaments made from GTP-tubulin are straight and allow the full microtubule to remain straight and stable; however, protofilaments of GDP-tubulin are curved and have a kink at the dimer-dimer interface of ∼12° (33). Based on this conformational change, strain energy should build up in the microtubule lattice after hydrolysis and/or phosphate loss since the protofilaments are held in a straight conformation, and a mechanochemical microtubule model concluded that the buildup of such strain energy could be the basis for dynamic instability (34). If Taxol solely functioned through stabilizing interprotofilament interactions, it would seemingly do nothing to mitigate this strain buildup and we would still expect to observe dynamic instability. Amos and Löwe postulated that Taxol-induced changes in the nucleotide-binding domain could allow the protofilaments to remain straight (7,35), and the recent observations of Elie-Caille et al. indeed show that individual protofilaments bound with Taxol are significantly less curved or kinked than protofilaments bound with either GDP or GMPCPP (8). Although we do see increased interactions between adjacent protofilaments, our results also suggest that changes in lateral interactions may be secondary to the allosteric effects that Taxol has on the T1–T5 and H11 loops. Since these loops make up the nucleotide-binding site, their enhanced flexibility should allow them to easily rearrange in response to hydrolysis, thereby counteracting larger-scale conformational changes and the resulting kinking of the protofilament. This effect would result in straighter protofilaments that would be less strained and hence a more stable microtubule.

In addition to surrounding the nucleotide, the T1–T5 and H11 loops also form the interface with the α-monomer of the next dimer along the protofilament. As such, we would conclude that the increased flexibility of this interdimer region should manifest itself at the level of the polymer. Indeed, multiple groups have found that microtubules stabilized with Taxol are more flexible and have a shorter persistence length than microtubules without Taxol (36–40); however, one group has reported the opposite result (38). VanBuren et al., on the basis of their mechanochemical model, also proposed that Taxol could function by reducing the flexural rigidity of the microtubule (34). Apart from these measurements of flexibility, a recent study that used osmotic stress to deform microtubules concluded that Taxol had no effect on the lateral interaction between protofilaments (41). These authors likewise postulated that Taxol might instead act by counteracting the straight-to-curved conformational change that follows GTP hydrolysis, similar to the hypothesis of Amos and Löwe (7). In our simulations, the T1–T5 loops all become approximately three times more flexible/dynamic when Taxol binds (Fig. 2). On the basis of relatively simple mechanics, we can approximately relate these changes in flexibility to changes in the bending rigidity of the microtubule. Since the thermal energy driving these fluctuations is the same in each case, an increase in flexibility by a factor of three should correspond to a decrease in the bending rigidity by the same factor. This is again in excellent agreement with experimental measurements and will be an important area for further study.