A Quantitative Model of Thermal Stabilization and Destabilization of Proteins by Ligands

Abstract

Equilibrium binding ligands usually increase protein thermal stability by an amount proportional to the concentration and affinity of the ligand. High-throughput screening for the discovery of drug-like compounds uses an assay based on thermal stabilization. The mathematical description of this stabilization is well developed, and the method is widely applicable to the characterization of ligand-protein binding equilibrium. However, numerous cases have been experimentally observed where equilibrium binding ligands destabilize proteins, i.e., diminish protein melting temperature by an amount proportional to the concentration and affinity of the ligand. Here, we present a thermodynamic model that describes ligand binding to the native and unfolded (denatured) protein states explaining the combined stabilization and destabilization effects. The model also explains nonsaturation and saturation effects on the protein melting temperature when the ligand concentration significantly exceeds the protein concentration. Several examples of the applicability of the model are presented, including specific sulfonamide binding to recombinant hCAII, peptide and ANS binding to the Polo-box domain of Plk1, and zinc ion binding to the recombinant porcine growth hormone. The same ligands may stabilize and destabilize different proteins, and the same proteins may be stabilized and destabilized by different ligands.

INTRODUCTION

The pharmaceutical industry uses a number of different methods to measure drug candidate ligand binding to target proteins of therapeutic interest. One of the main methods with wide applicability and generality is the thermal shift assay (1), also called ThermoFluor (2,3). This method is used in high-throughput screening of chemical compounds to search for strongly binding ligands that could be developed into therapeutic compounds (4). The ThermoFluor method has been used to discover compounds that inhibit protein-protein interaction, such as Hdm2-p53 interaction (5–7), and to measure ligand binding constants for enzymes such as carbonic anhydrase (8,9). In addition, the method is useful for the characterization of recombinant protein stability in various solutions and in the presence of various excipients (10–12), the optimization of conditions for protein crystallization (13), and the determination of the function of unknown proteins (14).

The thermodynamic model for estimating binding constants (9) is based on standard models from protein studies with differential scanning calorimetry (15). The method is based on the observation that ligands perturb protein thermal stability upon binding to the protein in its native state. However, the major limitation of this model is that it does not account for ligand binding to the unfolded state of a protein during the thermal shift assay.

Most ligands stabilize proteins upon binding, causing an increase in the protein melting temperature. Since most drug candidates are stabilizers, the model is well developed to quantitatively account for the dependence of the stabilization on ligand and protein concentrations (9). However, some ligands destabilize proteins by binding primarily to the unfolded state of the protein and destabilizing it (i.e., reduce the protein melting temperature). Ligands that stabilize proteins may be called N-binders (N-ligands, upshifters), and ligands that destabilize proteins may be called U-binders (U-ligands, downshifters).

Here, we present a model that takes into account ligand binding not only to the native state but also to the unfolded state of the protein and develop a quantitative description of protein destabilization by ligands. The dependence of protein stabilization and destabilization on the thermodynamic parameters of protein stability and ligand binding to two different states is presented. Simulated dependencies are presented for the enthalpy of unfolding, heat capacity of unfolding, Gibbs free energy of ligand binding, enthalpy of ligand binding, and protein concentration. Experimental examples that illustrate stabilization-destabilization events for proteins and ligands of biochemical or pharmaceutical significance are described.

MATERIALS AND METHODS

Production of recombinant porcine growth hormone

Escherichia coli strain BL21 (DE3) harboring a pET21a+-based expression vector was used for recombinant porcine growth hormone (rpGH) production. The vector contained a strong phage T7 promoter and a nucleotide sequence encoding porcine growth hormone (pGH) (16). E. coli cells were cultivated in a batch fermentation process previously described (17). Expression of the target protein was induced with 1 mM isopropyl-1-thio-β-D-galactopyranoside (IPTG). rpGH was expressed as an insoluble protein and accumulated in the inclusion bodies. pGH was refolded from solubilized inclusion bodies by a dilution protocol in the presence of the glutathione pair at a final concentration of 11.3 mM and pH 9.0. The (reduced glutathione)/(oxidized glutathione) ratio was 2:1. The renatured protein was purified by ion-exchange chromatography on Q-Sepharose followed by hydrophobic chromatography on Phenyl-Sepharose (17,18). A final protein solution in 25 mM Tris-HCl buffer pH 8.5 was frozen and stored at −20°C. The rpGH biological activity was determined in vitro on oGHR-FDC-P1 cells, as previously described (19,20).

Production of recombinant human carbonic anhydrase II

Complementary DNA (cDNA) of human carbonic anhydrase II (hCAII) was purchased from RZPD Deutsches Ressourcenzentrum für Genomforschung (Berlin, Germany). For recombinant protein expression, a nucleotide sequence encoding full-length (hCAII (amino acids 1–260)) was inserted into the pET-15b vector (Novagen, Madison, WI) via the NcoI and XhoI sites. The cloning procedure resulted in the removal of the His-tag sequence, enabling production of untagged hCAII construct.

For protein expression, the plasmid pET-15b-hCAII was transformed into E. coli strain BL21 (DE3). An overnight culture of plasmid-harboring cells was inoculated into fresh Luria-Bertani (LB) medium containing 60 μM ZnCl₂ and cultured at 37°C until an A₅₅₀ of 0.5–0.8 was reached. Expression of the target protein was induced by 0.2 mM IPTG. Cells cultured at 30°C in the presence of 0.4 mM ZnCl₂ were harvested 4 h after induction and lysed by sonication. Soluble protein was purified using a Sepharose-IDA-Ni⁺² affinity column, followed by anion exchange chromatography on CM-Sepharose (Amersham Biosciences, Uppsala, NY). Eluted protein was dialyzed into a storage buffer (20 mM HEPES (pH 7.8), 0.05 M NaCl, and 0.2 mM dithiothreitol (DTT)), lyophilized, and stored at −20°C. The purity of hCAII preparations was analyzed by sodium dodecylsulfate-polyacrylamide gel electrophoresis (SDS-PAGE) and determined to be higher than 95%. Protein concentrations were determined by ultraviolet-visible (UV-Vis) spectrophotometry using the extinction coefficient ɛ₂₈₀ = 50,420 M⁻¹cm⁻¹ and confirmed by the standard Bradford method. The catalytic activity of purified hCAII was measured in a 10 mM HEPES (pH 7.5), 50 mM Na₂SO₄ buffer, containing 10% acetonitrile (the standard buffer), using p-nitrophenyl acetate as a substrate (21). The enzyme activity was confirmed to be in the range of 1300–1400 pmol/(min×μg).

Production of recombinant Plk1-PBD

cDNA of human Polo-like kinase 1 (Plk1) was purchased from RZPD Deutsches Ressourcenzentrum für Genomforschung (Berlin, Germany). For the expression of the Polo-box domain (PBD) of Plk1, a nucleotide sequence corresponding to the C-terminal part of the protein (amino acids 326–603) was amplified by polymerase chain reaction (PCR) and inserted into a pSUMO prokaryotic expression vector (LifeSensors, Malvern, PA) via the Eco31I and HindIII sites. As a result, a His-tag containing SUMO protein was fused to the N-terminus of Plk1-PBD.

For protein expression, plasmid pSUMO-Plk1-PBD was transformed into the E. coli strain Rosetta-gami 2 (DE3) (Novagen, Madison, WI). An overnight culture of plasmid-harboring cells was inoculated into fresh LB medium, cultured at 37°C until an A₅₅₀ of 0.5–0.6, and put on ice. In the evening, expression of the target protein was induced by 0.1 mM IPTG. After the addition of IPTG, cells were cultured at 20°C overnight, harvested by centrifugation, and lysed by sonication in a buffer containing 20 mM HEPES (pH 7.0), 0.2 M NaCl, 0.1 M imidazole, 2 mM β-mercaptoethanol, 0.1% thioglycerol, and complete EDTA-free protease inhibitor cocktail (Roche Applied Science, Indianapolis, IN). Soluble protein was purified using a Sepharose-IDA-Ni⁺² affinity column and dialyzed against buffer containing 20 mM Tris-HCl (pH 8.0), 150 mM NaCl, and 2.0 mM DTT for 24 h. Cleavage of the SUMO-tag was performed at 4°C overnight, using 1 unit of SUMO protease (LifeSensors, Malvern, PA) per 100 μg of SUMO-Plk1-PBD fusion protein. SUMO, and Plk1-PBD proteins were separated on a Sepharose-IDA-Ni⁺² affinity column. Eluted Plk1-PBD protein was dialyzed into a storage buffer containing 50 mM Tris-HCl (pH 7.8), 0.2 M NaCl, and 2.0 mM DTT, flash frozen in liquid nitrogen, and stored at −80°C. The purity of the Plk1-PBD preparations was analyzed by SDS-PAGE and determined to be higher than 95%. Protein concentrations were determined by UV-Vis spectrophotometry using the extinction coefficient ɛ₂₈₀ = 36,245 M⁻¹cm⁻¹ and confirmed by the standard Bradford method.

Carbonic anhydrase inhibitors

Standard carbonic anhydrase inhibitors, AZM (acetazolamide), CARBS (p-carboxybenzene sulfonamide), and EZA (ethoxazolamide) were purchased from Aldrich Chemical Co. (Milwaukee, WI). TFMSA (trifluoromethanesulfonamide) was purchased from Alfa Aesar (Karlsruhe, Germany). The thermodynamics of binding of these inhibitors have been previously described (9,22). Inhibitor 3d (3-methylsulfonylbenzimidazo[1,2-c][1,2,3]thiadiazole-7-sulfonamide) was synthesized as previously described (23).

Peptides for Plk1-PBD

For Plk1-PBD-ligand binding studies, the phosphopeptide PMQS-pT-PL, representing the core of the optimal Polo-box binding ligand (24) and its unphosphorylated counterpart PMQS-T-PL were synthesized by JPT Peptide Technologies (Berlin, Germany).

Thermal-shift assay (ThermoFluor)

The thermal shift assay was performed using the iCycler iQ Real Time Detection System (Bio-Rad, Hercules, CA), originally designed for PCR. Protein unfolding was monitored by measuring the fluorescence of the solvatochromic fluorescent dye Dapoxyl sulfonic acid sodium salt. A temperature increment of 1°/min was applied. Samples contained 10–40 μM protein, 0–4 mM ligand, and 50 μM Dapoxyl sulfonate in the total volume of 10 μl, overlayed with 2.5 μl of silicone oil DC 200; 96-well iCycler iQ PCR plates were used for the assay.

RESULTS

Derivation of protein melting temperature T_m versus ligand concentration L_t

A ligand may bind to the native (N) and/or unfolded (U) protein. If the ligand binds to the unfolded state more strongly than to the native state, then the protein is destabilized by the ligand. On the other hand, if the ligand binds to the native form more strongly than to the unfolded state, then the protein is stabilized by the ligand. The binding reactions may be shown as linked equilibria:

(1)

where is the concentration of the unfolded protein-ligand complex, 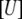is the concentration of unfolded free protein, 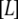is the concentration of free ligand, 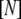is the concentration of native free protein, and 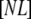is the concentration of the native protein-ligand complex. 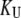is the equilibrium constant of protein unfolding in the absence of ligand, assuming that there are only two protein states at equilibrium. It may be expressed as

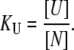(2)

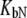and 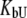are ligand binding constants to the native and unfolded protein states, respectively:

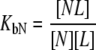(3)

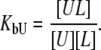(4)

Equations for the conservation of mass of the total protein (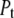) and total ligand (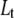) are

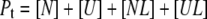(5)

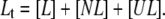(6)

The fraction of the unfolded protein may be expressed as

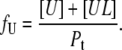(7)

The system of Eqs. 2–7 was solved to express the total added ligand concentration as a function of 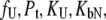and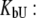

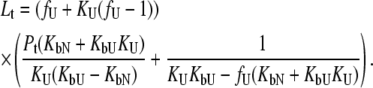(8)

However, this equation may be simplified by considering that at the protein melting temperature, the fraction of unfolded protein is equal to one half (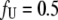), i.e., the concentrations of the folded and unfolded protein species are equal. Then, we obtain the relationship between the equilibrium constants and total concentrations of the ligand and the protein:

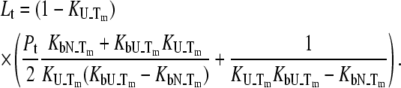(9)

This equation is valid only for the condition where 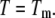Here, the subscript 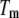of each equilibrium constant denotes the value of the appropriate constant at the temperature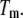

To find a relationship between total ligand concentration and protein melting temperature, the dependence of the equilibrium constant on temperature should be considered. Assuming the temperature-independent heat capacity of unfolding and binding, the temperature dependence of the equilibrium constant is given by

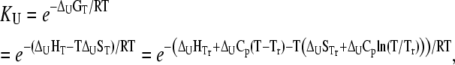(10)

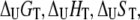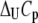where and are the Gibbs free energy, enthalpy, entropy, and heat capacity changes of unfolding, respectively, and R is the universal gas constant. The temperature 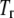is the reference temperature of protein melting without added ligand. The temperature dependence of the native form binding constant is given by

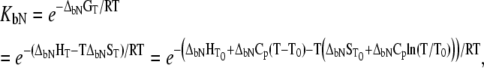(11)

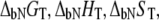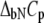where and are the Gibbs free energy, enthalpy, entropy, and heat capacity of ligand binding to the native state protein, respectively. The reference temperature 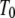is equal to 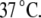The temperature dependence of the binding constant to the unfolded protein is given by

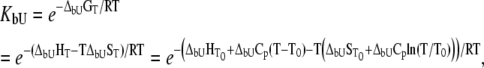(12)

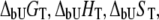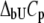where and are the Gibbs free energy, enthalpy, entropy, and heat capacity of ligand binding to the unfolded state protein, respectively.

Substituting Eq. 9 with Eqs. 10–12 at 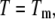we obtain the total required ligand concentration 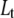to reach the protein melting temperature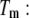

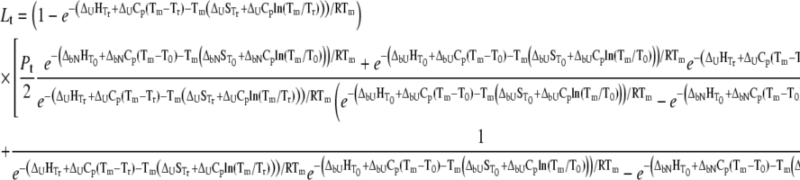(13)

This equation describes the relationship among all thermodynamic parameters of protein unfolding and ligand binding to two protein states and relates the parameters to the total protein and ligand concentrations. The model is valid only when the binding stoichiometries to the native and unfolded forms of the protein are equal to 1:1.

Equation 13 is quite complex and can be simplified with the assumption that a ligand does not bind either to the native or to the unfolded form. If a ligand does not bind to an unfolded protein (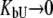) or binds to the unfolded state more weakly than to the native state, and conditions 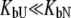and 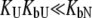are satisfied, then Eq. 9 simplifies to

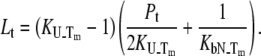(14)

This equation can be expressed in terms of thermodynamic parameters:Equations 14 and 15 were derived by Matulis et al. (9), where a partial model was derived without considering ligand binding to an unfolded protein.

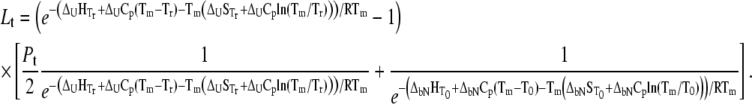(15)

The other limiting situation is that where a ligand does not bind to the native protein (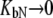) or where it binds to the native form more weakly than to the unfolded one, so that conditions 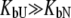and 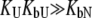are satisfied. Then, Eq. 9 simplifies to

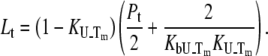(16)

This equation may be expressed in terms of thermodynamic parameters:

Equation 13 and its partial forms (Eqs. 15 and 17) are transcendental for 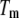and can be solved only numerically. The Brent algorithm (25) was used in writing the function 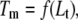which numerically solves Eq. 13. The obtained numerical function was fit to the additional experimental data for ligand concentration dependence on protein melting temperature. The fit was performed using the nonlinear Levenberg-Marquardt algorithm. Most parameters (except two: 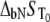and 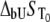) were set to reasonable values and/or fixed.

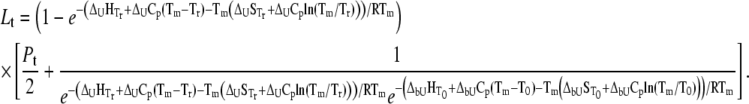(17)

Simulated T_m = f(L_t) curve dependence on thermodynamic parameters of unfolding and binding

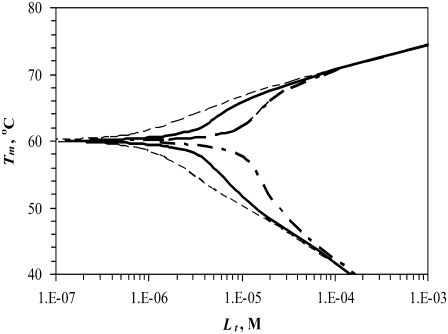
Figs. 1–5 show hypothetical protein melting temperature (T_m) dependencies on hypothetical ligand concentration (L_t). The curves were simulated according to Eq. 13 using the following thermodynamic parameters, except where noted otherwise: 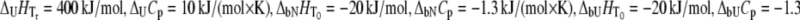for N-binders and approaches 0 for U-binders, 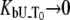for N-binders and for U-binders, and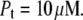

FIGURE 1.

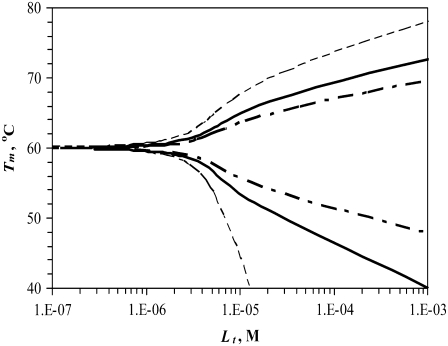
Simulated dependence of the protein melting temperature T_m on ligand concentration. Ligand stabilizers (N-binders) shift the T_m upward, whereas ligand destabilizers (U-binders) shift the T_m downward. Curves simulated for proteins with different enthalpies of unfolding (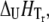 while keeping other parameters constant as described in Materials and Methods)—narrow dashed line: 300 kJ/mol, bold solid line: 500 kJ/mol, and bold dashed line: 700 kJ/mol.

FIGURE 2.

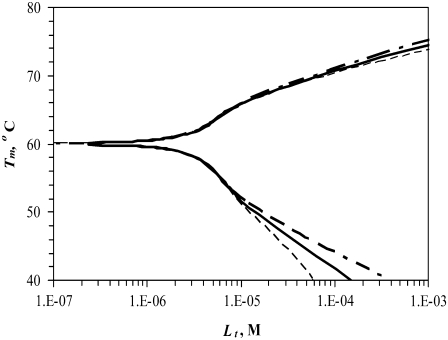
Simulated dependence of the protein melting temperature T_m on added ligand concentration for proteins with different heat capacities of unfolding (Δ_uC_p)—narrow dashed line: 15 kJ/(mol × K), bold solid line: 10 kJ/(mol × K), and bold dashed line: 6.3 kJ/(mol × K), while keeping other parameters constant. Ligand stabilizers shift the T_m upward, whereas ligand destabilizers shift it downward.

FIGURE 3.

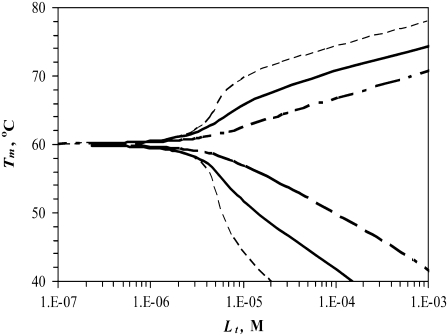
Simulated dependence of the protein melting temperature T_m on the concentration of ligand interacting with the following binding constants (37°C)—narrow dashed line: K_bN or K_bU = 10⁸ M⁻¹, bold solid line: K_bN or K_bU = 10⁷ M⁻¹, bold dashed line: K_bN or K_bU = 10⁶ M⁻¹. For N-binders, K_bU → 0, and for U-binders, K_bN → 0.

FIGURE 4.

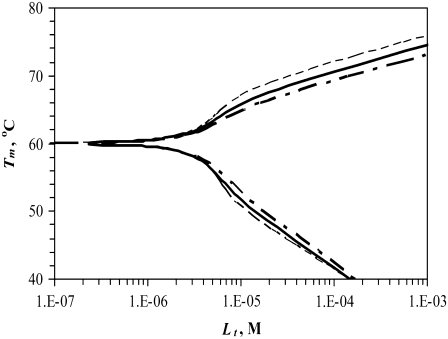
Simulated dependence of the protein melting temperature T_m on the concentration of ligand interacting with the following binding enthalpies (Δ_bNH for N-binders and Δ_bUH for U-binders)—narrow dashed line: 0 kJ/mol, bold solid line: −20 kJ/mol, bold dashed line: −40 kJ/mol. Other parameters were kept constant as explained in the Materials and Methods section.

FIGURE 5.

Simulated dependence of the protein melting temperature T_m on added ligand concentration L_t for various protein concentrations—P_t: narrow dashed line: 3 μM, bold solid line: 10 μM, and bold dashed line: 30 μM. Other parameters were kept constant as explained in Materials and Methods.

Fig. 1 shows the curves of the function T_m = f(L_t) simulated using various enthalpies of protein unfolding. Ligands that stabilize proteins upon binding are N-binders—they raise the protein T_m—whereas ligands that bind more strongly to the unfolded form and destabilize proteins are U-binders—they diminish the protein T_m. When all other parameters are equal, the U-binders are expected to have a stronger effect on proteins than N-binders (Fig. 1). In other words, the T_m is diminished to a greater extent for U-binders than it is increased for N-binders. The reason for such a result is a nonlinear relationship between ΔG and T_m. Equal addition to or subtraction from ΔG does not lead to an equal change in T_m.

Fig. 2 shows the same curve dependence on the heat capacity of unfolding. Here, we see a similar effect—the impact of U-binders on the protein T_m is greater than that for N-binders. However, the overall effect of the heat capacity is significantly less than the effect of the enthalpy (Fig. 1).

Fig. 3 compares the same curves at different binding constants to the native (N-binders) and unfolded (U-binders) forms. Stronger binding leads to a greater impact on the T_m. However, the effect of U-binders is greater than the effect of N-binders. Therefore, it takes less ligand-U-binder to reduce the T_m by the same amount that the ligand-N-binder raises the T_m.

Fig. 4 compares the same curve dependence on the enthalpy of binding to the native and unfolded forms. The difference between the binding enthalpies of 0 and −40 kJ/mol, a range of realistic ligand binding enthalpies, is not very large. However, different binding enthalpies may lead to an error in the T_m of 3°C–4°C.

Fig. 5 illustrates the expected curve dependence if the experiment is carried out at different protein concentrations. At greater protein concentrations, the curves become more sigmoidal, since it is expected to take more ligand to raise the T_m to the same extent.

Experimental illustration of N-binders and U-binders

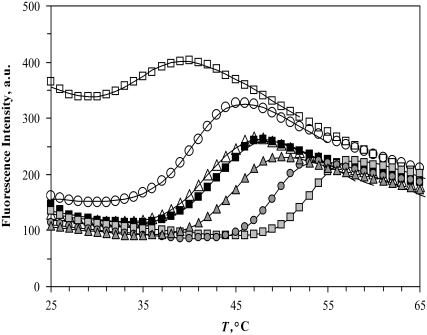
Fig. 6 shows experimental temperature denaturation curves of the Plk1-PBD protein with various added ligands. The midpoint of the transition without any ligand (42°C) is equal to the T_m of the protein. The experimental data were fit to the unfolding model as in Matulis et al. (9). U-binder ligand (ANS, 1,8-anilinonaphthalene sulfonate) addition shifted the T_m downward, whereas the addition of a specific binding peptide shifted the T_m upward.

FIGURE 6.

Temperature denaturation profiles of Plk1-PBD (10 μM). Black-filled symbols represent the denaturation profile of Plk1-PBD without added ligand. Addition of the ligand ANS (open symbols) destabilized the protein, shifting the T_m downward, whereas the addition of the phosphorylated peptide (gray solid symbols) stabilized the protein, shifting its T_m upward. The concentrations of the ligands: (triangles) 15.6 μM peptide and 31.3 μM ANS, (circles) 100 μM, (squares) 1000 μM. Data points are experimental observations; the lines are simulated according to the model of Eq. 13. The denaturation parameters of free Plk1-PBD were 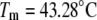and

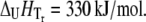
Stabilization of carbonic anhydrase

Plotting the various ligand effects on protein T_m as a function of the total added ligand concentration gives the T_m = f(L_t) functions. Fig. 7 shows the effect of three N-binders (stabilizers) on the T_m of carbonic anhydrase II. These specific sulfonamide inhibitors bind with 1:1 stoichiometry to the active site of the enzyme. The curves, drawn according to Eq. 13, match the experimental data points reasonably well. A slight discrepancy at the middle of the graph can be explained by the inexactness of the concentration of ligand or protein. Compounds that bind more strongly raise the T_m to a greater extent than the weaker binders. These results are similar to our previous results (9).

FIGURE 7.

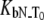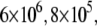Dependence of the hCAII melting temperature on ligand concentration: AZM (•), 3d (▪), and CARBS (▵). Lines are drawn according to the model of Eq. 13. Regressed values of ligand binding constants () are and 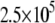for AZM, 3d, and CARBS, respectively.

Stabilization and destabilization of Plk1-PBD

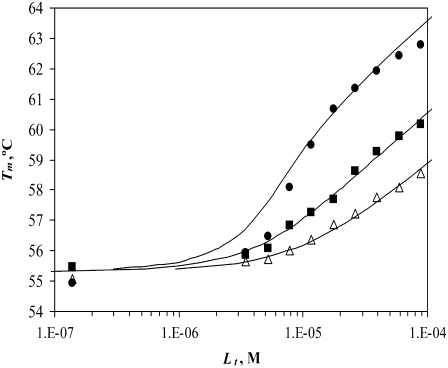
The recombinant Polo-box domain Plk1-PBD binds the phosphorylated peptide PMQS-pT-PL with a stoichiometry of 1:1 and a binding constant of K_bN (37°C) = 2.3 × 10⁵ M⁻¹. However, the nonphosphorylated peptide PMQS-T-PL did not bind the protein, and its K_bN was nondetectable.

The same protein may exhibit thermal destabilization in the presence of ligands that bind to the unfolded state more strongly than to the native state. A good example of such destabilization is ANS binding to Plk1-PBD. The addition of ANS at concentrations comparable to the concentration of the phosphorylated peptide in Fig. 8 produced a comparable destabilization of the protein. Addition of 1 mM phosphorylated peptide stabilized the protein by ∼10°C, whereas addition of 1 mM ANS destabilized the protein by ∼10°C (Fig. 9). Several representative curves of fluorescence dependence on temperature are shown in Fig. 6 for both stabilization and destabilization.

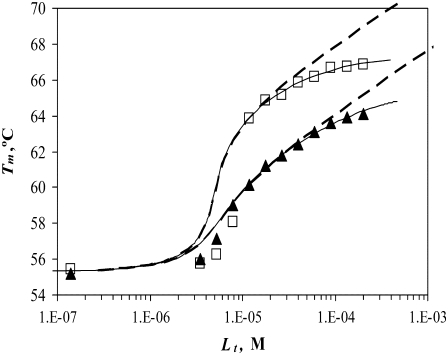
FIGURE 8.

Dependence of the Plk1-PBD melting temperature on the concentration of added peptide in two forms: phosphorylated (▪) and unphosphorylated (▵). Lines are drawn according to the model of Eq. 13, using the following parameters: 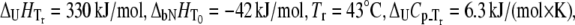and 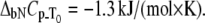For phosphorylated peptide, the binding constant was 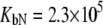M⁻¹. The unphosphorylated peptide binding constant was nondetectable ( 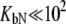M⁻¹).

FIGURE 9.

Dependence of Plk1-PBD melting temperature on ANS concentration. Lines are drawn according to the model of Eq. 13 using the following parameters: 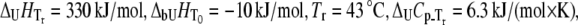and 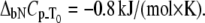The binding constant is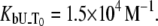

Zinc binding to the growth hormone

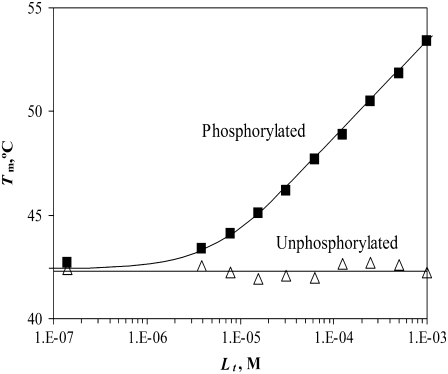
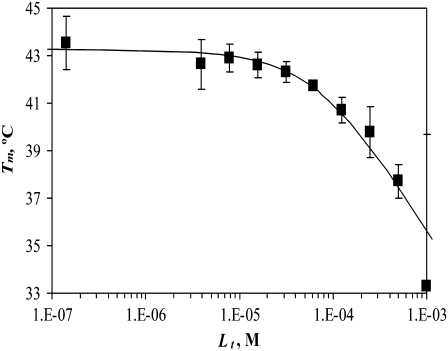
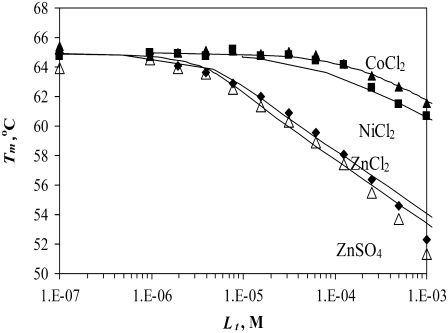
Another important example of protein destabilization by ligands is the binding of Zn²⁺ to rpGH. Our results show that zinc binds with the stoichiometry of one zinc cation per one hormone molecule, resulting in significant destabilization of the protein. For example, the addition of 100 μM Zn²⁺ decreased the melting temperature of the protein by ∼10°C (Fig. 10). There was little difference between the zinc chloride and sulfate, indicating that only the cation is important for this interaction. The binding constants to the unfolded state of the rpGH were 1.6 × 10⁶ M⁻¹ for zinc chloride and 2.3 × 10⁶ M⁻¹ for zinc sulfate. Therefore, the Zn²⁺ binding constant to unfolded rpGH (K_bU, 37°C) was equal to (2.0 ± 0.5) × 10⁶ M⁻¹. Other metals such as nickel and cobalt also destabilized the rpGH. However, their binding constants and destabilizing effects were significantly smaller than z.

FIGURE 10.

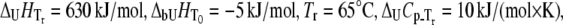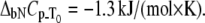Dependence of the rpGH melting temperature on added metal concentration: CoCl₂ (▴), NiCl₂ (▪), ZnCl₂ (♦), and ZnSO₄ (▵). Lines are drawn according to the model of Eq. 13. The following parameters were used to obtain binding constants to unfolded rpGH: and The binding constants 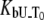for CoCl₂, NiCl₂, ZnCl₂, and ZnSO₄ are equal to 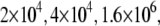and 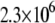M⁻¹, respectively.

Zinc preferentially binds to the unfolded state of the rpGH and destabilizes it. The binding constant for the unfolded form is greater than the binding constant for the native form, which is poorly determined by the method. The K_bN is somewhere between 0 and 10⁴ M⁻¹ and is hidden by the dominating K_bU.

Saturation effect

The model described by Eqs. 9 and 13 helps to explain the saturation effect. The saturation effect is a term we have used to describe the situation where the addition of ligand increases the T_m by a lesser extent than expected based on its binding affinity. It was often observed that the addition of ligands did not increase the melting temperature to the extent predicted by our previous models, which did not account for ligand binding to the unfolded state. For example, the binding of EZA and TFMSA to carbonic anhydrase exhibits the saturation effect (Fig. 11). At submillimolar concentrations, the ligands do not shift the T_m to the extent predicted by the model. At ∼200 μM, the T_m is ∼2°C lower than predicted, which does not account for the ligand binding to the unfolded state of the protein (dashed line, Fig. 11). However, the application of our model that does account for the ligand binding to the unfolded state shows a model curve (solid line, Fig. 11) that fits the experimental data much better.

FIGURE 11.

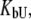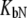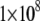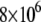Dependence of the recombinant human carbonic anhydrase II melting temperature on the total added concentration of EZA (□) and TFMSA (▴). Dashed lines represent the fit assuming K_bU → 0, Eq. 15, whereas solid lines are fit using Eq. 13. For vanishing the fitted constants have values of and M⁻¹ for EZA and TFMSA, respectively. 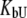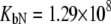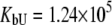The binding constants (under the condition when was allowed to vary) are as follows: and M⁻¹ for EZA, and 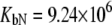and 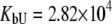M⁻¹ for TFMSA.

Fitting of the experimental data to the previous model (Eqs. 14 and 15) yielded the binding constants (K_b, 37°C) of 1.0 × 10⁸ M⁻¹ for EZA and 8.0 × 10⁶ M⁻¹ for TFMSA. However, application of the full model (Eqs. 9 and 13) yielded the following binding constants (37°C): 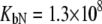M⁻¹, 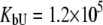M⁻¹ for EZA and 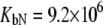M⁻¹, 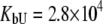M⁻¹ for TFMSA. The application of both models yields similar binding constants for the native state. However, the new model, which accounts for the binding to the denatured state of the protein, fully accounts for the saturation effect and determines the binding to the denatured state of the protein.

DISCUSSION

This model, which takes into account ligand binding to both the native and denatured protein states, is more detailed than the previously described model (9), helps to quantitatively account for protein destabilization by ligands, and determines the ligand binding constant to both protein states. As shown with several examples of unrelated proteins and ligands, some proteins may be stabilized or destabilized by various ligands. The destabilization effect is often hidden, since most ligands stabilize proteins upon their specific binding with 1:1 stoichiometry to sites such as the enzyme active site.

Ligand binding to the unfolded protein state is not well understood. There are no crystal structures of any unfolded proteins. We do not know exact sites of ANS binding to unfolded Plk1-PBD or Zn²⁺ binding to unfolded pGH, for example. However, the U-binder effect is obvious and indicates strong binding to the unfolded state.

An important implication of this model is that the binding constants routinely determined by the thermal shift assay may be incorrect. They may be lower than the constants determined by methods where the temperature is not raised and no denaturation occurs, such as isothermal titration calorimetry. If, for example, the K_b (37°C) by isothermal titration calorimetry (ITC) is determined to be equal to 10⁷ M⁻¹ and the K_bN (extrapolated to 37°C) by thermal shift is equal to 10⁷ M⁻¹, then we can be quite certain that we have determined the actual K_b (37°C). However, if we determine the K_bN only by the thermal shift assay, then there is no certainty that it is really equal to K_b (37°C), since the actual K_b may be greater than K_bN if there is a significant K_bU. However, the actual K_b cannot be smaller than K_bN. Therefore, the hits obtained by the thermal shift assay are real and the method is valid. In short, the thermal shift assay may somewhat underestimate the binding constant for the native state. The method, however, will not overestimate the constant.

A limitation of the model is that it assumes that there is only one unfolded state of the protein. It is likely that an unfolded protein exists in a large number of semiflexible conformational states. The model approximates the unfolded state of the protein as a single thermodynamic state. Another limitation is that the model analyzes binding as having 1:1 stoichiometry. In the case of U-binders, it is possible that a number of ligand molecules bind to the unfolded state with variable potency. A cumulative effect would probably be observed where several weakly binding ligands shift the T_m as much as one strongly binding ligand. Such cases would have to be analyzed by a significantly more complex model.

Stabilization of carbonic anhydrase

Inhibitors that bind specifically, such as sulfonamides, bind to the active site of the enzyme carbonic anhydrase with a stoichiometry of 1:1. Such inhibitors bind strongly to the native state protein and bind weakly, if at all, to the unfolded state of the protein. Therefore, inhibitor binding to carbonic anhydrase is well approximated by Eq. 15, where it is assumed that K_bU is negligible (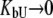) or the binding to the unfolded state is weaker than to the native state and conditions 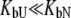and 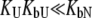are satisfied. Since all these conditions are met for inhibitor binding to carbonic anhydrase, the approximation is valid and the binding constants match those obtained by isothermal titration calorimetry, as previously discussed (9).

However, some strong carbonic anhydrase inhibitors, such as EZA and TFMSA (Fig. 11), exhibit nonlinear T_m dependence on ligand concentration (on a semilogarithmic scale). First, we discuss the reason for the expected linearity of the dependence, since there is a misconception that it results from the bonds formed between the ligand and protein and holds the protein in a more stable conformation. As previously discussed (26), it is important to note that the T_m shift caused by the ligand continues with increasing ligand concentration beyond the levels where the protein is fully saturated with ligand. The contribution from the entropy of mixing is dominant here. Enhanced stability arises from the additional Gibbs free energy required to remove the ligand from the protein before its unfolding, and this free energy has an important component arising from the entropy of mixing of dissociated ligand and depends on the concentration of free ligand in solution.

In addition to numerous examples where the protein T_m increases linearly with increasing concentration (e.g., Figs. 7, 8, and 9), there are examples where the T_m stops increasing (e.g., Fig. 11, and an example of Ca²⁺ binding to α-lactalbumin (26)). It has been suggested that saturation may be caused either by ligand binding to the unfolded state of the protein (26) or by the low solubility of the ligand (9). Both these reasons may cause the saturation effect. However, in the case of EZA and TFMSA binding to hCAII, ligand solubility is probably not the limiting factor, and the quantitative model, which takes into account ligand binding to the unfolded state accounts for the experimental data remarkably well (Fig. 11). Interestingly, the binding constants for the unfolded state were only ∼1000-fold weaker than those of the folded state.

Stabilization and destabilization of Plk1-PBD

The Plk1 PBD is a good example of the same protein being strongly stabilized and destabilized by various ligands. A specifically binding phosphorylated peptide was a strong stabilizer, whereas its unphosphorylated counterpart did not affect the stability, and the negatively charged ANS was a strong destabilizer. We do not know the mode or the exact stoichiometry of ANS binding to the unfolded state, but the data are consistent with the model of the stoichiometry of 1:1.

The thermal shift approach contributes data of peptide binding to Plk1-PBD. This protein binds the phosphorylated peptide PMQS-pT-PL with a stoichiometry of 1:1 and the binding constant K_bN = 2.3 × 10⁵ M⁻¹ (K_dN = 4.3 μM, 37°C). However, the binding of unphosphorylated peptide PMQS-T-PL was not detected. The literature lists controversial numbers for binding. It was determined by ITC that the peptide containing the same core (MAGPMQS-pT-PLNGAKK) binds to Plk1-PBD with K_d = 0.28 μM, whereas the binding of the same unphosphorylated peptide is undetectable (24). However, other authors determined by tryptophan fluorescence measurements that the binding of both peptides was similar; the K_d for the phosphorylated peptide was determined to be 2.77 μM, whereas the K_d of the unphosphorylated peptide was equal to 3.53 μM (27). Our results (Fig. 8) support the notion that the phosphorylation of the threonine is essential for the binding of the peptide to Plk1-PBD.

Zinc binding to the growth hormone

Zinc has been shown to be important for the function of growth hormones from humans and other organisms. For example, Zn²⁺ has been demonstrated to enhance the activity of human growth hormone (hGH) in a cell line based biological assay (28,29). The binding affinity of hGH with the extracellular binding domain of the human prolactin receptor was increased ∼8000-fold by the addition of 50 μM ZnCl₂, whereas Zn²⁺ was not required for hGH binding to the hGH receptor (30). Zinc has also been demonstrated to induce dimerization of hGH, and the resulting Zn²⁺-hGH dimer has been proposed as the major storage form of hGH in vivo. Mutational analysis indicated that His¹⁸, His²¹, and Glu¹⁷⁴ participate in coordinating Zn²⁺ and promoting formation of the hormone dimer (31).

Porcine growth hormone (pGH) used in this study shares 68% sequence identity with hGH (32). Studies on porcine growth hormone interaction with zinc are interesting from the evolutionary point of view, since there are some major differences between human and porcine growth hormones. For example, hGH has lactogenic activity, but pGH has no lactogenic activity (33). Moreover, zinc-protein precipitates may be useful for protein purification, storage, and formulation. Precipitation of hGH by zinc does not alter the secondary structure of hGH, and the process is fully reversible. Zinc binding induces only minor tertiary structural changes to the protein (34).

Our results on the interactions of rpGH with metals show that there is a specific effect of zinc on the protein. Zinc preferentially binds to the unfolded state of the rpGH and destabilizes it. The binding constant for the unfolded form is equal to ∼2 × 10⁶ M⁻¹, whereas the binding constant for the native form is poorly determined by this method. The K_bN is equal to somewhere between 0 and 10⁴ M⁻¹, and it is hidden by the dominating K_bU. There may be more than one Zn binding site in the U-state, but the consecutive binders, if any, should have weaker binding constants.

Zinc binding to rpGH is another example of a ligand that preferentially binds the unfolded state of the protein. Again, we do not know the exact mode or the stoichiometry of zinc binding to the unfolded protein. However, the model implies that the binding stoichiometry is one Zn²⁺ bound to one rpGH molecule. The binding constant (K_d = 0.5 μM) is rather strong, implying that there is a specific Zn²⁺-binding site available only in the unfolded state of the protein.

CONCLUSIONS

The above examples of three protein systems illustrate the applicability of the model of protein stabilization and destabilization by ligands. To conclude, this model, which takes into account ligand binding to both the native and denatured protein states, is more detailed and helps to quantitatively account for protein destabilization by ligands, determines the ligand binding constants to both protein states, and helps to explain the saturation effect.