A Hybrid Model for Three-Dimensional Simulations of Sprouting Angiogenesis

Abstract

Recent advances in cancer research have identified critical angiogenic signaling pathways and the influence of the extracellular matrix on endothelial cell migration. These findings provide us with insight into the process of angiogenesis that can facilitate the development of effective computational models of sprouting angiogenesis. In this work, we present the first three-dimensional model of sprouting angiogenesis that considers explicitly the effect of the extracellular matrix and of the soluble as well as matrix-bound growth factors on capillary growth. The computational model relies on a hybrid particle-mesh representation of the blood vessels and it introduces an implicit representation of the vasculature that can accommodate detailed descriptions of nutrient transport. Extensive parametric studies reveal the role of the extracellular matrix structure and the distribution of the different vascular endothelial growth factors isoforms on the dynamics and the morphology of the generated vascular networks.

INTRODUCTION

Sprouting angiogenesis, the process of new capillaries forming from existing vessels, can be observed in the human body under various conditions. Apart from angiogenesis in a physiological context which mainly takes place during embryogenesis and fetal development, angiogenesis can be observed under pathological conditions, such as wound healing, thrombosis, and tumor growth (1,2). In the case of wound healing and thrombosis, newly formed capillaries grow in a controlled manner and stop growing once the pathological condition has been alleviated; this is, however, not the case for tumor-induced angiogenesis (2).

Tumor-induced angiogenesis can persist for years, involving a disorganized, inefficient, and leaky vasculature (2). This vasculature supplies the tumor with nutrients and growth factors, enabling increased tumor cell proliferation and thus enhanced tumor growth. Furthermore, angiogenesis enables hematogenous spread of cancer: single cancer cells or cell clusters that detach from the primary tumor may enter the leaky vessels and use the vasculature to metastasize to remote organs (3). The regulation or even inhibition of tumor-induced angiogenesis can affect tumor growth. The inhibition of angiogenesis restrains nutrient supply, reducing the growth rate of the tumor and hindering migrating cell clusters from entering the vasculature, thus reducing the risk of metastasis (3,4). A complete inhibition promotes hypoxia (state of oxygen shortage) within the tumor that can increase the occurrence of aggressive migrating tumor cell phenotypes (5,6). The regulation of capillary growth may present a more efficient pathway for drug delivery, as the leaky vessels and the high interstitial pressure in the proximity of the tumor prevents effective supply of drugs through the blood vessels into the core of the tumor (7). Although antiangiogenic therapy is comparatively young, it has already been established as the fourth pillar of cancer therapy (4), next to surgery, radiation, and chemotherapy.

Tumor-induced sprouting angiogenesis

The maximal size a tumor can assume without relying on a vasculature for nutrient supply is restricted to ∼1 mm³ (4,8). In this stage of avascular growth, nutrients reach the tumor by the sole means of diffusion through the surrounding tissue. If the tumor grows beyond this size of ∼1 mm³, cells in the core of the tumor cannot obtain enough oxygen to survive. These cells become hypoxic and eventually starve, forming a necrotic region at the core of the tumor. Tumors can reside in this avascular state for a long time (4). However, one of the many responses of tumor cells to hypoxia and glucose deprivation is that they start to secrete angiogenic growth factors that are responsible for initiating sprouting angiogenesis (9). Several growth factors are involved in the process of angiogenesis. Vascular endothelial growth factors (VEGF) have been identified to be one of the main driving forces (10). VEGFs, upon release by hypoxic tumor cells, diffuse through the extracellular matrix (ECM) occupying the space between tumor and existing vasculature in the proximity of the tumor and establish a chemical gradient between the tumor and nearby vessels. Once VEGF has reached a vessel, it binds to receptors located on endothelial cells (EC), which line the blood vessel walls. This binding sets off a cascade of events (10–12).

In the early phase of angiogenesis, ECs stimulated by VEGF start releasing proteases that degrade the basal lamina, a fibril structure building the outermost layer of the vessel wall (1,13). This enables ECs to leave the vessel wall and enter the ECM. Further intercellular and intracellular signaling pathways, initially triggered by VEGF, increase EC proliferation and coordinate the selection of migrating ECs located at the tip of outgrowing sprouts (1). Migrating sprout tip cells probe their environment by extending filopodia and migrate along the VEGF gradient toward regions of higher concentration, a directed motion referred to as chemotaxis (14). ECs located initially behind the migrating tip cells proliferate, thus extending the sprouting blood vessel (1,14). Fibronectin, which is distributed in the ECM and at the same time released by the migrating tip cells, establishes an adhesive gradient which serves as another cue for the ECs following behind (13,15,16). Fibronectin released by the ECs binds to matrix components such as collagens and other fibers, which occupy roughly 30% of the ECM (17). Matrix-bound fibronectin in turn can bind to transmembrane receptors located on the EC membrane (18). This autocrine signaling pathway, promoting cell-cell and cell-matrix adhesion, accounts for a movement referred to as “haptotaxis” (1). In addition to chemotactic and haptotactic cues, the fibrous structures present in the ECM also influence cell migration by facilitating movement in fiber directions (19,20).

After the initial sprouts have extended for some small distance into the ECM, repeated branching of the tips can be observed. Sprout tips approaching others may fuse and form loops, a process called “anastomosis”. Anastomosis can be observed to occur either by sprout tips fusing with other sprout tips thus arresting their migration, or by sprout tips fusing with already established sprouts at some distance behind the tip. Along with anastomosis, the formation of lumen within the strands of endothelial cells establishes a network that allows blood circulation (1). Maturation, the final stage of angiogenesis, incorporates the rebuilding of a basal lamina and the recruitment of pericytes and smooth muscle cells to stabilize the vessel walls (21). In tumor-induced angiogenesis, the newly built vasculature is often disorganized and leaky, leading to high interstitial pressure and inefficient blood supply (22). Together with a growing tumor, which exerts pressure on the fragile capillaries and thus suppresses temporal and local blood delivery, ever new regions of acute hypoxia arise, releasing in turn VEGF, which sets off the process of angiogenesis anew (23). This process does not stop and full maturation is impaired (4).

Vascular endothelial growth factors

In addition to the soluble isoform of VEGF, several other VEGF isoforms influence the capillary network formation (24,25). Some VEGF isoforms express a binding site for heparan sulfate proteoglycans which is found on cell surfaces, in the ECM, and in body fluids. Such isoforms can therefore be bound by the ECM (26). These matrix-bound VEGF isoforms can be cleaved from the ECM by matrix metalloproteinases (MMPs) (24) establishing localized chemotactic cues. MMPs are expressed both by tumors and migrating ECs (15,27). Inflammatory cells stimulated by the tumor can also release VEGF and contribute to the chemotactic cues of the ECs (28).

Extracellular matrix

The extracellular matrix describes the material between cells in metazoans, including the space between the initial vasculature and the tumor and plays an important role in cell migration. Fibers such as collagen, laminin, and fibrillin are distributed throughout the ECM occupying roughly 30% of the ECM (17). These fibers form bundles that serve as guiding structures for migrating cells (13,19). The structures are in turn subject to remodeling by endothelial tip cells (29), facilitating migration through the matrix and playing a crucial role in lumen formation (13). The ECM further presents binding sites for fibronectin and matrix-bound VEGF isoforms that can be cleaved by MMPs.

COMPUTATIONAL MODELING OF ANGIOGENESIS

The modeling of vasculogenesis, the formation of blood vessels during embryogenesis, and angiogenesis has gained increased interest over the last 20 years. An increase in the availability of biological data, along with increased computational capabilities has enabled the formulation and computational exploration of these processes. In the following, we provide a short overview of the modeling work done in the field of angiogenesis, distinguishing between two broad model categories: 1), continuum models; and 2), discrete models, including cellular automata, agent-based models, and cellular Potts (CP) models. A comprehensive and more detailed overview of mathematical modeling in the field of angiogenesis can be found in Mantzaris et al. (30) and in the model comparison sheet (see Supplementary Material, Data S1).

Continuum models

Continuum models aim to describe the large-scale, average behavior of cell populations using a system of partial differential equations. Accordingly, capillary networks are described in terms of endothelial cell densities.

The work of Balding and McElwain (31) can be considered as the onset of continuum modeling of angiogenesis using partial differential equations. In their work, they describe vascular networks by endothelial tip cell and sprout cell densities, showing simulations of the outgrowth of networks in one dimension through the introduction of a chemotactic stimulus. Byrne and Chaplain (32) then considered one-dimensional systems of angiogenesis, which were extended to two dimensions and included effects of haptotaxis as EC-Fibronectin interaction by Orme and Chaplain (33), as well as Anderson and Chaplain (34,35).

The process of bud formation observable in the early stage of angiogenesis was first addressed mathematically by Orme and Chaplain (36). In a one-dimensional domain, reaction-diffusion dynamics and haptotaxis mechanisms lead to an aggregation of endothelial cells forming buds. Levine et al. (37,38) presented models based on the continuum theory of reinforced random walks (39), which described the inception of angiogenesis including accounting for macrophages and pericytes involved in the process of vessel maturation. The continuum model equations are derived from enzymatic Michaelis-Menten biochemical reactions. Levine et al. (40) then coupled these one-dimensional models of bud formation to a two-dimensional model describing the migratory response of endothelial cells within the ECM. This complex model considers the dynamics of tumor angiogenesis factor, protease enzymes, fibronectin, and EC concentrations and included the role of angiogenic inhibitors, namely angiostatin. An extension to this model including a maturation process for ECs and the dynamics of angiopoietin was presented by Plank et al. (41). Mechano-chemical models of vasculogenesis and angiogenesis have been proposed by Manoussaki et al. (42) and Holmes and Sleeman (43). In these models, the ECM is represented as a viscoelastic material interacting with the ECs.

Discrete models

Continuum models provide valuable insight into the processes of angiogenesis but they are limited in their prediction of the structure of vascular networks. To determine the physiology that governs nutrient, oxygen, and drug throughput of such networks, discrete models have been presented, describing the morphology of vascular networks. Discrete models are distinguished as cellular automata, agent-based, and cellular Potts (CP) models. One of the first works describing angiogenesis as a discrete process was introduced by Stokes and Lauffenburger (44). In this agent-based model, a two-dimensional, lattice-free model defines sprouts by the trace of individual tip cells and considers branching to occur according to predefined probabilistic rules. Tip cell migration is governed by a stochastic differential equation accounting for chemotaxis and random motion. The lattice-based model presented by Anderson and Chaplain (34) is derived from the discretization of a two-dimensional continuum model. Tip cells located at discrete lattice points are assigned probabilities to migrate to adjacent lattice points within the next simulation time-step. These probabilities account for chemotactic, haptotactic, and diffusive contributions corresponding to a continuum formulation. Capillaries are represented as masked points on the grid and probabilistic branching rules depend on the sprout age, tumor angiogenesis factor concentration, and the EC density. An extension to three dimensions is presented in Chaplain (35). Sun et al. (45) present a deterministic, two-dimensional model of angiogenesis. The ECM is explicitly modeled by an anisotropic directional field, influencing EC migration and branching behavior. These lattice-based models are based on the theory of cellular automata.

In the literature (46,47), mathematical modeling of flow in capillary networks has been presented in two- and three-dimensional networks, where blood is modeled as a non-Newtonian fluid. These works have been extended to define an interactive description of blood pressure and shear stress dependent vessel remodeling and branching during angiogenesis (48,49). Tip cell migration is determined by chemotaxis, haptotaxis, and random motion. Further, matrix-degrading enzymes released by the ECs are considered to degrade fibronectin in the ECM. More recently discrete agent-based models of angiogenesis have been coupled to models of tumor growth, in two and three dimensions (50,51). CP models were introduced in Glazier and Graner (52) to simulate the adhesion-driven rearrangement of biological cells. CP models have been used to model vasculogenesis by Merks et al. (53) and angiogenesis by Bauer et al. (54). In Bauer et al. (54), two-dimensional simulations of angiogenesis are presented that employ ECM representation consisting of structural cells, fibers, and interstitial fluid. Endothelial cell migration is governed by chemotactic and haptotactic stimuli, and branching and anastomosis occur in response to cell-cell and cell-matrix interactions.

A hybrid model of sprouting angiogenesis

In this article, we present a deterministic, hybrid model of sprouting angiogenesis. The model combines a continuum approximation of VEGF, MMPs, fibronectin, and endothelial stalk cell density with a discrete, agent-based particle representation for the tip cells. The particle representation of individual tip cells enables a grid-independent migration as proposed in Plank and Sleeman (55). Particle-mesh interpolation methods are employed to derive an implicit three-dimensional level-set representation of voluminous vessels. This continuous, grid-independent formulation of the developing capillary network is an extension of the discrete indicator functions considered in existing models. By modeling lumen formation as an implicit process that takes place during angiogenesis, we can derive tubular vessels that allow for blood flow simulations in complex geometries, the subject of ongoing research.

The chemotactic response of ECs to soluble VEGF gradient is considered to be the key driving force of angiogenesis in most mathematical models of sprouting angiogenesis. However, the influence of matrix-bound VEGF isoforms on the branching behavior of ECs (24,25) has not been considered in any model so far. Bauer et al. (54) present studies in the presence of a nondiffusing isoform, distributed according to the initial soluble VEGF profile, but the model does not consider the dynamics of protease-VEGF interactions that play a key role in cleaving the matrix-bound isoform from the ECM. Novelties in this work lie in the consideration of a localized matrix-bound VEGF isoform and its cleaving by proteases (MMPs) (Fig. 1) released at the endothelial tip cells (see Vascular Endothelial Growth Factors). Studies are presented that highlight the effects observable on the vessel geometries.

FIGURE 1.

Conceptual sketch of the different VEGF isoforms present in the ECM. Soluble and cleaved VEGF isoforms freely diffuse through the ECM, whereas matrix-bound VEGF isoforms stick to the fibrous structures composing the ECM and can be cleaved by MMPs secreted by the sprout tips.

Further, the model considers the explicit modeling of the ECM by introducing randomly distributed fiber bundles to influence EC migration and branching. This approach renders the model completely deterministic, removing the random migration component on EC migration (35,55,56). Sun et al. (45) addressed the ECM by a heterogeneous and anisotropic description of conductivity. Similar to this model, the ECM in the work presented herein acts as a tensor on the migration cues given by the VEGF and fibronectin gradients. In Bauer et al. (54), an explicit formulation of the ECM consisting of fibers, structural cells, and interstitial fluid is introduced, influencing EC migration through adhesive forces. This work additionally considers the fibers to offer binding sites for matrix-bound VEGF and fibronectin, which, to the best of our knowledge, has not been considered in mathematical modeling work so far.

Branching is modeled to occur in response to divergence in directional cues given by the VEGF and fibronectin gradients as well as the ECM fiber orientations. Filopodia are modeled explicitly to sense the migration cues in the vicinity of the tip cells, determining the branching direction. No branching probabilities (34,35,55) are introduced. To account for the cell cycle, the model assumes a threshold time span after a branching event has taken place, before which a tip cell cannot proliferate or branch. This is a common assumption that has been included into existing models (34,35,55). Other models that do not depend on probabilistic branching rules are presented in Sun et al. (45) and Bauer et al. (54). In the former, branching depends on the variation of the normal velocity on the transverse tip cell orientation. In the later model, branching occurs without any predefined rule, solely depending on diverging adhesive forces promoted by ECM fibers and structural cells.

HYBRID MODEL OF SPROUTING ANGIOGENESIS

We present the assumptions of the proposed model and their respective computational implementation. This model quantifies several biological assumptions and their dynamic interactions, thus enabling the identification of critical factors in the process of angiogenesis and paving the way for future integration of experimental data (57). We note that these assumptions do not address all the biological processes of angiogenesis and that they may be more pertinent to in vitro angiogenesis rather than in vivo angiogenesis, which is known to depend on the particular microenvironment (58).

Model overview

This model of tumor-induced sprouting angiogenesis distinguishes molecular species and cells. We use a hybrid approach representing molecular species by their concentration and migrating EC tip cells by particles. The evolution of molecular species is governed by reaction-diffusion equations that are discretized on the grid while a particle approach is employed to model the migrating EC tip cells. Newly formed capillaries are in turn represented by the endothelial cell density. The particle and grid descriptions are coupled as the ECs both serve as a source of fibronectin and MMPs and as sink for VEGF (binding to the cell surface receptors). As the tip cells migrate through the ECM following up the chemotactic and haptotactic cues, they define the morphology of the outgrowing sprouts. The migrating tip cells depose ECs along their way leaving a trail of endothelial cell density on the grid. From the voluminous three-dimensional representation of the vessels, a level-set approach can easily be employed to generate tubular structures capable of supporting blood flow. The ECM is explicitly modeled to consist of directed bundles of collagen fibers randomly distributed throughout the domain. A vector field describing the fiber directions modulates the migration velocity of the ECs in the presence of fibers.

Molecular species, cells, cell densities, and matrix properties are defined in Table 1.

TABLE 1.

Molecular species, cells, cell densities, and matrix property definitions

Symbol	Description	Equation or Subsection
[bVEGF]	Concentration of matrix-bound VEGF.	Eq. 1
[cVEGF]	Concentration of cleaved matrix-bound VEGF.	Eq. 2
[VEGF]	Concentration of soluble VEGF.	Eq. 3
[FIB]	Concentration of unbound fibronectin.	Eq. 4
[bFIB]	Concentration of matrix-bound fibronectin.	Eq. 6
[MMP]	Concentration of matrix metalloproteinases.	Eq. 7
[EC]	Endothelial tip cell density.	Parameter Estimation
ρ	Endothelial cell density lining capillary walls.	Eq. 19
K	Vector field representing the fiber orientation in the ECM.	ECM
Eρ	Fiber density in the ECM.	ECM
Eχ	Fiber indicator function in the ECM.	ECM

Model equations

In the following, we state the governing equations of the model, along with the assumptions that they implement. The assumptions are identified by acronyms (V₁) for VEGF through (ECM₃) for the ECM while they are referenced using {V₁}.

Vascular endothelial growth factors

VEGF is implicated as a key regulator of pathological, tumor-induced angiogenesis (10). In this work we assume a source of soluble VEGF (sVEGF), thus implicitly modeling its release from tumor cells (V₁). We consider in addition VEGF isoforms that bind to the ECM matrix-bound VEGF (bVEGF) (V₂).

Matrix-bound VEGF [bVEGF]. Matrix-bound VEGF (bVEGF) does not diffuse and it is assumed to be locally distributed in the ECM (25,59) (V₃). On initialization, bV_n spherical clusters of bound VEGF with radius bV_r and VEGF level bV_l are distributed in the domain. The spheres have a smooth interface mollified by a Gaussian function. The matrix-bound VEGF is then multiplied with the matrix indicator field E_χ to model VEGF binding to the matrix fibers. The bVEGF can be cleaved from the matrix by MMPs released from migrating ECs (24) (V₄). Endothelial cells express surface receptors that bind VEGF molecules (60), thus enabling the migrating tip cells to sense the VEGF concentration in their vicinity and to trigger chemotaxis (14) (V₅).

Matrix-bound VEGF evolution is given by

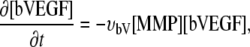(1)

with the cleaving rate υ_bv {V₄}.

Cleaved VEGF [cVEGF]. Cleaved bVEGF (cVEGF) diffuses through the ECM (V₆). Cleaved VEGF as well as soluble VEGF are subject to natural decay (V₇), with the decay rate given by d_V.

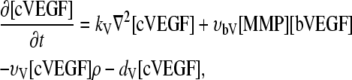(2)

with the endothelial uptake rate of VEGF given by υ_v and the endothelial cell density ρ {V₅}.

Soluble VEGF [sVEGF]. Upon release {V₁}, the soluble VEGF proteins diffuse through the ECM and establish a chemotactic gradient (V₈). Soluble VEGF is subject to endothelial uptake and decay {V_{5, 7}}. The diffusion constant is given by parameter k_V:

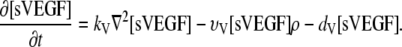(3)

Fibronectin

Fibronectin is a protein binding to cell integrin receptors and to extracellular matrix components (18).

Unbound fibronectin [FIB]. Depending on its local concentration, fibronectin is released by the migrating ECs (17) (F₁). We consider fibronectin released by ECs binding to integrins located at the EC membrane (F₂) and to matrix components such as collagen and fibrin, establishing an adhesive force between cells and fibers in the ECM (18)(F₃). Fibronectin diffuses through the ECM when not bound to the matrix (F₄) with a diffusion constant given by k_F and is subject to natural decay (F₅). The decay rate for unbound fibronectin is given by d_F,

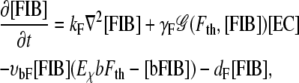(4)

with a creation rate γ_F and creation function

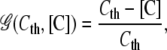(5)

depending on the local fibronectin concentration and the creation threshold level F_th {F₁}. The rate of fibronectin binding to the ECM is given by υ_bF and bF_th is a constant describing the threshold concentration level for bound fibronectin to account for binding site saturation in the ECM.

Matrix-bound fibronectin [bFIB]. Fibronectin is bound by the ECM, inhibiting further diffusion {F₃}. Bound to the ECM, fibronectin is degraded by MMPs at the specific degradation rate δ_bF (F₆) and decays at a rate given by d_bF. The matrix-bound fibronectin establishes a haptotactic gradient for the ECs (1)(F₇):

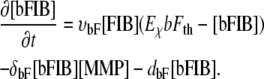(6)

Matrix metalloproteinases (MMPs) [MMP]. Matrix metalloproteinases (MMPs) are proteases involved in the degradation of matrix proteins and the cleavage of cell surface receptors. MMPs cleave the bVEGF isoforms from the binding sites in the ECM (24) (P₁). MMPs are assumed to be released at the migrating ECs depending on the local MMP concentration (15,27) (P₂). The specific release rate is given by γ_M and [EC] describes the endothelial tip cell density. MMP release is stopped when the local MMP level approaches the threshold level M_th. Upon release by the ECs, MMPs are assumed to diffuse through the ECM (P₃) with diffusion constant k_M. MMPs are subject to natural decay (P₄). The decay rate is given by d_M, and the MMP concentration evolves as

(7)

Endothelial cells

Endothelial cells are the constituents of blood vessels and have an active role in sprouting angiogenesis. During angiogenesis, ECs degrade the blood vessel basement membrane and proliferate in the external matrix, forming eventually new networks of blood vessels. ECs are assumed to occur in three states: quiescent ECs lining regular vessel walls; migrating cells located at the tip of outgrowing sprouts; and proliferating ECs located at a small region behind the migrating tip cell.

Sprout tip migration

The migrating tip cells determine the morphology of the outgrowing capillaries with proliferating cells filling the gap between the established sprout and the migrating tip cell (14) (M₁). The migration direction is determined by chemotactic {V₅} and haptotactic {F_2,6} cues in the matrix given by VEGF and fibronectin gradients (1,10,14) (M₂). As the VEGF level increases in the proximity of the tumor and the EC surface receptors become occupied, the cells ability to sense a gradient is affected and the chemotactic cue is attenuated (14,60) (M₃). The attenuation is represented by a function 𝒲. The sprout tip acceleration during migration is defined as

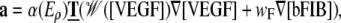(8)

where

(9)

with chemotactic parameters w_V and w_V2 and

(10)

The presence of fibers (E_ρ) enhances the migration speed of ECs as the fibers provide integrin receptors promoting mesenchymal motion of the tip cells (19) (M₄). A very dense matrix slows down the migration speed of the tip cells (13) (M₅) as characterized by the function

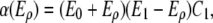(11)

where the threshold E₀ defines the migration factor in the absence of fibers, E₁ the maximal fiber density, and C₁ the ECM migration constant. The collagen fiber bundles composing the ECM provide a guiding structure for EC migration (13,19) (M₆). To model these directional cues, a tensor 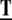is introduced acting on the migration velocity,

(12)

with

(13)

the ECM strength β_K and K being the vector field the tensor is applied on.

The particle positions x_p are updated according to

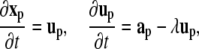(14)

with u_p and a_p being the velocity and acceleration at particle location x_p, and λ the drag coefficient.

Branching

Migrating tip cells extend filopodia equipped with cell surface receptors to sense the surrounding environment for chemo- and haptotactic cues (14) (B₁). The matrix structure may promote diverging migration directions, leading to branching of the endothelial tip cells and creation of new sprouts (25) (B₂). In our model, we locate regions of high anisotropy in the migration acceleration direction field V by a curvature measure k,

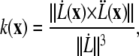(15)

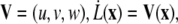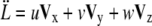with and (61).

Branching occurs in locations where the local curvature k exceeds a threshold level ai_th. To determine the preferred branching direction in three dimensions, six satellite particles are distributed radially around the tip cell particle in a plane perpendicular to the migration direction (Fig. 2) {B₁}. The velocity field is measured at these six locations and the angle between velocities at opposing satellite points is computed. The branching direction is then defined by the two satellite particles with the largest angle between velocities pointing away from the migrating direction. A new tip cell is then created and to guide the two tip cells apart, the particle velocity u_p on the right-hand side of Eq. 14 is changed to u′_p, a combination of the acceleration direction at the satellite and the direction pointing from the sprout tip position to the satellite particle position,

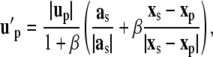(16)

with satellite velocity u_s at satellite position x_s and β = 0.8, resulting in a short acceleration toward the satellite positions. ECs are insensitive to branching cues immediately after a branching event has occurred (1) (B₃). To account for this effect, a sprout threshold age sa_th is introduced. Sprout tips of age smaller than sa_th are not considered for branching.

FIGURE 2.

The figure shows satellite particles placed in the plane perpendicular to the sprout migration direction. The values u₁–u₆ describe the local migration cues at sprout particle location {B₁}.

Anastomosis

Anastomosis, the formation of loops, occurs after the sprout tips have migrated some distance into the ECM and branching has taken place (1). Tip cells fuse either with existing sprouts or with other tip cells (A₁). When a sprout tip fuses with an existing sprout, a loop is closed and migration stops for the sprout tip (A₂). When two sprout tips fuse, a loop is closed and migration is stopped for both tip cells (A₃).

ECM

The ECM consists of fibrous structural glycoproteins such as collagens, elastin, and laminin, giving the ECM structure, strength, and resistance (13,29) (ECM₁). Collagens are the main component of the ECM in humans and cross link with neighboring collagens to form bundles (19) (ECM₂). Other components present in the ECM are cell-matrix adhesion promoting proteins such as fibrin and fibronectin, interstitial fluids like blood plasma, and various growth factors such as VEGF (13) (ECM₃).

In this work, the ECM is modeled as a collection of fiber bundles randomly distributed throughout the computational domain {ECM_1,2}. The ECM is represented by three grid-functions: 1), a vector field K that describes the fiber orientations; 2), a smooth indicator function E_χ, indicating the presence of fibers at any given point in space; and 3), a fiber density field E_ρ, which is used to regulate migration speed according to {M_4,6}.

These fields are constructed in a straightforward manner by generating Fb_n random fibers with a given length Fb_l, which is constant for all fibers. These fibers are then put on the grid much like lines are rasterized in computer graphics (62). In the case of K, the directions are rasterized onto the grid, and in the case of E_χ, we tag the grid points at the fiber locations with a value of 1, resulting in randomly distributed fibers.

The fields K and E_ρ are filtered with a Gaussian filter to achieve a smooth matrix representation. In the case of E_χ this is not possible, so the field is constructed by using smoothed fibers. In cases where fibers overlap, the maximum value of the two fibers is retained.

METHODS

The time-step constraint for diffusion on the molecular species is stricter than for the reaction part. A fractional step algorithm is used to solve the system efficiently. In this algorithm the nonlinear and linear reaction parts of the equations are solved simultaneously using explicit Euler steps. The linear diffusion part is solved using implicit time steps. The systems can be safely decoupled, as EC cell migration occurs on a much smaller timescale than molecular diffusion and steady state can be assumed for the source and sink of the different proteins. VEGF, fibronectin, and acceleration gradients for migration velocity and the curvature measure are calculated on the grid using second-order finite differences. To get the acceleration and curvature on the particle at location x_p = (x_p, y_p, z_p), mesh-particle interpolations are done using the M′₄ kernel

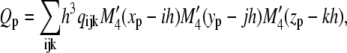(17)

with

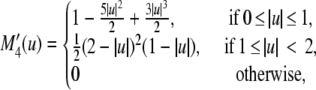(18)

with the grid value q_ijk at grid point [i, j, k] and grid spacing h. To interpolate the sprout tip density onto the grid, particle-mesh interpolations are performed using a fourth-order B-spline kernel. In the presence of only one particle, the B-spline kernel guarantees positive values for [EC] at all grid locations.

Endothelial cell density

To obtain the endothelial cell density defining the capillary sprouts, at every time step, we interpolate the sprout tip cell density Q_p at x_p onto the grid using a fourth-order B-spline kernel B₄ and add the maximum of the interpolated sprout tips and the ρ-field onto the ρ-field,

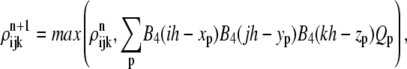(19)

with particle weight Q_p, and mesh size h, with n denoting the n^th time step.

COMPUTATIONAL DETAILS

Parameters

In the development of computational models of angiogenesis, a key issue is the estimation of parameters of the governing equations. Results from biological experiments provide a range of values for some parameters, such as the VEGF diffusion coefficient, uptake, and decay rates. On the other hand no experimental data has been provided so far for other parameters like MMP cleaving rate, bound VEGF distribution, and friction coefficient for the endothelial cell migration. In this article, we formulate the equations in nondimensional form and then use values for the parameters as they have been reported in the literature or we infer values of certain parameters based on parameters for related processes. An integrative experimental, computational study to quantify values for the parameters of our models is the subject of ongoing research activities.

Nondimensionalizing the parameters

We nondimensionalize the equations by scaling the concentrations c of the various substances with a maximum threshold concentration c₀ and the endothelial cell density [EC] with the close packing cell density [EC]₀.

Concentrations:

(20)

Further, we scale the distance with the domain size D_l, and time with 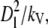where k_V is the VEGF diffusion coefficient.

Space and time:

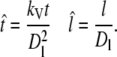(21)

Rescaling our set of parameters, we obtain the nondimensionalized set of parameters.

Model parameters:

(22)

Parameter estimation

Table 2 shows the estimated values of parameters in our model. These estimates were based on experimental data reported in the references. When no reference measurements were available, the parameters were estimated on data given for similar species. For model parameters such as the drag coefficient λ, anisotropy threshold level ai_th, or the ECM strength β_K, parameters were chosen to suit the model.

TABLE 2.

Model parameter values

Parameter	Description	Unit	Reference	Value
[VEGF]0
[FIB]0	Maximal concentration of molecules.	Mol cm−3	(22,34,45)	10−13
[MMP]0
[EC]0	Endothelial cell close-packing density.	EC cm−3	(12,45)	106
Dl	Domain length.	cm	(22)	1.5 × 10−1
kV	VEGF diffusion constant.	cm2 s−1	(11,34,45,54)	6 × 10−7
υbV	MMP-VEGF cleaving rate.	[VEGF]s−1 cm−3	—	2.67 × 108
υV	VEGF uptake rate of ECs.	[VEGF][EC]−1 s−1	(11,54)	2.67 × 10−23
dV	VEGF decay rate.	cm−1	(45,54)	1.8 × 10−5
kF	Fibronectin diffusion constant.	cm2 s−1	(34)	3 × 10−8
γF	EC release rate of fibronectin.	[FIB][EC]−1 s−1	—	3 × 10−22
υbF	Fibronectin-ECM binding rate.	[FIB]−1 s−1	—	2.67 × 108
δbF	MMP-fibronectin degradation rate.	[FIB]−1 s−1	—	2.67 × 109
dF	Fibronectin decay rate.	s−1	—	1.8 × 10−3
Fth	Fibronectin threshold level for creation.	[FIB]cm−3	—	10−10
dbF	ECM bound fibronectin decay rate.	s−1	—	1.8 × 10−5
bFth	Maximal fibronectin binding sites in ECM.	[FIB]cm−3	—	5 × 10−12
kM	MMP diffusion constant.	cm2 s−1	—	6 × 10−8
γM	EC release rate of MMPs.	[MMP][EC]−1 s−1	—	3 × 10−22
dM	MMP decay rate.	s−1	—	2.67 × 10−6
Mth	MMP threshold level for creation.	[FIB]cm−3	—	10−13
wV	Chemotactic parameter.	cm5[VEGF]−1 s−1	—	6 × 105
wV2	Chemotactic coefficient.	cm3[VEGF]−1	—	10−11
wF	Haptotactic parameter.	cm5[FIB]−1 s−1	—	5 × 10−14
λ	Drag coefficient.	—	—	0.95
βK	ECM strength.	—	—	0.95
Fbn	Number of fiber bundles.	—	—	105
Fbl	Fiber bundle length.	—	—	1.17 × 10−2
Fbi	Fiber bundle density.	—	—	1.2
E0	ECM constant.	—	—	0.05
E1	ECM constant.	—	—	1.0
C1	ECM constant.	—	—	4.0
bVn	Number of pockets of matrix-bound VEGF.	—	—	3.7 × 103
bVl	Level of VEGF in pockets.	cm−3[VEGF]	—	2.5 × 10−14
bVr	Radius of VEGF pockets.	cm	—	1.2 × 10−3
sath	Sprout threshold age for branching.	d	—	2.1
aith	Threshold level of anisotropy in ECM for branching.	—	—	15
Qp	Endothelial cells density at sprout.	cm−3 EC	—	106

Model parameter values

We use the estimates from the table above to define our nondimensional set of model parameters. Model parameters that are dimensionless will be assigned to the value defined in the table. For ease of understanding, we drop the hats from the notation of the nondimensional variables and from now on only refer to nondimensional variables:

(23)

The results reported in the article are based on simulations using the above values unless stated otherwise.

Initial and boundary conditions

The computational domain is defined as a cube of size 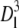discretized with a 128³ uniform grid. In the following, we set D_l = 1 and all spatial dimensions are appropriately normalized. A source of VEGF, representing a tumor, is distributed on the y-z plane at x = 1, which is at the boundary of the domain. Five vessel sprouts are initially placed along a line at z = 0.5 on the y-z plane at x = 0.0. The locations of the sprouts are at y = 0.15625, 0.3125, 0.46875, 0.625, and 0.78125 (see Fig. 3).

FIGURE 3.

The figure shows a conceptional x-z plane through the computational domain. Five sprout tips are initially placed on the y-z plane lower-end of the domain in x direction; a tumor source of soluble VEGF is modeled at the upper-end in x direction outside the computational domain.

The tumor source of VEGF is modeled via a Dirichlet boundary condition in the x direction for the governing equations of the soluble VEGF, with [sVEGF] = 1.0 at x = 1.0 and [sVEGF] = 0.0 at x = 0.0. For all other concentrations, we apply homogenous Neumann boundary conditions in the x direction. In y and z directions we apply periodic boundary conditions for all molecular species. Matrix-bound VEGF is distributed throughout the domain equally in y and z directions with an increased concentration toward the boundary at x = 1, accounting for the tumor as a source of VEGF. The distribution is given by

(24)

For the capillary sprouts, we apply periodic boundary conditions in y and z dimension. Sprouts leaving the domain in x direction are eliminated from the simulation. We note that periodic boundary conditions in the y and z dimensions imply homogeneity of the process in these directions. The use of periodic conditions can be justified when phenomena from the image domains do not interfere with the process of angiogenesis in the main domain. This is indeed the case in these simulations for the times that have been simulated.

RESULTS

We report results on the blood vessel morphology as influenced by large-scale parametric studies of the structure of the ECM, the distribution of matrix-bound VEGF, and the intensity of cell-cell and cell-matrix adhesion. These three-dimensional simulations are novel as they include explicitly soluble and bound growth factors, they account for the fibrous structure of the ECM and its binding sites for fibronectin, and they investigate their effects on guidance cues and endothelial cell migration. We present statistics of the branching points, branch lengths and frequency of anastomosis providing a quantitative, comparative analysis that may guide future experiments and simulations. See Movie S2 for a video of the simulation.

Matrix structure

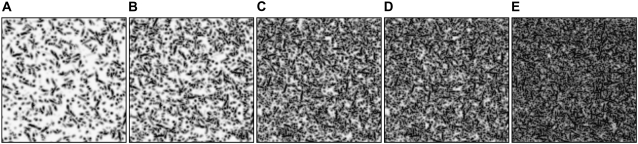
We first assess the effects of the ECM density on the resulting vessel networks. Random fiber fields were created with five different densities: 15,000 fibers resulting in a volume density of 6%; 30,000 fibers (11%); 70,000 fibers (26%); 100,000 fibers (38%); and 200,000 fibers (75%) (Fig. 4). The normalized volume density is given by the sum of the fiber density E_ρ over all grid points divided by the number of grid points. For each density value we performed 32 simulations with a different random seed for the fiber placement. If not stated otherwise, all results presented herein are ensemble averages over these 32 instances. Comparing the number of branches found in the computational domain at T = 22.0 (Fig. 5), we find a linear increase of the number of branches for logarithmic increasing fiber density up to a threshold density at ∼40%. After this point, the number of branches can be observed to decrease again. Examples of the structure of the corresponding vessel networks are depicted in Fig. 6: in very low density ECMs, hardly any branching occurs, while in very dense ECMs the EC sprouts branch very often. In the 75% density case the fiber density is high enough to impair the migration which leads to shorter capillary networks (Fig. 6 E).

FIGURE 4.

Slice of the [ECM] field for five different densities: (A) 6%, (B) 11%, (C) 26%, (D) 38%, and (E) 75%.

FIGURE 5.

Influence of the matrix density on the number of branches of the vessel network (error bars represent standard deviation of data).

FIGURE 6.

Capillary networks for different ECM densities: 6% (A), 11% (B), 26% (C), 38% (D), and 75% (E).

Haptotaxis

We investigated the effect of the weight of the haptotactic cues. We performed simulations with six different values for w_F (0.001, 0.005, 0.025, 0.125, 0.25, 0.5, and 1.0) in an ECM with a fiber density of 26%. We found no discernible effects on the length of the vessel branches (Fig. 7). As haptotactic cues become stronger the average number of branches in a vessel network is greatly reduced (Fig. 8). The reason for this behavior becomes evident when we inspect the morphology of the vessel networks (Fig. 9 ): we observe that an increased influence of fibronectin (i.e., increased values of w_F), results in narrower networks and an increased frequency of anastomosis (Fig. 10) Haptotaxis essentially represents a very localized autocrine directional cue, and thus serves as a recruiter for neighboring vessels.

FIGURE 7.

Effect of fibronectin weight w_F on branch lengths: mean branch length at t = 20.0 (error bars indicate standard deviation of data).

FIGURE 8.

Effect of fibronectin weight w_F on the number of vessel branches: average number of branches at t = 20.0 (error bars indicate standard deviation of data).

FIGURE 9.

Effect of cell-cell haptotaxis (w_F) on the vessel network morphology: w_F = 0.001 (A), w_F = 0.125 (B), and w_F = 1.0 (C).

FIGURE 10.

Effect of fibronectin weight w_F on the probability of branch fusion events at t = 20.0 (error bars indicate standard deviation of data).

Matrix-bound VEGF

To investigate the effect of matrix-bound VEGF we performed simulations with a decreased threshold age for branching of sa_th = 4 and an increased branching threshold level of anisotropy ai_th = 45. The model parameters governing the MMP evolution are set to: k_M = 0.01, γ_M = 250, and d_M = 100 and haptotaxis is switched off: w_F = 0.0. In a first set of simulations, we varied the amount of matrix-bound VEGF, distributing 500, 1400, 3700, and 10,000 pockets holding a VEGF level of bV_l = 0.25. With an increased number of pockets, we observed an increase in the number of branches (Fig. 11). The pockets induce strong chemotactic cues (Fig. 12). The probability of sprout tips hitting a pocket is increased for a higher pocket density, leading consequently to an increase in branching.

FIGURE 11.

Effect of number of VEGF pockets bV_n on the number of branches (error bars indicate standard deviation of the data). The horizontal line denotes the average number of branches for the case of no bound-VEGF; the dashed lines represent the standard deviation for that case.

FIGURE 12.

Effect of MMPs cleaving matrix-bound VEGF on chemotactic cues and anisotropy at pocket location for bV_n = 3700 and bV_l = 0.25: t = 13.21 (A), t = 16.89 (B), and t = 20.63 (C). The white cloud in the left figure denotes the MMP concentration; the orange dots indicate pockets of matrix-bound VEGF. The figure in the middle shows the evolution of the acceleration field at pocket location (see also Movie S1).

In a second set of simulations, we varied the VEGF level, comparing runs with 3700 pockets containing a VEGF level of bV_l = 0.01, 0.03, 0.09, and 0.25 (Fig. 13). We observe an increase in branching along with an increase in the VEGF level. The results show that not only the density of bound VEGF but also the pocket level has an effect on branching behavior. This is attributed to the MMPs cleaving the matrix-bound VEGF, effectively reducing the chemotactic cues together with the level of anisotropy at pocket location (Fig. 12). As pockets are being cleaved before the sprout tips reach them, their influence on the branching and migration behavior is reduced. For pockets with a low VEGF level, the cleaving removes most VEGF from the pocket before the sprout tips get there, making the influence of bound VEGF dependent on the level of the pocket.

FIGURE 13.

Effect of VEGF level bV_l on the number of branches (error bars indicate standard deviation of the data). The horizontal line denotes the average number of branches for the case of no bound-VEGF; the dashed lines represent the standard deviation for that case.

Comparing branch lengths in the absence of bound VEGF to the case of 100,000 distributed pockets (Fig. 14), no significant variation is observed in the mean branch length. The distributions of the two settings however vary considerably, leading to a narrower distribution in the branch length for the simulations including bound VEGF.

FIGURE 14.

Histogram of branch lengths for no bound VEGF (open bars), and 100,000 VEGF pockets (shaded bars).

Investigating the probability of anastomosis, we found an increase in the number of sprout fusions for an increasing number of pockets distributed (Fig. 15 ). Note that a similar effect has been observed for an increase in the weight of haptotactic cues. Comparing, however, the probability of anastomosis against the number of branches, we find that matrix-bound VEGF has quite an opposite effect on the fusion probability than the haptotactic cues. The morphology of the vessels (Figs. 16 and 17) indicates that the distributed VEGF introduces deviation in the migration of sprout tips toward pocket location, whereas the haptotactic cues introduce directed deviation toward existing sprouts (Fig. 9).

FIGURE 15.

Relationship between the average number of branches and the probability of anastomosis: varying the number of bound-VEGF pockets (solid circles), and increasing haptotaxis (open circles).

FIGURE 16.

Effect of pocket number of matrix-bound VEGF (bV_n) on the vessel network morphology: bV_n = 500 (A), bV_n = 1400 (B), bV_n = 3400 (C), and bV_n = 10,000 (D).

FIGURE 17.

Evolution of angioegenesis (red) in the presence of matrix-bound VEGF (blue). Bound VEGF is cleaved by MMPs (not shown) (see also Movie S3).

CONCLUSIONS

We presented a three-dimensional model of sprouting angiogenesis that incorporates for the first time, to the best of our knowledge, effects of the extracellular matrix structure on the vessel morphology and considers both soluble and matrix-bound growth factor isoforms.

The model is used to perform large-scale parametric studies to assess the vessel morphology as influenced by the structure of the ECM, the distribution of matrix-bound VEGF, and the intensity of cell-cell and cell-matrix adhesion. The simulations demonstrate that the structure and density of the ECM has a direct effect on the morphology, expansion speed, and number of branches observed in computationally grown vessel networks. The simulations reflect the influence of the extracellular matrix composition on endothelial cell migration and network formation corresponding to observations made by the literature (13,18,19). Simulation results presented for sprouting angiogenesis in the presence of matrix-bound VEGF isoforms demonstrate an increase in the number of observed branches for an increase in both the amount of distributed VEGF pockets and the level of VEGF at pocket location. In addition, a strong effect on the sprout morphology can clearly be observed. These results are consistent with the findings made by the literature (24,25) on sprouting angiogenesis in the presence of matrix-bound VEGF. With the number of branches depending on the matrix structure and level of matrix-bound VEGF isoforms, this model may be easier to tune against experiments compared to most other models where branching is modeled as a purely probabilistic process.

The method is formulated as a generalized particle method and is implemented upon a parallel particle-mesh framework (63); this renders the method scalable to massively parallel computer architectures, a crucial aspect for the study of angiogenesis at macroscopic scales, and integrative models of vascular tumor growth. The grid-independent particle representation of migrating tip cells provides a way to generate smooth vessel networks. Particle-to-mesh and mesh-to-particle interpolation schemes provide a straightforward way of coupling the two levels of representation. Limitations of the current model are related to the explicit definition of tip cells restricting the formation of new sprout tips to predefined locations on the initial vasculature. After initiation, new sprout tips can only emerge from branching migrating tip cells. Formulation of a tip cell selection method combined with cell-type-specific migration and proliferation rules are the subject of current work. We are currently working on addressing these limitations and on developing methods for vessel maturation and simulations of blood flow through the matured networks. The integration of this framework in studies of tumor-induced angiogenesis is a subject of coordinated investigations with experimental groups.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.