Saccades Exert Spatial Control of Motion Processing for Smooth Pursuit Eye Movements

Abstract

Saccades modulate the relationship between visual motion and smooth eye movement. Before a saccade, pursuit eye movements reflect a vector average of motion across the visual field. After a saccade, pursuit primarily reflects the motion of the target closest to the endpoint of the saccade. We tested the hypothesis that the saccade produces a spatial weighting of motion around the endpoint of the saccade. Using a moving pursuit stimulus that stepped to a new spatial location just before a targeting saccade, we controlled the distance between the endpoint of the saccade and the position of the moving target. We demonstrate that the smooth eye velocity following the targeting saccade weights the presaccadic visual motion inputs by the distance from their location in space to the endpoint of the saccade, defining the extent of a spatiotemporal filter for driving the eyes. The center of the filter is located at the endpoint of the saccade in space, not at the position of the fovea. The filter is stable in the face of a distracter target, is present for saccades to stationary and moving targets, and affects both the speed and direction of the postsaccadic eye movement. The spatial filter can explain the target-selecting gain change in postsaccadic pursuit, and has intriguing parallels to the process by which perceptual decisions about a restricted region of space are enhanced by attention. The effect of the spatial saccade plan on the pursuit response to a given retinal motion describes the dynamics of a coordinate transformation.

Introduction

Retinal inputs provide sensory drive for visually guided behaviors. Because the eyes move continuously, the retinal locus of a stimulus cannot provide unambiguous guidance about the correct location of objects in space. Yet, spatial information drives many behaviors. For example, saccadic eye movements are based on the location of targets in space, not on the retinal locus activated by a momentary flash (Mays and Sparks, 1980). Transformation of inputs that enter the brain in retinal coordinates into spatial behavior is a fundamental sensorimotor process. Saccadic selection of moving targets for smooth pursuit eye movements provides a specific example of this transformation that lends itself particularly well to study.

Recent reports have established that visual motion processing for smooth pursuit eye movements can be altered dynamically by saccades. An example occurs when a single target moves across a locus eccentric from the fovea: the initial pursuit response is weak, but the response after the saccade is strong, as if the visual motion drive for pursuit has been enhanced. Similarly, if two moving targets are present, the saccade to one is an oculomotor choice: postsaccadic smooth eye velocity is dominated by visual inputs from the moving target at the endpoint of the saccade, even if the initial pursuit was driven by the other target (Gardner and Lisberger, 2001, 2002; Liston and Krauzlis, 2005). These results illustrate the ability of the spatially specific saccade plan to enhance motion inputs that arise in a retinal coordinate frame. The preferential treatment of the motion of one target at the expense of the others resembles cued spatial attention.

Three features of perceptual attention parallel the effects of saccades on subsequent pursuit. First, both specify a region of space for enhanced processing: saccades determine the location of target motion to be preferentially processed by pursuit while spatial attention enhances perception at a region of space. Second, both can be triggered by the saccade plan. For pursuit, even subthreshold stimulation in the superior colliculus (SC) biases the subsequent pursuit choice toward targets in the movement field of the excited neurons (Carello and Krauzlis, 2004). For perception, stimulation of the frontal eye fields (FEFs) with current too weak to evoke a saccade is sufficient to cause the responses of extrastriate neurons in area V4 to mimic the effects of cued attention (Moore and Armstrong, 2003). Similarly, microstimulation in the SC enhances attentional processing in a spatially selective manner (Muller et al., 2005). Third, both depend on modulation of response gain. Target choice for pursuit reflects in an increase in the response to specific visual motion inputs. Likewise, attention manifests itself as increases in the gain of neural responses for stimuli falling within a restricted spatial locus. If the behavioral effects of target choice for pursuit and perceptual attention are so similar, then perhaps they use similar neural mechanisms.

We tested the hypothesis that saccades enhance the processing of visual motion within a specific spatial location, just as does cued attention. We show that the gain of the pursuit response to a given target motion is weighted spatially, by the distance from the endpoint of the upcoming saccade to the spatial location of the target. We propose that a spatial filter anticipating the movement of the eyes controls the gain of visual-motor transformation for pursuit.

Materials and Methods

Subjects and equipment.

Four male monkeys (Macaca mulatta) were used in experiments approved by the Institutional Animal Care and Use Committee of the University of California, San Francisco. All experimental procedures were in accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals. Briefly, eye position was monitored using the scleral search coil technique while the head was held stationary using custom hardware that had been implanted on the monkey's skull during sterile surgery under isoflurane anesthesia. Surgical procedures have been reported before (Ramachandran and Lisberger, 2005). All monkeys were experienced in smoothly tracking visual targets for a fluid reward, and needed no additional behavioral training for this study.

In a dimly lit room, visual stimuli were projected onto the back of a tangent screen placed 114 cm in front of the monkey. Projecting a stationary red light-emitting diode onto the center of the screen generated a fixation spot. The position of the tracking target, which was a small white 0.5° spot, was controlled by reflecting a beam of light off a pair of two orthogonal mirror galvanometers. Many of the experiments described here implicitly rely on displacing the target instantaneously; the galvanometers could complete our largest step (9°) within 4 ms. To verify that our data were not affected by the visual streak generated during the displacement, we also presented targets using two separate pairs of galvanometers and shutters to illuminate different targets before and after displacement, eliminating the visual streak. We did not find any differences in the results for the two methods of target presentation, and data from both are included.

Data collection and analysis.

Stimuli were presented as a series of trials, where each trial represented a different set of target trajectories, and the order of the trials was randomized. Each trial began when the fixation target appeared for a random time (500–1100 ms), followed by the appearance of the tracking target. The target usually appeared slightly eccentric (0–1.5°) to the position of fixation and immediately moved toward the position of fixation. On one-half of the trials, the target moved for a short interval (100–200 ms) and then underwent a step change in position, sometimes changing its direction of motion or speed as well. Whether or not the target underwent this step, it continued moving for a random duration (600–800 ms) during which the monkey was required to keep his gaze within 2° of the tracking target. Whenever the target was displaced, the monkey was allowed a 300 ms grace period when fixation requirements were suspended so that he could catch the target and complete the trial. In each experiment, all variables such as the initial and postdisplacement direction of motion were balanced to discourage any sort of learning, as well as efforts to anticipate the target motion. Monkeys were rewarded with droplets of fluid for ∼95% of all attempted trials they completed. They typically worked until satiated, for ∼1500–2500 trials.

Horizontal and vertical eye position signals were sampled at 1 kHz on each channel and differentiated digitally using a balanced difference algorithm over a 2 ms time window. The differentiated traces then were filtered digitally using a two-pole Butterworth filter with a cutoff at 25 Hz. For a discussion of the effects of filtering on the measurement of postsaccadic eye velocity, see Lisberger (1998). An automated threshold-crossing algorithm marked the beginning and end of each saccade with a threshold at 50°/s; the ends of the saccades were provisionally estimated to occur 15 ms after eye velocity crossed back below threshold. For target motion at 10°/s, we lowered the threshold to 40°/s to catch smaller saccades. After provisional marking of saccade start and end by the automated algorithm, all trials were inspected and, if necessary, the saccade marks were adjusted by hand using custom software. The measurements reported in this paper rest on a precise identification of saccade initiation; to confirm that our algorithm gave excellent results, we remarked the saccades by hand for selected experiments on the basis of the initial deflection on eye velocity traces that had been generated on-line using an analog circuit. The circuit differentiated signals up to a cutoff at 25 Hz and filtered signals of higher frequencies. Because the analog filter was causal, the latter assessment of the time of the start of the saccade is uncorrupted by the smoothing that arises with zero-phase digital filtering. Results did not depend on how the saccade start and end were determined.

Our analysis used standard statistical methodology, including t tests and linear regression techniques. Data were fit to simple linear models in a least-squares sense, and the p values for slopes and y-intercepts were estimated by generating a t statistic for each. We fitted plots of postsaccadic eye velocity as a function of the duration of the motion that drove it with either a sigmoid (1) or an exponential (2) as follows:

For these equations, m represents the slope of the function, τ the time constant, and β the point at which it reaches one-half of its maximum value. When fitting the sigmoid, we used only eye velocity data that had been normalized to the mean eye velocity on control trials; this removed our subjects' spatial bias from the analysis. Curve-fitting was done in a least-squares sense, using Levenberg–Marquardt minimization; 95% confidence intervals (CIs) were estimated from the residuals. To find the time at which the sigmoid was at 10 and 90% of its maximal value, we solved Equation 1 for t. The original data used in this paper, analysis code, and figure-generation code are available on the internet (http://keck.ucsf.edu/∼schoppik/).

Results

A stimulus paradigm for controlling the distance between tracking target position and saccade endpoint

Our experiments tested the hypothesis that saccades enhance the processing of visual motion inputs for pursuit in proportion to the proximity of the target to the endpoint of the saccade. We began by designing a behavioral task that would allow us to control the location of a moving target relative to the endpoint of a saccade, by disrupting the usual accuracy of saccades to moving targets. Specifically, we contrived for monkeys to make a saccade to a target that was no longer where they expected it to be, but instead had been displaced some distance at carefully controlled moments. Our approach bears some resemblance to the well explored double-step paradigm (Becker and Jurgens, 1979), and to remapping experiments in the parietal cortex (Duhamel et al., 1992).

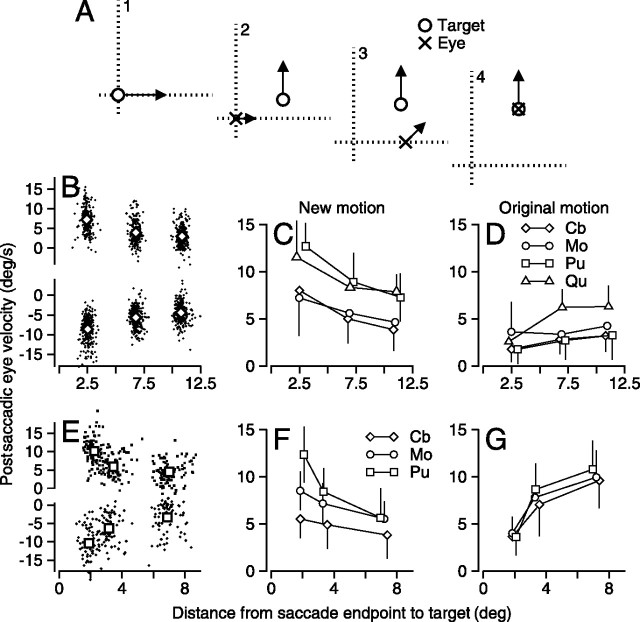
Our task, which can be described in four intervals, is diagrammed in two ways in Figure 1. First, the set of four Cartesian plots in Figure 1A1–A4 provide snapshots of both target and eye motion for each interval. Second, for an example trial, Figure 1B plots the position of the eyes and the target as a function of time, and Figure 1C similarly plots velocity. The black bars with numbers over them delineate the duration of each of the four intervals specified in Figures 1A1–A4, allowing the reader to cross-reference between the spatial and temporal presentations.

Figure 1.

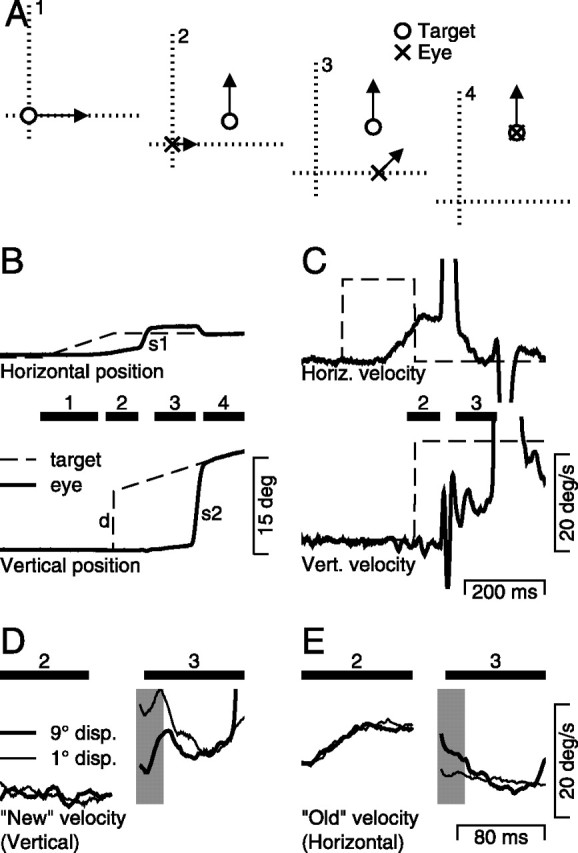
Schematic diagram of the behavioral task and sample responses. A, The task is shown in spatial coordinates as a sequence of four snapshots. In each panel, the open circle and the cross indicate the position of the target and eye. A1, Starting just off fixation point, the target moves to the right at 20°/s. A2, The eye moves rightward in response to the initial target motion, while the target steps up (the “new” position) and begins moving upwards at 20°/s (the “new” motion). A3, The eye makes a rightward saccade driven by the predisplacement location of the target, while the target continues to move up. A4, A second saccade takes the eye directly to the target, which is then tracked appropriately. B, The horizontal and vertical components of eye (solid line) and target (dashed line) positions are plotted as a function of time. Black bars with numbers over them mark the periods corresponding to the schematic in A. The labels “d,” “s1,” and “s2” mark the target displacement to the new position and motion, and the first and second saccades. C, The horizontal and vertical components of eye velocity (solid line) and target velocity (dashed line) as a function of time. The bold, horizontal bars correspond to intervals 2 and 3. D, E, Same data as in C, but with the time base expanded so that data are shown only for intervals 2 and 3. In D and E, the thick and thin lines show responses when the size of the target displacement was 9 and 1°, respectively, whereas the shaded vertical rectangles indicate the interval used for analysis.

Each trial begins with a brief period of fixation, after which the target moved rightward (Fig. 1A1). The initial motion of the target was designed both to necessitate a rightward saccade and to drive the initiation of pursuit. The short-latency pursuit response is shown as a small black arrow pointing rightward in Figure 1A2 (second interval). For the duration of the second interval, the initial saccade plan is locked in; the animal is now committed to use the target position at the end of interval 1 to drive a rightward saccade. During the second interval, however, the motion of the target changes: it is displaced vertically 0, 1, 5, or 9°, and its direction of motion changes from horizontal to vertical. In the third interval (Fig. 1A3), we see the consequences of the saccade planned to the target position in interval 1. The rightward saccade takes the eyes to the “wrong” location; however, the postsaccadic pursuit, which must be driven by presaccadic target motion, has already incorporated both the “old” target motion of interval 1 and the “new” target motion of interval 2 (diagrammed by an arrow moving both up and to the right). By analyzing the component of eye motion in the direction of the “new” target motion, as a function of the jump size, we test the hypothesis that the target motion affects pursuit eye velocity with a gain related to the location of the new target motion in space. Finally, in interval 4 (Fig. 1A4), the monkey makes a corrective saccade to the new location of the target, tracking accurately for a brief period of time to receive his reward.

Figure 1B diagrams the eye and target positions as a function of time, whereas Figure 1C similarly diagrams the corresponding velocities. The initial horizontal target motion marks the beginning of interval 1, and the eye's horizontal smooth response can be seen slightly before interval 2. The vertical target displacement and subsequent motion (marked “d”) marks the beginning of interval 2. The initial saccade (marked “s1”), driven by the horizontal target trajectory, defines the end of interval 2. Before the beginning of interval 3, the change in eye position is entirely horizontal, bringing the eye ahead of the target. At the end of saccade “s1,” interval 3 begins; the eye velocity traces reveal that despite the switch from horizontal to vertical target velocity, both horizontal and vertical eye velocity are present up until the point of the second, corrective saccade (marked “s2”), which marks the start of interval 4.

The success of our experiment depends on correctly timing the length of interval 1. The endpoint of saccade “s1” must be determined by the original position of the moving target, but the saccade latency must be long enough for pursuit to have seen the new target motion. Because pursuit has a shorter latency to respond to the new target motion, we can hope that interval 2 will interpose up to 100 ms of new target motion between displacement “d” and saccade “s1.” As a consequence, postsaccadic eye velocity is driven by the new target motion and is our dependent variable. Furthermore, because we displaced the target at the start of interval 2, the new motion is some distance above the endpoint of the first saccade, and so the distance from the endpoint of the saccade to the target becomes our independent variable. To ensure that the monkeys did not simply withhold their saccades until the target had changed direction, 50% of trials were controls in which the target did not change its trajectory, and the monkey received his reward by tracking accurately to the end of the trial.

On ∼45% of the trials, the monkey made his first saccade before the target had changed direction (interval 1 was too long) or made a saccade directly to the postdisplacement location of the target (interval 1 was too short); both outcomes are to be expected when the target trajectory changes in this manner (Lisberger et al., 1975). Such trials were excluded from additional analysis, because the presaccadic motion took place too close to the spatial endpoint of the saccade. After excluding control trials (50% of all trials) and those with unsuitable saccade timing (45–48% of all trials), we were left with usable trials that represented 2–5% of the all trials the monkeys performed. For the analyses in Figures 2–5, we further restricted the trials we analyzed to those in which the duration of the new motion was >50 ms. As a result, many days of experiments were needed to obtain sufficient data.

Figure 2.

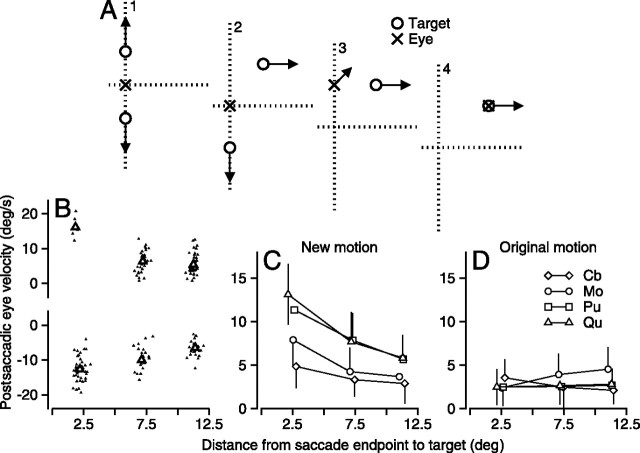
Relationship between postsaccadic eye velocity and the distance from the endpoint of the saccade to the target position when the direction of new motion was orthogonal to the original motion. A, Same schematic as Figure 1. B–D, Analysis of data when target displacement was orthogonal to the original motion, as shown schematically in A. E–G, Analysis of data when target displacement was parallel to the original motion. B, E, Plots of postsaccadic eye velocity in the direction of new motion as a function of the distance between target and eye at the end of the saccade for individual monkeys. Dots show data for individual trials, and larger symbols (diamonds in B for monkey Cb and squares in E for monkey Pu) show means for the three different amplitudes of displacement of target position. Positive and negative values of postsaccadic eye velocity were taken from trials in which the new target motion was upward or downward. C, F, Means and SDs of postsaccadic eye velocity in the direction of new motion for all monkeys used in each experiment. Different symbols correspond to different monkeys. E, G, The mean and SD of postsaccadic eye velocity in the direction of the original motion. The graphs in C and D summarize data for experiments in which the original direction of motion was horizontal and new motion vertical, whereas in F and G, original motion was vertical and new motion was horizontal. Before averaging, we took the absolute velocity of all eye velocities.

Figure 3.

Relationship between postsaccadic eye velocity and the distance from the endpoint of the saccade to the target position in the presence of a distracter. A, Schematic diagram showing the task as a sequence of four snapshots in time. A1, Two targets (open circles) began moving in opposite directions away from the fixation point and the eye (x). A2, One of the targets is displaced and begins to move orthogonally, whereas the other continues along the original trajectory. A3, A saccade is made to the old location of one of the targets, and the eyes begin to move smoothly; the second target disappears. A4, A saccade was made to the new location of the target, followed by proper tracking. B, Plot of postsaccadic eye velocity in the direction of new motion as a function the distance between target and eye at the end of the saccade for one monkey. Dots show data for individual trials, and larger symbols show means for the three different amplitudes of displacement of target position. Positive and negative values of postsaccadic eye velocity were taken from trials in which the new target motion was rightward or leftward. C, Means and SDs of the absolute value of postsaccadic eye velocity in the direction of new motion for all monkeys used in each experiment. Different symbols correspond to different monkeys. D, The mean and SD of the absolute value of postsaccadic eye velocity in the direction of the original motion.

Figure 4.

Relationship between postsaccadic eye velocity and the distance from the endpoint of the saccade to the target position when the first saccade is aimed at a stationary target. A, Schematic diagram showing the task as a sequence of four snapshots in time. A1, A target (open circle) appears stationary but offset from the current position of the eye (x). A2, The target steps and moves to the right at 20°/s. A3, A saccade is made to the old location of the target, and the eyes begin to move smoothly along the direction of target motion. A4, The eye saccades to the new location of the target and tracks it appropriately. B, Plot of postsaccadic eye velocity in the direction of new motion as a function the distance between target and eye at the end of the saccade for one monkey. Dots show data for individual trials, and larger symbols show means for the three different amplitudes of displacement of target position. Positive and negative values of postsaccadic eye velocity were taken from trials in which the new target motion was rightward or leftward. C, Means and SDs of the absolute value of postsaccadic eye velocity in the direction of new motion for all monkeys used in each experiment. Different symbols correspond to different monkeys.

Figure 5.

Effect of the distance from the endpoint of the saccade to the target position on the relationship between postsaccadic eye velocity and target speed. A, Schematic diagram showing the task as a sequence of four snapshots in time. A1, A target (open circle) began moving at the fixation point at 20°/s. A2, The target stepped and moved at a speed indicated by the marker: 10°/s (black filled circle), 20°/s (open circle), or 30°/s (gray circle). Only one target was visible to the monkey on the trial. The eye (x) begins pursuit in the direction of initial target motion. A3, The eye makes a saccade to the old location of the target and moves in the same direction. Only the 20°/s target is shown for clarity. A4, The eye makes a saccade to the new location of the target and tracks it appropriately. B, Four graphs plotting the mean and SD of the absolute value of postsaccadic eye velocity against the distance between target and eye, for three different speeds of target motion. Different axes and markers correspond to different monkeys. Black-filled markers are trials in which the target slowed to 10°/s, open markers are ones in which the target continued to move at 20°/s, and gray-filled markers are ones in which the targets sped up to 30°/s.

Finally, although it may appear as if the second saccade has a shorter latency than the first saccade, when measured relative to the onset of the driving target motion, they are quite similar. The average delay from the time the target changed position and direction to this second saccade (d→s2) was 141 ms (±28 ms SD). The average delay from the onset of target motion to the first saccade was similar at 146 ms (±32 ms). The time between the onsets of the first and second saccades (s1→s2) averaged 82 ms (±36 ms). As would be expected in a double-step-like task, the endpoints of the saccade were not influenced by the ongoing pursuit, and had a bimodal distribution, landing either directly on the target, or at the “incorrect” location.

A spatial filter for processing motion direction around the endpoint of a saccade

The expanded eye velocity traces in Figure 1, D and E, show examples of how the distance between the moving target and the endpoint of the saccade itself affects postsaccadic eye velocity. Each panel shows the eye velocity along one component, for two trials: one with a 1° step (thin traces) and one with a 9° step (thick traces). Figure 1D illustrates the eye velocity responses along the axis of new motion, here vertical, and Figure 1E illustrates the eye velocity responses along the axes of old motion, here horizontal. Compared with when the step was 1° (thin traces), the vertical, or new, component of postsaccadic eye velocity (Fig. 1D) at the start of interval 3 was smaller and the horizontal, or old, component (Fig. 1E) was larger when the target had been displaced 9° (bold traces) from the endpoint of the saccade. Consequently, pursuit was more nearly vertical when the endpoint of the saccade was close to the vertically moving target. Alternately, when the endpoint of the saccade was far from the vertical motion, pursuit was more nearly horizontal.

The records in Figure 1, D and E, present an example of our basic finding, and also underscore the challenges of performing and analyzing these experiments. First, both the horizontal and vertical eye velocity traces in the time between interval 2 and interval 3 are contaminated by rapid deflections associated with the saccade to the previous location of the original rightward-moving target. We have previously provided a detailed evaluation of the challenges of measuring immediate postsaccadic eye velocity and we are confident that the differences demonstrated in Figure 1, D and E, are well beyond the time when eye velocity is related directly to the saccades themselves (Lisberger, 1998). Second, because the feedback loop closes quickly after the end of the saccade, by design, our analysis is based on a brief 20 ms interval (Fig. 1D,E, shaded rectangle) when eye velocity depends on the distance from the endpoint of the saccade to the moving target. As the pursuit system naturally corrects the difference between target and eye velocity, the eye velocity traces for target displacements of 1 and 9° converge quickly, although they are quite different during the period under study.

Figure 2B uses data from monkey Cb to illustrate how we quantified the results of our experiments. Each of the 1672 points represents the postsaccadic pursuit velocity in a single trial plotted as a function of the radial distance in space between the target and the eye at the endpoint of the saccade. Variation in the latency and accuracy of the monkey's first saccade causes scatter along the x-axis for each cluster of points, and variation in the postsaccadic eye velocity causes scatter along the y-axis. The experiment summarized in Figure 2B contained targets that began to move along the horizontal meridian. In 50% of the trials, targets then stepped 1, 5, or 9° vertically and moved either upward or downward, shown as points plotted at negative or positive values along the y-axis. Both the clouds of points from the individual trials and the averages for monkey Cb (open diamonds) show that the postsaccadic vertical eye velocity depended strongly on the distance from the endpoint of the saccade to the spatial location of the new motion. Trials were included in this analysis only if the first saccade landed within 1° of the horizontal meridian, and if the interval of new motion was at least 50 ms long. Requiring a longer period of target motion before the saccade would have revealed larger effects, but at the cost of including fewer trials, a feature of the data that we will document later.

To summarize the results, we inverted the eye velocity traces from the trials that ended with downward motion, so that we could combine the data from both directions of target motion as if the new motion always had been upward. We then averaged the data for each displacement of target position (0/1, 5, or 9°) and plotted the mean and SD of postsaccadic eye velocity as a function of the mean distance from the target position to the eye position at the endpoint of the saccade (Fig. 2C). For all four monkeys, the postsaccadic eye velocity in the direction of the new target motion was largest when the distance between the target and eye position at the endpoint of the saccade was smallest. Postsaccadic eye velocity declined as the distance increased. In the same trials, the eye velocity response to the original, horizontal target motion showed the opposite trend (Fig. 2D); the greater the distance from target to saccadic endpoint, the faster the eyes moved along the original component of motion.

Statistical evaluation supported the qualitative effects seen in Figure 2B–D. Regression lines were fit to the collection of single-trial measurements from each monkey individually; complete statistical information can be found in Table 1. The mean slope across monkeys was −0.45 ± 0.14 (SD), and the mean y-intercept was 10.72 ± 2.88 (SD). All slopes and y-intercepts were significantly different from zero (p < 0.001). In Figure 2D, the mean slope was 0.35 ± 0.20 (SD), but was significantly different from zero for only two monkeys. The absence of a strong effect in Figure 2D is attributable to relationships we will document later between postsaccadic eye velocity in the original and new directions of motion and the duration of the interval of new motion.

Table 1.

Parameters of linear regression for text and Figures 2–4

Monkey, figure	No. trials	Slope (95% CI)	y-Intercept (95% CI)	R 2	F	p
Cb, 2C	1672	−0.50 (0.04)	8.96 (0.29)	0.28	664.81	0
Mo,2C	459	−0.28 (0.08)	7.74 (0.69)	0.09	44.85	0
Pu, 2C	42	−0.61 (0.26)	14.02 (2.13)	0.36	22.84	0
Qu, 2C	29	−0.41 (0.30)	12.15 (2.29)	0.22	7.71	0
Cb, 2D	1672	0.17 (0.02)	1.48 (0.16)	0.12	230.76	0
Mo, 2D	459	0.06 (0.09)	3.41 (0.71)	0	1.63	0.20
Pu, 2D	42	0.15 (0.20)	1.55 (1.66)	0.05	2.21	0.14
Qu, 2D	29	0.40 (0.20)	2.10 (1.57)	0.38	16.40	0
Cb new, text	1295	−0.18 (0.03)	5.48 (0.25)	0.08	111.31	0
Mo new, text	621	−0.10 (0.05)	7.59 (0.40)	0.03	17.76	0
Pu new, text	117	−0.47 (0.18)	12.55 (1.43)	0.19	26.94	0
Qu new, text	295	0.21 (0.09)	8.14 (0.64)	0.07	21.72	0
Cb old, text	1295	0.04 (0.40)	3.01 (0.30)	0.27	378.05	0
Mo old, text	621	0.46 (0.56)	1.95 (0.48)	0.27	230.14	0
Pu old, text	117	0.47 (0.13)	3.30 (1.06)	0.30	49.91	0
Qu old, text	259	0.37 (0.08)	3.06 (0.59)	0.21	81.87	0
Cb, 2F	188	−0.34 (0.13)	6.21 (0.66)	0.12	25.65	0
Mo, 2F	138	−0.52 (0.14)	9.20 (0.64)	0.28	52.32	0
Pu, 2F	285	−1.13 (0.81)	13.51 (0.81)	0.39	184.40	0
Cb, 2G	188	1.02 (0.15)	2.46 (0.76)	0.48	173.06	0
Mo, 2G	138	1.04 (0.16)	3.04 (0.73)	0.54	158.95	0
Pu, 2G	285	1.12 (0.16)	3.03 (0.81)	0.39	182.00	0
Cb, 3C	278	−0.22 (0.07)	5.39 (0.52)	0.12	37.69	0
Mo, 3C	141	−0.52 (0.13)	9.00 (0.95)	0.31	61.20	0
Pu, 3C	286	−0.66 (0.10)	13.00 (0.80)	0.35	154.62	0
Qu, 3C	181	−0.78 (0.13)	14.30 (1.05)	0.45	149	0
Cb, 3D	278	−0.15 (0.07)	3.88 (0.47)	0.07	21.56	0
Mo, 3D	141	0.24 (0.10)	1.92 (0.74)	0.13	21.61	0
Pu, 3D	286	0.01 (0.06)	2.48 (0.49)	0	0.21	0.64
Qu, 3D	181	0.03 (0.09)	2.46 (0.73)	0	0.44	0.51
Cb, 4C	248	0 (0.11)	4.45 (0.91)	0	0	0.96
Mo, 4C	780	−0.35 (0.06)	7.60 (0.50)	0.15	133.23	0
Pu, 4C	211	−0.61 (0.12)	10.41 (1.02)	0.31	93.92	0
Qu, 4C	615	−0.41 (0.07)	9.34 (0.56)	0.17	123.38	0

In the left column, the first entry indicates the monkey. When the data appeared in a figure, the second entry indicates the figure panel. When the data was mentioned only in the text, the second entry indicates whether the regression is for the old or new direction of motion, and the third entry is “text.”

We repeated the experiment in Figure 2A–D, with the motion rotated so that the original direction was vertical, and the new direction horizontal (data not shown) (details for each monkey in Table 1). Statistical evaluation demonstrated the same decrease in postsaccadic eye velocity with increasing distance between the target and the endpoint of the saccade. For four monkeys, neither the mean slope in the new direction, –0.14 ± 0.28 (SD), nor the mean y-intercept, 8.44 ± 2.97 (SD) was different from the data shown in Figure 2C (paired t test; p > 0.06; p > 0.08). Similarly, neither the mean slope in the old direction, 0.20 ± 0.14 (SD), nor the mean y-intercept, 2.83 ± 0.60 (SD), was different from the data shown in Figure 2D (paired t test; p > 0.36; p > 0.42).

To control for the effect of step direction, we also conducted a variation of the experiment in Figure 2A–D where the step of target motion at the start of interval 2 was parallel to the initial motion of the target, rather than orthogonal. Otherwise, the experimental design was the same: at the time of the target step, the direction of smooth target motion changed so that it was orthogonal to the original motion, and the amplitudes of the target steps again were 1, 5, or 9°. The step always moved the target away from the position of fixation, and the experiment was run only with target motion that was initially vertical and then changed to new motion that was horizontal.

For an example monkey (Pu), the cloud of points of postsaccadic eye velocity from individual trials (n = 285) and the averages (Fig. 2E, squares) indicate that the speed of eye motion in the direction of the new target motion was related inversely to the distance between target and eye position at the endpoint of the saccade. For all three monkeys tested on this experiment (Fig. 2F), the same trend is visible in the plots of average postsaccadic eye velocity as a function of the distance from the endpoint of the saccade to the target. Furthermore, for all three monkeys, the postsaccadic eye velocity in the direction of the original target motion scaled proportionately with the distance to the endpoint of the saccade (Fig. 2G). The fact that the new direction of motion was horizontal, the monkeys' best axis of pursuit, led to a better illustration of this feature of our data in Figure 2G than in Figure 2D. Statistical analysis supported the trends seen in the graphs. For eye velocity in the new direction of target motion, the mean slope of the three regression lines fitted to all trials from each monkey independently was −0.66 ± 0.41 (SD), and the mean y-intercept was 9.64 ± 3.67 (SD). Neither the slopes nor the y-intercepts for Figure 2F were significantly different from those for Figure 2C (two-tailed paired t test; p > 0.4). For eye velocity in the original direction of target motion (Fig. 2G), the mean slope of the relationship between postsaccadic eye speed and distance from saccade endpoint to target was 1.06 ± 0.06, and the mean y-intercept was 2.84 ± 0.33. Here, unlike Figure 2D, the slopes and y-intercepts were significant for all three monkeys tested (p < 0.001).

The data in Figure 2 show that the pursuit response to a given target motion is modulated by the distance from the endpoint of the saccade to the target. The modulation is consistent with the conclusion that a spatial filter surrounds the endpoint of a saccade. If the target is near the center of the spatial filter, its motion has priority access to the pursuit system and dominates the smooth eye velocity response.

Distracter targets do not affect the spatial filter

In experiments like that diagrammed in Figure 3A, interval 1 provided two targets moving in opposite directions along the vertical axis. The monkey was free to saccade to either target, and each had an equal likelihood of undergoing a displacement and a change to a new, horizontal direction of motion in interval 2, just as in the experiments of Figure 2. Software detected saccades, determined which target the monkey had chosen, and turned off the remaining target, allowing the monkey to track only one target and receive a reward. Trials were not included in the analysis if the monkey chose the target that did not displace (∼25% of all trials), or if neither target was displaced (50% of all trials). When the monkey chose the target that did displace, his behavior was mostly the same as during the single target case, in that his saccade was too early or late most of the time (∼23% of all trials), leaving us with only ∼2% of all trials for analysis.

Figure 3B shows the results of the experiment for one monkey (Qu). Each of the 181 points shows the pursuit response on a single trial. The y-axis plots the horizontal component of postsaccadic eye velocity when the step of target position in interval 2 was to the right or left (points plotting at positive or negative values on the y-axis); the x-axis shows the radial distance between target and eye at the end of the saccade. Both the clouds of points for the individual trials and their means (open triangles) indicate that the postsaccadic horizontal eye velocity tends to be slower when the distance from the endpoint of the saccade to the horizontally moving target is larger. The same relationship appears in the means of postsaccadic horizontal eye velocity of all four monkeys (Fig. 3C). Regression lines were fit to all trials from each monkey separately; detailed statistics are in Table 1. The regression slope of eye velocity versus distance for four monkeys averaged –0.55 ± 0.24, the y-intercept averaged 10.42 ± 4.04, and neither the slope nor the y-intercept was statistically different from those for the two experiments summarized in Figure 2 (two-tailed paired t test; p > 0.3). Regression analysis was performed on all trials that went into Figure 3D, and detailed statistics can be found in Table 1. As in Figure 2D, the relationship between original postsaccadic eye velocity and the distance from the eye to the target at the endpoint of the saccade is unimpressive (Fig. 3D).

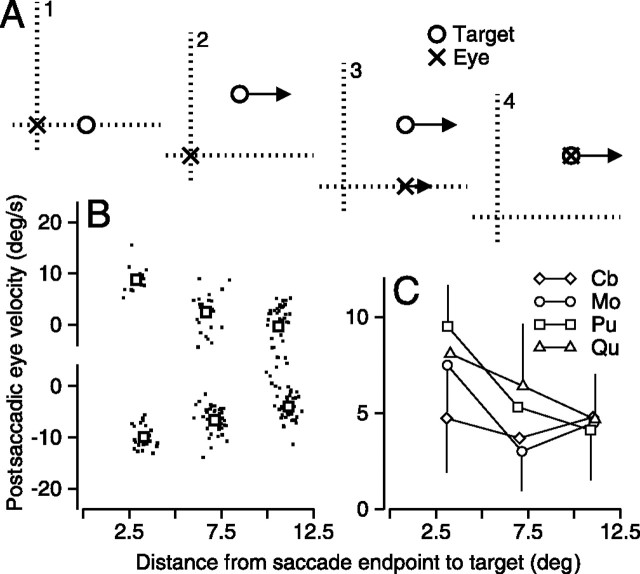
The spatial filter exists for saccades to stationary targets

The experiment diagrammed in Figure 4A follows same structure used before, except that in interval 1, the target does not move smoothly. Each trial began with the monkey fixating straight ahead. At the start of interval 1, the fixation target disappeared and another target appeared 3° eccentrically along the horizontal meridian, to provide the stimulus for a saccade. In interval 2, the target steps vertically and begins to move horizontally. The target remained stationary in 50% of the trials to encourage the animal to make a timely and accurate saccade; these control trials were removed from additional analysis.

As before, a falloff in postsaccadic eye velocity as a consequence of the distance between target and saccadic endpoint appears in the clouds of points for individual trials for one monkey (Fig. 4B), the means for those trials (Fig. 4B, open squares), and the means for all four monkeys used in this experiment (Fig. 4C). Regression lines were fit to data from all trials for each monkey separately, and detailed statistics can be found in Table 1. Coefficients for one monkey (Cb) were not significantly different from zero, indicating that a regression model was not appropriate. As such, his data were excluded from the following summary statistics. The average regression slope for the remaining three monkeys in Figure 4C was −0.46 ± 0.14, and the y-intercept was 9.12 ± 1.42. Neither the slope nor the y-intercepts were significantly different from those for the experiments summarized in Figures 2 and 3 (two-tailed paired t test; p > 0.15). For this experiment, it did not make sense to show plots of the orthogonal, vertical eye velocity, because there was never any vertical target motion.

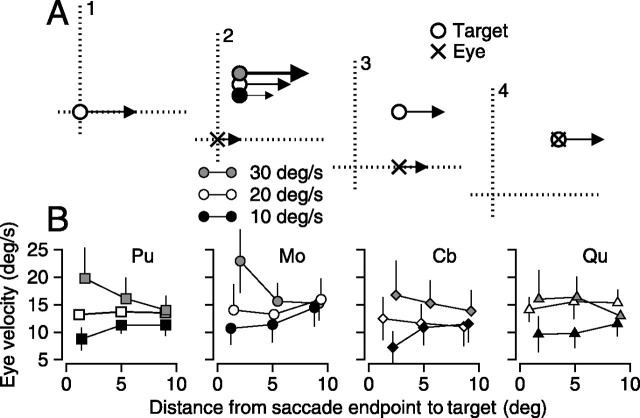
Processing of target speed within the spatial filter

The experiment diagrammed in Figure 5A has the same basic structure as the previous experiments but alters postdisplacement target speed, rather than direction. In interval 1, the target started from straight ahead gaze and moved to the right. At the start of interval 2, after the initiation of pursuit, but before the monkey executed a catch-up saccade for the initial target motion, the target stepped to a location that was 1, 5, or 9° off the horizontal meridian and continued to move in the same direction. At the time of the target step, the target either continued at its original speed of 20°/s (Fig. 5A, white circle), or changed to 10 or 30°/s (black and gray circles, respectively). As a result, the new motion comprised one of the three target speeds that was present in interval 2, before the catch-up saccade; the speed of new motion should affect postsaccadic eye velocity more strongly when the distance from the target to the eye position at the endpoint of the saccade is small, and less or not at all when the distance is large.

For each of the four monkeys, the effect of the speed of the new target motion on postsaccadic pursuit depended on the distance from the endpoint of the saccade to the target. For the smallest distances of ∼1°, the postsaccadic eye velocity was highest for new target motion at 30°/s (Fig. 5B, gray symbols), intermediate for new target motion at 20°/s (white symbols), and lowest for new target motion at 10°/s (black symbols). For the largest distances of ∼9°, the postsaccadic eye velocities are much more similar for the three target speeds. For the intermediate distances, the separation of the responses for the three target speeds also was intermediate. We performed two statistical analyses to quantify our observations. First, we compared the y-intercepts of regression lines fitted to the relationship between postsaccadic eye velocity and distance from saccade endpoint to target for each of the three final target speeds. When the presaccadic target speed was 10, 20, or 30°/s, the y-intercept was 9.05 ± 0.85, 13.45 ± 0.67, and 20 ± 3.56. All differences in y-intercept were statistically significant (t test; p < 0.05). Second, we ran an ANOVA using the speed of new motion (df = 2) and the size of the target step (df = 2) as factors on all data points (n = 2928). There was a main effect of the size of the target step, and no main effect of speed (F = 6.29, F = 0.53; p < 0.01, p = 0.53). Supporting our observations, there was an interaction between the size and speed (p < 0.01). Post hoc comparisons across factors failed to reach significance.

The effect of target speed on the postsaccadic eye velocity for a given distance between saccade endpoint and target is diagnostic for how strongly the new visual motion just before the saccade affects pursuit. Thus, the results in Figure 5 indicate that speed is processed within the spatial filter for pursuit, as is direction.

Frame of reference of the spatial filter for pursuit

The experimental design used so far shows that there is a spatial filter for pursuit, because the postsaccadic eye velocity depends on the location of the moving target relative to the endpoint of the saccade. However, it does not resolve the frame of reference of the spatial filter. In all of our experiments so far, the target was displaced away from both the endpoint of the saccade and the current location of the fovea. As such, our previous experiments cannot disambiguate whether the spatial filter is positioned in relation to the location of the target on the retina before or after the saccade. The experiment diagrammed in Figure 6A can do so.

Figure 6.

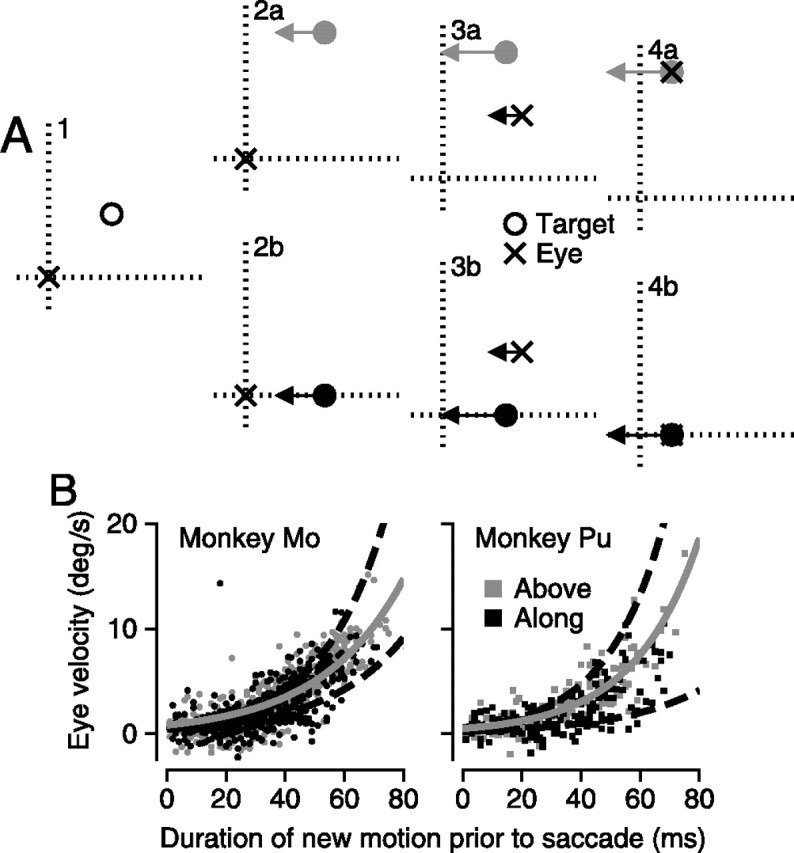
Analysis of the frame of reference of the relationship between postsaccadic eye velocity and the distance from the endpoint of the saccade to the target position. A, Schematic diagram showing the task as a sequence of four snapshots in time. A1, A stationary target (open circle) appeared 3° above and to the right of the eye (x). A2a,b, The target could follow one of two trajectories. It could step 3° upwards and begin moving to the left, “above” trials indicated by a gray-filled circle. Or it could step 3° downward to the horizontal meridian and begin moving to the left, “along” trials indicated by a black-filled circle. A3a,b, The eye makes a saccade to the original location of the target and begins to move smoothly to the left. A4a,b, The eye makes a saccade to the correct location of the target and continues to track it smoothly. B, Graphs that plot eye velocity as a function of the duration of target motion before the first saccade for two monkeys. Gray and black dots show data from individual trials in which the target stepped so that it moved either above or along the horizontal meridian. The solid gray curves show the exponential fit to the “above” trials, whereas the two dashed black curves delimit the 95% confidence intervals on the fit to the “along” data.

Each trial began with the monkey fixating straight ahead. At the start of interval 1, the fixation target disappeared and another target appeared eccentrically at 3° up and right. At the start of interval 2, before the saccade, the target stepped 3° up or down and began to move back toward the vertical meridian either along the horizontal axis (Fig. 6A, interval 2b, “along”) or along a parallel line 6° off the axis (Fig. 6A, interval 2a, “above”). Once the monkey makes a saccade to the original location of the target at 3° up and right, these two options disambiguate the coordinate system of the spatial filter. For both the “above” and “along” target motions, postsaccadic eye velocity is driven by new target motion that is ∼3° from the eye position at the endpoint of the saccade. If the spatial filter is centered on the endpoint of the saccade, then the responses to either target motion should be the same, because in both cases, the motion is 3° from the endpoint of the saccade. However, the “above” and “along” target motions provide new target motion at quite different retinal eccentricities just before the saccade. The target motion along the horizontal meridian is very close to the fovea, whereas the target motion that is above the meridian is >6° eccentric. If the filter is centered in retinal coordinates on the fovea just before the saccade, then postsaccadic eye velocity should be larger for the target that stepped back to the horizontal meridian.

Postsaccadic eye velocity was the same for both target trajectories. The symbols in Figure 6B plot two monkeys' postsaccadic eye velocity on individual trials, as a function of the duration of the new target motion that caused the pursuit response. The duration was defined as the interval between the step and ramp of target position at the start of interval 2 and the monkey's saccade at the start of interval 3. Postsaccadic eye velocity increased as a function of the duration of motion exposure, and the data overlapped extensively for the along target motion (black symbols) and above target motion (gray symbols) for both monkeys. To quantify this claim, we fitted an exponential to the data (Eq. 2), and calculated the 95% confidence intervals for our fit. The gray line representing the fit to the “above” trials sits well within the black dashed lines, which show the 95% confidence intervals of the fit to the “along” trials, demonstrating that the response of the pursuit system under these different conditions cannot be distinguished. For monkey Mo, the latency (β) and time constant (τ) were 0.19 and 0.04 for 471 “along” trials; for 436 “above” trials, β and τ were –0.64 and 0.04. For monkey Pu, β and τ for 148 “along” trials were –0.69 and 0.05; for 153 “above” trials, β and τ were −0.99 and 0.04. We conclude that the spatial filter for pursuit is centered on the endpoint of the saccade: the location of new motion relative to the endpoint of the saccade is more important in determining the magnitude of pursuit than is the actual retinal location of the target.

Dynamics of processing in the spatial filter for pursuit

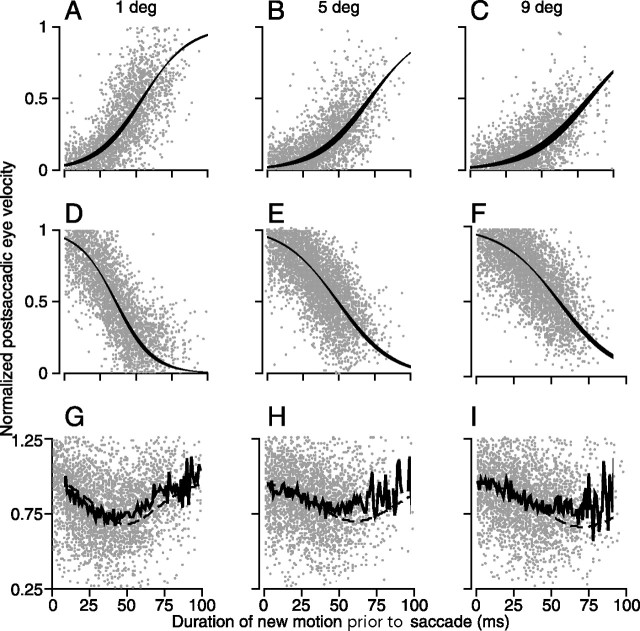
Figure 6B shows that postsaccadic eye velocity depends strongly on the duration of the new motion before the saccade. Figure 7A–F analyzes these dynamics further by replotting the data from the experiments reported in Figure 2 and the accompanying text. Recall that, in these experiments, the targets were displaced and assumed an orthogonal direction of motion at the start of interval 2. In Figure 7, for each of the three different step sizes (0/1, 5, or 9°) described earlier, we plot horizontal eye velocity when it was in the direction of new target motion in Figure 7A–C, and when it was in the direction of old target motion in Figure 7D–F. The gray clouds of points show normalized postsaccadic eye velocity as a function of the duration of new motion for each individual trial from four monkeys. Eye velocity was normalized relative to the average postsaccadic eye velocity measured on control trials in the same experiment, when the target started to move horizontally and continued without any changes.

Figure 7.

Temporal dynamics of the modulation of visual-motor transmission for pursuit. All plots show normalized horizontal postsaccadic eye velocity as a function of the duration of new motion before the beginning to the targeting saccade. Normalization was performed relative to the postsaccadic eye velocity on control trials in which a single target moved horizontally. Graphs are grouped by rows, which show a particular type of experiment, and columns, which show data when the displacement of the target was 1, 5, or 9°. In each graph, the tiny gray dots show the responses in individual trials across all four monkeys. A–C, Data from the experiment described in Figures 1–2. Initial target motion was vertical, and the new target motion was horizontal. The graphs plot the time course of the increase in postsaccadic eye velocity in the direction of new motion. D–F, The original direction of motion was horizontal, and the new direction of target motion was vertical. The graphs plot the time course of decay of the response to the old, horizontal target motion. In A–F, the black ribbons show the best fitting sigmoid function with the 95% confidence intervals on the fit. G–I, Data from the experiment diagrammed by open circles in Figure 5A, in which the target underwent a vertical displacement but continued to move horizontally at 20°/s so that the original and new motions were the same. The jagged solid line corresponds to the mean of the data. The dashed line shows the sum of the sigmoid fits from the data in the two graphs directly above each of the bottom graphs.

Figure 7A–C show that longer durations of presaccadic target motion in the new direction caused larger postsaccadic eye velocities. The duration of the rise from zero to 90% of maximal response is between 90 and 130 ms, and is similar to the initial response of the smooth pursuit system to optimal step-ramp target trajectories. For a direct comparison between the two, see Lisberger (1998), his Figure 5. The data are well approximated by the sigmoid curve in each graph; the solid ribbon shows 95% confidence intervals around the best fitting curve. Details about the fits and the exact values of the sigmoid can be found in Table 2. Figure 7D–F shows that postsaccadic eye velocity in the direction of original motion declines as a function of the duration of the new motion. The data could again be summarized by the superimposed decreasing sigmoid functions plotted as ribbons to show their 95% confidence intervals. The functions describing the decrease in postsaccadic eye velocity are related to the offset of the pursuit response, as analyzed in Luebke and Robinson (1988), their Figure 4; Soechting et al. (2005), their Figure 5B; and throughout Krauzlis and Lisberger (1994). The parameters of the sigmoid fits to the data (Eq. 1) reveal how the location of the visual stimulus within the spatial filter affects the dynamics of the gain of visual–motor transformations for pursuit. As shown in Table 2, the slope decreased and the half-maximum time of the best fitting sigmoid increased as a function of the distance from the saccade endpoint to the target. Thus, gain of visual–motor transformations rises more quickly to a higher level at the center of the spatial filter.

Table 2.

Parameters of sigmoid fits to dynamics of visual motion processing for pursuit

Step size	Slope (95% CI)	Half-maximum (95% CI)	No. trials	Time at 0.10	Time at 0.90
0/1°, new	0.061 (0.003)	53.9 (0.8)	2814	18.94	90.01
5°, new	0.053 (0.003)	73.4 (1.36)	3055	30.67	112.82
9°, new	0.045 (0.003)	86.3 (2.23)	3161	37.04	129.54
0/1°, old	−0.066 (0.003)	36.0 (0.7)	3446	64.24	7.39
5°, old	−0.050 (0.002)	52.4 (0.88)	4737	88.89	9.03
9°, old	−0.048 (0.003)	58.9 (1.21)	4234	97.38	12.76

Data are graphed in Figure 7.

The time courses of gain modulation in Figure 7 allow us to explain why the values of postsaccadic eye velocity in the direction of the original target motion were small and not strongly related to the duration of new motion in Figures 2D and 3D. Figure 7D–F indicates that postsaccadic eye velocity in the original direction of target motion decays quite rapidly, reaching 10% of its maximum value when there had been as little as 65 ms of new motion (Table 2). Because we included data in our graphs only if there had been in excess of 50 ms of new motion, the values of postsaccadic eye velocity should be small and therefore the effects of the distance from the endpoint of the saccade to the target difficult to see.

Motion processing within the spatial filter reflects the weighted vector superposition of old and new target trajectories

The bottom row of the graphs in Figure 7 plots data for the trials from Figure 5, in which the target moved horizontally at 20°/s, and underwent a step displacement but did not change direction or speed. Although the same direction and speed of target motion was present both before and after the step change in target position, the clouds of points in Figure 7G–I suggest a parabolic shape that is clarified by averaging the normalized eye velocity in 1 ms bins to yield the functions shown by the bold, jagged curves.

The transient dip in the relationships between postsaccadic eye velocity and the duration of the visual motion stimulus even when the target has not changed speed or direction suggests that a step of target position initiates two simultaneous components of the pursuit response: decay of the response to the original motion and build-up of a response to the new target motion. To test this hypothesis, we added the paired functions derived from the data in the first two rows of Figure 7, which provide direct estimates of the time courses of build-up and decay of the horizontal pursuit response. For each size of target step, the resulting curves (Fig. 7G–I, dashed curves) predict the means of the actual data quite well, diverging only as the number of points becomes small when the duration of “new” motion approaches 75–100 ms. The analysis in Figure 7 provides direct support for the conclusions of Soechting et al. (2005), who showed that the pursuit response to an abrupt change in target direction could be described as the vector superposition of two discrete responses.

The graphs in Figure 7G–I explain why the average postsaccadic eye velocity did not depend on the distance from the saccade endpoint to the target when the target underwent a step of position but did not change speed or direction (Fig. 5B–E, open symbols). Under these conditions, the expected change in postsaccadic eye velocity is subtle, and the effect of distance is only visible as a function of time.

Discussion

We have demonstrated that target motion is processed preferentially to guide smooth pursuit eye movements within a symmetric spatial region around the endpoint of a saccade. When the initial target motion at one location in one direction is followed closely by new target motion at a new location, the resulting pursuit eye movement reflects a weighted vector superposition of the two. The weighting is related to, and varies dynamically in time as a function of, the spatial distance between the endpoint of the saccade and the target. Intuitively, visual motion signals stimulating the foveal retina ought be more effective in driving pursuit; given the latency of visual processing, this effect would first be detectable ∼100 ms after the saccade brings the eye to point at the target. Instead, our results demonstrate that the weighting change is present immediately after the saccade and therefore, because of the latencies in sensory-motor processing for pursuit, must begin before the saccade. Thus, the pursuit system anticipates the spatial location of target motion with respect to the endpoint of a saccade, and responds unhampered by the visual latency. Our discussion will make the case that this very specific oculomotor interaction affords a comprehensive and mechanistic description of gain control for smooth pursuit eye movements.

Old and new concepts of gain control for pursuit

There is a marked difference between presaccadic and postsaccadic smooth eye velocity when comparing responses at comparable times after the onset of target motion (Lisberger, 1998; Ogawa and Fujita, 1998). Lisberger (1998) suggested that postsaccadic enhancement could be thought of as one consequence of a “volume control” turned to a high setting by the execution of a saccade. Gardner and Lisberger (2001, 2002) demonstrated that the saccade-driven increase in pursuit gain was inextricable from more cognitive processes of decision-making. When confronted with the motion of two targets, pursuit generates an initial, presaccadic eye velocity that is a weighted vector average of the independent responses to the two targets. A natural or electrically evoked saccade to one target is sufficient to drive postsaccadic smooth pursuit preferentially by the motion of the target closest to the endpoint of the saccade. The selective change in pursuit gain is sufficient to instantiate a “choice” between the two targets.

We propose a single model of pursuit that can explain our data as well as two previous observations: smooth pursuit results from a stereotyped response to visual motion, in which the response is modulated by a spatial filter that operates as though it moves with the eye. First, Lisberger and Westbrook (1985) demonstrated the existence of a comparable spatial filter in their exploration of the consequences of initial target eccentricity on presaccadic pursuit. They attributed the modulation to weaker visual motion signals from more eccentric retinal locations. Although the filter described in the present paper is centered on the endpoint of the saccade, rather than the current position of fixation, their filter is remarkably similar. Second, the temporal dynamics of the filter, revealed in our Figure 7 and Lisberger (1998), his Figure 5, follow a time course remarkably similar to that of the “best” presaccadic eye velocity initiated by a target that ramps toward the position of fixation from just eccentric (Lisberger and Westbrook, 1985). Given the similarity of the spatial and temporal properties of the filters that affect both presaccadic and postsaccadic pursuit, it seems reasonable to conclude that they are mediated by the same neural mechanisms. The saccade plan represents the upcoming locus of the fovea; as the plan is formulated and executed, the locus of the strongest positive modulation of visual motion inputs moves to the upcoming location of the fovea.

Liston and Krauzlis (2003, 2005) have proposed a different explanation based on data that fit well with ours. They used the shorter latency of pursuit to study the response of the oculomotor system to two targets. They contrived a situation in which the initial pursuit response could be in a different direction than the eye movement after a saccade, and studied pursuit dynamics in the presaccadic period. They posit that a single high-level “decision process” coordinates the tracking response, forcing the smooth eye movement to match that of the target closest to the endpoint of the saccade. Their data are consistent with our proposal for the role of the saccade: the formulation and execution of the saccade plan itself provides the “decision signal” for the pursuit system by enhancing the transmission of visual motion signals from the region of space at the endpoint of the saccade. Furthermore, the time course of their effect resembles the formulation of a plan to saccade. Our interpretation is consistent with their report that subthreshold microstimulation in the superior colliculus can bias pursuit toward the motion of targets passing through the movement field of the excited neurons (Carello and Krauzlis, 2004). Finally, our interpretation provides a mechanistic explanation for why space ought to be a primal cue for the pursuit system, as Adler et al. (2002) have described: a spatial cue provides direct information to the pursuit system about the upcoming location of the fovea, just as does the saccade plan. We conclude that our data provide a quantitative description of the influence of the upcoming locus of the fovea, as driven by the saccade plan, on smooth pursuit eye movements.

Features of the neural underpinnings of a moveable spatial filter, and perceptual consequences

We propose that weighting retinocentric visual motion by the upcoming position of the eye in space transforms the representation of visual motion into a spatial command for eye velocity. Saccades rely on a similar coordinate transformation, taking account of the former retinal position of a flashed stimulus and all subsequent changes in the position of the eyes (Mays and Sparks, 1980). Insights from computational studies provide a framework for thinking about how this kind of computation might be done in the brain. If model neurons combine extraretinal information about the locus of gaze with visual signals about the retinal position of a target, then they can learn and compute a movement command appropriate for bringing the eyes to the position of a target in space (Zipser and Andersen, 1988; Pouget and Sejnowski, 1994; Salinas and Abbott, 2001; Smith and Crawford, 2005). These models suggest that neurons involved in creating a spatial-weighting of the visual motion drive for pursuit ought to integrate two signals: a directional signal related to the retinal visual motion stimulus, and a direction-independent gain modulation related to eye position. The effects of electrical stimulation of pursuit-related neurons in the frontal eye fields were interpreted as having two similar components, suggesting a direct neural correlate of the interactions needed to explain our data (Tanaka and Lisberger, 2002).

It would be tempting, but unproductive, to speculate about the anatomical loci of either the filter itself or the signals that control it. It is unlikely that neural correlates of such fundamental sensorimotor transformations would be restricted to a single anatomical locus, because neurons across the sensorimotor spectrum show spatially selective enhancement in conjunction with saccades (Newsome et al., 1988; Tolias et al., 2001; Reppas et al., 2002). Even subthreshold microstimulation in an area that generates saccades (FEF) enhances visual responses in the extrastriate visual cortex (V4) to targets presented at the endpoint of saccades generated by stronger stimulation at the same site (Moore and Armstrong, 2003). Although it is likely that the effects of the filter will be felt across many anatomical areas, research into the neural correlates of attention suggests that these effects might be different in magnitude in tractable ways.

Our proposed filter fits well with concepts suggested by previous research on attention. For example, neurophysiologists have demonstrated many correlates of perceptual enhancement in which the neural responses to a given visual stimulus are larger if a monkey attends to the location of the stimulus or is going to use the stimulus as the target of an impending saccade (Goldberg and Wurtz, 1972; Mountcastle et al., 1981; Connor et al., 1997; Bisley and Goldberg, 2006). The magnitude of these effects can vary with the area. Consider two areas involved in representing retinal motion to drive smooth pursuit eye movements, the middle temporal area (MT) (Newsome et al., 1985; Carey et al., 2005) and the ventral intraparietal area (VIP) (Schlack et al., 2003). The magnitude of neural modulation after cued attention is considerably larger in VIP than in MT (Cook and Maunsell, 2002); crucially, VIP receives considerable information about the position of the eyes, whereas MT has little or no extraretinal input (Newsome et al., 1988; Bremmer et al., 1999; Cook and Maunsell, 2002). Correspondingly, we predict that the neural correlates of the spatial control of visual motion processing for pursuit will be clearest in areas that have responses related to visual motion and/or pursuit, and also are driven strongly by information about the direction of gaze.

Lastly, we note an intriguing parallel between perceptual and motor effects of saccades. In the face of many saccades, we maintain a stable perception of the world. As Dodge (1907) observed, the inverse of the command to saccade is the exact signal needed to maintain such perceptual constancy. Perception of both space and time is compromised in specific ways around the time of the saccade (Morrone et al., 2005). These perceptual effects have been modeled as resulting from a coordinate transformation similar to the one we proposed to explain our results (VanRullen, 2004). Perhaps use of the pursuit system to obtain continuous measures of the neural dynamics surrounding saccades will allow an understanding at the level of neural circuits into this most fundamental and intriguing perceptual phenomena.