A comparison of random vs. chemotaxis driven contacts of T cells with dendritic cells during repertoire scanning

Abstract

Generating adaptive immunity after infection or immunization requires physical interactions within a lymph node (LN) T-zone between antigen-bearing dendritic cells (DCs) that arrive from peripheral tissues and rare cognate T cells entering via high endothelial venules (HEVs). This interaction results in activation of cognate T cells, expansion of that T cell lineage and their exit from the LN T zone via efferent lymphatics (ELs). How antigen-specific T cells locate DCs within this complex environment is controversial, and both random T cell migration and chemotaxis have been proposed. We developed an agent-based computational model of a LN that captures many features of T cell and DC dynamics observed by two-photon microscopy. Our simulations matched in vivo two-photon microscopy data regarding T cell speed, short-term directional persistence of motion and cell motility. We also obtained in vivo data regarding density of T cells and DCs within a LN and matched our model environment to measurements of the distance from HEVs to ELs. We used our model to compare chemotaxis with random motion and showed that chemotaxis increased total number of T cell DC contacts, but decreased unique contacts, producing fewer activated T cells. Our results suggest that, within a LN T-zone, a random search strategy is optimal for a rare cognate T cell to find its DC match and maximize production of activated T cells.

1. Introduction

Lymph nodes (LNs) are an anatomic nexus of lymphatic and blood circulations, where specialized antigen presenting cells known as dendritic cells (DCs) interact with T cells (Chicz et al., 1993; Muller et al., 2003; Randolph et al., 2005). During infection, DCs transport antigen from peripheral sites to a T-zone of a LN via afferent lymphatics (AL), where they encounter T cells entering via high endothelial venules (HEV) (Cahalan and Parker, 2006; von Andrian and Mempel, 2003). T cells exit via medullary sinuses (MS) into efferent lymphatics, traversing an entire LN in ~ 24 hours (Catron et al., 2004). Intravital two-photon microscopy (2PM) within LNs has allowed novel observations of dynamics at the cellular level (Miller et al., 2002). Although DCs move more slowly than T cells (2–3 vs. 11 µm/min) (Miller et al., 2004a; von Andrian and Mempel, 2003), they contact many T cells by moving their dendrites to an average length of 19 µṃ with velocities approaching 40 µm/min (Miller et al., 2004b). Scanning efficiency of CD4⁺ T cells within the LN T-zone was estimated using serial cryosections over a 96 hour period (Westermann et al., 2005); more than 60% of T cells were < 5 µm from a DC and more than 95% were within 15 µm, i.e., within reach of DC dendrites. Cognate T cells (those T cells that can recognize the antigen being presented on a DC) are rare (10⁻⁵ to 10⁻⁷ frequency), but each DC briefly contacts from 500–5000 individual T cells/hour (Bousso and Robey, 2003; Miller et al., 2004b; Turner et al., 2006). If a peptide-MHC complex (pMHC) on a DC surface matches a T cell receptor (TCR), then contact and binding ultimately results in T cell activation and clonal expansion. T cells make multiple, transient (2–3 minute) contacts with DCs during T cell repertoire scanning (Miller et al., 2004b). Cognate T cells can bind for longer times to an antigen-bearing DC (10–15 hours) and later form clusters or swarms of T cells (Liu et al., 1996). These longer interactions are associated with secretion of interleukin-2 and interferon-γ (D'Souza and Lefrancois, 2004). Another class of antigen-bearing DCs, licensed DCs, have interacted with and been further stimulated by effector CD4⁺ T cells and are important for generation of long-lived memory CD8⁺ T cells (Ding et al., 1995; Lee et al., 2002; Sporri and Reis e Sousa, 2005).

On a short time scale, T cell motion is apparently hardwired to establish polarity and then to adjust it periodically without abruptly reversing direction. This leads to motion with a mean free path of ~ 20–30 µm interrupted by a change in direction every 2–3 minutes (Miller et al., 2004a; Miller et al., 2004b). On longer time scales (~ 40 minutes), T cell motion conforms to a random search, i.e., (displacement)² vs. time is linear and there is no preference to approach or leave DCs (Halin et al., 2005; Mempel et al., 2004; Miller et al., 2003; Miller et al., 2004a; Miller et al., 2004b). This short-term persistence does not depend on chemotaxis per se, but is an intrinsic property arising from establishment of T cell polarity by preferential formation of membrane protrusions on the leading edge of a moving cell, so that cell motion tends to be axial rather than lateral (Pankov et al., 2005). Once initiated, cell polarity has been described as a self-organizing mechanism (Wong et al., 2006). When present, chemotaxis utilizes and builds on these same inherent intracellular mechanisms of persistence of motion (Friedman et al., 2005; Pankov et al., 2005). Lymphocyte movement begins with actin-based protrusion via GTPases of the Rho/Rac/Cdc42 family, and these can act antagonistically to control not only cell speed but also directionality; activity of Rac and Cdc42 tend to increase membrane protrusions at the leading edge, while Rho appears to oppose them (Friedman et al., 2005). Lymphocyte chemotaxis is important for organizing the secondary lymphoid tissues (Cyster, 2005). Within the LN, B cells move via chemotaxis to the T-B boundary following antigen engagement (Okada et al., 2005). Chemotactic movement of CD8⁺ T cells towards activated CD4⁺ T cell-DC complexes has also been observed (Castellino et al., 2006). Evidence for chemotaxis included directed motion of CD8⁺ T cells towards interacting DC and CD4⁺ T cells and an increase in contacts (or “hit rate”) between a DC and its surrounding CD8⁺ T cells. Also, they observed upregulation of chemokine receptor CCR5 by CD8⁺ T cells, production of the corresponding ligands CCL3 and CCL4 by DC-CD4⁺ T-cell conjugates and a reduction in hit rate when ligand-blocking antibodies were introduced or if T cell CCR5 receptors were defective (Castellino et al., 2006). Additionally, there is an extracellular matrix architecture (i.e., fibroblastic reticular cell network) that may provide preferential pathways for T cell motion within the LN (Bajenoff et al., 2006; Mempel et al., 2006).

To help resolve whether random or chemotactic motion of T cells would enhance their interaction with DCs, we created an agent-based computer model (ABM) with quantitative anatomic features of a LN T-zone that captured the stochastic nature of individual cell motion and cellular interactions. Our ABM was validated by comparing in vivo observations of cellular motion from 2PM studies with simulations and we then used our ABM to extend both the space and time range of observation beyond that currently accessible experimentally. We used our ABM to compare how antigen presentation dynamics are affected by varying (1) anatomic positions of the afferent lymphatics, HEVs and MS in the LN and (2) rules of individual cell motion (i.e., random motion with short-term persistence vs. chemotactic motion).

2. Material and Methods

2.1. Overview

We built a first generation 2-dimensional (2-D) ABM, based on agents (cells), rules (binding, activation, proliferation etc), environment (T-zone of a LN represented as 100 × 100 lattice, with 5 × 5 µm square compartments) and time increments (30 seconds), to incorporate stochastic encounters between individual cells (Figure 1). We constructed a 2-D model both for greater speed of computation and because it mimics the typical presentation of time-lapse 2PM data. Cell motility estimates from 2PM data are based on 2-D observations (Miller et al., 2002; Miller et al., 2004a) and there is a trade-off between spatial resolution in X–Y vs. Z-planes using 2PM methodology, which becomes particularly important for short-term tracking (Cahalan et al., 2002). Cell types included CD4⁺ T cells (with naïve, activated and effector classes), CD8⁺ T cells (with naïve, activated and effector/memory classes), antigen-bearing DCs and licensed DCs. We also classified T cells as either naïve or primed, which included all non-naïve classes. To validate placement of HEV and MS on the grid environment, multiple measurements were obtained from murine LNs. Our estimates for density of cells and the ratio of CD4⁺ to CD8⁺ T cells and of T cells to CD11b⁺, CD11c⁻ DCs on the lattice were obtained from data on naïve murine LNs. Our simulations were patterned after biological experiments in which antigen is introduced by DCs that have been exposed to antigen (OVA) and in which the frequency of cognate T cells has been enhanced by using transgenic T cells and recipient mice (Miller et al., 2004a). To represent this, most of our simulations used a cognate T cell frequency of 1:300, although some illustrations use a higher frequency (1:10). Consistent with the inherent stochasticity of an ABM, T cell motion was captured in two ways. First, as random motion with a weighted probability of motion in the same direction as the previous step but with no 180° turns. Second, as chemotactic motion near a DC, from a DC-secreted chemokine and implemented as a weighted probability of motion towards that DC. Chemotaxis was studied independently for CD4⁺ and CD8⁺ T cells and was assumed to have variable strength (Butcher and Lin, 2006), duration (de-sensitization) (DeFea, 2007)and recovery times (re-sensitization) (Zaslaver et al., 2001).

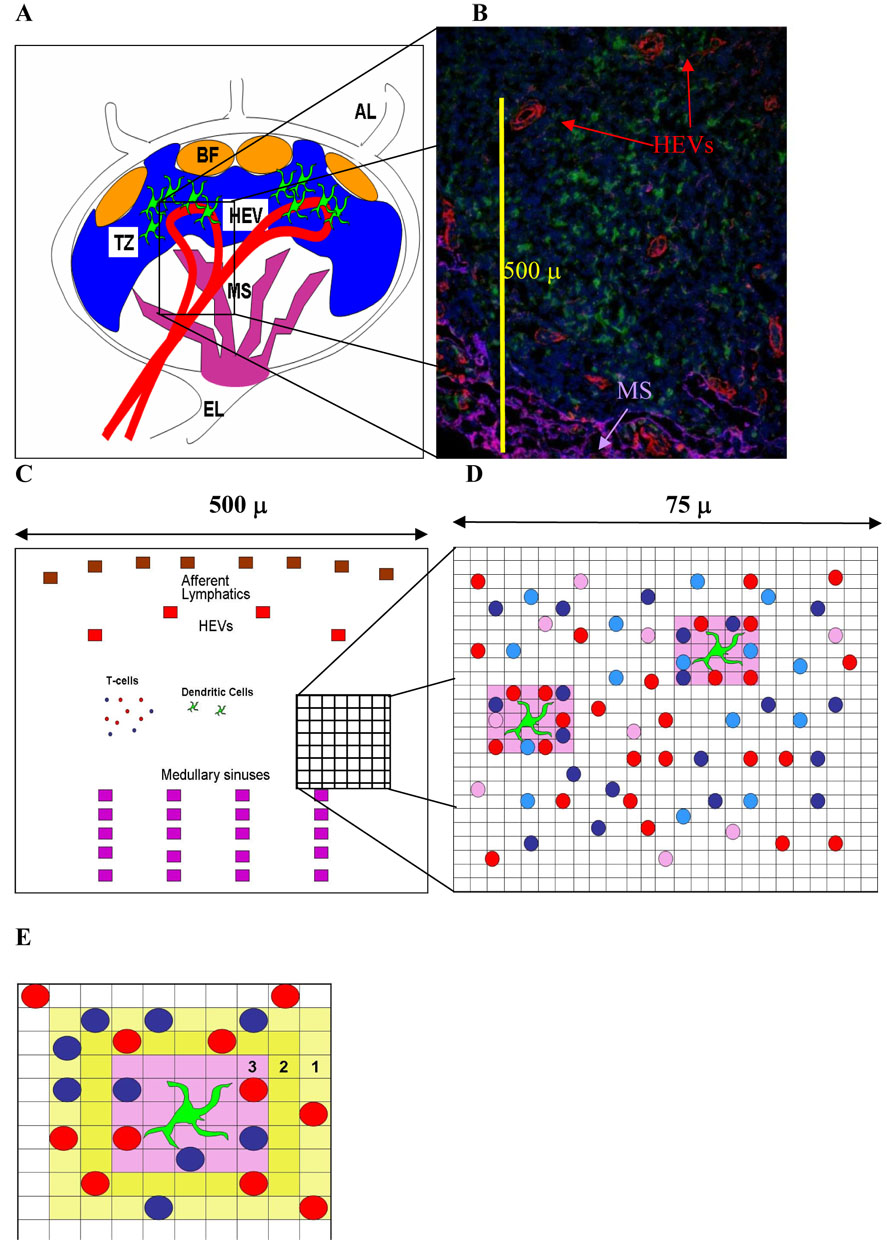
Figure 1. Diagrams of lymph node anatomy and our computer model.

Panel A: Diagram of lymph node (LN) anatomy. Naive CD4⁺ and CD8⁺ T cells enter a LN from the bloodstream via high endothelial venules (HEV) and eventually exit through a collection of medullary sinuses (MS) into efferent lymphatic vessels (EL). Dendritic cells (DCs) enter through afferent lymphatic vessels (AL), enter into the T-zone (TZ) of the paracortex while remaining outside B cell follicles (BF) and migrate toward HEV, positioned to efficiently scan newly arriving T cells. If a T cell does not recognize antigen (find an appropriate pMHC match on a DC) in a time-span of hours to days, it will exit a LN through EL and ultimately re-enter the bloodstream via the thoracic duct.

Panel B: This 5 µm thickness frozen section is taken from a murine LN and highlights a portion of the T-zone within a 480 × 600 µm area. T cells are stained blue with DAPI (nuclei), DCs are stained green, HEVs are stained red (PNAd) and MS are purple (LYVE-1). In this example, the HEV to MS distance is approximately 345 µm, but the average from 84 measurements was 325 µm (see Supplemental Material and Methods).

Panel C: Our model is a two-dimensional 100 × 100 lattice of 5 × 5 µm square micro-compartments, representing a tissue section that is 500 µm square. This includes a section of a LN T-zone, with accompanying afferent lymphatics (ALs), high endothelial venules (HEV) and MS, as shown in panel B. In our model there are 4 HEV entrances, 8 AL entrances and 20 MS exits, with an average distance from entrance to exit of 325 microns, based on data shown in panel B. The model has a cylindrical toroidal structure, so that cells leaving the right-hand side of the grid re-emerge on the left-hand side etc; thus each grid represents a module within the T-zone.

Panel D: A 25 × 25 lattice section (75 µm square) within a T-zone is shown in more detail. Each micro-compartment may contain at most one T cell (naïve CD4⁺ T cells are pink, activated and effector are shades of red, while naïve CD8⁺ T cells are light blue and activated/effector/memory are dark blue). The DCs (green) are larger and have extensions (dendrites); each DC can potentially interact with as many as 16 neighboring T cells simultaneously; the local “sweep area” surrounding each DC is pink.

Panel E. A close-up view of the chemotactic area surrounding a DC is shown in shades of yellow. Once a T cell has at least one adjacent square with chemokine, then its rules of motion are altered to move up the chemokine gradient. The values (3, 2, 1) represent increasing gradients of chemokine concentration. The sweep area of the DC is pink.

2.2. ABM Environment and Agents

An agent-based computer model (ABM) is an appropriate tool to investigate cellular interactions that depend on physical contact, since it incorporates random encounters between individual cells. We abstract a LN T-zone as the basic environmental module for interaction between DCs and T cells and we are able to track individual cells as they change their state and location, contact and potentially influence other cells. A list of rules governs the lifespan, movement, probability of activation and other changes of state for individual cells. The entire history of each cell is stored for analysis (e.g., all past and present locations, interactions, time from entry into the LN until exit etc). Figure 1 shows the LN environment and our model abstraction of a T-zone. Panels A and B illustrate the anatomy of a LN. Panel C shows the layout of the full model grid of a portion of a T-zone within a LN paracortex and Panel D shows a more detailed rendering of individual cells on the grid, in which elemental units (5 × 5 µm square micro-compartments) of our grid are scaled to the approximate diameter of a T cell (5 µm) (Janeway, 2005). Each micro-compartment may contain at most one T cell: CD4⁺ T cells (naïve, activated and effector are shown as pink, red and maroon, respectively), while CD8⁺ T cells (naïve and activated/effector/memory) cells are shown as shades of blue from light to dark. The DCs (green) are larger and have extensions (dendrites) that sweep the surrounding space as T cells meander by. We abstracted this by having DCs occupy a contiguous 15 µm square that extends out for another 5 µm in all directions, so that each DC could potentially interact with up to 16 neighboring T cells simultaneously. This local area of influence, or “sweep area” (Castellino et al., 2006), surrounding each DC is shown in pink (panel D).

2.3. Cellular motion rules (random vs. chemotactic)

Random Motion

T cell motion (both CD4⁺ and CD8⁺) was captured in our model using either random movement or chemotactic motion of T cells towards DCs. When motion was random, an unbound T cell could move every 30 seconds to an unoccupied adjacent position (5 µm steps; speed = 10 µm/min). Motion was implemented by weighting the probability of moving in the same direction as the previous step (“short-term persistence”) from 0.50 – 0.95. If a T cell had to pause because its chosen adjacent lattice position was occupied, then the direction at the next update time was chosen randomly.

Short-term Persistence

2PM observations have demonstrated that T cells have a mean free path ~ 20 – 30 µm and turned, on average, every 2–3 minutes (Mempel et al., 2004; Miller et al., 2004a; Miller et al., 2004b). Further, once a T cell established polarity, it was not altered every 30 seconds (the time step in our simulations) (Pankov et al., 2005; Wong et al., 2006). Thus, we had to account for these biological features in our model development. To this end, we define short-term persistence as the likelihood of a T cell moving in the same direction as its previous step. Our basic grid unit is a 5×5 µm square, and at this level of spatial resolution we performed studies testing what would occur if there were no short-term persistence of T cell motion (i.e. purely random T cell motion). Our results suggest that random T cell motion (i.e., less short-term persistence) at this spatial resolution would lead to more meandering paths and T cell mean free paths would be much shorter than those observed in vivo. Likewise, metrics such as cell motility, transit time or search time depended on how frequently T cells changed direction and our studies testing purely random motion (i.e., without short-term persistence) would lead to values for these metrics that were not consistent with in vivo data (data not shown). Based on a time step of 30 seconds and a step size of 5 µm, short-term persistence = 90% resulted in the best match between simulations and in vivo data for mean free path and cell motility and became our default value. A 90% short-term persistence obviously implies a strong likelihood of moving in the same direction as the previous step and the distribution of straight paths for 1,000 T cells closely conforms to an exponential distribution (data not shown). However, each T cell’s initial direction is randomly chosen and when a T cell stops because its path is obstructed, the direction for its next step is likewise randomly chosen. Typically, a T cell in our simulation would move about 4 steps (20 µm) in a given direction before turning, with some T cells changing direction after one step and some continuing for multiple steps in one direction. Motion observed in our simulations conforms closely to that seen in time-lapse 2PM studies. Once a cognate T cell became bound to a DC, it moved with the DC at its slower speed (2.5 µm/min). After release, if it was not activated, a T cell resumed its usual speed, but if activated, it moved more slowly (5 µm/min) (Miller et al., 2004b).

Chemotaxis

Alternatively, we modeled chemotaxis for antigen-bearing DCs to attract T cells. Four principles were incorporated into our model of chemotaxis:

1. A steady state gradient of chemokine concentration around each DC was established, for a total area of 45 × 45 µm, including the area occupied by a DC.

2. Strength of chemotaxis could be varied from random to completely directed motion (Butcher and Lin, 2006).

3. Duration of chemoattraction could be varied (a desensitization phenomenon) (DeFea, 2007).

4. Recovery (resensitization to chemotactic responsiveness) times could also vary (Zaslaver et al., 2001).

Chemotactic motion of T cells toward DCs was implemented independently for CD4⁺ and CD8⁺ T cells, to investigate them separately. For each T cell, its rules of motion were governed by random motion with short-term persistence until it encountered chemokine around a DC, after which its motion was directed by chemoattractant strength, for a duration determined by the desensitization time, and then motion returned to random motion with short-term persistence. After recovery (resensitization time) that particular T cell could again be responsive to chemokine around any DC. Snapshots of grids illustrating chemotaxis vs. no chemotaxis are shown in Figure 2.

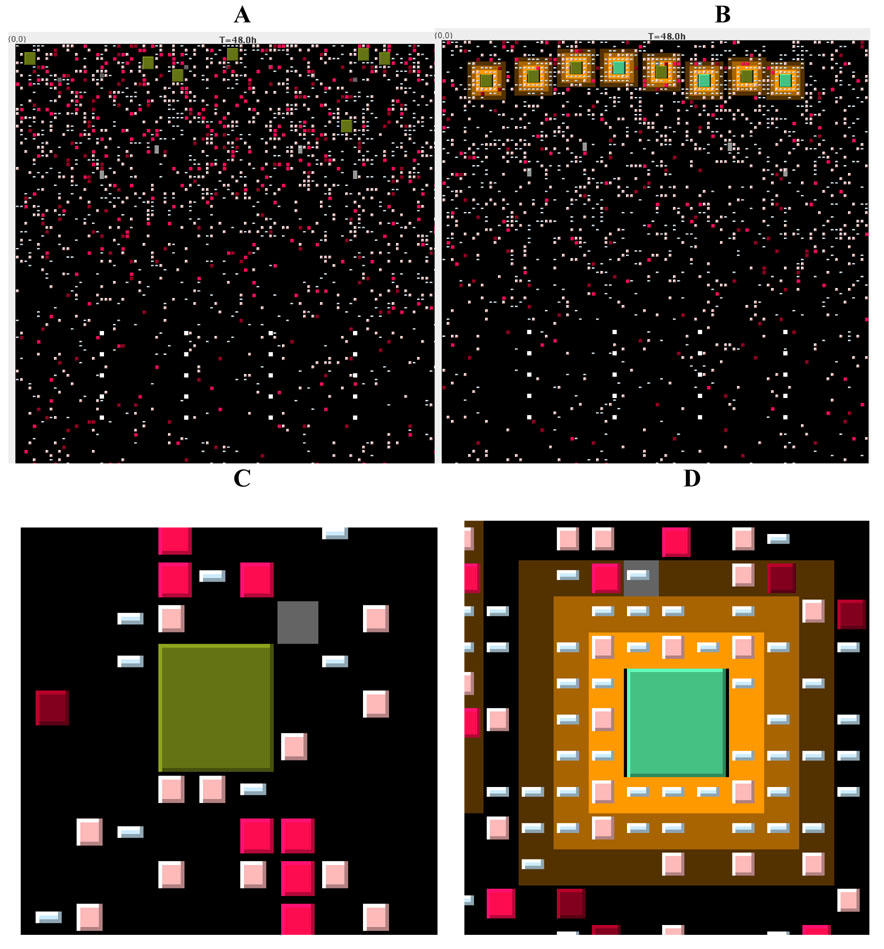
Figure 2. Snapshots of the full grid and zoom figures from our computer simulations taken at 48 hours.

Panel A. The complete layout of the T-zone grid is shown from a snapshot of a simulation at 48 hours after introduction of antigen via DCs (shown as large green squares) under conditions of no chemotaxis. DCs enter near the top of the grid, the T cells enter via HEVs that are placed in an arch about 1/3 of the distance from the top of the grid and later exit via MS that are arranged in rows near the bottom of the grid. CD4⁺ T cells are shown as squares in shades of pink to red, while CD8⁺ T cells are shown as rectangles in shades of blue (color shades are described in Figure 1). The chemotactic areas around DCs are shown in yellow.

Panel B. The complete layout of the T-zone grid is shown at 48 hours after introduction of antigen via DCs with chemotaxis.

Panel C. A close-up from panel A shows a DC without chemokine, and few T cells in the local vicinity.

Panel D. A close-up from panel B shows the chemokine area (shades of yellow) around a DC, along with multiple T cells that have been attracted. Note that these simulations and those posted online all use a cognate ratio of 1:10 for purposes of illustrating more activity on the grid. Movies from the simulations are available at: http://malthus.micro.med.umich.edu/LNcode/flash/series/1.html

2.4. Rules of cell motion (no chemotaxis)

• Naïve T cells attempt to move every 30 seconds to an adjacent (von Neumann) open position, with an average potential speed of 10 µm/min (Miller et al., 2004a; von Andrian and Mempel, 2003)

• T cells move sequentially to avoid collisions; the order is randomized at each time step

• T cells do not make a 180° turn, unless they were forced to stop for at least one time step

• The probability of moving in the same direction as the previous move was named “short-term persistence” ; the range examined was 50 – 95 %

• Since the grid is a cylindrical torus, if a T cell moves off one side of the grid, it appears on the other side

• DCs may move every 2 minutes to an open adjacent (von Neumann) position, with an average potential speed of 2.5 µm/min (Miller et al., 2004a)

• DCs do not move off the edge of the lattice

• Once a T cell is bound to a DC, its motion is updated with the DC, until it is freed

• Once a T cell becomes activated, effector or memory class, then it moves more slowly (updated every minute), with an average potential speed of 5 µm/min

2.5. Chemotaxis Rules for altering T cell motion around an Antigen-bearing DC

• Around an antigen-bearing DC, chemokine concentration and local gradients are assumed to have reached steady state

• Since the gradient is inversely proportional to the distance from its source, the area around the DC is defined by 3 concentric squares, for a total area of 45 × 45 µm

• Higher values have higher concentration of chemokine: closest grid positions to a DC are assigned the chemokine value = 3, the next outer grid positions have chemokine value = 2 and the farthest outer grid positions have chemokine value = 1; all other grid positions have chemokine value = 0

• Once a T cell encounters at least one grid position having a non-zero chemokine value, then new rules of T cell motion are invoked

• Three parameters of chemotaxis vary: (1) strength of chemoattraction, (2) duration until desensitized and (3) recovery and potential resensitization

• Strength of attraction was implemented as probability of movement towards a location with a higher chemokine value that varied from random motion to movement that was always towards the higher chemokine value; a weighting function was used that incorporated chemokine values of all adjacent cells; strength was varied from no chemotaxis (random motion) to allocating 100% probability to moving to a higher value of chemokine

• Algorithm for strength of attraction

  • “Prob_attract”, a continuous scale of chemotaxis strength, varies from 0 to 0.75, corresponding to random motion vs. never going down the gradient

  • First, check chemokine value of 4 adjacent squares

  • If all values = present location, then probability of motion = 0.25 in any direction

  • Else, count # of squares GT (>), # EQ (=) and # LT (<) present location chemokine value

  • Compute a weight function: for GT, wgt_GT = 0.25 + (Prob_attract /3), for EQUAL, wgt_EQ = 0.25 and for LT, wgt_LT = 0.25 – (Prob_attract /3)

  • Total = #GT*wgt_GT+ #EQ*wgt_EQ + #LT*wgt_LT

  • Probability move to GT = #GT*wgt_GT/Total

  • Probability move to EQ = #EQ*wgt_EQ/Total

  • Probability move to LT = #LT*wgt_LT/Total

  • Note that these represent the probability of moving to all GT, all EQUAL and all LT, so PROB move needs to be allocated equally to each member in that class.

  • These probabilities sum to 1

  • If Prob_attract = 0 (i.e., no chemotaxis, then all revert to 0.25, or random motion)

  • If Prob_attract = 0.75 (i.e., maximum chemotaxis, then a T cell has 0 probability of going down the gradient; at values < 0.75, there is always some small probability of going down a gradient)

  • In Table III, chemotaxis strengths of “weak”, “intermediate” and “strong” correspond to Prob_attract values of 0.25, 0.50 and 0.75, respectively, while “none” corresponds to 0, or random motion.

• Duration (time to desensitization) and recovery (resensitization) were implemented by turning off a T cell’s ability to respond to chemokine after a stipulated time and allowing that T cell to later respond to chemokine; each of these parameters was varied from 3–60 minutes (Butcher and Lin, 2006; DeFea, 2007; Zaslaver et al., 2001)

Table 3.

Sensitivity of T cell-DC contacts and production of T cells to chemotaxis parameters by PRC analysis

	Chemotaxis Parameters
	CD4+ T cell-DC			CD8+ T cell-DC
	Strength	Duration	Recovery	Strength	Duration	Recovery
Total contacts CD4+ T cell-DC	↑↑↑↑	↑↑		↓↓	↓↓
Unique contacts CD4+ T cell-DC		↓↓	↑	↓	↓
Total contacts CD8+ T cell-DC	↓↓			↑↑↑↑	↑↑↑
Unique contacts CD8+ T cell-DC	↓↓↓↓	↓↓↓			↓↓
Ratio primed: naïve CD4+ T cell output
Day 1
Day 2
Day 3
Day 4				↓
Day 5				↓
Day 6				↓
Day 7				↓
Ratio primed: naïve CD8+ T cell output
Day 1
Day 2
Day 3
Day 4	↓↓	↓
Day 5	↓↓	↓
Day 6	↓	↓
Day 7	↓	↓
Search time (hrs)		↑↑	↓↓	↑↑	↑↑
Transit time (hrs)	↑↑↑↑	↑↑↑

ns = p > 0.01 (all Table positions that are blank are “ns”)

↓ or ↑ = p < 0.01, with negative or positive association

↓↓ or ↑↑ = p < 0.001, with negative or positive association

↓↓↓ or ↑↑↑ = p < 10⁻⁶, with negative or positive association

↓↓↓↓ or ↑↑↑↑ = p < 10⁻⁹, with negative or positive association

2.6. Rules of Cell interaction

CD4⁺ and CD8⁺ T cells

• If a naïve, cognate CD4⁺ T cell comes in contact with a mature or licensed DC, or a naïve CD8⁺ T cell comes in contact with a LDC, the T cell binds with probability = 75 % (range 50 – 100 %)

• Binding-time duration is taken from a uniform distribution (10–15 hrs)

• After a CD4⁺ T cell is released from a DC or a CD8⁺ T cell is released from a LDC, then the T cells become activated with probability = 95% (range 90 – 100%)

• Activated T cells proliferate at a doubling period of 8 hrs (range = 7–9 hours) for 4 divisions (range = 2–6); after completion of proliferation, CD4⁺ T cells become effector T cells and CD8⁺ T cells become either effector or memory T cells.

Antigen-bearing Dendritic cells

• If a naïve, cognate CD4⁺ T cell is bound to an antigen-bearing DC for 14.5 hrs, then the Antigen-bearing DC differentiates into LDC

• An effector CD4⁺ T cell licenses an antigen-bearing DC with probability = 95 % (range 90–100 %) during contact

• By contact via exosomes or shared antigen, both antigen-bearing DCs and LDCs can convert IDCs to Antigen-bearing DCs with probability = 70 % (range 50–90%) (Wieckowski and Whiteside, 2006).

• A primed CD4⁺ T cell binds with an IDC with probability = 75% (range 50–100 %)

• A primed CD4⁺ T cell binds to an IDC for 30–90 minutes (taken from a uniform distribution)

• If bound for at least 60 minutes, a primed CD4⁺ T cell converts an IDC to an antigen-bearing DC with probability = 95 % (range 90–100%)

2.7. Lifespan for Cell types

• CD4⁺ T naïve cell age: 16 to 365 days (McCune et al., 2000)

• CD4⁺ effector maximum lifespan: 60 hours (Sprent and Tough, 2001)

• CD8⁺ T naïve cell age: 165 to 365 days (McCune et al., 2000)

• CD8⁺ activated cell maximum lifespan: 48 hours (Sprent and Tough, 2001)

• CD8⁺ effector maximum lifespan: 60 hours (Sprent and Tough, 2001)

• DC age: 1 to 11 days (Kamath et al., 2002)

• Antigen-bearing DC maximum lifespan: 60 hours (Kamath et al., 2002)

• LDC maximum lifespan: 36 hours (Lanzavecchia and Sallusto, 2004; Lindquist et al., 2004)

2.8. Validation of model grid and placement of HEV, MS and AL

To validate the dimensions on the grid and distance from HEV to MS (as shown in Figure 1, panel C), LNs were taken from 4 CD11c-eYFP transgenic mice bred on a C57 BL/6 background, as described in (Lindquist et al., 2004). Tissue was fixed for 1 hr in 4% paraformaldehyde, equilibrated overnight at 4°C in 30% sucrose, and embedded in OCT compound for sectioning. Tissues were stored at −80°C until use. 5 µm cryostat sections were stained for MS with anti-LYVE-1 (Upstate, 1:100) and revealed using an Alexa Fluor 555-coupled goat anti-rabbit IgG secondary mAb (Invitrogen, 2:100). Tissue sections were also stained for HEV with anti-PNAd (BD Pharminogen, 5ug) and revealed with an Alexa Fluor 647-coupled goat anti-rat IgM secondary mAb (Invitrogen, 2:100). Images were obtained using an Olympus BX51 system with a SPOT RT camera (Diagnostic Instruments, Inc.) and analyzed using SPOT Advanced software (Diagnostic Instruments, Inc). In total, 7 LNs were each sectioned 3 times as shown in Figure 1, panel B and the HEV to MS distance was determined 4 times, for a total of 84 measurements. The average distance was 325 µm, with a range of 150–600. Variation in size of the LNs and tissue plane of the cross-section contributed to this wide range.

2.9. Justification for cell density on model grid

Estimates of the number of cells (CD4⁺ and CD8⁺ T cells and DCs) in a healthy LN were obtained using data from murine LNs. Mediastinal LNs were obtained from 6 naïve C57BL/6 mice and crushed through a 70 µm cell strainer (BD Falcon, San Jose, CA) to obtain single cell suspension. Red blood cells were lysed using 0.144M Tris, 0.017M NH₄Cl buffer. Cells were washed with 2% FBS/1x PBS and counted. Approximately 4 × 10 ⁵ cells per LN were obtained. Cells were stained for surface markers anti-CD8 (clone 53-6.7) and anti-CD11c (clone HL3) at 0.5 µg/3 × 10⁵ cells; anti-CD4 (clone RM4–5), anti-CD86 (clone GL1), anti-CD11b (clone M1/70) at 0.08 µg/3 × 10⁵ cells. All antibodies were obtained from BD/PharMingen (San Jose, CA) and cells were stained in 0.1%BSA/1x PBS/20% mouse serum for 15 minutes at room temperature. Cells were then washed in FACS buffer (0.1% BSA/ 1x PBS) and resuspended in 1% paraformaldehyde. Cells were collected on a FACSCalibur (Becton Dickinsin Immunocytometry Systems, San Jose, CA) and analyzed using FlowJo software (TreeStar Inc., San Carlos, CA). Among the 400,000 live cells per LN, there were 20,000 monocytes, 120,000 CD4⁺ T cells and 100,000 CD8⁺ T cells. Among the monocytes, ~ 1400 were CD11b⁺, CDllc⁻. This results in the ratio CD4⁺:CD8⁺ T cells = 6:5 and the ratio 1:160 for DC:all T cells, the latter ratio is corroborated in data from human LN (Takahashi et al., 2001).

Initial conditions estimated from data derived above

• From the murine LN data, each LN had ~ 400,000 live cells, 20,000 monocytes, 120,000 CD4⁺ T cells and 100,000 CD8⁺ T cells

• The ratio of CD4⁺:CD8⁺ T cells was 6:5

• The ratio of CD11b⁺, CD11c monocytes (DCs) to all T cells was 1:160

• This compares well with the ratio of DCs to T cells in human LNs (Takahashi et al., 2001)

• We used these ratios and scaled from the entire LN to a grid (1/160).

• On the 500 × 500 µm grid there are initially 750 naïve CD4⁺ T cells, 625 naïve CD8⁺ T cells; 8 antigen-bearing DCs were introduced as a pulse over the first 24 hours, to simulate introduction of antigen from an acute introduction of infection or vaccination.

• Default values for recruitment rates for naïve CD4⁺ and CD8⁺ T cells were determined to have those cells reach a steady state over 28 days

• In our model, antigen is introduced via antigen-bearing DCs that enter the LN (Miller et al., 2004b)

2.10. Protocol for two-photon imaging

CD4⁺ T cells were isolated by magnetic negative selection (Miltenyi Biotec) from spleens and LNs of C57BL6 mice (The Jackson Laboratories). The T cell purity of this method is typically >90 % CD4⁺, CD3⁺ as assessed by flow cytometry. T cells were labeled with 5 µM CFSE (Molecular Probes) for 30 minute at 37° C, washed once, and 5–10 million cells were transferred into B6 mice by tail vein injection. 18 hours after T cell transfer, mice were euthanized by CO₂ asphyxiation and cervical LNs removed for microscopy. LNs were secured in the flow chamber with a thin film of VetBond (3M) and maintained at 37° C by perfusing the chamber with warm RPMI bubbled with a mixture of 95 % O₂ / 5 % CO₂ (Carbagen gas) (Miller et al., 2002). Time-lapse imaging was performed using a custom built two-photon microscope at the Washington University School of Medicine. CFSE labeled T cells were excited by a Chameleon Ti:sapphire laser (Coherent) tuned to 780 nm and fluorescence at 490–550 nm was collected. ImageWarp (A&B software) was used to control the various hardware devices during real-time acquisition and to process and archive the image data. Each 11.3 sec time point, consists of a 200 µm by 250 µm by 50 µm volume (x and y =2 pix/µm). Z-stacks were acquired by taking 21 sequential steps at 2.5 µm spacing. To increase signal contrast, we averaged 10 video frames for each z-slice. Multi-dimensional rendering and cell tracking were performed with Volocity (Improvision).

2.11. Model Parameters and Uncertainty and Sensitivity Analysis

Models include parameters describing a large number of known biological processes, thus it is critical to understand the role that each of these parameters plays in determining output. Uncertainty analysis measures the variation in model output based on the variation of inputs (i.e. parameter values). Sensitivity analysis involves the correlation of these variances in parameter values to variances in model output and is particularly useful when parameter values are not known with certainty. These techniques have recently been introduced into the biological sciences. Correlations between model output and parameter values can be determined using partial rank correlation coefficients (PRCC). Time dependent correlations can also be identified. We have used this approach to identify key parameters in ODE models (e.g., (Chang et al., 2005; Marino and Kirschner, 2004; Sud et al., 2006; Wigginton and Kirschner, 2001). In addition, we have adapted this approach, originally developed for ODEs, for use in agent-based model setting (Marino et al., submitted 2007; Segovia-Juarez et al., 2004)

To explore effects of uncertainty in our model, we used a C program to create a Latin Hypercube Sampling (LHS) (Blower and Dowlatabadi, 1994; Blower et al., 2000; Helton and Davis, 2003) of our parameter values. The LHS method is a stratified Monte Carlo sampling method that allows simultaneous, random sampling of each defined parameter over biologically plausible ranges. Each parameter is assigned a distribution, typically uniform or normal and centered on a baseline, estimated value.

We assessed how parameter variations affect our outcome measures by varying each parameter above and below the baseline values given in Table 1. The entire range of each distribution is evenly sampled to generate a set of values for each parameter range. For each continuous parameter, we sampled at 30 evenly spaced intervals over the range, replicating 50 times for a total sample size of 1500 combinations of all parameters. For many of the parameters in our ABM where events may transpire after physical contact between two cells, the biologically plausible range for probability of an occurrence was much narrower than the mathematical range (0, 1). In such cases, we narrowed the parameter range to a more realistic range. Although we completed a full model analysis using all model parameters (full model analysis), we also concentrated on a smaller set of parameters, or a local analysis. In this instance, six parameters affecting T cell motion (chemotaxis strength, duration and recovery, independently influencing CD4⁺ and CD8⁺ T cell motion) were studied simultaneously using 20 replications of 50 rows from an LHS matrix. The values obtained from LHS were read into our C++ model of the LN, which created various outputs (raw data). We then used C and Java code to abstract information from the raw data. Partial rank correlation (PRC) was then done using Matlab. PRC allows an assessment of how sensitive the system is to those variations from the LHS.

Table 1.

Parameter ranges for uncertainty and sensitivity analyses

Parameter	Minimum	Maximum	Default
CD4+ T cells
Recruitment of naïve T cells	5.0 %	11.0 %	8.0	Calc†
Doubling time for activated T cells	6 hrs	10 hrs	8hrs
	(Miller et al., 2004a)
Number of divisions for activated T cells	2	6	4
	(Miller et al., 2004a)
Probability cognate T cell binds with DC	50 %	100%	75%	Est§
Probability T-cell activation by Ag-bearing DC	90 %	100 %	95 %	Est§
CD8+ T cells
Recruitment of naïve T cells	4.0 %	10.0%	7.0%	Calc†
Doubling time for activated T cells	6 hrs	10 hrs	8hrs
	(Antia et al., 2003)
Number of divisions for activated T cells	2	6	4
	(van Stipdonk et al., 2001)
Probability cognate T cell binds with LDC	50 %	100 %	75 %	Est §
Probability T-cell activation by LDC	90 %	100%	95 %	Est §
Dendritic cells
Probability effector CD4+ licenses Ag-bearing DC	90 %	100%	95%	Est§
Probability LDC matures DC	50 %	90 %	70%
	(Hao et al.,2006; Segura et al., 2005)
Probability primed CD4+ binds to DC	50%	100%	75 %	Est §
Probability primed T cell matures DC	90%	100%	95 %	Est §
Rules of T cell motion
Short-term persistence (no chemotaxis) (Chemotaxis, varied separately for CD4+ and CD8+)	50 %	95 %	90 %	Calc†
Strength (Probability of attraction) See Material & Methods	0 %	100%
Duration (Time until desensitized)	3 mins	60mins
	(Foxman et al., 1997;Iijima et al.,2002; Narang et al., 2001)
Recovery (Time until resensitized)	3 mins	60 mins
	(Foxman et al.,1997;Iijima et al., 2002; Narang et al., 2001)

^†Calc = calculated

^§Est = estimated

Recruitment rates calculated to maintain steady-state populations for CD4⁺ and CD8⁺ T cells, e.g., 5% is the probability of a CD4⁺ naïve T cell entering via any HEV during each time step (30 seconds); Short-term persistence of 90 % as probability of continuing in same direction in next 5 micron step matches in vivo data of mean free path and motility for T cells.

We combine the resulting uncertainty data with a sensitivity analysis using Partial Rank Correlation (PRC) to ascertain the strength of association between outcome measures and each parameter, across its range of values (Blower and Dowlatabadi, 1994). Furthermore, this analysis can occur over time, so that we can identify those parameters that are significant at various times during the induction of an immune response. A Student's t-test was used to determine the significance of each PRC; pairs of correlation values can be compared using a Fisher’s Z-transformation of PRC (Meng et al., 1992). Since we are evaluating multiple parameters for significance, we used Holm’s modification of Bonferroni’s correction (Holland and Copenhaver, 1988) to the usual significance threshold p-value < 0.05, to more conservative value, e.g., p < 0.005, when testing 10 separate parameters). Although this is a stricter threshold for hypothesis testing, it decreases the likelihood of a spuriously positive inference, particularly when evaluating multiple parameters at multiple time points for multiple outcomes.

3. Results

Our LN simulations generate many quantitative outcome measures, allowing enumeration of all cell classes present in our simulated T-zone and each cell’s entire event history. Likewise, there are several metrics of efficient T cell output from the LN, suggested by questions such as: (1) After a T cell enters the LN, how long does it take to find a DC? (2) How quickly are T cells activated? (3) How many contacts does a DC make with T cells, and how many of these are unique contacts? (4) How fast is transit through a LN and therefore the turnover of newly arriving T cells? (5) Is there a trade-off between speed and magnitude of T cell production? To address these questions, we concentrated on the following:

3.1. Metrics from simulations

Distance naïve T cells travel from point of entry vs. time

In each simulation, 50 T cells were randomly chosen and their positions were tracked for 1000 minutes after their entry into the T-zone to compare with in vivo data estimates of motility coefficients.

Search time

The mean time that a naïve CD4⁺ T cell (regardless of its cognate status) takes from entry via HEV to first contact with a DC was calculated using 1000 T cells per simulation.

Transit time

The mean time taken by naïve CD4⁺ T cells to traverse the entire T-zone (from entry via the HEV to exiting the T zone via MS) was calculated from about 10,000 T cells per simulation.

Mean free path

The weighted average of straight path lengths (in µm) for naïve CD4⁺ T cells was determined by constructing a frequency count of ~ 10⁵ individual path lengths between turns from 1,000 CD4⁺ T cells per simulation.

T cell-DC contacts

Contacts between DCs and T cells (counted separately for CD4⁺ and CD8⁺ T cells per each DC) were recorded as total number of contacts with all T cells and total contacts with different T cells (unique contacts) over the entire lifespan of each DC.

Cumulative output of primed CD4⁺ and CD8⁺ T cells

Since a key result of antigen presentation is the magnitude and time course of primed T cell production, we counted the number of such cells that had exited the T-zone at particular time points (e.g., 2, 3, 4 days). This information on the output of CD4⁺ and CD8⁺ T cells was reported both as absolute number and as a ratio of primed to naïve T cells.

Time series

Data from the simulations were also represented using graphical display of cell population classes vs. time, movies and snapshots of the 2-D grid environment.

3.2. ABM recapitulates fundamental features of cell dynamics in LNs

We first studied T cell motion in the absence of any chemotaxis, where T cells moved randomly with short-term persistence as described in Methods. Equivalency of T cell motility in our model with in vivo 2PM studies is shown in Figure 3, Panels A & B. Our simulations matched in vivo average T cell speed (10 µm/min), mean free path length (~ 20 µm), and motility coefficient (68 µm/min^1/2) (Miller et al., 2002; Miller et al., 2003; Miller et al., 2004a; Miller et al., 2004b), suggesting that our ABM depicts the essential features of T cell motion in a LN T-zone.

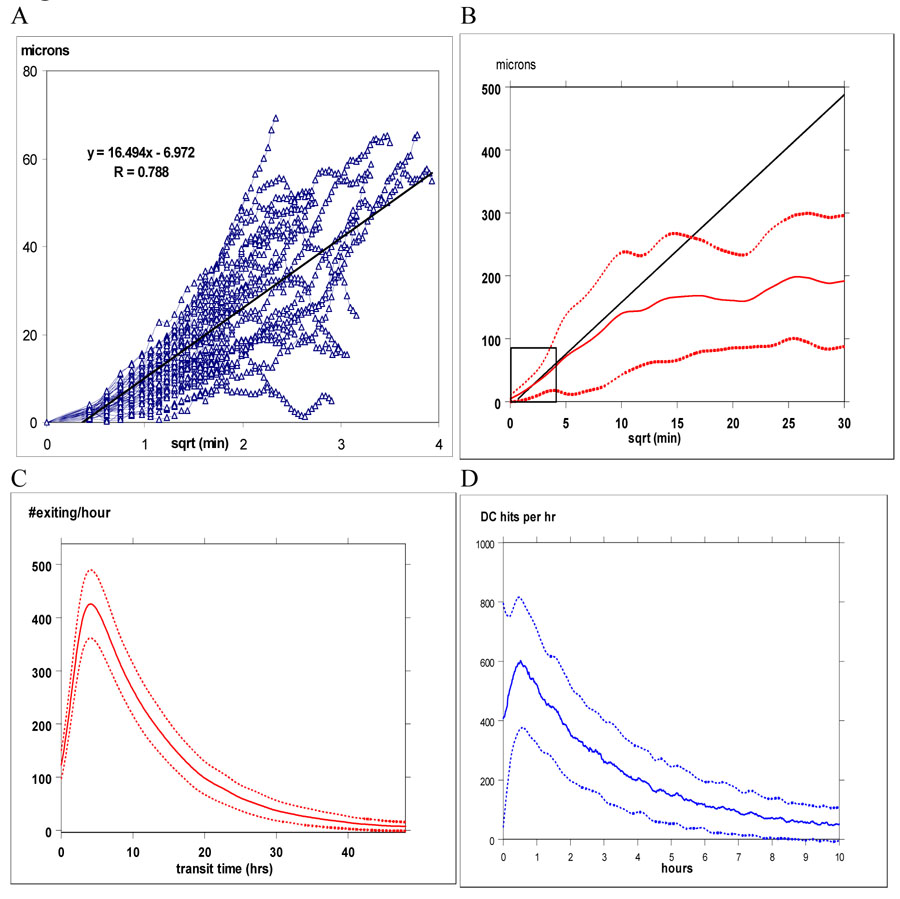
Figure 3. T cell motion in vivo vs. simulations.

Panel A shows the relationship between displacement (in µm) vs. min^1/2 from in vivo tracking of 46 CD4⁺ T cells. For random motion, this relationship is linear. In panel B, displacement vs. min^1/2 (solid line is the mean ± 1 S.D. shown as dashed lines) is plotted from 25 independent simulations using 1250 CD4⁺ T cell trajectories, superimposed on the regression line from panel A. Insert box within panel B marks the range for distance and time shown in panel A. Maximum duration of in vivo observations is about 40 minutes. Our simulations and in vivo data match for ~ 1 hour, after which T cell motility decreases as T cells bind to DCs. Panels C & D show the mean ± 1 S.D. for times elapsed for T cells to transit the T-zone and to first contact a DC, respectively called “transit time” and “search time”. Both distributions are right-skewed; in these examples, the mean transit time was 13 hrs and the mean search time was 2 hrs.

3.3. Transit time through a LN and Search time for T cell to encounter a DC

Average elapsed time from intravenous injection of labeled T-cells to their appearance in the thoracic duct ranges from 24–36 hours (Westermann et al., 1988; Westermann et al., 1993). However, transit times within component sections of a LN have not been studied systematically, nor are kinetics precisely known regarding how much time is required from entry of a T cell into the LN until its first encounter with a DC, although these encounters have been observed to occur within approximately 6 hours (Bajenoff et al., 2003). Distributions of search and transit times (in hours) from 25 independent simulations, using parameter values from Table 1 are shown in Figure 3, Panels C &, D. In our simulations, T cell-DC contacts begin less than 30 minutes after extravasation, with an average search time of several hours. Mean transit times through a T-zone are 12–16 hours. Considering the additional time required to exit the T-zone and traverse the MS to the efferent lymphatics, our transit times are consistent with data from whole animal experiments (Westermann et al., 1988).

3.4. Altering LN anatomy affects transit times, search times and T cell output

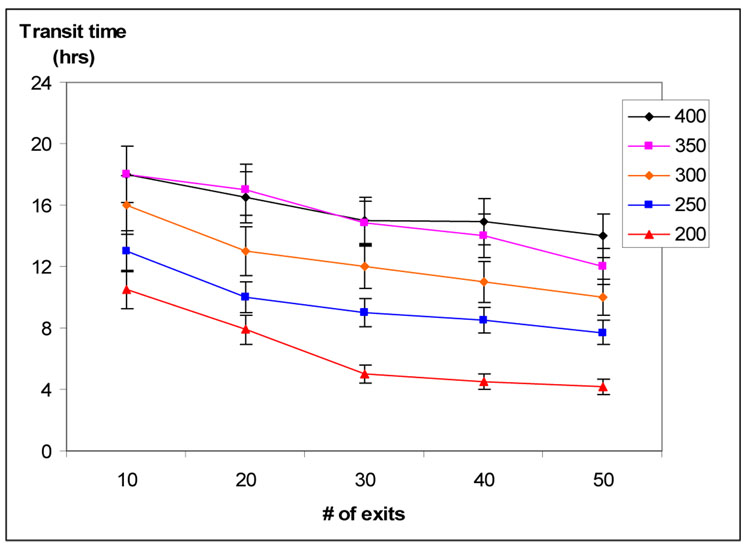
In Figure 1, panel B we show a typical section of a T-zone, where the distance from HEV to MS exits is 325 µm. To understand the importance of LN anatomy of dynamics of T cells in the LN, we examined how varying the number of exits and distance from entry to exit would affect transit time in 25 simulations in which the average distance from entry to exit varied from 200 to 400 µm, while the number of MS exits varied from 10 to 50. As expected, T cell transit times were longer when average distance from entry to exit increased and shorter when the number of exits increased. When our ABM had more than 30 exits, any further decrease in transit times was small (Figure 4). In all subsequent simulations, we placed 20 exits on our grid and made the average distance from HEV to MS equal 325 µm.

Figure 4. Transit time vs. # of exits and mean transit distance.

Transit time was affected by both mean distance from HEV to MS and the number of MS exits. The mean ± 1 S.D. for transit time is shown as mean distance varied from 200 to 400 µm and the number of exits increased from 10 to 50. Based on these data and 84 measurements like that shown in figure 1 B, our simulations had 20 exits and a mean HEV-MS distance of 325 µm.

For our simulations, ALs and HEVs were positioned on the 2D grid to imitate normal LN anatomy as shown in Figure 1. However, to again determine the impact of anatomy on T cell dynamics, we tested the hypothesis that normal LN anatomic placement of HEVs and ALs is optimal in terms of facilitating a large number of T cell-DC contacts and thus maximizing output of primed T cells (Table 2). We inverted grid positions of HEVs and ALs within a T-zone (from the normal position shown in Fig. 1, panel C to place ALs below HEVs), while maintaining the same distance from HEVs to MS and from ALs to HEVs, so that distance would not affect search or transit times. This alteration in anatomic arrangement of entry points for T cells and DCs, resulted in significant prolongation in search times, decreased contacts between T cells and DCs and diminished production of primed CD4⁺ and CD8⁺ T cells (Table 2). These observed changes were not due to alteration of T cell flow rates through the LN, since both transit times and output of naïve CD4⁺ and CD8⁺ T cells did not change significantly. The anatomic configuration where DCs migrate near HEVs so they can interact quickly with arriving T cells and effectively sample the circulating T cell population is clearly optimal (Bajenoff et al., 2003).

Table 2.

Anatomic placement of HEVs and AL Affects total and unique T cell contacts per DC and Primed T cell output

	AL above HEV (Baseline)	AL below HEV
Average number of T cell contacts per DC (×104)	1.84 ± 0.47	0.74 ± 0.25 c
Average number of Unique T cell contacts per DC	1200 ± 340	960 ± 275 b
Unique contacts (%)	6.7 ± 1.4	13.3 ± 4.5 b
Cells exiting per LN
naïve CD4+ T (× 106)	1.49 ± 0.01	1.48 ± 0.01
naïve CD8+ T (× 106)	1.30 ± 0.01	1.29 ± 0.01
primed CD4+ T (×104)	1.44 ± 0.40	0.83 ± 0.21 b
primed CD8+ T (×103)	2.88 ± 0.14	1.12 ± 1.12 b
Transit time (hrs)	11.8 ± 0.10	12.2 ± 0.11
Search time (hrs)	1.82 ± 0.20	3.46 ± 0.24 c

All comparisons are vs. baseline placement, using Student’s t-test to compute significance levels:

^ap < 0.05

^bp < 0.01

^cp < 0.001

25 simulations resulted in means ± S.D. based on 400 DCs, >250,000 individual transit times and > 50,000 T cell searches

3.5. Effect of chemotaxis on T cell-DC contacts and T cell output

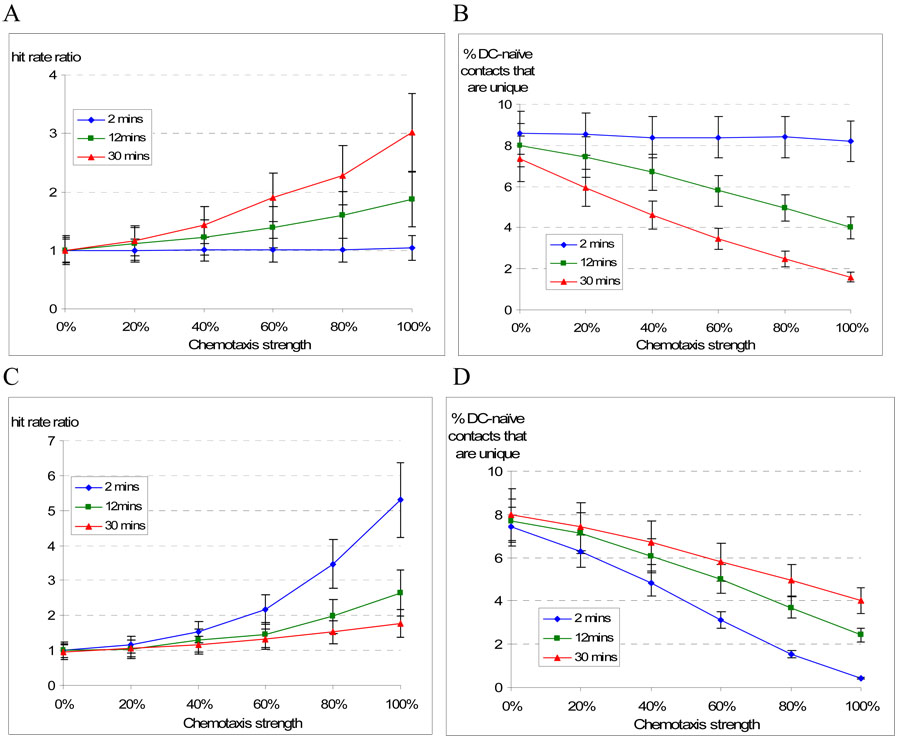
To evaluate DC inducing CD4⁺ T cell chemotaxis, we performed simulations in which we varied three parameters (chemotactic strength, duration and recovery). We varied chemotactic strength along a spectrum from random to completely chemotaxis directed (always moving up a chemokine gradient, with no stochasticity) and varied duration and recovery times from 2 to 30 minutes (Figure 5). Our output metrics were total number of CD4⁺ T cell contacts per DC and the percentage of those contacts that were with a unique naïve CD4⁺ T cell. We calculated a “hit rate ratio”, adapted from (Castellino et al., 2006), by comparing the total T cell-DC contacts vs. a control with no chemotaxis. As strength and duration of chemotaxis increased, the hit rate ratio increased several fold, while the percentage of unique contacts decreased. Similarly, as chemotactic strength increased and recovery time shortened (i.e., faster recycling back to chemotactic receptiveness), the hit rate ratio increased but the percentage of unique contacts again decreased. The decrease in percentage of unique contacts was due to both an increase in number of total contacts and a decrease in number of unique contacts. Whether by increased chemotactic strength, lengthened duration or by shortened recovery time, higher levels of chemotaxis interfered with efficient T cell repertoire scanning.

Figure 5. Chemotaxis strength, duration and recovery affect CD4⁺ T cell-DC contacts.

Effect of chemotactic strength, duration and recovery: In panel A, the number of T cell contacts per DC (hit rate) is expressed as a ratio vs. no chemotaxis (i.e., random motion) and with variable duration (time to desensitization = 2, 12 or 30 minutes). The number of contacts progressively increases with increasing strength and duration of chemotaxis, but the proportion of unique contacts decreases (panel B). In panels C and D, strength of chemotaxis and recovery (resensitization time = 2, 12 or 30 minutes) time are varied. Stronger chemotaxis and shorter recovery times increased the hit rate ratio, but also decreased unique contacts. All values represent mean ± 1 S.D. from 25 simulations.

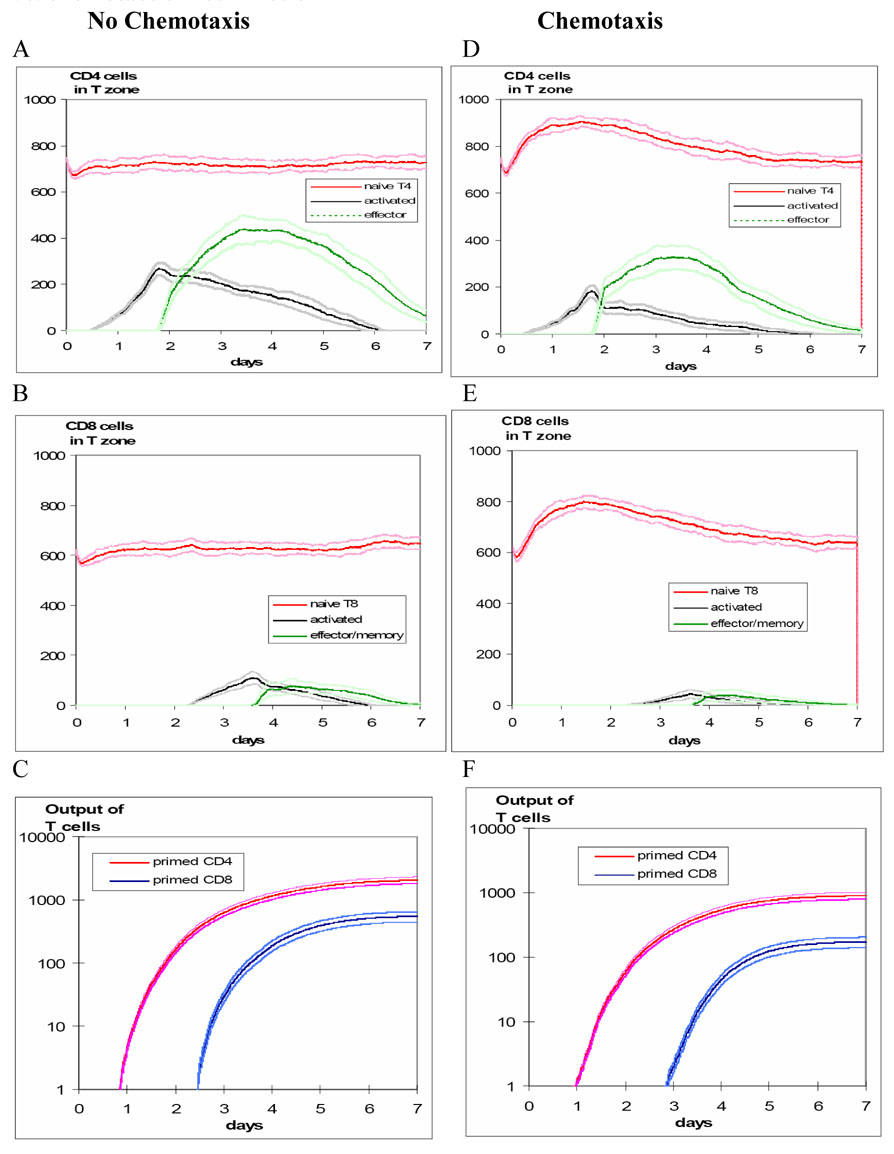
The effect of chemotaxis is also illustrated in Figure 6, which compares simulations with random vs. chemotactic T cell motion. For purposes of demonstrating activity, these scenarios use a cognate frequency of 1:10 (but the results are consistent at the 1:300 ratio). Chemotaxis results in both delayed and smaller cumulative production of primed T cells, especially CD8⁺ T cells. There is an initial rise in the density of naïve T cells for both CD4⁺ and CD8⁺ T cells since recruitment rates for naïve CD4⁺ and CD8⁺ T cells were the same for each scenario but chemotaxis prolonged search and transit times. This results in crowding and inefficient repertoire scanning.

Figure 6. Magnitude and timing of T cell production in the LN: comparing random vs. chemotactic T cell motion.

Time course of CD4⁺ and CD8⁺ T cell populations in the LN T-zone, under scenarios of random motion vs. chemotaxis, showing mean ± 1 SD (from 25 simulations) after introducing antigen-bearing DCs. For purposes of illustrating activity, these scenarios are based on a cognate frequency of 1:10. The left panels are based on random T cell motion, while the right panels are based on chemotactic motion for both CD4⁺ and CD8⁺ T cells.

In panel A, activated CD4⁺ T cells appear by 24 hours, reach a peak by about 48 hours, and are followed by effector CD4⁺ T cells reaching a peak around 3–4 days. In panel B, the CD8⁺ T cell response, dependent on CD4⁺ T helper cells, is delayed by about 1 day. In panel C, cumulative output of all primed T cells is plotted on a log scale as mean ± 1 SD. Maximum CD4⁺ and CD8⁺ T cell outputs are achieved by about 4 and 6 days, respectively.

The effect of chemotaxis is shown in the right panels (D, E and F) and results in lower production and later peaking of primed CD4⁺ and CD8⁺ T cells. Since the recruitment rates for naïve CD4⁺ and CD8⁺ T cells were the same for each scenario and chemotaxis caused prolonged search and transit times, there was an initial rise in the density of naïve T cells for both CD4⁺ and CD8⁺ T cells as a result of crowding and inefficient repertoire scanning.

3.6. Sensitivity analysis of chemotactic parameters

We confirmed how chemotaxis affects our output metrics by LHS/PRC analysis of 1000 simulations, summarized in Table 3. Stronger CD4⁺ T cell chemotaxis increased total CD4⁺ T cell-DC contacts, decreased total CD8⁺ T cell-DC contacts, and more importantly decreased the number of unique CD8⁺ T cell-DC contacts, implying steric competition. Similarly, increased duration of CD4⁺ T cell chemotaxis increased total CD4⁺ T cell-DC contacts, but decreased both unique CD4⁺ T cell-DC contacts and CD8⁺ T cell-DC contacts, while increasing recovery time (i.e., a longer time that T cells were non-receptive to chemotaxis) increased the number of unique CD4⁺ T cell-DC contacts. Stronger CD8⁺ T cell chemotaxis increased total CD8⁺ T cell-DC contacts, but decreased both total and unique CD4⁺ T cell-DC contacts. Again, chemotaxis increased contacts, but decreased efficient scanning and may result in competition on the same DC surface for CD4⁺ and CD8⁺ T cell binding. Similarly, increased duration of CD8⁺ T cell chemotaxis resulted in more total CD8⁺ T cell-DC contacts, but fewer CD4⁺ T cell-DC contacts and fewer unique CD4⁺ T cell-DC and CD8⁺ T cell-DC contacts.

Chemotaxis had only inhibitory effects on output of primed CD4⁺ or CD8⁺ T cells. Stronger or longer duration of CD4⁺ T cell chemotaxis inhibited output of primed CD8⁺ consistently on days 4–7, but did not increase output of primed CD4⁺ T cells. Stronger CD8⁺ T cell chemotaxis decreased output of primed CD4⁺ T cells on days 4–7, but did not increase output of primed CD8⁺ T cells. Search times were lengthened when chemotaxis lasted longer and were shortened when there were longer chemotaxis recovery times, since the local environment around a DC was more (or less) crowded. Transit times were longer under conditions of stronger or longer duration CD4⁺ chemotaxis (note that our metrics for mean free path, transit and search times were based on naïve CD4⁺ T cells). Therefore, whether measured by unique T cell-DC contacts, search time to first contact a DC, output of primed T cells or turnover (transit time), chemotaxis had only inhibitory effects on efficient repertoire scanning.

3.9 Sensitivity analysis of full model parameters

In the full model analysis, we focus on identifying parameters that significantly alter our output metrics: T cell path lengths, transit times, search times, T cell-DC contacts and output of primed CD4⁺ and CD8⁺ T cells. A subset of model parameters had this property and we summarize the results in Table A.1–Table A.4, in the Appendix. These include: (1) separate analysis of short-term persistence, (2) full model analyses of mean free path, search and transit times and T cell contacts per DC and (3) full model analyses of output of primed: naïve T cells, for both CD4⁺ and CD8⁺ T cells. However, in this full model analysis , chemotaxis still had only inhibitory effects on production of non-naïve T cells and did not qualitatively alter any conclusions from the local parameter analysis.

4. Discussion

Whether T cell-DC contacts in LNs occur because of random T cell migration or are driven by chemotaxis is a fundamental issue for vaccine design and understanding host responses during infection, cancer and autoimmune disease. Our work demonstrates that efficient T cell scanning requires only random migration, not chemotaxis. While directed motion moves cells rapidly from one point to another, a random search enhances full exploration of the local environment. An analogous observation is that foraging patterns of birds and insects exhibit a mixture of random exploration within a local vicinity with occasional longer directed flights to explore new areas as an optimal search strategy (Viswanathan et al., 1999; Viswanathan et al., 2001). Within a LN, less than 1% of cells are DCs (Takahashi et al., 2001) and the frequency of a cognate T cell that exactly matches a particular antigen may be as low as 1:10⁷ (Turner et al., 2006), so initial interactions between T cells and DCs must be both brief and numerous to produce an effective, timely T cell response. Although chemotaxis enhances directionality of T cells, our model predicts that it hinders cognate T cells from contact with DCs. There is great competition for T cells to access a DC surface, and given how rare cognate T cells are in an actual response, the strategy of attracting non-specific T cells appears inefficient. A better strategy for efficient scanning is to briefly contact and then clear irrelevant T cells away from a DC. Our model of chemotaxis is relatively simple, but it does include features of variable attraction strength, desensitization and resensitization times, rather than chemotaxis as an all or none phenomenon. Our model used cognate frequency that, although matched to published imaging experiments (Miller et al., 2002; Miller et al., 2003; Miller et al., 2004a; Miller et al., 2004b), is much higher than observed in vivo during an actual infection. We abstract a small section of a T-zone from a LN, through which ~ 10⁴ naïve T cells transit during a 7 day simulation, so cognate frequencies of 1:10⁶ are too low to reproducibly result in T cell activation in our simulations. However, our model results imply that if cognate frequency is lower than what we tested, T cell crowding around DCs induced by chemotaxis would create an even greater impediment to repertoire scanning. If chemoattraction is sufficiently strong and long lasting, then although total T cell contacts per DC increase significantly, the numbers of unique contacts decrease, thereby inhibiting efficient repertoire scanning and ultimately hindering generation of an adaptive immune response. Further, if there were separate chemotactic mechanisms involving CD4⁺ and CD8⁺ T cells, we found evidence of steric competition. This would suggest that there might be a strategic advantage to separating CD4⁺ and CD8⁺ expansion either spatially (different DCs) or temporally (different activation kinetics). In fact, recent work has described two distinct DC subsets for antigen presentation for CD4⁺ and CD8⁺ T cells (Dudziak et al., 2007).

Aside from T cell motility, efficient repertoire scanning is also dependent on LN microanatomy. Our model demonstrates that HEVs and ALs are positioned optimally to shorten the time required for entering naïve T cells to encounter a DC in a LN T-zone and to enhance the number of T cell-DC contacts and output of primed CD4⁺ and CD8⁺ T cells. Co-localization of T cells and DCs in a LN T-zone enhances likelihood of rare cognate encounters and positioning of DCs near the entry points for newly arriving T cells (Bajenoff et al., 2003) and rapid movement of their long dendrites contributes to efficient local scanning, despite a relatively slow DC velocity.

We constructed a 2-D model both for greater speed of computation and because it mimics the typical presentation of time-lapse intravital 2PM data. Building a 3-D model has obvious appeal as a more realistic representation of a 3-D anatomical structure and allows less restriction to cellular motion. However, there are some key issues that we benefit from using a 2-D representation initially. First, random walks in 3-D vs. 2-D differ with respect to motility coefficient; in 3-D an individual path might never return to its origin, but in 2D it will eventually. Second, experimental data used to calibrate the LN model (mean distance from HEV to EL, for example) are measured from photomicrographs, which are 2-D and do not have a 3-D orientation. Third, 2PM experimental data is constructed from stacks of planar representations of T cell motion, typically 2.5 µm apart. There is a trade-off in terms of more information in the x–y plane regarding position and speed and better depth resolution, so 3-D representations of T cell motility have inherently greater measurement error (Cahalan et al., 2002). Thus, calibration and estimation of key parameters is more complex in 3D. We also believe our results are extendable to 3-D as initial studies by our group using chemotaxis in a 3-D representation yield even more crowding effects that are observed in 2-D (not shown). These studies are currently being investigated.

LNs have a highly organized and complex architecture composed of distinct cellular compartments and structures, including a basement membrane that is comprised of non-hematopoietic, fibroblastic reticular cells (FRCs) present in the T cell area (Bajenoff, 2006). Much interest has recently centered on the FRC network (Bajenoff et al., 2006) in guiding T cell motion in the LN. One analysis of T cell motion from 2PM (Beltman et al., 2007) concluded that large velocity fluctuations of T cells were determined by the LN environment rather than by an intrinsic motility program. However, another analysis (Beauchemin et al., 2007) of 2PM found that T cell motion could be faithfully modeled using a combination of pause times and times to move at a constant speed. Interestingly, the estimates of T cell 'mean free path' determined by 2PM are about twice the average distance between branch points in the FRC network, suggesting that at an intersection a T cell will turn onto a new fiber only ~ 50% of the time. Clearly, T cell motion within a LN is more complex than simply conforming to a path on the FRC network.

Observations in vivo of T cell motion in LNs show an inherent cycle of establishing cell polarity, later pausing and re-adjusting course (Miller et al., 2002; Miller et al., 2003) and the same pattern is observed in vitro, even where there is no underlying scaffold structure (Butcher and Lin, 2006). So, random motion with short-term persistence, chemotaxis and an underlying guidance structure are not mutually exclusive mechanisms (Mempel et al., 2006). Our model does not directly contradict previously studies of chemokine-mediated motion of naïve CD8⁺ T cells towards dyads of DCs and activated CD4⁺ T cells (Castellino et al., 2006), nor are we attempting to diminish the importance of chemotaxis generally in T cell migration. While directed motion based on the inherent architecture of the LN or chemotaxis to facilitate entry or exit from a LN may aid in transit and turnover of T cells, our model suggests that chemotaxis directing T cells towards DCs does not enhance repertoire scanning, but appears to inhibit it.

Appendix

In the full model analyses, short-term persistence was included as a parameter whose value varied from 50–95% (see Methods for more info on short-term persistence). When varied over that wide range, greater persistence was strongly associated with longer mean free path, shorter search and transit times and more unique T cell-DC contacts (Table A.1). This resulted in a greater initial rise in ratio of primed to naïve CD4⁺ T cells exiting the T-zone, but lowered cumulative output of ratio primed to naïve CD8⁺ T cells. Our results may imply one aspect of evolutionary pressure that established short-term persistence of T cell motion.

Table A.1.

T cell “Short-term Persistence” vs. DC contacts and T cell output

Short-term Persistence	50 %	70 %	90 %
CD4+ T cell contacts per DC	25,700 ± 9,400	19,500 ± 7,800 ***	17,800 ± 5,970 ***
% Unique contacts	2.4 ± 0.66	4.3 ± 1.0 **	5.7 ± 0.9 ***
CD8+ T cell contacts per DC	21,200 ± 6,700	18,800 ± 7,800 *	17,600 ± 6,100 **
% Unique contacts	2.30 ± 0.60	4.2 ± 0.9 **	6.1 ± 1.3 ***
Search time (hrs)	4.34 ± 0.31	3.61 ± 0.22 **	3.17 ± 0.16 ***
Transit time (hrs)	19.7 ± 0.17	16.5 ± 0.18 **	13.1 ± 0.21 **
Mean free path (µm)	7.4 ± 0.1	11.9 ± 0.2 ***	21.0 ± 0.2 ***
Cumulative T cell output
naïve
CD4+ T cells (× 106)	0.784 ± 0.016	0.990 ± 0.138 ***	1.36 ± 0.024 ***
CD8+ T cells (× 106)	0.691 ± 0.014	0.878 ± 0.13 ***	1.21 ± 0.020 ***
primed (per 100 naïve cognates)
CD4+ T cells	208 ± 19	228 ± 15 **	201 ± 25 NS
CD8+ T cells	129 ± 26	106 ± 8 *	46 ± 9 ***

Cognate: non-cognate ratio = 1:10

All comparisons are vs. probability = 50% category, using Student’s t-test to compute significance levels:

^NSp > 0.05

^*p < 0.05

^**p < 0.01

^***p < 0.001

25 simulations resulted in means ± S.D. based on 200 DCs, >250,000 individual transit times and > 50,000 T cell searches

In the full model analysis (Table A.2), increased recruitment of naïve T cells lead to shorter mean free paths, longer search times for CD4⁺ T cells to encounter a DC. Search times also increased with an increased probability of an antigen-bearing DC activating a cognate CD4⁺ T cell or when DC chemotaxis for CD8⁺ T cells was stronger or had longer duration. Search times for CD4⁺ T cells were decreased with higher DC chemotaxis for CD4⁺ T cells, or when effector CD4⁺ T cells were more likely to license DCs. Transit time through a LN was prolonged and total contacts of CD4⁺ T cells with DCs were increased with stronger chemotaxis towards DCs. Number of unique contacts of CD4⁺ T cells with DCs was increased with higher naïve CD4⁺ T cell recruitment, but inhibited by longer duration of CD4⁺ T cell chemotaxis or by either stronger or longer lasting CD8⁺ T cell chemotaxis. Total contacts of CD8⁺ T cells with DCs were increased by recruitment of naïve CD8⁺ T cells, greater strength or duration of CD8⁺ T cell chemotaxis, higher probability of LDC activation, shorter doubling periods after CD4⁺ T cell activation, greater binding probability of CD4⁺ T cells with DCs, greater activation probability of DCs and more short-term persistence. Total contacts of CD8⁺ T cells with DCs were decreased when CD4⁺ T cell chemotaxis was stronger or lasted longer. Unique contacts of CD8⁺ T cells with DCs were inhibited by higher CD4⁺ T cell recruitment, stronger or longer lasting CD8⁺ T cell chemotaxis and were increased by greater short-term persistence.

Table A.2.

Sensitivity of T cell path length, transit time, search time and T cell contacts per DC to full model parameters by PRCC analysis

Parameter	Mean free path 1	Search time	Transit time	T-cell contacts per DC
				CD4 +		CD8 +
				All	Unique	All	Unique
CD4+ T cells
recruitment	↓	↑↑↑			↑↑		↓↓↓
binding with DC						↑↑
doubling time						↓↓
Antigen-bearing DC activation		↑↑				↑↑
CD8+ T cells
recruitment	↓	↑↑↑			↓↓↓	↑↑↑
LDC activation						↑↑
eCD4 licenses Antigen-bearing DC		↓↓
Short-term persistence	↑↑↑↑	↓↓↓↓	↓↓↓↓		↑↑↑↑	↑↑	↑↑↑
CD4+ T cell chemotaxis
strength		↓↓	↑↑	↑↑↑		↓↓↓↓	↓↓↓↓
duration					↓	↓↓	↓↓
recovery
CD8+ T cell chemotaxis
strength		↑↑			↓↓↓	↑↑↑↑
duration		↑↑↑			↓↓	↑↑↑
recovery

Cognate: non-cognate ratio = 1:300

¹mean free path before turning

ns = p > 0.000358 (threshold based on Bonferroni correction)

↓ or ↑ = p < 0.000358, with negative or positive association

↓↓ or ↑↑ = p < 10⁻⁵, with negative or positive association

↓↓↓ or ↑↑↑ = p < 10⁻⁶, with negative or positive association

↓↓↓↓ or ↑↑↑↑ = p < 10⁻⁹, with negative or positive association

In the full model analysis of CD4⁺ T cell output over 7-day simulations (Supplemental Table A.3), longer doubling periods were consistently associated with less output of primed T cells (days 2–7), while a higher number of divisions were associated with a higher output. Longer doubling times for CD8⁺ T cells resulted in more CD4⁺ T cell output on day 2, presumably related to less crowding. Higher probability of non-naïve CD4⁺ T cell binding to DCs resulted in higher output on days 3 and 4. Greater short-term persistence with resultant shorter search times resulted in higher output on days 1–4. Strength of chemotaxis had no significant effect on CD4⁺ T cell output, while longer lasting chemotaxis (for either T cell class) inhibited output.

Table A.3.

Sensitivity of CD4⁺ T cell output to full model parameters by PRC analysis

Parameter	1 day	2 days	3 days	4 days	5 days	6 days	7 days
CD4+ T cells (primed:naïve)
Recruitment		↓
doubling time		↓↓↓	↓↓↓	↓↓	↓↓	↓↓	↓↓
number of divisions		↑↑	↑↑	↑↑↑	↑↑	↑↑	↑↑
CD8+ T cells (primed:naïve)
recruitment
doubling time		↑↑
Primed CD4 binds DC			↑↑↑	↑↑
Short-term persistence	↑↑↑	↑↑↑	↑↑↑	↑↑
CD4+ T cell chemotaxis
strength
duration		↓↓	↓↓
recovery
CD8+ T cell chemotaxis
strength
duration		↓↓
recovery

Cognate: non-cognate ratio = 1:300

ns = p > 0.000358 (threshold based on Bonferroni correction)

↓ or ↑ = p < 0.000358, with negative or positive association

↓↓ or ↑↑ = p < 10⁻⁵, with negative or positive association

↓↓↓ or ↑↑↑ = p < 10⁻⁶, with negative or positive association

↓↓↓↓ or ↑↑↑↑ = p < 10⁻⁹, with negative or positive association

In the full model analysis of CD8⁺ T cell output over 7-day simulations (Table A.4), CD4⁺ T cell parameters played an important and often inhibitory role. Greater CD4⁺ T recruitment, longer activated T cell doubling periods or a greater number of cell divisions were consistently associated with less output of primed T cells (days 3–7). On the other hand, higher CD8⁺ T cell output was associated with greater probability of CD4⁺ T cell activation, higher probability of CD8⁺ T cell binding to LDC and higher probability of LDC activating a CD8⁺ T cell. Higher probability of binding of CD4⁺ T cells to DCs or a higher probability of maturation of a DC resulted directly in more effector CD4⁺ T cells and later (days 5–7), higher output of CD8⁺ T cells. Chemotaxis of CD8⁺ T cells had no significant effect in the full model to increase output of CD8⁺ T cells, while CD4⁺ T cell chemotaxis that lasted longer inhibited output of CD8⁺ T cells (days 4–7), while longer recovery times (day3) actually enhanced the output of CD8⁺ T cells.

Table A.4.

Sensitivity of CD8⁺ T cell output to full model parameters by PRC analysis

Parameter	1 day	2 days	3 days	4 days	5 days	6 days	7 days
CD4+ T cells
recruitment				↓	↓↓	↓↓↓	↓↓↓
doubling time			↓↓	↓↓	↓↓↓	↓↓↓	↓↓↓
number of divisions			↓↓	↓↓	↓	↓	↓
Antigen-bearing DC activation				↑	↑↑↑	↑↑	↑↑
CD8+ T cells
cognate binding to LDC					↑	↑	↑
LDC activation					↑	↑	↑
Primed CD4 binds DC					↑
Primed T cell matures DC					↑	↑	↑
Short-term persistence
CD4+ T cell chemotaxis
strength
duration				↓	↓	↓	↓
recovery			↑
CD8+ T cell chemotaxis
strength
duration
recovery

Cognate: non-cognate ratio = 1:300

ns = p > 0.000358 (threshold based on Bonferroni correction)

↓ or ↑ = p < 0.000358, with negative or positive association

↓↓ or ↑↑ = p < 10⁻⁵, with negative or positive association

↓↓↓ or ↑↑↑ = p < 10⁻⁶, with negative or positive association

↓↓↓↓ or ↑↑↑↑ = p < 10⁻⁹, with negative or positive association