Proton Solvation and Transport in Aqueous and Biomolecular Systems

Abstract

The excess proton in aqueous media plays a pivotal role in many fundamental chemical (e.g., acid-base chemistry) and biological (e.g., bioenergetics and enzyme catalysis) processes. Understanding the hydrated proton is, therefore, crucial for chemistry, biology, and materials sciences. Although well studied for over 200 years, excess proton solvation and transport remains to this day mysterious, surprising, and perhaps even misunderstood. In this feature article various efforts to address this problem through computer modeling and simulation will be described. Applications of computer simulations to a number of important and interesting systems will be presented, highlighting the roles of charge delocalization and Grotthuss shuttling, a phenomenon unique in many ways to the excess proton in water.

INTRODUCTION

The solvation structure and high mobility of excess protons in liquid water is a critically important phenomenon in numerous chemical and biological processes. Protons play a key role in acid-base reactions, enzyme catalysis, and many forms of energy transfer and conversion in biomolecules and complex materials. For these reasons, the mechanism of proton solvation and transport (PS&T) has been the focus of scientific exploration for over two centuries. The most recognized foundational theory was presented by the Lithuanian scientist C. von Grotthuss, who first postulated that charged bodies are transferred through water by hopping from molecule to molecule.¹ This mechanism, still referred to as “Grotthuss shuttling”, has been significantly modified since that time. It is now appreciated that the protonic charge is transferred from the hydronium ion (H₃O⁺) to surrounding water molecules via the rearrangement of covalent and hydrogen-bonds (h-bonds), thus resulting in structural diffusion that can be much faster than conventional diffusion under the proper conditions (e.g., along quasi-one-dimensional “water wires” in proteins). This shuttling mechanism also seems to explain why protons are significantly more mobile than other solvated cations of similar charge and size in aqueous media.

Although numerous theoretical and experimental efforts have synergistically and significantly advanced our understanding of PS&T over the last three decades, they have frequently provided conflicting and even contradictory conclusions. Indeed, we have yet to identify a complete and conclusive microscopic picture of the solvation and transport of excess protons in aqueous systems. This challenge will not likely be solved by experiment alone, but rather by computational simulations benchmarked against experimental results. It is within this context that the present feature article has been cast.

PS&T is one of the most challenging molecular processes to study through computer simulation for several reasons. First, it involves a chemical bonding topology that is dynamically rearranging, i.e. covalent and h-bonds are continuously formed and broken (cf. Fig. 1a). Second, the proton is light enough that quantum effects such as tunneling and zero-point energy contributions, might affect the mechanism of transfer. Third, the proton does not exist as a single “hydronium cation” (H₃O⁺, cf. Fig 1b), as is commonly taught in high school chemistry, but as a protonic charge that is delocalized over multiple water molecules and shuttled by numerous hydrogen nuclei. Thus, the identity of the protonic charge is constantly changing, predominantly in the form of either an Eigen (H₉O₄⁺) or Zundel cation (H₅O₂⁺) surrounded by a dynamically rearranging network of h-bonded water molecules (cf. Fig. 1c). The electrostatic interactions of the “excess proton” with its water environment therefore defy traditional solvation models for ions in polar media. Despite these challenges, computer simulations can play an important, even critical, role in determining the mechanism of PS&T. However, as with any computer simulation approach, care must be taken to ensure that as much of the relevant physics is represented in the modeling as possible, including an accurate and physically complete potential energy surface.

Figure 1.

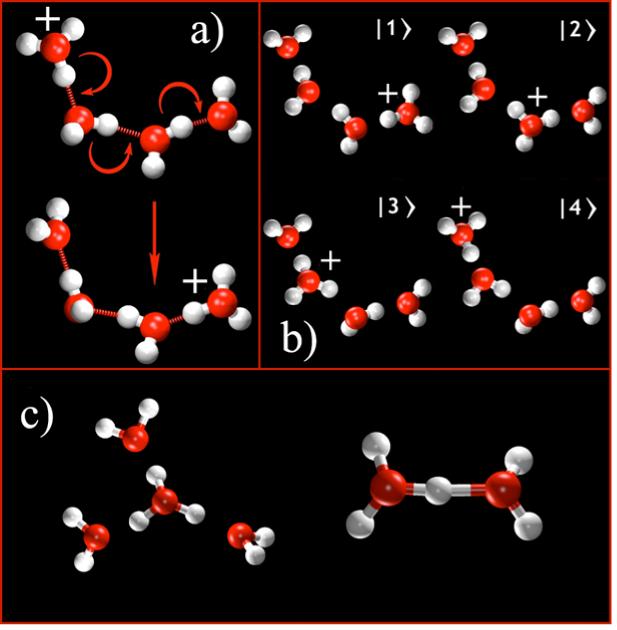
a) The Grotthuss shuttling process for the excess proton in a small chain of water molecules. Note that the chemical bonds and hydrogen bonds are rearranged, thereby moving the excess charge without any (or little) molecular diffusion. b) The MS-EVB basis states used to describe this process. Transitions between MS-EVB states via the MS-EVB algorithm allow for a continuous and deterministic trajectory describing Grotthuss shuttling and proton delocalization. c) The stable Eigen (left; H₉O₄⁺) and Zundel (right; H₅O₂⁺) cations

A variety of computational approaches have been presented to study PS&T. They range from pure quantum mechanical treatment of the system via ab initio molecular dynamics (MD), to mixed quantum/classical dynamics approaches, to empirical force field MD simulations, and even to non-deterministic, stochastic methods. In this article we will review how theory and computational simulations have contributed to our understanding of PS&T in aqueous and biomolecular systems, primarily focusing on our group’s long-standing efforts^2-37 to develop the multi-state empirical valence bond (MS-EVB) formalism. A number of aqueous and biomolecular systems will be described, including PS&T in bulk water,^4-14 in aqueous weak acids,^15-17 at the water liquid-vapor interface,¹⁸ in protonated water clusters,^19-21 in water-alcohol mixtures,²² in water-filled hydrophobic channels²³, in synthetic ion channels,^24,25 at the water/lipid bilayer interface,²⁶ through lipid bilayers,^27,28 in large transmembrane biomolecular proton channels^29-37 such as the aquaporin channels^33-35 and the M2 channel in influenza A,^29-32 and finally in enzymes such as carbonic anhydrase and cytochrome c oxidase.^36,37 Most of the aforementioned computational studies have relied upon experimental data for their development and validation. Since space limitations do not allow us to discuss them herein, we refer the reader to relevant reviews and literature on several related topics, including the experimental analysis of PS&T;³⁸ PS&T in complex materials, such as Nafion™, for which there are very high acid concentrations;^39,40 and “proton transfer” reactions in which the proton exchanges between donor and acceptor groups.^41-43

COMPUTATIONAL METHODOLOGIES

The most important component in a computer simulation of PS&T is a physically complete and accurate potential energy function for the system, especially given the fact that the Grotthuss shuttling involves the constant rearrangement of the chemical bonding topology (cf. Fig. 1a). If an accurate potential energy function is in hand, both the dynamics (e.g., self-diffusion) and free energies (e.g., solvation free energies or free energy barriers to proton transport) can be calculated from the dynamical simulations using deterministic (Newtonian) equations of motion subject to the proper ensemble constraints such as constant temperature, pressure, etc.. Replacing all-atom, deterministic MD with more phenomenological approximations (e.g., dielectric continuum models, stochastic dynamics, etc.), can introduce uncontrolled errors. Similarly, inadequate sampling in the MD or an intrinsically inaccurate or incomplete potential energy function can also introduce errors, although these errors are generally more controllable (via improved simulation statistics, potential energy function refinement, etc.). With this perspective in mind the MS-EVB approach that has been extensively developed and utilized in our group will be described along with other PS&T computer simulation approaches.

The Multi-State Empirical Valence Bond (MS-EVB) Method

In the MS-EVB method PS&T can be simulated explicitly by evolving the system on a reactive potential energy surface defined by a linear combination of multiple diabatic potentials. This reactive potential energy surface enables the formation and cleavage of molecular bonds in a deterministic classical MD simulation. Each of the diabatic potentials represents one possible protonation configuration, or a limiting “state” of the system. Thus, in the full MS-EVB potential the proton is represented as a protonic charge delocalized over multiple molecules surrounded by dynamically rearranging h-bonds and transferred by dynamically rearranging covalent bonds (i.e., the Grotthuss PT mechanism). The sum of states composes the basis states in an overall “Hamiltonian” matrix. Empirical potentials are used for the diagonal elements which describe the bonded and non-bonded interactions for a bonding topology. The off-diagonal elements allow for transitions between states as a function of the instantaneous nuclear configurations. Figure 1b shows the MS-EVB states necessary to model a proton shuttle through a short water wire. In the bulk liquid phase, many states are necessary (as many as 20-30 in order to describe the first three solvation shells of a hydronium ion) and their identities must be allowed to change dynamically in time. Each state contains all of the molecules of the condensed phase system and has the proton bonded to a different water molecule. During an MS-EVB MD simulation, the Hamiltonian matrix is diagonalized and the lowest eigenfunctions are determined at each time-step. The forces on the nuclei are calculated using the Hellmann-Feynman theorem for the lowest state then and fed into an MD integrator such as Velocity Verlet. Thus the resulting MD trajectory explicitly includes the excess proton delocalization and shuttling through the water molecules.

The MS-EVB parameters, which form the diagonal and off-diagonal matrix elements, are generally chosen to be compatible with molecular mechanics force fields such as AMBER and CHARMM. They have been optimized to accurately reproduce binding energies and proton transfer barriers calculated with high level ab initio methods,^5,6,11 as well as structural, transport, and spectroscopic properties of the proton in bulk water,^5-11,13 including nuclear quantum effects.^6,8 At any time-step in the simulation the protonic charge is defined by the ground state MS-EVB vector of state coefficients, $\overrightarrow{c}=(c_1,c_2,\dots ,c_N)$, reflecting the delocalization of the excess charge over the h-bond network and the weights of the N-different EVB states given by the amplitudes, $c_i^2$. The process of PS&T in an MS-EVB simulation is characterized by the constant and dynamically evolving redistribution of these amplitudes, as a function of the propagation of the nuclear coordinates. The distribution of the first (largest) MS-EVB amplitude, $c_i^2$, in bulk water is usually bimodal, with a maximum at $c_i^2\approx 0.65$, reflecting the Eigen cation, $H_9{O}_4^{+}$. The Zundel cation, with $c_i^2\approx 0.5$, is somewhat less thermodynamically stable than the Eigen in bulk water in the present version of the MS-EVB potential,¹¹ in agreement with other theoretical predictions.⁴⁴ The effective spatial position of the excess proton can be defined as the center of excess charge (CEC) of the MS-EVB complex:¹¹

$${\mathit{r}}_{cec}\left(t\right)=\sum _{i=1}^N{c}_i^2{\mathit{r}}_i\left(t\right),$$ (1)

where r_i(t) is the center of charge vector of the hydronium in the i^th MS-EVB state at time t. The (classical and non-Grotthuss-shuttling) hydronium ion is represented as a simple limit of the MS-EVB model corresponding to a single (1×1) diagonal element of the MS-EVB Hamiltonian. Throughout this article the terms “proton” and “hydronium” stand for the center of excess charge of the full MS-EVB model and the single state MS-EVB model (the “classical” hydronium cation), respectively.

Within any MD simulation methodology it is important to give careful consideration to the actual target of the calculation. Proton transport over long length and time scales is quite different from simpler kinetic proton transfer processes; it can involve numerous free energy barriers and subtle dynamical effects, such as h-bond network rearrangements in aqueous solution or long time scale protein conformational changes in a biomolecular environment. For systems in which there is a large free energy barrier influencing proton transport, the simulation may also involve the calculation of the potential of mean force for the excess protonic charge (which is, as described earlier, characterized as a function of the center of excess charge coordinate in the MS-EVB model). The potential of mean force, in essence, provides a picture of the free energy landscape sampled by an ensemble of excess protons as they diffuse through a confined space such as a proton channel. However, the potential of mean force alone is not always enough to determine the true transport behavior of the excess protonic charge. In some cases, the self-diffusion constant of the excess proton must be evaluated explicitly in addition to the potential of mean force to calculate the overall proton conductance.^34,35

It is important to describe how the MS-EVB methodology relates to the work of other researchers. The original Empirical Valence Bond (EVB) method was developed by Warshel and co-workers.^42,43,45,46 The EVB approach was in many ways a pioneering development in molecular simulation because it allowed for reactive processes to be described by a relatively simple empirical potential energy function. The original EVB method employs an insightful interpolation scheme that utilizes the concept of a superposition state in quantum mechanics. The EVB approach was developed in order to study proton and hydride transfer in enzymes, as well as electron transfer reactions. Generally these applications require only a few diabatic basis states in the EVB parameterization and the identity of those states is fixed with the molecular frame of the donor and acceptor species (and perhaps a few intervening water molecules).

By contrast, the MS-EVB approach represents an extensive generalization of these ideas to describe PS&T over much longer distances, involving Grotthuss shuttling through many moving (diffusing) water molecules and also possibly through ionizable molecular groups such as amino acids. A critical element of the MS-EVB approach is that the identity of the states included in the MS-EVB complex is constantly changing during the simulation. These states are selected by virtue of a rather intricate state-searching algorithm in order to ensure as much continuity in the molecular forces as possible, which in turn helps to ensure good energy conservation in the MD simulation so that the trajectory generates a reliable ensemble average of dynamical observables. This essential dynamically rearranging multi-state feature of the MS-EVB method allows the critical process of molecular diffusion to be included in the MS-EVB methodology. Including the physics of diffusion, in addition to Grotthuss shuttling, was essential to the development of an empirical simulation methodology for proton transport processes, as opposed to simpler proton transfer reactions between a fixed donor and acceptor group. The interplay between molecular diffusion and Grotthuss proton shuttling is indeed critical for understanding the process of PS&T in aqueous and more complex physical and biomolecular systems.

It should also be appreciated that Vuilleumier and Borgis^47-51 independently developed their own multi-state model for the excess proton in bulk water. Both this and our MS-EVB model are derived from the original 2-state EVB model for the excess proton in water of Lobaugh and Voth.⁴ However, there are important differences between the Vuilleumier and Borgis model and MS-EVB, particularly in the treatment of the off-diagonal matrix elements, the state selection algorithm, and the ability to conserve energy (the latter being related to the multi-state selection algorithm, which is at the heart of the MS-EVB methodology). The second generation MS-EVB model (denoted MS-EVB2)¹¹ and its underlying multi-state algorithm has significantly expanded upon some of the initial MS-EVB concepts, and the third generation model (soon to be published) will continue along this path of refinement. It should be also noted that Laria et al.⁵² have recently used the MS-EVB model to study protons in supercritical water and found that their simulations were in agreement with several experimental results.

Other Simulation Approaches for Proton Solvation and Transport

Parrinello and collaborators^53-60 have used the Car-Parrinello MD method to study the excess proton in water and other systems. In this approach, the electronic structure at the level of gradient-corrected density functional theory (DFT) is solved simultaneously with the nuclear dynamics. Ab initio MD approaches such as Car-Parrinello MD can describe the chemical bonding rearrangements that occur in the Grotthuss mechanism, and potentially offer the attractive reduction in the uncertainties and hard work involved in developing a more empirical potential such as the MS-EVB model. They suffer, however, from very high computational cost, which limits all ab initio MD simulations to rather small system sizes (on the order of 100 water molecules or less) and short simulation times (tens of ps). The computer simulation of proton transport, especially in biomolecular systems, can require as much as hundreds of nanoseconds of MD simulation time, for systems involving tens of thousands of atoms. However, the so-called quantum mechanics/molecular mechanics (QM/MM) implementation of Car-Parrinello MD⁶¹ promises to make that methodology more relevant to complex systems provided the underlying electronic structure is of sufficient accuracy (see below).

A second concern in Car-Parrinello MD simulations of PS&T is the accuracy of the underlying electronic DFT used in such simulations. As an example, recent work^14,62-64 has suggested that the simple Generalized Gradient Approximation (GGA) DFT required by the Car-Parrinello MD method may give poor structural and dynamical results for the underlying liquid water solvent, contrary to the reports of earlier simulations in the literature. In general, the Car-Parrinello MD water for the widely used Becke-Lee-Yang-Parr (BLYP) and Perdew-Burke-Ernzerhof (PBE) functional is too highly structured and slowly diffusing. It should be noted that these ab initio MD results on pure water have recently been called into question⁶⁵ through a Car-Parrinello MD simulation with the BLYP functional utilizing a “complete” basis set, as opposed to the incomplete plane-wave basis set used in all earlier Car-Parrinello MD simulations of aqueous systems. This latter paper reports what appears to be improved water structural properties in the complete basis set limit (namely a oxygen-oxygen radial distribution function in better agreement with experiment). However, no water self-diffusion data was reported. Moreover, given that GGA-DFT has been known for some time to be fairly inaccurate for proton transfer barriers for gas phase Zundel cations with various fixed oxygen-oxygen distances,⁶⁶ it seems unclear to what degree these functionals can be trusted to provide accurate proton hopping barriers in the more complex condensed phase environment of liquid water or solvated biomolecules. Indeed, it has been shown that the spurious (overly structured and slowly diffusing) properties of liquid water in GGA-DFT Car-Parrinello MD simulations, especially for the commonly used BLYP functional, can translate into a rather poor description of the excess proton diffusion rate.¹⁴ A different recent report⁶⁰ suggested a faster proton diffusion rate in BLYP-level Car-Parrinello MD simulations, attributing the difference to a more complete equilibration of the Car-Parrinello MD water simulation, although these results have not yet been reproduced by other researchers. Yet another prediction, made with ab initio MD combined with quasi-chemical theory,⁶² was that the Zundel cation is substantially more stable than the Eigen cation in liquid water at 300K, a prediction which is at odds with theoretical predictions⁴⁴ as well as other ab initio MD and empirical (e.g., MS-EVB) simulations. It seems, therefore, that there are some issues of reproducibility and accuracy in ab initio MD simulations that remain to be resolved. An important future challenge for both electronic structure theory and ab initio MD methods will be the accurate and statistically reliable simulation of liquid water, both with and without excess protons.

The inherent challenges in the “pure” ab initio MD simulation of PS&T have not deterred researchers from developing a number of mixed QM/MM approaches to the problem.^61,67,68 In such methods there is an ab initio quantum mechanical (QM) region embedded in a much larger empirical molecular mechanics (MM) environment. Space limitations do not allow us to delve into these methods in detail, but in short they could offer a solution to the “size issue” for ab initio MD simulations of PS&T in some complex systems (e.g., proteins in which the excess proton is solvated and transported in a fairly small region such as bacteriorhodopsin⁶⁸). The computational demands of the QM calculation in such systems are still formidable, so researchers have also sought more semi-empirical solutions for the QM calculation, e.g., a semi empirical DFT QM/MM approach based on the self-consistent charge density functional tight binding (SCC-DFTB) method.⁶⁷ It should be noted though that QM/MM approaches are still challenged by the issue of the overall accuracy of the underlying electronic structure calculation and, in the case of a semiempirical approach, the accuracy of the additional parameterizations inherent in that level of electronic structure theory. ⁶⁹ Another significant challenge for QM/MM approaches to PS&T is that in true proton transport problems there is a significant contribution from water diffusion, which greatly complicates the definition and treatment of the boundary region between the QM and MM regions (i.e., waters can diffuse from one region to the other and thus must somehow be “switched” from a QM water to an MM water or vice versa). In light of these complications, it remains to be seen if ab initio MD or OM/MM approaches offer any real advantage over more empirical MD modeling. Nevertheless, if these complications can be resolved our understanding of PS&T will certainly benefit from more “first principles” analyses. One example of this might be the recent prediction of “proton hole” (i.e., hydroxide) migration being favored over more standard Grotthuss proton shuttling in the active site of the enzyme carbonic anhydrase.⁷⁰ The inherent inaccuracies in the semi-empirical DFT approach used to make this prediction appear to undermine its reliability in the absence of any confirming experimental results. However, it is an intriguing prediction nevertheless and highlights the need for greater predictive accuracy in QM/MM approaches for PS&T in complex systems.

Empirical modeling of PS&T is also, however, not without its potential pitfalls. In some PS&T simulation studies (e.g., Ref. 71,72) the PM6 model⁷³ for the excess proton in water has been utilized. While appealing in some ways, this model has proven to be qualitatively inaccurate in describing PS&T bulk water and quantitatively inaccurate for proton hopping barriers in protonated water chains.³⁵ Other approaches^74,75 to simulate PS&T may be best described as approximations to a full multi-state MS-EVB methodology. In these approaches two EVB-like states are used to transfer an excess proton between two water molecules and then these two states are somehow moved along to the next proton hopping step. However, because they do not contain the full symmetry of the proton solvation process in water, these approaches tend to overemphasize the population of the Zundel cation;⁷⁶ more recent results suggest that this leads to an incomplete description of the physics of the PS&T process.^11,39 All of these alternative empirical MD approaches have nevertheless proven to be useful in the study of certain aspects of PS&T and thus contributed to our overall understanding of this phenomenon.

Another approach to simulating PS&T is the Q-HOP model,⁷⁷ which employs a stochastic hopping algorithm to describe the proton shuttling process. Stochastic algorithms are not deterministic, meaning that the dynamics are not directly derived from an underlying potential energy function in the form of Newton’s equations. It is therefore difficult to associate actual physical interactions with the underlying stochastic proton hopping dynamics, and several other assumptions must be made in order to define the stochastic proton hopping probability. Consequently, additional systematic errors may be introduced into the simulation results. Despite these shortcomings the Q-HOP method may be appealing to some researchers because it is fast and easy to implement in a simulation context. A more phenomenological stochastic approach for describing proton transport via a Monte Carlo algorithm has also recently been developed within the context of the enzyme and proton pump cytochrome c oxidase.⁷⁸

In light of the methodological advances described in this section (and their potential pitfalls) for simulating PS&T, the following sections will highlight selected results for a number of interesting and challenging systems. These results will be largely taken from a body of work using the MS-EVB simulation methodology.^2-37 In general, the objective in this body of work has been to study realistic systems for sufficiently long MD simulation times (tens to hundreds of nanoseconds) to calculate statistically converged structural and dynamical properties. Many interesting and sometimes unexpected results have been obtained, as summarized below. It is likely, however, that some of these results may require updating and even revision in the future as increasingly accurate versions of the overall PS&T simulation methodology become available (e.g., in the underlying MS-EVB method, ab initio MD approaches, protein force fields, altogether new methods, etc.).

PS&T IN BULK WATER

It is not only intrinsically interesting but also a crucial test of accuracy for simulation models to study PS&T in bulk water before moving on to more complex systems. This has been a central point of validation for the MS-EVB methodology. To a reasonable degree of accuracy, the model reproduces the self-diffusion properties for the hydrated proton^6,9, predicts a solvation structure composed of a roughly 65:35 mixture of the Eigen and Zundel cations⁵ (which can be modified to some degree by nuclear quantum effects^6,8), reproduces infrared spectroscopy results¹⁰, reproduces the activation energy for the excess proton self-diffusion constant, and agrees with the observed deuterium isotope effects.⁸ In the second-generation MS-EVB2 model a more advanced EVB state selection algorithm was introduced to improve energy conservation, which is also a crucial point of physical validation. Although the numerical value of the self-diffusion constant from MS-EVB classical MD simulations is below the experimental result, quantizing the MS-EVB model with quantum path integral simulations increases the excess proton diffusion rate such that it is in reasonable agreement with experiment.^6-8 Accounting for quantum effects must therefore correct the very small deviation in the PT activation barrier, lowering it from 2.7 kcal/mol in classical simulations such that it is closer to the experimental value of 2.5 kcal/mol. However, despite its demonstrated successes for simulating PS&T in bulk water, the MS-EVB model can and should be refined, as will be briefly discussed at the end of this article.

Once a simulation can reasonably reproduce these important experimental observables, i.e. the excess proton diffusion rate, spectroscopy, and activation energy, one can begin to address the question of the mechanism for Grotthuss-assisted diffusion in bulk water. In 1995, Agmon⁷⁹ proposed a mechanism in which the h-bond being donated to the acceptor water molecule must first be broken before the proton is transferred (donor to acceptor via an Eigen-Zundel-Eigen interconversion), and a new h-bond is finally formed with the donor water molecule that the proton leaves behind. According to this “Moses mechanism”, so coined due to its analogy to Moses parting the Red Sea, the rate limiting step to PT should be cleavage of the acceptor water molecule’s h-bond, and the coordination numbers of the 1st solvation shell water molecule and the hydronium cation should be approximately four and three, respectively. Early Car-Parrinello MD studies proposed a Zundel-Zundel transition mechanism,⁵³ but more recent simulations have supported the Eigen-Zundel-Eigen interconversion in the Moses mechanism.^55,56 (although the validity of these results may be influenced by the previously discussed concerns over the accuracy of Car-Parrinello MD for liquid water and the limited statistics available from those simulations).

By contrast, some experimental results suggest that 1st solvation-shell waters do not have a coordination number of four, as predicted by the Moses mechanism, but form stronger h-bonds with cations than other water molecules.⁸⁰ Moreover, extensive MS-EVB simulations lasting multiple nanoseconds indicate that 1st solvent-shell water molecules have coordination numbers that are not bulk-like (∼ 4) but closer to 3.6.^9,11,50 Thus, the h-bond being donated to the 1st shell acceptor water molecule is unfavorable 40% of the time, suggesting that its cleavage might not be rate limiting as predicted by the Moses mechanism. In 2005 Lapid et al.¹³ extended a Pauling bond order analysis to analyze tens of nanoseconds of MS-EVB2 simulation trajectory data and found evidence for a significantly more complicated bulk water PT mechanism that, in agreement with work by Ohmine and Saito,⁸¹ involves collective motion of clusters of water molecules that extend beyond the 1st solvation shell.¹³ In this mechanism PT is preceded by cleavage of h-bonds donated from the acceptor water molecule, which are favorable, and formation of those donated to the donor water molecule, which are unfavorable. Some number of these h-bonds must remain broken in order to disrupt the 3-fold solvation symmetry around the hydronium ion and induce proton transfer. Although each h-bond formation or cleavage event is fast (50-150 fs), they occur in a collective manner. The activation energy of transfer should be related to this collective process and, not surprisingly, its experimentally measured value is close to the strength of the collective rearrangement of h-bonding in liquid water (2.6 kcal/mol), a quantity which is often incorrectly described as the strength of a single h-bond. An important distinction between this latter PT mechanism and the original Moses mechanism is that PT is driven by the collective breaking of h-bonds as opposed to a single h-bond cleavage. Although this mechanism shows agreement with some available experimental results, it can be argued that the precise mechanism for the excess proton mobility in bulk water is still an unresolved question. Its ultimate resolution will require further studies, using increasingly accurate simulation models and statistical analysis, in conjunction with additional experimental measurements.

WEAK ACID IONIZATION AND PROTONATABLE RESIDUES

Weak acids play an essential role in both chemical and biological systems. In fact almost every biological system involves ionizable residues, such as glutamate or histidine, that must be modeled as proton donors and acceptors. To this end the MS-EVB methodology with an additional state representing the protonated residue and Car-Parrinello MD simulations have been used to evaluate the ionization of biologically relevant moieties. One interesting facet now demonstrated by both approaches is the formation of a metastable contact ion pair upon the deprotonation of an acidic residue. This is in agreement with and extends the earlier work of Ando and Hynes^82,83 who used ab initio quantum calculations along with Monte Carlo simulations to map out the preliminary stages of acid dissociation for HCl, a acid strong enough to form a stable contact ion pair, and HF, a weaker acid that must overcome a significant barrier to form a metastable contact ion pair. Similarly, a metastable contact ion pair was reported for glutamic acid with an MS-EVB study that clearly identified the stabilized proton acceptor as an Eigen cation.¹⁷ More recently a Car-Parrinello MD study⁸⁴ of acetic acid (the small molecule analogue of glutamic acid) identified the formation of a transient contact ion pair upon acid deprotonation. However, the precise identity of the contact cation (i.e., an Eigen cation versus a “free hydronium”, as referred to in the latter work) was unclear, as was the statistical significance of the contact ion pair due to Car-Parrinello MD sampling limitations. MS-EVB studies have also previously shown that moieties such as imidazole¹⁶ and histidine,¹⁷ although they lack a formal charge upon deprotonation, can form a stabilized Eigen cation in the first solvation shell.

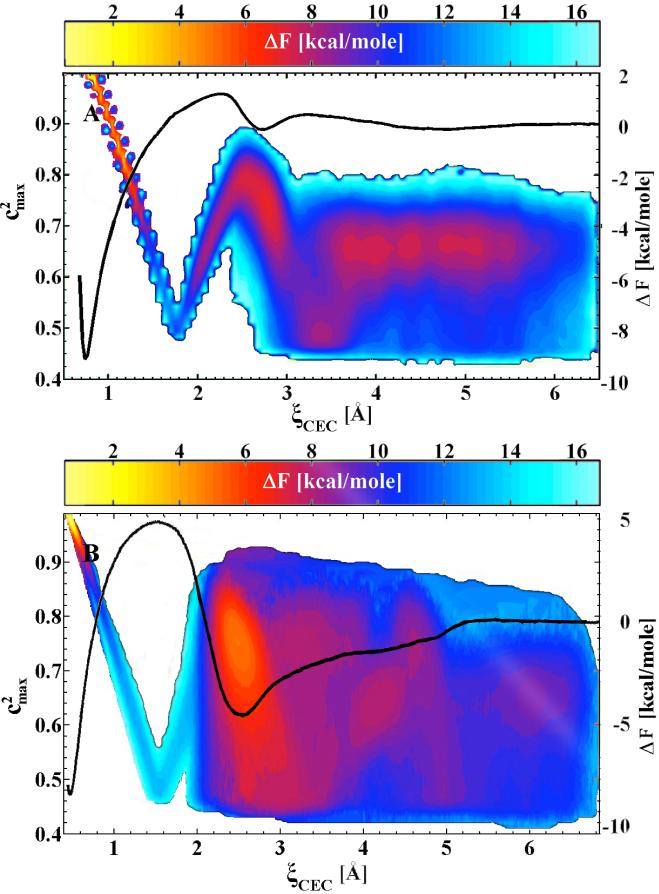
Figure 2 shows the potential of mean forces (free energy profiles) for the deprotonation of histidine and glutamic acid as a function of the distance of the excess proton center of excess charge from the histidine nitrogen or glutamic acid oxygen, respectively. The deep minimum in these potential of mean force curves corresponds to the protonated acid, while the second shallower minimum corresponds to the stabilized Eigen cation in a contact ion pair with the conjugate base moiety. Also shown in Fig. 2 is the value of the square of the maximum EVB state amplitude, which in general reflects the nature of the hydrated proton for a particular environment as described earlier, as a function of the acid dissociation coordinate. The behavior of the maximum EVB state amplitude squared is quite complex (i.e., there are a variety of dominant states) during the acid deprotonation. In particular, the excess proton first transitions from a protonated acid to a mixed (50-50%) state between an acceptor water molecule and the conjugate base of the acid. Then, it proceeds through a more hydronium-like localized species at the top of the potential of mean force free energy barrier, to the Eigen-conjugate base contact ion pair, and finally to the solvent-separated hydrated proton having the typical bulk-like mixture of Eigen and Zundel cation character, the former being somewhat more dominant.

Figure 2.

The potential of mean force (free energy profile), ΔF, and largest MS-EVB amplitude, $c_{\max }^2$, for deprotonation/protonation event in histidine (A) and glutamic acid (B). The reaction coordinate is the location of center of excess charge (CEC). The physical nature of the excess proton, reflected by the value of $c_{\max }^2$ (∼ 0.65 for an Eigen cation and ∼ 0.5 for Zundel), varies significantly over the range of the reaction coordinate. The color bar depicts the free energy cost of sampling these configurations (with their corresponding MS-EVB amplitudes) relative to the protonated amino acid.

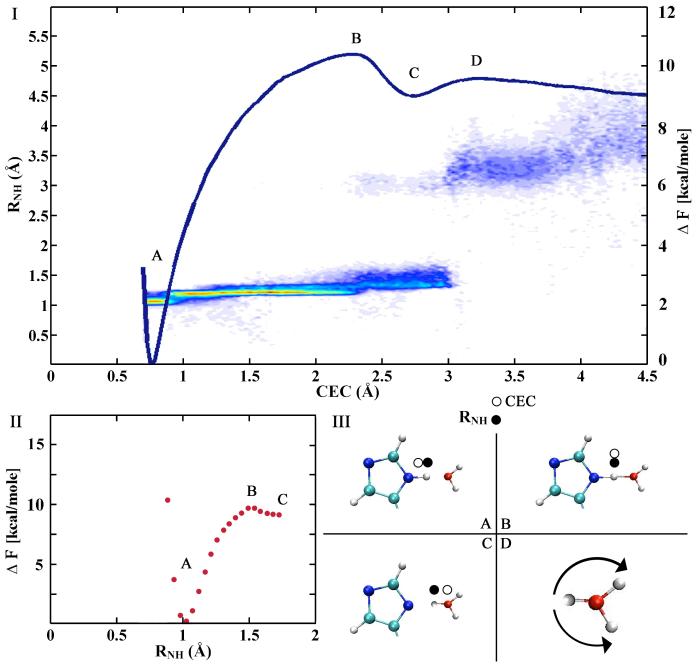
In addition to structural characterization of ionizable residues it is crucial that theoretical models be able to reproduce experimentally measurable pK_a values. Both the MS-EVB¹⁷ and Car-Parrinello MD^85,86 formalisms have been used to address this challenge, but the latter have focused on computing relative pK_a values due to the computational expense of Car-Parrinello MD. Comparing the MS-EVB simulation to a recent Car-Parrinello MD analysis of the histidine pK ⁸⁵_a highlights some important differences between the MS-EVB and Car-Parrinello MD approaches. First, the Car-Parrinello MD study defined the reaction coordinate as the distance between the histidine epsilon nitrogen and the neighboring hydrogen (R_NH), while the MSEVB study used the distance between the histidine epsilon nitrogen and the excess proton center of excess charge. Figure 3 shows both the MS-EVB (panel I) and Car-Parrinello MD (panel II) potential of mean forces of histidine deprotonation in terms of these respective coordinates, as well as the distribution of R_NH distances (panel I) in the MS-EVB simulation for a given center of excess charge value. Although the two potential of mean forces are very similar at short distances, the bimodal distribution of R_NH distances in the MS-EVB simulation suggests that the R_NH reaction coordinate breaks down as the center of excess charge traverses past the first stabilized Eigen contact ion pair and continues into the bulk environment. The R_NH reaction coordinate therefore can not sample the delocalized protonic charge in the stabilized first solvation shell Eigen cation or the subsequent transfer of the protonic charge via different protons into the bulk region. Thus, it cannot sample the true asymptotic solvated proton state that largely defines the value of the pK_a relative to the protonated acid state. Rather, the R_NH reaction coordinate likely samples the reorientation and/or diffusion of the nearest first solvation shell water, the original proton acceptor. In addition, the Car-Parrinello MD study calculated the pKa of histidine relative to that of water based on the assumption that the potential of mean force for histidine and water are equivalent past the initial proton transfer. From panel (I) of figure 3 it is evident that care must be taken in making this assumption. It should be noted, however, that the autoionization process in water has been directly studied via the Car-Parrinello MD approach combined with transition path sampling. ⁸⁷

Figure 3.

The MS-EVB (I) and Car-Parrinello MD (II) potential of mean forces (free energy profiles) for PT from histidine (A), through the Zundel transition state (B), to the stabilized Eigen cation (C), and into bulk solvent (D). The scatter plot in I represents the density (red for most dense, blue for least dense) of R_NH distances in the MS-EVB simulation along the center of excess charge (CEC) reaction coordinate, highlighting the fundamental difference between the CEC and R_NH coordinates. Each state is depicted in III where an open circle denotes the location of the CEC and filled circle denotes the R_NH hydrogen. The MS-EVB R_NH jump from ∼1.4_ to 3.5_ corresponds to the rotation of the 1^st-solvation shell water molecule, also shown in III D, after the CEC is transferred to a 2^nd-solvation shell water molecule and beyond.

The current body of work on acids in water illuminates the complexities and intricate nature of the dissociation of ionizable residues in bulk water, complications that will only increase in biomolecular environments. Continued careful study of the acid deprotonation event in bulk water will therefore be essential in establishing a solid foundation to evaluate the role of amino acids and other ionizable residues in PS&T in biological systems.

PS&T AT INTERFACES AND OTHER INHOMOGENEOUS ENVIRONMENTS

Liquid-Vapor Interface and Protonated Water Clusters

Recent experimental and computational developments have brought into doubt long held views of ionic solvation near the liquid/vapor interface. The conventional analysis of ion solvation near the dielectric boundary at the liquid vapor interface, first formulated by Wagner⁸⁸ and later quantified by Onsager and Samaras,⁸⁹ holds that ions should be expelled from the interface by the repulsive interaction with their associated image charges. Recently, however, the inability to reconcile the seemingly anomalous uptake of Cl₂ and Br₂ gases by halide salt aerosols led Hu et al. to question this conventional view and instead propose a concentration gradient that favors these anions at the interface.⁹⁰ Subsequent MD simulations have supported anion surface enhancement and further clarified that the degree of enhancement should increase with anion size and polarizability, but that cations should be repelled from the interface according to the conventional picture of ion solvation.^91-95 More recently, spectroscopic investigations^96-99 have indicated that specific anions are indeed present at the interface, and at greater concentration relative to the bulk.

As described earlier, the nature of solvation and transport of the smallest cation, the excess proton, is fundamentally different than that of other cations.^1,100,101 Nevertheless, MS-EVB simulations have predicted an enrichment of the solvated proton at the water liquid/vapor interface¹⁸ and the surface of water clusters.^19-21 The apparent reason for this behavior is the highly anisotropic solvation of the hydronium cation and to a lesser degree its intrinsic polarizability, which imparts to it an “amphiphilic” character, thus causing the interfacial preference. As shown in Fig. 4 the lone pair side of the hydronium cation (left arrow in the figure) preferentially orients toward the vacuum interface so that its O-H bonds can still participate in three strong hydrogen bonds with water molecules. Thus, an increased number of dangling water O-H bonds (c.f. right arrow in Fig. 4) become “tied up” by the surface hydronium.¹⁸ The interfacial enrichment of excess proton has also been demonstrated for non-dissociable hydronium potentials^18,102 as well as ab initio MD simulations of protonated clusters.^19,20 The predicted interfacial enrichment is now supported in second harmonic generation (SHG) spectroscopy^103-105 and sum frequency generation (SFG) spectroscopy studies,^106-113 as well as detailed thermodynamic analysis.¹¹⁴ It also appears to provide an explanation for the anomalous surface tension behavior of acids versus other salts^105,114 and the Jones-Ray effect.¹⁰⁵ This putative surface enrichment, assuming it stands further experimental and computational scrutiny, will likely have significant implications for atmospheric chemistry, biochemistry/biophysics, and materials science.

Figure 4.

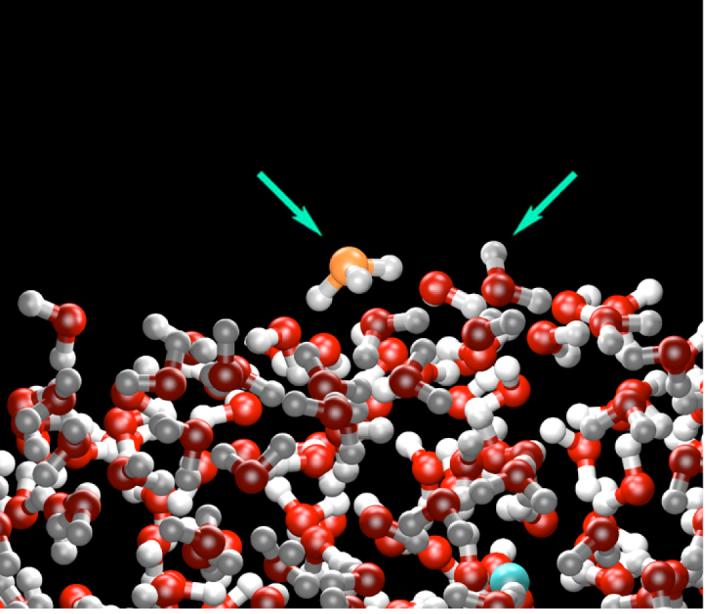
A representative configuration from an MS-EVB2 simulation of the water liquid/vapor interface. The hydronium cation (orange) is found to preferentially reside at the interface orienting its lone pair region (left arrow) into the vapor phase. The hydronium cation also “ties up” an increased number of dangling water O-H bonds, such as the one shown by the right arrow. The chloride counterion (blue) resides on average at least one water layer below the interface.

Water-Alcohol Mixtures

The previously discussed anisotropic ordering and enrichment at the liquid/vapor interface for the hydronium cation is akin in some ways to that for the small amphiphile methanol. Computer simulation¹¹⁵ and sum-frequency vibrational spectroscopy data¹¹⁶ have demonstrated a preferential ordering of methanol at the liquid/vapor interface in the neat liquid, such that the methyl groups of the interfacial molecules are directed away from the liquid into the vapor phase. Furthermore, both simulation¹¹⁷ and experiment^118,119 of water-methanol mixtures exhibit methanol surface enrichment and the same preferential orientation of the methanol methyl groups. In light of the similar anisotropic solvation and surface enrichment exhibited by both methanol and the solvated proton, one would naturally ask whether the previously demonstrated hydronium amphiphile-like behavior¹⁸ extends to other mixed dielectrics, such as water-amphiphile mixtures.

MS-EVB simulations of methanol-water solutions of varying concentration were performed and the solvated proton was found to have a significant anisotropic association with methanol’s hydrophobic methyl group.^3,22 Figure 5 contrasts atomic isodensity surfaces of bulk water and water-methanol solutions surrounding the hydronium cation. As shown in panel (a), the bulk solvation of the hydronium cation is marked by a highly anisotropic solvation: the three hydrogen atoms of the hydronium ion are each strongly solvated while the hydronium lone pair region is devoid of any appreciable density. The density plots for the water-methanol solution (cf Fig. 5b) display this same anisotropic solvation about the hydronium hydrogen atoms. The lone pair region, however, is occupied by a significant distribution of methyl carbon density at a distance equivalent to that for the second water solvation shell of the cation. This anisotropic hydrophilic/hydrophobic association, first noted for the water liquid/vapor interface, apparently also applies to an amphiphile-like solvation in water-methanol solutions.

Figure 5.

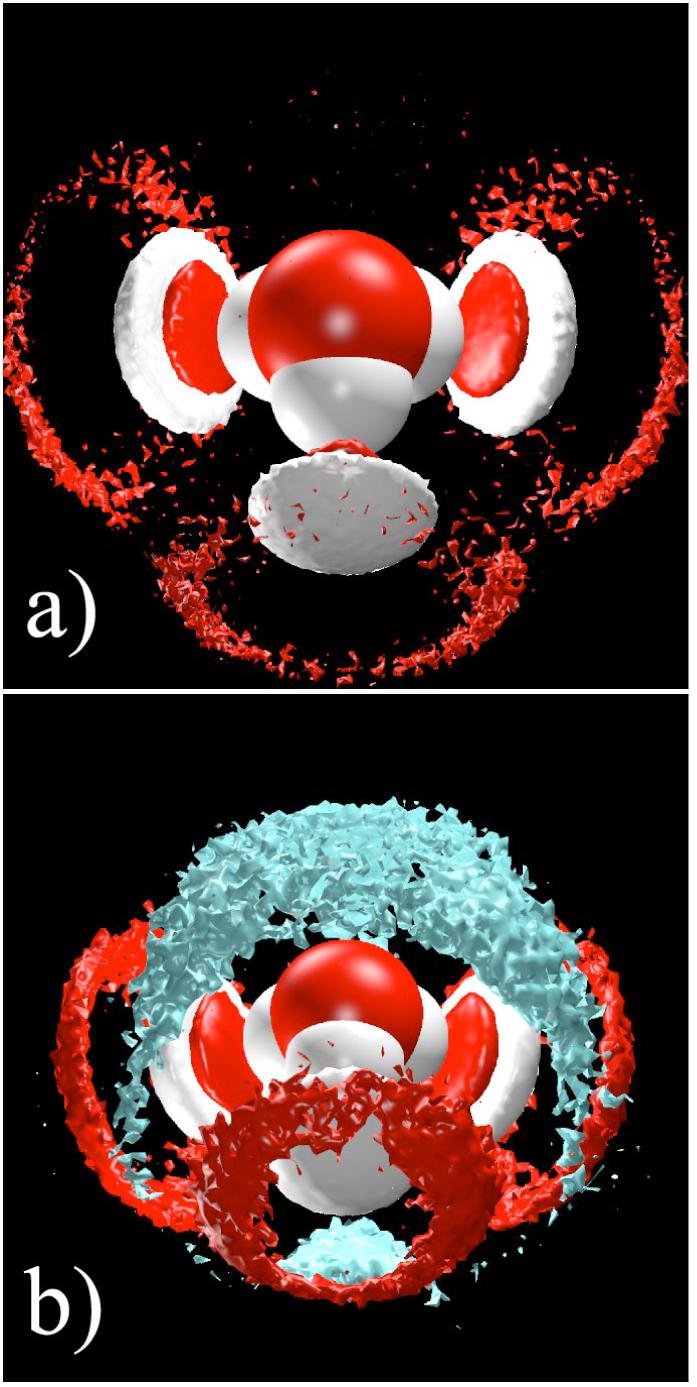
a) Isodensity surfaces from a bulk water simulation that contain three times the uniform atomic density for water oxygen (red) and water hydrogen (white) about the hydronium cation showing the 1^st solvation shell waters closely coordinated to all three hydronium hydrogen atoms. b) Isodensity surfaces from a bulk 50% methanol-water simulation that contain three times the uniform atomic density for water oxygen (red), water hydrogen (white), and methyl carbon (cyan) about the hydronium cation showing the asymmetric solvation structure in which the top (i.e., lone electron pair) of the hydronium prefers the low dielectric methyl group region of the methanol density.

The diffusion of the center of excess charge was also calculated across the range of concentrations.²² While the absolute diffusion for each concentration was smaller than measured in experiment, the diffusion trend across concentrations was accurately reproduced. As with proton diffusion in bulk water, the multiplicative correction factor is believed to largely result from a nuclear quantum correction^7,8 to the classical MS-EVB simulation. It should be noted that at larger concentrations (∼90% methanol) the protonated methanol states, which were excluded in this particular MS-EVB model, might also possibly impact the diffusion rates. It is, however, unclear what effect the inclusion of the methoxonium states may have in the MS-EVB model. Recent Car-Parrinello MD studies suggest a role for the protonation of methanol at water/methanol interfaces,⁵⁸ but the aforementioned concerns over the accuracy of the underlying electronic structure in these simulations remain an issue to be resolved. In addition, the absolute quantitative accuracy of the MS-EVB model for such mixtures should also be a future target for quantitative improvement.

Lipid Bilayers

One of the first applications of MS-EVB method for PS&T was to study the behavior of an excess proton at the water-phospholipid interface.²⁶ In this work, it was found that a favorable free energy exists for “trapping” the excess proton near the phospholipid head groups in “Eigen-like” and “Zundel-like” structures formed by the excess proton, some number of water molecules, and the lipid head group(s). The simulations also revealed that protons likely permeate pure lipid bilayers in a highly concerted mechanism involving charge delocalization and Grotthuss shuttling through complicated (non-single-file) water networks, a process which is different from Grotthuss hopping through a single-file chain of water molecules. Later work²⁸ has gone on to analyze this permeation mechanism in more detail, especially in comparison to the permeation of more “standard” cations such as Na⁺. Strikingly, the free energy barrier for permeation five Angstroms into the lipid bilayer is considerably lower for the excess proton than for Na⁺. This behavior likely translates into a substantially lower overall free energy to permeation, although the precise collective “coordinate” for this permeation process in lipid bilayers remains rather unclear. It is intriguing to consider the connection between the proton’s facilitated bilayer permeation and its aforementioned “amphiphilic” character in the previous two subsections.

Water-Filled Channels

Another early application of the MS-EVB model was to study PT through narrow water-filled hydrophobic channels as a function of the channel radius.²³ This study revealed a significant enhancement of the PT rate by more than an order of magnitude when the channel becomes so narrow that only a single-file chain of water molecules can fill it (i.e., a quasi-one-dimensional “water wire” or “proton wire” is formed). Subsequently, Dellago et al.¹²⁰ utilized the MS-EVB and Car-Parrinello MD approaches to study PS&T through water-filled carbon nanotubes and found a similarly enhanced PT rate. For both studies, however, it should be noted that the free energy cost was not calculated for moving the excess proton from the bulk water environment into the hydrophobic channel, so the enhanced rate of diffusion within the channel may be less relevant to the overall transport process if the proton desolvation penalty at the channel’s entrance is rate limiting. Indeed, the MS-EVB and other results for proton exclusion by water-filled biological aquaporin channels described later suggest that such free energy costs for the excess proton to leave the bulk water environment can be substantial (although not necessarily as large as for other cations - see the discussion the synthetic LS2 channel below).

PS&T IN BIOMOLECULAR SYSTEMS

Biomolecular systems have presented the most challenging and arguably important application for the MS-EVB simulation methodology to date.^29-37 Here we highlight our efforts, and summarize those of others, to characterize PS&T in variety of biomolecular systems including aquaporin channels, the M2 proton channel, the enzyme carbonic anhydrase, and the proton pump cytochrome c oxidase. Many of these simulations have not only been in basic agreement with experimental results but provided new insight into the mechanism and function of PT in biology.

Aquaporin Channels

One of the most interesting biological systems studied to date is the transmembrane water channel, aquaporin.^33-35 The aquaporin channels are unique in their ability to simultaneously conduct water and block all cations, including water-hopping protons.^121,122 Ion exclusion has been linked to several filtering properties, including the channel’s narrow selectivity filter, a narrow region thought to block most ions due to a high desolvation penalty, and the relatively small number of carbonyl groups lining the channel’s interior, which would otherwise aid ion desolvation as they do in ion channels. The mechanism of proton exclusion, however, is less clear given the excess proton’s ability to delocalize and shuttle, and this topic has been the subject of much debate, especially in the area of computational analysis. A variety of formalisms have been used to address this interesting phenomenon of PT blockage, including stochastic simulations,¹²³ continuum electrostatic calculations,⁷² MD simulations using a dissociable empirical potential,^72,124 phenomenological EVB treatments,^125,126 and explicit MS-EVB MD simulations.^33-35 Several of these studies have predicted that the free energy barrier to proton translocation occurs in the selectivity filter known as the Asn-Pro-Ala (NPA) motif, though the magnitude and interpretation of the origin(s) of this barrier have varied. Some have argued that the NPA region creates a bi-polar orientation in the water-file, which limits Grotthuss-like shuttling. Others argue that the barrier is electrostatic in nature from the opposing macrodipoles of two α-helices that line the channel¹²⁴ or primarily caused by the channel dehydration penalty, which should peak near the NPA region.^125,126

In an effort to clarify which of these factors is the true source of proton blockage, MS-EVB2 simulations were carried out^33-35 on aquaporin-1 (Aqp1), a member of the orthodox aquaporin subfamily, and the Escherichia coli glycerol facilitator (GlpF), a member of the aquaglyceroporin subfamily, as well as several mutants of Aqp1 (cf. Fig. 6).¹²⁷ In one study, the permeation free-energy profiles and the maximum proton conductance were calculated for both the delocalized proton, capable of Grotthuss-like charge delocalization and shuttling, and a classical hydronium ion (H₃O⁺).³⁵ Surprisingly, the results indicated that proton blockage is caused by not one, but a balance of multiple factors. Moreover, the mechanism of proton blockage for GlpF seems somewhat different from that of Aqp1. Confirming simulations on a number of mutants³⁴ (Fig. 6) further indicated that the selectivity filter inhibits PT not only via a desolvation penalty but by direct electrostatic repulsion. The macrodipoles of two α-helices that line the channel, HB and HE, were found to be responsible for the primary free energy peak located at the NPA domain, but this barrier alone does not block the proton permeation. The MS-EVB2 simulation studies,^33-35 taken together and in conjunction with the experimental mutation results,¹²⁷ present a reasonably conclusive picture that the bipolar field, direct electrostatic interactions with certain amino acid residues, and the dehydration penalty for the hydrated proton to enter the channel are all important in blocking PT through aquaporin channels.

Figure 6.

Snapshot of the Aqp1 H180A/R195V double mutant with helices HB and HE labeled. The Phe-56, Ala-180, Val-195 and Cys-189 residues are colored purple, red, yellow and green, respectively.

M2 Proton Channel in Influenza A

In contrast to the proton-blocking aquaporin channels, the transmembrane M2 channel¹²⁸ of the influenza A virus is highly proton-selective, conducting protons over 100-fold more efficiently than all other cations. The M2 channel is believed to play an essential role in the viral life cycle by allowing proton flux from endoplasm into virion and thus enabling the uncoating and release of the viral RNA into the host cell.^129,130 Before recent mutations of the M2 channel occurred, proton transport could be efficiently blocked by the anti-flu drug amantadine.¹³¹ A substantial amount of evidence has confirmed that PT in the M2 channel is activated by low pH,^132-135 and this behavior is related to the protonation of one or more of the four His37 residues (one on each monomer) that reside near the center of the channel (cf. Fig 7),¹³⁴ as well as their interactions with four proximal Trp41 residues.³² Nevertheless, the exact protonation states of the His37 residues and the conformational changes associated with different His37/Trp41 adducts during channel opening are still not entirely clear. Two PT mechanisms have been proposed to date: The “shuttling mechanism” suggests that PT is aided by the protonation, rotation, and deprotonation of the His37 imidazole rings,¹²⁸ while the “shutter mechanism” links the protonation of His37 residues to an electrostatic repulsion that opens the previously occluded channel to the formation of a continuous water wire (cf. Fig. 7) and proton conduction.¹³⁶ (Here, the phrase “protonation” of a His37 residue refers to it being doubly protonated.)

Figure 7.

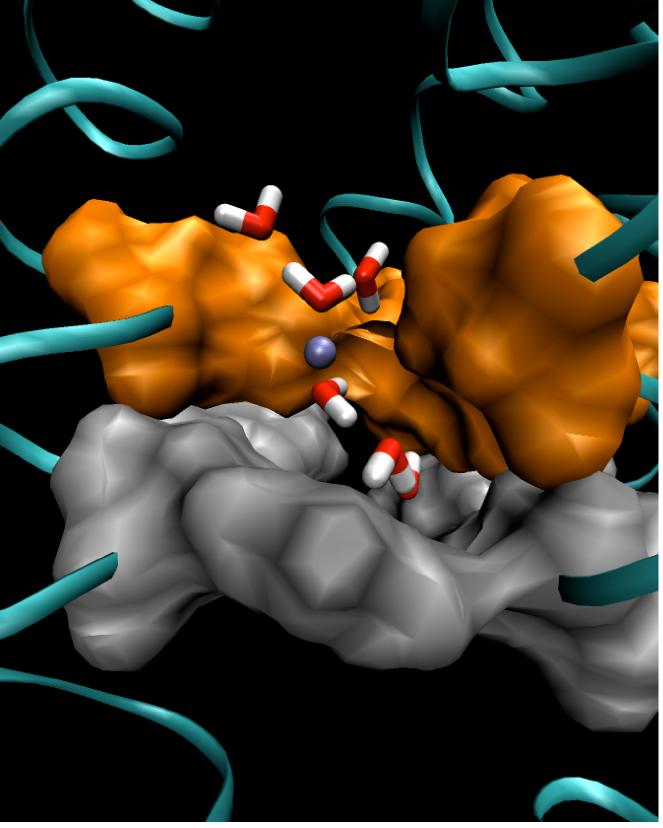
A snapshot of the His37/Trp41 domain of the M2 channel in the open state. The molecular surfaces of His37 and Trp41 are represented by solid surfaces colored orange and silver, respectively. The excess proton is represented by an ice blue ball with a segment of the proton transporting “water wire” also shown.

To shed a light on the PT mechanism in the M2 channel, especially in the His37/Trp41 domain, an explicit proton MSEVB2 simulation was carried out on the M2 transmembrane peptide domain channel in a fully solvated dimyristoylphosphatidylcholine (DMPC) bilayer.²⁹ This simulation showed that the proton was able to shuttle through a water wire temporarily formed in the gating His37/Trp41 domain in less than 1ns. More recently, the potential of mean force of proton permeation and the maximum ion conductance of the excess proton were calculated for all five possible His37 protonation states.¹³⁵ The results from these MS-EVB2 simulations indicate that, although all of the protonation states form stable α-helix tetramers in DMPC liposome, that with three protonated His37 residues has a substantially lower PT free energy barrier than the other protonation states. Moreover, these protonation states have different His37/Trp41 conformations than the proposed closed-state M2 structures. Thus, the open M2 channel is proposed to have three protonated His37 residues, in agreement with inferences from experimental results.^134,135 Furthermore, the pKa values, predicted by continuum calculations, of the different protonation-state conformations suggest the gating pH is 5.5, which is also in good agreement with experimental observations.¹³⁴ Future MS-EVB simulations will incorporate dynamically protonatable His37 groups,¹⁷ which should help to distinguish which of the two proposed PT mechanisms is more kinetically favored.

Carbonic Anhydrase

Carbonic anhydrase (CA), one of the fastest known enzymes, catalyzes the interconversion of carbon dioxide to bicarbonate and an excess proton at a rate close to the diffusion-controlled limit. The PT mechanism is thought to begin with the autoionization of a Zn-bound water molecule, which releases a proton that is subsequently transported through an intramolecular water wire. Although this autoionization would be very unfavorable in bulk-water, the Zn-mediated protein environment effectively lowers its barrier by ∼ 9 kcal/mol. In this way CA epitomizes the ability of biological systems to effectively solvate and transport an excess protonic charge. (Note, however, the alternative “proton hole” mechanism recently proposed and described earlier based on semiempirical DFT “QM/MM” calculations.⁷⁰) Human Carbonic Anhydrase II (HCA II), the fastest of the seven mammalian isozymes,^137,138 has become a key system for the experimental^137-154 and theoretical^{67,70,155-163} explorations of how the protein environment stabilizes PT. The intramolecular water wire in HCA II spans 8-10 Angstroms between the Zn-bound water in the active site and His-64, the latter amino acid residue being the enzyme’s likely final proton acceptor during catalysis. The exact structure and number of water molecules contributing to the intramolecular water wire is a matter of debate, but a consensus has been reached that two to four water molecules are involved. ^{145,150-152,158-160,163} Given the timescale discrepancies between water wire formation (ps) and the PT event (μs), it is possible that multiple water wire formations contribute to the PT event. In fact, CA represents an interesting and very well experimentally characterized system at the boundary of proton “transfer”, in which the proton exchanges between a single donor and acceptor group, and proton “transport” behavior, in which the proton is transferred through several water molecules over a longer distance via Grotthuss shuttling.

Given the key role believed to be played by the water wire(s) in the active site, a complete and accurate evaluation of CA’s PT mechanism will require accounting for all PT pathways (i.e., statistically-converged free energy sampling of multiple water-wire formations with proton transport through them). To this end, the MS-EVB2 methodology is currently being extended in our group to study HCA II. With the recent parameterization of histidine¹⁷ and the ongoing parameterization of the zinc active site, a complete HCA II model will soon be available. It will be used to sample dynamically over varying water wire sizes and long time scales to calculate the potential of mean force (free energy barrier) of PT in HCA II. This analysis will be compared to previous studies described below, which employed DFT on small molecular subsystems, semi-empirical calculations, and the two-state (or few-state) EVB approach.

The early DFT calculations indicated that increasing the number of bridging waters in the water wire from two to four causes PT to change from a concerted process, to a partially concerted process, and finally to a stepwise process.¹⁶⁰ These calculations suggested barriers that are somewhat smaller than the experimentally determined barrier, even with the inclusion of the water wire formation energy.¹⁵⁸ In order to improve on gas phase calculations and account for the protein environment, the SCC-DFTB method described earlier, a semiempirical approximation of DFT,⁶⁷ was used in a QM/MM-like approach. Due to the size of the system true dynamical simulations were prohibitive. Instead adiabatic mapping and minimum energy pathways were calculated for PT through 2 and 4 molecule water wires.^67,162,163 These calculations lead to two counter-intuitive results. First, instead of decreasing the PT activation energy as CA is expected to do, including the protein environment increased the PT activation energy to values close to that measured experimentally. Second, changing the water wire length from 2 to 4 molecules increased the activation energy by more than 10 kcal/mol. These conclusions will benefit from further validation because the absolute accuracy of the SCC-DFTB approach for PS&T remains to be established⁶⁹ and the calculated barriers in CA are not true free energy barriers, so they do not include entropic and other temperature-dependent (e.g., anharmonic) effects. In addition, as described earlier the same SCC-DFTB QM/MM approach has been utilized more recently along with some degree of free energy sampling and predicted a “proton hole” hydroxide transfer instead of a more standard Grotthuss shuttling PT event between the zinc-bound water and His64.⁷⁰

A two-state (or few-state) EVB methodology has also been applied in a collection of pioneering studies of CA by Warshel and co-workers, in order to evaluate the nucleophilic attack of the Zn-bound hydroxide by CO₂^156,157 and the deprotonation event of the Zn-bound water.^{155,157,161,164,165} The initial deprotonation event was modeled with a united-atom force field, utilizing the x-ray crystallographic waters. In spite of these approximations, the method accurately predicted the magnitude of the reaction barrier as well as the reaction rate.¹⁵⁵ More recently CA has been modeled with a framework involving EVB and modified Marcus theory.^155,161,164 The original study in this regard,¹⁶⁴ which used fixed EVB states along a water wire in implicit solvent, was subsequently reexamined to identify the origin of the observed linear free energy relationship in CA.¹⁶¹ All of these studies utilizing the simpler few-state EVB approach bode well for the eventual success of more comprehensive MS-EVB studies of PS&T in the various isozymes of CA, simulations which are currently underway.

Cytochrome c Oxidase

Another key application of the MS-EVB method has been PT in the D-channel of cytochrome c oxidase (CcO).^36,37 CcO, the terminal membrane-bound enzyme in the respiratory chain, catalyzes the reduction of dioxygen to water and simultaneously pumps protons across the mitochondrial or bacterial membrane. The enzymes ability to transport protons destined for both catalysis and pumping through the same proton channel has been a model bioenergetic curiosity, attracting extensive experimental and theoretical research.¹⁶⁶ Computational analyses other than the MS-EVB approach, including continuum calculations, classical MD simulations, Monte Carlo algorithms, the temperature-dependent Hartree approximation with adiabatic simulation method and quantum calculations,^167-174 have been used to postulate CcO’s proton pumping mechanism. None of these studies, however, incorporated full Grotthuss proton delocalization and transport over multiple water molecules, as has been done with the MS-EVB2 model.^36,37

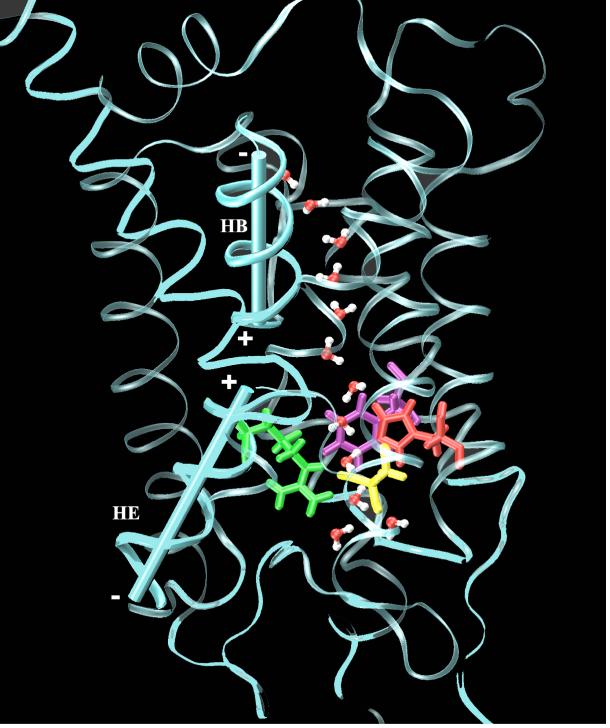
The MS-EVB2 simulations of the wild type enzyme have indicated that proton transport in the D-channel, one of two channels known to deliver the protons to the active site and to be pumped, is very rapid once Glu242 (bovine heart notation), a residue at the top of the channel, is deprotonated.³⁶ This is in agreement with experimental evidence that Glu242 plays a critical role in PT and proton pumping. When Glu242 is protonated, these simulations also revealed for the first time that a “proton trap” exists in the channel (cf. Fig. 8) where a proton resides “waiting” for the deprotonation of Glu242 and hence rapidly reprotonates it. The existence of a proton trap and D-channel proton was recently supported by a high resolution crystal structure.^175,176 If this discovery withstands the test of further experimental validation, it will have significant implications for CcO’s proton pumping mechanism, many details of which remain to be resolved. For example, a recent semi-quantitative analysis suggested a concerted mechanism that does not require Glu242 to be protonated/deprotonated.¹⁷⁰ This is at odds with the MS-EVB potential of mean force calculations, which indicate that the barrier for a proton to escape from the trap region and approach the protonated Glu242 is quite large.

Figure 8.

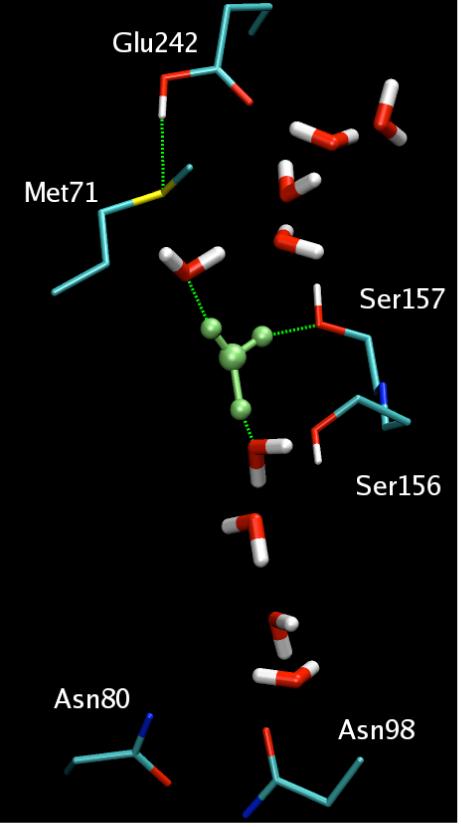
The hydration structure of the excess proton in the D-pathway proton trap region from MS-EVB simulations of bovine CcO with Glu242 in its protonated state. The solvated excess proton is colored in green; the H-bonds are represented as dashed green lines.

MS-EVB2 simulations have also been carried out on a N98D CcO mutant,³⁷ which decouples proton pumping and catalysis such that the enzyme can still transport protons to the active site to reduce oxygen to water, but it can not pump protons across the membrane. These simulations suggest that this mutation effectively perturbs the proton trap region, thus accelerating proton conductivity. This supports the hypothesis that the putative proton trap plays a critical role in proton pumping mechanism.

FUTURE CHALLENGES AND IMPROVEMENTS

There is an ongoing effort in our group and elsewhere to increase the accuracy and generality of the MS-EVB methodology. The original model was developed to study proton translocation phenomena in biomolecular systems. Accordingly, the water potential energy function for the original and second generation MS-EVB models was chosen because it is simple enough for large scale MD simulations and compatible with existing biomolecular force fields. A priority for the third generation MS-EVB model will be to incorporate a better empirical potential for the underlying water molecules¹⁷⁷ along with a revised MS-EVB parameter set and state-selection algorithm. The physical effects of nuclear quantization and electronic polarization are only implicitly included in such empirical water forcefields. One of the original MS-EVB papers⁶ showed that quantization of the MS-EVB potential enhances the proton hopping rate by about a factor of two, bringing it closer into agreement with experiment. The inclusion of electronic polarizibility is another important goal of future MS-EVB models, due to the growing evidence that the electronic polarizability of water is desirable for MD simulations that involve interfaces¹⁰² (with and without charged ions) or solvated systems of ions and charged amino acid groups in proteins.¹⁷⁸ Toward this goal, a polarizable version of the MS-EVB model has recently been published,¹⁷⁹ although its properties such as energy conservation remain to be elucidated.

An MS-EVB model for the hydroxide anion, OH^-, is also currently being developed. When combined with the Self-Consistent Iterative MS-EVB method,¹² the existence of a combined hydronium and hydroxide MS-EVB model will allow for the development of an autoionizable empirical model for water, something that has been a long-standing goal in the field of molecular simulation.

CONCLUSIONS AND FUTURE OUTLOOK

In this article we have reviewed our multi-year effort to develop a robust and accurate computer simulation methodology for the study of PS&T in a host of realistic physical and biological systems,^{2-37,158,159,180} as well as summarized related efforts on this topic. This combined body of computational research has yielded an unprecedented, yet in some ways incomplete, understanding of this complex and important phenomenon, a goal which dates back to the original work of Grotthuss 200 years ago.¹ In general the hydrated proton -- or to be more correct the charge defect associated with the excess proton -- possesses the ability to shuttle and delocalize in an aqueous environment. This behavior undoubtedly gives rise to the proton’s enhanced transport rates, yet the exact mechanism of PS&T remains enigmatic in certain systems. The system-specific mechanisms studied to date have been surprisingly complex and diverse, each uniquely fit to the physical or biomolecular system under investigation. The proton blockage in aquaporin channels epitomizes this complexity; it results from several complementary factors, including direct electrostatic interactions with specific protein residues, a bipolar field at the channel’s center that restricts the solvent structure and dynamics, and a proton dehydration penalty at the channel entrance. Given the subtleties that have proven to be essential in each system, it is unlikely that a single or even a handful of ‘universal’ PS&T mechanisms will emerge, making extrapolations between systems potentially unreliable. Nevertheless, each application of computer simulation to PS&T has offered insights into the nature of this process, and some have demonstrated trends that may be true for broader classes of systems. For example, the anisotropic solvation structure surrounding a hydronium ion, leading to its trend to be excluded from bulk water and a preference for interfaces, is expected to be a guiding principle that describes polar-apolar interfaces. On the other hand, we clearly still have much to learn. Computer simulations coupled with experimental validation and guidance will be critical in this pursuit. Continued improvement and extension of the underlying computer modeling and simulation approaches, in addition to diligent application of the MS-EVB and other PS&T simulation methodologies to important physical and biological systems, will therefore remain key priorities in computational chemistry, biophysics, and materials science for a long time to come.

Biography

Jessica M.J. Swanson received her B.S. in Biochemistry from the University of California, Davis in 2000 and her Ph.D. in Physical Chemistry from the University of California, San Diego in 2006 under the supervision of J. Andrew McCammon. In 2006 she was awarded a NIH NRSA fellowship to study the proton pumping mechanism in cytochrome c oxidase. Her long-term research interests are focused on the charge transport processes underlying important biomedical and alternative energy problems.

C. Mark Maupin received his B.S in Chemistry from Boise State University in 2000, an M.S. in Interdisciplinary Science: Biochemistry from Boise State University in 2002, and is currently a fifth year graduate student in Physical Chemistry at the University of Utah under the supervision of Gregory A. Voth. His graduate research has included computational methods development, force field parameterization, and the study of proton transport in a variety of systems including ionizable amino acids and human carbonic anhydrase II.

Hanning Chen received his B.S. in Polymer Science and Engineering from the University of Science and Technology of China in 1999 and his M.S. in Physical Chemistry from the University of New Orleans in 2003. In 2003, he joined Professor Gregory A. Voth’s research group as a Ph.D. student where he helps develop molecular simulations methods for proton transport in the condensed phase, as well as their applications to study proteins such as ion channels.

Matt K. Petersen received his B.S. in Professional Chemistry in 1998 and his B.S. in Mathematics with Physics Minor in 2000 from the University of Idaho. In 2006 he received his Ph.D. in Physical Chemistry from the University of Utah under the direction of Gregory A. Voth. His research interests include alternative energy technology, including proton conducting membranes for fuel cell applications.

Jiancong Xu received her M.S in Molecular and Cellular Biology from the University of Heidelberg, Germany in 2002 and began pursuing her Ph.D. in Physical Chemistry under the direction of Gregory A. Voth in August 2002. Her research interests include the mechanism of coupled proton-electron transfer in cytochrome c oxidase, molecular modeling of proton translocation in biological systems, and structure-function correlations.

Yujie Wu (not shown in photo) received his B.S. in Biochemistry and Molecular Biology from Nankai University (China) in 1994, his M.S. in Biochemistry and Biophysics from the Institute of Biophysics, Chinese Academy of Sciences in 1997, and his Ph.D. in Physical Chemistry from the University of Utah in 2004. His Ph.D. and postdoctoral research was supervised by Dr. Gregory A. Voth and focused on theoretical/computational studies of biological proton channel systems and the development of the relevant methods and force fields. He is now a senior scientist and developer at Schrödinger, Inc. in New York City.

Gregory A. Voth is Distinguished Professor of Chemistry at the University of Utah. He has authored or co-authored approximately 300 scientific publications and mentored over 70 postdoctoral fellows, 30 graduate students, and 10 undergraduates. His research interests include the theory and simulation of charge transport, solvation, and multiscale phenomena in liquid state, biomolecular, and materials systems.