The dynamics of memory as a consequence of optimal adaptation to a changing body

Abstract

The response of the motor apparatus to neural commands varies due to many causes. Fast timescale disturbances occur when muscles fatigue. Disturbances with a slow timescale occur when muscles are damaged, or limb dynamics change due to development. To maintain performance, motor commands need to adapt. Computing the best adaptation in response to any performance error results in a credit assignment problem: what timescale is responsible for this disturbance? Here we show that a Bayesian solution to this problem accounts for numerous behaviors of animals during both short and long-term training. Our analysis focuses on characteristics of the oculomotor system during learning, including effects of time passage. However, we suggest that learning and memory in other paradigms, such as reach adaptation, the adaptation of visual neurons, and retrieval of declarative memories, largely follow similar rules.

Suppose we are designing the control mechanism of an autonomous robot. We recognize that motors in various limbs will change their characteristics with use and with passage of time. For example, with repeated use over a short period, a motor may experience heating and change its response transiently until it cools. On the other hand, with repeated use over a long period the batteries may gradually discharge and the power will only return to near its original state after a recharge. Both of these conditions will produce movement errors, requiring our controller to adapt and send updated commands to the motors to produce the desired actions. However, our controller should interpret these errors differently: errors that have a fast time scale should result in rapid adaptive changes, but should be quickly forgotten. Errors that persist for extended periods of time should result in slow adaptive changes.

It appears to us that the nervous system faces similar problems in controlling the body. Properties of our muscles change due to a variety of disturbances, such as fatigue¹, disease, exercise, and development. The states of these disturbances affect the motor gain, i.e., the ratio of movement magnitude relative to the input signal. States of disturbances unfold over a wide range of timescales. Therefore, when the nervous system observes an error in performance, it faces a credit assignment problem: given that there are many possible perturbation timescales that could have caused the error, which is the most likely? We think that the solution to the credit assignment problem should dictate the temporal properties of the resulting memory. That is, adaptation in response to things that are likely to be permanent should be remembered, while adaptation in response to things that appear transient should be forgotten.

Results

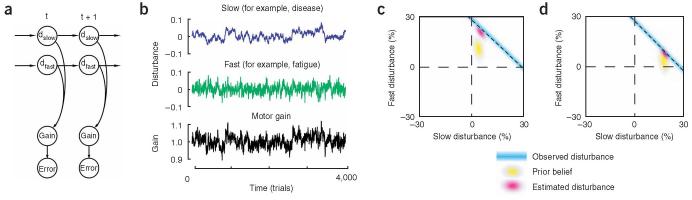
Bayesian statistics allows us to formalize this problem and predict the behavior of a rational learner. Suppose that the motor plant is affected by disturbances that can come in a variety of timescales. Each disturbance will have a state, here represented as a random variable, which evolves independent of other states (Fig. 1a). This implies that fatigue state does not directly affect disease state. A long timescale disturbance, such as the general health state, will have a state that goes up slowly and goes down slowly (Fig. 1b). A short timescale disturbance, such as fatigue state, will have a state that rapidly changes. We assume that the moment-to-moment variance of the states is higher for faster timescales (although all disturbances will have the same variance over long times; see methods for details). Finally, we assume that the various states combine linearly to affect the motor plant, resulting in perturbations to the motor gain. This motor gain defines the movement and thus the movement error. From these assumptions, the Bayesian formalism directly leads to our predictions about learning and memory.

Figure 1.

A generative model for changes in the motor plant and the corresponding response of a Bayesian learner to performance errors. For illustrative purposes, here we show the results of a simulation with just two timescales. a) Various disturbances d evolve over time as independent random walks that linearly combine to change the motor gain. The observed error is a noisy version of the gain disturbance. b) Sample disturbances and the resulting motor gain. c) The Bayesian learner’s belief during an experiment where a disturbance suddenly increases the gain of the motor plant. Before the learner observes the gain, it has a prior belief. The learner’s belief can be represented by its current estimate of the fast and slow disturbances and its uncertainty about this estimate. This is termed a prior and is shown in yellow. In this case, the prior has a larger uncertainty along the fast state. In each trial, the learner observes the disturbance to the motor gain (in this case a 30% increase). This observation is represented by the blue line. The observation is a line and not a point because the disturbance could be due to a fast timescale with magnitude of 30%, a slow timescale with magnitude of 30%, or any other point along this line. Because the learner has sensory noise, there is a probability distribution associated with its observation, and therefore the blue line is hazy. To solve the credit assignment problem, the learner integrates its observation (blue line) with the prior belief (yellow cloud) to generate a posterior estimate (red cloud). In this case, because uncertainty was greater for the faster timescales, the observation was mostly assigned to a fast timescale perturbation. d) The perturbation is sustained for 30 trials. Now the learner associates the perturbation with a slow timescale.

The Bayesian learner observes the motor error (deviations from unity gain), but it needs to estimate the states of the various potential disturbances. Is the error due to fatigue or something more serious? As the states of the various timescales can never be known, the learner represents its knowledge as a probability distribution. Before an observation is made, the learner has a prior belief. For example, if there are only two states, then the prior belief is characterized by a Gaussian distribution (yellow cloud in Fig. 1c). When the learner observes an error, it has effectively measured the sum contribution of all states: the which leads to a diagonal area of high likelihood (Fig. 1c). This measurement will be affected by noise, and so the uncertainty of the learner in its measurement is displayed as the thickness of the blue line. By combining the measurement with its prior knowledge, the learner comes up with a new estimate (the posterior, red cloud).

How did the learner solve the credit assignment problem? When on a given trial it observes a large error, the learner needs to estimate if this is due to a fast or due to a slow disturbance. In this example, the first time the large disturbance happens the system infers that it is most likely due to a fast disturbance as the prior belief is skewed into the direction of fast timescales. That is, the yellow cloud characterizing the distribution (Fig. 1c) has a larger variance along the fast state. This skew arises because of the assumption that disturbances that have fast timescales are affected by greater variability. Therefore, the red cloud in Fig. 1c is centered on a large contribution by the fast timescale. However, if the system keeps observing large errors, this finding is best explained in terms of a slow disturbance as a fast disturbance would be expected to quickly dissipate (Fig. 1d). This would explain why adaptation tends to show a rapid initial phase followed by a slower phase of performance changes.

This credit assignment also may work in more complex situations. For example, say averaged over the last hundred trials there is a negative perturbation while the last three trials had positive perturbations. The system would infer a long timescale negative and a short timescale positive disturbance. In this scenario, the sum of the states might be zero, indicating a motor gain of one, but the learner knows that the various states have not returned to their baseline. This would explain why adaptation followed by a limited period of de-adaptation does not wipe out the memory.

The Bayesian learner’s estimates of the contribution of each timescale, as well as the uncertainties of these estimates, are constantly changing in response to the observed outcomes of each motor command. Whenever a movement error is observed, the state estimates adapt and the uncertainty decreases. The learner thus becomes less sensitive to errors that follow. However, when time passes without the learner observing consequences of its actions (for example, in darkness or in sleep), the disturbances are expected to get smaller because each disturbance tends to vanish over its own timescale. Therefore, the learner’s beliefs will change even when it cannot observe motor error. However, when the learner is prevented from observing motor errors, its uncertainty increases. This makes the interesting prediction that the learner will be more sensitive to errors that follow a period of sensory deprivation, and will therefore learn at a faster rate after a period of darkness or sleep as compared to before that period.

Handling the motor errors in this way is the statistically optimal way for estimating the gain of the motor plant. Here we show that this simple computational framework is able to account for a large body of behavioral data.

Short and long-term effects of saccadic gain adaptation

Motor adaptation has been extensively studied in the context of saccades. Saccades are rapid eye movements that shift the direction of gaze from one target to another.

The eyes move so fast that visual feedback can not usually be used during the movement². For that reason, any changes in the properties of the oculomotor plant that are not compensated would lead to inaccurate saccades³. It has been observed that if saccades overshoot the target, the motor gain (i.e., the ratio of eye displacement to target displacement) tends to decrease and if they undershoot, the gain tends to increase. For example, when motor gain decreases to below one the nervous system must send a stronger command to produce a movement of the correct size. The saccadic jump paradigm⁴ is a way to probe such adaptation⁵: while the subject moves its eyes toward a target, the target is moved. For a monkey, the rate of adaptation to this disturbance is similar to adaptation in response to weakening of eye muscles^6,7, suggesting that the error is interpreted as a change in the eye plant. Using this paradigm it is possible to probe the mechanism that is normally used to adapt to ongoing changes of the oculomotor plant.

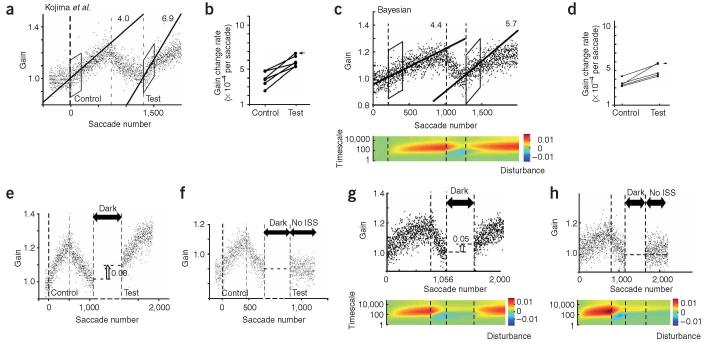
In an impressive range of experiments started by McLaughlin⁴, investigators have examined how monkeys adapt their saccadic gain. The gain changes over time so that saccades progressively become more precise (Fig. 2a). The rate of adaptation typically starts fast and then progressively gets slower. This is a classic pattern that is reflected in numerous motor adaptation paradigms, including reaching^8-10. The same patterns are seen for the Bayesian learner (Fig. 2b). When the gain rapidly changes, the credit is mostly assigned to fast states because the uncertainty is greater for these states, resulting in rapid adaptation. Between trials, fast states decay rapidly, but this decay is smaller in the slower states. If the perturbation is maintained, the relative contribution of the fast states diminishes in comparison to the slow states (the blue bank becomes darker and shifts to longer timescales in Fig. 2b). This implies that as training continues, the estimate of the gain change is assigned to progressively slower timescales. In practical terms, this results in the often reported observation that in response to a constant perturbation (i.e., a step change in the apparent gain), performance of the learner shows an initially rapid rate of adaptation followed by progressively slower rates.

Figure 2.

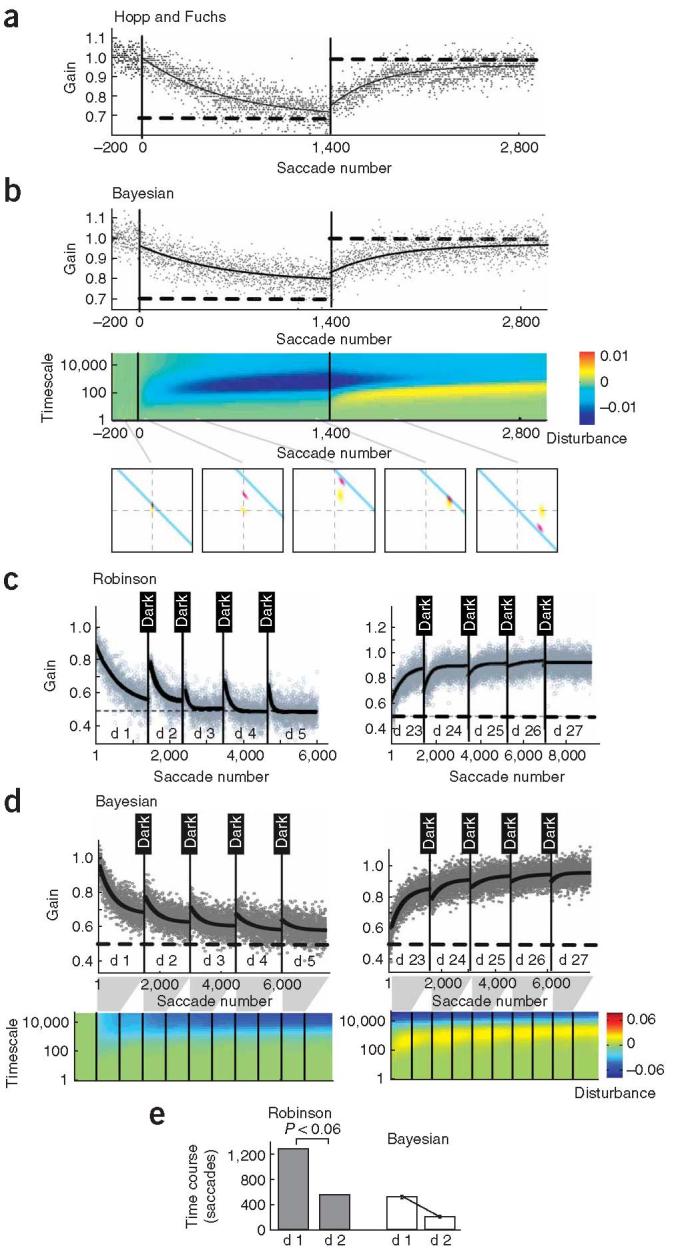
Short-term and long-term behavior in response to saccadic gain changes. a) Short-term training. Each dot represents one saccade, the thick lines are exponential fits to the intervals [0:1400] and [1400:2800]. Starting at saccade number 0,a target is displayed and as soon as the saccade starts, the target jumps back by 30%. The adaptation that would negate this target jump is indicated as horizontal dashed lines. This manipulation ends at saccade number 1400, beyond which are washout trials. Reprinted with permission³. b) The same plot is shown for the Bayesian learner. The color plot shows the learner’s estimates of the state of each disturbance (we have assumed 30 different states, ranging from very short to very long). The estimate of the mean of each disturbance, before updating with the new feedback, is plotted using a color that becomes blue for more negative values (gain less than unity), and red for more positive values (gain greater than unity). The sum of the various states is the expected gain of the motor plant with respect to unity. The sub-plots below this figure show the belief of the Bayesian learner during the initial stages of gain-decrease and then after 30 trials, approximated by two timescales. c) Long-term training. In this experiment¹¹ the saccadic gain was reduced over many days of training. At the end of each training session the monkey was blind-folded and held in darkness for the remainder of the day. Note that the rate of re-learning in day 2 following darkness is faster than initial learning. Black lines show exponential fits to the data. d) The same plot for the Bayesian learner along with a colorplot showing the estimate of the learner of the disturbance at each timescale. e) Comparison of the saccadic gain change time course obtained by fitting an exponential function to the set of all saccades during the day.

When the target no longer jumps (in trial 1,400, the dashed line returns to one in Fig. 2a), saccade gains return to one. However, note that the state estimates do not return to baseline: in trial 2,900, the faster states are positive while the slower states are negative. Adaptation followed by de-adaptation may not wash out the system.

Our model not only accounts for relatively brief periods of adaptation that are typically involved in laboratory settings, it also accounts for behavior during long term periods of training. For example, let us consider a recent experiment¹¹ where the saccadic gain adaptation was set to -50%. The monkey adapted for about 1500 saccades every day for 21 consecutive days, and then after several days of washout trials, de-adapted back to a gain of unity. Interestingly, after training in each day the monkey wore goggles that blocked vision. Multiple effects are visible in the data (Fig. 2c). First, we note that there are several timescales during adaptation: there is a fast (100 saccades) and a slow (10 days) timescale. Second, we note that the starting point of performance on each day is a bit higher than the final performance in the previous day. Third, re-learning rates are affected by the periods of darkness. For example, the learning rate on the second day is much faster than the first day. Finally, during the gain-down adaptation (days 1-22), performance following darkness has decayed toward a gain of unity. However, during wash-out (days 23-27), the decay is toward a gain of 0.5. That is, the system appears to “forget” in different directions during the two phases of learning.

Our model’s behavior (Fig. 2d) is surprisingly similar given that we used the same parameters that we inferred from the single session adaptation in Hopp and Fuchs³ (Fig. 2b). The quantification of the systems estimates of disturbances shows that indeed the system infers longer timescales and stronger deviations over time (deeper blues at longer timescales in Fig. 2d, colorplot). After the initial period of gain-down adaptation training, a period of darkness follows. This means that the monkey is allowed to make saccades, but is not allowed to observe the sensory consequences of its actions (effectively, the noise on the observation is set to infinity). During the darkness period, the learner becomes uncertain about its beliefs about the states of the motor system. Increased uncertainty means that new observations about motor gain are relatively more precise than old information which in turn leads to faster learning when the blind folds are removed. Consequently, while both the monkey and the model forget some of their learning during darkness, they learn faster during the second day than during the first day (quantified in Figs. 2e and f). Similar results were found in a recent study of ocular reflexes¹².

The model explains why forgetting is apparently in opposite directions during the first and second halves of this experiment. Passage of time produces substantial decay in the fast states. During gain-down adaptation, this results in a forgetting toward a gain of unity because the fast states return to zero. By the end of training on day 22, only the slow states are negative, while all the fast states are at zero. During washout, the training causes the fast states to rapidly become positive, pushing the performance away from 0.5 and toward unity. When the gain is retuned to unity, it causes the fast states to become positive (yellow in Fig. 2b). Even after 5 days of reversal the long timescales are still strongly negative (blue in Fig 2d). As a consequence, when time passes during the darkness period of the washout days, forgetting in the fast states now makes the gain estimate drop toward 0.5.

Double reversal training of saccades

Many motor learning studies have attempted to quantify timescales of memory using an interference paradigm. A common theme is a “double reversal” paradigm where the direction of visual errors is changed twice. For example, in Kojima et al. ¹³, the saccadic gain was initially increased, then decreased until it reached unity, and finally increased again (Fig. 3a). The animals learned faster during the second gain-up session than during the first (Fig. 3b). The reversal learning apparently reduced the estimated gain of the motor plant back to one, yet the monkey still had “saved” some aspect of its previous gain-up training as it showed savings.

Figure 3.

The double reversal paradigm. a) The gain is first adapted up until it reaches about 1.2 with a target jump of +35%. Then it is adapted down with a target jump of -35%. Once the gain reaches unity it is again adapted up with a positive target jump. Data from Kojima et al¹³. The box indicates the trials where the line was fitted. The number on the line indicates its slope. b) The speed of adaptation (slope of the lines in part a) is compared between the first gain-up and the second gain-up trials in different sessions of training. The monkey exhibits savings in that it re-learns faster despite the apparent washout. c) The performance of the Bayesian learner is shown along with a colorplot showing the estimate of the learner of the disturbance at each timescale. d) The rate of adaptation for the Bayesian learner. e) In this experiment, the reversal training is followed by a period of darkness, and then gain-up adaptation¹³. Saccade gain shows spontaneous recovery. f) The same plot for the Bayesian learner along with a colorplot showing the estimate of the disturbance at each timescale. g) In this experiment, the period of darkness is followed by a condition where the target does not change position during the saccade period (i.e., no intra-saccadic step, ISS)¹³. The animal does not show spontaneous recovery. h) The same plot for the Bayesian learner along with a colorplot showing the estimate of the disturbance at each timescale..

The Bayesian model (using the same parameter values as before) explains this phenomenon (Fig. 3c). At the end of the first gain-up session, most of the gain change is associated with the slow states (they are positive, yellow in Fig. 3c, colorplot). In the subsequent gain-down session, errors produce rapid changes in the fast state so that by the time the gain estimate reaches unity, the fast and slow states have opposite estimates: the fast states are negative, while the slow states are positive. Therefore, the gain-down session did not reset the system because the latent variables store the history of adaptation. In the subsequent gain-up session, the rate of re-adaptation is faster than initial adaptation (Fig. 3d) because the fast states decay toward zero in between trials, while the slow states are already positive. After about 100 saccades the speed gain from the low frequencies is over and is turned into a slowed increase due to the decreased error term.

In another set of experiments, the investigators¹³ observed that following a period of darkness where the animal was not allowed to view sensory consequences of its motor commands, there was a sudden jump in performance. In these experiments, gain-up training followed gain-down training until saccade gains were restored to unity. Now the animals spent some time in the dark. Afterwards, when the animal was tested in the gain-up task, saccade gain had spontaneously increased (Fig. 3e). The same effect is seen for the Bayesian learner (Fig. 3f). In the dark period, the Bayesian learner makes no observations and therefore cannot learn from error. However, the estimates are still affected by passage of time: the fast states are negative and rapidly decay toward zero, while the slow states are positive and only slowly decay (Fig. 3f, colorplot). The sum is a positive disturbance that after an initial transient, slowly decays. Consequently, by the end of the dark period, the estimate has become “gain-up”. This effect is enhanced by fast learning following the period of darkness.

A recent model of motor adaptation¹⁴ is functionally similar to the model introduced here and explains much of the data on saccadic gain adaptation (Fig. 3) using two integrators operating at different timescales. However, for the Bayesian model, the passage of time during darkness not only produces changes in the mean of the estimates, but it also makes the learner less certain of its belief. Therefore, the Bayesian model makes an important prediction: extended periods of darkness should lead to faster subsequent learning. We noted this earlier in the multi-day adaptation studies (Fig. 2e). However, the effect is present even in a single day study. Here, the Bayesian model predicts that re-learning will be faster when up-down adaptation is followed by a period of darkness than if the darkness period is replaced with saccades in full light. Indeed, in the available data¹³, after darkness the gain change is much faster (5.8 * 10^-4 vs. 3.8 * 10^-4 for one monkey, 9.3 * 10^-4 vs. 6.8 * 10^-4 for the other with p < 0.05 and p < 0.001, respectively). These effects of post-darkness change in rates of learning come about only if passage of time has an influence on the uncertainty of the learner. That is, passage of time affects the learner’s knowledge in terms of both its mean and variance, demonstrating that sensory deprivation leads to faster learning. Models of memory that do not consider uncertainty of the learner¹⁴ [?] generally cannot account for such data.

If the darkness period is followed by a period without intra-saccadic target jumps (Fig. 3g), then the animal does not show spontaneous recovery. At first glance this would suggest some kind of context dependent recall. However, the Bayesian learner shows a similar behavior (Fig. 3h) and the model explains that the effect is not due to context, but uncertainty. At the end of the darkness period, the slow states are at a positive gain while the fast states are near zero. When darkness is followed by gain-up training, all states are more uncertain and therefore rapidly move toward a positive gain. On the other hand, when darkness is followed by unity gain training, the gain-up status of the slow states is rapidly negated by the fast states that now become negative.

Adaptation outside the motor system

Many phenomena outside of the realm of muscle properties can be expected to happen on multiple timescales. For example, the contrast of visual scenes may follow similar rules¹⁵. To adapt optimally, the nervous system might need to estimate the current level of contrast from past values. Recently, investigators measured how visual neurons adapted to stimuli that changed on several different timescales¹⁶ (Fig. 4a). It was found that adaptation timescales among the neurons were longer as the interval between switches of contrast was lengthened. The Bayesian learner shows very similar effects (Fig. 4b). Multiple timescale learning and adaptation may be optimal even for sensory phenomena.

Figure 4.

The Bayesian learner outside of movement settings. a) The response of a neuron in the fly is shown to a visual stimulus that changes its standard deviation, switching between two levels (reprinted from ¹⁶). b) The data is modeled by a system with many timescales that drifts towards a mean of 40 spikes/second. c) Declarative memory data reprinted ²¹. For word translations that had been learned with different intervals between training sessions the retention function is shown. d) The retention function of a Bayesian learner

Analogous problems of multiple-timescale inference may also be solved by the nervous system in certain cognitive tasks. For instance, in the retrieval of long-term declarative memories, numerous studies over a century of research have explored “spacing effects”: a specific item will typically be remembered longer if the study trials for that item are spaced out over a long training period rather than clustered within a short training period^17-20. The spacing effect in one classic study of long-term memory for vocabulary words in a foreign language²¹ is shown in Figure 4c. Spacing effects might seem counterintuitive if we think of forgetting as a passive decay process with a fixed time-constant, but the phenomenon should be familiar, from the often-repeated (and often-ignored) advice of school teachers that steady studying over a whole term leads to better retention of learning than intensive cramming right before the exam.

Our framework can explain spacing-dependent forgetting curves (Fig. 4d) as follows. Let us assume that the strength of a memory trace reflects the modulation of a “cognitive gain” and that each encounter or study-trial with a specific item results in a measured gain of 1 for that item. Intuitively, the model attempts to infer the changing importance of a given item, allowing that the importance of different items could rise and fall over different timescales. These timescales are reflected in the item’s past use: when experience with an item has been spaced over a long period of time, it provides evidence that the item is of long-term relevance. In contrast, an item with clustered experience or practice is more likely to be of only short-term interest.

Discussion

Traditional models of adaptation simply change motor commands to reduce prediction errors^22,23. We approached the problem from a different point of view: if the CNS knows that the body is affected by perturbations that have multiple timescales, then the problem of learning in the CNS is really one of credit assignment. The rational approach would be to do three things: First, the learner should represent its knowledge of the properties of the motor system, including how disturbances of various timescales can affect it. Second, it should represent the uncertainty it has about its beliefs. Third, it should formulate the computational aim of adaptation in terms of optimally combining what it knows about the properties of the motor plant with the current observations. The experimental predictions of the presented model derive from the way knowledge about the state of the motor plant is combined with noisy feedback into a statistically optimal estimate.

While our work may be the first model of learning where all three of these points are considered together, we have been greatly influenced by earlier studies that have largely considered these points separately. Foremost among the previous works is the work of Smith et al. ¹⁴. In that model, it was proposed that the brain responds to error with at least two systems: one that is highly sensitive to error but rapidly forgets, and another that has poor sensitivity to error but has strong retention. That model explained savings and spontaneous recovery and demonstrated that during the period of darkness, motor estimates take the form of sum of two exponentials, one with a fast and the other with a slow time constant. However, because that model did not incorporate uncertainty, it could not explain the animal’s rapid re-learning after darkness and sensory deprivation, and it could not explain the lack of spontaneous recovery when darkness was followed by gain-one training (Fig. 3).

The idea of multiple timescales have also been proposed in the context of connectionist learning theory²⁴ and in motor learning^8,10. Connectionist models as well as earlier motor learning models have no systematic way of modeling uncertainty about timescales. The phenomenon of spontaneous recovery in classical conditioning²⁵ fits well into the framework presented here. In classical conditioning, it has been proposed that the nervous system should keep a measure of uncertainty about its current parameter estimates to allow an optimal combination of new information with current knowledge²⁶. That model included a measure of uncertainty and a mechanism mediated by neuro-modulators for allowing fast changes at catastrophic moments. The multiple timescales of potential disturbances proposed here may lead to similar results as fast timescales may take care of catastrophic fast changes. Moreover, Kalman filters have been used for systems identification in engineering to solve similar problems²⁷. Finally, even the earliest studies of oculomotor adaptation realized that the objective of adaptation is to allow precise movement with a relentlessly changing motor plant⁴. Our approach unifies these ideas in a coherent computational framework.

In the saccade experiments that we considered, darkness corresponds to a period of time where the animal makes eye movements but is not allowed to observe the visual consequences of its motor commands. Because our model shows how a rational learner would update its knowledge when it is faced with sensory deprivation, it gives one explanation as to why there are improved rates of learning after periods of darkness. It is interesting to view sleep in a similar framework: as essentially a period where the brain simulates movements but is deprived of actual feedback. The post-sleep improvements in rates of learning may be partly due to an increased uncertainty regarding the states of the internal model.

There are features of adaptation that our model in its current form does not explain. For saccades, three kinds of asymmetries are observed: Adaptation up is faster than adaptation down, unlearning after up adaptation is slower and spontaneous recovery is only observed in the up direction. It is an exciting question how these asymmetries arise. We know that our body is not symmetric with respect to strengthening and weakening of muscles. For example, we often experience errors due to rapid fatigue but errors due to fast strengthening are really quite rare. Such asymmetric history of perturbations can in principle explain both the fact that gain-down learning is slower than gain-up, and that spontaneous recovery is present only in the gain-up direction. The asymmetries may, however, also indicate effects stemming from suboptimal neural computation. Similarly, for the adaptation of visual neurons there exists a clear asymmetry between upward and downward adaptation. The nervous system should also have someway of learning the importance of each possible timescale. Hierarchical Bayesian models allow a straightforward modeling of such phenomena. Moreover, the model presented here uses a simple definition of time. For example, the nervous system may model that our motor system changes less if we do not move than if we move. Such a situation may be analogue to a Kalman filter that runs fast in the presence of movement and much slower in the absence of movement. It is known that adaptation is highly context dependent^28-30 and indeed we should only generalize from one situation to another situation that is similar. In this model we cut out all properties apart from time and error magnitude to predict purely temporal adaptation phenomena.

It should be clear that we modeled the animal’ s learning here as if the errors were due to the behavior of the motor plant, when in fact errors were due to clever manipulations in the outside world. As long as changes in the world happen according to similar rules or the subject does not know it is dealing with changes in the outside world, our model extends well to those situations. However, it is likely that the world goes through more step type changes than our body - in particular the world in a neuroscientist’s laboratory! In that case, the nervous system has to solve an additional credit assignment problem: Is the error due to a change in my body or due to a change in the world? We find it intriguing that different species may have different ways of solving this problem. Gain adaptation training in monkeys generalizes broadly to other types of saccades³¹, generally agreeing with our simple model of associating the errors to changes in the oculomotor plant. However, similar training in humans is context specific and shows more specific generalization patterns, suggesting that the credit assignment is mostly to the model of the world³². However, humans have ample experience with changes in the world, such as the wearing of glasses, that demand specific context dependent patterns of adaptation.

It should be emphasized that we did not model the mechanisms of any specific memory, but rather attempted to present a general model for all memories based on a generalization from how the brain would learn to control the motor plant. For example, let us consider spacing training trials. Spacing effects have been observed robustly across many timescales and stimuli^33-34. Spacing effects fall out naturally and quite generally from making rational statistical inferences about the timescales over which a given piece of information’s relevance is changing. This is the same kind of inference that the motor system must make about potential motor disturbances. Anderson³⁵ originally suggested a similar view of memory retrieval, inspired by a model for predicting library-book access, and he showed how this model could predict spacing effects and other dynamical aspects of declarative memory. Our results suggest that common principles of memory and forgetting may be at work more broadly across the nervous system. Both higher-level cognitive learning and lower-level sensorimotor learning face a shared challenge of adapting their behavior to processes in the world that can unfold over different timescales.

An important question for further inquiry is how the nervous system solves problems that require multiple timescale adaptation. Our idea that the general rules for learning and memory may have arisen from time-dependent properties of the motor system gains credence from a recent observation that saccades can fatigue the eye muscles, producing a short-term adaptive response in the cerebellum³⁶. The compensation of saccadic fatigue is based on the adjustment of a Purkinje cell simple spike population signal. If this adaptation process is happening in the cerebellum^37,38, the necessary effects could potentially be implemented directly by synapses that exhibit LTD with power-law characteristics^39,40. Alternatively, at least for small timescales, small groups of neurons may jointly represent the estimates along with their uncertainties. A second question is how the nervous system infers the timescale and noise properties of the disturbances. The Bayesian learner may begin with a prior assumption about the structure of the “generative model”, but adapt the parameters of this model as it experiences the world.

Methods

The Bayesian approach makes it necessary to explicitly specify all the assumptions we are making about how the motor plant may change over time.

Disturbances

Our problem of learning is one of state estimation, where state refers to the state of the disturbances. Each disturbance was modeled as a random walk that was independent of all other disturbances:

$${\text{disturbance}}_{\tau }(t+\Delta )=(1-1∕\tau ){\text{disturbance}}_{\tau }\left(t\right)+{\epsilon }_{\tau }$$ (1)

where ε_τ was drawn from a mean zero normal distribution of width σ_τ , and τ was the timescale. The larger the value for τ, the closer (1-τ ^-1) is to 1 and the longer a disturbance typically lasts. The motor gain was simply one plus the sum of all the disturbances:

$$\text{gain}\left(t\right)=1+\sum _{\tau }{\text{disturbance}}_{\tau }\left(t\right)$$ (2)

Eq. (1) is the state update equation. The problem of state estimation is to estimate the states from measured output (see below). We do this via a Kalman filter. In our simulations each saccade is simulated as one time step of the Kalman filter. The τ are thus defined in terms of saccades.

Parameters

Only those timescales will matter that are not much longer than the overall time of the experiment (because they would already have been integrated out) and that are not much shorter than the time of an individual trial (because they would average out). For that reason we chose the distribution of τ to be 30 values exponentially scaled between 2 and 33333 saccades. Choosing a larger number of disturbances while correcting for the overall variance hardly changes the results. We chose 30 timescales as an approximation to a continuous distribution to allow our simulation to run fast. Once chosen, the timescales remained fixed. The distribution of expected gains thus only depended on the distribution of σ_τ, a characterization of how important disturbances were at various timescales. It seemed plausible that disturbances with a short timescale tended to be more variable than those that had a long timescale: over the timescale of about a year we can double our strength through workout. Over the timescale of a week we can half our strength if we get ill. And over the timescale of a minute we can half our strength through fatigue. Each such effect seems to be similarly important - although we acknowledge that there are many more timescales. Therefore we choose: σ²_τ=cτ^-1 where c is one of the two free parameters of our model (see supplemental material for an analysis of the sensitivity of these variables). We have thus specified the prior assumption about the body that drives adaptation.

On each trial the learner made an observation about the state of the motor plant. We assumed that this observation was corrupted by noise:

$$\text{observation}\left(t\right)=\text{gain}\left(t\right)+w$$ (3)

where w was the observation noise with a width σ_w. This is the second free parameter in our model. Throughout this paper we choose σ_w = 0.05 which we estimated from the spread of saccade gains over typical periods of 200 saccades and c = 0.001 because that yielded good fits to the data by Hopp and Fuchs³. We chose to model all data using the same set of parameters to avoid issues of over-fitting.

Inference

Given this explicit model, Bayesian statistics allowed deriving an optimal adaptation strategy. MATLAB files for repeating these simulations are available online. We observed that the system was equivalent to the generative model of the Kalman filter⁴¹ with a diagonal state transition matrix M=diag(1-τ^-1), an observation matrix H that is a vector consisting of one 1 for each of the 30 potential disturbances, and a diagonal state noise matrix of Q=diag(cτ^-1). State noise was what was driving the changes of each of the disturbances. This Kalman filter represents its knowledge about disturbances by two entities, a state vector of length 30 containing the best estimates at each timescale as well as a matrix V characterizing the uncertainty about that estimate. We obtained the solution that is well known from the Kalman Filter literature. We used the Kalman filter toolbox written by Kevin Murphy to numerically solve these equations. To model target jump experiments we simply add the displacements to the error that is being used by the Kalman learner.

To model the sensory deprivation experiments (i.e., darkness), we made the measurement noise for those trials set to infinity. To model the experiments where the monkey spends some time in the dark (Fig. 3f) we simulated 500 saccades without any feedback. To model long-term learning in the monkey where he spends a whole night in the dark (Fig. 2d), we simulated 1500 saccades without sensory feedback.

Contrast adaptation of visual neurons

The adaptation state is modeled as a muscle that has a baseline gain of 40. c = 0.003 and σ_w = 1 are chosen to model the data. The contrast of the input stimulus that is varied in the experiment is modeled as a motor gain change from 20 to 60. Each second is modeled as 100 time steps for the Kalman filter. Otherwise the same distribution of time scales (in terms of simulation steps) is retained and the same methods are used.

Word learning

To model the retention of memories we treat each learned word as a gain perturbation of 100. c = 0.03 and σ_w = 1 are chosen to model the data. As words are not used in between we assume that apart from the learning trials the rest of the time consist just of no observations, equivalent to darkness in the saccade case. Each year is modeled by 100 time steps for the Kalman filter. The same distribution of time scales (in simulation steps) is used as in the motor case. The plotted retention function is the gain of the adapting system.