Role of selection in the emergence of lineages and the evolution of virulence in Neisseria meningitidis

Abstract

Neisseria meningitis is a human commensal bacterium that occasionally causes life-threatening disease. As with a number of other bacterial pathogens, meningococcal populations comprise distinct lineages, which persist over many decades and during global spread in the face of high rates of recombination. In addition, the propensity to cause invasive disease is associated with particular “hyperinvasive” lineages that coexist with less invasive lineages despite the fact that disease does not contribute to host-to-host transmission. Here, by combining a modeling approach with molecular epidemiological data from 1,108 meningococci isolated in the Czech Republic over 27 years, we show that interstrain competition, mediated by immune selection, can explain both the persistence of multiple discrete meningococcal lineages and the association of a subset of these with invasive disease. The model indicates that the combinations of allelic variants of housekeeping genes that define these lineages are associated with very small differences in transmission efficiency among hosts. These findings have general implications for the emergence of lineage structure and virulence in recombining bacterial populations.

A spectrum of population structures has been identified among bacterial pathogens by multilocus studies of genetic variation in housekeeping genes (1, 2). It ranges from the extremely low diversity observed in Yersinia pestis (3) and Salmonella enterica var Typhi (4) to the very high levels of unstructured diversity found in Helicobacter pylori (5). The majority of pathogenic bacteria investigated to date, however, occupy an intermediate position within this spectrum, being composed of distinct cocirculating lineages that constitute a small subset of the possible allele combinations (6). These intermediate population structures exhibit apparently conflicting signals of both clonal descent and genetic exchange, and the mechanisms whereby they arise and are maintained remain incompletely understood (7).

Neisseria meningitidis, the meningococcus, was one of the first bacteria where such an intermediate population structure was described (8–10). Populations of this highly recombining bacterium (11), which has an essentially commensal relationship with the human host, also present the intriguing feature that only certain lineages, the so-called hyperinvasive lineages, are associated with disease (12). These observations present two conceptual challenges: first, how does lineage structure arise in the face of the observed high rates of recombination; and, second, why are some lineages especially virulent, when invasive disease confers no benefit in terms of host-to-host spread (13)?

Here, we address these questions by means of a survey of 1,108 meningococci isolated from asymptomatic carriage and disease in the Czech Republic over a 27-year period. The isolates were characterized at seven housekeeping loci by multilocus sequence typing (MLST) (14) and at the porA locus, which encodes a major surface antigen and vaccine candidate PorA (15). None of the population genetic frameworks proposed to date for bacterial pathogens (9, 16, 17) were consistent with the patterns of genetic variation seen; neither could they explain the association of the invasive phenotype with a subset of lineages. We therefore developed a model invoking selection as the principal force driving lineage evolution and the persistence of virulence. The model generated a population structure comprising a limited set of lineages, only some of which were hyperinvasive, provided that competition among genotypes was present but incomplete. The observed shifting association between antigenic type and lineage was consistent with competition among types being mediated by immune selection. These results can be generalized and may be widely applied in studies of bacterial population structure and evolution.

Results

Diversity of Carried Meningococci Over Time.

Carried samples were collected in small groups, mainly of <10 individuals from each location at any particular time point, although some larger groups were sampled in the 20- to 24-year age range in 1993–1994 during a sequence type (ST)-11 serogroup C epidemic, with the largest being of 55 individuals. Over the study time period, the incidence of invasive meningococcal disease in the Czech Republic varied from 0.4/100,000 in 1970–1974 to a peak of 1.6/100,000 in 1995–1999. Most cases were sporadic until 1993 when elevated disease was reported because of the emergent serogroup C ST-11 strain (11). There were 11 years between 1971 and 1994 for which 33 or more meningococcal carriage isolates were available: 1971, 50; 1972, 135; 1973, 95; 1974, 102; 1975, 115, 1978, 46; 1979, 44; 1980, 60; 1993, 218; 1994, 79; and 1996, 33. These 977 isolates were characterized by MLST and yielded 455 unique combinations of MLST alleles (STs) and 27 clonal complexes [Table 1 and supporting information (SI) Table S1]. The data were stored in a database available at http://neisseria.org/nm/typing/mlstdb. F_ST values, calculated by pairwide comparisons of the concatenated nucleotide sequences of the MLST alleles for each year were low (−0.00969 to 0.05247), indicative of no temporal change in the bacterial population structure at the nucleotide sequence level (Table S2).

Table 1.

Observed frequencies of the most common clonal complexes per year

Clonal complex	Year											Total
	1971	1972	1973	1974	1975	1978	1979	1980	1993	1994	1996
cc41/44	5	26	11	9	25	8	4	8	31	7	3	137
cc549	1	34	14	2	4	1	1		5	2		64
cc376	7	11	5	17	6	2	2	3		1	1	55
cc22	2	2	5	11	10	2	3	5	3			43
cc92	2		1	3		4			21	5	6	42
cc11									33	4		37
cc174	2	9	6	2	7	1			1	3		31
Others	12	17	22	34	17	12	15	23	63	33	15	263
Unassigned	19	36	31	24	46	16	19	21	61	24	8	305
Total	50	135	95	102	115	46	44	60	218	79	33	977

Complexes with 30 or more members are shown.

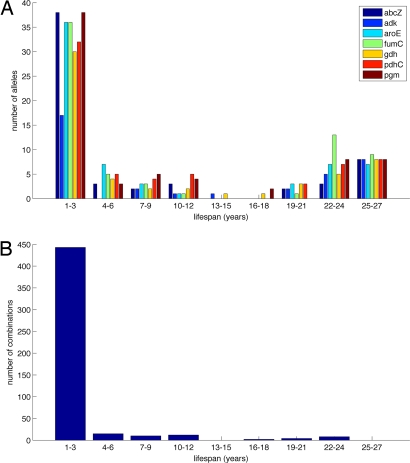
In the complete sample of 1,054 isolates from carriage, including years with <33 isolates, most alleles were short-lived, with 227 of 415 (54.7%) observed within a 1- to 3-year time period only, but 104 (25.1%) were seen for between 22 and 27 years, the time period of the study (Fig. 1A). Similarly, 443 of 494 (89.7%) STs were observed for no longer than 3 consecutive years but a few (ref. 12; 2.4%) persisted for 19 years or more (Fig. 1B). On average, 64% of isolates sampled each year had a ST not seen previously in the dataset. The lifespan of allele combinations was simulated by using the same rate of appearance of new STs as observed (Figs. S1 and S2). In this simulation, allele combinations did not persist >7 years at most, indicating that purely neutral processes did not provide an adequate explanation for the patterns observed in the data.

Fig. 1.

The observed lifespan, in years, of alleles at each of the seven housekeeping loci (A) and the unique allelic combinations of these loci (B) within the Czech dataset.

Of the clonal complexes present in the dataset, only the ST-41/44 clonal complex was present in all years, with the central genotype, ST-44, the only individual ST present throughout the survey, being isolated in all years except 1996. The other STs belonging to this clonal complex (22/47 of which were single-locus variants and 14/47 of which were double-locus variants of ST-44) were typically only identified in a single year and were absent from subsequent samples (Table 2). Of the 83 allele changes represented in these 47 variants, at least 73 were likely to have been the result of recombination events based on the number and position of nucleotide differences from ST-44.

Table 2.

Temporal distribution of STs belonging to the ST-41/44 clonal complex

ST	Year											Total
	1971	1972	1973	1974	1975	1978	1979	1980	1993	1994	1996
44	2	9	8	8	10	2	2	6	8	1		56
303*	1	1	1					1				4
314*	1											1
385	1											1
319†		4										4
43*		1								1		2
327*		1				1						2
386†		2										2
315*		1										1
316		1										1
317*		1										1
318*		1										1
358†		1										1
359*		1										1
390†		1										1
498†		1										1
525*			1				1					2
550*			1									1
436*				1								1
437*					6							6
146*					3	1				1		5
527*					2							2
438					1							1
513					1							1
526					1							1
1006†					1							1
691*						1						1
1008*						1						1
1041*						1						1
1177†						1						1
687*							1					1
723								1				1
110*									6	1		7
136									6			6
112									2	1		3
111†									2			2
108									1			1
109†									1			1
137*									1			1
142*									1			1
690†									1			1
721*									1			1
1086†									1			1
150†										1		1
224										1		1
252†											1	1
256											1	1
260†											1	1
Total	5	26	11	9	25	8	4	8	31	7	3	137

*Single locus variant of ST-44.

^†Double locus variant of ST-44.

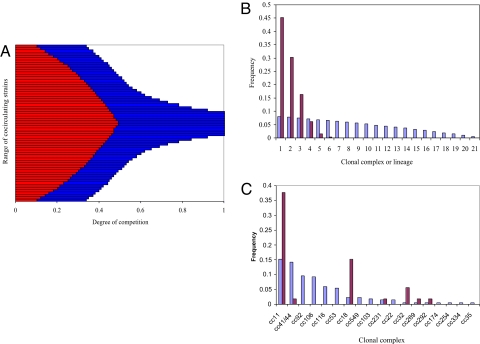
A comparison of isolates causing disease in 1993 (11), the year with most carriage isolates available, found that frequencies of the most virulent complexes were not related to the frequencies of carriage (Fig. 2C). For example, ST-11 complex accounted for 15.2% carriage in that year, but caused 37.7% of disease, whereas the next most common carried complex (ST-41/44 complex) represented 14.3% carriage but only 1.9% of disease.

Fig. 2.

Emergence of lineages. (A) The effects of competition (γ) on the coexistence of allelic combinations or strains, characterized by very small differences in transmission efficiency, within a hypothetical six-locus, two-allele system. The blue bars indicate the range of γ over which each strain can survive, overlaid on these in red is the (smaller) range of γ over which the strain can afford to carry excess virulence. Two features are to be noted: The number of cocirculating strains decreases as competition (γ) for available hosts increases, and fewer of the these strains are able to carry the burden of excess virulence. Parameters used: β_i = 1.76 + 0.1·i for strains 1–32, and the converse for strains 33–64; μ = 0.02/yr, σ = 10/yr, α_avirulent = 0, α_virulent = 2/yr. (B) The frequency distributions of strain types (now representing lineages caused by the purging of most allele combinations) among disease (brown) and carriage (blue) isolates for an intermediate value of γ (= 0.45). (C) Shown is the contrast between the distribution of clonal complexes among disease (brown) and carriage (blue) isolates obtained in 1993 within the Czech dataset.

Associations Between Clonal Complexes and Antigen Type.

Particular antigen combinations, as defined by PorA VR1 and VR2 epitopes, were strongly associated with certain clonal complexes at particular times but the frequencies of association varied over the time frame of the study (Table 3 and Table S3). For example, 76.9% (n = 13) of isolates with the P1.19,15 combination in 1972–1973 belonged to the ST-376 clonal complex [and these represented 62.5% (n = 16) of this complex]. In 1993–1994, however, 57.9% (n = 19) of this combination was represented by isolates belonging to the ST-41/44 complex [representing 29.0% (n = 38), the most common phenotype, of this complex] and with only a single ST-376 complex isolate.

Table 3.

Clonal complex association of PorA variants in the 1970s and 1990s

Variant	Clonal complex
	cc41/44		cc549		cc376		cc92		cc22		cc11		cc174		cc254		cc106
	70s	90s	70s	90s	70s	90s	70s	90s	70s	90s	70s	90s	70s	90s	70s	90s	70s	90s
18–1,3					2.0				31.0			14.3	25.0
5–1,2–2		25.0	69.8												4.8
19,15	2.0	59.1			72.5	4.5							2.0		2.0
5–1,10–1							50.0	45.2										52.4
5,2												100
21,16	13.3	3.7		7.4			6.7	3.7							46.7	11.1		3.7
18,25	89.3				3.6
22,14–6	77.8	50.0	3.7		7.4
12–1,13–1	19.0
5–2,10			25.0						18.8	50.0
7–1,1	13.6				9.1										9.1
5–1,10–4		16.7	7.7				7.7	41.7	3.8				3.8		3.8

Values are the percentages of each variant associated with each clonal complex in the decade specified. Clonal complexes with 25 or more isolates in the two decades are shown.

Competition as a Determinant of Lineage Structure and Its Nonrandom Association with Hyperinvasiveness.

We explored the behavior of a multilocus model of pathogen population structure (see Methods) within which STs were defined by combinations of alleles at housekeeping loci and were constantly generated by reassortment of preexisting alleles. The model made three assumptions: (i) that there are small differences in transmissibility between STs, (ii) that STs are in competition with each other, but (iii) coinfection with different STs is possible. Each of these STs could also acquire excess virulence, which within this framework had the simple effect of shortening the infectious period. Fig. 2A shows the range of model outcomes for a hypothetical six-locus, two-allele system under different levels of competition for available hosts (see also Fig. S3). Under low levels of competition, all possible STs can coexist and acquire excess virulence. As competition increases, the STs of lower transmissibility are lost, until the population is dominated by only a few of the many possible combinations of housekeeping genes, each constituting a distinct lineage, with excess virulence emerging only among the more transmissible lineages that are able to tolerate this penalty. Under these circumstances, the distribution of lineages among population samples of carriage and disease isolates would conform to the pattern shown in Fig. 2B. Under very intense competition, the population is dominated by a very limited number of STs, none of which possess excess virulence. Under full competition, and with no coinfection, the system would collapse to a single most transmissible strain type, as observed in the previous models (18, 19).

Effects of Immune Selection on the Association Between Lineage and Antigenic Type.

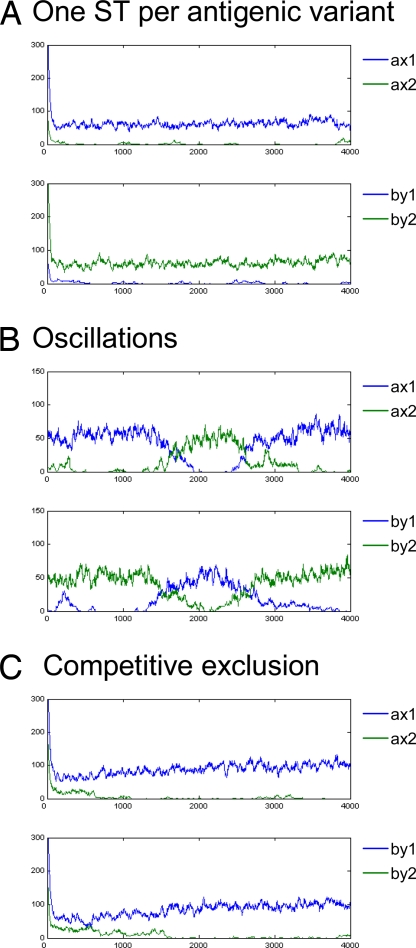
A stochastic model was used to examine the effects of competition through host immune selection. In this model strains were defined both by their combination of housekeeping genes (i.e., lineage) and two variable antigenic determinants. Simulations showed that, when immune selection was sufficiently high, lineages followed one of three distinct trajectories (Fig. 3): (i) when differences in transmissibility were low, each lineage stably associated with an antigenic type; (ii) as the differences in transmissibility among lineages increased, their relationship with antigenic type fluctuated over time, with the lineages oscillating in dominance within each antigenic type; and, (iii) once the differences in transmissibility between two lineages were sufficiently large, the lineage with lower transmissibility could not be sustained in the population.

Fig. 3.

Associations between ST1 (blue) and ST2 (green) with antigenic types ax, bx, ay, and by (representing the various epitope combinations possible within a two-locus, two-allele model) under strong immune selection. The different dynamic outcomes are each ST is uniquely associated with a dominant antigenic type (A), periodic replacement of antigenic type linked to a particular ST (B), and competitive exclusion of one ST (C). In this example, R₀ of ST1 = 5, R₀ of ST2 = 5.1 (A), 4.3 (B), and 4.05 (C). Other parameters used were: σ = 20.27 yr⁻¹, ς = 2.03 yr⁻¹, γ = 0.97. Population size = 1,000.

Discussion

Lineage structure in bacterial populations has been defined on the basis of linkage disequilibrium among housekeeping loci since the seminal multilocus enzyme electrophoresis enzyme (MLEE) studies of the early 1980s (2). Since that time it has been assumed the genetic variation in these loci is neutral (17) and lineage structure was initially rationalised as a product of clonal descent, i.e., the absence of appreciable genetic exchange combined with diversity reduction events such as periodic selection or bottlenecking (20). The clonal model was challenged by the discovery of widespread horizontal genetic transfer or “localized sex” (21) in bacteria, such as the meningococcus, that nevertheless exhibit lineage structure (22). This observation was accommodated by the proposal that short-term domination of lineages might arise in otherwise nonclonal populations as a consequence of the rapid spread of particular genotypes or “epidemic clones” (9).

A formalized “microepidemic” model of the oversampling of particular genetic types, as a consequence of their belonging to the same “short transmission chain,” can reproduce the results of cross-sectional studies of some bacterial pathogen populations (17). The results of the present study, however, demonstrate that this model cannot account for the persistence of certain STs in meningococcal populations. Simulations (SI Text) incorporating microepidemic processes over extended periods of time demonstrated that, under the assumptions that generate the observed cross-sectional diversity of STs within the Czech dataset (17), the likelihood of subsequently recovering the same ST decays rapidly with time. The persistence of ST-44 relative to other variants within the ST-41/44 complex in the Czech data set (Table 2) was not consistent with these results. Further evidence for the stability of ST-44 was provided by interrogation of the PubMLST website (http://pubmlst.org/neisseria), which demonstrated that the ST-44 type was observed globally from 1968 to 2006. There is extensive evidence for the persistence of particular multilocus genotypes among meningococcal disease isolates (8, 22, 23). Similar observations have been made in other bacteria (24, 25), including the early observation that the electrophoretic type associated with E. coli K12 persisted for >50 years (20). We observed that the differential survival of variant genotypes within a clonal complex has been demonstrated over extended time periods in carried meningococci, requiring the rejection of the microepidemic model as an explanation of meningococcal lineage structure.

The variation observed in meningococcal populations can be replicated by a selective model, built on the assumption of small differences in transmissibility between STs that are in competition with each other and that can coinfect different hosts. Within this framework, discrete lineage structure arises through any form of competition and leads to the long-term persistence of a small subset of the more transmissible STs. Importantly, the coexistence of several lineages is only possible when differences in transmissibility among these STs are very small. In essence, the more transmissible genotypes persist over long periods of time, always generating a transient cloud of less transmissible variants, constituting a clonal complex around the central persisting genotype, but consistently outcompeting them. In addition to the data reported here, this finding is consistent with patterns of variation seen previously in collections of disease-associated meningococci (8, 22, 23, 26).

The analysis demonstrates that the combinations of alleles at meningococcal housekeeping loci must be associated with transmission fitness and subject to selection, despite the similarity of the protein variants encoded by their alleles. This inference is strongly supported by the asymmetric distribution of the lifespan of alleles. If the variation among alleles were neutral, all alleles would have similar life spans; however, the data show that whereas most alleles at all loci are short-lived, some persist for extended periods of time: an observation that is replicated in the lifespan of STs (Fig. 1). Although variation in these housekeeping genes is largely synonymous, they do contain phenotypic variants, as evidenced by the success of MLEE, which measures variation in electrostatic charge (2). This variation provides a potential mechanism for the very small differences in metabolic efficiency that would be needed to generate the small differences in transmission fitness required by the model as, in the highly integrated metabolism of a bacterium, subtly different protein variants are likely to interact more or less efficiently (27). There is support for this idea from the observation that the evolutionary rate of genes depends on the number of intracellular interactions in which their protein product participates (28). Under this scenario, each stable set of housekeeping alleles encodes a set of coadapted metabolic enzymes. Hybrid genotypes will arise frequently by recombination (29) but will not persist (11) as they are very marginally less efficient at transmission. Such fitness differences have been observed for meningococcal surface proteins (23), but there is no a priori reason why this effect cannot be driven by metabolic efficiency of housekeeping proteins, particularly those used for characterization techniques such as MLEE and MLST, which have been chosen because they demonstrate interstrain variability. These observations imply that the concept of bacterial lineage has been successful because, for many organisms, it represents a unit of selection rather than simply reflecting descent by purely neutral processes.

Attaching a property of “excess virulence,” that is a proclivity to cause pathology that does not enhance host-to-host transmission, to the different STs within this framework led to a situation where only the more transmissible of the persisting lineages were capable of carrying excess virulence, i.e., be hyperinvasive. The expected distribution of lineages among disease and carriage isolates generated by this model was in agreement with data from 1993 (11) (Fig. 2C) and was also consistent with the general observation that populations of carried meningococci comprise multiple lineages (or clonal complexes), whereas collections of meningococcal isolates from cases of invasive disease typically contain a limited subset of lineages (11, 12). These hyperinvasive lineages are known to be persistent, having spread worldwide over many decades (22). Our model also accommodates the phenomenon of unencapsulated meningococci occurring commonly in carriage (30). The hyperinvasive phenotype of meningococci is polygenic with the possession of a capsule a necessary but not sufficient factor; thus, within our framework it may be treated as an element of excess virulence and the lack of it may be simply explained by the frequencies of avirulent forms of all cocirculating STs. Finally, our estimates of the pathogenicity, i.e., the disease-causing potential, of the hyperinvasive lineage was very low, which is consistent with characteristics of meningococcal outbreaks, as demonstrated by previous theoretical studies (31).

Our final result concerns immune selection as a particular means of competition among multilocus genotypes comprising both loci defining lineage (i.e., those that affect transmissibility) and loci defining antigenic type (i.e., those under strong immune selection). Multilocus models for immune selection have shown that discrete antigenic types, characterized by nonoverlapping combinations of antigenic variants, may emerge and stably dominate under conditions of strong immune selection (32). Here, by extending this framework to include the housekeeping genes, we have shown that a strong association can also arise between lineage (i.e., ST) and antigenic type but that these associations may shift with time. These model predictions were consistent with the data, which showed that a particular lineage tended to dominate within an antigenic type at a given point in time, but could undergo replacement (Table 3). We know of no other explanation for the association of particular antigenic types with lineages and the fluctuation in this association that is observed in this and other meningococcal populations (33, 34).

The selective model proposed here provides a number of advantages to the clonal and neutral frameworks. In addition to representing the data more accurately, it enables the key features of persistence and excess virulence to be accommodated within the same simple framework. Further, altering the level of a single parameter, which represents interstrain competition acting within the population, generates different population structures without recourse to the addition of other parameters. The assumption of selection is also consistent with the general features of the genomes of most bacteria that show signals of high levels of stabilizing selection including the conservation of gene order and GC skew, low levels of nucleotide and protein sequence diversity, and the lack of pseudogenes (35). A final advantage is that this framework is both predictive, and therefore refutable in any given system, and generalizable to other bacteria. Consequently, it can be used widely as a basis of further investigations of bacterial population structure.

Methods

Data Collection.

Meningococci were isolated from throat swab specimens obtained in the 1970s (610 isolates), 1980s (99 isolates), and 1990s (345 isolates) in the Czech Republic. The samples were from volunteers of all age groups and included school and workplaces from locations covering all areas of the country. Swabs were inoculated onto Thayer-Martin selective medium and incubated at 37°C in 5% CO₂ for 48 h. Presumptive meningococcal colonies were subcultured onto heated blood Mueller-Hinton agar, and species identification was performed by Gram staining, oxidase reaction, and with the Neisseria 4H system (Sanofi Diagnostics Pasteur) or API NH system (bioMérieux) panels of biochemical tests. None of the sampled individuals had known contact with patients with invasive meningococcal disease. Additionally, meningococci (54 isolates) from cases of invasive disease were available for 1993. Chromosomal DNA was extracted from stored samples by using the Isoquick Nucleic Acid Extraction Kit (Orca Research). Samples were characterized by MLST (14), with referral to the Neisseria MLST database (http://pubmlst.org/neisseria/) (36) for clonal complex assignment, and by sequencing of the variable regions of the PorA gene (15). MLST data from isolates from 1993 have been published (11, 29).

Deterministic Model of Competition Between Lineages.

Bacterial variants were designated as (i, j) where i represented their lineage, as defined by a particular combination of housekeeping genes, and j denoted a propensity to cause disease, the latter being equivalent to a virulence determinant or combination of virulence determinants. Horizontal genetic exchange was included by permitting i and j to associate randomly, such that all combinations could occur in the population. The proportion of the host population previously exposed to any variant was designated w. The rate of change in w with time can be given as:

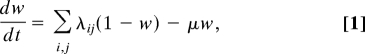where λ_ij is the force of infection associated with strain (i, j) and μ is the average death rate within the host population. The force of infection is defined as λ_ij = β_iy_ij, where β_i is the probability of lineage i being transmitted from an infected to a susceptible host. Interstrain competition was included in this model in a nonspecific manner by restricting infection within previously exposed hosts (w) by a factor γ that was allowed to vary between 0 (no competition) and 1 (complete cross-protection). Under these conditions, the proportion of hosts infectious at any given time with strain (i, j) is given by the following equation:

where σ denotes the basic rate of loss of infectiousness and α_j represents the contribution to loss of infectiousness caused by additional host death or clinical resolution of infection. The gain term of this equation indicates that unexposed hosts (1 − w) are fully susceptible, hosts currently infected with strain (i, j) cannot be reinfected by the same, and previously exposed hosts who are not currently infected with (i, j), in other words (w − y_ij), have their susceptibility reduced by (1 − γ). In contrast with models where strains are defined by antigenic characteristics, the mode of selection is independent of (i, j). It can be shown that the basic reproductive ratio [number of secondary cases produced by one primary case in a totally susceptible population (19)] of each variant (i, j) is given by R₀^ij = β_i/(σ + α_j + μ).

Stochastic Model of Immune Selection with Lineage Structure.

Strains were defined by two antigenic determinants, to which hosts gained allele-specific immunity. In addition, each strain had an ST, which determined the transmissibility of the strain, but had no effect on immunity. For simplicity, each locus had two alleles: one antigenic loci expressing a or b, and the other x or y, and the STs were simply labeled 1 or 2, leading to eight possible strains, ax1, ay1, bx1, by1 and ax2, ay2, bx2, by2. Two strains coinfecting the same host could recombine at a given rate, r, which was the same for each locus and allowed genes to respond to different types of selection pressure. Mutation also occurred at the same rate, m, for each locus, facilitating the emergence of new variants. Pathogen strains existed within a population of hosts, which were connected on a random network, updated at each time step to approximate random mixing (37). Upon infection, hosts remained infectious for a period, 1/σ, and then retained immunity to the antigenic determinants for a further period 1/ς. Cross-immunity (γ) was incorporated by allowing infection by one strain to confer partial protection against other strains expressing the same antigenic determinants, regardless of their ST. Competition between STs was generated by differences in their R₀ values, and it was assumed that ecological constraints did not allow for the coinfection of the same host by two strains belonging to the same ST. A total of 1,000 simulations were run for 3,000 time steps each, with varying levels of cross-immunity and competition. The ranges of the parameters explored were chosen to encompass what is known of meningococcal biology (38) and are outlined in Table S4. Parameter space was explored (see Fig. S4) by using the statistical technique of Latin Hypercube Sampling (39).