A Top-Down Approach to Mechanistic Biological Modeling: Application to the Single-Chain Antibody Folding Pathway

Abstract

A top-down approach to mechanistic modeling of biological systems is presented and exemplified with the development of a hypothesis-driven mathematical model for single-chain antibody fragment (scFv) folding in Saccharomyces cerevisiae by mediators BiP and PDI. In this approach, model development starts with construction of the most basic mathematical model—typically consisting of predetermined or newly-elucidated biological behavior motifs—capable of reproducing desired biological behaviors. From this point, mechanistic detail is added incrementally and systematically, and the effects of each addition are evaluated. This approach follows the typical progression of experimental data availability in that higher-order, lumped measurements are often more prevalent initially than specific, mechanistic ones. It also necessarily provides the modeler with insight into the structural requirements and performance capabilities of the resulting detailed mechanistic model, which facilitates further analysis. The top-down approach to mechanistic modeling identified three such requirements and a branched dependency-degradation competition motif critical for the scFv folding model to reproduce experimentally observed scFv folding dependencies on BiP and PDI and increased production when both species are overexpressed and promoted straightforward prediction of parameter dependencies. It also prescribed modification of the guiding hypothesis to capture BiP and PDI synergy.

INTRODUCTION

In systems biology, mathematical models are used to describe biological systems to obtain understanding of system behavior and predict system responses (1). The type of model used and its scale and scope vary with the desired behaviors and responses it is intended to capture and predict, the desired level of detail, and the size of the biological system of interest. Model types range from the highest-level regulatory graphs, which show how species interact, to Bayesian networks, which represent conditional interactions and dependencies, to Boolean models, which describe switching behavior, to nonlinear ODE models, which describe dynamic behavior, to the most highly detailed stochastic models, which capture random behavior caused by low molecule counts (2–4). Model scale may range from molecular to organismal, and from low-level mechanistic detail to higher-level lumped behavioral units. Model building on the mechanistic scale has been referred to as “bottom-up,” as the model includes previously-known interactions and regulatory feedbacks, which are pared down as analysis identifies the critical, behavior-defining ones. Building on the more abstract, lumped behavioral scale has been referred to as “top-down,” where input-output relations are used to identify and gradually fill in previously unknown interactions (5). This work combines these two approaches by applying the top-down methodology to biological model building on the mechanistic scale.

By and large, mechanistic modeling approaches have not been formalized and are as varied as the models and biological systems under study themselves. Additionally, no formal evaluation of the approaches' applicability to or advantages in modeling a particular biological system has been performed. The body of circadian rhythm mathematical models demonstrates the variety of approaches that have been employed to describe a system largely conserved across mammals and fruit flies. In developing their mathematical model for the mammalian circadian rhythm, Forger and Peskin (6) performed an exhaustive literature search to include many of the known molecular interactions and mechanisms involved in the circadian clock, when a basic negative feedback loop was all that was necessary to reproduce experimentally observed oscillations. This approach is clearly in the vein of bottom-up model building, and it produced a mathematical model containing 73 state variables (biological species) and 74 parameters. In stark contrast, Tyson et al. (7) sought to capture and analyze circadian behavior in Drosophila melanogaster with a higher-level model by reducing a three-state model consisting of mRNA and two forms (monomer and dimer) of protein to two: mRNA and total protein. Meantime, Leloup and Goldbeter developed 10-state Drosophila (8) and 19-state mammalian (9) models of intermediate complexity to fulfill their analytical purposes.

Still, one generalized approach to mechanistic modeling of biological systems has been proposed (10): start by identifying all of the reactions within the scope of the biological system and perform mass balances around the participating species. Then, simplify the resulting mathematical model consisting of a set of nonlinear ODEs with further assumptions and approximations, which often leads to algebraic expressions, Michaelis-Menten kinetics, and transfer functions such as the Hill function. Finally, employ analytical tools such as sensitivity analysis to identify components responsible for producing certain behaviors and stability and bifurcation analysis to assess what behaviors the system is capable of producing. This process description formalizes the bottom-up approach to mechanistic model building.

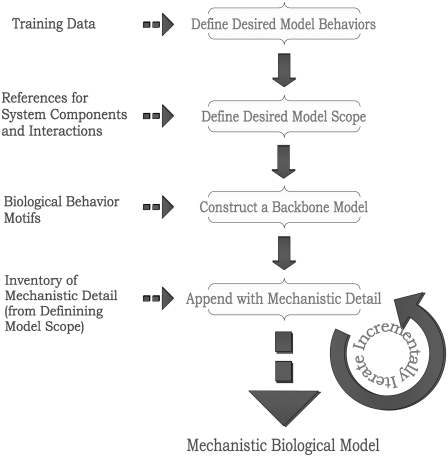
This work describes a contrasting approach similar to that outlined by Ideker and Lauffenburger (11), but on the scale of mechanistic modeling: with the full desired mechanistic scope of the model defined, develop the simplest imaginable representation of the biological system in an attempt to isolate the backbone structure and identify motifs responsible for the underlying behavior. Once this basic model has been established, gradually expand it to include the desired mechanistic details, so the contributions—or lack thereof—of these modifications to system behavior may be incrementally evaluated using systems biology analytical tools. (In the cited work by Ideker and Lauffenburger (11), a top-down approach to biological modeling across many levels of complexity, starting from high-level regulatory graphs and gradually appending them with more data to transition to lower-level model types like ODE models, is described.) This approach may then be referred to as a top-down approach to mechanistic modeling, and its methodology is outlined in Fig. 1. The strength of this approach lies in the fact that it necessarily acquaints the modeler with the inner workings—the behavioral contributions originating from each mechanistic component—of a model as the modeler constructs it.

FIGURE 1.

Overview of the top-down approach to mechanistic biological modeling methodology presented in this work. Inputs and outputs to the methodology are indicated with dotted arrows; methodology flow is indicated by solid arrows.

The top-down mechanistic modeling approach also benefits from a growing repertoire of known biological motifs and modules responsible for producing certain biological behaviors. The Escherichia coli toggle switch (12) and repressilator (13) are two well-known examples from synthetic biology. Other examples include positive feedback loops that can store information from transient signals, inhibitory feedback loops that guard against noise, and feed-forward loops that accelerate responses (14). Much work has gone into identifying and cataloguing recurring structural motifs within a variety of gene regulatory, protein-protein interaction, and other biological networks (15–19), with the intent of eventually characterizing their dynamic properties (21–22). One of the most extensive—though still quite limited—collections of already-characterized biological behavior motifs has been compiled by Wolf and Arkin (23). Familiarity with these motifs and modules can aid in construction of the basic backbone structure by allowing one to identify more readily the components and interactions that will be necessary to reproduce experimentally observed behaviors.

To demonstrate the top-down approach to mechanistic modeling, this work will develop a model for single-chain antibody fragment 4-4-20 (scFv) translocation into and folding within the endoplasmic reticulum (ER) lumen of Saccharomyces cerevisiae, or baker's yeast, by the chaperone binding protein (BiP) and foldase protein disulfide isomerase (PDI). The motivation for this study comes from the fact that single-chain antibodies have a variety of applications in biotechnology and medicine (24,25) and serve as useful models for the expression of other disulfide bond-containing therapeutic proteins. Additionally, yeast is a frequently-used platform, because it combines the ease of microbial genetics and growth characteristics with post-translational, eukaryotic processing (26–28). The goal of using systems biology to study this system is to optimize production of scFv in the S. cerevisiae platform.

It has been shown that overexpressing BiP or PDI individually increases scFv yields in the microorganism but overexpressing both species simultaneously amplifies yields beyond both of those individual increases (26,29). Xu et al. (29) hypothesized that these experimentally observed BiP and PDI dependencies and amplification resulting from co-overexpression originate from BiP assisting in/accelerating unfolded scFv translocation into the ER with no effect on protein folding rates and PDI actually facilitating protein folding. In this line of reasoning, increasing BiP increases the pool of scFv to be folded, and increasing PDI increases the amount of that pool that is exported from the cell. A mathematical model was developed using the top-down approach to mechanistic modeling to test this hypothesis. Steady-state analysis was employed as a primary analytical method for evaluating model performance. As the top-down approach was applied, its strengths were clearly highlighted as it identified a critical motif and three requirements for reproduction of experimentally observed BiP and PDI dependencies and enhanced scFv production with both species overexpressed, while suggesting that the hypothesis incompletely describes potentially more complex interactions between BiP and PDI in scFv folding that yield synergistic effects.

MODEL DEVELOPMENT METHODOLOGY

Establishing desired model behaviors

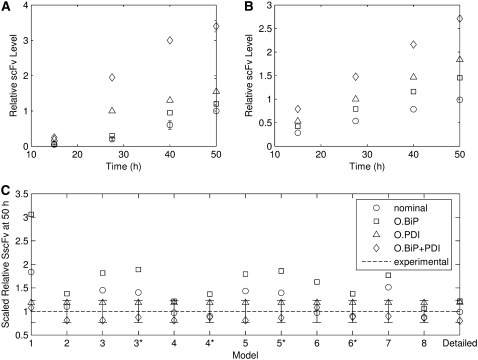
In implementing the top-down approach, one first identifies the experimental behavior(s) one wishes to capture with the mathematical model. One benefit of the top-down approach is that it begins with the construction of a high-level mathematical model, so the approach may be readily implemented even when existing biological data is sparse (which is often the case with biological systems). To reiterate, in the case of scFv folding, the model must display BiP and PDI dependence in secreted scFv production and increased scFv production when both BiP and PDI are overexpressed than when either is overexpressed independently. These behaviors are captured in a key set of experimental data from Xu et al. (29), reproduced in Fig. 2 A.

FIGURE 2.

(A) Experimental scFv secretion data reproduced from Xu et al. (29). “O.” refers to “overexpressed”. Overexpression levels are provided in the reference. (B) In silico reproduction of this data, using the fully detailed mathematical model. (C) 50 h time points for all model simulations normalized to the respective 50 h experimental time points in Fig. 2 A (e.g., the 50 h O.BiP model time points are divided by the experimental 50 h O.BiP data point). The similarly-scaled experimental 50 h time points to which this data is compared are represented by the horizontal dashed line of value one. Thus, models that have normalized 50 h time points close to one for all BiP and PDI expression levels are most successful at reproducing the experimental data. Scaled error bars for the experimental 50 h data point with the highest standard deviation (0.2 relative units for O.PDI) are provided on the plot (O.BiP and O.BiP+PDI had standard deviations of 0.05 relative units). BiP and PDI overexpression levels and the unscaled simulation and experimental values used to produce this plot are provided in Table 1.

Establishing desired model details

Next, one mines the experimental literature for known and hypothesized interactions and mechanistic details desired for inclusion in the final mechanistic model. In doing so, the model's scope is established. Since the scFv folding model was to be used for evaluating the validity of the hypothesis of Xu et al. (29), it was to include BiP assisting in unfolded scFv (UscFv; a detailed key to nomenclature, including definitions for prefixes such as the U-, used in this work is provided in Table 2) translocation into the ER and PDI catalyzing protein folding. Other details desired for inclusion in the model were those associated with transcription, translation, and post-translational translocation of the scFv; UscFv, BiP, and PDI binding states; and relative UscFv folding/misfolding rates in each of those binding states. Inclusion of these details would also require three compartments: the nucleus, cytoplasm, and ER.

TABLE 2.

Definitions for all states found in the equations and in Figs. 3 and 6, recurring prefixes used in state names, subscripts for SscFv production in the equations, all icons found in the aforementioned figures, and recurring prefixes and suffixes used in parameter subscript labels

State name	State definition
BiP	BiP (binding protein).
BiP·PDI·UP	BiP- and PDI (protein disulfide isomerase)-bound generic unfolded protein.
BiP·PDI·UscFv	BiP- and PDI-bound unfolded scFv (single-chain 4-4-20 antibody fragment) protein.
BiP·UP	BiP-bound generic unfolded protein.
BiP·UscFv	BiP-bound unfolded scFv protein.
Cytoplasmic scFv mRNA	Cytoplasmic scFv mRNA.
Cytoplasmic UscFv	Cytoplasmic unfolded scFv protein.
MscFv	Misfolded scFv protein.
Nuclear scFv mRNA	Nuclear scFv mRNA.
PDI	PDI.
PDI·UP	PDI-bound generic unfolded protein.
PDI·UscFv	PDI-bound unfolded scFv protein.
ptt'ing UscFv	Post-translational translocating unfolded scFv protein.
scFv mRNA	scFv mRNA.
SscFv	Secreted scFv.
UscFv	Unfolded scFv protein.
UP	Generic unfolded protein within the ER, excluding scFv.
State prefix	Significance
M-	Misfolded.
S-	Secreted.
U-	Unfolded.
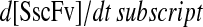	Subscript definition
-nominal	No BiP or PDI overexpressed.
-O.BiP	BiP overexpressed.
-O.BiP+PDI	Both BiP and PDI overexpressed.
-O.PDI	PDI overexpressed.
-SS	Steady-state.
Icon description	Icon definition
Double-headed arrow	Indicates reversible reaction.
k–	Rate constant defined in Table 3.
Multiplication sign	Indicates an additional reactant in a second-order reaction.
Orange sunburst	BiP.
Pink/turquoise banana-shape	PDI acting as a foldase.
Pink/turquoise tooth-shape	PDI acting as a chaperone.
Plus sign	Indicates additional products of a reaction.
Red box containing text “VscFv”	scFv mRNA input.
Red curved line bundle	Folded scFv destined for secretion (SscFv).
Red oval containing text	scFv state defined by text.
Red sun containing text “deg.”	Indicates degradation of the reactant.
Single-headed arrow	Indicates irreversible reaction.
Turquoise oval containing text	Generic unfolded protein state defined by text.
Rate constant subscript prefix/suffix	Significance
-b	Specific to a three-state model.
-bit	BiP-independent translocation into the ER.
(-)d	Degradation.
m-	Misfolding rate.
r-	Reverse reaction rate.

Constructing a backbone model

With the scope of the detailed mechanistic model established, one then identifies the components necessary for construction of a backbone model, the bare minimum that is required for capturing the desired experimental behaviors. This step may be facilitated by searching the literature for elements (modules, motifs, and interactions) known to be responsible for producing certain biological behaviors for homologies to the system at hand. If one or more plausible matches is/are found, the corresponding element(s) may be applied to the backbone model structure. Experimental validation of the utilization of such elements—notably, combinations thereof in gene regulatory networks—in mathematical model construction to represent and predict biological behavior was performed by Guido et al. (30). If no known modules, motifs, or interactions are appropriate for use in the backbone model, the modeler will need to identify such underlying mechanisms independently.

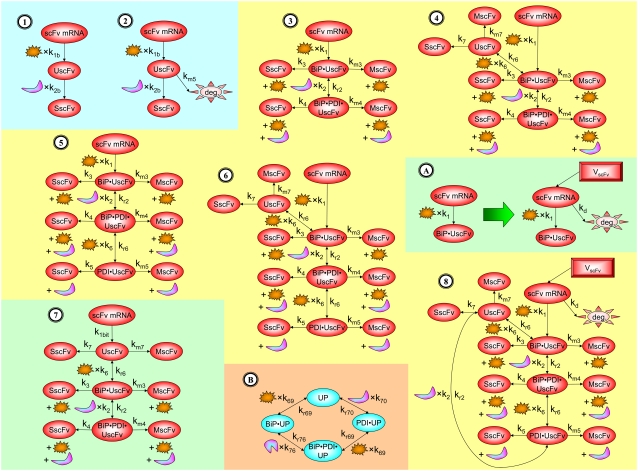
In the scFv folding example, there was no precedent for the experimentally observed scFv folding dependencies, so the latter approach was undertaken. Guidance in constructing a backbone model structure for this system originated from the hypothesis of Xu et al. (29). It was possible to capture this hypothesis most fundamentally in a two-state mathematical model, where UscFv entered the ER in a second-order, BiP-dependent step, and the UscFv folded in preparation for secretion (SscFv) in a second-order, PDI-dependent step. This reaction scheme is illustrated as Model 1 in Fig. 3, and its parameters are described and assigned values in Table 3.

FIGURE 3.

Schematics for the developmental models and their modifications. Models 1 and 2 were used in backbone model development. Models 3–6 represent the original four permutations of models containing explicit BiP and PDI binding and release. When Modification A was applied to these models, they were designated Models 3*−6*, which are not schematized here. Model 7 represents a binding permutation model where the branched dependency-degradation competition motif for BiP was introduced by eliminating BiP's role in post-translational translocation. Model 8 depicts a final permutation where UscFv may freely move between BiP and PDI binding states and has Modification A implemented in it. The figure legend that defines species, prefixes, icons, and rate constant subscript prefixes and suffixes is in Table 2. Parameter definitions and values are in Table 3.

TABLE 3.

Parameters definitions, values, and references

Developing models parameter	Detailed model parameters	Definition	Value	Units	Reference(s)
k1	N/A	Effective second-order rate constant for scFv translation and translocation into the ER by bound BiP.	1.2 × 10−8		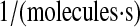(32,84,86)
k1b	N/A	Effective second-order rate constant for scFv translation and BiP-catalyzed translocation into the ER.	1.2 × 10−8		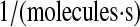(32,84,86)
k1bit	N/A	Effective first-order rate constant for scFv translation and BiP-independent translocation into the ER.	4.0 × 10−3		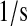(32,84,86)
k2	k61	PDI-UscFv binding rate.	2.3 × 10−7		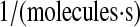(71–73)
k2b	N/A	PDI-catalyzed UscFv folding rate.	1.6 × 10−7		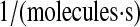(36,67,68,71–73)
kr2	kr61	PDI-UscFv release rate.	6.0 × 10−4		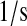(71–73)
k3	k63	BiP·UscFv folding rate.	7.0 × 10−3		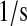(36,67,68)
kd	k3d	Cytoplasmic scFv mRNA degradation rate.	2.6 × 10−3		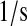(85)
km3	km63	BiP·UscFv misfolding rate.	3.9 × 10−2		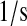(36,67,68)
k4	k65	BiP·PDI·UscFv folding rate.	3.4		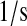(36,67,68)
km4	km65	BiP·PDI·UscFv misfolding rate.	3.9 × 10−2		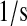(36,67,68)
k5	k66	PDI·UscFv folding rate.	8.5 × 10−2		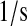(36,67,68)
km5	km66	PDI·UscFv misfolding rate.	3.4 × 10−1		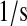(36,67,68)
k6	k60	BiP-UscFv binding rate.	1.2 × 10−8		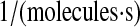(86)
kr6	kr60	BiP-UscFv release rate.	1.0 × 10−1		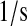(86,87)
k7	k64	UscFv folding rate.	7.0 × 10−3		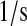(36,67,68)
km7	km64	UscFv misfolding rate.	3.4 × 10−1		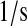(36,67,68)
N/A	k55	scFv mRNA nuclear translocation rate.	1.8		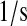(74–80)
N/A	k56	scFv translation rate.	6.2 × 10−2		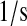(81,82)
N/A	k58	UscFv trafficking rate to the translocon.	2.2 × 10−9		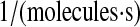(83)
N/A	k59	UscFv posttranslational translocation rate.	9.0 × 10−1		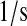(84)
N/A	k69	BiP-unfolded protein binding rate.	8.8 × 10−2		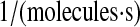(S. Hildebrandt, D. Raden, A. S. Robinson, and F. J. Doyle III, unpublished)
N/A	kr69	BiP-unfolded protein release rate.	1.0 × 10−1		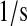(S. Hildebrandt, D. Raden, A. S. Robinson, and F. J. Doyle III, unpublished)
N/A	k70	PDI-unfolded protein binding rate.	2.3 × 10−7		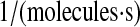(71–73)
N/A	kr70	PDI-unfolded protein release rate.	6.0 × 10−4		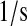(71–73)
N/A	k76	PDI-unfolded protein binding rate as a chaperone.	2.3 × 10−7		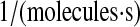(71–73)
N/A	kr76	PDI-unfolded protein release rate as a chaperone.	3.2 × 10−1		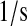(41,71–73)
N/A	k57	Cytoplasmic UscFv degradation rate.	4.0 × 10−4		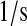(69)

When developing a backbone (or any mathematical) model, enumerating all assumptions and simplifications is an effective means of systematizing the process. If and when a model fails to capture the experimental behaviors, assumptions and simplifications may be altered or relaxed in a methodical fashion. Only when all of these potential alterations and relaxations have been exhausted should the insight gained from the unsuccessful modeling attempt be applied toward formulating a new model. The assumptions and simplifications used in construction of the scFv folding backbone model are listed below and explained in the following paragraph.

1. All reactions were modeled using lowest-order, deterministic kinetics.

2. No scFv protein of any form was initially present in the system.

3. Unfolded protein entry to the ER was assumed to have a first-order dependency on BiP.

4. Folding/secretion was assumed to have a first-order dependency on PDI.

5. Pools of 1 × 10³ scFv mRNAs, 3.37 × 10⁵ free BiPs, and 5.24 × 10⁵ free PDIs participated in their respective reactions, as described in the reaction equations and illustrated in Fig. 3, and were not consumed.

6. No scFv misfolding or degradation reactions were included.

7. All properly folded scFv was assumed to proceed to the Golgi and ultimately be secreted.

8. All compartments were assumed to be well mixed.

Assumptions 1 and 7 will be common to all mathematical models presented in this article. The second assumption was meant to mimic the experimental conditions under which the invalidation data were taken, where transfer to galactose-containing medium at time = 0 initiated scFv production. Assumptions 3 and 4 were meant to capture in basic form the central concepts of the hypothesis of Xu et al. (29), and the first-order dependencies arose from Assumption 1. Assumption 5 arose from literature-derived values for these concentrations (31–33), and embedded within it was the further, critical assumption that all BiP and PDI was available for reaction with scFv, and none was sequestered away by competing reactions/species. Assumption 6 was made for simplicity, even though it is well documented that proteins terminally misfold and are removed from the ER via ER-associated degradation (34). Assumption 7 was for pure model simplification reasons. Assumption 8 was also made for simplification, and although preliminary work exists suggesting that BiP is not homogeneously distributed throughout the ER (35), Fig. 4 A suggests these effects will not alter BiP dependency results presented here. The reaction equations follow. State definitions are provided in Table 2, rate constant definitions and values are provided in Table 3, and rate constant derivations are provided in the Appendix.

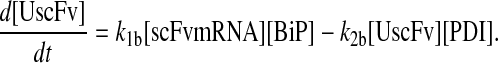(1)

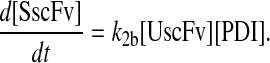(2)

All mathematical model simulations in this work were performed using MATLAB Simulink using the ode15s solver (The MathWorks, Natick, MA). Fig. 2 B, which contains trajectories from the fully detailed model, exemplifies typical simulation trajectories for all mathematical models from in silico runs intended to replicate the experimental results of Xu et al. (29) in Fig. 2 A. All model trajectories displayed the observed linear behavior, so that a concisely effective method for evaluating model performance in replicating the experimental trajectories could be developed by comparing 50 h time point values, as demonstrated in Fig. 2 C. These values, listed in Table 1, were scaled by the experimental data points to facilitate this simulation-experiment comparison. The table also lists the multiples by which BiP and PDI were overexpressed to yield the model results that most closely matched experiment, all of which are within an order-of-magnitude of the experimental values listed in the table, except for Model 8. Error bars from the experimental data point with the largest standard deviation (O.PDI at 50 h) were also included in the figure. Model numbers in the figure correspond to their assignments in Fig. 3 and the text, and asterisks indicate models that have been modified with Modification A, which is also schematized in Fig. 3.

FIGURE 4.

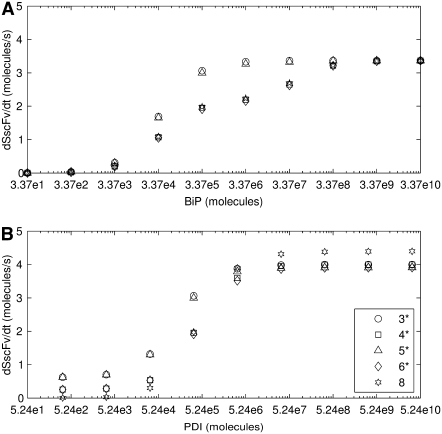
Curves depicting the Michaelis-Menten-like dependencies of steady-state SscFv production on BiP (A) and PDI (B) levels for Models 3*−6* and 8.

TABLE 1.

Relative BiP and PDI overexpression levels used to produce the corresponding relative SscFv levels 50 h into the in silico experiments (columns 2–14), which were normalized to provide the scaled relative SscFv level data found in Fig. 2 C

Model	1	2	3	3*	4	4*	5	5*	6	6*	7	8	Detailed	Experiment
Relative overexpression level
BiP	2	1.5	1.5	40	1.5	40	1.5	20	2	40	3	100	2	3–12
PDI	2	2	10	40	10	40	10	80	10	40	20	15	4	6–8
Relative scFv level
Nominal	1.8	1.1	1.5	1.4	0.97	0.90	1.4	1.4	0.97	0.90	1.5	0.87	0.99	1.0
O.BiP	3.7	1.7	2.2	2.3	1.5	1.6	2.2	2.2	2.0	1.7	2.1	1.3	1.5	1.2 ± 0.1
O.PDI	1.8	1.8	1.8	1.8	1.8	1.8	1.8	1.8	1.8	1.8	1.8	1.8	1.9	1.6 ± 0.4
O.BiP + PDI	3.7	2.8	2.8	3.0	2.8	3.0	2.8	2.9	3.7	3.0	3.1	2.9	2.7	3.4 ± 0.2

Experimental values of the BiP and PDI overexpression levels and the relative SscFv levels to which the data in Fig. 2 C were normalized are also included in the final column for comparison. Key: O., overexpressed; O.BiP, overexpressed BiP; O.PDI, overexpressed PDI; O.BiP+PDI, overexpressed BiP and PDI; Nominal, no overexpression.

One benefit of developing a backbone model is it generally facilitates analysis by eliminating the clutter associated with more detailed models. For example, with such a simple model for scFv folding, it was possible to derive analytically the steady-state production of SscFv from the model equations and evaluate its dependencies on BiP and PDI concentrations directly. Steady state was achieved within the first time step of the simulations, 1 × 10³ s, which is consistent with experiments that show pro-scFv (UscFv) reaching steady-state levels within 10 and 60 min of the initiation of scFv production. Consequently, the steady-state analysis was appropriate. For this most basic mathematical model, the steady-state SscFv production rate (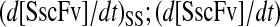 suffixes defined in Table 2), which was derived by expressing the SscFv production rate in terms of system parameters after having set the other states' time dependencies to zero, was

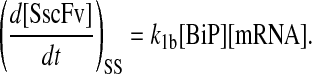(3)

This equation demonstrates that SscFv production was totally independent of PDI levels in this mathematical model. scFv flux through the system was constant and determined at the ER-entry step, modulated by BiP. Increasing/decreasing PDI levels would only decrease/increase, respectively, UscFv levels, but the flux would remain the same. As a result, this model was incapable of reproducing the experimentally observed scFv folding dependency data. These results indicated a fault in the backbone model formulation.

As previously discussed, modifications to the model should be made by systematically altering or relaxing assumptions and simplifications before discarding it completely. Assumption 6 was the first to be altered in the scFv folding model, as it was arguably one of the weakest. This alteration was justified biologically: in vivo, if a protein is not successfully folded after some time, it proceeds down the ER-associated degradation pathway, where it is retro-translocated from the ER to the cytoplasm and degraded (reviewed in (34)). Hence, protein folding may be viewed as a competition between achieving a properly folded state or a terminally misfolded state.

To include this detail in the backbone model, a generic degradation pathway was added to the UscFv state, illustrated as Model 2 in Fig. 3. Thus, Assumption 6 from the previous model was replaced with

• 6. UscFv misfolds/degrades in a first-order reaction

and all other assumptions remained the same. The corresponding model equations and steady-state SscFv production rate follow.

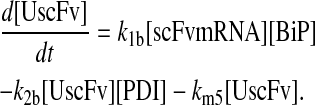(4)

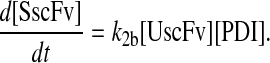(5)

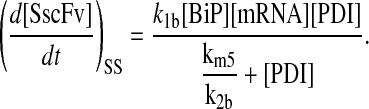(6)

From the steady-state SscFv production rate, it may be seen that the degradation pathway introduced PDI dependency, the magnitude of which varies depending on the ratio of the degradation to folding rate constants. The model predicts that as the assisted folding rate constant dominates over degradation, PDI dependence diminishes. For the literature-derived parameter values used in the model (see Appendix for all parameter derivations), there was sufficient PDI dependence to capture both of the two key experimental invalidation behaviors: scFv secretion showed a similar BiP- and PDI-dependency and was enhanced when BiP and PDI were simultaneously—as opposed to individually—overexpressed (Fig. 2 C). Based on this significant improvement in model performance, the first in a series of three requirements for the ultimate detailed model to reproduce the experimental data was formulated:

Requirement No. 1

Competition between degradation/misfolding and accelerated folding by PDI is necessary for PDI dependence.

Thus, with the addition of UscFv degradation, a successful backbone model was constructed, and the hypothesized folding process remained viable.

Further model development

Upon formulation of a successful backbone model, the top-down approach to mechanistic modeling proceeds with the gradual supplementation of the model with mechanistic detail until the desired level of detail, defined when the model's scope was being elaborated, has been reached. The order in which these details are added and the quantities added at a time will depend upon the model and its intended use and will consequently require the discretion of the modeler. One consideration to make when proceeding, though, is that one purpose of incrementally appending the model is to enable the modeler to observe and evaluate the discrete effects produced by each alteration. Consequently, it would be desirable to design each increment so as to maximize the insight gained from implementing it. This process is demonstrated with the scFv folding model below.

For the scFv folding model, further translocation or folding details could not be reasonably added without first including explicit BiP and PDI binding and release of the UscFv: it was desired to have BiP bind the UscFv at the translocon for entry to the ER, at which point BiP could theoretically release it, or PDI could also bind the BiP·UscFv complex. It has been hypothesized that PDI is largely incapable of binding unfolded protein on its own in its foldase capacity, and BiP is responsible for making unfolded protein accessible for PDI binding (36), thus increasing the extent to which BiP and PDI cooperate in the protein folding process. The model was later used to assess this hypothesis. UscFv could also transition between the BiP·PDI·UscFv and PDI·UscFv states with the respective release or binding of BiP. True to the top-down modeling approach, these binding states were added incrementally to evaluate their effects on the ability of the model to reproduce the experimentally observed BiP and PDI scFv folding dependencies. The resulting four model permutations are schematized as Models 3–6 in Fig. 3. Parameter descriptions and values are provided in Table 3.

With the model constructs established, it was then necessary to assign the folding and misfolding rates associated with each of the binding states. Derivation and references for the actual rate values are presented in the Appendix, but qualitative descriptions and logic are presented here. It is thought that chaperone proteins such as BiP do not actually promote faster protein folding but rather protect the unfolded protein against misfolding by binding hydrophobic regions (reviewed in (37)). Hence, a BiP-bound unfolded protein would be expected to fold at approximately the same rate as an unbound one, however its effective misfolding rate would be slower than the unbound one. A PDI-bound unfolded protein would be expected to have a faster folding rate but a similar misfolding rate (ignoring PDI's proposed chaperone behavior (38–40), reviewed in (41)) to an unbound one, and a BiP- and PDI-bound unfolded protein would be expected to have both a faster folding rate and a slower misfolding rate. Assumptions and simplifications for the four model permutations follow:

1. All reactions were modeled using lowest-order, deterministic kinetics.

2. No scFv protein of any form was initially present in the system.

3. Unfolded protein entry to the ER was assumed to have a first-order dependency on BiP.

4. Folding/secretion was assumed to be first-order and faster for BiP-PDI-bound and PDI-bound than BiP-bound and unbound UscFv.

5. A pool of 1 × 10³ scFv mRNAs participated in the lumenal UscFv production reaction but was not consumed.

6. 3.37 × 10⁵ free BiPs and 5.24 × 10⁵ free PDIs were available for UscFv binding and were consumed in the binding reactions and regenerated upon release.

7. All properly folded scFv was assumed to proceed to the Golgi and ultimately be secreted.

8. Misfolding/degradation was assumed to be first-order and equivalent for both BiP-PDI-bound BiP-bound UscFv but faster for both unbound and PDI-bound UscFv.

9. BiP binding was required for PDI binding to occur.

10. Multiple binding by BiP and PDI was ignored for simplicity, and folding/misfolding rates were based on overall folding/misfolding rates, as derived in the Appendix.

11. All compartments were assumed to be well mixed.

Due to the increasing size and number of models, their ODEs have been relegated to the Appendix, though it must be noted that the initial step of importing UscFv to the ER (BiP·UscFv production term) was always represented by k₁[BiP][scFv mRNA] in the BiP·UscFv equations, with k₁ representing the effective second-order scFv translation and translocation rate into the ER. Analytical solutions for the model permutations' steady-state SscFv production rates are presented below (Model 3, Eq. 7; Model 4, Eq. 8; Model 5, Eq. 9; and Model 6, Eq. 10). In deriving these solutions, a further assumption was employed to make the algebra tenable: unbound BiP and PDI were sufficiently abundant over UscFv, so their concentrations were not altered by binding UscFv. This assumption held during simulations, where BiP and PDI concentrations remained 3.37 × 10⁵ and 5.24 × 10⁵ molecules, respectively, while bound species never exceeded 100 molecules.

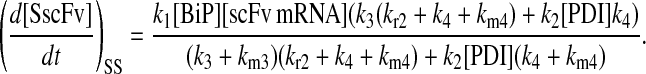(7)

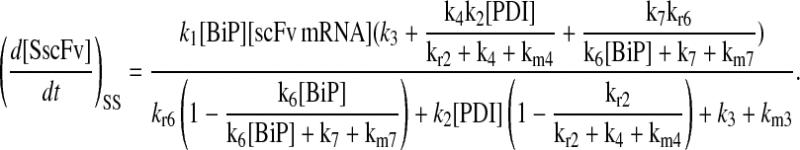(8)

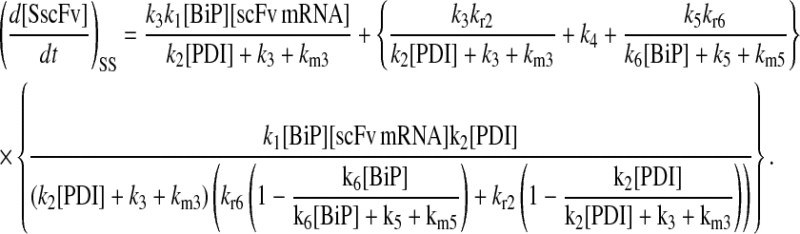(9)

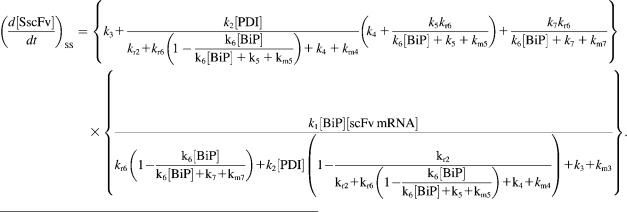(10)

As may be observed in these equations, the aforementioned BiP·UscFv production term, k₁[BiP][scFv mRNA], appears in the numerator in each of the model permutations' expression for steady-state SscFv production, indicating that production in each permutation was largely linearly dependent on BiP concentration. On the other hand, production dependence on PDI concentration assumed a Michaelis-Menten-like form. The linear BiP dependence overpowered PDI's contribution for a range of BiP and PDI concentrations (not shown), so to reproduce the experimental dependencies, it was necessary to overexpress PDI an order-of-magnitude times more than BiP (Fig. 2 C, Table 1). To modify this behavior, the assumptions and simplifications that went into deriving the models were reevaluated for alterations.

From the backbone model development, it was observed that including a degradation pathway to compete with a species-dependent pathway instilled the Michaelis-Menten-like dependence on PDI in the steady-state SscFv production rate expression. This branched dependency-degradation competition motif could then be applied to BiP's role in translocation, so steady-state SscFv production would have a Michaelis-Menten-like dependence on both BiP and PDI. Since BiP catalyzing translocation of UscFv into the ER was the dependency step, a degradation step, such as cytoplasmic scFv mRNA degradation, was necessary. A schematic representation of this modification is presented in Fig. 3 (Modification A); it is shown implemented in Model 8; and Models 3–6 with this modification will be denoted with an asterisk as Models 3*−6*. This theoretical alteration translated into the alteration of Assumption 5, whose revised version appears below:

• 5. scFv transcription was modeled by a step input of scFv mRNA that could be consumed by cytoplasmic degradation and lumped translation/translocation into the ER to yield 1 × 10³ scFv mRNA during steady-state SscFv production.

The fully modified differential equations for each model permutation appear in the Appendix; however, it is instructive to analyze the differential equation for scFv mRNA production—common to all model permutations—which resulted from the revised Assumption 5:

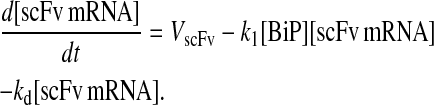(11)

When this equation is analyzed at the steady state,

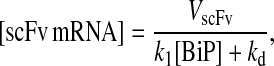(12)

a steady-state BiP·UscFv production term (i.e., the BiP-dependent translocation rate) for the altered models may be derived: 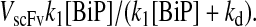This term, with its distinct Michaelis-Menten-like dependence on BiP, supplants k₁[BiP][scFv mRNA] in the previous models' expressions for steady-state SscFv production (Eqs. 7–8), so that both BiP and PDI have similar concentration dependencies. The similar steady-state BiP and PDI SscFv production value dependencies shown in Fig. 4 and the comparable BiP and PDI relative overexpression levels required to reproduce the experimentally observed BiP and PDI dependencies in Fig. 2 provided in Table 1 reinforce this result with simulation data. Consequently, an important biological structural motif has been identified, and a second requirement for the scFv folding model is claimed:

Requirement No. 2

Assuming post-translational translocation is BiP-dependent, competition between the translocation step and cytoplasmic degradation of the translocating species is required to make BiP and PDI expression level dependencies comparable.

It may also be noted that another way to introduce a branched dependency-degradation competition motif for BiP in the scFv folding model is by eliminating BiP's participation in post-translational translocation of the UscFv to the ER (Model 7 in Fig. 3). In this case, UscFv enters the ER unbound, where it may degrade by folding or misfolding (degradation branch of the motif) before being reversibly bound by BiP (dependency branch). The steady-state BiP·UscFv production term in this case, 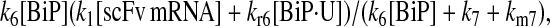demonstrates Michaelis-Menten-like dependency, so that the expression for steady-state SscFv production thus shows such a dependence on both BiP and PDI:

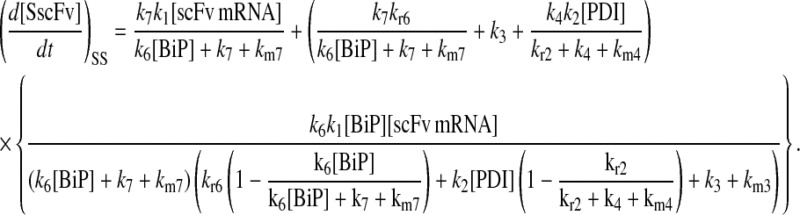(13)

From this result, one may conclude that the hypothesis of Xu et al. (29) is not exclusive in possessing the ability to reproduce experimentally observed BiP and PDI dependencies in scFv folding, though the BiP-independent translocation model is inconsistent with experimental evidence of BiP-scFv associations (42).

In returning to the hypothesis-based model development, there were four permutations of the model iteration that included explicit BiP and PDI binding details that were capable, to some extent, of capturing the experimentally observed BiP and PDI dependencies. One final permutation was established to evaluate the hypothesis that PDI requires BiP-bound UscFv for binding as a foldase, as previously described. This final permutation, which represented the alternative case where PDI may bind UscFv directly, is represented by Model 8 in Fig. 3 and already has Modification A implemented in it.

While the analytical solution for steady-state SscFv production in this final model permutation is fairly complex (see Appendix), it does exhibit Michaelis-Menten-like dependencies on both BiP and PDI. However, it deviated from experiment by an order of magnitude in the amount of BiP and PDI overexpression (Table 1) it required to reproduce the data in Fig. 2 A. A further means to evaluate model performance would be necessary to draw more definitive conclusions on this model permutation and the hypothesis that generated it.

Up to now, focus has been placed on evaluating the model permutations' ability to reproduce BiP and PDI dependencies. The other key experimental behavior desired for a successful mathematical model to exhibit was enhanced SscFv production by simultaneously—over independently—overexpressed BiP and PDI. The unscaled results recorded in Table 1 show that this behavior was in fact displayed by all of the models.

Xu et al. (29) proposed that the enhanced SscFv production from simultaneous BiP and PDI overexpression resulted from cooperativity, or synergistic effects, between the two species in the folding process. In the context of their hypothesized model, where BiP and PDI act serially upon scFv, synergy is mathematically defined as a steady-state SscFv production rate when both BiP and PDI are overexpressed (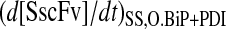) that is greater than the product of the production rates when each of the species is overexpressed independently (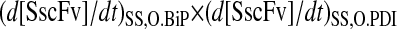) using the same relative overexpression levels. When these rates are normalized by the production rate when neither species is overexpressed (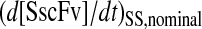), the following ratio

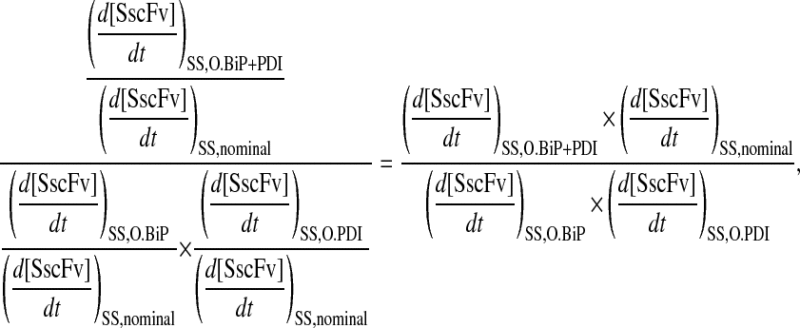(14)

indicates serial synergy for values >1. An experimental synergy value was obtained by evaluating the slopes for each BiP/PDI overexpression level data set in Fig. 2 A and implementing them in Eq. 14 as the respective steady-state SscFv production rates. The value, 1.9, supports the proposal that the experimental data reflects synergistic behavior between BiP and PDI.

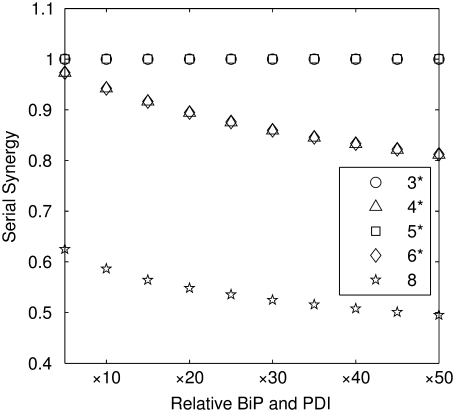
The models were also tested for their ability to display serial synergy, and results are plotted in Fig. 5. The synergy values in the plot are for BiP and PDI overexpression levels of the same relative amounts (e.g., both BiP and PDI were overexpressed 10-fold, 20-fold, etc.), though similar trends were observed for all other calculated permutations in BiP and PDI levels in the 10- to 100-fold overexpression range (e.g., BiP overexpressed 10-fold and PDI overexpressed 20-fold, BiP overexpressed 20-fold, and PDI overexpressed 10-fold, etc.). From the plot, it may be observed that none of the models exhibited serial synergy, indicating the likelihood of more complex interactions between BiP and PDI in the scFv folding process than hypothesized by Xu et al. (29), which may include the involvement of other species, such as co-chaperones, and/or PDI's chaperone activity.

FIGURE 5.

Curves depicting the serial synergy values (serial synergy defined by Eq. 14) calculated for Models 3*−6* and 8 over a variety of BiP and PDI overexpression levels. In this plot, “Relative BiP and PDI” indicates the factor by which both BiP and PDI were overexpressed for that particular value. Values for further permutations in relative BiP and PDI overexpression were calculated, but they displayed similar relative behavior and are not included on this plot for simplicity.

At this stage of model development, there was one final technical issue to be addressed pertaining to the biological validity of Assumption 6: 3.37 × 10⁵ free BiPs and 5.24 × 10⁵ free PDIs were available for UscFv binding and were consumed in the binding reactions and regenerated upon release. BiP has many roles in the ER (most reviewed in (37); karyogomy function described in (43)) and, consequently, interacts with many proteins there, and PDI accelerates the folding of any disulfide bond-containing species. To better represent this biological sequestration of BiP and PDI from UscFv, a pool of total (non-scFv) unfolded protein was introduced to which BiP and PDI could bind. This modification is schematized as Modification B in Fig. 3. Upon implementation of Modification B, one also introduces a useful means of tuning SscFv production rates.

That is, as available BiP and PDI levels are altered through introduction of this pool of generic unfolded protein, SscFv production dependencies are also altered per the BiP and PDI dependency curves in Fig. 4, as long as free BiP and PDI are available in excess (the assumption under which the dependency curves were generated). If either BiP or PDI concentrations approach or fall below UscFv levels, SscFv production dependence will be dominated by the limiting species—behavior that is not captured by the curves. To control the amount of BiP and PDI sequestered away by generic unfolded protein, the amount of generic unfolded protein present and/or BiP and PDI's affinities for unfolded protein may be altered. In this work, the amount of generic unfolded protein was kept constant at 1.5 × 10⁵, while the affinities were altered, so that an excess of 1.87 × 10⁵ unbound BiP and 3.74 × 10⁵ unbound PDI remained at steady state.

Completion of the fully detailed model

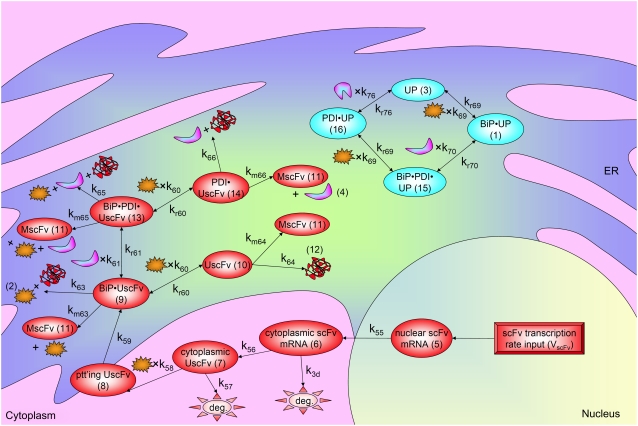
Even though all model permutations were similarly capable of capturing desired BiP and PDI dependencies and enhanced scFv production when both BiP and PDI were overexpressed, Model 6* was selected for further development, because its mechanistic structure most resembled the desired fully detailed model structure. In transforming Model 6* to the fully detailed model, details pertaining to scFv transcription and translation and an extra step to the post-translational translocation process were added (Fig. 6; legend in Table 2) with no effect on model performance with regard to capturing BiP and PDI dependencies and enhanced scFv production with BiP and PDI overexpression (Fig. 2 C). Additionally, it should be noted that in the fully detailed model, BiP-dependent translocation competes with cytoplasmic unfolded scFv rather than scFv mRNA degradation, but Michaelis-Menten-like dependence on BiP is retained because the branched dependency-degradation competition motif and Requirement No. 2 are conserved. The list of model assumptions and simplifications for the fully detailed model follows. System ODEs are included in the Appendix. Parameters, some of which were renamed from the simpler models, are listed in Table 3.

1. All reactions were modeled using lowest-order, deterministic kinetics.

2. No scFv transcript or protein of any form was initially present in the system.

3. BiP binds UscFv at the translocon in a second-order reaction, and UscFv enters in a first-order reaction step.

4. Folding/secretion was assumed be first-order and faster for BiP-PDI-bound and PDI-bound than BiP-bound and unbound UscFv.

5. scFv transcription was a step input.

6. 3.37 × 10⁵ total BiP and 5.24 × 10⁵ total PDI were available for UscFv and general unfolded protein binding and were consumed in the binding reactions and regenerated upon release.

7. All properly folded scFv was assumed to proceed to the Golgi and ultimately be secreted.

8. Misfolding/degradation was assumed be first-order and equivalent for both BiP-PDI-bound BiP-bound UscFv but faster for both unbound and PDI-bound UscFv.

9. BiP binding was required for PDI binding to occur.

10. Multiple binding by BiP and PDI was ignored for simplicity, and folding/misfolding rates were based on overall folding/misfolding rates, as derived in the Appendix.

11. Cytoplasmic species (scFv mRNA and UscFv) degraded.

12. All compartments were assumed to be well mixed.

FIGURE 6.

Schematic for the fully detailed scFv folding model. State numbers are provided for comparison with equations in the code. The figure legend that defines species, prefixes, icons, and rate constant subscript prefixes and suffixes is in Table 2. Parameter definitions and values are provided in Table 3.

RESULTS

Having developed a detailed mechanistic model using the top-down approach, analysis could proceed. The top-down model development process enables the more efficient and effective application of analytical methods, reviewed in Aldridge et al. (10), due to the insights one has attained in incrementally constructing the model. The insights gained in the scFv folding model development guided the prediction and evaluation of parameter dependencies of SscFv production. Development of the backbone model for scFv folding identified the core processes required for reproduction of experimental behaviors: translocation by BiP and branched folding by PDI that competed with degradation. The added details only elaborated, but did not alter, these basic processes. Consequently, predictions could be made for large groups of parameters within the processes as to how they would affect SscFv production.

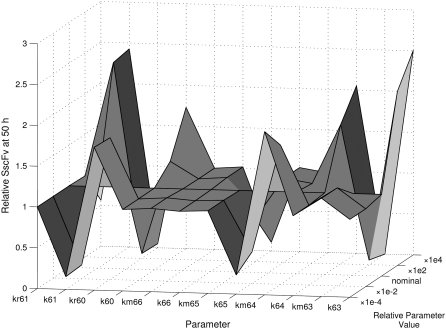
Starting with the PDI folding/degradation competition process, it would follow that changes in parameters associated with folding would similarly affect SscFv production, and changes in parameters associated with misfolding would inversely affect production. Thus, increasing folding rates and decreasing misfolding rates would be expected to increase SscFv production. Additionally, adjusting BiP- and PDI-UscFv binding/ dissociation rates so as to increase the production of the fastest folding, slowest misfolding UscFv binding state (BiP·PDI·UscFv) over slower folding and faster misfolding states would also increase SscFv production. Indeed, these predictions were verified when the parameter alterations were implemented in the mathematical model (see Fig. 7, which shows the relative SscFv dependencies to the various folding, misfolding, binding, and dissociation rates). Relative overall misfolded scFv production dependencies were simply the inverse of these results (not shown).

FIGURE 7.

Relative SscFv production dependency on UscFv folding and misfolding and BiP- and PDI-UscFv binding/release rate parameters, as defined in Table 3 and depicted in Fig. 6. Generally, parameter numbers with a corresponding r are binding rates, and the r rates are dissociation rates; parameter numbers with a corresponding m are folding rates, and the m rates are misfolding rates (see Table 2). SscFv levels were measured at 50 h.

Similar predictions and verifications could be performed for parameter dependencies in the BiP translocation process. In a logical fashion, it could be anticipated that increases/decreases in parameters associated with transcription and translation would result in increased/decreased SscFv production (verification not shown). However, there was one parameter that proved to be critical to model performance: the rate at which the translocation complex formed, which included UscFv trafficking to the translocon and BiP binding to it in a second-order reaction. Reasoning predicts that low values of this parameter would limit the translocation process, so SscFv production would be highly BiP-dependent. High values of this parameter would flood the ER with UscFv, so SscFv production would become folding—hence, PDI—limited. Consequently, this parameter could potentially dictate relative SscFv dependencies to BiP and PDI levels.

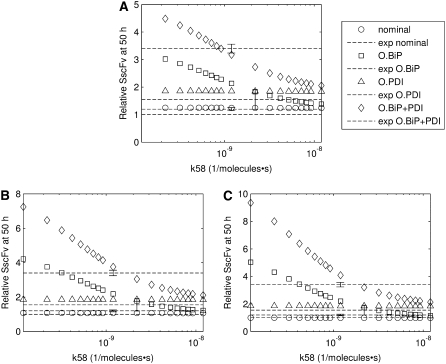
To verify this prediction, SscFv levels at 50 h were plotted against the experimental measurements for a range of translocation complex formation rates for various BiP and PDI overexpression levels, as shown in Fig. 8. In the plots it may be observed that, indeed, there is a gradual transition from total BiP dependence to total PDI dependence by SscFv production as the translocation rate increases. It is only within an intermediate range, at ∼2.2 × 10⁻⁹ 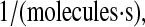that BiP and PDI dependencies are comparable. (The literature-derived value, 1.2 × 10⁻⁸ 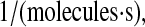used in model development falls within this range.) Since the value of this parameter is so critical for reproducing experimentally observed BiP and PDI dependencies, it becomes one final model requirement:

FIGURE 8.

Plots demonstrating SscFv production dependency on the rate at which cytoplasmic UscFv was trafficked to the translocon (k₅₈) for double BiP and PDI (A), triple BiP and PDI (B), and quadruple BiP and PDI (C) overexpression levels. SscFv levels were measured at 50 h and compared to the experimental values (dashed lines). Error bars for the experimental data are provided on one experimental data point for ease of interpretation but apply to all: O.BiP+PDI and O.BiP error bars are found at 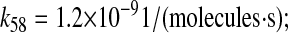O.PDI, at 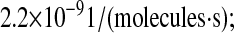and nominal, at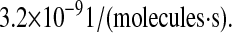

Requirement No. 3

The rate constant associated with the second-order BiP-dependent reaction step in translocation must not be so low compared to PDI-dependent folding rates that it excessively amplifies BiP over PDI expression level dependency. It also should not be so high that it eliminates BiP dependency altogether and makes the system PDI folding-dependent.

It is important to note that Fig. 8 and Requirement No. #3 suggest that relative secreted scFv dependencies on BiP and PDI concentrations are not robust to perturbations in the translocation rate constant. Robustness has been hypothesized to be a key feature of biological regulatory systems, which contain control elements responsible for conferring robustness on these systems (44,45). The isolated scFv folding model presented here lacks any such elements, so its consequent lack of robustness is not surprising. Biologically, the protein folding process is regulated by the unfolded protein response (reviewed in (46,47)), which does contain control elements that increase protein folding robustness. Prill et al. (20) has also hypothesized robustness to be a feature of recurring biological motifs, which is supported by the branched dependency-degradation competition motif, but warn that a motif that expresses robustness in isolation may not necessarily pass along that robustness to the entire system, which is also observed in this work.

CONCLUSIONS

In this work, a top-down approach to mechanistic modeling was presented and its implementation demonstrated through the development of a mathematical model for scFv folding in S. cerevisiae ER by BiP and PDI. This approach, represented schematically in Fig. 1, may be summarized as follows:

1. Establish the training data (i.e., the experimental data the mathematical model is expected to reproduce).

2. Establish the scope of the model (i.e., the biological details that the model will include).

3. Develop and analyze a backbone model (i.e., the most basic abstraction of the biological system that can reproduce the desired behaviors), potentially from known biological behavior motifs.

4. Incrementally append the backbone model with desired biological details and evaluate their effects on model performance until the desired level of mechanistic detail has been achieved.

As part of the model development, the importance of annotating all assumptions and simplifications was emphasized, as systematic alteration and relaxation of these assumptions and simplifications could be used to conclusively eliminate poorly performing model formulations.

When it was employed to develop a mechanistic mathematical model for scFv folding based on the Xu et al. (29) hypothesis, the strength of the top-down approach was demonstrated. The approach identified three requirements and a biological behavior motif necessary to reproduce experimentally observed BiP and PDI dependencies and augmented scFv production with combined BiP and PDI overexpression, thus supporting the hypothesis in these capacities. It also identified a shortcoming in the hypothesis, in that it cannot capture synergistic interactions between BiP and PDI in the scFv folding process. Elucidation of the requirements and motif, which naturally arose as part of the top-down process, would not have been so straightforward had a bottom-up approach been implemented. The requirements are reiterated below:

Requirement No. 1

Competition between degradation/misfolding and accelerated folding by PDI is necessary for PDI dependence.

Requirement No. 2

Assuming post-translational translocation is BiP-dependent, competition between the translocation step and cytoplasmic degradation of the translocating species is required to make BiP and PDI expression level dependencies comparable.

Requirement No. 3

The rate constant associated with the second-order BiP-dependent reaction step in translocation must not be so low compared to PDI-dependent folding rates that it excessively amplifies BiP over PDI expression level dependency. It also should not be so high that it eliminates BiP dependency altogether and makes the system PDI folding-dependent.

The scFv folding example is elementary in its size and complexity and in the amount of biological information readily available for model construction, but the top-down approach is applicable to systems of all sizes with all amounts of available biological information. One key to any successful modeling effort is the proper alignment of model scope with the amount of available information and goal(s) of model construction. Gradually applying detail to a highest-level model systematically heeds this charge by enabling the modeler to straightforwardly identify when the model is becoming needlessly and/or impractically bulky, especially with respect to available biological data and questions being asked of it. Even when systems become necessarily large and/or difficult to solve, the approach intimates the modeler with the modeling aspects that are pushing the ever-increasing upper bounds of computer technology (e.g., speed, memory, parallelization) and software (e.g., solvers for ordinary and differential-algebraic systems of equations, such as those within the powerful DASPK (48) and SUNDIAL (49)) capability, so a precise plan of action may be developed to cope with them.

One challenge present in the top-down approach is the possibility of missing certain mechanistic components or biological behavior motifs if their effects are masked within the data used to construct the model. For example, a feedforward regulatory loop may be overlooked if its influence on existing experimental data is adequately captured by employing a large value for one of the parameters when the precise value is unknown. Generally, this challenge may be addressed by comparing mechanistic model parameter values to known values for particular classes of reactions for discrepancies (e.g., check if a model's phosphorylation rate falls within the known range of values for this type of reaction). This parameter-check may also be used as a means of evaluating model performance. Additionally, and perhaps more importantly, an incomplete model produced by the top-down approach that captures known experimental behaviors is not technically invalid, unless experimental conditions in which the influence of the missing components or biological behavior motifs plays a critical role are defined and the influence observed. Again, the top-down approach offers the benefit of preventing the model from becoming overly-detailed relative to the amount of available information and the questions being asked of it. The process of amending a model with more biological information as it becomes available falls into the general framework of iterative, hypothesis-driven research in systems biology (1). Finally, one way to protect against overlooking the influence of a particular biological behavior motif is by ensuring that known motifs and their behaviors are thoroughly characterized for a wide range of conditions and parameter values, a task that has been undertaken for a variety of feedforward loop types (50–52) in the case of the feedforward loop example.

The field of systems biology is only recently emerging as a viable means for studying biological systems, thanks to recent advances in experimental data gathering and analysis techniques and tools (53). As the field continues to develop and become more standardized, a systematization of the approaches to mathematical modeling of biological systems will assist in this standardization. As these approaches are systematized, formal comparisons and evaluations of their appropriateness and performance for use in modeling particular systems will most certainly arise.

It is even possible that, eventually, certain aspects of modeling approach selection and implementation will become fully automated. Specific to the implementation of the top-down approach to mechanistic modeling, much effort is being placed into developing literature and database mining algorithms and software (54–58) to enumerate experimentally observed species interactions—a potential means of automating the process of defining model scope. If a formal biological behavior motifs database were ever to be compiled, algorithms and software could be developed to mine it for motifs for use in backbone model construction as well. Another approach may be the creation and cataloguing of a biological behavior motifs database using an algorithm similar to that developed and implemented by François and Hakim (59), which constructs basic modules and motifs from scratch (excluding even biologically known parameter values) to capture prescribed biological behaviors. The François and Hakim (59) evolutionary procedure may even be adapted to automate the process of appending a backbone model with mechanistic detail and assessing the effects on model performance, much the way attempts have been made to automate model reduction in bottom-up approaches to mechanistic modeling (60–64). Similarly, the top-down approach may borrow methods, such as those from metabolic engineering (65,66), to systematically explore the effects of altering model connectivity. Indeed, this work takes only an initial step into the systematization of mechanistic biological modeling, with much work yet to be done.

APPENDIX

Nomenclature

Table 2 enumerates definitions for all states, state prefixes, and prefixes and suffixes used in parameter subscript labels in model equations and Figs. 3 and 6 for straightforward interpretations of these model descriptions. Note that the brackets around the state names found in the equations simply indicate concentrations, which were always expressed in terms of number of molecules. The table also provides a legend for all of the characters used in the figures. Finally, all parameter definitions and values may be found in Table 3.

Parameter derivations

k₃/k₆₃, k_m3/k_m63, k₇/k₆₄, k_m7/k_m64, k₄/k₆₅, k_m4/k_m65, k₅/k₆₆, and k_m5/k_m66, UscFv folding and misfolding rates

For Fab antibody fragments, Mayer et al. (36) measured 2% nominal folding, 15% folding with BiP and ATP, 20% folding with PDI, and 40% folding with BiP, PDI, and ATP. These folding percentages were assumed to be loosely applicable to 4-4-20 scFv fragment folding, since Nieba et al. (67) has reported 2% nominal folding when the fragment is expressed in E. coli. Freund et al. (68) measured a fast folding phase rate of 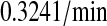and slow phase rate of 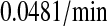for another scFv fragment. The overall folding rate

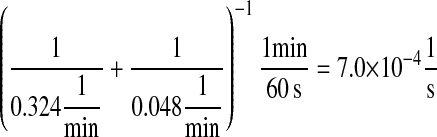was assumed to be applicable to the 4-4-20 fragment, so this was the nominal and BiP-assisted folding rate (k₃/k₆₃ and k₇/k₆₄) used in the mathematical models. The remaining folding rates could be derived from the collected information:

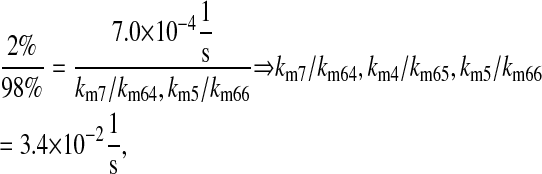(15)

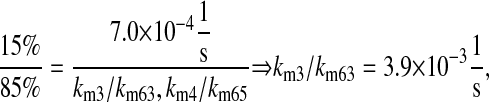(16)

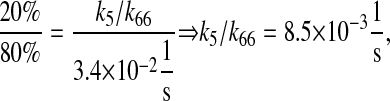(17)

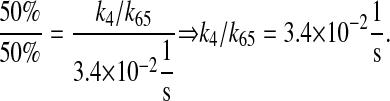(18)

To accelerate folding dynamics, all of these rate constant values were multiplied by a factor of 10. Further, k₄/k₆₅ was multiplied by another factor of 10 to emphasize the increase in folding rate caused by BiP and PDI binding.

k₆/k₆₀, k_r6/k_r60, k₆₉, k_r69, k₂/k₆₁, k_r2/k_r61, k₇₀, k_r70, k₇₆, and k_r76, BiP- and PDI-UscFv and general unfolded protein binding and dissociation rates

k₆/k₆₀ and k_r6/k_r60 are taken directly from Robinson and Lauffenburger (69), with the original references provided in Table 3. Units conversion was implemented using 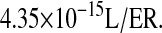BiP-general unfolded protein binding and release rates were taken directly from S. Hildebrandt, D. Raden, A. S. Robinson, and F. J. Doyle III, unpublished, which used an optimized value for binding, and the Robinson and Lauffenburger (69) value for release.

Darby and Creighton (71) measured a PDI binding rate of 600 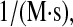which converts to 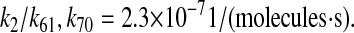Primm and Gilbert (72) and Puig et al. (73) measured the dissociation constant for various forms of PDI from various substrates to be ∼1 μM, which converts to 2.62 × 10³ molecules. This value was used to calculate the dissociation rate: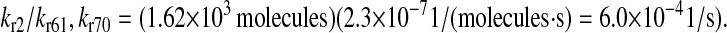

For PDI chaperone binding/dissociation, Gilbert (41) reviewed dissociation constants ranging from 50 to 1000 μM. The average of these values was used: 1.31 × 10⁶ molecules, after units conversion. The chaperone binding rate was arbitrarily taken to be identical to the foldase binding rate 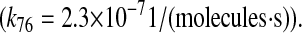The consequent chaperone release rate was then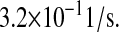

k₅₅, k₅₆, k₅₈, and k₅₉, scFv translation and transport rates

Ribbeck and Görlich (74), Siebrasse and Peters (75), and Smith et al. (76) place nuclear translocation at a rate of 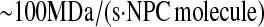in various vertebrates for various molecules. Ribbeck and Görlich (74) measured 2800 NPC molecules in the nuclear envelope of HeLa cells. These values were combined to produce a general value for the nuclear translocation rate, 2.8 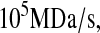which was assumed to apply to S. cerevisiae.

Calapez et al. (77), Lukacs et al. (78), Shav-Tal et al. (79), and Politz et al. (80) measured diffusion rates for a variety of species in the nucleus, including DNA, mRNA, and nascent ribosomes, to be 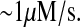Given an estimated S. cerevisiae nuclear volume of 1.74 × 10⁻¹⁵ L and an assumption of nuclear sphericity, the characteristic area (〈r²〉) of the nucleus may be calculated:

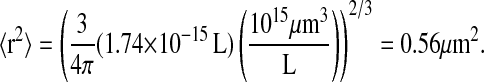(19)

The resulting effective diffusion rate was then

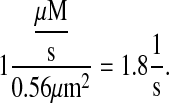(20)

Combining the diffusion rate with the nuclear translocation rate and the molecular weight of scFv mRNA (0.3200024 MDa) gave an overall nuclear translocation rate of

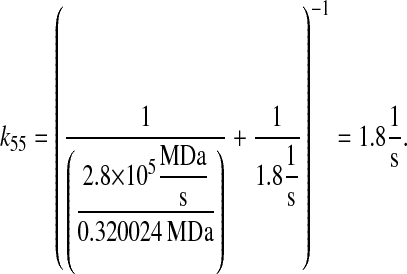(21)

Although ribosome occupancy density does not necessarily scale linearly with mRNA length (81), this assumption was made for simplification purposes. Using extrapolation points from Arava et al. (81), ribosome occupancy density could be estimated from the 963-nt-long scFv fragment mRNA:

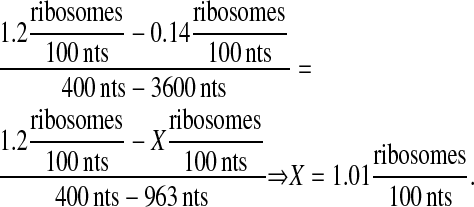(22)

From this density, it could be estimated that there is an average of 10 ribosomes on the scFv fragment mRNA. Freedman (82) estimated an overall translation rate of 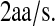The scFv fragment mRNA is 321-amino-acids long, so the overall scFv translation rate is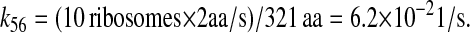

Goder et al. (83) estimated SRP binding and trafficking to the translocon to take place at a rate of 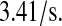The parameter k₅₈ also includes BiP binding at the translocon, which occurs at a rate of k₆/k₆₀ = 1.2 × 10⁻⁸ 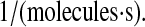Combining these two rates provides the overall rate constant:

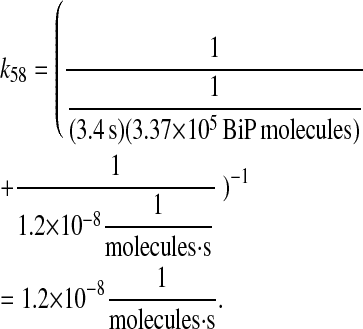(23)

The value in the table is optimized for desired secreted scFv dependencies on BiP and PDI levels, as discussed in the text.

Theoretical analyses by Elston (84) place translocation at a rate of 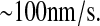The average length of an amino acid is 0.35 nm, and the scFv fragment protein length is 317 amino acids. Thus, k₅₉ is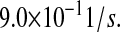

k_d/k_3d, scFv mRNA degradation rate

As an approximation for scFv mRNA degradation, Oliveira and McCarthy (85) gives half-lives for a variety of mRNAs ranging from 1.5 to 7.5 min. The average of 4.5 min gave a first-order rate constant of 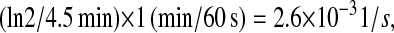which was used to for k_3d.

k_1b, k_1bit, and k_2b, developing models rates

The value k_1b encompasses the processes involved with k₅₅, k₅₆, k₅₈, and k₅₉. The value k₅₈ largely remained the rate-limiting step, so its derived value, 1.2 × 10⁻⁸ was used in these models. The value k_1bit is the equivalent rate without BiP dependence, so this dependence may be removed by the multiplication by 3.37 × 10⁵ BiP molecules. Thus, 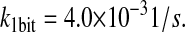The value k_2b was taken to be k₅ /k₆₆, made PDI-dependent by dividing by 5.24 × 10⁵ PDI molecules.

Model equations

Model 1

(24)

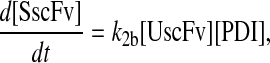(25)

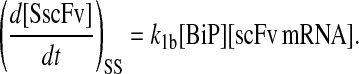(26)

Model 2

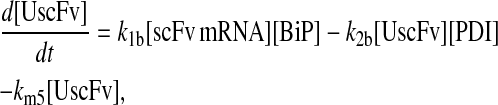(27)

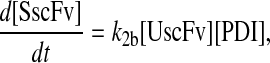(28)

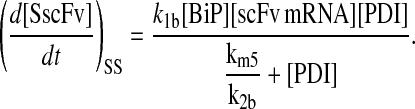(29)

Model 3

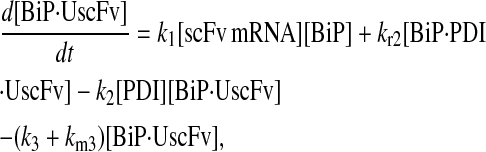(30)

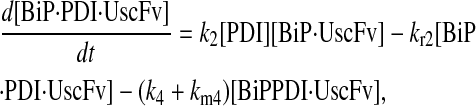(31)

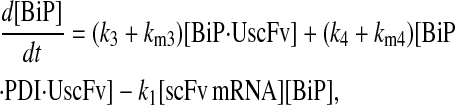(32)

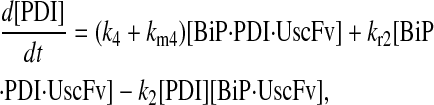(33)

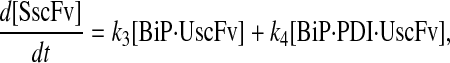(34)

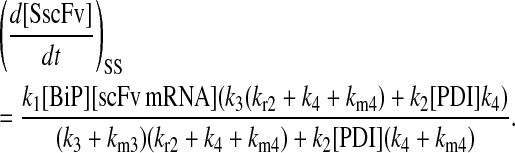(35)

Model 3*

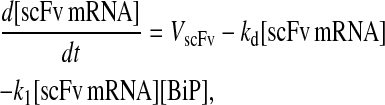(36)

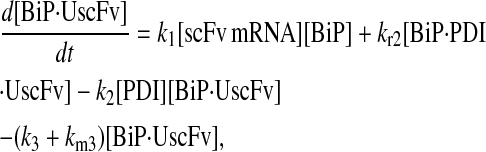(37)

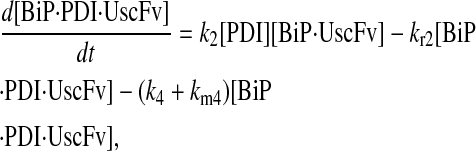(38)

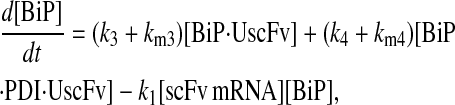(39)

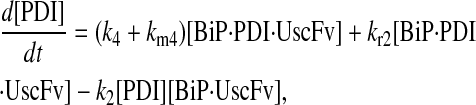(40)

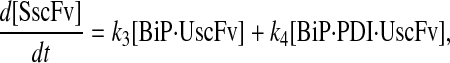(41)

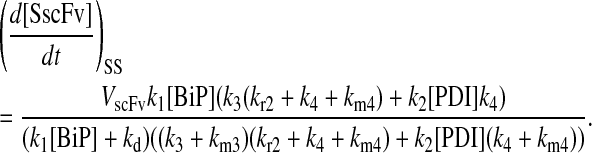(42)

Model 4

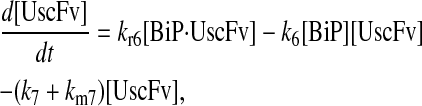(43)

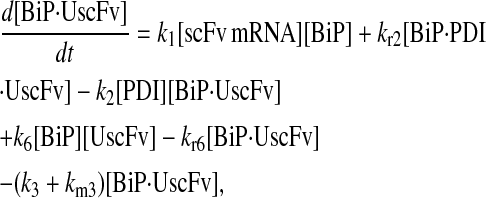(44)

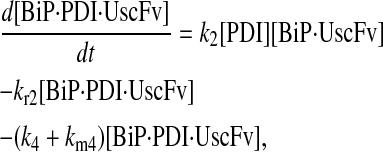(45)

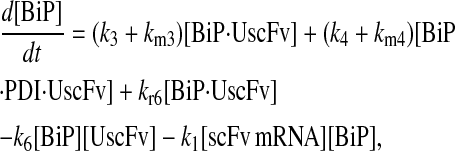(46)

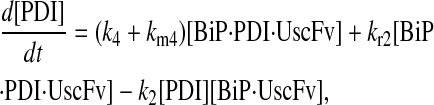(47)

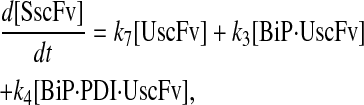(48)

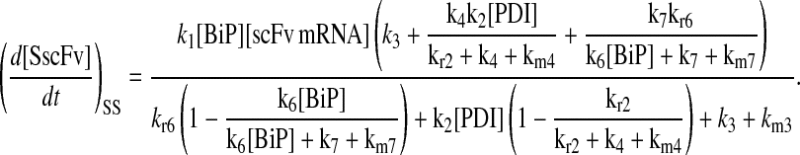(49)

Model 4*

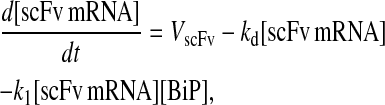(50)

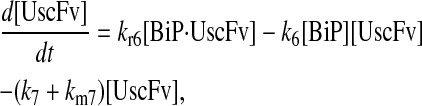(51)

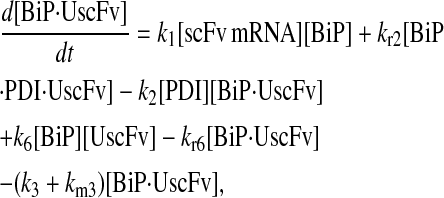(52)

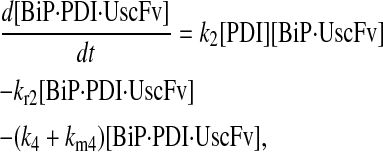(53)

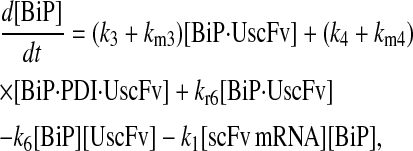(54)

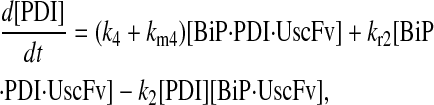(55)

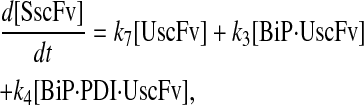(56)

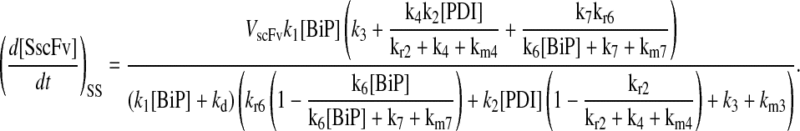(57)

Model 5

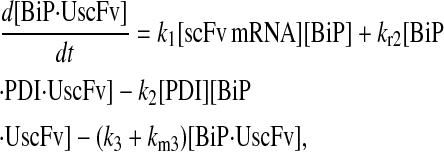(58)

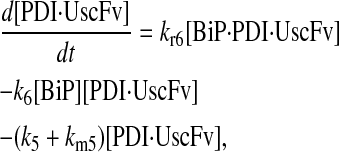(59)

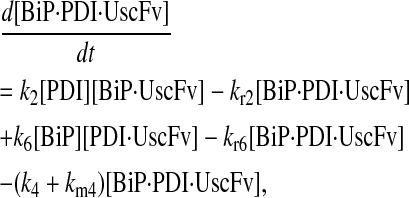(60)

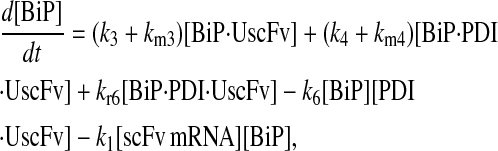(61)

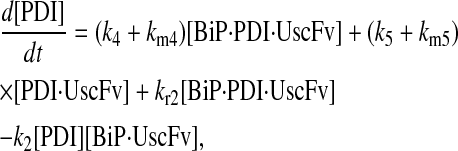(62)

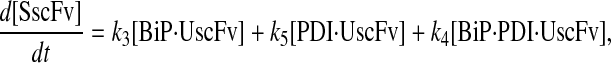(63)

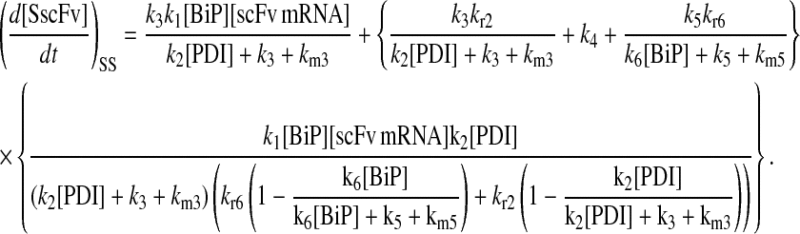(64)

Model 5*

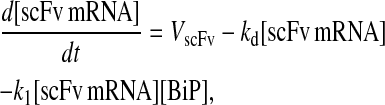(65)

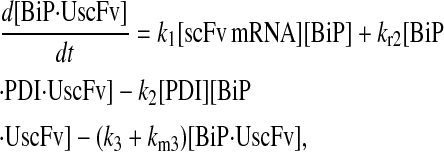(66)

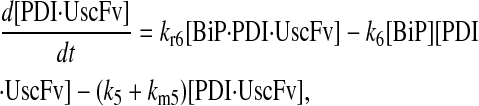(67)

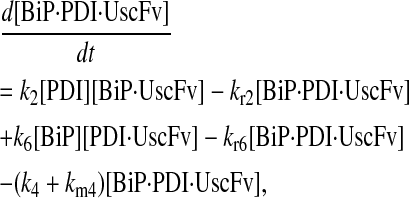(68)

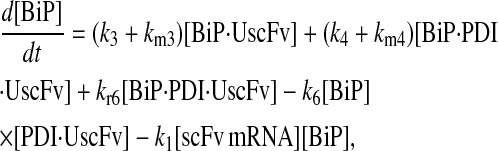(69)

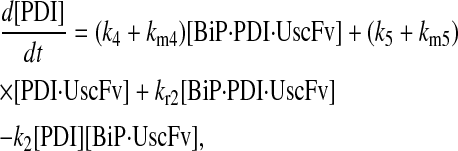(70)

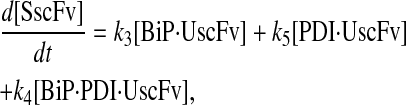(71)

(72)

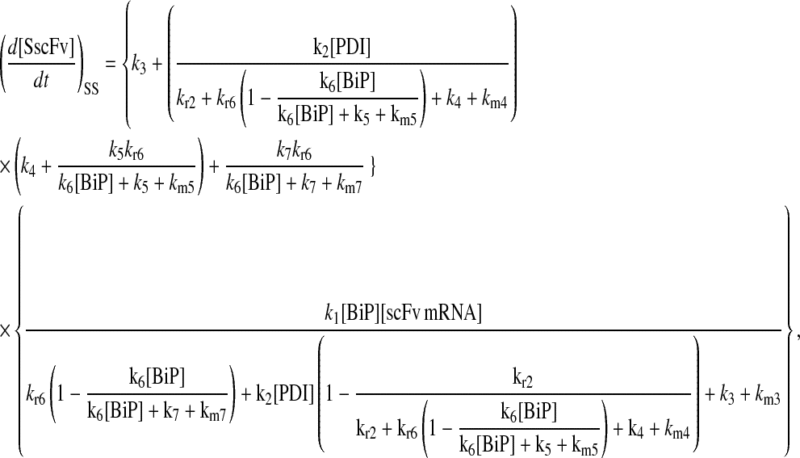
Model 6

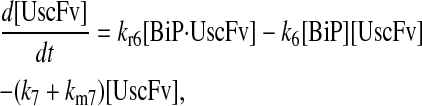(73)

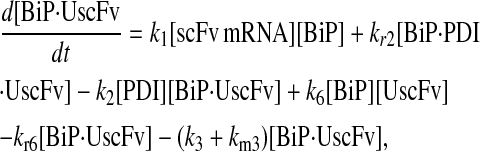(74)

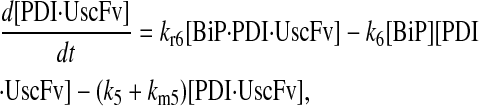(75)

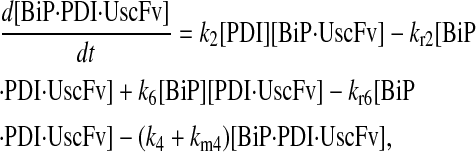(76)

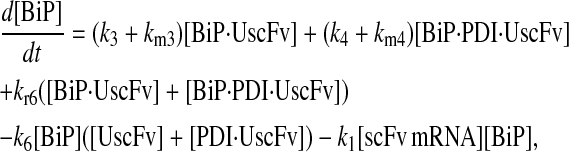(77)

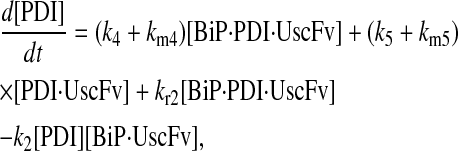(78)

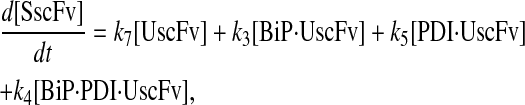(79)

(80)

Model 6*

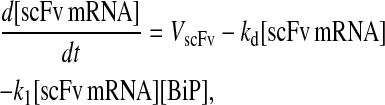(81)

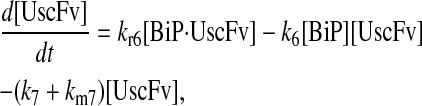(82)

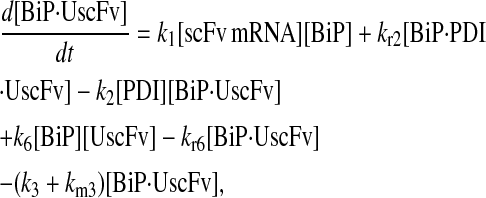(83)

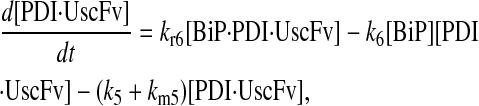(84)

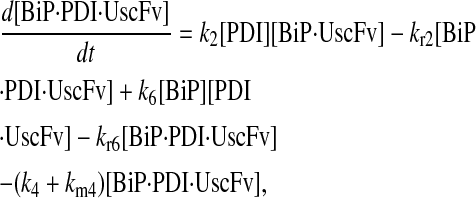(85)

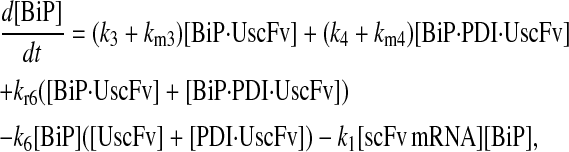(86)

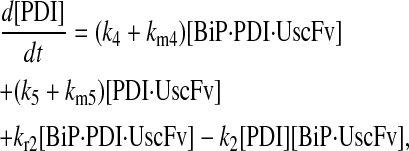(87)

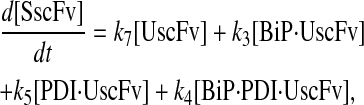(88)

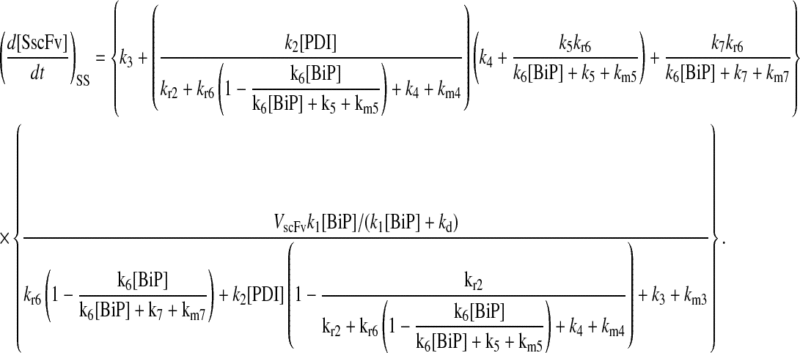(89)

Model 7

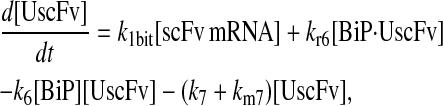(90)

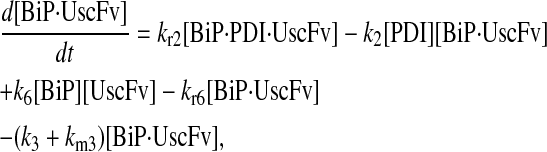(91)

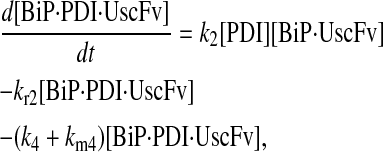(92)

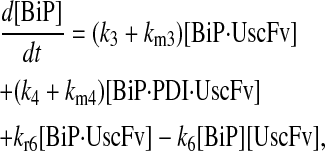(93)

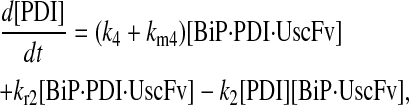(94)

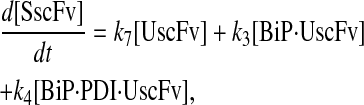(95)

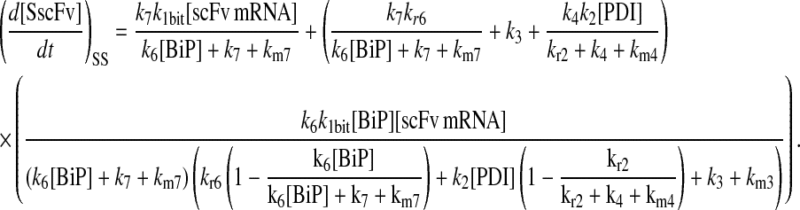(96)

Model 8

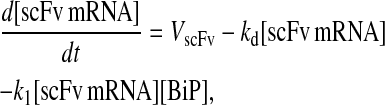(97)

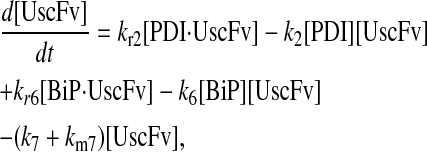(98)

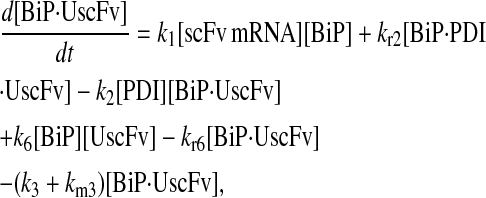(99)

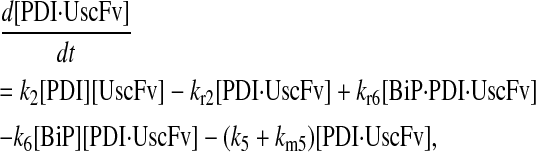(100)

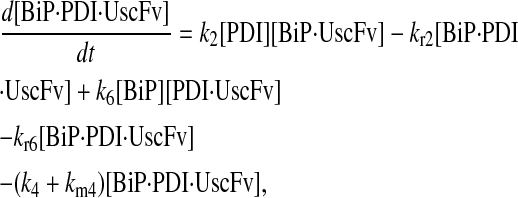(101)

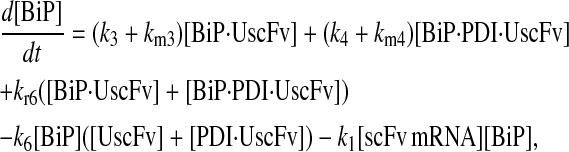(102)

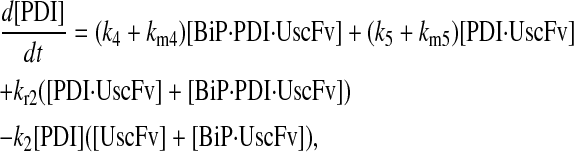(103)

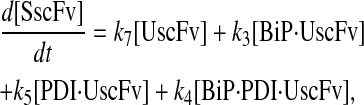(104)

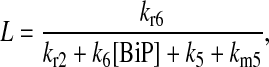(105)

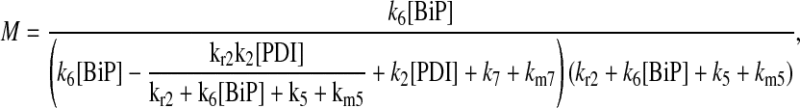(106)

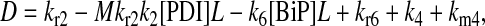(107)

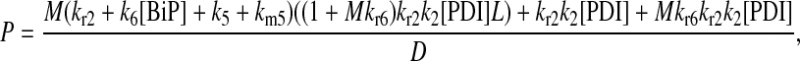(108)

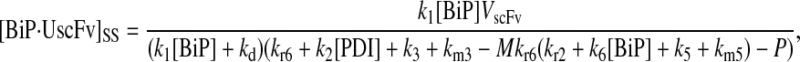(109)

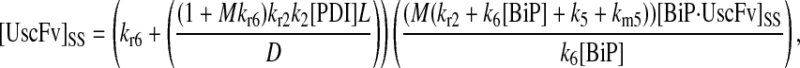(110)

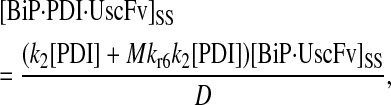(111)

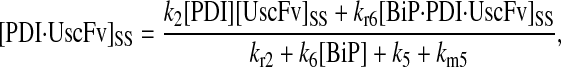(112)

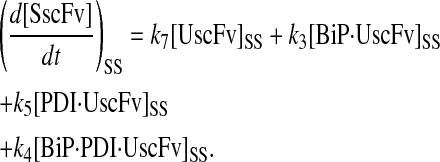(113)

Detailed model

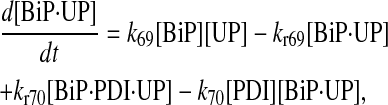(114)

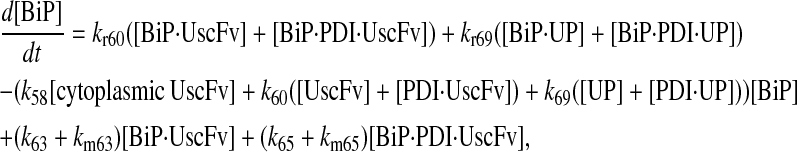(115)

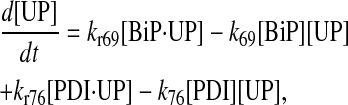(116)

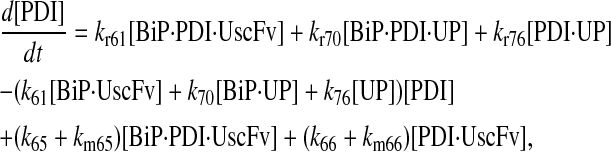(117)

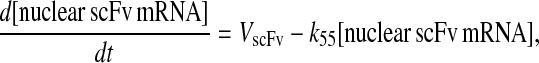(118)

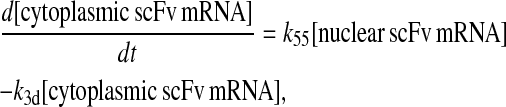(119)

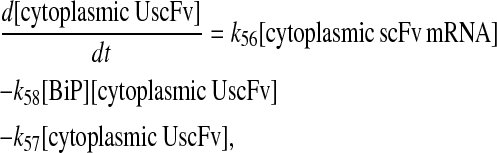(120)

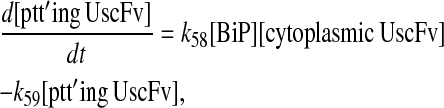(121)

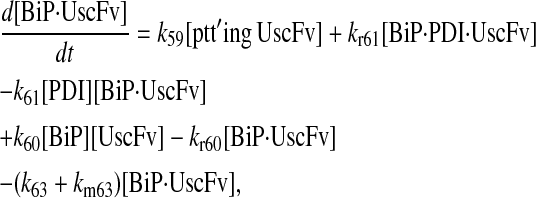(122)

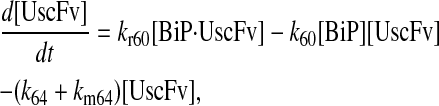(123)

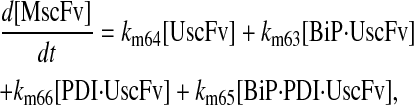(124)

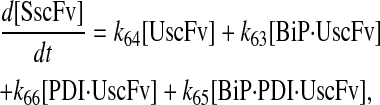(125)

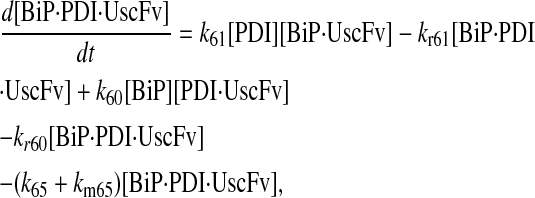(126)

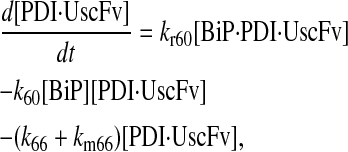(127)

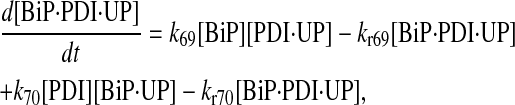(128)

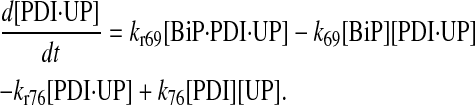(129)