Effect of Trehalose on a Phospholipid Membrane under Mechanical Stress

Abstract

Explicit solvent molecular dynamics simulations were used to investigate at atomic resolution the effect of trehalose on a hydrated phospholipid bilayer under mechanical stress (stretching forces imposed in the form of negative lateral pressure). Simulations were performed in the absence or presence of trehalose at 325 K, and with different values for negative lateral pressure. In the concentration regime (2 molal) and range of lateral pressures (1 to −250 bar) investigated, trehalose was found to interact directly with the membrane, partially replacing water molecules in the formation of hydrogen bonds with the lipid headgroups. Similar to previous findings in the context of thermal stress, the number, degree of bridging, and reaching depth of these hydrogen bonds increased with the magnitude of perturbation. However, at the concentration considered, trehalose was not sufficient to preserve the integrity of the membrane structure and to prevent its extreme elongation (and possible disruption) under the effect of stretching forces.

INTRODUCTION

The preservation of biostructures under unfavorable conditions by sugars has been a subject of increasing interest in the past few decades. It is well established that sugars, and in particular disaccharide trehalose (TRH), are able to stabilize membranes and proteins exposed to damaging conditions in vitro (1–5). The situation is more complicated in vivo, where other types of molecules may contribute to stress tolerance (4,6–10), e.g., in some species, anhydrobiosis is possible without sugars (9,10).

In the context of anhydrobiosis, three main hypotheses were proposed to explain the protective effect of saccharides on biomolecules. The water-replacement hypothesis suggests that, during drying, sugars can substitute water molecules (in particular by forming hydrogen bonds) around the polar and charged groups present in phospholipid membranes and in proteins, thereby stabilizing their native structure in the absence of water (11). The water-entrapment hypothesis, in contrast, proposes that sugars concentrate residual water molecules close to the biomolecular surface, thereby preserving to a large extent its solvation and native properties (12). Finally, the vitrification hypothesis suggests that sugars found in anhydrobiotic systems (known to be good vitrifying agents) protect biostructures through the formation of amorphous glasses, thereby reducing structural fluctuations and preventing denaturation or mechanical disruption (13). In the last few years, a consensus has emerged that these mechanisms may not be mutually exclusive (1,2,7,13). Vitrification may occur simultaneously with a direct interaction between the sugar and the biostructure or with an entrapment of residual water molecules at its surface, depending on the type of protected biostructure and on the nature of the environmental stress.

Recent molecular dynamics simulations (14–27) suggested that there is a qualitative difference in the way sugars interact with membranes and with proteins. Although sugars are seen to interact directly (through hydrogen bonds) with membrane headgroups, even in dilute solutions (14–21), they appear to be preferentially excluded from protein surfaces (trapped water layer), even in highly concentrated solutions (22–27). However, the suggestion that sugars are preferentially excluded from the surface of proteins in concentrated solutions or during dehydration remains very controversial (28).

Sugars can provide bioprotection in a wide range of stressful conditions, e.g., extreme dryness, cold, heat, pressure, oxygen deprivation, high salt concentrations, or irradiation (1,2,4,7,9,29). Among these, dehydration stress is by far the most commonly investigated. As a result, essentially all hypotheses for bioprotection mechanisms have been based on studies of dehydrated systems, and much less is known about the effect of sugars on biomolecules exposed to other types of perturbation. Here, we focus on the effect of mechanical stress applied to phospholipid membranes.

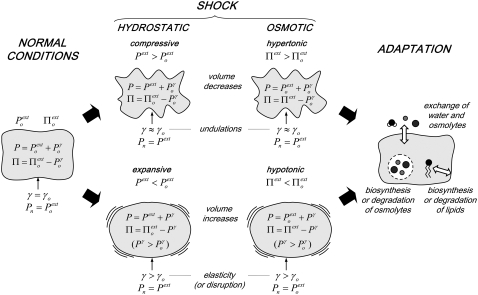
Three types of damaging external conditions can result in mechanical stress (in the form of large positive or negative surface tensions) on a lipid bilayer, presented here in the context of a cell membrane: (1), shear (e.g., when the shape of a cell is distorted by contact with a mobile surface); (2), hydrostatic pressure (when a cell is placed in a low-pressure or high-pressure environment); and (3), osmotic pressure (when a cell is placed in a hypotonic or hypertonic aqueous environment). Fig. 1 provides a schematic representation of the effects of hydrostatic (pressure) or osmotic (tonicity) shocks on a living cell (omitting the possible presence of a cell wall).

FIGURE 1.

Schematic representation of the effects of hydrostatic (pressure) or osmotic (tonicity) shocks on a living cell (omitting possible presence of a cell wall).

Under normal conditions (Fig. 1, left), the internal hydrostatic pressure (P) is equal to the external pressure (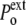) increased by a possible contribution (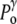) due to the surface tension (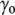) of the membrane at rest, whereas the internal tonicity (Π) is equal to the external tonicity (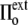) decreased by this same contribution 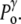This ensures both mechanical and chemical equilibrium (the latter relative to the diffusion of water across the membrane). The surface tension 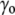may result from thermal undulations of the membrane or from its elasticity. Approximating the cell surface as a sphere of radius R, one has 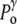= 2 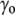/R. Finally, the normal pressure acting (from the exterior) on the cell membrane (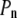) is equal to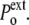

In a compressive hydrostatic shock (external pressure increased from 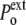to 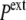> 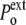), the cell volume decreases by compression of its content, whereas in hypertonic osmotic shock (external tonicity increased from 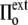to 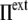> 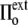), the cell volume decreases by an efflux of water (Fig. 1, center, top). The membrane instantaneously relieves the resulting lateral compression by undulating, so that the surface tension remains close to 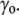However, in the compressive shock, the normal pressure 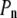increases to 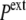(while it remains unchanged in the hypertonic shock). In an expansive hydrostatic shock (external pressure decreased from 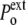to 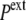< 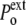), the cell volume increases by expansion of its content, whereas in a hypotonic osmotic shock (external tonicity decreased from 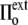to 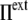< 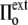), the cell volume increases by an influx of water (Fig. 1, center, bottom). The membrane is stretched, and its surface tension increases to 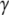> 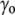(it may also disrupt if the perturbation is too large). This tension results in an increase of the corresponding pressure term 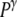above 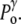In the expansive shock, the normal pressure 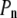also decreases to 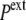(while it remains unchanged in hypotonic shock).

A number of adaptation mechanisms (Fig. 1, right) may come into play after some time to relieve the stress due to shock (30–35): (1), an exchange of water or osmolytes with the extracellular medium (regulation of the intracellular hydrostatic and osmotic pressures); (2), the biosynthesis or degradation of osmolytes within the cell (regulation of the intracellular osmotic pressure); and (3), the biosynthesis or degradation of membrane lipids, as well as changes in lipid composition (regulation of the membrane surface area). These observations do not strictly apply to cells presenting a surrounding rigid or moderately elastic wall (e.g., cells of bacteria, archaea, fungi, algae, and plants). In these cells, the expansion caused by a hypotonic shock is restricted by the wall, resulting in a pressure (analogous to 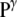in Fig. 1) exerted by the cell content on the wall, i.e., the so-called turgor pressure (32). In the presence of a cell wall, a hypertonic shock may result in the cytoplasmic membrane peeling away from the cell wall, a phenomenon called plasmolysis (32).

Elevated hydrostatic pressure exerts a broad range of effects on living cells, mainly associated with protein denaturation and lipid phase transitions (30). Pressure also interferes with the cell architecture, affecting the cell-wall integrity and several organelles, as well as with cellular growth and division (30,31). The compression of membranes causes the fatty-acid acyl chains to pack more tightly together, reducing membrane fluidity and promoting ordering in the bilayer (30,31). Conversely, membrane-stretching can lead to the formation of pores and, at sufficiently high negative lateral pressures, to the rupture of the bilayer (36). The critical tension for the rupture of membranes when laterally stretched varies in the range of ∼1–25 mN/m, depending on the loading rate of the applied tension as well as on the lipid composition (36,37). A number of studies addressed the effect of high hydrostatic pressure and the mechanisms of barotolerance in vivo for tardigrades (38), yeasts (39–45), or bacteria (30,31,46), and in vitro for proteins (30,31,47,48) and membranes (30,31,49,50). It appears that cells and biomolecules can remain functional even under compressions of up to thousands of bar (30,31,38–50). Much less is known about the effects of low hydrostatic pressure and expansive pressure shocks in vivo, a situation that could occur in practice, e.g., when a deep-sea organism is transferred to more shallow water, or when a living cell is released in space.

The phenomenon of barotolerance in living cells is not completely understood, although it seems to involve an interplay between TRH and heat-shock proteins (HSPs) (39,42,51), suggesting analogies with the mechanisms of thermotolerance (40). However, studies using yeasts indicated that TRH contributes more to barotolerance than to thermotolerance, whereas the opposite is observed for HSPs (41). This difference may be explained by the membrane-stabilizing properties of TRH, whereas HSPs appear to be predominantly (if not exclusively) protein stabilizers (41,45,50). However, the mechanisms whereby sugars such as TRH promote the stabilization of membranes under mechanical stress remain essentially unknown at the molecular level.

Many living organisms also present mechanisms to cope with osmotic stress (32–34). Because the cytoplasmic membrane of cells is permeable to water, but not to most other metabolites, hypertonic or hypotonic shocks cause an instantaneous efflux or influx of water, resulting in a decrease or increase of cytoplasmic volume, respectively (32–34). To some extent, hypertonic and compressive shocks have comparable effects on the cell, and a similar observation holds for hypotonic and expansive shocks (Fig. 1). However, an important difference pertains to the normal pressure acting on the membrane (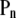 in Fig. 1; only altered in hydrostatic shocks), which may have an influence on lipid phase equilibria.

Traditionally, organisms are divided into two broad categories in terms of adaptation to osmotic stress: osmoregulators (most terrestrial and aquatic vertebrates) that present specialized organs to regulate internal osmotic pressures, and osmoconformers (most invertebrates) that use organic osmolytes to adjust intracellular osmotic pressure (34). In many species, osmolytes can be up- or down-regulated to prevent osmotic shrinkage or swelling (32–34). Sugars (mainly TRH) are produced in response to osmotic stress in bacteria, yeasts, fungi, algae, and plants (32–35,49). Many studies showed that TRH (as well as other osmolytes, called “counteracting solutes”) has an action that goes beyond the purely osmotic role, and is related to specific stabilizing interactions with cellular macromolecules (34,35,52).

Here, molecular dynamics (MD) simulations were performed to investigate the effect of TRH on the structure and dynamics of a dipalmitoyl phosphatidylcholine (DPPC) bilayer exposed to negative lateral pressure, mimicking the effect of mechanical stretching. Simulations of the bilayer in the absence or presence of the disaccharide were performed at different lateral pressures, to provide a better understanding of sugar-membrane interactions and how they modulate the response of a lipid membrane exposed to mechanical stress.

METHODS

All MD simulations were performed using the GROMOS96 program (53), together with the GROMOS 45A4 force field, including parameters recently developed for lipids (54) and carbohydrates (55), and the simple point charges water model (56). Newton's equations of motion were integrated, using the leapfrog algorithm (57) with a 2-fs time step. The SHAKE algorithm (58) was applied to constrain all bond lengths with a relative geometric tolerance of 10⁻⁴. The simulations were performed under periodic boundary conditions (rectangular box) in the isothermal-isobaric ensemble (with different reference values for normal and lateral pressures; see below). The temperatures of solute and solvent degrees of freedom were separately coupled to a heat bath at 325 K (relaxation time, 0.1 ps) (59), and the atomic coordinates and box dimensions were coupled to a pressure bath via anisotropic scaling (59) (relaxation time, 0.5 ps; isothermal compressibility, 0.46 × 10⁻³ kJ⁻¹ × mol × nm³). Mechanical stress was introduced by setting the reference pressure P_z along the z-axis of the box (perpendicular to the bilayer plane) to 1 bar for all systems, whereas reference pressures P_x and P_y along the x-axis and y-axis (in the bilayer plane) were jointly set to different values ranging from 1 to −250 bar. Systems with five different lateral pressures were considered: A (P_x = P_y = P_z = 1 bar), B (P_x = P_y = −100 bar, P_z = 1 bar), C (P_x = P_y = −150 bar, P_z =1 bar), D (P_x = P_y = −200 bar, P_z =1 bar), and E (P_x = P_y = −250 bar, P_z =1 bar). These lateral pressures can be related to an applied surface tension γ via (60)

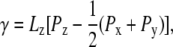(1)

where L_z is the box dimension along the z-axis (a positive value of γ indicating the application of stretching forces on the bilayer patch). Note that γ is defined here for the entire bilayer rather than for the two constituting leaflets (61).

Nonbonded interactions were truncated at a distance of 1.4 nm, and reevaluated at every time step in the range of 0.0–0.8 nm, or at every five time steps in the range of 0.8–1.4 nm (twin-range cutoff scheme (62)). A reaction-field correction was applied to account for the mean effect of neglected electrostatic interactions beyond 1.4 nm, using a relative dielectric permittivity of 54 as appropriate for the simple point charges water model (63). For all simulations, the atomic coordinates were saved every 1 ps for analysis.

The systems consisted of a hydrated membrane bilayer patch consisting of 2 × 64 DPPC molecules, simulated either in the absence or presence of 128 TRH molecules. The systems excluding TRH involved 3655 water molecules, whereas the systems including TRH involved 3339 water molecules, resulting in a TRH solution at a 2-molal (2 mol kg⁻¹) concentration (14). In total, 10 simulations were performed at 325 K, involving: (1), the DPPC bilayer in pure water at lateral pressures P_x = P_y of 1, −100, −150, −200, and −250 bar (control simulations labeled A_w–E_w); and (2), the DPPC bilayer in the 2 m TRH solution at lateral pressures P_x = P_y of 1, −100, −150, −200, and −250 bar (simulations labeled A_t–E_t).

A DPPC bilayer at full hydration (3655 water molecules, implying 28–29 water molecules per lipid) in the liquid-crystalline phase, previously equilibrated during 8.5-ns MD simulation at 325 K (no applied surface tension) (14), was used to initiate the 30-ns production runs of all simulations without TRH, with the exception of the simulation at 1 bar (20 ns only). For systems in the presence of TRH, the inclusion of TRH was followed by a thorough equilibration procedure (involving in particular the relaxation of the sugar-water mixture by a 5-ns simulation at 500 K, with positional restraints on the lipid molecules), as described previously (14). This equilibration was followed by a 6-ns simulation at 325 K (no applied surface tension) (14), the final configuration of which was used to initiate the 30-ns production runs of all simulations including TRH, with the exception of the simulation at 1 bar (20 ns only). A summary of the simulated systems and simulation conditions is provided in Table 1.

TABLE 1.

Summary of the simulated systems and simulation conditions: simulation code, applied lateral pressure (P_x, P_y; P_z = 1 bar), and TRH concentration, together with initial and final values of the area per lipid (A), box dimension along the z-axis (L_z), and applied surface tension (γ; calculated using Eq. 1.)

Simulation	Px,Py (bar)	TRH (m)	Ainitial (nm2)	Afinal (nm2)	Lz initial (nm)	Lz final (nm)	γinitial (mN/m)	γfinal (mN/m)
Aw	1	0	0.56	0.56	7.46	7.60	0.0	0.0
At	1	2	0.56	0.56	8.69	8.62	0.0	0.0
Bw	−100	0	0.56	0.67	7.46	6.26	75.32	63.20
Bt	−100	2	0.56	0.68	8.69	7.12	87.74	71.88
Cw	−150	0	0.56	0.82	7.46	5.36	112.60	80.91
Ct	−150	2	0.56	0.88	8.69	5.50	131.17	83.02
Dw	−200	0	0.56	1.02	7.46	4.15	149.89	83.39
Dt	−200	2	0.56	1.08	8.69	4.53	174.61	91.02
Ew	−250	0	0.56	1.47	7.46	2.89	187.31	72.56
Et	−250	2	0.56	1.65	8.69	2.95	218.19	74.07

Indicative fluctuations (in the form of standard deviations calculated over the initial and final 1 ns of the simulations and averaged over all simulations) are 0.016 (A_initial) and 0.005 nm² (A_final); 0.235 (L_{z initial}) and 0.033 nm (L_{z final}); and 4.45 (γ_initial) and 0.491 mN/m (γ_final). Initial and final values refer to first and last configurations of 30-ns simulations (except A_w and A_t, 20 ns only).

It is important to stress that whereas the applied normal (P_z) and lateral (P_x = P_y) pressures are constant throughout a simulation, the surface tension γ is not (Eq. 1). As L_z converges toward its equilibrium value L_{z final}, the latter quantity converges to a particular value γ_final (Table 1). Only at this point does the simulation represent an equilibrium situation at this particular surface tension. However, the application of a constant lateral pressure (rather than a constant surface tension) may provide a more realistic representation of the effect of a hydrostatic or osmotic stress on a cell membrane.

RESULTS

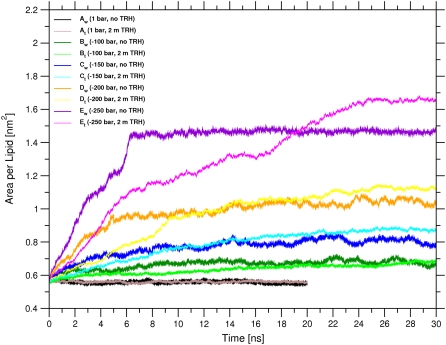
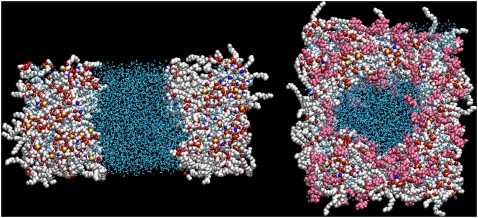
The time evolution of the area per lipid of the bilayer is shown in Fig. 2 for the 10 simulations performed. In the absence of TRH, the average values for the area per lipid are qualitatively similar to those observed in a previous MD study addressing the effect of mechanical stress on the physical properties and pore-formation mechanism in a DPPC bilayer (36). In the absence of surface tension (A_w), the area per lipid is essentially time-independent, with an average value of 0.56 nm². This value is compatible with previous results using the same force field and simulation conditions (54,61), but is on the low side compared with the best estimate of 0.64 nm² derived from a careful analysis of the different available experimental values (64). The area per lipid in the simulation at −100 bar lateral pressure (B_w) appears to converge to a value of ∼0.68 nm² (average over the final 5 ns), i.e., closer to the experimental result. These simulation conditions may actually be closer to the experimental situation. The simulated membrane patch, because of its microscopic size and artificial periodicity, cannot undergo undulations over a significant length-scale. In a real membrane, such thermal undulations would be responsible for a nonvanishing average surface tension, which could in principle be approximately reintroduced during the simulation by means of a relatively small negative lateral pressure (as in simulation B_w). However, the appropriateness of one choice or the other is still much debated (61,65–67). For higher values of negative lateral pressure (C_w, D_w, and E_w), the membrane significantly expands, with average values of the area per lipid of 0.81, 1.04, and 1.47 nm², respectively (averages over the final 5 ns). For the highest value of lateral pressure (E_w), this expansion results (after ∼6 ns) in the formation of a water channel that divides the bilayer plane into two distinct regions (Fig. 3, left). This disruption of the bilayer structure could represent the onset of a transition to a nonlamellar (e.g., hexagonal) phase (68,69). However, the very high expansion rate of the bilayer in this simulation does not allow for the extensive reorientation of the lipid molecules that would accompany such a transition (in particular, the final configuration of this simulation presents extensive headgroup-headgroup contacts through periodicity).

FIGURE 2.

Area per lipid as a function of time for the simulations of a hydrated DPPC bilayer at 325 K with different negative lateral pressures, either in pure water or in a 2-m TRH solution. See Table 1 for simulation codes.

FIGURE 3.

Final configurations (30 ns) of the simulations of a hydrated DPPC bilayer at 325 K and −250 bar lateral pressure, either in pure water (E_w; left) or in a 2-m TRH solution (E_t; right), viewed perpendicular to the bilayer plane. The DPPC and TRH molecules are represented using a spacefill model, and water molecules using a licorice model. For DPPC, carbon atoms are represented in white, oxygen atoms in red, phosphorus atoms in yellow, and nitrogen atoms in blue. Water molecules are represented in blue, and TRH molecules in pink. See Table 1 for the simulation codes.

Comparing the results of the simulation pairs at identical lateral pressure, differing only by the absence or presence of TRH, the following observations can be made: (1), the presence of the sugar leads to a slight increase in the final value of the area per lipid at the end of the simulation (except for A_w vs. A_t and B_w vs. B_t); and (2), the inclusion of TRH slows down the relaxation to this final value. At the highest negative lateral pressure of −250 bar (E_w vs. E_t), the final area per lipid is 1.66 nm² for the system with TRH (average over the final 5 ns), compared with a corresponding value of 1.47 nm² in pure water. As was the case in the absence of the sugar (E_w), the expansion in the presence of TRH (E_t) results (after ∼16 ns) in the disruption of the membrane. However, in this case, a toroidal water pore is formed rather than a dividing channel (Fig. 3, right). At intermediate lateral pressures of −150, and −200 bar, the bilayer is slightly more expanded in the presence of TRH, with values of the area per lipid of 0.86 nm² (C_t) and 1.10 nm² (D_t), respectively (averages over the final 5 ns), compared with corresponding values of 0.81 nm² (C_w) and 1.04 nm² (D_w), respectively, in pure water. For the lowest applied surface tensions corresponding to lateral pressures of 1 and −100 bar, the final area per lipid is essentially unaffected by the presence of TRH, with final values of 0.56 nm² (A_w and A_t) and 0.67 nm² (B_w and B_t), respectively (average over the final 5 ns).

The observation that TRH induces a slight expansion of the bilayer at constant negative lateral pressure (C_w vs. C_t and D_w vs. D_t) is in line with recent simulation studies suggesting that TRH (at a comparable concentration of ∼1.4 M) decreases the surface tension in bilayer systems simulated at constant area (17), and increases the surface area in bilayer systems simulated at constant surface tension (18). However, even if the thermodynamical driving force toward bilayer expansion appears to be somewhat larger in the systems including TRH, the kinetics of this expansion is slower. This probably results from the lower diffusivity (higher viscosity) of the sugar-water solution compared with that of pure water.

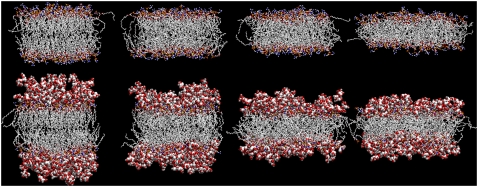
The final configurations of all simulated systems (except E_w and E_t, shown in Fig. 3) after 20 ns (Fig. 3 A) or 30 ns (Fig. 3, B–D) are displayed in Fig. 4. The lateral expansion and normal shrinkage of the bilayer upon increasing the magnitude of the negative lateral pressure (i.e., the surface tension) are evident, in agreement with the corresponding increase in area per lipid (Fig. 2); Fig. 4 also depicts a clustering of TRH molecules at the interface between the bilayer headgroups and the solvent (21).

FIGURE 4.

Final configurations (20 ns for A; 30 ns for B–D) of the simulations of a hydrated DPPC bilayer at 325 K and lateral pressures of (left to right) (A) 1 bar; (B) −100 bar; (C) −150 bar; and (D) −200 bar, either in pure water (top; A_w, B_w, C_w, and D_w) or in a 2-m TRH solution (bottom; A_t, B_t, C_t, and D_t). The DPPC molecules are represented using a licorice model, and TRH molecules using a space fill model. For DPPC and TRH, carbon atoms are represented in silver, oxygen atoms in red, phosphorus atoms in yellow, nitrogen atoms in blue, and hydrogen atoms in gray. See Table 1 for the simulation codes.

The total number of hydrogen bonds (H-bonds) present on average (final 10 ns of the simulations) between different species is reported in Table 2 for all simulations. In the absence of surface tension (A_w and A_t), TRH is seen to replace water at ∼20–25% of the H-bonding sites provided by the membrane surface (of an average of 545 DPPC-water H-bonds in pure water, 145 are lost in the presence of TRH, whereas 117 TRH-DPPC H-bonds are formed). Such a partial replacement is in line with the results of previous simulation studies that probed sugar-lipid H-bonded interactions (14–17,19–21). For the systems without TRH, an increase in the magnitude of the negative lateral pressure (and the concomitant increase in the area per lipid; Figs. 2 and 4) promotes a systematic increase in the number of DPPC-water H-bonds (by ∼10–20% relative to A_w, for simulations B_w–D_w). For simulation E_w, however, a small reduction (∼5%) in the number of DPPC-water H-bonds (relative to A_w) results from the dehydration of lipid headgroups caused by the clustering of water molecules within the water channel (Fig. 3, left). For simulations including TRH, the average number of DPPC-water H-bonds is approximately the same in simulations A_t, B_t, and C_t, and is slightly increased (∼10%) in simulations D_t and E_t. However, in these simulations, an increase in the magnitude of the negative lateral pressure (and the concomitant increase in the area per lipid) promotes a more pronounced and systematic increase in the average number of TRH-DPPC H-bonds (by 38%, 91%, 95%, and 127% relative to A_t, for simulations B_t–E_t). As a result, the fraction of all H-bonds to DPPC contributed by TRH molecules rises progressively, from 23% (A_t) to 37% (E_t). Simultaneously, the number of TRH-water and TRH-TRH H-bonds tends to decrease (although not systematically).

TABLE 2.

Average number of H-bonds (rounded to nearest integer) between all species present during the simulations of a hydrated DPPC bilayer at 325 K with different negative lateral pressures, either in pure water or in a 2-m TRH solution

Simulation	Px,Py (bar)	TRH (m)	DPPC-water	TRH-DPPC	TRH-water	TRH-TRH
Aw	1	0	545 (13)
At	1	2	400 (11)	117 (6)	1263 (34)	166 (15)
Bw	−100	0	598 (15)
Bt	−100	2	398 (13)	161 (8)	1279 (35)	146 (12)
Cw	−150	0	649 (16)
Ct	−150	2	402 (11)	223 (10)	1217 (33)	131 (12)
Dw	−200	0	658 (15)
Dt	−200	2	433 (18)	228 (10)	1180 (28)	134 (11)
Ew	−250	0	524 (14)
Et	−250	2	454 (22)	265 (11)	1055 (34)	141 (11)

Standard deviations are reported in parentheses. Values are averaged over the final 10 ns of the simulations. The criterion to define the presence of an H-bond is a hydrogen-acceptor distance shorter than 0.25 nm, and a donor-hydrogen-acceptor angle larger than 135°. See Table 1 for the simulation codes.

The increase in the average number of water-DPPC and TRH-DPPC H-bonds with increasing negative lateral pressure certainly results in large part from the lateral expansion of the bilayer (Figs. 2 and 4). This expansion not only allows for a better intercalation of the solvent and co-solute molecules between the lipid headgroups, but also facilitates the penetration of these molecules deeper into the membrane. This interpretation is confirmed by a substantial increase in the number and relative proportion of TRH-DPPC H-bonds involving the (relatively buried) ester oxygen atoms (Table 3) upon increasing the surface tension. In comparison, the increase in the number of TRH-DPPC H-bonds involving the (more superficial) phosphate groups is more limited, and the corresponding relative proportion decreases upon increasing the surface tension.

TABLE 3.

Average number of H-bonds (rounded to nearest integer) between TRH (hydroxyl groups) and either the phosphate or ester groups of lipid molecules during the simulations of a hydrated DPPC bilayer at 325 K with different negative lateral pressures in a 2-m TRH solution

Simulation	Px,Py (bar)	H-bonds to phosphate	H-bonds to ester	H-bonds to phosphate (%)	H-bonds to ester (%)
At	1	102	15	87	13
Bt	−100	114	47	71	29
Ct	−150	126	97	57	43
Dt	−200	122	106	54	46
Et	−250	137	128	52	48

Relative contributions (in percentages) to the total number of TRH-DPPC H-bonds are also presented. Values are averaged over the final 10 ns of the simulations. See legend of Table 2 for the H-bonding criteria. See Table 1 for the simulation codes.

The nature of TRH-DPPC H-bonds is analyzed in more detail in Table 4. The TRH molecules are able to form multiple H-bonds simultaneously, sometimes with the same DPPC molecule and sometimes with distinct ones (configurations were observed in the simulations where a single TRH molecule formed as many as eight H-bonds with lipid molecules). Comparing the occurrences of different H-bonding patterns (14) at different lateral pressures, interesting observations can be made. In the absence of surface tension (A_t), most of the TRH molecules (74%) belong to the patterns “0” and “1,” i.e., are either not H-bonded to the bilayer, or form a single H-bond with one DPPC molecule. Upon increasing the magnitude of the negative lateral pressure, the occurrences of these two patterns are reduced (to 62%, 48%, 45%, and 38% for simulations B_t–E_t, respectively). In contrast, the occurrences of all other patterns, involving more than two H-bonds to the same DPPC molecule or the bridging of multiple DPPC molecules by a common TRH molecule, nearly systematically increase. The occurrences of TRH molecules with a specific degree of bridging (i.e., forming at least one H-bond with a given number of distinct DPPC molecules) are shown in Table 5. The results clearly show that an increase in magnitude of negative lateral pressure (and the concomitant lateral expansion) leads to a substantial increase in number of TRH molecules H-bonded to two or more distinct DPPC molecules.

TABLE 4.

Average number of TRH molecules forming a specific H-bonding pattern with DPPC molecules during the simulations of a hydrated DPPC bilayer at 325 K with different negative lateral pressures in a 2-m TRH solution

Simulation	At	Bt	Ct	Dt	Et
Px,Py (bar)	1	−100	−150	−200	−250
Pattern
0	65.79	54.30	34.22	24.81	16.97
1	28.98	24.88	27.12	32.49	31.59
11	13.87	18.15	16.69	19.05	19.62
111	4.66	4.65	5.93	3.67	6.65
1111	0.65	1.40	0.90	0.21	0.81
2	4.96	7.58	10.45	17.02	15.05
21	4.20	7.42	14.50	14.92	16.39
211	2.81	3.81	7.84	6.13	9.28
2111	0.52	1.15	1.84	1.45	2.49
22	0.01	0.61	2.24	0.94	0.70
3	0.24	0.72	1.23	2.30	2.18
31	0.31	1.13	2.20	1.38	1.36
311	0.44	0.51	1.30	1.05	1.04
4	0.04	0.03	0.08	0.14	0.17
Others	0.52	1.66	1.46	2.44	3.70
Total	128	128	128	128	128

A pattern is noted by a series of integers (in descending order) indicating the number of H-bonds formed between a TRH molecule and each one of a series of distinct DPPC molecules (14,19). A zero indicates molecules forming no H-bonds to DPPC, whereas “Others” indicates TRH molecules forming H-bonds to five or more DPPC molecules. Values are averaged over the final 10 ns of the simulations. See legend of Table 2 for the H-bonding criteria. See Table 1 for the simulation codes.

TABLE 5.

Average number of TRH molecules bridging a specific number of distinct DPPC molecules through (possibly multiple) H-bonds during the simulations of a hydrated DPPC bilayer at 325 K with different negative lateral pressures in a 2-m TRH solution

Simulation	At	Bt	Ct	Dt	Et
Px,Py (bar)	1	−100	−150	−200	−250
Degree of bridging
0	65.79	54.30	34.22	24.81	16.97
1	34.19	33.21	38.88	51.95	48.99
2	18.46	27.39	36.07	36.43	38.15
3	8.01	9.40	15.80	12.32	18.09
4	1.47	3.07	2.96	2.25	4.25
Others	0.08	0.63	0.07	0.24	1.55
Total	128	128	128	128	128

A zero indicates molecules forming no H-bonds to DPPC, whereas “Others” indicates TRH molecules H-bonded to five or more distinct DPPC molecules. Values are averaged over the final 10 ns of the simulations. See legend of Table 2 for the H-bonding criteria. See Table 1 for the simulation codes.

DISCUSSION

This work represents a preliminary simulation study of the effect of mechanical stress on phospholipid membranes, and the modulation of their response by sugars. It is restricted to the effect of lateral stretching forces applied on a very short (30 ns) timescale, and to one type of lipid (DPPC) and sugar (TRH) in a moderately concentrated solution (2 m). It is not entirely obvious how the effect of hydrostatic or osmotic pressure variations on a living cell will map onto corresponding changes affecting a microscopic patch of its cell membrane. As schematized in Fig. 1, this mapping is also likely to be time-dependent, with the immediate response to a rapid variation in external conditions (shock) being followed by various possible adaptation processes. Furthermore, the immediate response of a membrane to mechanical stress is also known to be dependent on the loading rate of the tension, i.e., on the timescale of the shock itself (37). Our simulations are expected to be (qualitatively) representative for the (sugar-modulated) short time response of a membrane to a hypotonic osmotic shock or an expansive hydrostatic shock (implying membrane stretching). However, the response to hydrostatic pressure changes (and its modulation by sugars) is also likely to be influenced by the concomitant change in the normal pressure (P_n in Fig. 1), and by the influence of this change on lipid phase transitions. Such effects were not considered in this study (where the normal pressure was kept at 1 bar), and their investigation will be undertaken in future work.

Keeping these restrictions in mind, this study led to the following observations:

1. The presence of TRH slightly changes the final (equilibrated) structure and increases the area per lipid of the bilayer when subjected to important stretching forces. However, the bilayer structure is essentially unaffected by the presence of TRH (compared with pure water) in the absence of surface tension (A_w vs. A_t) or at the lowest negative lateral pressure considered (−100 bar; B_w vs. B_t). The simulations under the highest negative lateral pressure considered (−250 bar; E_w vs. E_t) result in the disruption of the bilayer. However, the sugar also appears to affect the mechanism of disruption (dividing water channel in E_w vs. toroidal water pore in E_t).

2. The presence of TRH slows down the relaxation of the bilayer structure and area per lipid toward equilibrium after activation of the stretching forces. This is likely attributable to: (1), the presence of TRH molecules bridging multiple lipid molecules through H-bonds, thereby providing additional “cohesive” forces between lipids (that would oppose membrane expansion); and (2), the higher viscosity (lower diffusivity) of the TRH solution compared with pure water (14,20,21).

3. With the increase in the surface tension (and the concomitant increase in the area per lipid), the number of TRH-DPPC H-bonds increases significantly. This increase is accompanied by: 1), a simultaneous (though more limited) increase in the number of water-DPPC H-bonds; 2), an increase in the proportion of TRH-DPPC H-bonds involving the ester (as opposed to the phosphate) groups of the lipids; and 3), an increase in the number of TRH molecules bridging two or more DPPC molecules through (possibly multiple) H-bonds. The latter two observations are probably related to an increase in the ability of TRH molecules to intercalate between lipid headgroups, and penetrate deeper into the membrane.

Interestingly, many of the features observed here in the context of mechanical stress (stretching) are similar to those observed in previous studies involving thermal stress (14,20) (elevated temperature; associated with a much more limited increase in the area per lipid): (1), clustering of the sugar molecules at the interface between the lipid headgroups and the solvent; (2), partial replacement of water molecules in the vicinity of the lipid headgroups, with direct sugar-lipid interactions through H-bonds; (3), reinforcement of these interactions upon increasing the magnitude of the stress factor; and (4), a concomitant increase in the proportion of H-bonds involving the ester groups as well as in the degree of bridging. However, these effects were found to correlate with a significant stabilization of the bilayer structure against thermal disruption, whereas no clear protective effect against mechanical stress was observed in this case. The results for negative lateral pressures down to −200 bar suggest (in line with previous studies (17,18)) that TRH slightly enhances (rather than prevents) a membrane expansion under the effect of stretching forces. At −250 bar, the system without TRH undergoes membrane disruption by the formation of a dividing water channel, whereas the system with TRH remains at the level of toroidal pore formation. This observation could be interpreted tentatively as resulting from a protective effect of TRH in this case. However, because of the very short timescale of the transition observed in simulation E_w (only ∼6 ns) and because of the bias introduced by artificial periodicity (bilayer stacking with direct headgroup-headgroup contacts after 6 ns), this interpretation remains speculative, and should be tested by additional simulations involving much lower expansion rates (to be addressed in future work).

CONCLUSIONS

These simulations suggest that, whereas TRH preserves the integrity of biological membranes under thermal stress, TRH alone does not preserve the integrity of biological membranes under mechanical stress (in the form of lateral stretching), at least in the surface tension and concentration regimes investigated. Even though the sugar establishes H-bonds with the lipid headgroups, the number, degree of bridging, and reaching depth of which increase with the magnitude of perturbation, these interactions are not sufficient to preserve the integrity of the membrane structure and to prevent its extreme elongation and possible disruption under the effect of stretching forces.