Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2008 Jul 18;95(8):4077–4088. doi: 10.1529/biophysj.108.132738

Mapping Local Matrix Remodeling Induced by a Migrating Tumor Cell Using Three-Dimensional Multiple-Particle Tracking

Ryan J Bloom *, Jerry P George *, Alfredo Celedon †,‡, Sean X Sun *,†,‡, Denis Wirtz *,‡
PMCID: PMC2553112  PMID: 18641063

Abstract

Mesenchymal cell migration through a three-dimensional (3D) matrix typically involves major matrix remodeling. The direction of matrix deformation occurs locally in all three dimensions, which cannot be measured by current techniques. To probe the local, 3D, real-time deformation of a collagen matrix during tumor cell migration, we developed an assay whereby matrix-embedded beads are tracked simultaneously in all three directions with high resolution. To establish a proof of principle, we investigated patterns of collagen I matrix deformation near fibrosarcoma cells in the absence and presence of inhibitors of matrix metalloproteinases and acto-myosin contractility. Our results indicate that migrating cells show patterns of local matrix deformation toward the cell that are symmetric in magnitude with respect to the axis of cell movement. In contrast, patterns of matrix release from the cell are asymmetric: the matrix is typically relaxed first at the back of the cell, allowing forward motion, and then at the cell's leading edge. Matrix deformation in regions of the matrix near the cell's leading edge is elastic and mostly reversible, but induces irreversible matrix rupture events near the trailing edge. Our results also indicate that matrix remodeling spatially correlates with protrusive activity. This correlation is mediated by myosin II and Rac1, and eliminated after inhibition of pericellular proteolysis or ROCK. We have developed an assay based on high-resolution 3D multiple-particle tracking that allows us to probe local matrix remodeling during mesenchymal cell migration through a 3D matrix and simultaneously monitor protrusion dynamics.

INTRODUCTION

Cell migration drives embryonic and tissue development, and sustains important physiopathological factors, including cancer metastasis, wound healing, and immunological responses. In part because of the limitations of current imaging techniques and biophysical assays, most of what we know about cell migration stems mostly from studies of cell motility on planar two-dimensional (2D) substrata. In particular, the introduction and subsequent refinements of traction microscopy (1–5) have provided critical insights into the fundamental mechanical aspects of cell migration. This method computationally transforms the movements of beads embedded in a stiff (polyacrylamide) gel placed underneath the cell into mechanical stresses induced by the cytoskeleton-driven contractile motion of the cell.

However, the physiological environment of most cells in vivo is three-dimensional (3D). Cells live and move within, not on top of, an extracellular matrix. Even endothelial and single-layered epithelial cells, which form 2D structures in vivo, move through the 3D extracellular matrix and 3D connective tissues in the context of disease, such as during wound healing and cancer metastasis. Although it is more relevant to cell behavior in vivo, mapping the local matrix deformation generated by cells moving through a 3D matrix poses a major challenge because cells that are fully embedded inside a matrix deform that matrix locally in all three directions (6–8).

Current methods that probe matrix deformation have led to important insights into the interplay among matrix remodeling, cell adhesion, and cell contractility. These methods can be categorized as 1), those that use embedded beads tracked by confocal microscopy (9–11) and 2), those that monitor the 2D projections of local 3D movements of matrix fibers by phase contrast (12), differential interference contrast (DIC) microscopy (13,14), or fluorescence microscopy (15). 3D single-particle tracking schemes have been devised to probe in real time the 3D displacements of a single bead, typically for single-molecule applications. These tracking methods take advantage of out-of-focus images and analyze the size and/or patterns of diffraction rings around the fluorescence (16–18) or bright-field images (19) of beads.

In this study we developed, tested, and exploited an experimental assay to map at the single-cell level the 3D matrix deformation field generated by individual cells migrating completely embedded inside a 3D matrix. This assay tracks simultaneously and in real time the 3D movements of multiple beads embedded in the 3D matrix. We establish proofs of principle for the assay by mapping the spatiotemporal patterns of local matrix deformation during single HT-1080 fibrosarcoma cell migration through a dense collagen I matrix in the absence and presence of inhibitors of matrix metalloproteinase (MMP) and myosin II-driven cytoskeleton contractility. We also take advantage of our assay, which can simultaneously monitor time-dependent cell-shape changes and matrix deformation, to investigate the correlation between local matrix remodeling and local membrane protrusion dynamics. This assay sheds light on the little-understood mechanism of cell migration inside 3D matrices, which more closely mimics the in vivo condition.

MATERIALS AND METHODS

Cell culture

HT-1080 cells (ATCC, Manassas, VA) were cultured in Dulbecco's modified Eagle's medium with 10% (v/v) fetal bovine serum (ATCC), and 100 units of penicillin/100 μg of streptomycin (Sigma, St. Louis, MO). For both culture and imaging, the cells were maintained at 37°C in a humidified, 5% CO2 incubator. The cells were passaged every 2–3 days for a maximum of 20 passages.

Collagen matrix

3D collagen matrices were prepared by mixing 3.64 mg/mL chilled acid-soluble rat tail type I collagen (final concentration 2 mg/mL; BD Biosciences, San Jose, CA), beads, and cells suspended in cell culture medium and reconstitution buffer inside a coverslip-bottom multiwell culture plate (LabTek, Campbell, CA). Reconstitution buffer contained 200 μM sodium bicarbonate and 200 μM HEPES (Sigma) in deionized water. All ingredients were mixed thoroughly on ice, with care taken to avoid introducing bubbles into the collagen solution. The pH of the collagen gel was maintained at 7.0 by 30–60 μl 1 M NaOH. Collagen samples containing the cells were allowed to solidify overnight in an incubator at 37°C and 5% CO2 before use. The concentration of the collagen matrix (2 mg/mL) was selected so that the matrix mesh size (<1 μm) was significantly smaller than the sizes of the cell and nucleus. Cells were seeded at extremely low density within the matrix to avoid potential confounding effects of local matrix deformation by neighboring cells.

Young's modulus of the collagen matrix

To approximately estimate forces from bead displacements in the matrix (see Discussion section), we measured the Young's modulus of the collagen gel. Briefly, gels immersed in medium were subjected to weights of increasing mass placed on top of the gel (surface area: 2.2 mm2) and the gel deformation in the z direction was measured. The Young's modulus was obtained from the slope of the line of the applied pressure (weight per unit area) as a function of the gel strain, 1 − t/t0, where t is the measured thickness and t0 is the initial thickness of the specimen. We found that a 2-mg/mL collagen gel has a Young's modulus of ∼200 Pa.

3D multiple-particle tracking

To capture the local 3D mechanical traction and relaxation of the collagen matrix induced during the migration of HT-1080 cells inside the matrix, bright-field images of the beads embedded in the matrix were captured using a Cascade 1K CCD camera (Roper Scientific, Tucson, AZ) mounted on a Nikon TE2000E microscope and a 60× Plan Fluor oil-immersion lens (N.A. 1.4; Nikon, Melville, NY). Cells in the matrix were maintained at 37°C in a humidified, 5% CO2 incubator (Pathology Devices, Westminster, MD) mounted on the microscope stage. To accurately capture the deformations of the matrix along the entire height of each cell, five positions of the microscope stage were memorized in parallel planes 8–10 μm apart (depending on the size of the cell) using a built-in Nikon z-motorized lens with 50 nm accuracy (Fig. 1). The time required for collection of these five images was 5 s. Using the Metavue software (Universal Imaging, West Chester, PA), a set of five images of each cell was collected every minute for typically 90 min, resulting in five separate 90-min videos of each cell in different z planes. Embedded in the matrix were 3.6-μm-diameter carboxylated polystyrene beads (Duke Scientific, Palo Alto, CA). These beads were large enough to negate Brownian displacements and were effectively tethered to the collagen matrix fibers by the reactive carboxyl group, which acted as faithful fiduciary markers of the local deformations of the collagen matrix induced by migrating cells.

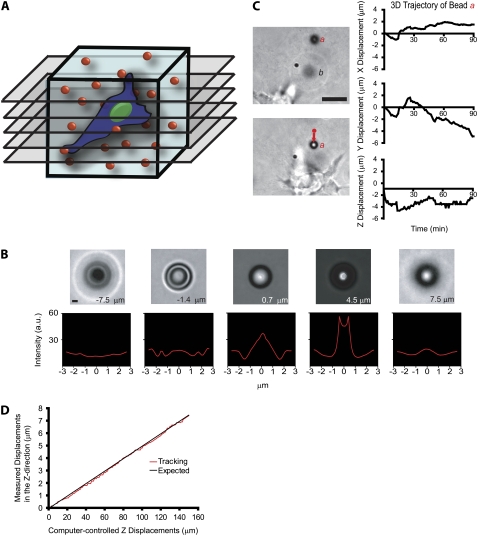
FIGURE 1.

FIGURE 1

Open in a new tab

Method to probe the local 3D deformation of the 3D matrix induced by a migratory cell. (A) Schematic of the method used to quantify the local deformation of a 3D collagen matrix (light blue) during cell migration. 4D bright-field microscopy is used to track in equally spaced planes of focus the time-dependent 3D movements of individual 3.6-μm-diameter carboxylated polystyrene beads dispersed in the matrix with high x, y, and z resolution. (B) To calibrate bead movements and before each experiment, randomly selected beads in the matrix are moved by the motorized microscope stage in the z direction to generate a reference image set. High z-movement resolution is achieved by analyzing the diffraction rings of the bead (see text for details). Scale bar, 3 μm. (C) Typical x, y, and z movements of a single polystyrene bead a near a migrating HT-1080 cancer cell (left panel). The initial coordinates of bead a were subtracted (right panel). Bead b is an example of a bead that becomes out of focus, illustrating the 3D deformation of the matrix. Scale bar, 20 μm. (D) Typical vertical displacement of a bead embedded in the matrix (i.e., “output” displacement) as a function of the computer-imposed vertical displacement of this bead by the microscope stage (i.e., “input” displacement). The root mean-squared difference between these two displacements is 120 nm, the spatial resolution of our particle-tracking method in the z direction.

The beads were tracked using customized software developed in MATLAB (The MathWorks, Natick, MA). For each bead in the collagen matrix, the coordinates x and y of the center of the bead were measured using the average of three intensity profiles in the x and y directions, f(x) and f(y), respectively. The x coordinate was obtained from the displacement in the x direction required to match f(x) and f(−x) given that the intensity profile is symmetric with respect to the center of the bead. The x coordinate is half of the distance at which the maximum of the correlation function C(Δx) = ∫f(x)f(−x + Δx)dx occurs (19). The same applies for the y coordinate of the center of the bead. This method allowed us to track the center of the bead with subpixel resolution (∼20 nm). The z coordinates of the beads were measured using the change in the diffraction rings as a function of the off-focus distance (19). First, a calibration set of 200 profiles spanning 10 μm was obtained from an immobile bead embedded in the collagen matrix in planes of focus 50 nm apart, using the z-motorized microscope stage. Then, the relative z-position of a bead in the collagen matrix containing the cells was obtained by comparing its intensity profile (e.g., Fig. 1 C) with the calibration set. Square error minimization followed by interpolation between the closest profiles in the calibration set allowed us to find the z value with an accuracy of ∼120 nm. This accuracy corresponds to the root mean-square (RMS) difference between measured and imposed displacements of beads in the matrix in the z direction (Fig. 1 D).

Cell speed

Cell speed within the matrix was measured using image recognition software (Metamorph/Metavue). The nucleus of each cell was tracked for 90 min, with cell speed (displacement/time) calculated every minute.

Immunofluorescence microscopy

To visualize actin filament architecture and nuclear DNA, cells were incubated with Alexa Fluor 568 phalloidin (Invitrogen, Carlsbad, CA) and 100 nM 4′,6-diamidino-2-phenylindole (DAPI; Invitrogen), respectively, for 1 h. Images of cells were collected using a Cascade 1K CCD camera (Roper Scientific) mounted on a Nikon TE2000E epifluorescence microscope equipped with a 60× oil-immersion objective (Nikon) and controlled by the Metamorph imaging software (Universal Imaging).

Cell treatments

The protease inhibitor cocktail added to the medium before the HT 1080 cells were embedded in the collagen matrices consisted of 50 μM GM 6001 (Calbiochem, La Jolla, CA) dissolved in dimethyl sulfoxide (J. T. Baker, Phillipsburg, NJ), 250 μM E-64 protease inhibitor (Calbiochem) dissolved in medium, 2 μM leupeptin (Sigma) dissolved in medium, 100 μM pepstatin A from microbial source (Sigma) dissolved in dimethyl sulfoxide, and 2.2 μM aprotinin from bovine lung (Sigma) dissolved in medium, as described previously (20). Nonmuscle myosin II, ROCK, and Rac1 were inhibited using blebbistatin (Sigma), 50 μM Y27632 (Sigma), and 100 μM NSC23766 (Calbiochem), respectively. These drugs were added to the medium before cell embedding and matrix gelation, and after gelation by adding these drugs in medium on top of the solidified matrix, as described previously (20).

Statistics

The mean values, standard error of measurement (SEM), and statistical analysis of bead displacements were calculated using Graphpad Prism (Graphpad Software, San Diego, CA). Two-tailed unpaired t-tests were conducted to determine significance, which was indicated using the standard Michelin Guide scale (***p < 0.001, **p < 0.01, and *p < 0.05). Unless indicated, comparisons are with control conditions. All experiments were conducted at least in triplicate.

RESULTS

Measurement of local 3D matrix deformation by 3D multiple-particle tracking

A cell migrating through a 3D collagen matrix deforms it locally in all three directions. To monitor matrix deformation, 3.6-μm-diameter polystyrene beads were incorporated inside a type-I collagen gel matrix before cells were seeded in the matrix (Fig. 1 A). The 3D movements of the beads embedded in the solidified matrix were tracked using a multiple-particle tracking method based on bright-field microscopy (Fig. 1, B and C) to monitor local 3D deformations of the matrix around the cell. We chose large beads so that their spontaneous Brownian motion would be negligible compared to the movements of the beads induced by cell-mediated deformations of the matrix. The surface of the beads was carboxylated so that the beads would adhere firmly to the collagen matrix, and faithfully report its local deformation by the cell. This was verified by applying known small and large displacements in the x, y, and z directions to the matrix using a motorized stage (see more details in Materials and Methods and Fig. 1 D).

We monitored the time-dependent coordinates x, y, and z of each bead in the matrix in real time after the initial calibration of the z displacements of the beads (Fig. 1 B; see more details under Materials and Methods). The displacements of the beads in the x and y directions were obtained by monitoring the intensity-weighted center of mass of each bead with 20-nm spatial resolution. The displacements of the beads in the z direction were obtained by analyzing the rings of diffraction of each bead with 120-nm resolution (Fig. 1 B).

The local displacements of the beads in the collagen matrix in the vicinity of single HT-1080 fibrosarcoma cells were generally on the order of several microns along each coordinate axis for 90-min tracking (Fig. 1 C). By comparison, the magnitude of the spontaneous displacements of the beads in the matrix in the absence of cells, presumably caused by the thermally-excited spontaneous movements of collagen fibers and (small) microscope stage drift, were <20 nm (Fig. 3 C). These large cell-mediated bead displacements and the large size of the cells prevented us from holding the position of the plane of focus constant and being able to simultaneously track all the beads in the vicinity of the cell over long periods of time. Therefore, we devised a scheme whereby the positions of the beads in the matrix were recorded in a stack of five 8–10-μm spaced parallel planes spanning the cell in the collagen matrix (Fig. 1 A). The collection of such a stack took <5 s and was typically conducted every minute for 90 min. This approach, based on high-resolution 3D multiple-particle tracking, allowed us to detect and quantify local time-dependent 3D deformations of the matrix in the vicinity of single motile cells while simultaneously monitoring cell-shape changes, such as membrane protrusion dynamics.

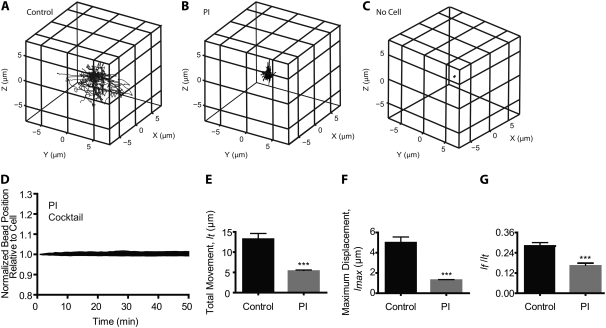
FIGURE 3.

FIGURE 3

Open in a new tab

Local 3D deformation of the collagen matrix during tumor cell migration in the presence and absence of protease inhibitors. (A–C) 3D trajectories (reported to an arbitrary origin) of randomly selected beads embedded in a collagen matrix for control HT-1080 fibrosarcoma cells (A), PI cocktail-treated HT-1080 cells (B), and far away from any cell (C). Beads were tracked in 3D for 90 min and their initial positions in the matrix were subtracted. (D) Changes in the distances between beads and points on a migrating HT-1080 cell treated with PI cocktail (see details in Fig. 2). (E–G) Analysis of the bead trajectories for 90-min 3D tracking in terms of their averaged total movement, lt (E); averaged maximum displacement (maximum excursion from their initial position), lmax (F); and averaged ratio of the net distance between initial and final positions of the bead, lf, and the total movement (G). ***p < 0.001. For panels D–G, at least five individual PI-treated cells were probed and a total of at least 50 beads were tracked in 3D per condition.

Patterns of 3D matrix deformation during 3D cell migration

Using our 3D multiple-particle tracking assay, we analyzed the location, direction, magnitude, and timing of local 3D matrix remodeling induced by HT-1080 cells (Fig. 2). Analysis of the bead trajectories in 3D revealed that the local deformation of the matrix never occurred in the direction away from the cell during cancer cell migration. The only beads that showed movement away from the cell were those located right next to the cell surface and pushed by the bulk motion of the cell body, and those that accompanied outward matrix relaxation after the initial inward movement (see more below). These local measurements are consistent with previous observations that showed global contraction of the collagen matrix impregnated with fibroblasts (21,22).

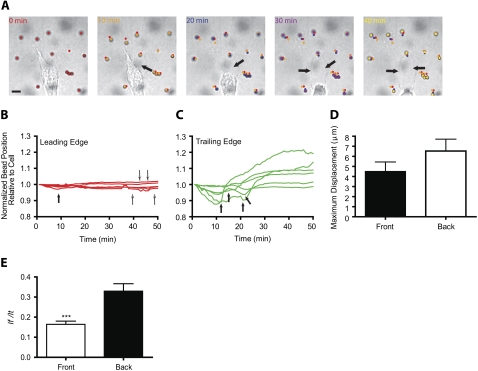
FIGURE 2.

FIGURE 2

Open in a new tab

Deformation of the matrix at the leading and trailing edges of a migrating cell. (A) Initial deformation of the collagen matrix toward the back of a migrating HT-1080 cell followed by the relaxation of the matrix away from the cell. Arrows indicate the formation of a growing defect in the collagen matrix in the wake of the migrating cell. Scale bar, 20 μm. See also Movie S1, Data S1. (B and C) Changes in the distances between beads and fixed points in the image in the matrix regions near the leading edge (B) and near the back (C) of a migrating HT-1080 cell (shown in panel A). Distances were normalized by their initial value. Beads and curves in panels B and C are color-coded according to their position in panel A. Thick arrows indicate onsets of relaxation; narrow arrows in panel B indicate beads that have not relaxed yet. (D) Averaged maximum displacements of the beads toward the cell, lmax, in regions of the matrix at the back and front of control HT-1080 cells. (E) Averaged ratios of the net distance between the initial and final positions of the beads, lf, and their total displacements, lt, in regions of the matrix near the front and back of the cell. A ratio close to zero indicates an elastic, reversible deformation of the matrix; a ratio close to one indicates an irreversible “rupture” deformation of the matrix. ***p < 0.001. In panels D and E, at least 10 cells were probed and a total of at least 100 beads were tracked.

Multiple-particle tracking revealed patterns of local matrix deformation toward and away from the cell that were qualitatively different in the regions of the matrix near the front and back of the migrating cells (Fig. 2, B and C). The magnitude of matrix deformation at the back and front of the cell was (on average) typically symmetric in magnitude and direction (toward the cell). In particular, the averaged maximum displacements toward the cell, lmax, of the beads located in regions of the matrix near the leading and trailing edges of migrating cells were similar (Fig. 2 D). This result indicates that the magnitude of matrix deformation toward the cell was, on average, similar in regions of the matrix at the back and the leading edge of the cell.

For each tracked bead, we observed that after an initial matrix deformation toward the cell, the matrix then relaxed away from the cell. This matrix relaxation was asymmetric in magnitude and timing with respect to the axis of movement of the cell. Beads in the vicinity of the leading cell edge moved first toward the cell surface and then relaxed away from the cell back to their initial positions. Accordingly, distances between beads and the closest points on the cell surface (normalized by the initial values of these distances) first became smaller than one and then returned to a value close or equal to one (Fig. 2 B). Hence local cell-mediated matrix deformation was typically “elastic” in regions of the matrix near the leading edge of the cell (e.g., Fig. 2 B).

In contrast, in regions of the matrix near the rear of the cell, the beads initially moved toward the cell with a magnitude similar to or slightly larger than that of the beads at the front of the cell (Fig. 2, C and D), but then underwent movement away from the cell that was typically much larger than the initial distance between the cell and the beads (e.g., Fig. 2 C). Accordingly bead-cell distances at the rear of the cell became first smaller than one, and then became larger than one (Fig. 2 C). In classical mechanics, this is the signature of the fracture of a material subjected to large stresses. Indeed, large global relaxation of the matrix at the rear of the cell was accompanied by both forward cell motion and the formation of a rapidly growing hole (or defect) in the collagen matrix in the wake of the migrating cell (arrows in Fig. 2 A; more easily seen in the Supplementary Material, Movie S1, Data S1). Moreover, matrix relaxation at the front of the cell was typically delayed with matrix relaxation at the back of the cell (Fig. 2, B and C). We observed that global relaxation of the matrix from the back of the cell occurred when a sufficient number of cell protrusions at the rear of the cell had released their attachments from the matrix fibers (e.g., arrows in Fig. 2 C).

We observed that some rare beads at the front relaxed away from the cells before or at the same time as beads near the back of the cell (e.g., closed arrow in Fig. 2 B), but these did not lead to global matrix relaxation or release from the cell (thin semi-open arrows in Fig. 2 B). In some less frequent instances (<10% cells), we observed that some cells did not delay matrix relaxation at the front: cells released the matrix in the back while they simultaneously generated thin protrusions to pull the matrix at its front. Moreover, cells often contracted the collagen matrix at the back with a large magnitude as it moved forward, while they simultaneously contracted the matrix at their front with a smaller magnitude (e.g., Fig. 2, B and C). This larger contraction at the back mediated rapid mechanical breakdown of the matrix, which propelled the cell forward and therefore presumably precluded the need for the cell to pull the matrix at its leading edge (Movie S1, Data S1).

To quantify matrix relaxation away from the cell after the initial deformation of the matrix toward the cell, we introduced the parameter lf/lt, which is the ratio of the distance between the initial and final positions of each bead, lf, to the total displacement of the bead, lt. This ratio is close to zero for an elastic (reversible) recovery after matrix contraction (since lf = 0 μm), akin to a “perfect” elastic recoil after stretching, and is one if only net bead movement toward the cell occurs without matrix relaxation (since, in this case, lf = lt). We found that the parameter lf/lt was significantly lower in regions of the matrix near the front than in regions of the matrix near the back of the cell. Therefore, the deformation of the matrix near the front of the cell is mostly elastic, whereas that at the back of the cell is more irreversible.

Taken together, these results indicate that HT-1080 cell migration inside a 3D matrix involves only the deformation of the matrix toward the cell without large-scale pushing of the surrounding matrix, the elastic relaxation of the matrix near the front of the cell, and the irreversible rupture deformation of the matrix near the back of the cell. In general, for each cycle of motility, the cell deforms the matrix with equal magnitude at its front and back, then releases the matrix first at the back, moves forward, and finally releases the matrix at its front.

Effect of protease inhibitors on local matrix contraction and relaxation

To functionally validate our assay, we subjected cells to inhibitors that are known to reduce or abrogate cell migration (at least in 2D motility). In the first series of experiments, we investigated 3D local matrix deformation when the cells had been treated with multiple MMP inhibitors (denoted PI cocktail, Fig. 3), which were expected to reduce the magnitude of matrix deformation since such treatment blocks pericellular proteolysis (see more in Discussion). We found that the magnitude of the deformation of the collagen matrix was greatly reduced in PI-treated cells (Fig. 3, A, B, and D, and Movie S2, Data S1). Analysis of the bead trajectories showed that the mean maximum displacements (i.e., maximum excursions of the beads toward the cell from their initial position, lmax) and the mean total (curvilinear) displacements of the beads (lt) were drastically reduced in cells treated with the PI cocktail compared to control untreated cells (Fig. 3, E and F). Accordingly, the averaged speed of migration of PI-treated cells was drastically reduced compared to control cells (Fig. 4 E).

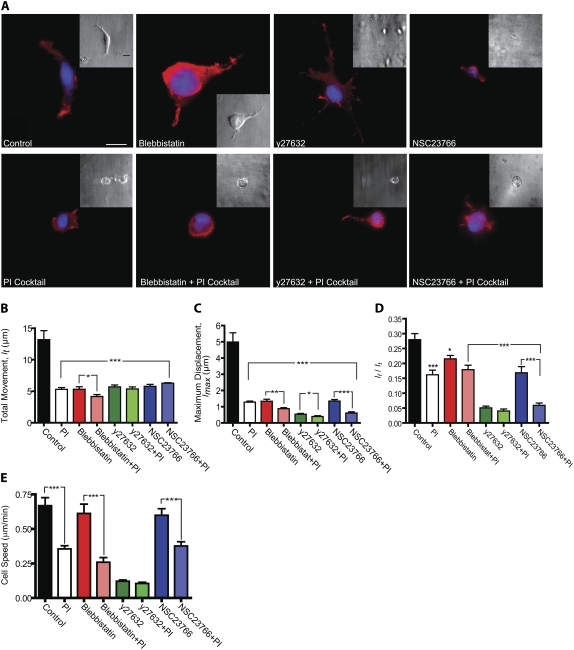
FIGURE 4.

FIGURE 4

Open in a new tab

ROCK, Rac1, and myosin II mediate local cell matrix deformation. (A) Morphology (through phase-contrast microscopy, insets) and actin filament architecture (through fluorescence microscopy) of control cells and cells treated with specific ROCK inhibitor Y27632, 5 μM myosin II inhibitor blebbistatin, and specific Rac1 inhibitor NSC23766 in the presence/absence of the PI cocktail. Cells were fixed and stained for actin using Alexa-488 phalloidin and nuclear DNA using DAPI. Scale bar, 20 μm; scale bar in insets, 40 μm. (B–D) Analysis of bead trajectories in terms of the mean total displacement of each bead (C), the mean maximum displacement of each bead (D), and the mean ratio of the net distance traveled by each bead to its total movement (E) for control cells and cells treated with either Y27632, NSC23766, or blebbistatin in the presence and absence of the PI cocktail. Beads were tracked for 90 min. (E) Averaged cell speed for conditions shown in panel A. For each condition in panels B–D, at least five individual cells were probed and a total of at least 50 beads were tracked in 3D per condition. ***p < 0.001, **p < 0.01, and *p < 0.05.

PI-cocktail treatment also significantly reduced the mean ratio lf/lt (Fig. 3 G), which indicates that the deformation of the matrix became dominantly elastic, presumably because it did not induce the formation of matrix defects that would prevent a perfect recovery after cell-induced stretching of the matrix. Moreover, no significant difference in the magnitude and type of matrix deformation (elastic versus rupture deformation) occurred between the front and back of the PI-treated cells.

Rac1, ROCK, and myosin II mediate local cell matrix deformation

In a second series of experiments to functionally validate our assay, we investigated the effect of RhoGTPase inhibitors that are known to reduce single-cell migration, at least on planar substrates. Using our 3D multiple-particle tracking assay, we mapped the magnitude of matrix remodeling after inhibition of myosin II-induced cell contractility and F-actin architecture regulators Rho/ROCK and Rac1 (23). We targeted ROCK and nonmuscle myosin II because they are two key regulators of membrane ruffling dynamics (24), and Rac1 because it is the small GTPase that regulates the persistence of migration (25,26).

Control HT-1080 cells in collagen matrix displayed mostly cortical actin, with few actin filament bundles (Fig. 4 A). Cells treated with 5 μM of the specific myosin II inhibitor blebbistatin (27) displayed a morphology similar to that of control cells (Fig. 4 A). In particular, cells continued to display ruffling protrusions. At 5 μM, ∼50% myosin II activity is inhibited (28). Actin staining appeared mostly at the cell periphery (cortex) and the number of F-actin bundles in the cell body was reduced (Fig. 4 A). Application of the 3D multiple-particle tacking assay indicated that partial myosin II inhibition greatly reduced the magnitude of local matrix contraction (Fig. 4, B–D). Accordingly, the speed of migration of blebbistatin-treated cells was slightly reduced compared to that of control untreated cells (Fig. 4 E). At 85% myosin II inhibition using 50 μM blebbistatin (28), membrane ruffling was dramatically reduced, further diminishing both the magnitude of matrix deformation and cell speed (data not shown).

Cells treated with Y27632 (29,30), which inactivates ROCKI and ROCKII, displayed a dendritic morphology with a thin protruding leading edge that was longer than in control cells (Fig. 4 A) (31). Inhibition of ROCK, which is upstream of myosin II and regulates actin filament assembly, significantly reduced both the magnitude of matrix contraction (Fig. 4, B and C) and cell speed (Fig. 4 E). Moreover, inhibition of ROCK rendered the relaxation of matrix deformation much more elastic-like than in cells treated with 5 μM blebbistatin (Fig. 4 D). Cells treated with specific inhibition of GTPase Rac1 by NSC23766 (32) displayed a blebbing morphology, and membrane ruffling disappeared (Fig. 4 A). The effect of Rac1 inhibition on the magnitude of matrix contraction was intermediate between those of ROCK and myosin II inhibitions (Fig. 4, B–D). Combining MMP inhibition with inhibition of either ROCK, Rac1, or myosin II synergistically reduced the magnitude of matrix contraction, lmax, more than in cells treated with any one of these inhibitors (Fig. 4 C) and drastically reduced cell migration (Fig. 4 E) (26).

Taken together, these results suggest that our assay can quantify matrix remodeling when cells inside a matrix are subjected to cytoskeleton inhibitors. We find that the inhibition of either ROCK, Rac1, or myosin II greatly reduces the magnitude of matrix deformation and cell speed, and that combining PI treatment with the inhibition of either ROCK or myosin II or Rac1 synergistically inhibits matrix deformation.

Spatial correlation between localized protrusive activity and matrix contraction

Exploiting the fact that our assay can visualize simultaneously both the surface morphology of the cell and the deformation of the matrix, we tested the hypothesis that local membrane ruffling would induce local matrix deformation. The surface of control cells displayed rapidly growing and retracting protrusions terminated by long finger-like protrusions, which dynamically shifted their position along the cell surface. The position of the main growing protrusion correlated with the direction of cell movement (e.g., Fig. 5 A). We detected each actively growing ruffling membrane protrusion and scored whether local matrix deformation occurred, and if it did, we assessed its magnitude. We found a near-perfect correlation between the position of the growing ruffling protrusions from the cell surface and the position of contraction in the matrix (first set of bars in Fig. 5 D). Moreover, regions along the cell surface where protruding ruffling was absent, such as along the relatively smooth sides of a moving cell, correlated with regions of the matrix that showed no significant deformation.

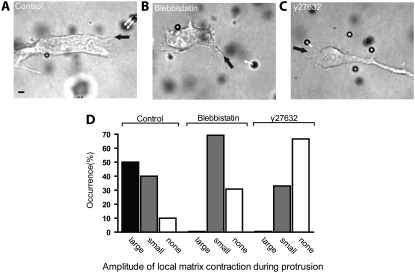
FIGURE 5.

FIGURE 5

Open in a new tab

Correlation between protrusive activity and matrix deformation during 3D cell migration. (A–C) Examples of actively growing membrane protrusions (black arrow) and associated local matrix deformations (white arrows) for a control HT-1080 cell (A), a 5 μM blebbistatin-treated cell (B), and a Y27632-treated cell (C). Scale bar, 20 μm. (D) Occurrence and magnitude of local collagen matrix deformations in the vicinity of actively growing cell membrane protrusions (see text for details). This shows that matrix deformations toward a control occurred only in the presence of growing cell protrusions. This correlation largely disappeared after inhibition of ROCK or partial inhibition of myosin II. Ten individual cells were probed and a total of at least 100 beads were tracked in three dimensions per condition.

Both the occurrence of membrane protrusions and the spatial correlation between the location of a membrane protrusion and local matrix deformation diminished significantly when myosin II was inhibited, and diminished further when ROCK was inhibited (second and third sets of bars in Fig. 5 D, respectively; see also Fig. 5, B and C). Rac1 inhibition and PI treatment separately eliminated membrane ruffling completely and induced cell blebbing (Fig. 4 A). For blebbing cells (i.e., for PI-treated cells and NSC26633-treated cells), matrix contraction was drastically reduced (Figs. 3 and 4). Therefore, we could not reliably test for a possible correlation between local membrane blebbing and local matrix contraction. Together, these results show that our assay can probe simultaneously membrane protrusion dynamics and local matrix remodeling. The results suggest that localized plasma membrane protrusion dynamics correlates with local matrix remodeling, and that this correlation is mediated by ROCK and myosin II activity.

DISCUSSION

Cells induce and exploit symmetric matrix tension and asymmetric release to move forward

Our 3D multiple-particle tracking results reveal that migrating cells deform the matrix in regions of the matrix behind the cell in a fundamentally different manner from that in regions in front of the cell. In general, the matrix in the space ahead of cell movement is deformed elastically, i.e., initial matrix deformations toward the cell induced by actively growing thin protrusions are almost completely recovered after the matrix fibers are detached from the protrusions. In contrast, the matrix behind the cell undergoes “fracture deformation”, i.e., the initial pulling deformation toward the cell by growing cell protrusions breaks down the matrix irreversibly. Indeed, migrating cells often leave in their wake large and rapidly growing matrix defects that correlate with large and rapid matrix relaxation as measured by our assay. We speculate that the large tension induced by the cells in their wake, combined with local MMP-mediated local pericellular proteolysis, renders the matrix highly susceptible to mechanical breakdown. Biochemical breakdown of the matrix is initiated by MMPs, followed by a large-scale mechanical breakdown induced by the large tension in the matrix itself, mediated by ROCK/myosin II. This matrix defect quickly releases the tension in the back of the cell and, in turn, allows the front of the cell to move forward.

This asymmetric deformation of the matrix is likely to cause a corresponding asymmetry in the mechanical properties of the matrix since the stiffness of a gel depends directly on its local microstructure (33,34). The elastic deformation of the matrix in front of the cell suggests that the mechanical properties of the matrix in the space near the cell's leading edge remain mostly unchanged during cell movements. In contrast, the matrix pore size is greatly increased in the wake of the cell, which may render the matrix softer and more fragile. Such induced spatial asymmetry in the mechanical properties of the matrix does not occur during cell migration on planar stiff substrata such as extracellular matrix-coated glass. The induced asymmetry in the matrix microstructure may contribute to the observed higher persistence of migration of cells embedded in a 3D matrix compared to migration on 2D substrata (25). Once the cell has spontaneously created a locally asymmetric matrix microstructure, the cell can only continue to move in the same direction, and mechanical breakdown at the rear of the cell prevents it from moving back. We are currently using particle-tracking microrheology (35) to probe directly the mechanical properties of the matrix near a migrating tumor cell. Results will be presented in a future publication.

Our 3D multiple-particle tracking assay reveals that, upon MMP inhibition, the magnitude of matrix contraction is drastically reduced and patterns of matrix remodeling become uniformly distributed around the cell. Moreover, the matrix responds purely elastically to local mechanical traction by the cell. These results suggest that when a cell adopts a rounded or blebbing morphology induced by PI treatment, asymmetric release of the matrix after its contraction does not occur. Moreover, PI treatment greatly reduces the motility of HT-1080 cells.

Although this result is inconsistent with early observations of tumor cell migration (20,26), it is consistent with observations in more recent studies (36,37) that used native collagen similar to the one used in this work. Friedl and co-workers originally observed that PI-treated HT-1080 cells could still invade a collagen matrix thanks to a mesenchymal-to-amoeboid switch in morphology and switch in mode of migration (20). PI-induced amoeboid migration requires active Rho/ROCK, as Y27632 or C3 treatment (which inactivates RhoA, RhoB, and RhoC) blocks motility (26). Moreover, these early studies suggested that to migrate through a collagen matrix (20) or Matrigel (which contains collagen IV, laminin, and growth factors) (26), colon carcinoma cells LS174T undergo amoeboid migration and do not require pericellular proteolysis to migrate, but require Rho/ROCK, as Y27632 treatment blocks LS174T cell motility. However, Wolf et al. (20), Sahai and Marshall (26), and Zaman et al. (38) suggested that this amoeboid migration in certain tumor cells treated with the PI cocktail can only be observed in cells embedded in a matrix composed of pepsin-extracted collagen and in Matrigel, not in native collagen. Pepsin extraction produces collagen telopeptides that miss Schiff base crosslinks (39–41). Our results suggest that Rho/ROCK/myosin, Rac1, and pericellular proteolysis are all required for the net migration of HT-1080 cells through native collagen I. Our results also suggest that both the magnitude of matrix deformation and the speed of migration are synergistically reduced by simultaneous blockade of pericellular proteolysis and Rac1 or the Rho/ROCK/myosin pathway. Clearly, more studies are needed to understand these differences; in particular, a more thorough characterization of the microstructure and microrheology of the collagen matrix during cell migration is required.

Traction force microscopy indicates that cells on a planar substrate use mainly traction from the lamellipodium at the leading edge for forward locomotion (1). During the 2D migratory process, the mid-body and trailing edge of the cell are mostly passive elements and are towed by the lamellipodium. In contrast, our quantitative measurements using 3D multiple-particle tracking show that ruffling protrusions at the front and back edge of the cell pull the matrix toward the cell surface with equal magnitude. Therefore, these results suggest that asymmetry during locomotion in a 3D matrix does not necessarily stem from an imbalance of traction forces between front and back, but rather from an imbalance in the magnitude and timing of matrix relaxation after initial contraction. Moreover, there seems to be little correlation between the protrusive activity of the plasma membrane of cells migrating on planar substrates and the local traction of the underlying substratum (42). In contrast, our results reveal a near-perfect spatiotemporal correlation between matrix contraction and active filopodial protrusions. These fundamental differences underlie the importance of matrix dimensionality (2D versus 3D) not only in guiding cell morphology and function (37,43–46), but also in regulating the patterns of matrix traction and release that drive cell migration.

Elastic deformation ahead of mesenchymal cell migration, and rupture deformation in the wake of cell migration

Recent measurements indicate that the forces induced by a keratocyte crawling on a planar substrate and pushing against an AFM cantilever are on the order of 1–5 nN (47). An extrapolation of these results obtained with a 2D model of cell motility to the current 3D case would predict that the matrix in the vicinity of the leading edge of a migrating cell should display outward deformation, away from the cell surface, due to growing membrane protrusions. Indeed, actin assembly-mediated forces against cell membrane would be transmitted to the contiguous collagen matrix. Even when the fact that matrix digestion occurs is taken into account, the growing protrusions of the plasma membrane should be accompanied by bead movements away from the cell. Instead, beads in the vicinity of migrating cells always move first toward the cell and then away from the cell after matrix relaxation from the cell—never the other way around. If pushing forces of magnitude similar to those produced during 2D cell migration (∼nN) existed during 3D cell migration, they would be readily detected with our assay. Our observations are consistent with previous results obtained using global matrix contraction assays (9–11,13,48) or by monitoring the apparent movements of collagen fibers in the vicinity of migrating cells (49)

The absence of significant pushing forces during 3D migration can partly be explained thanks to close observations by DIC or phase-contrast microscopy of how a single cell moves in a 3D collagen fiber matrix. Thin filopodial protrusions at the leading edge do not push against a continuum of collagen, but proceed along individual fibers, often until they encounter a denser, more disorganized region of the collagen fiber matrix. During their progression along the collagen fibers, these actively protruding structures at the back and front of the cell pull on their supporting fibers, which, due to the high connectivity among collagen fibers, cause large-scale movement of the matrix toward the cell body. At the front of the cell, the protrusions ultimately detach from the collagen fibers, generating a rapid large-scale elastic relaxation of the surrounding matrix fibers. At the back of the cell, the protruding filopodia, which are pulling on the fibers, often create a hole in the matrix during the initial traction of the collagen fibers toward the cell body. This hole becomes larger as the cell moves forward. Of importance, the magnitudes with which thin cell protrusions pull on the collagen fibers at the front and the back of the cell are similar (Fig. 2 D). In contrast, the fracture of the matrix at the back of the cell renders matrix relaxation asymmetric: it is reversible or elastic at the front of the cell and irreversible at the back of the cell (Fig. 2 E). This asymmetric relaxation between the front and back of the cell is mediated by acto-myosin contractility and Rac1, and is completely eliminated after the inhibition of MMPs.

In contrast to the present 3D cell migration case, the stresses generated during 2D cell migration can be measured quantitatively using traction force microscopy because the measuring substratum embedded with probing beads and top-coated with extracellular matrix molecules is not in direct contact with the cell. Here the matrix inside which the cells move is also used to probe local matrix deformation. These displacements cannot readily be transformed into stresses because the matrix undergoes local degradation. Nevertheless, one can use the displacements of the beads to obtain an approximate estimation of the order of magnitude of the contractile forces exerted by migrating HT-1080 cells. The local force f generated by the cell is approximately given by 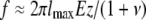Inline graphic (see the Supplementary Material, Data S1, for the derivation), where E is the Young's modulus of the collagen gel, ν is its Poisson ratio, lmax is the magnitude of bead movement during matrix contraction, and z is the distance between the bead and the cell. For instance, for beads z = 5 μm away from the location of the contractile force on the cell and moving lmax = 5 μm during matrix contraction (Fig. 2 D), using the above estimate, the maximum force exercised by the cell is 4200 pN = 4.2 nN, assuming that the Poisson ratio of the collagen gel is 0.2 (50,51). This is an underestimate because during matrix contraction the cell partially digests the matrix; moreover, the direction of the contractile force is unknown. The cell also exerts forces over a region, not just at a point along its periphery. To obtain a more detailed estimate of the forces exerted by a cell within a 3D matrix, a quantitative estimate of the digestion rate of the matrix and a mathematical formalism for describing a shrinking elastic body under tension are needed, which are beyond the scope of this article.

Advantages and limitations of 3D multiple-particle tracking mapping of matrix deformation

One of the salient advantages of our assay over current techniques is that it monitors with high resolution the spatiotemporal, 3D deformations of a matrix near a live cell fully embedded in the matrix. Although our use of bright-field microscopy instead of fluorescence microscopy somewhat reduces the spatial resolution of bead displacements in the z direction due to the diffraction from the matrix fibers and the cell, it allows us to monitor simultaneously local shape changes of the cell and local matrix remodeling. Nevertheless, our preliminary experiments suggest that extending our assay to take advantage of fluorescence microscopy would be straightforward, and it could be used to map both cytoplasmic and extracellular matrix microrheology simultaneously using fluorescent nanoparticles of different colors (46,52).

Our current assay could be used in other biological applications where the displacement of nanoparticles in real time and in all three directions is central to the cell function being tested, including monitoring endocytic and phagocytic events in real time (18), mapping the microrheological properties of the cytoplasm (53) or the nucleus (54) in real time and in 3D, and tracking viral particles (21,55) or gene/protein delivery vehicles (56) from their initial binding interactions with host cell receptors on the apical surface to their translocation toward the nucleus.

Our current approach presents limitations. Unlike the conventional 2D case, subtraction of bead movements after cell removal cannot be done here because of the irreversible cell matrix digestion that occurs during cell migration. Moreover, our assay does not transform the measured maps of local matrix deformations into maps of local stresses. This is because cells crawling through a matrix partially degrade it to overcome the steric hindrance caused by the dense mesh of matrix fibers, inducing time-dependent changes in the mechanical properties of the matrix. Unlike traction microscopy, where the underlying matrix serves as a measuring device that is not in direct contact with the cell, here the matrix is both deformed and locally degraded, which precludes the computation of the stress tensor from the measured strain tensor. Transformation of our measured 3D maps of matrix deformations into local 3D maps of mechanical stresses is left to future studies.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.

Supplementary Material

[Supplement]
108.132738_index.html (941B, html)

Acknowledgments

D.W. thanks B. W. Schafer, S. J. Weiss, and V. Damljanovic for fruitful conversations.

This work was supported by National Institutes of Health grants GM075305-01 (S.X.S. and D.W.) and EB006890-02 (D.W.). A.C. was partially supported by the Howard Hughes Medical Institute-funded graduate training program in Nanotechnology for Biology and Medicine in the Johns Hopkins Institute for NanoBioTechnology.

Ryan J. Bloom and Jerry P. George contributed equally to this work.

Editor: Elliot L. Elson.

References

  • 1.Dembo, M., and Y. L. Wang. 1999. Stresses at the cell-to-substrate interface during locomotion of fibroblasts. Biophys. J. 76:2307–2316. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Munevar, M., Y. L. Wang, and M. Dembo. 2001. Traction force microscopy of migrating normal and H-ras transformed 3T3 fibroblasts. Biophys. J. 80:1744–1757. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Beningo, K. A., M. Dembo, I. Kaverina, J. V. Small, and Y. L. Wang. 2001. Nascent focal adhesions are responsible for the generation of strong propulsive forces in migrating fibroblasts. J. Cell Biol. 153:881–888. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Wang, H. B., M. Dembo, S. K. Hanks, and Y. Wang. 2001. Focal adhesion kinase is involved in mechanosensing during fibroblast migration. Proc. Natl. Acad. Sci. USA. 98:11295–11300. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Harris, A. K. 1986. Cell traction in relationship to morphogenesis and malignancy. Dev. Biol. 3:339–357. [DOI] [PubMed] [Google Scholar]
  • 6.Bellows, C. G., A. H. Melcher, and J. E. Aubin. 1981. Contraction and organization of collagen gels by cells cultured from periodontal ligament, gingiva and bone suggest functional differences between cell types. J. Cell Sci. 50:299–314. [DOI] [PubMed] [Google Scholar]
  • 7.Grinnell, F., and C. R. Lamke. 1984. Reorganization of hydrated collagen lattices by human skin fibroblasts. J. Cell Sci. 66:51–63. [DOI] [PubMed] [Google Scholar]
  • 8.Elsdale, T., and J. Bard. 1972. Collagen substrata for studies on cell behavior. J. Cell Biol. 54:626–637. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Roy, P., W. M. Petroll, H. D. Cavanagh, C. J. Chuong, and J. V. Jester. 1997. An in vitro force measurement assay to study the early mechanical interaction between corneal fibroblasts and collagen matrix. Exp. Cell Res. 232:106–117. [DOI] [PubMed] [Google Scholar]
  • 10.Roy, P., W. M. Petroll, H. D. Cavanagh, and J. V. Jester. 1999. Exertion of tractional force requires the coordinated up-regulation of cell contractility and adhesion. Cell Motil. Cytoskeleton. 43:23–34. [DOI] [PubMed] [Google Scholar]
  • 11.Tamariz, E., and F. Grinnell. 2002. Modulation of fibroblast morphology and adhesion during collagen matrix remodeling. Mol. Biol. Cell. 13:3915–3929. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Harley, B. A., T. M. Freyman, M. Q. Wong, and L. J. Gibson. 2007. A new technique for calculating individual dermal fibroblast contractile forces generated within collagen-GAG scaffolds. Biophys. J. 93:2911–2922. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Petroll, W. M., L. Ma, and J. V. Jester. 2003. Direct correlation of collagen matrix deformation with focal adhesion dynamics in living corneal fibroblasts. J. Cell Sci. 116:1481–1491. [DOI] [PubMed] [Google Scholar]
  • 14.Vanni, S. B., C. Lagerholm, O. Otey, D. L. Taylor, and F. Lanni. 2003. Internet-based image analysis quantifies contractile behavior of individual fbroblasts inside model tissue. Biophys. J. 84:2715–2727. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Krahn, K. N., C. V. C. Bouten, S. van Tuij, A. M. J. van Zandvoort, and M. Merkx. 2006. Fluorescently labeled collagen binding proteins allow specific visualization of collagen in tissues and live cell culture. Anal. Biochem. 350:177–185. [DOI] [PubMed] [Google Scholar]
  • 16.Toprak, E., H. Balci, B. H. Blehm, and P. R. Selvin. 2007. Three-dimensional particle tracking via bifocal imaging. Nano Lett. 7:2043–2045. [DOI] [PubMed] [Google Scholar]
  • 17.Speidel, M., A. Jonáš, and E. L. Florin. 2003. Three-dimensional tracking of fluorescent nanoparticles with subnanometer precision by use of offfocus imaging. Opt. Lett. 69:69–71. [DOI] [PubMed] [Google Scholar]
  • 18.Levi, V., Q. Ruan, and E. Gratton. 2005. 3-D particle tracking in a two-photon microscope: Application to the study of molecular dynamics in cells. Biophys. J. 88:2919–2928. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Gosse, C., and V. Croquette. 2002. Magnetic tweezers: micromanipulation and force measurement at the molecular level. Biophys. J. 82:3314–3329. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Wolf, K., I. Mazo, H. Leung, K. Engelke, U. H. von Andrian, E. I. Deryugina, A. Y. Strongin, E. B. Brocker, and P. Friedl. 2003. Compensation mechanism in tumor cell migration: mesenchymal-amoeboid transition after blocking of pericellular proteolysis. J. Cell Biol. 160:267–277. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Chang, M. I., P. Panorchan, T. M. Dobrowsky, Y. Tseng, and D. Wirtz. 2005. Single-molecule analysis of human immunodeficiency virus type 1 gp120-receptor interactions in living cells. J. Virol. 79:14748–14755. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Grinnell, F. 2000. Fibroblast-collagen-matrix contraction: growth-factor signalling and mechanical loading. Trends Cell Biol. 10:362–365. [DOI] [PubMed] [Google Scholar]
  • 23.Ridley, A. J. 2001. Rho GTPases and cell migration. J. Cell Sci. 114:2713–2722. [DOI] [PubMed] [Google Scholar]
  • 24.Delanoe-Ayari, H., R. Al Kurdi, M. Vallade, D. Gulino-Debrac, and D. Riveline. 2004. Membrane and acto-myosin tension promote clustering of adhesion proteins. Proc. Natl. Acad. Sci. USA. 101:2229–2234. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Pankov, R., Y. Endo, S. Even-Ram, M. Araki, K. Clark, E. Cukierman, K. Matsumoto, and K. M. Yamada. 2005. A Rac switch regulates random versus directionally persistent cell migration. J. Cell Biol. 170:793–802. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Sahai, E., and C. J. Marshall. 2003. Differing modes of tumour cell invasion have distinct requirements for Rho/ROCK signalling and extracellular proteolysis. Nat. Cell Biol. 5:711–719. [DOI] [PubMed] [Google Scholar]
  • 27.Ramamurthy, B., C. M. Yengo, A. F. Straight, T. J. Mitchison, and H. L. Sweeney. 2004. Kinetic mechanism of blebbistatin inhibition of nonmuscle myosin IIB. Biochemistry. 43:14832–14839. [DOI] [PubMed] [Google Scholar]
  • 28.Shu, S., X. Liu, and E. D. Korn. 2005. Blebbistatin and blebbistatin-inactivated myosin II inhibit myosin II-independent processes in Dictyostelium. Proc. Natl. Acad. Sci. USA. 102:1472–1477. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Uehata, M., T. Ishizaki, H. Satoh, T. Ono, T. Kawahara, T. Morishita, H. Tamakawa, K. Yamagami, J. Inui, M. Maekawa, and S. Narumiya. 1999. Calcium sensitization of smooth muscle mediated by a Rho-associated protein kinase in hypertension. Nature. 389:990–994. [DOI] [PubMed] [Google Scholar]
  • 30.Kole, T. P., Y. Tseng, L. Huang, J. L. Katz, and D. Wirtz. 2004. Rho kinase regulates the intracellular micromechanical response of adherent cells to rho activation. Mol. Biol. Cell. 15:3475–3484. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Carragher, N. O., S. M. Walker, L. A. Scott Carragher, F. Harris, T. K. Sawyer, V. G. Brunton, B. W. Ozanne, and M. C. Frame. 2006. Calpain 2 and Src dependence distinguishes mesenchymal and amoeboid modes of tumour cell invasion: a link to integrin function. Oncogene. 25:5726–5740. [DOI] [PubMed] [Google Scholar]
  • 32.Gao, Y., J. B. Dickerson, F. Guo, J. Zheng, and Y. Zheng. 2004. Rational design and characterization of a Rac GTPase-specific small molecule inhibitor. Proc. Natl. Acad. Sci. USA. 101:7618–7623. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Tseng, Y., K. M. An, and D. Wirtz. 2002. Microheterogeneity controls the rate of gelation of actin filament networks. J. Biol. Chem. 277:18143–18150. [DOI] [PubMed] [Google Scholar]
  • 34.Tseng, Y., K. M. An, O. Esue, and D. Wirtz. 2004. The bimodal role of filamin in controlling the architecture and mechanics of F-actin networks. J. Biol. Chem. 279:1819–1826. [DOI] [PubMed] [Google Scholar]
  • 35.Tseng, Y., E. Fedorov, J. M. McCaffery, S. C. Almo, and D. Wirtz. 2001. Micromechanics and microstructure of actin filament networks in the presence of the actin-bundling protein human fascin: a comparison with a-actinin. J. Mol. Biol. 310:351–366. [DOI] [PubMed] [Google Scholar]
  • 36.Sabeh, F., I. Ota, K. Holmbeck, H. Birkedal-Hansen, P. Soloway, M. Balbin, C. Lopez-Otin, S. Shapiro, M. Inada, S. Krane, E. Allen, D. Chung, and S. J. Weiss. 2004. Tumor cell traffic through the extracellular matrix is controlled by the membrane-anchored collagenase MT1-MMP. J. Cell Biol. 167:769–781. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37.Chun, T. H., K. B. Hotary, F. Sabeh, A. R. Saltiel, E. D. Allen, and S. J. Weiss. 2006. A pericellular collagenase directs the 3-dimensional development of white adipose tissue. Cell. 125:577–591. [DOI] [PubMed] [Google Scholar]
  • 38.Zaman, M. H., L. M. Trapani, A. L. Sieminski, D. Mac, H. Kellar, K. R. D. Gong, A. Wells, D. A. Lauffenburger, and P. Matsudaira. 2006. Migration of tumor cells in 3D matrices is governed by matrix stiffness along with cell-matrix adhesion and proteolysis. Proc. Natl. Acad. Sci. USA. 103:10889–10894. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 39.Hotary, K., X. Y. Li, E. Allen, S. L. Stevens, and S. J. Weiss. 2006. A cancer cell metalloprotease triad regulates the basement membrane transmigration program. Genes Dev. 20:2673–2686. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 40.Demou, Z. N., M. Awad, T. McKee, J. Y. Perentes, X. Wang, L. L. Munn, R. K. Jain, and Y. Boucher. 2005. Lack of telopeptides in fibrillar collagen I promotes the invasion of a metastatic breast tumor cell line. Cancer Res. 65:5674–5682. [DOI] [PubMed] [Google Scholar]
  • 41.Woodley, D. T., M. Yamauchi, K. C. Wynn, G. Mechanic, and R. A. Briggaman. 1991. Collagen telopeptides (cross-linking sites) play a role in collagen gel lattice contraction. J. Invest. Dermatol. 97:580–585. [DOI] [PubMed] [Google Scholar]
  • 42.Lo, C. M., H. B. Wang, M. Dembo, and Y. L. Wang. 2000. Cell movement is guided by the rigidity of the substrate. Biophys. J. 79:144–152. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43.Walpita, D., and E. Hay. 2002. Studying actin-dependent processes in tissue culture. Nat. Rev. Mol. Cell Biol. 3:137–141. [DOI] [PubMed] [Google Scholar]
  • 44.Hotary, K. B., E. D. Allen, P. C. Brooks, N. S. Datta, M. W. Long, and S. J. Weiss. 2003. Membrane type I matrix metalloproteinase usurps tumor growth control imposed by the three-dimensional extracellular matrix. Cell. 11:33–45. [DOI] [PubMed] [Google Scholar]
  • 45.Cukierman, E., R. Pankov, and K. M. Yamada. 2002. Cell interactions with three-dimensional matrices. Curr. Opin. Cell Biol. 14:633–639. [DOI] [PubMed] [Google Scholar]
  • 46.Panorchan, P., J. S. Lee, T. P. Kole, Y. Tseng, and D. Wirtz. 2006. Microrheology and ROCK signaling of human endothelial cells embedded in a 3D matrix. Biophys. J. 91:3499–3507. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 47.Prass, M., K. Jacobson, A. Mogilner, and M. Radmacher. 2006. Direct measurement of the lamellipodial protrusive force in a migrating cell. J. Cell Biol. 174:767–772. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 48.Miron-Mendoza, M., J. Seemann, and F. Grinnell. 2008. Collagen fibril flow and tissue translocation coupled to fibroblast migration in 3D collagen matrices. Mol. Biol. Cell. 19:2051–2058. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 49.Wolf, K., Y. I. Wu, Y. Liu, J. Geiger, E. Tam, C. Overall, M. S. Stack, and P. Friedl. 2007. Multi-step pericellular proteolysis controls the transition from individual to collective cancer cell invasion. Nat. Cell Biol. 9:893–904. [DOI] [PubMed] [Google Scholar]
  • 50.Barocas, V. H., A. G. Moon, and R. T. Tranquillo. 1995. The fibroblast-populated collagen microsphere assay of cell traction force. Part 2: Measurement of the cell traction parameter. J. Biomech. Eng. 117:161–170. [DOI] [PubMed] [Google Scholar]
  • 51.Parekh, A., and D. Velegol. 2007. Collagen gel anisotropy measured by 2-D laser trap microrheometry. Ann. Biomed. Eng. 35:1231–1246. [DOI] [PubMed] [Google Scholar]
  • 52.Tseng, Y., T. P. Kole, and D. Wirtz. 2002. Micromechanical mapping of live cells by multiple-particle-tracking microrheology. Biophys. J. 83:3162–3176. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 53.Kole, T. P., Y. Tseng, I. Jiang, J. L. Katz, and D. Wirtz. 2005. Intracellular mechanics of migrating fibroblasts. Mol. Biol. Cell. 16:328–338. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 54.Tseng, Y., J. S. Lee, T. P. Kole, I. Jiang, and D. Wirtz. 2004. Micro-organization and visco-elasticity of the interphase nucleus revealed by particle nanotracking. J. Cell Sci. 117:2159–2167. [DOI] [PubMed] [Google Scholar]
  • 55.Dobrowsky, T. M., Y. Zhou, S. X. Sun, R. F. Siliciano, and D. Wirtz. 2008. Monitoring early fusion dynamics of human immunodeficiency virus type 1 at single-molecule resolution. J Virol. 82:7022–7033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 56.Suh, J., D. Wirtz, and J. Hanes. 2003. Efficient active transport of gene nanocarriers to the cell nucleus. Proc. Natl. Acad. Sci. USA. 100:3878–3882. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplement]
108.132738_index.html (941B, html)
108.132738_Supplem._material_Bloom_etal.doc (37KB, doc)
Download video file (808.5KB, mov)
Download video file (774.1KB, mov)

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES