3′-Phosphoinositides Regulate the Coordination of Speed and Accuracy during Chemotaxis

Abstract

The PI3K/PTEN pathway, as the regulator of 3′-phosphoinositide (3′-PI) dynamics, has emerged as a key regulator of chemoattractant gradient sensing during chemotaxis in Dictyostelium and other cell types. Previous results have shown 3′-PIs to be important for regulating basal cell motility and sensing the direction and strength of the chemoattractant gradient. We examined the chemotaxis of wild-type cells and cells lacking PTEN or PI3K1 and 2 using analytical methods that allowed us to quantitatively discern differences between the genotype's ability to sense and efficiently respond to changes in gradient steepness during chemotaxis. We found that cells are capable of increasing their chemotactic accuracy and speed as they approach a micropipette in a manner that is dependent on the increasing strength of the concentration gradient and 3′-PI signaling. Further, our data show that 3′-PI signaling affects a cell's ability to coordinate speed and direction to increase chemotactic efficiency. Using to our knowledge a new measurement of chemotactic efficiency that reveals the degree of coordination between speed and accuracy, we found that cells also have the capacity to increase their chemotactic efficiency as they approach the micropipette. Like directional accuracy and speed, the increase in chemotactic efficiency of cells with increased gradient strength is sensitive to 3′-PI dysregulation. Our evidence suggests that receptor-driven 3′-PI signaling regulates the ability of a cell to capitalize on stronger directional inputs and minimize the effects of inaccurate turns to increase chemotactic efficiency.

INTRODUCTION

Cell motility is an intriguing biological process that requires the direct coordination of multiple spatially and temporally complex subcellular processes, including signal transduction, cell-substrate adhesion, and cytoskeletal dynamics. Cell motility can be divided into two categories: nondirected (or isotropic) motility and directed motility. An example of directed motility that is of particular interest is chemotaxis. In chemotaxis, cells sense direction in chemoattractant concentration gradients via signal transduction and use this information to direct their motility to regions of higher concentration. In addition to being important during cancer progression, chemotaxis is essential for predation by cells of the immune system and the model organism Dictyostelium discoides, where it also offers a developmental mechanism for multicellular structures to form from differentiating cells that are initially dispersed over long distances.

The identification of the signaling pathways responsible for chemoattractant gradient sensing is currently a vigorous area of research (1–3). The PI3K-PTEN pathway responsible for the regulation of 3′-phosphoinositide (3′-PI) dynamics was identified as a strong candidate for regulating directional sensing in Dictyostelium (4,5). Cells lacking two PI3Ks were shown to have reduced cell polarity as well as a reduced ability to maintain proper directionality during chemotaxis. Artificially targeting PI3K to the membrane or genetic deletion of PTEN led to increased pseudopodia formation and a poorly defined leading edge during chemotaxis, which in turn resulted in reduced chemotactic efficiency. Furthermore, during chemotaxis PI3K was shown to localize to the leading-edge membrane, whereas PTEN localized to the lateral and anterior cell membrane. This spatial distribution of PI3K and PTEN provided a mechanism to sharply regulate the spatial accumulation of 3′-PIs to the region of the cell membrane experiencing the highest concentration of the chemoattractant, cAMP. The leading-edge localization of 3′-PIs was hypothesized to provide membrane-binding sites for a host of signaling proteins that governed efficient F-actin assembly and pseudopod protrusion. Recently, we showed that inhibition of PI3K by wortmannin in HL60 cells expressing CSCR2 resulted in reduced cell motility but normal chemotaxis in response to a gradient of CXCL8, and that wortmannin inhibition of PI3K impaired the ability of cells to reorient their polarity and respond quickly to a change in the direction of the CXCL8 gradient (6,7). Similar results in a variety of cellular systems suggest that 3′-PI signaling is a rather general mechanism for regulating the cytoskeletal-dependent processes of cell polarity and chemotaxis (8–10).

In addition to directional sensing, the 3′-PI signaling system is also thought to play an important role in another aspect of gradient sensing: gradient amplification (11). During gradient amplification, the weak external chemoattractant gradient is amplified into a strong internal signaling gradient, providing clear, reliable instruction from a noisy message. Gradient amplification is no mean feat considering that cells can consistently sense and respond to concentration gradients so shallow as to occupy only on the order of 50 receptors, with minute differences in receptor occupancy across the cell body (12). Of importance, both directional sensing and gradient amplification were shown to occur in cells treated with the actin polymerization inhibitor Latrunculin, which causes cells to lose morphological polarity (and presumably F-actin-based cytoskeletal structure) (11,13–15). These results led to a model in which the 3′-PI signaling system is independent of the cytoskeleton and therefore likely sends an instructive signal to the F-actin-based cell protrusions that play a key role in displacing the cell body (16).

Increased scrutiny has led to a more complex picture of the role of 3′-PIs in Dictyostelium cell motility and chemotaxis. A detailed analysis of pseudopod dynamics during chemotaxis suggested that 3′-PIs regulated the frequency, but not the directional accuracy, of pseudopod extension, calling into question the role of 3′-PIs in directional sensing (17). Subsequently, a Dictyostelium mutant lacking all five known type I PI3Ks was reported to undergo chemotaxis with “near wildtype efficiency”, further bringing into question the role of 3′-PIs in chemotaxis (18). Curiously, the speed of random motility, but not chemotaxis, is reduced in the pentuple knockout, suggesting that 3′-PIs may only play a role in regulating basal cell motility. Likewise, a detailed comparison of pseudopod dynamics during isotropic and directed motility found that pten- cells had an increased number of lateral pseudopodia, a defect that was manifested to the same degree in both of these paradigms of cell motility (19). The similarity of the defect in both conditions led to the conclusion that PTEN function is largely independent of receptor activation. Finally, PI3K (and reporters for 3′-PI accumulation) have been shown to spontaneously localize to the membrane independently of the G-protein-dependent constitutive activity of the chemoattractant receptor (20). Similarly, PTEN was observed to delocalize from the membrane at sites of random pseudopod extension. Although a clear role for 3′-PIs in isotropic motility and chemotaxis has yet to emerge, it is becoming apparent that the precise function of 3′-PIs in regulating cell motility is more complex than originally supposed.

We have investigated a specific role for receptor-regulated 3′-PI signaling in chemotaxis by measuring directional accuracy and speed for wt, pi3k1/2-, and pten- cells in chemoattractant gradients produced by micropipette and a microfluidic device. In the micropipette assay, a nonlinear gradient with radial symmetry is produced that a cell chemotaxing toward areas of higher concentration would experience as an increasingly stronger directional signal. In contrast, the gradient produced by the microfluidic device we used is linear, i.e., it has a constant steepness in one direction and is translationally invariant in the other. A comparison of chemotaxis as a function of position in the differing gradients revealed that all three genotypes are capable of increasing directional accuracy as they approach regions of higher chemoattractant concentration in the nonlinear micropipette assay. A similar analysis of cells in a linear gradient suggests that the change in gradient steepness in the micropipette assay is responsible for the increase in accuracy, since all three genotypes were incapable of increasing their accuracy as they moved into regions of higher concentration. In the nonlinear gradient, wt cells were capable of increasing their speed as they approached the micropipette, whereas only pi3k1/2- and pten- were capable of doing so in the linear gradient. An examination of the relationship between the direction and magnitude of chemotactic movements revealed that, although these parameters are often reported as independent measures of chemotaxis, they are in fact coordinated by the cell in both linear and nonlinear gradients to increase chemotactic efficiency. Both pi3k 1/2- and pten- cells had an overall decreased ability to coordinate their speed and directional accuracy and had an impaired ability compared to wt to increase their coordination as they moved into regions of higher concentration in the micropipette assay. These results suggest that receptor-driven 3′-PI signaling plays a key role in coordinating speed and accuracy, thereby increasing chemotactic efficiency.

MATERIALS AND METHODS

Cell culture and preparation

Cells were cultured axenically in HL5 supplemented with glucose and penicillin-streptomycin. For chemotactic competence, the cells were shaken for a maximum of 2 days, washed three times in Na/K phosphate buffer, and resuspended for a final density of 5 × 10⁶ cells/mL in 30 mL of buffer. cAMP was delivered every 6 min for 5 h. The cells were plated (micropipette assay) or injected (microfluidic device) and allowed to adhere and disperse. Recording commenced no more than 6½ h after the pulsing began. The pten- cells were obtained from the Dictyostelium Stock Center.

Imaging and cell tracking

All imaging was done on a Nikon TE-30 inverted microscope using 20× DIC optics (Nikon), NA = 1.4, and a CoolSnap camera. Using 2-by-2 binning resulted in a field 430 μm wide and 321 μm high and a pixel density of 2.6 pixels per μm². The cells were imaged for 1½ h at a frequency of 1/3 Hz. The following criteria were established to ensure consistency throughout experimentation and analysis: 1), cells were tracked for a minimum of 100 frames (i.e., 300 s); 2), cells were only tracked if the entire cell body remained completely within the field of view; 3), cells that made physical contact with other cells were avoided; and 4), care was taken to avoid cells that were closely following other cells to eliminate any influence from streaming or cell-to-cell signaling. Tracking was done using the Metamorph (Molecular Probes, Eugene, OR) “track objects” function and logged to Excel (Microsoft, Redmond, WA). For more data regarding the sample sizes and tracking times, see Table 1.

TABLE 1.

Sample sizes, tracking times, and mean measures for each genotype in every condition tested

	Micropipette	Microfluidic device
wt
N =	6	5
n =	99	61
Mean tracking time (minutes)	10.91 (4.94)	21.15 (11.82)
pi3k1/2−
N =	9	4
n =	124	28
Mean tracking time (minutes)	14.06 (11.46)	18.09 (12.88)
pten−
N =	6	6
n =	52	41
Mean tracking time (minutes)	16.49 (10.54)	31.51 (18.70)

Values are for the mean with standard error in parentheses, except for tracking time, which is shown as the mean with the standard deviation in parentheses; N and n are the number of experiments and the number of cells, respectively, for the given genotype in a particular condition.

To obtain estimates of the concentration field produced by the micropipette, we first imaged dilute, uniform concentrations of fluorescein (MW 332.2) to determine the range for which its fluorescence was linearly related to imaged intensity. We then imaged a gradient resulting from highly concentrated fluorescein. The gradient was rapidly produced with intensity values within the predetermined linear range. An exponential curve was found to fit the data obtained from line scans of the original images with minimal error.

Microfabrication and device operation

All microfabrication was performed using soft lithographic, rapid prototyping methods (21,22). Briefly, SU-8 150 (Microchem, Newton, MA) was deposited on dried, acetone-cleaned silicon wafers and spun to a thickness of ∼100 μm. Film masks were printed at a resolution of 3556 dpi. After UV exposure and baking, the remaining photoresist was washed away, leaving a positive master. Devices were created by pouring mixed and degassed polydimethylsiloxane (PDMS):PDMS crosslinker at a ratio of 1:10 over a master in a 30 mm petri dish. After incubation for at least 2 h at 80°C, the PDMS was removed, the devices were trimmed to size, and channels were punched. After plasma treatment for 10 s, the PDMS devices were then bonded to glass. The resulting devices ranged from 100 to 185 μm high with a chemotaxis chamber 500 μm wide.

Devices were operated using 1 mL syringes driven by a Harvard syringe pump. To maintain consistent shear flow across numerous experiments, the programmed flow rates were adjusted according to Walker et al. (23).

Data analysis

Our definition of accuracy is a transformation of the direction, θ, of a chemotactic movement as measured on the interval [0°–180°] relative to the direction of the gradient, and was defined as: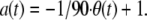 As for the more familiar chemotactic index, defined as 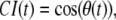the accuracy transformation provides an index ranging between −1 and +1. However, the accuracy index used here differs importantly from the chemotactic index in that it is a linear transformation of angle values and therefore does not contain the distortions introduced by the cosine function. Therefore, the linear transformation is preferred for statistical analysis. All analyses done here were performed with data from 3-s sampling intervals.

Mean accuracy, speed, and coordination were compared by means of a two-way analysis of variance (ANOVA) using, in the case of chemotaxis, the concentration profile and genotype as factors. After obtaining evidence that concentration profiles and genotypes were significantly different by two-way ANOVA, genotypes were compared using the Bonferroni t-test. All mean values from the simulations of coordination were compared using ANOVA. Regression coefficients and their associated errors were obtained by regressing the mean speed, accuracy, or coordination averaged over 10 μm intervals using the MATLAB function robustfit.m. To assess the significance of the slope and y-intercept coefficients (or differences between them) and their associated p-values, t-values were calculated according to Glantz et al. (24). All analyses were done in MATLAB (The MathWorks, Natick, MA).

Simulation of coordination

Stochastic simulations of coordination were performed in MATLAB as follows: The n pooled chemotactic speeds and directions of wt cells in the micropipette assay were separately ranked by increasing speed and accuracy, respectively. For every discrete time step of the simulation, t, a uniformly distributed random integer, r, with a value between one and n was generated, and the speed with rank r was chosen from the experimental distribution. The accuracy of the movement at time t was chosen to be either the direction with rank r or an independently chosen rank. A free parameter of the model, λ, defined to be between zero and one, determined the fraction of the time that the model randomly chose directions with the same rank as the speed, and therefore the degree of coordination between speed and direction in the simulation. For each degree of coordination in the simulation, 80 cells were simulated for 500 time steps each.

RESULTS

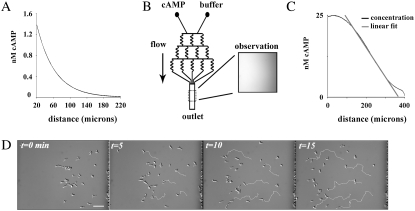
Using a micropipette to create a chemoattractant concentration gradient, Van Haastert and Postma (25) recently showed that wt cells increase their directional accuracy as they approach the gradient source. In the standard micropipette assay, the chemoattractant concentration falls off nonlinearly with increased distance from the micropipette, creating for a cell approaching the gradient source a gradient of ever-increasing steepness and mean concentration (Fig. 1 A). Since 3′-PI signaling has been shown to be involved in adaptation to mean concentrations, and to amplify the chemoattractant gradient (11,13) and regulate directional accuracy (5), we hypothesized that two features of this experiment were essential for this result: 1), the ever-increasing steepness, or nonlinearity, of the chemoattractant gradient; and 2), regulated 3′-PI signaling as required for the amplification of the consistently stronger gradient and the regulation of leading-edge F-actin dynamics. We resolved to test this notion through the comparison of wt, pi3k1/2-, and pten- cells in the micropipette assay and in a linear gradient generated by the microfluidic device (Fig. 1, B and C). The gradient in the micropipette assay was created by free diffusion of the chemoattract cAMP from a micropipette containing ∼30 μL of 100 μM cAMP. With this concentration, a nonlinear gradient with a mean concentration in the low-nM range was created within ∼250 μm of the micropipette, and cells of all three genotypes were capable of sensing and responding from distances of at least 220 μm. The exact concentration profile resulting from the diffusion from the pipette tip at the bottom of the dish depends on a number of geometric and temporal factors; the curve shown in Fig. 1 A is consistent for x > ∼10 μm with the expected steady-state, 1/r concentration profile for a constant-concentration point source (26)

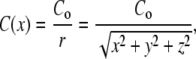where the bottom of the dish is the x-y plane and z is the vertical distance. When the pipette is first inserted into the dish, the falloff will be transiently steeper than this because the chemoattractant will not yet have diffused out into the bulk fluid. Since the microscope sums the fluorescence intensity over a range of z values, the observed intensity profile, such as in Fig. 1 A, is obtained by integrating the concentration from z = 0 to Z_max to produce an intensity profile given by

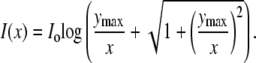A pilot study to determine the optimal conditions in the microfluidic device revealed that the chemotaxis of wt cells was most efficient in a gradient of 50 pM/μm cAMP with a midpoint of 12.5 nM cAMP (data not shown). For an example of the chemotaxis of wt cells in these conditions, refer to Fig. 1 D. These conditions are in good agreement with those found in Song et al. (27). The stability of the gradient in the device is driven by fluid flow, which also creates shear force on adherent cells perpendicular to the direction of the gradient (23). By varying the flow, we determined that a flow rate of 1.4 μL/min produced a stable gradient and had no apparent effects on motility (see Fig. S1 of the Supplementary Material, Data S1). At this low rate, the estimated 10 pN shear force is ∼½ as large as that required to initiate Ca²⁺-regulated, shear flow-driven motility, and considerably lower than that shown to activate the 3′-PI signaling pathway in vegetative cells (28,29). Furthermore, chemotaxis in higher shear forces (40 pN) also showed no obvious directional bias by flow (data not shown). For all three genotypes, cells were more accurate and faster in the linear gradient than in the micropipette assay (Fig. 2, B and E).

FIGURE 1.

Experimental and analytical paradigm to measure directed and persistent random motility. (A) Quantitation of fluorescein (MW 332.3) diffusing from a micropipette reveals the nonlinear concentration profile in the assay. (B) Schematic of the microfluidic device used in the study; manipulation of the flow into the two inlets (labeled cAMP and buffer) enables the production of stable concentration gradients. Inset, image of fluorescein fluorescence in the device. (C) Quantification from a line scan of fluorescein image in B detailing experimental control over chemoattractant profiles. Flowing buffer and cAMP at identical flow rates creates linear chemoattractant concentration gradients for chemotaxis that are stable over experimental timescales (<90 min). (D) Time series showing the chemotaxis of wt cells in the microfluidic device when exposed to a linear cAMP gradient of 50 pM/μm cAMP with a midpoint of 12.5 nM (concentration increases from right to left and flow is from top to bottom). For clarity, five cells were chosen and their respective tracks are shown in white.

FIGURE 2.

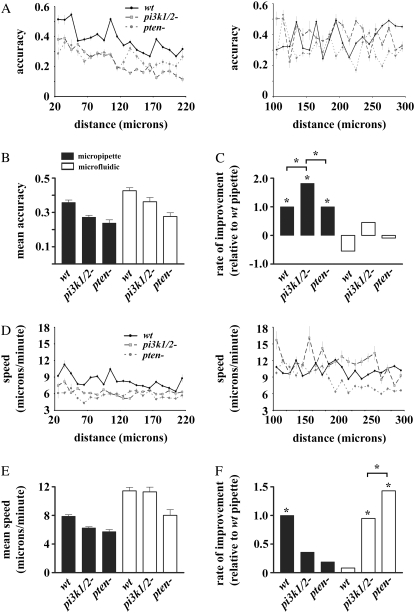
Chemotactic accuracy and speed in linear and nonlinear concentration gradients. The chemotactic accuracy (A) and speed (D) of the three genotypes versus distance from the highest concentration in the nonlinear gradient (left) and linear gradient (right). Mean accuracy (B) and speed (E) for wt, pi3k1/2-, and pten- in the micropipette (nonlinear) and microfluidic (linear) assay, respectively. Statistical comparison of the rate of improvement of accuracy (C) and speed (F) in the micropipette assay and the linear region of the microfluidic device. For comparison, the rate of increase in each chemotactic parameter was normalized to the rate of wt cells in the micropipette assay. Stars represent statistically significant differences at p < 0.05.

To test the role of 3′-PIs and chemoattractant concentration profile in increasing efficiency with increased proximity to higher concentrations, we plotted the directional accuracy and speed (Fig. 2, A and D, respectively) of wt, pi3k1/2-, and pten- cells chemotaxing in linear and nonlinear gradients. The directional accuracy ranges from −1 for movements directly away from the highest concentration, to +1 for movements directly toward the highest concentration (see Materials and Methods for complete definition). As the gradient steepness increases with increased proximity to the highest concentration in the micropipette assay, distance is used as a proxy for gradient steepness. To address the magnitude and statistical significance of any potential trend, we performed linear regression for each measure of chemotactic behavior as a function of distance from the micropipette (see Table S1 of the Supplementary Material (Data S1) for regression coefficients). The slopes were compared statistically as measures of a genotype's rate of improvement with increasing proximity to higher concentrations. Statistically significant increases in directional accuracy were seen in all three genotypes tested (Fig. 2 C). Although pi3k1/2- cells were capable of increasing their accuracy to a greater degree than wt and pten-, both pi3k1/2- and pten- cells displayed an overall lower chemotactic accuracy and speed in the micropipette assay. In the micropipette assay, only wt cells were capable of increasing their speed as they experienced steeper concentration gradients. The lack of increased speed in pi3k1/2- and pten- cells reveals that proper regulation of 3′-PIs is required for increasing chemotactic speed with increased proximity to the micropipette.

To verify that the improvement in directional accuracy by all three genotypes was due to the varying gradient steepness in the micropipette assay, we repeated our analysis of chemotactic accuracy and speed as a function of distance from the highest concentration in the linear gradient where the gradient steepness is held constant. Chemotaxis over distance in the shallow, linear gradient was considerably more variable than in the micropipette assay, and no genotype showed a statistically significant ability to increase accuracy as it approached regions of higher concentration (Fig. 2, A and D). Although wt cells in the linear gradient apparently decreased their accuracy as they moved into regions of higher concentration (Fig. 2 C), this negative relationship was not statistically significant. Thus, the increases in accuracy by cells seen in the micropipette assay are likely due to either the rate at which the mean concentration increases in the different assays or the ever-increasing gradient steepness experienced by a cell. We have not yet addressed the question of whether any of the observed behavior was the result of the radial nature of the diffusion from the micropipette, since a lateral or directional error in a cell trajectory could produce a larger change in concentration for the pipette than would a corresponding error in the translationally invariant microfluidic device. This issue could be resolved by using a microfluidic gradient generator that produces nonlinear, translationally invariant gradients (33).

Of interest, despite having mean speeds lower than wt (Fig. 2 E), both pi3k1/2- and pten- cells, unlike wt, were capable of increasing their speed with increased proximity to the highest concentration in the linear gradient (Fig. 2 F). Thus, for the mutants with impaired 3′-PI signaling, increases in speed are not dependent on the presence of a nonlinear gradient. This discrepancy may indicate that the mechanism relating speed to gradient strength may be uncoupled in 3′-PI signaling mutants.

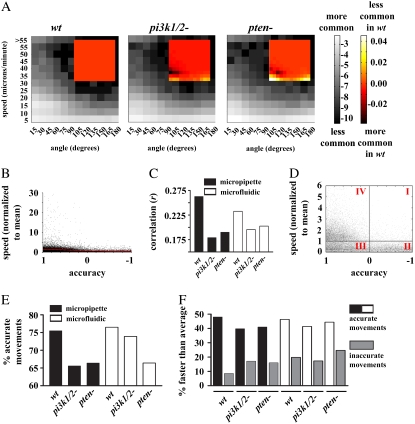
Speed and direction are the two most commonly utilized measures of chemotactic efficiency (for example, see Andrew and Insall (17), Hoeller and Kay (18), and Loovers et al. (30)). It is likely that when these two parameters are considered separately (and thus implicitly assumed to be independent of each other), there is a possibility of neglecting the prospect that a cell might coordinate its direction and speed to increase the efficiency of chemotaxis. To examine how these two common measures of chemotactic efficiency may depend on one another and explore how that potential dependence may differ between wt and 3′-PI signaling mutants, we computed the two-dimensional probability distributions of speed and direction as measured between 0° and 180° (with 0° being perfectly accurate and 180° being perfectly inaccurate) for wt and both mutant cell lines during chemotaxis in the micropipette and microfluidic assay (Fig. 3). The full ranges of angles and speeds were divided into bins with widths of 15° and 5 μm/min, respectively, and labeled with the upper limit of each bin. A grayscale color map was used to depict the probability that a cell of a given genotype would make a movement in a particular range of speed and angles. Although the most common movements in all three cell lines fall within the 0–5 μm/min range, a fair number also occur in the range of 5–20 μm/min. Of those movements that were faster than typical, the majority were associated with directions that brought the cell closer to the micropipette (i.e., angles < 90°). Therefore, the majority of the probability gathers in the lower left-hand quadrant of each genotype's distribution, indicating dependence between the speed and direction of movement. In biological terms, cells tend to adjust the magnitude of their movements according to their accuracy (and/or vice versa). To provide a comparison between the distribution of the mutants to wt, the two-dimensional distribution of wt cells was subtracted from each respective mutant and presented as insets in Fig. 3. Two regions contrasting the coordination of wt and the mutants can be seen in the difference distributions. First, for both mutants in both assays there is a substantial decrease in the faster (i.e., > 5 μm/min) movements associated with accurate directions, and a corresponding increase in slower (0–5 μm/min) movements also associated with accurate directions. This shifting of probability from higher speeds to lower speeds while directional accuracy remains roughly constant is consistent with the observation that the largest defect in pi3k 1/2- cells or wt cells treated with the PI3K inhibitor LY429009 is a reduction in speed (but not directional accuracy), and is suggestive of a role of 3′-PIs in regulating basal cell motility (30). The role of PI3K in sensing a change in gradient direction has been demonstrated by blocking PI3K with wortmannin (6), but it is not yet clear whether this treatment also affects chemotactic accuracy between linear and radial gradients. However, a second region of difference can also be seen as an increase in large, inaccurate directions, suggesting a role for 3′-PIs in directional accuracy. Thus, Dictyostelium cells coordinate their “choice” of direction with their “choice” of speed in a manner that is dependent, in part, on 3′-PI signaling.

FIGURE 3.

During chemotaxis, accurate movements tend to be faster movements. (A) Two-dimensional histograms displaying the log of the probability that a cell will make a movement during chemotaxis in the micropipette and microfluidic assay with a particular angle (x axis) and speed (y axis) represented in grayscale. Speed values are separated in bins 5 μm/min wide; angles are in bins 15° wide and each bin is labeled with the upper limit for that bin. The heat-mapped insets show the difference between a given mutant and wt. Doubling and halving the bin widths had no appreciable effect on the general conclusion. Similar patterns can be seen in 2-D histograms of movements from the microfluidic device. (B) Scatter plot of the accuracy of wt movements versus their speed after normalized to each individual cell's mean speed. A linear fit (red line) indicates the correlation between accuracy and speed. (C) Correlation coefficients between each genotype's accuracy and normalized speed (as in B). Each correlation was found to be significant at p < 0.05 level. (D) A magnification of the plot from B. This plot, containing >99% of the total data, can be divided into four regions (labeled I, II, III, and IV) that describe the accuracy and speed of the cell (see text). (E) Percent of movements from each genotype with positive accuracy (quadrants III and IV in D). (F) Percent of accurate and inaccurate movements with faster than average speeds.

For a quantitative understanding of the relationship between speed and direction, we first determined the mean speed of each cell and used this to normalize the speed of all its movements. The normalized speed of each movement was then plotted versus its accuracy for all three genotypes in each experimental assay (for an example, see Fig. 3 B). Correlation coefficients were computed and their significance ascertained. The magnitudes of the correlation coefficients are plotted in Fig. 3 C. All cell lines in both assays displayed a statistically significant correlation between their accuracy and their normalized speed, although the correlation coefficients for both mutants were considerably reduced compared to wt.

In addition to the presence of correlation, the scatter plots of normalized speed versus accuracy further exemplify the argument that accurate movements tend to be faster movements. The plot can be divided into the following four regions: region I with inaccurate directions and above-average speeds, region II with inaccurate directions and below-average speeds, region III containing accurate movements with below-average speed, and region IV with accurate movements and above-average speed (Fig. 3 D). An examination of the distribution of the data points with above-average speed suggested there were considerably more above-average speed movements that were accurate than inaccurate. However, since there are also far more accurate movements than inaccurate movements, regardless of speed (Fig. 3 E), comparisons solely between accurate and inaccurate above-average speed movements could be misleading. To account for the fact that there are more accurate than inaccurate movements, we determined the percentage of total accurate movements that also had above-average speed, and similarly, the percentage of total inaccurate movements that also had above-average speed (Fig. 3 F). With this analysis, it can be seen that accurate movements were two to five times more likely to be faster than average as compared to inaccurate movements.

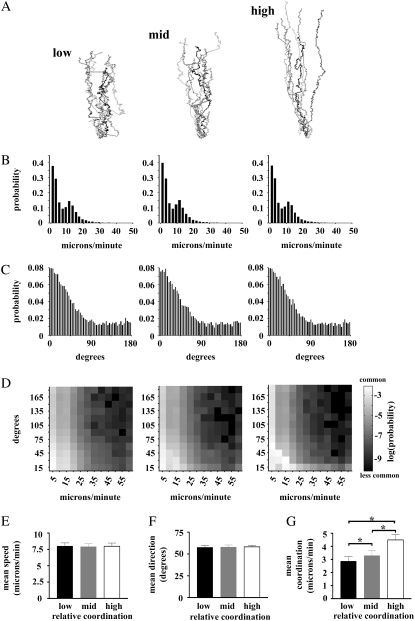
To better demonstrate the consequences of the interdependence between speed and direction on chemotactic efficiency, and the usefulness of our definition of coordination, we performed simulations of chemotaxis in which the coordination between the speed of cell movement and the directional accuracy could be varied. For each relative level of coordination, the cell tracks, means, and distributions of speed and angle were determined (Fig. 4). It is easy to see that the cell tracks displayed in Fig. 4 A qualitatively show widely varying degrees of chemotactic efficiency. As coordination between speed and accuracy increases, the simulated “cells” produce tracks that become less tortuous, with fewer and fewer “runs” of inaccurate movements, and the overall distance covered is increased. It should be noted that these apparent differences exist despite the fact that the probability distributions of the speed and direction of each simulation, considered separately, fail to suggest any significant differences in the different simulations (Fig. 4, B and C). Only the two-dimensional probability distributions (Fig. 4 D) are capable of revealing any difference between the simulations, as more probability gathers in the lower left-hand quadrant as the degree of coordination is increased. Most interestingly, a statistical comparison of the mean values of speed or angle reveals the inadequacy of population means to differentiate the striking variability in chemotactic efficiency seen in the tracks, since the simulations proved to be statistically identical (Fig. 4, E and F).

FIGURE 4.

Simulations of coordination reveal its effect on chemotactic efficiency. (A) “Tracks” of cells from a stochastic simulation of chemotaxis with varying degrees of coordination between directional accuracy and speed. (B and C) The probability distribution of the speed and direction, respectively, of cells in A. (D) The two-dimensional probability distributions reveal the dependency of directional accuracy and speed in the simulations in A. (E and F) Mean speed and direction for each simulation in A. (G) Mean coordination index for each simulation. The stars indicate differences at the p < 0.05 level by Bonferroni t-test after ANOVA.

Given that speed and directional accuracy alone proved to be inadequate to describe chemotactic efficiency, we developed a measurement that could combine information on the speed with the direction of cell movement. This measurement, called the coordination index, was obtained by multiplying the accuracy index, which, again, ranges between −1 and +1 (with −1 being a movement directly away, and +1 being a movement directly toward the highest concentration) by the speed of that particular movement. The coordination index, therefore, weighs the speed of the cell movement according to the accuracy of the movement. An additional desirable property of the coordination index is that negative values are allowed, in contrast to speed, which, by definition, is always positive. A statistical comparison of the mean coordination index of the simulations in Fig. 4 A proved that the simulations were significantly different from each other (Fig. 4 G). This result underscores the limitations of considering speed and accuracy separately and highlights the usefulness of the coordination index for describing chemotactic efficiency.

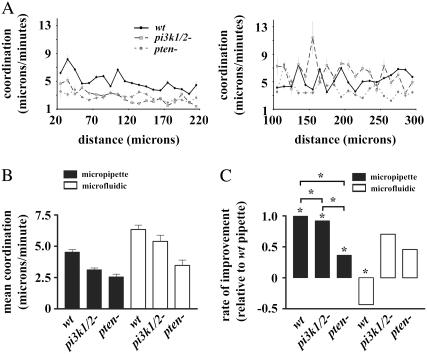
Since chemotactic efficiency is dependent on direction and speed, and accuracy is known to increase as cells approach regions of higher concentration in the micropipette assay, we asked whether the coordination between speed and accuracy might also increase in a similar manner. For both speed and accuracy, the mean coordination of all cells in the linear gradient was higher than in the micropipette assay. For both gradient profiles, wt cells had significantly higher coordination compared to pi3k1/2- and pten-, whereas pi3k1/2- had higher coordination than pten- (Fig. 5 A). An examination of the coordination as a function of distance from the micropipette revealed that not only were wt cells capable of increasing their accuracy and speed as they approached the micropipette, they were also capable of increasing the coordination between accuracy and speed (Fig. 5 B). Both mutants also showed an ability to increase their coordination as they approached the micropipette, although their ability to do so was significantly reduced compared to wt. None of the genotypes tested were capable of improving coordination as they approached the highest concentration in the linear gradient, and in fact the wt cells showed a significant decrease in coordination over distance. This suggests that the nonlinear gradient generated in the micropipette assay was required for improvements in coordination. Thus, assuming that the sensing system is not saturated in the regions measured here, the regulation of 3′-PI signaling is required for increases in the coordination of accuracy and speed by cells during chemotaxis in nonlinear gradients.

FIGURE 5.

Coordination in linear and nonlinear concentration gradients. (A) Coordination versus distance from the highest chemoattractant concentration present in the nonlinear gradient (left) and linear gradient (right). (B) Comparison of the mean coordination of the three genotypes in the linear and nonlinear gradients. (C) Statistical comparison of the rate of improvement of coordination in the micropipette assay and the linear region of the microfluidic device. For comparison of the increase in the coordination, the rate of increase was normalized to the rate of wt cells in the micropipette assay. Stars represent statistically significant differences at p < 0.05.

DISCUSSION

It was recently shown that wt cells increase their directional accuracy as they approach the micropipette (25). Our data corroborate and extend these findings by showing that wt cells also increase their speed and the coordination between the speed and direction as they approach the gradient source. Given the nonlinear nature of the concentration gradient generated in the micropipette assay, a cell moving toward the micropipette would experience a gradient whose steepness would be consistently increasing. According to the model in which the steepness of the 3′-PI signaling gradient is directly related to the steepness of the chemoattractant gradient, we hypothesized that an ever-steeper chemoattractant gradient would result in ever-steeper 3′-PI signaling polarity and more efficient chemotaxis. As they approached the micropipette, wt and pi3k1/2- cells were capable of increasing their directional accuracy. Dictyostelium possesses five type I PI3Ks, so the improvement in chemotaxis seen here most likely results from the residual PI3K activity in the pi3k1/2- mutant. Chemotactic efficiency in the microfluidic device was statistically higher than in the micropipette assay. This is likely due to the increased stability of the concentration gradient present in the microfluidic device. In the linear gradient the chemotactic ability of all three genotypes over distance was more erratic (Figs. 2, A and D, and 4 B), and no increase in accuracy or coordination was seen for any genotype. A similar result was seen by Arrieumerlou and Meyer (31) when they qualitatively compared the movements of immune cells in linear and nonlinear gradients, whereas our quantitative examination suggests that the change in gradient steepness or mean concentration experienced by a cell can account for the increased erratic behavior in the linear gradient.

There are at least four possible explanations for differences in the regulation of chemotactic efficiency in linear and nonlinear gradients: 1), a temporal effect whereby the directional accuracy and speed of a cell improve during a prolonged chemotactic run; 2), a temporally induced chemokinetic effect whereby changes in mean concentration result in changes in motility; 3), changes in gradient steepness; and 4), effects of the radial concentration profile lead to changes not only in the magnitude of the local gradient but also in its direction. Although there does qualitatively appear to be an increase in the speed and accuracy of a cell over time (data not shown), it is likely that this phenomenon is not responsible for the increased accuracy seen in the micropipette, for several reasons. For example, an increase in accuracy over time should result in increases in accuracy in the linear gradient as well, but we found no evidence of any such behavior. Also, in the micropipette assay (as well as the linear gradient), the initial distributions of cells were thoroughly scattered at various distances from the highest concentration, which would tend to obscure any effect that temporal increases would have on measures of accuracy as a function of distance. In this study it is impossible to rule out a temporally induced chemokinetic effect because the difference in the rate of change in mean concentration, by definition, differs between the two assays. Although Dictyostelium has been shown to be capable of sensing purely spatial chemoattractant gradients (11), it must be noted that chemokinesis in Dictyostelium has been measured for cAMP concentrations ranging from pM to μM, and the mean speed was only appreciably increased over buffer in 10 nM cAMP (32). As the result of either increased gradient steepness or a novel, temporally induced chemokinetic effect, the increases in accuracy and coordination seen here clearly indicate a receptor-dependent 3′-PI regulation of chemotaxis. A comparison of the radial gradients with a 1/r profile with translationally invariant 1/x gradients would require more complex microfluidic gradient generators than the ones used in these experiments (33).

It has been shown that eukaryotic chemotaxis displays characteristics of a biased random walk, in which individual movements are, on occasion, directionally random, but over the long term the directions are biased enough to produce efficient chemotaxis (25,31,34). Our detailed examination revealed that during chemotaxis, Dictyostelium cells are capable of coordinating the speed of their motility with the direction such that faster-than-average movements tend to be accurate in direction. To better capture chemotactic efficiency, we have introduced a new, to our knowledge, descriptive parameter, the coordination index, which is capable of describing the coordination between speed and directional accuracy. A similar definition was suggested but not applied by Loovers et al. (30) as best representing chemotactic efficiency. Coordination, while not absolutely required for chemotaxis, nonetheless serves to deemphasize directionally inaccurate movements and increase the efficiency with which the cells are capable of reaching their destination. We hypothesize that coordination comes about as a result of directionally biasing the extension and/or extending the lifetime of cytoskeletal projections during chemotaxis. Of interest, pi3k1/2- and pten- cells both showed a decreased ability to coordinate their speed and accuracy, suggesting a role for 3′-PIs in regulating coordination. Consistent with this notion, both pi3k1/2- and pten- cells, unlike wt, were capable of increasing their speed in the microfluidic device. We interpret this ability that is present in mutants but not in wt to be a further indication of the loss of coupling between speed and direction after the dysregulation of 3′-PI signaling.

Recent attempts to understand theoretically the motile response to eukaryotic gradient sensing have only focused on explaining the directional accuracy of the cell (25,31,34). Despite the impressive results in explaining the directional component of eukaryotic chemotaxis provided by these efforts, our data argue that a more complete model must take into account speed in addition to directional accuracy. Introducing speed into a model that relates the chemoattractant gradient to the motility of the cell also requires the introduction of time into the model. This is the subject of ongoing work.

The molecular mechanisms responsible for chemoattractant gradient sensing and the manner in which sensory pathways integrate with cytoskeletal dynamics are, in many ways, the largest open questions in eukaryotic chemotaxis. We examined the role of the 3′-PI signaling pathway, a leading candidate in regulating gradient sensing, by comparing the movement of wt and mutant cells with defects in 3′-PI signaling in linear and nonlinear gradients. We found that cells coordinate speed and directional accuracy during chemotaxis to raise chemotactic efficiency, and that their ability to take advantage of increased directional strength in a nonlinear gradient and increase both accuracy and coordination as they approach higher concentrations requires the degradation of 3′-PI by pten-. We suspect that the coordination of speed and accuracy during chemotaxis is a complex process that is regulated by multiple, potentially redundant pathways, as we have shown here that receptor-driven 3′-PI signaling, in part but not in toto, regulates the coordination of chemotaxis in Dictyostelium. We hypothesize that the coordination of speed and directional accuracy is likely to be universal for chemotactic cells since higher overall chemotactic efficiency is likely to offer a selective advantage for the system.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.