Insights into Subunit Interactions in the Heterotetrameric Structure of Potato ADP-Glucose Pyrophosphorylase

Abstract

ADP-glucose pyrophosphorylase, a key allosteric enzyme involved in higher plant starch biosynthesis, is composed of pairs of large (LS) and small subunits (SS). Current evidence indicates that the two subunit types play distinct roles in enzyme function. The LS is involved in mainly allosteric regulation through its interaction with the catalytic SS. Recently the crystal structure of the SS homotetramer has been solved, but no crystal structure of the native heterotetrameric enzyme is currently available. In this study, we first modeled the three-dimensional structure of the LS to construct the heterotetrameric enzyme. Because the enzyme has a 2-fold symmetry, six different dimeric (either up-down or side-by-side) interactions were possible. Molecular dynamics simulations were carried out for each of these possible dimers. Trajectories obtained from molecular dynamics simulations of each dimer were then analyzed by the molecular mechanics/Poisson-Boltzmann surface area method to identify the most favorable dimers, one for up-down and the other for side-by-side. Computational results combined with site directed mutagenesis and yeast two hybrid experiments suggested that the most favorable heterotetramer is formed by LS-SS (side-by-side), and LS-SS (up-down). We further determined the order of assembly during the heterotetrameric structure formation. First, side-by-side LS-SS dimers form followed by the up-down tetramerization based on the relative binding free energies.

INTRODUCTION

Starch is an important carbohydrate and the primary energy source for plants. It has numerous industrial applications as reviewed in Slattery et al. (1). Starch biosynthesis occurs by the participation of three main enzymes: ADP-glucose pyrophosphorylase (AGPase), starch synthase, and branching enzyme (2,3). The first enzyme in starch biosynthesis is the AGPase that catalyzes the conversion of Glc-1-P and ATP to ADP-glucose and pyrophosphate (PP_i). ADP-glucose is then used by starch synthase for the synthesis of polyglucans. Ample evidence has indicated that the AGPase catalyzes the rate limiting step in starch biosynthesis in higher plants (1,2,4).

AGPase from higher plants has a heterotetrameric structure (α₂β₂) composed of pairs of small (SS) and large (LS) subunits encoded by at least two different genes (5). The molecular mass of AGPases ranges from 200 to 240 kDa depending on plant species. In particular, the apparent molecular mass of potato SS and LS is shown to be 50 and 51 kDa, respectively (6). Although the primary amino acid sequence comparison of small subunits from different plant species exhibits 85–95% identity, the level of primary amino acid identity among large subunits is 50–60% for various plant species. LS and SS amino acid sequences share relatively less but still significant homology. For example, there is a 53% sequence identity between the potato tuber AGPase small and large subunits (7). Such a high homology between different subunits suggests that these two genes might have evolved from a common ancestor, most probably by a gene duplication event (8). Almost all plant AGPases, with a few exceptions, are allosterically regulated by metabolites that are indicative of the major carbon assimilatory pathway used in plant tissue. AGPases are regulated by 3-phosphoglyceric acid/inorganic phosphate (3-PGA/P_i) ratio in cells with 3-PGA being the main activator whereas P_i is the main inhibitor (5) with a few exceptions. The enzyme is also subject to post-translational redox modification by oxidation/reduction of the Cys12 residues in the small subunits (9). When oxidized, a disulfide bond forms between the Cys12 residues, which covalently links the small subunits. In the reduced state, the enzyme shows more intersubunit flexibility, has higher affinity for its substrates, is more sensitive to 3-PGA activation and more resistant to P_i inhibition (9,10). This regulation is believed to be important for fine tuning the activity of the enzyme.

Different approaches have been used in attempts to decipher the role of the two subunit types in higher plant AGPase function. Genetic, mutagenesis, and biochemical studies suggest that the SS has both catalytic and regulatory activities and the LS is mainly responsible for modulating the allosteric regulatory properties of the SS in the heterotetrameric enzyme (11–14). The small subunit (SS) is capable of forming a homotetrameric enzyme exhibiting normal catalytic properties but is defective in allosteric regulatory properties. This SS enzyme requires more than 30-fold greater amounts of 3-PGA for activation and is more sensitive to P_i inhibition as compared with the heterotetrameric enzyme. The large subunit, which is incapable of forming an active enzyme, increases the allosteric regulatory response of the SS to effectors (5,11,15). Alternatively, recent studies have implicated that the LS may bind to substrates Glc-1-P and ATP (16,17). The binding of the LS to substrates may allow the LS to interact cooperatively with the catalytic SS in binding substrates and effectors and, in turn, influence net catalysis. In addition, specific regions from both the LS and the SS were found to be important for subunit association and enzyme stability. Laughlin et al. (18) showed that deletion of a 19-amino acid segment at C-terminus of either subunit results in a decrease in enzyme activity due to inability of subunits to assemble into a heterotetrameric enzyme. They also identified a region composed of 28 residues at N-terminus of LS that is essential for the stability of the enzyme. In addition, Cross et al. (19), using chimeric maize/potato small subunits, found a polymorphic motif in the SS that is critical for subunit interaction. They have concluded that a 55-amino acid region between the residues 322–376 directly interacts with LS and significantly contributes to the overall enzyme stability.

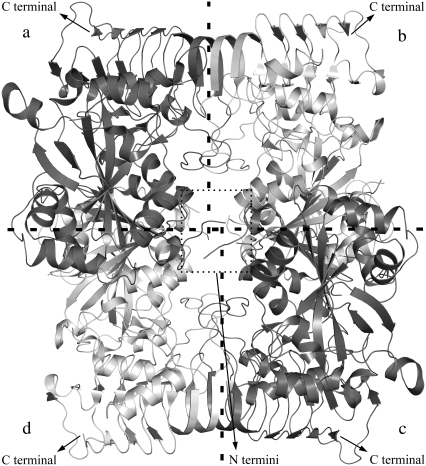
Recently, three-dimensional (3-D) structure of the homotetrameric SS was determined by x-ray crystallography in its inhibited state. Three structures were extracted in that study: the enzyme in the absence of substrates and effectors, the enzyme in complex with ATP and in complex with ADP-glucose, with the resolutions of 2.1 Å, 2.2 Å, 2.6 Å, respectively (20). This recombinant homotetrameric enzyme elucidates structural information about the assembly of the subunits and also gives structural insights into the heterotetrameric enzyme. Fig. 1 displays the crystal structure of the homotetrameric SS. The x-ray crystallographic structure of heterotetrameric AGPase is not available, because it is difficult to obtain a highly pure and stable form of the enzyme. Obtaining the native structure of the heterotetrameric enzyme is important to understand the structure-function relationships between the subunits and its reaction mechanism. This will enable us to rationally manipulate the enzyme to obtain different engineered variants that may be used for crop plant improvement.

FIGURE 1.

Crystal structure of homotetrameric SS composed of four identical chains in different color shades, chains a–d.

In this effort, we first carried out homology modeling for potato AGPase LS. To elucidate the heterotetrameric AGPase structure, we have proposed three possible tetrameric models between the subunits based on the crystal structure of the homotetramer. Then, 10 ns of explicit solvent molecular dynamics (MD) simulations were carried out for each combination of dimeric interaction possibilities between the subunits. To further investigate the nature of these interactions, relative binding free energies between the subunits were calculated by molecular mechanics/Poisson-Boltzmann surface area (MM-PBSA) methodology using the trajectories taken from the MD simulations. Based on these binding free energy calculations, the most favorable interactions between the subunits were determined. These results, together with site directed mutagenesis and yeast two hybrid experiments, were used to propose a complete model for the heterotetrameric AGPase. Further, a list of interfacial amino acids that might play critical roles in the interaction between the LS and SS were identified. The detailed computational techniques used in this work allowed us to model the heterotetrameric assembly of the enzyme as well as to postulate the order of assembly during heterotetramerization. This study establishes the groundwork for understanding the subunit-subunit interactions of the native structure of AGPase for what we believe is the first time.

MATERIALS AND METHODS

Homology modeling of the large subunit and construction of the heterotetrameric models

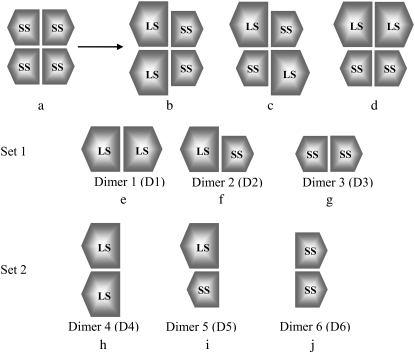
The sequence alignments of the LS and SS using CLUSTALW (1.83) (21) with default parameters show that there is a 53% of sequence identity between LS and SS. SWISS–MODEL homology modeling server (first-approach method) (22,23) was used to construct the 3-D structure of the LS. When the near-full-length cDNA clones of potato tuber AGPase large and small subunits were compared, the LS and SS were found to consist of 470 and 521 residues, respectively (7). Both subunits carry amyloplast targeting sequences at their N-terminus regions. The ribbon diagram displaying the homotetrameric complex is shown in Fig. 1. Each of the subunits is shaded differently to illustrate the symmetry of the complex. In the crystal structure of homotetrameric SS (pdb id: 1YP2), one chain consists of 442 amino acids, thereby excluding the amyloplast target sequence of the first 79 residues at the N-terminus. Twenty-nine residues at the N-terminus of the LS, including the plastid targeting sequence, were removed before submission to the SWISS–MODEL server to exclude the random coil fragment at this region and to achieve a better global superimposition with the SS. The crystal homotetrameric structure of the SS contains structural gaps where the C-chain (1YP2_C) is the most complete. In the crystal structure of this chain, fragments between the residues 27–32 and 91–98 were missing. To fill these gaps 1YP2_C was initially submitted to SWISS-MODEL and used as the model SS in further calculations. After the 3-D structure of the LS was generated; the homotetrameric structure was used as a template to construct the heterotetrameric AGPase with two large and two small subunits. Three models were proposed: a schematic presentation of the three proposed models is illustrated in Fig. 2, b–d, together with the homotetrameric SS (Fig. 2 a). Each model was built by superimposing the large (or small) subunit with the template homotetrameric structure using backbone atoms. Models were named as Model-1 (Fig. 2 b), Model-2, (Fig. 2 c), Model-3 (Fig. 2 d).

FIGURE 2.

Schematic presentation of (a) the crystal structure of homotetrameric SS and (b–d) proposed models. For construction of the models each large and small subunits were superimposed with the corresponding chain in the crystal structure and the original SS chains were than deleted. (b–d) Correspond to Model-1, Model-2, and Model-3, respectively. (e–j) Schematic presentation of dimeric interactions between the subunits that constitute the heterotetrameric models. LS and SS are composed of 441 and 442 residues respectively. Set 1 contains the D1, D2, D3, and set 2 contains the D4, D5, D6.

To predict the correct model for the heterotetrameric AGPase structure among the proposed models, we followed different computational approaches as explained below. Because the enzyme has a twofold symmetry, six different dimeric interactions were possible as displayed in Fig. 2, e–j. Three dimer models representing the side-by-side organization were named as set1 dimers (D1–D3), whereas the remaining three dimer models, representing the up-down organizations, were named as set2 (D4–D6). Each possible model was subjected to additional analysis. First, MD simulations were carried out for each of these possible dimer models. Trajectories obtained from MD simulations of each postulated dimer model were then analyzed by MM-PBSA method to identify the most favorable interactions.

MD simulations

All of the six dimer models (D1-D6) were solvated in different rectangular boxes including TIP3P water molecules (24). Distances between the edge of the water boxes and the closest atom of solutes were at least 10 Å. Counter ions were added to neutralize the systems. All the histidine residues were treated as carrying +1 charge at their Nɛ atoms. Simulations were carried out with the NAMD software (25) using the parm96 force field (26) and periodic boundary conditions (27). A direct-space nonbonded cutoff value of 9 Å was used with particle mesh Ewald method (28) to treat the long range electrostatic interactions. SHAKE algorithm (29) was applied to water molecules to treat them as rigid bodies and to hydrogen atoms to constrain their movements. Langevin piston Nose-Hoover method (30,31) was used to keep the pressure constant. Time step of all simulations were 2 fs. Systems were minimized by conjugate gradient method for 10⁴ steps keeping the backbone atoms of solutes fixed followed by an additional 10⁴ steps with relaxed backbone atoms. The systems were then gradually heated from 0 K to 300 K in 150 ps using NVT ensembles in which the Cα atoms of the solutes were restrained by applying 2 kcal mol⁻¹ Å⁻² force constant. Isothermal-isobaric ensembles (NPT) were then applied for 80 ps during which the restraints on Cα atoms were removed gradually with an additional 100 ps of equilibration simulation. Subsequent NPT simulations were carried out for 10 ns and the last 8 ns of the simulations were analyzed for binding free energy calculations by MM-PBSA method. MD simulations were also used to obtain insights about the flexibility of interface residues (32).

Identification of interface residues

Snapshots taken from the last 8 ns of the simulations were separated as complex, receptor, and ligand structures. Interface residues at each snapshot were identified based on the implementation of Lee and Richards method (33) using the NACCESS program (34) and by HotSprint (prism .ccbb.ku.edu.tr/hotsprint) (35). Probe radius used for calculation of the atomic accessible surface area was taken 1.4 Å together with a z-slice value of 0.05 Å. Hydrogen atoms were not included during the calculations. The set of interface residues was completed by a two-step approach. First, residues that show >1 Ų decrease in their accessible surface area on complexation were considered as part of the initial interface set. Second, residues from the initial set that hold the above criteria at least for 50% (200 snapshots) of the last 8 ns part of the simulations were chosen as the actual set of interface residues. (The list of interface residues is provided in Table S1 of the Supplementary Material, Data S1.)

Binding energy calculations

Molecular mechanics Poisson-Boltzmann surface area (MM-PBSA) or a related approach of generalized born surface area (MM-GBSA) methods (23) can be used to calculate the binding free energy of molecules in an equilibrium state. In these approaches, binding free energy of a complex is calculated by taking snapshots from a molecular dynamics trajectory and computing the average energy of these snapshots according to the formula in Eq. 1,

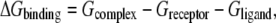(1)

where G_complex, G_receptor, and G_ligand are the energies of the complex, receptor, and ligand respectively. Snapshots of the complex, receptor and ligand can either be taken from separate trajectories or a single trajectory in which the coordinates of receptor and ligand are extracted from the complex molecule in the latter approach. Energy of a molecule in Eq. 1 can be represented as shown in the following equation:

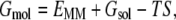(2)

where E_MM is the total mechanical energy of the molecule in gas phase, G_sol is the solvation free energy and TS is the entropic term. Each term in Eq. 2 can be divided into individual energetic components as shown below:

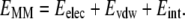(3)

In Eq. 3, E_MM represents the bonded and nonbonded interactions as a sum of electrostatic (columbic), van der Waals (Lennard-Jones), and internal strain (bonds, angles, and dihedrals) energies. This term is calculated by classical molecular-mechanics methods using standard force fields such as parm96 force field (26). Solvation free energy of a molecule is calculated as the sum of a polar and a nonpolar term:

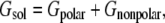(4)

where electrostatic contribution to the solvation energy (G_polar) is computed in a continuum solvent environment by solving either the Poisson-Boltzmann equation (36), or using a GBSA method. Nonpolar solvation energy (G_nonpolar), which is considered to be the sum of a solute-solvent van der Waals interactions and solvent-solvent cavity formation energy, is approximated by using an empirical formula such as G_nonpolar = α × SASA + β. According to this formula, nonpolar solvation energy of a molecule is proportional to the solvent accessible surface area (SASA) of that molecule in a solvent, where α and β are constants (37,38).

The entropic term in Eq. 2 is considered as the summation of vibrational, rotational, and translational contributions where vibrational term can be calculated by normal-mode analysis or quasi-harmonic analysis:

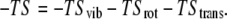(5)

The entropic term is found to be much smaller than the other two terms (in Eq. 2) in many applications of estimating relative binding free energies (39). Because the calculation of entropic contribution is computationally expensive, this term can be omitted if qualitative results, rather than quantitative, are considered to be more important. This is also true for different ligands that show similar binding affinities and modes for a given receptor (40–42).

The last 8 ns of the simulations for each dimeric interaction between the LS and SS pairs were analyzed by MM-PBSA method as implemented in AMBER8 package (43). The trajectories were postprocessed to strip off the water molecules and counter ions before the calculations. Four hundred snapshots with 20 ps intervals were extracted for each complex, receptor, and ligand structures from single trajectories. We analyzed the autocorrelation functions of effective free energies for the six dimers (D1–D6) and found that the correlations drop to 0.1 in 20 ps meaning that the consecutive snapshots (structures) are not correlated (Fig. S1 of the Supplementary Material, Data S1). In our simulations, we do not have the crystal structures of the isolated monomers, which would make the separate trajectory inappropriate in our case. However, because we are interested mainly in the relative binding free energies of the models rather than the absolute free energies, and all models have the same reference states, we assume that having the same hypothetical reference in all cases, would introduce similar errors and would cancel out in comparisons of the stabilities of the dimers.

In all of the calculations the LS was treated as the receptor and the SS as the ligand. Gas phase energies (E_MM) of the proteins were calculated by the SANDER module applying no cutoff value for nonbonded interactions. The electrostatic contribution to the desolvation free energy was computed by solving the finite difference Poisson-Boltzmann equation using the PBSA module of AMBER8 with PARSE parameter set (44). Dielectric constants for the solute and solvent were taken as 1 and 80, respectively; and the solvent probe radius was adjusted to 1.4 Å. Nonpolar solvation energies were calculated according to SASA dependent empirical formula by using the LCPO method (45) as implemented in AMBER8. The surface tension parameters, α and the β, were taken as 0.0542 and 0.92, respectively (44).

Cloning and site-directed mutagenesis of large subunit

The LS and SS cDNA of potato AGPase were obtained by PCR with appropriate primer sets. PCR products were digested and cloned into pGADT7 and pGBKT7 vectors and constructs were named as pGBT-LS and pGAD-SS. Escherichia coli DH5α host strain was used during the manipulation of plasmids. Selection of pGBT-LS was done in the presence of kanamycin (50 μg/mL) and selection of pGAD-SS was done in the presence of the ampicillin (100 μg/mL). Site-directed mutagenesis was carried out using the Stratagene Quick-change Mutagenesis kit. The PCR reaction contained 30 fmol of DNA, 20 pmol of primers, 0.2 mM dNTPs, and 2.5 units of Pfu Turbo DNA polymerase. The PCR was carried out for 12 cycles under the following conditions: 40 s at 94°C, 40 s at 55°C, and 11 min at 68°C. The PCR products were digested with DpnI to remove template plasmid DNA and transformed into E. coli DH5α. The presence of the mutation was verified by DNA sequencing through Iontek (Istanbul, Turkey).

Yeast manipulations

Transformation of constructs into the yeast strain AH109 followed the protocol outlined by Clontech (Palo Alto, CA). AH109 yeast cells containing both plasmids were selected on a synthetic minimal medium containing 6.7 g/L yeast nitrogen base (Difco, Detroit, MI) without amino acids (Trp and Leu), 2% glucose, amino acid dropout supplement without Leu and Trp (Clontech), and 20 g/L agar (plates only). The constructs containing wild-type (WT) and mutant form of LS were sequentially transformed into the cells as in the following procedure. First, pGAD-SS was transferred into AH109 cells. Transformed cells were selected in minimal media that lacks Leu for 3 days at 30°C. A single colony was picked and grown in liquid media (without Leu) for competent cell preparation. Then, constructs that contain WT LS and mutant LS were transferred into AH109/pGAD-SS cells. Transformed cells were seeded onto selective media that lacked both Trp and Leu. Then interaction between SS and LS including the mutant form was scored on the media that lacked Leu, His, and Trp.

RESULTS AND DISCUSSION

Modeled structure of the AGPase large subunit

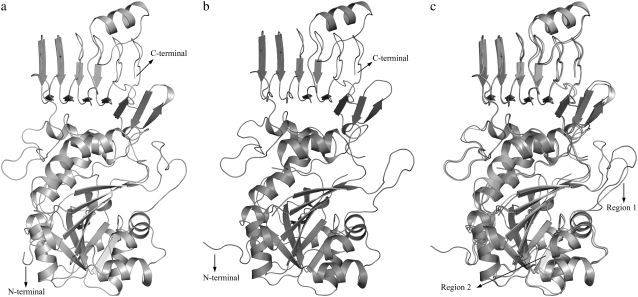
The plastid targeting peptide was removed before modeling of the LS as described in Materials and Methods. The homology modeling of potato AGPase LS resulted in a structure similar to the crystal structure of the SS (C chain) as expected (Fig. 3 a). The modeled structure of the LS, the crystal structure of the SS and the superimposed images of both can be seen in Fig. 3, a–c. The LS model shows a root mean-square value of 1.3 Å when superimposed with the C-chain of the crystal structure of the SS (Fig. 3 c) using heavy backbone atoms. This relatively small difference indicates a high structural similarity between the subunits. Visual inspection of the superimposed structures shows two regions where the subunits differ most. These regions correspond to residues between 95–108 (region 1) and 122–126 (region 2) in the LS and 108–119 and 133–134 in the SS (Fig. 3 c) and may reflect different functions for the subunits. For example, amino acids 112–117 undergo a conformational change on Glc-1-P binding in SS. Also residues from 106 to 119 are forced to move significantly on ATP binding (20). Although both regions constitute loop structures in LS, the first fragment in the SS is a loop and the second one is part of an α-helix.

FIGURE 3.

Three-dimensional structures of (a) LS, (b) SS, and (c) their superimposed images. See Materials and Methods for details about the missing regions in SS.

Possible heterotetrameric models and analysis of interactions between small and large subunits of potato AGPase

Three heterotetrameric models were proposed for the potato AGPase. A schematic presentation of the three proposed models is illustrated in Fig. 2, b–d, together with the schematic model of the homotetrameric SS (Fig. 2 a). MM-PB(GB)SA methodologies have been used widely to predict protein structures (46), and to estimate the binding energies of protein-ligand (23) and protein-protein interactions (47–49). As mentioned earlier, we have investigated six different possible dimeric interactions that could exist between the subunits (Fig. 2, e–j). Because the MM-PB(GB)SA methods require the systems to reach equilibrium, the first 2 ns parts of the simulations were considered as the transition phase from the starting structures into the equilibrium state. This was essential because the starting configurations of the dimers were not taken from experimentally determined crystal structures and the size of the dimers were relatively large that might require a significant amount of time to reach an equilibrium state. The root mean-square profiles of the six dimers with reference to the initial structures (at t = 0 ns) are provided in Fig. S2, Data S1. To test the stability of the systems, gas-phase energies and solvation energies were calculated for each snapshot and plotted as shown in Fig. S3, Data S1. Based on the regression lines, the graphs show that only D6 shows increasing E_MM + G_sol values whereas the rest of the systems exhibit a decreasing trend in these terms. We also observe that the energetic values of the LS and SS in the set2 dimers (D4, D5, D6) fluctuate less than the set1 dimers. This is especially true if the corresponding dimer contains the SS as in D5 and D6 for which the slopes of the regression lines are 1.43 × 10⁻¹ kcal/(mol ps) and 5.3 × 10⁻² kcal/(mol ps), respectively (Fig. S3 b, Data S1). D6 and its components, with 10⁻³ kcal/(mol ps), 1.1 × 10⁻² kcal/(mol ps) slopes for the receptor and ligand respectively (Fig. S3 b, Data S1), can be considered to be most stable structures in terms of E_MM + G_sol values. This is an expected result because the starting structure of this dimer was taken from the homotetrameric crystal structure of the SS. However, in the set1 dimers the most stable structure is D1 with a slope of 1.05 × 10⁻¹ kcal/(mol ps) whereas D3 is the most unstable with a slope of 2.86 × 10⁻¹ kcal/(mol ps) (Fig. S3 a, Data S1).

In the single trajectory approximation used here, the same coordinates were used for the separated ligand and receptor atoms as for the complex. Thus the bonded energies (dihedral, bond, and bond angle) in E_MM (Eq. 2) will cancel when applied to Eq. 1. The change in E_coul and E_vdw will result from the nonbonded interactions between the receptor and ligand on complexation. This approximation is considered to be valid when the ligand or receptor do not show conformational changes on complexation or, as in this case, when very similar ligands are being compared (23,49–55) in which case any enthalpic and entropic penalties on complexation are approximately constant (48,56). We further estimated the conformational entropy contribution (translational, rotational, and vibrational) to the binding free energy using normal mode analysis (NMODE module of AMBER8). The results showed that entropy is smaller with an order of magnitude compared to the other contributions (for example, for the SS in D2, we obtained a TS value of 4857 kcal/mol compared to −27,000 kcal/mol from other effective free energy terms, and vibrational entropy changes were found to be less significant with a value of 10 kcal/mol). Entropic contributions were not included in the calculations because we are interested mainly in relative binding energies between the subunits and the subunits have similar binding modes because of the high structural similarity. Therefore, we assumed that entropy contributions are similar for different dimers and would cancel out in the relative binding free energies. Because all three models tested are composed of two SS and two LS, all the tetramerization reactions can be thought as

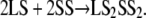Because the initial molecules were the same in all three tetramers, we assumed that we could choose hypothetical reference states for the LS and SS, and calculate the relative energies with respect to these references.

To construct the native structure of heterotetrameric AGPase, we used two of the interactions from six different possibilities shown in Fig. 2, e–j. Binding free energies along the trajectories of all dimers are presented in Fig. S4 (Data S1) and the averages of 400 snapshots are listed in Table 1. This table shows that subunit interactions in set1 have dominant roles in maintaining the stability of native AGPase tetrameric structure. In other words, the interaction between the lateral subunits is much stronger compared to the longitudinal interaction. Indeed, the number of interface residues of set1 dimers is higher than the number of set2 dimer interface residues. In all the cases, internal energies (ΔE_int = Δ(bond + angle + dihedral)) converge to zero that is a characteristic of single trajectory approach. For all dimers in set1, ΔE_VDW values range from −190.27 kcal/mol to −179.56 kcal/mol and are very close to each other. Differences among the set2 dimers for this energy component are more pronounced, but still very close to each other (between −116.74 kcal/mol and −99.14 kcal/mol). In addition to ΔE_VDW energies, ΔG_nonpolar energies also show very similar values in each set of dimers. Values in set1 dimers are more negative (stable) than the values in set2. This is an expected result because nonpolar solvation energy is directly related to the solvent accessible surface area by a relation of G_nonpolar = α × SASA + β and the number of interface residues that are buried on complex formation in set1 complexes is higher than the set2 complexes. Gas-phase electrostatic (E_elec) and polar solvation (G_polar) energies are also observed to be discriminating terms among the dimers. It is also seen that ΔE_elec for D2 is 1.8 times greater than D1 and 3.2 times greater than D3. This indicates a better electrostatic complementation between large and small subunits. For set2 dimers, the most favorable steric complementarity is achieved by the association of two small subunits in D6. ΔE_elec for this dimer is 1.6 and 1.2 times greater than Dimer 4 and 5, respectively. Whereas gas-phase electrostatic energies favor binding, polar solvation energies contribute negatively to the interactions. These two components generally tend to cancel the effect of each other. In our study, dimers that have higher E_elec values can better compensate the desolvation penalties of complexation (Dimer 2 and 6, Table 1), but the overall contribution from ΔG_elec disfavors binding of subunits. However, contributions from van der Waals and nonpolar solvation energies drive the association of dimers, thus yielding overall favorable complexes. These results are consistent with the studies reported previously (48,49,57).

TABLE 1.

Binding free energy components for each of the dimers averaged over the 400 snapshots

	Set 1 (kcal/mol)			Set 2 (kcal/mol)
	Dimer 1	Dimer 2	Dimer 3	Dimer 4	Dimer 5	Dimer 6
ΔEelec	−277.02 (2.67)	−511.49 (1.90)	−157.58 (2.17)	−248.21 (3.35)	−330.53 (2.31)	−393.96 (2.38)
ΔEVDW	−190.27 (0.43)	−191.05 (0.42)	−179.56 (0.49)	−116.74 (0.48)	−105.22 (0.38)	−99.14 (0.38)
ΔEint	0.01 (0.0)	0.01 (0.0)	0.01 (0.0)	0.01 (0.0)	0.01 (0.0)	0.01 (0.0)
ΔGgas	−467.28 (2.77)	−702.53 (2.00)	−337.13 (2.38)	−364.93 (3.47)	−435.74 (2.28)	−493.09 (2.35)
ΔGnonpolar	−18.51 (0.03)	−19.03 (0.04)	−17.01 (0.04)	−12.30 (0.05)	−11.10 (0.03)	−10.97 (0.03)
ΔGpolar	414.20 (5.71)	600.53 (3.49)	267.49 (2.89)	342.09 (4.41)	416.02 (3.79)	454.75 (2.66)
ΔGsol	395.69 (5.70)	581.50 (3.49)	250.48 (2.85)	329.79 (4.39)	404.91 (3.78)	443.78 (2.64)
ΔGelec	137.19 (4.97)	89.03 (2.87)	109.90 (1.50)	93.88 (2.70)	85.48 (3.05)	60.79 (1.13)
ΔGTotal	−71.58 (4.94)	−121.03 (2.86)	−86.65 (1.28)	−35.14 (2.73)	−30.83 (3.08)	−49.31 (1.02)

Values in parentheses are standard errors of the means. Explanation for the abbreviations can be found in methods section. ΔG_elec corresponds to sum of gas-phase electrostatic energy and polar solvation energy.

Modeled structure of heterotetrameric AGPase and the mechanism of tetramerization

Table 1 shows that D2 has a more favorable interaction with a binding free energy of −121.03 kcal/mol compared to D1 and D3 that have values of −71.58 kcal/mol and −86.65 kcal/mol, respectively. This means that association of LS and SS is more likely to happen than a homodimer formation (if lateral interaction of heterotetramer is considered: E = −121.03 × 2 = −242.06 kcal/mol versus E = −71.58 + (−86.65) = −158.23 kcal/mol). We observe that the binding free energies in set2 dimers are very close to each other. Among set2 dimers (up-down interactions) D4 and D6 have slightly more favorable interaction energies than D5 constituting a total energy of −84.45 kcal/mol (E = −35.14 kcal/mol + (−49.31 kcal/mol)) compared to interactions of LS and SS in D5 that gives a −61.66 kcal/mol (E = −30.83 kcal/mol × 2) of total energy.

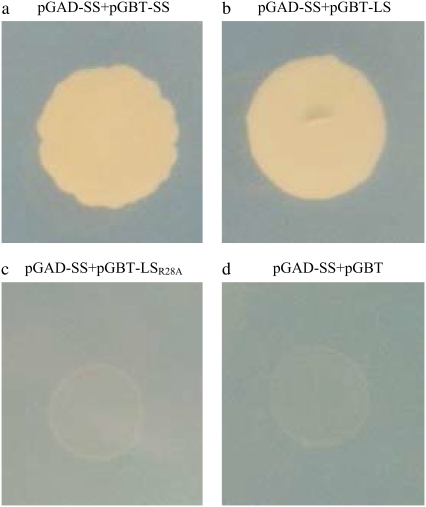
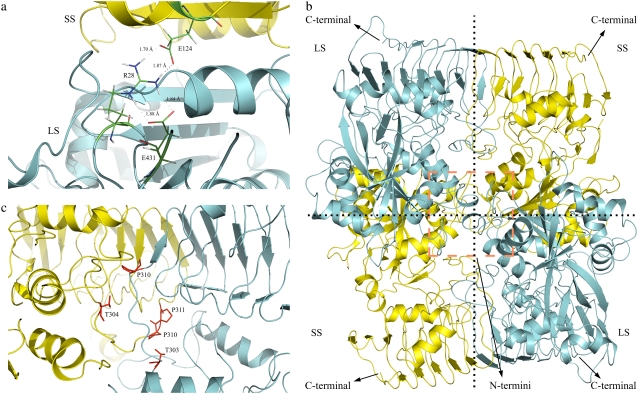
These results indicate that side-by-side interactions are much stronger when compared to the up-down interactions. Among the set1 dimers, D2 is clearly more favorable based on the free energy results. Additionally, the set2 dimers exhibit competitive results, although D4+D6 is slightly more favorable than the two D5 associations, the difference between their binding free energies is not as strong as in the set1 dimers. We carried out site directed mutagenesis and Y2H experiments where we mutated the interface residues in D4, D5, and D6. Table S1 (Data S1) lists the interface residues in all six dimers. We found that Arg²⁸ (of the LS) was an interface residue in D5 but not in D4 and D6. When this residue was mutated to alanine, we observed no growth in the selective interaction media (Fig. 4), indicating the importance of this residue in the tetramerization of the complex and validating the involvement of D5 in the tetrameric assembly. When a detailed analysis was done on this residue, we observed that Arg²⁸ of the LS makes several hydrogen bonds with Glu¹²⁴ in SS and Glu⁴³¹ in LS. We also noticed that Glu⁴³¹ in the LS is found in the C-terminal β-helix domain and Arg²⁸ is found in the N-terminus (Fig. 5 a). Thus, Arg²⁸ provides interactions between the SS and the C-terminus of the LS. Similarly, mutating Gln¹⁰⁰ (of the SS) to alanine inhibits the colony growth in the media. This residue has many intersubunit contacts as well. Based on these data, we suggest that Model-2 is the most probable heterotetrameric structure when the overall stability of the enzyme is considered. In addition, a possible homodimer formation between the SS as in D6 does not allow a disulfide bridge between the Cys¹² residues of this subunit because of the spatial restrictions. It was found that a disulfide bond forms between the Cys¹² residues covalently linking the small subunits when the heterotetramer is in the active state (9).

FIGURE 4.

Yeast two-hybrid analysis of potato AGPase subunit interactions (a) SS_WT:SS_WT; (b) SS_WT:LS_WT; (c) SS_WT:LS_R28A; and (d) SS_WT:empty GBT vector. AH109 yeast cells expressing the designated plasmids are selected on a synthetic growth medium without Leu and Trp. Selections for interactions were carried out in the absence of Leu, Trp, and His.

FIGURE 5.

(a) LS_R28 makes several hydrogen bonds (dashed lines) with SS_E124 and LS_E431 throughout the simulation. In this snapshot it forms total of four H-bonds with SS_E124 and LS_E431. Note that LS_E431 is found in C-terminal β-helix domain and LS_R28 is found in the N-terminus. The H-bonds formed by LS_R28 makes a significant contrbution to LS-SS interaction by connecting the LS C-terminal β-helix domain and the SS.(b) Modeled structure of the heterotetrameric potato AGPase; subunits LS (cyan) and SS (yellow). The model was generated from the final snapshots of the D2 and D5 simulations. Schematic presentation of the model can also be seen in Fig. 2 c. (c) Snapshot showing the highly conserved residues (red), Thr³⁰³, Pro³¹⁰ in LS, and Thr³⁰⁴, Pro³¹⁰, Pro³¹¹ in SS in Dimer 2 interface. LS is cyan and SS is yellow.

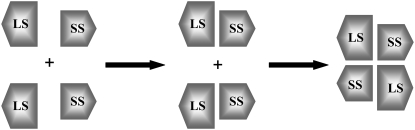
These results allow us to further speculate on the mechanism of heterotetramer formation. We propose that first LS-SS dimers form as shown in Fig. 2 c (D2), then, most probably, this LS-SS dimer interacts with another LS-SS dimer. The rationale behind this hypothesis is that side-by-side LS-SS interactions are much stronger compared to up-down LS-SS interactions and other possible dimer associations. Both Model 1 and Model 2 are possible in this case (based on the comparable binding free energies), however, in the active state of the enzyme there might be a population shift toward Model 2 (i.e., an increase in the concentration of the Model 2 contrary to a decrease in the Model 1 concentration). Because Model 2 will allow the Cys¹² residues of the SS monomers to form a disulfide bridge in the tetramer structure, this heterotetramer will be favored energetically. Therefore, we propose that the order of assembly during the heterotetramerization (Fig. 6) should be first side-by-side interaction between the LS and the SS and then up-down complexation.

FIGURE 6.

Order of assembly formation. First LS and SS associate to form a side-by-side dimer. Up-down complexation then takes place.

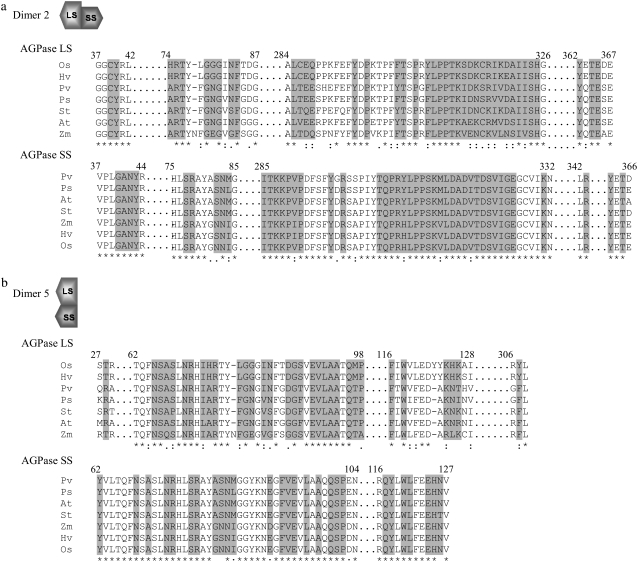
After establishing the native structure of AGPase (Fig. 5 b), we have further investigated D2 and D5, to get a more detailed picture of the interactions. A complete list of the interface residues for D2 and D5 can be seen in Fig. 7 (Table S1, Data S1). Comparison of these residues with other plant AGPases showed strong conservation of amino acids in both the LS and the SS. Although the number of interface residues for D2 is 86, this number decreases to 59 for D5. Consequently, average buried surface area between the subunits of D2 and D5 are 3454.03 Ų and 2078.27 Ų, respectively. Our recent study shows that hot spots, critical for binding are mostly conserved and clustered tightly (58). Using CONSURF server (59) we found that large and small subunits contain highly conserved residues at their interfaces. All of the residues with a conservation score of 9, Thr³⁰³ and Pro³¹⁰ in LS and Thr³⁰⁴, Pro³¹⁰, and Pro³¹¹ in SS, are found in the loop regions taking a role in subunit interactions and structural stability as further shown in Fig. 5 c. Laughlin et al. (18) reported that deletion of 10 amino acids from C-termini of both LS and SS of potato AGPase disrupt formation of heterotetrameric enzyme. They have concluded that removing 10 amino acids from the LS C-termini may affect folding and/or stability of the enzyme. In addition, Greene and Hannah (60) have identified a mutant form of the maize endosperm LS of AGPase. Analysis of this mutant indicated that due to a frame shift mutation in the LS coding region the last 100 amino acids were missing. Their yeast two-hybrid results showed that there was no interaction between the LS and SS in that case. On the other hand, our analysis of models indicates that the C-terminal β-helix domains of both subunits does not participate in up-down subunit-subunit interactions, but rather participate in lateral interactions, and alternatively are involved in the binding of effectors. Our result supports Laughlin et al. (18) as they concluded that C-terminal domains are most probably involved in the proper folding of the monomers. Furthermore, Greene and Hannah (61) have identified an amino acid residue (His³³³) from the maize endosperm LS AGPase that participates in interactions with the SS. Our analysis of interface residues of potato LS indicated that Tyr²⁵⁸ (corresponding to maize His³³³ LS AGPase) is not found in the interface. This might be due to additional amino acids required for the maize endosperm AGPase LS to interact with the SS. Alternatively, this specific residue may be solely responsible for heat stability rather than any interaction between the subunits.

FIGURE 7.

Interface residues (shaded) in Model-2. Residues that show >1 Ų change in their solvent accessible surface area on complexation and hold this condition for at least 50% (200 snapshots) of the last 8 ns of the simulations were taken as interface residues. Conserved residues were obtained from CONSURF (59). As representatives, alignments were carried out by picking up large and small subunit primary amino acid sequences from different plants. OS, Oryaza sativa; Hv, Hordeum vulgare; Pv, Phaseolus vulgaris; St, Solanum tuberosum, At, Arabidopsis thaliana; and Zm, Zea mays.

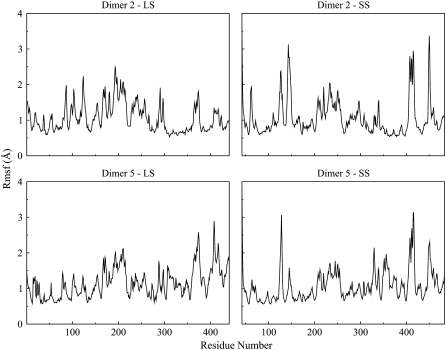
To compare the flexibilities of the subunits, average root mean-square values along the trajectories were analyzed. For the LS in D2 and D5, root mean-square values were found to be 1.06 Å and 1.15 Å, respectively. The values for the SS are 1.06 Å and 1.07 Å for the corresponding dimers. In general, residues in both of the dimers show similar modes of fluctuations, but a closer examination shows two regions (in D2) in the LS and SS: the first region comprises 65 residues, between 299–363 in the LS with an average root mean-square of 0.69 Å and the second region comprises 105 residues between 300–404 in the SS with an average root mean-square of 0.92 Å (Fig. 8). It should be pointed out that 23 of the interface residues in the LS and 27 of the interface residues in the SS lie within these regions. In the LS, residues between 299 and 310 are part of a loop region that connects the N-terminal domain with the C-terminal β-helix domain. The corresponding region in the SS is between residues 300 and 311. This region exhibits smaller relative fluctuations in D2 when compared to its equivalent region in D5. It is surprising that a loop region is more restricted; a possible explanation for the smaller root mean-square values may be that this region makes interactions with their counterparts in the other subunits. These interactions might restrict the movement of amino acids in the region, thus resulting in smaller fluctuations. Indeed, Jin et al. (20) have also reported that residues between 300 and 320 (291–311 in our case) make several interactions with their equivalent regions in the other subunit. The rest of the residues, 311–363 in LS and 312–364 in SS, mostly make up the C-terminal β-helix domains of their corresponding subunits. These results are also in agreement with study of Cross et al. (19). The region they have identified in the SS, which is important for the interaction with the LS and enzyme stability, comprises the amino acids between 322 and 376 (289–343 in our case). This 55-residue long fragment correlates with our smaller root mean-square region and 30 of them make up the interface with the LS. Overall, we can conclude that residues interacting with their counterparts in the partner subunit or being a part of the structurally rigid β-helix domain experience smaller root mean-square values. In contrast to D2, we do not observe any obvious stretches in D5 that represent rigid fragments (Fig. 8). This might be due to the fact that number of interface residues in this interaction type is lower and they are more scattered than in D2, however they still make important interactions. For instance, Glu⁹⁰, Glu⁹⁴, Gln¹⁰⁰, Trp¹²⁰, and Glu¹²⁴ residues in SS, which were also reported by Jin et al. (20) in the crystal structure of the SS, were found to be at the interface in all of the 400 snapshots taken from the last 8 ns of the simulations except for the Glu⁹⁰ that was part of the interface for 93% of the simulation time. Moreover, residues such as Arg⁷⁴, Arg⁷⁸, Glu⁹⁰, and Glu¹²⁴ in the SS make salt bridges with Glu⁹⁰, Asp⁸⁶, Arg⁷⁵, and Arg⁷¹ in the LS respectively.

FIGURE 8.

Root mean-square fluctuations (Rmsf) of backbone atoms (C, CA, and N) versus residue number for Dimer 2 and Dimer 5 subunits.

CONCLUSIONS

Higher plant AGPases consist of pairs of large and small subunits (5,6). Although the SS was crystallized in a homotetrameric form, the native structure of the heterotetrameric enzyme is still unknown. However, a 53% sequence identity, thus a highly comparable structural architecture with an root mean-square of 1.3 Å, between the large and small subunits suggest that the heterotetrameric enzyme should have a similar assembly when compared with the homotetrameric SS. To predict the native form of AGPase we have proposed three models based on the crystal structure of the SS (Fig. 2, a–d) and further investigated the possible subunit interactions (Fig. 2, e–j) by combining molecular dynamics simulations and MM-PBSA methodology. Results from binding free energy calculations and yeast-two-hybrid experiments show that the Model-2 in Fig. 2 c allows the most favorable interactions between the subunits. Interfaces of Dimer 2 and Dimer 5, building heterodimers of the modeled AGPase, contain many conserved residues that are part of the interacting regions. These regions also overlap with the fragments that were experimentally found to be important in subunit-subunit interactions. This study will enable engineering of potato AGPase to obtain a more stable enzyme and the engineered AGPase can be used for improvement of plant yield.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.