Stress-Strain Experiments on Individual Collagen Fibrils

Abstract

Collagen, a molecule consisting of three braided protein helices, is the primary building block of many biological tissues including bone, tendon, cartilage, and skin. Staggered arrays of collagen molecules form fibrils, which arrange into higher-ordered structures such as fibers and fascicles. Because collagen plays a crucial role in determining the mechanical properties of these tissues, significant theoretical research is directed toward developing models of the stiffness, strength, and toughness of collagen molecules and fibrils. Experimental data to guide the development of these models, however, are sparse and limited to small strain response. Using a microelectromechanical systems platform to test partially hydrated collagen fibrils under uniaxial tension, we obtained quantitative, reproducible mechanical measurements of the stress-strain curve of type I collagen fibrils, with diameters ranging from 150–470 nm. The fibrils showed a small strain (ɛ < 0.09) modulus of 0.86 ± 0.45 GPa. Fibrils tested to strains as high as 100% demonstrated strain softening (σ_yield = 0.22 ± 0.14 GPa; ɛ_yield = 0.21 ± 0.13) and strain hardening, time-dependent recoverable residual strain, dehydration-induced embrittlement, and susceptibility to cyclic fatigue. The results suggest that the stress-strain behavior of collagen fibrils is dictated by global characteristic dimensions as well as internal structure.

INTRODUCTION

Collagen was first produced by animals ∼700 million years ago. Every extant vertebrate and invertebrate species studied contains this protein (1). From the skin of primitive multicellular animals such as sea cucumbers (Cucumaria frondosa) (2), to the bones of giant dinosaurs such as tyrannosaurus rex (3), to our own human bones (4), this molecule has played a central role in providing structural support. Combining collagen's three-dimensional molecular structure and charge distribution with the fundamental laws of thermodynamics affords a glimpse into how thousands of these molecules self-assemble into a discrete crystalline structure known as a fibril (5). It is becoming increasingly clear that to determine how the structure of tissues such as skin, tendon, and bone confers mechanical properties to those tissues requires a better understanding of the mechanics of individual fibrils. We present mechanical tests on single fibrils that provide what to our knowledge are first measurements of large deformation stress-strain relationships and of the strength of these biologically ubiquitous submicron-size objects.

In addition to a better scientific understanding of biological structures, this work has clinical applications in areas such as bone fracture. An improved understanding of the initiation and propagation of cracks in bone structures will aid in the development of better clinical procedures for assessing and mitigating fracture risk. Clinicians assess the risk of bone fracture using empirical correlations between risk of fracture and bone mass or projected “areal” bone mineral density (aBMD), as measured by dual energy x-ray absorptiometry. The significance of aBMD was established through clinical trials performed on thousands of postmenopausal women, showing that a low aBMD was associated with an increased probability of fracture. However, this test fails to predict fractures in a large segment of the population (6,7). Lack of a better test is attributable to an incomplete knowledge of how the chemistry and hierarchical structure of bone confer mechanical strength and fracture toughness to the tissue. The bone density-fracture risk correlation originally led to a focus on the contribution of bone's mineral phase to its mechanical properties. Subsequent experiments showed that collagen plays an important role in the origins of bone's resistance to fracture, as quantified by its fracture toughness (8).

The relevance of collagen fibrils (∼100 nm in diameter) and fibers (∼1 μm in diameter) to bone's resistance to crack initiation and propagation can be established theoretically, using linear elastic fracture mechanics (LEFM) to make a conservative estimate of the critical flaw size tolerated by a bone operating at a prescribed stress level. In this one-parameter theory, a preexisting crack subjected to mechanical loads will extend when the stress intensity factor, K, which is a measure of the intensity of stress and strain in the vicinity of its front, reaches the material's fracture toughness, K_c. The stress intensity factor is related to the applied stress, 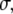the crack's characteristic length, a, and a constant reflecting the structural geometry and applied loading, Y, by the relation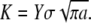

Bone's fracture toughness is anisotropic and varies with type and condition of loading. For the illustrative value, 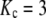MPa-m^1/2, and demanding that an isolated crack (Y = 1) not extend until the operating stress reaches the reported bending strength of bone, σ_max = 200 MPa (9), the critical crack size is 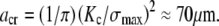In addition to the critical flaw size, LEFM provides an estimate of the characteristic length of the process zone near the crack front that is damaged by the stress intensification and is directly responsible for toughness, 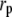∼ 0.1 ≈ 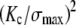23 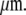The first implication of these simple calculations is that a bone structure cannot allow the presence of crack-like flaws with characteristic lengths greater than a few hundred microns. Instead, it must detect and resorb cracks before they reach these sizes. The presence of extrinsic toughening and crack-arresting mechanisms (10) associated with bone's hierarchical structure render the LEFM-based critical flaw size overly conservative. However, recent calculations (11) and experimental observations (12,13) suggest that these mechanisms are not capable of preventing the propagation of cracks longer than a few millimeters in bones subjected to monotonic and cyclic loads (11). Taylor et al. (13) reviewed the ability of bone to detect and repair the damage it experiences continuously from fatigue loading, and they observed that cracks longer than a few millimeters are rarely found in bone structures.

The second implication is that micron-scale and perhaps submicron-scale structures such as osteons, collagen fibers, and fibrils play a critical role in retarding the initiation and growth of small cracks by acting like reinforcing rods that resist the crack-opening displacements. Evidence of such extrinsic toughening mechanisms, as discussed in Nalla et al. (10) and shown in Fig. 1, can explain the experimental observations of Akkus and Rimnac (12) that under fatigue loading, the crack growth rate (increase in crack length per unit cycle of loading) decreases for crack lengths smaller than 150 μm, and then starts to accelerate. We conclude that experimental measurements of the stiffness, strength, and toughness of collagen fibrils and fibers can shed light on the origins of bone's fracture toughness and fracture risk.

FIGURE 1.

Evidence of extrinsic toughening mechanisms in bone: (a) crack bridging attributable to a secondary lamella, and (b) possible collagen fibril-based bridging (from Nalla et al.) (10).

Measurements and modeling of the mechanical properties of collagen and bone have been performed at molecular, micron, and millimeter scales. However, the scale around a few hundred nanometers, corresponding to the diameter of one fibril, is relatively unexplored. The experimental technique described here offers great promise for guiding and assessing the development of multiscale theoretical and computational models for collagen-based tissues that will lead to theories relating the response of bone's small-scale structural features to its global mechanical behavior.

Theoretical and computational studies of collagenous structures include composite mechanics (14), network (15), and molecular dynamics (16–18) simulations. The molecular dynamics models developed by Buehler (16–18) incorporate information obtained at both the quantum and molecular scales, and are very promising in the determination of variables that control collagen's mechanical response to applied forces. For example, these models predict that the shape of the stress-strain curve of collagen fibrils is dictated by cross-link density. Highly cross-linked fibrils behave like hardening springs that rupture in a brittle manner at their peak stress, whereas low-density cross-linking results in energy dissipating postpeak deformations and graceful failure. This difference in the response to mechanical forces will likely be reflected in bone's resistance to crack initiation and propagation. Buehler also showed that the interaction between nanoapatites and collagen in mineralized bone increases not only the stiffness but also the toughness of the material (16). The fundamental phenomenon here is similar to that in the case of cross-linking. Localized high stiffness and strength regions in the fibril prevent slippage of collagen molecules, resulting in enhanced energy storage during loading of the fibril. The data we present below are consistent with this general idea, and indicate that the fibrils we tested possessed cross-links. However, we also show that structural effects not taken into account in previous models are clearly present in the experimental measurements of isolated fibrils.

Experiments at the tissue level were performed on bone (4) and tendon (19). At smaller length scales, laser tweezers (20) and atomic force microscopy (AFM) (21) were used to test collagen molecules. Modified microtensile test systems (22,23) were applied to investigate collagen fibers with diameters ≥1 μm. However, little is known at the intermediate size scale around a few hundred nanometers. Although synchrotron x-ray diffraction (24,25) detected the deformation of collagen fibrils inside tissue samples by monitoring the change of D-spacing upon loading, those results represent the averaged response of many fibrils, and not the response of an individual fibril. Recently, AFM-based force spectroscopy (26,27) was used to probe individual collagen fibrils. However, those experiments were limited to strains of only a few percent and did not provide any strength or toughness information.

We present stress-strain data from 13 type I collagen fibrils tested using a novel microelectromechanical systems (MEMS) technique. To the best of our knowledge, we show for the first time the strength behavior of individual isolated fibrils that only becomes apparent at strains >10%. The results are discussed in the context of a modern multiscale theoretical model. We show that structural size-dependent effects are clearly present in the postyield behavior of single collagen fibrils.

MATERIALS AND METHODS

Type I collagen fibrils were isolated from the dermis of sea cucumber, Cucumaria frondosa (28,29). This structure is several dozen microns long, has cross-sectional dimensions ∼10–500 nm, and is easily obtainable as an isolated fibril. Sea cucumber fibrils are similar to those found in vertebrates. They have the same length, assemble with the same repeat period, and possess the same gap/overlap ratio (30) and cross-linking chemistry (31). The habit of echinoderm fibrils is spindle-shaped rather than cylindrical, as found in mammals. In addition, the collagen amino and carboxy termini are arranged in a bipolar manner, with their center of symmetry at the middle of the long axis of the spindle, rather than monopolar as found in mammals. This spindle structure can also be obtained using mammalian collagen monomers to reconstitute synthetic fibrils (32). Clear evidence of the proteoglycans used to aggregate echinoderm fibrils was found, but these molecules are all removed in the purification procedure for obtaining the fibrils that we measured (33). The major difference between echinoderm collagen fibrils and those of other animals is at the systemic level (28,30). Echinoderms have the ability to change the mechanical properties of their collagen fibrillar networks in a way that is interfaced with their neural systems over physiologically relevant timescales. However, the set of molecules relevant to this process is not present in the structure we studied. Collagen cross-link density is expected to play a strong role in the mechanics of the fibril as based on both modeling (17) and straightforward physical arguments. There are relatively few published data on the degree of cross-linking in sea cucumber collagen (28,34,35). Because our source of fibrils was highly dispersed in solution, it was not possible to determine the degree of cross-linking in the tested samples with direct spectroscopic measurements.

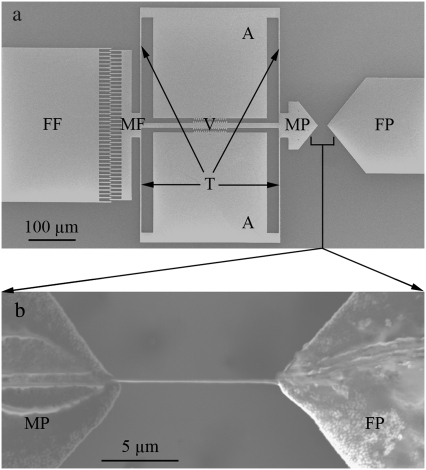
MEMS devices were designed to test single collagen fibrils as previously described (36). The fabrication of these devices is briefly summarized as follows: 100-mm-diameter silicon wafers were sequentially coated with 3.5 μm of sacrificial SiO₂, 6 μm of polycrystalline Si (polysilicon), and 0.6 μm of masking SiO₂, via low-pressure chemical vapor deposition. The devices (Fig. 2 a) were patterned using optical lithography. Then the masking SiO₂ was etched in CHF₃/C₂F₆ plasma, and the polysilicon was etched in a Cl₂ plasma. The device was released by immersion in aqueous hydrofluoric acid for 15 min, followed by rinsing in methanol and critical point CO₂ drying. The release etch dissolved all of the remaining masking SiO₂ and the sacrificial SiO₂ beneath the movable portions of the polysilicon device. The majority of sacrificial SiO₂ beneath the large areas (labeled A, FF, and FP in Fig. 2 a) remained to anchor the device. After release, ∼20 nm of palladium were sputtered onto the device to provide sufficient electrical conductivity.

FIGURE 2.

Representative MEMS mechanical testing device. (a) Low magnification SEM image of MEMS device, consisting of fixed (FF) and movable (MF) comb-fingers, fixed (FP) and movable (MP) pads, a Vernier scale (V), anchors (A), and tether beams (T). (b) Higher magnification SEM image of a fibril attached to movable (MP) and fixed (FP) pads.

The device (Fig. 2 a) contains a movable pad actuated by an electrostatic comb-drive. The previously described actuator (36,37) allows constant, monotonically increasing, or cyclic loading (up to ∼10 kHz), depending on whether direct-current or alternating-current voltages are applied. Using tungsten probes, one anchor (labeled A in Fig. 2 a) is electrically grounded, and a voltage is applied to the fixed fingers (FF in Fig. 2 a). The resulting electrostatic attraction between the fixed fingers and movable fingers pulls the device to the left, as oriented in Fig. 2 a. Fibrils were visualized in solution, using either fluorescently tagged antibodies or dark field illumination. A pulled glass micropipette attached to a micromanipulator was used to transfer a fibril out of a solution droplet and position it across the two MEMS device pads (Fig. 2 b). An electrochemically etched ultrasharp tungsten probe attached to another micromanipulator was used to apply epoxy (8265-S, J.B. Weld Co., Sulphur Springs, TX) droplets on both ends of the fibril, fixing it to the device. To determine if the epoxy had spread along the fibril surface during this procedure, a test fibril was visualized using dark field microscopy, allowing us to label it fluorescently after the application of epoxy. Under fluorescence imaging, antibodies clearly adhered to the fibril and not the epoxy. Thus, antigenic sections of the collagen surface were still accessible for antibody binding after the epoxy was applied, supporting the conclusion that the epoxy remained on the pads where it was placed, and did not significantly wet the fibril.

Thirteen different fibrils loaded onto 13 individual MEMS devices were tested. The diameters of the fibrils extracted using the antibody labeling were 330 nm and 470 nm. The diameter of the fibrils extracted using dark field illumination was smaller, 210 ± 40 nm (mean ± SD; range, 150–280 nm; n = 11). Because our displacement measurement was fairly coarse compared with the gauge lengths (minimum measureable displacement of 0.25 μm, with gauge lengths from 5–21 μm), we did not perform any preconditioning. Instead, each fibril was loaded and unloaded four times by manually increasing and decreasing the applied direct-current voltage. It took ∼5 s to make each increment in force, adjust the force to correspond to 0.25 μm of displacement, and then record the voltage. Each loading-unloading cycle took ∼7 min to complete. To minimize dehydration, we placed several wet paper towels next to the test platform, and wrapped the setup with cellophane. This procedure tended to raise the humidity only a few percent above ambient. Tests were performed at relative humidities of 31–60%, as determined using a digital relative humidity/temperature meter (Fisher Scientific, Pittsburgh, PA). Displacement of the movable pad, which represents the stretch of the fibril, was measured by visualizing the Vernier scale using a 50× long working distance objective lens. This measurement is associated with a 0.25-μm resolution. The epoxy droplets were extremely large compared with the fibril diameters and no decohesion of the fibril-epoxy interface was observed for the data presented here, thus confirming the correlation between device movement and fibril extension. It is quite possible that nonuniform strains existed along the fibril. However, we have no way to measure this directly so the analysis presented here assumes uniform strain.

Precise measurements of fibril diameters, as needed to calculate stress, could not be performed simultaneously with the tensile testing because the optical microscope resolution was too low. To overcome this problem, we used scanning electron microscopy (SEM) after tensile testing to record fibril diameters as well as gauge lengths. We expected fibrils to dehydrate in the SEM resulting in aberrantly small diameter measurements. To account for differences between the measured area and the area during tensile testing, we performed a separate calibration experiment. We deposited several fibrils onto a glass substrate and compared the heights measured by AFM at high humidity with those after the same fibrils were imaged by SEM. Using 14 separate fibrils and 10 measurements per fibril, we determined an average shrinkage upon dehydration of 27%, with a standard error of 1.8%. For the tension-tested fibrils, the SEM measured diameters were enlarged accordingly and the new values were used for calculation of the cross-sectional areas of unloaded fibrils. We tested some fibrils after they were imaged by SEM to investigate the effect of dehydration in the SEM vacuum chamber on the mechanical properties of collagen fibrils.

The force-displacement curves were used to calculate nominal stress (force divided by area of unloaded fibril)-engineering strain (change in length divided by original length) curves. We recognize that for experiments associated with large strain and significant reduction in cross-sectional area, the true stress (force divided by instantaneous area) and a higher-order strain may be preferable. However, our choice allows for a more direct comparison with the molecular dynamics results of Buehler (16–18) for the same measures, and eliminates the need to measure the change in cross-sectional area during testing (which we are unable to do). It should be kept in mind that true strengths are likely larger than what we report and the qualitative shapes of stress-strain curves may change when using true stress and true strain.

Scatter in the stress-strain data presented below is typical of what we observed. When MEMS devices are actuated without a fibril loaded onto them, they show repeatable force-displacement curves that, on the scale shown here, are practically noise-free. Thus, the scatter in these data is unlikely to be from noise in our power supply or measurement technique. Instead, it is a reflection of the “noisy” behavior of the fibrils themselves.

RESULTS AND DISCUSSION

Our discussion focuses primarily on strength and postyielding behavior. The first-generation MEMS device used did not provide sufficient displacement to fracture all of the fibrils. However, its displacement capacity was sufficient to apply strains much larger than reported previously, to take several fibrils past their yield point and to bring a small number of them to failure.

As expected for a multiphase biological structure of varying global characteristic dimensions (e.g., diameter and length) and internal structures (e.g., cross-link density), we found substantial variability in mechanical behavior among the 13 specimens. First, we present the qualitative responses of four fibrils that clearly illustrate the range of stress-strain responses. Second, we present the stress-strain response of a fibril that received substantial time to recover after it was strained beyond its yield point. Third, we present quantitative details of all 13 fibrils tested. And fourth, we discuss these results in light of some relevant modeling from the literature.

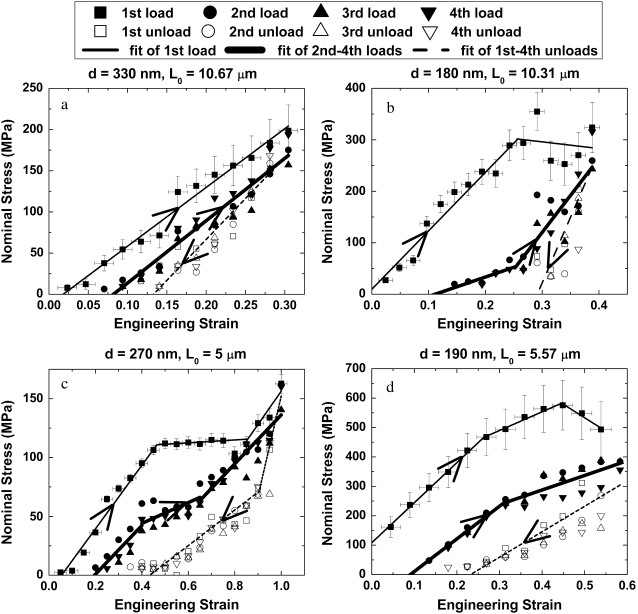
Fig. 3 shows the fibrils' response to loading and unloading. For all cases, the first loading curve is distinct and is fit to a single straight line or multiple straight lines. The four unloading curves for each fibril are treated as a single data set because the stress-strain relationship of each individual curve was indistinguishable within the experimental error. The three subsequent loading curves were treated as a single data set for the same reason. Fig. 3 a shows a fibril that remained linear up to the maximum strain achieved by the device. Fig. 3, b–d, shows that during initial loading collagen fibrils can exhibit three qualitatively different behaviors upon departure from the initial linear region. The stress-strain curve can be “perfectly plastic” (flat yield regime) (Fig. 3 b), perfectly plastic-strain hardening (Fig. 3 c), or nonlinear strain softening (Fig. 3 d).

FIGURE 3.

Mechanical behavior of four representative fibrils. Solid squares and thin solid lines represent the first load, open symbols and dotted lines represent the four unloads, and other solid symbols and thick solid lines represent the 2nd–4th loads. The diameter (d) and the gauge length (L₀) of each fibril are shown at the top of each subplot. The four fibrils display differing behavior during the first load: (a) linear up to the maximum strain, (b) elastic-perfectly plastic, (c) elastic-perfectly plastic-strain hardening, and (d) nonlinear strain softening.

All of the fibrils exhibit qualitatively similar unloading behavior. The unloading curves are steeper than the initial loading curves, resulting in residual strains. Because the unloading procedure brings the displacement of the device back to zero, the subsequent loading curves do not begin to create stress in the fibril until an offset strain is reached (the fibril sags between its attachment points when the device is unloaded). However, the strain at which the fibril picks up a force is less than the residual strain of the just-completed unloading curve, indicating that a portion of the residual strain is recovered. The subsequent unloading-loading cycles repeat this hysteresis. The sizes of the residual strain and the strain recovery are expected to depend on the test conditions. For example, going to a higher strain on the first pull is expected to result in a higher residual strain upon unloading. Likewise, the amount of time spent at zero force is expected to control the degree of residual strain recovery seen upon subsequent loading.

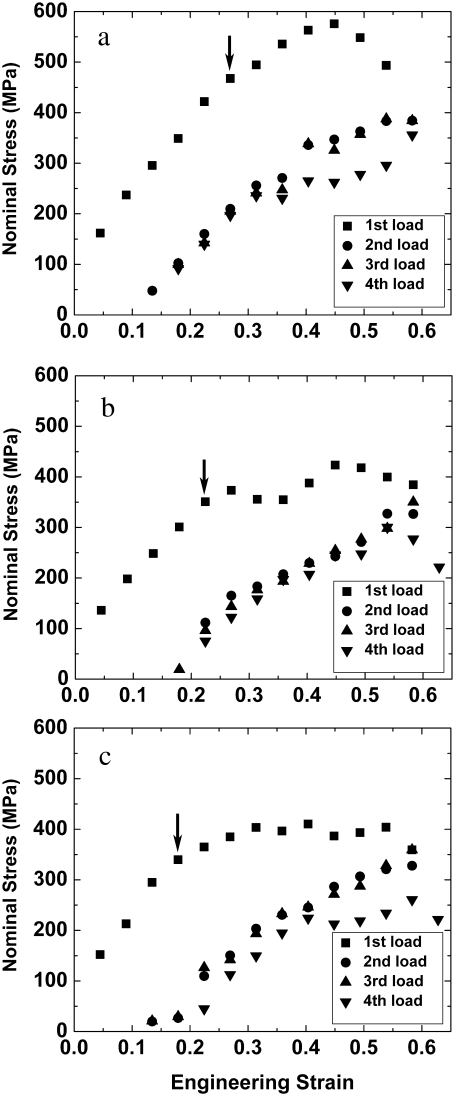
To determine whether a fibril is capable of fully recovering the residual strain that develops at the end of the first loading-unloading cycle, we exposed one fibril to four loading-unloading cycles, stored it at ∼90% relative humidity for >100 min, and repeated the mechanical test. Fig. 4 shows the loading stress-strain curves of this fibril (the same fibril shown in Fig. 3 d). The curves in Fig. 4, a–c, demonstrate substantial recovery back to the initial condition after prolonged rest in a humid environment. This recovery may be attributable to a combination of time (i.e., intramolecular relaxation of the collagen molecules or intermolecular relaxation between them) and rehydration from the highly humid environment. Although some recovery is present, it is also clear that the yield point in each subsequent set of tensile tests decreases, indicating some accumulation of damage.

FIGURE 4.

Nominal stress-engineering strain curves of a fibril (same fibril shown in Fig. 3 d) tested three times, showing the data for the first loads (solid squares) and 2nd–4th loads (other solid symbols) for (a) test 1, (b) test 2, and (c) test 3. The yield point (indicated by arrow in the first load) in each subsequent set of tensile tests decreases, indicating some accumulation of damage.

In the four first loads shown in Fig. 3, as in all 13 fibrils tested, linear behavior at low strain was observed. The elastic modulus obtained from least-squares fits to these low-strain portions of the data was 0.86 ± 0.45 GPa (mean ± SD; range, 0.36–1.60 GPa; n = 13). Six of the 13 fibrils showed linear behavior similar to that shown in Fig. 3 a, with maximum strains ranging from 0.1–0.5. Three of these linear fibrils experienced brittle rupture at stress levels of σ_max ∼ 0.20 GPa (ɛ ∼ 0.4). All three of these fibrils broke at the edges of the testing pads, which was likely because of stress concentration around the fibril-epoxy interface. The other seven fibrils showed various yielding behaviors similar to those in Fig. 3, b–d. The first deviation from linearity occurred at a yield strength of 0.22 ± 0.14 GPa (mean ± SD; range, 0.07–0.47 GPa; n = 7) and a yield strain of 0.21 ± 0.13 (mean ± SD; range, 0.09–0.46; n = 7). These results are similar to those predicted by Buehler (17) for uncross-linked fibrils, i.e., a yield strength and strain of 0.4 GPa and 0.05, respectively. His model predicted the yield strength of even lightly cross-linked fibrils to be substantially >1 GPa, whereas our maximum yield strength was <0.5 GPa.

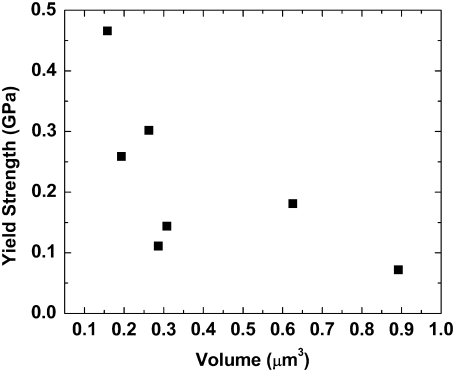
However, the model of Buehler (17) contains no intrinsic diameter. It is a material model and not a structural model. If the fibrils we tested support this assumption, then we should not find any size-dependent effects in our stress-strain curves. The seven fibrils that demonstrated yielding had diameters ranging from 150–280 nm, and gauge lengths ranging from 5–21 μm. Fig. 5 shows the yield strength plotted versus the volume of the tested fibrils. As the volume increases, the yield strength decreases. The fibrils clearly do not behave as homogenous materials. Rather, the stress-strain curves are dependent on fibril geometry. Structural features within the fibrils, such as defects in the molecular arrangement or spatial variations in cross-linking density, may control the observed mechanical behavior. Our experimentally determined yield strengths are lower than the computed strengths of Buehler (17), and this finding is consistent with the idea that structural features control the system. These structural inhomogeneities would act to concentrate stress and thus lower the apparent yield strength.

FIGURE 5.

Yield strength versus volume of seven fibrils that showed yielding behavior. The yield strength decreases as volume increases, indicating size-dependent effects.

Regarding the modeling of strain recovery that we measured, simple deterministic models of collagen intermolecular interactions that take the fibrils beyond their yield point would not be expected to display strain recovery upon unloading. However, molecular dynamics simulations that contain temperature effects may well show this behavior. Buehler has not published unloading or cyclic loading curves using his multiscale model that uses a molecular dynamics simulation to model collagen molecule conformations. It would be very interesting to see if these temperature dependent effects result in strain recovery upon unloading. Another possible physical source for the strain hardening and strain recovery we measured may be related to the movement of water in the system. If loading the sample in tension results in a reduction in fibril radius, this could create an internal pressure that would drive water out of the fibril, making it stiffer. Unloading the fibril might allow the water back into the fibril to some extent, causing a recovery of the original state.

At very low applied loads, one might expect a nonlinear entropic hardening behavior of the collagen molecules, as measured by Sun et al. using optical tweezers (20) and as subsequently modeled by Buehler and Wong (38). There are two reasons why our data do not exhibit this type of response. First, quantitatively, the entropic effects provide a restoring force in the 1–10 pN range/molecule that would likely translate into the 1–10 nN range/fibril. We designed our MEMS devices to look at the large strain behavior of fibrils and so their sensitivity is not high enough to measure these small forces. Second, qualitatively, once the single molecules are included in a fibril, they stack in a pseudocrystalline array. This lowers the system's entropy significantly making entropic hardening an unlikely mechanism of mechanical response. Neither our experimental data nor the modeling data of fibrils (16–18) showed the classic toe-region response of larger tissue samples such as whole tendon (39). This is consistent with the accepted theory that this response is attributable to suprafibrillar “hinge” structures in the larger tissue samples.

The experiments described above show that the collagen fibrils we tested are capable of sustaining stresses as high as 0.47 GPa without yielding, as well as stresses up to 0.60 GPa and strains up to 100% without fracturing. The maximum force applied by the first-generation MEMS device (∼35 μN) was insufficient to break hydrated fibrils in the middle of the gauge region under monotonically increasing loads. However, we were able to break fibrils by exposing them to two damaging scenarios. One fibril broke in tension in the middle of the gauge region after cycling at 0.08 ± 0.007 strain and at 1 kHz for 5 min (Fig. 6). The corresponding fracture strength and strain were 0.1 GPa and 0.13, respectively. Several other fibrils were broken after exposure to dehydration in the SEM chamber. The fibril shown in Fig. 7 is typical and it broke at a strain of 0.05, with a corresponding fracture strength of 0.03 GPa. This same fibril underwent stress up to 0.05 GPa (and strain up to 0.18) when hydrated (before insertion into the SEM). The fracture surfaces appeared smooth and perpendicular to the long axis of the fibril (Fig. 7 c). Although it is known that water acts as a plasticizing agent in collagenous tissues (40), to our knowledge these are the first experimental data showing that these effects are at play within a single fibril. This suggests that water molecules inside the fibrils play an important role in preventing embrittlement.

FIGURE 6.

Optical images of a fibril attached with epoxy across two pads of a MEMS device. (a) The fibril was intact before loading in tension. (b) The fibril broke in the middle of the gauge region under tension after cyclic loading. The broken pieces of fibril were curved, indicating they were hydrated and flexible.

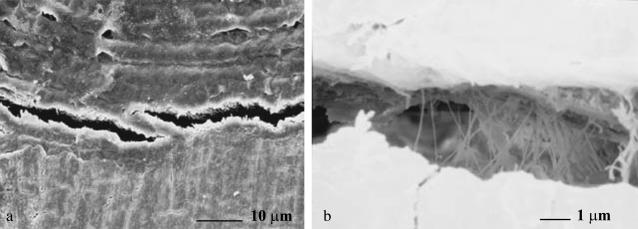
FIGURE 7.

SEM images of a fibril strained before and after dehydration. (a) The fibril was not broken after the first tensile test. (b) The fibril broke at very small strain (∼0.05) during the second test performed after SEM imaging. The broken pieces of fibril were straight, consistent with embrittlement because of dehydration in the SEM chamber. (c) Image of broken fibril at higher magnification. The fracture surfaces of the fibril were smooth, and perpendicular to the long axis of the fibril.

CONCLUSIONS

We tested the mechanical properties of single type I collagen fibrils isolated from sea cucumber using a MEMS-based method. Four stress-strain curves representative of those obtained from 13 fibrils with diameters of 150–470 nm were presented. The most important result is that the yield stress and qualitative behavior of the stress-strain curve in the postyield region depend on fibril volume. This implies that collagen fibrils cannot be considered representative volume elements and that an understanding of their strength behavior requires a structural analysis, and not merely a material analysis. The fibrils withstood tensile stresses (strains) up to 0.60 GPa (100%) without fracturing. The fibrils exhibited time-dependent recoverable residual strains. Collagen structures at the level of a single fibril are susceptible to cyclic fatigue and dehydration-induced embrittlement. The dehydration of collagen fibrils was shown to lower their strength. Further examination of the subtleties of this effect under various levels of hydration may offer new insights into the declining strength of tissues such as bone, tendon, and ligament with aging.