Effect of Nonuniform Interstitial Space Properties on Impulse Propagation: A Discrete Multidomain Model

Abstract

This work presents a discrete multidomain model that describes ionic diffusion pathways between connected cells and within the interstitium. Unlike classical models of impulse propagation, the intracellular and extracellular spaces are represented as spatially distinct volumes with dynamic/static boundary conditions that electrically couple neighboring spaces. The model is used to investigate the impact of nonuniform geometrical and electrical properties of the interstitial space surrounding a fiber on conduction velocity and action potential waveshape. Comparison of the multidomain and bidomain models shows that although the conduction velocity is relatively insensitive to cases that confine 50% of the membrane surface by narrow extracellular depths (≥2 nm), the action potential morphology varies greatly around the fiber perimeter, resulting in changes in the magnitude of extracellular potential in the tight spaces. Results also show that when the conductivity of the tight spaces is sufficiently reduced, the membrane adjacent to the tight space is eliminated from participating in propagation, and the conduction velocity increases. Owing to its ability to describe the spatial discontinuity of cardiac microstructure, the discrete multidomain can be used to determine appropriate tissue properties for use in classical macroscopic models such as the bidomain during normal and pathophysiological conditions.

INTRODUCTION

Cardiac tissue can be viewed as a network of interconnected cells (myocytes) that are organized within and tethered to an extracellular matrix to produce a synchronous contraction that is triggered by the highly coordinated spread of electrical activity. The currents underlying the propagation of impulses from cell to cell flow across the cell membrane and through both the intracellular and extracellular spaces in the heart. Over the past 30 years, there has been considerable interest in the gap junction structures that couple the intracellular spaces of myocytes to one another and their role in arrhythmia generation (1,2). Unlike the intracellular space, however, the role of the interstitial space in the spread of electrical activity is less well understood or appreciated. The extracellular space, or interstitium, occupies 20–25% of the total heart volume (3). In one of the more comprehensive studies of the cardiac interstitium, Frank and Langer found that the extracellular space is highly complex and comprised of ground substance (23%), blood vessels (60%), connective tissue cells (e.g., fibroblasts) (7%), collagen (4%), and “empty” space (6%) (3).

Because current must flow in a closed circuit, the transmembrane ion flux must flow through both the intracellular and interstitial spaces. For a given membrane potential gradient, the total current in each space and, ultimately, the speed of impulse propagation depend on the resistance of the spaces and capacitance of the membrane, which in turn depend on the material composition and geometry of the space at the micro- and macroscales. Factors that modulate the resistance of the intracellular space, such as cell geometry, cell size, and changes in the number and types of gap junctions, have all been implicated in conduction disturbances (4). It is surprising that factors that modulate the resistance of the interstitial space, such as the number of fibroblasts, the proportion of collagen, the permeability of the ground substance, the size of the vessels, the extent of cell packing, etc., have been generally ignored or considered to have a negligible influence on the nature of impulse conduction. Although the studies are less numerous, there is growing evidence that the properties of the interstitial space must be considered in propagation disturbances (5,6).

Classical cable theory predicts that the speed of conduction will slow as the fraction of the interstitial space decreases, due to the resulting increase in interstitial resistance. Kleber and Cascio showed that in the early stages of ischemia, the interstitial space is reduced by 50% and the conduction velocity slows by 12%. A few studies, however, have revealed an apparent paradox, in which the conduction velocity (θ) is highest in tissues that have very tight cell packing (i.e., small interstitial space). Draper recorded propagating action potentials in large and small mammalian muscle from specialized conducting fibers of the Purkinje and ventricular fibers of the working myocardium. In this study, measured conduction velocities in Purkinje fibers were three to six times faster than in ventricular fibers. This increase in θ was found only in large mammals, where the Purkinje fibers were tightly packed and neighboring fibers were separated by 20- to 40-nm-wide interstitial pathways over considerable distances (7). The conduction velocities in loosely packed bundles can be predicted under cable theory, but when applied to tightly packed bundles, cable theory predicted a conduction velocity 50% slower than what is experimentally measured (8).

Sommer hypothesized that the tight packing in Purkinje fibers causes propagation to primarily occur along the outer membranes of the bundle facing the larger extracellular space (7), decreasing the effective membrane capacitance. Furthermore, since the intracellular space of the fibers is highly connected, the effective diameter for conduction becomes the bundle diameter instead of the diameter of a single fiber. Consequently, the effective intracellular resistance is decreased, causing conduction velocity to increase. As noted, an increase in conduction velocity with decreasing extracellular space is not predicted by classical cable theory. One reason for this is that most models of propagation assume radial symmetry. To understand the role of tight cell packing on conduction, a computational model is needed that can account for interstitial current flow both along and around a given cardiac fiber.

In this article, we present a multidomain model of propagation in which the intracellular and interstitial spaces are represented as spatially distinct regions in three dimensions. In contrast to the bidomain model in which the intracellular and interstitial properties are adjusted to occupy the same volume, the intracellular and interstitial spaces in the multidomain model are separated by a membrane interface and can have different volumes. As a result, the multidomain model allows the dimensions of the interstitial space and its electrical properties to vary around the cell. The simulations presented here show that although the multidomain and the bidomain models predict similar conduction velocities, the nature of propagation and the shapes of the predicted transmembrane potentials around the cell are very different when the interstitial space in not uniformly distributed. The results also show that the influence of internal membranes on conduction can be effectively eliminated if the local extracellular resistance is sufficiently high, leading to significantly greater conduction velocity along the fiber.

METHODS

Idealized cardiac structure

The results presented in this article were simulated in a fiber with a simple geometry to clearly present the formulation of the discrete multidomain model. In addition, the simplified geometry allowed us to test the fundamental assumptions made in the bidomain model, such as the notion that the intracellular and extracellular spaces can be represented as two overlapping linear cables. Fig. 1 A depicts the underlying geometrical model, and Table 1 lists the physical constants used to compare both model formulations. The domain consisted of a fiber 0.5 cm long surrounded by a layer of extracellular space of finite thickness. An extracellular bath 0.05 cm long was added to the end of the fiber and the boundary of the bath was set to 0 mV as a reference potential.

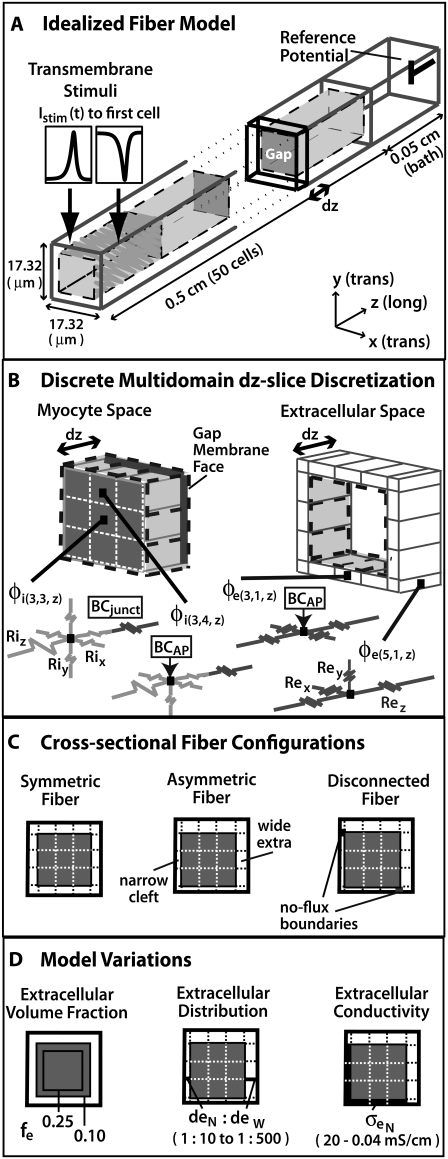
FIGURE 1.

(A) Depiction of the first two and last cells in an idealized cardiac fiber used to simulate longitudinal propagation. The model consisted of 50 rectangular cells (100 μm long) connected via intercellular junctions (Gap). Propagation was initiated via a time-variant transmembrane stimulus (shown by the two traces) applied to the entire first cell. (B) Discretization of the discrete multidomain for a single dz slice defined by nine intracellular voxels and 16 encompassing extracellular voxels. For each space, two sample resistor networks are shown. φ_i and φ_e represent the intracellular and extracellular potentials at a uniquely defined (x, y, z) coordinate within the tissue space. The boxed BC_AP and BC_junct are assigned boundary conditions at locations where two domains interface. (C) Three model configurations were used that described a 1), symmetric; 2), asymmetric; and 3), asymmetric, but also discontinuous extracellular space in the tissue cross section. (D) In all model configurations, the fraction of extracellular space was varied between 0.10 and 0.25. In the asymmetric configurations, the extracellular depth was skewed such that 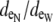biased the distribution of extracellular space in the cross section. In an asymmetric fiber model defined by f_e = 0.10 and 1:500 bias in distribution, the conductivity in the narrow cleft (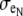) was isotropically increased from normal to 0.04 mS/cm.

TABLE 1.

Electrical constants used in discrete multidomain and bidomain computational models

Electrical constants of fiber model
Parameter	Value	Reference
Myocyte conductivity	4 mS/cm	(26,27)
Junctional resistance	1.125 Ωcm2	(26,28)
Membrane capacitance	1 μF/cm2	(29,30,26)
Extracellular conductivity	20 mS/cm	(30,31)
Extracellular volume fraction	0.25 and 0.10	(3,32)

The fiber consisted of 50 brick-shaped cells with a length of 100 μm and a cross section of 300 μm² that were aligned end to end (9). The cells were delineated from the extracellular space by an enveloping membrane, represented as an interface. The terminal membrane faces of the cells were tightly opposed such that no interstitial space was defined between abutting cells. Gap junctions were assumed to be fixed resistances evenly dispersed over the membrane faces of abutting cells. For simplicity, the intracellular and extracellular spaces were modeled as isotropic, ohmic volume conductors. The distribution of extracellular space consumed either 25% or 10% of the overall cross-sectional area by varying the thickness of the layer of extracellular space that surrounded the fiber. The physical constants of the domain (Table 1) were defined in an earlier study (10) and fall within the measured value ranges given in the references cited in the table.

Bidomain

Governing equations

In the bidomain model, the cardiac fiber is modeled using a typical one-dimensional bidomain formulation where current flow is described along the fiber axis only (the z axis). The governing one-dimensional bidomain equations are

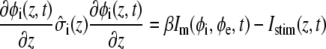(1)

and

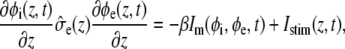(2)

where 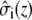and 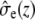describe the macroscopic effective conductivities (mS/cm) of the intracellular and extracellular spaces, respectively. These effective conductivities were derived by multiplying the conductivity of the intracellular and extracellular fluids with their respective volume fractions, f_i and f_e.

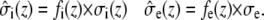(3)

The electrical properties of the two fiber spaces are nonuniform (i.e., the intracellular and extracellular parameters change as a function of location along the fiber). Thus, the model is piecewise homogeneous, with discontinuities between adjacent nodes of different conductivity. The intracellular conductivity was assumed to be heterogeneous, discriminating between the resistivity of the myocyte cytoplasm and the junctional resistances between abutting cells. The extracellular conductivity remains constant along the fiber and within the terminal bath. However, in the bath, f_e increased to 1, whereas f_i decreased to 0. Thus, a single discontinuity existed in the extracellular space between the end of the fiber and the bath. I_stim(z,t) is the time-dependent transmembrane stimulus (μA/cm³) applied to the first cell of the fiber, and β is the surface/volume ratio (cm⁻¹) that averages the membrane current density (I_m) to a current/tissue volume. I_m is defined by the equation

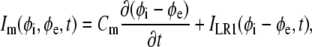(4)

where C_m is the membrane capacitance (μF/cm²) and I_LR1 is the sum of ionic currents (μA/cm²) as described by the Luo-Rudy I cardiac action potential (11). Finally, we assumed that the fiber was electrically insulated, applying no-flux boundary conditions at the outer extent of the model.

Nodal network representation

For the bidomain, the fiber domain was discretized into a mesh using a cell-centered, finite-volume scheme with 10 μm spacing. Each node represented both the intracellular and extracellular potentials and could be interpreted as connected by resistors. Every 10th element in the intracellular space was assumed to contain the gap junction resistance. Hence, the conductivity of that element was accordingly lowered, resulting in a heterogeneous distribution of conductivities in the intracellular space. At each location along the fiber, the intracellular space connected to the overlapping extracellular space via a membrane current. The entire domain consisted of 500 intracellular nodes, 550 extracellular nodes (500 plus 50 bath nodes) and 500 membrane connections.

Discrete multidomain

Governing equations

In the discrete multidomain model, the volume of cardiac tissue is subdivided into discrete three-dimensional domains that together form a continuous space. In this model, each cell was described as a single domain encapsulated by a membrane and surrounded by a separate extracellular domain. We assume that each domain acts as a volume conductor and can be described by a quasistatic approximation (12). Assuming no current sources inside individual domains, the potential within each domain (Ω_n) is governed by Laplace's equation,

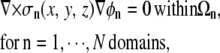(5)

with k boundary condition(s) that cumulatively describe the current flow through the entire defining domain surface (∂Ω_n),

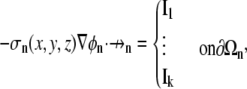(6)

where σ_n(x, y, z) describes the conductivity tensor (mS/cm²) as a function of space within the nth domain and 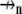is the normal vector to the domain's surface. Each domain can be broadly characterized as a cell or the extracellular space. A cell domain can define any cell type that spans a volume in the tissue model; however, for the purpose of this article, only cardiomyocytes were described in the fiber. The boundary conditions on each domain described how a particular domain within the tissue model was coupled to its neighboring domains. In this particular model, we defined three spatially unique boundary conditions at the interface of 1), a myocyte-myocyte domain; 2), a myocyte-extracellular domain; and 3), any domain at the tissue boundary. Note that at the interface of two domains, there existed a pair of applied boundary conditions, one for each domain to maintain conservation of current.

As in the bidomain model, no interstitial space was assumed to exist between two abutting cells. The myocyte-myocyte interface of a junctional boundary condition was defined as

(7)

where R_junct(x, y, z) defines the increased resistance (KΩ·cm²) between the intracellular space of two myocytes (Ω_n and Ω_{n neigh}) that accounts for the junctional boundary. The potential difference (φ_{n neigh} – φ_n) (mV) was calculated between the locations that immediately flank the junctional boundary in each domain. Although the model formulation would allow for the membrane resistance to be a function of space, the model used here did not have the spatial discretization to warrant the inclusion of spatially localized gap junctions. Instead, we assumed that gap junctions are homogeneously distributed everywhere that two myocytes touch; therefore, σ_junct was constant over the intercalated disc.

At the interface of a myocyte domain with the surrounding extracellular space, we defined the transmembrane potential as φ_m = φ_i(x, y, z) – φ_e(x, y, z), where φ_i is inside the myocyte, φ_e is within the extracellular space, and the pair immediately flank the myocyte-extracellular (myo-extra) boundaries. It is important to note that even though we are describing a single fiber, the circumferential transmembrane potential was not held constant. At this myocyte-extracellular interface, the boundary condition I_AP was applied to describe the action potential dynamics of the membrane:

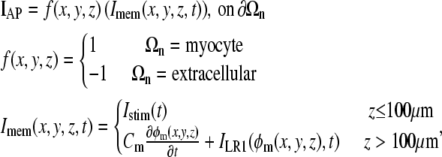(8)

where I_mem (μA/cm²) describes the current that transverses this interface. I_stim is a time-variant stimulus (see Fig. 1 A) used to initiate a propagating action potential from the first cell by adding current to the intracellular space and subtracting current from the extracellular space across a myo-extra interface. The 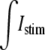was evenly divided between the 120 myo-extra interfaces that defined the first cell, and a time-variant stimulus was used to decrease the number of iterations needed to solve the system during the initiation of the action potential. For all other myocytes, the boundary condition is governed by the capacitive current, where C_m defines the membrane capacitance (μF/cm²) and the sum of ionic currents, I_LR1, as described in the Luo-Rudy I cardiac action potential (11). Notice that the model formulation has the flexibility of defining spatially variable membrane dynamics around the perimeter of a single cell. However, in this study, we assumed that the membrane channels described in I_LR1 were homogeneously distributed over the myo-extra interface.

Last, we assumed the outer boundaries of the intracellular and interstitial domains to be electrically insulated, with a no-flux boundary condition similar to the bidomain formulation. This resulted in a full set of boundary conditions:

For Ω_n = myocyte,

(9)

and for Ω_n = extracellular,

(10)

Nodal network representation

In the discrete multidomain, the fiber was discretized into a three-dimensional rectilinear mesh using a cell-centered, finite-volume scheme with 10-μm-thick voxels that varied in cross-sectional area (13). The discretization for a single z-plane in the discrete multidomain is shown in Fig. 1 B. In contrast to the bidomain representation, each voxel in the mesh existed entirely within a myocyte or the extracellular domain and had a unique (x, y, z)-coordinate in the tissue space. The cytoplasmic space of each myocyte was defined by a lattice of 3 × 3 × 10 voxels connected via resistors representative of the cytoplasmic conductivity. The surrounding extracellular space was defined by a single voxel layer that wrapped around the lateral surface of the myocyte and extended into the terminal bath. As is the case with the bidomain, adjacent extracellular nodes could be interpreted as connected by resistors, representing a homogeneous or heterogeneous interstitial conductivity or geometry. Adjacent nodes transversing separate domains were connected via spatially and dynamically defined boundary conditions. The entire domain consisted of 4500 intracellular nodes, 9250 extracellular nodes (8000 plus 1250 bath nodes), and 6000 membrane connections.

Heterogeneous fiber configurations

Because of the increased discretization in the discrete multidomain, we were able to vary the structural and electrical properties within the fiber cross-section. As depicted in Fig. 1 C, there were three different model configurations: 1), symmetric; 2), asymmetric; and 3), disconnected fiber morphology. As implied by the name, the symmetric fiber had uniform structural and electrical properties around the perimeter of the myocyte and was most similar to the bidomain representation. The asymmetrical fiber had nonuniform electrical and geometrical properties around the fiber. Finally, the disconnected fiber was electrically uncoupled between opposing extracellular spaces at two locations in the fiber cross-section by defining no-flux boundary conditions at corner nodes.

Furthermore, the dimensions and/or the electrical properties of the extracellular space of the generalized model configurations were varied (shown in Fig. 1 D). For all three configurations, two fiber morphologies that described a 0.25 or 0.10 volume fraction of extracellular space (f_e) were defined. In the asymmetric model, a nonuniformity was introduced around the fiber perimeter by biasing the depth of extracellular space on opposing sides of the myocyte cross section. Maintaining all other structural parameters, this spatial bias created a narrow extracellular depth (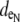) around half of the myocyte perimeter and a wider depth (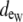) around the opposite half. The depths of the opposing halves were varied such that the ratio of distributed extracellular space, defined from narrow to wide, ranged from 1:10 to 1:500, maintaining the extracellular volume fraction. In the asymmetric fiber model defined by f_e = 0.10, four cases were considered that defined a narrow extracellular depth around half the fiber perimeter: 1), 81 nm for the 1:10 case; 2), 17 nm for the 1:50 case; 3), 4 nm for the 1:250 case; and 4), 2 nm for the 1:500 case. In the case with a 1:500 bias in distribution, the extracellular conductivity was varied around the fiber. The wider extracellular region had a normal conductivity (σ_e) of 20 mS/cm, whereas the narrow cleft (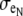) had a conductivity that varied from normal to 0.04 mS/cm.

Computer simulation

Longitudinal propagation was initiated by applying a transmembrane stimulus pulse (μA/cm²) at time zero to the first myocyte by adding current to the intracellular space and subtracting current from the extracellular space across a myo-extra interface (see Fig. 1 A for the I_stim profile). Both the one-dimensional bidomain model and the multidomain models were stimulated with the same amount of total current. In the multidomain, the 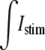was evenly divided between the 120 myo-extra interfaces that defined the first cell, and in the bidomain, 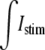was divided between the 10 nodes of the first cell. A time-variant stimulus was used to decrease the number of iterations needed to solve the system during the initiation of the action potential. The nodes located at the most terminal part of the bath were grounded.

In both models, a semi-implicit Crank-Nicolson scheme (14) was used to define the system of equations and a GMRES approach solved the linear system for the next time step. A fixed time step of 0.05 μs was used for all simulations to maintain numerical accuracy. The small mesh resolution is driving the small time step. Unlike in the traditional bidomain formulation, where the membrane dynamics drive the time step, in the multidomain, the resistive elements in the stiffness matrix need to be of the same order of magnitude as the capacitive elements to ensure that an accurate solution will be reached with a reasonable number of iterations. Ultimately, it allowed a solution to be found (relative error <0.01%) within a maximum of 100 iterations, including during initiation of the action potential. The time step was extensively investigated and optimized to solve the problem accurately in the shortest simulation time. The simulations were implemented using CardioWave software (15) that has been upgraded to also solve more complex systems defined by the discrete multidomain model (16). The discrete multidomain simulations were run in parallel on multiprocessor machines. Simulating 10 ms of activation required 4–8 h on two quad-core 3GHz Intel Xeon processors. Conversely, the bidomain simulations required 30 min on a single processor for the same time step and total simulation time.

Calculations

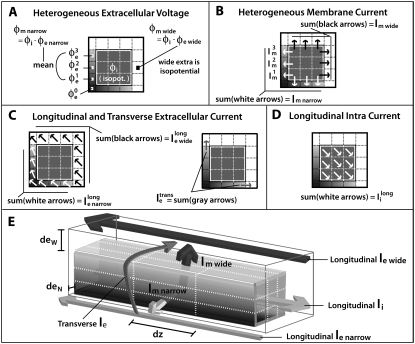
Results were obtained from the middle portion of the fiber at the center of a myocyte, where boundary effects are negligible. Conduction velocity (θ) was calculated between action potentials recorded 10 cell lengths apart. The maximum amplitude, (φ_m)_max and maximum upstroke velocity, (∂φ_m/∂t)_max were calculated from an action potential in the center of the fiber. The time constant of the action potential foot (τ_foot) was calculated as the slope of the phase-plane plot during the initial 15-mV rise in transmembrane potential. In the discrete multidomain, two action potentials were analyzed. Fig. 2 depicts the recording sites for the two opposing locations in the fiber cross section.

FIGURE 2.

Discrete multidomain measurements and calculations used in the results section for comparison to bidomain measurements and analysis. The shaded voxels in the extracellular space define the narrow cleft, and the open voxels define the wider extracellular region. Arrows denote current flow across a single node. Diagonal arrows represent longitudinal current flow along the fiber axis. (A) The potentials φ_{e narrow}, φ_{e wide}, and φ_i represent the average potential in the the narrow extracellular cleft, the wider extracellular region, and the intracellular space, respectively. (B) The perimetrical current crossing the myo-extra boundaries is split into two membrane components: 1), I_{m narrow} represents the sum of current entering/leaving the narrow extracellular region; and 2), I_{m wide} represents the sum of current entering/leaving the opposite, wider region. (C) Extracellular current flow is described by three current components: 1), 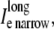representing the sum of current flow along the fiber axis within the narrow cleft; 2), 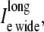representing the sum of current flow along the fiber axis within the wider region; and 3), 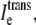representing the sum of current flow perpendicular to the fiber axis, leaving the narrow cleft and entering the wider extracellular region. (D) The current 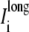represents the total of current along the fiber axis within the cytoplasmic space. (E) A three-dimensional representation depicting the current flow patterns defined in A–D.

RESULTS

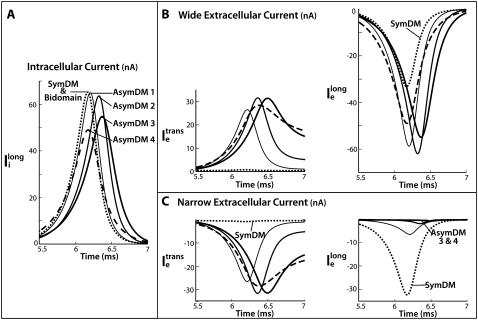
Both the one-dimensional bidomain model and three-dimensional discrete multidomain model allow for computation of potentials in the intracellular and extracellular spaces. In the bidomain model, both potentials are defined at each computational node. In the discrete multidomain, potentials are defined at separate computational nodes. A study was performed that compared the predicted bidomain potentials to the predicted potentials from various forms of the discrete multidomain. To facilitate the comparison, the discrete multidomain potentials were averaged, and currents were summed in five regions of the fiber cross section: 1), the intracellular region; 2), the wide extracellular region; 3), the membrane adjacent to the wide extracellular space (nonconfined membrane); 4), the narrow extracellular region; and 5), the membrane adjacent to the narrow extracellular space (confined membrane). These five cross-sectional regions are illustrated in Fig. 2. Fig. 2 A depicts the regionally averaged potentials from the discrete multidomain mesh. The intracellular region was nearly isopotential for all simulations, and the wide extracellular region was also nearly isopotential for all simulations. Fig. 2, B–D, depicts the regionally summed currents for the two opposing membranes, the two extracellular regions, and the intracellular region.

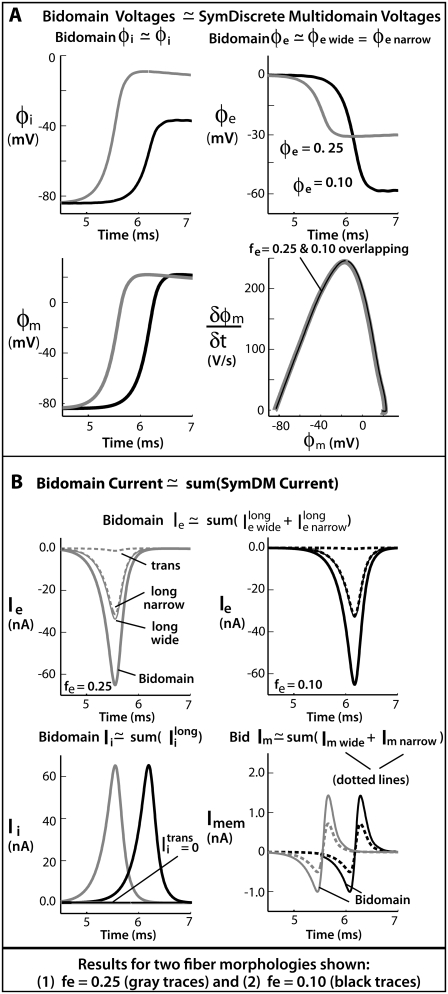
Comparison of bidomain and symmetric discrete multidomain models

Because the one-dimensional bidomain assumes radial symmetry, the predicted potentials and currents are expected to correspond to the symmetric discrete multidomain model (SymDM), where the thickness of extracellular space is uniform around the perimeter of the fiber. Fig. 3 A shows the comparisons of the potentials and currents generated by the two models for extracellular volume fractions of 0.25 or 0.10. The intracellular and extracellular spaces of the multidomain are isopotential, and the magnitudes are equal to the corresponding bidomain model. Consequently, the shape of the propagating transmembrane potential also is identical in both models. As given in Table 2, the maximum transmembrane potential (φ_m)_max is 22 mV and the upstroke velocity, (∂φ_m/∂t)_max, is 245 mV/ms. The time constant for the first 15-mV rise in transmembrane voltage, τ_foot is 218 μs. As expected from cable theory, the decrease in the fraction of extracellular area, f_e, from 0.25 to 0.10 reduced the conduction velocity (θ) from 56.8 cm/s to 49.4 cm/s, as predicted by the theoretical relationship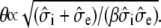

FIGURE 3.

Results comparing a symmetrically defined discrete multidomain model to an equivalent bidomain representation for two fiber morphologies: 1), f_e = 0.25 (shaded traces), θ = 56.7 cm/s; and 2), f_e = 0.10 (solid traces), θ = 49.5 cm/s. Although the depth of the surrounding extracellular space is consistently defined in the SymDM model, results differentiate the narrow from the wide regions (defined in the asymmetric models) for comparison purposes. Definitions for these two regions are depicted in Fig. 2. (A) Recorded bidomain potentials and the corresponding averaged potentials from the symmetric discrete multidomain were equivalent. Depicted from left to right are intracellular, extracellular, transmembrane, and corresponding phase-plane plots. As predicted by cable theory, the resulting action potentials for the two fiber morphologies were the same. (B) Calculated bidomain currents were equivalent to the corresponding current sum from the symmetric discrete multidomain. Depicted from left to right are membrane, extracellular (f_e = 0.25), extracellular (f_e = 0.10), and intracelluar. Since the intracellular and extracellular spaces were isopotential within a SymDM dz slice, the perimetrical membrane current was homogenous, i.e., I_{m wide} = I_{m narrow}. Since the defined narrow region is smaller than the wide region, the SymDM extracellular current traces show this bias with a slightly smaller 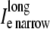to 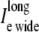and a nonzero 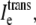which is even more slight in the f_e = 0.10 case.

TABLE 2.

Comparison of bidomain to AsymDM AP waveshapes

fe	Model	Extra bias	θ (cm/s)	(φm)max (mV)			(∂φm/∂t)max (mV/ms)			τfoot (μs)
0.25	Bidomain		56.8	22			246			218
0.25	Symmetric DM	1:1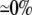
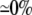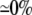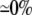0.25	Asymmetric DM	1:10		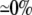		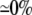	+2%		−1%	+1%
		1:50	−2%	−2%			+10%		−3%	+5%
		1:250	−4%	+1%		−4%	+34%		−14%	+18%
		1:500	−4%	+19%		−3%	+40%		−20%	+25%
		1:1000	−1%	+36%		+1%	+31%		−25%	+27	+29%
0.10	Bidomain		49.4	22			244			217
0.10	SymDM	1:1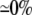
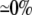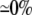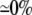0.10	AsymDM 1	1:10	−1%	−1%			+5%		−2%	+2%
	AsymDM 2	1:50	−3%	−2%		−4%	+21%		−8%	+10%
	AsymDM 3	1:250	−3%	+25%		−1%	+37%		−22%	+26%
	AsymDM 4	1:500	+1%	+41%		+1%	+18%		−24%	+28%

Table shows the percent change in AP characteristics from AsymDM models with a nonuniform distribution of extracellular space compared to the equivalent bidomain representation (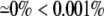). The two percentages correspond to divergent values of the confined membrane and the nonconfined membrane (bold values). If only one percentage is given, the measured values for the pair were nearly equivalent.

Fig. 3 B plots the calculated currents from both the bidomain and symmetric discrete multidomain simulations. As noted, the currents within each dz slice of the SymDM were summed to compare to the nodal currents predicted by the bidomain model. For example, the sum of the perimetrical membrane currents of the discrete multidomain is equivalent to the bidomain membrane current. As shown, the sum of the membrane currents from the narrow side (left and bottom patches) and the sum from the wide side (right and top patches) of the multidomain are each half the magnitude of the bidomain membrane current. The longitudinal and transverse currents in the intracellular and extracellular spaces in the multidomain model are also compared to the longitudinally confined bidomain current. Note that because the two extracellular regions comprised a different number of nodes (seven versus nine), the SymDM extracellular traces show a slightly unequal magnitude of longitudinal current in the two regions, which becomes less apparent when f_e is decreased. The slight nonzero transverse current is due to the fact that the model is not truly radially symmetric. The summation of the intracellular longitudinal currents in the SymDM is, for all purposes, equivalent to the longitudinally described intracellular current of the bidomain.

Comparison of bidomain and asymmetric discrete multidomain models

The bidomain model only considers the fraction of extracellular space and not the distribution around the myocyte perimeter. In contrast, the distribution of extracellular space can vary in the discrete multidomain model; however, the effects of an unequal distribution are unknown. Simulations were peformed to compare potentials and currents in the bidomain model with those predicted in the discrete multidomain model with unequal distributions of extracellular space, while still maintaining the same f_i/f_e ratio. In the multidomain model, the surrounding extracellular space was redistributed by shifting the myocyte center toward the lower left corner of the fiber model (Fig. 1 C). This manipulation led to a thinner layer of extracellular space on the bottom and left side of the myocyte (narrow region) and a thicker layer on the top and right side (wide region). The asymmetric shift of the fiber in the extracellular space was defined by the ratio of the opposing extracellular depths ().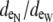

Table 2 summarizes the simulation results of the discrete multidomain for increasing asymmetry ratios from 1:10 to 1:500 or 1:1000 as a percent change from the simulated bidomain value. The limiting asymmetry case was reached when the narrow interstitial depth diminished to 2 nm, the smallest membrane apposition experimentally observed (17). The results show that for moderate extracellular distributions where the surrounding extracellular depth was >50 nm, the bidomain and asymmetric discrete multidomain models predict similar potentials and conduction velocities. These moderate asymmetrical distributions included the 1:50 bias when f_e = 0.25 and the 1:10 bias when f_e = 0.10.

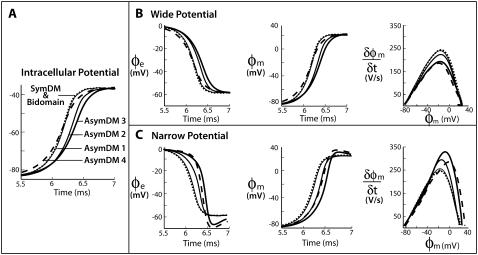
Confining the depth of the narrow extracellular space below 50 nm in the discrete multidomain, however, produced significant differences in potential and currents compared to the bidomain predictions. The differences in resistance in the narrow and wide extracellular region leads to a heterogeneous distribution of potentials in the fiber cross section. Fig. 4 shows the time course of the potentials from the asymmetric models, referred to as AsymDM 1–4, and the SymDM potential model (see Table 2 for model profiles). In the intracellular region, the multidomain nodes are nearly isopotential, but the rise in potential was less steep than in the bidomain (Fig. 4 A). In the wide extracellular region, the peak potential was slightly smaller (less negative) and also showed a less steep decline than that predicted in the bidomain (Fig. 4 B). In the narrow region, the peak magnitude was larger (more negative). The initial decline in the narrow extracellular potential was initially slow (Fig. 4 C), almost flat compared to the opposing decline in the wide extracellular potential. However, the potential difference between the two regions increases as the narrow extracellular potential reaches a more negative value (as seen in AsymDM 3 and 4). As a result, the transmembrane potential was nonuniform around the fiber perimeter and the nonconfined membrane leads impulse propagation. The shift in impulse propagation of opposing membranes is shown in the transmembrane potential plots, whereas the difference in opposing action potential shapes is shown in the corresponding phase-plane plots (Fig. 4, B and C). Results are only shown for the fiber with f_e = 0.10, but these qualitative changes are observed for both extracellular volume fractions.

FIGURE 4.

Perimetrical changes in multidomain potentials for unequal distributions of extracellular space: AsymDM 1 = 1:10 (thin line), AsymDM 2 = 1:50 (medium line), AsymDM 3 = 1:250 (thick line), and AsymDM 4 = 1:500 (dashed line) in comparison to an equivalent bidomain representation, f_e = 0.10 (dotted line). The graphs show (A) intracellular potentials, and (B and C) extracellular potentials, transmembrane potentials, and phase-plane plots for the narrow and wide regions, respectively.

The upstroke velocity decreases by 24% from the nonconfined membrane and increases 37% from the confined membrane as compared to the bidomain (∂φ_m/∂t)_max. Although the depolarization of the confined membrane is delayed more than the depolarization of the nonconfined membrane, the initial 15-mV rise in the transmembrane potential (τ_foot) uniformly increases around the fiber perimeter. Initially, the action potential amplitude (φ_m)_max decreases 2% and 4% on the nonconfined and confined membranes, respectively, as compared to the bidomain (φ_m)_max. However, (∂φ_m/∂t)_max then increases 41% on the nonconfined membrane and 1% on the confined membrane. It is surprising that although the transmembrane potentials of the discrete multidomain varied significantly around the perimeter of the fiber, the conduction velocity decreased only slightly. The most noticeable decrease in conduction velocity (−4%) occurred when the extracellular depth fell to ∼5 nm. Note that a slightly greater decrease (∼3% greater) was obtained with a finer discretization (not shown). The differences between the discrete multidomain potentials and bidomain potential are quantified in Table 2.

As with the potentials, the cumulative longitudinal currents are different in the asymmetric multidomain models as compared to the SymDM and bidomain models. In the multidomain model, there is a decrease in the longitudinal extracellular (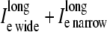), intracellular (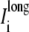) and perimetrical membrane (I_{m wide} + I_{m narrow}) currents. Because the bidomain formulation only describes longitudinal current flow, we compared the transverse current flow of the AsymDM models to the SymDM model with equivalent volume ratio.

Fig. 5 shows the current distributions for fiber configurations of AsymDM 1–4 as compared to the bidomain and/or SymDM models. The longitudinal intracellular current decreases as the asymmetry increases from SymDM to AsymDM 4 (Fig. 5 A). The time to peak intracellular current increases until AsymDM 3. For AsymDM 4, however, the time to peak approaches that of the SymDM model. The longitudinal extracellular current increases in the wide extracellular region but decreases in the narrow region (Fig. 5, B and C). The reduction of longitudinal current in the narrow region was accompanied by an increase in transverse current. Hence, the fundamental difference between the AsymDM and SymDM cases is the conversion of current flow in the narrow extracellular region from longitudinal to transverse (Fig. 5 C). Even for the least asymmetric configuration (1:10), the current within the narrow extracellular region was primarily directed around the fiber perimeter (transverse), flowing into the wide extracellular region and then flowing along the fiber axis (longitudinally).

FIGURE 5.

Alterations in the multidomain intracellular and extracellular currents for unequal distributions of extracellular space: AsymDM 1 = 1:10 (thin line), AsymDM 2 = 1:50 (medium line), AsymDM 3 = 1:250 (thick line), and AsymDM 4 = 1:500 (dashed line) in comparison to an equivalent bidomain or corresponding SymDM representation with f_e = 0.10 (dotted line). (A) In the intracellular space, current consistently decreases with an increasing asymmetry. (B) In the wide extracellular region, the current along and across the fiber are larger compared to the bidomain case. (C) In the narrow extracellular region, current shifts from the longitudinal to the transverse direction.

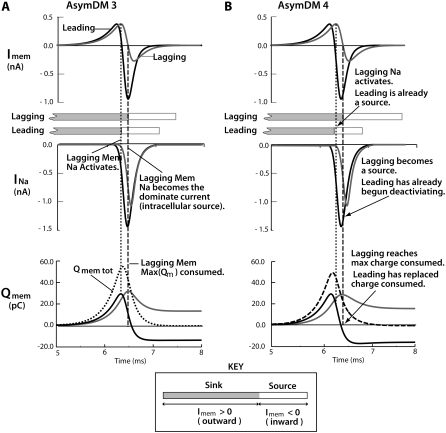
The conversion from longitudinal to transverse current flow in the narrow extracellular region was accompanied by a redistribution of perimetrical membrane current. In Fig. 6, A and B, opposing membrane contributions are shown for the AsymDM 3 and 4 models. The initial depolarization of the membrane, as the result of the membrane being charged by the capacitive current, is an outward current (with respect to the intracellular space) and acts as a sink for upstream intracellular current. Thus, the further depolarization of the membrane, as the result of the activation of the sodium current (I_Na), is an inward current and is an intracellular source. In AsymDM 3 (Fig. 6 A), the nonconfined membrane charges first, activating the inward sodium current first and, hence, leading propagation. Sodium activation of the confined membrane is delayed by 115 μs, causing a lag in propagation; however, activation occurs before the leading membrane becomes a source (the capacitance current remains the dominant current). The load of the confined membrane results in a 21% increase in the sodium current from the leading action potential and a 19% decrease in the lagging action potential compared to the SymDM membrane current predictions. This results in the nonconfined membrane contributing more charge to downstream depolarization than the region consumes (shown in the bottom plots). In contrast, in AsymDM 4, sodium activation of the confined membrane occurrs after the leading membrane has already become a source for intracellular current (Fig. 6 B, dotted line). In addition, sodium inactiviaton of the leading membrane begins before the confined membrane has ever become a source for intracellular current (dashed line). Note that even though the velocities of the AsymDM 4 model and SymDM model are similar, the lagging membrane acts as a large load on downstream propagation, shown as a 26% increase in sodium current over that in the SymDM model.

FIGURE 6.

Increased extracellular resistance (due to the narrower depth) delays downstream charging of the confined membrane, redistributing I_Na and shifting I_mem contributions from opposing membrane regions. I_Na from the leading membrane increases, contributing more charge (Q_mem) than the region consumes for downstream depolarization. In contrast, I_Na from the lagging membrane decreases, contributing less charge (Q_mem) than the region consumes. The time during which the shaded and open boxes overlap is when the leading membrane is a source (contributing current) and the lagging membrane is a sink (consuming current). (A) In AsymDM 3, all patches of the lagging membrane reach threshold (I_Na activation) before the leading membrane becomes a source for intracellular current, i.e., I_Na becomes the dominant current. (B) In AsymDM 4, I_Na from the leading membrane activates and begins deactivating before the lagging membrane ever becomes a source of intracellular current. In addition, the leading membrane is able to replace the intracellular current consumed from the downstream membrane (confined and nonconfined), whereas the lagging membrane remains a sink for intracellular current.

In the bottom plots in Fig. 6, A and B, I_mems from the leading and lagging membrane regions were integrated over time. As the activation delay between the opposing regions widens, less intracellular current is consumed by the lagging membrane and, thus, less inward current from the leading membrane is lost to the depolarization of the lagging membrane. However, because there is still a load from the confined membrane, sodium current from the leading membrane increases. Together, the decrease in current consumed from the confined membrane and the increase in sodium current contributed from the leading action potential results in the nonconfined membrane replacing the amount of current consumed downstream at a faster rate. In AsymDM 4, Q_mem from the leading membrane has returned to zero before the lagging membrane is able to contribute to the intracellular current, and an incremental increase in conduction velocity is observed. Notice that the additional sodium current contributed from the leading action potential (AP) replaces the current that the confined membrane consumed but could not replace due to the decrease in sodium current.

Eliminating membrane participation in impulse propagation

As noted in the Introduction, the tight packing of cardiac fibers in large mammalian Purkinje bundles has been proposed as a possible mechanism to prevent intimately juxtaposed membranes from participating in impulse propagation, thereby increasing conduction velocity (7). It has also been suggested that in normal ventricular tissue, impulse propagation may primarily occur along cardiac fiber membranes adjacent to larger interstitial gaps (6). Table 2 shows that restricting half of the extracellular thickness to 2 nm did not significantly impact the speed of impulse propagation, although the time courses of the action potentials around the myocyte perimeter exhibited significant variation.

Several studies have suggested that resistance of the extracellular space may not be linearly related to the cross-sectional area as the thickness approaches the dimensions of the basement membrane, 30–50 nm (18). As a result, simulations have been performed in which the resistivity of the extracellular space was increased from 0.05 to 25.60 KΩ·cm. We used the case with a 0.10 fraction of extracellular space because it was more representative of the permeable space of the interstitium (3).

Table 3 quantifies the percent change in action potential characteristics from narrow and wide regions in fiber models with an increased narrow extracellular resistivity. When the narrow resistivity is twice normal (0.10 KΩ·cm), there is an immediate change in AP characteristics along the confined membrane. Most notable is the significant reduction in upstroke velocity (from +18% to −11%) that is accompanied by a 7% increase in conduction velocity. When the narrow resistivity is four times normal (0.20 KΩ·cm), τ_foot diverges across opposing membranes, requiring a longer time to depolarize the confined membrane. As the narrow resistivity increases, the more restricted patches of the confined membrane never depolarize, until eventually no patches of the confined membrane depolarize.

TABLE 3.

Comparison of SymDM to AsymDM and Discon AP waveshapes

Model*	ρe narrow (KΩ·cm)	θ (cm/s)	(φm)max (mV)			(∂φm/∂t)max (mV/ms)			τfoot (μs)
SymDM	0.05	49.5	22			244			219
AsymDM 4	0.05	+1%	+41%		+1%	+18%		−24%	+28%
AsymDM 5	0.10	+7%	+44%		−1%	−11%		−23%	+24%
AsymDM 6	0.20	+15%	+39%		−10%	−34%		−19%	+22%	+19%
AsymDM 7	0.40	+23%	+27%		−21%	−39%		−15%	+35%	+13%
AsymDM 8	0.80	+29%	+13%		−21%	−42%		−10%	+83%	+9%
AsymDM 9	1.60	+34%	−2%		−25%	−43%		−7%	+126%	+5%
AsymDM 10	3.20	+37%	−147%		−17%	−45%		−4%	+137%	+3%
AsymDM 11	6.40	+39%	−10%			−2%			+1%
AsymDM 12	12.80	+40%	−6%			−1%			+1%
AsymDM 13	25.60	+41%	−3%			−1%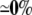
Discon	0.05	70.2 (+42%)	22 (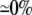)			243 (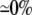)			217 (−1%)

Table shows the percent change in the discrete multidiomain AP characteristics in models that described an increased resistivity in the narrow extracellular region compared to the corresponding symmetric discrete multidomain with equivalent volume fraction ratio (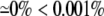). The two percentages given correspond to inconsistent values of the confined membrane and the nonconfined membrane (bold values). When only one percentage is given, the difference in measured values for the pair was <1% (bold) or only the nonconfined membrane was excited (bold).

^*All AsymDM model configurations had an extracellular volume fraction of 0.10 at 1:500 bias.

The action potential of the nonconfined membrane approaches the shape of that predicted by the SymDM, whereas conduction velocity increases by 41%. As the load from the confined membrane lessens, τ_foot decreases to 219 μs and upstroke velocity increases to 243 mV/s. When the load from the confined membrane is nearly zero, (φ_m)_max increases to 22 mV. Conduction velocity steadily increases to 69.9 cm/s, nearly equal to that predicted from a bidomain model with half the surface/volume ratio (2434 μm⁻¹).

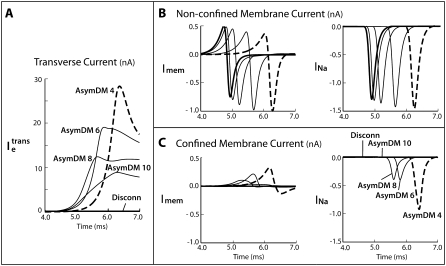
As the resistance in the narrow extracellular region increases, impulse propagation in the narrow and wide regions disassociates. This dissociation is revealed as a longer delay in the activation of sodium current from the lagging membrane and a reduction in the transverse current in the extracellular space (see Fig. 7 A). As a result, the impulse from the nonconfined (leading membrane) experiences a decreased load from the confined (lagging) membrane, and thus the sodium current of the leading membrane decreases to the predicted value of the SymDM case (Fig. 7 B). The sodium current of the lagging membrane decreases to zero, at which point no membrane patches are able to reach threshold (Fig. 7 B).

FIGURE 7.

(A) Extracellular transverse current decreases in the extracellular space as the resistivity is increased in the narrow region. (B) The current contributions from the nonconfined membrane approach the case where the extracellular regions have been disconnected (thick solid line), which is half the predicted bidomain current. (C) The extracellular regions uncouple and the sodium current of the confined membrane is no longer activated, thereby eliminating the membrane contribution to propagation.

As the resistance in the narrow extracellular region increases, the downstream load from the confined membrane decreases and is effectively disconnected from the wide region, eliminating half the membrane from impulse propagation. A limiting case was simulated in which the narrow extracellular region was physically disconnected form the wide region. This disconnected model (Discon) was created by defining no-flux boundaries at opposing domain corners in the extracellular space (see Fig. 1 C). We used the same fiber configuration as in AsymDM 4, with an f_e of 0.10, extracellular bias of 1:500, and normal resistivity. The results are shown in Table 3. As expected, the membrane adjacent to the cleft space does not participate in propagation due to the loss of the transverse current flow necessary to depolarize the membrane. The conduction velocity increases 41% to 70.2 cm/s (consistent with a fiber with a membrane surface/volume ratio that has been halved) and the shape of the propagating action potential follows that simulated in the SymDM or bidomain models.

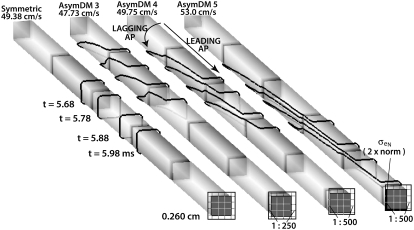
Fig. 8 shows isopotential lines (φ_m = −60 mV) for the SymDM and AsymDM 3–5 models. In the symmetric model, the wavefront is radially homogeneous, as assumed in the bidomain model. In the asymmetric models, the unequal membrane load creates a radially heterogeneous wavefront that stretches over multiple cells. Impulse propagation is determined by the nonconfined membrane, whereas the delayed depolarization of the confined space creates a transverse load on longitudinal propagation.

FIGURE 8.

Radial load asymmetry stretches the propagating wavefront, shown by isochrones of φ_m = −60 mV, at four time points in the center of the fiber.

In the asymmetric multidomain models, we observed an initial slowing in conduction velocity (−3% in AsymDM 3) before observing propagation speeding up (+41% in AsymDM 13). We attribute the initial slowing to the increase in transverse extracellular current, flowing from the narrow to the wide side, which decreased the intracellular current gradient. Because we observed this upturn in conduction velocity when the length constant in the confined space decreased (λ_narrow ≈ 8.8 μm) to a magnitude near the mesh size (in the transverse direction), we reran select cases near this transition point to confirm that the biphasic observation was not a computational error manifested by an inadequate mesh size. The mesh of the intracellular space was increased to a 9 × 9 voxel grid, decreasing the spatial resolution in the transverse direction to a 1.83-μm step, instead of the 3 × 3 grid with a 5.48-μm step used previously. We observed the same biphasic response in conduction velocity, with a slightly more pronounced decline in conduction velocity near the transition point. In AsymDM 3, AsymDM 4, and AsymDM 13, we computed θs of 45.8 cm/s (instead of 47.7 cm/s), 48.0 cm/s (instead of 49.7 cm/s), and 69.3 cm/s (instead of 69.9 cm/s), respectively.

DISCUSSION

In the classical bidomain model (19), the known variability of interstitial spaces around myocytes from narrow spaces between tightly connected fibers to wide gaps between bundles can only be represented as an averaged, homogenized resistance. The discrete multidomain model presented in this work provides a means to investigate the effects on impulse propagation of heterogeneity or discontinuity in both the intracellular and extracellular spaces at the microscale. Comparison of a multidomain model, describing a narrow depth of extracellular space around half of the membrane, with an equivalent bidomain model demonstrates that although the conduction velocity slows with a decreasing fraction of interstitial space, the magnitude of the conduction velocity is relatively insensitive to the distribution of extracellular space around the fiber. This result supports the generally held assumption that the bidomain predicts the effects of the macroscopic intracellular and extracellular properties on conduction. At the microscale, however, the potentials and patterns of current flow predicted by both models show significant differences due to the differences in the mechanisms of propagation.

In the discrete multidomain, a narrow extracellular pathway bordering half the membrane creates an unequal perimetrical load on the depolarizing intracellular current that acts to break the symmetry of the wavefront conducting on a single fiber. As shown in Fig. 8, the leading edge of the wavefront advances along the membrane adjacent to the wider extracellular space followed by the progressive depolarization of the confined membrane. The delayed depolarization along the confined membrane is the result of decreased electrotonic effects between the narrow extracellular space and the upstream inward (toward the intracellular space) membrane current. In contrast, the depolarization of the leading membrane creates a large potential gradient in the extracellular space transverse to the fiber axis, which depolarizes the confined membrane. This is revealed as the complete redirection of current in the narrow extracellular space from longitudinal to transverse. As a result, impulse propagation advances down the fiber axis via activation of the nonconfined membrane adjacent to the wide extracellular space and then propagates around the fiber perimeter via activation of the confined membrane. Thus, the nonconfined membrane is driving propagation.

Although impulse propagation along 50% of the membrane is transverse, the confined membrane impacts longitudinal propagation by acting as a large downstream load to intracellular current. For the case of AsymDM 3, the lagging membrane acts as a load during the initial depolarization of the leading membrane, thereby increasing τ_foot. However, the depolarization of the leading membrane (while the capacitance current is the dominant current) creates enough of a potential gradient transverse to the fiber axis to also sufficiently depolarize the confined membrane. Because the depolarization of half the membrane is delayed, there is a time when the nonconfined membrane is acting as a source and the confined membrane is acting as a sink to downstream axial intracellular current. During this time, the lagging membrane is an additional load to the upstream intracellular current, causing the leading action potential to activate at a lower transmembrane potential and to extend the time the sodium channels are open, thus increasing the charge contributed by the inward sodium current by as much as 26% along the nonconfined membrane. The increase in sodium current along the nonconfined membrane is accompanied by a decrease in upstroke velocity and an insignificant decrease in amplitude of the leading action potential (Fig. 4 B).

Conversely, impulse propagation along the confined membrane experiences a smaller downstream load due to the collision of the clockwise and counterclockwise action potentials that propagate from the leading membrane and around the fiber perimeter. The lagging action potentials have a decreased inward current, increased upstroke velocity, and increased amplitude. The time constant of the initial rise in transmembrane voltage increases concurrently with τ_foot from the leading action potential as long as the extracellular gradient created by the depolarization of the leading membrane can also drive the initial 15-mV depolarization of the lagging membrane.

The changes in sodium current with load are consistent with the findings of Spach and Kootsey (20), who compared changes in sodium current and AP characteristics during longitudinal propagation under three conditions: 1), at steady state within a uniform fiber (“normal” downstream load); 2), near a stimulus site (increased downstream load); and 3), near an AP collision site (decreased downstream load). They found that the sodium current increases near the stimulus site while it decreases near the collision site, in comparison to the sodium current from the uniform action potential. Spach and Kootsey concluded that the changes in downstream load affected the kinetics of activation and inactivation of the sodium channels, similar to the effects observed in Fig. 6. In addition, they observed the same changes in action potential characteristics with variations in downstream load during longitudinal propagation. In the multidomain model studied here, the downstream load on intracellular current was transverse to the direction of propagation.

Sommer hypothesized that tight extracellular spaces may eliminate membrane participation in downstream propagation (7). The results of our simulations showed that although the conduction near the tight spaced lagged, the conduction velocity was nearly constant, even for an extremely narrow space of 2 nm. Although, at this narrow depth, the confined membrane begins to disassociate from longitudinal propagation, it remains a large downstream load to the depolarizing current of the leading membrane, hindering an increase in conduction velocity. Although the confined space has a larger interstitial resistance than the wide space, the magnitude of the resistance is proportional to the thickness. Several studies have suggested that the resistance of the extracellular space may depend on more than the thickness (18,21,22).

In a comprehensive review, Levick discusses the implications of flow through porous media, such as the interstitium, by building on the Carman-Kozeny equation as it relates to the composition of the extracellular space and the presence of cells, i.e., impermeable volumes. He concluded that interstitial conductivity is nonlinearly related to the extracellular fiber concentration. In addition, he found that a heterogeneous composition of extracellular matrix proteins, such as that found in cardiac tissue, could further decrease conductivity that is not accounted for by simple application of the Carman-Kozeny equation (21). Filion et al. argue that because 30–50 nm of basement membrane is composed of concentrated extracellular matrix proteins (22), this membrane may be 35 times more resistant than the larger interstitial matrix (18). As a result, the microscale heterogeneity in the interstitial space may significantly contribute to very large interstitial resistance in tight clefts.

The simulation results showed that when the resistivity of the confined space is increased relative to that in the nonconfined space, the narrow extracellular region becomes functionally disconnected from the wide region. As a result, the leading wavefront dominates longitudinal conduction and the confined region acts less and less as a load. Eventually, when the extracellular resistance becomes 65 times larger than normal, the membrane covered by a narrow 2-nm depth of extracellular space never depolarizes, as shown in Fig. 7. Because the narrow region no longer serves as a load, the action potentials on the wide side have an increased upstroke velocity, a decreased τ_foot, and an increased conduction velocity. The increase in velocity and the change in shape reach their limiting values when the resistivity of the confined extracellular space is 32 times greater than normal.

The drag observed in the propagating wavefront as the result of a nonuniform, and at times confined, distribution of extracellular space has been observed in other theoretical studies using different modeling approaches (23–25). Henriquez and Plonsey (23) and Roth (24) modeled longitudinal propagation in a strand of cardiac tissue using a two-dimensional bidomain approach expressed in cylindrical coordinates. The strand was immersed in a large bath while the interstitial space within the strand was confined. Wang et al. used a boundary element method that computationally separated the intracellular and extracellular spaces as in the discrete multidomain (25). In contrast to the case considered here, the fibers in the bundle models were assumed to be radially symmetric, but because of a large volume conductor surrounding the tissue, an effective nonuniformity in the interstitial resistance from the surface to the center of the bundle was created during longitudinal propagation.

Roth (24) and Wang and co-workers (25) reported a decrease in conduction velocity as the interstitial space became more confined within the bundle. In Wang et al.'s study, when the fibers are uncoupled and tightly packed, separated by <1 μm, the conduction velocity is lower along the center fiber than along the surface fiber because of each fiber's location with respect to the surrounding bath. The authors demonstrated that the transverse coupling of fibers leads to a uniform conduction velocity along the bundle by increasing θ along the inner membrane and decreasing θ along the outer membrane compared to the respective velocities in an uncoupled fiber bundle. Wang et al.'s analysis of this result is similar to the analysis presented here for a single, isolated fiber. The small decrease in θ observed for AsymDM 1–3 arose because the leading membrane is loaded by the lagging membrane, decreasing the amount of current available to depolarize the downstream membrane in the longitudinal direction.

Neither bundle model produces an increase in conduction velocity as the interstitial space becomes more resistive, as observed in the multidomain representation of the single fiber with nonuniform interstitial space. In the multidomain model, conduction velocity does not begin to increase until the depth of the extracellular space is ∼2 nm in the narrow region at a normal extracellular resistivity of 50 Ωcm (σ_e = 20 mS/cm). In Roth's model, ρ_e was 66.7 Ωcm (σ_e = 15 mS/cm) and f_e decreased to 0.005, which is equivalent to a 6-nm depth of interstitial space surrounding the membrane of the inner-bundle fibers. In the Wang et al. model, the interfiber distance was decreased to 1 nm; however, ρ_e was 3.3 times lower than 50 Ωcm. Thus, this would be equivalent to a confined depth of 3.3 nm with a ρ_e of 50 Ωcm, which is still wider than the transition case, AsymDM 4. In the multidomain, a very large resistance adjacent to part of the membrane is required for the increase in conduction velocity. The resistance is larger than can be obtained by simply reducing the interstitial space. As we note, there is evidence that the interstitial resistance can increase nonlinearly when the interstitial space is reduced significantly. It is interesting to note that Wang et al. observe action potential changes in the inner fiber similar to those we report for the lagging action potential before conduction begins to increase. The results from the multidomain model show that the changes in waveshape and wavespeed observed in bundle models due to an effective nonuniformity in interstitial properties can be realized even at the level of a single fiber. This suggests that it may be possible to build a two-dimensional or three-dimensional bidomain representation of a Purkinje bundle to reproduce the speedup and waveshape changes seen in the multidomain with decreasing interstitial space, assuming that the properties of extracellular space can be appropriately represented.

One limitation of the model we describe here is the idealized fiber structure of regular and repeating myocytes surrounded by an unequal but constant depth of extracellular space along the fiber length. In real tissue, a cardiac fiber is composed of irregular and variable-sized myocytes that branch, rejoin, and terminate, changing not only the volume fraction ratio but also the extracellular distribution around the fiber. For the purpose of this article, we used a simple geometry to better control the distribution of extracellular space; however, the multidomain model can be applied to more realistic tissue geometries. Another limitation is that we assumed that diffusion, and not ionic availability, is the limiting factor in impulse propagation, which may not hold true in confined tissue spaces. Further study, using more sophisticated membrane models, is needed to determine how best to account for the ion concentrations in the extracellular spaces of the multidomain model.

In summary, our simulations showed that over a wide range of asymmetry in the extracellular space, the bidomain model predicts the conduction velocity and average action potential time course in a single fiber. When asymmetry is combined with nonuniform material properties, it is possible to reduce the impact of half the membrane on conduction. For this to occur, half of the membrane must serve as an intracellular source for downstream charging before the other half reaches threshold. Although this was accomplished here by increasing the resistance of the confined space, this elimination of half the membrane could also be accomplished by reducing the number of Na channels (and hence the Na current) in the confined region. Although it is not yet practical for modeling all scenarios, the multidomain model can be very useful in helping to determine which electrical and membrane properties, as well as volume fractions, to assign in classical macroscopic models such as the bidomain, which requires significantly less computational time.