Polymerization and Bundling Kinetics of FtsZ Filaments

Abstract

FtsZ is a tubulin homolog essential for prokaryotic cell division. In living bacteria, FtsZ forms a ringlike structure (Z-ring) at the cell midpoint. Cell division coincides with a gradual contraction of the Z-ring, although the detailed molecular structure of the Z-ring is unknown. To reveal the structural properties of FtsZ, an understanding of FtsZ filament and bundle formation is needed. We develop a kinetic model that describes the polymerization and bundling mechanism of FtsZ filaments. The model reveals the energetics of the FtsZ filament formation and the bundling energy between filaments. A weak lateral interaction between filaments is predicted by the model. The model is able to fit the in vitro polymerization kinetics data of another researcher, and explains the cooperativity observed in FtsZ kinetics and the critical concentration in different buffer media. The developed model is also applicable for understanding the kinetics and energetics of other bundling biopolymer filaments.

INTRODUCTION

FtsZ is a bacterial homolog of tubulin that is essential for bacterial cytokinesis (1–3). FtsZ polymerizes into filaments that associate laterally to form bundles in vitro (4–10). Early during the cell cycle, FtsZ, interacts with membrane-associated proteins FtsA and ZipA and assembles into a ring structure (Z-ring) at the midcell (11–13). The Z-ring persists as a coherent structure until the completion of cytokinesis, but fluorescence recovery after photobleaching studies indicate that there is a continuous turnover of FtsZ monomers (14,15). Several other proteins are recruited to the Z-ring to form a complete septal ring capable of carrying out cytokinesis (reviewed in (16–18)). It has been postulated that the Z-ring generates a contractile force at the midcell. Mechanical analysis of the contraction step has been performed, and because there is substantial cell wall growth and turnover, the Z-ring force does not have to be large to accomplish cell division (19).

The question that remains is how does the Z-ring generate the contractile force to accomplish division? To reach an answer, composition and structure of the Z-ring have to be analyzed. Toward this end, in vitro polymerization of FtsZ filaments has been investigated (4,5,7,8,20–23). The polymerization of FtsZ requires a minimum concentration of protein, termed the critical concentration. Below the critical concentration, polymers are a negligible species and above the critical concentration, polymers dominate the reaction (21). This critical behavior indicates that the assembly of FtsZ is cooperative. The presence of cooperativity has been problematic because FtsZ polymers are single-stranded and the origin of the critical nucleus is therefore not obvious (such as in actin or tubulin). Furthermore, existing kinetic and thermodynamic models do not address lateral interactions between FtsZ filaments. Therefore, it is desirable to understand the nature of the critical nucleus and develop a kinetic model to explain FtsZ polymerization and filament bundling. The model should reveal the strength of the filament bonds, and estimate the strength of lateral interactions between filaments in bundles.

In this article, we introduce a kinetic model that quantitatively explains the polymerization kinetics of FtsZ filaments. We incorporate bundling activity of FtsZ by introducing a lateral interaction (perpendicular to the filament direction) between filaments. FtsZ filaments and bundles can break longitudinally as well as laterally. Our modeling confirms the presence of a relatively weak dimer nucleus that contributes to cooperativity. However, we show that cooperativity in FtsZ polymerization is partly entropic in origin, resulting from continuous fragmentation and annealing of filaments. We quantitatively predict that at high FtsZ concentrations, bundle formation is favored; at low FtsZ concentrations, single filament formation is favored. At short times, single filaments are favored, and only at long times do bundles form. To completely explain polymerization kinetics in all buffer conditions, we postulate that an FtsZ subunit in a filament can form three kinds of longitudinal bonds. Subunits having only one longitudinal bond are less favorable than subunits having two longitudinal bonds. The former situation occurs during the formation of a dimer, or addition of a monomer to the end of an existing filament. The latter situation occurs when the subunit is in the middle of a filament. With this combination of ingredients, our modeling is able to correctly reproduce available kinetic data. We obtain quantitative estimate of FtsZ activation rates, and longitudinal and lateral bond energies.

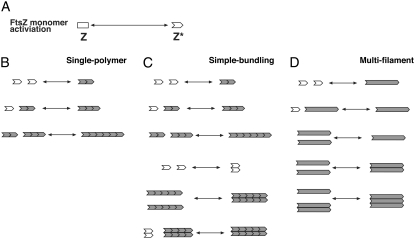
When considering all possible species of FtsZ filaments and bundles, it becomes clear that a fully comprehensive kinetic model is computationally prohibitive. Instead, we examine three reduced models. Scheme One (single-polymer scheme, Fig. 1 B) is a single-filament model where the explicit length of the filament is computed, but there is no bundle formation. Scheme Two (simple-bundling scheme, Fig. 1 C) allows formation of bundles with two filaments, and the lengths of the filaments are computed. However, the filaments in the bundle are of equal length. Scheme Three (multifilament scheme, Fig. 1 D) considers bundles with an arbitrary number of filaments. However, the lengths of the filaments are not explicitly computed. These models cover different limits of FtsZ kinetics, and complement each other. Together, the results form a consistent picture of FtsZ filament and bundle formation. We show that during the timescale of in vitro fluorescence experiments, single filaments and bundles with two filaments are the dominant species, and the single-polymer scheme and the simple-bundling scheme are sufficient to explain the data. However, for longer reaction times, only the simple-bundling scheme is able to explain filament length distributions, bundle formation and the turnover from single filaments to polymers. Therefore, the simple-bundling scheme is the best model for explaining FtsZ polymerization up to several minutes of reaction time.

FIGURE 1.

Schematic depictions of three simplified schemes of our kinetic model. (A) The activation step which converts Z to Z* is common to all three schemes. (B) The single-polymer scheme. The activated monomers form single filaments that can elongate, break, and anneal. The number of monomers or the length of the filament is computed in the model. (C) The simple-bundling scheme. The activated monomers can form filaments and bundles with two protofilaments. The lengths of the protofilaments are identical in the bundle; however, the filaments and bundles can break and anneal. (D) The multifilament scheme. The activated monomers can form filaments and bundles, although the model does not contain information about the longitudinal length. This scheme assesses whether bundles with more than two filaments are important during the timescales of the experiments.

MODELS

FtsZ forms complex structures in vitro and in vivo. In particular, FtsZ filaments form multistranded bundles and even polymer networks under different buffer and concentration conditions (4,6,9,10,24). Each FtsZ monomer can form longitudinal bonds in the filament direction as well as lateral bonds (perpendicular to the filament) (6,25). Therefore, a model of FtsZ filament polymerization must include the possibility of forming lateral interactions. Indeed, from fits to published kinetic data, it is possible to estimate the lateral interaction energy, which is a crucial parameter in establishing the structure of FtsZ bundles.

When FtsZ is activated and free to form any number of longitudinal and lateral bonds, the number of possible reacting species is enormous. Even in a bundle with two filaments with lengths i and j, because the filaments can form any number of lateral bonds and can align in any number of ways, the number of distinct species for the two-filament bundle is (i + j)/2. If we allow filaments of any length up to a maximum of N, all possible double-stranded bundles would include ∼N³ species (10⁶ species for N = 100). If the number of filaments in the bundle can vary, it is clear that the number of possible species increases geometrically. A full kinetic model that includes all possible numbers of lateral bonds and filaments becomes computationally impossible. Thus, simplifications and approximations must be made; models covering different regimes with different degrees of complexity must be developed to examine the kinetics of FtsZ filament formation.

To compare and contrast different aspects of FtsZ dynamics, we study three simplified models of FtsZ polymerization: the single-polymer scheme, the simple-bundling scheme, and the multifilament scheme (Fig. 1). All the schemes include fragmentation and annealing, i.e., an FtsZ polymer can dissociate to form two filaments and two FtsZ polymers can combine and form a longer polymer. The relationships between rate constants that describe the formation of different bundles are discussed below. We note that our models have features in common with fragmentation and annealing models of F-actin that have been examined previously (26).

Fluorescent measurements of filament formation shows that there is a noticeable lag time before FtsZ starts to polymerize (20), implying that FtsZ monomers go through several relatively slow activation steps before polymer formation. Before adding GTP, FtsZ is in the inactive monomer state, denoted as Z. After GTP is added (time t = 0), FtsZ binds GTP, and then become the activated monomer (Z*). Polymerization can proceed for Z*. Therefore, the first part of FtsZ kinetics is described by the reaction

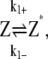(1)

where k_1± values are activation rate constants and the ± sign denotes the forward and backward reactions, respectively. Note that the activation step modeled here effectively included several steps, and can include GTP turnover. To reduce complexity, we have modeled these steps as a single step with an effective rate constant.

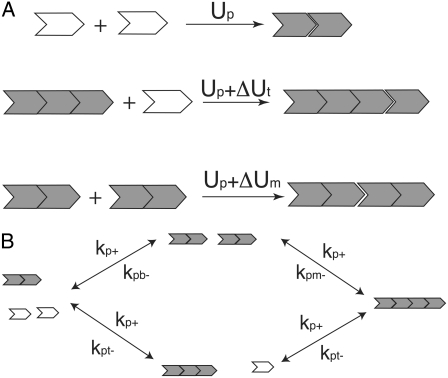
After FtsZ monomers reach the activated Z* state, they can interact with each other's states either longitudinally or laterally to form polymers and bundles. An important postulate of our model is that the longitudinal interaction varies depending on the position of the monomer in the filament (Fig. 2). This implies that an FtsZ molecule can form three kinds of longitudinal bonds, depending on whether it has formed bonds at one or both longitudinal interfaces. Monomers forming a dimer bond have an energy U_p; a monomer at the end of a filament has an energy U_p + ΔU_t; bonds in the middle of a filament have an energy U_p + ΔU_m. This assumption implies that the equilibrium constants for forming these bonds are different. However, due to energy conservation, kinetic rate constants are not independent. Fig. 2 shows two different pathways to form a filament with four subunits. A similar mechanism of single FtsZ elongation was suggested by Huecas et al. (27).

FIGURE 2.

(A) We propose that FtsZ can form three kinds of bonds, depending on whether one or both longitudinal interfaces are occupied. We denote the longitudinal bond energy of a monomer with a monomer that occurs in a dimer as U_p (top). The bond energy of a monomer at the tip of a filament is U_p + ΔU_t (center). The bond energy of monomers in the middle of a filament is U_p + ΔU_m (bottom). (B) The reaction rates and equilibrium constants are not independent. Here, a filament with four monomers can be formed in two ways. The relationships between the equilibrium constants are explained in the text.

FtsZ polymerization reactions are diffusion-limited. To simplify calculations, we assume that all the forward reactions have a similar polymerization rate constant k_p+. The depolymerization (fragmentation) reaction has different rates. From detailed-balance (energy conservation), k_pb–k_pm– must be equal to k_pt–k_pt– (see Fig. 2 B), where k_pb– is the longitudinal dimer breakage rate, k_pm– is the filament breakage rate, and k_pt– is the monomer breakage rate from the tip. If there are bundles, a similar argument can be made for the bundle fragmentation rates. Formation and fragmentation rates for bundles of different lengths are also related to the longitudinal (U_p, ΔU_t, and ΔU_m) and lateral (U_b) interaction energies. These relationships are derived and explained in the Appendices. The fragmentation rate also effectively models several steps, and describes the net rate of GTP hydrolysis and filament breakage. (In some buffer conditions, GTP hydrolysis is also not present.) Therefore, the fragmentation rate contains further information about GTPase activity of FtsZ. Our model does not explicitly describe GTPase activity, although estimates of some of these rates are available (28). GTPase activity of FtsZ can be explored with more data.

Single-polymer scheme

In this scheme, we only consider the longitudinal interaction between Z* monomers. There are only single-stranded polymers in solution. We use Z*_i to describe a FtsZ polymer with i monomers. We assume that in each filament, any longitudinal bond can break, with a breaking rate that is related to the position of the bond (see above and Fig. 2). Furthermore, we assume that any two Z*_i polymers can anneal to form one longer polymer (see Fig. 1 A). Thus, under this scheme, there are only monomers and single-filament polymers of different lengths. Concentration of each species is computed as a function of time. The complete set of reactions for this scheme is

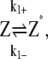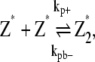(2)

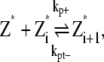(3)

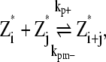(4)

where k_p+ is the polymerization rate for the single filament. As explained earlier, we use the same polymerization rate for dimerization, tip growing, and reannealing reactions. k_pb– is the dimer breaking rate, k_pt– is the depolymerization rate from the polymer tip, and k_pm– is the fragmentation rate at the middle of long polymer. We propose that depolymerization is the easiest for the dimer because it has no conformational constraints; the monomer at the tip of a long polymer is slightly more stable. Fragmentation in the middle of a filament is the most difficult because the monomer has formed two longitudinal contacts. In the model, the maximum polymer length is N, and as long as N is sufficiently large, the exact value of N does not affect the results. We set N = 500, and the maximum length of polymers is 2.5 μm. This value is obtained after the results are converged with respect to increasing N. The detailed equations and rate relationships for these reactions are listed in the Appendices.

Simple-bundling scheme

The single-filament scheme ignores any bundling activity. An increase in complexity is to consider the formation of a two-filament bundle (Fig. 1 B). Previous modeling work (20) only considered a bundle with sequential addition of monomers, and the filament bundle could not fragment or break into protofilaments. In our model, the filaments in the bundle are of equal length. However, the bundle can fragment longitudinally as well as laterally. Fragmenting longitudinally generates two shorter bundles. Note that to allow a bundle with two filaments of unequal length, the number of possible species increases dramatically, approaching N³ where N is the maximum length of the filaments. Such a model is beyond our available computational power.

The set of reaction for the simple-bundling scheme includes Eq. 1 and

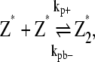(5)

(6)

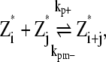(7)

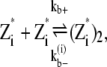(8)

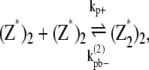(9)

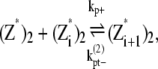(10)

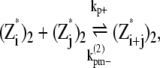(11)

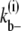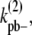
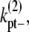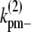where k_b+ is the lateral association rate; is the lateral dissociation rate for a bundle with length i; and and are the fragmentation rates for a double-stranded bundle at different positions. (The nomenclature follows our convention in the single-filament scheme.) The superscript 2 denote a two-filament bundle species. Note that due to detailed balance (energy conservation), the lateral dissociation rate is a function of the filament length, i. The specification is given in the Appendices. Also, since we assume that bundles are filaments of equal length, the rates associated with bundling (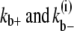) should be considered as effective bundling rates modeling a set of bundling reactions.

Multifilament scheme

To examine possible higher order bundling activity, we also consider a simplified model where there may be an arbitrary number of filaments in a bundle. Again, due to the large number of possible species, simplifications must be made. We only consider FtsZ in the monomer (Z*) or the polymer (P) states. Activated monomers and polymers can form bundles, denoted as (Z*)_α and (P)_α, where α is the number of filaments in the bundle. We assume that filaments in the bundle form a maximal number of lateral bonds. The energetics and the rate constants of these bond formation are summarized in the Appendices.

The reactions considered in the multifilament scheme consist of Eq. 1 and

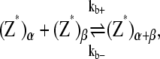(12)

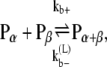(13)

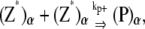(14)

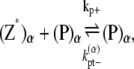(15)

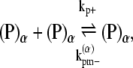(16)

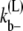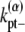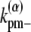where k_b± are the bundling/dissociation rates for a single monomer; is the adjusted bundle dissociation rate for polymer FtsZ with average length L; and and are the longitudinal breaking rates at the ends or in the middle of a bundle of width α. For large α, it is more difficult to depolymerize the bundle to shorter bundles, therefore 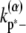decreases with α. The precise relationships are specified in the Appendices. By assuming a uniform bundling rate, we are also assuming that multifilament bundles are two-dimensional sheets instead of three-dimensional clusters.

From the conservation of mass, we can obtain the average polymer length L as

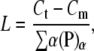(17)

where C_t is the total amount of FtsZ protein and C_m is the amount of FtsZ in monomer or bundled monomer states. When L becomes large, 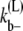becomes small because there are more lateral bonds to break to dissociate the bundle. The detailed equations for this model are given in the Appendices.

RESULTS

Applying the models described above, we fitted the polymerization kinetics of FtsZ by comparing the fluorescent intensities of FtsZ polymers obtained from our model to the experimental results of Chen et al. (20). A mutant FtsZ construct, L68W, was used in the study, and the fluorescence intensity of Tryptophan was enhanced if longitudinal contact between monomers was maintained. We assume that lateral bundling in our model does not change the fluorescent intensity. The formula to compute the fluorescent intensity, F(t), is (20)

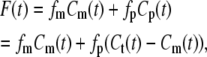(18)

where f_m is the monomer fluorescence; C_m(t) is the concentration of monomer at different times; f_p is the fluorescence for FtsZ protein in the polymer state; C_p is the concentration of protein in the polymer state; and C_t = C_m + C_p is the total/initial concentration of FtsZ. The values f_m and f_p are both measured and normalized using Chen et al's measurements (20). Starting from four different monomer concentrations (1.6 μM, 2.9 μM, 4.6 μM, and 6.1 μM), we computed the fluorescence intensity curves as functions of time.

For each scheme, we varied the corresponding kinetic parameters to fit the computation result to experimental data. We used a Metropolis-Hastings Monte Carlo algorithm to vary the kinetic parameters. This method allowed us to minimize the distance between simulated results and the measured results by adjusting these parameters. After a satisfactory set of parameters was reached, we extend the simulation time to 3 min and allow the system to reach equilibrium. At equilibrium, we computed the length distribution of the filaments, studied the cooperativity of FtsZ assembly, and computed the critical polymerization concentration (C_c). Our schemes all give a cooperative behavior during assembly.

Short-time kinetics

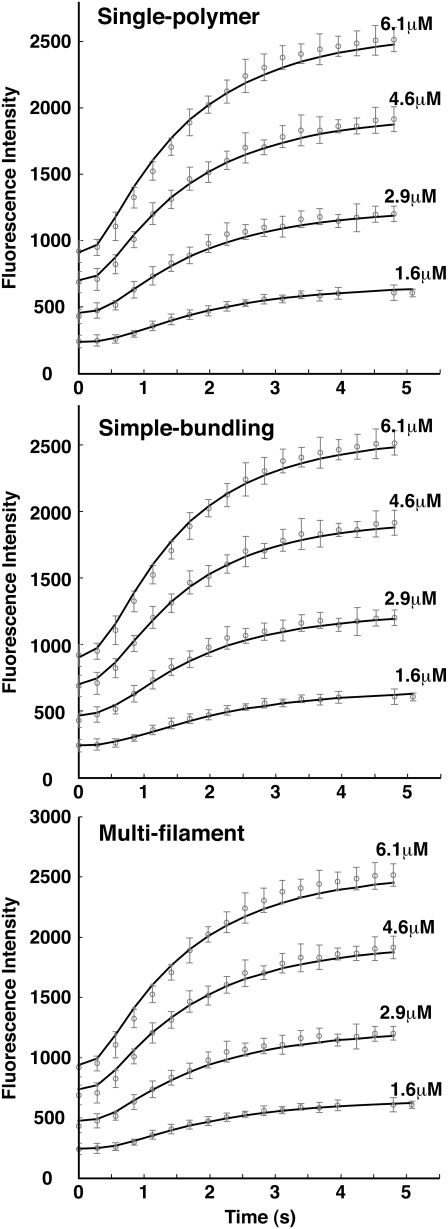
We first describe our results for the kinetic data of Chen et al. (20), which records fluorescence data for L68W up to 20 s. As we will see, within this timescale, the reaction is not fully complete and has not reached equilibrium. Therefore, we call this set of data the “short time” data. The data shows at least three regimes: the initial lag region; the rapidly growing region; and the plateau region. As shown in Fig. 3 and Table 1, for all three schemes, we found similar set of parameters to fit the experimental results in MMK buffer: the slow activation rate (∼1.0 s⁻¹) give rise to the lag region; a fast polymerization rate (∼10⁶ M⁻¹ s⁻¹) gives rise to the rapidly growing region; and, together with a slow depolymerization rate (∼10 s⁻¹), this determines the height of the plateau region. The slow activation rate and different affinities to polymer ends are similar to what were found previously (20). However, our model is able to reveal the bundling rate, which has not been discussed before.

FIGURE 3.

Model results for L68W polymerizing in MMK buffer. Four initial concentrations of FtsZ are shown. The symbols are the experimental data of Chen et al. (20); the error bars show the spread of the data points. The solid lines are model results. All three schemes describe the data quite well, although the multifilament scheme is not as good as the single-polymer or the simple-bundling scheme. Average error per data point is 27.23 for the single polymer scheme, 23.01 for the simple-bundling scheme, and 23.77 for the multifilament scheme.

TABLE 1.

Fitted parameters for L68W in MMK buffer from three modeling schemes

Parameter	Single-polymer	Simple-bundling	Multifilament
k1+(s−1)	0.86	0.87	0.75
k1–(s−1)	5.0e-4	1.0e-3	1.0e-4
kp+(μM−1 s−1)	5.1	5.0	5.0
kpb–(s−1)	34.5	13	100.0
kb+(μM−1 s−1)	—	5.0	5.0
kb–(s−1)	—	17	3.0
Up(kBT)	—	12.0	16.0
ΔUt(kBT)	3.9	3.0	5.0
ΔUm(kBT)	7.8	6.0	10.0
Ub(kBT)	—	0.25	0.15

The maximum time of the data is 5 s. Within this timescale, a small portion of filaments have formed bundles. All three schemes give consistent kinetic parameters. Here, k_B is the Boltzmann constant and T is the room temperature.

A result of our modeling is that FtsZ polymerization is a highly dynamic process. Polymer is exchanging its monomer components with the solution constantly. The lifetime of an FtsZ monomer in a polymer was estimated to be ∼10 s when there is GTPase activity (14,15). Our schemes allow for breaking of every longitudinal bond, which implies that each monomer in a polymer could return to the solution by breaking longitudinal bonds. The fitted fragmentation rate (k_pm ∼ 0.1 s⁻¹, MMK buffer) is consistent with a previous estimate (24). The finite monomer lifetime also shows the importance of fragmentation and annealing in FtsZ kinetics.

For schemes that include bundling, the fitted parameters reveal the longitudinal bond energies (U_p, ΔU_t, ΔU_m) and the lateral interaction energy per monomer, U_b, between FtsZ filaments. These energies are important in establishing the morphologies of FtsZ bundles. The simple-bundling scheme and the multifilament scheme obtain similar energies. The results show that the longitudinal interactions are strong, but lateral interaction is weak. For instance, in MMK buffer, the longitudinal interaction energy (12.0–18 k_BT) is much stronger than the lateral energy (∼0.25 k_BT). However, the lateral interaction is extensive, i.e., bundling for filaments becomes progressively more favorable as the filament length increases. This explains why FtsZ eventually forms long and narrow bundles. The obtained interaction energies are also consistent with previous modeling estimates (10).

Fig. 3 shows that all three schemes can fit the short time kinetics (<20 s) reasonably well. This is because lateral interactions are weak and within this timescale, a small portion of the filament population has begun to bundle. The fluorescence assay also does not preferentially detect bundles. Nevertheless, the simple-bundling scheme gives a slightly better fit, which implies that bundles are beginning to form. (Average error per data point is 27.23 for the single polymer scheme, 23.01 for the simple-bundling scheme, and 23.77 for the multifilament scheme.) A kinetic study to longer timescales will differentiate these schemes even further.

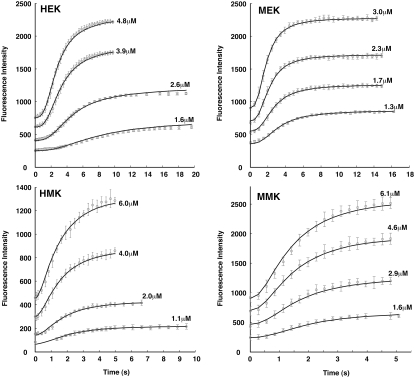
Our model also explains different polymerization kinetics under other buffer conditions (Fig. 4). We apply the simple-bundling scheme to the MEK buffer which lacks Mg, and there is no GTP hydrolysis activity. The model fits the much slower kinetics in MEK buffer with similar polymerizing and bundling rates but faster dimer fragmentation rates when compared to the MMK buffer. These results are reasonable because FtsZ polymerization and bundling are diffusion-limited processes. Therefore, the forward reaction rates are relatively buffer-independent. The MMK buffer contains Mg⁺², and allows GTP hydrolysis. HEK and MEK buffers contain EDTA, which blocks GTP hydrolysis. We find that the fragmentation rates in HEK and MEK are slower than HMK and MMK, indicating that GTP hydrolysis probably increases filament fragmentation rates. The fitted parameters for all four buffer conditions are summarized in Table 2. Again, the simple-bundling scheme with a maximum of two filaments in a bundle is sufficient to explain FtsZ polymerization for short timescales (<20 s). The reaction systems have not reached equilibrium after 20 s.

FIGURE 4.

Model results for the simple-bundling scheme for L68W in all four buffer conditions. The initial concentrations of the FtsZ are shown. The symbols are the experimental data and the solid lines are the simple-bundling model results. The parameters obtained for these buffer conditions are summarized in Table 2.

TABLE 2.

Fitted parameters obtained from the simple-bundling scheme for L68W in all four buffer conditions for data shown in Fig. 4

Parameter	MMK	HMK	MEK	HEK
k1+(s−1)	0.87	0.86	1.14	1.43
k1–(s−1)	1e-3	1e-3	1e-3	0.03
kp+(μM−1 s−1)	5.0	5.0	5.0	4.3
kpb–(s−1)	13	11	372	4300
kb+(μM−1 s−1)	5.0	5.0	3.4	3.9
kb–(s−1)	17	15	110	210
Up(kBT)	12.0	10.0	8.0	7.0
ΔUt(kBT)	3.0	2.9	5.55	7.9
ΔUm(kBT)	6.0	5.8	11.1	15.8
Ub(kBT)	0.25	0.3	0.1	0.08

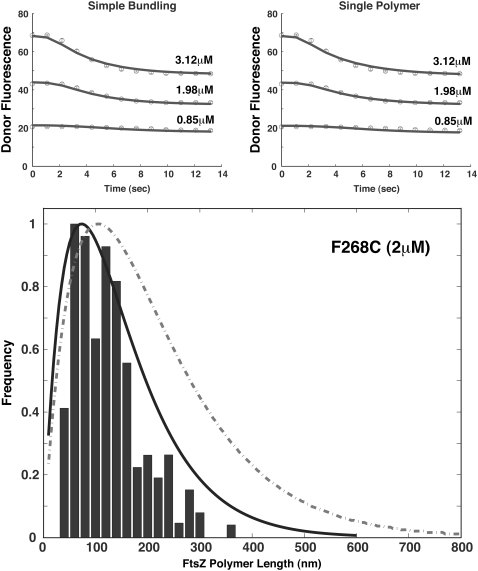
In addition to L68W, the single-polymer and simple-bundling schemes can also explain polymerization data for the F268C mutant. The results are shown in Fig. 5 and Table 3. For F286C, length distribution data is available. We use the fitted parameters to explain the length distribution data (next section).

FIGURE 5.

Model results for the F268C mutant. The fitted short-time data are shown in the upper panels where the solid lines are model results and symbols are data from Chen and Erickson (21). Again the single-polymer and simple-bundling schemes can both explain the short-time data. For longer times (3 min), the length distributions computed from these schemes are different (lower panel). The solid line is the simple-bundling scheme and the dashed line is the single-polymer scheme. The bars are also from data in Chen and Erickson (21). The fitted parameters are shown in Table 3.

TABLE 3.

Fitted parameters for F268C FtsZ

Parameter	Single polymer	Simple bundling
k1+(s−1)	0.31	0.35
k1–(s−1)	0.01	0.01
kp+(μM−1 s−1)	5.5	5.5
kpb–(s−1)	140.0	120.0
kb+(μM−1 s−1)	—	5.0
kb–(s−1)	—	30.0
Up(kBT)	—	10.0
ΔUt(kBT)	4.4	4.0
ΔUm(kBT)	8.8	8.0
Ub(kBT)	—	0.05

The plots are shown in Fig. 5.

Equilibrium steady state

From experiments, kinetic equilibrium is reached after reacting for several minutes. FtsZ filaments are both in bundles and a single filament forms. We use the simple-bundling scheme to examine filament length distribution over time. Data for longer reaction times are available, but for a different mutant, F268C (21). We refitted the single-polymer and simple-bundling schemes for the F268C data (Fig. 5). This allows us to examine the length distribution at 3 min and 2 μM F268C concentration (Fig. 5). We see that from the length distribution, the single-polymer scheme no longer shows good agreement. This result indicates that bundling must be considered for longer timescales and the simple-bundling scheme is able to explain the data at 3 min.

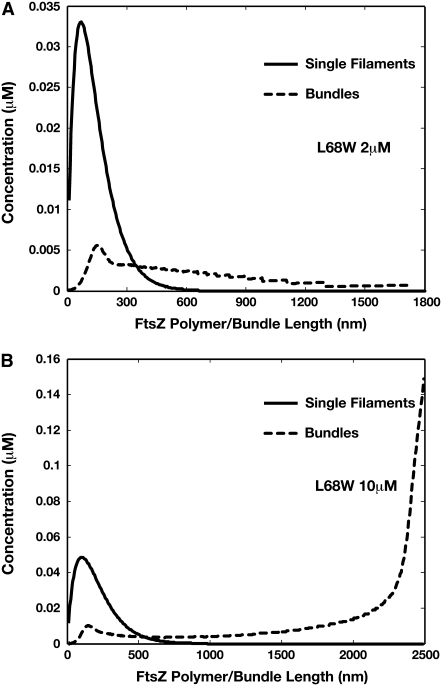
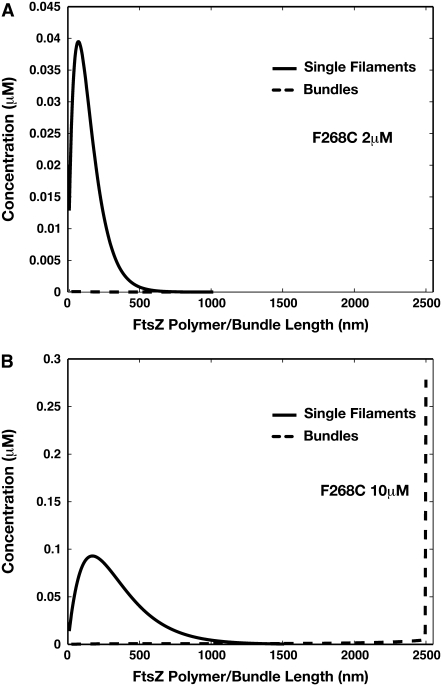
The simple-bundling scheme also gives the correct behavior when the initial FtsZ concentration is increased. We performed the same computation for 10.0 μM of FtsZ. The computed length distributions of single-stranded polymers and double-filament bundles are plotted for L68W in Fig. 6, and F268C in Fig. 7. Comparing to the polymer and bundle distributions at 2.0 μM, there is clearly a shift of dominant species from single-stranded polymer (2.0 μM) to long bundle (10.0 μM). This shift has been observed in experiments and can only be explained by including lateral interactions between FtsZ monomers. Therefore, the simple-bundling scheme is a more complete description of FtsZ kinetics, and completely explains both short and long time results up to several minutes.

FIGURE 6.

Distributions of single filaments and bundles obtained from the simple-bundling scheme for L68W in MMK after 3 min of reaction. (A) If the initial FtsZ monomer concentration is 2 μM, our model predicts that single filaments, not bundles, dominate the system. The single filament length is ∼80 nm. (B) If the concentration is >10 μM, bundles are the dominant species. Longer bundles (more than a micron) are stabilized by lateral interactions. This result is more relevant for in vivo conditions where FtsZ concentration in the cell is ∼7 μM.

FIGURE 7.

Distributions of single filaments and bundles obtained from the simple-bundling scheme for F268C after 3 min of reaction. A similar behavior as L68W is seen. Although at 2 μM, there are hardly any bundles. At 10 μM, there is significant bundling and the concentration for longest bundles diverge. To fully converge the results with respect to N is computationally difficult. However, the results show that bundles eventually dominate.

The multifilament scheme cannot compute length distributions of filaments and bundles. However, it is able to compute the average length of all filaments and bundles. Using the parameters fitted to the short-time data (Table 1), we obtain an average length of ∼300 nm at 3 min and 2 μM initial concentration. This average includes filaments and bundles, and is too long when compared to experimental data (Fig. 5). More significantly, the multifilament scheme shows that at 3 min, the system is dominated by bundles of 2–3 filaments. Therefore, at 3 min, the simple-bundling scheme is the best model in describing all available data.

Cooperativity

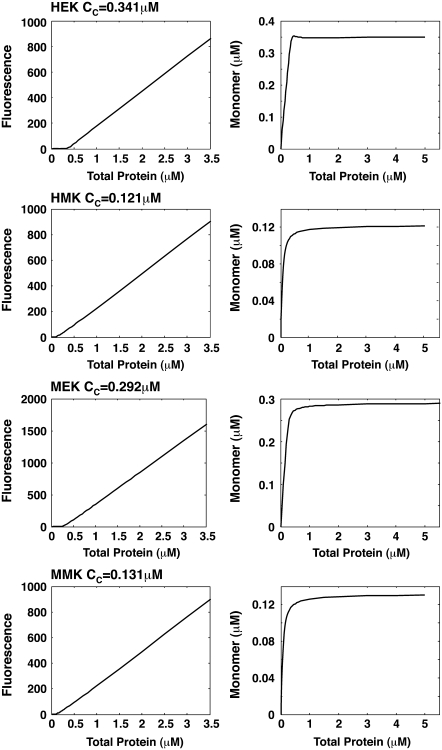
FtsZ assembly is cooperative. After a critical monomer concentration is reached, any additional monomers increase only the polymer concentration. We studied the monomer concentration at kinetic equilibrium as a function of total protein concentration. The single-polymer and simple-bundling schemes both show cooperative behavior and both schemes give C_c ∼ 0.15 μM for MMK and HMK buffers, and C_c ∼ 0.35 μM for MEK and HEK buffers (Fig. 8). These results are in good agreement with the measured C_c under four buffers (0.45 μM for HEK, 0.36 μM for MEK, 0.12 μM for HMK, and 0.19 μM for MMK). For the multifilament scheme, although the monomer concentration is decreasing when more protein is added, it does not reach a plateau at high protein concentrations. The bundling activity of FtsZ is also cooperative (29,30) and our multifilament scheme shows that a critical concentration exists for generating bundles of more than two filaments. Here cooperativity is enthalpic and is the result of lateral interaction that becomes progressively more favorable as the filament lengths increase.

FIGURE 8.

Cooperativity during FtsZ assembly for L68W. The fluorescence of the polymers (left panel) and the monomer concentration (right panel) as functions of the total protein concentration are plotted for each buffer. These results are obtained from the simple-bundling scheme. All four panels show a clear critical concentration where formation of polymers becomes the more favored. The critical concentrations depend on the buffer and the model results are in accord with experimental data.

DISCUSSION AND CONCLUSIONS

To understand the role of the Z-ring in cell division and its possible force-generation properties, it is necessary to establish the structure and energetics of FtsZ filaments and bundles. In vitro kinetic studies are a useful approach for obtaining the physical properties of FtsZ bundles. In this article, we developed models to explain FtsZ polymerization observed in vitro, and obtained quantitative results that describe the energetics and dynamics of FtsZ formation. We postulate that a longitudinal bond in the middle of a filament is different from a longitudinal bond at the end of the filament, indicating that multiple longitudinal bonds stabilize the filament. A possible structural explanation for this postulate is that FtsZ can be in several conformations, and the longitudinal interactions are stabilized by the presence of a next-nearest neighbor. By examining data at different timescales, we conclude that the simple-bundling scheme best describes the FtsZ kinetics. Results from this scheme are able to broadly explain FtsZ polymerization kinetics, length distribution of filaments, and bundling activity up to 3 min of reaction time. There is, however, a lack of length distributions of filaments and bundles at different concentrations. More extensive data should allow us to quantify the bundling activity of FtsZ further.

Previous modeling of FtsZ polymerization utilized an actinlike model where the filament grows as a two-stranded bundle (20). This model did not consider lateral interactions, and also did not incorporate filament fragmentation and annealing, but did include a favorable unimolecular activation step. The model also introduced different affinities for dimers and for polymer elongation. However, the previous model is only adequate to address short time kinetics and low concentrations. Additional investigation has shown that FtsZ are in single filaments at low concentrations and bundles at high concentrations (4–10,21). Thus, the previous model must be revised. Here, we developed a model that takes into account bundle formation and estimated the bundling energy. We showed that cooperativity can arise in single-filament models if we take into account fragmentation and annealing. Therefore, the current work simultaneously explains the bundling activity of FtsZ filaments and cooperative assembly. The current work is also more relevant for physiological conditions where FtsZ concentration is ∼7 μM.

Our modeling also revealed the longitudinal and lateral interaction energy between FtsZ filaments. The longitudinal interaction energy is between 7 and 23 k_BT per bond, depending on the buffer composition. The lateral interaction energy is significantly weaker, between 0.1 and 0.3 k_BT per monomer. However, this weak lateral interaction energy leads to bundle formation if the filaments are long enough (since the net lateral interaction energy is extensive). The lateral interaction also stabilizes long and bundled filaments, and is responsible for the shift from single filaments to bundles seen in Fig. 6. Thus, the morphology of FtsZ is strongly dependent on the lateral interaction energy. The longitudinal and lateral interaction energies obtained from the model also can serve as a basis for further modeling studies of FtsZ dynamics.

Our modeling shows that a superior fit is achieved when in addition to monomer activation, fragmentation of growing polymers is taken into account. When polymerization reaction commences, as polymer concentration starts to grow, so does the fragmentation rate. The increasing number of available ends causes a geometric increase in the number of reaction paths through which monomers can become incorporated into polymers. This leads to cooperative behavior where a small change in the concentration leads to large changes in the state of organization of FtsZ: at the critical concentration a transition occurs from a system dominated by disorganized monomers to a system of polymers.

Biologically, cooperativity is significant because small changes in some parameter can lead to large changes in the organization of FtsZ in the cell. This permits the living cell to rapidly and efficiently respond to changing conditions. It should be noted that the transition from single-stranded polymers to a bundled network of polymers is also cooperative (9,10). These two layers of cooperativity form the a priori points of physiological control over the organization of FtsZ in the cell over which proteins act. For example, SulA, a DNA-damage inducible inhibitor of FtsZ, acts on the cooperative transition between monomers and polymers (30). On the other hand, MinC, a spatial regulator of FtsZ function, acts on the cooperative transition between polymers and a bundled polymer network (10).

In bacterial cells, FtsZ also interacts with membrane-bound FtsA and ZipA, and many other division-related gene products. Colocalization of FtsZ and FtsA is observed during the initial formation of the Z-ring. In addition to anchoring FtsZ filaments to the membrane, ZipA also modulates the interaction between FtsZ (31), possibly by changing the local electrostatic environment of the Z-ring just as the presence of Mg⁺² in buffer changes the interaction energy in vitro. Thus, bacterial cells can change the structure and morphologies of the Z-ring by modulating the longitudinal and lateral interaction energies of FtsZ filaments. The role of other Z-ring-associated proteins in modulating these interactions should be considered more extensively.

Available fluorescence measurements have focused on the formation of FtsZ longitudinal contacts. Once these contacts are formed, our modeling shows that complicated processes such as polymer-polymer annealing, polymer-polymer bundling, and bundle-bundle annealing are important. These processes do not lead to fluorescent intensity change, but are sensitive to lateral interaction between FtsZ filaments. Experiments that can probe the lateral interactions are needed to further elucidate the roles of these contacts in FtsZ dynamics.

APPENDIX A: KINETIC EQUATIONS AND COMPUTATIONAL DETAILS

Here we summarize the kinetic equations used in the three schemes presented in this article. For all schemes, the activation step is the same. From Eq. 1, the kinetic equation for this step is

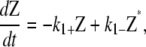(19)

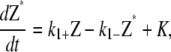(20)

where K is a term due to polymerization of activated FtsZ to form polymers and filaments. K is different for each scheme. The polymerization and bundling steps are summarized below.

Single-polymer scheme

Only monomer and protofilaments are considered in this scheme. All the fragmentation/annealing reactions of FtsZ protofilament are included. Therefore,

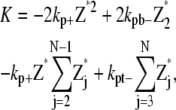(21)

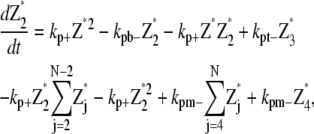(22)

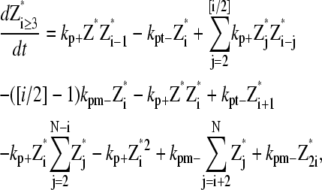(23)

where N is the maximum longitudinal length of the filament.

Simple-bundling scheme

The simple-bundling scheme not only includes all the reactions in the single-polymer scheme, but also takes identical polymer bundling as well as bundle breaking and multiparallel-polymer fragmentation/reannealing into account. The mathematical equations for single filaments are

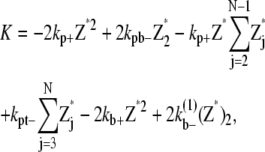(24)

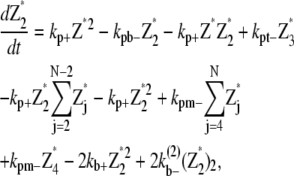(25)

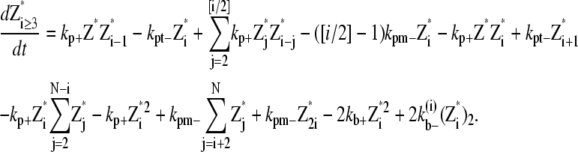(26)

And the equations for double-filament bundles are

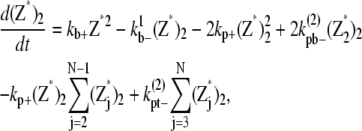(27)

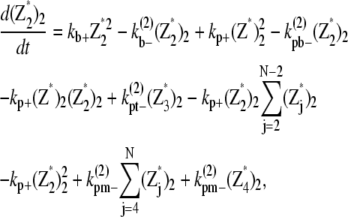(28)

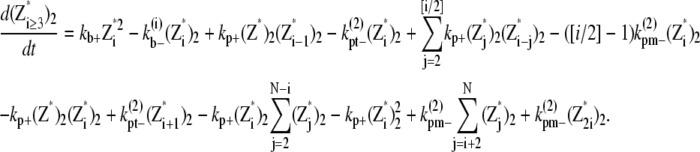(29)

Multifilament scheme

The multifilament scheme only considers lateral bonds and does not explicitly account for filaments and bundles of different longitudinal length. The kinetic equations for this scheme is

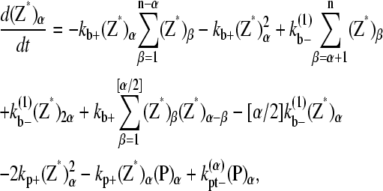(30)

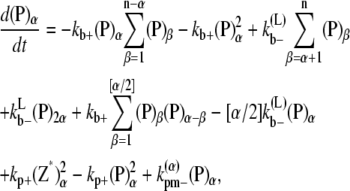(31)

where n is the maximum number of filaments in a bundle.

Computational details

Although the presented models are simplifications of a more complete kinetics model, the computational complexity is still very high, especially when the maximum polymer length is large. For the single-polymer scheme, total number of species is N + 1, and total number of reversible chemical reactions is

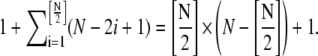Here, N is the maximum length of the polymers. When simple-bundling is introduced, the total number of species doubles and the number of reversible chemical reactions becomes

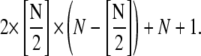For example, if N = 100, there would be 2501 and 5101 reversible chemical reactions in single-polymer and simple-bundling schemes, respectively. Because experiments have shown that the polymer or bundle length can reach several microns when the reaction reaches equilibrium, the maximum polymer length allowed in our simulation must be sufficiently large to contain most of the important species, but not so large that it cannot be solved using reasonable computing resources. To achieve this, we test the convergence property of all three models with respect to N.

For the short time kinetics results shown in Figs. 3 and 4, our results varies very little when N > 150. This is because that within the first 20 s, although the fluorescence intensity has plateaued, FtsZ has not formed long polymers. The solution is dominated by short polymers within this timescale. For longer reaction times, polymers start to anneal and form longer filaments. After 2 ∼ 3 min at 2 μM initial FtsZ concentration, the solution reaches equilibrium where all species reach stable concentrations. When studying the longer timescale, a much larger N is needed. We tested different N values from 300 to 1000, and the results indicate that for both single-polymer and simple-bundling schemes, any N ≥ 500 gives very similar equilibrium state concentrations for all the species. In the presented results for FtsZ in different buffers, we use N = 500, in which case the total number of reversible chemical reactions is 62,501 and 125,501 for single-polymer and simple-bundling schemes, respectively. For the 10 μM results, much larger N that is beyond our computational resources is needed. Figs. 6 B and 7 B are simply to indicate that bundling is more dominant at 10 μM.

For the multifilament scheme, analogous to the maximum polymer length N in the other two schemes, the maximum bundle width n affects the result. We performed convergence test for n and find that with any n ≥ 50, the results do not change with increasing of n. In this case, we have 1254 equations.

To solve the equations for all the chemical reactions, we use an ordinary differential equation solver that is based on a fourth order Runge-Kutta method. Numerical routines from the Numerical Algorithm Group (http://www.nag.com) are used to compute the results.

APPENDIX B: REACTION RATES

In the kinetic schemes described in Models, some of the dissociation rate constants for polymers and bundles depend on the location of the bond and the bundle length and width. The dependence can be inferred from the energetics of the longitudinal and lateral bonds. In this Appendix, we explain this dependence.

For single filaments, we proposed that FtsZ monomer dissociation rate from a polymer depends on its relative position in the polymer. As discussed in Models and Fig. 2, monomers can form three types of longitudinal bonds. We denote the association rate of the dimer bond as k_p+ and the dissociation rate as k_pb–. The longitudinal interaction energy of the dimer bond is U_p. For the bond at the tip of a filament, the rates are k_p+ and k_pt–, and the bond energy is U_p + ΔU_t. For the bond in the middle of a filament, the rates are k_p+ and k_pm–, and the bond energy is U_p + ΔU_m. The corresponding dissociation rate constants are modified as

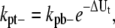(32)

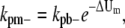(33)

where ΔU_t,m are in units of k_BT. From the energy conservation condition k_pb–k_pm– = k_pt–k_pt–, it is also clear that 2ΔU_t = ΔU_m. Some typical values for L68W are k_pt– = 0.65 s⁻¹, k_pm– = 0.032 s⁻¹ in MMK; k_pt– = 1.45 s⁻¹, and k_pm– = 0.005 s⁻¹ in MEK.

In the simple-bundling scheme, 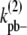is the fragmentation rate of a two-dimer bundle, breaking two longitudinal bonds. Assuming that a single longitudinal bond in a dimer has a bond energy of U_p, and U_p remains constant when additional strands are added to the bundle, then the rate to fragment two longitudinal bonds is

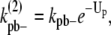(34)

where k_pb– is the rate of breaking a single dimer. The additional energetic cost slows down the breakage of bundled filaments. With the same reasoning, the general expression for 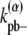in a multidimer bundle is

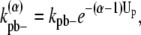(35)

where α is the number of dimers in the bundle. By assuming U_p is constant as more filaments are added, we are also assuming that the filaments are not staggered but are aligned.

A similar argument can be made about the longitudinal bonds at different locations in a bundle. When we break longitudinal bonds at the end of a α-filament bundle (longer than 2), or a fragmentation of a α-filament bundle (longer than 3), the rates become

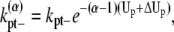(36)

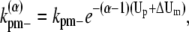(37)

for the lateral bonds. When a bundle with longitudinal length i dissociates into two bundles (both with longitudinal length i), the process breaks i lateral bonds. The dissociation rate for this process, 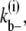would be

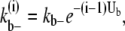(38)

where U_b is the bond energy per lateral bond. For the multifilament scheme, we do not keep track of the length of the bundles. But an estimate of the average bundle length is obtained from the average length of Eq. 17. Therefore, 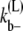for the multifilament scheme is

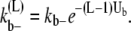(39)

Thus, from the schemes that include multiple bond-breaking reactions, it is possible to obtain estimates of the interaction energy between FtsZ monomers. The lateral and longitudinal interaction energies are crucial for determining the equilibrium state topology of FtsZ filaments and the ultrastructure of the filament bundles.