Intracellular Calcium Release Channels Mediate Their Own Countercurrent: The Ryanodine Receptor Case Study

Abstract

Intracellular calcium release channels like ryanodine receptors (RyRs) and inositol trisphosphate receptors (IP₃Rs) mediate large Ca²⁺ release events from Ca²⁺ storage organelles lasting >5 ms. To have such long-lasting Ca²⁺ efflux, a countercurrent of other ions is necessary to prevent the membrane potential from becoming the Ca²⁺ Nernst potential in <1 ms. A recent model of ion permeation through a single, open RyR channel is used here to show that the vast majority of this countercurrent is conducted by the RyR itself. Consequently, changes in membrane potential are minimized locally and instantly, assuring maintenance of a Ca²⁺-driving force. This RyR autocountercurrent is possible because of the poor Ca²⁺ selectivity and high conductance for both monovalent and divalent cations of these channels. The model shows that, under physiological conditions, the autocountercurrent clamps the membrane potential near 0 mV within ∼150 μs. Consistent with experiments, the model shows how RyR unit Ca²⁺ current is defined by luminal [Ca²⁺], permeable ion composition and concentration, and pore selectivity and conductance. This very likely is true of the highly homologous pore of the IP₃R channel.

INTRODUCTION

Intracellular Ca²⁺ signaling is associated with many cellular phenomena. The Ca²⁺ signals are generated either by Ca²⁺ entry through the surface membrane or by Ca²⁺ release from intracellular Ca²⁺ stores like the sarcoplasmic reticulum (SR) or endoplasmic reticulum. Surface membrane Ca²⁺ entry is mediated by the L-type calcium channel and/or its homologs (e.g., T-, N-, and P/Q-type calcium channels), while Ca²⁺ entry from intracellular stores is generally mediated by either ryanodine receptor (RyR) or inositol trisphosphate receptors (IP₃R) channels.

The RyR and IP₃R channels share significant homology (1,2), but have little homology with the L-type channel (with the possible exception of their selectivity filters (3–7)). Their single-channel permeation properties reflect this dichotomy: the RyR and IP₃R channels have high conductance and low (millimolar) Ca²⁺ affinity (8–11) while the L-type channel has relatively low conductance and high (micromolar) Ca²⁺ affinity (12,13). In this article, we show that the high conductance and low Ca²⁺ affinity of the intracellular calcium channels make them ideal for their physiological role of conducting a large Ca²⁺ flux over a long time (>5 ms). Our test case here is the RyR channel of striated muscles.

The RyR channel of striated muscle is found in the SR membrane and can mediate large SR Ca²⁺ release events lasting >10 ms. Such long release events would not be possible if only Ca²⁺ moved across the SR membrane; the rapid movement solely of Ca²⁺ would quickly bring the SR membrane potential to the Ca²⁺ Nernst potential (E_Ca, the Ca²⁺ equilibrium potential), stopping Ca²⁺ release. Some other ion species like K⁺, Mg²⁺, or Cl⁻ must provide a countercurrent to prevent the SR membrane potential from coming close to E_Ca.

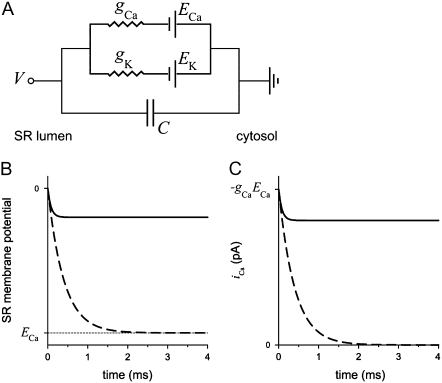
The need for countercurrent in Ca²⁺ release—known for many years (14–20)—can be illustrated using an equivalent circuit model of a patch of membrane that contains conduction pathways for two ion species (e.g., K⁺ and Ca²⁺). These pathways could be either two separate channels or through the same channel (Fig. 1 A). At steady state (with conduction pathways open), the net ionic current is 0 and the membrane voltage is (see Eq. 4)

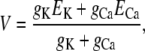(1)

where g_j and E_j are the conductance and Nernst potential, respectively, of ion species j. Thus, if there is no K⁺ current (g_K = 0), the Ca²⁺ current will stop because the membrane potential V becomes the Ca²⁺ Nernst potential (E_Ca = −118 mV, assuming normal resting physiological ion concentrations). On the other hand, if other ions (K⁺ in this example) can cross the membrane (assuming equal K⁺ concentrations on both sides of the membrane), then any change in the membrane potential generated by the Ca²⁺ current will drive K⁺ in the opposite direction. This countercurrent attenuates the Ca²⁺-driven change in the membrane potential and will ultimately clamp potential at some value away from E_Ca (Eq. 1). At this potential, there will be a constant driving force for Ca²⁺ release. The predicted time course of the membrane potential change in each of these cases is shown in Fig. 1 B. How this affects the unit Ca²⁺ current is shown in Fig. 1 C. Equivalent circuit modeling and interpretations like this were presented decades ago (14).

FIGURE 1.

(A) Equivalent circuit of Ohmic ion currents across a capacitive membrane. (B) Time course of membrane potential with countercurrent (solid line) and without (dashed line) for the equivalent circuit in panel A. (C) Time course of Ca²⁺ current with countercurrent (solid line) and without (dashed line) for the equivalent circuit in panel A. g_K = 100 pS, g_Ca = 25 pS, E_K = 0 mV, and E_Ca = −120 mV.

How the SR membrane potential may be affected or generated by Ca²⁺ release has been experimentally explored. In 1976, Chandler et al. (21) proposed a mechanical model of Ca²⁺ release control that did not involve SR potential changes. A few years later, Mathias et al. (22) proposed an alternative model where SR potential changes stimulate Ca²⁺ release. Indeed, several studies (using a variety of techniques) have reported signals that were attributed to SR membrane potential changes (23–28). However, the disagreement between these studies has made it difficult to access particular models describing SR membrane potential changes that may be caused by (or generated by) Ca²⁺ release. In a now classic work, Somlyo et al. (29) used electron-probe x-ray analysis to monitor total intra-SR ion concentrations before and after Ca²⁺ release. They provided compelling evidence against the existence of a large and/or sustained SR membrane potential change, but the possibility of small transient changes in SR membrane potential during Ca²⁺ release remains.

Many groups have also attempted to identify the required countercurrent and the channel that mediates it. The SR K⁺ channel has been perhaps most often considered the SR countercurrent pathway (16,26,30–34). However, block of this pathway alters SR Ca²⁺ uptake, but does not appear to eliminate SR Ca²⁺ release (19,35). Furthermore, K⁺ and Cs⁺ act almost equally well as counterions during prolonged (>10 ms) Ca²⁺ release (16,36)—even though Cs⁺ barely goes through the SR K⁺ channel (31,37). This is also true for the briefer Ca²⁺ release associated with Ca²⁺ sparks in amphibian skeletal muscle (38) and mammalian cardiac muscle (39–41). Overall, the clear implication is that the SR K⁺ channel may not carry the required countercurrent during Ca²⁺ release.

Recently, a new SR cation channel called TRIC has been identified (42) and suggested to mediate countercurrent during SR Ca²⁺ release. However, TRIC knockout mice have large, fast, caffeine-induced Ca²⁺ transients, implying that sufficient countercurrent exists in the absence of TRIC current (42). Countercurrent during SR Ca²⁺ release could also be mediated by the SR Cl⁻ channel (43). However, many studies of SR Ca²⁺ release in skeletal and cardiac muscle have been done using large impermeable anions like glutamate or aspartate instead of Cl⁻ (14,16,38–41). This suggests that SR Cl⁻ channels also do not carry a substantial countercurrent during Ca²⁺ release. Somlyo et al. (29) proposed that H⁺ may also play a role in SR charge compensation. Kamp et al. (44) showed that, although there was significant acidification (∼0.2 pH units) inside the SR during Ca²⁺ release, proton fluxes could reasonably account for just 5–10% of the necessary charge compensation.

Here, we propose here that the RyR channel mediates its own countercurrent during SR Ca²⁺ release for the following reasons:

1. Only countercurrent through RyR is consistent with previous experimental results. RyR conducts Cs⁺ with high conductance and does not conduct anions. Thus, substituting Cs⁺ for K⁺ or use of large anions instead of Cl⁻ would not substantially affect Ca²⁺ release.

2. RyR is poorly Ca²⁺ selective and has millimolar Ca²⁺ affinity (8). Therefore, it is improbable that all the current through RyR is Ca²⁺ current under physiological conditions (e.g., ∼1 mM intra-SR [Ca²⁺] with symmetric 150 mM K⁺ and 1 mM Mg²⁺). This is not the case for the L-type calcium channel, which is highly Ca²⁺ selective and has 1000-fold greater Ca²⁺ affinity. Thus, other permeable cations (K⁺ and Mg²⁺) very likely move through open RyR channels.

3. A robust model of ion permeation through a single open RyR predicts that there is a substantial K⁺ current under physiological conditions (45,46). The model has reproduced all the known permeation and selectivity data wild-type and mutant RyR channels. It has predicted previously unknown permeability attributes that were later verified experimentally (45,46).

In this article, we use this model (46) and the equivalent circuit approach to compute unit Ca²⁺ current, K⁺ and Mg²⁺ currents, and SR membrane potential (as well as their time courses) when a RyR channel opens under (approximately) physiological ionic conditions. We conclude that the large K⁺ and Mg²⁺ countercurrent through an open RyR is sufficient to clamp the SR membrane potential far from E_Ca. Therefore, RyR channels (and probably IP₃R channels as well) most likely mediate their own countercurrent during Ca²⁺ release, while the other SR ion channels likely mediate the countercurrent required for efficient SR Ca²⁺ uptake (after RyR channels have closed).

THEORY AND METHODS

Equivalent circuits

In our analysis, we consider two variants of the same equivalent circuit (Fig. 1 A, and see Fig. 3 A). The membrane is always modeled as a capacitor with capacitance C.

FIGURE 3.

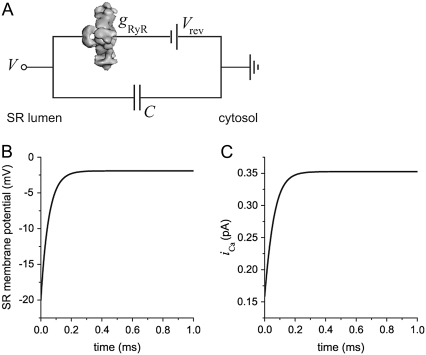
(A) Equivalent circuit of net RyR current across a capacitive membrane. The representation of RyR is reproduced from Orlova et al. (72). (B) Time course of SR membrane potential for the equivalent circuit in panel A. (C) Time course of unit Ca²⁺ current for the equivalent circuit in panel A. The initial applied potential at time t = 0 is −20 mV. g_RyR = 192 pS and V_rev = −1.9 mV.

In one circuit (Fig. 1 A), two ion species cross the membrane, each with a linear current/voltage relation

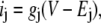(2)

where i_j, g_j, and E_j are the current, conductance, and Nernst potential of species j, respectively, and V is the applied voltage. The ions could be moving through two separate channels or through the same channel. This circuit was used to illustrate the need for countercurrent in the Introduction.

Such a simple equivalent circuit is not, however, a reasonable description of RyR permeability. Specifically, the RyR permeation model (see below) shows that Eq. 2 is not true for Ca²⁺ under physiological conditions; the Ca²⁺ current through RyR is very nonlinear (approximately exponential) for applied voltages between the SR membrane potential (normally ∼0 mV) and the Ca²⁺ Nernst potential (∼−118 mV). However, the net conductance through RyR (due to all the ion species) is nearly linear around the reversal potential V_rev under physiological conditions (Fig. 2 A). Therefore, we model (see circuit in Fig. 3 A) net RyR conductance (not the individual ion conductances) as a single resistor with its conductance g_RyR calculated using the RyR permeation model.

FIGURE 2.

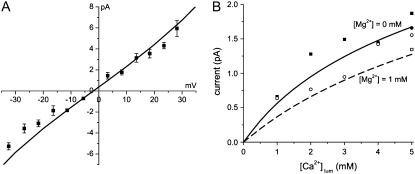
Comparison of the permeation (PNP/DFT) model predictions (lines) to experimental data (symbols) collected under physiological ionic conditions. (A) Current/voltage curve under our approximate physiological concentrations at ∼V_rev. Currents are from single RyR2 channels reconstituted in planar lipid bilayers. These data were collected using the methods described by Kettlun et al. (55). The mean ± SE are shown and n = 4–8. Between ±15 mV, a linear least-squares fit (not shown) indicated a g_RyR = 197 pS and V_rev = −2.3 mV, which is almost identical to the permeation model curve (g_RyR = 192 pS and V_rev = −1.9 mV). (B) Comparing the model to data published in Kettlun et al. (55). (Solid line/solid symbols) The current at 0 mV applied voltage with symmetric [K⁺] = 150 mM as luminal Ca²⁺ is added. (Dashed line/open symbols) The current at 0 mV applied voltage with symmetric [K⁺] = 150 mM and [Mg²⁺] = 1 mM as luminal Ca²⁺ is added. Squares are from mammalian cardiac muscle RyR and circles are from amphibian skeletal muscle RyR.

For both circuits, the net unitary current 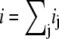and membrane potential V at time t is the solution of the equation

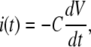(3)

namely

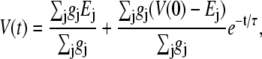(4)

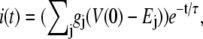(5)

where the time constant of the voltage and current change is

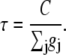(6)

In all calculations, we assume a [Ca²⁺]_cytosol of 0.1 μM and a membrane capacitance C of 0.01 pF, which approximately corresponds to a 1 μm² patch of membrane. This is similar to the experimental value of 0.013 pF/μm² quoted by Baylor et al. (28).

Model of RyR permeation

We use a model of a single, open RyR pore to compute the net current, as well as the currents carried by each permeant ion species (46). The ions are modeled as charged, hard spheres and their flux through the open pore is described by a combination of one-dimensional Poisson-Nernst-Planck theory and density functional theory of fluids (47,48) (the PNP/DFT model):

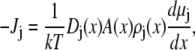(7)

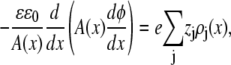(8)

where ρ_j and μ_j are the concentration and electrochemical potential, respectively, of ion species j throughout the pore and baths. J_j is the flux of ion species j and A(x) is the area of the equichemical potential surfaces that is estimated as previously described (49,50). The dielectric constant ɛ of the system is 78.4. The value ɛ₀ is the permittivity of free space, k is the Boltzmann constant, and T = 298.15K is the temperature. The chemical potentials μ_j are described with DFT of electrolytes (51,52).

The model of the pore includes the five conserved, charged amino acids found by Gao et al. (5), Wang et al. (6), and Xu et al. (7) to significantly affect RyR selectivity and permeation. These amino acids are Asp-4899, Glu-4900, Asp-4938, Asp-4945, and Glu-4902 in the RyR1 numbering scheme (53). The current/voltage relations (−150 to +150 mV) in over 50 ionic solutions (45,46) (and another 50 solutions as yet unpublished by D. Gillespie, L. Xu, and G. Meissner) of wild-type and mutant RyR channels are reproduced by the model without changing any parameters. The model also predicted—before the confirming experiments were done—anomalous mole fraction effects (54) in mixtures of Na⁺ and Cs⁺ (45), Ca²⁺ and Na⁺, and Ca²⁺ and Cs⁺ (46).

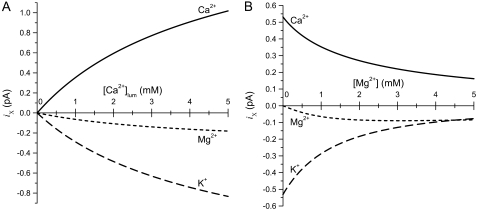
This article focuses on ionic solutions that approximate intracellular, physiological conditions at small applied voltages: symmetric 150 mM KCl and 1 mM MgCl₂, 1 mM SR luminal CaCl₂ and a ±10 mV applied voltage range. To show that the model is accurate under these conditions, we compare it—without changing any parameters from those listed in Gillespie (46)—to experimental current/voltage data collected under these conditions (Fig. 2 A). These single RyR channel data were collected with standard methods described elsewhere (55). Note the close correspondence of the experimental results (squares) and theoretical prediction (line). We also compared the model to previously published experimental results reported by Kettlun et al. (55) in Fig. 2 B (symbols). The solid line in Fig. 2 B shows the current predicted by the model in the absence of Mg²⁺ (0 mV, symmetric 150 mM K⁺, various luminal Ca²⁺ levels). The dashed line in Fig. 2 B shows the current predicted by the model in the presence of 1 mM Mg²⁺ (again 0 mV, symmetric 150 mM K⁺, various luminal Ca²⁺ levels). The model reproduces the experimental results very well with no adjustable parameters. These data/theory comparisons and many other published ones (45,46) show that the model can accurately compute the net current, but also—and most importantly for this article—the contributions of each permeable ion species to that net current (see Figs. 5 and 6).

FIGURE 5.

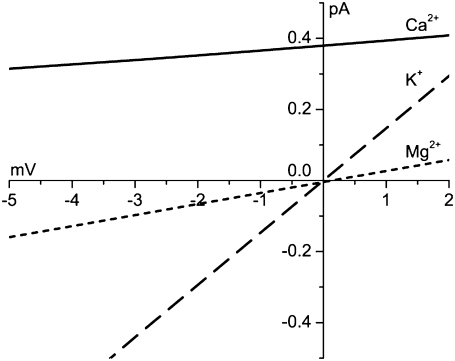
Individual Ca²⁺ (solid line), K⁺ (dashed line), and Mg²⁺ (dotted line) currents at small applied voltages, as computed by the PNP/DFT model. The conductances are 14 pS for Ca²⁺, 31 pS for Mg²⁺, and 147 pS for K⁺, which were obtained by linear least-squares fits between ±3 mV. [K⁺] = 150 mM and [Mg²⁺] = 1 mM symmetric and [Ca²⁺]_lum = 1 mM. The model results for the net current under these conditions are compared to experiments in Fig. 2 A.

FIGURE 6.

(A) Individual Ca²⁺ (solid line), K⁺ (dashed line), and Mg²⁺ (dotted line) currents as a function of [Ca²⁺]_lum (0 to 5 mM), as computed by the PNP/DFT model. [K⁺] = 150 mM and [Mg²⁺] = 1 mM, symmetric. (B) Currents of Ca²⁺ (solid line), K⁺ (dashed line), and Mg²⁺ (dotted line) as symmetric [Mg²⁺] is increased from 0 to 5 mM, as computed by the PNP/DFT model. [K⁺] = 150 mM, symmetric, and [Ca²⁺]_lum = 1 mM. For each x-axis concentration, the reversal potential is calculated and each ionic species current at that potential is shown. The reversal potential was used because equivalent circuit analysis indicates that this is the stationary SR membrane potential (Eq. 4). The ionic concentrations and applied potential are very close to the conditions of Fig. 2 B, where the permeation model reproduced experimental results. [Ca²⁺]_lum and [Mg²⁺]_lum are also changed in Gillespie (46), and the model reproduced those results (shown in that article).

Details of the model have been described previously (46).

RESULTS AND DISCUSSION

RyR opening can change local SR membrane potential quickly

To study the time course of local membrane potential due to the opening of a single RyR, we consider a 1 μm² patch of SR membrane (C = 0.01 pF). In the equivalent circuit shown in Fig. 3 A, the SR membrane potential is Eq. 4,

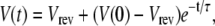(9)

with time constant τ = C/g_RyR where g_RyR is the net conductance of RyR at the reversal potential V_rev (Eq. 6).

Our experiments show (Fig. 2 A) that g_RyR = 197 pS gives a time constant τ of 51 μs. With this time constant, the SR membrane potential and unit Ca²⁺ current reach 95% of their eventual steady-state values in ∼150 μs. This is illustrated in Fig. 3, B and C. This time constant is likely an upper limit because a smaller patch of SR membrane or a 1 μm² patch with more RyR channels would decrease τ by decreasing C or increasing g_RyR, respectively. This implies that that RyR opening (by itself) will clamp the SR membrane potential to a steady-state value in much less than a millisecond (∼150 μs). If this steady-state potential is well away from E_Ca, then an open RyR will continue to conduct Ca²⁺ out of the SR. Experimentally, the minimum detectable RyR open event duration in bilayers is probably near 358 μs (i.e., 2 × 0.179/Fc; recording system dead time assuming Fc = 1 kHz (56)). Thus, RyR autocountercurrent probably clamps the SR membrane potential in less time than the briefest single RyR open events detected in typical planar lipid bilayer studies.

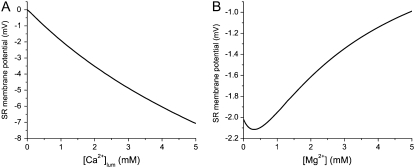
At steady state (t > 0.5 ms), the SR membrane potential becomes the single-channel reversal potential V_rev (Eq. 9). Here, we compute V_rev with the model (46), but experimentally measured V_rev could be used as well. V_rev—and consequently SR membrane potential—depends on the ionic composition of the cytosol and SR lumen. In the cytosol, the normal physiological divalent concentrations are believed to be 1 mM Mg²⁺ and 0.1 μM Ca²⁺. Inside the SR (luminal), there is 1 mM Mg²⁺ and 1 mM Ca²⁺. Luminal Ca²⁺ concentration [Ca²⁺]_lum (i.e., SR Ca²⁺ load) is an important and variable physiological parameter in cardiac muscle and some nonmuscle cells. Also, Mg²⁺ concentrations can and have been experimentally manipulated in studies of RyR-mediated SR Ca²⁺ release. Therefore, we have evaluated how different [Mg²⁺] and [Ca²⁺]_lum affect V_rev (and, later, RyR autocountercurrent).

Fig. 4 A shows how V_rev, achieved after a RyR channel opens, varies as SR load ([Ca²⁺]_lum) is increased with symmetric 1 mM Mg²⁺ present. Fig. 4 B shows V_rev as a function of symmetric [Mg²⁺] at a constant [Ca²⁺]_lum (1 mM). Note that the V_rev values here are all between 0 and −7 mV and far from E_Ca. For example, V_rev is ∼−2 mV and E_Ca is −118 mV under physiological conditions (at 1 mM Ca²⁺ in Fig. 4 A). Such small V_rev values have been measured in single RyR channel studies, even under Ca²⁺ and Mg²⁺ gradients of >5 mM (46). A reversal potential so far from the Ca²⁺ Nernst potential is consistent with the relatively poor Ca²⁺ selectivity of the RyR channel and implies that there must be a large countercurrent of other permeable cations through the open channel.

FIGURE 4.

Changes in stationary SR membrane potential as divalent concentrations vary, as computed by the PNP/DFT model. (A) [Ca²⁺]_lum is increased with symmetric [K⁺] = 150 mM and [Mg²⁺] = 1 mM. (B) [Mg²⁺] is increased symmetrically as [K⁺] = 150 mM and [Ca²⁺]_lum = 1 mM. The minimum in the potential is probably due to an anomalous mole fraction effect similar to the one previously discovered by the model from Gillespie (46).

There are, albeit indirect, measurements of the SR membrane potential (e.g., (14,28)). These studies generally have applied a model to convert an optical signal into a predicted SR potential change. Vergara et al. (14) and Baylor et al. (28) used an equivalent circuit model similar to the one we apply here. Both computed that a stationary SR membrane potential is achieved when there is zero net current flowing across the membrane—which is our conclusion as well (Eq. 5). However, they predicted that there is a large SR potential and we predict a small one (−2 mV). The difference in these predictions is generated by the assumptions used to describe ion permeation and selectivity. For example, Vergara et al. (14) described—very reasonable at the time—that SR Ca²⁺ currents were Ohmic (i.e., linear). As described above, the RyR-mediated Ca²⁺ current is highly nonlinear between 0 mV and E_Ca, and the linear assumption resulted in Ca²⁺ current being severely overestimated. Baylor et al. (28), on the other hand, used a Goldman-Hodgkin-Katz model to model individual ion currents. Because their study was performed before RyR permeation properties were characterized, they reasonably assumed that the Ca²⁺ current was conducted by a highly Ca²⁺ selective channel; the smallest Ca²⁺/K⁺ permeability ratio they considered was 100. We now know that this value is near 7, and if that were used in their formulation, then they would have predicted an SR potential close to −2 mV.

RyR mediates a large countercurrent

The equivalent circuit model of the capacitive membrane (Fig. 3 A) indicates that the stationary net current through the membrane will be 0 (Eq. 5). If the RyR channel is the only channel present, then the membrane potential is V_rev (Fig. 4) and the net current through the RyR channel will be 0. Since there is a large Ca²⁺ driving force (E_Ca − V_rev = −118 − (−2) = −116 mV), there will be a substantial Ca²⁺ efflux. To have zero net current, there must be an equal countercurrent of other permeable cations, K⁺ and Mg²⁺. This is illustrated in Fig. 5 where the individual ion currents around the predicted V_rev (Fig. 4) under physiological conditions are shown. Note that the unit Ca²⁺ current at 0 mV here (0.38 pA) is quite close to the extrapolated unit Ca²⁺ (0.48 pA) experimentally defined by Kettlun et al. (55) in such salt solutions.

Since the ionic concentrations of Ca²⁺ and Mg²⁺ in cells may vary (e.g., during exercise or SR overload), we calculated unit currents (at the V_rev of Fig. 4) over a range of [Ca²⁺]_lum (SR loads) and symmetric [Mg²⁺]. Fig. 6 A shows how unit currents vary as SR load ([Ca²⁺]_lum) is increased with symmetric 1 mM Mg²⁺ present. As SR Ca²⁺ load is increased from 0 to 5 mM, K⁺ consistently provides the vast majority (82%) of the countercurrent while Mg²⁺ provides the rest (18%). Larger Ca²⁺ loads result in larger Ca²⁺ currents, but the unit Ca²⁺ current changes sublinearly with intra-SR Ca²⁺ levels: doubling intra-SR [Ca²⁺] (from 1 to 2 mM) increases unit Ca²⁺ current by ∼70%; halving intra-SR [Ca²⁺] (to 0.5 mM) reduces the current ∼43%. Some modeling of SR release and sparks (e.g., (57)) assume a linear i_Ca-versus-[Ca²⁺]_lum relationship. The nonlinearity illustrated here could alter the interpretation of those studies.

Fig. 6 B shows how unit Ca²⁺ currents vary as symmetric Mg²⁺ is increased at a constant SR load (1 mM). Increasing [Mg²⁺] has the opposite effect of increasing SR load: stationary Ca²⁺ current decreases as [Mg²⁺] increases. Also, as [Mg²⁺] increases from 0 to 5 mM, Mg²⁺ provides a larger percentage of the countercurrent, from 0% to 52%. Both of these results are because Mg²⁺ competes very effectively with Ca²⁺ for the RyR pore; high [Mg²⁺] displaces Ca²⁺ from the pore, decreasing Ca²⁺ current and increasing the Mg²⁺ current (46,54,58–62).

The effect of elevated cytosolic Mg²⁺ on RyR-mediated SR Ca²⁺ release has been studied experimentally and our predictions are consistent with those results. For example, elevated cytosolic Mg²⁺ reduces both the amplitude and spatial width of local Ca²⁺ release (63). Our calculations suggest that one contributing factor is that the extra Mg²⁺ reduces the unitary Ca²⁺ current. Likewise, the marked increase in cytosolic Mg²⁺ associated with skeletal muscle fatigue (64) will also reduce RyR unitary Ca²⁺ current, contributing to tension decline.

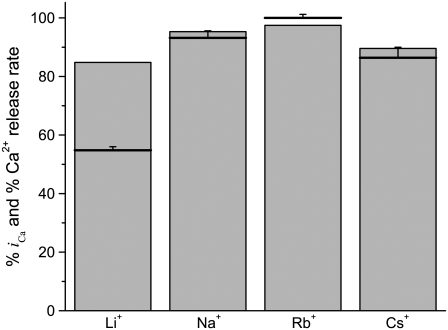
Substituting K⁺ for other monovalent cations

One prediction of the autocountercurrent idea is that any cation conducted by the open RyR channel can provide countercurrent. Fig. 7 (bars) shows that the permeation model predicts that Li⁺, Na⁺, Rb⁺, and Cs⁺ can all provide substantial countercurrent (relative to that provided by K⁺). The predictions shown in Fig. 7 use salt solutions used by Abramcheck and Best (16) in early Ca²⁺ release (i.e., initial rate of rise) studies in skinned fiber with different monovalent cations. The Abramcheck and Best (16) results are shown as bold horizontal lines in Fig. 7. Our predictions match very well with the Abramcheck and Best (16) results—except for the Li⁺ case. They reported that Ca²⁺ release rate in Li⁺ was reduced to 55%, not 85% as our permeation model predicts.

FIGURE 7.

Substituting K⁺ for other monovalent cations X⁺ = Li⁺, Na⁺, Rb⁺, and Cs⁺. The shaded bars show the percent i_Ca compared to when K⁺ is present, as computed by the PNP/DFT model at V_rev. The solutions contain symmetric 103 mM X⁺, 7 mM Na⁺, and 0.1 mM Mg²⁺; [Ca²⁺]_cytosol = 0.1 μM and [Ca²⁺]_lum = 1 mM. These are the same solutions used by Abramcheck and Best (16) for their 100% K⁺ substitution experiments. The Abramcheck and Best (16) measurements (percent of initial rate of rise of Ca²⁺ release) are shown as bold horizontal lines with error bars.

The skinned fiber studies assume open probability (P_o) of RyR is the same in each monovalent cation tested. However, ryanodine binding studies suggest this may not be true. Ryanodine binding is often used to assess RyR channel P_o since binding is nearly always proportional to P_o (65). Ryanodine binding (and presumably P_o) is substantially suppressed when Li⁺ is present compared to when K⁺, Na⁺, or Cs⁺ are present (66,67). Thus, the reduced Ca²⁺ release in skinned fibers observed by Abramcheck and Best (16) likely reflects a Li⁺-dependent P_o reduction rather than a reduction of countercurrent effectiveness.

Another prediction of the autocountercurrent idea is that Ca²⁺ release should be severely diminished if permeant counterions are replaced by an impermeant cation. Consistent with this, Abramcheck and Best (16) reported a substantial reduction in Ca²⁺ release when K⁺ was replaced by choline. However, they reported that 50% and 100% exchange of K⁺ for choline were equally effective. This is likely explained by slow choline permeation through open RyR channels (68) and occlusion of the pore. Our own pilot measurements of unit Ca²⁺ current in the presence and absence of choline are consistent with this notion (data not shown).

Possible role of other SR channels

If RyR is not the only channel providing countercurrent, then the stationary SR membrane potential is (by Eq. 4)

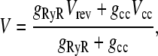(10)

where g_cc and V_cc are the other countercurrent channel's conductance and reversal potential, respectively. For both K⁺ and Cl⁻, V_cc is 0. The SR membrane potential V with another countercurrent channel present will be a fraction of V_rev. Because V_rev is already close to zero (∼−2 mV; Fig. 4) with only the RyR present, the contribution of another countercurrent channel is limited to 2 mV. For example, if g_cc = g_RyR = ∼200 pS, then the presence of g_cc would change SR membrane potential from −1.9 mV to ∼−1 mV. Even with a large countercurrent carried by another channel, there would still be significant and sufficient RyR autocountercurrent. That is, there is little gained by having another channel providing countercurrent. For every millivolt of SR membrane potential controlled by another high conductance channel, the Ca²⁺ current changes only ∼4% because of calcium's small conductance (see Fig. 5).

If RyR carries its own countercurrent, then what do the SR K⁺ and Cl⁻ channels do? A growing body of work suggests that these channels likely provide the counterion flux necessary for efficient SR Ca²⁺ uptake (69) and perhaps carry the countercurrent necessary to return SR potential to resting conditions after the RyR channels close. The SR of striated muscle is divided into two functionally/structurally distinct regions (70,71). The longitudinal SR contains few RyR channels but many SR Ca²⁺ pumps (i.e., SERCA). It could be that the countercurrent function of SR K⁺ and Cl⁻ channels is important in the longitudinal SR during Ca²⁺ uptake, which is slower and more dispersed than Ca²⁺ release. On the other hand, the fast, localized SR Ca²⁺ release requires fast, focal countercurrent—exactly what RyR autocountercurrent provides.

CONCLUSION

We propose that open RyR channels carry their own counterion flux. This follows directly from the equivalent circuit analysis which demonstrates that the stationary SR membrane potential must be between the RyR reversal potential and zero (Eq. 10 for V_cc = 0). Since the experimentally defined V_rev is already very close to zero (46) (see also Figs. 2 A and 4), significant autocountercurrent is inevitable given the poor selectivity of the RyR channel. This general result is independent of the PNP/DFT permeation model used here. Indeed, in many ways the model used here simply plays a pedagogical role by enabling the decomposition of the current into species components (Figs. 5 and 6).

We showed that SR membrane potential will change to E_Ca in <1 ms in the absence of countercurrent. Thus, any SR Ca²⁺ release event lasting >1 ms requires a counterion flux be present. This includes SR Ca²⁺ release observed in cells during prolonged voltage-clamp depolarizations which last >10 ms. It very likely includes the release underlying spontaneous Ca²⁺ sparks which have rise times lasting >5 ms. It may even include the very fast and brief Ca²⁺ release events stimulated by an action potential in mammalian skeletal muscle (rise times ∼1 ms). In fact, autocountercurrent may be essential to nearly any RyR-mediated SR Ca²⁺ release observed in a cell.

Since IP₃R and RyR channels have homologous pores and permeation characteristics, we predict this may also be true for IP₃R-mediated Ca²⁺ release as well. We would also predict that mutations in or near the RyR (and IP₃R) selectivity filter could be pathogenic if they alter the autocountercurrent process. In wild-type channels, we predict that the early rate of rise of Ca²⁺ transients and sparks should depend nonlinearly on ion composition and concentrations.

Lastly, it is possible that TRIC, K⁺, or Cl⁻ channels may contribute countercurrent during SR Ca²⁺ release, but their contribution is relatively small and perhaps not necessary. However, these other ion channels likely carry the required counterion flux during the SR Ca²⁺ uptake process.