Control of Transcriptional Variability by Overlapping Feed-Forward Regulatory Motifs

Abstract

In yeast, β-oxidation of fatty acids (FAs) takes place in the peroxisome, an organelle whose size and number are controlled in response to environmental cues. The expression of genes required for peroxisome assembly and function is controlled by a transcriptional regulatory network that is induced by FAs such as oleate. The core FA-responsive transcriptional network consists of carbon source-sensing transcription factors that regulate key target genes through an overlapping feed-forward network motif (OFFNM). However, a systems-level understanding of the function of this network architecture in regulating dynamic FA-induced gene expression is lacking. The specific role of the OFFNM in regulating the dynamic and cell-population transcriptional response to oleate was investigated using a kinetic model comprised of four core transcription factor genes (ADR1, OAF1, PIP2, and OAF3) and two reporter genes (CTA1 and POT1) that are indicative of peroxisome induction. Simulations of the model suggest that 1), the intrinsic Adr1p-driven feed-forward loop reduces the steady-state expression variability of target genes; 2), the parallel Oaf3p-driven inhibitory feed-forward loop modulates the dynamic response of target genes to a transiently varying oleate concentration; and 3), heterodimerization of Oaf1p and Pip2p does not appear to have a noise-reducing function in the context of oleate-dependent expression of target genes. The OFFNM is highly overrepresented in the yeast regulome, suggesting that the specific functions described for the OFFNM, or other properties of this motif, provide a selective advantage.

INTRODUCTION

Peroxisomes are highly dynamic and responsive eukaryotic organelles whose dysfunction is linked to a host of severe neuropathologies (1–9). Peroxisomes play roles in many metabolic processes (10), most notably the β-oxidation of fatty acids (FAs) (11). Accordingly, the peroxisome compartment is rapidly and dramatically induced in the presence of FAs. This induction is mediated at the level of transcription (12). In both animals and fungi, lipid-binding heterodimeric transcription factors (TFs) regulate cellular lipid levels by controlling the transcription of lipid metabolizing enzymes, many of which are localized to peroxisomes (3,5,13).

In the budding yeast Saccharomyces cerevisiae, peroxisomes are induced in response to oleic acid, and the transcription of many peroxisomal proteins and proteins required for assembly and growth of the organelle is controlled by oleate response elements (OREs) recognized by the FA-bound heterodimer Oaf1p-Pip2p (12–16). This heterodimer operates within the context of a feed-forward transcriptional network involving four core TFs: Adr1p, Oaf1p, Pip2p, and Oaf3p (17,18). The individual roles of Adr1p, Oaf1p, and Pip2p in regulating the expression of oleate-responsive genes are known (12), and recent work has established that Oaf3p is a transcriptional inhibitor with a significantly increased number of target genes when cells are grown in oleate-containing medium (17). Key oleate-responsive genes, such as the catalase CTA1, the peroxisomal lipase LPX1, and the TF PIP2, are regulated by all four TFs under oleate growth conditions (17). We refer to such genes as AOPY-regulated genes due to their regulation by Adr1p, Oaf1p, Pip2p, and Ykr064p (Oaf3p) (17). Although the combinatorial roles played by these factors in regulating oleate-responsive genes are known and the pathway-level structure of the transcriptional network has been mapped (17), little is known about the specific role of the feed-forward network architecture in regulating the transcriptional response to oleate. In a recent study of the heterogeneity of response in the yeast galactose transcriptional network, kinetic model simulations and experiments demonstrated that dual feedback loops in the galactose transcriptional network ensure a more homogeneous transcriptional response by filtering out molecular noise (19). Like the galactose network, the oleate-responsive transcriptional network is extremely sensitive (2) and possesses positive feedback, raising the question of how the transcriptional network prevents inappropriate proliferation of the organelle in response to transient exposure to FA. Mathematical studies have showed that feed-forward (20) and heterodimeric (21) transcriptional network motifs can reduce noise. These considerations led us to investigate whether the feed-forward, heterodimeric architecture of the oleate-responsive transcriptional network acts to reduce transcriptional noise. Using a kinetic model, we demonstrate that the Adr1p-driven feed-forward loop (FFL) reduces the steady-state variability of expression of oleate-responsive genes combinatorially regulated by these factors, and that the Oaf3p-driven inhibitory FFL modulates the transient variability of FA-responsive genes in the cell population.

MATERIALS AND METHODS

Computational methods

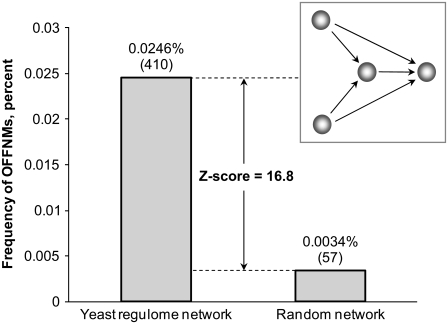
The ordinary differential equation (ODE) kinetic model equations were solved using the standard ODE solver of MATLAB (The MathWorks, Natick, MA). Model optimization was carried out using the constrained optimizers ga and fmincon in the MATLAB Genetic Algorithm, Direct Search, and Optimization Toolboxes. The undetermined model parameters (see the Supplementary Material, Data S1) were optimized to minimize the χ² for the model agreement with time-course and steady-state gene expression measurements (Table 4 in Data S1). The stochastic simulations were carried out using the chemical kinetics simulation software Dizzy (22), running in the Sun Java runtime environment version 1.4.2 on a 32-bit Intel Xeon processor system running CentOS 5 GNU/Linux. Network motifs were detected in the yeast regulome using the FANMOD software (23). For the random network generation (see Fig. 6), the following parameter values were used: number of networks = 1000, exchanges per edge = 3, and exchange attempts = 3 (23).

FIGURE 6.

OFFNMs are enriched in yeast regulome. Frequency of OFFNMs in the yeast regulome (extracted from the Yeast Proteome Database (33), see Fig. S1) and in random networks.

Experimental methods

The YOR084W-GFP (encoding Lpx1-GFP) and deletion strains are from the haploid GFP-clone and deletion collections, respectively (Invitrogen, Carlsbad, CA). Strains containing both a gene deletion and GFP tag were made by mating, sporulating, and dissecting tetrads. All strains used for flow cytometry are haploid spores otherwise isogenic to BY4742. For each strain, three individual yeast colonies were each seeded into 2 mL YEPD (1% yeast extract, 2% peptone, 2% glucose) and cultures were grown overnight at 30°C. Cells were washed with water and transferred to 2 mL YPBO (0.3% yeast extract, 0.5% potassium phosphate (pH 6.0), 0.5% peptone) 0.5% Tween 40 (w/v) and 0.15% (w/v) oleate) and grown for 48 h at 30°C to final densities of ∼1.5 × 10⁷ cells/mL. The cells were pelleted and resuspended in water, and fluorescence intensities of individual cells were measured using a FACSCaliber flow cytometer (BD Biosciences, San Jose, CA). For each culture, 20,000 events were counted with a flow rate of 100–600 cells/s and a forward scatter threshold of 25. Data analysis was done using WinMDI 2.9 (available from http://facs.scripps.edu). Cells were selected using a polygon gate region in the dot plot of forward scatter counts versus side scatter counts (to select viable, single-cell events for analysis). A second polygon gate region in the dot plot of forward scatter counts versus GFP fluorescence counts was used to eliminate uninduced cells from being included in the calculation of the coefficient of variation (CV) of Lpx1p-GFP expression, to obtain the most conservative possible estimate for the CV of Lpx1p-GFP expression in adr1Δ cells.

MODEL DEVELOPMENT AND RESULTS

FA-responsive gene regulatory network in Saccharomyces cerevisiae

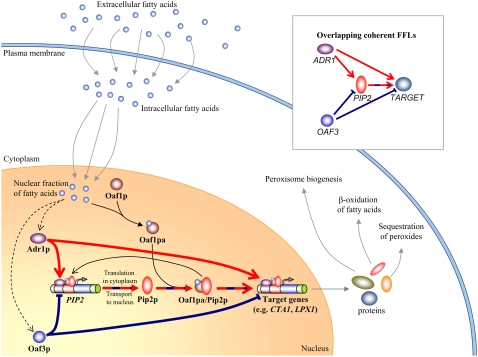
In response to the presence of FA, the four TFs (Oaf1p, Pip2p, Adr1p, and Oaf3p) regulate transcription of target genes through a transcriptional network characterized by an overlapping feed-forward network motif (OFFNM) (Fig. 1). Intracellular FA (oleate) binds Oaf1p, activating the TF. Oaf1p forms a heterodimer with Pip2p, and this heterodimer targets the ORE on promoter regions as a transcriptional activator. The promoter of the gene PIP2 contains an ORE, and thus PIP2 is transcriptionally autoregulated in the presence of oleate. Adr1p is rapidly activated in the presence of nonfermentable carbon sources (such as oleate), and binds UAS1 elements in the promoters of the target genes (e.g., PIP2, CTA1, and LPX1) (12). Adr1p therefore drives a coherent FFL (coherent type 1, in the classification scheme of Mangan and Alon (24)) involving PIP2 and targeting downstream target genes (e.g., CTA1 and LPX1) (Fig. 1, thick red lines). Oaf3p, which is a transcriptional inhibitor, also binds to the promoters of CTA1 and PIP2 under oleate growth conditions (17). Thus, Oaf3p drives a coherent inhibitory feed-forward network motif (coherent type 2, in the Mangan-Alon classification (24)) involving PIP2 and CTA1, as well as many other targets of Oaf1p, Pip2p, and Adr1p (Fig. 1, thick blue lines). The two FFLs share the regulatory cascade PIP2 → Pip2p → Oaf1p Pip2p → TARGET (where TARGET represents a typical target gene for this regulatory network, such as CTA1 or LPX1), and thus form an overlapping regulatory architecture.

FIGURE 1.

The yeast oleate-responsive transcriptional network contains an OFFNM. Lines terminating in open arrows and blunted lines represent transcriptional up- and down-regulation, respectively. Lines terminating in solid arrows indicate molecular processes such as transport, transcription/translation, and dimerization. Dotted black arrows indicate indirect carbon-source-dependent activation. Red and blue arrows and blunted lines represent the Adr1p- and Oaf3p-driven coherent feed-forward motifs, respectively. The alternating red/blue dashed line represents the overlapping region. The inset panel demonstrates schematically the OFFNM. Intracellular FA (oleate) binds Oaf1p, activating the TF. Active Oaf1p forms a heterodimer with Pip2p, and this heterodimer targets the ORE on DNA as a transcriptional activator. The promoter of the gene PIP2 contains an ORE, and thus PIP2 is transcriptionally autoregulated in the presence of oleate. Adr1p is rapidly activated in the presence of nonfermentable carbon sources and targets UAS1 elements in the promoters of the target genes PIP2 and CTA1. Adr1p therefore drives a coherent feed-forward network motif targeting PIP2 and CTA1 (thick red lines). Oaf3p is a transcriptional inhibitor whose target footprint (in terms of number of genes) is strongly increased under oleate growth conditions (17). It drives a coherent inhibitory feed-forward network motif targeting PIP2 and CTA1 (thick blue lines).

Mathematical model of the oleate-responsive transcriptional network

To investigate the functional roles of network structural elements in controlling the dynamic response to oleate, a mathematical model was developed that describes the response of the core oleate-inducible gene regulatory network in yeast under a carbon source transition from a nonfermentable carbon source (glycerol) to FA (oleate). A complete description of the mathematical model, including the values of all kinetic parameters and source material used for parameter estimation, is given in the Supplementary Material (Data S1). The model describes the transcriptional regulatory interactions governing peroxisomal protein production in response to intracellular oleic acid. The model incorporates the oleate-dependent expression and activity of four TF genes (ADR1, OAF1, PIP2, and OAF3), as well as the expression of two archetypical oleate-inducible target genes, CTA1 (Catalase A) and POT1 (3-ketoacyl-CoA thiolase, also known as FOX3), the products of which are peroxisomal and which are commonly used as transcriptional indicators of peroxisome induction (16,25,26). For each gene in the model, both the gene-specific mRNA and protein are represented by dynamical variables in a set of ODEs:

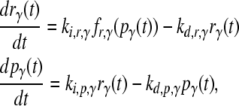(1)

where the index γ labels a gene, with possible values (a, c, o, y, p, f) mapping to genes as follows: a = ADR1, o = OAF1, p = PIP2, y = OAF3, c = CTA1, and f = POT1. The dynamical variables r_γ and p_γ represent the concentrations of mRNA and protein, respectively, for gene γ. The fractional transcriptional activity of each gene γ is modeled using a rational function f_r,γ involving the protein concentrations of the relevant transcriptional regulators of the gene. The rate of initiation of transcription of gene γ is given by the product of this fractional activity and the rate constant k_i,r,γ. The rate of initiation of translation is given by the product of the rate constant k_i,p,γ and the concentration of the mRNA. The constants k_d,r,γ and k_d,p,γ are the degradation rate constants for the mRNA and protein of gene γ, respectively. The transport of FA across the plasma membrane and subsequent esterification with coenzyme A (CoA) are modeled using an ODE for intracellular oleate, O_ic, based on the following assumptions: 1), the rate of transport of FA across the plasma membrane is a hyperbolic saturating function of extracellular oleate concentration; and 2), the rate of fatty acyl-CoA synthesis is of the Michaelis-Menten form (see Data S1 for details).

Direct and indirect activation of TFs by oleate

In the model, the activity levels of the TFs Oaf1p, Oaf3p, and Adr1p are altered by the presence or absence of intracellular FA, consistent with the literature (12,13,17). The molecular interactions underlying activation of Oaf1p, Adr1p, and Oaf3p are assumed to occur rapidly, so the rates of activation and deactivation are at quasi-steady state (27) with respect to the slowly varying total concentrations of these TFs, and with respect to the time-varying concentration of intracellular oleate. In each of these three cases, activation of the TF is modeled phenomenologically using a Michaelis-Menten-type function of intracellular oleate concentration. For example, oleate binding-dependent activation of Oaf1p is modeled using the equation:

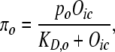(2)

where π_o is the concentration of activated Oaf1p, and K_D,0 is the equilibrium dissociation constant for Oaf1p protein activation by oleate. The corresponding equation for modeling the concentration of activated Oaf3p (π_y) is given in Data S1. In the case of Adr1p, the TF is active in glycerol-growth conditions, but in oleate-growth conditions it has increased DNA-binding activity for oleate-responsive genes (17). The concentration of activated Adr1p in oleate-growth conditions was modeled using a sum of a constitutive activity level and a Michaelis-Menten-type function of O_ic:

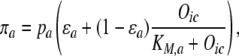(3)

where π_a is the concentration of activated Adr1p; ɛ_a is a constitutive fractional activity of Adr1p protein, and K_M,a is the equilibrium dissociation constant for Adr1p activation in the presence of oleate.

Heterodimerization of activated Oaf1p with Pip2p

The reactions for binding and dissociation of the Oaf1p-Pip2p heterodimer are assumed to be in quasi-steady state with respect to the time-varying concentrations of total activated Oaf1p and total Pip2p. Thus, the concentration of Oaf1p-Pip2p heterodimer h is given by

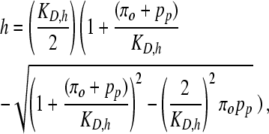(4)

where p_p is the total concentration of Pip2p, and K_D,h is the dissociation constant.

Fractional gene activity

For each gene, the fractional transcriptional activity was modeled using a rational function involving the concentrations of the transcriptional regulators of that gene. As an example, the fractional transcriptional activity of PIP2 was modeled as a function of h, π_a, and π_y:

(5)

where ɛ_p is the constitutive term in the fractional activity of PIP2; A_p is the activation constant for PIP2 induction; q represents the cooperativity of Adr1p and Oaf1p-Pip2p binding to the promoter region; and K_h, K_a, and K_y are equilibrium constants for Oaf1p-Pip2p, Adr1p, and Oaf3p, respectively, binding to their corresponding cis-regulatory elements in the promoter. The fractional transcriptional activity functions for OAF1, PIP2, ADR1, OAF3, and POT1 were similarly constructed based on available information from the literature regarding their carbon source-dependent and TF-dependent transcriptional activities; the specific functional forms are given in Data S1.

Comparison of model simulations with experimental data

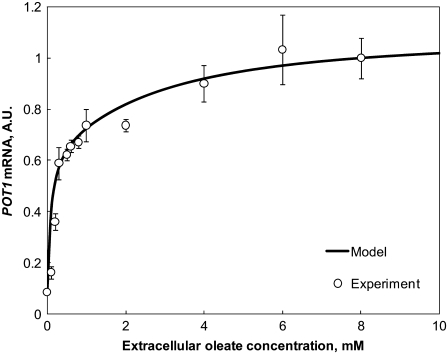
The kinetic parameters of the model were obtained from the literature or directly estimated from steady-state and wild-type (WT) time-course expression data for the four core TFs and the target genes POT1 and CTA1 (6,17) (see Data S1). The remaining 14 undetermined kinetic parameters were varied to minimize the model error for recapitulating time-course (6) and dose-response (13) expression measurements in WT yeast and in deletion strains for the four core TFs (see Data S1). The dose-response for POT1 induction under varying concentrations of oleate (Fig. 2) shows agreement between model and experiment for oleate concentrations varying over two orders of magnitude. Simulated and measured time-course transcript abundance ratios under a carbon source switch from glycerol to oleate are shown in Data S1. The optimized model reproduced both the measured dynamic and steady-state responses, with the exception of a transient effect at 9 h in the time-course data. To further assess the model, each of the 14 undetermined parameters was varied eightfold up and down relative to the value in the best-fit model to determine the sensitivity of the model prediction error to the individual parameter values. The model prediction error increased strongly over the range of alternative parameter values explored for 13 of the 14 parameters (Fig. S1 of the Supplementary Material). These findings suggest that the available number and diversity of measurements used for model training are adequate to discern the best-fit model in the space of these parameter values. Varying the remaining parameter (K_M,s, see Data S1) up or down twofold from the value in the best-fit model did not alter the main findings discussed below. Furthermore, a quantitative analysis of model complexity indicates that the model is not overfitted (Data S1).

FIGURE 2.

The model recapitulates the measured relative dose response for POT1 expression. Data points indicate the activity of a luciferase reporter gene with the POT1 promoter in yeast cells grown overnight in media with oleate at the indicated initial concentration (13). The predicted POT1 expression levels from the model (line plot) have been normalized relative to the luciferase activity in 8 mM oleate.

To investigate the possibility that the overlapping feed-forward network architecture serves to regulate the variability of downstream target gene expression by reducing the strength of molecular noise, the ODE-based kinetic model was translated into a stochastic model in which the dynamics of the transcriptional network within each cell are modeled as a stochastic process. Formally, the dynamics of the stochastic process are governed by a chemical master equation that can be obtained from the ODE kinetic model as described by Gillespie (28). A simplified stochastic model was defined using the quasi-steady-state approximation (QSSA)-based Rao-Arkin method to model the stochastic reaction propensity for reaction channels that are not governed by simple mass-action kinetics (29), consistent with previous experimentally validated models of transcriptional regulation (19,30,31). The stochastic dynamics were solved using Monte Carlo simulations based on the Gibson-Bruck algorithm (32). The resulting ensemble-averaged stochastic dynamics are consistent with the deterministic ODE-based kinetic model, and allow the estimation of the contribution of molecular noise to the steady-state distribution of target gene expression.

Adr1p-driven FFL reduces variability of oleate-responsive gene expression

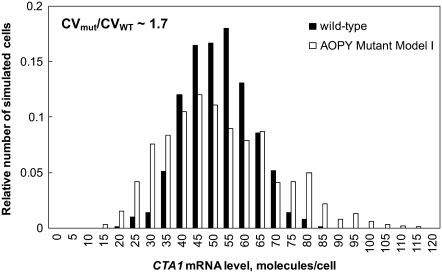
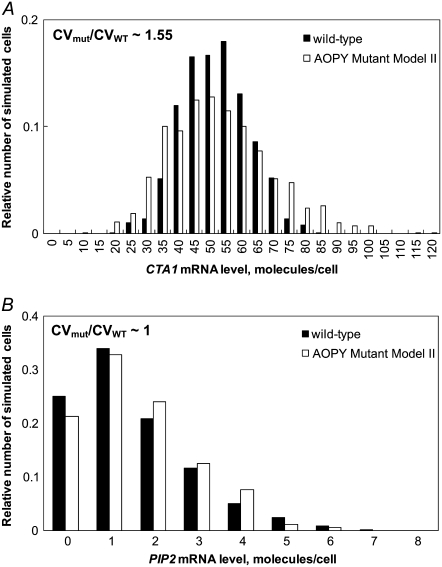
In silico modeling was used to investigate the role of Adr1p in regulating the dynamics and cell population distribution of expression of a gene activated by both an ORE (Oaf1p-Pip2p) and Adr1p, i.e., CTA1. The model was modified to simulate a hypothetical mutant strain (AOPY Mutant Model I) in which CTA1 is fully inducible on oleate by Oaf1p-Pip2p alone, and is not directly regulated by Adr1p, thus eliminating Adr1p-driven feed-forward regulation of CTA1 (Fig. 1, red lines). In the mutant model, the activating effect of the ORE was increased so that CTA1 would have comparable oleate dose-responses in the mutant and WT models. To quantify the cell population heterogeneity of expression of CTA1 on oleate in the two models, the steady-state stochastic dynamics in both models were simulated for 100 min. The simulations revealed that at steady state, the histogram of CTA1 transcript levels showed a broader distribution in the mutant model than in the WT model (Fig. 3), indicating greater heterogeneity of gene expression across the stochastic ensemble. The CV of CTA1 transcript levels was 1.7-fold higher in the mutant model than in the WT model. To investigate the transcriptional heterogeneity for the case in which Adr1p regulates neither PIP2 nor downstream targets, but these genes fully induce on oleate, an alternate version of the model (AOPY Mutant Model II) was constructed that represents a mutant in which both PIP2 and CTA1 are regulated only via the ORE (corresponding to an adr1Δ strain with elevated ORE-binding affinity). Stochastic simulations of this model also showed a more broadly distributed histogram of expression of CTA1 (ratio of CVs = 1.55) in the mutant than in the WT; this effect was not observed for PIP2 (Fig. 4). The steady-state variability of CTA1 expression was also studied using stochastic simulations of two other mutant models (AOPY Mutant Models III and IV, consisting of the deletions oaf3Δ and adr1Δoaf3Δ, respectively, with compensation in the ORE-binding affinity to allow full induction). The CTA1 variability was 1.44-fold higher in the adr1Δoaf3Δ model than in the WT model, whereas the ratio of the variability between the oaf3Δ model and the WT model was only 1.18 (Fig. S2).

FIGURE 3.

An in silico model of a mutant strain in which CTA1 is solely ORE-activated (AOPY Mutant Model I) is predicted to have greater variability of CTA1 expression than the WT model. The histogram shows the simulated population heterogeneity of reporter expression (CTA1 mRNA level) in WT (black bars) and mutant strain (in which Adr1p does not regulate CTA1) (white bars) in oleate growth conditions. The abscissa is the CTA1 mRNA concentration after 100 min of stochastic simulation with initial conditions given by species concentrations obtained from the steady-state solution to the ODE kinetic model with constant 0.12% (w/v) oleate. Stochastic simulations were carried out for an ensemble of 1000 realizations of the stochastic process. CV_mut represents the steady-state CV of reporter expression levels for the AOPY Mutant Model I, and CV_WT represents the CV in the WT model.

FIGURE 4.

An in silico model of a mutant strain in which both PIP2 and CTA1 are solely ORE-activated (AOPY Mutant Model II, corresponding to an adr1Δ strain with the ability to fully induce ORE-driven expression) is predicted to have greater variability of CTA1, but not PIP2 expression, than the WT model. The histograms show the simulated population heterogeneity of (A) CTA1 and (B) PIP2 mRNA levels in WT (black bars) and a mutant adr1Δ strain in which PIP2 and CTA1 have increased ORE-driven transcriptional activity (white bars) in oleate growth conditions. The abscissas represent the distribution of the (A) CTA1 and (B) PIP2 mRNA concentrations after 100 min of stochastic simulation with initial conditions given by the steady-state solution to the ODE kinetic model with constant 0.12% oleate. Stochastic simulations were carried out for an ensemble of 1000 realizations of the stochastic process. CV_mut represents the steady-state CV of expression levels of the indicated reporter in AOPY Mutant Model II, and CV_WT represents the CV of the indicated reporter in the WT model.

To investigate the model prediction that Adr1p-initiated feed-forward regulation can serve as a noise reducer, the variability of expression of an AOPY target gene, LPX1 (17), was tested experimentally. LPX1 (YOR084W) is highly induced in response to oleate, and the protein product is peroxisomal (6). The abundance of a chimera of Lpx1p and green fluorescent protein (GFP) reporter (Lpx1-GFP) was measured in WT and adr1Δ yeast strains in the presence of oleate using flow cytometry (see Materials and Methods). Consistent with simulation results, the CV of Lpx1-GFP in adr1Δ cells was 1.8-fold higher than in WT cells (Fig. S3).

Oaf3p acts to modulate transcriptional changes in a fluctuating environment

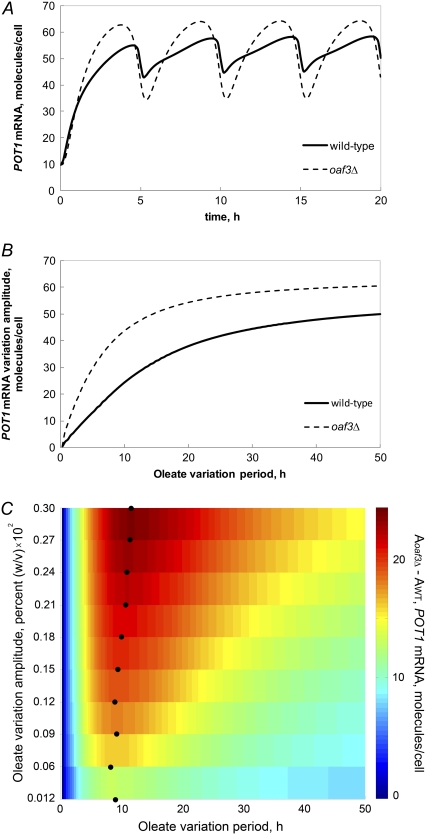
Next, the mathematical model was used to investigate whether the feed-forward inhibitor, Oaf3p, acts to buffer the induced genetic switch against variations in the level of intracellular FA. ORE-driven gene (POT1) expression kinetics were simulated in the WT and oaf3Δ model strains exposed to a sinusoidal oscillating oleic acid concentration. For the mutant strain, the amplitude of oleate oscillation was decreased so that POT1 would have comparable oleate dose-response to the WT. The kinetic model predicts that the transcriptional repressor Oaf3p modulates the amplitude of variation of expression levels of ORE-driven genes in a fluctuating environment. The results (Fig. 5 A) showed larger-amplitude variations in POT1 expression in the oaf3Δ model than in the WT model, indicating that in the model, the loss of Oaf3p impaired the ability of the genetic switch to compensate for transient oleate oscillations. The ability of the network to compensate for transient oleate oscillations was also examined in two other mutant models, adr1Δ and adr1Δoaf3Δ. Comparing the time course of POT1 expression levels across all four models (WT, oaf3Δ, adr1Δ, and adr1Δoaf3Δ) revealed that the smallest-amplitude POT1 oscillations occurred in the WT and adr1Δ models, and the largest-amplitude oscillations occurred in the oaf3Δ and adr1Δoaf3Δ models (Fig. S4). Additionally, the most rapid transient induction from the noninduced state occurred in the adr1Δoaf3Δ model.

FIGURE 5.

Deletion of Oaf3p in the model makes POT1 transcriptional activity undergo larger-amplitude oscillations in response to a temporally varying concentration of intracellular FA. WT and oaf3Δ models of POT1 transcription were solved for the case of a temporally oscillating concentration of oleate. (A) POT1 undergoes higher-amplitude oscillations in the oaf3Δ model than in the WT model. (B) The difference between POT1 mRNA variation amplitudes in the oaf3Δ model and WT increases with increasing period of oleate pulsing. When the period exceeds 10 h, the difference between the oaf3Δ model and WT model amplitudes starts to decrease. (C) The difference between the POT1 mRNA variation amplitudes in the oaf3Δ (A_oaf3Δ) and WT (A_WT) models, for different values of the period and amplitude of oleate concentration oscillation. Color indicates the POT1 amplitude difference between the oaf3Δ model and the WT model. Overall, the difference between the amplitude of POT1 variation in the two models is stronger at higher values of the oleate oscillation amplitude. Furthermore, as the oleate oscillation amplitude increases, the maximum POT1 amplitude difference (dark red) is observed at slightly increasing values of the oleate oscillation period (black circles).

The dependence of POT1 expression amplitudes (in the oaf3Δ and WT models) was also systematically explored on the timescale and the amplitude for varying the oleate concentration. The model simulations showed that the POT1 amplitude difference between the oaf3Δ model and the WT model increased with decreasing frequency of an oleate pulse (Fig. 5 B), indicating that the oaf3Δ strain is less able than the WT to filter out oleate variations on a timescale of >40 min (Fig. 5 B). Varying both the amplitude and period of the oleate concentration oscillations revealed a nonlinear relationship between amplitude and period. The maximal differences between oaf3Δ and WT strains slightly shifted toward greater period as the amplitude increased (black circles, Fig. 5 C), suggesting a complex mechanism for modulating role of Oaf3p on target gene expression under fluctuating oleate environments.

The OFFNM network architecture occurs frequently in the yeast regulome

To determine whether the oleate-responsive transcriptional network architecture consisting of the OFFNM is commonly found in the yeast regulome, a network representing 3515 gene regulatory interactions extracted from the literature-based Yeast Proteome Database (33) was analyzed. The OFFNM was found to be highly overrepresented in the yeast regulome (Fig. S5). In the yeast regulatory interaction network, there were 410 instances of OFFNMs and 25 instances of overlapping coherent FFLs of the specific subtype represented in the yeast oleate-responsive transcriptional network (i.e., overlapping coherent type 1 and 2 FFLs) (Fig. S6). The frequency of OFFNM motif in the yeast regulome is thus almost 10-fold higher than in random networks generated from random edge reassignment of the network (Fig. 6).

DISCUSSION

Here we present for the first time, to our knowledge, a detailed kinetic model of the core FA-responsive transcriptional network in yeast. A key structural motif in this network that has not been previously studied using mathematical modeling is an overlapping pair of FFLs driven by Adr1p and Oaf3p, respectively (see Fig. 1, inset). We refer to this network architecture as the OFFNM. Simulations of the model suggest two functional roles of this network motif. First, the Adr1p-driven FFL reduces the steady-state expression variability of an ORE- and Adr1p-driven target gene. Second, the Oaf3p-driven inhibitory FFL modulates the dynamic response of the target gene to a transiently varying concentration of intracellular FA.

Simulations of the kinetic model in the absence of Adr1p (AOPY Mutant Model I) revealed significantly higher target gene expression than the corresponding WT strain with an intact FFL. In the Mutant Model I, the target gene induction is driven entirely by Oaf1p-Pip2p, whereas in the WT, the target gene induction is driven by the combined effect of two factors (Adr1p and Oaf1p-Pip2p). We speculate that acting alone, Oaf1p-Pip2p-mediated expression is noisy because PIP2 mRNA has a high level of fluctuations in the model (as defined by the steady-state CV), and this variability is presumably due to the low copy number of PIP2 mRNA (see Data S1) and the fact that PIP2 is positively autoregulated. Previous studies have established that a low copy number of a gene's mRNA (34,35) and positive autoregulation of a gene (36) can both contribute to variations in the protein level, and, in the case of a TF, to increased variability of expression of downstream gene targets (extrinsic noise) (37). In the presence of Adr1p, this noise is expected to be buffered because of its direct regulatory influence on the target gene, which increases AOPY gene expression, thereby decreasing the relative variation in expression from the target. Furthermore, the lack of a significant effect of oaf3Δ on target gene stochastic variation suggests that, at steady state, the Adr1p-driven FFL is primarily responsible for reducing stochastic fluctuations in the expression of target genes. We note that although PIP2 is a target of Adr1p, its low level of expression leads to Pip2p variation likely having a high proportion of intrinsic noise (34,35,38,39), whereas highly expressed AOPY targets are dominated by extrinsic noise (e.g., by fluctuating levels of Pip2p).

The hypothesis that the Adr1p-containing FFL reduces (extrinsic) noise was tested experimentally by comparing the cell population heterogeneity of expression of the oleate-inducible lipase Lpx1p (a known target of all four TFs) in WT and adr1Δ cells in oleate growth conditions, and a higher level of dimensionless variability (1.8-fold) was observed in adr1Δ cells than in WT cells.

The Oaf3p effect in modulating the gene expression response is likely due to the rapid response of Oaf3p activation to a changing oleate concentration, relative to the slower response of the positively autoregulated Pip2p. Previous studies have established that positive autoregulation leads to a slower response (40), whereas the activation of Oaf3p is presumed to occur through rapid molecular interactions and not through transcriptional regulation. We did not observe a strong effect of deletion of Adr1p on the ability of the network to compensate for a dynamically varying oleate level. Although previous modeling studies have suggested that dimerization of a TF can reduce transcriptional variability of its target (21,41,42), we did not observe a significant noise reduction associated with heterodimerization of Oaf1p-Pip2p in the context of our model of the core network (results not shown). Since Oaf1p in the absence of Pip2p appears to be a transcriptional repressor (17), perhaps the role of heterodimerization in this network is instead to provide a carbon-source-dependent, inducible mechanism to inhibit the transrepressive activity of Oaf1p. From the results of the network motif frequency analysis of the OFFNM in the yeast regulome, it appears that this network structure is frequently used in yeast transcriptional regulation, suggesting that the specific functions described for the OFFNM provide cells with a selective advantage.