Abstract
The transmembrane (TM) domain of the M2 channel protein from influenza A is a homotetrameric bundle of α-helices and provides a model system for computational approaches to self-assembly of membrane proteins. Coarse-grained molecular dynamics (CG-MD) simulations have been used to explore partitioning into a membrane of M2 TM helices during bilayer self-assembly from lipids. CG-MD is also used to explore tetramerization of preinserted M2 TM helices. The M2 helix monomer adopts a membrane spanning orientation in a lipid (DPPC) bilayer. Multiple extended CG-MD simulations (5 × 5 μs) were used to study the tetramerization of inserted M2 helices. The resultant tetramers were evaluated in terms of the most populated conformations and the dynamics of their interconversion. This analysis reveals that the M2 tetramer has 2× rotationally symmetrical packing of the helices. The helices form a left-handed bundle, with a helix tilt angle of ∼16°. The M2 helix bundle generated by CG-MD was converted to an atomistic model. Simulations of this model reveal that the bundle's stability depends on the assumed protonation state of the H37 side chains. These simulations alongside comparison with recent x-ray (3BKD) and NMR (2RLF) structures of the M2 bundle suggest that the model yielded by CG-MD may correspond to a closed state of the channel.
INTRODUCTION
Membrane proteins comprise ∼25% of most genomes, and in humans are a major target for drugs (1,2). Yet of the ∼47,000 structures deposited in the Protein Data Bank (3), only ∼300 are for membrane proteins, corresponding to <150 unique structures (http://blanco.biomol.uci.edu/Membrane_Proteins_xtal.html). Thus, despite the progress made in determining membrane protein structures (4), it is of some importance to develop methods that enable prediction of membrane protein structures either ab initio or as an adjunct to methods for determining low-resolution structures (5).
Models of membrane protein folding suggest that it may occur via two major stages (6–9). First, upon insertion into the bilayer, the polypeptide forms independently stable transmembrane (TM) α-helices. Second, these TM helices subsequently pack together to form the tertiary structure of the protein. Subsequent to and/or in parallel with the initial insertion phase, TM helices can start to seek out their most stable native conformations. This search for the native protein conformation may include the reorientation of the helices from their original insertion positions to alignments that will lead to the most stable packing arrangement of the helices. This search may itself proceed via several steps. For example, bacteriorhodopsin has several folding intermediates (10), and indeed there may exist multiple folding pathways leading to the native structure (11), consistent with the more general concept of protein folding on a funnel-shaped energy landscape (12).
Recent studies with small water-soluble proteins suggest that molecular dynamics (MD) and Monte Carlo simulations can be used to explore aspects of protein folding (13). For example, simulation folding studies on small soluble peptides, e.g., Trpcage (14,15), yielded predicted structures with an accuracy close to that of NMR. However, Trpcage folds in ∼10 ns, whereas the folding and assembly of small membrane peptides occurs on the microsecond timescale (16), i.e., beyond the range of most atomistic MD simulations of membrane systems (17–19). However, coarse-grained (CG) approaches, in which small groups of atoms are treated as single particles, allow one to expand the length of MD simulations of membranes to tens of microseconds (20–30). Recent works have adapted CG lipid models for use with proteins (27,28,31–33), and demonstrated that CG-MD may be used to simulate, e.g., the self-assembly of TM helix dimers of the simple model membrane protein glycophorin A (31) and the folding of a TM α-helical hairpin (28).
The M2 channel protein from influenza A virus (Fig. 1) provides a good test case for modeling studies of simple membrane proteins (34,35). It is a 97-residue protein containing a single TM α-helix. The protein exists as a tetramer, with the ion channel formed by a parallel bundle of four TM helices. M2 has been the subject of extensive experimental (36–58) and computational (59–65) studies in the past few years. In particular, it has been used in simulations based on an implicit membrane and solvation model to study folding/self-assembly of the TM helix tetramer (64,65). It therefore provides a well-documented test case for analysis of TM helix bundle self-assembly and dynamics using CG-MD. Furthermore, two recent structures of the M2 TM helix tetramer, as revealed by x-ray crystallography in the presence of detergent (octyl glucoside) (66) and by NMR in detergent (DHPC) micelles (67), enable the model structures to be compared with those determined experimentally, albeit in different environments.
FIGURE 1.
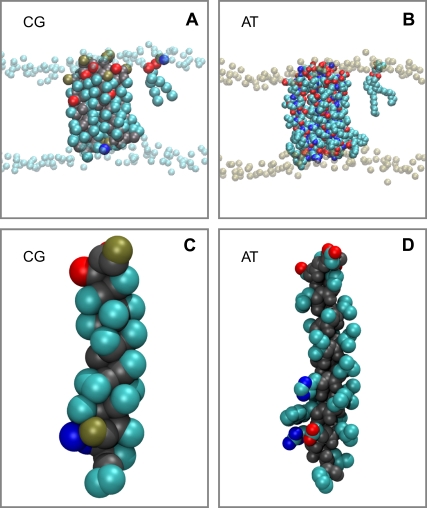
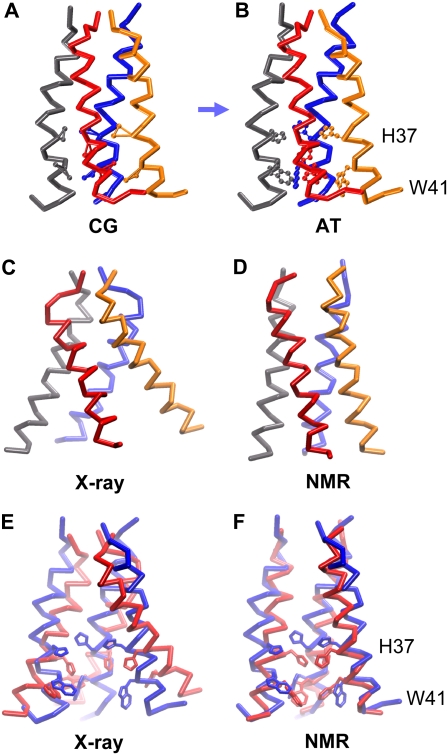
CG (A) and atomistic (B) systems, with the M2 tetramer, one DPPC lipid molecule, and the phosphate particles/atoms of the remaining DPPC molecules represented. Colors for the atoms: cyan, carbon; red, oxygen; blue, nitrogen; and bronze, phosphorous. Colors for CG particles: cyan, apolar; red, polar; blue, positively charged; and bronze, negatively charged. The CG (C) and atomistic (D) single M2 helices are shown using the same color schemes, although the atomistic backbone has been colored gray for clarity.
In this study, CG-MD simulations are used to study the partitioning of isolated TM helices into a lipid bilayer during self-assembly of a bilayer. CG-MD is also used to explore the self-assembly of a tetrameric bundle of M2 TM helices in a bilayer, and the conformational dynamics of the resultant helix bundle. The resultant M2 bundle model is converted from CG to atomistic (AT) form and shown to be stable in ∼15 ns duration simulations in an atomistic lipid bilayer.
METHODS
M2 TM helix and bilayer models
A 27-mer peptide (residues D21SSDPLVVAASIIGILHLILWILDRLF47) was used to model the TM region of M2 plus several residues on either side (68). This region was chosen on the basis of experimental evidence (69,70) in combination with results of a TM helix prediction server (71). Modeller v7.7 (72–74) was used create a structure with an α-helical region for the proposed TM domain (residues 22–46) with an additional residue at either end in a random coil conformation. This atomistic model was converted to CG using the protocol described previously (31). The result was a monomer 27 amino acids in length, with the central 25 amino acids held together in a comparatively rigid α-helical structure. Since the CG backbone particles cannot form hydrogen bonds, harmonic restraints were used to maintain the α-helical conformation.
To simulate bilayer formation and partitioning of a single TM helix into the membrane, a simulation box (of dimensions 100 × 100 × 100 Å3) containing the CG α-helical peptide was filled with 256 randomly placed and orientated CG dipalmitoylphosphatidylcholine (DPPC) lipids, ∼3000 CG water particles, and four CG Na+ ions. This primary simulation resulted in a stable membrane-spanning M2 TM helix (see Fig. 2). This monomeric helix was replicated to produce four monomers of similar orientation, which were inserted into a preformed and equilibrated CG DPPC bilayer, ∼45 Å apart from one another. This system was the basis of five subsequent tetramer simulations, each of 5 μs duration.
FIGURE 2.
Snapshots of the system during the bilayer-forming simulation, showing the helix partitioning into the bilayer as it forms (water particles omitted for clarity). The helix partitions into the arranging lipids that form a stable bilayer after ∼23 ns. This bilayer remains intact (and the helix continues to span the bilayer) for the remainder of the simulation.
CG simulation parameters and protocols
All simulations were performed using GROMACS (www.gromacs.org) (75,76). CG simulations were performed as described by Bond and Sansom (31). The CG parameters for lipids (DPPC), ions, and water molecules were as described by Marrink et al. (21). The CG parameters for amino acids were a modified version of that described by Bond and Sansom (31), and the same as that described by Bond et al. (28) and Bond and Sansom (32). Briefly, a CG peptide model was generated from the atomistic model, yielding a chain of backbone particles with attached side-chain particles. Interparticle bond potentials used a force constant of 50 kJ mol−1Å−2. The equilibrium bond length was 3.6 Å for the backbone particles. Different amino acids had different equilibrium bond length(s) for their side-chain particle(s). Harmonic restraints were applied between backbone particles to mimic secondary structure H-bonds in the atomistic structure. The target distance was 6 Å, with a force constant of 10 kJ mol−1 Å−2.
For all CG simulations, Lennard-Jones interactions were smoothly shifted to zero between 9 Å and 12 Å, and electrostatics were smoothly shifted to zero between 0 Å and 12 Å, with a relative dielectric constant of 20 used for explicit screening. The nonbonded neighbor list was updated every 10 steps. All simulations were performed at constant temperature, pressure, and number of particles. The temperatures of the protein, DPPC, and solvent were each coupled separately using the Berendsen algorithm (77) at 323 K, with a coupling constant τT = 1 ps. The system pressure was anisotropically coupled using the Berendsen algorithm at 1 bar with a coupling constant τP = 1 ps and a compressibility of 5 × 10−6 bar−1. The time step for integration was 40 fs, and coordinates were saved every 400 ps for subsequent analysis. Analyses were performed using GROMACS tools and locally written code. Visualization used VMD (78).
Atomistic simulations
Atomistic simulations used an extended united atom version of the GROMOS96 force field (79,80). All energy minimizations used <1000 steps of steepest descents to relax any steric conflicts generated during setup. Long-range electrostatic interactions were treated using the particle mesh Ewald method (81) with a 10 Å cutoff for the real space calculation. A 10 Å cutoff was used for the van der Waals interactions. All simulations were performed in the constant number of particles, pressure, and temperature (NPT) ensemble. The temperatures of the protein, lipids, water, and ions were coupled separately using the Berendsen thermostat (77) at 323 K with a coupling constant τT = 0.1 ps. The pressure was coupled semiisotropically using the Berendsen barostat at 1 bar with coupling constant τP = 1 ps. The time step for integration was 2 fs. The LINCS algorithm (82) was used to restrain bond lengths.
General analysis
Simulation results were analyzed using GROMACS tools and locally written code. The clustering of tetramer structures was carried out using NMRclust (83). Secondary structure analyses used DSSP (84). Pores within the helical bundle were analyzed and visualized using HOLE (85). Visualization used VMD (78).
RESULTS
M2 helix partitioning into a lipid bilayer
The initial set of simulations (CG-M1 to CG-M10) consisted of self-assembly simulations starting from a box of randomly positioned lipids plus a single 27-mer M2-TM peptide in an α-helical conformation (Table 1). The aim of the simulation was to test the assumption of a preferred TM orientation of the M2 peptides. For 90% of the simulation time, as the lipids self-assemble into a bilayer, the peptide helix partitions into the bilayer and remains spanning it (Fig. 2). This occurs after an average of ∼25 ns, after which time both the bilayer and membrane-spanning helix remain stable throughout the remainder of the simulation. It should be noted that the dynamics of CG simulations may be faster than that of a corresponding AT simulation, with a 3–6-fold speed-up factor depending on the molecules in question (21). Thus from 75 to 150 ns of “atomistic time” was needed for bilayer/helix self-assembly. This is comparable to the estimate of 50–100 ns obtained from earlier atomistic simulations, albeit on a smaller system (86).
TABLE 1.
| Simulation | Setup | Duration (ns) |
|---|---|---|
| CG-M1 to CG-M10 | 27-mer M2-TM peptide, 256 DPPCs, ∼3000 water particles, 4 Na+ ion particles | 10 × 1000 |
| CG-T1 to CG-T5 | 4 × 27-mer M2-TM peptides, preequilibrated bilayer (195 DPPCs), ∼3000 water particles, 16 Na+ ion particles | 5 × 5000 |
| CG-T6 | 4 × 27-mer M2-TM peptides (randomly orientated) in a preequilibrated bilayer (196 DPPCs), ∼3000 water particles, 16 Na+ particles | 5000 |
| CG-T+ | 3 × 27-mer M2-TM peptide with neutral H37, 1 × 27-mer M2-TM peptide with positive H37, preequilibrated bilayer (195 DPPCs), ∼3000 water particles, 14 Na+ particles | 5000 |
| CG-T2+ | 2 × 27-mer M2-TM peptide with neutral H37, 2 × 27-mer M2-TM peptide with positive H37, preequilibrated bilayer (195 DPPCs), ∼3000 water particles, 12 Na+ particles | 5000 |
| CG-T3+ | 1 × 27-mer M2-TM peptide with neutral H37, 3 × 27-mer M2-TM peptide with positive H37, preequilibrated bilayer (195 DPPCs), ∼3000 water particles, 10 Na+ particles | 5000 |
| CG-T4+ | 4 × 27-mer M2-TM peptide with positive H37, preequilibrated bilayer (195 DPPCs), ∼3000 water particles, 8 Na+ particles | 5000 |
| AT-T0 | 4 × 27-mer M2-TM peptides, preequilibrated bilayer (195 DPPCs), ∼8000 water molecules, 8 Na+ ions | 15 |
| AT-T4+ | 4 × 27-mer M2-TM peptides, preequilibrated bilayer (195 DPPCs), ∼8000 water molecules, 4 Na+ ions | 15 |
| CG-x-ray | 4 × 25-mer (x-ray-to-CG*), preequilibrated bilayer (203 DPPCs), ∼3000 water molecules, 8 Na+ ions | 500 |
| CG-D4 | 4 × 25-mer (AT model-to-CG†), preequilibrated bilayer (203 DPPCs), ∼3000 water molecules, 8 Na+ ions | 2000 |
For this simulation, the crystal structure was converted into a CG model.
For this simulation, the D4 model adapted from the crystal structure was converted into a CG model.
The tilt angle of the helix in the TM orientation simulations relative to the bilayer normal (i.e., the z axis) has an average of 16° (±7°). The N-terminal of the M2 TM helix contains several charged and polar residues (D21, S22, S23, and D24), whereas the C-terminal contains both charged and aromatic residues (R45 and F47). These residues interact with the lipid headgroups and appear to act as anchors of the helix in the membrane.
Thus, this relatively simple CG-MD simulation is consistent with both experimental studies (36,87) and implicit bilayer simulations (64,88) indicating that the M2-TM helix adopts a membrane-spanning orientation.
M2 TM helix tetramerization
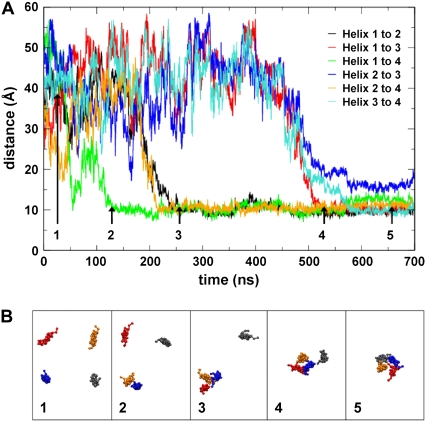
Five independent self-assembly simulations of the influenza M2 tetramer (CG-T1 to CG-T5; see Table 1), each of duration 5 μs, were performed, starting from four isolated M2-TM helices inserted in a parallel fashion and similar orientation (at an interhelix separation of ∼45 Å) in a preformed DPPC bilayer. Thus, this simulation mimics the second stage of membrane protein folding, i.e., oligomerization and packing together of the helices. The formation of helix bundles was assessed by monitoring the distances between the centers of mass of the Cα particles of the various pairwise combinations of helices as a function of time (Fig. 3).
FIGURE 3.
Distances between the centers of mass of the helices as they aggregate together into a tetramer (A), and snapshots of the positions of the helices (B) as tetramerization takes place. Helix 1, blue; helix 2, red; helix 3, gray; and helix 4, orange. This indicates that helices 1 and 4 form a dimer after ∼120 ns, which becomes a trimer (with helix 2) ∼100 ns later. A four-helix aggregate is formed after ∼530 ns, which then rearranges into a left-handed helical bundle.
In each of the five simulations a tetrameric bundle was formed. It can be seen that this occurs by initial formation of dimer, which subsequently grows by addition of helices until the tetramer is formed. Averaging across the five simulations, the mean time taken for formation of a tetramer was 550 ns (± 120 ns). It is worth noting that in each simulation a loose tetrameric assembly formed within a shorter period of time; the mean time quoted is for formation of a plausible homotetrameric left-handed helix bundle. However, to allow equilibration of each bundle before analysis, only data from 1 μs onward were considered, giving 4 μs per simulation and 20 μs of tetramer simulation time in total.
Conformation of the four-helix bundle
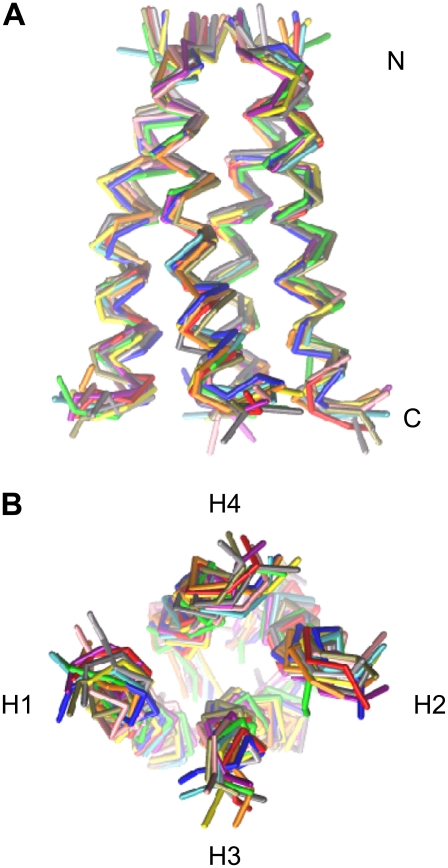
The five simulations were each clustered (using NMRclust (83) on their Cα RMSDs) to yield representative frames from the three top clusters per simulation. A comparison of the 15 structures, via calculation of a Cα RMSD matrix, yielded four major conformations, combinations of which were present in all of the simulations. Furthermore, a more detailed examination of these four major conformations revealed that they corresponded to the same structure, but with different numbering (i.e., permutation) of the helices. Manual renumbering of the helices resulted in a single cluster of structures (see Fig. 4) with an overall Cα RMSD of 3 Å between one another. Note that this is comparable to, e.g., the RMSD of an NMR ensemble structure for the TM domain of the F1F0 ATPase c-subunit (89).
FIGURE 4.
Ensemble represents conformations 1–4 rotated by 90°, 180°, or 270° so that they can all be superimposed upon one another.
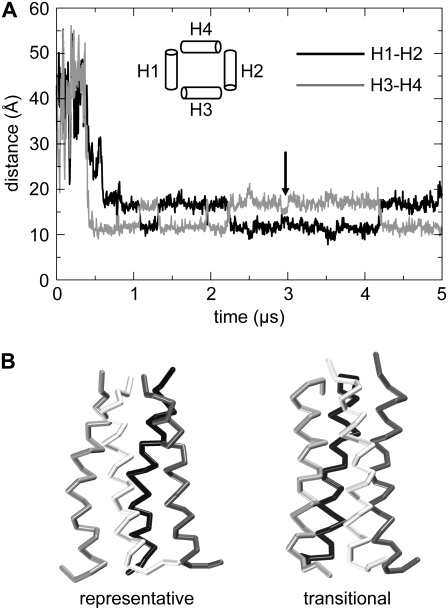
Previous modeling studies of M2 have assumed fourfold rotational symmetry (44,61,65) for the tetramer, such that the two diagonal distances across the bundle (distances H1-H2 and H3-H4 in Fig. 5) are by definition equal to one another. However, in the final ensemble of 11 structures (four structures having been excluded during the clustering as outliers/minor conformations) of the tetramer, the two average diagonal distances are 11.5 ± 0.3 Å and 16.8 ± 0.2 Å. Thus, the ensemble structure shown in Fig. 4 has 2× rotational symmetry. Interestingly, such symmetry has been seen in some atomistic simulations of M2 models (90).
FIGURE 5.
(A) Helix distances show that helices 1 and 2, and helices 3 and 4 are opposite each other in the arrangement of the helical bundle. It can be seen that at several points the two diagonal distances “switch” so that the closer helices move apart, whereas the distant helices approach one other. (B) Comparison of 2×-symmetrical (“representative”) and 4×-symmetrical (“transitional”) M2 helix bundle structures.
From visual inspection, the helix bundle is clearly left-handed, in agreement with previously published data (36). During the simulation, the average tilt angle of the helices is 16° ± 7°. This result is comparable to some experimental estimates of the tilt angle (14° ± 5° (91)), but somewhat less that other findings (33° ± 3° (36), 37° ± 3° (40), 32° ± 6° (87)). Although there appears to be a discrepancy between the calculated tilt angle for the CG system and some other experimental data, it is worth noting that these experiments were carried out in DMPC (36,40,87), whereas the CG-MD simulations presented here utilized DPPC, which would be expected to result in a ∼4 Å thicker hydrophobic core than in a DMPC bilayer (92). However, it should be mentioned that due to the granularity of the CG lipid model, the CG-DPPC molecule in our simulations represents lipid tails of 14–18 carbons in length (21,33). Despite this, however, our simulations reveal a bilayer thickness (defined by the phosphate–phosphate distance) of ∼39 Å, which more closely resembles the corresponding distance in DPPC (37 Å) (93). It might be anticipated that in a wider lipid bilayer the tilt angle will be lower. Indeed, previous work stated that the conformation of M2 depends on the lipid bilayer environment (55), with a thicker hydrophobic distance resulting in a shallower tilt angle. It is also worth noting that the experimentally derived model that most closely matches the CG simulation (14° ± 5° (91)) was based on data obtained from M2 channels expressed in Xenopus laevis oocytes. Furthermore, the tilt angle in the recent NMR structure in DHPC micelles (67) is ∼15°.
The average crossing angle between sequential helices was calculated at 21° ± 7° This compares well with the experimentally derived model value of 19° (91). The orientation of the helices relative to each other was such that the proposed pore-lining residues (V27, A30, S31, G34, H37, F38, and W41) (91,94,95) are indeed facing the center of the helix bundle. The side-chain particles for the important pore-gating residues, H37 and W41 (see Fig. 6), were also observed to form two rings of constriction within the center of the helix bundle that occluded the pore (see below). In agreement with recent atomistic simulations (96), the V27 region was also seen to form a narrow passage in the pore.
FIGURE 6.
Comparison of the CG (A) and atomistic (B) models that was based on the CG structure. The trace of the CG backbone particles and the atomistic α-carbons are represented (helix 1, blue; helix 2, red; helix 3, gray; and helix 4, orange). The side-chain particles for the CG residues H37 and W41, and the heavy atoms of the equivalent atomistic residues are shown in more detail. (C) The x-ray structure (66) and (D) the NMR structure (67) of the M2 TM helix bundle are shown fitted to the converged CG model. E and F show (respectively) the Cα traces of the x-ray and NMR structures (red) fitted onto our atomistic model (blue) with the H37 and W41 side chains also represented. The nearest helix has been removed from E and F for clarity.
The interhelix distances discussed so far were calculated using the center of mass of all of the backbone particles. Further analysis of the interhelix distance was carried out by dividing the helices into N- and C-terminal segments (where the N-terminus was defined as the center of mass of the backbone particles for the first five residues of the helix, and the C-terminus for the last five residues). The average adjacent (i.e., not diagonal) helix–helix distance for the N-terminus was 9.6 ± 0.1 Å (9.5 Å, 9.4 Å, 9.6 Å, and 9.7 Å for helices 1-3, 3-2, 2-4, and 4-1, respectively), whereas for the C-terminus the corresponding distance was 14.0 ± 0.2 Å (14.1 Å, 14.2 Å, 13.7 Å, and 14.1 Å for helices 1-3, 3-2, 2-4, and 4-1, respectively). Thus the N-terminal segments of the helices are packed more closely together than the C-terminal segments. Again, this seems to agree with available structural data. A further simulation (simulation CG-T6, Table 1) was also run in which the helices were orientated randomly (by random rotations about their bilayer normal axes) in the bilayer. This resulted in the same converged conformation, with representatives being within 2 Å of the central structure of the main ensemble produced from simulations CG-T1 to CG-T5 (Fig. 4).
Thus, overall, the ensemble of bundle structures agrees well with previous structural data, other than in the departure from exact 4× rotational symmetry. Indeed, recent x-ray studies of the M2 TM tetramer (66) suggest that local deviations from exact 4× symmetry may occur.
Dynamics of the helical bundle
The CG simulations of the tetrameric helix bundle were further analyzed in terms of possible switching between alternative conformations. From analysis of the interhelical distances (Fig. 5), it is evident that switching occurs on a ∼1 μs timescale between two alternative twofold symmetrical structures. In one of these two conformations, helices H1 and H2 are farthest from each other, whereas in the other the most distant helices are H3 and H4. The distances between these helices versus time (Fig. 5) suggest that these two conformations switch back and forth in a concerted motion, with helices H1 and H2 moving toward each other as helices H3 and H4 move apart. In addition, occasionally a “transitional conformation” between the two is observed (e.g., as indicated by the vertical arrow in Fig. 5). A more detailed examination of this structure suggests that during the transition the average tilt angle of the helices (∼10°) is less than that during the simulation as a whole (∼16°). This decrease in tilt angle helps to accommodate the larger residues (H37 and W41) that face toward the center of the pore. It also appears that as the two 2×-symmetrical conformations switch between one another the transitional bundle is closer to being 4× symmetrical (see Fig. 5 B), with less tilted helices such that the overall shape of bundle is less “conical”.
Charge state of the histidine
The two recent experimental structures of M2 have been suggested to represent open (x-ray (66)) and closed (NMR (67)) conformations of the helical bundle. Our initial CG tetramerization simulations (CG-T1 to CG-T5) treated the H37 side-chain particles as neutral. Thus, the model generated most likely corresponds to the proposed closed state. This is in agreement with the better fit of the model to the NMR than to the x-ray structure. To see whether we could simulate the open (or intermediate) states of the channel, we turned the H37 residues into a positively charged side chain by altering the secondary side-chain particle from type Nda (nonpolar) to Qda (charged). Thus systems with one, two, three, and four positively charged H37 side chains were created (CG-T1+, CG-T2+, CG-T3+, CG-T4+; see Table 1). Tetramerization of these systems was simulated as described above, and the resultant tetramers were analyzed.
Of interest, it was found that the average tilt of the helices in the bundle did not significantly alter with an increase in the protonation state of the histidine residues. However, it did seem that there were some more subtle changes in the packing of the helices as more of the H37 residues were charged. The conical shape of the converged (H37 neutral) CG M2 tetramer could be defined by the ratio as of the area (AN) formed by the centers of mass (for each helix) of the five residues at the N-terminus of each monomer to the corresponding area (AC) formed by centers of mass of the five residues at the C-terminus of each monomer. So, for example, for simulation CG-T3 (all H37 residues neutral) AN : AC = 1:2.1, whereas for CG-T4+ (all H37 residues charged) AN : AC = 1:2.3, indicating a somewhat wider C-terminal packing when in CG-T4+. To explore this further, the area between the centers of mass of the four H37 residues was calculated. For CG-T3 this area was 43 Å2, whereas for CG-T4+ this area had almost doubled to 77 Å2. Thus, even at the CG-MD level (which truncates the electrostatic interactions somewhat (21,28)), our model simulations suggest an opening of the M2 channel at the C-terminal mouth as a result of the repulsion of charged H37 residues, which move away from each other via reorientation of the helices without large changes in tilt angle.
Conversion to an atomistic model
To more fully assess the conformational dynamics and stability of the M2 TM tetramer model generated by the CG self-assembly simulations, the CG structure was converted to an atomistic model, which was then the starting point for conventional atomistic simulations. To convert the CG protein model, Modeller v7.7 (http://www.salilab.org/modeller/) was used, with the backbone particles of the CG model as a template for the Cα atoms. An ensemble of 1000 models was produced, which was subsequently filtered in terms of RMSD (for the backbone positions and also for key side-chain positions) to yield the atomistic model that best fitted the input CG model. To convert the CG lipid bilayer to an atomistic equivalent, we used a library of 1500 different conformations of DPPC molecules derived from an atomistic simulation of a pure DPPC bilayer. For each CG lipid, the entire library was searched to determine which atomistic conformation provided the best matches (defined via the RMSD of the 12 CG particles against their atomistic equivalents). These AT lipid molecules were then superimposed onto their CG counterparts, and concatenated together with the AT protein model. The resultant AT system was then energy-minimized before solvation and addition of counterions.
The outcome of this conversion procedure is illustrated in Fig. 6, A and B. The RMSD between the CG protein conformation and the modeled atomistic structure is 1.9 Å (calculated using the CG backbone particles versus the Cα atoms plus the side-chain particles against the corresponding side-chain atoms), with a backbone-Cα RMSD of 0.7 Å. In particular, it can be seen that the AT model has an overall conical shape, with the side chains of H37 and W41 directed toward the interior of the pore.
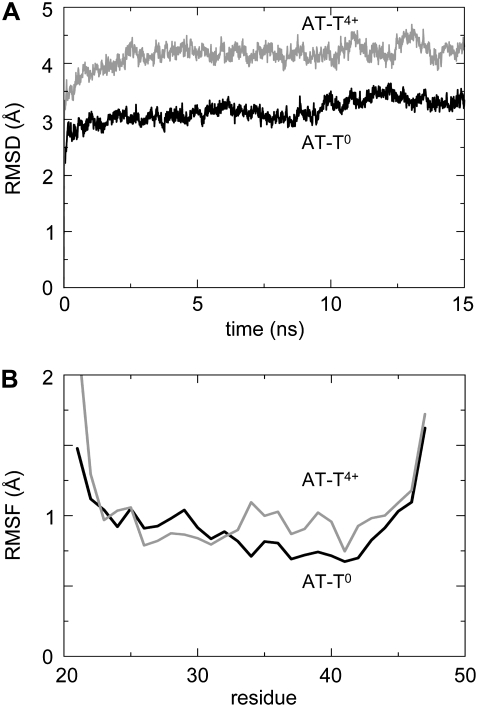
The conformational dynamics and stability of the resultant AT model were assessed in a pair of related MD simulations (Table 1 and Fig. 7). In simulation AT-T0 the four H37 residues were in their neutral (i.e., unprotonated) state, whereas in simulation AT-T4+ all four histidines were protonated. Comparing the Cα RMSDs for the two simulations (Fig. 7 A), it can be seen that the conformational drift is, as anticipated, substantially less for the AT-T0 simulation than for the AT-T4+ simulation. For the AT-T0 simulation the Cα RMSD after ∼15 ns is ∼3.5 Å relative to the starting structure. This is comparable to that seen in, e.g., simulations of low-resolution x-ray or EM structures (97). The profile of Cα root mean-square fluctuation versus residue (Fig. 7 B) suggests that fluctuations in the vicinity of the H37 are low for AT-T0, and somewhat higher for AT-T4+. Significantly, over the 15 ns of the simulations (for both AT-T0 and AT-T4+), the diagonal helix–helix distances (i.e., between H1 and H2, and between H3 and H4) change by <1 Å. Thus, these simulations confirm that switching between the two 2×-symmetrical structures (seen in the CG simulations on a ∼1 μs timescale) is not seen on the much shorter timescale of the atomistic simulations.
FIGURE 7.
RMSD (top) and RMSF (bottom) for the two atomistic simulations containing the histidine-neutral (solid) system and the histidine-4+ (shaded) system.
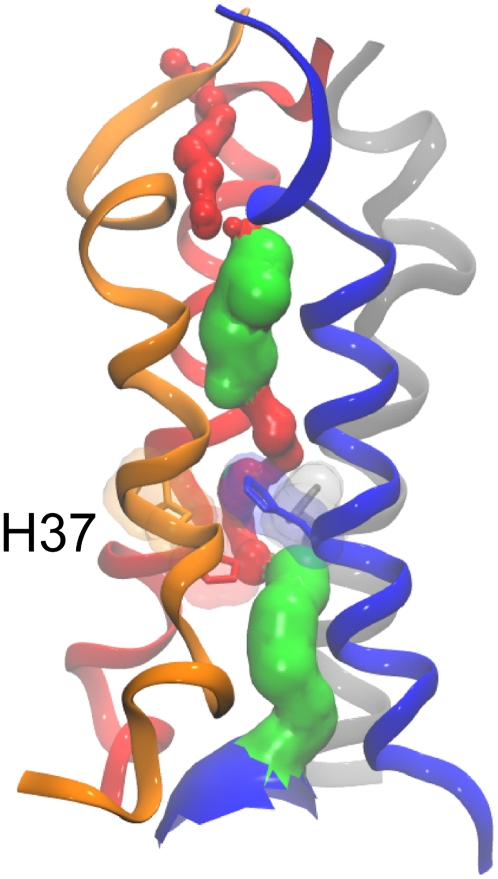
The atomistic model pore (at t = 0.25 ns from AT-T0; Fig. 8) was analyzed in terms of the central pore using HOLE (85). Two constrictions to the central pore were observed: one at the N-terminus and one in the vicinity of the H37 side chains, the latter suggesting that this model may correspond to a closed conformation of the channel. A comparable N-terminal constriction is observed in the recently determined x-ray structure (66) and in some recent simulations based on models (e.g., (62,90). This N-terminal constriction is also in the vicinity of V27, which has been suggested to form an amantadine-sensitive “second gate” (96). A constriction is also seen in the recent NMR structure (67) around the H37 region. The pore radius profile of the atomistic model (see Supplementary Material, Data S1) shows that whereas the N-terminal region more closely resembles the N-terminal of the x-ray structure, the C-terminal region more closely resembles that of the NMR structure, with a smaller cavity in the center.
FIGURE 8.
Pore profile of the atomistic channel, taken from a snapshot during the histidine-neutral simulation. The side chains of the key gating residues (H37) are shown. The color scheme for the pore surface is as follows: red, radius < 1.15 Å (no water can pass); green, 1.15 Å < radius < 2.30 Å (single-file water); and blue, radius > 2.30 Å (multiple waters). Helix 1, blue; helix 2, red; helix 3, gray; and helix 4, orange.
This model was also compared with the crystal structure of the M2 TM helix bundle (Fig. 6 C) (66). The initial RMSD for the Cα atoms of the AT-T0 starting conformation against the x-ray structures is relatively high (5 Å) and the corresponding plateau value during the AT-T0 simulation was 5.6 Å. The x-ray structure was also compared with the initial CG simulations that were used to form the tetramer (CG-T3 in particular) to see whether the crystal conformation was sampled at any point throughout the CG bundle dynamics. The minimum RMSD observed was 3.9 Å. In a further comparison, the x-ray structure (Fig. 6 C) was converted into a CG model and used to initiate a further simulation (CG-x-ray; see Table 1). The D4 model constructed from the x-ray structure (which is suggested to represent a more closed state of the channel (66)) was also converted to a CG model and used as the initial structure for a subsequent CG-MD simulation (CG-D4; Table 1). The Cα RMSD for CG-x-ray after 500 ns was quite high at ∼6 Å, and the Cα RMSD for the CG-D4 simulation also reached a plateau value of ∼6.5 Å after 500 ns (and subsequently fluctuated about this for the remainder of the simulation). This degree of conformational drift could be attributed to two factors: a degree of collapse of the more “open” regions between the C-termini of the helices, and interhelix movement (the longest interhelix distance switching between H1-H2 and H3-H4, as seen in CG-T1 to CG-T5). It is interesting that in the x-ray structure, two β-octyl glucoside molecules seem to help hold the C-termini of the helices open. To evaluate whether this collapse of the structure had resulted in convergence of the CG-x-ray simulation with the bundle orientation formed from the CG-T3 simulation, an RMSD matrix between the two simulations was calculated. During some limited regions a degree of convergence (<4 Å) was seen (a similar trend, but to a lesser extent, was seen for the CG-D4 simulation).
DISCUSSION
In this study we have demonstrated that an ensemble of 5 μs CG-MD simulations may be used to self-assemble a four-TM helix bundle, i.e., the influenza M2 ion channel TM helix tetramer. Furthermore, this approach yields a converged structure for the M2 TM helix bundle in a lipid bilayer. The resultant model of the M2 TM bundle is compatible with the majority of the available structural, mutational, and biophysical data. A novel aspect of the CG-MD simulations is that the converged model shows ∼2× rotational symmetry, rather than the exact 4× symmetry assumed in many previous modeling and structural studies. The M2 helix bundle undergoes a concerted switching motion between two related 2×-symmetrical structures on a ∼1 μs timescale. Conversion of the CG to an AT model yielded a structure that was stable in 15 ns duration AT-MD simulations. As expected, the conformational switching seen in the CG-MD simulations was not seen in the (substantially shorter timescale) AT-MD simulations.
To test the sensitivity of the CG simulations to changes in the sequence of the M2 helix, self-assembly simulations (data not shown) were performed in which the sequence of the M2 TM peptide was scrambled. Simulations on this helix resulted in partitioning into the bilayer for 66% of the simulation time (cf., 90% for the wild type). The residual partitioning of the scrambled M2 helix into the bilayer is perhaps not surprising since bilayer partitioning of a helix (to a first approximation) depends on its amino acid composition (98). However, self-assembly simulations using this scrambled M2 helix (carried out in the same manner as for the wild-type M2 helix) resulted in “ejection” of one of the helices to the surface of the membrane whenever an aggregate formed. Thus the CG-MD self-assembly of a stable and converged M2 helix tetrameric bundle appears to be sensitive to (large-scale) changes in the sequence the peptide used.
These studies, in a broader context, illustrate the potential for CG-MD simulations to model the second stage of membrane protein folding, namely, the self-assembly/packing together of TM α-helices. It thus extends previous CG-MD simulations of formation of dimers of glycophorin A TM helices (31), and AT-MD simulations of association of model TM helices within a bilayer environment (99,100). Taken together, these studies indicate that MD simulation may provide a valuable tool to probe the process of association of TM helices, and the nature and stability of TM helix/helix interactions within a lipid bilayer environment.
It is perhaps useful here to reflect critically on the more general applicability of CG-MD to modeling helix packing within membrane proteins. Based on experience with M2 tetramerization (this article) and glycophorin A helix dimerization (31,101), it would seem that CG-MD can be used to pack simple oligomers of relatively undistorted TM helices. However, to model the packing of more complex assemblies of TM helices, possibly including helices, e.g., kinked by the presence of proline residues (102) and interacting via side-chain-mediated H-bonds (103,104), a more complex, multiscale simulation approach is likely to be required.
It is important to examine the relationship of the CG-MD model of the M2 TM tetramer with available experimental and computational data. In terms of the mutational and related functional data, the CG-MD model is consistent in that it suggests that the key side chains (e.g., H37 and W41) are directed toward the center of the four-helix bundle.
A number of previous studies of self-assembly of the M2 tetramer (64,65) and of the stability of the related HIV Vpu channel TM helix pentamer (105) have employed MD simulations combining an atomistic protein model with a continuum model for the lipid bilayer and solvent. These simulations assumed N-fold rotational symmetry of the helix bundle. Here we relax this assumption, and the resultant simulations suggest the existence of a 2×-symmetrical (closed) state. There is also some evidence for departure from exact 4× rotational symmetry of the M2 channel in the recent x-ray crystallographic structure (66). Indeed, this structure seems to more closely match our model than the subsequent (exactly 4× rotationally symmetric) model, D4, that was generated from the crystal structure. It is possible that such loss of symmetry would be more difficult to detect in NMR experiments. For example, the recent NMR structure (Fig. 6 D) determined in DHPC micelles was generated using C4 rotational symmetry (67). However, the helix tilt angle in the NMR model (∼15°) is close to that of the CG-MD generated model (∼16°).
It is also productive to reflect on some of the limitations of the computational methodology used in this study. The CG force field employed is relatively simple, although it has been tested for membrane peptides and protein against a range of experimental data (28,30). Furthermore, this and related CG models have been used successfully to characterize the interactions of integral proteins (106) with lipid bilayers, to probe lipid bilayer deformation by integral membrane proteins (32,33), and to explore bilayer/protein coupling in gating of mechanosensitive channels (107). Refinement of the force field for lipids was recently reported (29), and this refinement has been extended to peptides and proteins (108). It will therefore be important to explore the sensitivity/robustness of our conclusions to such improvements in the CG force field.
We used our converged CG model of the M2 helix bundle as the starting point for a (brief) AT-MD simulation. Another possible means of capturing atomistic detail is to combine CG and AT components within the same simulation (25,26,109–111). Such an approach may provide a more accurate, yet still computationally feasible, route to modeling self-assembly of TM helix bundles. We also would like to explore a more sophisticated (and possibly automated (112)) approach to initiation and implementation of CG → AT switching. For example, one might consider that an appropriate switch time would be shortly after a transition between the two 2×-symmatrical bundle conformations. This can be determined by monitoring, e.g., the pattern of interhelix distances as the CG-MD simulation proceeds and thus automatically initiating the switch to AT-MD. Thus a single long (multi-microseconds) CG-MD simulation could spawn an ensemble of shorter (multi-nanoseconds) AT-MD simulations.
In terms of future directions of these studies, it will be of interest to extend the approach to self-assembly of TM helix bundles (e.g., phospholamban (J. Vorel and M. S. P. Sansom, unpublished results)), to TM helix hairpins fragments from more complex membrane proteins (28), and ultimately to multipass membrane protein helix bundles. In this way it may be possible to develop CG-MD as a component of a multiscale approach for predicting membrane protein structure via simulation.
SUPPLEMENTARY MATERIAL
To view all of the supplemental files associated with this article, visit www.biophysj.org.
Supplementary Material
Acknowledgments
We thank the Biotechnology and Biological Sciences Research Council (BBSRC) and the Wellcome Trust for funding. T.C. was supported by a BBSRC research studentship. We also thank our colleagues (especially Philip Biggin and Chee Chew) for helpful discussions concerning this article, and Bill DeGrado for valuable discussions and for providing us with access to the M2 x-ray structure for comparison with the CG models.
Peter J. Bond's present address is Max Planck Institute of Biophysics, Frankfurt/Main, Germany.
Syma Khalid's present address is School of Chemistry, University of Southampton, Highfield, Southampton, UK.
Editor: Gregory A. Voth.
References
- 1.Hopkins, A. L., and C. R. Groom. 2002. The druggable genome. Nat. Rev. Drug Discov. 1:727–730. [DOI] [PubMed] [Google Scholar]
- 2.Russ, A. P., and S. Lampel. 2005. The druggable genome: an update. Drug Discov. Today. 10:1607–1610. [DOI] [PubMed] [Google Scholar]
- 3.Berman, H. M., J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov, and P. E. Bourne. 2000. The Protein Data Bank. Nucleic Acids Res. 28:235–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.White, S. H. 2004. The progress of membrane protein structure determination. Protein Sci. 13:1948–1949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Fleishman, S. J., V. M. Unger, and N. Ben-Tal. 2006. Transmembrane protein structures without X-rays. Trends Biochem. Sci. 31:106–113. [DOI] [PubMed] [Google Scholar]
- 6.Popot, J. L., and D. M. Engelman. 1990. Membrane protein folding and oligomerization: the two-state model. Biochemistry. 29:4031–4037. [DOI] [PubMed] [Google Scholar]
- 7.Engelman, D. M., Y. Chen, C. Chin, R. Curran, A. M. Dixon, A. Dupuy, A. Lee, U. Lehnert, E. Mathews, Y. Reshetnyak, A. Senes, and J. L. Popot. 2003. Membrane protein folding: beyond the two stage model. FEBS Lett. 555:122–125. [DOI] [PubMed] [Google Scholar]
- 8.White, S. H., and G. von Heijne. 2004. The machinery of membrane protein assembly. Curr. Opin. Struct. Biol. 14:397–404. [DOI] [PubMed] [Google Scholar]
- 9.Bowie, J. U. 2005. Solving the membrane protein folding problem. Nature. 438:581–589. [DOI] [PubMed] [Google Scholar]
- 10.Booth, P. J., S. L. Flitsch, L. J. Stern, D. A. Greenhalgh, P. S. Kim, and H. G. Khorana. 1995. Intermediates in the folding of the membrane-protein bacteriorhodopsin. Nat. Struct. Biol. 2:139–143. [DOI] [PubMed] [Google Scholar]
- 11.Lu, H., and P. J. Booth. 2000. The final stages of folding of the membrane protein bacteriorhodopsin occur by kinetically indistinguishable parallel folding paths that are mediated by pH. J. Mol. Biol. 299:233–243. [DOI] [PubMed] [Google Scholar]
- 12.Dill, K. A., and H. S. Chan. 1997. From Levinthal to pathways to funnels. Nat. Struct. Biol. 4:10–19. [DOI] [PubMed] [Google Scholar]
- 13.Snow, C. D., E. J. Sorin, Y. M. Rhee, and V. S. Pande. 2004. How well can simulation predict protein folding kinetics and thermodynamics? Annu. Rev. Biophys. Biomol. Struct. 34:43–69. [DOI] [PubMed] [Google Scholar]
- 14.Simmerling, C., B. Strockbine, and A. E. Roitberg. 2002. All-atom structure prediction and folding simulations of a stable protein. J. Am. Chem. Soc. 124:11258–11259. [DOI] [PubMed] [Google Scholar]
- 15.Chowdhury, S., M. C. Lee, G. Xiong, and Y. Duan. 2003. Ab initio folding simulation of the trp-cage mini-protein approaches NMR resolution. J. Mol. Biol. 327:711–717. [DOI] [PubMed] [Google Scholar]
- 16.Kubelka, J., J. Hofrichter, and W. A. Eaton. 2004. The protein folding “speed limit.” Curr. Opin. Struct. Biol. 14:76–88. [DOI] [PubMed] [Google Scholar]
- 17.Bond, P. J., and M. S. P. Sansom. 2003. Membrane protein dynamics vs. environment: simulations of OmpA in a micelle and in a bilayer. J. Mol. Biol. 329:1035–1053. [DOI] [PubMed] [Google Scholar]
- 18.Ash, W. L., M. R. Zlomislic, E. O. Oloo, and D. P. Tieleman. 2004. Computer simulations of membrane proteins. Biochim. Biophys. Acta. 1666:158–189. [DOI] [PubMed] [Google Scholar]
- 19.Gumbart, J., Y. Wang, A. Aksimentiev, E. Tajkhorshid, and K. Schulten. 2005. Molecular dynamics simulations of proteins in lipid bilayers. Curr. Opin. Struct. Biol. 15:423–431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Shelley, J. C., M. Y. Shelley, R. C. Reeder, S. Bandyopadhyay, and M. L. Klein. 2001. A coarse grain model for phospholipid simulations. J. Phys. Chem. B. 105:4464–4470. [Google Scholar]
- 21.Marrink, S. J., A. H. de Vries, and A. E. Mark. 2004. Coarse grained model for semiquantitative lipid simulations. J. Phys. Chem. B. 108:750–760. [Google Scholar]
- 22.Murtola, T., E. Falck, M. Patra, M. Karttunen, and I. Vattulainen. 2004. Coarse-grained model for phospholipid/cholesterol bilayer. J. Chem. Phys. 121:9156–9165. [DOI] [PubMed] [Google Scholar]
- 23.Nielsen, S. O., C. F. Lopez, G. Srinivas, and M. L. Klein. 2004. Coarse grain models and the computer simulation of soft materials. J. Phys. Condens. Matter. 16:R481–R512. [Google Scholar]
- 24.Stevens, M. J. 2004. Coarse-grained simulations of lipid bilayers. J. Chem. Phys. 121:11942–11948. [DOI] [PubMed] [Google Scholar]
- 25.Izvekov, S., and G. A. Voth. 2005. A multiscale coarse-graining method for biomolecular systems. J. Phys. Chem. B. 109:2469–2473. [DOI] [PubMed] [Google Scholar]
- 26.Shi, Q., S. Izvekov, and G. A. Voth. 2006. Mixed atomistic and coarse-grained molecular dynamics: simulation of a membrane bound ion channel. J. Phys. Chem. B. 110:15045–15048. [DOI] [PubMed] [Google Scholar]
- 27.Shih, A. Y., A. Arkhipov, P. L. Freddolino, and K. Schulten. 2006. Coarse grained protein-lipid model with application to lipoprotein particles. J. Phys. Chem. B. 110:3674–3684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bond, P. J., J. Holyoake, A. Ivetac, S. Khalid, and M. S. P. Sansom. 2007. Coarse-grained molecular dynamics simulations of membrane proteins and peptides. J. Struct. Biol. 157:593–605. [DOI] [PubMed] [Google Scholar]
- 29.Marrink, S. J., J. Risselada, S. Yefimov, D. P. Tieleman, and A. H. de Vries. 2007. The MARTINI forcefield: coarse grained model for biomolecular simulations. J. Phys. Chem. B. 111:7812–7824. [DOI] [PubMed] [Google Scholar]
- 30.Sansom, M. S. P., K. A. Scott, and P. J. Bond. 2008. Coarse grained simulation: a high throughput computational approach to membrane proteins. Biochem. Soc. Trans. 36:27–32. [DOI] [PubMed] [Google Scholar]
- 31.Bond, P. J., and M. S. P. Sansom. 2006. Insertion and assembly of membrane proteins via simulation. J. Am. Chem. Soc. 128:2697–2704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Bond, P. J., and M. S. P. Sansom. 2007. Bilayer deformation by the Kv channel voltage sensor domain revealed by self-assembly simulations. Proc. Natl. Acad. Sci. USA. 104:2631–2636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Periole, X., T. Huber, S. J. Marrink, and T. P. Sakmar. 2007. G protein-coupled receptors self-assemble in dynamics simulations of model bilayers. J. Am. Chem. Soc. 129:10126–10132. [DOI] [PubMed] [Google Scholar]
- 34.Forrest, L. R., W. F. DeGrado, G. R. Dieckmann, and M. S. P. Sansom. 1998. Two models of the influenza A M2 channel domain: verification by comparison. Fold. Des. 3:443–448. [DOI] [PubMed] [Google Scholar]
- 35.Sansom, M. S. P., L. R. Forrest, and R. Bull. 1998. Viral ion channels: molecular modelling and simulation. Bioessays. 20:992–1000. [DOI] [PubMed] [Google Scholar]
- 36.Kovacs, F. A., and T. A. Cross. 1997. Transmembrane four-helix bundle of influenza A M2 protein channel: structural implications from helix tilt and orientation. Biophys. J. 73:2511–2517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Song, Z., F. A. Kovacs, J. Wang, J. K. Denny, S. C. Shekar, J. R. Quine, and T. A. Cross. 2000. Transmembrane domain of M2 protein from influenza A virus studied by solid-state 15N polarization inversion spin exchange at magic angle NMR. Biophys. J. 79:767–775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Mould, J. A., J. E. Drury, S. M. Frings, U. B. Kaupp, A. Pekosz, R. A. Lamb, and L. H. Pinto. 2000. Permeation and activation of the M2 ion channel of influenza A virus. J. Biol. Chem. 275:31038–31050. [DOI] [PubMed] [Google Scholar]
- 39.Mould, J. A., H. C. Li, C. S. Dudlak, J. D. Lear, A. Pekosz, R. A. Lamb, and L. H. Pinto. 2000. Mechanism for proton conduction of the M(2) ion channel of influenza A virus. J. Biol. Chem. 275:8592–8599. [DOI] [PubMed] [Google Scholar]
- 40.Kovacs, F. A., J. K. Denny, Z. Song, J. R. Quine, and T. A. Cross. 2000. Helix tilt of the M2 transmembrane peptide from influenza A virus: an intrinsic property. J. Mol. Biol. 295:117–125. [DOI] [PubMed] [Google Scholar]
- 41.Wang, J., S. Kim, F. Kovacs, and T. A. Cross. 2001. Structure of the transmembrane region of the M2 protein H(+) channel. Protein Sci. 10:2241–2250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Okada, A., T. Miura, and H. Takeuchi. 2001. Protonation of histidine and histidine-tryptophan interaction in the activation of the M2 ion channel from influenza A virus. Biochemistry. 40:6053–6060. [DOI] [PubMed] [Google Scholar]
- 43.Lin, T. I., and C. Schroeder. 2001. Definitive assignment of proton selectivity and attoampere unitary current to the M2 ion channel protein of influenza A virus. J. Virol. 75:3647–3656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Nishimura, K., S. Kim, L. Zhang, and T. A. Cross. 2002. The closed state of a H+ channel helical bundle combining precise orientational and distance restraints from solid state NMR. Biochemistry. 41:13170–13177. [DOI] [PubMed] [Google Scholar]
- 45.Tang, Y., F. Zaitseva, R. A. Lamb, and L. H. Pinto. 2002. The gate of the influenza virus M2 proton channel is formed by a single tryptophan residue. J. Biol. Chem. 277:39880–39886. [DOI] [PubMed] [Google Scholar]
- 46.Howard, K. P., J. D. Lear, and W. F. DeGrado. 2002. Sequence determinants of the energetics of folding of a transmembrane four-helix-bundle protein. Proc. Natl. Acad. Sci. USA. 99:8568–8572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Tian, C. L., K. Tobler, R. A. Lamb, L. H. Pinto, and T. A. Cross. 2002. Expression and initial structural insights from solid-state NMR of the M2 proton channel from influenza A virus. Biochemistry. 41:11294–11300. [DOI] [PubMed] [Google Scholar]
- 48.Cristian, L., J. D. Lear, and W. F. DeGrado. 2003. Use of thiol-disulfide equilibria to measure the energetics of assembly of transmembrane helices in phospholipid bilayers. Proc. Natl. Acad. Sci. USA. 100:14772–14777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Chizhmakov, I. V., D. C. Ogden, F. M. Geraghty, A. Hayhurst, A. Skinner, T. Betakova, and A. J. Hay. 2003. Differences in conductance of M2 proton channels of two influenza viruses at low and high pH. J. Physiol. 546:427–438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Tian, C. L., P. F. Gao, L. H. Pinto, R. A. Lamb, and T. A. Cross. 2003. Initial structural and dynamic characterization of the M2 protein transmembrane and amphipathic helices in lipid bilayers. Protein Sci. 12:2597–2605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Vijayvergiya, V., R. Wilson, A. Chorak, P. F. Gao, T. A. Cross, and D. D. Busath. 2004. Proton conductance of influenza virus M2 protein in planar lipid bilayers. Biophys. J. 87:1697–1704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Czabotar, P. E., S. R. Martin, and A. J. Hay. 2004. Studies of structural changes in the M2 proton channel of influenza A virus by tryptophan fluorescence. Virus Res. 99:57–61. [DOI] [PubMed] [Google Scholar]
- 53.Venkataraman, P., R. A. Lamb, and L. H. Pinto. 2005. Chemical rescue of histidine selectivity filter mutants of the M2 ion channel of influenza A virus. J. Biol. Chem. 280:21463–21472. [DOI] [PubMed] [Google Scholar]
- 54.Kass, I., and I. T. Arkin. 2005. How pH opens a H+ channel: the gating mechanism of influenza A M2. Structure. 13:1789–1798. [DOI] [PubMed] [Google Scholar]
- 55.Duong-Ly, K. C., V. Nanda, W. F. Degrad, and K. P. Howard. 2005. The conformation of the pore region of the M2 proton channel depends on lipid bilayer environment. Protein Sci. 14:856–861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Stouffer, A. L., V. Nanda, J. D. Lear, and W. F. DeGrado. 2005. Sequence determinants of a transmembrane proton channel: An inverse relationship between stability and function. J. Mol. Biol. 347:169–179. [DOI] [PubMed] [Google Scholar]
- 57.Betakova, T., F. Ciampor, and A. J. Hay. 2005. Influence of residue 44 on the activity of the M2 proton channel of influenza A virus. J. Gen. Virol. 86:181–184. [DOI] [PubMed] [Google Scholar]
- 58.Hu, J., R. Fu, K. Nishimura, L. Zhang, H. X. Zhou, D. D. Busath, V. Vijayvergiya, and T. A. Cross. 2006. Histidines, heart of the hydrogen ion channel from influenza A virus: toward an understanding of conductance and proton selectivity. Proc. Natl. Acad. Sci. USA. 103:6865–6870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Zhong, Q., T. Husslein, P. B. Moore, D. M. Newns, P. Pattnaik, and M. L. Klein. 1998. The M2 channel of influenza A virus:- a molecular dynamics study. FEBS Lett. 434:265–271. [DOI] [PubMed] [Google Scholar]
- 60.Zhong, Q., D. M. Newns, P. Pattnaik, J. D. Lear, and M. L. Klein. 2000. Two possible conducting states of the influenza A virus M2 ion channel. FEBS Lett. 473:195–198. [DOI] [PubMed] [Google Scholar]
- 61.Forrest, L. R., A. Kukol, I. T. Arkin, D. P. Tieleman, and M. S. P. Sansom. 2000. Exploring models of the Influenza A M2 channel:- MD Simulations in a lipid bilayer. Biophys. J. 78:55–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Smondyrev, A. M., and G. A. Voth. 2002. Molecular dynamics simulation of proton transport through the influenza A virus M2 channel. Biophys. J. 83:1987–1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Wu, Y., and G. A. Voth. 2005. A computational study of the closed and open states of the influenza a M2 proton channel. Biophys. J. 89:2402–2411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Im, W., M. Feig, and C. L. Brooks. 2003. An implicit membrane generalized Born theory for the study of structure, stability, and interactions of membrane proteins. Biophys. J. 85:2900–2918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Bu, L., W. Im, and C. L. Brooks. 2007. Membrane assembly of simple helix homo-oligomers studied via molecular dynamics simulations. Biophys. J. 92:854–863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Stouffer, A. L., R. Acharya, D. Salom, A. S. Levine, L. Di Costanzo, C. S. Soto, V. Tereshko, V. Nanda, S. Stayrook, and W. F. DeGrado. 2008. Structural basis for the function and pharmaceutical inhibition of an influenza virus proton channel. Nature. 451:596–599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Schnell, J. R., and J. J. Chou. 2008. Structure and mechanism of the M2 proton channel of influenza A virus. Nature. 451:591–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Forrest, L. R., D. P. Tieleman, and M. S. P. Sansom. 1999. Defining the transmembrane helix of M2 protein from influenza A by molecular dynamics simulations in a lipid bilayer. Biophys. J. 76:1886–1896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Lamb, R. A., S. L. Zebedee, and C. D. Richardson. 1985. Influenza virus M2 protein is an integral membrane protein expressed on the infected-cell surface. Cell. 40:627–633. [DOI] [PubMed] [Google Scholar]
- 70.Grambas, S., M. S. Bennett, and A. J. Hay. 1992. Influence of amantadine resistance mutations on the pH regulatory function of the M2 protein of influenza A viruses. Virology. 191:541–549. [DOI] [PubMed] [Google Scholar]
- 71.Cuthbertson, J. M., D. A. Doyle, and M. S. P. Sansom. 2005. Transmembrane helix prediction: a comparative evaluation and analysis. Protein Eng. Des. Sel. 18:295–308. [DOI] [PubMed] [Google Scholar]
- 72.Sali, A., and T. L. Blundell. 1993. Comparative protein modeling by satisfaction of spatial restraints. J. Mol. Biol. 234:779–815. [DOI] [PubMed] [Google Scholar]
- 73.Marti-Renom, M. A., A. Stuart, A. Fiser, R. Sanchez, F. Melo, and A. Sali. 2000. Comparative protein structure modelling of genes and genomes. Annu. Rev. Biophys. Biomol. Struct. 29:291–325. [DOI] [PubMed] [Google Scholar]
- 74.Fiser, A., R. Kinh Gian Do, and A. Sali. 2000. Modeling of loops in protein structures. Protein Sci. 9:1753–1773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Berendsen, H. J. C., D. van der Spoel, and R. van Drunen. 1995. GROMACS: a message-passing parallel molecular dynamics implementation. Comput. Phys. Commun. 95:43–56. [Google Scholar]
- 76.Lindahl, E., B. Hess, and D. van der Spoel. 2001. GROMACS 3.0: a package for molecular simulation and trajectory analysis. J. Mol. Model. 7:306–317. [Google Scholar]
- 77.Berendsen, H. J. C., J. P. M. Postma, W. F. van Gunsteren, A. DiNola, and J. R. Haak. 1984. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 81:3684–3690. [Google Scholar]
- 78.Humphrey, W., A. Dalke, and K. Schulten. 1996. VMD—visual molecular dynamics. J. Mol. Graph. 14:33–38. [DOI] [PubMed] [Google Scholar]
- 79.van Gunsteren, W. F., P. Kruger, S. R. Billeter, A. E. Mark, A. A. Eising, W. R. P. Scott, P. H. Huneberger, and I. G. Tironi. 1996. Biomolecular Simulation: The GROMOS96 Manual and User Guide. Zurich, Switzerland/Groningen, The Netherlands, Biomos & Hochschulverlag AG an der ETH Zurich.
- 80.Scott, W. R. P., P. H. Hunenberger, I. G. Tironi, A. E. Mark, S. R. Billeter, J. Fennen, A. E. Torda, T. Huber, P. Kruger, and W. F. van Gunsteren. 1999. The GROMOS biomolecular simulation program package. J. Phys. Chem. A. 103:3596–3607. [Google Scholar]
- 81.Darden, T., D. York, and L. Pedersen. 1993. Particle mesh Ewald—an N.log(N) method for Ewald sums in large systems. J. Chem. Phys. 98:10089–10092. [Google Scholar]
- 82.Hess, B., H. Bekker, H. J. C. Berendsen, and J. G. E. M. Fraaije. 1997. LINCS: a linear constraint solver for molecular simulations. J. Comput. Chem. 18:1463–1472. [Google Scholar]
- 83.Kelley, L. A., S. P. Gardner, and M. J. Sutcliffe. 1996. An automated approach for clustering an ensemble of NMR-derived protein structures into conformationally related subfamilies. Protein Eng. 9:1063–1065. [DOI] [PubMed] [Google Scholar]
- 84.Kabsch, W., and C. Sander. 1983. Dictionary of protein secondary structure: pattern-recognition of hydrogen-bonded and geometrical features. Biopolymers. 22:2577–2637. [DOI] [PubMed] [Google Scholar]
- 85.Smart, O. S., J. G. Neduvelil, X. Wang, B. A. Wallace, and M. S. P. Sansom. 1996. HOLE: a program for the analysis of the pore dimensions of ion channel structural models. J. Mol. Graph. 14:354–360. [DOI] [PubMed] [Google Scholar]
- 86.Esteban-Martin, S., and J. Salgado. 2007. Self-assembling of peptide/membrane complexes by atomistic molecular dynamics simulations. Biophys. J. 92:903–912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Kukol, A., P. D. Adams, L. M. Rice, A. T. Brunger, and I. T. Arkin. 1999. Experimentally based orientational refinement of membrane protein models: a structure for the influenza A M2 H+ channel. J. Mol. Biol. 286:951–962. [DOI] [PubMed] [Google Scholar]
- 88.Ulmschneider, M. B., M. S. P. Sansom, and A. Di Nola. 2006. Evaluating tilt angles of membrane-associated helices: comparison of computational and NMR techniques. Biophys. J. 90:1650–1660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Girvin, M. E., V. K. Rastogi, F. Abildgaard, J. L. Markley, and R. H. Fillingame. 1998. Solution structure of the transmembrane H+-transporting subunit c of the F1Fo ATP synthase. Biochemistry. 37:8817–8824. [DOI] [PubMed] [Google Scholar]
- 90.Chen, H. N., Y. J. Wu, and G. A. Voth. 2007. Proton transport behavior through the influenza a M2 channel: insights from molecular simulation. Biophys. J. 93:3470–3479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Pinto, L. H., G. R. Dieckmann, C. S. Gandhi, C. G. Papworth, J. Braman, M. A. Shaughnessy, J. D. Lear, R. A. Lamb, and W. F. DeGrado. 1997. A functionally defined model for the M2 proton channel of influenza A virus suggest a mechanism for its ion selectivity. Proc. Natl. Acad. Sci. USA. 94:11301–11306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Kandasamy, S. K., and R. G. Larson. 2006. Molecular dynamics simulations of model trans-membrane peptides in lipid bilayers: a systematic investigation of hydrophobic mismatch. Biophys. J. 90:2326–2343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Tieleman, D. P., and H. J. C. Berendsen. 1996. Molecular dynamics simulations of a fully hydrated dipalmitoylphosphatidycholine bilayer with different macroscopic boundary conditions and parameters. J. Chem. Phys. 105:4871–4880. [Google Scholar]
- 94.Hay, A. J., A. J. Wolstenholme, J. J. Skehel, and M. H. Smith. 1985. The molecular basis of the specific anti-influenza action of amantadine. EMBO J. 4:3021–3024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Holsinger, L. J., D. Nichani, L. H. Pinto, and R. A. Lamb. 1994. Influenza A virus M2 ion channel protein: a structure-function analysis. J. Virol. 68:1551–1563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Yi, M., T. A. Cross, and H. X. Zhou. 2008. A secondary gate as a mechanism for inhibition of the M2 proton channel amantadine. J. Phys. Chem. B. 112:7977–7979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Law, R. J., C. Capener, M. Baaden, P. J. Bond, J. Campbell, G. Patargias, Y. Arinaminpathy, and M. S. P. Sansom. 2005. Membrane protein structure quality in molecular dynamics simulation. J. Mol. Graph. Model. 24:157–165. [DOI] [PubMed] [Google Scholar]
- 98.Hessa, T., H. Kim, K. Bihlmaier, C. Lundin, J. Boekel, H. Andersson, I. Nilsson, S. H. White, and G. von Heijne. 2005. Recognition of transmembrane helices by the endoplasmic reticulum translocon. Nature. 433:377–381. [DOI] [PubMed] [Google Scholar]
- 99.Stockner, T., W. L. Ash, J. L. MacCallum, and D. P. Tieleman. 2004. Direct simulation of transmembrane helix association: role of asparagines. Biophys. J. 87:1650–1656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Ash, W. L., T. Stockner, J. L. MacCallum, and D. P. Tieleman. 2004. Computer modeling of polyleucine-based coiled coil dimers in a realistic membrane environment: insight into helix-helix interactions in membrane proteins. Biochemistry. 43:9050–9060. [DOI] [PubMed] [Google Scholar]
- 101.Psachoulia, E., P. J. Bond, P. W. Fowler, and M. S. P. Sansom. 2008. Helix-helix interactions in membrane proteins: coarse grained simulations of glycophorin helix dimerization. Biochemistry. In press. [DOI] [PubMed]
- 102.Cordes, F. S., J. N. Bright, and M. S. P. Sansom. 2002. Proline-induced distortions of transmembrane helices. J. Mol. Biol. 323:951–960. [DOI] [PubMed] [Google Scholar]
- 103.Choma, C., H. Gratkowski, J. D. Lear, and W. F. DeGrado. 2000. Asparagine-mediated self-association of a model transmembrane helix. Nat. Struct. Biol. 7:161–166. [DOI] [PubMed] [Google Scholar]
- 104.Senes, A., D. E. Engel, and W. F. DeGrado. 2004. Folding of helical membrane proteins: the role of polar, GxxxG-like and proline motifs. Curr. Opin. Struct. Biol. 14:465–479. [DOI] [PubMed] [Google Scholar]
- 105.Ulmschneider, J. P., and M. B. Ulmschneider. 2007. Folding simulations of the transmembrane helix of Virus Protein U in an implicit membrane model. J. Chem. Theory Comput. 3:2335–2346. [DOI] [PubMed] [Google Scholar]
- 106.Scott, K. A., P. J. Bond, A. Ivetac, A. P. Chetwynd, S. Khalid, and M. S. P. Sansom. 2008. Coarse-grained MD simulations of membrane protein-bilayer self-assembly. Structure. 16:621–630. [DOI] [PubMed] [Google Scholar]
- 107.Yefimov, S., E. van der Giessen, P. R. Onck, and S. J. Marrink. 2008. Mechanosensitive membrane channels in action. Biophys. J. 94:2994–3002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Monticelli, L., S. K. Kandasamy, X. Periole, R. G. Larson, D. P. Tieleman, and S. J. Marrink. 2008. The MARTINI coarse grained force field: extension to proteins. J. Comput. Theor. Chem. 4:819–834. [DOI] [PubMed] [Google Scholar]
- 109.Neri, M., C. Anselmi, M. Cascella, A. Maritan, and P. Carloni. 2005. Coarse-grained model of proteins incorporating atomistic detail of the active site. Phys. Rev. Lett. 95:218102. [DOI] [PubMed] [Google Scholar]
- 110.Chang, R., G. S. Ayton, and G. A. Voth. 2005. Multiscale coupling of mesoscopic- and atomistic-level lipid bilayer simulations. J. Chem. Phys. 122:244716. [DOI] [PubMed] [Google Scholar]
- 111.Ayton, G. S., and G. A. Voth. 2007. Multiscale simulation of transmembrane proteins. J. Struct. Biol. 157:570–578. [DOI] [PubMed] [Google Scholar]
- 112.Sun, Y., S. McKeever, K. Balali-Mood, and M. S. P. Sansom. 2008. Integrating multi-level molecular simulations across heterogeneous resources. In Proceedings of the 8th IEEE/ACM International Conference on Grid Computing (Grid 2007). Austin, Texas, 2007. 161–168.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.