Abstract
Many physiological characteristics of living cells are regulated by protein interaction networks. Because the total numbers of these protein species can be small, molecular noise can have significant effects on the dynamical properties of a regulatory network. Computing these stochastic effects is made difficult by the large timescale separations typical of protein interactions (e.g., complex formation may occur in fractions of a second, whereas catalytic conversions may take minutes). Exact stochastic simulation may be very inefficient under these circumstances, and methods for speeding up the simulation without sacrificing accuracy have been widely studied. We show that the “total quasi-steady-state approximation” for enzyme-catalyzed reactions provides a useful framework for efficient and accurate stochastic simulations. The method is applied to three examples: a simple enzyme-catalyzed reaction where enzyme and substrate have comparable abundances, a Goldbeter-Koshland switch, where a kinase and phosphatase regulate the phosphorylation state of a common substrate, and coupled Goldbeter-Koshland switches that exhibit bistability. Simulations based on the total quasi-steady-state approximation accurately capture the steady-state probability distributions of all components of these reaction networks. In many respects, the approximation also faithfully reproduces time-dependent aspects of the fluctuations. The method is accurate even under conditions of poor timescale separation.
INTRODUCTION
Stochastic simulation is important for the study of chemical reaction systems where the number of molecules of some species can become small. The exact stochastic simulation algorithm of Gillespie (1,2) is the standard approach to simulation in this setting, but can become too slow to be useful in cases where fast reactions dominate the calculations but slow reactions determine the interesting evolution of the overall system. This may be the case, for example, in enzyme-catalyzed reactions where binding and unbinding of the enzyme and substrate often occur much more frequently than the product-producing reaction. Gillespie's algorithm will spend most of its time tracking binding and unbinding reactions that essentially cancel each other out and produce no net conversion of substrate into product.
Many approximations to Gillespie's algorithm have been proposed to reduce the bottleneck that occurs in systems with disparate timescales. Tau-leaping (3–6) uses Poisson random variables to allow multiple firings of reaction channels per time step. This approach can speed up simulations, but the explicit version has difficulty with the stiff systems we consider. The implicit version (5) was proposed to solve stiff systems; however, practical τ-selection formulas were only proposed (6) for the explicit version. A τ-selection formula based on reversible reactions was proposed, but a formula for a general stiff system is not yet available. Other approaches rely on separating the system into slow and fast reactions or species. The slow reactions can be simulated with Gillespie's algorithm and the fast reactions can be handled in a more efficient manner. One approach is to simulate fast reactions using chemical Langevin equations (7,8). Other techniques avoid simulating the fast reactions altogether, instead using their average values to derive the firing propensities of the slow reactions. The average values are obtained using the quasi-steady-state approximation (QSSA) (9) or the quasi-equilibrium approximation (also known as the partial equilibrium assumption) (10–12).
In this article, we apply an idea, called the total QSSA (TQSSA), to provide an algorithmic, fast, and accurate way to stochastically simulate enzyme-catalyzed reactions. The TQSSA was developed in a deterministic setting to remove the restrictions associated with the standard QSSA applied to enzyme-catalyzed reactions (13). The TQSSA accurately tracks intermediate complexes and can be extended straightforwardly to complex systems of interacting enzymes (14). In the stochastic setting considered here, TQSSA allows Gillespie's algorithm to be used to simulate the slow reactions while analytically accounting for the abundances of the fast species, as in the methods mentioned above. Thus, it avoids the bottleneck associated with simulating the fast reactions directly. The main contribution of this article is to show that stochastic TQSSA generalizes the QSSA results of Rao and Arkin (9) and can improve the accuracy of the partial equilibrium assumption employed by others (10–12) by allowing the slow timescales to affect the quasi-steady-state of the fast complexes. We provide a general framework for applying stochastic TQSSA to chemical reaction networks and illustrate its usefulness on a complex network exhibiting alternative stable steady states. Our results show that for cases having reasonable timescale separation between fast and slow reactions, the stochastic TQSSA simulations are nearly identical to direct simulation of all the reactions using Gillespie's stochastic simulation algorithm.
MICHAELIS-MENTEN KINETICS
Consider a simple chemical reaction where a substrate (S) is converted irreversibly to a product (P) by an enzyme (E):
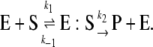 |
(1) |
In these reactions,  and
and  are the rate constants for formation and dissociation of the enzyme-substrate complex (E : S), and
are the rate constants for formation and dissociation of the enzyme-substrate complex (E : S), and 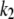 is the rate constant for the enzymatic conversion of S to P. With square brackets denoting the concentration of a chemical species, the rate equations corresponding to the above elementary reactions can be written as
is the rate constant for the enzymatic conversion of S to P. With square brackets denoting the concentration of a chemical species, the rate equations corresponding to the above elementary reactions can be written as
 |
(2) |
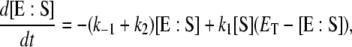 |
(3) |
where  is the total enzyme concentration. We always use subscript T to indicate the total amount of a chemical moiety. If the concentration of substrate is very much greater than
is the total enzyme concentration. We always use subscript T to indicate the total amount of a chemical moiety. If the concentration of substrate is very much greater than 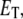 then the change in concentration of the enzyme-substrate complex (Eq. 3) will be fast in comparison to the change in concentration of the free substrate. Under these conditions, the enzyme-substrate complex rapidly reaches its stationary state, i.e.,
then the change in concentration of the enzyme-substrate complex (Eq. 3) will be fast in comparison to the change in concentration of the free substrate. Under these conditions, the enzyme-substrate complex rapidly reaches its stationary state, i.e.,
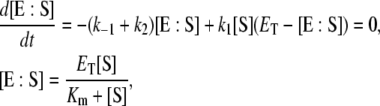 |
(4) |
where Km = (k−1 + k2)/k1 is called the Michaelis constant of the enzyme. Equation 4 is the QSSA for the enzyme-substrate complex. In this case, the conversion of substrate into product is described by the well known Michaelis-Menten rate law:
 |
(5) |
The condition for validity of the QSSA is 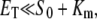 where
where  is the initial substrate concentration.
is the initial substrate concentration.
When this condition is not satisfied, then both [S] and [E:S] change on the same timescale. However, when k2 ≪ k−1, the “total” substrate concentration, 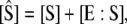 changes on a slower timescale than the enzyme-substrate complex (13):
changes on a slower timescale than the enzyme-substrate complex (13):
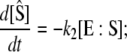 |
(6) |
 |
(7) |
Applying the QSSA, d[E:S]/dt = 0, to Eq. 7, one finds that
 |
(8a) |
or
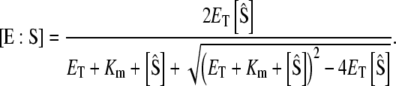 |
(8b) |
Equation 8b as the solution of Eq. 8a is a standard formula in numerical analysis to avoid a cancellation error when 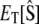 is much smaller than
is much smaller than  Borghans et al. (13) called Eq. 8 the TQSSA.
Borghans et al. (13) called Eq. 8 the TQSSA.
Tzafriri and Edelman (15) derived the following sufficient condition for the validity of TQSSA:
 |
(9) |
where  and
and  Tzafriri and Edelman also showed that
Tzafriri and Edelman also showed that
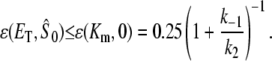 |
(10) |
Therefore, the condition for validity of TQSSA, Eq. 9, is satisfied if 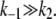 From Eq. 10, it is clear that the condition is also satisfied to some extent even when
From Eq. 10, it is clear that the condition is also satisfied to some extent even when  So TQSSA seems to be a good approximation for any ratio of
So TQSSA seems to be a good approximation for any ratio of  to
to  and for any values of the rate constants.
and for any values of the rate constants.
To examine the stochastic characteristics of a Michaelis-Menten reaction mechanism when enzyme and substrate are in comparable concentrations, we turn to the chemical master equation, which describes the evolution of the probability distribution of each potential state of the system. Under normal circumstances, this probability distribution function would be written in terms of the numbers of molecules of S and E:S (i.e., 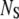 and
and  ), but to isolate the slow reaction, according to the idea of TQSSA, we use the random variables
), but to isolate the slow reaction, according to the idea of TQSSA, we use the random variables 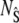 and
and 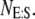 The equation for the probability of the state
The equation for the probability of the state  is given by
is given by
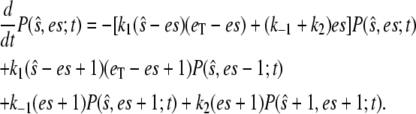 |
(11) |
Allowing for a slight abuse of notation, es refers to the numerical value of the random variable 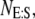 not the product of two numbers, e and s. In addition, we use an upper-case italic letter to denote the concentration of a particular species and a lower-case italic letter to denote its number of molecules in a specified volume (e.g., the volume of a yeast cell). For example,
not the product of two numbers, e and s. In addition, we use an upper-case italic letter to denote the concentration of a particular species and a lower-case italic letter to denote its number of molecules in a specified volume (e.g., the volume of a yeast cell). For example, 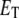 = total concentration of enzyme, whereas
= total concentration of enzyme, whereas  = total number of enzyme molecules.
= total number of enzyme molecules.
To obtain an equation for the probability of the composite variable, 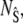 we write the joint probability as
we write the joint probability as 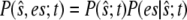 at each occurrence of this expression in Eq. 11 and sum Eq. 11 over all possible values of es. Denoting the conditional expectation of a function of the complex E:S by
at each occurrence of this expression in Eq. 11 and sum Eq. 11 over all possible values of es. Denoting the conditional expectation of a function of the complex E:S by
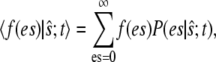 |
(12) |
the master equation for the slow variable becomes
 |
(13) |
because all terms relating to the fast reactions cancel out. For cases of large timescale separation, the distribution of es should reach steady state quickly compared to the evolution of 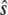 and we can eliminate the dependence on t in the expected value of es in Eq. 13. In this case, Eq. 13 exactly describes the noise in the chemical reaction
and we can eliminate the dependence on t in the expected value of es in Eq. 13. In this case, Eq. 13 exactly describes the noise in the chemical reaction
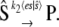 |
(14) |
Since in most cases we expect the differential equation description of chemical reactions to track the mean values of the reactants, it seems reasonable to replace  by the steady-state value of es from the TQSSA, given by
by the steady-state value of es from the TQSSA, given by
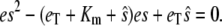 |
(15) |
To investigate the accuracy of our approach, we compute the exact value of 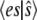 and compare it to the TQSSA value. Assuming that
and compare it to the TQSSA value. Assuming that 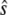 is constant on the short timescale, the evolution of the probability of
is constant on the short timescale, the evolution of the probability of  is governed by the equation
is governed by the equation
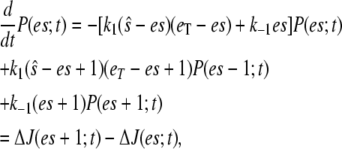 |
(16) |
where 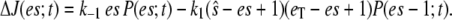 At steady state (on the fast timescale),
At steady state (on the fast timescale), 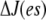 is a constant, and (considering the case
is a constant, and (considering the case  ) the constant must be zero. This equation provides a recurrence relation for P(es) whose solution is
) the constant must be zero. This equation provides a recurrence relation for P(es) whose solution is
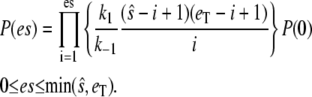 |
(17) |
The condition that the total probability sums to 1 allows the determination of P(0), and then the moments 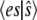 and
and 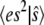 can be computed exactly. Fig. 1 a compares the function
can be computed exactly. Fig. 1 a compares the function 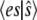 with the deterministic TQSSA result for the case
with the deterministic TQSSA result for the case 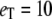 with
with  and
and  (arbitrary units). Clearly the stochastic mean
(arbitrary units). Clearly the stochastic mean 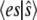 is very close to the deterministic value of es given by Eq. 15, even for this case of very small numbers of molecules. The variance
is very close to the deterministic value of es given by Eq. 15, even for this case of very small numbers of molecules. The variance 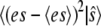 is shown in Fig. 1 b and is quite small, on the order of one molecule or less.
is shown in Fig. 1 b and is quite small, on the order of one molecule or less.
FIGURE 1.
Michaelis-Menten kinetics. (a) Comparison of steady-state mean of enzyme-substrate complex as a function of 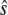 for
for 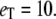 The solid line plots
The solid line plots 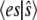 calculated from the steady-state probability distribution, P(es), and the dashed line plots deterministic TQSSA results from Eq. 12. (b) Steady-state variance of the enzyme-substrate complex as a function of
calculated from the steady-state probability distribution, P(es), and the dashed line plots deterministic TQSSA results from Eq. 12. (b) Steady-state variance of the enzyme-substrate complex as a function of  calculated from P(es).
calculated from P(es).
This analysis is quite similar to that in Goutsias (10) and Cao et al. (11,12). Our approach differs in using Eq. 15 for the mean value of the complex. Goutsias and Cao assume that the association and dissociation of the enzyme-substrate complex reaches equilibrium independently of the substrate-to-product conversion reaction, and so their value for 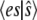 will not depend on the slow rate constant
will not depend on the slow rate constant  whereas our value does. For cases of extreme timescale separation (
whereas our value does. For cases of extreme timescale separation ( > 100
> 100 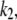 say), all these approaches tend to the same solution, and
say), all these approaches tend to the same solution, and  in Eq. 15 will tend quickly to a constant independent of
in Eq. 15 will tend quickly to a constant independent of  For less extreme cases, the term
For less extreme cases, the term 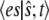 approaches a steady value dependent on both fast and slow reactions. Only the TQSSA captures this average value accurately, and the reaction (Eq. 14), using the corresponding time-invariant propensity, will satisfy a master equation that approximates the actual master equation (Eq. 11). Thus the TQSSA is expected to be more accurate than the other approaches in cases where the timescale separation is not large. An example of this behavior is shown in the Supplementary Material (Data S1).
approaches a steady value dependent on both fast and slow reactions. Only the TQSSA captures this average value accurately, and the reaction (Eq. 14), using the corresponding time-invariant propensity, will satisfy a master equation that approximates the actual master equation (Eq. 11). Thus the TQSSA is expected to be more accurate than the other approaches in cases where the timescale separation is not large. An example of this behavior is shown in the Supplementary Material (Data S1).
We examine the accuracy and efficiency of stochastic TQSSA by simulating both the full reaction mechanism (Eq. 1) (we call this “full Gillespie simulation”) and the simplified reaction (Eq. 14), with propensity 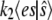 given by the steady-state value of es from the TQSSA expression (Eq. 15). We do the comparison for different initial numbers of enzyme and substrate molecules. Of two roots obtained from the quadratic equation (Eq. 15), we take only the root that satisfies
given by the steady-state value of es from the TQSSA expression (Eq. 15). We do the comparison for different initial numbers of enzyme and substrate molecules. Of two roots obtained from the quadratic equation (Eq. 15), we take only the root that satisfies  We have chosen
We have chosen  and
and 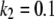 (arbitrary units), and the numerical simulations are averaged over 50,000 realizations. In Fig. 2, we plot the mean number of product
(arbitrary units), and the numerical simulations are averaged over 50,000 realizations. In Fig. 2, we plot the mean number of product 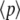 and its standard deviation as a function of time for two different cases: 1),
and its standard deviation as a function of time for two different cases: 1),  and 2),
and 2), 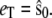 From the figure, it is clear that in both cases the stochastic TQSSA is in excellent agreement with the full Gillespie simulation. The stochastic QSSA proposed by Rao and Arkin does not give correct results in the two cases considered here. (For the case
From the figure, it is clear that in both cases the stochastic TQSSA is in excellent agreement with the full Gillespie simulation. The stochastic QSSA proposed by Rao and Arkin does not give correct results in the two cases considered here. (For the case 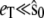 (not shown), stochastic QSSA is accurate, as expected.) The approximation proposed by Goutsias gives good results in the cases we consider, but our results are more accurate (see the Supplementary Material, Data S1, Fig. S2, a–c). As expected, the stochastic TQSSA simulation is very much faster than the full Gillespie simulation (15 times faster in the cases considered here).
(not shown), stochastic QSSA is accurate, as expected.) The approximation proposed by Goutsias gives good results in the cases we consider, but our results are more accurate (see the Supplementary Material, Data S1, Fig. S2, a–c). As expected, the stochastic TQSSA simulation is very much faster than the full Gillespie simulation (15 times faster in the cases considered here).
FIGURE 2.
Michaelis-Menten kinetics. Time evolution of mean product  (solid line) ± 1 SD (dashed lines) calculated from the full Gillespie simulation. (a)
(solid line) ± 1 SD (dashed lines) calculated from the full Gillespie simulation. (a) 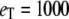 and
and 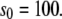 (b)
(b) 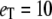 and
and 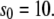 The lines for stochastic TQSSA simulations are indistinguishable from the full Gillespie simulations.
The lines for stochastic TQSSA simulations are indistinguishable from the full Gillespie simulations.
GOLDBETER-KOSHLAND SWITCH
We now extend our stochastic TQSSA method to coupled enzymatic reactions: the well-known Goldbeter-Koshland (GK) ultrasensitive switch (16). The GK switch consists of a substrate-product pair (S and Sp) that are interconverted by two enzymes (D and E). One can imagine that Sp is the phosphorylated form of the protein S, enzyme E is a kinase acting on S, and enzyme D is a phosphatase acting on Sp. The six reactions involved are
 |
(18) |
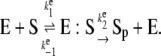 |
(19) |
If these reactions (Eqs. 18 and 19) can be described by Michaelis-Menten rate laws, then the time evolution of the switch is given by
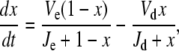 |
(20) |
where 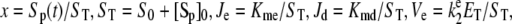 and
and 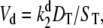 and Kme and Kmd are standard Michaelis constants for enzymes E and D. The superscript on a rate constant indicates the enzyme and the subscript indicates the particular reaction. The conditions for Michaelis-Menten rate laws to apply are
and Kme and Kmd are standard Michaelis constants for enzymes E and D. The superscript on a rate constant indicates the enzyme and the subscript indicates the particular reaction. The conditions for Michaelis-Menten rate laws to apply are 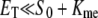 and
and 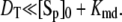 The steady-state solution of Eq. 20 is known as the Goldbeter-Koshland function:
The steady-state solution of Eq. 20 is known as the Goldbeter-Koshland function:
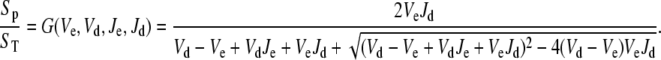 |
(21) |
The steady-state response of 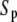 as a function of
as a function of 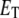 shows a steep sigmoidal shape if
shows a steep sigmoidal shape if 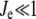 and
and 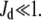 The steepness originates from the kinetic interplay of the two substrate-saturated enzymes acting in opposite directions.
The steepness originates from the kinetic interplay of the two substrate-saturated enzymes acting in opposite directions.
The classic GK ultrasensitive switch requires that substrate concentrations be much larger than enzyme concentrations, which can be expected for metabolic control networks, where concentrations of metabolites are much larger than those of enzymes. But the applicability of Michaelis-Menten kinetics is limited in the context of protein interaction networks, because a particular enzyme may act on multiple substrates, a particular substrate may be acted upon by multiple enzymes, and enzymes and substrates often alternate their roles. When the enzyme and substrate swap roles, Michaelis-Menten kinetics is no longer applicable, since the condition  cannot possibly be true for both reactions simultaneously. In this case it is better to write the rate equations in terms of
cannot possibly be true for both reactions simultaneously. In this case it is better to write the rate equations in terms of 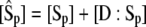
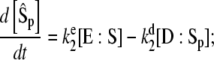 |
(22) |
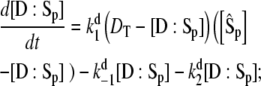 |
(23) |
 |
(24) |
where  and
and 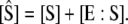 Invoking the TQSSA on Eqs. 23 and 24, as done by Ciliberto et al. (14), we find that the reactions portrayed in Eqs. 18 and 19 are governed by a single “slow” differential equation (Eq. 22) with
Invoking the TQSSA on Eqs. 23 and 24, as done by Ciliberto et al. (14), we find that the reactions portrayed in Eqs. 18 and 19 are governed by a single “slow” differential equation (Eq. 22) with  and
and 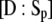 given as functions of
given as functions of  by the solution of the pair of quadratic equations:
by the solution of the pair of quadratic equations:
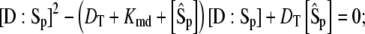 |
(25) |
 |
(26) |
with 0 ≤ [D:Sp] ≤ DT and 0 ≤ [E:S] ≤ ET.
As before, we can write a chemical master equation for the entire system and then sum over the fast variables to get a master equation for the slow composite variable  :
:
 |
(27) |
(for details, consult the Supplementary Material, Data S1). Assuming that the expected values equilibrate on a faster timescale, we can reduce Eq. 27 to a master equation for the reactions
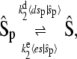 |
(28) |
with propensities  and
and 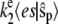 for the forward and backward reactions, respectively. If we look at the evolution of the fast variables in between transitions of the slow variables, the equations for es and
for the forward and backward reactions, respectively. If we look at the evolution of the fast variables in between transitions of the slow variables, the equations for es and  are analogous to the equation for es in the simple enzyme-catalyzed reaction.
are analogous to the equation for es in the simple enzyme-catalyzed reaction.
For the stochastic TQSSA, numerical simulation of the reactions in Eq. 28 is carried out using Gillespie's stochastic simulation algorithm. At each time step, we calculate the propensities by solving the quadratic equations (Eqs. 25 and 26) in terms of numbers of molecules rather than concentrations. Of the multiple roots obtained from the solution of the quadratic equations we take only that root for which 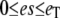 and
and 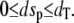 To compare the full Gillespie simulation involving six reactions (Eqs. 18 and 19) with the stochastic TQSSA simulation, we consider the parameter set
To compare the full Gillespie simulation involving six reactions (Eqs. 18 and 19) with the stochastic TQSSA simulation, we consider the parameter set  molecules,
molecules,  and
and 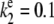 (all the rate constants with subscript “1” have the unit molecule−1 min−1, and the other rate constants have the unit min−1). These parameter values are consistent with Ciliberto et al. (14). In Fig. 3, we plot the time evolution of mean
(all the rate constants with subscript “1” have the unit molecule−1 min−1, and the other rate constants have the unit min−1). These parameter values are consistent with Ciliberto et al. (14). In Fig. 3, we plot the time evolution of mean 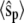 for three different total numbers of kinase and phosphatase: (a),
for three different total numbers of kinase and phosphatase: (a), 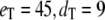 ; (b),
; (b), 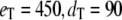 ; and (c),
; and (c),  In each case, the middle line corresponds to the mean value of
In each case, the middle line corresponds to the mean value of 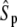 and the lines above and below are ± σ (1 SD) from the mean. For the initial condition, we used
and the lines above and below are ± σ (1 SD) from the mean. For the initial condition, we used  and
and  To get the mean, we have averaged each case over 50,000 trajectories. In Fig. 3, we have plotted the results from both the full Gillespie and stochastic TQSSA simulations; the agreement is so good that it is difficult to distinguish between the two results.
To get the mean, we have averaged each case over 50,000 trajectories. In Fig. 3, we have plotted the results from both the full Gillespie and stochastic TQSSA simulations; the agreement is so good that it is difficult to distinguish between the two results.
FIGURE 3.
Goldbeter-Koshland switch. Time evolution of mean 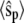 (solid line) ± 1 SD (dashed lines) for three different total numbers of enzyme molecules: (a)
(solid line) ± 1 SD (dashed lines) for three different total numbers of enzyme molecules: (a) 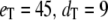 ; (b)
; (b) 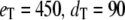 ; and (c)
; and (c) 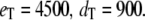 Results of the full Gillespie and stochastic TQSSA simulations are indistinguishable.
Results of the full Gillespie and stochastic TQSSA simulations are indistinguishable.
Fig. 4 compares the steady-state probability distributions of 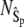 calculated from full Gillespie and stochastic TQSSA simulations. We have chosen
calculated from full Gillespie and stochastic TQSSA simulations. We have chosen 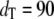 and
and  with the same initial conditions as used previously. The agreement between the two distributions is so good that it is difficult to distinguish between the two lines. We have found that the steady-state probability calculated from stochastic TQSSA matches very well with full Gillespie simulations for both Ŝp and Ŝ for any numbers of total enzymes, dT and eT.
with the same initial conditions as used previously. The agreement between the two distributions is so good that it is difficult to distinguish between the two lines. We have found that the steady-state probability calculated from stochastic TQSSA matches very well with full Gillespie simulations for both Ŝp and Ŝ for any numbers of total enzymes, dT and eT.
FIGURE 4.
Goldbeter-Koshland switch. Steady-state probability distributions of Ŝp for 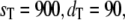 and
and  The solid line represents the full Gillespie, and the dashed line the stochastic TQSSA.
The solid line represents the full Gillespie, and the dashed line the stochastic TQSSA.
In Fig. 5, we compare full Gillespie simulations with stochastic TQSSA for steady-state means and standard deviations of Ŝp and D:Sp. We choose the same parameters as before, with 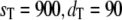 and with different values of
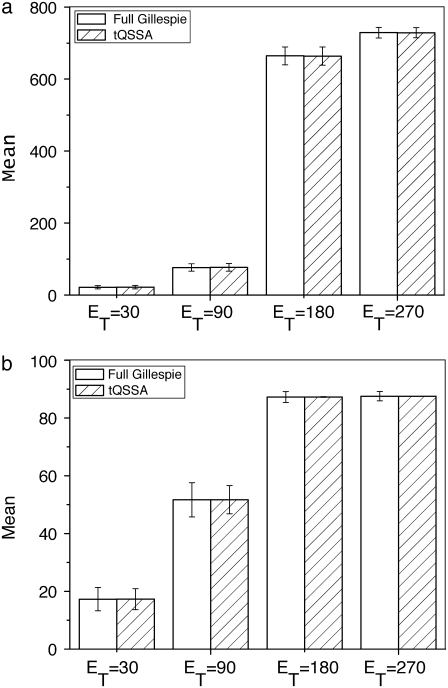
and with different values of 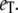 It is clear that for any values of initial enzyme and substrate concentrations, stochastic TQSSA always predicts the mean accurately for both Ŝp and the complex D:Sp. It always predicts the standard deviation for Ŝp accurately. For the complex, the standard deviation of D:Sp predicted by stochastic TQSSA is generally good. It fails for the cases where the number of free enzyme molecules is very small (see Fig. 5 b, ET = 180 and 270; see also Table S3 in the Supplementary Material, Data S1). Fig. 5 a also illustrates the switching behavior of Ŝp with increasing
It is clear that for any values of initial enzyme and substrate concentrations, stochastic TQSSA always predicts the mean accurately for both Ŝp and the complex D:Sp. It always predicts the standard deviation for Ŝp accurately. For the complex, the standard deviation of D:Sp predicted by stochastic TQSSA is generally good. It fails for the cases where the number of free enzyme molecules is very small (see Fig. 5 b, ET = 180 and 270; see also Table S3 in the Supplementary Material, Data S1). Fig. 5 a also illustrates the switching behavior of Ŝp with increasing  (In the Supplementary Material (Data S1), we present more comparisons of full Gillespie with stochastic TQSSA simulations.)
(In the Supplementary Material (Data S1), we present more comparisons of full Gillespie with stochastic TQSSA simulations.)
FIGURE 5.
Goldbeter-Koshland switch. Steady-state mean (bars) and standard deviation (error bars) of Ŝp (a) and D:Sp (b) for 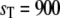 and
and 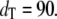 The open bars represent the full Gillespie, and the hatched bars the stochastic TQSSA. In some cases, the standard deviations in stochastic TQSSA are so small that the error bars are not visible.
The open bars represent the full Gillespie, and the hatched bars the stochastic TQSSA. In some cases, the standard deviations in stochastic TQSSA are so small that the error bars are not visible.
In Fig. 6, we report the time autocorrelation function, 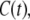 of steady-state fluctuations around the mean for different variables. We define the autocorrelation function for any variable x as
of steady-state fluctuations around the mean for different variables. We define the autocorrelation function for any variable x as
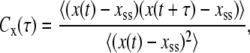 |
(29) |
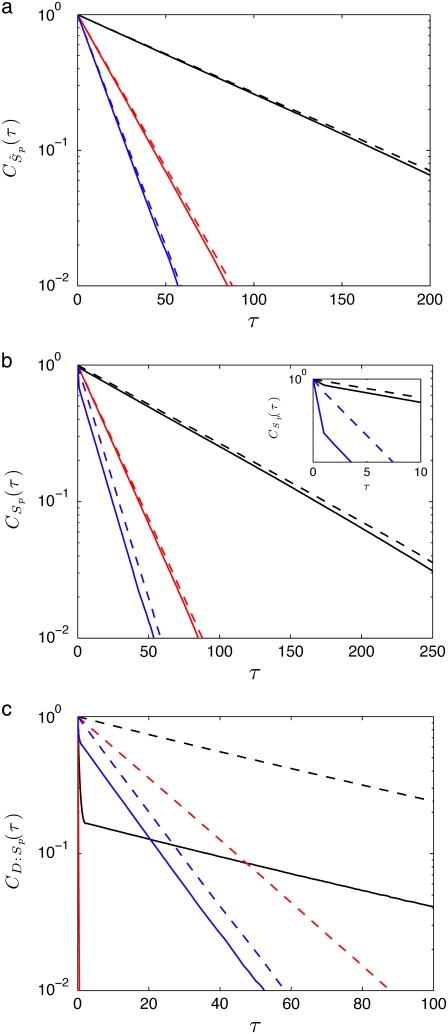
where 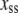 is the steady-state value of x. To get a smooth profile for an autocorrelation function, we averaged results over 10,000 trajectories. In general, the autocorrelation functions for various species in this network decay exponentially. In Fig. 6 a we show that the autocorrelation function of Ŝp calculated from stochastic TQSSA simulations matches very well with full Gillespie simulations. In Fig. 6 b, we compare autocorrelation functions for free species Sp. TQSSA always predicts a single exponential decay of the autocorrelation function, but in some cases, full Gillespie calculations show biexponential decay with a short and a long component of the decay. From the figures, it is clear that stochastic TQSSA predicts the long time component accurately but it can't predict the short time component. We find a similar trend for the complex D:Sp (Fig. 6 c) as well. The failure of stochastic TQSSA simulations to capture the fast timescale of decaying autocorrelations is to be expected, because all fast-timescale events are averaged out in the quasi-steady-state approximations (Eqs. 25 and 26).
is the steady-state value of x. To get a smooth profile for an autocorrelation function, we averaged results over 10,000 trajectories. In general, the autocorrelation functions for various species in this network decay exponentially. In Fig. 6 a we show that the autocorrelation function of Ŝp calculated from stochastic TQSSA simulations matches very well with full Gillespie simulations. In Fig. 6 b, we compare autocorrelation functions for free species Sp. TQSSA always predicts a single exponential decay of the autocorrelation function, but in some cases, full Gillespie calculations show biexponential decay with a short and a long component of the decay. From the figures, it is clear that stochastic TQSSA predicts the long time component accurately but it can't predict the short time component. We find a similar trend for the complex D:Sp (Fig. 6 c) as well. The failure of stochastic TQSSA simulations to capture the fast timescale of decaying autocorrelations is to be expected, because all fast-timescale events are averaged out in the quasi-steady-state approximations (Eqs. 25 and 26).
FIGURE 6.
Goldbeter-Koshland switch. Autocorrelation functions of fluctuations for the species (a) Ŝp, (b) Sp, and (c) D:Sp, calculated from full Gillespie simulation (solid lines) and from stochastic TQSSA simulation (dashed lines) for different numbers of enzymes: 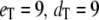 (black);
(black);  (red); and
(red); and  (blue).
(blue).
GENERAL FORMULATION OF THE TQSSA
To provide a general setting for the TQSS approach to stochastic simulation taken in this article, we first develop a general framework for the deterministic TQSSA and then extend it to a stochastic formulation. Systems of enzyme-catalyzed reactions, the focus of this article, fit naturally into this general framework, but the framework encompasses a much broader class of systems.
Consider a chemical reaction network with N species participating in M independent reactions. The deterministic chemical rate equations can be written as dx/dt = S·r(x(t)), where x(t) is an N-vector of concentrations of reacting chemical species, S is an N × M matrix of stoichiometric coefficients, and r is a vector of time-dependent fluxes through the M reactions of the network. (These fluxes are, in general, nonlinear functions of the concentrations of the reacting species.) We assume that the reactions have been partitioned into Ms slow reactions and Mf fast reactions,  where Ms + Mf = M. If the reactions are ordered in this fashion, then the stoichiometric matrix can be separated into two submatrices, S = [Sslow × Sfast], where Sslow is an N × Ms matrix of stoichiometric coefficients for the slow reactions, and Sfast is an N × Mf matrix of stoichiometric coefficients for the fast reactions.
where Ms + Mf = M. If the reactions are ordered in this fashion, then the stoichiometric matrix can be separated into two submatrices, S = [Sslow × Sfast], where Sslow is an N × Ms matrix of stoichiometric coefficients for the slow reactions, and Sfast is an N × Mf matrix of stoichiometric coefficients for the fast reactions.
Although it may be possible to separate reactions into slow and fast categories, it is usually impossible to separate chemical species into these categories because most chemical species participate in both fast and slow reactions. Using the TQSS idea, we seek linear combinations of the original chemical species (e.g., 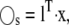 where l is an N × Ns matrix of constants) such that
where l is an N × Ns matrix of constants) such that 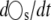 involves only slow reactions, rs. In such a case,
involves only slow reactions, rs. In such a case,
 |
(30) |
Hence, the condition for a slow combination of species, 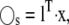 is that the columns of l span the left null space of the N × Mf matrix Sfast. The number of slow variables, Ns, is the dimension of this left null space. A linear transformation matrix L can be constructed by choosing the first Ns rows of L as appropriate linearly independent components of the null space, and the remaining rows as standard basis vectors that are linearly independent of the first Ns rows. (It is clear that L is not unique, and this freedom can be used for other purposes.) The transformation
is that the columns of l span the left null space of the N × Mf matrix Sfast. The number of slow variables, Ns, is the dimension of this left null space. A linear transformation matrix L can be constructed by choosing the first Ns rows of L as appropriate linearly independent components of the null space, and the remaining rows as standard basis vectors that are linearly independent of the first Ns rows. (It is clear that L is not unique, and this freedom can be used for other purposes.) The transformation  produces chemical rate equations of the form (the hat is dropped for notational simplicity):
produces chemical rate equations of the form (the hat is dropped for notational simplicity):
 |
(31) |
where the slow variables, 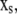 participate only in slow reactions, and the fast variables,
participate only in slow reactions, and the fast variables, 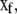 are governed by both fast and slow reactions. The 0 matrix in Eq. 31 has Ns rows and Mf columns, and the stoichiometry matrix is equal to L·[SslowSfast].
are governed by both fast and slow reactions. The 0 matrix in Eq. 31 has Ns rows and Mf columns, and the stoichiometry matrix is equal to L·[SslowSfast].
In terms of the preceding examples, the association and dissociation of enzyme-substrate complexes are chosen as the fast reactions, xs corresponds to the total variables defined by TQSSA (denoted with hats in our examples), and xf corresponds to the original complexes in the system. Any conservation relations in the system show up as all zero rows of Ss and can be eliminated from the differential equation. By construction there are no linear combinations of species that are governed only by slow reactions among the Nf = N – Ns “fast” variables.
In the deterministic formulation of TQSSA, the derivatives of the fast variables are set equal to zero and the resulting equations solved for the quasi-steady-state values of the fast variables in terms of the slow variables. This in turn allows for the simulation of the slow subsystem with the values for the fast variables replaced by their quasi-steady-state values.
To see how this idea transfers to the stochastic setting, consider the chemical master equation for the entire system (dropping the bold face):
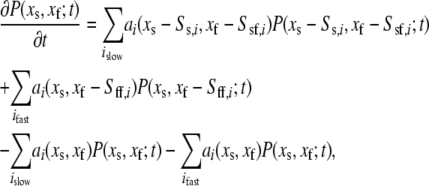 |
(32) |
where  is the propensity of the ith reaction. Writing
is the propensity of the ith reaction. Writing  in the above and summing over the fast species gives
in the above and summing over the fast species gives
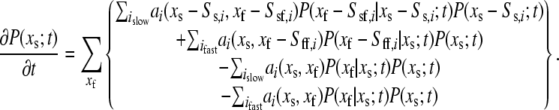 |
(33) |
Defining
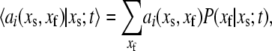 |
(34) |
and recognizing that 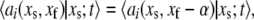 allows us to write
allows us to write
 |
(35) |
This can be recognized as the master equation of the system consisting of just the slow reactions involving the species  having stoichiometric matrix
having stoichiometric matrix 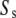 and propensities
and propensities 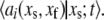
If the original slow reaction rates depend at most linearly on the fast variables 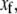 which will be the case if no slow variable is the result of a bimolecular reaction where both reactants are fast variables, then
which will be the case if no slow variable is the result of a bimolecular reaction where both reactants are fast variables, then 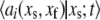 will depend only on the slow variables and the means of the fast variables given the values of the slow variables. (This was the major restriction in Goutsias (10).) We make the further assumption that the differential equations governing the system provide accurate information concerning the means of the variables. Then, assuming that the fast variables go to steady state quickly compared to the evolution of the slow variables (the standard TQSSA assumption), we can set the derivatives of the fast variables to zero, yielding
will depend only on the slow variables and the means of the fast variables given the values of the slow variables. (This was the major restriction in Goutsias (10).) We make the further assumption that the differential equations governing the system provide accurate information concerning the means of the variables. Then, assuming that the fast variables go to steady state quickly compared to the evolution of the slow variables (the standard TQSSA assumption), we can set the derivatives of the fast variables to zero, yielding
 |
(36) |
Equation 36 provides  coupled equations in N unknowns. Given the assumption of mass-action kinetics, these equations will be at most second order in the variables, xs and xf. In most cases, we can solve these equations for the
coupled equations in N unknowns. Given the assumption of mass-action kinetics, these equations will be at most second order in the variables, xs and xf. In most cases, we can solve these equations for the 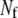 fast variables in terms of the slow variables, providing us with the means of the fast variables needed to compute the rates of the slow reactions of the reduced stochastic system. Clearly, as pointed out by Goutsias (17), the solution of the deterministic chemical reaction equations can differ from the mean values of the solution of the stochastic reaction equations when the molecular populations approach zero. Although not a concern for the problems considered in this article, this potential limitation must be kept in mind for the general case.
fast variables in terms of the slow variables, providing us with the means of the fast variables needed to compute the rates of the slow reactions of the reduced stochastic system. Clearly, as pointed out by Goutsias (17), the solution of the deterministic chemical reaction equations can differ from the mean values of the solution of the stochastic reaction equations when the molecular populations approach zero. Although not a concern for the problems considered in this article, this potential limitation must be kept in mind for the general case.
COUPLED GK SWITCHES (BISTABILITY)
We now apply this general approach to coupled GK switches (Fig. 7 a). To reactions shown in Eqs. 18 and 19, we add a second GK switch, which converts unphosphorylated E to a phosphorylated form Ep and back. The conversion of E to Ep is catalyzed by S, and the dephosphorylation reaction of E is catalyzed by the phosphatase, F. In this network, S and E act as mutual antagonists. This network describes the transition from the G2 phase to mitosis (the M phase) in the eukaryotic cell cycle, where S = MPF (M-phase promoting factor, a dimer of Cdc2 and cyclin B) and E = Wee1 (a kinase that phosphorylates and inactivates Cdc2). Novak and Tyson (18) used this module in a mathematical model for the G2-to-M transition during early embryonic cell cycles of Xenopus. Using GK rate laws, like Eq. 20, they showed that the concentration of S may exhibit two stable steady-state values, 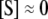 and
and 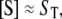 for intermediate values of
for intermediate values of  That is to say, the control system (Fig. 7 a) can exhibit bistability for
That is to say, the control system (Fig. 7 a) can exhibit bistability for 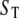 in a certain interval (
in a certain interval ( ). Ciliberto et al. (14) showed that bistability is maintained after unpacking the reaction network into elementary steps, provided that Sp has some ability to bind E but limited ability to convert E to Ep. To apply the TQSSA to the resulting network, they introduced the definitions
). Ciliberto et al. (14) showed that bistability is maintained after unpacking the reaction network into elementary steps, provided that Sp has some ability to bind E but limited ability to convert E to Ep. To apply the TQSSA to the resulting network, they introduced the definitions
 |
(37) |
In terms of these variables, the TQSSA equations are
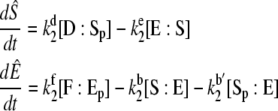 |
(38) |
and
 |
(39) |
Using these equations and the parameter values given in Table 1 (taken from Marlovits et al. (19)), Ciliberto et al. found that 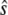 is a bistable function of
is a bistable function of  (Fig. 7 b).
(Fig. 7 b).
FIGURE 7.
Bistability for coupled GK switches. (a) Reaction scheme. (b) Bifurcation diagram.
TABLE 1.
Parameter values for coupled GK switches
| Enzyme | S | Dp | Sp | E | F |
| Substrate | E | Sp | E | S | Ep |
| Letter, l | b | d | b′ | e | f |
 |
0.625 | 0.0001125 | 0.00625 | 0.0125 | 0.00125 |
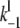 |
10.6 | 0.005 | 0.005 | 0.05 | 0.001 |
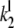 |
0.4 | 0.085 | 0.0001 | 0.05 | 0.2 |
| Kml | 17.6 | 800 | 0.816 | 8 | 160.8 |
| LT | 1600 | 160 | 40 |
The association rate constants (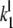 ) are in units molecule−1 min−1, and dissociation (
) are in units molecule−1 min−1, and dissociation ( ) and catalytic (
) and catalytic (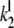 ) rate constants are min−1. Units for Michaelis-Menten constants (
) rate constants are min−1. Units for Michaelis-Menten constants (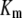 ) are molecules. LT is the total number of molecules of enzymes D, E, and F.
) are molecules. LT is the total number of molecules of enzymes D, E, and F.
In the same way as before, we can obtain a master equation for the slow reactions:
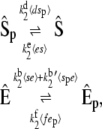 |
(40) |
with propensities based on the expected values of the numbers of enzyme-substrate complexes. We calculate the expected values of the complexes by solving the coupled algebraic equations (Eq. 39). In Fig. 8, we compare the steady-state probability distribution of Ŝ obtained from full Gillespie simulations of this reaction network with stochastic TQSSA simulations of Eq. 40. We calculate the steady-state probability distributions for different values of  In the monostable zone (
In the monostable zone ( ), the prediction of stochastic TQSSA is good (Fig. 8 a). As
), the prediction of stochastic TQSSA is good (Fig. 8 a). As 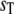 increases into the bistable zone, the prediction of stochastic TQSSA is still fine (Fig. 8 b), although the relative intensities of the two peaks in the bistable zone differ from the “exact” result of full Gillespie simulations. In the upper monostable region (
increases into the bistable zone, the prediction of stochastic TQSSA is still fine (Fig. 8 b), although the relative intensities of the two peaks in the bistable zone differ from the “exact” result of full Gillespie simulations. In the upper monostable region (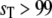 ), the probability distribution calculated from the stochastic TQSSA is a little shifted from the exact result (Fig. 8 c). In the deterministic case, the system settles to a particular steady state depending on initial conditions. In the stochastic case, the system jumps back and forth between the alternative stable steady states.
), the probability distribution calculated from the stochastic TQSSA is a little shifted from the exact result (Fig. 8 c). In the deterministic case, the system settles to a particular steady state depending on initial conditions. In the stochastic case, the system jumps back and forth between the alternative stable steady states.
FIGURE 8.
Bistable switch. Steady-state probability distributions of Ŝ. The solid lines represent the full Gillespie, and the dashed line the stochastic TQSSA. (a)  (b)
(b) 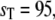 and (c)
and (c) 
In Fig. 9, we plot a sample trajectory of Ŝ in the bistable regime (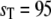 ); we initialize the system with
); we initialize the system with 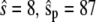 molecules. The upper panel shows a trajectory calculated from a full Gillespie simulation and the lower panel shows a stochastic TQSSA simulation. It appears from this example that the residence time in the upper steady state is much shorter in the stochastic TQSSA calculation than in the full Gillespie calculation. To investigate the apparent discrepancy, we calculate the residence time distributions of lower and upper steady states in both full Gillespie and stochastic TQSSA simulations. We initialize the system at the lower steady state (
molecules. The upper panel shows a trajectory calculated from a full Gillespie simulation and the lower panel shows a stochastic TQSSA simulation. It appears from this example that the residence time in the upper steady state is much shorter in the stochastic TQSSA calculation than in the full Gillespie calculation. To investigate the apparent discrepancy, we calculate the residence time distributions of lower and upper steady states in both full Gillespie and stochastic TQSSA simulations. We initialize the system at the lower steady state (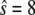 ) and record the time
) and record the time  when
when  reaches for the first time its upper steady-state value (
reaches for the first time its upper steady-state value (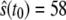 ). Then we follow the trajectory until
). Then we follow the trajectory until 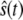 next reaches its lower steady-state value (
next reaches its lower steady-state value ( ). Continuing this process, we record a sequence of times
). Continuing this process, we record a sequence of times 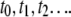 when
when 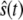 flips back and forth between its upper and lower steady states. We define (
flips back and forth between its upper and lower steady states. We define ( ) as a sample residence time in the upper steady state, (
) as a sample residence time in the upper steady state, ( ) as a sample residence time in the lower steady state, and so on. From a long simulation, we compute many sample residence times for both steady states. In Fig. 10, we plot cumulative distributions of these residence times. The top panel compares the cumulative probability distribution for residence times in the upper steady state from full Gillespie and stochasticTQSSA simulations (Fig. 10, a and b, respectively). The dashed lines are single exponential fits to the cumulative distribution. The bottom panel is the same for the lower steady state. Though the stochastic TQSSA calculation produces an exponential decay distribution, the mean residence times for the upper (TU = 42.15 × 103 min) and lower (TL = 5.55 × 103 min) steady states do not agree with the full Gillespie simulation (TU = 129.96 × 103 min; TL = 20.84 × 103 min).
) as a sample residence time in the lower steady state, and so on. From a long simulation, we compute many sample residence times for both steady states. In Fig. 10, we plot cumulative distributions of these residence times. The top panel compares the cumulative probability distribution for residence times in the upper steady state from full Gillespie and stochasticTQSSA simulations (Fig. 10, a and b, respectively). The dashed lines are single exponential fits to the cumulative distribution. The bottom panel is the same for the lower steady state. Though the stochastic TQSSA calculation produces an exponential decay distribution, the mean residence times for the upper (TU = 42.15 × 103 min) and lower (TL = 5.55 × 103 min) steady states do not agree with the full Gillespie simulation (TU = 129.96 × 103 min; TL = 20.84 × 103 min).
FIGURE 9.
Bistable switch. The trajectory of Ŝ in the bistable zone ( ). (Upper) Full Gillespie simulation. (Lower) Stochastic TQSSA simulation.
). (Upper) Full Gillespie simulation. (Lower) Stochastic TQSSA simulation.
FIGURE 10.
Bistable switch. Plot of cumulative probability (pt) of residence times (tR) for 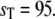 (Upper) Upper steady state. (Lower) Lower steady state. The labeled lines represent full Gillespie (a), and stochastic TQSSA (b). Dashed lines are best-fitting exponential curves to the cumulative probability distributions.
(Upper) Upper steady state. (Lower) Lower steady state. The labeled lines represent full Gillespie (a), and stochastic TQSSA (b). Dashed lines are best-fitting exponential curves to the cumulative probability distributions.
Suspecting that these divergent results might be attributable to poor timescale separation (see the Supplementary Material, Data S1) in our parameter set (Table 1), we repeated the simulations for a new parameter set with large rate constants for association and dissociation of enzyme-substrate complexes, while keeping the rate constant for enzymatic conversion of substrate to product unchanged (see the Supplementary Material, Table S6, Data S1). In this case, we find that stochastic TQSSA simulations are in excellent agreement with full Gillespie simulations with respect to steady-state probability distributions (see the Supplementary Material, Fig. S4, a–c, Data S1) and mean residence times in the lower and upper steady states.
DISCUSSION
The stochastic TQSSA approach differs from tau-leaping and chemical Langevin approaches in that it does not simulate the fast reactions. In tau-leaping (3–6), the number of fast-reaction events that occur during each time interval is estimated using a Poisson random variable, whereas Haseltine and Rawlings (8) simulate the fast reactions using chemical Langevin equations. These methods can work for enzyme-catalyzed reactions, but tau-leaping can be slow for stiff systems and the accuracy of the chemical Langevin equation can be a problem when the number of molecules of reacting species becomes small.
Other approaches rely on the separation of timescales that often occurs in enzyme-catalyzed reactions. Rao and Arkin (9) separate the species according to whether they evolve on fast or slow timescales and show how to obtain a master equation for the slow species that depends on the average values of the fast species. Furthermore, assuming that the timescale separation allows the fast species to equilibrate quickly, they show that in the Michaelis-Menten case the master equation for the slow species corresponds to the reduced reaction obtained using the quasi-steady-state approximation (QSSA). Thus, simulating the reduced reaction using Gillespie's stochastic simulation algorithm will accurately reproduce the noise in the reaction system while avoiding the bottleneck created by the fast reactions.
Goutsias (10) takes a similar approach, but separates the reactions, not species, according to timescale. His approach is more general than Rao and Arkin in terms of how he determines the average values of the fast species, and for the Michaelis-Menten case his approach is not limited by the conditions under which QSSA is valid. In the general case, his approach requires the solution of a system of quadratic equations subject to a linear inequality constraint after each occurrence of a slow reaction.
Cao et al. (11,12) also identify fast- and slow-reaction channels, but propose a framework using the steady-state probability function for the fast species to calculate the moments of the fast species. Recognizing that this calculation will not always be feasible, they explore several approximate methods, the simplest of which involves using equilibrium values from the associated reaction-rate equations.
The TQSSA approach differs from the quasi-equilibrium assumption of Goutsias (10) and Cao (11,12) in that it allows the slow-timescale reactions to impact the steady state of the fast reactions. For the case of large timescale separation, all three approaches will give comparable results. This case is nice theoretically since the average values of the complexes decay quickly to their steady-state values after the firing of a slow reaction, and the master equation governing the slow reactions using the steady-state average propensities is a good approximation to the actual master equation that has time-varying coefficients. In cases with less timescale separation, the time-varying coefficients of the actual master equation do not settle out between firings of the slow reactions. In these cases, the TQSSA approach can still provide a good approximation, as shown in our examples.
For the Goldbeter-Koshland ultrasensitive switch, our stochastic results (means and standard deviations) for the slow variables using TQSSA are all but identical to the results obtained by simulating the full system using Gillespie's stochastic simulation algorithm. In addition, the means for the complexes, which are not directly simulated, are very accurate in all cases, and the standard deviations are accurate except in cases where the free enzyme populations are reduced to only a few molecules. In these problem cases, the inaccuracies in the standard deviations are of the order of 1 molecule. This accuracy for variables that are not directly simulated is surprising. It is due largely to the fact that the standard deviation is composed of components from both the fast and slow reactions, and the fast (unsimulated) component is very small (see Fig. 1 b).
Furthermore, for slow variables, the TQSSA technique accurately captures the autocorrelation function of fluctuations about a steady state. For the complexes, free enzyme, and free substrate variables that are not directly simulated, the autocorrelation functions can consist of multiple exponential components, and our approach will find only the slowest components of the autocorrelation functions. This is to be expected, since all information about fast transients is lost in the TQSSA approach.
Our final example of a coupled Goldbeter-Koshland switch exhibiting bistability is a particularly sensitive test of the accuracy of the stochastic TQSSA, since small changes in stochastic trajectories near the unstable steady state can change the stable steady state that is approached. For the parameter values considered here (Table 1), there is little timescale separation between complex formation and product formation. Even so, TQSSA produces reasonably accurate probability distributions, as seen in Fig. 8, a–c, although the residence time distribution is inaccurate (Fig. 10).
In summary, our results show that stochastic simulations based on the TQSSA can be implemented in a straightforward, algorithmic manner to efficiently calculate accurate trajectories for the slow variables in a multiple-timescale system of chemical reactions.
SUPPLEMENTARY MATERIAL
To view all of the supplemental files associated with this article, visit www.biophysj.org.
Supplementary Material
Acknowledgments
This work has been supported by a grant from the National Institutes of Health (GM078989). We also acknowledge generous support from Virginia Tech's Advanced Research Computing facility for a grant of computing resources on System X.
Editor: Arthur Sherman.
References
- 1.Gillespie, D. T. 1976. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys. 22:403–434. [Google Scholar]
- 2.Gillespie, D. T. 1977. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 81:2340–2361. [Google Scholar]
- 3.Gillespie, D. T. 2001. Approximate accelerated stochastic simulation of chemically reacting systems. J. Chem. Phys. 115:1716–1733. [Google Scholar]
- 4.Cao, Y., L. R. Petzold, M. Rathinam, and D. T. Gillespie. 2004. The numerical stability of leaping methods for stochastic simulation of chemically reacting systems. J. Chem. Phys. 121:12169–12178. [DOI] [PubMed] [Google Scholar]
- 5.Rathinam, M., L. R. Petzold, Y. Cao, and D. T. Gillespie. 2003. Stiffness in stochastic chemically reacting systems: The implicit tau-leaping method. J. Chem. Phys. 119:12784–12794. [DOI] [PubMed] [Google Scholar]
- 6.Cao, Y., D. T. Gillespie, and L. R. Petzold. 2007. The adaptive explicit-implicit tau-leaping method with automatic tau selection. J. Chem. Phys. 126:224101–224108. [DOI] [PubMed] [Google Scholar]
- 7.Gillespie, D. T. 1992. A rigorous derivation of chemical master equation. Physica A. 188:404–425. [Google Scholar]
- 8.Haseltine, E. L., and J. B. Rawlings. 2002. Approximate simulation of coupled fast and slow reactions for stochastic chemical kinetics. J. Chem. Phys. 117:6959–6969. [Google Scholar]
- 9.Rao, C. V., and A. P. Arkin. 2003. Stochastic chemical kinetics and the quasi-steady-state assumption: application to the Gillespie algorithm. J. Chem. Phys. 118:4999–5010. [Google Scholar]
- 10.Goutsias, J. 2005. Quasiequilibrium approximation of fast reaction kinetics in stochastic biochemical systems. J. Chem. Phys. 122:184102–184116. [DOI] [PubMed] [Google Scholar]
- 11.Cao, Y., D. T. Gillespie, and L. R. Petzold. 2005. The slow-scale stochastic simulation algorithm. J. Chem. Phys. 122:014116–014123. [DOI] [PubMed] [Google Scholar]
- 12.Cao, Y., D. T. Gillespie, and L. R. Petzold. 2005. Accelerated stochastic simulation of the stiff enzyme-substrate reaction. J. Chem. Phys. 123:144917–144928. [DOI] [PubMed] [Google Scholar]
- 13.Borghans, J. A., R. J. de Boer, and L. A. Segel. 1996. Extending the quasi-steady state approximation by changing variables. Bull. Math. Biol. 58:43–63. [DOI] [PubMed] [Google Scholar]
- 14.Ciliberto, A., F. Capuani, and J. J. Tyson. 2007. Modeling networks of coupled enzymatic reactions using the total quasi-steady state approximation. PLoS Comput. Biol. 3:e45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Tzafriri, A. R., and E. R. Edelman. 2004. The total quasi-steady-state approximation is valid for reversible enzyme kinetics. J. Theor. Biol. 226:303–313. [DOI] [PubMed] [Google Scholar]
- 16.Goldbeter, A., and D. E. Koshland. 1981. An amplified sensitivity arising from covalent modification in biological systems. Proc. Natl. Acad. Sci. USA. 78:6840–6844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Goutsias, J. 2007. Classical versus stochastic kinetics modeling of biochemical reaction systems. Biophys. J. 92:2350–2365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Novak, B., and J. J. Tyson. 1993. Numerical analysis of a comprehensive model of M-phase control in Xenopus oocyte extracts and intact embryos. J. Cell Sci. 106:1153–1168. [DOI] [PubMed] [Google Scholar]
- 19.Marlovits, G., C. J. Tyson, B. Novak, and J. J. Tyson. 1998. Modeling M-phase control in Xenopus oocyte extracts: the surveillance mechanism for unreplicated DNA. Biophys. Chem. 72:169–184. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.