Effects of a distal mutation on active site chemistry

Abstract

Previous studies of E. coli dihydrofolate reductase (ecDHFR) have demonstrated that residue G121, which is 19Å away from the catalytic center, is involved in catalysis and long distance dynamical motions were implied. Specifically, the ecDHFR mutant G121V has been extensively studied by various experimental and theoretical tools, and the mutation’s effect on kinetic, structural, and dynamical features of the enzyme explored. The current work examined the effect of this mutation on the physical nature of the catalyzed hydride transfer step by means of intrinsic kinetic isotope effects (KIEs), their temperature dependence and activation parameters as described before for the wild type ecDHFR (Sikorski et al. 2004, J. Am. Chem. Soc., 126, 4778–4779). The temperature dependence of initial velocities was used to estimate activation parameters. Isotope effects on the preexponential Arrhenius factors, and the activation energy could be rationalized by an environmentally coupled hydrogen tunneling model, similar to the one used for the wild type enzyme. Yet, in contrast to the wild type, fluctuations of the donor-acceptor distance were now required. Secondary (2°) KIEs were also measured for both H and D transfer and, as in the case of the wild type enzyme, no coupled motion was detected. Despite these similarities, the reduced rates, the slightly inflated 1° KIEs and their temperature dependence, together with relatively deflated 2° KIEs, indicate that the potential surface prearrangement was not as ideal as for the wild type enzyme. These findings support theoretical studies suggesting that the G121V mutation lead to a different conformational ensemble of reactive states and less effective rearrangement of the potential surface, but has only small effect on H-tunneling.

Dihydrofolate reductase from Escherichia coli (ecDHFR) is a small monomeric enzyme (18 kDa) that consists of eight-stranded β-sheet and four α-helices connected with several loop regions. It catalyzes the reduction of 7,8-dihydrofolate (DHF) to 5,6,7,8-tetrahydrofolate (THF) with the concomitant oxidation of NADPH (nicotinamide adenine dinucleotide phosphate, reduced form) to NADP⁺, in which a hydride is stereospecifically transferred from the pro-R C4 position of the nicotinamide ring to the si face of the C6 position of pterin. This enzyme helps maintain intracellular pools of THF used in the biosynthesis of purine nucleotides and some amino acids. Furthermore the essential role of DHFR in DNA synthesis and in a variety of anabolic pathways makes it a common target for antiproliferative therapeutics. Due to its biological and pharmacological importance, and it being a small monomeric enzyme, DHFR has been the subject of intensive structural and kinetic investigation over many years, serving as a paradigm of enzymatic systems in many experimental and theoretical studies (1–8).

The complete kinetic scheme for wild type ecDHFR was derived from equilibrium binding, steady-state, and pre-steady-state kinetic experiments (9, 10). That kinetic scheme revealed that the entire kinetic cascade is rather complex, and that the slowest step at neutral pH is THF release, while the hydride transfer step (the chemical step) is mostly rate-limiting at pH over 8.0. Similar kinetic schemes were constructed for mutant enzymes, laying down the foundation for studies of relationships between kinetics and mutations (11–20). In addition to kinetic studies, structural studies suggested that residues 9–24, denoted as the Met-20 loop, adopt three different conformations (closed, occluded, and open) during the catalytic cycle, and that these conformations are stabilized by interactions between the Met-20 loop and the βF-βG loop (residues 117–131) (21).

Two-dimensional heteronuclear (1H-15N) nuclear magnetic relaxation studies of DHFR demonstrated that glycine-121, though 19 Å away from the catalytic center of the enzyme, had large-amplitude backbone motions on the nanosecond time scale (22–24). Equilibrium binding studies of G121V-ecDHFR indicated that the mutant retained wild-type binding properties with respect to dihydrofolate and tetrahydrofolate; however, binding to NADPH and NADP⁺ was decreased by 40-fold and 2-fold, respectively, relative to wild-type DHFR (23). In yet another study of G121V-ecDHFR that is relevant to this paper, adiabatic compressibility that was determined by the sound velocity indicated a modified volume fluctuation of the native state (25). These results emphasized the role of G121 in packing and stability affecting the enzyme function, via long-range interactions (26, 27). Finally, CD and fluorescence spectroscopy studies indicated that the folding pattern of the enzyme was also altered by G121V mutation (6), which is in accordance with substantial effect of G121V on the protein thermal dynamics.

Support for the connection between enzyme dynamics and catalysis in DHFR came from various theoretical studies. Very different simulations and molecular dynamic studies suggested strong correlated and anticorrelated side chain motions involving spatially removed residues, including G121 (3–5, 28). A computational study by Thorpe & Brooks III (29) suggested that DFT and NADPH populate preferentially a region of configurational space of DHFR that is conducive to the reaction, while substrate and cofactor become trapped in unproductive configurations in G121V-ecDHFR. Hybrid quantum-classical molecular dynamics simulations done by Hammes-Schiffer and coworkers (3, 5) indicated that the decrease in the hydride transfer rate for G121V-DHFR was due to an increase in the free energy barrier but not to a decrease in the transmission coefficients, suggesting that this mutation may interrupt the network of motions coupled to the H-transfer. According to these studies mutations spatially removed from the active site caused nonlocal structural perturbations and significantly affected the catalysis by altering the conformational motions of the entire protein.

These, and other studies, suggested that the G121V mutant affects the dynamic, kinetic and folding properties of the enzyme. This mutant is probably the mutant of ecDHFR that has been studied most intensively. The goal of the present work is to check whether and how this mutation affects the chemical step (C-H-C hydride transfer) of the DHFR catalyzed reaction, and its coupling to the protein dynamics.

Previous studies of G121V that attempted to better isolate the H-transfer from other kinetic steps used stopped-flow methods (11, 30). These pre-steady-state experiments at pH 7 indicated that the rate of hydride transfer was reduced from 220 (for wild type) to 1.3 s⁻¹. The kinetic analysis was complicated by a conformational change, which preceded H-transfer and occurred at a rate of 3.5 s⁻¹. If this step exists in the kinetic mechanism of the wild-type enzyme, then it would be predicted to occur at a rate higher than 2000 s⁻¹. In order to test the suggested dynamic coupling between a remote residue to the H-transfer step at the active site, the effect of the mutation on the H-transfer step has to be isolated from other kinetic steps. Then, effects on the coupling between the active site environment and the nature of the H-transfer have to be compared to these of the wild type enzyme.

While studying the wild type ecDHFR, we have demonstrated that intrinsic KIE can be extracted from competitive KIE experiments of 1° H/T and D/T KIE and that these KIEs appeared to expose the nature of the chemical step better than most other methods (31). The temperature dependence of the intrinsic KIEs indicated possible contributions of quantum mechanical hydrogen tunneling and enzyme motion to the wild type enzyme catalysis. Additionally, 2° KIEs were used to test possible coupling between the 1° and 2° hydrogens on the donor carbon (4C of NADPH). The present study used the same kinetic tools to investigate the effect of G121V on the nature of the hydride transfer step. A comparison of the findings to the wild type enzyme isolated effects of the mutation on the H-transfer event from its effects on other kinetic steps. This in turn, afforded direct comparison to relevant theoretical studies, which most generally focus on that step.

MATERIALS AND METHODS

Materials

All materials were obtained from Sigma unless otherwise indicated. 7,8-Dihydrofolate (DHF) was prepared by dithionite reduction of folic acid as described by Blakely (32). [1-²H]-glucose available from Sigma came with ~98 % deuterium content, which is insufficient for use in competitive KIE measurements. [1-²H]-glucose was prepared by reduction of δ–gluconolactone with 5% sodium mercury amalgam in 99.96% deuterium oxide (D₂O) (33). The C1 deuterium content of the product was over 99.9% as determined by ¹H-NMR.

Synthesis of labeled cofactors for 1° KIEs

R [4-²H]-NADPH was prepared through stereospecific reduction of NADP⁺ with 2-propanol-d₈ (>99.7% D at 2C as determined by ¹H-NMR) using alcohol dehydrogenase from Thermoanaerobium brockii (tbADH) (34, 35). R [4-³H]-NADPH (680 mCi/mmol) was synthesized by reduction of NADP⁺ using glucose dehydrogenase from Cryptococcus uniguttulatus (GluDH), followed by oxidation of the resulting NADPH with acetone using tbADH, followed by a second reduction with unlabeled glucose using GluDH as described in more details elsewhere (36). [Ad-¹⁴C]-NADPH (50 mCi/mmol) was prepared by 2′-phosphorylation of [Ad-¹⁴C]-NAD⁺ using an NAD⁺ kinase from chicken liver to produce [Ad-¹⁴C]-NADP⁺, followed by reduction with glucose using GluDH as described elsewhere (37). R [4,4-²H,³H]-NADPH (680 mCi/mmol) was prepared by following a three-step procedure: NADP⁺ was reduced to S [4-³H]-NADPH with [1-³H]-glucose using GluDH, oxidized by acetone using tbADH, and finally the resulting [4-³H]-NADP⁺ was reduced with [1-²H]-glucose using GluDH. Prior to the final reduction, tbADH was removed by ultrafiltration. [Ad-¹⁴C, 4-²H₂]-NADPH (50 mCi/mmol) was prepared from [Ad-¹⁴C]-NADP⁺, which was synthesized as described above, and then reduced with [1-²H]-glucose to produce 4S [Ad-¹⁴C, 4-²H]-NADPH using GluDH. 4S [Ad-¹⁴C, 4-²H]-NADPH was then oxidized with acetone to produce [Ad-¹⁴C, 4-²H]-NADP⁺ using tbADH, following by a second reduction with [1-²H]-glucose.

Synthesis of labeled cofactors for 2° KIEs

S [4-³H]-NADPH was prepared by reduction of NADP⁺ with [1-³H]-glucose using GluDH. R [Ad-¹⁴C, 4-²H]-NADPH was prepared by reduction of [Ad-¹⁴C]-NADP⁺ (37) with [1-²H]-glucose using GluDH. S [4,4-³H, ²H]-NADPH was prepared by reduction of NADP⁺ with [1-²H]-glucose using GluDH, followed by oxidation with acetone using tbADH and second reduction with [1-³H]-glucose using GluDH. Prior to the final reduction tbADH was removed by ultrafiltration.

A mixture of S [4-³H]-NADPH with [Ad-¹⁴C]-NADPH for 2° H/T KIE measurements with H-transfer was prepared by reducing [Ad-¹⁴C]-NADP⁺ with [1-³H]-glucose using GluDH. A mixture of S [4,4-³H, ²H]-NADPH with R [Ad-¹⁴C, 4-²H]-NADPH for 2° H/T KIE measurements with D-transfer was prepared by reduction of a mixture of [4-³H]-NADP⁺ and [Ad-¹⁴C]-NADP⁺ (36, 37) with [U-²H]-isopropanol (> 99.3 % D in 2C as determined by ¹H-NMR) using tbADH.

All synthesized cofactors were purified by semipreparative reverse-phase HPLC on a Supelco Discovery C18 column (25 cm × 10 mm, 5 μl) as described before (38) and lyophilized for long-term storage at −80 °C.

Enzyme preparation

The G121V mutant of Escherichia coli DHFR (G121V-ecDHFR), was expressed, purified and stored as discussed elsewhere (11, 30).

Methods

Preparation of samples for competitive KIE experiments

For 1° KIE measurements, [Ad-¹⁴C]-NADPH and R [4-³H]-NADPH (H/T experiments) or [Ad-¹⁴C, 4-²H₂]-NADPH and R [4,4-²H, ³H]-NADPH (D/T experiments) were combined in radioactivity ratio close to 1:6 (¹⁴C/³H, compensating for the lower efficiency of tritium scintillation counting). Each of the mixtures was copurified by reverse-phase HPLC on a Supelco Discovery C18 column (25 cm × 4.6 mm, 5 μl), divided into aliquots containing 300,000 dpm of ¹⁴C and frozen in liquid nitrogen for short-term storage (<3 weeks) at −80 °C.

For 2° H/T KIE measurements, mixtures of [Ad-¹⁴C]-NADPH and S [4-³H]-NADPH or R [Ad-¹⁴C, 4-²H]-NADPH and S [4,4-³H, ²H]-for experiments with H or D transfer, respectively, were repurified by HPLC, divided into 300,000 dpm ¹⁴C aliquots (sufficient for ten HPLC injections) and stored at −80 °C for less than three weeks.

Competitive kinetic isotope effects (KIE)

All experiments were performed in MTEN (50mM 2-morpholinoethanesulfonic acid, 25mM Tris, 25mM ethanolamine, and 100mM NaCl) at pH 8.0 under an atmosphere of oxygen over a range of 5–45 °C. In each experiment, one aliquot of the copurified labeled NADPH was thawed just before use. DHF was added to the reaction mixture to a final concentration of 0.85 mM, (approximately 200 fold excess over the 4 μM NADPH). The final volume was brought to 1040μl by adding MTEN and the pH was readjusted to 8.0 at the experimental temperature. Oxygen was bubbled through the reaction mixture for 5 min to ensure the trapping of the product (THF). Before initiating the reaction, two 100 μl samples (t = 0) were withdrawn. Two other 100 μl aliquots for infinite time samples (t = ∞) were also removed and w.t. ecDHFR (approx. 0.2 unit) was added to each of the latter two samples to ascertain complete fractional conversion. The reaction was initiated by adding G121V-DHFR. At various time points 100 μl aliquots were withdrawn at fractional conversions (f) ranging from 25% to 85% as determined from the ¹⁴C distribution between NADPH and NADP⁺. All samples were quenched with methotrexate (final conc. 1.8mM). The overall reaction ran between 15–40 min. and all quenched samples were immediately frozen and stored in dry ice.

Prior to HPLC-LSC analysis, the samples were thawed and bubbled with oxygen for 3 minutes. The samples were then injected into reverse phase HPLC for separation of the reactants and products using the analytical method described elsewhere (38). Fractions (0.8 ml) were collected every minute, mixed with 10 ml Ultima Gold liquid scintillation cocktail (PerkinElmer) and stored in the dark for over 24 hours before β-emission analysis with a Packard Tricarb Tr2900 liquid scintillation counter (LSC) for 5 min/sample. Infinite time samples (t=∞) were processed identically as the time points to estimate background levels of radiation and the ratios of ³H/¹⁴C at t=∞ (R_∞). Blank samples (t=0) were used to assure the quality and purity of the label NADPHs. The observed KIEs were calculated according to (39):

$$\text{KIE}=\frac{ln(1-f)}{ln[1-f\cdot ({\text{R}}_{\text{t}}/{\text{R}}_{\infty })]}$$ [1]

where the fractional conversion (f) was determined from the ratio of ¹⁴C in product to the total ¹⁴C, which was calculated from:

$$f=\frac{[\text{Ad}{-}^{14}\text{C}]{\text{NADP}}^{+}}{[\text{Ad}{-}^{14}\text{C}]{\text{NADP}}^{+}+[\text{Ad}{-}^{14}\text{C}]\text{NADPH}}$$ [2]

and R_f and R_∞ are ratios of ³H/¹⁴C in products at various fractional conversions and at 100% conversion, respectively. Each experiment resulted in at least 5 time points and was performed at least in duplicate.

Intrinsic KIEs

The intrinsic D/T KIEs were derived by numerically solving the following equation (40–44):^•

$$\frac{{}^{\text{T}}{(V/K)}_{\text{D},\text{obs}}^{-1}-1}{{}^{\text{T}}{(V/K)}_{\text{H},\text{obs}}^{-1}-1}=\frac{{(k_{\text{D}}/k_{\text{T}})}^{-1}-1}{{(k_{\text{D}}/k_{\text{T}})}^{-3.34}-1}$$ [3]

where ^T(V/K)_H,obs and ^T(V/K)_D,obs are the observed H/T and D/T KIEs, respectively, and k_D/k_T is the intrinsic D/T KIE. The intrinsic H/T KIE is formulated as (k_D/k_T) (41, 45). In the procedure it is assumed that the Swain-Schaad relationship holds or have little temperature dependence for intrinsic primary KIEs (41, 44, 46). In systems where non-classical isotope effects have been suggested from temperature dependency or theoretical simulation, the experimental relationship between 1° H/T and D/T KIEs have been shown to be very close to the semiclassical limit (44, 47–50). Several recent gas phase calculations for small model reaction also result in Swain-Schaad exponent that at ambient temperature (300–350 °K) did not deviate significantly from its semiclassical value (51–55). Furthermore, even if the magnitude of the exponent (3.3) was altered for a full tunneling model, it would not be expected to change over the narrow temperature range under study and, hence, wouldn’t affect the trend manifested in the temperature dependence of the intrinsic isotope effects (31, 46). To eliminate other common assumptions associated with this procedure (44), the overall reaction should be irreversible in the procedure. Accordingly, the experiments were designed to ensure the irreversibility of the overall reaction by trapping the product THF with oxygen (38). Values for intrinsic H/T and H/D KIEs were calculated numerically using the appropriate modification of Equation 3 (44). Standard errors on the intrinsic KIEs were calculated by calculating the intrinsic KIEs from the raw data (without averaging procedure) followed by standard error analysis as described by Francisco et al. (46), Sikorski et al. (31), and in more details in the Supplementary Information.

The isotope effects on the activation parameters for the intrinsic KIEs were calculated by fitting them to the Arrhenius equation for KIEs:

$$k_{\text{L}}/k_{\text{I}}=(A_{\text{L}}/A_{\text{I}}){\text{e}}^{\mathrm{\Delta }{\text{Ea}}_{\text{I}-\text{L}}/\text{RT}}$$ [4]

where L represents H or D and I represents D or T. A_L /A_I and ΔEa_I-L are the isotope effect on the preexponential Arrhenius factors and the difference in activation energy between L and I respectively.

Non-competitive KIEs

Initial velocity measurements were obtained under saturating conditions of both the substrate and cofactor (100 μM) by monitoring the decrease in 340 nm absorbance (Δε₃₄₀ = 13.2mM⁻¹ cm⁻¹) (56). Experiments were carried out over a temperature range of 5–45°C using a Hewlett-Packard 8453 series UV/Vis spectrophotometer equipped with a water-jacketed cuvette holder. All assays were performed in MTEN buffer (pH 8.0, adjasted at the experimental temperature) containing 1mM DTT. In a typical experiment, 30μl 100nM enzyme was pre-incubated with 100 μM cofactor, and the reaction initiated by addition of 100 μM substrate. DHF and NADPH saturation was ensured by doubling the concentrations of DHF and NADPH at the temperature extremes, which did not affect the measured rates. Turnover rates were also determined with 100 μM R [4,4-¹H, ²H]-NADPH using the same procedure. All measurements were performed at least in triplicate and standard deviations for each temperature set were computed. Calculated k_cat values for each temperature were fit to the Arrhenius equation using a non-linear least-squares regression, in which errors were weighted using the standard deviations. The resulting parameters were used to calculate the activation parameters, and the noncompetitive KIEs on k_cat.

RESULTS AND DISCUSSION

Competitive 1° KIEs

Mixed labeling experiments were conducted with G121V-ecDHFR using the same method previously used to study the wild type ecDHFR (31). Primary H/T and D/T V/K KIE measurements were conducted as described briefly in Ref (31) and in more details here (Materials and Methods). As for the wild type enzyme, the intrinsic H/D, H/T and D/T KIEs were calculated numerically from the observed H/T and D/T KIEs through the methodology developed by Northrop (40, 44, 57). The average intrinsic KIEs and their respective standard errors were then used in calculating the isotope effects on the activation parameters. Tables summarizing the observed and intrinsic 1° H/T and D/T isotope effects over a temperature range from 5°C to 45°C are given in the Supplementary Information. Figure 1 presents the observed (open structures) and intrinsic (close structures) KIEs for both wild type (panel a) (31) and G121V (panel b) ecDHFRs. Figure 2 presents only the intrinsic H/T KIEs for the wild type (blue) and G121V (red) to better asses the differences between these two enzymes. The same trend is also observed for the H/D and D/T KIEs. Apparently, all the KIEs of G121V are slightly larger than those measured with wild-type DHFR and are slightly temperature dependent.

Figure 1.

Arrhenius plot of observed (open structures) and intrinsic (close structures) 1° KIEs for the wild type ecDHFR (Panel a. From Ref (31)) G121V-ecDHFR (Panel b. From Tables 1 and 2 in the Supplementary Information to this paper). The lines represent the non-linear regression to Equation 2.

Figure 2.

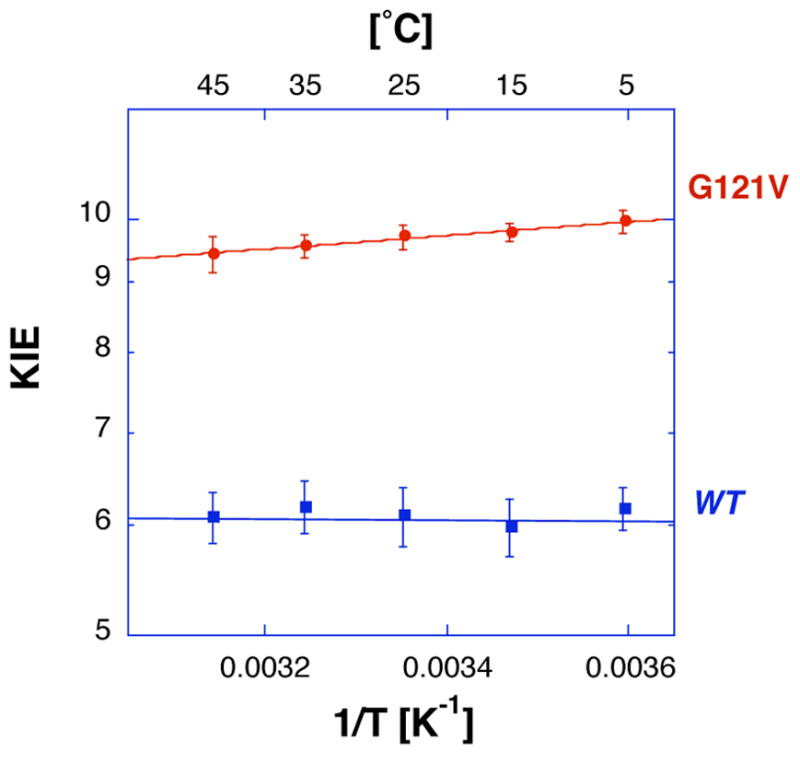
Arrhenius plot of intrinsic H/T KIEs for the wild type (blue) and G121V (red) ecDHFR (same as the blue points and lines in both panels of Figure 1).

The reason that the observed KIEs are often smaller than their corresponding intrinsic KIEs is that isotopically insensitive kinetic steps “mask” the intrinsic KIEs. In the current work the KIEs were measured under irreversible reaction conditions and the kinetic complexity can be formulated as follows (44, 58):

$${}^{\text{T}}{(\text{V}/\text{K})}_{\text{L},\text{obs}}=\frac{{\text{k}}_{\text{L}}/{\text{k}}_{\text{I}}+{\text{C}}_{\text{f}}}{1+{\text{C}}_{\text{f}}}$$ [5]

where C_f represents the forward commitment to catalysis, which is the ratio of the forward isotopically insensitive step over preceding reverse steps. The intrinsic H/D KIE at 25°C afforded calculations of the commitment on the pre-steady-state hydride transfer rate at the same temperature and pH 7 as reported in Ref. (11). The KIE measured for G121V by pre-steady-state kinetics using UV absorbance and fluorescence resonance energy transfer (FRET) at 25°C was 2.4 (30). The intrinsic KIE that we report here is 4.9 ±0.2, suggesting a commitment close to 1.8 on the pre-steady-state KIEs. In accordance with Ref s. (30) and (31), a model that may explain the commitment on the pre-steady-state hydride transfer rate includes two kinetic steps, the isotopically insensitive flip of the nicotinamide ring out of the active site (the reverse of flip-in observed by FRET (30)), and the hydride transfer itself. Taken together, the much slower flip-in of the nicotinamide ring (3.5 s⁻¹ and 2000 s⁻¹ for G121V-DHFR and w.t. ecDHFR, respectively) and the increased pre-steady-state commitment for the G121V-DHFR suggest that the flip-out is also slower for the mutant. Similar conclusions were reached by Wright et al. from their NMR studies (23, 59), identifying the effect of the G121V mutation on the rates and thermodynamic distribution of the different conformational ensembles of the same wild type and mutant enzymes studied here (24). According to Wright’s experiments, the motion of the nicotinamide ring seems to be correlated to the motion of the M20 loop from occluded to closed conformation. It is important to note that the protein-substrate coherent motion, suggested from the NMR studies, is not an indication of protein modes coupled to the H-transfer coordinate, which is the focus of the current work. The coupled motion identified by Wright and coworkers (24, 59) is involved in the orientation of the reactants in the active site prior to the chemical step (H-transfer). Such motion might be relevant to the formation of near attack conformation (NAC) as suggested by Bruice and co-workers (60–62), but is part of the commitment and not the chemical step. As emphasized in the following section, the current work examine the effect of the dynamically altered mutant G121V on the C-H-C transfer step, which is the only step in which covalent bonds are cleaved or made (cf., the chemical step).^••

Temperature dependence of intrinsic KIEs and rates

The measured H/T and D/T KIEs were used to calculate the intrinsic KIEs. Figure 1 presents Arrhenius plots (KIE on a logarithmic scale vs. the reciprocal of the absolute temperature) for the observed and intrinsic KIEs for both wild type (reproduced from Ref. (31)) and G121V mutant (from this study, see Tables in the Supplementary Information). While the intrinsic KIEs for the wild type enzyme appeared temperature independent, those of G121V were a little larger and some temperature dependency is apparent (Figure 2). The temperature dependence was further examined by fitting the intrinsic KIEs to Eq. 4 (the lines in Figure 1 and 2) and the fitting parameters are summarized in Table 1.

Table 1.

Rates and isotope effects on Arrhenius factors.

EcDHFR:a	Wild Typeb	G121V
Rate c [s−1]	228 ±8	1.4 ±0.2	S.C. Al/Ahd
AH/AT	7.0 ±1.5	6.6 ±1.3	0.5 – 1.6
AH/AD	3.5 ±0.5	3.7 ±0.5	0.6 – 1.4
AD/AT	1.70 ±0.14	1.8 ±0.1	0.9 – 1.2
ΔEa H-T	−0.1 ±0.4	0.22 ±0.12
ΔEa H-D	−0.07 ±0.3	0.16 ±0.08
ΔEa D-T	−0.03 ±0.1	0.07 ±0.03
ΔG‡ 25 °C c	14.3 ±0.5	17.3 ±0.5
ΔH‡	3.1 ±0.2	2.6 ±0.3
TΔS‡25 °C	−11.2 ±0.5	−14.7 ±0.6

^aAll energy units are in kcal/mol

^bFrom Ref. (31).

^cPre-steady state rates at pH = 7 from Refs (11) and (30).

^dSemiclassical limits of isotope effects on Arrhenius preexponential factors A_l/A_h where A_l and A_h are the factors for the light and the heavy isotopes, respectively (39, 41, 57, 64–67).

Initial velocity studies between 20 to 45 °C (pH = 9, at which chemistry is more rate limiting on k_cat for both enzymes (9, 11)) resulted in similar activation energies for both enzymes (E_a = 3.7 ±0.2 and 3.2 ±0.3 kcal/mol for wild type and G121V, respectively). Below 20 °C E_a for both enzymes was larger indicating a change in rate limiting step. These E_as are in accordance with a pre-steady-state study (for the chemical step) and steady state (for product release step) measurements by Maglia and Alemann (63). Naturally, ΔH^‡s for both enzymes (above 20 °C) were also similar (ΔΔH^‡ = 0.5 ±0.5 kcal/mol). Apparently, the difference in rates between the two enzymes results from TΔΔS^‡ = 3.5 ±0.8 kcal/mol at 297 K (Table 1).

The initial velocities were also measured with R [4-²H]-NADPH (under the same conditions), and the resulting KIEs on k_cat were all temperature independent and within the range of 2.8 ±0.6. This value is similar (within experimental errors) to the one measured by pre-steady-state experiments, supporting the conclusion of Cameron et al. (11) that at pH 8 the same kinetic steps limited k_cat and k_H-transfer. As discussed below, this provides additional support to the suggested interpretation.

This paper focuses on the effect of the distal mutation on the chemical step, so effects on the intrinsic KIEs are discussed in detail. As apparent from Table 1, all isotope effects on the Arrhenius preexponential factors lie well above the semiclassical limits (39, 57, 64–67). Traditionally, using a tunneling correction to transition state theory (39, 64), such phenomenon would be interpreted as an indication for tunneling of both heavy and light isotopes (68). Yet, the relatively small size of the KIEs and the measured energy of activation cannot be explained by such a tunneling correction, which predict very large KIEs and no energy of activation at the regime where both isotopes tunnel, leading to temperature independent KIEs (68, 69). “Marcus like” models (discussed in the following section) appear to explain the findings better. These models can also be used to rationalize the lack of isotope effects on the activation energy for the wild type enzyme and the small, but non-zero E_a for the mutant (Table 1).

“Marcus Like” models (Environmentally Coupled Tunneling)

Models assuming 1-dimensional rigid potential surface successfully reproduced temperature independent large KIEs with no activation energy of the isotopically sensitive step (48). For temperature independent small KIEs with a significant activation energy a different kind of model is required. The Markus theory of electron and proton transfer in condensed phase offered a relevant procedure (70–73). Several phenomenological models were developed in recent years that fall under the title “Marcus like” models (e.g., Refs (74–80)). All these models were constructed assuming that rates and KIEs can be measured for a single kinetic step (the chemical step), and thus are relevant to the experimental efforts described here. Although these different models were constructed from very different basic principles, they all share several mathematical and physical aspects. Mathematically, they separate the temperature dependence of the reaction rate from that of the KIEs. This enables rationalization of systems with or without temperature dependent KIEs whether the barrier for the reaction is significant or not. From the physical point of view, all these models suggest that (i) the hydrogen should be treated quantum mechanically throughout the reaction coordinate (including tunneling); (ii) fluctuations of the reaction’s potential surface are at a time scale similar or slower than the H-transfer rate, and thus determine the overall rates (81) (the solvent coordinate is the reaction coordinated as stated by Kiefer and Hynes (51, 52); and (iii) these fluctuations can be treated as two orthogonal vibrations, one that represents fluctuations of the donor-acceptor distance and second that represents changes in the system’s symmetry (Figure 3). Various terms have been coined recently to characterize H-transfer in enzymatic systems, including “vibrationally enhanced tunneling” (79), “rate-promoting vibrations” (80) and “environmentally coupled tunneling” (74, 75). In this paper we use the term “Environmentally Coupled Tunneling” (ECT) that was coined by Knapp and Klinman (74), although other terms coined by others are as valid. This model follows the treatment of Kuznetsov and Ulstrup (82), and the changes in the system’s symmetry are addressed as system “rearrangement” (the “Marcus” term) and fluctuations of the donor-acceptor distance as “gating” (the “Franck-Condon“ term). The first term (represented by the p coordinate in Figure 3) is not dependent on the mass of the transferred particle (no KIE) but determine most of the energy of activation of the rate. The second term (represented by the q coordinate in Figure 3) determines the KIEs and their temperature dependence (e.g., no “gating”, no temperature dependence on the KIEs).

Figure 3.

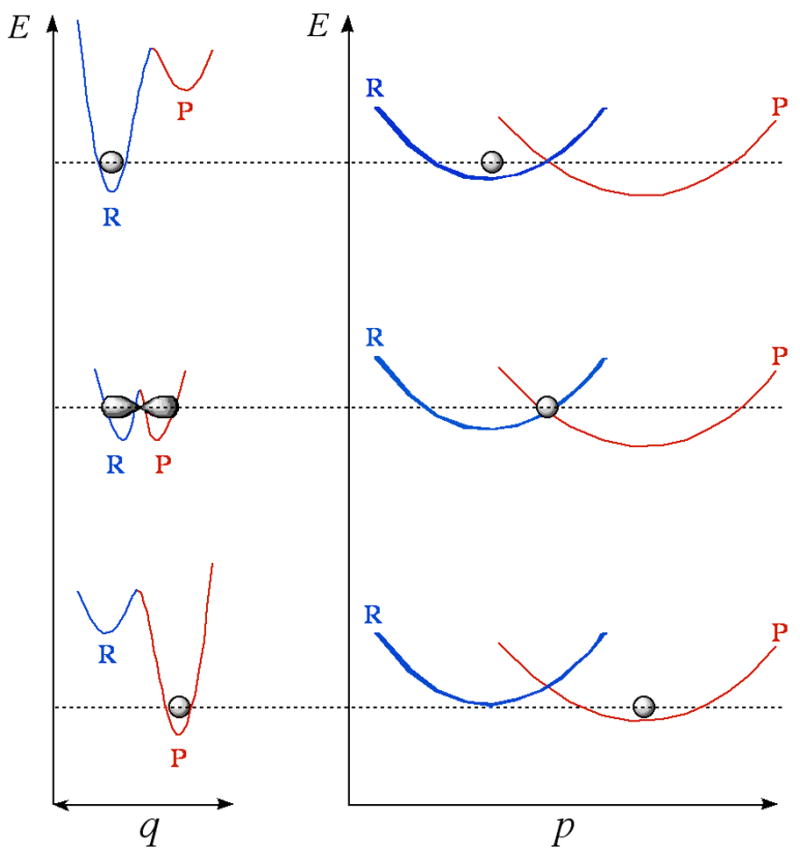
Illustration of “Marcus-like” models: energy surface of environmentally coupled hydrogen tunneling. Two orthogonal coordinates are presented: p, the environmental energy parabolas for the reactant state (R) and the product state (P); and q, the H-transfer potential surface at each p configuration. The gray shapes represent the populated states (e.g., the location of the particle). Thermal fluctuations of the distance between donor and acceptor along the q coordinate (denoted “gating” by Knapp and Klinman (74)) leads to the temperature dependency of the KIE.

According to this interpretation the lack of temperature dependence of the KIEs and the large A_l/A_h for the wild type ecDHFR are rationalized as a perfect “rearrangement” (the p coordinate in Figure 3) of the potential surface, so that the average donor-acceptor distance is right for tunneling and no “gating” (fluctuations along the q coordinate, Figure 3) is needed. For the G121V mutant on the other hand, the slightly inflated KIEs and their small, but non-zero, temperature dependence, would indicate that the “rearrangement” is not perfect, and that the average donor-acceptor distance is larger than for the wild type enzyme. Accordingly, some thermally activated “gating” is required which leads to the slight temperature dependence of the KIEs. Additionally, this model is also in accordance with the slightly inflated KIEs as H tunnels from longer distance than D.•••

An alternative to the phenomenological models would be QM/MM studies such as these described in Refs (2), (83), and (84). While studying ecDHFR for example, Garcia-Viloca et al. (7) predicted a 2° KIE (which is a sensitive probe of the reaction’s potential surface and was later confirmed experimentally (31)); Pu et al. (8) could reproduce the trends of temperature dependence for 1° KIEs, and Agarwal et al. (28) could reproduce and predict several experimental data. All these studies could address the role of protein motion and other mechanistic features that are not directly accessible by experimental studies. Since the substantial features of “Marcus like” models are embedded in the QM/MM simulation, it would be worthwhile to “extract” features like “gating” from such simulations. Such efforts by Hammes-Shiffer and co-workers while studying the enzyme lipoxygenase (85) and by Warshel and co-workers while studying alcohol dehydrogenase (86) resulted in very interesting insights.

Interestingly, the isotope effect on the preexponential Arrhenius factors for the wild type and mutant enzymes are practically the same (within experimental errors). This in turn, suggests that despite the 163 fold difference in rates (11, 30), the mutation has not substantially altered the nature of the hydride transfer. This conclusion is also in agreement with MM/QM calculations by Hammes-Shiffer and co-workers (1, 28) that suggested a similar nature of H-transfer (κ) but larger free energy barrier (ΔG^‡). Interestingly, the effects of the mutation on the activation parameters (TΔS^‡ = 3 ±1 kcal/mole at 300 K and ΔH^‡= 0.5 ±1.7 kcal/mol), suggest that most of the difference between the wild type and G121V is entropic and not on the enthalpy of activation. A deconvolution of the free energy of activation calculated from the simulation reported in Ref. (28) into entropic and enthalpic components might be able to give insight to these findings.

Wright and co-workers compared the conformational ensembles of the reactant and product states of both wild type and G121V ecDHFRs (23, 24). They concluded that the “close” conformation of loop M20 (believed to be the productive one) is more prevalent in the reactant state of the wild type enzyme. Taken together with the present kinetic findings, it is ttempting to suggest that their findings can now be extended beyond these two stable states to indicate different conformational ensembles at the transition state. Yet, this extension is only circumstantial, because the spectroscopic data examined two stable states while the kinetic data are also affected by the transition state and thus reflect its nature.

The hybrid quantum-classical molecular dynamic simulation conducted by Watney et al. (5) also suggested that the conformational ensemble at the transition state is affected by the G121V mutation. That simulation compared the wild type enzyme to the G121V mutant and the results suggested that the mutation affected both the conformational ensembles of the mutant along the reaction coordinate and the coupling of its dynamics to the H-transfer event. Furthermore, the calculations indicated that most of the effect of the mutation on the enzyme’s activity was by altering the potential surface reorganization, and only small change in the degree of tunneling and the transmission coefficient was observed. The findings presented here provide experimental support to both conclusions. Apparently, the nature of the H-transfer was not altered significantly, and less perfect reorganization is in accordance with the slightly inflated KIEs and their temperature dependence.

Finally, 2° H/T KIEs for the G121V mutant (at 25 °C) were measured with S [4-³H]-and with S [4,4-³H,²H]-NADPH, namely with H- and D-transfer from the 1° I position. The observed 2° KIEs were 1.087 ±0.005 and 1.125 ±0.007, for H- and D-transfer, respectively. The observed 2° KIE and the commitments for H and D reported above (C_f of 0.7 ±0.1 and 0.15 ±0.05 for H- and D-transfer, respectively) were used to calculate the intrinsic KIEs (Eq. 5). These intrinsic 2° KIEs were identical within experimental errors (1.15 ±0.01 and 1.14 ±0.02 for H- and D-transfer, respectively). As in the case of the wild type enzyme (31), no breakdown of the rule of geometrical mean (87) was apparent, providing no evidence for 1°–2° coupled motion (57, 67, 88–90). These intrinsic 2° H/T KIEs are smaller than these measured for the wild type enzyme 1.19 ±0.2 (31), suggesting different transition state conformations, and possibly different carbon center rehybridization. The lack of coupled motion for both enzymes agrees with a similar nature of the H-transfer mechanism, but reduced 2° KIEs indicate some differences in the system’s vibrational states, which could be in agreement with different rearrangements of the potential surface close to the transition state. Interestingly, a more rigorous MM/QM study of the 2° KIEs for the wild type ecDHFR indicated non-synchronized hybridization of the donor and acceptor carbons and slightly associative transition state (91). A similar study of the G121V mutant is under way, and it’s findings may shed light on the differences between the transition state ensembles of the wild type and G121V ecDHFRs.

CONCLUSIONS

The H-transfer step in the reaction catalyzed by the mutant G121V-ecDHFR was examined and compared to that of the wild type ecDHFR. The temperature dependence of the intrinsic 1° KIEs with G121V yields isotope effects on Arrhenius parameters that lie well above the semiclassical limits, and were identical (within experimental errors) to the wild type enzyme. The enthalpy of activation for both enzymes at high pH (where the chemical step is more rate limiting for both enzymes) was also similar, and most of the rate differences appear associated with change in entropy. The findings with both the wild type ecDHFR (31) and G121V-ecDHFR are consistent with environmentally coupled hydrogen tunneling (74) and other “Marcus like” models in which the motion of the active site is coupled to the H-transfer coordinate. The G121V mutation seems to have little effect on the nature of H-transfer, yet, while the wild type ecDHFR reaction presented no temperature dependence of the KIEs, that of the mutant did indicate small, but non-zero, temperature dependence of these KIEs. Several phenomenological working-models can be used to rationalize our current findings. Using the terminology coined the Knapp and Klinman model, the wild type reaction involves environmentally coupled H-tunneling with perfect pre-organization of the potential surface (no donor-acceptor gating motion needed). Alternatively, the models such as Truhlar (81) or of Kiefer and Hynes (51, 52) would suggest that for the wild type enzyme the rearrangement of the “solvent coordinate” leads to an average distance of donor and acceptor that is ideal for tunneling. The G121V mutation (~19 Å from the reaction center) seems to affect the preorganization of the system so that some thermally activated donor-acceptor fluctuations now affect H-tunneling, resulting in slightly larger and more temperature dependent KIEs. These findings are in accordance with this remote residue being part of a dynamic network that is coupled to the catalyzed chemistry (1, 3, 5, 7, 30). These QM/MM models did not deconvolute their simulation in terms used by the “Marcus like” models mentioned above. Consequently, direct comparison of simulation and phenomenological studies is yet to come.

The 2° H/T KIEs measured with either H- or D-transfer were identical (within experimental errors). This result does not indicate coupled motion between the 1°and 2° C4 hydrogens (68, 69). A similar conclusion has been drawn for the wild type enzyme from the “mixed labeling” experiment (in which 2° H/T is measured with H-transfer and 2° D/T with D-transfer (67, 88, 92). The comparison of the two enzymes is again in accordance with similar nature of H-transfer. The size of the 2° KIEs on the other hand was smaller for the G121V indicating differences in transition state structure and vibrational states. A QM/MM study, similar to the one conducted with the wild type (91), is under way to explore the differences in these 2° KIEs on the molecular level.

In the future tools similar to those described above will be used to examine the effect of dynamic perturbation of DHFR on its catalyzed chemistry. Different theoretical studies suggested that other residues (specifically, M42 and S148) also participate in the same network of protein motions as G121, and that this network is directly coupled to the H-transfer event (1–3, 29). Of special interest are the mutants M42W and M42W-G121V, for which non-additive decrease in rates suggested synergism between residues 121 and 42 (30). Recent study (3) suggested that several other residues, and specifically S148, were also part of the same network. Detailed examination of different combinations of the G121V-M42W-S148A single, double and triple mutants, using the tools described above, is yet to be conducted.

Abbreviations

DHFR

dihydrofolate reductase

KIE

kinetic isotope effect

RP HPLC

Reverse Phase High Pressure Liquid Chromatography

LSC

Liquid Scintillation Counter

DHF

7,8-dihydrofolate

THF

5,6,7,8-tetrahydrofolate

TEAA

triethyl ammonium acetate

NADPH

nicotinamide adenine dinucleotide 2′-phosphate (reduced form)

NADP⁺

nicotinamide adenine dinucleotide 2′-phosphate (oxidized form)