Abstract
Epidemiological studies routinely use central-site particulate matter (PM) as a surrogate for exposure to PM of ambient (outdoor) origin. Below we quantify exposure errors that arise from variations in particle infiltration to aid evaluation of the use of this surrogate, rather than actual exposure, in PM epidemiology. Measurements from 114 homes in 3 cities from the Relationship of Indoor, Outdoor and Personal Air (RIOPA) study were used. Indoor PM2.5 of outdoor origin was calculated: 1) assuming a constant infiltration factor, as would be the case if central-site PM were a “perfect surrogate” for exposure to outdoor particles; 2) including variations in measured air exchange rates across homes; 3) also incorporating home-to-home variations in particle composition, and 4) calculating sample-specific infiltration factors. The final estimates of PM2.5 of outdoor origin take into account variations in building construction, ventilation practices, and particle properties that result in home-to-home and day-to-day variations in particle infiltration. As assumptions became more realistic (from the first, most constrained model to the fourth, least constrained model), the mean concentration of PM2.5 of outdoor origin increased. Perhaps more importantly, the bandwidth of the distribution increased. These results quantify several ways in which the use of central site PM results in underestimates of the ambient PM2.5 exposure distribution bandwidth. The result is larger uncertainties in relative risk factors for PM2.5 than would occur if epidemiological studies used more accurate exposure measures. In certain situations this can lead to bias.
Introduction
Numerous epidemiological studies have shown a positive association between ambient (outdoor) particulate matter (PM) concentrations and cardiovascular and respiratory morbidity and mortality (1-4). Adverse effects are more closely associated with fine particles (PM2.5) than coarse (3, 5-7). Since a causal association requires exposure (8), the epidemiological findings have prompted initiation of many exposure studies (9). Pooled (frequently called cross-sectional) exposure studies have consistently found poor correlations between ambient PM2.5 concentrations and personal exposure to PM2.5 (9-16). These poor correlations were initially used to argue that ambient PM is a poor surrogate for exposure to PM and to question the epidemiological conclusions (11, 17, 18). In response, Wilson (6) and Mage (19) argued that the seeming contradiction between the exposure studies and epidemiological findings is “a logical syllogism”. They argued that the composition and properties of ambient particles differ substantially from those generated in other microenvironments and that the epidemiological studies use central-site ambient PM as a surrogate for exposure to “PM of ambient origin”, not as a surrogate for total PM exposure. This argument is now supported by longitudinal exposure studies, which show higher outdoor – personal PM correlations for individuals (20-22). As a result, recent exposure analyses are being conducted to characterize exposure to ambient and non-ambient particles (i.e., when, where, how and how much), to quantify exposure errors arising from the use of a central site surrogate, and to understand the effect of such errors on epidemiological conclusions.
The indoor environment is an important location for exposure because people spend more than 85% of their time indoors (23). PM in indoor environments consists of (a) ambient particles from regional and local sources that have infiltrated indoors and persist (1), (b) primary particles emitted indoors (24), and (c) secondary PM formed indoors from reactions of precursor gases of indoor and outdoor origin (25, 26). Particles generated indoors and outdoors have different sources and are likely to have different chemical and physical properties and different toxicities (27,28).
In this work PM2.5 mass and species and air exchange rates measured in the Relationship of Indoor, Outdoor and Personal Air (RIOPA) study were used to quantify the residential outdoor contribution to indoor PM2.5 concentrations using several approaches with increasingly more realistic assumptions (i.e., decreasing constraints on particle infiltration behavior). The results provide an improved mechanistic understanding of parameters influencing indoor PM2.5 of ambient origin and thus a subset of parameters influencing community exposure to ambient PM2.5. Results aid assessment of exposure error in epidemiological studies.
Methods
Sample collection and analysis
Study design, sampling, analysis, and quality control measures are described in Supporting Information and in previous publications (5,16). Briefly, residential indoor and outdoor PM2.5 samples were collected from summer, 1999 to spring, 2001 in 212 homes in Houston (TX), Los Angeles County (CA), and Elizabeth (NJ) as part of the RIOPA study (29). One hundred sixty-two of these homes were sampled a second time approximately three months later. PM2.5 samples were collected in Harvard Impactors on Teflon filters for 48 hours at 10 lpm (16) and analyzed for mass (16) and functional groups (30); a subset were analyzed for trace elements (31).
Indoor and outdoor samples were also collected concurrently on a quartz fiber filter (QFF) followed by polyurethane foam (PUF) for 48 h at 10 l/m (25 cm/s face velocity) in a subset of homes for measurement of particulate organic carbon (OC), elemental carbon (EC), and gas- and particle-phase polycyclic aromatic hydrocarbons and chlordanes (32-35). In this study, a QFF was also placed downstream of the Teflon filter in the Harvard Impactor. This quartz fiber backup filter sample provides an estimate of the organic vapor adsorbed on the concurrently collected quartz fiber front filter in the second sampler. Backup filter OC was subtracted from the concurrently collected front filter OC to obtain particulate OC concentrations (32, 36). The air exchange rate for each home during each 48-hr sampling period was determined from the house volume and concentration of a perfluorocarbon tracer emitted at a constant rate (29, 37).
The contribution of outdoor PM2.5 to the indoor environment
As described below, PM2.5 mass and species concentrations were used to calculate the contributions of outdoor and indoor-generated PM2.5 to indoor PM2.5 concentrations using several approaches with increasingly more realistic assumptions. Results from these methods were then compared, and insights into exposure errors discussed.
The 114 RIOPA homes that had one complete set of 48 hr measurements (i.e., OC, EC, elements, mass, and air exchange rate) were used. Samples from these homes were selected for “complete chemical analysis” in order to create a PM speciation data set reasonably evenly distributed between the three cities, across seasons and between homes in close proximity (< 200 m) and farther from identified local sources. Table S1 in Supporting Information summarizes measurements for these 114 homes. Table S2 in Supporting Information provides the distribution of measurements across cities and seasons.
Assuming perfect instantaneous mixing and assuming that factors affecting indoor concentrations are constant or change slowly throughout the monitoring period, the steady state indoor PM2.5 mass concentration can be described with a single compartment mass balance model. Indoor PM2.5 concentrations are described as the sum of PM generated outdoors (ambient contribution) and PM generated indoors (non-ambient contribution), as follows:
| (1) |
where Ci is the indoor PM2.5 mass concentration, Ca is the ambient (outdoor) PM2.5 mass concentration, FINF is the dimensionless infiltration factor, Cpig is the concentration of indoor-generated PM found indoors, and Cai is the concentration of ambient-generated PM found indoors. In the mass balance model, FINF is given by Pa/(a+k), where P is the dimensionless penetration coefficient, a is the air exchange rate (h-1), and k is the particle loss rate (h-1). Also in the mass balance model, Cpig is Qi/V(a+k), where Qi is the indoor source strength (μg/h), and V is the house volume (m3). In reality, air exchange rate, P and k differ from home-to-home, day-to-day and species-to-species.
The residential outdoor contribution to indoor PM2.5 was calculated in four ways with increasingly more realistic assumptions. The first approach (the Random Component Superposition Model; RCS) assumes the infiltration factor, FINF, is constant across homes (38) as would be the case if central site PM2.5 were a perfect surrogate for PM2.5 of outdoor origin. The second approach (Mass Balance Model) uses the measured air exchange rate for each home and assumes that the penetration of particles into the home (P) and loss rate coefficient (k) of particles indoors are constant across the homes. In this way FINF varies only with air exchange rate. The third approach (External Mixture Model) uses measured air exchange rates and determines species-specific P and k values that do not vary from home-to-home or day-to-day. In this way FINF varies with PM composition as well as air exchange rate. The fourth approach (Microscopic Mixture Model) uses all measured major PM2.5 species collected concurrently at the same home to calculate an infiltration factor for that sample. Because only concurrently-collected data at a single home are used to determine the infiltration factor for that home and day, the distribution of infiltration factors across all sampled homes (many sampled on different days) takes into account the possibility that variations in building construction, ventilation practices, particle size distributions, particle composition, and the chemical/thermodynamic properties of particles might occur across homes and days, introducing home-to-home and day-to-day variations in particle infiltration behavior.
Random Component Superposition Model
The random component superposition statistical (RCS) model (38) computes a constant infiltration factor, FINF, from the linear regression of all measured outdoor PM2.5 mass concentrations on indoor concentrations (see Equation 1). The product of FINF with each outdoor concentration, Ca, provides an estimated mean, median and standard deviation of the outdoor contribution (Cai) to indoor PM2.5. This model assumes a linear superposition of the ambient and non-ambient contributions to indoor PM2.5, and lack of correlation between these two components. The accuracy of FINF obtained this way increases as the number of measurements increases. This is because the slope (FINF) is easily influenced by outliers. The standard deviation of the outdoor contribution to indoor PM2.5 obtained by the RCS model is not affected by this limitation.
Mass Balance Model
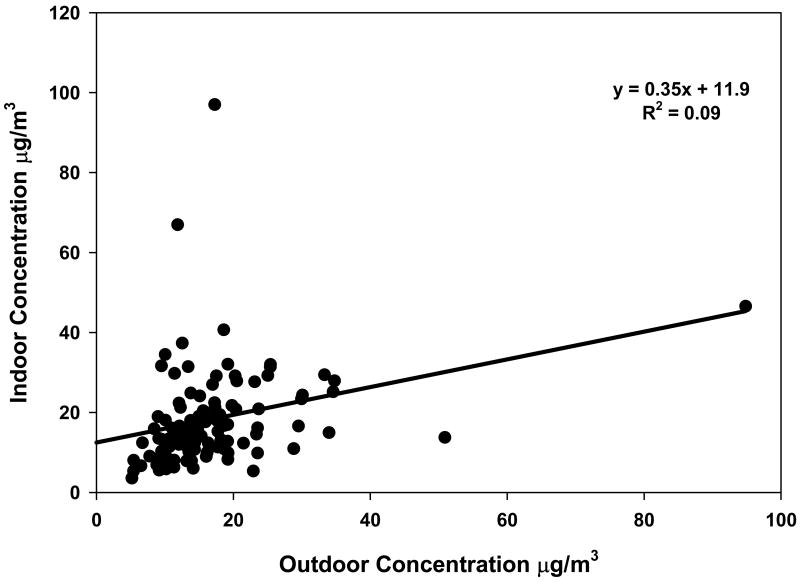
Indoor and outdoor PM2.5 mass concentrations are shown in Figure 1. Mass balance model results were obtained by fitting measured indoor (Ci) and outdoor (Ca) PM2.5 mass concentrations and air exchange rates (a) to the mass balance equation (Equation 1) using nonlinear regression (NLIN in SAS). This results in the estimation of a single particle penetration coefficient (P) and particle loss rate coefficient (k) for the 114 home dataset. P was constrained to be physically plausible (0 ≤ P ≤ 1). Ambient and nonambient contributions to indoor PM2.5 concentrations were then calculated for each home using these constant values of k and P, measured indoor and outdoor PM2.5 concentrations, measured air exchange rates and Equation 1. The biggest limitation of this method is that the estimates of P and k obtained by nonlinear regression are not truly independently determined. P and k estimates are more stable when indoor source strengths are not highly variable. The impact of reasonable variations in P and k on the outdoor contribution are quantified in the sensitivity analyses below.
Figure 1. Indoor and outdoor PM2.5 mass concentrations from 114 RIOPA homes. Line is the linear least squares regression line.
External Mixture Model
In the previous section, infiltration factors were calculated allowing air exchange rate to differ from home to home but using a fixed P and k across homes. In reality, P and k will vary from home to home and day to day. P varies with particle size and house structure. The indoor particle loss rate coefficient, k, is determined by many factors including the indoor surface-to-volume ratio, housing structure, near-surface air flows, turbulence and the particle size distribution. Particle composition and size distribution are dictated by particle formation mechanisms. If variations in P and k are predominantly dictated by the particle size distribution, the next most logical model improvement would be to provide species-specific P and k values. Assuming fixed species-specific P and k values is like treating the aerosol as an external mixture of chemical species. The overall PM2.5 infiltration factor for a single home could then be calculated as a linear combination of its components' infiltration factors:
| (2) |
where
FINF --- infiltration factor for a single home (dimensionless)
FINFi --- infiltration factor of the ith component of PM2.5 in a single home (dimensionless)
wi --- mass fraction of the ith component of PM2.5 in a single home (dimensionless)
Pi --- Penetration coefficient of the ith component in a single home (dimensionless)
a --- air exchange rate of a single home (h-1)
ki --- loss rate of the ith component in a single home (h-1)
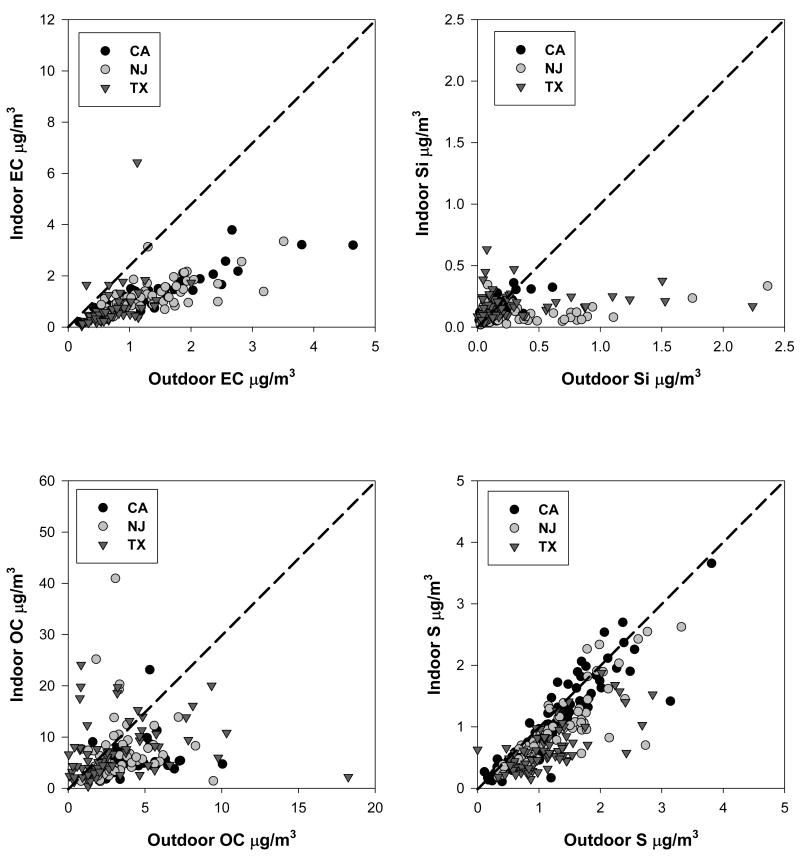
Indoor and outdoor concentrations of four PM2.5 species are shown in Figure 2. Species-specific but home-averaged P and k values were estimated for each of 22 measured species by nonlinear regression (NLIN in SAS) of the 114 measured indoor concentrations of species i (Ci) on the concurrently measured outdoor concentrations of species i (Ca) and air exchange rate (a). P was constrained to values between 0 and 1. Species-specific P and k values were used to calculate FINF for each home as described in Equation 2. To calculate wi (see Equation 2) sulfur was converted into (NH4)2SO4; OC was converted into organic matter multiplying by an estimated molecular weight/carbon weight of 1.4; oxides of Al, Si, Ca, Ti, K and Fe were used to calculate soil weight; and other elements were also converted to oxidant form (39, 40). Each species mass was divided by the sum of measured species to calculate wi. It is recognized that mass reconstruction is not perfect (i.e., sulfate is not always fully neutralized in the east, the organic molecular weight per carbon weight is sometimes greater than 1.4, and a portion of the measured mass was not accounted for by measured species), however it provides a reasonable weighting of the species-specific P and k values. As for the mass balance model, P and k are not truly independent and P and k values are more stable for species with less variable indoor source strengths. Also, it must be noted that one major species, nitrate, was not measured. The impacts of these limitations on estimates of the outdoor contribution to indoor PM2.5 are explored in sensitivity analyses below.
Figure 2. Indoor and outdoor concentrations of sulfur, silicon, organic carbon (OC) and elemental carbon (EC) by location: California (CA), New Jersey (NJ) and Texas (TX).
Microscopic Mixture Model
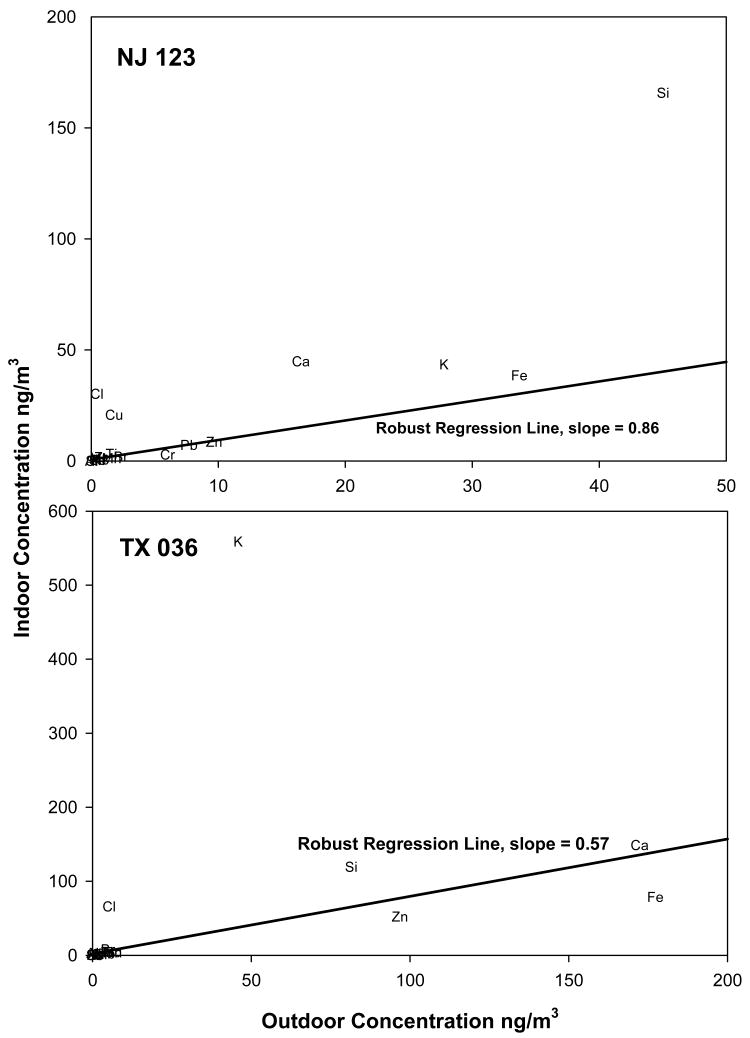
The microscopic mixture model uses all measured PM2.5 species and allows P, k and a to differ from home to home and species to species. Figure 3 shows the indoor and outdoor concentrations of individual PM2.5 species measured concurrently in a New Jersey (Fig. 3a) and Texas (Fig. 3b) home. The data in each figure represent individual PM2.5 species measured concurrently in the same home. Some species have substantial indoor sources, as evidenced by indoor concentrations that exceed their outdoor concentrations. Other species appear to be distributed around a regression line. All concurrently measured species in the same home are acted upon by the same air exchange rate. If all species also had the same size distribution, and were chemically/thermodynamically stable, then concurrently measured species in the same home would all have the same infiltration factor, which would be given by the slope in the regression of Ci on Ca. However, PM species have varying size distributions and some have indoor sources. Assuming indoor and outdoor generated PM2.5 are independent, the PM2.5 infiltration factor for one home during the 48 hr sampling period can be estimated by regressing the indoor species concentrations on the outdoor species concentrations measured concurrently in that home using robust regression. Because the infiltration factor is calculated independently for each home and sampling period, the distribution of infiltration factors across all homes (many sampled on different days) allows for variations in the size distribution and chemical stability of individual species. One reason for the variation in species size distribution is that species are to some degree externally mixed and to some degree internally mixed. Because the infiltration factor is calculated independently for each home and sampling period, variations in the microscopic mixing properties of the particles are taken into consideration.
Figure 3. Indoor and outdoor PM2.5 species concentrations and robust regression lines for a New Jersey (NJ123) and a Texas (TX 036) home. Organic carbon and sulfur are off scale.
A robust regression method, called least-trimmed squared regression (S-plus, Insightful, Inc.), was used to regress the indoor PM2.5 species concentrations on the outdoor PM2.5 species concentrations collected concurrently at a single home, yielding a PM2.5 infiltration factor (slope) for each home. In this analysis outliers represent species for which there are significant indoor sources. Therefore it is desirable to considerably down-weight outliers in the regression used to estimate the infiltration factor. The least-trimmed squared regression is very robust with respect to outliers in the response and predictor variables, even when as many as half of the data points are outliers (41). The product of the estimated home infiltration factor and the corresponding measured outdoor PM2.5 concentration is the contribution of outdoor PM2.5 to the indoor PM2.5 concentration in μg/m3 (i.e., “PM of outdoor origin”) for that home.
This method allows for home-to-home and day-to-day variations in air exchange rate, particle penetration, and particle loss rate that can occur due to variations in parameters such as house structure, air conditioner use, ventilation practice, particle size distribution, particle composition, and the thermodynamic stability of particle species. It assumes that indoor and outdoor sources are independent, perfect instantaneous mixing indoors, that factors affecting indoor concentrations are constant or change slowly throughout the monitoring period. The biggest limitation is that one major PM2.5 species, nitrate, was not measured. The impact of this limitation is explored below.
Results and Discussion
Random Component Superposition Model
With this model (38) a constant infiltration factor, FINF, of 0.35 was obtained (Figure 1). Regression results were not unduly influenced by outliers or by the highest point on the x-axis. (Removal of the two outliers alone and with the highest point on the x-axis yielded FINF = 0.35 and 0.36, respectively, where outliers were defined as having an absolute studentized residual greater than three.) [Note the coefficient of determination between indoor and outdoor PM2.5 mass concentrations was quite low (R2 = 0.09), as expected since indoor sources vary considerably from home-to-home and day-to-day and, in reality, particle infiltration behavior varies as well.] The mean, median and standard deviation of the estimated residential outdoor contribution (Cai) to indoor PM2.5 was 5.9 μg/m3 (40%), 5.2 μg/m3 (35%) and 3.6 μg/m3 (22%) for the 114 study homes, respectively.
Mass Balance Model
A particle penetration coefficient (P) of 1.0 and particle loss rate coefficient (k) of 1.5 were obtained for the 114 home dataset. These values of the penetration coefficient and particle loss rate are in reasonable agreement with previous literature values (16 and references contained therein) including controlled dynamic experiments of PM2.5 penetration which includes diffusional flow through cracks and fissures in the building envelope (42). PM2.5 mass is dominated by accumulation mode particles (i.e., particles 0.1 – 1.0 μm in diameter). Accumulation mode particles are not easily removed from an airstream by diffusion or impaction. Therefore particles of this size are expected to have larger P values (i.e., P ≈ 0.9-1.0) than coarse mode or ultrafine particles. The mean, median, and standard deviation of infiltration factors for the 114 homes are 0.40, 0.38, and 0.19, respectively, calculated by the mass balance approach. The estimated contributions of outdoor PM2.5 to indoor PM2.5 have a mean, median and standard deviation of 6.7 μg/m3 (43%), 5.8 μg/m3 (42%), and 4.7 μg/m3 (26%), respectively.
In a previous publication (16), the RCS model and the mass balance model were applied to all 212 RIOPA homes with measured PM2.5 mass. For this larger dataset, the average infiltration factor was 0.46 calculated by both models. For the subpopulation in this paper, the selected 114 homes, the mean infiltration factor was 0.35 and 0.40 for RCS model and mass balance model, respectively. The FINF in the earlier publication is most likely larger because the dataset contained more data from California homes, and the mean air exchange rate for California study homes is greater than the overall study mean.
To test the sensitivity of outdoor contribution estimates to uncertainties in P and k, the outdoor contribution was estimated for three reasonable scenarios: 1) using P = 1.0 and k = 1.5, as estimated for the 114 homes; 2) using P = 1.0 and k = 1.2, obtained by nonlinear regression of 114 homes without the 2 outliers (outliers defined as having an absolute value of studentized t > 3.0); and 3) using P = 0.91 and k = 0.79, the parameters estimated by Meng et al (16) for all 212 homes with measured PM2.5 mass. The biggest difference in the outdoor contribution to indoor PM2.5 was found between scenarios 1 and 3. For scenario 3 the mean outdoor contribution was 7.8 μg/m3 or 50%.
External Mixture Model
Selected species scatter plots are found in Figure 2. Species-specific P and k values are provided in Table S3 (Supporting Information). Penetration coefficients and loss rates were more stable for species expected to have little or no indoor sources, such as S, V, and EC, than for elements expected to have large and variable indoor source contributions, such as soil elements: Al, Si, Ca, Ti (i.e. through resuspension). This is seen in the variation in calculated P and k values when data from all RIOPA homes were included in the calculations and when different subsets of data were used (see Supporting Information for species specific P, k estimates and sensitivity analyses Tables S3-S4). The reason is that non-linear regression considers P, k and Cpig to be constant, but Cpig varies considerably from home to home for species with indoor sources. Generally, elements associated with coarse mode aerosol, such as soil elements, have smaller penetration coefficients and larger loss rates than elements associated with fine mode particles, such as S, V and EC.
The mean, median, and standard deviation of the resulting infiltration factors for the 114 homes were 0.54, 0.54, and 0.16, respectively. FINF varies with home because air exchange rate and species concentrations vary with home. The mean, median, and standard deviation of the outdoor contribution to the indoor PM2.5 mass concentration were 8.4 μg/m3 (59%), 7.2 μg/m3 (58%), and 5.8 μg/m3 (29%), respectively.
Microscopic Mixture Model
The mean, median and standard deviation of the infiltration factors obtained by robust regression are 0.69, 0.70 and 0.23, respectively. Indoor PM2.5 of outdoor origin had a mean, median and standard deviation of 12.0 μg/m3 (73%), 10.0 μg/m3 (74%), and 10.1 μg/m3 (36%), respectively, using this approach. Additional robust regression results are provided in Table S5 of Supporting Information.
Nitrate, a major component of PM2.5 in California that can have large losses during outdoor-to-indoor transport (43), was not measured in the RIOPA study. A sensitivity analysis was performed by conducting robust regression on RIOPA data from one California home (CA239) after adding indoor and outdoor nitrate concentrations from another California study (43) with similar atmospheric conditions. Robust regression results were unchanged with the addition of nitrate.
Discussion
In this analysis we first assumed a constant infiltration factor across homes (RCS model), as would be the case if central site PM were a perfect surrogate for exposure to PM of ambient origin. Next we allowed air exchange rate to vary (mass balance model). Recognizing that size distributions differ from species-to-species due to different formation mechanisms, we next allowed both P and k to vary from PM2.5 species to species but required the behavior of a given species to be constant across homes (external mixture model). Finally we estimated an infiltration factor independently for each sample (home and day), allowing P, k and a to be different from home to home and day-to-day in recognition of variations in particle, ventilation and/or house characteristics (microscopic mixture model). The microscopic mixture model provides a unique infiltration factor for each home, providing minimal constraints on the particle infiltration behavior. Table 1 summarizes the infiltration factors and the residential outdoor contribution to indoor PM2.5 from each method. In Table S5 (Supporting Information) infiltration factors obtained from the microscopic mixing model are provided by location. Figure 4 shows the cumulative distributions of infiltration factors and of PM2.5 of outdoor origin for the 114 homes for each model.
Table 1. PM of ambient origin calculated using four methods with increasingly more realistic assumptions.
| Infiltration and Contribution | RCS Model | Mass Balance Model | External Mixture Model | Microscopic Mixture Model | |
|---|---|---|---|---|---|
| Infiltration Factor | Mean | 0.35 | 0.40 | 0.54 | 0.69 |
| Median | 0.35 | 0.38 | 0.54 | 0.70 | |
| Standard Deviation | 0.0 | 0.19 | 0.16 | 0.23 | |
|
| |||||
| Contribution (%) | Mean | 40 | 43 | 59 | 73 |
| Median | 35 | 42 | 58 | 74 | |
| Standard Deviation | 22 | 26 | 29 | 36 | |
|
| |||||
| Contribution (μg/m3) | Mean | 5.9 | 6.7 | 8.4 | 12.0 |
| Median | 5.2 | 5.8 | 7.2 | 10.0 | |
| Standard Deviation | 3.6 | 4.7 | 5.8 | 10.1 | |
Figure 4. Cumulative distribution of indoor PM of outdoor origin (a) and infiltration factor (b) calculated by the four methods.
These estimates of PM2.5 of outdoor origin are important in part because they demonstrate that PM2.5 emitted and formed outdoors is a substantial source of total PM2.5 exposure. This is not at odds with the poor indoor – outdoor PM2.5 correlations observed in pooled exposure studies since home-by-home and day-by-day variations in air exchange rate, particle properties, house characteristics, ventilation practices, and indoor source strengths all introduce scatter in indoor – outdoor relationships. With increasingly more realistic assumptions (i.e., decreasing constraints on particle infiltration behavior) the mean contribution of outdoor sources to indoor PM2.5 shifted from 40% (RCS) to 43% (mass balance), to 59% (external mixture) and to 73% (microscopic mixture). The shift in the mean can be explained as follows:
| (3) |
The left hand side of the inequality is the infiltration factor calculated as with the RCS model, from the mean penetration coefficient, mean air exchange rate and mean loss rate, i.e., assuming the particle infiltration behavior is the same across all study homes. The right hand side is the mean infiltration factor calculated using the least constrained method, i.e., the microscopic mixture model. In this case, the infiltration factor for the ith home is calculated from a set of home-specific parameters Pi, ki and ai. Because the mean of the function does not equal the function of the means, it is not surprising that the mean infiltration factors estimated by RCS and microscopic mixture approaches differ. The reason for the directionality of the shift is not known.
This work also illustrates several ways in which the use of central-site PM2.5 as an exposure surrogate underestimates the bandwidth of the distribution of exposures to PM of ambient origin. Because people spend a large majority of time indoors this assessment of residential indoor-outdoor relationships provides insights into several key exposure errors. With increasingly more realistic assumptions (i.e., decreasing constraints on particle infiltration behavior) the standard deviation of outdoor contributions across homes increased. If central site PM2.5 were a perfect surrogate, then exposure variations across homes would occur only because homes were sampled on different days. This is the case with the RCS method, which yielded a standard deviation of 22%. When variations in the air exchange rate were taken into consideration (mass balance model), the distribution of values of “PM of ambient origin” was broadened to 26%. Accounting also for variations in particle properties (external mixture model) broadens the distribution to 29%. Accounting also for variations in infiltration due to differences in housing properties and the microscopic mixing properties of particles day-to-day and home-to-home (microscopic mixture model) broadens the distribution to 36%. Spatial variations in ambient PM2.5 concentrations and inter-personal variations in the time spent in each microenvironment are likely to broaden exposure distributions as well. Thus, particle infiltration behavior is a substantial contributor to exposure error. Air exchange rate, particle properties and housing characteristics all appear to contribute substantially to home-by-home and day-by-day variations in infiltration.
The use of central site PM2.5 as a surrogate for exposure to PM of ambient origin in longitudinal PM epidemiology does not account for the variation in exposures encountered across a population on a given day. This limitation leads to larger error bars around relative risk factors, which makes it less likely that relative risk factors will be significant. Improved exposure metrics would lead to smaller error bars around relative risk factors, improving the sensitivity of PM epidemiology. However, in itself, exposure variability across the population is a Berksonian error and will not lead to bias in longitudinal PM epidemiology (44).
Exposure errors introduced because of differences between the population average exposure to “PM2.5 of ambient origin” and central site PM2.5 could introduce bias in relative risk factors in certain situations (44). It is worth noting that the physically based model of Equation 1 suggests that these exposure errors are not uncorrelated with, but in fact proportional to, the ambient concentration since a major contributor to this error is the difference, Ca – Cai. In chronic epidemiological studies, time-averaged central site PM2.5 concentrations are assigned to individuals retrospectively as surrogates for PM2.5 dose. It is possible, at least in theory, for the mean ambient PM2.5 concentration to be higher in City A than City B, but the mean exposure to ambient PM2.5 to be higher in City B because of a difference in the infiltration behavior between cities. In fact, particle infiltration factors estimated for Texas homes are smaller than for California homes in the RIOPA study, presumably due to the more extensive use of air conditioning in Texas homes. Such a situation could result in a surrogate (a single-time averaged central-site PM2.5 concentration) that does not vary with actual exposure to PM of ambient origin. Seasonal variations in particle infiltration behavior in longitudinal (time series) epidemiology could potentially cause bias in relative risk factors as well. The effect is likely to differ with location. For example, FINF is higher in New Jersey study homes and lower in Texas study homes in the summertime, when 24 hr average PM2.5 concentrations tend to be highest. This introduces seasonal variations in exposure error. (Differences in the seasonality of infiltration behavior in Texas and New Jersey are presumably due to differing ventilation practices, e.g., air conditioner and window use.)
A particular strength of the RIOPA study is that measurements were made in three geographically diverse locations with distinctly different climates and different mixes of ambient sources (29). Thus insights derived from these 3 cities can largely be generalized to other US locations. Between city differences (i.e., Table S5) provide some insight into regional differences in infiltration behavior. Two US locations that are not well represented by RIOPA are: 1) woodsmoke-dominated areas of the Northwest and 2) areas of the Upper Midwest with extremely cold winters and well-insulated homes.
This paper focuses on PM2.5 mass, the concentration of which is reasonably homogeneous across urban areas (1). Some PM2.5 components, for example primary motor vehicle combustion products, have more dramatic spatial variations. In addition, changes in particle composition with outdoor-indoor transport are likely to occur because the size distribution and thermodynamic behavior of major PM2.5 species vary considerably. Changes in the composition of ambient PM2.5 with outdoor to indoor transport warrant further examination. Presentation of this type of species-specific exposure information is needed to evaluate the plausibility of PM and health hypotheses.
Supplementary Material
The following additional materials are provided in Supporting Information: 1) additional details concerning sample collection, analysis and quality control, 2) summary statistics describing major PM2.5 mass and species concentrations and air exchange rates for the 114 RIOPA homes, Table S1, 3) the number of homes across cities and seasons that make up the 114 study homes used for this analysis, Table S2, 4) penetration coefficients and loss rate constants estimated for PM2.5 species for the external mixture model, Table S3, 5) description and results of a sensitivity analysis for that analysis, Table S4, 6) a brief discussion regarding the potential use of sulfur as a tracer for determination of PM2.5 infiltration behavior, including Figure S1, and 7) microscopic mixture (robust regression) results by city, Table S5.
Acknowledgments
This research was supported by the Health Effects Institute, the Mickey Leland National Urban Air Toxics Center, the NIEHS Center of Excellence, the NJ Agricultural Experiment Station, and an EPA STAR Graduate Fellowship (for D. Shendell). We gratefully acknowledge the hard work of all the students and technicians in the field and laboratories of RIOPA investigators and the hospitality of the RIOPA participants, and valuable discussions with Dr. Melissa Lunden.
Research described in this article was conducted, in part, under contract to the Health Effects Institute (HEI), an organization jointly funded by the United States Environmental Protection Agency (EPA: Assistance Agreement R828112) and automotive manufacturers. The contents of this article do not necessarily reflect the views of HEI, nor do they necessarily reflect the views and policies of EPA or of motor vehicle and engine manufacturers.
Literature Cited
- 1.USEPA. Air quality criteria for particulate matter. USEPA; Research Triangle Park, NC: 1996. [Google Scholar]
- 2.Norris G, YoungPong SN, Koenig JQ, Larson TV, Sheppard L, Stout JW. An association between fine particles and asthma emergency department visits for children in Seattle. Environ Health Persp. 1999;107:489–493. doi: 10.1289/ehp.99107489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Schwartz J, Norris G, Larson T, Sheppard L, Claiborne C, Koenig J. Episodes of high coarse particle concentrations are not associated with increase mortality. Environ Health Persp. 1999;107:339–342. doi: 10.1289/ehp.99107339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Goldberg MS, Burnett RT, Bailar JC, Brook J, Bonvalot Y, Tamblyn R, Singh R, Valois MF, Vincent R. The association between daily mortality and ambient air particle pollution in Montreal, Quebec, 2. Cause-specific mortality. Environ Res. 2001;86:26–36. doi: 10.1006/enrs.2001.4243. Section A. [DOI] [PubMed] [Google Scholar]
- 5.Schwartz J, Dockery DW, Neas LM. Is daily mortality associated specifically with fine particles? J Air Waste Manage Assoc. 1996;46:927–939. [PubMed] [Google Scholar]
- 6.Wilson WE, Suh HH. Fine particles and coarse particles: Concentration relationships relevant to epidemiologic studies. J Air Waste Manage Assoc. 1997;47:1238–1249. doi: 10.1080/10473289.1997.10464074. [DOI] [PubMed] [Google Scholar]
- 7.Klemm RJ, Mason RM, Heilig CM, Neas LM, Dockery DW. Is daily mortality associated specifically with fine particles? Data reconstruction and replication of analyses. J Air Waste Manage Assoc. 2000;50:1215–1222. doi: 10.1080/10473289.2000.10464149. [DOI] [PubMed] [Google Scholar]
- 8.Zartarian VG, Ott WR, Duan N. A quantitative definition of exposure and related concepts. J Exposure Anal Environ Epidemiol. 1997;7:411–437. [PubMed] [Google Scholar]
- 9.Wallace L. Indoor particles: a review. J Air Waste Manage Assoc. 1996;46:98–126. doi: 10.1080/10473289.1996.10467451. [DOI] [PubMed] [Google Scholar]
- 10.Sexton K, Spengler JD, Treitman RD. Personal exposure to respirable particles: A case study in Waterbury, Vermont. Atmos Environ. 1984;18:1385–1398. [Google Scholar]
- 11.Spengler JD, Treitman RD, Tostenson TD, Mage DT, Soczek ML. Personal exposures to respirable particulates and implications for air pollution epidemiology. Environ Sci Technol. 1985;19:700–707. doi: 10.1021/es00138a008. [DOI] [PubMed] [Google Scholar]
- 12.Morandi MT, Stock TH, Contant CF. A comparative study of respirable particulate microenvironmental concentrations and personal exposures. Environ Monit Assess. 1988;10:105–122. doi: 10.1007/BF00401776. [DOI] [PubMed] [Google Scholar]
- 13.Pellizzari ED, Clayton CA, Rodes CE, Mason RE, Piper LL, Fort B, Pfeifer G, Lynam D. Particulate matter and manganese exposures in Toronto, Canada. Atmos Environ. 1999;33:721–734. doi: 10.1038/sj.jea.7500186. [DOI] [PubMed] [Google Scholar]
- 14.Lachenmyer C, Hidy GM. Urban measurements of outdoor-indoor PM2.5 concentrations and personal exposure in the deep south. Part I. pilot study of mass concentrations for nonsmoking subjects. Aerosol Sci Tech. 2000;32:34–51. [Google Scholar]
- 15.Oglesby L, Kunzli N, Roosli M, Fahriander CB, Mathys P, Stern W, Jantunen M, Kousa A. Validity of ambient levels of fine particles as surrogate for personal exposure to outdoor air pollution---results of the European EXPOLIS-EAS study (Swiss center Basel) J Air Waste Manage Assoc. 2000;50:1251–1261. doi: 10.1080/10473289.2000.10464156. [DOI] [PubMed] [Google Scholar]
- 16.Meng QY, Turpin BJ, Korn L, Weisel CP, Morandi M, Colome S, Zhang J, Stock T, Spektor D, Winer A, Zhang L, Lee JH, Giovanetti R, Kwon J, Alimokhtari S, Shendell D, Jones J, Farrar C, Maberti S. Influence of outdoor sources on indoor and personal fine particle concentrations: analyses of RIOPA data. J Exposure Anal Environ Epidemiol. 2005;15:17–28. doi: 10.1038/sj.jea.7500378. [DOI] [PubMed] [Google Scholar]
- 17.Lipfert FW, Wyzga RE. Air pollution and mortality: The implications of uncertainties in regression modeling and exposure measurement. J Air Waste Manage Assoc. 1997;47:517–523. doi: 10.1080/10473289.1997.10464417. [DOI] [PubMed] [Google Scholar]
- 18.Gamble JF. PM2.5 and mortality in long-term prospective cohort studies: cause-effect or statistical association? Environ Health Persp. 1998;106:535–549. doi: 10.1289/ehp.98106535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Mage D, Wilson W, Hasselblad V, Grant L. Assessment of human exposure to ambient particulate matter. J Air Waste Manage Assoc. 1999;49:1280–1291. doi: 10.1080/10473289.1999.10463964. [DOI] [PubMed] [Google Scholar]
- 20.Ebelt ST, Petkau AJ, Vedal S, Fisher TV, Brauer M. Exposure of chronic obstructive pulmonary disease patients to particulate matter: relationships between personal and ambient air concentrations. J Air Waste Manag Assoc. 2000;50:1081–1094. doi: 10.1080/10473289.2000.10464166. [DOI] [PubMed] [Google Scholar]
- 21.Janssen N, de Hartog J, Hoek G, Brunekreef B, Lanki T, Timonen KL, Pekkanen J. Personal exposure to fine particulate matter in elderly subjects: relation between personal, indoor, and outdoor concentrations. J Air Waste Manag Assoc. 2000;50:1133–1143. doi: 10.1080/10473289.2000.10464159. [DOI] [PubMed] [Google Scholar]
- 22.Rojas-Bracho L, Suh HH, Catalano PJ, Koutrakis P. Personal exposures to particles and their relationships with personal activities for chronic obstructive pulmonary disease patients living in Boston. J Air Waste Manag Assoc. 2004;54:207–217. doi: 10.1080/10473289.2004.10470897. [DOI] [PubMed] [Google Scholar]
- 23.Robinson J, Nelson WC. National human activity pattern survey data base. USEPA; Research Triangle Park, NC: 1995. [Google Scholar]
- 24.Abt E, Suh HH, Allen G, Koutrakis P. Characterization of indoor particle sources: A study conducted in the metropolitan Boston area. Environ Health Persp. 2000;108:35–44. doi: 10.1289/ehp.0010835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Weschler CJ, Shields HC. Potential reactions among indoor pollutants. Atmos Environ. 1997;31:3487–3495. [Google Scholar]
- 26.Wainman T, Zhang JF, Weschler CJ, Lioy PJ. Ozone and limonene in indoor air: a source of submicron particle exposure. Environ Health Persp. 2000;108:1139–1145. doi: 10.1289/ehp.001081139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Monn C, Becker S. Cytotoxicity and induction of proinflammatory cytokines from human monocytes exposed to fine (PM2.5) and coarse particles (PM10-2.5) in outdoor and indoor air. Toxicol Applied Pharm. 1999;155:245–252. doi: 10.1006/taap.1998.8591. [DOI] [PubMed] [Google Scholar]
- 28.Long CM, Suh HH, Kobzik L, Catalano PJ, Ning YY, Koutrakis P. A pilot investigation of the relative toxicity of indoor and outdoor fine particles: In vitro effects of endotoxin and other particulate properties. Environ Health Persp. 2001;109:1019–1026. doi: 10.1289/ehp.011091019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Weisel CP, Zhang J, Turpin BJ, Morandi MT, Colome S, Stock TH, Spektor DM, Korn L, Winer A, Alimokhtari S, Kwon J, Mohan K, Harrington R, Maberti S, Shendell D, Giovennetti R, Lee JH. The relationships of indoor, outdoor and personal air (RIOPA) study: study design, methods and quality assurance/control results. J Exposure Anal Environ Epidemiol. 2004;15:123–137. doi: 10.1038/sj.jea.7500379. [DOI] [PubMed] [Google Scholar]
- 30.Reff A, Turpin BJ, Porcja RJ, Giovennetti R, Cui WX, Weisel CP, Zhang J, Kwon J, Alimokhtari S, Morandi M, Stock T, Maberti S, Colome S, Winer A, Shendell D, Jones J, Farrar C. Functional group characterization of indoor, outdoor and personal PM2.5: Results from RIOPA. Indoor Air. 2005;15:53–61. doi: 10.1111/j.1600-0668.2004.00323.x. [DOI] [PubMed] [Google Scholar]
- 31.Meng QY. Ph D Thesis. Rutgers University; New Brunswick, NJ: 2004. Mechanistic investigation of the relationship of indoor, outdoor and personal PM2.5 mass concentration and associated species. [Google Scholar]
- 32.Polidori A, Turpin BJ, Meng QY, Lee JH, Weisel C, Morandi M, Colome S, Stock T, Winer A, Zhang J, Kwon JM, Alimokhtari S, Shendell D, Jones J, Farrar C, Maberti S. Analysis of RIOPA OC/EC data. J Exposure Anal Environ Epidemiol. doi: 10.1038/sj.jes.7500476. in preparation. [DOI] [PubMed] [Google Scholar]
- 33.Naumova YY, Totten LA, Eisenreich SJ, Turpin BJ, Colome SD, Morandi MT, Weisel CP, Stock TH, Winer AM, Alimokhtari S, Kwon J, Maberti S, Shendell D, Jones J, Wall SJ. Polycyclic aromatic hydrocarbons in the indoor and outdoor air of three cities in the U.S.: Results from the RIOPA study. Environ Sci Technol. 2002;36:2552–2559. doi: 10.1021/es015727h. [DOI] [PubMed] [Google Scholar]
- 34.Offenberg JH, Naumova YY, Eisenreich SJ, Turpin BJ, Morandi MT, Stock T, Colome SD, Winer AM, Weisel CP. Chlordanes in the indoor and outdoor air of three cities in the U.S. Environ Sci Technol. 2004;38:2760–2768. doi: 10.1021/es035404g. [DOI] [PubMed] [Google Scholar]
- 35.Naumova YY, Offenberg JH, Eisenreich SJ, Polidori A, Meng QY, Turpin BJ, Weisel CP, Morandi MT, Colome SD, Stock TH, Winer AM, Alimokhtari S, Kwon J, Maberti S, Shendell D, Jones J, Farrar C. Gas-Particle Distribution of Polycyclic Aromatic Hydrocarbons in Coupled Outdoor/Indoor Atmospheres. Atmos Environ. 2003;37:703–719. [Google Scholar]
- 36.Turpin BJ, Saxena P, Andrews E. Measuring and simulating particulate organics in the atmosphere: problems and prospects. Atmos Environ. 2000;34:2983–3013. [Google Scholar]
- 37.Dietz RN, Goodrich RW, Cote EA, Wieser RF. Detailed description and performance of a passive perfluorocarbon transfer system for building ventilation and air exchange measurements. In: Trechel HR, Laqus, editors. Measured Air Leakage of Buildings. American Society of Testing and Materials; Philadelphia, PA: 1986. pp. 203–264. ASTM STP 904. [Google Scholar]
- 38.Ott W, Wallace L, Mage D. Predicting particulate (PM10) personal exposure distributions using a random component superposition statistical model. J Air Waste Manage Assoc. 2000;50:1390–1406. doi: 10.1080/10473289.2000.10464169. [DOI] [PubMed] [Google Scholar]
- 39.Turpin BJ, Lim HJ. Species contributions to PM2.5 mass concentrations: revisiting common assumptions for estimating organic mass. Aerosol Sci Technol. 2001;35:602–610. [Google Scholar]
- 40.Lee JH, Yoshida Y, Turpin BJ, Hopke PK, Poirot RL, Lioy PJ, Lioy PJ, Oxley JC. Identification of sources contributing to Mid-Atlantic regional aerosol. J Air Waste Manage Assoc. 2002;52:174–185. doi: 10.1080/10473289.2002.10470850. [DOI] [PubMed] [Google Scholar]
- 41.Rousseeuw PJ, Leroy AM. Robust regression and outlier detection. John Wiley & Sons, Inc; New York: 1987. [Google Scholar]
- 42.Thatcher TL, Layton DW. Deposition, Resuspension, and Penetration of Particles within a Residence. Atmospheric Environment. 1995;29:1487–1497. [Google Scholar]
- 43.Lunden MM, Revzan KL, Fischer ML, Thatcher TL, Littlejohn D, Hering SV, Brown NJ. The transformation of outdoor ammonium nitrate aerosols in the indoor environment. Atmos Environ. 2003;37:5633–5644. [Google Scholar]
- 44.Zeger SL, Thomas D, Dominici F, Samet JM, Schwartz J, Dockery D, Cohen A. Exposure measurement error in time-series studies of air pollution: Concepts and consequences. Environ Health Perspect. 2000;108:419–426. doi: 10.1289/ehp.00108419. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
The following additional materials are provided in Supporting Information: 1) additional details concerning sample collection, analysis and quality control, 2) summary statistics describing major PM2.5 mass and species concentrations and air exchange rates for the 114 RIOPA homes, Table S1, 3) the number of homes across cities and seasons that make up the 114 study homes used for this analysis, Table S2, 4) penetration coefficients and loss rate constants estimated for PM2.5 species for the external mixture model, Table S3, 5) description and results of a sensitivity analysis for that analysis, Table S4, 6) a brief discussion regarding the potential use of sulfur as a tracer for determination of PM2.5 infiltration behavior, including Figure S1, and 7) microscopic mixture (robust regression) results by city, Table S5.