Luminal Mg²⁺, A Key Factor Controlling RYR2-mediated Ca²⁺ Release: Cytoplasmic and Luminal Regulation Modeled in a Tetrameric Channel

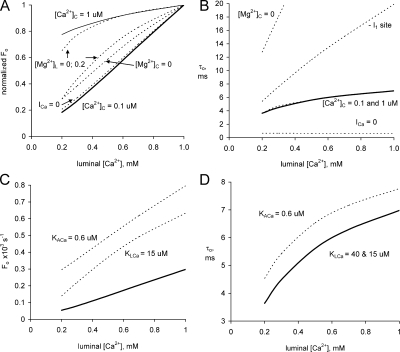
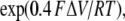Abstract

In cardiac muscle, intracellular Ca²⁺ and Mg²⁺ are potent regulators of calcium release from the sarcoplasmic reticulum (SR). It is well known that the free [Ca²⁺] in the SR ([Ca²⁺]_L) stimulates the Ca²⁺ release channels (ryanodine receptor [RYR]2). However, little is known about the action of luminal Mg²⁺, which has not been regarded as an important regulator of Ca²⁺ release.

The effects of luminal Ca²⁺ and Mg²⁺ on sheep RYR2 were measured in lipid bilayers. Cytoplasmic and luminal Ca²⁺ produced a synergistic increase in the opening rate of RYRs. A novel, high affinity inhibition of RYR2 by luminal Mg²⁺ was observed, pointing to an important physiological role for luminal Mg²⁺ in cardiac muscle. At diastolic [Ca²⁺]_C, luminal Mg²⁺ inhibition was voltage independent, with K_i = 45 μM at luminal [Ca²⁺] ([Ca²⁺]_L) = 100 μM. Luminal and cytoplasmic Mg²⁺ inhibition was alleviated by increasing [Ca²⁺]_L or [Ca²⁺]_C. Ca²⁺ and Mg²⁺ on opposite sides of the bilayer exhibited competitive effects on RYRs, indicating that they can compete via the pore for common sites.

The data were accurately fitted by a model based on a tetrameric RYR structure with four Ca²⁺-sensing mechanisms on each subunit: activating luminal L-site (40-μM affinity for Mg²⁺ and Ca²⁺), cytoplasmic A-site (1.2 μM for Ca²⁺ and 60 μM for Mg²⁺), inactivating cytoplasmic I₁-site (∼10 mM for Ca²⁺ and Mg²⁺), and I₂-site (1.2 μM for Ca²⁺). Activation of three or more subunits will cause channel opening. Mg²⁺ inhibition occurs primarily by Mg²⁺ displacing Ca²⁺ from the L- and A-sites, and Mg²⁺ fails to open the channel.

The model predicts that under physiological conditions, SR load–dependent Ca²⁺ release (1) is mainly determined by Ca²⁺ displacement of Mg²⁺ from the L-site as SR loading increases, and (2) depends on the properties of both luminal and cytoplasmic activation mechanisms.

INTRODUCTION

Excitation–contraction (E–C) coupling is the process by which muscle contracts in response to depolarization of its surface membrane during an action potential. Depolarization permits a Ca²⁺ influx via the L-type calcium channels and a small increase in cytoplasmic [Ca²⁺]. In the heart, this activates Ca²⁺ release channels (RYR2) in the SR via their cytoplasmic Ca²⁺ activation sites. The subsequent release of Ca²⁺ from the SR leads to a large increase in cytoplasmic [Ca²⁺], which is the signal for contraction (i.e., systole). The increase in cytoplasmic [Ca²⁺] strongly reinforces RYR activation and SR Ca²⁺ release, a process known as CICR. The process of CICR underlies the large amplification of the Ca²⁺ signal in which the SR supplies up to 95% of the Ca²⁺ entering the cytoplasm during systole (i.e., the amplifier gain of ∼20) (Fabiato, 1985). During diastole, the cytoplasmic [Ca²⁺] decreases as Ca²⁺ is sequestered into the SR by the ATP-driven Ca²⁺ pump (SERCa2) and extruded from the cell via the Na⁺/Ca²⁺ exchanger in the surface membrane. As a result of these Ca²⁺ uptake and release mechanisms, the free [Ca²⁺] within the SR varies between ∼0.3 and 1.0 mM during normal cardiac cycling (Ginsburg et al., 1998; Bers, 2001).

The Ca²⁺ content of the SR is a strong stimulator of CICR and a major determinant of E–C coupling gain (Fabiato and Fabiato, 1977). The dependence of Ca²⁺ release on SR Ca²⁺ content is a fundamental process underlying the function of smooth and cardiac muscle. It is believed that the cyclic variations in SR free [Ca²⁺], and its cyclic modulation of the E–C coupling gain constitutes a pacemaking mechanism in addition to that driven by the surface membrane current in pacemaking cells (Van Helden, 1993; Van Helden and Imtiaz, 2003; Vinogradova et al., 2005). Moreover, aberrant regulation of Ca²⁺ release by store load has been shown to generate cardiac arrhythmias (Venetucci et al., 2008).

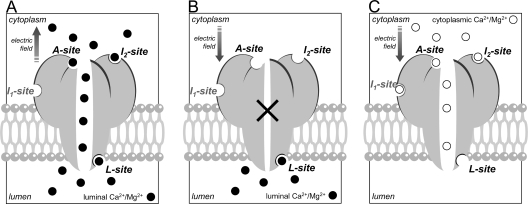
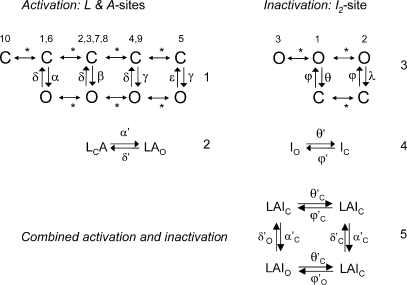
Single-channel studies of RYRs using artificial bilayers have now shown that the activity of RYRs is modulated by luminal Ca²⁺ (Sitsapesan and Williams, 1994; Herrmann-Frank and Lehmann-Horn, 1996; Tripathy and Meissner, 1996; Gyorke and Gyorke, 1998). The regulation of RYRs by luminal Ca²⁺ has complex dependencies on membrane potential and luminal [Ca²⁺] (Xu and Meissner, 1998; Laver, 2007a) that indicate the presence of both Ca²⁺-dependent activation and inhibition mechanisms (Tripathy and Meissner, 1996). The effects of luminal Ca²⁺ have been attributed in different studies to either Ca²⁺ sites on the luminal side of the RYR2 (Sitsapesan and Williams, 1995) or to cytoplasmic Ca²⁺ sites via the flow of Ca²⁺ through the pore “Ca²⁺ feedthrough” (Herrmann-Frank and Lehmann-Horn, 1996; Xu and Meissner, 1998). It has been suggested that luminal regulation of RYRs could somehow involve Ca²⁺-sensing mechanisms on both the luminal and cytoplasmic sides of the membrane (Sitsapesan and Williams, 1997; Gyorke et al., 2002). A recent single-channel study has shown that Ca²⁺ regulation of RYR2 is due to a process of “luminal-triggered Ca²⁺ feedthrough” (see Fig. 1 A), in which both luminal and cytoplasmic Ca²⁺ sites meditate channel activation, and where these sites are functionally linked by Ca²⁺ feedthrough (Laver, 2007a). This process involved three Ca²⁺-sensing mechanisms on both the luminal and cytoplasmic side of the RYR. These were (1) a novel luminal Ca²⁺ activation site (L-site; 40-μM affinity), (2) the well-described cytoplasmic Ca²⁺ activation site (A-site; ∼1-μM affinity), and (3) a novel cytoplasmic Ca²⁺ inactivation site (I₂-site; ∼1-μM affinity. There is also a low affinity Ca²⁺/Mg²⁺ inhibition site (I₁-site, previously referred to as the I-site) (Laver, 2007a, 2007b).

Figure 1.

Model for luminal-triggered Ca²⁺ feedthrough. (A) Three Ca²⁺-sensing sites on each subunit have been linked to regulation of cardiac RYRs by luminal Ca²⁺: the luminal activation site (L-site), the cytoplasmic activation site (A-site), and the cytoplasmic Ca²⁺-inactivation site (I₂-site). In addition, we show here that the low affinity Ca²⁺/Mg²⁺ inhibition site (I₁-site) has a small effect on RYR2 activity under physiological conditions. Cardiac RYR activation by luminal Ca²⁺ (•) occurs by a multistep process in which Ca²⁺ binding to the L-site initiates brief (1-ms) openings at rates up to 1 per second. Once the pore is open, luminal Ca²⁺ has access to the A-site–producing prolongation of openings and to the I₂-site–causing inactivation at high levels of Ca²⁺ feedthrough. (B) Optimal conditions for measuring L-site properties. Cytoplasmic [Ca²⁺] (≤0.1 μM) is at subactivating levels and (1) during intervals when the channel is shut (×) or (2) when there is a sufficiently large electrochemical gradient in opposition to Ca²⁺ feedthrough (e.g., +40 mV and luminal [Ca²⁺] ≤100 μM) can effectively prevent luminal Ca²⁺ from binding to the cytoplasmic sites. (C) Optimal conditions for measuring A- and I₂-site activation by cytoplasmic Ca²⁺ (○). Luminal [Ca²⁺] (≤10 μM) is at subactivating levels and when electrochemical gradient opposes Ca²⁺ feedthrough.

Less recognized, but of similar general importance to Ca²⁺, is Mg²⁺, which antagonizes the excitatory effects of Ca²⁺. Magnesium in the cytoplasm (9 mM) is buffered by ATP (∼8 mM) so that the free cytoplasmic [Mg²⁺] is ∼1 mM (Godt and Maughan, 1988). Mg²⁺ deficiency has been linked to hypertension, cardiac arrhythmia, and sudden cardiac death (Eisenberg, 1992; Seelig, 1994; Touyz, 2004; Tong and Rude, 2005). Cytoplasmic Mg²⁺ is an inhibitor of RYRs, and it is now understood that it inhibits RYRs by a dual mechanism (Meissner et al., 1986; Laver et al., 1997). First, Mg²⁺ competes with Ca²⁺ for the A- site where it causes channel closure. Second, Mg²⁺ binds to a low affinity divalent cation site (I₁-site, see above) where it also causes channel closure. The I₁-site in RYR2 has a very low affinity (∼10 mM), but we show that it should have a minor inhibitory role at physiological [Mg²⁺].

The recent identification of two novel Ca²⁺ regulatory sites on the cytoplasmic and luminal sides of RYR2 complex (L- and I₂-sites; Laver, 2007a) reveals new ways in which Mg²⁺ can potentially regulate RYR2. As yet, the free concentration of Mg²⁺ in the SR has not been directly determined but because there is no known active transport of Mg²⁺ across the SR membrane, the free [Mg²⁺] in the cytoplasm and lumen should be similar. In resting frog muscle, the total [Mg²⁺] in the terminal cisternae is approximately half that of Ca²⁺ (Somlyo et al., 1985). Because the calsequestrin (the main Ca²⁺ chelator in the SR) has about the same affinity for Ca²⁺ and Mg²⁺ (Ikemoto et al., 1974), it is likely that the free [Mg²⁺] will also be approximately half that of free Ca²⁺. During Ca²⁺ release in frog muscle (Somlyo et al., 1985), approximately half of the Ca²⁺ that is lost from terminal cisternae is replaced by Mg²⁺. Hence, over the course of the heartbeat, the free Mg²⁺ concentration in the SR most likely cycles between 0.7 mM in diastole and 1.0 mM in systole. However, no one has yet identified any role for luminal Mg²⁺ in regulating Ca²⁺ release from the SR. One study has measured the effect of luminal Mg²⁺ on RYRs (Xu and Meissner, 1998), which reported that physiological concentrations of luminal Mg²⁺ had no significant effect on the RYR2 in the presence of elevated cytoplasmic [Ca²⁺]. Here, we measure the effects of luminal Mg²⁺ on RYR2 over a range of cytoplasmic and luminal [Ca²⁺] and identify a novel, high affinity inhibition of RYR2 by luminal Mg²⁺.

In the previous formulation of the luminal-triggered Ca²⁺ feedthrough, a phenomenological set of equations was used to describe the action of Ca²⁺ binding at each site (Laver, 2007a). Here, we extend this model in two ways. First, we account for inhibition by luminal and cytoplasmic Mg²⁺ by allowing for competitive binding of Ca²⁺ and Mg²⁺ at the A-, L-, I₁-, and I₂-sites. This predicts an important physiological role for luminal Mg²⁺ in cardiac muscle. Second, we reconcile the luminal-triggered Ca²⁺ feedthrough model with the homotetrameric structure of the RYR using a similar approach to Zahradnik et al. (2005), who were the first to interpret its cytoplasmic Ca²⁺ activation in this way. Kinetic schemes now explicitly include contributions to channel gating from identical sites on the four RYR subunits.

MATERIALS AND METHODS

Lipid Bilayers, Chemicals, and Solutions.

SR vesicles (containing RYR2) were obtained from sheep hearts and reconstituted into artificial lipid bilayers as described previously (Laver et al., 1995). Lipid bilayers were formed from phosphatidylethanolamine and phosphatidylcholine (8:2 wt/wt) in 50 mg/ml n-decane. Vesicles were added to the cis solution and vesicle incorporation with the bilayer occurred as described by Miller and Racker (1976). During vesicle fusion the cis (cytoplasmic) and trans (luminal) solutions contained 250 mM Cs⁺ (230 mM CsCH₃O₃S, 20 mM CsCl) and 50 mM Cs⁺ (30 mM CsCH₃O₃S, 20 mM CsCl), respectively. Due to the orientation of RYRs in the SR vesicles, RYRs added to the cis chamber incorporated into the bilayer with the cytoplasmic face of the channel orientated to the cis solution. The osmotic gradient across the membrane and the Ca²⁺ (1–5 mM) in the cis solution aided vesicle fusion with the bilayer. The cesium salts were obtained from Aldrich Chemical Company, and Ca²⁺ and Mg²⁺ were added to these solutions as CaCl₂, MgCl₂, and MgSO₄ from BDH Chemicals. Before channel recording, the trans [Cs⁺] was raised to 250 mM by the addition of an aliquot of 4 M CsCH₃O₃S.

Solutions were pH buffered with 10 mM TES (N-tris[hydroxymethyl]methyl-2-aminoethanesulfonic acid; MP Biomedicals) and solutions were titrated to pH 7.4 using CsOH (optical grade from MP Biomedicals). Free [Ca²⁺] up to 10 μM was buffered with 4.5 mM 1,2-bis(o-aminophenoxy)ethane-N,N,N',N'- tetraacetic acid (BAPTA; obtained as a tetra potassium salt from Invitrogen) and titrated with CaCl₂. Free [Ca²⁺] between 10 and 50 μM in the luminal solution was buffered with either sodium citrate (up to 6 mM in the absence of Mg²⁺) or dibromo BAPTA (up to 2 mM). Determination of free [Ca²⁺] up to 100 nM was estimated using published association constants (Marks and Maxfield, 1991) and the program “Bound and Determined” (Brooks and Storey, 1992). A Ca²⁺ electrode (Radiometer) was used to determine the purity of Ca²⁺ buffers and Ca²⁺ stock solutions and was used to measure free [Ca²⁺] higher than 100 nM. Because all solutions contained ATP and ATP buffers Mg²⁺ and Ca²⁺, we took this into account when calculating free levels of Mg²⁺ and Ca²⁺. The required free [Mg²⁺] was determined using the estimates of ATP purity and effective Mg²⁺ binding constants determined previously under experimental conditions (Laver et al., 2004). ATP was obtained as sodium salts from Sigma Chemicals. During recordings, the composition of the cis solution was altered either by the addition of aliquots of stock solutions or by local perfusion of the bath. The local perfusion method allowed solution exchange within ∼1 s between solutions in random sequence (O'Neill et al., 2003). The perfusion method allowed us to apply solutions to the RYR in which free [Ca²⁺] and [Mg²⁺] had been accurately adjusted.

Acquisition and Analysis of Ion Channel Recordings.

Recording and analysis of ion channel activity were performed as described previously (Laver, 2007a). Electrical potentials are expressed using standard physiological convention (i.e., cytoplasmic side relative to the luminal side at virtual ground). Measurements were performed at 23 ± 2°C. During experiments the channel currents were recorded using a 50-kHz sampling rate and 5-kHz low pass filtering. Before analysis the current signal was digitally filtered at 1 kHz with a Gaussian filter and resampled at 5 kHz. Unitary current and time-averaged currents were measured using Channel2 software (P.W. Gauge and M. Smith, Australian National University, Canberra, Australia). Mean open and closed durations were generally calculated from recordings of 100–1,000 opening events. However, under conditions that produced extremely low channel activity, the mean durations were obtained from as few as 25 events covering >400 s of recording (sampling error of <25^−1/2, i.e., < 20%).

RESULTS

Inhibition of Cardiac RYRs by Luminal Mg²⁺

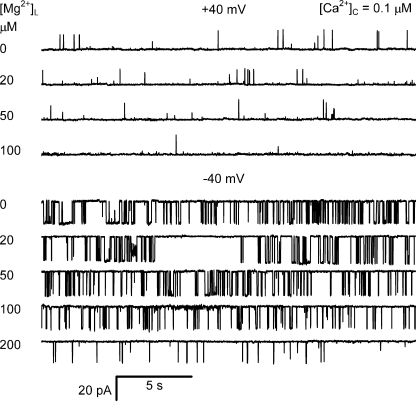
To explore the action of Mg²⁺ binding to the luminal facing L-site of RYR2, we measured the effect of luminal Mg²⁺ on RYR2 under experimental conditions previously shown to highlight channel gating associated with the L-site (Fig. 1 B). We used diastolic cytoplasmic [Ca²⁺] ([Ca²⁺]_C = 0.1 μM), which is too low to trigger channel openings via the cytoplasmic activation site (A-site), whereas the luminal [Ca²⁺] ([Ca²⁺]_L = 0.1 mM) is sufficiently high to trigger openings via the L-site. (All recordings were made in the presence of near maximally activating concentrations of ATP [2 mM]). A negative membrane potential favors the flow of Ca²⁺ and Mg²⁺ from the luminal to cytoplasmic baths where these ions may interact with the A- and I₂-sites. A positive membrane potential opposes that flow and will tend to restrict the site of action for luminal Ca²⁺ and Mg²⁺ to the luminal side of the channel. In fact, positive membrane potentials might support retrograde feedthrough (cytoplasmic to luminal bath) of Ca²⁺ or Mg²⁺ large enough to affect the L-site when their cytoplasmic concentrations exceed 0.1 mM. However, we cannot detect the effect of retrograde feedthrough because we show later that under these conditions the L-site does not contribute significantly to channel gating.

Fig. 2 shows the activity of a representative cardiac RYR under these conditions. In accord with previous findings (Laver, 2007a), RYRs were more active at −40 mV than at +40 mV. The addition of sub-mM levels of luminal Mg²⁺ was found to strongly inhibit the channel at both positive and negative potentials. Fig. 3 summarizes the effects of luminal Mg²⁺ on the gating kinetics of RYRs at a [Ca²⁺]_L of 0.1 and 1 mM (−40 mV). Increasing [Mg²⁺]_L decreased channel open probability, P_o (Fig. 3 A), via reductions in both opening frequency, F_o (Fig. 3 B), and mean open time, τ_o (Fig. 3 C). The kinetics of inhibition were quantified by fitting the data to the Hill equation (fits not depicted). The fit parameters for the data in Fig. 3 are shown in Table I (nos. 1–6). The half inhibitory [Mg²⁺]_L, K_i, for P_o, F_o, and τ_o in the presence of 0.1 mM luminal [Ca²⁺] were ∼0.1 mM (Table I, nos. 1, 3, and 5). K_i was increased to ∼1 mM (Table I, nos. 2, 4, and 6) by increasing [Ca²⁺]_L from 0.1 to 1 mM, indicating that inhibition involves competition between Mg²⁺ and Ca²⁺ for regulatory sites on the channel.

Figure 2.

Inhibition of RYR2 activity by luminal Mg²⁺. The traces were taken from a single experiment, and the luminal [Mg²⁺] is shown at the left of each trace. The cytoplasmic bath contained 2 mM ATP and 0.1 μM Ca²⁺ and did not contain any Mg²⁺. The luminal bath contained 0.1 mM Ca²⁺. Cytoplasmic and luminal baths also contained 230 mM CsCH₃O₃S and 20 mM CsCl, pH 7.4. Recordings obtained at +40 mV (top four traces) show channel openings as upward current jumps, whereas recordings at −40 mV show channel openings as downward current jumps.

Figure 3.

The effects of luminal Mg²⁺ on RYR2 open probability, P_o (A), opening frequency, F_o (B), and mean open time, τ_o (C). (A) The membrane potential was −40 mV, which favors the flow of Ca²⁺ and Mg²⁺ from luminal to cytoplasmic baths (arrow). Increasing luminal [Ca²⁺] caused a decrease in channel sensitivity to luminal [Mg²⁺]. Data points show the mean ± SE, with labels indicating the number of samples (corresponding points in B and C have the same sample numbers). Note that the data in B and C is taken from a subset of channel recordings used in A. This is because not all recordings used in P_o measurements were suitable for determining F_o and τ_o. The parameters derived from fitting Hill curves to the data are listed in Table I. The solid curves show theoretical fits to the data of the luminal-triggered feedthrough model as discussed in Results. The model parameters are listed in Table V.

TABLE I.

A Summary of the Hill Fit Parameters for Luminal Mg²⁺ Inhibition of Cardiac RYRs

No.		[Ca2+]L mM	[Ca2+]C μM	V mV	Ki μM	ni	Pmax, Fmax, and τmax	n	Figure
1	Po	0.1	0.1	−40	45 ± 5	1.8 ± 0.8	0.33 ± 0.07	17	3 A, 4 A
2	Po	1.0	0.1	−40	800 ± 180	1.5 ± 1.3	0.071 ± 0.020	11	3 A, 4 A
3	Fo	0.1	0.1	−40	76 ± 27	1.3 ± 1.0	8.8 ± 1.1	6	3 B, 4 B, 6 A
4	Fo	1.0	0.1	−40	876 ± 224	1.3 ± 1.0	11.8 ± 0.9	9	3 B, 4 B
5	τo	0.1	0.1	−40	123 ± 23	1.9 ± 1.6	10.0 ± 3.4	6	3 C, 4 C, 6 B
6	τo	1.0	0.1	−40	1,000 ± 330	2a	9.4 ± 5.0	9	3 C, 4 C
7	Po	0.1	0.1	+40	84 ± 12	1.2 ± 0.5	0.051 ± 0.036	3	4 A
8	Po	1.0	0.1	+40	1,600 ± 1,000	2.6 ± 7.9	0.16 ± 0.05	11	–
9	Fo	0.1	0.1	+40	73 ± 29	1.3 ± 1.0	3.4 ± 0.5	5	4 B
10	τo	0.1	0.1	+40	506 ± 83	1.0 ± 3.0	3.2 ± 2.0	5	4 C
11	Po	0.1	3.0	−40	18,000 ± 5,000	1a	0.78 ± 0.12	6	–
12	Po	0.1	3.0	+40	>105	–	0.88 ± 0.05	6	–
13	Fo	0.1	3.0	−40	2,400 ± 2,000	0.7 ± 1.2	70 ± 15	9	6 A
14	τo	0.1	0.1	−40	123 ± 23	1.9 ± 1.6	10.0 ± 3.4	6	6 B
15	τo	0.1	3.0	−40	480 ± 100	2.2 ± 2.0	73.0 ± 4.0	9	6 B
16	τo	0.1	10	−40	790 ± 150	1.5 ± 1.3	16.0 ± 7.0	7	6 B

The luminal Mg²⁺ dependencies of P_o were characterized by fitting data shown in the figures plus additional data not shown with Hill curves using the following equation for inactivation:

P_max is the maximal activity of the channel in the absence of luminal Mg²⁺, K_i is the [Mg²⁺] for half-inhibition, and n_i is the Hill coefficient. Similar equations were used to fit F_o and τ_o. The equations were fitted with the data using the method of least squares. n is the number of channels studied.

^aThe Hill coefficient was fixed during fitting.

To understand the possible role of Mg²⁺ feedthrough in Mg²⁺ inhibition, we compared the effects of luminal Mg²⁺ seen at negative membrane potentials (Fig. 3) with those at positive potentials that oppose the flow of Mg²⁺ through the channel (Fig. 4). Ion conduction models (Tinker et al., 1992) predict that at +40 mV the Mg²⁺ flux is 10-fold less than at −40 mV so that the Mg²⁺ inhibition will be more dependent on luminal facing sites and less dependent on cytoplasmic sites. Fig. 4 shows the kinetics of [Mg²⁺]_L inhibition at both +40 and −40 mV. Although the K_i for [Mg²⁺]_L inhibition of P_o (Fig. 4 A and Table I, nos. 1 and 7) and F_o (Fig. 4 B and Table I, nos. 3 and 9) are similar at both voltages, the K_i for τ_o was fourfold higher at +40 mV than at −40 mV (Fig. 4 C and Table I, nos. 5 and 10). The substantial voltage dependence in the K_i for inhibition of τ_o suggests that [Mg²⁺]_L inhibition during channel openings has contributions arising from Mg²⁺ binding with cytoplasmic sites on the RYR. The lack of any voltage dependence in the [Mg²⁺]_L sensitivity of F_o is consistent with it being associated with luminal facing sites on the RYR2, as one would expect from a closed channel (the rate of channel openings is a property of the closed channel).

Figure 4.

The effect of membrane potential on luminal Mg²⁺ inhibition of RYR2 open probability, P_o (A), opening frequency, F_o (B), and mean open time, τ_o (C). Changing the membrane potential from −40 to +40 mV, thereby opposing the flow of Ca²⁺ and Mg²⁺ from luminal to cytoplasmic baths, slightly decreased the sensitivity of P_o and F_o to luminal [Mg²⁺] but had a substantial effect on the Mg²⁺ dependence of τ_o. Data points show the mean ± SE. Labels indicate the number of samples for +40 mV (corresponding points in B and C have the same sample numbers). Sample numbers for −40 mV data are displayed in Fig. 3. The parameters derived from fitting Hill curves to the data are listed in Table I. The solid curves show theoretical fits to the data of the luminal-triggered feedthrough model as discussed in Results. The model parameters are listed in Table V.

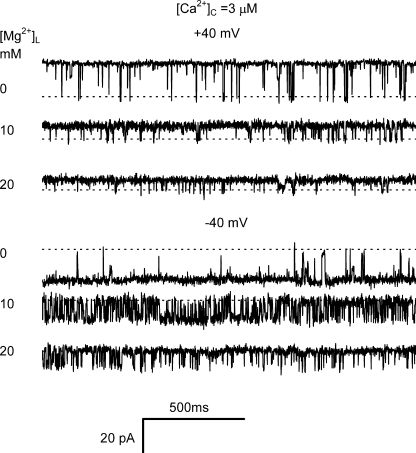
If the [Mg²⁺]_L-induced reduction in τ_o is indeed due to Mg²⁺ passing through the pore and binding to the A-site, one would expect that elevated [Ca²⁺]_C would alleviate this effect by competing with Mg²⁺ for the same site. To test this hypothesis, we measured the dose responses of luminal Mg²⁺ inhibition in the presence of [Ca²⁺]_C's of 0.1, 3, and 10 μM. It is important to realize that at elevated [Ca²⁺]_C, the A-site is the main trigger for channel openings. It has been shown that [Ca²⁺]_C of 3 and 10 μM is sufficient to trigger channel openings via the A-site at rates of ∼100 Hz (Laver, 2007a), which is an order of magnitude faster than the maximal triggering rates observed with the L-site (10 Hz).

Fig. 5 shows single channel recordings of RYRs in the presence of 3 μM [Ca²⁺]_C. Comparing the recordings in Figs. 2 and 5 shows that raising [Ca²⁺]_C from 0.1 to 3 μM substantially decreased the channel's sensitivity to luminal Mg²⁺. At negative voltages, the K_i for [Mg²⁺]_L inhibition of P_o was raised from 45 μM at 0.1 μM [Ca²⁺]_C to 18 mM at 3 μM [Ca²⁺]_C (Table I, nos. 1 and 11), and the inhibition was virtually abolished at positive membrane potentials that oppose Mg²⁺ feedthrough (K_i > 100 mM; Table I, no. 12). These values of K_i tally well with the description of [Mg²⁺]_L inhibition at 4 μM cytoplasmic Ca²⁺ reported by Xu and Meissner (1998).

Figure 5.

Inhibition of RYR2 activity by luminal Mg²⁺ in the presence of 3 μM cytoplasmic Ca²⁺. The traces were taken from a single experiment, and the luminal [Mg²⁺] is shown at the left of each trace. The cytoplasmic bath contained 2 mM ATP and 3 μM Ca²⁺, and the luminal bath contained 0.1 mM Ca²⁺. The dashed lines depict the closed current level in each trace.

The combined effects of cytoplasmic Ca²⁺ and luminal Mg²⁺ on F_o and τ_o are shown in Fig. 6 (−40 mV). Although increasing [Mg²⁺]_L caused a marked reduction in F_o at 0.1 μM [Ca²⁺]_C (the L-site being the main trigger; see above), it had very little effect at elevated [Ca²⁺]_C where the A-site is the main trigger for channel openings (Fig. 6 A and Table I, no. 13). This indicates that although luminal Mg²⁺ can prevent RYR activation by luminal Ca²⁺ (see Fig. 3), it does not prevent triggering of the RYR by the cytoplasmic Ca²⁺. The effect of luminal Mg²⁺ on τ_o is shown in Fig. 6 B. The K_i for [Mg²⁺]_L inhibition of τ_o was increased from 123 μM at 0.1 μM [Ca²⁺]_C to 480 μM and 790 μM at 3 and 10 μM [Ca²⁺]_C, respectively (Table I, nos. 14–16). This alleviation of [Mg²⁺]_L inhibition by cytoplasmic Ca²⁺ is consistent with the hypothesis that the [Mg²⁺]_L-induced reduction in τ_o is due to feedthrough of luminal Mg²⁺ to the A-site where it competes with cytoplasmic Ca²⁺.

Figure 6.

Antagonistic effects of cytoplasmic Ca²⁺ and luminal Mg²⁺ on RYR2. The effect of cytoplasmic Ca²⁺ on the luminal Mg²⁺ sensitivity of opening frequency (A) and mean open time (B). Data points show the mean ± SE. Labels indicate the number of samples in □ (A) and • (B; corresponding points in A and B have the same sample numbers). Sample numbers for ▪ are displayed in Fig. 3. The solid curves show theoretical fits to the data of the luminal-triggered feedthrough model as discussed in Results. The model parameters are listed in Table V.

Activation of Cardiac RYRs by Luminal and Cytoplasmic Ca²⁺

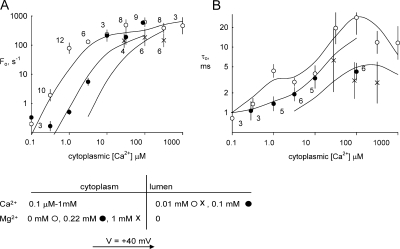
The first experiments described in this section were aimed at characterizing the [Ca²⁺]_C-dependent gating kinetics associated with the A-site. The experimental conditions were designed so that channel openings were triggered primarily by the A-site. Therefore, we kept [Ca²⁺]_L below 10 μM to minimize triggering by the L-site (Fig. 7, •) or the membrane potential was +40 mV (Fig. 8, ○) to minimize Ca²⁺ feedthrough from the luminal side when the channel was open. At +40 mV, F_o had a biphasic dependence on [Ca²⁺]_C (Fig. 8 A, ○). At [Ca²⁺]_C above 100 nM, F_o increased as third power of [Ca²⁺]_C until it plateaued to ∼1,000 Hz at high concentrations. Corresponding measurements of τ_o show an increase in two stages: τ_o increases from 1 to 4 ms over the [Ca²⁺]_C range 100 nM to 1 μM, and then from 4 to 20 ms between 10 and 100 μM. In the higher range of [Ca²⁺]_C, we noticed substantial scatter in channel kinetics, which was associated with the modal gating phenomenon reported previously (Laver et al., 1995). Measurements at −40 mV revealed another aspect to the [Ca²⁺]_C dependence of F_o (Fig. 7, •). At [Ca²⁺]_C below 100 nM, F_o had a weak dependence on [Ca²⁺]_C, increasing by a factor of 10 between 1 and 100 nM. Over this range F_o was extremely low, being equivalent to approximately one channel opening per minute. These measurements were only made possible because in some experiments bilayers contained 5–10 RYRs. The [Ca²⁺]_C dependence of τ_o at −40 mV was larger than that seen at +40 mV for [Ca²⁺]_C below 10 μM, but above this the [Ca²⁺]_C dependencies were very similar. The [Ca²⁺]_C dependencies of τ_o in Figs. 7 B and 8 B are quite complex, and the bases for these phenomena will be discussed in connection with the model (see below).

Figure 7.

Activation of RYR2 by luminal and cytoplasmic Ca²⁺. Cytoplasmic Ca²⁺ dependencies of opening frequency (A) and mean open time (B) in the presence of 2 mM ATP. Data points show the mean ± SE. Labels indicate the number of samples in • (A) and ○ (B; corresponding points in A and B have the same sample numbers). The inset shows the same data with F_o plotted on a linear scale. The solid and dashed curves show theoretical fits to the data of the luminal-triggered feedthrough model as discussed in Results. The model parameters are listed in Table V. (A and B) Dashed curves, 0.01 mM luminal Ca²⁺; solid curves, 0.1 mM luminal Ca²⁺.

Figure 8.

Inhibition of RYR2 by cytoplasmic Mg²⁺. The effect of Mg²⁺ (0.22 and 1 mM) on the cytoplasmic Ca²⁺ dependencies of opening frequency (A) and mean open time (B). Mg²⁺ shifts both Ca²⁺ dependencies of channel gating to higher [Ca²⁺]_C. Data points show the mean ± SE. Labels indicate the number of samples in ○ and × (A) and • (B; corresponding points in A and B have the same sample numbers). The solid curves show theoretical fits to the data of the luminal-triggered feedthrough model as discussed in Results. The model parameters are listed in Table V.

In accord with previous findings (Laver, 2007a), raising [Ca²⁺]_L from 10 to 100 μM caused a substantial increase in both F_o and τ_o (Fig. 7, ○) when [Ca²⁺]_C was <1 μM. The inset in Fig. 7 A shows F_o on a linear scale that makes it quite apparent that raised [Ca²⁺]_L increases the activating effect of [Ca²⁺]_C. Thus, [Ca²⁺]_C and [Ca²⁺]_L can have a synergistic effect on F_o. This cannot be due to Ca²⁺ feedthrough because F_o is a property of close channels. Rather, it indicates that there is an allosteric interaction between the luminal and cytoplasmic activation sites.

Inhibition of Cardiac RYRs by Cytoplasmic Mg²⁺

The addition of Mg²⁺ to the cytoplasmic bath (0.22 and 1 mM free Mg²⁺; i.e., 1 mM and 2.7 MgCl₂ mixed with 2 mM ATP, respectively) decreased τ_o and shifted the [Ca²⁺]_C dependence of F_o by ∼10-fold to higher concentrations (Fig. 8). These results indicate that cytoplasmic Ca²⁺ and Mg²⁺ compete for the A-site as proposed by previous studies (Meissner et al., 1986; Laver et al., 1997), and they also provide the basis for quantifying the action of luminal Mg²⁺ at the A-site in the luminal-triggered Ca²⁺ feedthrough model (see below).

The effects of luminal Ca²⁺ on RYR inhibition by cytoplasmic Mg²⁺ are shown in Fig. 9. These experiments were designed so that most channel-triggering events were due to the interaction of luminal Ca²⁺ with the L-site (i.e., [Ca²⁺]_C = 0.1 μM). The ability of luminal Ca²⁺ to trigger channel openings can be clearly seen in the [Ca²⁺]_L dependence of F_o (Fig. 9 A, ○), which shows half-maximal activation, K_a, of 45 ± 17 μM (K_a value is seen to be a measure of the Ca²⁺ affinity of the L-site; Laver, 2007a). Cytoplasmic Mg²⁺ caused a marked reduction in F_o in the presence of both 0.1 and 1 mM [Ca²⁺]_L (Fig. 9 C). However, in spite of its strong effect on channel gating, 0.22 mM [Mg²⁺]_C had no significant effect on the [Ca²⁺]_L sensitivity of the L-site (K_a = 60 ± 21 μM), indicating that cytoplasmic Mg²⁺ does not alter the Ca²⁺ affinity of the L-site.

Figure 9.

The effect of luminal [Ca²⁺] on the inhibition of RYR2 by cytoplasmic Mg²⁺. The effect of cytoplasmic Mg²⁺ on the luminal Ca²⁺ dependencies of opening frequency (A) and mean open time (B). The inset shows the corresponding absolute values of F_o (s⁻¹) plotted on a linear scale. The effect of luminal Ca²⁺ on the cytoplasmic Mg²⁺ dependencies of opening frequency (C) and mean open time (D). Data points show the mean ± SE, with labels indicating the number of samples (corresponding points in A and B, and C and D have the same sample numbers). The solid and dashed curves show theoretical fits to the data of the luminal-triggered feedthrough model as discussed in Results. The model parameters are listed in Table V. (A and B) Dashed curves, zero cytoplasmic Mg²⁺; solid curves, 0.22 mM cytoplasmic Mg²⁺. (C and D) Dashed curves, 0.1 mM luminal Ca²⁺; solid curves, 1 mM luminal Ca²⁺.

In the absence of cytoplasmic Mg²⁺, τ_o had a bell-shaped [Ca²⁺]_L dependence (Fig. 9 B, ○) reflecting reinforcement of channel activation via the A-site over the [Ca²⁺]_L range of 0 to 0.1 mM and inactivation via the I₂-site at higher [Ca²⁺]_L (Laver, 2007a). The addition of cytoplasmic Mg²⁺ decreased τ_o at low [Ca²⁺]_L (Fig. 9, B and D, ▵) but had no significant effect at [Ca²⁺]_L of 1 mM Ca²⁺ (Fig. 9, B and D, ▴), indicating competitive interactions between luminal Ca²⁺ and cytoplasmic Mg²⁺. This is the converse of our earlier result (Fig. 6) showing competition between luminal Mg²⁺ and cytoplasmic Ca²⁺. In Fig. 9 B, it appears that the activating part of the [Ca²⁺]_L bell curve for τ_o shifts to the right in the presence of cytoplasmic Mg²⁺. This would be expected from a mechanism in which feedthrough of luminal Ca²⁺ to the A-site is determining τ_o and where the apparent Ca²⁺ sensitivity of the A-site is decreased in the presence of cytoplasmic Mg²⁺ as seen in Fig. 8.

A Luminal-triggered Ca²⁺ Feedthrough Model for Mg²⁺ and Ca²⁺ Incorporating a Homotetrameric Channel Structure

Our previous study (Laver, 2007a) characterized the channel gating kinetics associated with three Ca²⁺ sites (A-, L-, and I₂-sites) on the RYR2 and/or associated proteins that underlie regulation of RYR2 by cytoplasmic and luminal Ca²⁺ (see schematic representations in Fig. 1). It is envisaged that the channel can open if Ca²⁺ is bound to either the A- or L-sites. Thus, even in the absence of cytoplasmic Ca²⁺, luminal Ca²⁺ can open the channel by binding to the L-site. The subsequent flow of Ca²⁺ through the pore can increase the cytoplasmic [Ca²⁺] in the vicinity of the pore mouth and reinforce channel activation (increasing τ_o) by binding to the A-site or inactivate the channel by binding to the I₂-site (decreasing τ_o).

Feedthrough of Mg²⁺ and Ca²⁺.

I_Ca and I_Mg were calculated using a rate theory model of RYR conductance (Tinker et al., 1992) (RYRs have nearly identical permeabilities to Ca²⁺ and Mg²⁺). The Ca²⁺ current through the RYR, I_Ca (pA), leads to an increase in the concentration of Ca²⁺ in the micro domain of the pore mouth. According to ion diffusion theory (Stern, 1992), the Ca²⁺ concentration profile, [Ca²⁺]_r at a distance, r (nm), is given by:

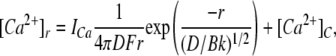(1a)

where D is the diffusion coefficient of Ca²⁺, k and B are the binding rate and concentration of the Ca²⁺ buffer, respectively, and F is the Faraday constant. In the experiments here (4.5 mM BAPTA with k = 1.7 × 10⁹ (Ms)⁻¹) and D = 3 × 10⁻¹⁰ m²s⁻¹ for Ca²⁺, the equation is expressed as:

(1b)

where a = 2,750 m⁻²A⁻¹ (or 2,750 μM nm/pA) and b = 6 nm. Examination of equations 1a and 1b reveals that the Ca²⁺ concentrations at the A- and I₂-sites ([Ca²⁺]_A and [Ca²⁺]_I2, respectively) will have linear dependencies on I_Ca.

(2)

(3)

A similar equation (Eq. 4) is used for [Mg²⁺] at the A-site:

(4)

The values of the parameters, X_Ca, Y_Ca, and X_Mg, were determined from fits of the model to the experimental data.

Ca²⁺ Activation Sites (A- and L-Sites).

Previous work by Zahradnik et al. (2005) established that each subunit has independent Ca²⁺ sites that cause channel opening by an allosteric mechanism. We have incorporated these findings into the gating model for luminal and cytoplasmic Ca²⁺ and Mg²⁺ (Fig. 10, scheme 1). In this model, the pairs of open and closed states (C↔O) are associated with particular subunit stoichiometries of the RYR (i.e., particular combinations of subunits with bound sites). The Ca²⁺ and Mg²⁺ dependencies in gating arise from the transition rates between different subunit stoichiometries (Fig. 10, scheme 1, asterisks), whereas the rates within each C↔O pair are independent of Ca²⁺ and Mg²⁺.

Figure 10.

Kinetic schemes for luminal-triggered Ca²⁺ feedthrough. Ca²⁺ activation (scheme 1, A- and L- sites) and Ca²⁺ inactivation (scheme 3, I₁ and I₂-sites). Each pair of open and closed states is associated with different functional states of individual RYR2 subunits, and the numbers refer to the entries in Table IV describing these stoichiometries. Asterisks indicate changes in subunit stoichiometry, and these depend on binding of Ca²⁺ or Mg²⁺. Also shown are their corresponding simplified schemes (schemes 2 and 4) and the overall scheme (scheme 5) resulting from the combined action of activation and inactivation. The reaction rates in scheme 5 have complex dependencies on [Ca²⁺] and [Mg²⁺], and these are derived in Eqs. 2–13. Reaction rates that depend on the Ca²⁺ and Mg²⁺ concentrations at the cytoplasmic pore mouth will depend on the permeability of these ions in the channel (Eqs. 1–4). Hence, they are given subscripts “o” and “c” to indicate the different rates associated with open and closed channels, respectively. In scheme 5, the open and closed status of the channel associated with each kinetic state is indicated by the subscripts “O” and “C,” respectively.

From the following data, we derive a scheme for the way in which the binding of Ca²⁺ and Mg²⁺ to the A- and L-sites promotes high opening frequencies (H), low opening frequencies (L), or channel closures (C) (Table II A, H and L states are not the same as the H and L gating modes of the RYR analyzed by Zahradnikova and Zahradnik [1995]). (1) Both [Ca²⁺]_L and [Ca²⁺]_C trigger channel openings, and [Mg²⁺]_L and [Mg²⁺]_C exhibit competitive inhibition (Figs. 3 and 8). This indicates that the A- and L-sites cause channel opening in response to Ca²⁺ binding, and Mg²⁺ inhibits by competing with Ca²⁺ at these sites. (2) [Ca²⁺]_C can trigger channel openings at high rates (1 kHz in Fig. 7 A), whereas the maximum for [Ca²⁺]_L alone is much lower (10 Hz in Figs. 3 B, 4 B, and 8 C). This indicates that the A-site can promote high activity, whereas the L-site can only promote low activity. (3) Although [Mg²⁺]_L inhibits triggering of the channel by [Ca²⁺]_L, it does not prevent its triggering by [Ca²⁺]_C (Fig. 6 A, □ and •). Thus, Ca²⁺ binding to the A-site will open the channel regardless of the Ca²⁺ or Mg²⁺ occupancy of the L-site. (4) Cytoplasmic Mg²⁺ decreases F_o regardless of luminal [Ca²⁺] (Fig. 8 C), indicating that at the L-site, Mg²⁺ inhibits simply by preventing luminal Ca²⁺ activation, whereas Mg²⁺ binding to the A-site will close the channel even if Ca²⁺ is bound to the L-site. From this functional matrix (see Table II A), one can calculate the probability that each subunit will contribute to high activity, low activity, and closed states of the channel, P_H, P_L, and P_C, respectively.

(5)

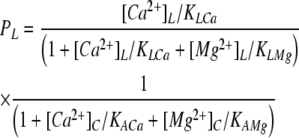(6)

(7)

where the K terms are the Ca²⁺ and Mg²⁺ binding affinities for the A- and L-sites as indicated by the subscripts.

TABLE II.

A Summary of the Functional Outcomes of the Various Binding States of the Luminal L-Site and the Cytoplasmic A- and I₂-Sites Derived from the Data

A		A-site
		Ca2+	empty	Mg2+
L-site	Ca2+	H	L	C
	empty	H	C	C
	Mg2+	H	C	C
B		I2-site
		Ca2+	empty	Mg2+
		I	O	I

(A) Three levels of channel activity are promoted by the A- and L-sites. H, high F_o state; L, low F_o state; C, closed channels. Ca²⁺ binding to the A-site lead to high activity, whereas Mg²⁺ binding causes channel closure regardless of the state of the L-site. In the absence of ion binding to the A-site, Ca²⁺ binding to the L-site generates low activity, whereas Mg²⁺ binding leaves the channel closed. (B) The binding of either Ca²⁺ or Mg²⁺ to the open channel (O) is considered to promote channel inactivation (I). The activity of the channel depends on the number of subunits in each state (see Tables III and IV).

Here, we present [Ca²⁺]_C dependencies of τ_o and F_o over an extended range (six orders of magnitude) to reveal new aspects of luminal and cytoplasmic Ca²⁺ activation. This data provides several clues about how the A-sites on each of the four RYR subunits contribute to channel gating. The fact that F_o increases as the third power of [Ca²⁺]_C over the range of 1–10 μM (Fig. 7 A) suggests that Ca²⁺ needs to be bound to A-sites on three subunits to trigger channel opening. It also appears that several subunits are involved in [Ca²⁺]_L activation because the Hill coefficients for F_o are ∼2 (Table I). The synergistic action of [Ca²⁺]_C and [Ca²⁺]_L on F_o in the [Ca²⁺]_C range of 1–100 nM and the lack of any dependence of F_o on [Ca²⁺]_L at high [Ca²⁺]_C indicate the existence of specific cooperative interactions between the luminal- and cytoplasmic-triggered gating mechanisms (see below). Finally, the large increase in τ_o at high [Ca²⁺]_C (Fig. 7 B) points to a stabilizing of the open conformation occurring when Ca²⁺ is bound to A-sites on all four subunits. To account for all these properties, we propose a gating scheme in which the gating mechanism has (1) a high opening rate (γ = 60 s⁻¹) when either three or four subunits are in the H state (see Table II A for the conditions for the H, L, and C states), (2) an intermediate opening rate (β = 7 s⁻¹) when at least three subunits are not in the C state and at least one subunit is in the H state, and (3) a low opening rate (α = 1 s⁻¹) when no subunits are in the H state but at least three are in the L state. The closing rate of the gating mechanism is relatively fast (δ = 1,500 s⁻¹) when three or fewer subunits are in the H state and slow (ε = 1.5 s⁻¹) when all four are in the H state. It has been shown (Laver, 2007a) that opening rate associated with the L-site is voltage dependent. This effect can be accommodated in the model by introducing a voltage dependence in α and β (Fig. 10). The various subunit stoichiometries, their probabilities, and associated opening and closing rates are summarized in Table III.

TABLE III.

The RYR2 Activation Associated with Various Combinations of Functional States among Its Four Subunits

Subunit stoichiometry	i	Opening rate constant, RO	Closing rate constant, RC	Probability of stoichiometry PS	Probability of stoichiometry given closed, PSC	Probability of stoichiometry given open, PSO
4L 0H	1	α	δ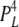
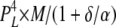3L 1H	2	β	δ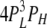
2L 2H	3	β	δ
1L 3H	4	γ	δ
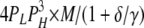0L 4H	5	γ	ε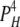
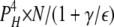3L 0H 1C	6	α	δ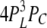
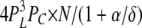2L 1H 1C	7	β	δ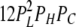
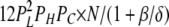1L 2H 1C	8	β	δ
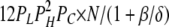0L 3H 1C	9	γ	δ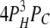
others	10	0	δ			0

The kinetic scheme for channel gating is shown in Fig. 10 (scheme 1). States C, L, and H depend on Ca²⁺ and Mg²⁺ binding to the A- and L-sites, which is described in Table II A. Subunit stoichiometries (i = 1–5) are the combinations of four active subunits that produce channel openings and stoichiometries 6–9 are combinations of three active subunits. Other stoichiometries are deemed not to produce channel openings. Associated with each stoichiometry is the channel opening and closing rate constants, the probability that the channel has that stoichiometry, and the probabilities of the channel open and closed states. Values for the rate constants are given in Table V. The values M and N are normalizing factors:

To calculate mean open and closed times, the gating scheme for the A- and L-sites can be simplified to the two states shown in Fig. 10 (scheme 2). To calculate the total opening and closing rates of the A-site, we use the simplifying assumption that the transition rates between stoichiometries are faster than the O↔C transitions. Estimates of the Ca²⁺ on and off rates at the A-site are 2 × 10⁸ (Ms)⁻¹ and 200 s⁻¹, respectively (Schiefer et al., 1995), suggesting that the O↔C transition rates are not likely to be slower than those for transitions between stoichiometries. Hence, we approximate the total opening and closing rates, α' and δ', respectively, by the sums of the rates (the R terms) associated with the 10 subunit stoichiometries (P_S; Table III) weighted by the open and closed state probabilities (P_SO and P_SC, respectively).

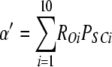(8)

(9)

Ca²⁺ Inactivation Sites (I₁- and I₂-Sites).

The cytoplasmic I₂-site was found to underlie the marked reductions in τ_o that occur with increasing [Ca²⁺]_C in the presence of elevated [Ca²⁺]_L (Figs. 7 B, ○, and 9 B, ○) (Laver, 2007a). Although we were unable to resolve an effect of Mg²⁺ binding to the I₂-site in this study (see below), we make the initial proposition that inactivation is promoted when either Ca²⁺ or Mg²⁺ bind to the I₂-site (Table II B). The probability that each subunit will contribute to inactivation (I), P_I, is given by:

(10)

(11)

In this study, we found a substantial decrease in τ_o between 0.1 and 10 μM [Ca²⁺]_C, followed by an increase in τ_o at [Ca²⁺]_C above 10 μM (e.g., Fig. 7 B, ○). This onset and alleviation of inactivation could be explained by a model in which inactivation occurs when the I₂-sites on three subunits are occupied (θ = 800 s⁻¹) but not when sites are occupied on all four subunits (λ = 0). The subunit stoichiometries associated with the I₂-sites, their probabilities, and associated opening and closing rates are summarized in Table IV. The gating scheme can be simplified to the two states shown in Fig. 10 (scheme 4) in which the opening and closing rates, φ' and θ', respectively, are given by:

(12)

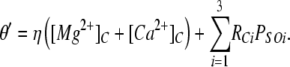(13)

TABLE IV.

The RYR2 Inactivation Associated with Various Combinations of Functional States among Its Four Subunits

Subunit stoichiometry	i	Opening rate constant, RO	Closing rate constant, RC	Probability of stoichiometry PS	Probability of stoichiometry given closed, PSC	Probability of stoichiometry given open, PSO
3I 1O	1	φ	θ
4I 0O	2	φ	λ
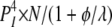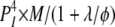others	3	φ	0		0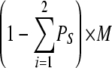

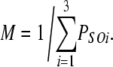The kinetic scheme for channel gating is shown in Fig. 10 (scheme 3). States O and I depend on Ca²⁺ and Mg²⁺ binding to the I₂-site, which is described in Table II B. Three inactivated subunits are needed to permit channel inactivation. Associated with each stoichiometry is the channel opening and closing rate constants, the probability that the channel has that stoichiometry, and the probabilities of the channel open and closed states. Values for the rate constants are given in Table V. The values M and N are normalizing factors:

We find that as [Ca²⁺]_C is increased to mM levels, τ_o decreases again as a result of the I₁-site. Even though the degree of Ca²⁺/Mg²⁺ inhibition is minor at 1 mM (<10% change in P_o; not depicted), it has a substantial effect on τ_o. The contribution of the I₁-site to inactivation is included in the model as an additional empirical term in the inactivation rate involving η in Eq. 13. The existence of the I₁-site has been known for some time. It was previously referred to as the I-site and was found to underlie low affinity (∼10 mM) Mg²⁺ inhibition (Laver et al., 1997). Because the effects of this site are minor, we have not developed a full allosteric scheme for this gating mechanism.

The combined effects of activation and inactivation mechanisms in schemes 2 and 4 in Fig. 10 were calculated by combining these into a four-state scheme (Fig. 10, scheme 5). The theoretical mean opening frequency (1/τ_c) and mean open times were calculated from scheme 5 using the Q-matrix method of Colquhoun and Hawkes (1981 and 1987). The tetrameric luminal-triggered Ca²⁺ feedthrough model accounts for the [Ca²⁺]_L, [Ca²⁺]_C, and voltage dependencies of P_o, τ_o, and F_o (solid and dashed curves in Figs. 3, 4, and 6–9). The model was also able to account for quite complex [Ca²⁺]_L and [Ca²⁺]_C dependencies of the RYR gating properties and fitted the increase in τ_o at [Ca²⁺]_C > 10 μM (Figs. 7 B, ○ and •, and 8 B, ○) without the benefit of an adjustable parameter. The model parameters (Table V) are only slightly different to the values quoted for the empirical predecessor of this model (Laver, 2007a; the data obtained here is consistent with this previous study).

TABLE V.

Parameters of the Luminal-triggered Ca2+ Feedthrough Model

	Affinity	Opening rates	Closing rates	Feedthrough
L-site	KCaL = 40 μM
		KMgL = 40 μM	α = 1 s−1a
		β = 7 s−1a	δ = 1,500 s−1
A-site	KCaA = 1.2 μM	γ = 60 s−1	ε = 1.5 s−1	XCa = 12 μM/pA
		KMgA = 60 μM			XMg = 120 μM/pA
I2-site	KCaI = 1.2 μM	φ = 800 s−1	θ = 1,000 s−1	YCa = 0.35 μM/pA
			KMgI unknown			λ = 0 s−1
I1-site			η = 1.5 ×105 (Ms)−1

The parameters are described in the text (see Eqs. 2–13 and schemes 1–5 in Fig. 10). The voltage-dependencies are given by the multiplying factor

where ΔV is the difference in the voltage from −40 mV.

^aParameters that depend on voltage where the values given are those measured at −40 mV.

Mg²⁺ Inhibition of RYR2.

The model accounts for luminal and cytoplasmic Mg²⁺ inhibition using an additional three free parameters (solid and dashed curves in Figs. 3, 4, 6, 8, and 9). The Mg²⁺ affinity parameter for the A-site (K_MgA in Eqs. 5 and 6) was adjusted until the model fitted the [Mg²⁺]_C dependencies of τ_o and F_o (Figs. 8, A and B, and 9, C and D). The parameter for Mg²⁺ affinity of the L-site (K_MgL in Eqs. 5 and 6) was determined by fitting the model to the [Mg²⁺]_L dependency of F_o (Figs. 3 B and 4 B). We then calculated the parameter associated with Mg²⁺ feedthrough (X_Mg in Eq. 4) by fitting the voltage/[Mg²⁺]_L dependencies of τ_o (Figs. 4 C and 6 B). Although there were no free parameters in the model for fitting the [Mg²⁺]_L dependencies of F_o in Fig. 6 A (□ and •), the model did fit the data at [Ca²⁺]_C = 3 μM fairly well, but it overestimated Mg²⁺ inhibition at [Ca²⁺]_C = 10 μM. This probably reflects the existence of subtle inter-subunit interactions in the RYR that are not included in the current model. We were unable to detect any inhibition of RYR2 resulting from Mg²⁺ binding to the I₂-site. The reason for this is that Mg²⁺ has a strong inhibitory effect at the A-site that probably masks any effect that it has at the I₂-site. We found that adjusting the Mg²⁺ affinity of the I₂-site in the model did not influence the overall fit of the model to the data. Therefore, we have assumed that Mg²⁺ binding to the I₂-site did not have a significant role in regulating RYRs in bilayer or in the cell and have omitted this binding reaction from the model. The model parameters are listed in Table V. The binding of Mg²⁺ at the I₁-site accounted for a modest reduction in τ_o (Figs. 7 B and 8 B) in the presence of elevated (1 mM) [Mg²⁺]_C. The parameter associated with Mg²⁺ inhibition at the I₁-site (η) was determined by Ca²⁺ inhibition at high [Ca²⁺]_C so that is was not a free parameter for fitting the model to Mg²⁺ inhibition.

Alternative Models.

The fact that F_o was dependent on both [Ca²⁺]_C and [Ca²⁺]_L could not be explained by the independent triggering of channel openings by the A- and L-sites as proposed in the previous study (Laver, 2007a). According to that model, F_o should be virtually independent of [Ca²⁺]_C over the range of 1–100nM when [Ca²⁺]_L is in the range of 100–1,000 μM.

We also investigated schemes in which Ca²⁺ binding at either A- or L-sites modified either the affinity and/or gating rates associated with the contra-lateral site. However, these models predicted that a [Ca²⁺]_L increase from 10 to 100 μM would cause a 10-fold increase in F_o in the presence of [Ca²⁺]_C in excess of 10 μM, whereas our data shows that the effect of [Ca²⁺]_L is very small once [Ca²⁺]_C exceeds 1 μM.

Our proposal that the channel opens when three or more subunits get activated via L- or A-sites fitted well with the data. We also explored a model in which channel openings could be triggered by combinations of at least two active subunits and another model where four active subunits were required for a channel opening. These models could not fit simultaneously the [Ca²⁺]_C dependencies of τ_o and F_o. In the case when two subunits could trigger an opening, we were unable to generate an increase in τ_o as [Ca²⁺]_C increased from zero to 1 μM at the same time as fitting the [Ca²⁺]_C dependencies of F_o. When four subunits were required to trigger openings, we were unable to generate any increase in τ_o with increasing [Ca²⁺]_C.

DISCUSSION

The data reveals a multiplicity of mechanisms by which luminal and cytoplasmic Ca²⁺ and Mg²⁺ can regulate RYR2. We show that Ca²⁺/Mg²⁺ regulation of RYR2 involves two Ca²⁺ activation mechanisms (L- and A-sites) and two inactivation mechanisms (I₁- and I₂-sites) associated with different parts of the RYR molecule (Fig. 1). Mg²⁺ in either the cytoplasm or SR lumen inhibits RYR2 by binding to the L-, A-, and I₁-sites. Mg²⁺ binding to the L-site has not been previously identified, and this study makes the first measurement of its Mg²⁺ affinity. We find that the L-site is nonselective with an affinity of 40 μM for both Ca²⁺ and Mg²⁺.

There are some important differences in how luminal and cytoplasmic Ca²⁺ activation mechanisms operate in RYR2. First, there is two orders of magnitude difference in the maximal opening frequencies attainable with the L- and A-sites. Second, the A-site has a relatively high (1.2 μM) Ca²⁺ affinity, which is ∼50-fold selective for Ca²⁺ over Mg²⁺, whereas the L-site has the same low affinity for Ca²⁺ and Mg²⁺. Finally, Mg²⁺ has different inhibitory actions at the A- and L-sites. Mg²⁺ at the L-site inhibits simply by preventing luminal Ca²⁺ activation, whereas Mg²⁺ binding to the A-site will close the channel even if Ca²⁺ is bound to the L-site. Therefore, just like we have previously seen in skeletal RYRs (Laver et al., 2004), Mg²⁺ at the A-site is an antagonist that does not simply prevent Ca²⁺ activation; it closes the channel even if it has been opened by another process (e.g., L-site activation).

Models incorporating several subunit interaction schemes were tested (see Results), but the only scheme that fitted the data was one in which channel activation or inactivation required ion binding to corresponding sites on at least three subunits. The same requirement for three subunits has also been reported for cytoplasmic activation of the IP₃R calcium release channels (Shuai et al., 2007), indicating that similar molecular mechanisms may underlie gating in these closely related channels. Here, we develop the first subunit-based model for both luminal and cytoplasmic regulation of any Ca²⁺ release channel type. The synergistic activation by luminal and cytoplasmic Ca²⁺ was explained by a process in which channel opening required at least three active subunits where each subunit may be activated from both luminal and cytoplasmic sides. Although the molecular structure of the divalent cation sites has not been determined, bilayer studies have showed that the luminal proteins, calsequestrin, triadin, and junctin, play an important role in regulating the RYR2 response to luminal Ca²⁺ (Gyorke et al., 2004). RYR2 incorporated into lipid bilayers from SR vesicles appear to retain their association with these luminal proteins (Gyorke et al., 2004, and Beard, N.A., personal communication). Therefore, the Ca²⁺/Mg²⁺ mechanisms of RYRs explored in this study should encompass the regulatory actions of those co-proteins.

Accessibility of Cytoplasmic Sites to Luminal Ca²⁺ and Mg²⁺

Several studies have now proposed that divalent ions on the luminal side of the membrane can flow through the pore and bind to sites on the cytoplasmic domain of the RYR and regulate channel activity. This proposal is based on several lines of evidence. First, RYR sensitivities to both activation and inhibition by luminal Ca²⁺ are closely correlated with the magnitude of Ca²⁺ feedthrough (Tripathy and Meissner, 1996; Laver, 2007a). Biasing the membrane voltage against Ca²⁺ feedthrough reduces the Ca²⁺ sensitivities of activation and inhibition. Second, heavy Ca²⁺ buffering of the cytoplasmic bath alleviates inactivation by luminal Ca²⁺, indicating that luminal Ca²⁺ must be traversing the cytoplasmic solution to reach the inactivation site (Tripathy and Meissner, 1996). Finally, the effects of luminal and cytoplasmic Ca²⁺ are not additive, indicating that Ca²⁺ competes for the same activating and inactivating sites from opposite sides of the membrane (Laver, 2007a).

We can estimate the distances of the A- and I₂-sites from the pore mouth by substituting the experimentally derived ratios of local [Ca²⁺]/I_Ca at each site (X_Ca and Y_Ca in Table V) into Eq. 1b and solving for the variable r in each case. Thus, we estimate that the A- and I₂-sites are 16.5 and 34 nm from the pore, respectively. Given that the RYR protein does not extend beyond 20 nm from the pore mouth, it is likely that the I₂-site involves inhibitory effects via interacting accessory proteins. A candidate for this is calmodulin, which has been shown to cause Ca²⁺-dependent inactivation of cardiac RYRs in lipid bilayers (Xu and Meissner, 2004).

Here, we have used the antagonistic effects of Ca²⁺ and Mg²⁺ on τ_o to provide stronger tests for the presence of feedthrough-mediated regulation of the channel (during openings it is possible for luminal Ca²⁺ and Mg²⁺ to have access to cytoplasmic domains of the RYR via the pore). Our data (Fig. 8 B) and those of others (Xu and Meissner, 1998) have shown that in the presence of ATP, τ_o increases with increasing cytoplasmic [Ca²⁺] and upon the addition of cytoplasmic Mg²⁺, it decreases τ_o in a competitive manner. We now show that luminal Mg²⁺ also decreases τ_o and that this is alleviated by cytoplasmic Ca²⁺ (Fig. 6 B), indicating that cytoplasmic Ca²⁺ and luminal Mg²⁺ compete for a common site (the A-site). In the converse experiment, we found that luminal Ca²⁺ alleviated the effect of cytoplasmic Mg²⁺ on τ_o (Fig. 8 B). These results clearly demonstrate that Ca²⁺ and Mg²⁺ compete from opposite sides of the open channel. Moreover, in agreement with the findings of Xu and Meissner (1998), we find that the effect of luminal Mg²⁺ on τ_o is abolished when the membrane potential is biased against Mg²⁺ feedthrough (Fig. 4 C). Collectively, these results strongly support the existence and importance of feedthrough regulation of RYR2 in vitro.

Efficacy of Luminal Ca²⁺ Activation Is Increased by Cytoplasmic Agonists and Reduced by Antagonists

A clear pattern is emerging in which cytoplasmic and luminal regulation of RYRs are closely linked. The results here and those of our recent studies (Laver, 2007a, 2008) suggest that this link occurs via two distinct mechanisms. First, activation of subunits by luminal Ca²⁺ may reduce the number of subunits that need to be activated by cytoplasmic agonists to achieve channel opening. This accounts for the synergy we observe in [Ca²⁺]_L and [Ca²⁺]_C activation and how this is antagonized by [Mg²⁺]_C. It is possible that the same inter-subunit processes underlie the ability of other cytoplasmic regulators to modify the responsiveness of RYR2 to [Ca²⁺]_L. Second, luminal Ca²⁺ can alter τ_o via Ca²⁺ feedthrough to the A-site. The luminal-triggered Ca²⁺ feedthrough model predicts that any antagonist that shortens channel openings triggered by cytoplasmic Ca²⁺ (the A-site) will reduce RYR activation by luminal Ca²⁺. The converse has already been found to hold true for the cytoplasmic agonists ATP (Laver, 2007a) and activating peptide DPc10 (Laver et al., 2008), which increase [Ca²⁺]_L activation of RYRs by lengthening channel openings triggered by [Ca²⁺]_C. ATP was found to increase τ_o in response to Ca²⁺ binding at the A-site. The model calculations showed that Ca²⁺ feedthrough could fully account for marked increase in the [Ca²⁺]_L dependence of τ_o (Fig. 9 B, ○ and dashes). Moreover, in the presence of ATP, [Mg²⁺]_C, which reduces τ_o by shifting its [Ca²⁺]_C dependence to higher concentrations (Fig. 8 B), reduces the [Ca²⁺]_L dependence of τ_o (Fig. 9 B, ○ and •), and this effect of [Mg²⁺]_C is in close alignment with predictions of the model.

Physiological Implications

Applying the Model to Ca²⁺ Release in Cardiomyocytes.

To gain an understanding of how RYRs might be regulated by Ca²⁺ and Mg²⁺ in cardiomyocytes, we extrapolate the luminal-triggered feedthrough model to the physiological situation. This is done here in four respects: (1) The free concentrations of Mg²⁺ in the cytoplasm and lumen are both set to 1 mM to match the likely intracellular concentrations (see Introduction); (2) The membrane potential across the SR membrane is considered to be zero. Although this has not been directly measured, electron probe analyses indicate that SR potentials are near zero at rest and during tetanus in skeletal muscle (Somlyo et al., 1981; Baylor et al., 1984); (3) Feedthrough of Ca²⁺ and Mg²⁺ was calculated in the presence of 150 mM K⁺ rather than the 250 mM Cs⁺ used in the bilayer experiments. I_Ca and I_Mg calculated in the presence of K⁺ were only 10% larger that those in the presence of Cs⁺; and (4) The values of the Ca²⁺ feedthrough parameters were set according to predictions of diffusion theory (Stern, 1992) for the Ca²⁺ buffering conditions in the cytoplasm as follows: In the cell, the cytoplasmic Ca²⁺ buffering is believed to be equivalent to that provided by ∼0.05 mM EGTA (Fabiato, 1983), and the Ca²⁺ binding rates for intracellular buffers (k = 10⁸ (Ms)⁻¹; Sipido and Wier, 1991) are 17-fold slower than for BAPTA, which was used in the bilayer experiments. Incorporating these cellular buffering parameters values into Eq. 1a gives [Ca²⁺]_r = 2750 × I_Ca/r. (Note that the exponential term in Eq. 1a vanishes because k is very large.) By substituting the values of r for the A- and I₂-sites (see above), we get the cellular values for X_Ca = 2,750/16.5 = 167 μM/pA and Y_Ca = 2,750/34 = 80 μM/pA. Therefore, the concentrations of Ca²⁺ reaching the A- and I₂-sites on the RYR as a result of feedthrough will be >10-fold higher in cardiomyocytes than in these bilayer experiments.

Luminal [Ca²⁺] Dependence of RYR Is Different in Diastole and Systole.

Fig. 11 (A and B) shows the model predictions of the dependence of F_o and τ_o on [Ca²⁺]_L in the SR at diastole ([Ca²⁺]_C = 0.1 μM). The opening frequency increases fourfold with increasing [Ca²⁺]_L over the physiological range (0.3–1 mM), whereas the increase in τ_o is 1.8-fold over this range. Collectively, these data indicate that the open probability of RYRs increases approximately eightfold between 0.3 and 1 mM [Ca²⁺]_L. Note that under diastolic conditions the RYR opening frequency is extremely low (<3.0 × 10⁻⁴ s⁻¹) and equates to less than one channel opening per hour, far too infrequent to be reliably measured in bilayer experiments. Examination of the legend for Fig. 11 reveals that these low triggering rates are due both to the lack of stimulation by the low [Ca²⁺]_C (0.1 and 1 μM [Ca²⁺]_C) and to the strong inhibitory effect of 1 mM [Mg²⁺]_C.

Figure 11.

Theoretical predictions of RYR2 modulation by free Ca²⁺ in the SR lumen. The calculations are derived from application of the luminal-triggered feedthrough model to the physiological context as described in the Discussion (Physiological implications). (A and B) The effect of various factors on the opening frequency, F_o, normalized to their values at [Ca²⁺]_L = 1 mM and mean open time, τ_o, of RYRs. See below for the absolute values of F_o at [Ca²⁺]_L = 1 mM for each condition. Diastolic conditions ([Ca²⁺]_C = 0.1 μM) and systole ([Ca²⁺]_C = 1 μM; in B both lines coincide). The contribution of various factors is seen by setting associated parameters to zero (dashed lines). For Ca²⁺ feedthrough, the Ca²⁺ current was set to zero (I_Ca = 0). Elimination of luminal Mg²⁺ inhibition ([Mg²⁺]_L = 0 and 0.2 mM; they coincide with the thick line in B). Elimination of cytoplasmic Mg²⁺ inhibition from the I₁- and A- sites ([Mg²⁺]_C = 0) and from the I₁-site only (–I₁). (C and D) The effects of perturbing A- and L-sites on SR load dependence of F_o and τ_o under diastolic conditions (solid line, K_ACa = 1.2 μM and K_LCa = 40 μM). Dashed lines show the effect of increasing Ca²⁺ sensitivities of either the A-site (K_ACa = 0.6 μM) or L-site (K_LCa = 15 μM; in B this coincides with the solid line). (A and B) [Ca²⁺]_C = 0.1 μM (normalizing factor, 3.0 × 10⁻⁴); [Ca²⁺]_C = 1 μM (normalizing factor, 2.9 × 10⁻²); [Mg²⁺]_C = 0 (normalizing factor, 1.07); [Mg²⁺]_L = 0 (normalizing factor, 1.2 × 10⁻³); [Mg²⁺]_L = 0.2 (normalizing factor, 0.8 × 10⁻³); -I₁ site (normalizing factor, 2.9 × 10⁻⁴); I_Ca = 0 (normalizing factor, 1.6 × 10⁻⁴).

During systole ([Ca²⁺]_C =1 μM), the model predicts that F_o varies by <20% over the physiological [Ca²⁺]_L. This is because at 1 μM [Ca²⁺]_C, the A-sites on three or more subunits have Ca²⁺ bound so that the A-site alone is sufficient to trigger openings and consequently the channel opening rates are independent of luminal Ca²⁺.

Luminal Mg²⁺ Is the Main Contributor to Store Load Dependence of RYR Activity in Diastole.

What is particularly striking in Fig. 11 A is the weakening of the [Ca²⁺]_L dependence of F_o when Mg²⁺ is removed from the SR lumen ([Mg²⁺]_L = 0). Although F_o at 1 mM [Ca²⁺]_L is elevated approximately fourfold, its relative dependence on [Ca²⁺]_L is reduced to only 20% over the physiological range. The reason for this is that the Ca²⁺ occupancy of the L-site determines the [Ca²⁺]_L dependence of F_o, but in the absence of luminal Mg²⁺ this site is saturated at physiological [Ca²⁺]_L and generates channel openings at a nearly constant maximal rate between 0.3 and 1 mM. However, in the presence of 1 mM [Mg²⁺]_L, the apparent affinity of the L-site for Ca²⁺ is raised from 40 μM to 1 mM, causing F_o to increase over this concentration range. Because [Mg²⁺]_L has not been measured, we examined the range of [Mg²⁺]_L that could retain a substantial [Ca²⁺]_L dependence on F_o. Even if the SR lumen only contained 0.2 mM Mg²⁺, the model predicts that there would be a [Ca²⁺]_L dependence on F_o nearly as large as that seen at [Mg²⁺]_L = 1 mM ([Mg²⁺]_L = 0.2; Fig. 11 A). The removal of luminal Mg²⁺ had no effect on τ_o and, the [Ca²⁺]_L dependence of τ_o at zero [Mg²⁺]_L in Fig. 11 B is obscured by the line for the [Ca²⁺]_L dependence in the presence of 1 mM [Mg²⁺]_L. Thus, the model predicts that luminal Mg²⁺ is a strong contributor to the store load dependence of F_o but not τ_o.

The removal of cytoplasmic Mg²⁺ caused a 300-fold increase in F_o (from 3.0 × 10⁻⁴ s⁻¹ to 1.07 s⁻¹; Fig. 11 legend; [Mg²⁺]_C = 0) and a 10-fold increase in τ_o. However, in spite of this strong effect, [Mg²⁺]_C did not contribute to the relative [Ca²⁺]_L dependence of channel activity as this form of Mg²⁺ inhibition was the same over the physiological [Ca²⁺]_L range.

Ca²⁺ and Mg²⁺ Micro-domains Are Minor Contributors to the Store Load Dependence of Host Channel Activity.

We used the model to examine the role of feedthrough on the activity of the channel passing the ions. Tinker's permeation model (Tinker et al., 1992) predicts that the Ca²⁺ current through a single RYR during Ca²⁺ release will be ∼1 pA per mM of [Ca²⁺]_L, which we expect to cause the cytoplasmic Ca²⁺ levels to rise to 167 μM/mM [Ca²⁺]_L at the A-site and 80 μM/mM [Ca²⁺]_L at the I₂-site. The contribution of Ca²⁺ feedthrough can be seen by comparing the solid curve with the dashed curve (labeled I_Ca = 0 in Fig. 11 B) showing τ_o when Ca²⁺ feedthrough is set to zero. Ca²⁺ feedthrough increased τ_o by up to 10-fold and produced the [Ca²⁺]_L dependence of τ_o. Although Ca²⁺ feedthrough had a large effect on τ_o, it is only a minor contributor to the [Ca²⁺]_L dependence of overall RYR activity as it had no effect on F_o (Fig. 11 A) so that even in the absence of feedthrough, RYR open probability would retain most of its dependence on [Ca²⁺]_L.

Based on estimates of Somlyo et al. (1985), the Mg²⁺ current through the RYR is approximately half that of the Ca²⁺ current. The model predicts that perturbations in the [Mg²⁺] near the A-site will be 120 μM/pA of Mg²⁺ current. Even if the Mg²⁺ current is as large as the Ca²⁺ current itself, feedthrough of Mg²⁺ is unlikely to cause a [Mg²⁺] perturbation >120 μM near any of the Ca²⁺ sites. Consequently, Mg²⁺ feedthrough will not make a big enough relative change in [Mg²⁺] at any sites to have an effect on Ca²⁺ release.

Luminal Activation Can Be Increased by Changes in Either L- or A-Site.

RYR2 mutations associated with sudden cardiac death are known to enhance activation by luminal Ca²⁺ (Jiang et al., 2005). Many of these mutations are known to reside in the cytoplasmic domains of the RYR, which raises the question of how can luminal activation be increased by cytoplasmic mutations (George et al., 2007). The model predicts that the enhanced luminal activation of mutant RYR2 may result from changes in gating associated with either luminal (L-site) or cytoplasmic (A-site) domains of RYR2. This is shown in Fig. 11 for the case where the affinities of these sites to Ca²⁺ were increased. The solid line shows the dependencies of F_o (Fig. 11 C) and τ_o (Fig. 11 D) for RYRs studied here. The dashed lines show the predicted outcomes if the Ca²⁺ affinity of the A-site is changed from 1.2 to 0.6 μM or the affinity of the L-site is changed from 40 to 15 μM. In both cases, the [Ca²⁺]_L dependence of F_o increased as a result of the synergistic interactions between RYR2 subunits. The channel open time was only affected by a change in the A-site, which increased channel open times in conjunction with Ca²⁺ feedthrough.

Concluding Remarks.

Bilayer experiments have revealed a multiplicity of mechanisms by which luminal and cytoplasmic Ca²⁺ and Mg²⁺ can regulate RYR2. However, processes that play an important role in RYR gating in bilayer experiments are not necessarily important for store load–dependent regulation of Ca²⁺ release in cardiomyocytes. The role of ion feedthrough depends on the creation of dynamic micro-domains of Ca²⁺ and Mg²⁺ at the cytoplasmic face of the channel. Feedthrough of Mg²⁺ contributed to RYR inhibition via τ_o in the bilayer experiments but is unlikely to play a significant role in the cell because of the high ambient [Mg²⁺]. The model predicts that Ca²⁺ micro-domains do play a role in stimulating RYR activity. Although much has been made of Ca²⁺ feedthrough in regard to luminal activation of RYRs in bilayer experiments, we find that it is not likely to be the main contributor to store load dependence of Ca²⁺ release in vivo. A more substantial contributor to this is luminal Mg²⁺, which competes with Ca²⁺ for the L-site. Even though the Mg²⁺ concentrations within the cell are relatively constant, luminal triggering of RYR2 is an interplay between Ca²⁺ and Mg²⁺ where increased luminal [Ca²⁺] leads to displacement of Mg²⁺ from the L-site. Thus, the inhibitory effects of Mg²⁺ vary during the cardiac cycle because the effects of Mg²⁺ are quite different between diastole and systole. In the absence of Mg²⁺, the L-site would saturate at sub-physiological [Ca²⁺]_L causing a loss of luminal regulation of RYR activity at physiological [Ca²⁺]_L and SR depletion.

At present, it is unclear what precise concentrations of Mg²⁺ exist in the SR and how [Mg²⁺]_L changes throughout the cardiac cycle. We demonstrate the robustness of our predication that luminal Mg²⁺ is important to load dependent Ca²⁺ release by showing that this prediction is valid over the [Mg²⁺]_L range of 0.2–1 mM; a range likely to bracket physiological concentration. Nevertheless, this study highlights the importance of gaining precise measurements of the free Ca²⁺ and Mg²⁺ concentrations in the SR lumen.

This study elucidates several new aspects of the close link between luminal and cytoplasmic regulation of RYRs reported in many studies. The synergy we observe between [Ca²⁺]_L and [Ca²⁺]_C activation can be understood in terms of molecular processes that may equally apply to transmembrane synergies between other regulators of RYRs. The model, which explains this synergy, also predicts that regulation of RYR2 activity by store load can result from changes in gating associated with either luminal or cytoplasmic Ca²⁺ activation sites on the channel protein, thus providing an explanation for how luminal Ca²⁺ activation of RYRs is increased by mutations in their cytoplasmic domains.