Gating Pore Currents in DIIS4 Mutations of NaV1.4 Associated with Periodic Paralysis: Saturation of Ion Flux and Implications for Disease Pathogenesis

Abstract

S4 voltage–sensor mutations in CaV1.1 and NaV1.4 channels cause the human muscle disorder hypokalemic periodic paralysis (HypoPP). The mechanism whereby these mutations predispose affected sarcolemma to attacks of sustained depolarization and loss of excitability is poorly understood. Recently, three HypoPP mutations in the domain II S4 segment of NaV1.4 were shown to create accessory ionic permeation pathways, presumably extending through the aqueous gating pore in which the S4 segment resides. However, there are several disparities between reported gating pore currents from different investigators, including differences in ionic selectivity and estimates of current amplitude, which in turn have important implications for the pathological relevance of these aberrant currents. To clarify the features of gating pore currents arising from different DIIS4 mutants, we recorded gating pore currents created by HypoPP missense mutations at position R666 in the rat isoform of Nav1.4 (the second arginine from the outside, at R672 in human NaV1.4). Extensive measurements were made for the index mutation, R666G, which created a gating pore that was permeable to K⁺ and Na⁺. This current had a markedly shallow slope conductance at hyperpolarized voltages and robust inward rectification, even when the ionic gradient strongly favored outward ionic flow. These characteristics were accounted for by a barrier model incorporating a voltage-gated permeation pathway with a single cation binding site oriented near the external surface of the electrical field. The amplitude of the R666G gating pore current was similar to the amplitude of a previously described proton-selective current flowing through the gating pore in rNaV1.4-R663H mutant channels. Currents with similar amplitude and cation selectivity were also observed in R666S and R666C mutant channels, while a proton-selective current was observed in R666H mutant channels. These results add support to the notion that HypoPP mutations share a common biophysical profile comprised of a low-amplitude inward current at the resting potential that may contribute to the pathological depolarization during attacks of weakness.

INTRODUCTION

Hypokalemic periodic paralysis (HypoPP) is a dominantly transmitted genetic disorder characterized by attacks of sustained sarcolemmal depolarization accompanied by low serum potassium (Cannon, 2006). These attacks are manifested clinically as prolonged episodes of flaccid paralysis. The pathogenesis of sarcolemmal depolarization during these attacks is poorly understood. In most affected kindreds, the disorder is caused by missense mutations at charged residues of the S4 voltage–sensing segments in either the L-type voltage-gated Ca²⁺ channel (CaV1.1) or voltage-gated Na⁺ channel (NaV1.4) of skeletal muscle (Jurkat-Rott et al., 1994; Ptacek et al., 1994; Bulman et al., 1999; Jurkat-Rott et al., 2000; Sternberg et al., 2001).

These charge-altering mutations impair the normal function of NaV1.4 and CaV1.1 channels. HypoPP mutations in CaV1.1 slow the kinetics of channel activation and may also cause reductions in CaV1.1 expression levels (Lapie et al., 1996; Lerche et al., 1996; Morrill et al., 1998; Morrill and Cannon, 1999). These observations have led investigators to speculate that HypoPP caused by CaV1.1 mutations may be the consequence of alterations in myoplasmic Ca²⁺ homeostasis, which might indirectly influence other conductances important for maintaining the resting potential. In contrast, HypoPP mutations in NaV1.4 enhance inactivation and consequently reduce Na⁺ channel availability, thereby limiting the ability of sarcolemma to propagate action potentials normally (Jurkat-Rott et al., 2000; Struyk et al., 2000). These functional impairments, however, have so far failed to yield a unified explanation for why homologous S4 segment mutations in two different channels might exert a convergent downstream influence on the stability of the sarcolemmal resting potential and cause hypokalemia with myoplasmic sequestration of K⁺.

Recently, it was reported that three HypoPP mutations in NaV1.4 create accessory ionic permeation pathways, separate from the central Na⁺-conducting pore (Sokolov et al., 2007; Struyk and Cannon, 2007). These permeation pathways most likely extend through the aqueous crevices in which the mutant S4 segments reside, structures referred to as gating pores. Similar ion-permeable gating pores have been reported in other channels harboring charge-altering mutations in S4 segments, including the Shaker K⁺ channel and NaV1.2 (Starace et al., 1997; Starace and Bezanilla, 2001, 2004; Sokolov et al., 2005; Tombola et al., 2005). These findings lend support to a structural model of the voltage-sensing domain wherein communication between intracellular and extracellular compartments is normally blocked by the positioning of one or more charged S4 side chains within a focal constriction in a water-filled gating pore (Starace and Bezanilla, 2004). When substituted residues are positioned within this corseted region, a transmembrane ion permeation pathway through the gating pore is created. Currents flowing through gating pores therefore typically exhibit robust voltage dependence, attributable to the normal voltage-dependent translocation of the S4 segments, which moves substituted side chains into and out of the permissive position.

The notion that aberrant gating pore currents created by S4 segment substitutions might account for the pathophysiology of HypoPP offers an attractive explanation for the convergence of phenotype arising from HypoPP mutations in CaV1.1 and NaV1.4. One critical step in supporting this hypothesis is to determine whether all HypoPP mutations create an ion-permeable gating pore, and to characterize the resultant currents.

Sokolov et al. (2007) reported an inwardly rectifying gating pore current with limited cation selectivity in the arginine to glycine mutation at position 666 in the rat Nav1.4 isoform (the human HypoPP mutant R672G ortholog). Currents with similar amplitude and voltage dependence were recorded from R666H and R663H mutant channels (human R672H and R669H orthologs), and were interpreted as evidence that monovalent cations were also permeable through gating pores in these mutants. The amplitude of the R666G gating pore current was estimated as ∼1.25% the amplitude of the peak Na⁺ ionic current flowing through the central pore. Using this estimate, the authors calculated that the magnitude of the R666G gating pore conductance in sarcolemma from heterozygotes was ∼69 μS/cm², rivaling the resting K⁺ conductance for influence over the resting potential and therefore sufficient to cause massive depolarization of muscle. Indeed, it was noted that the addition of a depolarizing gating pore conductance of this magnitude would necessitate a compensatory alteration to the normal resting conductances of muscle to maintain a hyperpolarized sarcolemmal resting potential between attacks of paralysis.

A contemporaneous report from our laboratory also demonstrated a gating pore current in rat NaV1.4-R663H mutant channels, which exhibited similar rectification and voltage dependence as that described by Sokolov et al. (2007; Struyk and Cannon, 2007). Our data indicated that the current flowing through the R663H gating pore was carried by protons, and that larger monovalent cations were impermeant. Moreover, we estimated the R663H proton current amplitude to be only ∼0.1% of the peak Na⁺ ionic current. This smaller conductance is probably inadequate to cause significant depolarization of resting sarcolemma. It is possible that the addition of a low-amplitude depolarizing current may potentiate the normal sarcolemmal propensity to depolarize when exposed to low external potassium, arising from effects attributable to the inward rectifier K current (Struyk and Cannon, 2008). In this manner, fibers that contain an accessory gating pore current would be characterized by a stable hyperpolarized resting potential in normal physiological conditions, but may be poised for massive depolarization in response to modest perturbations of extracellular K⁺.

We sought to clarify the reported differences between gating pore currents in different mutant channels and to expand the number of HypoPP mutants tested for a gating pore conductance. To do so, we initially focused on characterizing gating pore currents created by the R666G HypoPP mutation in the rat NaV1.4 isoform. In agreement with Sokolov et al. (2007), we found that R666G supports a gating pore current exhibiting limited selectivity between monovalent cations K⁺ and Na⁺. However, the amplitude of the R666G gating pore current we observed was comparable to the amplitude of the R663H proton current we previously reported, which is ∼0.1% of the predicted peak ionic current through the Na-selective pore, and not >1%. We also observed several unique properties for the voltage dependence and inward rectification of the R666G gating current, which were accounted for by a barrier model of ion permeation. Gating pore currents were also detected in other HypoPP mutations at the R666 site, with features consistent with a monovalent cation conductance in R666S and -C HypoPP mutants, and a proton-selective conductance in the R666H HypoPP mutant. These results support the notion that HypoPP mutations may exert their pathological effect by introducing low-amplitude depolarizing leakage currents to the sarcolemma.

MATERIALS AND METHODS

Expression of Nav1.4 Channels

The rat adult skeletal muscle Na⁺ channel α subunit cDNA (rNaV1.4) subcloned into the EcoRI site of the Xenopus expression vector pGEMHE (Liman et al., 1992) was used as a template for site-directed mutagenesis using the QuickChange Mutagenesis kit (Stratagene). Primers were designed to alter codons specifying the substitution mutation and to introduce a translationally silent restriction site to facilitate rapid screening by restriction digest. Point mutations were confirmed by direct sequencing through the codon position.

cRNA was synthesized by in vitro transcription using the mMessage mMachine kit (Ambion) from 2 μg of each expression construct linearized with NheI. Xenopus laevis were housed in an AAALAC-accredited facility, and all experiments were performed within guidelines established by the UTSW Institutional Animal Care and Use Committee. Xenopus oocytes between 1 and 7 d after harvest were injected with ∼50 ng of cRNA encoding either wild-type (WT) or mutant NaV1.4 protein, along with ∼50 ng (approximately twofold molar excess) of cRNA encoding the β1 subunit. Injected oocytes were incubated between 1 and 5 d at 17°C in ND96 medium (in mM: 96 NaCl, 2 KCl, 1.8 CaC₁₂, 1 MgC₁₂, 5 HEPES, pH 7.6, supplemented with 2.5 mg/ml pyruvate and 50 μg/ml gentamicin).

Electrophysiology

In all experiments, oocytes were voltage clamped in the cut-open configuration, with active clamp of the upper and guard compartments controlled by a CA-1B amplifier (Dagan Corporation) using the mainframe clamp circuitry. The lower oocyte membrane was permeabilized with 0.1% saponin to gain low-resistance electrical access to and facilitate ionic control over the intracellular compartment. The amplifier was controlled and signals were recorded with a Pentium-3–based PC running pClamp 7 software, interfaced using a DigiData 1200 A/D converter (MDS Analytical Technologies).

Voltage-sensing electrodes were fabricated from borosilicate capillary glass (1.5-mm OD thin wall with filament; World Precision Instruments) using a multistage puller (Sutter Instrument Co.) and filled with 3 M KCl. Tip resistances were between 0.2 and 2 MΩ. The leads of the amplifier headstage, attached to Ag⁺/AgCl pellets in plastic wells containing 1 M NaCl solution, were connected to the upper, guard, and lower oocyte compartments using glass agarose bridges containing 110 mM Na⁺ methanesulfonate, 10 mM HEPES, pH 7.4, and threaded with platinum wire. Correction of linear capacitance transients was accomplished using the amplifier's analogue circuitry. No analogue compensation for linear leak current was used during the experiments.

Current signals were filtered at 5 kHz and sampled at 100 kHz (for recordings of gating currents) or filtered at 500 Hz and sampled at 5 kHz (for recordings of steady-state leak currents). For gating current (charge displacement) measurements, a P/−8 subtraction protocol was used to subtract linear leak and residual capacitance current from a holding potential of −160 mV. No online leak subtraction was applied to measurements of gating pore currents. Rather, passive membrane leak conductance was compensated offline by generating a linear fit to the I-V relationship at voltages between +30 and +50 mV, and subtracting this linear current from the current records.

All experiments were performed in Cl⁻-free solutions to minimize contamination with endogeneous oocyte Cl⁻ currents. For initial experiments characterizing the amplitude, voltage dependence, and ionic permeability of R666G gating pore currents, the external solution (applied to the external and guard compartments) contained the following (in mM): 115 KOH (or equimolar amounts of NaOH or NMDG⁺ in substitution experiments), 1.5 CaOH₂, 2.5 BaOH₂, 10 HEPES, pH 7.4, with methanesulfonic acid. Internal solution contained (in mM): 120 NMDG⁺ (or equimolar amounts of KOH or NaOH in substitution experiments), 10 EGTA, 10 HEPES, pH 7.4, with methanesulfonic acid. For experiments approximating the mammalian physiological monovalent cation gradient, the external solution contained the following (in mM): 112 NaOH, 3 KOH, 1.5 CaOH₂, 2.5 BaOH₂, 10 HEPES, pH 7.4, with methanesulfonic acid. Internal solution contained (in mM): 103 KOH, 7 NaOH, 10 EGTA, 10 HEPES, pH 7.4. All bath solutions contained 1 μM tetrodotoxin (Tocris Chemicals) to block ionic currents through the central pore. Recordings were not begun until >40 min after saponin permeabilization of the oocyte membrane to allow for equilibration of the intracellular compartment with the lower bath.

Data Analysis

Data were analyzed using a combination of ClampFit 9 (MDS Analytical Technologies), Excel (Microsoft), and OriginPro 6.1 (OriginLab) software packages. For gating currents, Q_On was measured by integration of the leak-corrected current transient recorded over a 15-ms voltage step. To compensate for the presence of small leak subtraction errors arising from the combination of linear-nonspecific leak and nonlinear gating pore conductance, the steady-state current recorded during the last 0.5 ms of the voltage step in each trace was subtracted from the full current record before integration. The Q_On–V relationship was then determined by normalizing charge movement to the maximal charge displacement at saturating voltages (Q_On,Max), derived from fits with the Boltzmann function:

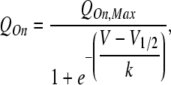where V_1/2 is the voltage of half-maximal charge movement, and k is the slope.

Steady-state currents, composed of ionic currents permeating rNaV1.4 gating pores and residual nonspecific leak across the oocyte membrane, were measured as the mean current elicited during the last 100 ms of a 300-ms voltage command. Leak correction of these raw current records to segregate gating pore currents from nonspecific oocyte background leak was accomplished as described above. In all figures, error bars represent ± SEM.

Modeling the Gating Pore Permeation Properties

Relative open probability of the permeation pathway was assumed to be governed by voltage-dependent conformational changes of the DIIS4 voltage–sensing segment, wherein the resting state at hyperpolarized potentials is permissive for ion permeation, and the “activated” state favored by depolarization occludes the gating pore. Transition between these two states was modeled by the voltage-dependent Boltzmann function:

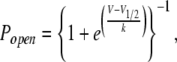where V_1/2 is the voltage of half-maximal availability, and k is the slope factor.

The cation permeation pathway was modeled as a barrier scheme, with a single cation binding site flanked by two energy barriers (Scheme 1).

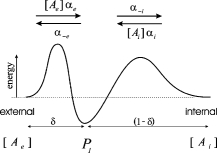(SCHEME 1)

The cation binding site was located eccentrically within the electrical field at a fractional electrical distance δ from the outside to account for the voltage-dependent and rectification features of the R666G gating pore currents (see Results). The binding interaction of all permeant cations was constrained to the same site (i.e., at an identical electrical distance). The outward flux for cation “A,” J_A, is proportional to the rate of ions moving from an occupied binding site to the external side, minus the concentration-dependent rate of ions moving from the external solution into the binding site:

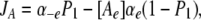(1)

where P₁ is the probability the binding site is occupied, P₀ = 1 − P₁ (empty), [A_e] is the activity of ion A on the external end of the gating pore relative to a reference of 1 M, α_e is the entry rate from the external side, and α_−e is the transition rate from an occupied site to the external side. The steady-state occupancy of the binding site (assuming no change in the activity of permeant ions in the compartments on either side of the membrane) is:

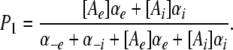(2)

Combining Eqs. 1 and 2 and scaling by the valence and elementary charge yield the outward current:

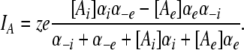(3)

The energy barriers are assumed to be symmetrical, and so the voltage dependence of the rate constants is expressed in terms of the fractional electrical distance:

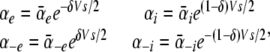(4)

where the 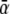terms are the transition rates at V = 0 mV, and Vs = z_sVF/(RT) is the normalized membrane potential. The constraint that I_A = 0 for the case where V = 0 and the concentration of A is identical on the external and internal sides requires that 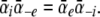To simulate gating pore currents under physiological conditions wherein more than one type of permeant ion may be present at either end of the pore, we expanded Scheme 1 to include multi-ion competition for a single binding site (see Appendix).

Parameter estimates for voltage-dependent gating and transition rates governing ion permeation were derived by minimization of the square of the residual differences between the mean I-V relationships for K⁺ or Na⁺ currents flowing independently through the R666G gating pore (see data in Fig. 3, A and B). The model responses were calculated as the unitary flux through the gating pore using Eqs. 3 and 4 multiplied by the voltage-dependent probability of accessibility, P_open. For comparison to the experimental data, the resultant membrane currents were calculated assuming a maximal translocation of 12 charges per Na⁺ channel (Hirschberg et al., 1995). Parameter values for the transition rates are listed in Table I. These parameters were then fixed and used to independently compute the predicted behavior of the R666G current under a physiologically distributed cationic gradient (high external Na⁺ and internal K⁺) and compared with the experimentally derived I-V relationship.

Figure 3.

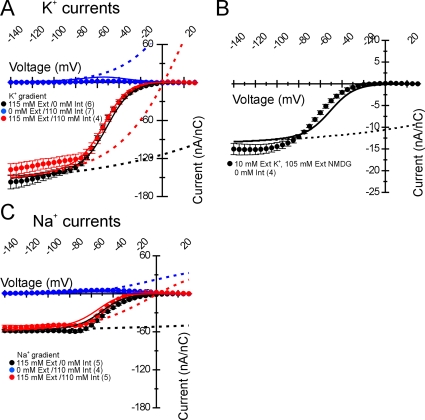
R666G K⁺ and Na⁺ steady-state gating pore currents. The permeability of the R666G gating pore for different monovalent cations was tested. The transmembrane cation gradient was manipulated as described in the insets, such that either cation was present exclusively in the internal or external compartments, or was distributed nearly symmetrically in both compartments. The normalized, leak-corrected I-V relationships of resultant K⁺ (A and B) and Na⁺ (C) gating pore currents are shown. The different colors in A and C represent current recordings made in different ionic gradients, with the legend in each figure inset. The number of samples recorded for each condition is also denoted in parenthesis. Very small outward currents were seen when either Na⁺ or K⁺ were present exclusively on the inside, despite significant outward driving force for both cations. In external solutions consisting of 10 mM K⁺ and 105 mM NMDG, low-amplitude K⁺ currents were observed (note the normalized current scale in B), indicating that NMDG does not block the pore from outside and therefore cannot account for the lack of outward currents. Furthermore, inward current amplitudes were nearly equivalent whenever K⁺ or Na⁺ was present on the outside, despite significant changes to the overall driving force due to differences in the internal cation concentration. Overlying the data are curves from the permeation model depicted in Fig. 6 and described (see Results), representing the best parameter fits listed in Table I. Solid lines represent currents from the full model, which includes voltage-dependent accessibility of the R666G gating pore due to movement of the DIIS4 voltage sensor, whereas the dotted lines demonstrate the predicted open-channel voltage dependence of currents flowing through an R666G gating pore in the absence of gating.

TABLE I.

Transition Rates (s⁻¹)

Ion	External→Internal		Internal→External
	αe	α-i	α-e	αi
K+	1.49 × 104	2.15 × 104	3.56 × 103	9.00 × 104
Na+	5.56 × 103	4.49 × 104	4.87 × 102	5.12 × 105

Online Supplemental Material

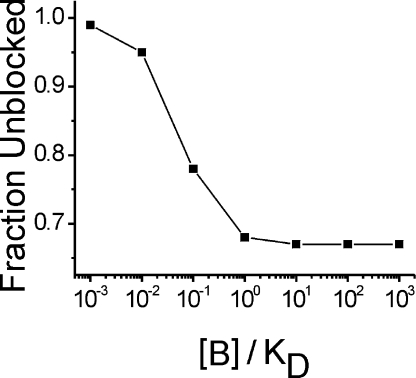
The possibility that voltage-dependent divalent cation block could account for the saturation of the gating pore current at hyperpolarized potentials was considered as an alternative to the energy barrier model presented in Fig. 6. The model described by Eq. 5 (see Results) was used to fit the data recorded using K⁺ as the permeant cation.

The model assumes that all divalent cations used in the study bind to the putative blocking site with similarly high affinity; thus, the block is directly related to the total divalent concentration in the bath, rather than the concentration of a specific divalent cation. The possibility that another charged molecule in the bath might function as a blocking cation (e.g., the charge-bearing fraction of HEPES) was excluded by the fact that in baths in which HEPES was substituted with different buffers (e.g., Tris), the saturating behavior of the I-V relationship persisted (not depicted in Fig. 2 B). This model can provide a reasonably good fit to these data (Fig. S1 A), provided a high-affinity block ([B]/K_D > 10) is used to emulate the saturation of current at voltages <−80 mV. The notion of high affinity divalent block is problematic, however, because a 50% increase in blocker concentration (from 4 to 6 mM) would produce a substantial reduction in current amplitude of ∼30%, which was not observed in the experimental data (Fig. S1 B). Fig. S1 is available at http://www.jgp.org/cgi/content/full/jgp.200809967/DC1.

RESULTS

We characterized gating pore currents in the rat NaV1.4 isoform (rNaV1.4) expressing missense mutations at position R666 (ortholog of the human R672 position, which is the second arginine from the outermost one in DIIS4). Xenopus oocytes were injected with RNA encoding either mutant or WT rNaV1.4 (Trimmer et al., 1989), along with the β1 subunit (McClatchey et al., 1993), and membrane currents were studied under voltage clamp in the cut-open configuration. Expression of rNaV1.4 mutant constructs at the plasma membrane was confirmed by recording current transients arising from nonlinear charge displacement (gating current). Corresponding steady-state currents, consisting of a combination of nonspecific oocyte membrane leak and rNaV1.4-specific gating pore current (if present), were subsequently assessed at higher amplifier gain.

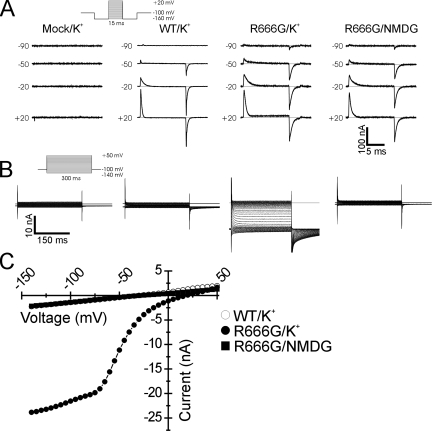
Representative current recordings from WT and R666G mutants are shown in Fig. 1. Translocation of rNaV1.4 gating charge was detectable in oocytes expressing both WT and R666G channels and absent in water-injected control oocytes. Significant differences in the steady-state background currents, however, could be discerned between WT and R666G-expressing oocytes, despite similar amounts of gating charge movement. In bath solution containing K⁺ as the predominant extracellular cation, oocytes expressing WT rNav1.4 exhibited a small amplitude membrane leak current with linear voltage dependence, indistinguishable from the nonspecific leak currents recorded from mock-injected oocytes. However, oocytes expressing R666G mutant channels revealed larger amplitude inward currents with nonlinear voltage dependence, consistent with ionic current flowing through an accessory gating pore created by the S4 missense mutation. This current was abolished when NMDG was substituted for K⁺ (Fig. 1 B), suggesting that the R666G gating pore is permeable for K⁺ but not NMDG. Examination of the steady-state I-V relationships reveals that at voltages >+20 mV, currents recorded from R666G-expressing oocytes are identical to the nonspecific membrane leak currents recorded in mock-injected oocytes and in oocytes expressing comparable levels of WT channels. An inward current appears at more negative voltages, however, in R666G-expressing oocytes. This inward current has steep voltage dependence in a midrange of membrane potentials and transitions to reduced voltage dependence (shallower slope conductance) at more hyperpolarized potentials (Fig. 1 C).

Figure 1.

Charge movement and gating pore currents in rNaV1.4-R666G channels. Oocytes expressing WT and R666G mutant channels were recorded using different bath solutions in which either K⁺ or NMDG was substituted as the predominant external cation (denoted at top of figure). For comparison, currents recorded from a mock-injected oocyte in K⁺-containing bath solution are also shown. Representative raw gating current traces are shown in A. Gating charge displacement was assessed by recording the nonlinear transient current responses elicited by 15-ms voltage steps from a prepulse potential of −160 mV (see voltage protocol in inset). Membrane potential commands (in mV) eliciting charge movement are denoted to the left of each trace. Scale bars for the current records in A are shown at the bottom right. In B, representative steady-state background current recordings are shown for the same oocytes whose gating currents are depicted in A. Steady-state currents were elicited by a 300-ms voltage command from a holding potential of −100 mV (see voltage protocol in inset). Scale bars for the current records in B are shown at the bottom left. The mean I-V relationships of the steady-state background currents from the oocyte recordings depicted in B are shown in C. The symbol legend is to the right. In K⁺-containing bathing solutions, oocytes expressing R666G mutant channels exhibit robust inward currents at voltages <+20 mV that are not seen in oocytes expressing comparable levels of WT channels under the same conditions (open circles are not fully visible beneath filled squares). Steady-state currents in R666G-expressing oocytes recorded in NMDG bath solution, however, are indistinguishable from the nonspecific membrane leak seen in mock-injected oocytes and oocytes expressing WT rNav1.4.

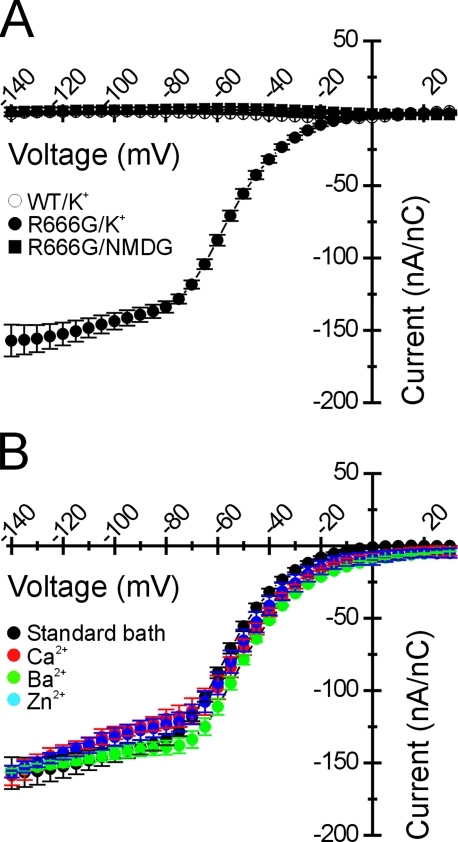
To segregate the R666G-specific steady-state current from the nonspecific oocyte membrane leak, the contribution of nonspecific leakage current at hyperpolarized voltages was extrapolated from a linear fit to the current responses to command potentials between +30 and +50 mV (a voltage range in which the R666G-specific conductance appears to be closed). The amplitudes of inward currents that remained after this leak correction were proportional to the maximal gating charge displacement in each oocyte (unpublished data), consistent with the notion that the R666G-specific inward current is the consequence of a gating pore conductance created by the mutation. For subsequent analyses, gating pore currents were normalized to the maximal gating charge displacement for comparison between oocytes with different levels of rNaV1.4 expression. Leak-corrected currents normalized in this manner are compared in Fig. 2 A for WT oocytes and R666G-expressing oocytes recorded in K⁺ and NMDG bath solutions.

Figure 2.

Normalized leak-corrected R666G gating pore currents are not altered by divalent substitution in the bath. Gating pore currents were segregated from the nonspecific oocyte membrane leak as described (see Results) and scaled to the maximal rNaV1.4 gating charge in the corresponding oocyte. The mean I-V relationship of these normalized steady-state currents is shown in A. A nonlinear current component was not detected for WT-expressing oocytes in K⁺-containing bath solutions (n = 5). Inward gating pore current is seen when R666G channels are recorded in K⁺-containing bath solution (n = 6), whereas the gating pore current is abolished by NMDG substitution in the bath (n = 4; symbol key in figure inset). In B, R666G gating pore K⁺ currents were recorded in the presence of different divalent cations in the bath. No difference in the amplitude or voltage-dependent plateau of the R666G gating pore current is seen despite substitution with either 6 mM Ca²⁺ (n = 4), Ba²⁺ (n = 4), or Zn²⁺ (n = 3; symbol legend in the figure inset).

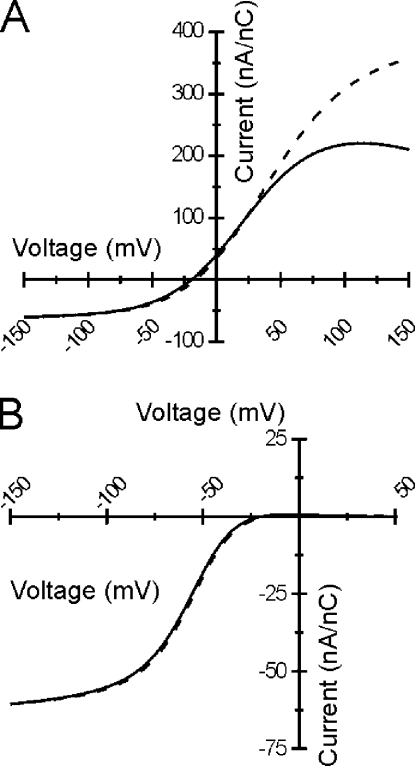
Several disparities in the current amplitude, selectivity, and voltage dependence were evident between the R666G gating pore currents we recorded and those reported in Sokolov et al. (2007). Because the recording solutions we used were slightly different, it was important to rule out the possibility that these differences in ionic composition might account for these discrepancies. Specifically, in addition to Ca²⁺, our external bath contained Ba²⁺, which we found was critical to suppress the background leak conductance of the oocyte membrane sufficiently to discern the low-amplitude gating pore current (note the ratio of nonspecific leak to gating pore current in Fig. 1 C). When oocytes were bathed in solutions identical to those used by Sokolov et al. (2007), high-amplitude background leak currents were observed roughly 100-fold higher than the typical oocyte leak current recorded in our standard bath solutions. Because the R666G-specific gating pore current was a minor component of the total current under these low-divalent conditions, we instead sought to test whether bath solutions with different divalent cation compositions affected the R666G gating pore current. Sokolov et al. (2007) reported that the addition of 6 mM Zn²⁺ fully blocked the R666G gating pore current, whereas 6 mM Ba²⁺ partially blocked the current (∼50%). In no instance did they report current saturation in the hyperpolarized voltage range, even in bathing solutions characterized by high divalent cation concentrations.

Various divalent cations were substituted in K⁺ bath solution (Fig. 2 B). K⁺ currents flowing through the R666G gating pore recorded using our standard divalent cation concentrations (2.5 mM Ba²⁺, 1.5 mM Ca²⁺) were not discernibly different from K⁺ currents recorded when these divalent cations were fully substituted with 6 mM Ca²⁺, 6 mM Ba²⁺, or 6 mM Zn²⁺. These data are consistent with two alternative interpretations: either all the divalent cations that were tested exert similar blocking effects on the R666G gating pore, or the divalent composition of the bath has no significant influence over the gating pore current. These alternative possibilities are considered below. These results do indicate, however, that the differences between our data and those reported in Sokolov et al. (2007) are probably not due to differences in bath divalent cation composition.

The ionic selectivity of the R666G gating pore was explored in greater detail through substitution of monovalent cations in the internal and external solutions, and the R666G conductance was found to exhibit several further unexpected features. When the ionic driving force for K⁺ was biased outwardly by raising the internal K⁺ to 110 mM and using NMDG as the predominant external cation, very low amplitude outward currents were observed, despite the strong outward driving force for K⁺ at all voltages (Fig. 3 A, blue symbols). The possibility that such small outward currents were due to external block by NMDG was excluded by recording inward K⁺ currents in bath solutions composed of 10 mM K⁺ and 105 mM NMDG (Fig. 3 B). K⁺ currents under these conditions are proportionately reduced in amplitude compared with the 105-mM K⁺ bath (notice the change in current scale for Fig. 3 B). When nearly equal concentrations of K⁺ were present on both sides of the membrane (Fig. 3 A), thereby reducing the inward electrochemical K⁺ driving force at hyperpolarized voltages (E_K ∼ +1 mV), the gating pore current amplitude was nearly identical to the currents recorded when K⁺ was limited to the extracellular compartment (e.g., E_K→∞). When Na⁺ was substituted for K⁺, nonlinear currents were also observed that exhibited the same voltage dependence as the K⁺ currents (Fig. 3 C). However, the normalized amplitude of the Na⁺ currents was reduced, suggesting that Na⁺ was less permeable through the R666G gating pore. Like the K⁺ currents, the amplitude of inward Na⁺ currents at hyperpolarized potentials was largely independent of changes to the inward Na⁺ driving force, and only very small outward currents were observed under conditions strongly favoring outward flow of Na⁺ ions at hyperpolarized voltages.

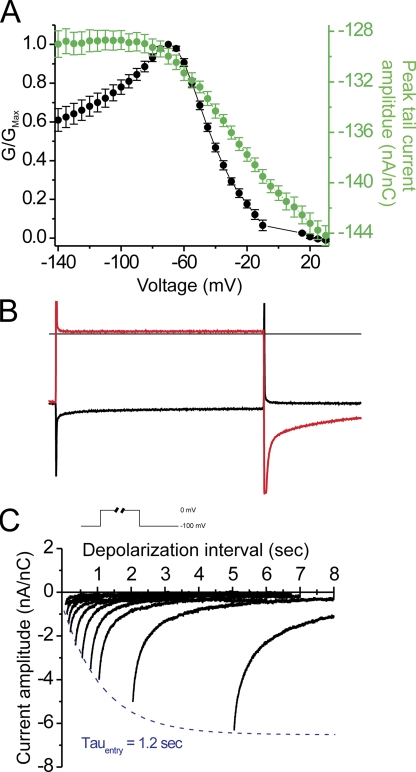
We sought to understand whether the unusual current saturation at hyperpolarized voltages was the consequence of changes in the open probability, P_OPEN, voltage-dependent block, or whether this was an intrinsic feature of the permeation pathway in the R666G gating pore. The relative open probability of a putative R666G gating pore exhibiting Ohmic conductance properties can be estimated by transforming the I-V relationship recorded in symmetric K⁺ into a normalized G-V relationship, assuming a E_REV ≈ 0. This transformation is demonstrated in Fig. 4 A (black circles). As anticipated, the gating pore permeation pathway is closed by membrane depolarization favoring outward movement of the DIIS4 voltage sensor, but this model also requires an ∼40% decline from peak in normalized P_OPEN to account for the saturation of the I-V curve at hyperpolarized voltages. As another index of P_OPEN, we examined whether the amplitudes of the tail currents observed upon membrane repolarization to the holding potential of −100 mV (Fig. 1 B) also support the notion that P_OPEN declines at potentials <−80 mV. Instantaneous tail current amplitudes were estimated by extrapolating a single exponential fit to the tail current decay after leak correction and normalization to gating charge. No change in normalized tail current amplitude was observed at voltages <−80 mV (Fig. 4 A, filled green circles), and thus these data fail to provide support for the notion that a reduction in P_OPEN at increasingly hyperpolarized potentials accounts for the current saturation at voltages <−80 mV. Furthermore, the aggregate behavior of the R666G gating pore currents, including the low amplitude of the outward currents, and the relative independence of inward currents from the ionic driving force cannot be explained parsimoniously with the assumption of a simple Ohmic conduction pathway.

Figure 4.

Anomalous R666G tail currents do not support a change in P_OPEN to explain the current saturation at hyperpolarized voltages. The I-V relationship of the steady-state currents in a symmetrical K⁺ gradient (from Fig. 3 A) was transformed to a G-V relationship in A by assuming a reversal potential of 0 mV and therefore a linear open-state current through the origin. These conductance values were then normalized to the peak conductance (filled black circles). Normalized peak tail current amplitudes (after leak correction) are plotted against the voltage of the preceding pulse at which the normalized conductance values were obtained (filled green circles, right axis). No change in the amplitudes of these tail currents (all measured at −100 mV) was observed at voltages <−80 mV in a region where the normalized conductance declines. (B) A comparison of individual raw current traces extracted from Fig. 1 A confirms that the tail currents exhibit an anomalous increase in amplitude after more depolarizing voltage pulses during which the gating pore is occluded (red trace) and are absent after hyperpolarized pulses during which the gating pore remains open (black trace). The slow activation kinetics of the tail currents are shown C, in which tail currents were recorded at −100 mV after depolarizing pulse to 0 mV of different durations (see inset at top of figure). Current traces are arranged along the abscissa in proportion to conditioning pulse duration, and the peak current is fit with a single exponential function (dashed blue line), revealing an activation time constant of 1.2 s at 0 mV.

The unexpected, anomalous behavior of the tail currents, which exhibited increased amplitudes after more depolarizing voltage pulses that close the gating pore conductance (Fig. 4; note larger transient tail current amplitudes are indicated by symbols nearer to the bottom edge of the plot in A), suggested that more than one open state is traversed during the recovery from nonconducting state(s) at depolarized potentials. In addition, the slow relaxation of the tail currents indicated that this recovery occurred over several hundred milliseconds, much slower than the fast transitions anticipated due to rapid movement of a single voltage sensor. The slow decay of the tail current suggested that entry to closed state(s) at depolarized potentials (from which recovery results in the tails) might also occur on a slow time scale. To test this hypothesis, we measured the time course for the development of the transient tail currents after progressively longer conditioning pulses to 0 mV (Fig. 4 C). Inward tail currents are small after short depolarizations (<100 ms), whereas longer depolarizations elicit progressively larger inward tail current transients, which approach a maximal saturating amplitude with a time constant of ∼1.2 s. The possible significance of these tail currents is discussed below, but the pertinent issue at hand is that these anomalous instantaneous tails do not reflect the P_OPEN of the R666G gating pore for the antecedent conditioning pulse.

The gating pore current saturation (shallow slope conductance) at hyperpolarized voltages suggests the presence of an impediment to current flow with low-voltage sensitivity in this range. This might either be the consequence of voltage-dependent ionic block at a shallow electrical distance from the outside, or intrinsic saturability of the permeation pathway. In either circumstance, the steep portion in the midrange of the I-V relationship is likely due to voltage-dependent changes to the accessibility of the permeation pathway due to translocation of the mutant DIIS4 segment. The possibility of ionic block was considered in a model with a two-state gating transition to account for the steep decrease in current amplitude as membrane voltage becomes depolarized. The open channel I-V was modeled using the GHK current equation to account for the effects of the asymmetrical permeant ion gradients. Bath divalent cations were considered the most likely voltage-dependent blocking candidates (see Materials and methods, Online supplemental material). Divalent block occurs as the result of binding at a site within the gating pore located at electrical distance δ from the external side. The complete model, assuming K⁺ as the permeant ion, is thus given by:

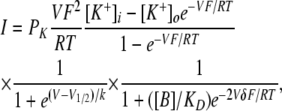(5)

where P_K is the K⁺ permeability of the gating pore, and [B]/K_D is the ratio of external divalent cation concentration to blocking affinity. First, we fit this equation to the special case of symmetrical K⁺ to determine P_K, [B]/K_D, and δ (the gating parameters V_1/2 and k were already known). Parameter estimation was somewhat limited because for high-affinity block ([B]/K_D > 1), the current is scaled by the ratio of P_K/([B]/K_D), and so separate determination of P_K and [B]/K_D is difficult. Nevertheless, it was clear that high-affinity block is required for an adequate fit; otherwise, the predicted I-V was too curvilinear in the −80 to −140 mV range. The best fit, obtained with [B]/K_D = 30 and δ = 0.1, is shown in Fig. S1. As the [B]/K_D ratio was further increased, the fit did not improve. This configuration was sufficient to account for the strong rectification of the permeation pathway in which outward current flow was impeded (only a small fraction of the block is relieved by depolarization before the gating pore becomes occluded by outward S4 movement). The model fails, however, to simulate the effect of increasing [B] by 50%, which was done experimentally when we increased the divalent from 4 to 6 mM (Fig. 2 B). The model predicts that steady-state K⁺ currents should decline by ∼33% under these conditions if the block is of very high affinity ([B]/K_D ≥ 10). The relationship between the expected current reduction due to a 50% increase in the concentration of a putative divalent blocker, starting from different [B]/K_D baseline values, is shown in Fig. 5. If the block is high affinity, such that [B]/K_D is any value >1, the prediction is a reduction in gating pore current amplitude by ∼30%. This magnitude block would have easily been detected but was not observed for our measurements in 6 versus 4 mM divalent (Fig. 2 B). Alternatively, if a low-affinity scenario is proposed, [B]/K_D < 1, to explain the failure to observe divalent block, the voltage dependence of the I-V would be too curvilinear and cannot simulate the saturation observed for V <−80 mV. Therefore, we reject the hypothesis that R666G gating pore current saturation at negative potentials is a consequence of voltage-dependent block by an external cation.

Figure 5.

High-affinity ionic block predicts a reduced current after a 50% increase in blocker concentration The model described by Eq. 5 was used to predict the effect on current amplitude of changing the divalent cation concentration from 4 to 6 mM (as is Fig. 2 B) for different blocking affinities. High-affinity block ([B]/K_D ≥ 10) predicts a ∼33% decline in current amplitude, which is inconsistent with the experimental data (see Fig. S1). The lack of a significant change in amplitude in Fig. 2 B would be consistent with a low-affinity block ([B]/K_D ≤ 10), but low-affinity block is not sufficient to account for the broad voltage range of current saturation.

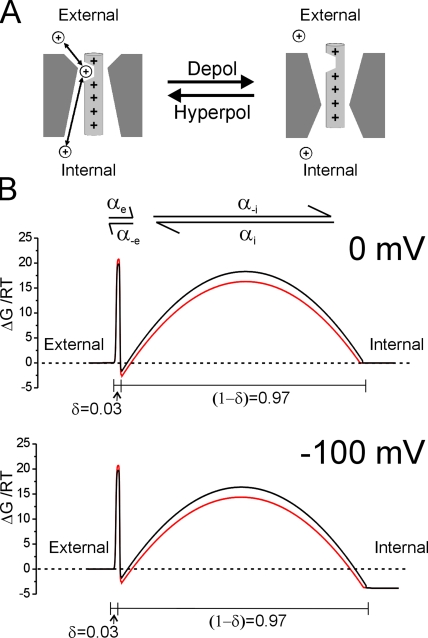
Our preferred model, which parsimoniously accounts for the saturation at negative voltages and the apparent independence from permeant ion driving force, is based on a single binding site scheme for ion permeation. As in the ionic block model, accessibility of the permeation pathway is gated by a two-state voltage-dependent rearrangement of the mutant voltage–sensing domain. The components of this model are displayed schematically in Fig. 6. At hyperpolarized voltages favoring inward movement of the S4 segment, the position of the R666G mutant residue renders the gating pore permissive for cation permeation, whereas membrane depolarization (outward S4 movement) abolishes the permeation pathway (Fig. 6 A). This scheme accounts for most of the steep voltage dependence of the R666G current between −80 and −20 mV and explains why no gating pore current is observed at depolarized voltages (>0 mV) under any ionic conditions. The exposed permeation pathway is modeled as a pore with a single cation binding site, flanked by two energy barriers (Fig. 6 B). The pronounced eccentric location of the binding site at a very shallow electrical distance from the external surface (δ = 0.03) accounts for the reduced voltage dependence exhibited by R666G gating pore currents. The maximal ion flux at hyperpolarized voltages is determined predominantly by the relatively voltage-independent rate of cation transitions over the external barrier. For the model in Scheme 1, as the membrane potential becomes very negative, the net current is approximately equal to 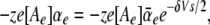which has a very shallow voltage dependence because δ is very small. The electrical distances of the binding sites of the two different monovalent cations can be estimated from fitting the above equation to the saturating portions of individual I-V curves at voltages <−100 mV. This yields δ = 0.07 ± 0.04 (n = 6) for K⁺ and 0.02 ± 0.02 (n = 5) for Na⁺ (statistically insignificant), suggesting that the two cations probably bind to the same site.

Figure 6.

A barrier model of R666G cation permeation. In the proposed model, accessibility of the R666G gating pore is due to voltage-dependent movement of the DIIS4 voltage sensor as depicted schematically in A. At hyperpolarized voltages favoring inward gating charge movement, the gating pore is accessible for cation binding and permeation, whereas outward movement of gating charges favored by membrane depolarization occludes the permeation pathway. The permeation pathway was modeled as a free-energy barrier profile calculated using Eyring rate theory. Profiles at 0 mV (top panel) and −100 mV (bottom panel) membrane potential of the proposed ion permeation pathway through the R666G gating pore are depicted in B. The black and red lines represent the proposed barrier profiles encountered by K⁺ and Na⁺, respectively. The shallow voltage dependence of the I-V relation at negative potentials (Fig. 2 A) is accounted for by a barrier model with a cation binding site that is very near the external face of the electrical field (δ = 0.03). Proposed transition rate constants for K⁺ and Na⁺ over the external and internal energy barriers at 0 mV are listed in Table I.

In contrast to both the Ohmic and divalent block models, the barrier model of the R666G gating pore is able to reproduce almost all of the fundamental features of the steady-state R666G currents (Fig. 3, solid lines). The dashing lines in Fig. 3 show the “open channel” I-V relationship (P_OPEN fixed at 1.0) for the single binding site model of permeation. Notice that the saturation of gating pore currents at negative potentials is accounted for entirely by permeation features of the external barrier model. When permeant ions are present intracellularly, steep outward rectification is noted only when the membrane potential approaches 0 mV and then becomes positive; however, in these instances the voltage-dependent movement of the DIIS4 segment occludes the gating pore (Fig. 3, solid lines), and so these changes to the gating pore current cannot be detected. Similarly, for inward currents the ionic concentration effect on driving force (dashed lines; V > −20 mV) is masked by voltage-dependent gated access to the permeation pathway. Finally, because voltage-dependent block is not a component of this model, it is also consistent with the independence of external divalent concentration, as shown in Fig. 2 B.

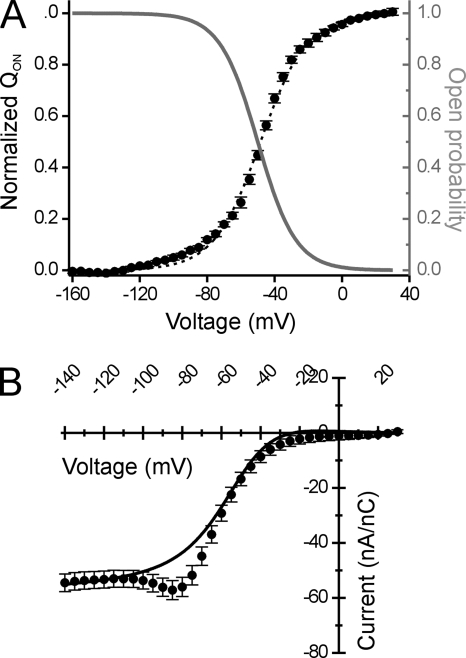
In our model, the occlusion and availability of the gating pore are simulated as a two-state transition with voltage-dependent rates, described by a single Boltzmann function. The relation between the voltage dependence of gating pore accessibility and measured charge displacement is shown in Fig. 7 A. The solid gray curve shows the voltage dependence for P_OPEN of the gating pore, as determined from the fits to the steady-state I-V data in Fig. 3. The black circles and dashed curve show the measured gating charge displacement of R666G channels (S4 translocation). These curves exhibit a close, inverse relationship, supporting our contention that accessibility of the R666G permeation pathway is coupled to the resting conformation of the DIIS4 segment and, conversely, that outward movement of gating charge favored by membrane depolarization occludes the R666G gating pore.

Figure 7.

Comparison of the model P_OPEN to the Q_On-V relationship and steady-state ionic currents in a physiologically relevant cation gradient. In A, the Q_On-V relationship of R666G gating charge displacement is compared with the voltage dependence of the relative open probability of the R666G gating pore derived from the best fit parameters of the model in Fig. 6. The solid black line represents the least-squares fit of a single Boltzmann function to the experimental Q_On-V data, yielding the following parameters: V_1/2 = −48.4 ± 1.0 mV, k = 13.8 ± 0.3 mV, n = 9. In comparison, the gray line represents the single Boltzmann function describing the voltage dependence of relative open probability of the R666G gating pore permeation pathway. The best fit parameters from this function are as follows: V_1/2 = −50 mV, k = 11.3 mV. The inverse relationship between R666G gating pore accessibility (note the inverted scale to the right) and the voltage dependence of gating charge movement supports the notion that cation access to the permeation pathway is controlled by S4 translocation (presumably the DIIS4 voltage sensor). In B, the I-V relationship of normalized cation currents flowing through the R666G gating pore in oocytes exposed to bath and internal solutions approximating the normal mammalian physiological Na⁺/K⁺ gradient is shown (n = 5). The solid line represents the behavior of the R666G gating pore current under these conditions, as predicted by the model (using parameters listed in Table I).

Because the permeation pathway is open only at hyperpolarized voltages, the bulk of the current carried by the R666G gating pore under normal physiological conditions is likely to be inward Na⁺ flow. To test this, we recorded R666G gating pore currents under conditions approximating the physiological monovalent cation gradient (scaled to account for differences in the osmolarity of solutions used to record from oocytes). These experimentally determined currents were compared with the model predictions (Fig. 7 B) using parameters for Na⁺ and K⁺ permeation derived independently. Under these approximate physiological conditions, the bulk of the R666G gating pore current is indeed directed inwardly and is of similar magnitude as currents recorded when Na⁺ was the sole external monovalent cation (compare the normalized current amplitudes in Fig. 7 B to Na⁺ currents in Fig. 3 B). The model predictions (solid line) lie in close agreement with the experimental data. These results suggest that in the presence of a normal physiological ionic gradient, the R666G gating pore conductance is likely to introduce a small Na⁺-predominant leak to the sarcolemma.

One notable deviation is the amplitude inflection (hump) between −90 and −60 mV where the inward current amplitude exceeds the model curve. This hump was prominent in recordings with asymmetrical ionic solutions wherein Na⁺ was the major extracellular cation, and the predominant internal cation was either K⁺ or an impermeant species (see also Fig. 3 C and Fig. 8). Similarly, the amplitude of the anomalous tail current transients was larger in Na⁺-containing bath solutions (for instance, Fig. 8). Both of these observations can be reconciled with a modification to our model wherein a second open state can be elicited in the R666G gating pore at intermediate depolarizations (to account for the hump in steady-state behavior) or during recovery after prolonged depolarizations (to account for the anomalous tails). In this scenario, both the permeability and ionic selectivity may differ from the primary open state (e.g., higher Na⁺ permeability). This possibility is discussed below.

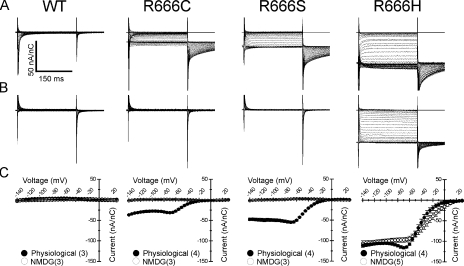
Figure 8.

Gating pore currents from other HypoPP mutations at site R666. Steady-state gating pore currents were recorded from R666S, -C, and -H mutant channels and compared with currents recorded in WT channels (denoted at top). Representative current traces, after leak correction and normalization to the corresponding maximal gating charge displacement, are shown for recordings made in bath and internal solutions approximating the normal mammalian physiological cation gradient (A) or in bath and internal solutions containing NMDG (B). Scale bars for all traces are shown in the inset to A. The mean I-V relationships of gating pore currents seen in each mutant under these conditions is shown in C. For each panel, the filled circles represent currents recorded in the physiological cation gradient, whereas open circles represent currents recorded when NMDG was present in both internal and external compartments. Number of samples recorded for each condition is denoted in parenthesis in the inset legend for each figure. Gating pore currents presumably carried by monovalent cations and abolished by NMDG substitution are seen in R666S and R666C mutant channels. In contrast, inward gating pore currents of similar magnitude are seen in R666H channels in both ionic conditions, consistent with the notion that the charge carriers of this gating pore current are protons rather than larger monovalent cations.

We tested whether other HypoPP mutations at the R666 position might create gating pores with similar currents. Representative traces of steady-state currents are shown in Fig. 8 for WT and rNaV1.4 channels expressing cysteine, serine, and histidine substitutions at the R666 position, after leak correction and normalization to maximal gating charge displacement. Currents were recorded in either a physiological cation gradient, as in Fig. 7 B, or in external and intracellular solutions in which the predominant cation was NMDG. As expected, no gating pore currents could be detected in WT channels. However, inward currents were observed in R666C, -S, and –H mutants, which exhibited the same sigmoidal voltage dependence with saturation of the current amplitude at hyperpolarized potentials, as with the R666G gating pore current. The magnitudes of normalized inward currents were each slightly different from the normalized amplitude of the R666G inward current, ranging between smaller currents (R666C) to currents that were nearly twice as large (R666H). These differences suggest that specific mutations expose pathways with different permeation characteristics. In R666C and –S channels, both steady-state gating pore and transient tail currents were abolished in recording solutions containing NMDG, consistent with the notion that these mutant gating pores predominantly conduct small monovalent cations. In contrast, when NMDG was substituted as the predominant cation in R666H channel recordings, the steady-state inward current persisted (Fig. 8, B and C, rightmost column). Although these results could be interpreted as demonstrating equivalent permeability for NMDG and Na⁺, it is more likely that the steady-state R666H gating pore current is carried by protons and not these larger monovalent cations. This view is consistent with previous findings that gating pores created by histidine substitutions in Shaker K⁺ channels (Starace et al., 1997; Starace and Bezanilla, 2001, 2004), and at the more exterior R663 position in rNaV1.4 (Struyk and Cannon, 2007) are selective for protons. Inward gating pore currents with similar amplitude and voltage dependence were recorded from R666H channels bathed in solutions predominantly consisting of Tris-HEPES buffer as described in Struyk and Cannon, (2007), which does not contain Na⁺ or NMDG (unpublished data), supporting the notion that protons are the charge carriers of this current. However, the tail currents recorded from R666H channels in each of the two conditions exhibit marked differences in amplitude and suggest that the tail current permeation pathway (the putative second open state) has a different ionic selectivity compared with the steady-state permeation pathway (as mentioned above to account for the hump in the I-V relation in the voltage range of −60 to −80 mV). Possible interpretations of this observation are discussed below, but it does suggest that the R666H gating pore is capable of conducting cations other than protons under the appropriate conditions.

DISCUSSION

We found that all the missense mutations at position R666 in rNaV1.4 that are linked to HypoPP create gating pores capable of carrying aberrant, small amplitude ionic currents. These results lend support to the notion that the pathological alteration of excitability in HypoPP fibers may be the consequence of these gating pore leaks.

Our results differ from those reported by Sokolov et al. (2007), who studied gating pore currents in the R666G/H mutants. One major difference was the predicted amplitudes of the gating pore currents in skeletal muscle, and by extension, their ability to influence the sarcolemmal resting potential. Sokolov et al. (2007) estimated the gating pore current density to be ∼1.25% of the peak ionic current through the pore based on a few observations where the expression level was favorable to measure both ionic current and then gating pore current after application of TTX to the same prep. In our experience, however, we predict a much lower gating pore current density relative to the Na⁺ current through the pore under physiological conditions. We consistently observe a gating pore current density of ∼100 nA/nC when normalized to the amplitude of the gating charge displacement. Assuming 12 elementary charges per channel, our normalized gating pore current density is equivalent to 0.0002 pA/channel = (100 A/Coul) * (1.6 × 10⁻¹⁹ Coul/e) * (12 e/channel), or 0.05% of the typical unitary Na⁺ current of 1 pA. Indeed, in our experience the channel expression level must be sufficient to produce a peak gating current of >100 nA in the cut-open configuration to reliably detect the gating pore current. The second major difference between the two studies is that we consistently observe saturation of gating pore current amplitudes at strongly hyperpolarized potentials. We observed gating pore current saturation for all four mutations tested at R666 and consider this behavior to be a fundamental property of the R666 gating pore. It is not clear why Sokolov et al. (2007) did not observe saturation. We have shown that the differences cannot be accounted for by ionic conditions and therefore must surmise that it may relate to the large leakage currents in their study, which were two orders of magnitude larger than in our prep and may have obscured the gating pore current for voltages far from the reversal potential at 0 mV.

Our standard bath conditions used to record the gating pore currents were not identical to those used by Sokolov et al. (2007), raising the question of whether this difference may account for the discrepancies in the reports. We were not able to discern differences in either the amplitude or voltage dependence of the R666G gating pore current when different divalent cations Ca²⁺, Ba²⁺, or Zn²⁺ were substituted in the bath at a concentration of 6 mM. This observation has two possible interpretations: either all three divalent cations exert similar effects on the R666G gating pore current at this concentration (which would be inconsistent with the potent block by Zn²⁺ reported in Sokolov et al. [2007]), or there is no substantial influence of divalent cations on the gating pore current at this concentration. We believe the latter interpretation is more likely. Although the saturating behavior of the R666G gating pore current may resemble the effects of high affinity divalent cation block, alteration of the putative blocker concentration (Fig. 2 B) did not change the current amplitude as predicted by this model. Therefore, our data are more consistent with a scheme in which ion flux through the permeation pathway is intrinsically saturable, and do not support a model with block by external divalent cations.

Inclusion of Ba²⁺ in the bath solution reduced the nonspecific oocyte leak and enhanced long-term membrane stability sufficiently to enable us to reliably detect the very low-amplitude gating pore currents. For several trials in which we attempted to replicate the recording conditions used by Sokolov et al. (2007), we were unable to maintain the high resistance of the oocyte membrane over the time period required for ionic equilibration in the intracellular compartment (unpublished data). There was some degree of overlap, however, in the recording conditions for the two studies, which permits some direct comparisons. The experiments in Fig. 2 B illustrate that with bath solutions composed of higher divalent cation compositions, equivalent to those used by Sokolov et al. (2007) in some of their experiments, the reported R666G gating pore still differed between the two studies. First, in our experience the amplitudes did not substantially change with substitution of 6 mM Ca²⁺, Ba²⁺, or Zn²⁺, whereas Sokolov et al. (2007) reported a mild block by Ca²⁺, an ∼50% block by Ba²⁺, and complete block by Zn²⁺ at that concentration. Moreover, the current saturation at hyperpolarized voltages was not a feature of the data reported by Sokolov et al. (2007), despite using similar concentrations of these different divalent cations. Therefore, there appear to be fundamental disparities between our data and those of Sokolov et al. (2007) that cannot be readily reconciled by invoking differences in recording conditions.

Voltage Dependence: Insights into the Structure of the DIIS4 Voltage-sensing Domain

The structural orientation of the canonical voltage-sensing domain shared by many voltage-gated ion channels remains the subject of contention because of apparent conflicts between several different investigations. Several lines of evidence have supported models in which S4 charges reside within an aqueous environment, with the N-terminal portion of the S4 segment oriented near the extracellular surface (Yang et al., 1996; Mitrovic et al., 1998; Ahern and Horn, 2004). In contrast, other studies, including structural data derived from x-ray crystallography of voltage-gated K⁺ channels, have supported the notion that S4 segments are part of a hinged paddle structure, which undergoes large amplitude movements across the lipid bilayer in response to changes in membrane voltage (Jiang et al., 2003; Long et al., 2005; Ruta et al., 2005). At rest, these putative S4-containing paddles are oriented such that nearly all charged side chains are in proximity to the intracellular compartment and are at least partially embedded within the lipid portion of the bilayer, and it is only with membrane depolarization that these charged sites approach the external surface.

Our observations of rNaV1.4-R666 gating pore currents are more readily accounted for by a model in which DIIS4 charged side chains reside within a hydrophilic environment. More specifically, our data suggest that the R666 residue must maintain aqueous contact with both intracellular and extracellular compartments at hyperpolarized voltages that favor the resting orientation of the DIIS4 segment. Similar gating pore currents have been described in mutant Shaker K⁺ channels (Tombola et al., 2005) and in Nav1.2 channels harboring paired glutamine substitutions at neighboring S4 sites (Sokolov et al., 2005). Although the organization of membrane phospholipids in the immediate vicinity of charged S4 segments may undergo significant distortion, and thus create aqueous accessibility to S4 sites oriented more deeply within the lipid bilayer (Freites et al., 2005, 2006), it is not likely that this distortion would be sufficient to support a transmembrane permeation pathway for cations. Our data are thus compatible with both the simple gating pore model of S4 movement, as well as a more recently proposed hybrid model in which one face of the S4 segment is exposed to the lipid bilayer, but the gating charges are stabilized in an aqueous crevice (Pathak et al., 2007).

Simultaneous accessibility to intracellular and extracellular compartments while the DIIS4 segment is in its resting conformation is a characteristic that appears to apply to the R663 site in rNav1.4 as well, which is capable of mediating a transmembrane proton current when a histidine residue is substituted for the native arginine (Struyk and Cannon, 2007). Combined with our results here, this suggests that both these charged S4 sites do not occupy strictly single file sequential positions within an aqueous canaliculus, but rather that internal and external aqueous continuity extends to both residues in the resting state. One caveat to this interpretation is that H⁺ permeation mediated by the R663H residue might be accomplished through “proton wire” transfer between several proton binding sites embedded within the channel protein or phospholipid bilayer, and thus the R663 site may not otherwise be directly exposed to both aqueous compartments. This is unlikely to be a mechanism for monovalent cation permeation, which is most likely the consequence of diffusion of cations through an aqueous milieu.

One novel aspect in the present report is the notion that the unusual saturating voltage dependence of R666 site–gating pore currents can be explained by postulating a cation binding site located in close proximity to the external face of the electrical field. This model offers possible insights into the structural orientation of the NaV1.4-DIIS4 segment. One simple interpretation of this model is that the cation binding site represents a favorable region for occupancy by the positively charged guanidinium group of residue R666 when the DIIS4 segment is in its resting conformation. Channels expressing charge-neutralizing mutations at R666 might therefore expose this favorable site to opportunistic access by monovalent cations from either side of the membrane. This in turn would suggest that the resting location of the R666 residue is near the external extreme of the electrical field. However, it is equally valid to suppose that an externally oriented site favorable for cation binding is a normal feature of WT voltage-sensing domains, and that gating pore currents mediated by mutations at R666 arise due to the creation of transmembrane aqueous continuity at a second, more internal location within the gating pore. Thus, the R666 residue might be located more deeply within the electrical field.

One observation that lends support to the former possibility is the fact that the steady-state proton-selective current in R666H mutant channels exhibits the same shallow voltage dependence at hyperpolarized voltages as the cation currents carried by other R666 mutants. The selectivity for protons over other larger monovalent cations is most consistent with a protonation–deprotonation reaction directly mediated by the substituted histidine side chain. Because the shallow voltage dependence of the inward proton current (Fig. 8 C) is primarily due to the eccentric orientation of the permeant ion binding site, it follows that this is probably also the location of the substituted histidine residue mediating proton selectivity. The simplest overall interpretation is therefore that the external orientation of these sites (for cation binding in R666G, -S, and -C mutants, and proton binding in R666H) closely approximates the normal, resting position of the R666 site. This suggests that the R666 residue and, presumably, the more exteriorly oriented R663 residue as well contribute only nominally to the total gating charge movement associated with rapid state transitions in rNaV1.4. One caveat to this interpretation is that the presence of a charge-neutralizing substitution at R666 may itself alter the topography of the electrical field within the gating pore, which may normally be concentrated in such a way to effect translocation of large amounts of gating charge with small physical motions of the S4 segment (Starace and Bezanilla, 2004; Ahern and Horn, 2005). Thus, the estimates arising from these mutant data may not indicate the true contribution of the R666 residue bearing a normal charge.

Finally, we modeled the gating transition mediated by S4 segment translocation as a two-state distribution, which oversimplifies the conformational rearrangements undergone by the S4 segment in response to changes in membrane voltage. Thus, it is possible that the unusual shape of the R666 gating pore I-V relationship might be influenced by multiple voltage-dependent conformational rearrangements in the mutant voltage-sensing domain, which in turn might conceivably alter the relative open probability of a static conduction pathway. In a related manner, it is also possible to propose a model in which the saturating I-V relationship at hyperpolarized voltages can be explained through an external ionic block mechanism characterized by shallow voltage dependence. However, neither a more complex gating scheme nor external ionic block by themselves can account for the aggregate features of the R666 site–gating pores. In contrast, the proposed permeation model, with an externally located barrier that is relatively voltage independent, is sufficient to account for all these characteristics with a single parsimonious mechanism. With this emphasis on the role of the permeation pathway, however, it is possible that the potential modulating influence of changes to accessibility arising from complex voltage-sensor conformational rearrangements may be undervalued in the present model.

The simple permeation and gating model offered in Fig. 6 offers an explanation for most of the steady-state experimental data, but there are a several characteristics of the R666G gating pore currents that are not explained. One of these is the transient inward tail currents elicited by membrane repolarization, whereas a second is the inward inflection of the I-V relationship or hump observed in Na⁺-containing bathing solutions. The open probability of the tail current permeation pathway exhibits an unexpected inverse voltage dependence relative to P_OPEN of the steady-state gating pore permeation pathway (largest tail currents were observed after strongly depolarized conditioning potentials where the gating pore is closed). Moreover, the ionic selectivity of the tails appears to be different, most notably in the R666H gating pore (Fig. 8). These features both suggest that domain II gating pores created by R666 site mutations can adopt more than one open state conformation, characterized by differences in permeability and ionic selectivity. The delay that characterizes the onset of the tail currents after prolonged depolarizations, and the slow relaxation of the tail currents upon repolarization, both indicate that the kinetics of this alternative conformation are slow, occurring over the course of several hundred milliseconds. Thus, a more complex scheme than the simple two-state model presented in Fig. 6 will be necessary to describe the full range of behavior of these gating pores. The data presented herein can be accounted for by a four-state gating model of the R666 gating pore, depicted in Scheme 2 below:

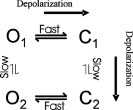(SCHEME 2)

In this scheme, O₁ represents the open state whose permeation characteristics are described in Fig. 6 B, whereas the O₂ state differs substantially in ionic selectivity from O₁, notably, by being more permeable to Na⁺ ions. Both the fast horizontal and slow vertical transitions are voltage dependent, with rightward/downward transitions favored by depolarization. With this scheme, the “hump” in the steady-state I-V relation observed in Na⁺-containing baths is the consequence of fractional occupancy of the O₂ state at intermediate voltages. The transient inward tail currents (larger in Na⁺-containing baths) are a consequence of slow recovery through the O₂ state from the C₂ state, which becomes populated during long depolarizations. More extensive investigation of these tail currents may yield further refinements of this model and should provide greater insight into slow conformational rearrangements of the voltage-sensing segments that may have an important role in Na⁺ channel gating, such as slow inactivation.

Amplitude and Composition of Gating Pore Currents: Implications for the Pathogenesis of HypoPP

The steady-state gating pore currents arising from mutations at the R666 site under physiological conditions are only ∼5–10% the size of the corresponding peak gating currents arising from movement of S4 charges. For all of the R666 mutants we studied, the gating pore currents were between 1.5 and 3 times larger than the magnitude of the R663H proton current we reported previously (after normalization to gating charge and accounting for differences in oocyte and mammalian ionic composition). Based on estimates, that peak ionic current in Na⁺ channels is 50–100 times larger than corresponding gating current (Armstrong and Bezanilla, 1974), or based on the calculation with 12e charges per channel above, the gating pore currents we measured are probably ∼0.02–0.1% the amplitude of the peak NaV1.4 ionic current.

In light of the low amplitude of these gating pore currents, their impact on the normal resting potential of quiescent sarcolemma is likely to be small, inducing membrane depolarization of only a few millivolts. This estimate is consistent with measurements from intact muscle fibers biopsied from human HypoPP patients, which in several independent studies have shown that the mean resting potential of HypoPP muscle is generally several millivolts depolarized from that of WT fibers (Rüdel et al., 1984; Ruff, 1999). Thus, it is likely that the gating pore currents themselves are insufficient to be the sole, direct cause of the massive depolarization of 30–40 mV underlying a HypoPP attack. Moreover, gating pore conductances in R666 and R663 mutants are persistently open in affected sarcolemma at rest, and thus if they were sufficient to exert a large influence over the resting potential, it would require a considerable additional increase in a hyperpolarizing conductance to maintain a normal resting potential in between attacks. No increase of the resting sarcolemmal conductance has been observed in muscle fibers from HypoPP patients that would support this notion (Rüdel et al., 1984; Ruff, 1999).

One alternative possibility is that aberrant permeation of ions through HypoPP gating pores may exert a secondary deleterious effect on the stability of the sarcolemmal resting potential. In the context of this proposal, one pattern that is emerging is the distinction between the ionic selectivity of gating pores created by histidine, which exhibit selectivity for protons under most circumstances, versus nonhistidine mutations, which are permissive for larger monovalent cations. This finding is in agreement with the ionic selectivity of gating pore currents recorded from Shaker K⁺ channel mutants in which proton selectivity is a feature limited to histidine substitution (Starace et al., 1997; Starace and Bezanilla, 2001, 2004; Tombola et al., 2005). This distinction may not be fully valid for the R666H mutation because the prolonged tail currents observed after depolarizing voltage pulses are smaller when larger monovalent cations are not present, therefore suggesting that the R666H tail current permeation pathway may become permeable to larger cations under appropriate conditions. Despite the differences in ionic selectivity, the amplitudes of monovalent cation and proton currents flowing through gating pores in all the NaV1.4 mutants are quantitatively similar. We have so far been unable to detect significant proton flux through gating pores established by nonhistidine substitutions at R666. These data therefore make it less likely that an abnormality of myoplasmic proton homeostasis alone, which might occur due to histidine-mediated proton influx present in R663H and in R666H mutants, is the primary mechanism of disease.

It has been suggested that gating pore-mediated cation currents in NaV1.4 mutants, which consist mostly of Na⁺ influx when the membrane is at rest, might result in an abnormal Na⁺ burden in affected myoplasm (Jurkat-Rott and Lehmann-Horn, 2007; Sokolov et al., 2007). This in turn might promote activity of the Na⁺/K⁺ ATPase as the sarcolemma attempts to maintain a normal electrochemical gradient. Augmented outward extrusion of Na⁺ would be coupled to increased active inward pumping of K⁺, which in turn might explain the persistent, modest hypokalemia observed in human patients, and may also contribute to the abnormal sequestration of K⁺ in the myoplasm during paralytic attacks. This proposed mechanism also offers an explanation for the pathophysiological effect of proton-selective gating pore currents, as the myoplasmic proton burden imposed by this subset of HypoPP mutations might also generate abnormalities of internal Na⁺ levels because active extrusion of myoplasmic protons against their electrochemical gradient may be tightly coupled to inward Na⁺ flow. The notion that HypoPP muscle is abnormally burdened by a high internal Na⁺ concentration is supported by findings of abnormally raised intracellular Na⁺ levels in biopsied HypoPP muscle fibers (Engel et al., 1965) and in MRI spectroscopy of human patients (Weber et al., 2006), although these observations have not been replicated elsewhere (Niall and Pak, 1966). Given the size of the currents in the present study, the estimated Na⁺ influx in resting sarcolemma heterozygous for the R666G mutation would be ∼17.5 pmol cm⁻² s⁻¹, assuming ∼500 channels/μm² (Bay and Strichartz, 1980). This flux is roughly sixfold greater than measurements of normal Na⁺ influx in quiescent rat sarcolemma, but is considerably less (by one to two orders of magnitude) than the total myoplasmic Na⁺ load attributable to repetitive stimulation (Kotsias and Venosa, 2001). Therefore, it is not clear if an additional, persistent Na⁺ burden of this magnitude is sufficient by itself to predispose to attacks of hypokalemia and depolarization.

We favor another proposed pathomechanism wherein low-amplitude gating pore leaks impair sarcolemmal ability to withstand the effects of modest reductions in extracellular K⁺ on the normal resting potential. Although in most circumstances the resting potential of mammalian muscle fibers is closely coupled to the reversal potential of K⁺ (E_K), when extracellular K⁺ is reduced beyond a threshold value (generally <1 mM) the resting potential abruptly depolarizes (Adrian, 1956; Hodgkin and Horowicz, 1959; Ruff, 1999). The mechanism for this behavior rests with the fact that the bulk of the resting K⁺ conductance flows through inward rectifier K⁺ channels and competes with a small, K⁺-independent depolarizing leak conductance to set the resting potential (Carmeliet, 1982; Siegenbeek van Heukelom, 1991; Geukes Foppen et al., 2001, 2002; Geukes Foppen, 2004). As extracellular K⁺ is reduced and E_K becomes hyperpolarized, reduction in the inward rectifier K⁺ conductance renders it too small to compete with the antagonistic leak, and the sarcolemma depolarizes. The addition of a gating pore current component would augment this background leak, and therefore shift this K⁺-dependent depolarization threshold toward the physiological range of extracellular K⁺ concentrations. Modeling from our laboratory has suggested that gating pore currents with amplitudes similar to those exhibited by the R663H mutant and R666 site mutants may be sufficient to predispose to sarcolemmal depolarization in response to only modest reductions in external K⁺ concentration (∼3 mM) (Struyk and Cannon, 2008). In this model, the only relevant characteristic determining the pathological impact of the gating pore current is its magnitude relative to the other resting sarcolemmal conductances. Sarcolemma beset by either Na⁺ or H⁺ gating pore currents of equivalent magnitude may therefore be equally poised for pathologically sustained depolarization.

APPENDIX

Multi-Ion Competition for a Single-Well Two-Barrier Model of Permeation through the R666 Gating Pore

The permeation model in Scheme 1 was extended to consider the consequences of competition for occupancy of the binding site by multiple types of ions present simultaneously on the external or internal face of the membrane, as would occur under physiological conditions. If the probability of binding site occupancy is very small (P₁ < 0.01), ions will act independently, and the total ionic current will be a simple linear superposition of the individual currents predicted with a single ionic species present: I_total = I_A + I_B + I_C + for ions A, B, C as in Eq. 3. Consider the alternative case of two types of permeant ion, A and B, present on both sides of the membrane, and competing for the same binding site along the permeation pathway of the gating pore. The net outward flux for A and B taken together is given by:

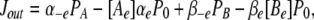(A.1)

where P_A is the probability of binding site occupancy by A, P_B by B, and P₀ is the probability of being empty. The α terms are the transition rates for A as in Scheme 1, and the β terms are the analogous rates for B. The mutually competitive binding interactions are summarized by the state diagram shown below, which is equivalent to the three-state kinetic model in Scheme 3.

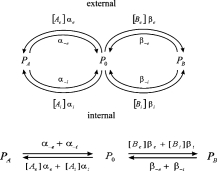(SCHEME 3)

From Scheme 3, the steady-state probability of occupancy by A is:

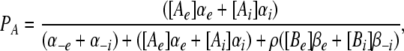(A.2)

with 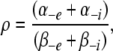which represents the ratio of the leaving rates (to both external and internal sides) when the binding site occupied by A is divided by the leaving rates for B. Combining equations A.1, A.2, and the constraint (P_A + P_B + P₀ = 1) yields the expression for the net outward current (with contributions from A and B), as:

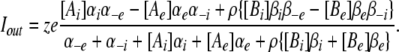(A.3)

Eq. A.3 was used to predict the net current, carried by Na⁺ and K⁺, under conditions where a physiological gradient was present (Fig. 7 B). Recall, the parameter values used for the rate constants were determined from other experiments in which only a single permeant ion was present (Fig. 3).

A test for independence of ion flux was performed by comparing the net current predicted by Eq. A.3 (competition for a single binding site in Scheme 3) to a linear superposition of Na⁺ and K⁺ currents predicted by Scheme 1 (independence). The open-channel current voltage behavior of the two models diverges at positive potentials as shown by the reduced outward current in the competitive model (Fig. 9 A, solid line). The reduction in current results from competition for the binding site by entry of Na⁺ and K⁺ from the inside. Conversely, at strongly negative potentials the two models converge because the (nearly) voltage-independent barrier for access to the binding site from the external side becomes rate limiting, and the binding site occupancy is low. The model demonstrates that when the probability of binding site occupancy >50%, the current is reduced in the competitive model. When the voltage dependence of gating pore accessibility is added to the model (Fig. 9 B), the region of current divergence is obscured by loss of accessibility. Therefore, it was not possible to experimentally differentiate between Schemes 1 and 3. Nevertheless, the saturation behavior of the I-V data at negative potentials provides strong evidence that the permeation pathway must contain a rate-limiting barrier that is relatively voltage independent, as would occur for a binding site very near the external end of the gating pore.

Figure 9.

Permeation for a single-well two-barrier model. Steady-state ion flux and occupancy of the binding site were computed for the case of two permeant ions present at physiological concentrations on either side of the gating pore (in mM [K]_e = 3, [K]_i = 103, [Na]_e = 112, [Na]_i = 7). The “open-channel” current–voltage relation that is in absence of gating is compared in A for the assumption of independence (Scheme 1, dashed line) or competition by Na⁺ and K⁺ for the single binding site (Scheme 3, solid line). When voltage-dependent gated accessibility of the pore is included (B), the current–voltage relation has strong inward rectification and the distinction between Schemes 1 and 3 is no longer discernable.