Comparison of algorithms for pre-processing of SELDI-TOF mass spectrometry data

Abstract

Motivation: Surface-enhanced laser desorption and ionization (SELDI) time of flight (TOF) is a mass spectrometry technology. The key features in a mass spectrum are its peaks. In order to locate the peaks and quantify their intensities, several pre-processing steps are required. Though different approaches to perform pre-processing have been proposed, there is no systematic study that compares their performance.

Results: In this article, we present the results of a systematic comparison of various popular packages for pre-processing of SELDI-TOF data. We evaluate their performance in terms of two of their primary functions: peak detection and peak quantification. Regarding peak quantification, the performance of the algorithms is measured in terms of reproducibility. For peak detection, the comparison is based on sensitivity and false discovery rate. Our results show that for spectra generated with low laser intensity, the software developed by Ciphergen Biosystems (ProteinChip^© Software 3.1 with the additional tool Biomarker Wizard) produces relatively good results for both peak quantification and detection. On the other hand, for the data produced with either medium or high laser intensity, none of the methods show uniformly better performances under both criteria. Our analysis suggests that an advantageous combination is the use of the packages MassSpecWavelet and PROcess, the former for peak detection and the latter for peak quantification.

Contact: rguerra@rice.edu; marina@rice.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Mass spectrometry (MS) technology is used to measure the mixture of proteins/peptides of biological tissues or fluids, such as serum or urine. Such measurements can be used to identify disease-related patterns, which hold potential for early diagnosis, prognosis, monitoring disease progression, response to treatment and drug target research.

A commonly used mass spectrometry technique uses matrix-assisted laser desorption and ionization (MALDI) ion source and a time-of-flight (TOF). A variant of MALDI is the method of surface-enhanced laser desorption and ionization (SELDI) that uses a solid chromatography surface to capture different types of proteins followed by ion detection. The data collected by SELDI is a vector of counts, each corresponding to the number of ions detected during a small, fixed interval of time. A quadratic transformation is used to derive the mass to charge (m/z) value of the protein from the TOF. This procedure is called calibration. Thus, the experimental data produced is an MS spectrum with the x-axis representing the mass/charge (m/z) ratio and the y-axis representing the intensity of the protein or peptide ions.

The key features of scientific interest are the MS peaks because they can be used to infer the existence of a peptide with a particular m/z ratio. A typical approach to analyzing MS data has the following two steps. First, peak locations are detected and their intensities are quantified for each spectrum. This is sometimes referred to as the pre-processing step of the data. The second step is to search for proteins that are differentially expressed among samples under different experimental conditions; clustering and classification of the differentially expressed proteins may also be performed (Kwon et al., 2007; Li et al., 2006; Shen et al., 2007).

The pre-processing of MS data can be divided into several subtasks, including:

• Alignment of the spectra is often required when different instruments are used to obtain the spectra or when the spectra are generated over a long period of time. Misalignment must be corrected to ensure that the same protein intensities are correctly identified in a sample (Wong et al., 2005).

• Filtering or denoising to remove high-frequency interfering signal caused by sources unrelated to the bio-chemical nature of the sample. Such sources can be electrical interference, random ion motions, statistical fluctuation in the detector gain or chemical impurities (Shin et al., 2007).

• Baseline subtraction to remove systematic artifacts produced from small clusters of the matrix material, which needs to be added to the sample of interest. In general, the baseline exhibits a decreasing behavior from low m/z to high m/z (Shin and Markey, 2006).

• Normalization to correct for systematic variation between spectra due to differences in the amount of protein in the sample, degradation over time and variation in the instrument detector sensitivity (Sauve and Speed, 2004).

• Peak detection refers to the process of identifying peak locations on the time or m/z scales. It can be performed using the individual spectra or a mean spectrum.

• Clustering of peaks is required when peak detection is performed using individual spectra. It decides which peaks in different samples correspond to the same biological molecule and determines a single m/z value for each cluster.

• Peak quantification to compute the intensity of each detected peak in each pre-processed spectrum. This task is usually performed by computing a local maximum within some range of the location of the detected peak. A typical range is between 0.1% and 0.3%.

No standard method has been established so far regarding the pre-processing steps, including the order in which the steps might be performed. Furthermore, the pre-processing of the data before peak detection may differ from the pre-processing prior to peak quantification. For example, Du et al. (2006) use the raw data to perform peak detection, while Morris et al. (2005) use the same algorithm to pre-process the spectra before both peak detection and peak quantification, albeit with different parameters in each case.

Because of the potential applications of mass spectrometry studies, the development of algorithms for pre-processing MS data has been an active area of research (Coombes et al., 2007; Du et al., 2006; Fung and Enderwick, 2002; Kwon et al., 2008; Li et al., 2005; Malyarenko et al., 2004; Wong et al., 2005). The pre-processing of MS data can influence the results of subsequent statistical analysis; thus it is important to identify those methods with the best performance. To date, limited research has been done in this direction. Meuleman et al. (2008) performed an extensive study to compare different algorithms for normalization, while Beyer et al. (2006) compare the performance of the package Ciphergen Express Software 3.0 produced by Ciphergen and the R package PROcess.

In this work, we present the results of an extended and up-to-date study that compares the performance of five popular and current methods for pre-processing of SELDI data. Our comparison is divided into two major parts, one for each of the two primary goals of the pre-processing of MS data: location of peaks and quantification of peak intensities.

2 METHODS

We list and briefly describe the algorithms for pre-processing that are being compared in this study, explain the methodology used to perform the comparison and give a description of the data.

2.1 Algorithms for pre-processing

In this study, we compare the performance of five algorithms for pre-processing of SELDI data. These algorithms were chosen based on their application in several published studies. Below we list and describe the corresponding software.

ProteinChip^© Software 3.1 and Biomarker Wizard are commercial software produced by Ciphergen Biosystems (Fremont, CA, USA). In the rest of the article we will refer to this combination as Ciphergen. By using the default options, the pre-processing steps available with this software include: denoising based on a moving average filter; baseline subtraction with the baseline being estimated with a piecewise convex-hull; normalization that takes the total ion current used for all the spots, averages its intensity and adjusts the intensity scales for all the spectra; and peak detection that looks for peaks in each individual spectra. A feature that distinguishes this peak detection algorithms is that it operates in two passes, the first uses low sensitivity to determine the peak locations of obvious and well-defined peaks, while the second pass look for smaller peaks at those peak locations by using higher sensitivity (Ciphergen Biosystems, 2002).

PROcess is a BioConductor package written by Xiaochun Li and available through R. Pre-processing steps with default options are as follows. The baseline is estimated by partitioning the m/z range on the log scale into n equally spaced interval, finding the local minimum within each interval, and smoothing these local minima by either local regression (loess) or local interpolation. Normalization is performed using total ion normalization; that is, for each spectrum its area under the curve (AUC) is calculated for m/z values greater than a user-defined threshold and all spectra are scaled to the median AUC. The algorithm for peak detection smooths the normalized, baseline subtracted spectrum by a moving average, identifies local maxima in the smoothed spectrum, and finally, a local maximum is considered a peak when its signal-to-noise ratio, intensity and area, exceed user-defined thresholds. The PROcess library also includes functions to assess the quality of a set of spectra (Li et al., 2005).

Cromwell is a set of Matlab scripts implementing the algorithms for pre-processing of MS data developed by the bioinformatics group at the MD Anderson Cancer Center (Coombes et al., 2007; Morris et al., 2005). Denoising is performed via wavelet regression using the undecimated discrete wavelet transform. The baseline is estimated by computing a monotone local minimum curve. Normalization is performed by scaling each individual spectrum so that the mean of its intensities is equal to 1. The algorithm for peak detection finds local maxima in the denoised, baseline subtracted spectrum and retains as peaks those with a signal-to-noise ratio greater than a user-defined threshold.

SpecAlign is freely available software developed by Wong et al., (2005). The algorithms in this package works on the individual spectra. For smoothing it uses the Savitzky–Golay filter. Denoising is performed using the Symmlet wavelet transform and then applying soft thresholding. The baseline is estimated using a restrained moving average, where only values smaller than the local average intensity are added to the global moving average. The peak detection algorithm requires three user-defined parameters: (1) a ‘baseline cutoff’ which represents the fraction of baseline under the baseline intensity at which the algorithm ignores selection peaks, (2) a ‘window size’ for defining a peak and (3) a ‘height ratio’ that works as a threshold for the signal-to-noise ratio. As a distinguished feature, it includes an algorithm for the alignment of spectra. Guidelines for combining the various subtasks available in this software are not provided for the authors. Some insights can be found in Whistler et al., (2007). Such information is important because the interaction of the pre-processing steps is complex and the results vary according to the specific order in which they are applied.

MassSpecWavelet is a Bioconductor package developed by Du et al. (2006). Peak detection is performed by using the continuous wavelet transform. A remarkable feature of this method is that no pre-processing of the spectra is required before peak detection. This package does not include any other pre-processing steps.

2.2 Methods of comparison

To assess the performance of these algorithms for pre-processing of SELDI data, we considered two aspects: the reproducibility of the quantified peaks and their false positive rate of peak detection.

2.2.1 Reproducibility

A functional model for the observed data is

(1)

where t takes values in the m/z scale, f(t) denotes the observed signal, B(t) is the baseline, N is a normalization factor, S(t) is the true signal and ɛ(t) refers to the high-frequency noise (Coombes et al., 2007).

An algorithm for pre-processing of MS data produces estimators for the baseline, noise and the normalization constant. The better those estimators, the closer the pre-processed spectrum would be to the true signal. Therefore, one way to measure its performance is by analyzing the variability that appears when it is used to pre-process a set of spectra that reflects the same true signal. Such analysis is possible by using replicates of a given sample. The best algorithm for pre-processing will be the one that minimizes the variability of the pre-processed spectra, or in other words, the one whose output is more reproducible.

Variability in a set of pre-processed spectra can be measured by performing peak quantification and then measuring the variability of the quantified intensities at each peak location. Because of the varying scales in peak intensities, a commonly used statistic to summarize their variability is the coefficient of variation (CV), which is equal to the SD divided by the mean. A pre-processing algorithm yielding relatively small CVs will be said to have high reproducibility, and thus, better performance than competing algorithms.

Note that a requirement to perform peak quantification is to have a set of peak locations. We used the same set of peak locations to perform peak quantification across all algorithms. This procedure has the advantage that the results are not influenced by the performance of peak detection algorithms. Ideally, if we knew the biological composition of the sample, we would be able to establish the location where quantification of intensities matters. However, with real data we do not have that information so the peak locations have to be estimated. Two factors become relevant: the quality of the peaks, that is, we need to verify by visually inspecting the spectra where the plausible peaks locate, and the robustness of our results to different sets of detected peaks. As shown in Section 3.1, we took into account those two factors in our analysis.

2.2.2 Peak detection

A ‘true’ peak is a peak associated with a peptide in the biological sample of interest. A peak detection algorithm estimates the locations of the true peaks by producing a set of m/z values. In this study, a detected peak is matched to a true peak if the former is in the 0.3% error range around the location of the latter.

In this study, we evaluated the performance of peak detection algorithms using sensitivity and false discovery rate (FDR). As suggested by Du et al., (2006), given a set of detected peaks, the sensitivity is estimated as the proportion of true peaks correctly detected, while the FDR is defined as the proportion of falsely detected peaks. By modifying the parameters of a peak detection algorithm, we obtained combinations of sensitivity and FDR and plotting these combinations we obtained a curve which can be interpreted similarly as a receiver operating characteristic curve. Given a value for the FDR, the higher the sensitivity, the better the performance of a peak detection algorithm. The ideal combination is having 100% sensitivity and 0% FDR.

We used simulated data to compare the performance of peak detection algorithms. With real data the number and location of protein peaks are unknown and therefore neither sensitivity nor FDR are estimable. The simulated data were generated using the simulation engine developed by Coombes et al., (2005), the details are given in Section 2.4.

2.3 Experimental data

Eighteen aliquots of the normal human serum control (Ciphergen Biosystems) were randomly spotted on a 96-well plate and then fractionated by an anion exchange procedure into six fractions. Each fractionated serum was spotted in duplicates on weak cation exchange (CM10) Arrays (Ciphergen Biosystems). Then, each spot were analyzed by three laser power settings, resulting totally 648 spectra for the analysis of different algorithms—36 spectra per combination of fractionation and laser power setting. The details of the fractionation and spotting procedures were previously reported (Li et al., 2006). In brief, a commercially available pooled human control serum was purchased from Ciphergen Biosystems. The sample were randomly spotted on a 96-well plate together with other samples and then fractionated by an anion exchange fractionation procedure. Twenty microliters of each sample were denatured by 30 μl of 50 mM Tris–HCl buffer containing 9 M urea and 2% 3-[(3-cholamidopropyl)dimethylammonio]-1-propanesulfonic acid (pH 9). The proteins were fractionated in an anion-exchange Q HyperD F 96-well filter plate (Ciphergen Biosystems). Six fractions, including those from the flow through (Fraction 1), pH 7 (Fraction 2), pH 5 (Fraction 3), pH 4 (Fraction 4), pH 3 (Fraction 5) and organic eluant fractions (Fraction 6), were collected by stepwise decreases in pH gradient. For ProteinChip array binding, 20 μl of each fractionated serum were diluted in 80 μl of CM Low Stringency Buffer (0.1M sodium acetate, pH 4.0) and profiled on Weak Cation Exchange (CM10) Arrays (Ciphergen Biosystems). Sinapinic acid (Ciphergen Biosystems), which served as an energy absorbing molecule, was used to facilitate desorption and ionization of proteins on the ProteinChip arrays. All fractionation and on-chip spotting steps were performed on a Biomek 2000 Robotic Station (Beckman Coulter, Fullerton, CA, USA).

The MS profiles of the serum samples on the ProteinChip arrays were acquired by a Protein Biology System (Model PBSIIc, Ciphergen Biosystems) using three different laser spot protocols (low, medium and high power settings). The high mass setting for the low laser protocol was 25 kDa, with an optimization range from 1 to 7.5 kDa and a deflector setting of 1 kDa. The medium and high laser spot protocol had a high mass setting of 200 kDa and deflector setting of 10 kDa, with an optimization range from 10 to 50 kDa and from 10 to 75 kDa, respectively. The laser intensities were between 170 and 250, and detector sensitivities between 4 and 10. These settings were optimized manually for each fraction to achieve a maximum yield of protein peaks. The final MS profiles were generated by averaging 65 laser shots with 5 shots on 13 positions of each array spot, preceded by two warming shots at intensities 10 units higher than the laser power. The data of the warming shots were not included in the final spectra. The starting and end positions of the spot were incrementally changed for each laser setting to avoid depletion of signal. Mass detection accuracy of PBSIIc was calibrated externally by using the All-in-1 peptide and All-in-1 protein II molecular mass standards (Ciphergen Biosystems). As suggested by the manufacturer's protocol, the m/z regions used to perform peak detection and quantification were set to 1500–10 000, 10 000–30 000 and 30 000–200 000 for profiles that were acquired using low, medium and high laser power settings, respectively.

The reproducibility among the competing algorithms at a given peak location will be evaluated by the CV of the peak intensities across the 36 replicates. Note that a specific peak location is not only determined by its m/z ratio, but also by a combination of fractionation and laser intensity. Based on the experimental design, the calculated CV of a peak includes variations in both experimental procedures and data analysis.

2.4 Simulated data

To compare the performance of peak detection algorithms, we worked with simulated data. We generated 100 experiments, each of them with 50 spectra.

To generate the component B(t)+N*S(t) in Equation (1) for each simulated spectrum, we used the simulation engine developed by Coombes et al. (2005) following the guidelines provided by Morris et al. (2005). In brief, such guidelines include the following steps. First, the characteristics of the population which will be reflected in the simulated data has to be determined. Specifically, two distributions must be specified, one for the m/z values corresponding to true peaks in the population and other for the abundance of each protein across samples. This task is accomplished by using real data, in our study we used the real spectra described in Section 2.3 produced with low laser intensity corresponding to fractionation 1. The next step is to generate experiments using the characteristics of the population. Three factors must be generated per experiment: the location of the true peaks, the abundance for each protein and the prevalence of the peaks across spectra. Note that we can use the given population to generate as many experiments as needed. Finally, the settings of the experiment are used to obtain the component B(t)+N*S(t) for each individual spectrum.

The only missing component in Equation (1) is ɛ(t). Morris et al. (2005) proposed the use of Gaussian white noise, however, by estimating the autocorrelation function and the partial correlation function of the noise in our experimental data, we found dependence structure. To take into account this factor, we propose the model

(2)

where, γ(t) follows a stationary autoregressive moving average (ARMA) process with variance of 1, while σ(t) is a positive function reflecting the variance of the noise.

The function ɛ(t) is intended to replicate the noise found in the 36 experimental spectra corresponding to fractionation 1 and low laser intensity. To attain this goal we proceeded as follows. To generate the component γ(t), we started by finding a common m/z interval where the 36 spectra had no noticeable peaks. Then, we used the intensities in that interval to fit an ARMA process, one per spectrum. We found that in all cases an ARMA process with 1 autoregressive term and 3 moving average terms provided a good approximation—using as diagnostic tools the autocorrelation function of the residuals and the Ljung-Box statistics. Finally, every time we simulated a spectrum we generated its respective component γ(t) by first randomly selecting one of the 36 fitted models, then generating an ARMA process from that model, and finally scaling the simulated process to have variance of 1. On the other hand, for each simulated spectrum the function σ(t) was defined as follows. We considered the experimental spectrum corresponding to the fitted ARMA model that was used to generate γ(t). Such spectrum was denoised using the undecimated discrete wavelet transform (the same algorithm used for denoising in the Cromwell algorithm), the denoised spectrum was substracted from the raw spectrum to obtain an estimator of the noise, 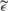(t). For each m/z value, t₀, we defined σ(t₀) as the SD of 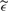(t) in a windows of length 1000 in the time scale and centered at .

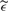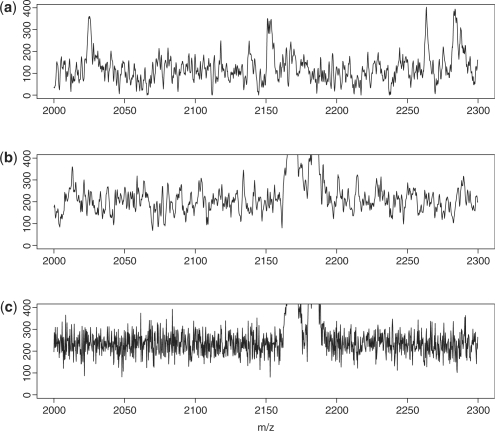
Figure 1 contains plots for (a) real data, (b) simulated data with noise generated using model (2) and (c) simulated data with Gaussian white noise. The axis limits in that figure were chosen to appreciate the characteristics of the noise. Clearly, noise generated with model (2) has a better agreement with real data than Gaussian white noise. Though the plot only shows spectra in the m/z range from 2000–2300, similar results were found in the m/z range from 2000–25 000.

Fig. 1.

Comparison of the noise in the (a) experimental data and simulated data using (b) an ARMA process and (c) a white noise.

We simulated 100 experiments, each of them with 150 true peaks and 50 spectra. The peaks are distributed in the m/z range from 1500 to 25 000. For each experiment, we used the approach by Morris et al. (2005) to generate the component B(t)+N*S(t) of the individual spectra and we added the noise, ɛ(t), using model (2).

3 RESULTS

3.1 Peak quantification

The experimental profiles were obtained by fractionating the sample into six parts and analyzing each of them with three laser intensities: low, medium and high. Therefore, the biological information in the sample is reflected in 18 spectra. We obtained 36 replicates for each of the 18 spectra. (see details in Section 2.3). To guarantee that we were using the raw data, we extracted the vector of counts from the XML files produced by the ProteinChip© Software 3.1 rather than using its automatic procedures to export the data in comma-separated values (csv) files. The correct alignment of the spectra was verified by using heatmaps (plots not shown). Each spectra was pre-processed using the algorithms described in Section 2.1. MassSpecWavelet was not included in this part of the analysis because it only performs peak detection. PROcess has two algorithms to estimate the baseline, one uses local interpolation while the other applies local regression, we included both variants and denoted them as PROcess1 and PROcess2, respectively. The specific settings used for each package can be found in the Supplementary Material.

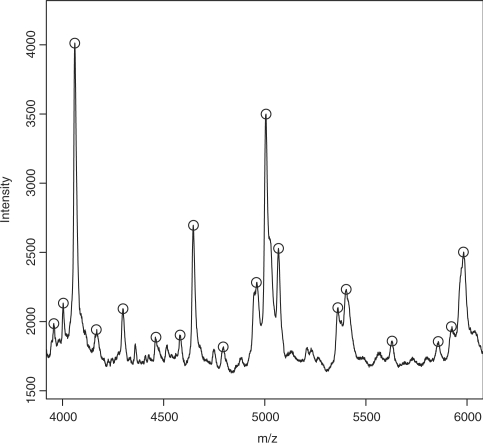
We identified a set of plausible peaks using the Ciphergen's software. From the set of detected peaks produced by Ciphergen, we only kept the peak locations that were detected in at least half of the replicates and were located within the m/z range corresponding to the laser power protocol used to acquire the profiles: 1500–10 000, 10 000–30 000 and 30 000–200 000 for low, medium and high laser power settings, respectively. We found 455 peaks, which split into 233, 123 and 99 peaks for data acquired using low, medium and high laser intensity, respectively. Figure 2 shows that these peaks match well with the peaks that appear in the mean raw spectrum. Similar results were found for all fractionations and laser intensities.

Fig. 2.

Mean (n=36) raw spectrum for spectra generated for fractionation 1 with low laser intensity. Detected peaks produced by Ciphergen appear in circles.

For each detected peak, x, we quantify its intensity in the individual spectra as the local maximum within the m/z interval [(1−0.003)x,(1+0.003)x]. The reproducibility of the pre-processed spectra was calculated as the CV of the peak intensity for x across all 36 replicates.

To analyze the CVs, we used a repeated measures ANOVA with between-subject factors. This model is adequate for this application because we have both, within- and between-subject factors. At each peak location (subject), we measure five CVs, each corresponding to a particular algorithm (within-subject factor). In addition, the peak locations are grouped according to laser intensity (between-subject factor).

We applied the repeated measures ANOVA model to the log-transformed data. The transformation helps to better satisfy the assumptions of normality and equal variances. Not all the algorithms for baseline subtraction guarantee that the intensities in the baseline-subtracted spectra will be positive, as a consequence the CVs do not need to be positive. We removed the peak locations with any negative CV, they accounted for 1, 6 and 2 peak locations detected with low, medium and high laser intensity, respectively.

Let y_kij denote the logarithm of the CV using algorithm j from the i-th peak location obtained with laser intensity k. The repeated measures ANOVA model with between subjected factors can be written as

(3)

where

• μ is the overall mean,

• γ_k is the fixed effect of laser intensity k, with ∑_k=1³γ_k=0,

• τ_j is the fixed effect of the algorithm j, with ∑_j=1⁵τ_j=0,

• (γ τ)_kj is the fixed effect for the interaction of the k-th group and the algorithm j, with ∑_k=1³(γ τ)_kj=∑_j=1⁵(γ τ)_kj=0,

• π_i(k) are independent random effects for the i-th subject in the k-th group, with π_i(k) ∼ N(0,σ_π²),

• e_kij are independent random error terms, with e_kij ∼ N(0,σ_e²).

To test differences among laser intensities, algorithms and their interaction we used F-tests. The specific expressions for the F-statistics are given by Davis (2002). The P-values were all smaller than 0.0001. The between group test indicates that the laser intensity used to produce the data has a significant effect on the performance of the algorithms. The within-subject test indicates that there are significant differences on the reproducibility attained by each pre-processing algorithm. And finally, the test for the interaction between the variables’ laser intensity and algorithm suggests that the differences among the performances of the pre-processing algorithms change when we analyze data produced with different laser intensities.

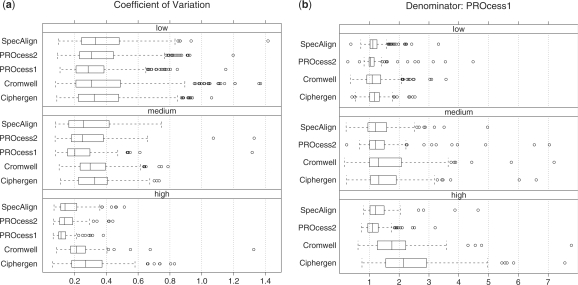
Figure 3a shows the CVs by algorithm and laser intensity. The CVs associated with peak locations detected with the high laser intensity are relatively smaller than low and median intensities. Taking ratios of CVs at each peak location, with PROcess1 in the denominator, we find (Fig. 3b) that all algorithms tend to be less reproducible than PROcess1. Furthermore, the ratios increase with laser intensity ranging from low to high, for example, with Ciphergen the percentage of peak locations with a ratio greater than 2 goes from 2% at low laser intensity to more than 20% and 50% at medium and high laser intensities, respectively.

Fig. 3.

(a) Comparison of algorithms based on the CV of peak intensities. We include two algorithms from the PROcess package. PROcess1 uses local interpolation to estimate the baseline, while PROcess2 applies local regression. The number of CVs per laser intensity is n_low=233, n_med=123 and n_high=99, respectively. Those cases when the CV is negative or higher than 1.5 are not shown, they account for 1.5% and 2.8% of the location peaks, respectively. (b) Ratio of CVs with PROcess1 in the denominator. Negative ratios or ratios higher than 8 are not shown, they represent 0.9% and 2.8% of the location peaks, respectively.

To verify the robustness of our results to different sets of detected peaks, we performed peak detection using MassSpecWavelet. In this case, the set of detected peaks has 495 elements and includes 80% of the peaks detected with Ciphergen. The results using this new set of peaks were similar to those reported here. See Supplementary Material for an analogous Figure 3.

For any given spectrum, there is a low-mass region where the spectrum is not reliable because is dominated by the matrix signal. Such region is typically ignored by pre-processing algorithms, such as those we consider in this study. The results reported here were obtained using a cutoff equal to 1500 m/z. We verified by visual inspection of the spectra that the magnitude of the noise above 1500 m/z was relatively stable. For spectra acquired using medium and high laser intensity, the cutoff could be increased since the data were used to quantify peaks in the m/z range from 10 000 to 30 000 and 30 000 to 200 000, respectively. We repeated the analysis using the m/z cutoffs 1500, 9000 and 28 000 for low, medium and high laser intensity, respectively. The results were similar to those reported here, an analogous Figure 3 can be found in the Supplementary Material.

3.2 Peak detection

To compare the performance of the algorithms in terms of peak detection, we used an extensive simulation study that includes 100 experiments. Each experiment has 50 spectra and 150 true peaks distributed in the range from 1500 to 25 000 m/z.

MassSpecWavelet, PROcess and Cromwell were applied over the 100 experiments. For SpecAlign and Ciphergen only 10 experiments were considered because for those packages the modification of the settings for peak detection must be done manually. See Supplementary Material for the specific settings used for each algorithm. The sensitivity and FDR for each set of detected peaks were computed as explained in Section 2.2.2. We used different signal-to-noise thresholds and obtained, for each algorithm, a set of FDR–sensitivity curves, one per experiment.

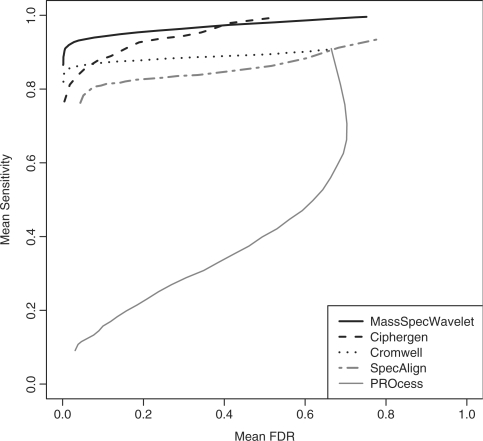
We summarized the results by computing the mean of the FDR–sensitivity curves. For each algorithm and signal-to-noise threshold there are as many combinations of FDR and sensitivity as the number of analyzed experiments. By computing for each signal-to-noise threshold the mean of its FDRs and sensitivities, respectively, we obtained a mean version of the FDR–sensitivity curves. Figure 4 shows the mean FDR–sensitivity curves by algorithm. On average, MassSpecWavelet has the highest mean sensitivities, and thus, the best performance. Ciphergen is the only competing package that reached mean sensitivity levels similar to those produced by MassSpecWavelet, but only with mean FDRs above ∼ 0.4. On the other hand, PROcess showed the worst performance with a mean sensitivity below 0.5 for any mean FDR in the range from 0 to 0.6. Since the poor performance of this algorithm was evident by visually comparing the sets of detected peaks with the spectra, we tried to obtain better results by modifying the peak detection settings; however, we were not able to find a combination with good visual results, this situation is reflected in its mean FDR–sensitivity curve.

Fig. 4.

Mean FDR–sensitivity curve for peak detection algorithms. The mean was computed across 100 experiments for PROcess, MassSpecWavelet and Cromwell, and 10 for Ciphergen and SpecAlign. Each curve represents the combinations of mean FDR and mean sensitivity corresponding to different signal-to-noise thresholds. See Supplementary Material for a figure, where the mean FDR–sensitivity relations are presented with dots.

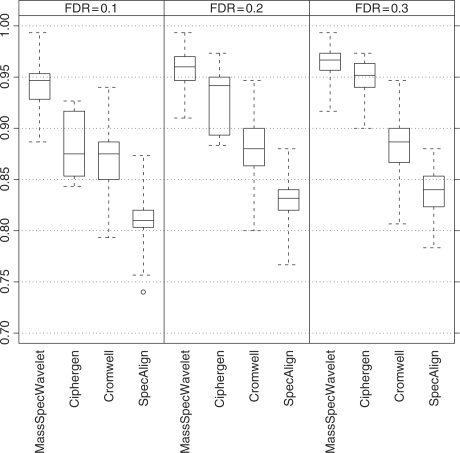
To take into account the variability of the sensitivity across experiments, we computed the sensitivity of the algorithms at given values of FDR. Specifically, we used every FDR–sensitivity curve to approximate, by linear interpolation, the sensitivity associated with a FDR of 0.1, 0.2 and 0.3, respectively. Figure 5 contains boxplots of those sensitivities grouped by algorithm and FDR. PROcess is not included because its sensitivities were all below 0.5. The results are similar to those found using the mean FDR–sensitivity curves. MassSpecWavelet is clearly the algorithm with the best performance, being the only algorithm that reaches sensitivities above 0.95 with a FDR of 0.1. It is followed by Ciphergen whose sensitivities increase constantly when the FDR goes from 0.1 to 0.3. The results in Figure 5 can also be presented in terms of peak counts. See Supplementary Material for a table summarizing the numbers of missed peaks and falsely discovered peaks by various methods.

Fig. 5.

Sensitivities by FDR and algorithm. Each boxplot represents the sensitivities at the given level of FDR computed across the experiments. The number of sensitivities that each boxplot represents is equal to the number of analyzed experiments: 100 for MassSpecWavelet and Cromwell, and 10 for Ciphergen and SpecAlign.

4 DISCUSSION

MS data requires several pre-processing steps in order to identify the location of peaks and quantify their intensities. Since any high-level statistical analysis relies on the quality of the pre-processing, it is of interest to compare the performance of competitive methods.

In this article, we considered MS data produced with the method of SELDI-TOF MS. Our comparison of pre-processing algorithms/approaches for this type of data included the Bioconductor packages PROcess and MassSpecWavelet available through R, the freely available software SpecAlign, the set of Matlab scripts, Cromwell, developed by the bioinformatics group at the MD Anderson Cancer Center and the commercial software produced by Ciphergen, which is commonly used in SELDI studies but whose relative performance with other competing algorithms had not been systematically explored. We evaluated their performances in terms of their primary functions: peak detection and peak quantification.

Regarding peak quantification, we found that the R package PROcess produced more reproducible results (Fig. 3). However, the results were not homogeneous across laser intensities. The differences among the methods were larger with data produced at high and medium laser intensities. In terms of peak detection, we found that the packages with the best performance were MassSpecWavelet and Ciphergen (Figs 4 and 5).

In working with the peak detection algorithms we noticed the following. In general, when performing peak detection it was easier to tune the parameters for MassSpecWavelet, Ciphergen and SpecAlign; we were able to get sensible results by only modifying the threshold for the signal-to-noise ratio while using the defaults settings for the other parameters. In terms of the required pre-processing steps, all the packages, with the exception of MassSpecWavelet, perform peak detection on the pre-processed spectra. Thus, MassSpecWavelet is the only algorithm, from among those we considered in this study, not sensitive to the previous pre-processing steps. Finally, our experience using Ciphergen's software suggests that with both, real and simulated data, there exists very good agreement between the detected peaks and those that can be visually detected in the mean spectrum (Fig. 2). Our results thus indicate that analyzing individual spectra is aceptable for peak detection; at least as implemented by the Ciphergen software.

Our peak detection comparison included corroboration with Du et al. (2006). In that study, curves of FDR–sensitivity were used to compare MassSpecWavelet, PROcess and Cromwell, and it was argued that the relative performance among the algorithms is explained by the estimate of the signal-to-noise ratio used in each case. The main difference between the peak detection study conducted by Du et al. (2006) and the one reported in this article is the data set that was used to perform the comparison. Experimental data set with 60 spectra and 21 true peaks was used by Du et al. (2006), while we considered simulated data with 50 spectra and 150 true peaks. Thus, the comparison of the algorithms in terms of peak detection is robust to different number of peaks.

Combining the results for the two criteria, we obtain some guidelines regarding the best algorithms for pre-processing of SELDI-TOF MS data. For data generated with low laser intensity, our results suggest that the software developed by Ciphergen is able to produce relatively good results, i.e. its reproducibility when measuring peak intensities is comparable to that of other algorithms, while its performance for peak detection is only surpassed by MassSpecWavelet. On the other hand, for medium and high laser intensity, none of the methods show uniformly better performances under both criteria. For these laser intensities, our results suggest that an advantageous combination is the use of the Bioconductor packages, MassSpecWavelet and PROcess, the former for peak detection and the latter for peak quantification.

The results reported in this article may be able to apply to other variants of MALDI-TOF MS. However, a cautionary note is that some of the methods included in this study were specifically developed for pre-processing of data collected by SELDI. For other types of MS data, our approach based on considering the reproducibility of the peak quantification as well as the FDR and sensitivity of the peak detection could be used to compare the performance of pertinent algorithms.