Abstract
The twist, rise, slide, shift, tilt and roll between adjoining base pairs in DNA depend on the identity of the bases. The resulting dependence of the double helix conformation on the nucleotide sequence is important for DNA recognition by proteins, packaging and maintenance of genetic material, and other interactions involving DNA. This dependence, however, is obscured by poorly understood variations in the stacking geometry of the same adjoining base pairs within different sequence contexts. In this article, we approach the problem of sequence-dependent DNA conformation by statistical analysis of X-ray and NMR structures of DNA oligomers. We evaluate the corresponding helical coherence length—a cumulative parameter quantifying sequence-dependent deviations from the ideal double helix geometry. We find, e.g. that the solution structure of synthetic oligomers is characterized by 100–200 Å coherence length, which is similar to ∼150 Å coherence length of natural, salmon-sperm DNA. Packing of oligomers in crystals dramatically alters their helical coherence. The coherence length increases to 800–1200 Å, consistent with its theoretically predicted role in interactions between DNA at close separations.
INTRODUCTION
Sequence dependence of the double helix structure and elasticity appear to play an important role in many fundamental processes involving DNA. X-ray and NMR structures of DNA oligomers reveal that the sequence affects the twist, rise, roll, tilt and other parameters characterizing the conformation of adjoining base pairs within the double helix (base pair step parameters) (1–5). The resulting intrinsic preference of the double helix to bend and twist at certain sequences may be important, e.g. for nucleosome binding, recognition of DNA by regulatory proteins, DNA–DNA interactions and synthesis of RNA on DNA templates (6–11 and references therein).
The actual twisting, stretching and bending of the double helix (hereafter referred to as the DNA conformation) may not only reflect the tendency of the base pairs to stack at distances and angles dependent on their identity but may also depend on interactions with other molecules. For instance, the same molecule has ∼10.5 bp per helical turn in solution (12–15) and 10.0 bp/turn in hydrated fibers (15,16). The conformation of DNA may also depend on other environmental factors, e.g. cations in the crystallization buffer appear to affect the conformation of DNA oligomers (17).
Analysis of how the DNA conformation depends on the nucleotide sequence is complicated by variations in the stacking geometry of the base pairs at each specific step with the surrounding sequence (18–20). This dependence of the base pair step parameters on the sequence context is not only poorly understood but is sometimes left unnoticed.
In other words, the sequence-dependent DNA conformation may both affect and be affected by the DNA environment and function. One approach to understanding these structure–function relationships is through computer simulations that explicitly account for each base pair, e.g. within ab initio, all-atom or wedge models (see 21–24 and references therein). This approach, however, is limited by our knowledge of microscopic interaction potentials and by other inherent restrictions and assumptions.
Another approach is through relating important DNA properties to cumulative statistical parameters rather than to conformations of individual base pair steps. So far this approach has been limited primarily to a simplified elastic rod model of DNA (10,21,25–27). For instance, bending of the central axis of DNA has been described by the bending elasticity modulus and bending persistence length. Twisting of DNA has been described by the torsional elasticity modulus and the corresponding persistence length. These parameters have proved to be very useful in characterizing a number of DNA properties and interactions (25–28), but they contain no information about the helical conformation of the molecule and its sequence.
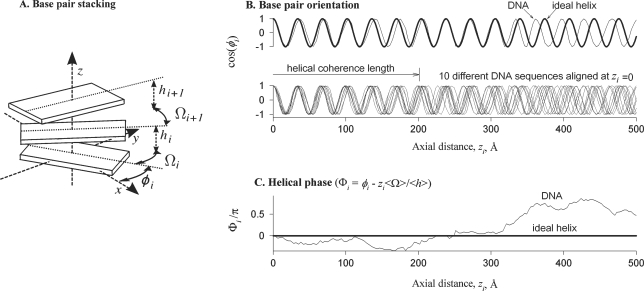
To incorporate cumulative parameters of the sequence-dependent helical structure into the latter approach, we proposed to describe sequence and thermal variations in the twist between adjoining base pairs with the twist coherence length (29–31). This length characterizes the ability of DNA to follow a structure close to a geometrically perfect double helix in the same way as the bending persistence length characterizes the ability of DNA centerline to follow a straight line (Figure 1).
Figure 1.
Schematic illustration of non-ideal helical geometry and helical coherence of straight DNA. (A) The base pairs are depicted as rigid blocks oriented at azimuthal angles φi with the twist Ωi and rise hi between them, where the index i numbers the base pairs. (B) The bold line in the top panel shows the dependence of base pair orientations on the distance zi along the helical axis in an ideal helix, in which the twist Ω and rise h per base pair are constant. Sequence dependence of the twist and rise in a DNA molecule (thin line) with the same average twist and rise (<Ωi> = Ω and <hi> = h) results in accumulating mean-square deviation of base pair orientations from the ideal helix. This loss of helical coherence is best illustrated by aligning several molecules with uncorrelated sequences at zi = 0 (bottom panel). Since twist and rise variations at each base pair step are small, these molecules remain close to the ideal helical alignment over many steps. However, accumulating twist and rise displacements eventually disrupt their alignment. (C) To characterize this effect, we introduce the helical phase Φi, which is the difference between the azimuthal angle φi in a DNA molecule and the azimuthal angle expected in the corresponding ideal helix (zi<Ωi>/<hi>). The helical phase of each DNA is determined by its sequence, as illustrated by the plot. The mean-square displacement of Φi averaged over all possible sequences accumulates linearly with zi [Equation (5)]. The helical coherence length is the axial distance at which this mean-square displacement exceeds 1 rad2. At larger distances, azimuthal orientations of base pairs on molecules with different sequences become uncorrelated (B, bottom panel). We describe the contributions of variations in the twist and rise by the twist and rise coherence lengths, correspondingly [Equation (8)]. For instance, the total helical coherence length would be equal to the twist coherence length if the variations in the rise were negligible. The contribution of correlations between the twist and rise is characterized by the twist–rise coherence length. Note that the latter is a mathematical construct rather than a physical length. It may be positive or negative, depending on the sign of twist–rise correlations. All these concepts can be generalized to bent DNA as discussed in the text.
In the present study, we introduce a more general concept of helical coherence that accounts also for sequence-dependent variations in the rise and other base pair step parameters. From the structures reported in the Nucleic Acid Database (NDB) (2), we find a dramatically different helical coherence of DNA oligomers in crystals (X-ray structures) compared to those in solution (NMR structures). The solution helical coherence length estimated from the NMR structures appears to be consistent with that for natural, salmon-sperm DNA. After describing the corresponding results, we discuss their implications for understanding the relationship of the double helix structure with the environment and functional properties of DNA.
BASIC CONCEPTS
Helical geometry of straight DNA
The geometry of an ideal, continuous, straight helix is described by a simple equation
| 1 |
where φ is the azimuthal orientation of the helix (e.g. one of its strands) at the coordinate z along the helical axis, H is the helical pitch and Φ0 = φ(z = 0) is the helical phase.
In DNA, the twist, rise and other base pair step parameters are affected by the nucleotide sequence (1,2,32) and thermal motions (21,33). Despite its discreteness and non-ideal helical geometry, straight DNA can still be described by
| 2 |
where zi is the z-coordinate of the base pair i along the helical axis, φi is the azimuthal orientation of the base pair, Φi is the helical phase,
| 3 |
is the reciprocal pitch (in an ideal helix Ω/h = 2π/H), Ωi and hi are the twist and rise between the adjoining base pairs i-1 and i (Figure 1), and < > indicates sequence and thermal averaging. The helical phase of DNA
| 4 |
may be different at different base pairs, but its average value is still the same as in an ideal helix, <Φi>=Φ0.
Helical coherence of straight DNA
The displacement of the helical phase from the average value increases with the length, disrupting the helical coherence of the molecule (Figure 1C). Over large spans of DNA, the mean-square displacement accumulates as
| 5 |
where λc is the helical coherence length (29,30). In straight DNA with only short-range correlations in the nucleotide sequence, Equation (5) fully describes the disruption of the helical coherence at large distances. Thus, λc is a single parameter that is needed to characterize the effects of such disruption, e.g. on intermolecular interactions and X-ray diffraction by DNA (10). It is the correlation length for azimuthal orientations of the base pairs; the orientations of base pairs separated by a larger distance along the DNA molecule become uncorrelated (Figure 1B).
The total coherence length has contributions from thermal fluctuations as well as sequence-dependent variations in both the twist and rise. These contributions add up as
| 6 |
(the derivation will be reported elsewhere). Here lp is the helical persistence length, which in straight DNA is determined primarily by thermal fluctuations
| 7 |
where kB is Boltzmann's constant, T is the absolute temperature and Ct and Cs are the torsional and stretching elasticities of the molecule, respectively. The intrinsic coherence length associated with sequence-dependent variations in the most energetically favorable values of Ωl and hl is given by,
| 8 |
where
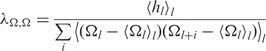 |
9 |
is the intrinsic twist coherence length,
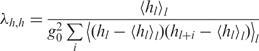 |
10 |
is the intrinsic rise coherence length,
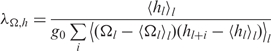 |
11 |
is the intrinsic twist-rise coherence length, and < >l indicates sequence averaging over all base pairs l. In the case of no sequence-dependent variations in the twist and rise,
Note that the intrinsic coherence length and the helical persistence length describe the ability of DNA to follow an ideal helical geometry in exactly the same way as the static (intrinsic) and dynamic (thermal) contributions to the bending persistence length (34) describe the ability of DNA centerline to follow an ideal straight line.
From the reported values of Ct and Cs [most recently reviewed in (10)] we find lp ∼700 Å, which is slightly longer than the 500 Å (25) bending persistence length of DNA. In ‘Results’ section, we estimate λΩ,Ω, λΩ,h, λh,h and the corresponding λ(0)c from Ωi and hi measured by X-rays in crystals and by NMR in solution of different DNA oligomers.
Helical coherence of curved and nearly straight DNA
Natural curvature of some sequences, thermal motions and interactions with proteins may cause DNA bending. The helical coherence length of curved DNA can be calculated along the centerline of the molecule using a similar approach, as discussed above, but the choice of a reference frame for defining the base pair step parameters with respect to the centerline is not a trivial issue (35–37). In the present study, we use a different, less general approach that is more convenient for analyzing effects of the helical coherence on X-ray diffraction and interaction between DNA in hydrated fibers and liquid-crystalline aggregates. In such aggregates DNA remains ‘nearly straight’ over long stretches, i.e. its centerline exhibits only small displacements from a straight axis. The helical coherence length of a nearly straight DNA can be calculated not only along its centerline but also along this global helical axis. It is the latter ‘axial’ helical coherence length that determines X-ray diffraction patterns and intermolecular interactions in hydrated DNA fibers. Note that the coherence length along the centerline of nearly straight DNA should be only slightly larger and it may be used as an upper bound approximation for the coherence length along the global axis.
The actual value of the helical coherence length of ‘nearly straight’ DNA along the global axis can be calculated from Equations (2–11) with all twist and rise values defined in a reference frame associated with this axis. In this reference frame, variations in the other base pair step and conformation parameters (tilt, roll, slide, propeller twist, etc.) do not result directly in accumulation of deviations from the ideal helical conformation (to be reported elsewhere).
X-ray diffraction
The intensity of X-ray scattering by a single, long and straight DNA double helix at the scattering vector (K, kz)
| 12 |
is the sum of scattering intensities along layer lines n, which can be approximated by (10)
| 13 |
We assume that the molecule is oriented along the z-axis and perpendicular to the incident beam. Here K is the coordinate of the scattering vector perpendicular to the incident beam and the z-axis, kz is the z-coordinate of the scattering vector, a is the DNA radius, Jn(x) is a Bessel function of order n, g0 is the reciprocal DNA pitch defined by Equation (3), and λc is the helical coherence length of DNA defined by Equations (6–11).
The interpretation of X-ray diffraction from non-crystalline, hydrated DNA fibers is more difficult due to intermolecular interactions and complex coherent scattering effects (38). Nevertheless, our recent analysis indicates that the scattering intensity at the n = ±5 layer lines may have the form of Equation (13) with λc approximately equal to the helical coherence length of an undeformed double helix in solution (to be reported elsewhere). In ‘Results’ section, we use the latter diffraction peaks from previously reported patterns (16,39), to provide an independent estimate of the helical coherence length in natural DNA.
METHODS
Analysis of DNA oligomer structures from the Nucleic Acid Database
For the analysis of quenched, sequence-dependent variations in the twist and rise, we utilized the structures of B-DNA oligomers from the NDB (2), which were determined in crystals by X-ray diffraction and in solution by NMR. We excluded DNA oligomers with modified/substituted/mismatched base pairs, cross-links, and large defects as well as DNAs co-crystallized with drugs, peptides or other macromolecules. From the remaining set of 50 crystal structures, we picked several overlapping subsets: (i) 22 structures with no kinks or significant bending apparent upon examination with a 3D viewer, (ii) dodecamers only, (iii) decamers only, (iv) decamers without spermine in the crystallization buffer and (v) decamers with spermine in the buffer. Independent analysis based on the full set and all these subsets produced similar results, as discussed in the Supplementary material. Because fewer NMR structures were available, we selected only one set of 26 oligonucleotides for their analysis. A list of NDB names and sequences of these oligonucleotides is provided in the online Supplementary material.
The reasoning behind this conservative and somewhat limited selection of oligomers was to avoid artificially enhancing differences between the base pair step parameters in crystal and solution structures as well as to discount those structures with defects and sharp bends in the DNA. Our stringent sampling may, therefore, underestimate some of the structural differences between different sequences.
To account for possible correlations between the structural parameters at different (mostly adjacent) base pair steps along a molecule, we constructed models of DNA with 106 base pairs by stacking 4–10 bp fragments from the selected oligomers. Fragments of these sizes were chosen, as opposed to simply using individual base pair steps of these oligomers, to illustrate the effects of longer range (>1 bp step away) correlations of the base pair step parameters.
These randomly sized fragments, eliminating the terminal base pairs of the oligomers to avoid end effects, were randomly selected within the oligomers. They were spliced by matching the last base pair step of the preceding fragment with the first step of the fragment to be added to build up the model DNA molecule. For example, if the final base pair step of a stacked sequence was T-C, the next fragment to be connected to this sequence was required to have a T-C step for its first step. Upon stacking of the new fragment, the values of the twist and rise of the last T-C step of the preceding sequence were replaced by those of the first T-C step of the new fragment. This construction (matching the two base pairs of the step rather than matching only the last and first individual base pairs of the previous and succeeding fragments, respectively) provides consistency in the base pair sequence text of the long molecule as well as subsumes any possible correlated behavior along the whole molecule. The stacking was performed either only with crystalline structures, resulting in DNA-cry models, or only with NMR structures, resulting in DNA-nmr models.
Note that large (≥106 base pairs) length of DNA-cry and DNA-nmr was required to achieve relatively small errors for the correlations in the base pair step parameters and in calculations of the coherence lengths. The analysis was repeated many times with different random seeds to test the reproducibility and determine standard deviations for the extracted correlation functions and coherence lengths.
These very long and unconfined DNA models remained nearly straight over large stretches but not over the entire length, so that the global helical axis could not be defined for the entire molecule. To evaluate the average helical coherence length for the large nearly straight stretches, we used the following three approximations.
(i) As an upper bound approximation, we calculated the intrinsic helical coherence length (λ(0)c) along the curved centerline. We used the NDB twist (Ωi) and rise (hi) values at the base pair step i defined in a standard local reference frame (1,35–37) and determined with the 3DNA program (40). We calculated the coherence length by direct fitting of Equation (5), where we replaced the axial coordinate z with the coordinate along the rise trajectory (used here as the DNA centerline). The helical phase at each point along this trajectory was calculated from Equation (4). Alternatively, we calculated the coherence length from Equations (8–11). Both procedures returned the same λ(0)c.
(ii) For a lower bound approximation, we used Ωi and hi determined from PDB coordinates with respect to the global helical axis of each oligonucleotide with the Freheelix98 program (41). We calculated λ(0)c from Equations (4,5 or 8–11) as above. This procedure underestimates λ(0)c for the following reasons. (i) It is equivalent to introducing small kinks at joints between different oligonucleotide fragments in the DNA construct (so that the global axes of these fragments match and the whole construct remains nearly straight). The kinks may exaggerate twist and rise variations, reducing the calculated λ(0)c. (ii) The Freehelix algorithm may further exaggerate rise variations because of the reference frame implemented in it (42), reducing λ(0)c even more.
(iii) Finally, we calculated λ(0)c using the same procedure as in the upper bound estimate described above but with Ωi and hi determined in a local reference frame for each base pair step with the Freehelix98 program. Comparison of this calculation based on local Freehelix base pair step parameters with the calculation based on local 3DNA parameters allowed us to get a better idea of the effect of using different reference frames and definitions of the step parameters.
Both 3DNA and Freehelix98 programs used in this study can be found online at http://ndbserver.rutgers.edu/services/index.html.
Analysis of fiber diffraction patterns
Original X-ray films with diffraction photographs of oriented, hydrated fibers of salmon sperm DNA at different densities, initially reported in (16), were generously provided by S. Zimmerman. The photographs were digitized on Arcus II (AGFA, Brentford, UK) or FUJI FLA5000 (Fuji Medical Systems, Stamford, CT, USA) scanners. The patterns were calibrated using the known diffraction angle of calcite crystals, placed in the X-ray beam together with DNA fibers as an internal standard during the diffraction experiments. The density profiles of the diffraction patterns in the kz direction were analyzed at the position of the maximum intensity at the n =±5 layer lines. The peaks at all layer lines contributing to this cross section were simultaneously fitted by Lorentzian functions [Equation (13)] with Systat PeakFit software. This fitting procedure was repeated for each quadrant in the diffraction pattern, providing four width measurements for the n =±5 diffraction peaks. The value of λc and its standard deviation were estimated from averaging of these four measurements.
The diffraction pattern of calf thymus DNA from (39) was analyzed based on a digital copy of the paper from http://www.nature.com. The pattern was calibrated using the kz = 2πn/H positions of the helical layer lines associated with the H = 34 Å pitch of DNA. Although the pattern reproduction could distort the image contrast and reduce the accuracy of the analysis, these results were consistent with those obtained from the original X-ray films of salmon sperm DNA described above.
RESULTS
Oligonucleotide-based DNA models
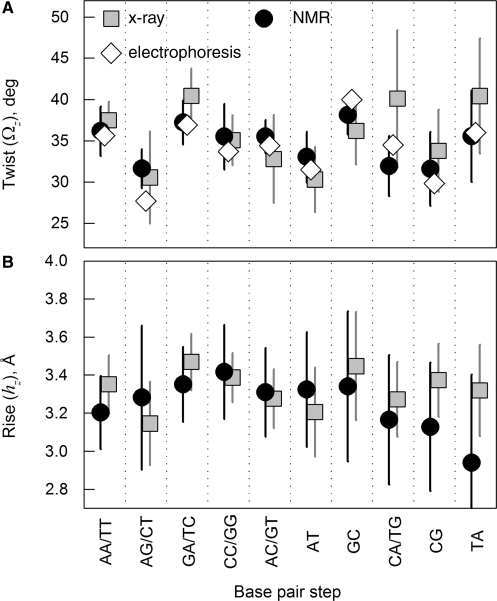
To characterize sequence effects in the double helix structure, we generated DNA-cry models based on known X-ray crystal structures of different oligomers with no visible defects, nucleotide modifications and co-crystallized macromolecules (see ‘Methods’ section). We built separate models based on a full set of 50 such oligonucleotide structures and its different subsets, all of which produced similar results discussed in Supplementary material. Here we show the results obtained for a subset of 22 oligonucleotides with no kinks or bending apparent upon examination with a 3D viewer. We similarly generated DNA-nmr models based on known NMR solution structures of 26 oligomers, also with no defects, apparent kinks or bending. The NDB names and nucleotide sequences of all oligomers are listed in the Supplementary material. The average values of the twist and rise and their dispersions for different base pair steps in these oligomers (Figure 2) were consistent with the corresponding values reported (32,43) from less selective data sets (see Figure S1A and C in the Supplementary material).
Figure 2.
Statistical analysis of twist and rise for different possible base pair steps in the standard reference frame (local z/3DNA). Squares show the values for 22 selected straight oligomers with known X-ray structures, circles show the values for 26 selected straight oligomers with known NMR structures, and diamonds show the average twist values reported in (32) based on electrophoretic measurements. The error bars show standard deviations based on measurements of the same step parameters within different contexts. Note that the same base pair step may be denoted, e.g. AG (5′-A to 3′-G) based on one strand or CT (5′-C to 3′-T) based on the complementary strand. Both possible notations for such steps are shown, separated by a slash.
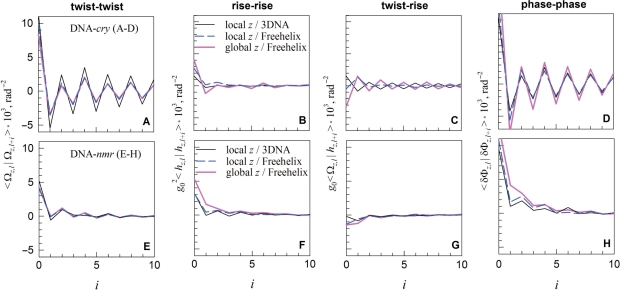
Using the DNA-cry and -nmr models, we calculated the pair correlation functions 〈 x|y〉 ≡ 〈(x − 〈x 〉) (y − 〈 y〉)〉, for the twist (<Ωl |Ωl+i >, rise (g20<hl|hl+i >), twist-rise (g0<Ωl|hl+i>), and helical phase step (<δΦl|δΦl+i> where δΦl ≡ Φl − Φl−1) as outlined in the ‘Methods’ section. Here the indices l and i indicate the number of the base pair step in the DNA construct. We used three different sets of Ωi and hi (see ‘Methods’ section): (i) based on the standard local reference frame implemented in NDB, to which we refer to as a local z/3DNA set; (ii) based on the global helical axis for each oligonucleotide and Freehelix reference frame, to which we refer to as a global z/Freehelix set and (iii) based on the local Freehelix reference frame, to which we refer to as a local z/Freehelix set. All three sets produced similar pair correlation functions (Figure 3).
Figure 3.
The twist (A and E), rise (B and F), twist–rise (C and G) and helical phase (D and H) correlations within DNA-cry (A–D) and DNA-nmr (E–H) at base pair steps separated by i intervening base pairs (i = 0 for correlations at the same step, i = 1 for adjoining steps, etc.).
Despite similar average values of the crystal and solution parameters for each base pair step (Figure 2), the correlations between these parameters in DNA-cry and DNA-nmr appear to be markedly different (Figure 3). A pronounced saw-tooth like pattern of the pair correlations in DNA-cry and large, negative 〈 xl|yl +1〉 indicate strong anti-correlation between successive base pair steps in oligonucleotide crystals. The step parameters deviate in opposite directions from the average on successive steps. Each step appears to correct distortions at the preceding one. Similar anti-correlations were observed when a larger set of 50 crystal structures and its different subsets were used to construct DNA-cry (see Supplementary material).
No anti-correlations were found in DNA-nmr. Positive correlations in the helical phase step (<δΦl|δΦl+i>) in DNA-nmr suggest that the local pitch deviations on successive steps within DNA in solution tend to occur in the same direction, contrary to DNA in crystals. As one may expect, the DNA-nmr correlation functions appear to be shorter range than in crystals.
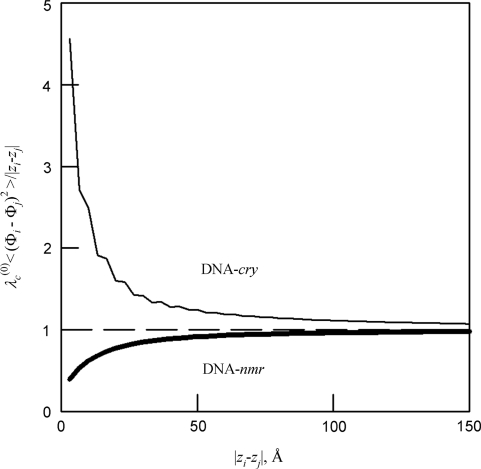
As expected, by direct averaging we found linear accumulation of mean-square deviations in the helical phase from that of an ideal helix [Equation (5)]. Figure 4 shows that Equation (5) becomes accurate in both DNA-cry and DNA-nmr at length scales larger than ∼50 Å. This accumulation results in the loss of correlations between azimuthal orientations of the base pairs with increasing separation between them along the molecule, which is described by the intrinsic helical coherence length λ(0)c (Figure 1B).
Figure 4.
Relative accuracy of Equation (5) at different length scales (shown for local z/3DNA but similar for all models). The dashed line is the prediction from Equation (5).
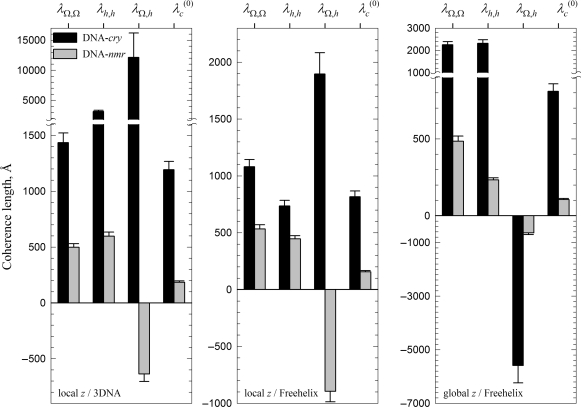
All three sets of Ωi and hi produced close values of λ(0)c (Figure 5). These values are consistent with the expected role of the calculation based on the local z/3DNA set as an upper bound approximation and the calculation based on the global z/Freehelix set as the lower bound approximation. Thus, we estimate 800 < λ(0)c < 1200 Å in DNA-cry and 100 < λ(0)c < 200 Å in DNA-nmr. The intrinsic helical coherence length of DNA appears to be 6–8 times smaller in solution than in crystals. The nearest neighbor anti-correlations in the local pitch within DNA-cry reduce the accumulation of the helical phase distortion, thereby increasing the helical coherence length. The positive correlations within DNA-nmr have an opposite effect, they decrease the helical coherence.
Figure 5.
Intrinsic helical coherence length λ(0)c and its components, as described by Equations (8–11).
Salmon sperm DNA in hydrated fibers
One drawback in using NMR versus X-ray structures for analyzing helical coherence is that NMR structures often have lower resolution and may be more dependent on the force fields and algorithms employed for their computer refinement (4). Since we could not exclude potential inconsistency in compiling the data for oligomers refined by different authors, we also evaluated the helical coherence length based on X-ray diffraction patterns from hydrated DNA fibers.
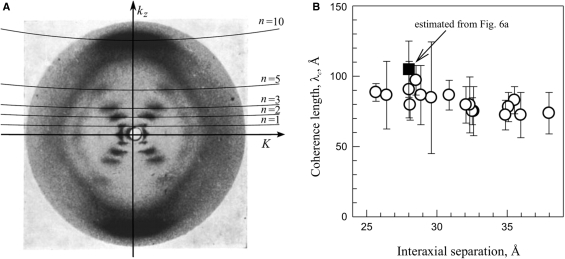
A typical diffraction pattern from hydrated, oriented fibers of B-DNA is illustrated in Figure 6A by a reproduction of the classical Franklin and Gosling picture (39). The two strong peaks on the equator (n = 0 line) at 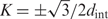 are coherent scattering on DNA packed in a hexagonal array with the interaxial separation dint (intermolecular scattering). For a long time the diffraction peaks at n=±1, ±2, ±3 and ±5 lines were believed to be incoherent scattering on separate molecules (intramolecular scattering) (39,44). A recent study showed that intermolecular scattering may contribute to the latter peaks as well, but this contribution decreases exponentially with n2 and becomes small already at n= ±3 (38). While different interpretation of the n=±1, ±2, ±3 peaks may still be possible, it is clear that the n=±5 peaks in hydrated fibers should not be affected by intermolecular scattering.
are coherent scattering on DNA packed in a hexagonal array with the interaxial separation dint (intermolecular scattering). For a long time the diffraction peaks at n=±1, ±2, ±3 and ±5 lines were believed to be incoherent scattering on separate molecules (intramolecular scattering) (39,44). A recent study showed that intermolecular scattering may contribute to the latter peaks as well, but this contribution decreases exponentially with n2 and becomes small already at n= ±3 (38). While different interpretation of the n=±1, ±2, ±3 peaks may still be possible, it is clear that the n=±5 peaks in hydrated fibers should not be affected by intermolecular scattering.
Figure 6.
(A) A typical diffraction pattern of hydrated DNA fibers (39) showing the layer lines. Imperfect vertical alignment results in broadening of these lines, but average tilt may be estimated from the width of the equatorial Bragg peak. (B) The helical coherence length extracted from experimental diffraction patterns taken from DNA fibers at different degrees of hydration (fiber density); open circles from data provided kindly by S. Zimmermann (16,38) and the filled square from the pattern shown in (A). The plotted values of λc were extracted by direct fitting of kz cross sections of n = ±5 peaks with Equation (13) without any corrections. The correction for the imperfect vertical alignment discussed in the text (‘Results’ section) increases estimated λc by 20–30% to 100–130 Å.
Moreover, a more detailed theoretical analysis shows that the effect of structural adaptation of DNA due to intermolecular interactions on the latter peaks may also be minimal, provided that the fibers are sufficiently hydrated. In such fibers, intermolecular interactions may alter the average twist angle and cause significant deviations from Equation (5) at large |zi−zj| (30) and from Equation (13) at n=±1, ±2 (to be reported elsewhere). Still, the form of the shorter-range correlations (smaller |zi−zj|) is given by Equation (5). Also, the n= ±5 diffraction peaks, described by Equation (13), may be unaffected at sufficiently large intermolecular separations (to be reported elsewhere). Fitting of the cross sections of the latter peaks at constant K with Equation (13) can then be used to extract λc for the solution structure of DNA.
Fitting of the n=±5 peaks in the Franklin and Gosling picture (39) produced λc ∼ 90–130 Å (Figure 6B), but this estimate could be affected by distortions of the diffraction intensity in the process of picture reproduction. For more accurate measurements, we reanalyzed 17 diffraction patterns of hydrated DNA fibers from reference (16), for which the original X-ray films were generously provided to us by S. Zimmerman. Direct fitting of the n=±5 peaks in the latter patterns produced λc ∼ 80–100 Å (Figure 6B), consistent with fitting of the Franklin and Gosling pattern. The fitted values of λc were virtually independent of the interaxial spacing, consistent with the theoretical prediction for minimal or no effect of intermolecular interactions on the diffraction peaks at n=±5.
However, such fitting underestimates λc. It assumes that λc is inversely proportional to the peak width in the kz direction, neglecting an unrelated peak broadening due to imperfect vertical orientation of DNA in fibers. Arcing of the peaks on the equator and meridian and tilting of the diagonal peaks in Figure 6A clearly indicate that imperfect DNA orientation does contribute to the width of the n = ±5 peaks. By examining all these experimental manifestations, we estimated the latter broadening as ∼ 20–30% at smaller dint and even larger in more hydrated fibers (potentially contributing to the small downward trend in λc in Figure 6B). Thus, our estimate of λc should be increased by the same amount to λc ∼ 100–130 Å.
From this estimate and Equation (6) with lp ∼ 700 Å, we find λ(0)c ∼ 120–160 Å, in good agreement with 100 < λ(0)c < 200 Å deduced from DNA-nmr but clearly different from 800 < λ(0)c < 1200 Å deduced from DNA-cry.
DISCUSSION
Sequence-dependent variations, fluctuations and correlations between base pair step parameters were discussed by many authors in application to DNA structure and mechanics (see e.g. 1,3,5,19–24,32,33,45–47 and references therein). The new question posed by the present study is how these variations and correlations affect the double helix coherence, i.e. its ability to follow a geometrically perfect helical structure. The helical coherence was proposed to play a significant role in DNA interactions (10).
To answer this question, we analyzed several different sets of crystal oligonucleotide structures, all of which produced similar results independent of the oligonucleotide selection and the crystallization method. A much smaller number of solution structures were available with only a handful measured with high-resolution NMR techniques. Insufficient representation of some base pair steps precluded the analysis based just on the high-resolution NMR structures. Even with the addition of lower-resolution, NOE-based structures, we were still able to analyze only a single set of oligonucleotides. Nevertheless, predictions for this set were in complete agreement with an independent analysis of X-ray diffraction patterns from highly hydrated, non-crystalline DNA fibers, giving us reasonable confidence at least in our qualitative conclusions.
Probably the most interesting aspect of these new findings is that intermolecular interactions dramatically alter the helical coherence of DNA in crystals compared to solution. The underlying changes in the twist and rise between adjoining base pairs are rather subtle, despite their dramatic effect on the helical coherence. It may not be surprising that these changes have not been delineated before.
Forces affecting helical coherence of DNA in solution and crystals
First, we should emphasize that the helical coherence of DNA directly depends only on the twist and rise variations. The other base pair step parameters change the helical coherence only through their effect on the twist and rise. A comparison of X-ray and NMR structures of synthetic DNA oligomers (Figure 2) reveals that the average values and dispersions of the twist and rise at each base pair step except CA/TG are similar in solution and crystals (2,4,48 and Supplementary material). The difference in the twist at CA/TG may be related to bimodal distribution with distinct low and high twist conformations at this step in dodecamer and decamer crystals, correspondingly (3, see also Figure S1B in the Supplementary material). At the same time, our analysis suggests that the correlations between these parameters and correlations of individual step parameters among adjoining steps along the sequences may be different, dramatically altering the ability of the DNA backbone to retain its helical coherence.
In solution, a larger than average twist between adjoining base pairs is more likely to be accompanied by a smaller than average rise, amplifying the distortion in the helical pitch at this base pair step (Figure 3G). A higher probability of a similar distortion and similar deviation in the helical phase at the next step (Figure 3H) exacerbates helical coherence disruptions, causing accumulation of significant deviations from the ideal helical geometry over a shorter axial distance.
In crystals, a totally different trend is observed. In contrast to solution, larger than average twist is more likely to be followed by smaller than average twist at the next base pair step (Figure 3A). As a result, the distortions in the helical pitch and deviations in the helical phase occur in opposite rather than similar directions at successive steps, reducing the helical coherence disruptions.
In solution, correlations between the base pair step parameters are determined by base pair stacking (in which we include steric clashes) and mechanics of the sugar-phosphate backbone (in which we include all intramolecular interactions within the backbone). The stacking interactions define preferential conformation at individual base pair steps. The backbone mechanics couples conformation parameters within each step and between adjacent steps. A smaller than the average rise upon larger than the average twist may reduce stretching while gradual relaxation of helical pitch variations may prevent sharp bending of the backbone.
In crystals, correlations between the base pair step parameters are in addition affected by steric clashes between the molecules and their hydration layers and by electrostatic interactions between the charged backbones. All these intermolecular interactions depend on the alignment between the ridges and grooves on opposing surfaces formed by the backbone, with the ridges facing the grooves being the most favorable alignment (10). Anti-correlated pitch distortions at consecutive steps may introduce an extra mechanical strain into each molecule, but they favor more beneficial alignment between molecules. Apparently the latter constraint is more important; inverting the helical phase correlations compared to those in solution and dramatically increasing the helical coherence. The only other way to enhance the helical coherence would be to make all twists and rises more uniform, independent of the sequence. But, this is not what we observe.
Note that only twist–rise correlations in crystals appear to be altered by the choice of the reference frame (Figure 3C). This is consistent with the previous report that the reference frame may affect the rise but not the twist (42). The calculated helical coherence length of DNA, however, is less affected by the choice of the reference frame, making it a convenient measure of sequence-dependent variations in the double helix conformation.
Helical coherence of DNA in non-crystalline, hydrated fibers
While easier to study, the double helix conformation in relatively dilute solutions or in crystals may not fully represent that inside cells. Packaging of meters of nucleic acids inside micron size compartments in cells necessitates close intermolecular interactions; yet the double helices remain more hydrated and not as tightly packed as in crystals, and they participate in more heterogeneous interactions. In vitro studies of DNA in hydrated fibers and liquid crystals designed to mimic some of the intracellular interactions revealed a surprising variety of phenomena, most recently reviewed in (10). Better understanding of the DNA helical coherence in such aggregates may help in understanding molecular mechanisms underlying these phenomena.
The adaptation of the double helix structure to intermolecular interactions does occur in hydrated DNA aggregates too, e.g. unwinding of the double helix from ∼10.5 bp/turn to 10.0 bp/turn (15,16). However, this adaptation is predicted to be more subtle than in crystals (to be reported elsewhere). Instead of altering short-range correlations between the base pair step parameters, the interaction between hydrated DNA results in the appearance of a new length scale, the ‘torsional adaptation length’ (30). The interaction alters the correlations between the base pair step parameters at larger length scales, preventing unlimited accumulation of the helical coherence distortions. As a result, the molecules gain the longer range coherence necessary for more energetically favorable alignment over a large juxtaposition length. At the same time, the correlations between the base pair step parameters and the helical coherence within shorter stretches of DNA remain essentially the same as in solution. The stronger the intermolecular interaction is, the shorter the torsional adaptation length will be (30). Crudely, one may think of crystals as a limiting case, in which the torsional adaptation length becomes so small that the correlations between base pair step parameters are affected by intermolecular interactions at all distance scales.
Helical coherence length of natural DNA
To quantify helical coherence distortions, we introduced a helical coherence length, λc, which is the length scale at which accumulation of displacements from an ideal helical structure disrupts correlations in the helical phase [Figure 1B and C; Equation (5)]. Azimuthal orientations of the base pairs separated by a larger distance along the molecule become uncorrelated. This cumulative, statistical parameter depends both on the deviation of the base pair step parameters from the average and the correlations between these parameters. At scales smaller than λc DNA can be perceived as an ideal double helix, but at longer scales this is not the case. The sequence dependence of preferential base pair step parameters determines the intrinsic coherence length λ(0)c of DNA [Equations (8–11)]. Thermal fluctuations reduce the total coherence length λc compared to λ(0)c [Equations (6 and 7)].
Analysis of the helical coherence based on DNA models, constructed by stacking oligomers with known structures, yielded λ(0)c ∼ 100–200 Å when using NMR structures in solution and λ(0)c ∼ 800–1200 Å when using X-ray structures in crystals (Figure 5). The difference in λ(0)c by almost an order of magnitude is associated primarily with the changes in base pair step parameter correlations, induced by the above discussed DNA–DNA interactions. Just as they suppress bending (33,43), crystal packing forces suppress helical pitch fluctuations, dramatically increasing the intrinsic helical coherence length.
Evaluation of the helical coherence length of natural, salmon sperm DNA in solution from X-ray diffraction on hydrated fibers yielded λc∼100–130 Å (Figure 6) and λ(0)c ∼ 150 Å, in agreement with the λ(0)c ∼ 100–200 Å estimate based on NMR structures. However, neither the X-ray data analysis nor the models of stacked oligomers are perfect. For instance, splicing and stacking of the oligomers could affect the model analysis; and imperfect vertical alignment of the molecules in fibers and non-linear response of the X-ray film could affect interpretation of the diffraction patterns. The uncertainty in λc and λ(0)c associated with these factors, however, cannot be responsible for the large difference between the helical coherence of DNA in solution and crystals. In any case, we expect these estimates to be accurate at least by an order of magnitude.
Effect of helical coherence on DNA interactions and homology recognition
While helical coherence may also be important, e.g. for interactions of DNA with proteins, we currently can say more about its potential role in DNA–DNA interactions. The potential importance of helical coherence for such interactions at biologically relevant intermolecular distances (packing densities) is suggested by the following observations and arguments.
Detailed theoretical analysis (10) suggests the following. Close juxtaposition of DNA is more energetically favorable when their sugar-phosphate backbones are aligned in such a register that minimizes the repulsion between negatively charged phosphates (49). This in-register alignment may become even more favorable upon binding of positively charged counterions in DNA grooves and juxtaposition of bound counterions with phosphates on the opposing surface (50). Disruptions of helical coherence preclude undeformed molecules from establishing such a register (29). Torsional deformation restores more favorable alignment, but at a corresponding energetic cost. This cost is an essential part of the interaction energy. It is determined by the balance between the torsional rigidity and the helical coherence length (30).
The tendency of hydrated DNA assemblies to form chiral, cholesteric liquid crystalline phases both in vitro and in vivo [see e.g. (51) and references therein] is direct experimental evidence for the importance of an in-register alignment. Without such an alignment, chirality of most important interactions between the molecules (e.g. electrostatic interactions between sugar-phosphate strands) would simply be averaged out (52). The alignment is also supported by the observation of strong azimuthal correlations between DNA helices, even in highly hydrated fibers (38). The observed double helix unwinding to 10 bp/turn in fibers (15,16) appears to be a manifestation of the torsion deformation accompanying this alignment.
The in-register alignment without torsional deformation is possible only upon juxtaposition of homologous (identical or nearly identical) sequences, when helical imperfections of the two molecules match. The energetic advantage of the juxtaposition between homologous sequences versus non-homologous sequences (sequence recognition), is determined by the cost of the torsional adaptation (30). A greater torsional adaptation is required for the in-register alignment of non-homologous molecules with shorter helical coherence length, resulting in a larger sequence recognition energy.
The recognition may be sufficiently strong, e.g. to explain segregation and pairing of homologous sequences recently observed within cholesteric spherulites formed by mixtures of two fragments with the same length and base pair composition but different sequences (53). Note that the recognition energy calculations reported in the latter study assumed λ(0)c ∼ 300 Å. Our current estimates of shorter λ(0)c suggest even stronger sequence recognition.
Additional experiments are still needed before the observed sequence homology recognition is established as a general feature of interactions between any double-stranded DNA fragments. Alternative interpretations of such recognition, e.g. via bubble formation and cross hybridization of the resulting single strands, should also be tested. Nevertheless, the possibility is not just intriguing but also potentially crucial. Pairing of homologous sequences within intact double-stranded DNA was proposed to precede double strand breaks that trigger homologous recombination in cells (54,55). Can the potential intrinsic ability of double-stranded DNA to recognize sequence homology from a distance contribute to the pairing? This question remains to be answered by future studies.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
ACKNOWLEDGEMENTS
We are grateful to Steven Zimmerman for providing the X-ray diffraction photographs originally described in reference (16). We thank Donald Rau and Victor Zhurkin for valuable discussions.
FUNDING
This work was supported by a fellowship from the Alexander von Humboldt foundation (A.W.). It was funded by the Engineering and Physical Sciences Research Council (GR/S31068/01, A.A.K and D.J.L.), the Royal Society (A.A.K. and A.W.), the Liverhulme Trust (F/07058/AE, A.A.K.), and the Intramural Research Program of the National Institute of Child Health and Human Development, National Institutes of Health (S.L.). Funding for Open Access publication charge: Intramural Research Program, NICHD, NIH.
Conflict of interest statement. None declared.
REFERENCES
- 1.Dickerson RE. DNA structure from A to Z. Meth. Enz. 1992;211:67–111. doi: 10.1016/0076-6879(92)11007-6. [DOI] [PubMed] [Google Scholar]
- 2.Berman HM, Olson WK, Beveridge DL, Westbrook J, Gelbin A, Demeny T, Hsieh S.-H, Srinivasan AR, Schneider B. The Nucleic Acid Database: A comprehensive relational database of three-dimensional structures of nucleic acids. Biophys. J. 1992;63:751–759. doi: 10.1016/S0006-3495(92)81649-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Gorin AA, Zhurkin VB, Olson WK. B-DNA twisting correlates with base pair morphology. J. Mol. Biol. 1995;247:34–48. doi: 10.1006/jmbi.1994.0120. [DOI] [PubMed] [Google Scholar]
- 4.Ulyanov NB, James TL. Statistical analysis of DNA duplex structural features. Meth. Enz. 1995;261:90–120. doi: 10.1016/s0076-6879(95)61006-5. [DOI] [PubMed] [Google Scholar]
- 5.Neidle S. Principles of Nucleic Acid Structure. London: Academic Press; 2008. [Google Scholar]
- 6.Bloomfield VA, Crothers DM, Tinoco I., Jr . Nucleic Acids. Structures, Properties, and Functions. Sausalito, CA: University Science Books; 2000. [Google Scholar]
- 7.Richmond TJ, Davey CA. The structure of DNA in the nucleosome core. Nature. 2003;423:145–150. doi: 10.1038/nature01595. [DOI] [PubMed] [Google Scholar]
- 8.Minsky A. Information content and complexity in the high-order organization of DNA. Annu. Rev. Biophys. Biomol. Struct. 2004;33:317–342. doi: 10.1146/annurev.biophys.33.110502.133328. [DOI] [PubMed] [Google Scholar]
- 9.Sarai A, Kono H. Protein-DNA recognition patterns and predictions. Annu. Rev. Biophys. Biomol. Struct. 2005;34:379–398. doi: 10.1146/annurev.biophys.34.040204.144537. [DOI] [PubMed] [Google Scholar]
- 10.Kornyshev AA, Lee DJ, Leikin S, Wynveen A. Structure and interaction of biological helices. Rev. Mod. Phys. 2007;79:943–996. [Google Scholar]
- 11.Dai X, Rothman-Denes LB. DNA structure and transcription. Curr. Opin. Microbiol. 1999;2:126–130. doi: 10.1016/S1369-5274(99)80022-8. [DOI] [PubMed] [Google Scholar]
- 12.Griffith JD. DNA-structure – evidence from electron-microscopy. Science. 1978;201:525–527. doi: 10.1126/science.663672. [DOI] [PubMed] [Google Scholar]
- 13.Levitt M. How many base-pairs per turn does DNA have in solution and in chromatin – some theoretical calculations. Proc. Natl Acad. Sci. USA. 1978;75:640–644. doi: 10.1073/pnas.75.2.640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wang JC. Helical repeat of DNA in solution. Proc. Natl Acad. Sci. USA. 1979;76:200–203. doi: 10.1073/pnas.76.1.200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Rhodes D, Klug A. Helical periodicity of DNA determined by enzyme digestion. Nature (London) 1980;286:573–578. doi: 10.1038/286573a0. [DOI] [PubMed] [Google Scholar]
- 16.Zimmerman SB, Pheiffer BH. Helical parameters of DNA do not change when DNA fibers are wetted – X-ray diffraction study. Proc. Natl Acad. Sci. USA. 1979;76:2703–2707. doi: 10.1073/pnas.76.6.2703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sines CC, McFail-Isom L, Howerton SB, VanDerveer D, Williams LD. Cations mediate B-DNA conformational heterogeneity. J. Am. Chem. Soc. 2000;122:11048–11056. [Google Scholar]
- 18.Yanagi K, Prive GG, Dickerson RE. Analysis of local helix geometry in three B-DNA decamers and eight dodecamers. J. Mol. Biol. 1991;217:201–214. doi: 10.1016/0022-2836(91)90620-l. [DOI] [PubMed] [Google Scholar]
- 19.Subirana JA, Faria T. Influence of sequence on the conformation of the B-DNA helix. Biophys. J. 1997;73:333–338. doi: 10.1016/S0006-3495(97)78073-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Packer MJ, Dauncey MP, Hunter CA. Sequence-dependent DNA structure: Tetranucleotide conformational maps. J. Mol. Biol. 2000;295:85–103. doi: 10.1006/jmbi.1999.3237. [DOI] [PubMed] [Google Scholar]
- 21.Olson WK, Zhurkin VB. Modeling DNA deformations. Curr. Opin. Struct. Biol. 2000;10:286–297. doi: 10.1016/s0959-440x(00)00086-5. [DOI] [PubMed] [Google Scholar]
- 22.Gardiner EJ, Hunter CA, Packer MJ, Palmer DS, Willett P. Sequence-dependent DNA structure: A database of octamer structural parameters. J. Mol. Biol. 2003;332:1025–1035. doi: 10.1016/j.jmb.2003.08.006. [DOI] [PubMed] [Google Scholar]
- 23.Dixit SB, Beveridge DL, Case DA, Cheatham TE, Giudice E, Lankas F, Lavery R, Maddocks JH, Osman R, Sklenar H, et al. Molecular dynamics simulations of the 136 unique tetranucleotide sequences of DNA oligonucleotides. II: Sequence context effects on the dynamical structures of the 10 unique dinucleotide steps. Biophys. J. 2005;89:3721–3740. doi: 10.1529/biophysj.105.067397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Cooper VR, Thonhauser T, Puzder A, Schroder E, Lundqvist BI, Langreth DC. Stacking interactions and the twist of DNA. J. Am. Chem. Soc. 2008;130:1304–1308. doi: 10.1021/ja0761941. [DOI] [PubMed] [Google Scholar]
- 25.Hagerman PJ. Flexibility of DNA. Annu. Rev. Biophys. Biophys. Chem. 1988;17:265–286. doi: 10.1146/annurev.bb.17.060188.001405. [DOI] [PubMed] [Google Scholar]
- 26.Travers AA. The structural basis of DNA flexibility. Philos. Trans. R. Soc. London, Ser. A. 2004;362:1423–1438. doi: 10.1098/rsta.2004.1390. [DOI] [PubMed] [Google Scholar]
- 27.Schlick T. Modeling superhelical DNA - recent analytical and dynamic approaches. Curr. Opin. Struct. Biol. 1995;5:245–262. doi: 10.1016/0959-440x(95)80083-2. [DOI] [PubMed] [Google Scholar]
- 28.Crothers DM, Drak J, Kahn JD, Levene SD. DNA bending, flexibility, and helical repeat by cyclization kinetics. Meth. Enz. 1992;212:3–29. doi: 10.1016/0076-6879(92)12003-9. [DOI] [PubMed] [Google Scholar]
- 29.Kornyshev AA, Leikin S. Sequence recognition in the pairing of DNA duplexes. Phys. Rev. Lett. 2001;86:3666–3669. doi: 10.1103/PhysRevLett.86.3666. [DOI] [PubMed] [Google Scholar]
- 30.Cherstvy AG, Kornyshev AA, Leikin S. Torsional deformation of double helix in interaction and aggregation of DNA. J. Phys. Chem. B. 2004;108:6508–6518. doi: 10.1021/jp0380475. [DOI] [PubMed] [Google Scholar]
- 31.Lee DJ, Wynveen A, Kornyshev AA. DNA-DNA interaction beyond the ground state. Phys. Rev. E. 2004;70:051913. doi: 10.1103/PhysRevE.70.051913. [DOI] [PubMed] [Google Scholar]
- 32.Kabsch W, Sander C, Trifonov EN. The ten helical twist angles of B-DNA. Nucleic Acids Res. 1982;10:1097–1104. doi: 10.1093/nar/10.3.1097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Olson WK, Marky NL, Jernigan RL, Zhurkin VB. Influence of fluctuations on DNA curvature – a comparison of flexible and static wedge models of intrinsically bent DNA. J. Mol. Biol. 1993;232:530–551. doi: 10.1006/jmbi.1993.1409. [DOI] [PubMed] [Google Scholar]
- 34.Trifonov EN, Tan RK-Z, Harvey SC. Olson WK, Sarma MH, Sarma RH, Sundaralingam M. Structure and Expression Volume 3: DNA Bending and Curvature. Schenectady, NY: Adenine Press; 1987. Static persistence length of DNA; pp. 243–253. [Google Scholar]
- 35.Dickerson RE, Bansal M, Calladine CR, Diekmann S, Hunter WN, Kennard O, von Kitzing E, Lavery R, Nelson HCM, Olson WK, et al. Definitions and nomenclature of nucleic acid structure parameters. J. Mol. Biol. 1989;205:787–791. doi: 10.1016/0022-2836(89)90324-0. [DOI] [PubMed] [Google Scholar]
- 36.Olson WK, Bansal M, Burley SK, Dickerson RE, Gerstein M, Harvey SC, Heinemann U, Lu X-J, Neidle S, Shakked Z, et al. A standard reference frame for the description of nucleic acid base-pair geometry. J. Mol. Biol. 2001;313:229–237. doi: 10.1006/jmbi.2001.4987. [DOI] [PubMed] [Google Scholar]
- 37.Lu X-J, Babcock MS, Olson WK. Mathematical overview of nucleic acid analysis programs. J. Biomol. Struct. Dynam. 1999;16:833–843. doi: 10.1080/07391102.1999.10508296. [DOI] [PubMed] [Google Scholar]
- 38.Kornyshev AA, Lee DJ, Leikin S, Wynveen A, Zimmerman SB. Direct observation of azimuthal correlations between DNA in hydrated aggregates. Phys. Rev. Lett. 2005;95:#148102. doi: 10.1103/PhysRevLett.95.148102. [DOI] [PubMed] [Google Scholar]
- 39.Franklin RE, Gosling RG. Molecular configuration in sodium thymonucleate. Nature (London) 1953;171:740–741. doi: 10.1038/171740a0. [DOI] [PubMed] [Google Scholar]
- 40.Lu XJ, Olson WK. 3DNA: a software package for the analysis, rebuilding and visualization of three-dimensional nucleic acid structures. Nucleic Acids Res. 2003;31:5108–5121. doi: 10.1093/nar/gkg680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Dickerson RE. DNA bending: The prevalence of kinkiness and the virtues of normality. Nucleic Acids Res. 1998;26:1906–1926. doi: 10.1093/nar/26.8.1906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Lu XJ, Olson WK. Resolving the discrepancies among nucleic acid conformational analyses. J. Mol. Biol. 1999;285:1563–1575. doi: 10.1006/jmbi.1998.2390. [DOI] [PubMed] [Google Scholar]
- 43.Olson WK, Gorin AA, Lu XJ, Hock LM, Zhurkin VB. DNA sequence-dependent deformability deduced from protein-DNA crystal complexes. Proc. Natl Acad. Sci. USA. 1998;95:11163–11168. doi: 10.1073/pnas.95.19.11163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Vainshtein BK. Amsterdam: Elsevier; 1966. Diffraction of X-rays by Chain Molecules. [Google Scholar]
- 45.Calladine CR. Mechanics of sequence-dependent stacking of bases in B-DNA. J. Mol. Biol. 1982;161:343–352. doi: 10.1016/0022-2836(82)90157-7. [DOI] [PubMed] [Google Scholar]
- 46.Olson WK, Swigon D, Coleman BD. Implications of the dependence of the elastic properties of DNA on nucleotide sequence. Phil. Trans. R. Soc. Lond. A. 2004;362:1403–1422. doi: 10.1098/rsta.2004.1380. [DOI] [PubMed] [Google Scholar]
- 47.El Hassan MA, Calladine CR. Conformational characteristics of DNA: Empirical classifications and a hypothesis for the conformational behaviour of dinucleotide steps. Philos. Trans. R. Soc. London, Ser. A. 1997;355:43–100. [Google Scholar]
- 48.Zhurkin VB, Tolstorukov MY, Xu F, Colasanti AV, Olson WK. Sequence-dependent variability of B-DNA: an update on bending and curvature. In: Ohyama T, editor. DNA conformation and transcription. Chapter 2. Landes Bioscience. NY: Springer; 2005. [Google Scholar]
- 49.Kornyshev AA, Leikin S. Theory of interaction between helical molecules. J. Chem. Phys. 1997;107:3656–3674. [Google Scholar]
- 50.Kornyshev AA, Leikin SL. Electrostatic zipper motif for DNA aggregation. Phys. Rev. Lett. 1999;82:4138–4141. [Google Scholar]
- 51.Livolant F, Leforestier A. Condensed phases of DNA: Structures and phase transitions. Prog. Poly. Sci. 1996;21:1115–1164. [Google Scholar]
- 52.Harris AB, Kamien RD, Lubensky TC. Molecular chirality and chiral parameters. Rev. Mod. Phys. 1999;71:1745–1757. [Google Scholar]
- 53.Baldwin GS, Brooks NJ, Robson RE, Wynveen A, Goldar A, Leikin S, Seddon JM, Kornyshev AA. DNA double helices recognize mutual sequence homology in a protein free environment. J. Phys. Chem. B. 2008;112:1060–1064. doi: 10.1021/jp7112297. [DOI] [PubMed] [Google Scholar]
- 54.Weiner BM, Kleckner N. Chromosome pairing via multiple interstitial interactions before and during meiosis in yeast. Cell. 1994;77:977–991. doi: 10.1016/0092-8674(94)90438-3. [DOI] [PubMed] [Google Scholar]
- 55.Zickler D. From early homologue recognition to synaptonemal complex formation. Chromosoma. 2006;115:158–174. doi: 10.1007/s00412-006-0048-6. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.