Kinetics and thermodynamics of salt-dependent T7 gene 2.5 protein binding to single- and double-stranded DNA

Abstract

Bacteriophage T7 gene 2.5 protein (gp2.5) is a single-stranded DNA (ssDNA)-binding protein that has essential roles in DNA replication, recombination and repair. However, it differs from other ssDNA-binding proteins by its weaker binding to ssDNA and lack of cooperative ssDNA binding. By studying the rate-dependent DNA melting force in the presence of gp2.5 and its deletion mutant lacking 26 C-terminal residues, we probe the kinetics and thermodynamics of gp2.5 binding to ssDNA and double-stranded DNA (dsDNA). These force measurements allow us to determine the binding rate of both proteins to ssDNA, as well as their equilibrium association constants to dsDNA. The salt dependence of dsDNA binding parallels that of ssDNA binding. We attribute the four orders of magnitude salt-independent differences between ssDNA and dsDNA binding to nonelectrostatic interactions involved only in ssDNA binding, in contrast to T4 gene 32 protein, which achieves preferential ssDNA binding primarily through cooperative interactions. The results support a model in which dimerization interactions must be broken for DNA binding, and gp2.5 monomers search dsDNA by 1D diffusion to bind ssDNA. We also quantitatively compare the salt-dependent ssDNA- and dsDNA-binding properties of the T4 and T7 ssDNA-binding proteins for the first time.

INTRODUCTION

The bacteriophage T7 replication process requires the cooperation of four proteins that are involved in multiple protein–protein interactions within the phage replisome: DNA polymerase with its processivity factor thioredoxin, helicase/primase, and ssDNA-binding protein. These proteins associate with each other at the replication fork to form a highly efficient replication machine. Bacteriophage T7 gene 2.5 protein (gp2.5), encoded by gene 2.5 of the bacteriophage T7, is a ssDNA-binding protein (1) that binds to and stabilizes transiently formed regions of ssDNA. It physically interacts with both T7 DNA polymerase and with the T7 helicase/primase (2–6) and plays multiple roles in T7 DNA replication and recombination (5,7–16). Single-stranded DNA-binding proteins are identified from all three domains of life, as well as in viral genomes (17). Because of their important role in many processes involving DNA transactions, understanding the mechanism of DNA helix-destabilization by ssDNA-binding proteins is crucial.

gp2.5 forms a stable homodimer in solution (9). It has a core that is well adapted for interactions with ssDNA and a highly acidic C-terminal tail (CTT) that is required for dimer formation and for interactions with other proteins of the bacteriophage T7 replication system (18). A deletion mutant lacking the C-terminal 26 residues, gp2.5-Δ26C, binds ssDNA more tightly than does the full length protein (2,19).

In our previous work (19), we utilized DNA stretching to study the effect of wild-type gp2.5 and gp2.5-Δ26C on DNA duplex stability and melting. Both proteins were observed to lower the DNA melting force. The observed decrease in the DNA melting force indicates that the binding ligand destabilizes the DNA helix (20–23). To quantify this helix-destabilization, we previously determined the equilibrium DNA melting force in the presence of protein over very long times (∼20 min) (19). The equilibrium melting force was then used to determine equilibrium binding constants of these proteins to ssDNA as a function of salt concentration. We observed several orders of magnitude difference between the salt-dependent binding affinity of full length gp2.5 and its C-terminal deletion mutant in low salt. We developed a quantitative model in which a dimeric gp2.5 must dissociate to bind to ssDNA (19). According to our model, the dimer dissociation requires disruption of weak nonelectrostatic and strong electrostatic interactions. Recently, Marintcheva et al. (24) showed that the gp2.5 CTT competes for the same binding surface as ssDNA, consistent with the results from our single-molecule measurements.

There are two primary open questions concerning the mechanism of gp2.5 interactions with DNA. First, it is known from previous studies that gp2.5 binds ssDNA much more weakly than other ssDNA-binding proteins, yet it appears to serve a very similar function as an ssDNA-binding protein (SSB) during bacteriophage replication (19). Thus, given such weak ssDNA binding, it is not clear how gp2.5 is able to find and bind to ssDNA-binding sites at the replication fork to stabilize and protect ssDNA. Second, gp2.5 is believed to bind ssDNA noncooperatively or only with weak cooperativity (9). In contrast, T4 gp32 binds highly cooperatively, and its cooperative interactions account for three of its four orders of magnitude preferential binding to ssDNA. Thus, it is not clear how a noncooperatively binding SSB such as T7 gp2.5 can stabilize ssDNA relative to dsDNA at the replication fork upon binding.

To address these questions in the current study, we determine the association rate for gp2.5 and gp2.5-Δ26C binding to ssDNA, which we find to be enhanced by one-dimensional sliding of the protein on dsDNA prior to ssDNA binding. From this data, we also determine the equilibrium association constant of both proteins, gp2.5 and gp2.5-Δ26C, to dsDNA as a function of salt concentration for the first time. These results, along with the previously determined salt-dependent equilibrium binding affinity of gp2.5 to ssDNA as well as the salt-dependent equilibrium binding affinity of T4 gene 32 protein (gp32) and its C-terminal truncation mutant *I to both ssDNA and dsDNA, allow us to compare the DNA-binding properties of the SSB proteins from these two model replication systems. Our comparison of these two proteins allows us to address quantitatively for the first time how these ssDNA-binding proteins can both function properly as SSB proteins in their respective replication systems when their overall equilibrium ssDNA-binding affinities and the cooperative nature of their binding differ substantially. Our results show for the first time that T7 gp2.5 exhibits a three to four orders of magnitude preferential binding to ssDNA over dsDNA, and that this must be achieved by additional single-strand specific interactions. This preferential binding to ssDNA, accompanied by weak nonspecific electrostatic interactions that promote binding to dsDNA, allow T7 gp2.5 to search dsDNA in one dimension and stabilize ssDNA at the bacteriophage replication fork without significant cooperative binding.

MATERIALS AND METHODS

Protein preparation and purification

Wild-type gp2.5 and gp2.5-Δ26C were purified from BL21(DE3)pLysS cells overexpressing histidine-tagged version of their genes as previously described (25). Following the purification, the histidine tag was proteolytically cleaved using PreScission protease (GST-tagged, Amersham, Piscataway, NJ). The cleaved histidine tag and the protease were subsequently removed using nickel-NTA agarose (Qiagen, Valencia, CA) and GSTTrap™HP columns, respectively. The purified proteins were dialyzed against storage buffer (50 mM Tris–HCL, pH 7.5, 0.1 EDTA, 1 mM DTT, 50% glycerol) and stored at −20°C. The storage buffer for gp2.5-Δ26C contained additional 150 mM NaCl. For experiments requiring high concentrations of gp2.5, the protein solution was concentrated using an Amicon Ultra centrifugal filter device (Millipore, Billerica, MA) with 10 kDa cut off.

DNA stretching

The optical tweezers instrument used here was described previously (19). Briefly, an optical trap is formed by focusing two counter-propagating diode lasers, each with ∼200 mW of near-infrared laser power (JDS Uniphase, San Jose, CA) to a diameter of ∼1 μm using 60×, 1.0 numerical aperture water immersion microscope objectives (Nikon, Tokyo, Japan). The light leaving the trap is directed onto a lateral effect photodiode detector (UDT Sensors, Hawthorne, CA), which determines the deflection of each beam and outputs a voltage that is directly proportional to the force being exerted on the bead in the optical trap.

Two 5-μm streptavidin-coated polystyrene beads (Bangs Laboratories, Fishers, IN) were trapped in the optical tweezers and on the end of a glass micropipette (World Precision Instrument, Sarasota, FL). Captured Phage-λ DNA molecules, ∼48 500 base pairs (New England Biolabs, Ipswich, MA), were biotin-labeled on each 3′ terminus and were repurified by extraction with phenol and chloroform and ethanol precipitation. The glass micropipette mounted on a feedback-compensated piezoelectric stage (Melles Griot, Carlsbad, CA) was moved causing the single DNA molecule captured between two beads to be stretched, resulting in a force-extension measurement, as described previously (26).

To obtain measurements of DNA helix destabilization, the pipette was moved in different size steps of 5–250 nm/s at a rate of ∼1 step per second, and after each step, the force was measured 100 times and averaged, thus averaging out contributions of thermal motion to the force measurement.

RESULTS

DNA melting force: effects of the experimental pulling rate and protein concentration

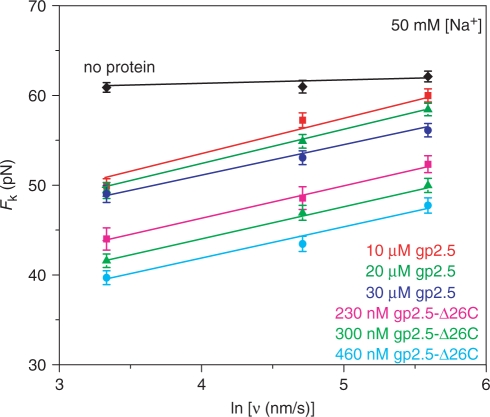
We used DNA stretching to probe the effect of gp2.5 and gp2.5-Δ26C on the DNA melting force as a function of pulling rate. Stretching curves for a single λ-DNA molecule in the absence or presence of gp2.5 and gp2.5-Δ26C are shown in Figure 1a and b, respectively. In both cases, the presence of the protein reduces the DNA melting force. However, to observe considerable reduction in the overstretching force, higher concentrations of gp2.5 compared to gp2.5-Δ26C are required. As the dsDNA molecule is pulled at different rates of v = 5–250 nm/s, the molecule extends to the B-form contour length and then begins to melt at the particular force F_k (v) (where the subscript k indicates that this kinetically determined force is likely to depend on pulling rate v) (27,28). In the absence of protein, the DNA melting force is independent of the pulling rate and shows very little hysteresis. However, in the presence of both gp2.5 and gp2.5-Δ26C, the melting force is significantly lowered and moreover depends on the pulling rate. The hysteresis observed in the release part of the stretching cycle clearly demonstrates the nonequilibrium nature of the DNA melting by gp2.5 and its C-terminal deletion mutant. The observed nonequilibrium DNA melting force is determined by the rate of protein binding to ssDNA during duplex melting. Therefore, this force is analog to dsDNA thermal melting studies and different from the equilibrium DNA melting force that was used in our previous studies (19). However, while in thermal melting studies, the DNA melting temperature varies linearly with the logarithm of the heating rate (29,30), in nonequilibrium DNA force-induced melting, the melting force varies linearly with the logarithm of the pulling rate [this work, Figure 2, and (27,28)].

Figure 1.

(a) Stretching (solid line)–relaxation (dashed line) curves in the absence of protein (black) at a pulling rate of 250 nm/s and in the presence of 30 μM gp2.5 at pulling rates of 250 nm/s (red), 100 nm/s (green), 25 nm/s (blue) and 5 nm/s (light blue) in 10 mM Hepes (pH 7.5), 50 mM Na⁺ (45 mM NaCl and 5 mM NaOH). (b) Stretching (solid line)–relaxation (dashed line) curves in the absence of protein (black) at a pulling rate of 250 nm/s and in the presence of 530 nM gp2.5-Δ26C at pulling rates of 250 nm/s (red), 100 nm/s (green), 25 nm/s (blue) and 5 nm/s (light blue) in 10 mM Hepes (pH 7.5), 100 mM Na⁺ (95 mM NaCl and 5 mM NaOH).

Figure 2.

Measured nonequilibrium DNA melting force, F_k (ν), as a function of pulling rate ν. Data are shown in the absence of protein (black diamond) and in the presence of 10 μM gp2.5 (red square), 20 μM gp2.5 (green triangle), 30 μM gp2.5 (blue circle), 230 nM gp2.5-Δ26C (pink square), 300 nM gp2.5-Δ26C (light green triangle) and 460 nM gp2.5-Δ26C (cyan circle). Linear fits are shown as continuous lines. Each data point is obtained by averaging three or more measurements, and error bars are determined from the standard error. Data is taken in 10 mM Hepes (pH 7.5) and 50 mM Na⁺ (45 mM NaCl and 5 mM NaOH).

At any given pulling rate v, the effect of gp2.5-Δ26C on F_k (v) is larger than the effect of gp2.5. The unwinding forces decrease as the amount of either protein increases, reflecting the faster protein association with ssDNA. Over the entire range of pulling rates, the nonequilibrium DNA melting force F_k (v) is always smaller than the equilibrium DNA melting force in the absence of protein, , and is larger than or equal to the equilibrium melting force in the presence of protein, , which was previously studied under the same solution conditions (19). Ideally, if we were able to stretch DNA slowly enough, the kinetically determined force of protein-supported strand separation F_k (v) should saturate at its equilibrium value, . However, in the presence of gp2.5 and gp2.5-Δ26C, even our slowest pulling rate of v = 5 nm/s was not slow enough to reach equilibrium, as evident from observed large residual hysteresis (Figure 1a and b). The hysteresis of DNA stretching in the presence of gp2.5 and gp2.5-Δ26C proteins is significantly smaller than that in the presence of bacteriophage T4 ssDNA-binding protein, gp32, and its CTD deletion mutant *I (27,28,31). For example, examination of Figure 1 shows that, at forces of 5–10 pN, the relaxation curve has a slope similar to that of dsDNA, and the DNA appears to almost completely reanneal. In contrast, at these forces, in the presence of T4 gp32, the DNA still very strongly resembles ssDNA (see Figure 2, Ref. 27). Therefore, gp2.5 dissociates from ssDNA faster than gp32.

Determining the gp2.5–ssDNA association rate from DNA stretching

We have used our experimental results to determine the association kinetics of gp2.5 and gp2.5-Δ26C binding to ssDNA. Pulling rate-dependent DNA melting occurs when the pulling rate is equal to the rate at which thermal fluctuations cause a certain number of base pairs to open, and these exposed regions of ssDNA are captured by protein binding (27,28). Based on this model, the pulling rate (v) can be expressed as follows:

1

where n_ss is the protein–ssDNA-binding site size in nucleotides and Δx is the increment in length per base pair of protein-bound ssDNA relative to dsDNA. Thus, n_ssΔx is the length released upon a single protein-binding event. N_b is the number of helix/coil boundaries in the DNA molecule. As long as the melting force is significantly lower than , such that there are no significant base pair opening fluctuations in the DNA molecule, ssDNA-binding protein-supported DNA melting occurs primarily from the ends of the molecule; so, N_b≈ 2 (A. Hanke, L. Shokri, I. Rouzina, and M. C. Williams, manuscript in preparation). The variable k_a is the rate of the single protein finding its contiguous binding site, which is created by the melting of n_ss base pairs at the boundary between the dsDNA and protein-covered ssDNA. The statistical weight s = e^ΔG/k_BT is the DNA base pair stability. Thus, the factor k_a/s^n_ss in Equation (1) is the rate at which the melting of n_ss base pairs occurs along with subsequent protein binding. Because we apply a force to the ends of the DNA molecule, the stability of each base pair becomes a function of the force. For our melting forces, which are always >20 pN, we can use the linear approximation ΔG = ΔG⁰ − FΔx (27). Here, ΔG⁰ is the extrapolated free energy of the DNA helix-coil transition per base pair in the absence of force and protein. By substituting the DNA base pair stability and the linear approximation of the DNA melting free energy into Equation (1), and solving for F_k (v), we obtain

2

where

3

In accord with our experiments, it follows from Equation (2) that as long as our stretching is slow enough, such that the ssDNA-binding protein has time to bind, i.e. when k_a > k_ν, the apparent DNA unwinding force is decreased, i.e., . As the pulling rate becomes faster, the protein has less time to affect the force-induced DNA melting, and the apparent unwinding force increases, until at k_ν ≅ k_a, it reaches the equilibrium DNA melting force in the absence of protein, i.e. .

We measured the DNA melting force F_k (v) as a function of v in the presence of variable concentrations of both proteins over a range of salt concentration of 5–50 mM Na⁺ for gp2.5 and 25–100 mM Na⁺ for gp2.5-Δ26C. Measured F_k (v) versus ln (v) dependencies in 50 mM Na⁺ in the absence and presence of both proteins are shown in Figure 2. In the absence of protein, the DNA melting force is practically independent of the pulling rate. In contrast, in the presence of both proteins, the observed linear dependence is consistent with the prediction of Equation (2). Because Δx, the extension per base pair, is known from the stretching curves, we could obtain the number of nucleotides of ssDNA that bind to the full length gp2.5 or its deletion mutant from the slope of our measured F_k (v) versus ln (v). We used the stretching curves for ssDNA in the presence of gp2.5-Δ26C in a buffer containing 5 mM Na⁺ to determine Δx, which is not expected to depend significantly on ionic strength (32). From the slopes of the lines shown in Figure 2, we found n_ss to be 7 ± 1 for gp2.5 and 6 ± 1 for gp2.5-Δ26C, which is in agreement with previous measurements of these quantities (9).

We determine k_a for each F_k (v) versus ln (v) data set by extrapolating this dependence to the point , which according to Equation (2) is expected to correspond to the condition k_ν ≅ k_a. These determinations of k_a are shown in Figure 3a and b. Here, k_a is a function of the protein concentration C, and exceeds the 3D diffusion limit for almost all conditions studied with gp2.5-Δ26C, given by k_diff = 4πDR = 2k_BT/3η ≈10⁹M⁻¹s⁻¹, where R is the protein size, estimated as 1 nm, D = k_BT/6πηR is the 3D diffusion coefficient and η is the solution viscosity (27,28). The 3D diffusion limit is not exceeded for gp2.5 under these conditions.

Figure 3.

(a) Protein association rate (k_a) as a function of protein concentration for gp2.5 in 5 mM salt (red diamond), 25 mM salt (green triangle) and 50 mM salt (blue circle). (b) Protein association rate (k_a) as a function of protein concentration for gp2.5-Δ26C in 25 mM salt (green triangle), 50 mM salt (blue circle) and 100 mM salt (brown square). Lines are fit to the data using Equation (5). Dashed lines show the three-dimensional (3D) diffusion limit as discussed in the text (48).

T4 and T7 ssDNA-binding proteins find new sites at the ds/ssDNA boundary by prebinding dsDNA and sliding on it to the new site

There are several possible models that could describe protein translocation along nucleic acids, such as intersegment transfer, hopping and sliding (33). Since in our experimental conditions the DNA molecule is straightened out by force and the protein-binding kinetics are fast (27), sliding is most likely the best model to explain the observed rate enhancement beyond that expected from diffusion in solution. Therefore, we assume that the proteins bind to dsDNA noncooperatively and weakly, such that they can slide on dsDNA (while they are still bound to dsDNA) until they can find a specific binding site between dsDNA and the protein-bound ssDNA newly created by thermal fluctuations. It has been shown (27,34,35) that under certain experimental conditions, ssDNA-binding proteins find their binding site generated by fluctuational opening of dsDNA to form ssDNA at the ds/ssDNA boundary under the action of force primarily via facilitated 1D motion along the dsDNA molecule, which means that most of the time proteins find their binding sites before dissociating from the dsDNA. If this is the case, the rate of binding to ssDNA is given by (27)

4

where k_s ∼ 10⁷ s⁻¹ is the conventional 1D sliding rate on dsDNA (36), n_ds is the protein-binding site size on dsDNA in nucleotides and Θ is the fraction of dsDNA bases bound by protein described by the McGhee and von Hippel isotherm (37):

5

Here, K_ds is the equilibrium association constant for protein binding to dsDNA.

After applying the above model to our data for gp2.5, fits of experimental k_a(C) to Equation (4) with Θ given by Equation (5) for gp2.5 for 5 mM < [Na⁺] < 50 mM and for gp2.5-Δ26C for 25 mM < [Na⁺] < 100 mM are shown in Figure 3a and b. The fitting parameters are the equilibrium binding constants to dsDNA (K_ds) and binding site size to dsDNA (n_ds), while k_s, which only weakly affects our fitting, is held constant. Our data for k_a versus C fits very well to the model represented by Equations (4 and 5), and therefore T7 gp2.5 binds ssDNA by first sliding on dsDNA, as was previously shown for T4 gp32 (27,28). A model in which proteins dissociate from dsDNA on average before binding to ssDNA, which would result in a linear dependence on protein concentration, does not fit our data well. We obtained a measurement of n_ds and K_ds as a function of salt concentration for the same solution conditions used previously to determine K_ss (19). As expected, n_ds did not vary significantly with salt concentration and from our fitting, we found n_ds = 5 ±1 for gp2.5 and n_ds = 7 ± 2 for gp2.5-Δ26C. These values for n_ds are very close to the values found above for n_ss. Although the 3D diffusion limit is not exceeded for g2.5, this model still fits the data well for that protein. This suggests that the 3D diffusion limit is in fact exceeded for gp2.5, but the concentration used to calculate this rate would need to be replaced by the effective concentration of monomers available for DNA binding, which is significantly reduced by the dimerization interaction described in our earlier work (19). Thus, if we assume that the effective concentration of gp2.5 is reduced by the probability of dimer dissociation, then the effective concentration of gp2.5 is reduced by a factor given by the ratio of K_ss for gp2.5 relative to that of gp2.5-Δ26C, which ranges from 10⁻³ to 10⁻² over the salt concentrations examined for both proteins. Therefore, the gp2.5 association rate exceeds the theoretical 3D diffusion limit at low salt concentrations.

The results of K_ds measurement for gp2.5 as a function of salt concentration are shown in Figure 4a along with the K_ss data for gp2.5 from our previous work (19). Presented in the same panels are the analogous data for the T4 gp32 protein obtained previously with the same approach (27,28,31,38). The Discussion section below will compare these two representative bacteriophage ssDNA-binding proteins. gp2.5-Δ26C shows stronger and more salt-dependent binding to both ssDNA and dsDNA (compare data points shown by the blue squares in Figure 4a and b) relative to that of gp2.5. Based on these and other (19,24,39) data, we conclude that these differences between gp2.5 and gp2.5-Δ26C are due to the fact that the DNA-binding site of gp2.5 is normally occluded by the CTT of its dimer partner when in solution, and the CTT must dissociate prior to DNA binding, as previously shown (19).

Figure 4.

The measured dependence of logarithm of the equilibrium association constants of SSB proteins to ssDNA (K_ss) and dsDNA (K_ds) as a function of logarithm of salt concentration. (a) Equilibrium association constants to ssDNA (solid symbols) and dsDNA (open symbols) for T7 gp2.5 (squares) and T4 gp32 (circles). (b) Equilibrium association constants to ssDNA (solid symbols) and dsDNA (open symbols) for T7 gp2.5 gp2.5-Δ26C (squares) and T4 gp32 C-terminal truncation mutant *I (circles). The linear fits to the data are shown for both proteins as continuous (ssDNA binding) and dashed (dsDNA binding) lines. The error in measurements is shown for all cases. ssDNA-binding results for gp2.5 are taken from Ref. (19), while results for T4 gp32 are taken from Ref. (28).

DISCUSSION

Comparing gp2.5 and gp2.5-Δ26C binding to dsDNA and ssDNA

Our current results suggest that gp2.5 and gp2.5-Δ26C bind both dsDNA and ssDNA via the same cationic binding site. Indeed, the modeled ssDNA-binding cleft of gp2.5 is large enough to accommodate a dsDNA molecule. More importantly, the salt dependence of gp2.5 binding to both forms of DNA is very similar, and the same is true for gp2.5-Δ26C. In addition, the similar ∼10⁴ difference between gp2.5 and gp2.5-Δ26C binding to ssDNA relative to dsDNA suggests that the same CTT conformational change regulates binding of these proteins to both DNA forms. gp2.5 binds DNA via an OB-fold (oligosaccharide/oligonucleotide binding fold) that is an universal structural element of all ssDNA-binding proteins regardless of the system of origin (39). The OB-fold contains a β-barrel with a distinct cleft lined with cationic residues and several aromatic side chains. Cationic residues provide the electrostatic component, which is apparently rather similar for dsDNA and ssDNA binding. Thus, the CTT deletion mutant gp2.5-Δ26C binds both DNA forms, releasing on average ∼2 Na⁺ cations into solution (i.e. the log–log slope of K versus Na⁺ is ∼−2) (40,41). In contrast, wild-type gp2.5 binds both dsDNA and ssDNA with a negligible slope, implying that about as many Na⁺ cations are associated with the CTT upon its unfolding into solution, such that there is no net ion uptake upon protein–DNA association. The salt-independent difference between the dsDNA and ssDNA binding then likely comes from stacking or other nonelectrostatic interactions of the aromatic residues within the inner surface of the OB-site with unpaired DNA bases. The free energy of this interaction can be estimated as Δ G_{destabilization} = k_B Tln (K_ss /K_ds) = k_B Tln (10⁴) = 9.2 k_B T = 5.5 kcal/mol. It is likely that the preferential interactions described by this free energy ensure the duplex-destabilizing ability of gp2.5 and make it an efficient ssDNA-binding protein.

Determining free energy of gp2.5 dimer dissociation from gp2.5 and gp2.5-Δ26C binding constants

The importance and generality of this ‘electrostatic shielding mechanism’ was discussed in the recent study (24). However, in contrast to gp32, the gp2.5 protein forms homodimers in solution (5), while it binds DNA as a monomer. Moreover, it is known that the CTT deletion mutant does not dimerize (39). These observations reflect the current well-supported model that the CTT of gp2.5 binds not to its own DNA-binding site, but rather to the site of its partner, thereby stabilizing the homodimer. We can use our gp2.5 and gp2.5-Δ26C dsDNA- and ssDNA-binding data to estimate the maximum free energy of this protein dimerization, assuming that the DNA binding of the two dimerized gp2.5 proteins differs from that of the two gp2.5-Δ26C proteins by the probability of the thermal dissociation of the gp2.5 dimer, P_dimer = e^{(− Δ G_dimer /k_BT)} − (e^{− Δ G_dimer / k_BT} + 1), i.e.

6

Here ΔG_dimer is the dimer dissociation free energy, which can be expressed as

7

Presented in Figure 5 is the dimerization free energy per gp2.5 monomer protein, Δ G_dimer /2, as a function of solution ionic strength estimated from our dsDNA-binding data obtained in this work, as well as from the data for ssDNA binding from our previous work on gp2.5 (19). Both estimates are in good agreement. As expected, the dimerization free energy is salt dependent. This implies that the electrostatic interaction of the anionic CTT with the DNA cationic-binding site of the protein partner contributes significantly to dimerization.

Figure 5.

The measured free energy of dimer dissociation (gp2.5) or C-terminus dissociation (gp32) as a function of logarithm of salt concentration. Equilibrium association constants of gp2.5 and gp2.5-Δ26C to dsDNA (K_ds, blue open squares and dashed line) and ssDNA (K_ss, blue filled squares and solid line) in 25 and 50 mM Na⁺ buffer were used to determine the values of Δ G_dimer^{ss, ds} directly by using Equation (7), and the interaction per protein, Δ G_dimer^{ss, ds} /2, is shown here. ssDNA results were obtained from Ref. (19). The blue lines are to guide the eye. Note that for the values measured here, Δ G_dimer from Equation (7) of Ref. (19) is equivalent to Δ G_dimer^{ss, ds} /2 from Equation (7) in this work. The analogous calculation was repeated for T4 gp32 C-terminal domain binding to the protein core domain, based on measured T4 gp32 interactions with dsDNA (red open circles and dashed line) and T4 gp32 interactions with ssDNA (red filled circles and solid line), calculated using previously obtained equilibrium binding constants (28). The red lines are fits to the data.

Comparing the properties of T7 gp2.5 and T4 gp32

The current work further develops an approach first introduced in a series of previous single-molecule DNA stretching studies for characterizing the thermodynamics and kinetics of ssDNA-binding protein interactions with DNA (27,28,31,38). The two complementary approaches allowed us to independently determine the binding constants, and the ssDNA- and dsDNA-binding site sizes of T4 gp32. The ssDNA-binding characteristics K_ss and n_ss were obtained from measurement of the equilibrium DNA melting force as a function of protein concentration (28). The dsDNA-binding parameters of gp32 were obtained from the measurements of the unwinding force dependence on the DNA pulling rate (27,28,31). Such measurements yield the rate of this protein finding its new binding site on ssDNA at the boundary with dsDNA. The binding site appears as a melting thermal fluctuation that is enhanced by the applied force. We have shown that this rate is determined by sliding to this new site of the protein prebound to dsDNA. Fitting the dependence of this protein's association rate on its concentration allows for the determination of K_ds and n_ds. In previous work on gp2.5 (19), we have applied the method of equilibrium force measurement to characterize this protein's binding to ssDNA. Here, we use the complementary approach of measuring the DNA unwinding force as a function of pulling rate to determine the gp2.5 ssDNA association rate, and subsequently its dsDNA-binding characteristics. In this section, we will compare the two ssDNA-binding proteins gp32 and gp2.5 studied so far by this single-molecule approach.

The binding constants for gp2.5 [this work and Ref. (19)] and gp32 (27,28,31,38), as well as of their CTT deletion mutants gp2.5-Δ26C and *I to ssDNA and dsDNA, are compared in Figure 4a and b. Similar to that expected for gp2.5, gp32 has a highly acidic unstructured CTT that is folded into this protein's cationic OB-site in the DNA-unbound state of gp32 (27,28,31,42–44). The CTT must unfold upon gp32–DNA binding. Consequently, as illustrated by Figure 4, the general features of the gp32 and gp2.5 DNA-binding data are very similar: stronger and more salt-dependent binding of the CTT truncation mutant, and the salt-independent difference between the dsDNA and ssDNA binding for each protein. Moreover, this salt-independent ∼10⁴-fold difference between ssDNA and dsDNA binding for gp32 and *I is similar to that observed for gp2.5 and gp2.5-Δ26C binding. Taking into account the similar ssDNA-binding site size (∼7 nt) for both gp2.5 [this work and Refs. (9,19)] and gp32 (27,28,43–46), we conclude that both destabilize every DNA base pair to a very similar extent, i.e. maximum destabilization per base pair is Δ G_{destabilization} × 2/7 ≈ 1.7 kcal/mol. The latter quantity is close to the average DNA base pair stability under physiological conditions of ∼2 kcal/mol (47,48), indicating that both gp2.5 and gp32 should be able to melt a significant fraction of dsDNA, given enough time. Another important similarity between T7 gp2.5 and T4 gp32 as characterized by our studies [this work and (27)] is the analogous kinetic mechanism of their ssDNA binding, which is enhanced by prebinding to dsDNA and 1D diffusion. This may therefore represent a common theme for many ssDNA-binding proteins, in which they bind nonspecifically and electrostatically to both ssDNA and dsDNA, but have an additional preference for ssDNA due to the other more specific interactions, as discussed above for gp2.5.

However, the data in Figure 4 also illustrate several differences between gp2.5 and gp32. First, the latter protein's C-terminal truncation mutant, *I, exhibits a slightly stronger salt dependence (average log–log slope of K_ss and K_ds versus Na⁺ is ∼−3.0 ± 0.3) compared to gp2.5-Δ26C (−2.0 ± 0.5 slope). This result implies a slightly higher cationic charge of the DNA-binding site of gp32 compared to gp2.5, as well as a higher anionic charge on its CTT. This effective charge of the OB-site of the protein and its CTT most likely does not include all the physical charges of these protein regions, but only the ones with high surface charge density that release or bind strongly associated ions upon protein–DNA interaction, as discussed previously in relation to gp32 (38).

This stronger electrostatic contribution to protein–DNA binding might well be responsible for the 10- to 100-fold stronger equilibrium DNA-binding constant of gp32, as compared to gp2.5, as this effect becomes very important as the salt concentration is lowered (Figure 4). In turn, this stronger binding of gp32 and *I to ssDNA is, most likely, responsible for the slower dissociation of these proteins from ssDNA, as indicated by much stronger hysteresis upon DNA relaxation after its force-induced melting in the presence of gp32 and *I (compared to gp2.5 and gp2.5-Δ26C) in our experiments. Our studies of the kinetics of ssDNA-binding protein dissociation from ssDNA will be discussed elsewhere. Here, we only note that it is possible that the kinetic differences between these ssDNA-binding proteins are primarily responsible for their inability to substitute for each other in in vivo (8) and in in vitro (5) DNA replication processes.

The other important difference between gp2.5 and gp32 is that the former binds ssDNA practically noncooperatively (9), while the latter binds ssDNA with a cooperativity factor of ∼1000 (43,44,46). Therefore, the 10⁴-fold preference for ssDNA in the case of gp2.5 is primarily the result of stacking or other nonelectrostatic interactions with DNA unpaired bases. At the same time, in the case of gp32, the same difference is a combination a ∼10-fold preference for ssDNA (weak stacking with the ssDNA bases), and its ∼1000-fold preference for ssDNA binding next to an already bound protein, which is absent for dsDNA binding. The latter fact restricts the protein unbinding from ssDNA to the boundary of the ssDNA–protein filament, thereby further slowing down the protein–ssDNA dissociation rate. The faster gp2.5 dissociation from ssDNA is probably the reason that this protein is the most efficient among other ssDNA-binding proteins at mediating DNA homologous base pairing (9,12) and strand annealing (12).

Finally, the most obvious difference between gp2.5 and gp32 is that the CTT-OB fold binding interaction in the former protein occurs not within the same protein, but rather with another gp2.5 monomer, thereby promoting its dimer formation in the DNA-unbound state. Based on our data presented in Figure 5, the free energy of CTT opening for gp32 is more salt dependent and, at physiological salt concentration (Na⁺ > ∼100 mM), weaker when compared to the dimerization free energy per gp2.5 monomer. When extrapolated to higher salt, the CTT opening free energy for gp32 vanishes at a much lower salt concentration (200 mM Na⁺) relative to gp2.5, which vanishes above 1 M Na⁺. This result further explains the weaker ssDNA binding of the wild-type gp2.5 compared to gp32 under physiological conditions. It also implies that gp2.5 interactions with other proteins of the T7 replication machinery, such as the DNA polymerase or primase-helicase (4), which bind to and unfold the CTT of this protein, will have a stronger regulatory effect on gp2.5 interactions relative to the effect of similar interactions with gp32 in the T4 replication system.

CONCLUSIONS

We have identified several similarities as well as several key differences in the behavior of the two bacteriophage ssDNA-binding proteins T7 gp2.5 and T4 gp32. The most important similarity between the proteins is the fact that both proteins bind weakly to dsDNA and search along the DNA to rapidly find ssDNA-binding sites. The ability to perform this search relies on the existence of two distinct binding modes, an electrostatic binding mode to dsDNA as well as a much stronger binding mode to ssDNA that consists of both electrostatic and other nonelectrostatic interactions. Interestingly, the preference for ssDNA-binding over dsDNA-binding for both gp2.5 and gp32 proteins is the same ∼10⁴, although, as discussed above, it comes from different interactions. Consequently, these two ssDNA-binding proteins destabilize the DNA duplex to the same extent. In addition, in both cases, the two binding modes are regulated by an acidic C-terminus that is known to interact with other replication proteins in their respective bacteriophage replication system. In contrast to such similar biophysical behavior, we also find that the equilibrium association constant for gp2.5 binding to both dsDNA and ssDNA is one to two orders of magnitude lower than that of T4 gp32. The same is true of the respective C-terminal deletion mutants of these proteins. Since this binding difference is salt dependent, it is primarily the higher effective charge of gp32's DNA-binding site, as determined from the salt dependence of its DNA binding, that is responsible for its stronger DNA binding in physiological salt conditions (Figure 4). The main consequence of the stronger gp32 binding is its slower dissociation from ssDNA, apparent in our DNA relaxation experiments. We expect that rapid gp2.5 dissociation from ssDNA is the main feature of this protein that distinguishes it from other ssDNA-binding proteins in in vivo functioning.

In contrast to the bacteriophage ssDNA-binding proteins discussed above, E. coli SSB, which is often compared to gp2.5 and gp32, binds ssDNA in a completely different manner (49–60). While it also has an OB-fold ssDNA-binding site (55), and an unstructured CTT able to regulate its ssDNA binding (51), E. coli SSB binds as a dimer or a tetramer, winding the ssDNA on itself (49,52,58). The binding site size and the binding constant of E. coli SSB to ssDNA are much larger than those for gp2.5 and gp32 under the conditions discussed here, and its binding kinetics are very different (49,52). This comparison illustrates the diversity of ssDNA-binding protein characteristics, and suggests that another single-molecule DNA stretching approach should be devised in this case to complement the existing solution studies.

While it is possible that T4 and T7 could be competing for DNA binding in the same infected E. coli cell, this is not likely a typical situation. However, it is still important to be able to compare T4 gp32 and T7 gp2.5 to understand how each protein in its respective biological system can facilitate phage replication. In particular, how can two replication systems with ssDNA-binding proteins whose equilibrium binding to ssDNA differs by two orders of magnitude achieve the same function? We have shown here that, while the overall ssDNA binding may be weaker, the preferential binding to ssDNA over dsDNA is the same in both cases, and this is therefore likely a critical property for facilitating phage replication.

FUNDING

National Institutes of Health (GM 72462 to M.C.W., ST32A107245-20 to B.M., F32GM72305T to B.M., GM068855-03S1 to A.H.); National Science Foundation (MCB-0744456 to M.C.W.). Funding for open access charge: NSF MCB-0744456.

Conflict of interest statement. None declared.