A two-stage neural spiking model of visual contrast detection in perimetry

Abstract

Perimetry is a commonly used clinical test for visual function, limited by high variability. The sources of this variability need to be better understood. In this paper, we investigate whether noise intrinsic to neural firing could explain the variability in normal subjects. We present the most physiologically accurate model to date for stimulus detection in perimetry combining knowledge of the physiology of components of the visual system with signal detection theory, and show that it requires that detection be mediated by multiple cortical cells in order to give predictions consistent with psychometric functions measured in human observers.

Introduction

Perimetry (functional testing of contrast detection in the human visual field) is an important tool in clinical practice, both for detecting and following certain diseases such as glaucoma. In recent years, great advances have been made in the neurophysiology literature in understanding components of the mechanisms involved in visual detection tasks. However, application of these advances requires combining these constituent parts and utilizing signal detection theory. In this paper we construct a model of perimetric response based on the known physiology of the early stages of the visual system, aiming to predict not only the sensitivity of the system but also the intrinsic variability as seen in the psychometric function.

The most commonly-used testing paradigm, standard automated static perimetry (Anderson & Patella, 1999), measures the contrast sensitivity to a briefly presented circular luminance increment stimulus presented at different field locations within 30° of fixation. The standard form of perimetry we model uses a detection task with a 0.43° diameter white stimulus presented for 200ms upon a 10cd/m² white background, as used in the Humphrey Field Analyzer (Carl Zeiss Meditec Inc, Dublin, CA, USA). The output gives the contrast sensitivities at each tested location, using an adaptive psychophysical procedure designed to estimate the 50% correct point on the psychometric function. The utility of conventional perimetry is limited by its high intra-test and inter-test variability (Henson, Chaudry, Artes, Faragher & Ansons, 2000), which increases with the amount of damage in glaucoma and other conditions, resulting in 95% confidence limits for test-retest that can cover more than half of an instrument's dynamic range (Chauhan & House, 1991). The sources of this variability, both intrinsic and extrinsic to the visual system, are not fully understood.

There is a long history of physiologically accurate modeling in the visual neurophysiology literature (Heeger & Simoncelli, 1991, Itti & Koch, 2001). However, modeling work in the clinical vision literature to date has largely concentrated on producing numerically realistic simulations of patient data. Typically these studies have focused on estimating the contrast sensitivity, with less emphasis on the magnitude or causes of variability in that measure. Most authors have simply sampled from a Gaussian distribution to generate variability (Gardiner & Crabb, 2002, Spry, Bates, Johnson & Chauhan, 2000, Vesti, Spry, Chauhan & Johnson, 2002), using a standard deviation taken from patient data (Henson et al., 2000); or other purely empirical methods (Harwerth, Carter-Dawson, Smith, Barnes, Holt & Crawford, 2004). Although these studies have produced useful results, they may have little theoretical basis (Anderson, 2006). More recently, models have started to incorporate aspects of the physiology. Gardiner et al suggested that dysfunctional retinal ganglion cells (RGCs) could cause the observed increase in variability with damage in glaucoma (Gardiner, Demirel & Johnson, 2006), but their model was based on detection being principally mediated by RGCs rather than in the visual cortex. Swanson et al produced a two-stage neural model incorporating cortical filtering of RGC signals (Swanson, Felius & Pan, 2004), but their model assumed the existence of intrinsic variability of the neural system without simulating its sources (Pan, Swanson & Dul, 2006).

This study aimed to develop a model of the visual system response to standard perimetric stimuli that enables the prediction of both contrast sensitivity and the intrinsic variability of the system. The model described is based on known neurophysiology of the normal visual system up to and including cortical area V1, and we compare the model output with psychophysical data collected from normal human observers. The model presented here aims to make it possible to examine the effect of individual components of the visual system on contrast sensitivity and its variability, and subsequently to identify those components whose properties may be changed in a diseased eye.

Methods

The study conformed to the tenets of the Declaration of Helsinki. All subjects gave informed consent prior to participation. Ethical approval was obtained from the Victorian College of Optometry / Department of Vision Sciences Human Research Ethics Committee at the University of Melbourne before the start of testing.

Model Description

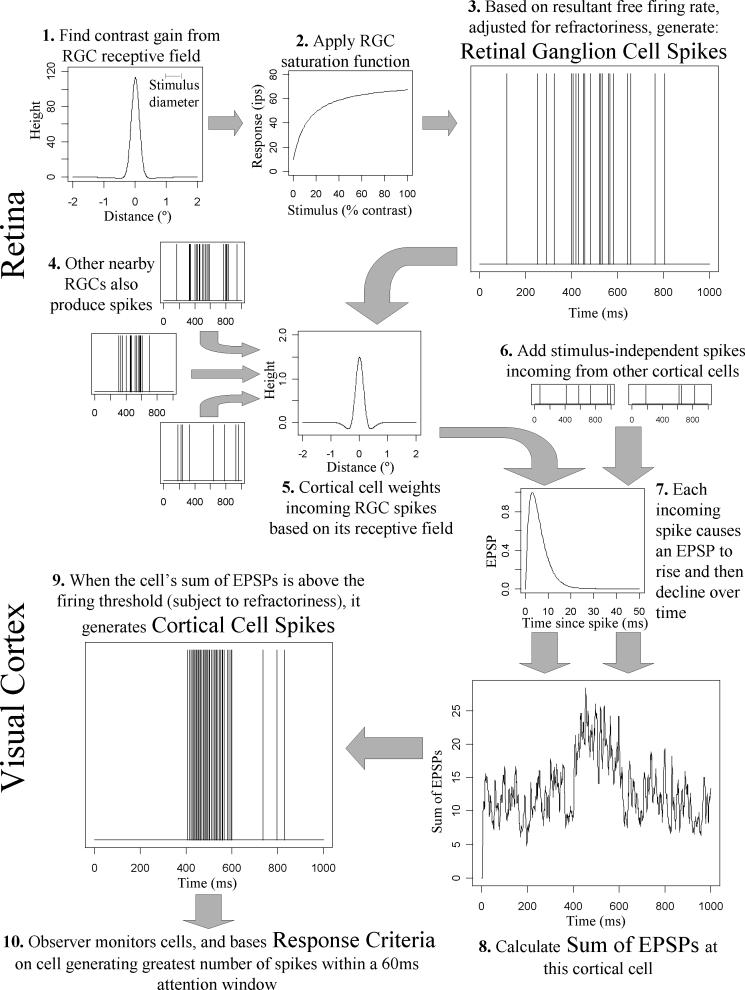
We model the propagation of a signal from the retina through the visual cortex, resulting in the observer attending to a single decision variable based on firing rates across a population of cortical simple cells. The steps in the model are outlined in Figure 1. Parameter values were taken from the literature wherever possible, using values estimated for magnocellular detection mechanisms at four non-foveal locations (±9°, ±9°), these being the first four visual field locations tested by the Humphrey perimeter in a clinical situation. Where significant contrast nonlinearity exists in the system, parameters were chosen to model behavior at / near the detection threshold, since these are the stimulus intensities that are of interest for constructing the psychometric function.

Figure 1.

An outline of the model, showing sequentially the steps used to determine whether the observer responds to the stimulus. Graphs at each stage were generated from a randomly-chosen run using a 100% contrast supra-threshold stimulus. The receptive field of the cortical cell shown was centered on an RGC positioned directly under the center of the stimulus. Therefore a large response is seen between 400−600ms, the period during which the modeled stimulus was presented.

RGCs take input from photoreceptor cells via associated retinal circuitry, and output neural spikes. The receptive field of each RGC was modeled as a 2-dimensional circularly symmetric difference-of-Gaussians (Step 1 in Figure 1). The contribution to the RGC input from a unit Weber contrast stimulus at a location in the retina distance x from the center of the RGC was given by G_cΦ_c(x) + G_sΦ_s(x), where Φ_a gives the probability density of a normal distribution of mean 0 and standard deviation σ_a. Weber contrast is given by C = (L_max - L_mean) / L_mean. The center of the RGC receptive field had height G_c=115.0 and standard deviation σ_c=0.18°; and the surround had G_s=−2.0 and σ_s=1.19° (Croner & Kaplan, 1995). The contrast gain of the RGC, in units of impulses per second per percent contrast, was found by integrating this receptive field over the area covered by the stimulus. In Step 2, the free firing rate of the RGC was determined by applying a Michaelis-Menton function; Rate = Base + Max*x / (Max/Gain + x) (Kaplan & Shapley, 1986). Here, x represents the stimulus luminance in units of percent contrast; Gain represents the calculated contrast gain given the relative positions of the stimulus and the RGC; Max represents the asymptotic maximum driven firing rate of 65 impulses per second (ips); and Base represents the free firing rate in the absence of a stimulus and is set to 10 ips (Carandini, Demb, Mante, Tolhurst, Dan, Olshausen, Gallant & Rust, 2005, Kaplan & Shapley, 1986).

To model RGC spiking (Step 3 in Figure 1), time was split into discretized bins of 0.5ms, with a probability of the cell firing within that time period given by the stimulus-dependent firing rate (in impulses per 0.5ms), adjusted for refractoriness by multiplying by a weighting function (Uzzell & Chichilnisky, 2004):

$$w\left(t\right)=\frac{{\lfloor t-t_{abs}\rfloor }^p}{{\lfloor t-t_{abs}\rfloor }^p+{t_{rel}}^p}$$

Here, exponent p=4 (Uzzell & Chichilnisky, 2004), the absolute refractory period t_abs=1.5ms (Berry II & Meister, 1998), and the time constant for the relative refractory period t_rel=2ms. Therefore, the probability of a spike being generated is zero during the first t_abs since the previous spike, and is reduced below the free firing rate subsequently while the cell recovers. Using Monte-Carlo random number generation, a spike train output from the RGC was generated. This process was repeated for each RGC (Step 4, Figure 1), with their positions relative to the stimulus determined by a hexagonal grid (for repeatability and simplicity the grid was regular and centered so that one RGC was directly under the center of the stimulus; results are given in the robustness checks when adding in random small fixation movements on each stimulus presentation, or adding randomly sampled ‘jitter’ to the positions of the RGCs instead of having a regular array).

These retinal-originating signals are relayed by the lateral geniculate nucleus (LGN) to the visual cortex. It is thought that nonlinear contrast gain control may occur at the LGN (Kaplan, Purpura & Shapley, 1987, Kozyrev, Silveira & Kremers, 2007), although this is disputed (Lee, Virsu & Creutzfeldt, 1983). At present there is no universally accepted mathematical model of any nonlinearity at this location. Since its consequences may be smaller near the detection threshold than at supra-threshold intensities, the simplifying assumption of lossless linear transmission was made.

The visual cortex was modeled in terms of responses of simple cells in the primary visual cortex (V1), simplified as an array of cortical cells with identical receptive field shapes and differing only in the visual field location from which they receive information. This is similar to a cortical filter in spatial vision models, where each filter element has the same form but a different location (Pan & Swanson, 2006). Each cortical cell receives input from a number of RGCs (Step 5, Figure 1), as well as from other cortical cells. For simplicity and repeatability there was one cortical cell “centered” directly over each RGC. The cortical cell received neural spikes from both the thalamic relay of RGC spikes via the LGN, and from random firing of 5.6ips from each of 250 other cortical cells (McAdams & Reid, 2005). These cortical-originating spikes were assumed to be independent of the stimulus and therefore independent of the input from retinal-originating spikes (Step 6, Figure 1). The total number of cortical-originating spikes within any given 0.5ms time interval was therefore modeled as a Poisson process with mean 0.7; the individual firing rate of each of these 250 cells is sufficiently low that the effect of refractoriness can be ignored when summing over them.

Incoming neural spikes were modeled in terms of excitatory postsynaptic potentials (EPSPs) in cortical cells. The EPSP at time t from a spike incoming at time t₀ was given by EPSP(t)=w.f(t-t₀).e^1-f(t-t0), where f(t)=t/t_rise, with t measured in seconds, and an EPSP rise time of 2.9ms (Veredas, Vico & Alonso, 2005) (Step 7, Figure 1). In this formulation, w represents a spatial weighting function. Each cortical cell was modeled as having a two-dimensional receptive field; when a spike arrives from a given RGC, w was calculated based on the spatial position of that RGC within the receptive field of the cortical cell. Physiologically, cortical cells are tuned to different orientations and spatial frequencies. However, for circularly symmetric stimuli as most often used in perimetry, previous modeling has found relatively little difference between results for oriented and non-oriented cortical cell receptive fields (Pan & Swanson, 2006, Swanson et al., 2004). Using non-oriented filters instead of a range of oriented filters reduces the dimensionality of the parameter space, and so vastly reduces the amount of computation required and eases interpretation of the results. Therefore, the cortical receptive field was modeled as a two-dimensional difference-of-Gaussians function (as seen in Step 5 in Figure 1), where the center had height 2 and space constant 0.25*0.83252/SF, and the surround had height −0.5 and space constant 0.5*0.83252/SF (Swanson et al., 2004); the spatial frequency SF was set at 0.5 cycles per degree defining the spatial extent of the receptive field. The cortical cell thus operates as a circularly symmetric spatial filter with no DC component, with the surround having sensitivity one quarter of the center, and space constant twice as large (so that the center and surround responses to a uniform field are of equal magnitude and opposite sign).

The effect of linear LGN contrast gain can be convolved with the multiplicative effect on the signal of parallel thalamic pathways (Feldmeyer, Lubke, Silver & Sakmann, 2002), and also with differences between the weightings given in the visual cortex to signals from the LGN and spikes originating elsewhere in the cortex. Here, cortical-originating spikes incoming to the cell were assigned a weighting of w=1, while the height of the cortical receptive field center was w=2. This 2:1 ratio shall be referred to in this paper as the retino:cortico-EPSP ratio. At Step 8 (Figure 1), all EPSPs at a given cell are added together.

When the sum of the EPSPs of a given cortical cell was higher than that cell's firing threshold, a cortical spike was produced (Step 9, Figure 1). The firing threshold had a fixed value (the free firing threshold) when there had been no spikes recently, and was elevated following a spike using the same refractoriness properties as for the RGCs described above. The free firing threshold was found by a binary search based on 10 seconds of simulated stimulus-free firing, and was set to give an average of 5.6ips during that time (McAdams & Reid, 2005). This meant that each cortical cell had a slightly different free firing threshold due to the random nature of the incoming EPSPs.

Signal detection theory was used to derive contrast threshold and intrinsic variability. The ‘observer’ attends to many filter elements, each corresponding to the spike train output from one or more cortical cells (Step 10 in Figure 1). If any filter element produces a spike count (within any 60msec window) greater than a criterion number of spikes, the observer was assumed to ‘respond’ to the stimulus. This window width was chosen because temporal summation of perimetric stimuli begins to decline after 0.06 seconds (Anderson & Patella, 1999). The decision variable is therefore the maximum 60msec spike count output by any of the filter elements; this formulation introduces spatial and temporal uncertainty to the model (Pelli, 1985). A similar decision variable has been used for analysis of spike trains from macaque midget ganglion cells (Swanson, Pan & Lee, 2008). For each stimulus presentation, the model generated cortical spikes over a 1000 msec period; the stimulus was ‘on’ between 400 and 600msec, giving a stimulus duration of 200msec. This 1000 msec period was chosen to approximately match the average response window allowed by a perimeter, whereas shorter intervals (500 msec) were used in the 2-alternative forced choice (2AFC) data we gathered from human observers. For modeling purposes it was assumed that the observer made no stimulus-independent response errors, i.e. the false positive and false negative rates were set to zero.

For improved computing speed, we fully modeled the observer attending to ‘near-stimulus’ channels covering a 3°×3° hexagonal grid centered on the stimulus; and in the rest of the retina we modeled channel elements as randomly firing cortical cells at an average rate of 5.6ips (adjusted for refractoriness as before), since these latter cells will not be significantly affected by the stimulus. The number of RGCs in the retina varies twofold between normal eyes, with an average of 1,500,000, of which approximately 10% are magnocellular (Lee, 1996, Perry, Oehler & Cowey, 1984). The average magnocellular RGC center-to-center spacing at location (±9°, ±9°) in humans has been reported to be near 0.16° (Sjöstrand, Olssona, Popovica & Conradi, 1999), corresponding to a 19×19 grid of ‘near-stimulus’ channels. Since the primary calculations have one cortical cell centered over each magnocellular RGC, the observer monitors signals from a total of 150,000 cortical cells.

When modeling a psychometric function, the first stage was to determine the free firing thresholds for each cortical cell as detailed above (this was determined for each psychometric function modeled). The decision variable was then used to derive simulated responses over 1000 stimulus-free runs, and a cumulative distribution function of the response variable in the absence of a stimulus was generated. The observer effectively compares the decision variable at a given moment against this distribution to decide whether to respond. Next, 20 initial stimulus presentations at 100% Weber contrast were simulated, to find the sample cumulative distribution function of the decision variable at this contrast. Plotting the probability that the decision variable is greater than k when a stimulus is presented against the probability that it is greater than k when a stimulus is not presented, for all possible values of k, gives a Receiver Operating Characteristic (ROC) curve. The area under this ROC curve, calculated by numerical integration, gives the probability of a correct response for a 2AFC task (Green & Swets, 1966). This is repeated decreasing the stimulus contrast in steps of 0.2 log₁₀ units, until the probability is below 0.6 (note that the program will also increase the contrast from 100% in steps of 0.2 log units until there is at least one probability greater than 0.9, but this was not needed here since the threshold was considerably lower than 100% contrast). A Quick function (Quick, 1974), a variant on the Weibull curve, is fitted to these probabilities using maximum likelihood estimation. This equation is given by P = 1 − 2^{-(Contrast/Threshold)Slope}. This then gives initial estimates of both the threshold (the contrast at which the area under the ROC curve is 0.75, corresponding to 50% detection) and the slope parameter. Based on these initial estimates, six intensities at equally-spaced intervals (in log units) are determined that will ensure that the range from 25% to 75% detection is covered (area under the ROC curve from 0.625 to 0.875). Lastly, 200 presentations are simulated at each of these intensities, and a Quick function fit through the resulting probabilities, to give the final estimates of threshold and slope. Note that the Quick functions fit to the data in this paper are for the psychometric function of a 2AFC task, and so have a lower asymptote of 50%; the psychometric function of a detection task as used in clinical perimetry will asymptote to the false positive rate.

The model was implemented in the C programming language. Generating one psychometric function took about 4−5 minutes on a 2GHz processor with 16GB of RAM.

Model experiments

First, 200 psychometric functions were generated using the parameter values given above. The intermediate stage graphics shown in this paper in Figures 3 and 4 were taken from one randomly-chosen run. Next, each parameter in turn was tested for robustness; 100 runs were done with that parameter set at each of two alternative values, as given in Table 1. To model fixation jitter, the stimulus center was moved relative to the central RGC according to a random sample from a 2D-Gaussian, with standard deviation 0.3° horizontal and 0.2° vertical (Demirel & Vingrys, 1994, Fendrich, Demirel & Danziger, 1999). To model a non-uniform grid of RGCs, the position of each was moved relative to the regular hexagonal grid according to a random sample from a 2D-Gaussian, with standard deviation 0.02° horizontal and 0.02° vertical. Note that the parameter “Retino:Cortico-EPSP ratio”, as mentioned in the Methods section, encompasses changing any one out of the LGN contrast gain, the height of the cortical filter receptive fields, and/or the relative magnitudes of EPSPs caused by spikes arriving from the retina and from cortical sources. The decision variable used in the primary calculations bases detection on the largest response from any cortical cell; the alternatives shown here are for detection being mediated by the 4^th and 8^th largest responses from the population of cortical cells respectively.

Figure 3.

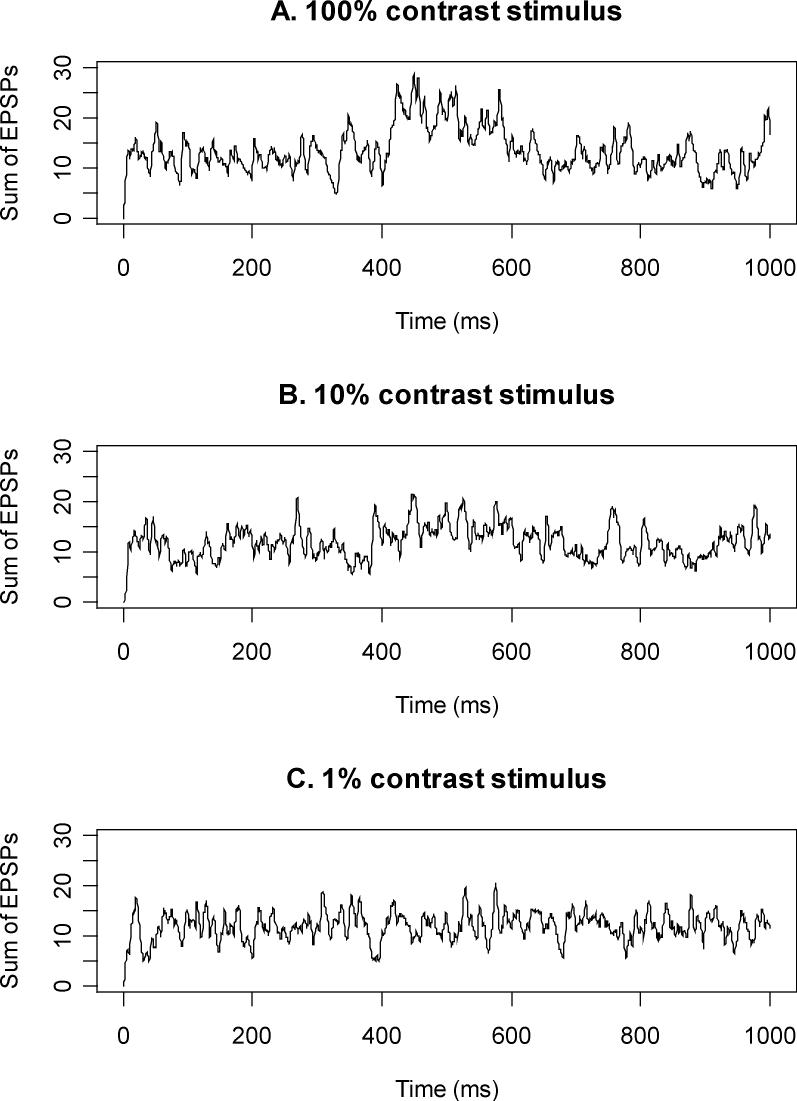
The sum of EPSPs for the cortical cell whose receptive field is centered on an RGC directly under the centre of the stimulus, for three different stimulus intensities. The modeled stimulus is presented between 400−600ms. During this period, the sum of EPSPs is visibly higher than outside this period for the supra-threshold 100% contrast; slightly higher for the near-threshold 10% contrast stimulus; and not noticeably higher for the sub-threshold 1% contrast stimulus.

Figure 4.

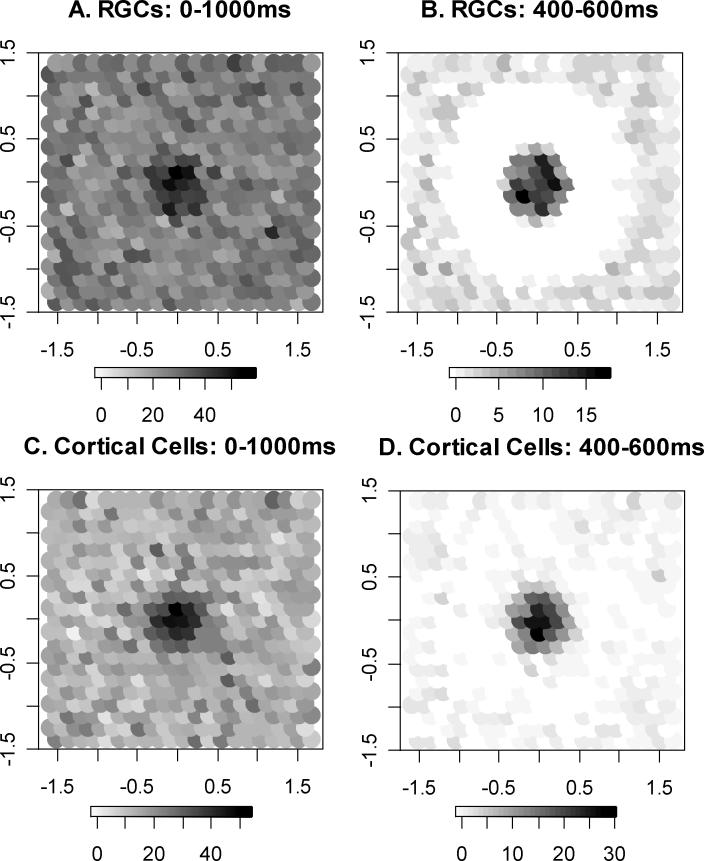
The number of spikes produced by different cells during one randomly-chosen simulated presentation of a 100% contrast stimulus, presented between 400−600ms. Darker shading corresponds to a higher spike count for that cell. Note the different grayscales in each case, chosen to give a full range from white (no spikes from that particular cell) through to black in each case. Figures 4A and 4C show the spike counts during the entire response window; Figures 4B and 4D show the spike counts restricted to the interval during which the stimulus was presented. In Figures 4A and 4B, the RGCs are positioned according to the center of their receptive field. In Figures 4C and 4D, the cortical cells are positioned according to the location of the RGC on which the cell's receptive field is centered. The cells shown cover an area on the retina ±1.5° horizontally and vertically from the center of the stimulus, with a center-to-center RGC spacing of 0.16°.

Table 1.

Results for parameter robustness checks. For each new parameter value in turn, 100 psychometric functions were generated. The numbers in the columns headed `Threshold' and `Slope' refer to the median of the values from those 100 runs. Values are given in units of % contrast. For details on the meaning of the individual parameters, and the abbreviations used, see the Methods section. For quick comparison, the equivalent results using the standard parameter values as given in the Methods section are included at the top of the table.

Parameter	Default value	New Value	Threshold	Slope
	All Defaults		11.2	2.0
Fixation Jitter:	None	Jittered	11.0	2.0
RGC Parameters:
Spatial organization	Regular	Jittered	10.9	2.0
Spacing	0.16°	0.14°	6.7	2.2
		0.18°	18.2	1.7
Total number of cells	150000	100000	10.5	1.8
		200000	11.6	2.0
Receptive Field Height	Center 115	1.5 × default	22.1	2.0
	Surround −2	0.5 × default	7.4	2.0
Maximum Driven Firing Rate	65 ips	40 ips	17.9	1.4
		100 ips	9.0	2.4
Baseline Firing Rate	10 ips	5 ips	10.1	2.1
		15 ips	12.3	2.0
Absolute Refractory Period	1.5 ms	1 ms	7.9	1.6
		2 ms	13.9	2.1
Relative Refractory Period	2.0 ms	1.5 ms	3.8	0.6
		2.5 ms	15.5	2.2
Cortical parameters:
Retino:Cortico-EPSP Ratio	2:1	1:1	58.0	1.1
		4:1	4.5	2.2
EPSP rise time	2.9 ms	2 ms	24.0	2.4
		3.5 ms	3.8	0.6
Filter Spatial Frequency	0.5 cycles/°	0.4 cycles/°	9.3	2.0
		0.6 cycles/°	15.1	1.8
Baseline Firing Rate	5.6 ips	3 ips	8.4	2.2
		8 ips	12.6	1.5
Attention Window	60 ms	30 ms	16.0	1.5
		120 ms	9.1	2.1
Decision Variable: nth largest signal	n=1	n=4	16.0	3.0
		n=8	29.0	3.4

Finally, to further examine the effect of RGC density, which is reported to vary twofold among normal human eyes (Curcio & Allen, 1990, Kerrigan-Baumrind, Quigley, Pease, Kerrigan & Mitchell, 2000), 200 psychometric functions were generated using randomly chosen densities within a set range; note that as well as the RGC spacing changing, the number of cortical cells modeled also changed (to maintain the one-to-one relation between RGCs and cortical cells), and the total number of RGCs / detection channels in the retina also changed using the assumption that the density was increased or decreased uniformly across the retina.

Human observer testing

Five normal observers were tested. The mean age was 33 years (range 21 to 47). The right eye of each observer was tested.

A contrast detection experiment was conducted using custom software developed with Matlab 7.1 (Mathworks, Natick, MA, USA) controlling a Cambridge Research Systems (Cambridge Research Systems, Kent, UK) ViSaGe attached to a 2.8GHz PC. Stimuli were presented on a gamma corrected monitor (Sony G520 [Sony, Tokyo, Japan], resolution 1024 × 768 pixels, frame rate 100Hz, maximum luminance 120cd/m2) viewed at a distance of 50 cm with the aid of a chin-rest. Participants were refractively corrected for working distance. Subject responses were recorded using an infrared Cambridge Research Systems CB6 button box.

Contrast detection thresholds were determined for circular luminance increment stimuli. The background luminance was 10 cd/m2 (31.5 apostilbs). Stimuli were 0.43° in diameter, and were presented at four locations at (±9°, ±9°) on the diagonal meridia (i.e. upper right, upper left, lower left, lower right). Testing at all four locations was interleaved within a single experimental run.

Subjects were instructed to maintain fixation on a central circular black fixation target (16 minutes of arc). A two-interval forced choice procedure was used. On each trial, a temporal interval was chosen at random to display the stimulus, with the other interval displaying the background luminance only. Each interval was 200ms in duration and was preceded by an auditory tone. A 500ms inter-stimulus interval was used. Subjects were required to indicate whether the stimulus appeared in the first or second interval. For each location, nine contrast levels were interleaved within a single run (Method of Constant Stimuli, MOCS). Contrast levels were chosen for individual subjects based on pilot testing, with nine luminances per location chosen to cover most of the range from guessing (50% correct) to the upper asymptote of performance (1.0 minus the false negative rate). Luminances were equally spaced on a scale of log(contrast). Within the MOCS, five repeats of each contrast level were included per run (making a total of 180 presentations per run: four locations at nine contrasts repeated five times). A single run required approximately 6 minutes to complete. The procedure was conducted twenty times to obtain psychometric functions at each location with a total of 100 presentations per contrast.

A two-stage process was used to fit psychometric functions to the data. Unlike the modelling experiments described above, with human subjects there are three parameters to be fit; threshold, slope and false negative rate (FN). False negatives, caused largely by lapses in attention or button-pushing errors, were assumed to be independent of stimulus contrast and location. Such errors do not affect the model results, and so FN was zero for the modelled psychometric functions. For the human data, at the first stage maximum likelihood estimation was used on all three parameters simultaneously, treating each of the four locations as being independent. A Quick function was fit to the probabilities as for the modelling experiments described above but with an extra free parameter FN, so that the fitted probabilities ranged from 50% to (100-FN)%. The four resultant estimates of FN were then averaged to give a single value per subject. The psychometric functions were then re-fit, using maximum likelihood estimation to find threshold and slope but keeping FN fixed at this average value.

Results

Results from the model

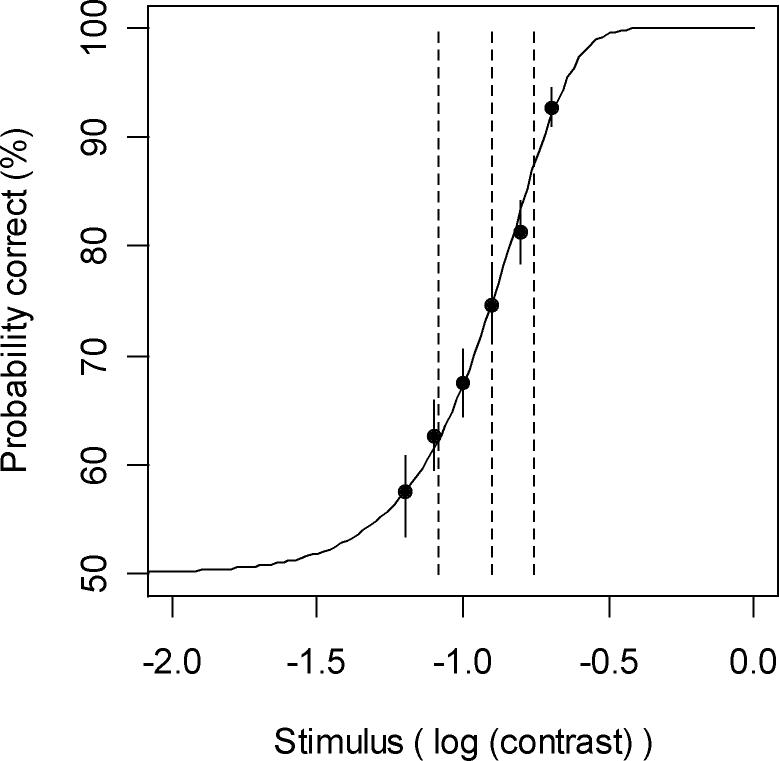
From 200 generated psychometric functions, the median detection threshold was 11%, and the median slope was 2.0. Figure 2 shows an example psychometric function generated by one randomly-chosen run of the model, with a 90% confidence interval for the area under the ROC curve (and hence the probability of a correct response to the 2AFC detection task) for each stimulus contrast shown by a vertical line through each point, as calculated using nonparametric bootstrap approximation using ROCKIT software (downloadable from http://xray.bsd.uchicago.edu/krl/KRL_ROC/software_index6.htm). Asymptotically, a zero contrast stimulus will give an area under the ROC curve of 0.5, corresponding to a 50% probability of making a ‘correct’ response to the 2AFC task, which is equivalent to 0% detection.

Figure 2.

A sample psychometric function generated by the model, for a two-alternative forced choice stimulus detection task. Solid circles represent the stimuli presented and their probabilities of detection. Solid vertical lines passing through these circles represent the 90% confidence interval for this probability. The dashed vertical lines represent the median and lower and upper quartiles of the fitted curve, corresponding to 25%, 50% and 75% detection probabilities. This psychometric function has a detection threshold of 12.6% contrast and a slope parameter of 2.1.

Figure 3 shows the sum of EPSPs at one cortical cell over time, for three different contrast stimuli. This cortical cell is centered on the stimulus, so sums EPSPs from spike trains giving maximum weighting to spikes from the RGC whose receptive field is centered directly under the center of the stimulus. The sum of EPSPs rises with stimulus contrast during the period the stimulus is being presented, between 400−600msec.

Figure 4 shows the total number of spikes output by the RGCs whose receptive fields are centered within ±1.5° of the center of the stimulus, and also spikes output by the cortical cells whose receptive fields are centered on these RGCs, for a 100% contrast supra-threshold stimulus. For clarity, the cortical cells are arranged in Figures 4C and 4D based on the spatial position of their corresponding central RGC. Cells are assigned a shading based on the number of spikes output, ranging from white for zero spikes to black for the maximum number of spikes over all cells shown. This maximum is different in each case, hence the different grayscales as shown in the respective keys. An increase in the number of spikes output by the cells in close proximity to the 0.43° diameter stimulus is clearly seen, especially when restricted to those spikes output while the stimulus is on (Figures 4B and 4D). The inhibitory surround can also be seen as a reduction in spike count below the usual random firing rate, and is especially clear in Figures 4B and 4D.

Table 1 shows the effect on the sensitivity and slope of the psychometric function when changing the parameter values of the model individually. The statistical significances of the changes in the median sensitivity and slope of the psychometric functions shown in Table 1 depend on the magnitudes of the changes made to the parameter values, and so formal significance tests are not presented here. Neither fixation jitter nor jittering the locations of the RGCs had a large effect on the results. In the case of the RGC receptive field height, the slope will not be changed regardless of the magnitude of the parameter value change, since this is exactly equivalent to the contrast of the stimulus being changed by the same amount. The only parameter adjustment found that could plausibly give slopes as steep as those from human observers was changing the decision variable so that detection was mediated by the responses from multiple cortical cells, rather than just the largest response.

To examine the effect of eccentricity, 100 runs were carried out with parameters based on a more central non-foveal location. Using RGC receptive field parameters for 0°−10° eccentricity instead of 10°−20° (Croner & Kaplan, 1995), and an RGC spacing of 0.10° instead of 0.16°, the median threshold was reduced to 7%. Although it is not possible to match either these results or the primary results to exact eccentricities due to a lack of available exact parameter values, qualitatively this agrees with the known decrease in sensitivity with increasing eccentricity.

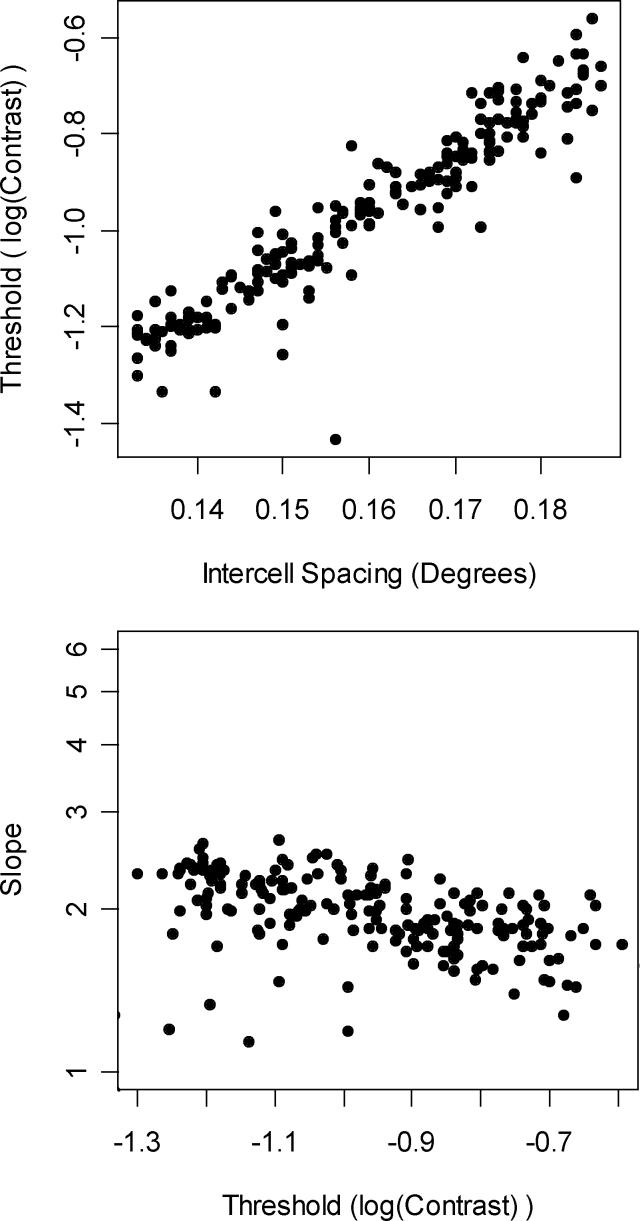
Perhaps the most important of the parameters that can be varied is the RGC spacing. This is because the RGC density has been reported to vary up to twofold between normal human eyes (Curcio & Allen, 1990), and by a log unit as eccentricity increases from 10° to 30°(Kerrigan-Baumrind et al., 2000). Increasing the density (i.e. decreasing the RGC center-to-center spacing, and increasing the total number of RGCs in the retina and hence the total number of detection channels) increases the sensitivity of the system and decreases the variability. Figure 5 shows the result of varying the spacing parameter randomly for each run between 0.13° and 0.19°, giving a twofold range of densities. Figure 5A shows the effect on threshold; halving the density results in threshold increasing sevenfold in linear units. RGC number, proportional to the reciprocal of the square of RGC spacing, is approximately linearly related to sensitivity (1/threshold) in either linear units (R²=0.91) or log units (R²=0.93), both significant with p<0.0001. The slope of the psychometric function decreases (equivalently, the variability increases) as spacing increases; Figure 5B shows the relation between sensitivity and variability as measured by the slope. This negative correlation between threshold and slope, equivalent to a negative correlation between sensitivity and variability, has been reported for human observers (Chauhan, Tompkins, LeBlanc & McCormick, 1993, Henson et al., 2000).

Figure 5.

The effect of varying center-to-center RGC spacing on the psychometric function. In Figure 5A, threshold increases as spacing increases. In Figure 5B, slope decreases as threshold increases.

Comparison with human data

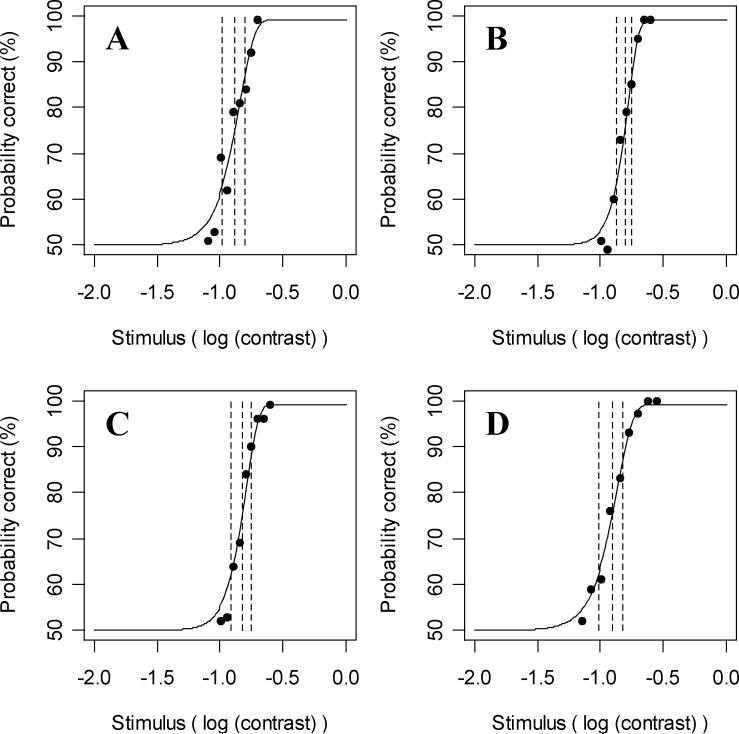
Figure 6 shows the four psychometric functions measured in one of the five subjects (Subject 4 in Table 2). Figure 6A shows the results at the superior nasal location (−9°, 9°); based on maximum likelihood estimation to fit a Quick function to the data, the threshold (stimulus intensity with 75% correct) was 13% contrast and the slope was 3.6. Figure 6B shows the results at the superior temporal location (9°, 9°) giving a threshold of 16% and slope of 5.2. At the inferior nasal location (−9°, −9°) in Figure 6C, threshold was 15% and slope 4.5; and at the inferior temporal location (9°, −9°) in Figure 6D, the threshold was 12% and slope 3.5. Stimulus intensities were chosen at intervals 0.05 log units apart for Figures 6A-C and 0.075 log units apart for Figure 6D, and the estimated false negative rate for this subject was 1.7%.

Figure 6.

The psychometric functions as recorded in one experimental subject at four locations in the visual field (±9°, ±9°) of the right eye. Figure 6A shows the psychometric function at the superior nasal location; Figure 6B superior temporal; Figure 6C inferior nasal; and Figure 6D inferior temporal. The data points show the percentage correct in the two-alternative forced choice contrast detection task at each of nine stimulus intensities per location. The curved line shows a Quick function fit to the data using maximum likelihood estimation. The three vertical dashed lines show the median (75% correct) and quartiles (87.5% and 62.5% correct) of the fitted curve.

Table 2.

Summary of experimental results by subject. Values are the mean of the fitted parameters from the four visual field locations tested, given in units of % contrast, and the estimated false negative rate FN.

Subject	Age	FN	Mean Threshold	Mean Slope
1	29	4%	12%	4.2
2	21	3%	12%	4.2
3	30	4%	14%	4.2
4	47	2%	14%	4.2
5	37	1%	13%	4.2

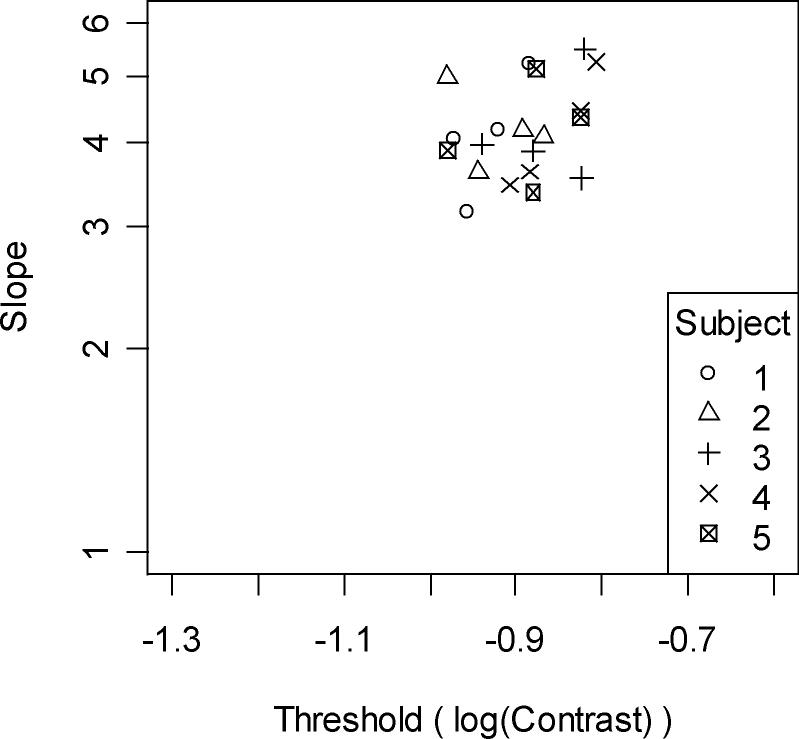
Figure 7 shows the thresholds and slopes from the four fitted psychometric functions for all five subjects (with different plotting symbols used for each subject). Table 2 summarizes the results for each of the five subjects. The overall mean threshold was 12.9%, with a slope of 4.2. The thresholds were significantly higher than those obtained from the primary calculations from the model (non-parametric Mann-Whitney test, p=0.0001), and the slopes were also significantly higher (p<0.0001).

Figure 7.

The threshold and slope of each fitted psychometric function from experimental subjects. Axes are the same as in Figure 5B. Different symbols represent the data for each subject, using the same numbering as in Table 2.

Discussion

In this paper, we used modeling to investigate the effect that the intrinsic noise associated with neural spiking has on the variability in perimetric sensitivities. Replicating the slopes of psychometric functions from human observers required that detection be mediated by responses from multiple V1 simple cortical cells, rather than just the largest response from a single cortical cell.

There are three main criteria for assessing the usefulness of a model: does it accurately simulate observed results, does it accurately represent human physiology, and can it be used to tell us useful things that we don't already know. The third (and most crucial) criteria cannot be truly satisfied unless the first two criteria are satisfied. In clinical visual psychophysics, work to date has largely concentrated on the first of those criteria, and the previously published models have to various extents ignored the physiology. In particular, this is the first model to properly attempt to explain the causes of intrinsic variability. The model presented here is firmly grounded in both signal detection theory and the known physiology of the visual system, with its constituent parts taken from the neurophysiology literature and parameters measured in vivo in experimental animals, while its integrative principles are derived from human psychophysics. Therefore, although there are caveats, the model can be said to approximate the true nature of the system as we currently understand it. Consequently, the model goes further towards satisfying the second criterion than has been previously achieved for perimetry.

Perimeters typically attempt to estimate the magnitude of noise from causes extrinsic to the visual system (Newkirk, Gardiner, Demirel & Johnson, 2006), such as false negatives and false positives from attention lapses, and fixation losses (Wyatt, Dul & Swanson, 2007). Testing algorithms (Turpin, McKendrick, Johnson & Vingrys, 2002) and post-processing techniques (Gardiner, Crabb, Fitzke & Hitchings, 2004) have been used to manage and reduce the variability present in perimetry, to improve the efficiency of clinical testing. However, noise intrinsic to the visual system is harder to quantify. There are three main sources of variability present in the model. Firstly, the free firing thresholds of cortical cells are found from binary search based on a ten second period of simulated stimulus-free RGC firing. This causes the free firing thresholds of individual cortical cells to differ. However, these differences are small (typically <1%) and so the variability due to this source is low. Secondly, each cortical cell receives EPSPs from randomly-firing cells elsewhere in the cortex; this noise is considered to be uncorrelated between cells. Thirdly, RGC firing is modeled as an essentially random process with a set probability. The resultant noise is strongly correlated between cortical cells with adjacent receptive fields, due to common input. The human cortex may take advantage of these correlations to improve detectability of stimuli (Bair, Zohary & Newsome, 2001, De La Rocha, Doiron, Shea-Brown, Josic & Reyes, 2007), but this process is not yet characterized sufficiently to be incorporated into the model.

Although thresholds of the psychometric functions generated by the model are statistically significantly different to those measured in human subjects, the magnitude of this difference is small, averaging 0.07 log units of contrast. They also match well with those reported in the literature. The median threshold from the model was 11%, equivalent to 35dB in the units used by the Humphrey Field Analyzer. The median slope was 2.0, which converts to an interquartile range of 3.3dB (Strasburger, 2001). Chauhan et al. (Chauhan et al., 1993) found a median threshold of 30%, with a wide range of slopes with median 2.2. Henson et al. (Henson et al., 2000) had normal thresholds ranging between 4% and 100% at the same four locations per subject tested in this study, and predict that at a threshold of 11% the slope would be 2.8. Both these studies were carried out using clinical perimeters rather than a 2AFC detection task; the perimeters can only present stimuli at fixed contrasts (tenths of a log₁₀ unit); the curve fitting procedure differed from that used here; and they also used fewer presentations per contrast level than was used in this study causing a greater spread of results. The psychometric functions we report in this study were collected using more robust and accurate psychophysical techniques than used in perimetry, in particular with regard to the number of presentations per intensity.

The experiments described in this paper as well as those discussed above produce human psychometric functions with significantly steeper slopes than the principal calculations from the current model. Similar conclusions were derived by a previous study. Neurometric analysis of cortical cell spike trains found that slopes of neurometric functions for individual cells were not as steep as those of psychometric functions from observers (Tolhurst, Movshon & Dean, 1983), implying that the observer may require that the signal be detected by multiple channels for a response to be generated. This would increase both contrast threshold and the slope of the psychometric function. A more recent study utilizing sinusoidal gratings and Gabor patches found that the best fits to psychophysical data were obtained using between 12 and 22 channels for detection, although with some caveats (Chirimuuta & Tolhurst, 2005). This is equivalent to changing the decision variable to be the number of spikes produced by the cortical cell with the nth largest response, instead of the largest response; that is, n cortical cells producing a response equal to or greater than the criterion. To our knowledge there is currently no universally accepted experimental data to favor using one decision variable over another, in particular for choosing a specific value for n>1, and so n=1 was used for our primary results, as it remains the maximum likelihood estimate. This ‘greatest-signal’ formulation is equivalent to probability summation as developed in spatial vision models (Pelli, 1985). Psychometric analysis of the effects of observer uncertainty demonstrates that an observer attending to many different channels will have a steeper psychometric function than the same observer attending to only a single channel (Pelli, 1985, Tyler & Chen, 2000). A perimetric observer attends to many locations in visual space (typically over 50 locations spanning 1000 degrees squared of visual angle), so there will be a high degree of spatial uncertainty. To our knowledge, uncertainty analysis has not been included in neurometric models, and modeling perimetric variability should be an ideal way to assess the possible role of observer uncertainty in neurometric analysis of cortical spike trains. Other formulations for decision rules have been suggested in the literature. For example, it has been suggested that detection is based on the time taken for N spikes to be emitted by a simple cortical cell (Rudd, 1996), rather than (as here) the number of spikes output within a fixed time window. There are possible advantages to that formulation, including a better adherence to Bloch's Law. A thorough exploration of decision rules is beyond the scope of this paper, but is certainly a fertile area for future work.

Because of inter-individual differences in each component of the model, combining the components requires simplifications to produce meaningful and interpretable results. A key aim is therefore ensuring that simplifications are chosen so as not to infringe on the integrity of the components that are of most interest. In the case of perimetry, which is a test most commonly used in glaucoma testing, this means that the retinal section of the model should be kept as physiologically accurate as is feasible; simplifications to the thalamic and cortical section of the model should still be minimized but can be more readily tolerated. For example, the model presented here is at the level of V1 simple cells; it does not consider extrastriate processing, since glaucomatous damage is thought to occur prior to that stage. Another section of the model where the visual system is less well understood is at the LGN. Physiologically it is not certain whether there is just signal gain (Lee et al., 1983) or also signal control (Kaplan et al., 1987, Przybyszewski, Gaska, Foote & Pollen, 2000). The understanding of this process is improving (Bonin, Mante & Carandini, 2006, Kozyrev et al., 2007), and it is hoped that it will soon be possible to incorporate these recent findings into future refinements of the model. At present, simple linear contrast gain was implemented. This gain is indistinguishable from changes in the height of the cortical filter receptive fields, and from the ratio of the EPSP magnitudes resulting from retinal-originating and cortical-originating signals. This combined parameter, which we have referred to as the retino:cortico-EPSP ratio, may well turn out to be the most crucial of the remaining unknown aspects of the model in terms of determining psychophysical detection thresholds for spot stimuli.

Results from the model are dependent on the parameters used at each stage, as shown in Table 1. The parameters were taken from the literature as cited in the Methods section, but are of course subject to measurement errors and natural variability. In reality, the values of each will vary between individuals, and will almost certainly vary during a lifetime. Further, almost all of the parameters were measured in animals rather than humans. For example, the spatial properties of RGC receptive fields are based on as few as five macaque retinas, that were presented sinusoidal gratings with mean luminance 40 cd/m² (Croner & Kaplan, 1995). Many of the cited papers used macaque monkeys due to the similarities between their visual system and that of humans, but other animals were also used such as larval tiger salamanders (Berry II & Meister, 1998). With further alterations to these parameters, it could be possible to exactly replicate the median slope and threshold values from the human psychometric functions. However, given that we are working towards a model that reflects the physiology rather than one that is as accurate as possible empirically, it is difficult to justify switching to essentially arbitrary values instead of using values taken from the literature.

Various simplifications were made to improve repeatability across trials (for example using a perfectly regular RGC array), or to reduce computing time (for example modeling cortical-originating spikes causing stimulus-independent EPSPs as arriving according to a pure Poisson process), or because a suitable model was not available. All RGCs had exactly the same properties, including the spatial organization of their receptive fields. The RGCs were also centered on a regular hexagonal grid. Neither of these reflects the actual physiology of the retina, but the effects of these simplifications appear to be small when tested by adding spatial jitter to the array of RGCs. The true physiology may result in slightly higher variability particularly when fixation movements are taken into account, but the results should average out to produce similar outcomes. The biphasic temporal response of RGCs was not included in the current model; this will become more important when modeling temporally flickering stimuli such as that used clinically in Frequency Doubling Technology (FDT) perimetry, and so it will be included in the future development of the model. In the visual cortex, it is known that the receptive fields of simple cells are tuned to different orientations and spatial frequencies. However this has been shown to have little effect on the results for circularly symmetric stimuli when using a non-neural spike model. For example, using a vertically-oriented filter with a peak spatial frequency of 1 cycle/° (Swanson et al., 2004), the median threshold decreased slightly to 5.24% contrast, with a median slope of 2.1. To implement a more realistic model of the cortical processing would require not only accurate knowledge of the proportions of filters possessing each possible combination of orientation and spatial frequency, but also of the lateral inhibitions between them and of cortical-cortical suppression. At suprathreshold contrasts cortical-cortical inhibition can have substantial effects on responsiveness of cortical simple cells (Miller, 2003), but we expect these effects should be minimal at the near-threshold contrasts considered in this study. Processing in the higher visual cortex is not included in the model, under the assumption that the V1 cortex is exclusively responsible for determining psychophysical thresholds for this very simple detection task (Chirimuuta & Tolhurst, 2005), but this is uncertain. While the model incorporates adaptation to the constant background luminance, rapid adaptation to the stimulus is not included (Rudd & Brown, 1997). Finally, only magnocellular detection mechanisms were modeled. Initial experiments suggest that very similar results (thresholds within 0.1−0.2 log units of those presented here) would be achieved using parameters taken from parvocellular mechanisms. However there are many times more parvocellular than magnocellular mechanisms, and the need for a much denser array currently causes the computing time required to be highly impractical. It is hoped to test the model more extensively using parvocellular mechanisms in the near future.

Moving forward, the model can be refined as more results from experimental physiology become available, both in terms of those components discussed above and the parameter values throughout the model. Concurrently, the model can be used to further our knowledge of the pathology of the diseased visual system, by comparing the consequences of altering components of the modeled system against patient psychophysical data. For example, the temporal and spatial characteristics of glaucomatous damage are uncertain, in particular whether damage is characterized purely by RGC death or by an extended period of RGC dysfunction (Weber & Harman, 2005). It is also unknown how the retina and visual cortex adapt to diminish the effect of RGC death or damage, for example whether the free firing thresholds of cortical cells reduce if they receive fewer input spikes from the LGN. Improved knowledge of these characteristics of the pathophysiology, in glaucoma and in other diseases, will help in the development of new non-invasive tests of visual function (improving upon or replacing current perimetric techniques); and potentially also direct development of new treatment regimens. A principle purpose of this work is the ability to generate clinically meaningful results and conclusions, and this aim will direct the future course of this project.

In conclusion, we have demonstrated that it is possible to construct a usable model of perimetric detection based on the known physiology of the visual system. To obtain psychometric functions from the model with slopes as steep as those from human subjects requires that detection be mediated by multiple cortical cells rather than just that with the largest response. We are hopeful that this model will provide a useful tool in improving understanding of clinically important problems and diseases of the visual system.