Learning Dynamics of Reaching Movements Results in the Modification of Arm Impedance and Long-Latency Perturbation Responses

Abstract

Some characteristics of arm movements that humans exhibit during learning dynamics of reaching are consistent with a theoretical framework where training results in motor commands that are gradually modified to predict and compensate for novel forces that may act on the hand. At a first approximation, the motor control system behaves as an adapting controller that learns an internal model of the dynamics of the task. It approximates inverse dynamics and predicts motor commands that are appropriate for a desired limb trajectory. However, we had previously noted that subtle motion characteristics observed during changes in task dynamics challenged this simple model and raised the possibility that adaptation also involved sensory-motor feedback pathways. These pathways reacted to sensory feedback during the course of the movement. Here we hypothesized that adaptation to dynamics might also involve a modification of how the CNS responds to sensory feedback. We tested this through experiments that quantified how the motor system’s response to errors during voluntary movements changed as it adapted to dynamics of a force field. We describe a non-linear approach that approximates impedance of the arm, i.e., force response as a function of arm displacement trajectory. We observe that after adaptation, the impedance function changes in a way that closely matches and counters the effect of the force field. This is particularly prominent in the long-latency (>100 ms) component of response to perturbations. Therefore, it appeares that practice not only modifies the internal model with which the brain generates motor commands that initiate a movement, but also the internal model with which sensory feedback is integrated with the ongoing descending commands in order to respond to error during the movement.

Introduction

Quantification of how the human arm responds to a perturbation is motivated by the idea that muscles and the associated neural control structures describe a complex control system that provides feedforward as well as feedback flow of information. When a reaching movement is initiated, the neural commands to the muscles are “feedforward” in the sense that they rely on an internal model that predicts dynamics of the upcoming movement (Thoroughman and Shadmehr 1999). However, as the movement proceeds, these neural signals may be augmented by “feedback” components that incorporate the sensory information from the moving limb, sense errors in performance, and modify descending commands (Smith et al. 2000). For example, consider the events that take place as an external perturbation displaces the hand from its nominal trajectory after a movement has initiated: 1) The displacement will stretch some muscles with respect to the length trajectory that they would have followed if the arm had not been perturbed. This generally results in an increase in the force that those muscle will produce for a constant neural input. Therefore, the perturbation might elicit a restoring force in the stretched muscles with nearly zero delay. 2) The stretch will result in changes in the afferent signals, which through spinal networks may augment the neural driving signal to the muscle at a time scale of 30-50 ms (Ghez and Shinoda 1978). 3) The afferent signals resulting from the stretch may reach the cortex and cause further changes in the muscle’s driving signal at a time scale of 100-150 ms (Gielen et al. 1988; Petersen et al. 1998). The total sum of these mechanisms is a restoring force that can be represented as a function of displacement. This function is named impedance.

Previous work has found significant evidence for adaptability of the feedforward component of the control system (Shadmehr and Mussa-Ivaldi 1994). When humans make simple reaching movements while holding a novel dynamical system, the motion characteristics of their arm are rather similar to one that results from the control system outlined in Fig. 1A. In this figure, adaptation is through changes in the internal model that represents an inverse of the dynamics of the limb. Computational properties of the adaptation process have suggested that the internal model may be forming in the brain with elements that resemble properties of certain cells in the cerebellum (Thoroughman and Shadmehr 2000).

Figure 1.

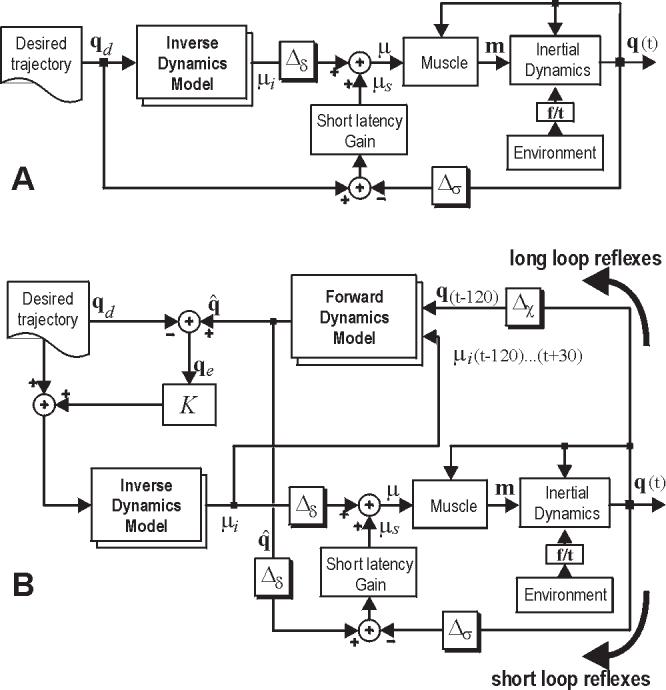
Two hypothetical representations of the motor control system for performance of reaching movements. While both systems rely on internal models to generate descending commands, the system in the lower figure also relies on an internal model to monitor afferent feedback and actively respond to potential errors in movement. (A) A controller that relies on an adaptive inverse model. Feedback is integrated with descending commands from the inverse model via a short-latency error correcting system. This short-latency system represents the reflex networks of the spinal cord. Δ_σ = 30 ms, Δ_δ = 60 ms. (B) A controller that evalulates delayed sensory feedback from the moving limb via a model of forward dynamics of the system. This allows the “long-latency” feedback pathway to estimate potential differences between ongoing action and desired behavior. These errors modify the desired trajectory, resulting in a change in the descending commands. Δ_χ = 120 ms .

While the model in Fig. 1A has been reasonably successful in describing simple reaching movements, it has clear limitations in that it provides a perturbation response pathway that only relies on the spinal system and the muscles’ intrinsic length-tension properties. There are no mechanisms of long-latency perturbation responses that rely on transcortical pathways. In effect, the descending commands are generated quite independently of the sensory feedback from the limb.

The problem is that because of the long sensory delays, it is not apparent how to incorporate feedback into the generation of descending commands. One idea is to use another kind of internal model to compensate for this delay (Fig. 1B). This new model, called a forward model, receives a copy of descending commands (efference copy) as well as delayed sensory feedback (for a recent review, see Wolpert and Ghahramani 2000). The forward model then simulates the dynamics of the limb starting from a state specified by the delayed sensory signal with a driving command specified by the efference copy. The result of this computation is a prediction of the state that the descending commands will have taken the limb to, and is the best estimate of where the limb is now. This estimate is compared with where we would like the limb to go, and descending motor commands are generated, via the inverse model, to guide the limb toward this goal. Therefore, the forward model provides a continous estimate of the sensory consequences of the descending commands based on the latest sensory feedback.

The resulting control scheme is complex. Because the system components are non-linear, we resorted to simulations in order to understand whether the controller’s performance had any resemblance to how subjects reacted to sensory feedback during their reaching movements. Bhushan and Shadmehr (1999) quantified performance in force fields when subjects were naïve, movements had large errors, and internal models were inappropriate for the dynamics of the task. It was found that much of the motion characteristics late into a movement were consistent with a control system that was reacting to sensory feedback and modifying descending commands. The characteristics suggested that as subjects trained, not only the inverse model changed, but that the forward model might have also adapted.

Here we sought to explicitly test the idea that with training, the motor system modifies how it responds to sensory feedback. A readily testable prediction of the model in Fig. 1B is that adaptation of either internal model should alter perturbation response of the system.

A theoretical framework to quantify the effect of adaptation on perturbation response

Consider the human arm holding the handle of a robotic system, as shown in Fig. 2D. Let us represent the joint torques produced by the muscles of the human arm with the vector m, passive torques due to the motion of the arm with the vector Ψ, and external torques (for example, from the robot held at the hand) with the vector τ. The equation of motion for the system is:

$$\Psi (\theta ,\stackrel{.}{\theta },\ddot{\theta })=\mathbf{m}(\theta ,\stackrel{.}{\theta },\mu )+\tau$$ (1)

where the passive torques depend on an inertia matrix H and Corriolis/Centripal matrix C:

$$\Psi (\theta ,\stackrel{.}{\theta },\ddot{\theta })\equiv \mathbf{H}\left(\theta \right)\ddot{\theta }+\mathbf{C}(\theta ,\stackrel{.}{\theta })\stackrel{.}{\theta }$$ (2)

These equations depend on joint positions θ, velocities $\stackrel{.}{\theta }$, and accelerations $\ddot{\theta }$. Let us define a generalized state-space vector $\mathbf{q}={\left[{\theta }^T{\stackrel{.}{\theta }}^T\right]}^T$. Term m(q,μ) implies that torques developed by muscles depend on the neural command μ as well as the state of the arm. Suppose now that in the null field condition (robot motors disabled), neural commands μ_o(t) are applied to the muscles and the hand makes a movement along the path ${\mathbf{x}}_o\left(t\right)\equiv [{\xi }_o^T{\stackrel{.}{\xi }}_o^T{]}^T$, or in joint coordinates ${\mathbf{q}}_o\left(t\right)\equiv {\left[{\theta }_o^T{\stackrel{.}{\theta }}_o^T\right]}^T$. The robot has a small mass that will result in forces T_o(t) on the hand, resulting in torques τ_o(t) = J^TT_o(t), where J = dξ/dθ. The equation of motion in this condition is:

$$\Psi ({\mathbf{q}}_o,{\stackrel{.}{\mathbf{q}}}_o)=\mathbf{m}({\mathbf{q}}_o,{\mu }_o)+{\tau }_o\left(t\right)$$ (3)

where the muscle torques may be labeled as m_o ≡ m(q_o,μ_o). It is reasonable to assume that the motor command μ_o(t) is composed of at least two components: a component that relies on a model of the inverse dynamics of the system, as specified by descending commands from the brain, and a component that relies on spinal structures that perform a function of error feedback control (Fig. 1A):

$${\mu }_o={\mu }_i\left({\mathbf{q}}_d\right)+{\mu }_s({\mathbf{q}}_o,{\mathbf{q}}_d)$$ (4)

where q_d is the desired trajectory of motion: ${\mathbf{q}}_d\equiv {\left[{\theta }_d^T{\stackrel{.}{\theta }}_d^T\right]}^T$.

Figure 2.

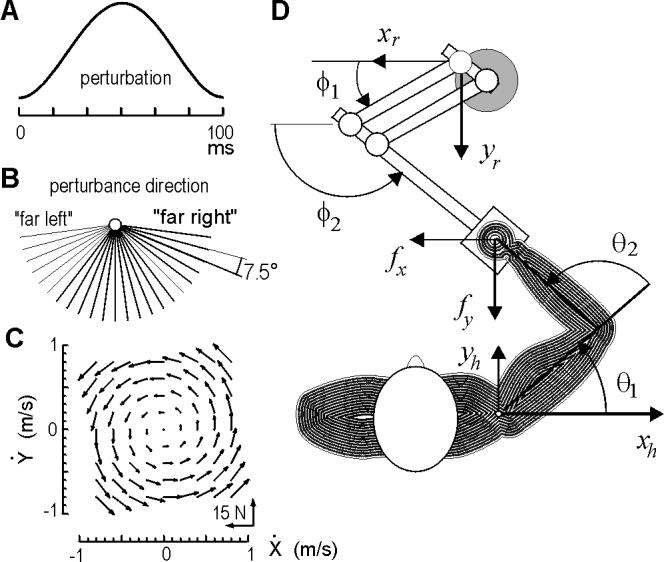
Experimental setup. Subjects made reaching movements of length 10 cm to a target at 90 degrees. (A) On some trials, a perturbation was imposed (probability of 1/6), at 100 ms after movement initiation (detected via a velocity threshold of 0.03 m/s). Perturbations were smooth, rapid functions of 100 ms in length and varying peak magnitude force (7 to 15 N). (B) Direction of the pertubation force vector was selected randomly from among these directions. (C) Subjects made reaching movements in the null field, and then in a force field. The forces in the field depended on hand velocity and are shown here. (D) Top view of the subject and the manipulandum.

Now consider the condition (condition 1) where the robot is programmed to produce a force field defined by $\Omega \stackrel{.}{\xi }$, where ${\stackrel{.}{\xi }}^T\equiv \left[\stackrel{.}{x}\stackrel{.}{y}\right]$ and Ω is a square matrix that linearly transforms hand velocity to forces. In terms of torques on the subject’s arm, the field is $\omega \stackrel{.}{\theta }$, where ω = J^T ΩJ. After extensive practice, the subject adapts and hand paths are similar to the condition where the robot motors were disabled, i.e., q(t) ≈ q_o(t). Because of the adaptation, the inverse model now produces a new command ${\tilde{\mu }}_i\left({\mathbf{q}}_d\right)$. The total command to the muscles becomes

$${\mu }_1={\tilde{\mu }}_i\left({\mathbf{q}}_d\right)+{\mu }_s({\mathbf{q}}_o,{\mathbf{q}}_d)$$ (5)

where ${\tilde{\mu }}_i\left({\mathbf{q}}_d\right)={\mu }_i\left({\mathbf{q}}_d\right)-\phi \left(\omega {\stackrel{.}{\theta }}_d\right)$, i.e., the inverse model produces a command that incorporates an estimate of the imposed force field. Finally, the equation of the motion after adaptation to the force field is

$$\Psi ({\mathbf{q}}_o,{\stackrel{.}{\mathbf{q}}}_o)=\mathbf{m}({\mathbf{q}}_o,{\mu }_1)+{\tau }_o\left(t\right)+\omega \stackrel{.}{\theta }.$$ (6)

By comparing Eqs. 3 and 6, muscle torques generated along trajectory q_o after adaptation can be written as:

$$\mathbf{m}({\mathbf{q}}_o,{\mu }_1)=\mathbf{m}({\mathbf{q}}_o,{\mu }_o)-\omega {\stackrel{.}{\theta }}_d,$$ (7)

where the muscle torques may be labeled as m₁ ≡ m(q_o,μ₁). Equation (7) simply restates the hypothesis that adaptation affected the feedforward component of the control system in Fig. 1A and did not affect the feedback system. However, in this way, the hypothesis becomes immediately testable: a measure of function of the feedback system is how it responds in terms of force to a perturbation that caused a displacement. If adaptation was solely through formation of an inverse model, then the perturbation response should not change as the system adapts.

To clarify the concept of perturbation response, let us assume that in the null field condition, the arm is perturbed by a small perturbation Δτ_o while reaching to a target. The perturbation will force the arm to move away from the unperturbed path: ${\mathbf{q}}_o+\Delta {\mathbf{q}}_o={\left[{({\theta }_o+\Delta {\theta }_o)}^T{({\stackrel{.}{\theta }}_o+\Delta {\stackrel{.}{\theta }}_o)}^T\right]}^T$. Muscles will produce a response to the perturbation that depends on both the change in muscle states and the change in neural input due to spinal reflexes: m(q_o + Δq_o,μ_o + Δμ_o). The change in muscle forces due to the perturbation will be:

$$\Delta {\mathbf{m}}_o\equiv \mathbf{m}({\mathbf{q}}_o+\Delta {\mathbf{q}}_o,{\mu }_o+\Delta {\mu }_o)-\mathbf{m}({\mathbf{q}}_o,{\mu }_o).$$ (8)

The change of muscle forces, Δm, with respect to displacement, Δq, is called impedance. The function Δm_o is a measure of impedance of the arm along a particular displacement from the unperturbed path q_o. Similarly, in the condition where a force field is present and the system has adapted through formation of an inverse model, imposition of a perturbation will accompany forces in the muscles:

$$\Delta {\mathbf{m}}_1\equiv \mathbf{m}({\mathbf{q}}_o+\Delta {\mathbf{q}}_o,{\mu }_o+\Delta {\mu }_o)-\omega {\stackrel{.}{\theta }}_d-\mathbf{m}({\mathbf{q}}_o,{\mu }_o)+\omega {\stackrel{.}{\theta }}_d.$$ (9)

However, in this adapted condition the change in muscle force due to the perturbation will be identical to Eq. 8. Therefore, the hypothesis predicts that adaptation of an inverse model should result in no changes in arm impedance:

$$\Delta {\mathbf{m}}_1(\Delta \mathbf{q},t)-\Delta {\mathbf{m}}_o(\Delta \mathbf{q},t)=0.$$

Now consider a condition where the control system gathers delayed sensory information and integrates this into descending commands during the execution of the reaching movement (Fig. 1B). The function of the forward model is to estimate current state of the system $\widehat{\mathbf{q}}$ from the delayed sensory feedback and a copy of efferent commands. As a result, now the input to the inverse model is not an invariant desired trajectory, but a trajectory that depends on the sensory information that is gathered during the movement:

$$\begin{array}{c}\mu ={\mu }_i({\mathbf{q}}_d+{\mathbf{Kq}}_e)+{\mu }_s({\mathbf{q}}_o,{\widehat{\mathbf{q}}}_o)\hfill \\ {\mathbf{q}}_e={\mathbf{q}}_d-{\widehat{\mathbf{q}}}_o\hfill \end{array}$$ (10)

where K is a gain matrix. In case of a perturbation to the arm, the transcortical feedback system will produce a response, resulting in a meaningful change in the impedance of the arm. In order to measure change in impedance during adaptation, the following problems need to be solved:

1. For any given trajectory, we need an estimate of the inertial forces Ψ. Knowing these forces and the measured forces at the handle will allow for an estimate of muscle forces m.

2. When a movement is perturbed, it will be necessary to estimate the inertial forces and muscle forces that would have been recorded if the movement had not been perturbed. Because some movements of a given subject may be slow while others may be faster, it is not sufficient to use a mean of unperturbed movements as a standard. Rather, it will be necessary to predict the unperturbed path the limb would have gone for each perturbed motion.

3. To estimate the change in impedance, we must be able to compare perturbation responses before and after adaptation at the same state and time.

The approaches we used to solve these problems are described below.

Methods

Estimating inertial dynamics of the arm

We represent the human arm as a chain of two segments, with each segment a three dimensional rigid body. Assume that the segments move in a horizontal plane defined by x and y coordinates. The segments may be complex in shape, but let us assume that the center of mass of each segment lies on the horizontal plane, and that the inertia of each segment written with respect to its center of mass has the shape:

$${}^{c}I\equiv \left[\begin{array}{ccc}\hfill \sum _i{m}_i({}^{c}r_{iy}^2+{}^{c}r_{iz}^2)\hfill & \hfill -\sum _i{m_i}^c{r_{ix}}^c{r}_{iy}\hfill & \hfill 0\hfill \\ \hfill -\sum _i{m_i}^c{r_{ix}}^c{r}_{iy}\hfill & \hfill \sum _i{m}_i(r_{ix}^2+r_{iz}^2)\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \sum _i{m}_i({}^{c}r_{ix}^2+{}^{c}r_{iy}^2)\hfill \end{array}\right]$$

where ${}^{c}r_{ix}$ and ${}^{c}r_{iy}$ are the x and y components of a vector ^cr that points from the center of mass of this segment to location of particle i that has mass m_i. When this inertia is written with respect to the point of rotation of each segment (shoulder or elbow), kinetic energy of the system may be computed, and its integral over any particular time period minimized to arrive at Eq. 2. This equation has components that are:

$$\begin{array}{c}\hfill \mathbf{H}\left(\theta \right)\equiv \left[\begin{array}{cc}\hfill a_1+a_2+2a_3\cos {\theta }_2\hfill & \hfill a_2+a_3\cos {\theta }_2\hfill \\ \hfill a_2+a_3\cos {\theta }_2\hfill & \hfill a_2\hfill \end{array}\right]\hfill \\ \hfill \mathbf{C}(\theta ,\stackrel{.}{\theta })\equiv \left[\begin{array}{cc}\hfill -a_3{\stackrel{.}{\theta }}_2\sin {\theta }_2\hfill & \hfill -a_3({\stackrel{.}{\theta }}_1+{\stackrel{.}{\theta }}_2)\sin {\theta }_2\hfill \\ \hfill -a_3{\stackrel{.}{\theta }}_1\sin {\theta }_2\hfill & \hfill 0\hfill \end{array}\right]\hfill \end{array}$$ (11)

with physical parameters derived from the inertia matrix that are:

$$a_1\equiv I_{1c}+p_1{l}_{c1}^2+p_2{l}_1^2,a_2\equiv I_{2c}+p_2{l}_{c2}^2,a_3\equiv p_2{l}_1{l}_{c2}$$ (12)

where l_c1 denotes the length from shoulder joint to the center of gravity of the upper arm, and l₁ and l₂ denote the length of the upper arm and forearm, and I_1c and I_2c denote the inertia of each link. For example, in the case of the shoulder segment:

$$I_{1c}\equiv \sum _i{m}_i({}^{c}r_{ix}^2+{}^{c}r_{iy}^2),p_1\equiv \sum _i{m}_i.$$

A lumped parameter estimation technique (Gautier and Khalil 1989; Gomi and Kawato 1996) was used to estimate the inertial parameters (Eq. 12) of each subject’s arm. Briefly, subjects held the handle of a high performance robot in hand (Fig. 2) and maintained equilibrium at configuration θ_o. The robot has been described elsewhere (Shadmehr and Brashers-Krug 1997). Their arm was supported in the horizontal plane with a sling hung from the ceiling. They were told to relax while the robot vigorously moved the hand about a region roughly three times the workspace where the reaching movements were to be performed. This procedure was repeatedly performed over a two week period to establish stability of the estimation. We measured state of the robot ${\mathbf{q}}_r={\left[{\varphi }^T{\stackrel{.}{\varphi }}^T\right]}^T$, ϕ^T = [ϕ₁ ϕ₂] and interaction forces at the handle f = [f_x f_y]^T. We then used a simple 2-link kinematic model, adjusted for each subject, to estimate the state of the subject’s arm ${\mathbf{q}}^T=\left[{\theta }^T{\stackrel{.}{\theta }}^T\right]$, θ^T = [θ₁ θ₂]. To estimate the arm’s inertial parameters, we assumed that during the procedure three kinds of forces dominated the motion of the arm: interaction forces at the handle, forces produced by the muscles, and inertial forces. We approximated the muscle forces in this procedure as a linear system being displaced from equilibrium:

$$\mathbf{m}(\mathbf{q},\mu )\cong -\left[\begin{array}{cc}\hfill \mathbf{K}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \mathbf{B}\hfill \end{array}\right]\Delta \mathbf{q},$$

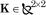where $\Delta {\mathbf{q}}^T=\left[{(\theta -{\theta }_o)}^T{\stackrel{.}{\theta }}^T\right]$ with and 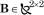representing passive stiffness and viscosity of the arm. The resulting equation of motion becomes:

$$\mathbf{H}\left(\theta \right)\ddot{\theta }+\mathbf{C}(\theta ,\stackrel{.}{\theta })\stackrel{.}{\theta }=-\mathbf{K}\Delta \mathbf{q}-\mathbf{B}\stackrel{.}{\mathbf{q}}+{\mathbf{J}}^T\mathbf{f}.$$ (13)

There are 11 unknown parameters a₁, a₂, a₃,k₁₁,···,k₂₂,b₁₁,···,b₂₂ that all appear linearly in the above equation. Bootstrapping was used to determine confidence intervals on the estimations. A second method of validation was through assessment of the physical plausibility of the inertia matrix, i.e., whether it was positive definite in all workspace regions. Third, we attached known weights to arm, re-estimated the parameters, and asked whether the change in inertia reflected the added weights.

Predicting the unperturbed path of a perturbed trial

The task for the subject was to make a reaching movement to a single target (displayed on a monitor facing the subject). The target was at 90 degrees at a displacement of 10 cm. At random trials (with a probability of 1/6), a torque pulse of width 100 ms perturbed the arm (Fig. 2A). The pulse was always delivered at the same time (100 ms) into the movement, but with varying magnitude or direction.

In order to estimate impedance, it was essential to be able to predict where the limb would have gone, q_o, and muscle forces that would have been produced, m_o, had the limb not been perturbed. Instead of averaging all unperturbed movements and taking this as an approximation of where the hand might have gone in any particular trial, we used a different approach. We used the portion of the limb’s movement before perturbation in any given trial as a key to estimate the intention of the subject for that movement.

The first step was to parameterize unperturbed movements. Unperturbed trials were organized in a data matrix with one row per movement. The number of columns equaled number of data samples per movement. Let us name this data for unperturbed trials as S. It can be represented as:

$$\mathbf{S}=[{\mathbf{S}}^a\mid {\mathbf{S}}^b]$$

where S^a represents the data samples from onset of the movement until the time perturbation is expected, $[t_0,t_p^{-}]$, and S^b represents the data from expected perturbation time to end of movement. The movement that we are trying to predict will be represented by q = [q^a | q^b], where q^a is the unperturbed portion of the trial (and is known), while q^b is where the system would have gone if it had not been perturbed (and is unknown).

Two methods of prediction were considered. In the first method, all unperturbed movements were used as bases to represent the perturbed trial:

$${\mathbf{q}}^a={\mathbf{k}}_1^T{\mathbf{S}}^a.$$

Assuming the same relationship between the vector and sample data matrix after perturbation onset time, we have:

$${\mathbf{q}}^b={\mathbf{k}}_1^T{\mathbf{S}}^b={\mathbf{q}}^a{\left[{\mathbf{S}}^a\right]}^{-1}{\mathbf{S}}^b.$$

In the second method, principal components of the unperturbed trials were used as bases to predict q^b. Initially, the unperturbed trials were represented through their principal components, and a relation Q between the period before and after the expected perturbation was established:

$$\begin{array}{c}\hfill {\mathbf{S}}^a={\mathbf{K}}_a{\mathbf{S}}_{pc}^a\hfill \\ \hfill {\mathbf{S}}^b={\mathbf{K}}_b{\mathbf{S}}_{pc}^b\hfill \\ \hfill Q={\mathbf{K}}_a^{-1}{\mathbf{K}}_b\hfill \end{array}$$

Then the perturbed trial q^a was fitted to ${\mathbf{S}}_{pc}^a$ and qb was predicted. To evaluate the method, we divided the unperturbed trials into two groups, bases and test, and used each method to predict motion of the limb in the test subgroup. We found the second method to be superior in prediction accuracy and report only those results arrived at with this method.

Experiments

Healthy volunteers (n=3, age 23, 27 and 36, one female and two males) began by practicing movements with the robot in the null field. We recorded three blocks of 96 movements, all toward target at 90 degrees (movements back to center were not analyzed). We recorded position and velocity of the robot and used measured kinematic parameters of the subject’s arm to estimate position, velocity, and acceleration of the elbow and shoulder joints. We measured forces at the hand and directly estimated the external torques τ acting on each joint (in Eq. 1). From the estimated inertial parameters, an estimate of inertial forces was made and by subtracting measured external forces at the handle, an estimate of muscle forces m_o(q,t) was arrived at for each recorded hand trajectory in this null field. No perturbations were applied in this initial set of movements,.

Next, 27 blocks of 96 movements (all toward 90 degrees) were performed. Perturbations of random magnitude (probability 1/9, range 7 to 15 N) and direction (probability of 1/23, range 7.5 to 172.5 deg) were applied to randomly selected movements (probability of 1/6). The perturbation directions are shown in Fig. 2B. We chose perturbations that resisted movements because assisting movements proved nearly destabilizing for subjects in force fields.

For each perturbed trial, the resulting muscle force m_o(q + Δq,t) was estimated. Next, the principal component approach was used to predict where the limb would have gone if it had not been perturbed in that trial, arriving at q, and the estimated muscle forces along that trajectory m_o(q,t). The difference between this and the perturbed trial were then represented with function Δm_o(Δq,t), representing impedance along the perturbation Δq(t).

Next, five blocks of 96 movements were performed (all toward 90 degrees) with the robot producing a force field defined by $\mathbf{f}=B\stackrel{.}{\xi }$, where B=[0, 13; -13, 0] N·s/m (Fig. 2C). Performance parameters demonstrated essentially complete adaptation by the end of the first block of movements, with hand trajectories converging onto those observed in the null field. Forces at the handle were then subtracted from inertial forces to arrive at an estimate of muscle forces in unperturbed trials in the force field, m₁(q,t) .

Next, the arm was perturbed during motion in the force field. Similar to the null field condition, 27 blocks of 96 movements were performed. Perturbation directions were as before, but their magnitude was limited to 9 N. This was because these perturbations were on top of an existing force field and together would approach the limits of the torque motors. For each trial, forces at the handle were subtracted from inertial forces to estimate m₁(q + Δq,t). The trajectory and forces that would have been recorded if the limb had not been perturbed were then estimated and the difference was an estimate of the impedance along the perturbed trajectory, Δm₁(Δq,t). This impedance was compared to the values measured in the null field.

In order to compare our results with a control condition, we performed a final experiment where the subjects were instructed to try to stiffen their arms as they moved in the null field. The change in impedance with respect to the baseline condition in the null field was estimated.

Comparing impedances: state and time matching

Functions Δm_o(Δq,t) and Δm₁(Δq,t) must be compared along identical displacement and time trajectories in order to establish impedance changes during adaptation. However, these functions are only known for specific histories of state transitions: they have been estimated from a finite number of perturbations. For example, a perturbation in the force field might result in a particular state trajectory and associated muscle forces. At each time sample into this trajectory in the force field, we need to know what the muscle forces would have been if the limb was moving in the null field and had reached this same state at this same time after the perturbation.

The procedure that we used is a parametric nonlinear approximation of the sampled data Δm_o(Δq,t), called Successive Approximations (SA), as described by Dordevic et al. (2000). Once the model of Δm_o(Δq,t) is constructed via SA, it allows for interpolation between the sampled data points. Given a set of parameters like perturbation direction and magnitude in the null field, the approximation will produce the states that the limb will follow and forces that the muscles will generate. More importantly, however, the model can be addressed randomly: given a particular state at a particular time, one can compute the expected restoring forces (Dordevic et al. 1999).

To estimate impedance in the null field, we used 23 directions and 9 magnitudes of perturbation. Each perturbation was given at least twice. The state and force trajectories recorded for each combination of perturbation direction and magnitude were averaged. Each component of the resulting trajectory (i.e., position along the x and y axis, velocity along the x and y axis, and muscle forces transformed to hand force along the x and y axis) was approximated with a 10^th order polynomial in time. The very high order was necessary for the high frequencies encountered at the moment of perturbation. This resulted in eight three dimensional matrices of size 23 × 9 ×11, one matrix for each component of the state and force vectors. Next, the dimension representing perturbation direction was fitted with polynomials, and finally the dimension representing perturbation magnitude was fitted with polynomials. The result was a model that given a perturbation vector produced a trajectory of states and forces in the null field condition. Quality of the model was determined through bootstrapping to arrive at an estimate of confidence intervals.

To validate the model, one of the subjects was asked to return for a second day of testing. On this second day, new perturbations were given and force responses were measured in the null field. These perturbations were not among the directions and magnitudes with which the model was trained on day 1. We quantified the accuracy of the model in predicting perturbation responses to these perturbations.

The next step was to compare force changes in the null field with that in the force field. Each perturbed trajectory in the force field resulted in a particular state trajectory. For each sampled time in this trajectory, the model of the null field was repeatedly ran to find the perturbation vector that produced the closest state in that time after the perturbation. State distance was measured by an L2 norm of the state vectors. In order words, we searched the null field impedance model to match the state of the limb that we had observed at a given time after perturbation in the force field. This time and state matching allowed us to compare functions Δm_o(Δq,t) and Δm₁(Δq,t) at similar states and time. Our implicit assumption in this comparison was that after training in the force field, the unperturbed trajectory q(t) was the same as the unperturbed trajectory in the null field. This is based on previous observations that there is a convergence of trajectories during adaptation to the one observed in the null field (Shadmehr and Mussa-Ivaldi 1994).

Results

The parameters of the inertia matrix (Eq. 12) were estimated from fitting Eq. (13) to trajectories where the robot vigorously moved the subject’s arm. Sessions were repeated 6-8 times over a two week period. Confidence intervals on the estimates were arrived through bootstrapping. The results are shown in Table 1. We also attached known weights to the upper and forearms and compared the change in the estimates of inertial parameters with the predicted values. The error in prediction was consistently less than 8%. The small size of the confidence intervals, the fact that in all three subjects the estimated inertia matrix is positive definite, and the similarity of the values to previously published results (Hodgson and Hogan, 2000), suggested that the inertial parameter estimation process was reasonably accurate.

Table 1.

Estimated inertial parameters (mean ± SD) for three subjects

Subject	a1 [kg m2]	a2 [kg m2]	a3 [kg m2]
A	0.2347 ± 0.0034	0.0990 ± 0.0014	0.0730 ± 0.0014
B	0.2936 ± 0.0041	0.0788 ± 0.0009	0.0882 ± 0.0012
C	0.4296 ± 0.0081	0.1433 ± 0.0017	0.1323 ± 0.0010

We next evaluated the technique to predict where the limb would have gone if it was not perturbed. The procedure relied on the characteristics of the movement during the interval before the perturbation (i.e., interval 0-100 ms into the movement). We divided the unperturbed trials into two equal groups, bases and test. The Principal Component procedure was used to represent the unperturbed trajectories in the bases set. The 0-100 ms interval in a given test movement was used to predict the remainder of that movement’s trajectory, given the observations in the bases set. An example of a typical test movement is shown in Fig. 3A, and statistics over all movements in the test set are shown in Fig. 3B. We found that the technique was generally very accurate in predicting position and velocity, and less so in predicting acceleration. The average rectified acceleration error was 17%, with 0.25 N of average force error. In comparison, there was a consistent increase in estimation error when we did not use this principal component approach but instead relied on an average of movements in the bases set.

Figure 3.

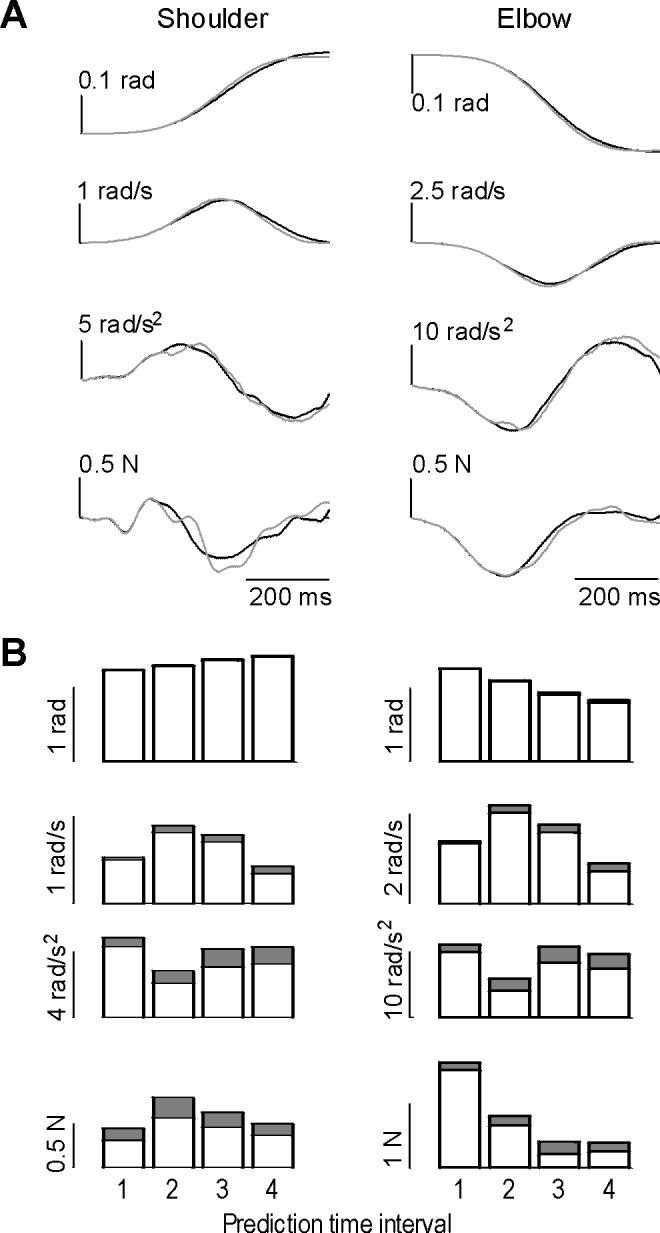
A principal component algorithm was used to parameterize trajectory of unperturbed movements during the interval 0-100 ms, and to predict the remainder of the movement’s trajectory. To evaluate the procedure, a set of unperturbed movements was divided into bases and test sets. (A) Sample movement in the test set, as predicted by the algorithm. Solid line is the measured trajectory, gray line is the predicted trajectory. (B) Performance over all movements and subjects. Average of absolute error is plotted on top of average of absolute state and force values over four intervals after movement initiation. Interval 1: 0.1-0.2. Interval 2: 0.2-0.3 ms. Interval 3: 0.3-0.4 ms. Interval 4: 0.4-0.5 ms.

A typical perturbed trajectory in the null field is shown in Fig. 4A along with the predicted unperturbed trajectory. The perturbation is a force vector along the x axis that displaces the hand 100 ms after hand velocity crosses a threshold of 0.03 m/s. We computed the torques produced by the muscles in the unperturbed case, m_o(q,t), and in the perturbed case, m_o(q + Δq,t), and the difference between the two, Δm_o, which is a measure of impedance along the perturbation Δq. We then represented each torque vector in terms of forces on the hand, and then plotted its x component in Fig. 4B. Note the bi-phasic force response that is generated in response to the perturbation: a rapid force change that resists the perturbation with a time scale of about 100 ms, followed by a second response that starts at around 120 ms. We consistently observed this bi-phasic response with little or no change in its timing for all perturbation vectors (Fig. 5).

Figure 4.

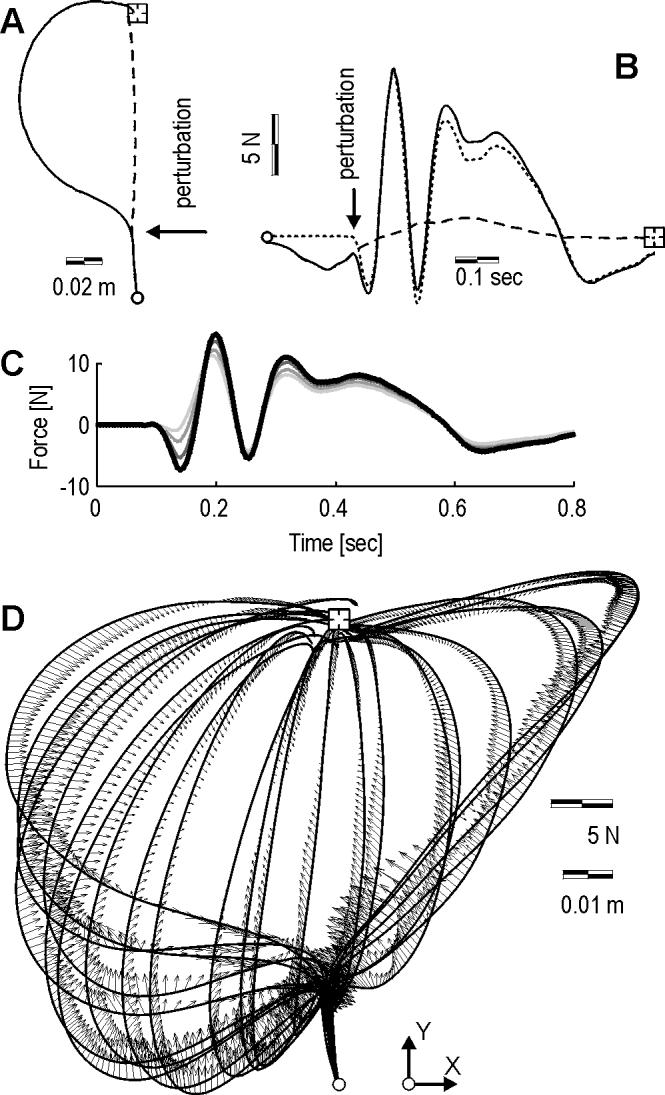
Typical trajectories and computed perturbation response forces in the null field. Perturbation is applied 100 ms after movement initiation is detected. (A) Hand paths to the target (square). The solid line is the perturbed path. The dash line is the path that is predicted to occur if the movement was not perturbed. (B) Solid line: muscle torques in the perturbed trajectory m_o(q + Δq,t), plotted in terms of forces on the hand (x component of the vector only). Dash line: muscle forces expected in the unperturbed trajectory m_o(q,t). Dot-dash line: muscle forces produced in response to the perturbation: m_o(Δq,t) ≡ m_o(q + Δq,t) - m_o(q,t). (C) Sensitivity of the muscle response force m_o (Δq,t) to potential errors in parameter estimation of the inertia matrix. Here, the results are shown for the case where parameters were scaled incrementally to 30% larger. An underestimation of inertial parameters primarily affects the first 50 ms of muscle response force estimation. (D) Muscle responses torques m_o(Δq,t) are plotted as forces on the hand for a set of perturbed trajectories.

Figure 5.

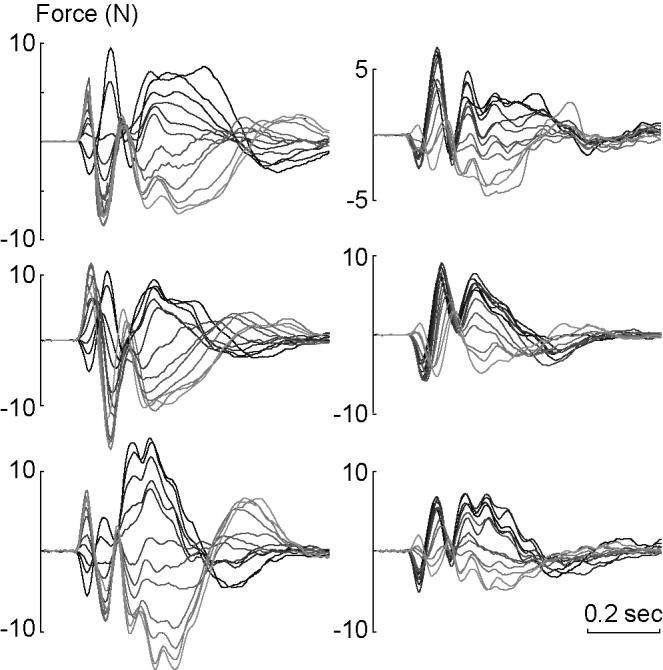
Muscle response forces, x-axis component only, in the null field m_o(Δq,t), and in the force field m₁(Δq,t), for the three subjects. Left column: null field. Right column: force field. The response forces are plotted as the direction of perturbation vector rotates from one extreme (light gray corresponds to the far right in Fig. 2B) to another (black corresonds to the far left in Fig. 2B). Whereas the responses are symmetric in the null field, they are clustered toward positive values in the force field.

We next calculated the extent to which potential errors in inertial parameter estimation might have influenced the estimation of the perturbation response forces. We systematically varied each parameter by up to 30% and reestimated the muscle forces for each perturbation. In general, we found that in the 50 ms period after onset of the perturbation, muscle force estimation was highly sensitive to inertial parameters. An under estimation of inertia resulted in significant over estimation of muscle forces during this period. Beyond 50 ms after the onset of the perturbation, potential errors in inertial parameters had significantly less effect on estimated muscle forces. This is shown for a typical movement in Fig. 4C. Close examination of the data led us to believe that while the biphasic force response pattern was a repeatable feature of the system, uncertainty in estimation of the human arm’s inertia would reduce our confidence for estimation of muscle forces during the first 50 ms after a perturbation. In Fig. 4D the torques Δm_o are transformed to hand forces and plotted for all perturbed trajectories.

Subjects then practiced in a force field (Fig. 2C). Because the target appeared in only one direction, we expected and observed rapid improvements in performance. From the unperturbed movements the function m₁(q,t) was estimated. In a fraction of movements, perturbations were imposed and muscle torques, m₁(q + Δq,t), were estimated. Comparing the perturbed and unperturbed movements resulted in an estimation of muscle torques in response to the perturbation, Δm₁. In Fig. 5 (right column), Δm₁ is plotted in terms of forces on the hand (x component) for a range of perturbation directions. The bi-phasic response was again present, but comparison of the left and right columns of this figure, corresponding to perturbation response in null and force fields, suggested that there had been a change in the way the motor system responded to a perturbation.

In the null field, as the perturbation vector rotated from one extreme to another, the restoring forces also rotated. This resulted in a symmetric behavior of the restoring forces with respect to perturbation direction, especially during the interval 50-150 ms after the onset of the perturbation. However, when perturbations were applied in the force field, rotation of the perturbation vector no longer produced a symmetric rotation of the muscle force response 50-150 ms after perturbation onset. Rather, there was a tendency for the restoring muscle forces to be positive regardless of perturbation direction. This is intriguing because the force field that the subjects had adapted to always pointed in the negative x direction during the unperturbed reaching movements (Fig 2C). However, a quantitative comparison of the left and right columns in Fig 5 would require an algorithm that matched trajectories along the same paths in time and space.

To perform this matching we used an algorithm called Successive Approximation (Dordevic et al. 2000). The algorithm uses polynomials in time to represent states and force trajectories for a given perturbation direction and magnitude in the null field. Polynomials in direction and magnitude are then used to represent the change in the coefficients of the polynomials in time. The result is a nonlinear representation of states visited and forces produced as a function of perturbation direction, magnitude, and time. The next step is to effectively “invert” this model so that for any given state and time, we would know what the restoring forces would have been in the null field. To do this, a search was performed for each given state to find the direction and magnitude of perturbation that at the given time would produce the state that in terms of an L2 norm was closed to the input state. The result was the restoring force expected at this state and time.

To test the algorithm, we first performed a bootstrapping procedure and then a validation experiment. In the bootstrap, confidence intervals were calculated on the model’s predicted states and forces for a given perturbation vector, and presented in terms of how well it correlated to the measured data. The correlations were extremely high for position variables (average of 0.99 with negligible confidence intervals), slightly lower for velocity variable (average of 0.97+/-0.005), and similarly high for force (average of 0.96+/-0.005) (Wang 2000).

In the validation experiment, one set of perturbations was imposed on the hand and a model via Successive Approximation was constructed. The subject then returned on a subsequent day and a new set of perturbations (not among the first set) was given. Restoring forces at the states visited for these new perturbations were calculated. For each state and time point in the data of the second set, the Successive Approximation model of the first set was used to predict what the forces should be. The measured data along with errors in the model’s predictions are plotted in Fig. 6. In general, errors peaked at 50 ms after perturbation onset, and then were negligible for up to 500 ms. Errors became significant near the end of the movement (600 ms after perturbation onset). This underlines our difficulty in precisely accounting for behavior of the limb during the perturbation (which lasted 100 ms), but gives some confidence that the procedures are robust for other periods.

Figure 6.

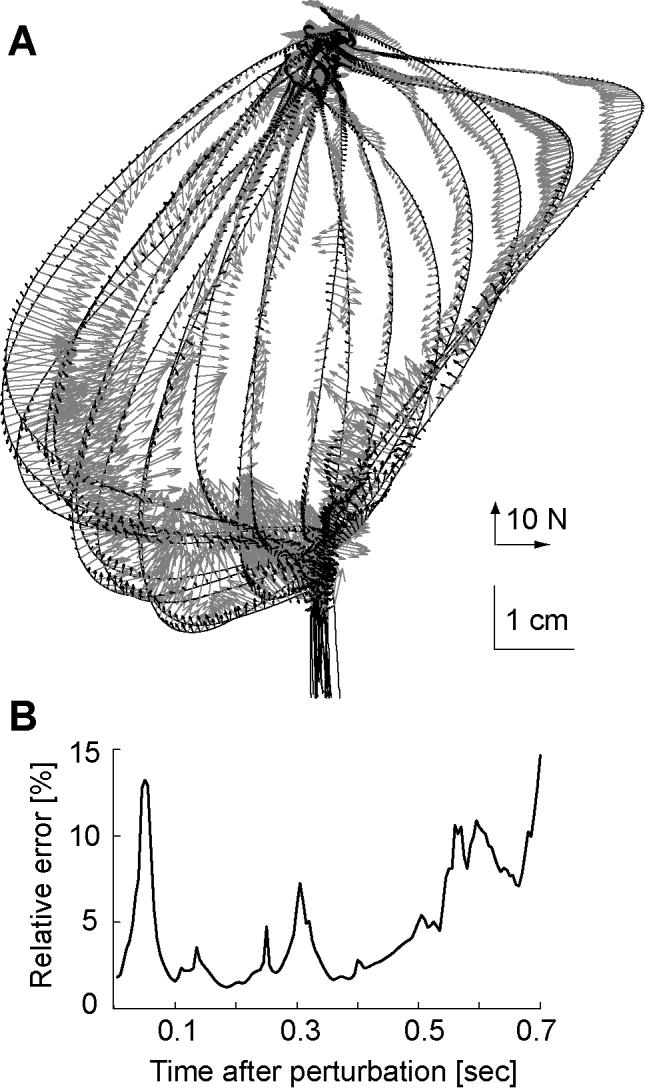
Test of the matching algorithm. Successive Approximation was used to model state and force trajectories that resulted for a set of perturbations in the null field. Muscle response forces were then measured for a novel set of perturbations and the model of the first set was used to predict behavior in the second set. (A) The measured forces (shown in gray) and the error in model’s predictions (black arrows) are shown along measured trajectories. (B) Error in prediction, measured as a percentage of the magnitude of the actual force, is plotted as a function of time after perturbation onset.

The perturbed trajectories recorded for a subject in the null and force field conditions are plotted in Fig. 7. In order to ensure that the states visited in the force field would be a subset of those visited in the null field, smaller magnitude perturbations (9 N) were used in the force field than the maximum values (15 N, range of 7-15 N) used in the null field. The figure illustrates that grossly, positions and velocities visited in the null field were indeed a superset of those visited in the force field. We did find, however, that in some cases y velocity in the field exceeded by about 25% the maximum values recorded in the null field perturbations. This is the range of extrapolation required of the model of the null field forces.

Figure 7.

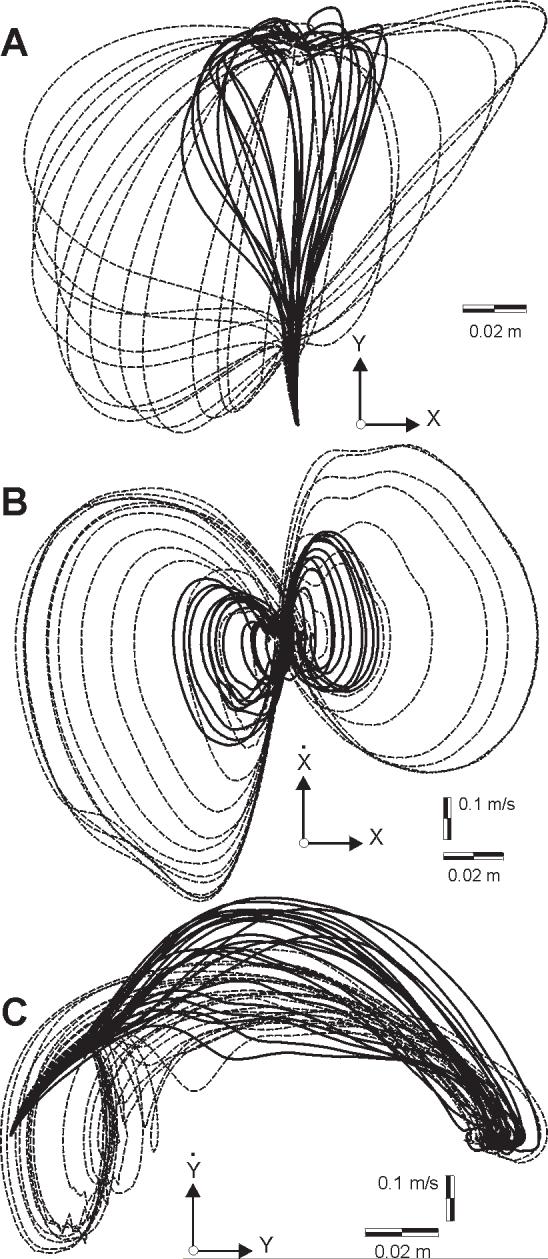
State trajectories of perturbed movements in null field (dashed line) and force field (solid line) for a typical subject. Generally, the states visited in the null field are a superset of those visited in the force field. Null field data is for the highest magnitude of perturbation vector (15N). Force field data is for 9N perturbation vector. (A) Position paths. (B) Position and velocity in x. (C) Position and velocity in y.

We next applied these tools to estimate the change in perturbation response forces due to adaptation of the controller. For each subject, perturbation responses computed in the force field (e.g., Fig. 5) were considered. For each movement, a transition of state trajectories and associated forces were observed, Δm₁(Δq,t). We used the Successive Approximation model of the trajectories recorded in the null field to estimate response forces along a matched state trajectory, Δm_o(Δq,t). In Fig. 8A, the difference in these two function is plotted along the hand’s trajectory for each subject. We found a consistent pattern of change: a perturbation to the adapted controller resulted in a response from the muscles that took into account the pattern of the imposed force field and attempted to compensate for it. In effect, the impedance of the arm had changed to reflect the behavior of the environment. This is inconsistent with an adaptive controller (Fig. 1A) that relies only on an inverse model. Instead, the results suggest that the controller has changed not only its feedforward pathways, but also in the way it processes sensory information and the way it responds to errors that result from perturbations.

Figure 8.

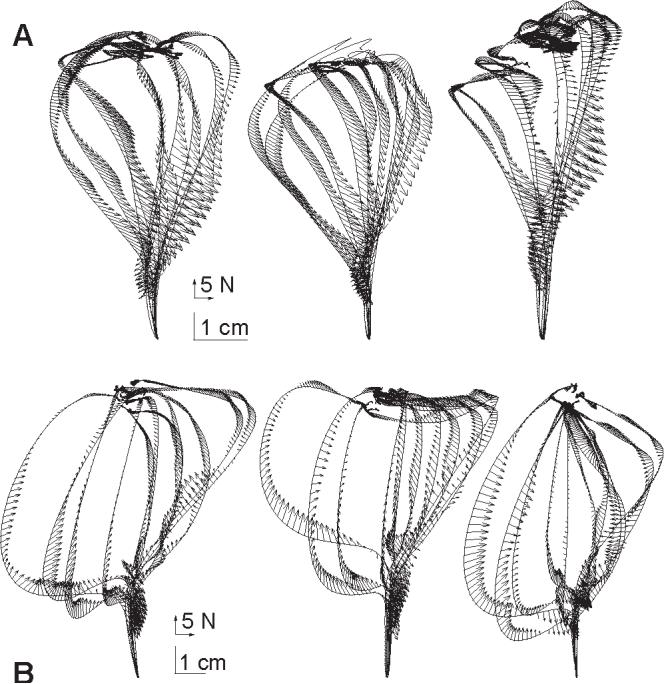
Change in muscle perturbation response as compared to responses measured in a baseline condition. (A) As subjects practiced movements in the force field, the change in perturbation response with respect to baseline conditions in the null field was measured and is plotted here along perturbed trajectories in the force field. Beyond the 80 ms period after perturbation onset, the change in force response is consistently a vector that points against the force field. (B) Control experiment. Subjects were asked to co-contract their arm muscles as they performed movements in the null field. The change in perturbation response with respect to baseline conditions in the null field is plotted along perturbed trajectories in the co-conctracted condition. Beyond the 80 ms period after perturbation onset, the change in force response is generally a vector that points toward the straight-line path to the target.

To test the validity of the entire process of estimating impedance changes, we performed a control experiment where there was a clear expectation of the shape of the impedance change. In this control experiment, the three subjects were asked to perform reaching movements, but now with increased levels of co-contraction in their arm. Perturbations were again delivered and the change in the impedance was estimated with respect to each subject’s “natural” movements in the null field. The results are in shown in Fig 8B. As expected, the changes in impedance are forces that converge toward the unperturbed trajectory (straight line to the target), indicating an increase in the strength of the perturbation response of the system, which is consistent with increased stiffness.

Discussion

A number of previous reports have estimated human arm impedance during multi-joint voluntary movements (Gomi and Kawato 1997; Gomi and Osu 1998; Dolan et al. 1993; Lacquaniti et al. 1993). In these works, small perturbations were applied to the limb and the restoring forces were approximated as a function of displacement. A linear approximation of this relation resulted in measures of arm impedance in terms of time varying stiffness and viscosity. This has revealed that arm stiffness and viscosity are not constant during a movement but may be modulated depending on task constraints. In an elegant example, Lacquaniti et al. (1993) considered a ball catching task and measured how the limb responded to small perturbations as a function of time to the expected impact of the ball. They found that perturbation response changed to increase resistance of the limb mostly along the expected perturbation direction at around the expected perturbation time. In effect, the work illustrated that when the perturbation (ball impact) was predictable, the brain had the capacity to anticipate it and modify feedback response mechanisms to match task requirements.

Response to a perturbation is mediated via at least three distinct pathways: intrinsic muscle length-tension properties (near instantaneous response), short-latency neural responses that depend on spinal circuitries (latency of 30-50 ms), and long-latency responses that depend on transcortical pathways (latency of 75-120 ms). When a perturbation is predictable, only the long-latency response appear to undergo a modification (Strick 1978). This is an example of modification in a sensory-motor feedback control pathway.

However, there is also evidence that learning of some movements involves modification of a feedforward control pathway. For example, in learning to reach for a target, muscle activations during the period that precedes the movement systematically change to reflect compensation for the expected dynamics of the task (Thoroughman and Shadmehr 1999). This implies that the brain relies on an internal model that transforms desired trajectories into motor commands, and that training modifies this internal model. Taken together with the work on modifiability of long-latency pathways, it appears that the brain might have the potential to adapt both the feedforward pathways that initiate movements and the feedback pathways that responds to a perturbation as the movement proceeds.

Here we sought to test the hypothesis that during learning of simple reaching movements, coincident with a change in the feedforward neural commands there may be a change in the way that the motor system responds to sensory feedback. We had some evidence for this hypothesis from previous work where a set of simulations used a control system (Fig. 1B) that included a model of the inverse dynamics in the feedforward pathway and a model of the forward dynamics in the long-latency feedback pathway (Bhushan and Shadmehr 1999). We had found experimentally that during the adaptation process, if the force field was suddenly changed, the motion of the human arm could not be fully explained with a control system that only had an adapted inverse model. In particular, while the simple model of Fig. 1A could account for motion of the hand up to about 250 ms, beyond this point the behavior had characteristics that could not be produced by the model. This is around the time that one expects an influence from the long-latency feedback system. Indeed, when simulations used the system of Fig. 1B and assumed a change in the model of direct dynamics, simulations faithfully produced the characteristics observed in our subjects.

Because modification of the forward model would result in a change in the error response of the control system, a direct test would be to quantify response to perturbation before and after adaptation. Therefore, we asked if the response to perturbation changed and whether the change incorporated information about the novel dynamics that the limb was interacting with. This is another way of asking whether the impedance changed to match the dynamics of the task.

Methodological Considerations

In this work, we used on a lumped parameter approximation of the inertial dynamics of the upper arm. This is similar to the approach taken by Dolan (1991) and Gomi and Kawato (1997). However, the approach suffers from uncertainties about the lengths of the links and non-rigidity of the muscle mass. Furthermore, perturbation based estimation of inertia often results in weaker excitation of the proximal link because the robot is connected to the hand, resulting in possible under-estimation of this link’s inertial parameters. This in fact may explain some of the difficulties that we had in precisely estimating forces in the 0-50 ms period after the onset of the perturbation. Our results were most sensitive to errors in inertial parameters during this period, but fairly insensitive for period beyond this.

An alternate approach would have been to build an analytic model based on approximation of the shape of each link (for example, a cylinder for the upper arm and a cone for the forearm), as done by Hodgson and Hogan (2000). To determine validity of either approach, a reasonable way is to determine whether the results agree with the physical constraint that the inertia matrix be positive definite at arbitrary joint angles. In all subjects, the estimated inertia met this criterion. Furthermore, the parameter values found here were very similar to those reported by Hodgson and Hogan (2000).

Here we chose not to linearly approximate impedance via time-dependent stiffness and viscosity matrices. Although the linear approach has been used in nearly all previous reports on this subject, consideration of the effect of time delays raises significant issues which, in our view, merit its reevaluation (e.g., Stroeve 1999). To demonstrate the weakness of the linear approach, consider a mass-spring-damper system where the spring forces depend on a time delayed sensory feedback of position:

$$m\ddot{x}\left(t\right)+b\stackrel{.}{x}\left(t\right)+kx(t-\Delta )=0$$

If we use Taylor series expansion to represent the time delay, we have:

$$x(t-\Delta )=x\left(t\right)+\frac{dx}{dt}(-\Delta )+\frac{1}{2}\frac{d^{2}x}{d{t}^2}{(-\Delta )}^2+\cdots$$

If we drop all but the first three terms, we get an approximation to our original system that looks like:

$$\left(m+\frac{k{\Delta }^2}{2}\right)\ddot{x}+(b+k\Delta )\stackrel{.}{x}+kx=0$$

which demonstrates that time delays in position feedback result in increased apparent mass but decreased apparent viscosity. The longer the time delay, the more the stiffness term will appear as viscosity and inertia. In the case of perturbation response of the human arm, this has the potential to distort the long-latency component that relies on the transcortical pathways.

An alternate approach is to consider that perturbation response of the biological system is a nonlinear force function of state and time. One draw back is that evaluation of the function would require an extremely large set of observations. For this reason, our measurement of impedance was limited to force responses with respect to perturbations at only one interval after movement initiation. This precluded us from describing a full measure of impedance, but allowed us to compare impedance changes at this one perturbation interval due to adaptation. A second draw back is that impedances would have to be compared at identical state trajectories. We approached this problem through application of a novel method called Successive Approximation (Dordevic et al. 2000), which resulted in an addressable model of impedance in the null field.

Modification of Error Feedback Response

We found that perturbations consistently produced a bi-phasic force response from the muscles (Fig. 5). The timing of these responses were approximately consistent with those typically associated with short-latency spinal mechanisms and long-latency transcortical mechanisms (Strick 1978). The responses, however, qualitatively changed after the subject had adapted to a force field. Whereas in the null field, a rotation in the direction of perturbation resulted in a similar rotation in the direction of force response, in the force field this pattern no longer held true. Rather, perturbations that displaced the hand in either direction resulted in muscle forces that were no longer symmetric about zero but biased toward one direction: the direction that opposed the force field that the subject had adapted to.

This observation is inconsistent with the control framework of Fig. 1A, where all learning takes place in the feedforward pathway. Instead, when considered along with the simulation of results of Bhushan and Shadmehr (1999), the present results suggest that the motor system also adapts its sensory-motor feedback pathways during practice, perhaps through a system similar to Fig. 1B. In this system, practice results in formation of a model of forward dynamics of the system. When a perturbation takes place, sensory feedback and efferent copy are used to estimate current position. This is compared to the desired position, and the error changes the desired trajectory to the target. This process of updating the desired trajectory modifies the input to the inverse model, effectively changing the descending commands. Because the inverse model has also adapted, the change in the desired trajectory results in a change in the output that incorporates knowledge about the force field. The result is a force response that is different from that when the system is expecting a null field.