Abstract
Co-evolution has an important function in the evolution of species and it is clearly manifested in certain scenarios such as host–parasite and predator–prey interactions, symbiosis and mutualism. The extrapolation of the concepts and methodologies developed for the study of species co-evolution at the molecular level has prompted the development of a variety of computational methods able to predict protein interactions through the characteristics of co-evolution. Particularly successful have been those methods that predict interactions at the genomic level based on the detection of pairs of protein families with similar evolutionary histories (similarity of phylogenetic trees: mirrortree). Future advances in this field will require a better understanding of the molecular basis of the co-evolution of protein families. Thus, it will be important to decipher the molecular mechanisms underlying the similarity observed in phylogenetic trees of interacting proteins, distinguishing direct specific molecular interactions from other general functional constraints. In particular, it will be important to separate the effects of physical interactions within protein complexes (‘co-adaptation') from other forces that, in a less specific way, can also create general patterns of co-evolution.
Keywords: co-evolution, protein–protein interaction, interactome, phylogenetic tree, mirrortree
Introduction
Co-evolution is a well-documented phenomenon that is both an important force in the organization of biological communities and a key component of current evolutionary theory. The knowledge we have accumulated regarding the co-evolution of species is particularly relevant in the context of this review as the relationship between pairs of genes and proteins can be described in terms of co-evolution, extrapolating the concepts and methodologies developed for the study of species co-evolution to the molecular level.
The original formulation of the term co-evolution is usually attributed to Ehrlich and Raven (1964), even if the initial ideas on mutual influence between species can be traced back to Darwin's (1862) work on orchids and pollinators. Strictly defined, co-evolution is the joint evolution of ecologically interacting species (Thompson, 1994) and it implies the evolution of a species in response to selection imposed by another. In this definition, co-evolution requires the existence of mutual selective pressure on two or more species.
Ecologists have described a number of examples of co-evolution from paired species, including inter-specific competition for resources, the interaction between parasites and their hosts, the relationship between predator and prey, as well as symbiotic relationships (see for example, Moya et al, 2008). In some cases, it has been possible to pinpoint morphological traits developed as a consequence of co-evolution, including direct or inverse concordances between characters (Thompson, 1994). In general, some similarity of the corresponding phylogenetic trees would be expected in these cases, for example the taxonomy of parasites and their hosts tend to be topologically similar (see for example, Stone and Hawksworth, 1985; Hafner and Nadler, 1988). However, it is important to note here that although the congruence of such trees reflects a similarity between the evolutionary processes (co-evolution) this is not sufficient evidence to demonstrate the existence of mutual influence (co-adaptation). Indeed, this resemblance does not necessarily imply that one has influenced the shape and structure of the other, or vice versa.
In general, a species evolves in response to a complex interaction with many other species. In extreme cases, when the process of co-evolution involves whole groups of species and specific examples of co-evolution between pairs of species cannot be identified, the process is called ‘diffuse co-evolution' or ‘guild co-evolution' (Thompson, 1994; Futuyma, 1997). This general ‘diffuse co-evolution' is the background process behind the constant improvement in the fitness of species (often referred to as the ‘arms race between competing species' and formulated as the ‘Red Queen Hypothesis'; Van Valen, 1973, 1977).
To study the molecular mechanisms that cause co-evolution, it is important to bring back the concept of ‘co-adaptation', which was first introduced by Dobzhansky (1950, 1970); see also Wallace (1953, 1991). The concept of co-adaptation was coined to refer to the coordination of specific changes in functional features (initially to the selective superiority of inversion heterozygotes; Ridley, 2003). In a number of cases, it has been possible to detect the adaptation of a set of genes to optimize physiological performance and reproductive success (see for example, Burton et al, 1999).
Taking this concept to the molecular level, co-adaptation can be applied to direct mutual interaction between proteins, for example physical contact as part of protein complexes, that are ‘complex and that require mutually adjusted changes' following the definition of co-adaptation by Ridley mentioned above.
Here, we will use the term ‘co-evolution' to refer to the similarity of evolutionary histories, which can be quantified through the similarity of the corresponding phylogenetic trees. By way of contrast, we will use ‘co-adaptation' to refer to the molecular mechanism that would explain co-evolutionary changes by the specific influence of protein families on each other's evolutionary histories. According to our definition, co-adaptation will imply that changes in one family will influence those in the other, and vice versa, in a way that will be mostly specific for those proteins. With this definition, co-adaptation will be a mechanism that requires a direct relationship between the corresponding families (e.g. physical interaction), but it will not necessarily the only cause of co-evolution. Other factors that would have a common general influence on two proteins, without requiring interaction between them, could also influence their evolution and cause them to present co-evolutionary characteristics.
Here, we shall review the evidence for co-evolution and co-adaptation at the molecular level, indicating the practical consequences of their study on our understanding of the organization of protein interactions, and how they are exploited to predict protein interactions.
Co-evolution at the residue level
It is tempting to think that mutations at a given position in a protein are not completely independent of mutations at other positions within the same protein. The most widely studied characteristic related to concerted mutational behaviour is the so-called ‘correlated mutations' within multiple sequence alignments (MSAs).
In MSAs, homologous proteins are represented in such a way that equivalent residues are placed in the same column. Hence, a column in an MSA contains a representation of amino-acid changes permitted during evolution at that position. As functional and structural requirements impose constraints on these changes, MSAs are a rich source of structure–function information. In some cases, it is possible to observe concerted mutations at two positions (columns) in MSAs, the amino-acid changes in one position being related to those in the other. Some time ago, a weak but consistent relationship was found between this correlated mutational behaviour and spatial proximity (Göbel et al, 1994; Olmea and Valencia, 1997). One hypothesis to explain such relationships states that destabilizing changes in one position can be evolutionarily fixed if they are ‘accommodated' or ‘compensated' by a modification nearby. Co-evolution between residues in the same proximity seems to have an important function in protein structure and function (Shim Choi et al, 2005; Socolich et al, 2005). Nevertheless, the relationship between correlated mutations (evident in MSAs) and compensatory changes (a possible explanation for these observations) has remained largely elusive. In practice, a number of variations in the specific methods to predict physical proximity based on the detection of correlations have been implemented with moderate success (see Fodor and Aldrich, 2004; Shackelford and Karplus, 2007 for systematic comparisons of methods).
Various arguments can be used to explain the difficulties in detecting signs of compensatory mutations in MSAs. For example, the presence of binding sites and active sites imposes a strong constraint on the variability of sequences that is difficult to separate from the purely structural one. The conservation of apolar residues in the protein core and the constraints imposed during folding tend to occlude possible signs of correlated changes. Furthermore, the relationship between correlated changes and physical proximity is complicated by the dependence between distant residues that cooperate in signal transmission processes (e.g. induced fit movements).
In any case, it is important to take into account that compensation can be achieved by cooperation between relatively close sets of residues organized into local structures without the need of direct physical contact between all the participating residues. This type of local compensation fits well with the co-variation model (Fitch, 1971; Shindyalov et al, 1994; Susko et al, 2002; Wang et al, 2007). In this model, the induction of mutations can be explained in terms of the increased local capacity to accept mutations after the introduction of an initial isolated change, with no need of direct interactions between the mutated residues.
The relationship between correlated mutations and spatial proximity (not always direct contact) has not only been found between residues in the same protein but also between residues in different proteins (Pazos et al, 1997; Yeang and Haussler, 2007; Burger and van Nimwegen, 2008). The hypothesis invoked to explain these inter-protein correlations is the same as that for the intra-protein ones, and involves co-adaptation between interacting proteins at the residue level. In some cases, it has been shown experimentally that compensatory changes at interfaces can indeed recover the stability of complexes lost due to an earlier mutation (Mateu and Fersht, 1999; del Alamo and Mateu, 2005). Correlated inter-protein changes seem to be more evident in obligate complexes, in which the two proteins must constantly interact to perform their biological function (Mintseris and Weng, 2005). Signs of inter-protein correlation can be used in some cases as constraints to select the arrangement of two interacting proteins or protein domains (Pazos et al, 1997), or to guide protein docking experiments (Tress et al, 2005), even though the corresponding residues might not enter in direct physical contact (Halperin et al, 2006). Moreover, inter-protein correlated pairs can also be used to look for interaction partners (Pazos and Valencia, 2002).
Co-evolution at the protein level, similarity of phylogenetic trees
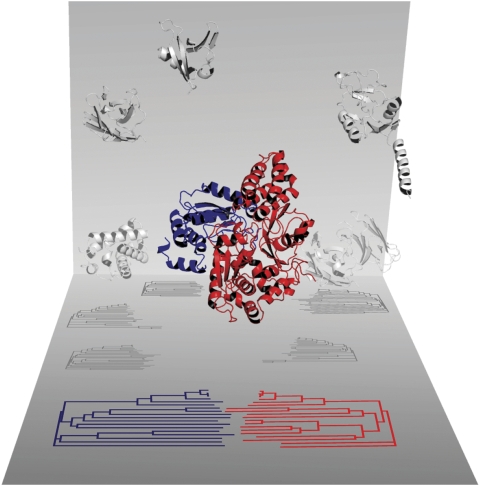
As mentioned in the Introduction, the protein feature most intuitively related to co-evolution is the similarity of the phylogenetic trees of interacting protein families. Qualitative similarities between phylogenetic trees have been observed in a number of interacting families (e.g. insulins and their receptors (Fryxell, 1996), dockerins/cohexins (Pages et al, 1997) and vasopressins/vasopresin receptors (van Kesteren et al, 1996)). Recent studies that have quantified the relationship between tree similarities and protein interactions in large data sets (Goh et al, 2000; Pazos and Valencia, 2001) have demonstrated that such similarity is not anecdotal. For example, the phylogenetic trees of the NuoE and NuoF subunits of the Escherichia coli NADH dehydrogenase complex display a clear similarity (0.86 in a 0–1 scale; in this methodology, the similarity between the phylogenetic trees is quantified indirectly as the Pearson's correlation coefficient between the sequence similarity matrices of the two families). These two subunits interact tightly as reflected in the 3D structure of the complex (PDB: 2fug; Sazanov and Hinchliffe, 2006; Figure 1). Many pairs of proteins in the flagellar machinery also co-evolve, as reflected by the similarity of their corresponding trees (Juan et al, 2008). Additionally, the similarity of phylogenetic histories can be used to predict the function of hypothetical proteins. For example, the hypothetical E. coli protein YecS strongly co-evolves with the flagellar protein FliY, suggesting that it is potentially acting in the flagella machinery.
Figure 1.
Co-evolution of interacting proteins. Example of two E. coli proteins that are tightly interacting (nuoE––blue and nuoF––red) and co-evolving (as reflected in the similarity of their phylogenetic trees, below). The observed co-evolution between these proteins is affected by many factors besides the co-adaptation of the two proteins, such as the interactions with other proteins in the cell (grey).
It has recently been shown that the tree similarity of interacting proteins is more evident when it is calculated for the residues that make up the actual interaction surfaces (Mintseris and Weng, 2005) or when relatively conserved regions are used rather than the full protein sequences (Kann et al, 2007). Co-evolution is also evident between interacting domains to such an extent that it is possible to pinpoint the domains responsible for the interaction using domain-restricted calculations of tree similarity (Jothi et al, 2006).
Obviously, the trees of any pair of protein families share a certain degree of similarity due to the underlying speciation of the host organisms. This similarity is in part related to the archetypal ‘tree of life' that represents the global evolutionary relationship of the species. Indeed correcting for this ‘background similarity' improves the performance of these methods (Pazos et al, 2005; Sato et al, 2005). Such background similarity can be extracted from an accepted ‘tree of life', for example that obtained from a molecular marker such as 16SrRNA or from a set of conserved genes (Pazos et al, 2005; Sato et al, 2005), or it can be directly inferred from the main tendencies in the data (Sato et al, 2005). An additional advantage of incorporating this information about the species tree is that non-standard evolutionary events (such as horizontal gene transfer) can be detected along with the predictions of interactions. This can be achieved by looking for incongruences between the species phylogeny represented in the ‘tree of life' and that of a given protein family (Pazos et al, 2005).
Because of its simple and intuitive nature, this ‘mirrortree' method (Pazos and Valencia, 2001) has been applied to many protein families (i.e., Devoto et al, 2003; Labedan et al, 2004; Dou et al, 2006) and different variations have been developed for a variety of applications (i.e., Goh and Cohen, 2002; Gertz et al, 2003; Ramani and Marcotte, 2003; Kim et al, 2004; Tan et al, 2004; Jothi et al, 2005; Pazos et al, 2005; Sato et al, 2005, 2006; Izarzugaza et al, 2006; Tillier et al, 2006; Waddell et al, 2007). For example, the concept of tree similarity was used to look for the correct mapping between two families of interacting proteins, that is, to choose which ligand within a family interacts with which receptor within another family. The idea is that the correct mapping (set of relationships between the leaves of both trees) will be that which maximizes the similarity between the trees (Gertz et al, 2003; Ramani and Marcotte, 2003; Jothi et al, 2005; Izarzugaza et al, 2006; Tillier et al, 2006). Mirrortree can also be used in a ‘supervised' way by training machine learning systems with examples of interacting and non-interacting pairs, using descriptors based on the phylogenetic trees of the proteins and the species involved (Craig and Liao, 2007).
The main problem of mirrortree-like approaches is the need to construct good phylogenetic trees on a genomic scale. These are necessary to assess the similarity of all possible pairs in the search for those that are correlated. The automatic generation of reliable phylogenetic trees, with all the steps involved (orthologue detection, distance estimation, methods to generate the tree and so on) is not trivial. Thus, advances in generating reliable phylogenetic trees on a genomic scale will greatly improve this approach (Huerta-Cepas et al, 2007).
Similarity of phylogenetic profiles as another case of co-evolution at the protein level
An extreme case of co-evolution involves the simultaneous loss of two interdependent proteins. One hypothesis seeks to explain this concerted disappearance of interacting proteins as ‘reductive evolution'. If the two proteins are needed to perform a given function and one of them is lost for any reason, the evolutionary pressure to maintain the other disappears as it cannot work alone. In a similar way, if one of the two proteins is ‘acquired' (i.e., horizontal gene transfer), the required partner must also be acquired. This is related to the concept of ‘selfish operons' (Lawrence, 1997), groups of related genes that are subject to concerted horizontal transfer. In practical terms, all this means that two related proteins will tend to be present in the same subset of organisms and absent in the rest. The pattern of presence/absence of a given protein (gene) in a set of genomes was termed ‘phylogenetic profile'. The similarity of phylogenetic profiles has been used extensively to detect protein functional relationships from genomic information (Gaasterland and Ragan, 1998; Marcotte et al, 1999; Pellegrini et al, 1999). These profiles constitute the simplest way of looking for protein co-evolution.
Initial attempts to detect protein interactions and functional relationships using ‘phylogenetic profiles' represented the distribution of proteins qualitatively, as binary vectors where ‘1' coded for the presence of the protein in an organism and ‘0' for its absence. Later, quantitative information was added by incorporating the similarity of a protein in an organism with respect to a reference organism (Date and Marcotte, 2003) into the vector positions. Once these vectors of species distributions (phylogenetic profiles) are defined, different measures of similarity can be used. It has repeatedly been shown that similar vectors are related to interactions or functional relationships between the corresponding proteins. For example, the phylogenetic profile of E. coli ribosomal protein RL7 reflects that this protein is present in most eubacterial genomes but not in archaea. Indeed, if we look for families with similar distributions, many ribosomal proteins functionally related to RL7 show up (Pellegrini et al, 1999). Other examples of functionally related families with similar species distributions include flagellar proteins (which also display similar phylogenetic trees as mentioned earlier) and proteins involved in amino-acid metabolism (Pellegrini et al, 1999). As with the similarity of phylogenetic trees or any other method for predicting functional relationships, the similarity of phylogenetic profiles can also be used for the ‘context-based' prediction of cellular activity. For example, the hypothetical E. coli protein YBGR has a species distribution similar to many proteins involved in amino-acid biosynthesis, supporting its function in this activity (Pellegrini et al, 1999).
Gene copy number appears to be another protein feature that co-evolves, in the sense that gene expansion in one family could be ‘accommodated' by corresponding expansions in a related family, and vice versa. In this sense, ‘quantitative' phylogenetic profiles coding the number of copies of a given protein family in a set of organisms can also be used to detect functionally related families (Ranea et al, 2007).
The selection of the set of organisms used to build such profiles has been shown to affect the performance of the method in predicting interactions (Sun et al, 2005). Indeed, the optimal set of organisms depends on the type of functional relationship we are trying to detect, a given set of organisms being better for detecting relationships between proteins of a specific functional class (Jothi et al, 2007). Incorporating evolutionary models into the methodology to differentially weight the gain/loss of genes depending on the phylogenetic context also improves performance (Zhou et al, 2006; Barker et al, 2007; Cokus et al, 2007). As with mirrortree, phylogenetic profiles encoding the presence/absence of protein domains rather than entire proteins can also be used to detect functional relationships (Pagel et al, 2004).
‘Anticorrelated' phylogenetic profiles (a protein is present when the other is absent, and vice versa) can also be informative and they have been linked to enzyme ‘displacement' in metabolic pathways (Morett et al, 2003). Recently, phylogenetic profiling was extended to triplets of proteins, facilitating the search for more complicated distributions (e.g. ‘protein C is present if A is absent and B is also absent'). This allows the detection of interesting cases related to biological phenomena beyond binary functional interactions, such as complementation (Bowers et al, 2004b). Phylogenetic profiling also helps in structure-based functional transfer: similar structures do not ensure similar functions (Devos and Valencia, 2000, 2001). However, if the phylogenetic profiles of two structurally similar proteins are also related, the chances that the two proteins have the same function are much higher (Shakhnovich, 2005).
This powerful and intuitive approach has some disadvantages. The main one is that it can only be applied to complete genomes, as only then is it possible to be sure of the absence of a given gene. In addition, it cannot be used with essential proteins that are present in most organisms as they would produce ‘flat' profiles (‘1' in all the positions) without information to match with other profiles. Moreover, this approach is more suitable for species with a strong tendency towards genomic reduction of unnecessary genes (bacteria and archea).
The idea of functional relationships between proteins has been extended to include other features together with the co-evolution related ones discussed above, leading to the concept of ‘functional neighbourhoods' (Danchin, 2003). Apart from the two methods discussed in detail here, there are many others for the prediction of functional associations between proteins based on co-evolution and other genomic features, which are termed ‘context-based' methods (Valencia and Pazos, 2002; Shoemaker and Panchenko, 2007). At the practical level, many of these methods are available through web resources such as STRING (von Mering et al, 2003), Prolinks (Bowers et al, 2004a) and ECID (Pazos et al, 2008)). As illustrated above with some examples, these methods can be used for the context-based functional transfer and, in this aspect, are orthogonal and complementary to the traditional homology-based strategy.
Co-evolution at the protein network level
Network concepts are becoming increasingly popular in molecular biology (Barabasi and Oltvai, 2004; Xia et al, 2004). Some biological phenomena cannot be deduced by simply summing the properties of the molecular components, but are ‘hidden' in the complex networks representing the relationships that exist between them. In the case of protein co-evolution, it is clear that if a given protein interacts with many different partners, the changes in its amino-acid sequence (and therefore in the topology of the tree) will be a complex combination of the effects produced by the interactions with all these partners. In this sense, the full network of molecular interactions in a cell can be seen as a co-evolving system.
Recently, a new method based on the construction of the whole network of inter-protein tree similarities has been proposed (Juan et al, 2008). In this case, the significance of the similarity of the trees of two protein families is evaluated in the context of the similarities to the trees of the rest of the proteome. Taking the complete co-evolutionary context into account substantially improves the detection of interacting proteins (Juan et al, 2008). This procedure not only corrects the interdependence between the pairwise co-evolutions discussed above but it also corrects for other factors that influence tree similarity. These factors include the bias introduced by the underlying species phylogeny (discussed above) and methodological errors during the detection of orthologues and the construction of the trees. Additionally, the information contained in this whole network of co-evolutions enables specific co-evolutionary trends to be separated from global trends (affecting many pairs), thereby providing important information on the structure and functioning of molecular complexes. For example, the interactions between members of the flagellar machinery are detected by this method with sensitivity and specificity higher than those obtained using the pairwise similarities alone (Juan et al, 2008).
The origin of co-evolution between protein families
One important question that arises is to what extent the observed co-evolution is due to direct compensatory changes in the corresponding proteins (co-adaptation) or to indirect factors that affect the sequences of both families in a similar magnitude. These include similar expression patterns, common functions in a given pathway, participation in a metabolic channelling event or collaboration in a specific cellular process.
It would make sense, and it is probably the first hypothesis that one might formulate, to think that coordinated changes in protein sequences are mechanistically related to the co-adaptation of the corresponding sequences and structures. The importance of compensatory changes can be justified in terms of maintaining the stability of protein complexes and/or the specificity of their binding to other proteins. As described above (see ‘Co-evolution at the residue level'), inter-protein compensatory changes, whereby a destabilizing mutation at the interface of one interacting partner is compensated for by a mutation in the other partner, have been found experimentally in different systems. Inter-protein compensatory mutations have also been proposed as an explanation for mutations that are pathogenic in one organism and neutral in others (Kondrashov et al, 2002; Kulathinal et al, 2004; Ferrer-Costa et al, 2007), as well as in cases where protein families are evolving very fast while having to maintain highly specific interactions with no cross-talk (Watanabe et al, 2000; Kachroo et al, 2001; Liu et al, 2001; Wang and Kimble, 2001; Haag et al, 2002). Given that inter-protein co-adaptation at the residue level has been repeatedly observed and it has a plausible physical interpretation, it makes sense to think that the observations of co-evolution at other ‘subprotein' levels (i.e., protein regions or domains) could, to some extent, also be the result of physical compensation. As mentioned above, co-evolution has been detected between entire proteins, protein domains (Jothi et al, 2006), conserved regions (Kann et al, 2007) and between protein surfaces in obligate complexes (Mintseris and Weng, 2005).
Alternatively, a number of forces affecting sets of proteins and genes can generate similar evolutionary rates, such as similar expression patterns, common cellular localization and functioning in a given biochemical pathway. These external forces can create in sets of genes under common pressure signatures of co-evolution without the need for specific co-adaptation between the corresponding proteins. Families with similar evolutionary rates in different organisms would ultimately present similar trees, because the changes that occur in both families and that are responsible for shaping their trees will be of a similar magnitude. Indeed, direct (Fraser et al, 2002; Hakes et al, 2007) and indirect (Eisen et al, 1998; Pal et al, 2001; Fraser et al, 2004; Subramanian and Kumar, 2004; Chen and Dokholyan, 2006; Drummond et al, 2006) relationships between similar evolutionary rates and protein interactions have been found.
Therefore, even if there are indications that compensatory co-adaptive changes occur between interacting proteins and they could moderately influence the similarity of the corresponding trees, it is difficult to think that co-adaptation is the only process responsible for the observed co-evolution. It is clear that a large number of accumulated compensatory changes would be needed to affect the inter-sequence distances and hence the phylogenetic trees. In summary, it is possible that a large proportion of the observed tree similarity is due to similarities in evolutionary rates (‘diffuse co-evolution' under general selective pressure) and that specific co-adaptation (directly related to mutual effects) has a function in shaping the details of the regions of interaction.
One factor that could provide some insight into the causes of any observed co-evolution is its specificity. One would intuitively relate specific co-evolution (particular of a given pair of proteins) to co-adaptation between these proteins, whereas broader nonspecific co-evolution (‘diffuse co-evolution') involving many proteins would be more easily related to the similarity in evolutionary rates. It is even possible to think of a gradient of specificity in the factors affecting the evolution of proteins, from highly specific factors affecting only a pair of proteins to highly unspecific factors (i.e., grown temperature, osmolarity, …) which affect the whole proteome (i.e. through the differential use of codons).
Further progress in this area will require a better understanding of the co-adaptation process at the molecular level, identifying the residues/positions in the protein sequences and structures, as well as the chain of events leading to compensation and their consequences for adaptation. It has been shown that inter-protein-correlated residues are closer than the average (Pazos et al, 1997; Yeang and Haussler, 2007), although co-evolution is not always evident at the protein interface itself (Hakes et al, 2007). Indeed, compensation could occur even over relatively large distances through chains of interactions (i.e., allosteric effects).
The discussion of co-evolution versus co-adaptation has scientific and practical implications. The first is related to the role of natural selection in the organization of molecular networks (e.g. gene control and protein interaction networks) and to what extent co-adaptation shapes the structure and evolution of protein networks. A practical consequence is the improvement of co-evolutionary-based methods to detect protein interactions, as discussed earlier. Other practical consequences are related to the possibility of modelling protein interactions, engineering specific interactions and designing molecules to interfere with the protein–protein recognition process (i.e., in signalling pathways), which would certainly benefit from a more precise understanding of the potential physical co-adaptation between proteins in protein complexes.
Acknowledgments
We sincerely thank David Juan (CNIO, Madrid) for interesting discussions and earlier contributions to some of the topics reviewed here. We thank Andres Moya (U Valencia), Antoine Danchin (Institute Pasteur, Paris), Victor de Lorenzo, (CNB-CSIC, Madrid) and Angel Nebreda (CNIO, Madrid) for critical comments on the paper. Finally, we thank Gloria Fuentes for help in preparing the figure and Michael Tress for reviewing the text. This study was funded in part by the grants BIO2006-15318 and PIE 200620I240 from the Spanish Ministry for Education and Science, and EU grants LSHG-CT-2003-503265 (BioSapiens) and LSHG-CT-2004-503567 (ENFIN).
References
- Barabasi AL, Oltvai ZN (2004) Network biology: understanding the cell's functional organization. Nat Rev Genet 5: 101–113 [DOI] [PubMed] [Google Scholar]
- Barker D, Meade A, Pagel M (2007) Constrained models of evolution lead to improved prediction of functional linkage from correlated gain and loss of genes. Bioinformatics 23: 14–20 [DOI] [PubMed] [Google Scholar]
- Bowers P, Pellegrini M, Thompson MJ, Fierro J, Yeates TO, Eisenberg D (2004a) Prolinks: a database of protein functional linkages derived from coevolution. Genome Biol 5: R35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowers PM, Cokus SJ, Eisenberg D, Yeates TO (2004b) Use of logic relationships to decipher protein network organization. Science 306: 2246–2249 [DOI] [PubMed] [Google Scholar]
- Burger L, van Nimwegen E (2008) Accurate prediction of protein–protein interactions from sequence alignments using a Bayesian method. Mol Syst Biol 4: 165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burton RS, Rawson PD, Edmands S (1999) Genetic architecture of physiological phenotypes: empirical evidence for coadapted gene complexes. Am Zool 39: 451–462 [Google Scholar]
- Cokus S, Mizutani S, Pellegrini M (2007) An improved method for identifying functionally linked proteins using phylogenetic profiles. BMC Bioinformatics 8: S7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Craig RA, Liao L (2007) Phylogenetic tree information aids supervised learning for predicting protein–protein interaction based on distance matrices. BMC Bioinformatics 8: 6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y, Dokholyan NV (2006) The coordinated evolution of yeast proteins is constrained by functional modularity. Trends Genet 22: 416–419 [DOI] [PubMed] [Google Scholar]
- Danchin A (2003) The Delphic Boat: What Genomes Tell Us. Cambridge, Massachusetts: Harvard University Press [Google Scholar]
- Darwin CR (1862) On the Various Contrivances by which British and Foreign Orchids are Fertilised by Insects, and on the Good Effects of Intercrossing. London: John Murray [PMC free article] [PubMed] [Google Scholar]
- Date SV, Marcotte EM (2003) Discovery of uncharacterized cellular systems by genome-wide analysis of functional linkages. Nat Biotechnol 21: 1055–1062 [DOI] [PubMed] [Google Scholar]
- del Alamo M, Mateu MG (2005) Electrostatic repulsion, compensatory mutations, and long-range non-additive effects at the dimerization interface of the HIV capsid protein. J Mol Biol 345: 893–906 [DOI] [PubMed] [Google Scholar]
- Devos D, Valencia A (2000) Practical limits of function prediction. Proteins 41: 98–107 [PubMed] [Google Scholar]
- Devos D, Valencia A (2001) Intrinsic errors in genome annotation. Trends Genet 17: 429–431 [DOI] [PubMed] [Google Scholar]
- Devoto A, Hartmann HA, Piffanelli P, Elliott C, Simmons C, Taramino G, Goh CS, Cohen FE, Emerson BC, Schulze-Lefert P, Panstruga R (2003) Molecular phylogeny and evolution of the plant-specific seven-transmembrane MLO family. J Mol Evol 56: 77–88 [DOI] [PubMed] [Google Scholar]
- Dobzhansky T (1950) Genetics of natural populations. XIX. Origin of heterosis through natural selection in populations of Drosophila pseudoobscura. Genetics 35: 288–302 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dobzhansky T (1970) Genetics of the Evolutionary Process. New York: Columbia University Press [Google Scholar]
- Dou T, Ji C, Gu S, Xu J, Ying K, Xie Y, Mao Y (2006) Co-evolutionary analysis of insulin/insulin like growth factor 1 signal pathway in vertebrate species. Front Biosci 11: 380–388 [DOI] [PubMed] [Google Scholar]
- Drummond DA, Raval A, Wilke CO (2006) A single determinant dominates the rate of yeast protein evolution. Mol Biol Evol 23: 327–337 [DOI] [PubMed] [Google Scholar]
- Ehrlich PR, Raven PH (1964) Butterflies and plants: a study in coevolution. Evolution 18: 586–608 [Google Scholar]
- Eisen MB, Spellman PT, Brown PO, Botstein D (1998) Cluster analysis and display of genome-wide expression patterns. Proc Natl Acad Sci USA 95: 14863–14868 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferrer-Costa C, Orozco M, Cruz X (2007) Characterization of compensated mutations in terms of structural and physico-chemical properties. J Mol Biol 365: 249–256 [DOI] [PubMed] [Google Scholar]
- Fitch WM (1971) Rate of change of concomitantly variable codons. J Mol Evol 1: 84–96 [DOI] [PubMed] [Google Scholar]
- Fodor AA, Aldrich RW (2004) Influence of conservation on calculations of amino acid covariance in multiple sequence alignments. Proteins 56: 211–221 [DOI] [PubMed] [Google Scholar]
- Fraser HB, Hirsh AE, Steinmetz LM, Scharfe C, Feldman MW (2002) Evolutionary rate in the protein interaction network. Science 296: 750–752 [DOI] [PubMed] [Google Scholar]
- Fraser HB, Hirsh AE, Wall DP, Eisen MB (2004) Coevolution of gene expression among interacting proteins. Proc Natl Acad Sci USA 101: 9033–9038 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fryxell KJ (1996) The coevolution of gene family trees. Trends Genet 12: 364–369 [DOI] [PubMed] [Google Scholar]
- Futuyma DJ (1997) Evolutionary Biology. Stamford, Connecticut: Sinauer Associates [Google Scholar]
- Gaasterland T, Ragan MA (1998) Microbial genescapes: phyletic and functional patterns of ORF distribution among prokaryotes. Microb Comp Genomics 3: 199–217 [DOI] [PubMed] [Google Scholar]
- Gertz J, Elfond G, Shustrova A, Weisinger M, Pellegrini M, Cokus S, Rothschild B (2003) Inferring protein interactions from phylogenetic distance matrices. Bioinformatics 19: 2039–2045 [DOI] [PubMed] [Google Scholar]
- Göbel U, Sander C, Schneider R, Valencia A (1994) Correlated mutations and residue contacts in proteins. Proteins 18: 309–317 [DOI] [PubMed] [Google Scholar]
- Goh C-S, Bogan AA, Joachimiak M, Walther D, Cohen FE (2000) Co-evolution of proteins with their interaction partners. J Mol Biol 299: 283–293 [DOI] [PubMed] [Google Scholar]
- Goh CS, Cohen FE (2002) Co-evolutionary analysis reveals insights into protein–protein interactions. J Mol Biol 324: 177–192 [DOI] [PubMed] [Google Scholar]
- Haag ES, Wang S, Kimble J (2002) Rapid coevolution of the nematode sex-determining genes fem-3 and tra-2. Curr Biol 12: 2035–2041 [DOI] [PubMed] [Google Scholar]
- Hafner MS, Nadler SA (1988) Phylogenetic trees support the coevolution of parasites and their hosts. Nature 332: 258–259 [DOI] [PubMed] [Google Scholar]
- Hakes L, Lovell S, Oliver SG, Robertson DL (2007) Specificity in protein interactions and its relationship with sequence diversity and coevolution. Proc Natl Acad Sci USA 104: 7999–8004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halperin I, Wolfson H, Nussinov R (2006) Correlated mutations: advances and limitations. A study on fusion proteins and on the Cohesin–Dockerin families. Proteins 63: 832–845 [DOI] [PubMed] [Google Scholar]
- Huerta-Cepas J, Dopazo H, Dopazo J, Gabaldon T (2007) The human phylome. Genome Biol 8: R109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Izarzugaza JM, Juan D, Pons C, Ranea JA, Valencia A, Pazos F (2006) TSEMA: interactive prediction of protein pairings between interacting families. Nucleic Acids Res 34: W315–W319 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jothi R, Cherukuri PF, Tasneem A, Przytycka TM (2006) Co-evolutionary analysis of domains in interacting proteins reveals insights into domain–domain interactions mediating protein–protein interactions. J Mol Biol 362: 861–875 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jothi R, Kann MG, Przytycka TM (2005) Predicting protein–protein interaction by searching evolutionary tree automorphism space. Bioinformatics 21: i241–i250 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jothi R, Przytycka TM, Aravind L (2007) Discovering functional linkages and uncharacterized cellular pathways using phylogenetic profile comparisons: a comprehensive assessment. BMC Bioinformatics 8: 173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Juan D, Pazos F, Valencia A (2008) High-confidence prediction of global interactomes based on genome-wide coevolutionary networks. Proc Natl Acad Sci USA 105: 934–939 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kachroo A, Schopfer CR, Nasrallah ME, Nasrallah JB (2001) Allele-specific receptor-ligand interactions in Brassica self-incompatibility. Science 293: 1824–1826 [DOI] [PubMed] [Google Scholar]
- Kann MG, Jothi R, Cherukuri PF, Przytycka TM (2007) Predicting protein domain interactions from coevolution of conserved regions. Proteins 67: 811–820 [DOI] [PubMed] [Google Scholar]
- Kim WK, Bolser DM, Park JH (2004) Large-scale co-evolution analysis of protein structural interlogues using the global protein structural interactome map (PSIMAP). Bioinformatics 20: 1138–1150 [DOI] [PubMed] [Google Scholar]
- Kondrashov AS, Sunyaev S, Kondrashov FA (2002) Dobzhansky–Muller incompatibilities in protein evolution. Proc Natl Acad Sci USA 99: 14878–14883 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kulathinal RJ, Bettencourt BR, Hartl DL (2004) Compensated deleterious mutations in insect genomes. Science 306: 1553–1554 [DOI] [PubMed] [Google Scholar]
- Labedan B, Xu Y, Naumoff DG, Glansdorff N (2004) Using quaternary structures to assess the evolutionary history of proteins: the case of the aspartate carbamoyltransferase. Mol Biol Evol 21: 364–373 [DOI] [PubMed] [Google Scholar]
- Lawrence JG (1997) Selfish operons and speciation by gene transfer. Trends Microbiol 5: 355–359 [DOI] [PubMed] [Google Scholar]
- Liu J-C, Makova KD, Adkins RM, Gibson S, Li W-H (2001) Episodic evolution of growth hormone in primates and emergence of the species specificity of human growth hormone receptor. Mol Biol Evol 18: 945–953 [DOI] [PubMed] [Google Scholar]
- Marcotte EM, Pellegrini M, Thompson MJ, Yeates TO, Eisenberg D (1999) A combined algorithm for genome-wide prediction of protein function. Nature 402: 83–86 [DOI] [PubMed] [Google Scholar]
- Mateu MG, Fersht AR (1999) Mutually compensatory mutations during evolution of the tetramerization domain of tumor suppressor p53 lead to impaired hetero-oligomerization. Proc Natl Acad Sci USA 96: 3595–3599 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mintseris J, Weng Z (2005) Structure, function, and evolution of transient and obligate protein–protein interactions. Proc Natl Acad Sci USA 102: 10930–10935 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morett E, Korbel JO, Rajan E, Saab-Rincon G, Olvera L, Olvera M, Schmidt S, Snel B, Bork P (2003) Systematic discovery of analogous enzymes in thiamin biosynthesis. Nat Biotechnol 21: 790–795 [DOI] [PubMed] [Google Scholar]
- Moya A, Pereto J, Gil R, Latorre A (2008) Learning how to live together: genomic insights into prokaryote–animal symbioses. Nat Rev Genet 9: 218–229 [DOI] [PubMed] [Google Scholar]
- Olmea O, Valencia A (1997) Improving contact predictions by the combination of correlated mutations and other sources of sequence information. Fold Des 2: S25–S32 [DOI] [PubMed] [Google Scholar]
- Pagel P, Wong P, Frishman D (2004) A domain interaction map based on phylogenetic profiling. J Mol Biol 344: 1331–1346 [DOI] [PubMed] [Google Scholar]
- Pages S, Belaich A, Belaich JP, Morag E, Lamed R, Shoham Y, Bayer EA (1997) Species-specificity of the cohesin–dockerin interaction between Clostridium thermocellum and Clostridium cellulolyticum: prediction of specificity determinants of the dockerin domain. Proteins 29: 517–527 [PubMed] [Google Scholar]
- Pal C, Papp B, Hurst LD (2001) Highly expressed genes in yeast evolve slowly. Genetics 158: 927–931 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pazos F, Helmer-Citterich M, Ausiello G, Valencia A (1997) Correlated mutations contain information about protein–protein interaction. J Mol Biol 271: 511–523 [DOI] [PubMed] [Google Scholar]
- Pazos F, Juan D, Izarzugaza JM, Leon E, Valencia A (2008) Prediction of protein interaction based on similarity of phylogenetic trees. Methods Mol Biol 484: 523–535 [DOI] [PubMed] [Google Scholar]
- Pazos F, Ranea JAG, Juan D, Sternberg MJE (2005) Assessing protein co-evolution in the context of the tree of life assists in the prediction of the interactome. J Mol Biol 352: 1002–1015 [DOI] [PubMed] [Google Scholar]
- Pazos F, Valencia A (2001) Similarity of phylogenetic trees as indicator of protein–protein interaction. Protein Eng 14: 609–614 [DOI] [PubMed] [Google Scholar]
- Pazos F, Valencia A (2002) In silico two-hybrid system for the selection of physically interacting protein pairs. Proteins 47: 219–227 [DOI] [PubMed] [Google Scholar]
- Pellegrini M, Marcotte EM, Thompson MJ, Eisenberg D, Yeates TO (1999) Assigning protein functions by comparative genome analysis: protein phylogenetic profiles. Proc Natl Acad Sci USA 96: 4285–4288 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramani AK, Marcotte EM (2003) Exploiting the co-evolution of interacting proteins to discover interaction specificity. J Mol Biol 327: 273–284 [DOI] [PubMed] [Google Scholar]
- Ranea JA, Yeats C, Grant A, Orengo CA (2007) Predicting protein function with hierarchical phylogenetic profiles: the Gene3D Phylo-Tuner method applied to eukaryotic genomes. PLoS Comput Biol 3: e237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ridley M (2003) Evolution. Boston, MA: Blackwell Publishing [Google Scholar]
- Sato T, Yamanishi Y, Horimoto K, Kanehisa M, Toh H (2006) Partial correlation coefficient between distance matrices as a new indicator of protein–protein interactions. Bioinformatics 22: 2488–2492 [DOI] [PubMed] [Google Scholar]
- Sato T, Yamanishi Y, Kanehisa M, Toh H (2005) The inference of protein–protein interactions by co-evolutionary analysis is improved by excluding the information about the phylogenetic relationships. Bioinformatics 21: 3482–3489 [DOI] [PubMed] [Google Scholar]
- Sazanov LA, Hinchliffe P (2006) Structure of the hydrophilic domain of respiratory complex I from Thermus thermophilus. Science 311: 1430–1436 [DOI] [PubMed] [Google Scholar]
- Shackelford G, Karplus K (2007) Contact prediction using mutual information and neural nets. Proteins 69: 159–164 [DOI] [PubMed] [Google Scholar]
- Shakhnovich BE (2005) Improving the precision of the structure–function relationship by considering phylogenetic context. PLoS Comput Biol 1: e9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shim Choi S, Li W, Lahn BT (2005) Robust signals of coevolution of interacting residues in mammalian proteomes identified by phylogeny-aided structural analysis. Nat Genet 37: 1367–1371 [DOI] [PubMed] [Google Scholar]
- Shindyalov IN, Kolchanov NA, Sander C (1994) Can three-dimensional contacts in protein structures be predicted by analysis of correlated mutations? Protein Eng 7: 349–358 [DOI] [PubMed] [Google Scholar]
- Shoemaker BA, Panchenko AR (2007) Deciphering protein–protein interactions. Part II. Computational methods to predict protein and domain interaction partners. PLoS Comput Biol 3: e43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Socolich M, Lockless SW, Russ WP, Lee H, Gardner KH, Ranganathan R (2005) Evolutionary information for specifying a protein fold. Nature 437: 512–518 [DOI] [PubMed] [Google Scholar]
- Stone AR, Hawksworth DL (1985) Coevolution and Systematics. Oxford: Clarendon Press [Google Scholar]
- Subramanian S, Kumar S (2004) Gene expression intensity shapes evolutionary rates of the proteins encoded by the vertebrate genome. Genetics 168: 373–381 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun J, Xu J, Liu Z, Liu Q, Zhao A, Shi T, Li Y (2005) Refined phylogenetic profiles method for predicting protein–protein interactions. Bioinformatics 21: 3409–3415 [DOI] [PubMed] [Google Scholar]
- Susko E, Inagaki Y, Field C, Holder ME, Roger AJ (2002) Testing for differences in rates-across-sites distributions in phylogenetic subtrees. Mol Biol Evol 19: 1514–1523 [DOI] [PubMed] [Google Scholar]
- Tan S, Zhang Z, Ng S (2004) ADVICE: automated detection and validation of interaction by co-evolution. Nucleic Acids Res 32: W69–W72 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson JN (1994) The Coevolutionary Process. Chicago: University of Chicago Press [Google Scholar]
- Tillier ER, Biro L, Li G, Tillo D (2006) Codep: maximizing co-evolutionary interdependencies to discover interacting proteins. Proteins 63: 822–831 [DOI] [PubMed] [Google Scholar]
- Tress M, de Juan D, Grana O, Gomez MJ, Gomez-Puertas P, Gonzalez JM, Lopez G, Valencia A (2005) Scoring docking models with evolutionary information. Proteins 60: 275–280 [DOI] [PubMed] [Google Scholar]
- Valencia A, Pazos F (2002) Computational methods for the prediction of protein interactions. Curr Opin Struct Biol 12: 368–373 [DOI] [PubMed] [Google Scholar]
- van Kesteren RE, Tensen CP, Smit AB, van Minnen J, Kolakowski LF, Meyerhof W, Richter D, van Heerikhuizen H, Vreugdenhil E, Geraerts WP (1996) Co-evolution of ligand–receptor pairs in the vasopressin/oxytocin superfamily of bioactive peptides. J Biol Chem 271: 3619–3626 [DOI] [PubMed] [Google Scholar]
- Van Valen L (1973) A new evolutionary law. Evol Theor 1: 1–30 [Google Scholar]
- Van Valen L (1977) The Red Queen. Am Nat 11: 809–810 [Google Scholar]
- von Mering C, Huynen M, Jaeggi D, Schmidt S, Bork P, Snel B (2003) STRING: a database of predicted functional associations between proteins. Nucleic Acids Res 31: 258–261 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waddell PJ, Kishino H, Ota R (2007) Phylogenetic methodology for detecting protein interactions. Mol Biol Evol 24: 650–659 [DOI] [PubMed] [Google Scholar]
- Wallace B (1953) On coadaptation in Drosophila. Am Nat 87: 343–358 [Google Scholar]
- Wallace B (1991) Coadaptation revisited. J Hered 82: 89–96 [DOI] [PubMed] [Google Scholar]
- Wang HC, Spencer M, Susko E, Roger AJ (2007) Testing for covarion-like evolution in protein sequences. Mol Biol Evol 24: 294–305 [DOI] [PubMed] [Google Scholar]
- Wang S, Kimble J (2001) The TRA-1 transcription factor binds TRA-2 to regulate sexual fates in Caenorhabditis elegans. EMBO J 20: 1363–1372 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watanabe M, Ito A, Takada Y, Ninomiya C, Kakizaki T, Takahata Y, Hatakeyama K, Hinata K, Suzuki G, Takasaki T, Satta Y, Shiba H, Takayama S, Isogai A (2000) Highly divergent sequences of the pollen self-incompatibility (S) gene in class-I S haplotypes of Brassica campestris (syn. rapa) L. FEBS Lett 473: 139–144 [DOI] [PubMed] [Google Scholar]
- Xia Y, Yu H, Jansen R, Seringhaus M, Baxter S, Greenbaum D, Zhao H, Gerstein M (2004) Analyzing cellular biochemistry in terms of molecular networks. Annu Rev Biochem 73: 1051–1087 [DOI] [PubMed] [Google Scholar]
- Yeang CH, Haussler D (2007) Detecting coevolution in and among protein domains. PLoS Comput Biol 3: e211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou Y, Wang R, Li L, Xia X, Sun Z (2006) Inferring functional linkages between proteins from evolutionary scenarios. J Mol Biol 359: 1150–1159 [DOI] [PubMed] [Google Scholar]