A Bridge to Coordination Isomer Selection in Lanthanide(III) DOTA-tetraamide Complexes

Abstract

Interest in macrocyclic lanthanide complexes such as DOTA is driven largely through interest in their use as contrast agents for MRI. The lanthanide tetraamide derivatives of DOTA have shown considerable promise as PARACEST agents, taking advantage of the slow water exchange kinetics of this class of complex. We postulated that water exchange in these tetraamide complexes could be slowed even further by introducing a group to sterically encumber the space above the water coordination site, thereby hindering the departure and approach of water molecules to the complex. The ligand 8O₂-bridged-DOTAM was synthesized in a 34% yield from cyclen. It was found that the lanthanide complexes of this ligand did not possess a water molecule in the inner coordination sphere of the bound lanthanide. The crystal structure of the ytterbium complex revealed that distortions to the coordination sphere were induced by the steric constraints imposed on the complex by the bridging unit. The extent of the distortion was found to increase with increasing ionic radius of the lanthanide ion, eventually resulting in a complete loss of symmetry in the complex. Because this ligand system is bicyclic, the conformation of each ring in the system is constrained by that of the other, in consequence inclusion of the bridging unit in the complexes means only a twisted square antiprismatic coordination geometry is observed for complexes of 8O₂-bridged-DOTAM.

Introduction

Control of the hydration state and water exchange kinetics in the complexes of lanthanide(III) ions is of considerable importance in the development of contrast media for MRI.¹ For the development of more efficient gadolinium-based contrast agents it is desirable that water exchange be extremely rapid. In sharp contrast to this avenue of investigation, a new technique for generating image contrast has recently been proposed that requires much slower water exchange.² This technique, known as chemical exchange saturation transfer (CEST), employs a pre-saturation pulse to selectively saturate exchangeable protons on the contrast agent. Chemical exchange of these protons with the bulk solvent results in an apparent decrease in the total water concentration, which appears as a darkening of the image.^2,3

The water exchange kinetics of the lanthanide(III) complexes of tetraamide derivatives of DOTA are found to be much slower than those of the polyamino carboxylate systems traditionally used for MRI contrast agents.^4–6 This, and the large lanthanide induced shifts (LIS) of the exchanging amide and coordinated water protons, make this type of complex attractive systems to study as CEST agents.³ These paramagnetic CEST (PARACEST) agents offer some significant advantages over the diamagnetic molecules originally proposed as CEST agents;^3,7,8 most importantly, the large chemical shift difference between the exchanging protons on the agent and the bulk water reduces off-resonance direct saturation of the bulk water signal.

The extent of the reduction of the bulk water signal intensity arising from CEST is inherently connected to the exchange rate of protons with the bulk solvent. First, the protons must meet the slow exchange condition of the NMR time-scale, i.e. k_ex ≤ Δω, where Δω is the chemical shift difference between the two exchanging pools in Hz. The next consideration is the amount of power that is applied in the pre-saturation pulse. Clearly, if a CEST agent is to be used in clinical medicine it is desirable that the applied pre-saturation power be as low as possible to fall within acceptable SAR limits for the patient. A recent complete solution⁹ of the Bloch equations¹⁰ has been used to show that the optimal CEST efficiency varies with both pre-saturation power and proton exchange rate. The results of this analysis show that as the pre-saturation power is reduced the exchange rate required to produce the largest CEST effect becomes slower and slower.^7,9 In consequence, the design of more efficient CEST agents for use at lower pre-saturation powers requires the design of lanthanide complexes with extremely slow water exchange rates, τ_M > 1 ms (τ_M = 1/k_ex).^7,9

In order to achieve this goal it is necessary to have a good understanding of the factors that affect water exchange in DOTA-tetraamide complexes. The first consideration is the coordination geometry of the lanthanide ion. In the lanthanide(III) complexes of DOTA, and its derivatives, two conformational isomers are observed: a mono capped square antiprism (SAP) and a mono capped twisted square antiprism (TSAP).^11–13 It is now well established that the rate of water exchange in the TSAP isomer is much faster than that in the SAP isomer, as much as one or two orders of magnitude faster.^6,14–17 It is important therefore that a PARACEST agent derived from DOTA adopt a SAP coordination geometry. For complexes of a simple tetraamide ligand such as DOTAM (Chart 1) it can be seen that the proportion of the SAP isomer present in solution is dependent upon which lanthanide ion is used to from the complex (Figure 1). As the ionic radius of the lanthanide ion becomes smaller, the proportion of SAP isomer present increases. This would seem to limit enquiry to the later lanthanide ions; however, it is also found that as the size of the amide substituent increases so the SAP isomer becomes increasingly favored and in most cases it is the only isomer observed in solution.^8,18

Chart 1.

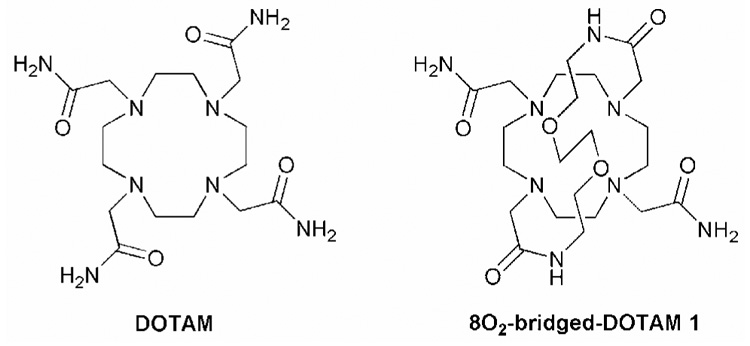
Figure 1.

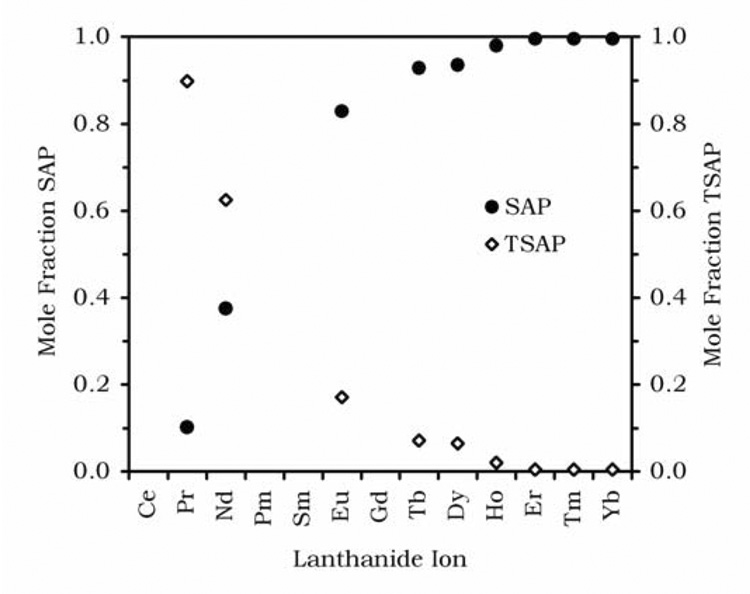
The mole fractions of the SAP (closed circles) and TSAP (open diamonds) isomers of DOTAM for each lanthanide ion, determined by integration of resonances in the ¹H NMR spectra of each complex recorded in D₂O at 500 MHz.

The amide substituent can affect the exchange rate in more ways than simply favoring the SAP isomer through steric bulk. It has been shown that the size and hydrophobicity of the amide substituent influences access of second sphere water molecules to the water coordination site.¹⁸ Although exchange in these octadentate systems occurs via a dissociative mechanism, it cannot occur unless there is a second water molecule available to replace that which is coordinated to the metal ion. Bulkier and more hydrophobic groups that hinder the access of these other water molecules have been shown to slow water exchange.¹⁸ To explore the potential effects of amide substituents further, we hypothesized that introducing a bridged substituent over the water coordination site would hinder dissociation of the coordinated water molecule and thereby slow exchange. To further reinforce this restriction upon the coordinated water molecule, two ether oxygen atoms were incorporated into the bridging group with the idea that they may induce a hydrogen bonding interaction with the protons of the coordinated water molecule. Accordingly, the new ligand, 8O₂-bridged-DOTAM 1, was prepared and its lanthanide complexes investigated as potential CEST agents.

Results and Discussion

Synthesis

8O₂-bridged-DOTAM 1 was prepared according to Scheme 1. Two of the nitrogen atoms of cyclen were selectively protected in trans-positions with benzyl carbamates using established procedures.^19,20 The two unprotected nitrogen atoms of 2 were then alkylated using bromoacetamide, with potassium carbonate as a base, in acetonitrile. Subsequent crystallization from hot acetonitrile afforded 3 in 69% yield. The protecting groups were then removed by hydrogenolysis over a palladium on carbon catalyst to yield DO2AM 4 in 91% yield. The bridging unit was then prepared by condensing 2.5 equivalents of chloroacetyl chloride with 2,2′(ethylenedioxy)bis(ethylamine) in dichloromethane. The resulting diamide 5 was purified by recrystallization from ethyl acetate. The disubstituted cyclen 4 and the bridging fragment 5 were then coupled together in a macrocyclization reaction. To promote macrocyclization and minimize the extent of polymerization side reactions, this reaction was performed at high dilution (3 mM) in acetonitrile using a stoichometric ratio of the reactants. After an aqueous workup and recrystallization from ethanol, ligand 1 was afforded in 60 % yield (the overall yield from cyclen was 34%), a good yield for the formation of a 21-membered macrocycle.²¹ Complexation of lanthanide ions with this ligand proved somewhat more difficult than is usually observed with tetraamide derivatives of DOTA. Eventually it was found that complexes could be formed by increasing the pH of the complexation reaction above 8 by addition of sodium hydroxide, and heating the reaction for several hours.

Scheme 1.

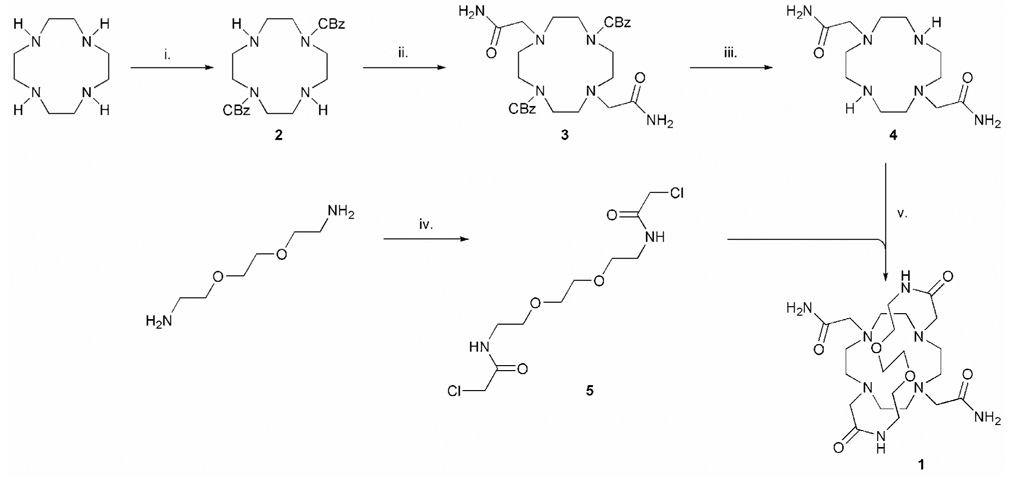
The synthesis of 1. Reagents and conditions: i. BnOCOCl/CH₂Cl₂/0 °C (91 %); ii. BrCH₂CONH₂/CH₃CN/K₂CO₃/55 °C (69 %); iii. H₂/Pd on C /EtOH (91 %); iv. ClCH₂COCl/ CH₂Cl₂/K₂CO₃/0 °C (84 %); v. CH₃CN/K₂CO₃/50 °C (60 %).

Crystal Structure of Yb8O₂-bridged-DOTAM

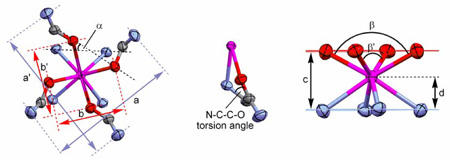
An X-ray quality crystal of Yb-8O₂-bridged-DOTAM³⁺(NO₃ ⁻)₃ was grown by slow evaporation of an aqueous solution of the complex at room temperature. The structure obtained by X-ray diffraction is shown in Figure 2 and selected geometrical parameters are presented in Table 1 and Table 2. Three complexes, each with three nitrate counter ions, crystallized in a P₃₁₂₁ space group along with six water molecules. The three complexes of each unit cell are rotated 120° with respect to one another (see packing diagram, S1 of ESI). Each complex in the unit cell adopts the same, highly ordered structure, and is completely C₂-symmetric. The cyclen ring adopts the usual [3,3,3,3] conformation with N-C-C-N torsion angles of −59.3° and −54.1°, indicating that the macrocycle is under some strain that distorts two of the ethylene bridges slightly from the usual gauche conformation. Despite this distortion the nitrogen atoms of the cyclen ring continue to adopt the coplanar arrangement that is usually observed in cyclen complexes (Figure 2 top).²² The coordinating amide oxygen atoms also adopt a coplanar arrangement that is characteristic of this type of complex,²² and although the ytterbium ion is, as is usual, sandwiched between these planes, its position is quite unusual.^23,24 A number of geometric parameters for Yb1, three complexes of DOTAM^23–25 and two DOTA²⁶ complexes are collected in Table 1. From this information, and that available elsewhere,^27,28 it is clear that the lanthanide ion in complexes of DOTA, or its derivatives, lies much closer to the oxygen donor atoms than it does to the macrocycle. Generally speaking the lanthanide ion is approximately twice as far from the N₄ plane as it is from the O₄ plane, however, in Yb1 the ytterbium ion lies almost half way between these two planes (c/d = 0.57) (Table 1).

Figure 2.

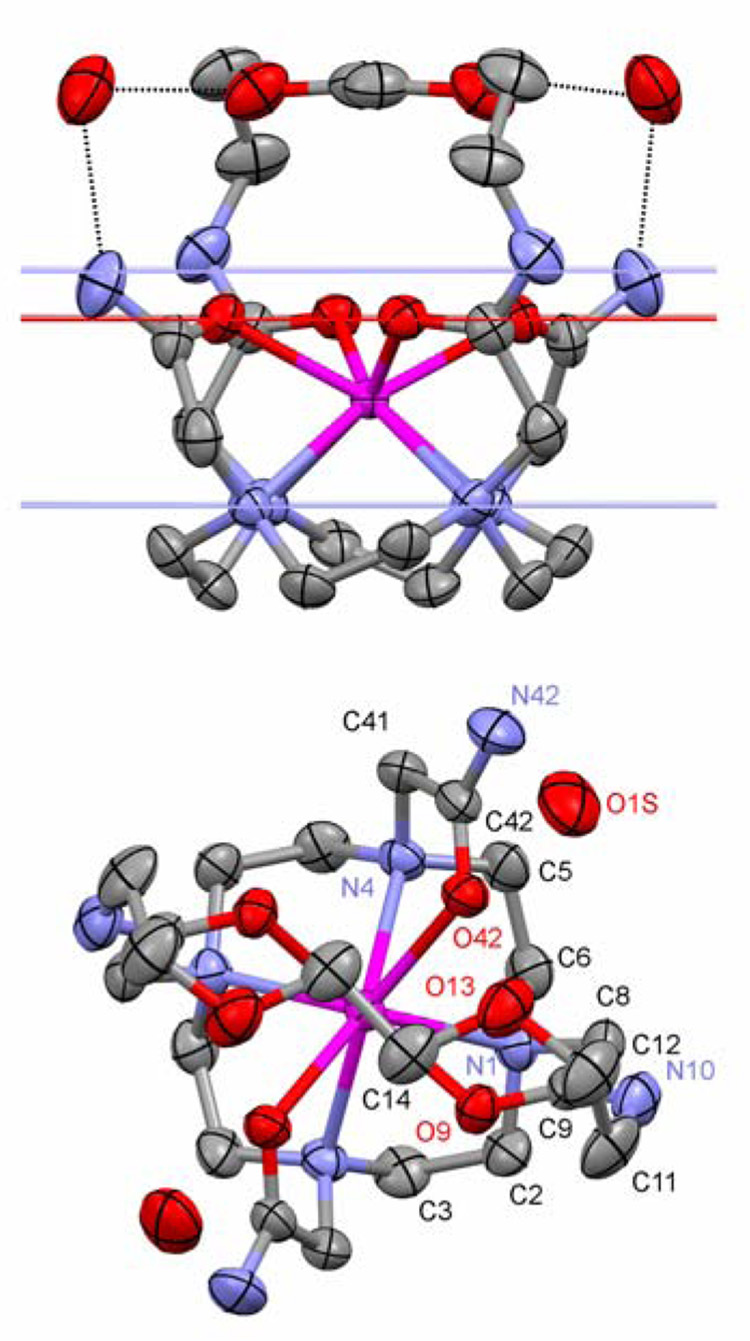
The crystal structure of Yb1 with hydrogen atoms and nitrate counter ions omitted for clarity. The side view (top) shows the mean planes of the macrocyclic nitrogen atoms, the amide nitrogen atoms and the amide oxygen atoms. It also shows the hydrogen bonding interactions between the two water molecules of crystalization and a primary amide proton and the ether oxygens. The hydrogen bonding interactions are represented as dotted lines. The top view (bottom) clearly shows the twisted square antiprismatic geometry of the complex.

Table 1.

Selected geometric parameters from the crystal structures of Yb1.

Complex	Yb1	YbDOTAMa	GdDOTAMb	PrDOTAMc	NdDOTAd	CeDOTAd
Coordination geometry	TSAP	SAP	SAP	TSAP	SAP	TSAP
α[°]	26.8	40.1	37.1	22.9	39.0	24.4
q	0	1	1	1	1	1
β [°]	122.3	141.9	142.7	140.9	145.9	143.5
β′ [°]	124.4	143.2	144.7	143.3	148.2	145.0
a [Å]	7.562	8.574	8.876	8.776	-	-
a′ [Å]	8.239	8.688	8.914	8.829	-	-
b [Å]	3.957	4.354	4.494	4.611	4.621	4.657
b′ [Å]	4.073	4.363	4.522	4.632	4.648	4.706
Max N-C-C-O [°]	−23.4	28.7	37.2	29.4	33.9	31.7
Min N-C-C-O [°]	−5.9	17.5	28.0	16.5	12.7	23.2
c [Å]	2.496	2.304	2.339	2.528	2.360	2.528
d / c	0.57	0.68	0.68	0.69	0.71	0.70

^a)Data from reference²³

^b)Data from reference²⁴

^c)Data from reference²⁵

^d)Data from reference²⁶

Table 2.

Selected bond lengths [Å] and angles [°] for Yb1 ³⁺(NO₃ ⁻)₃

Yb-O(9)	2.260(2)	Yb-O(42)	2.303(2)
Yb-N(1)	2.519(3)	Yb-N(4)	2.529(3)
O(9)′-Yb-O(9)	122.27(13)	O(9)-Yb-O(42)′	77.83(9)
O(9)-Yb-O(42)	76.14(10)	O(42)′-Yb-O(42)	124.41(13)
O(9)-Yb-N(1)′	155.82(10)	O(42)-Yb-N(1)′	85.67(9)
O(9)-Yb-N(1)	67.65(9)	O(42)-Yb-N(1)	126.12(9)
N(1)′-Yb-N(1)	113.13(14)	O(42)′-Yb-N(4)′	67.14(9)
N(1)′-Yb-N(4)	71.09(10)	O(42)-Yb-N(4)′	156.87(9)
N(1)-Yb-N(4)	72.33(10)	O(9)′-Yb-N(4)	126.97(10)
N(4)′-Yb-N(4)	110.57(14)	O(9)-Yb-N(4)	87.04(9)
O(42)-Yb-N(4)	67.14(9)	O(42)′-Yb-N(4)	156.87(9)

Although it is almost universally the case that DOTA-tetraamide complexes of ytterbium adopt a SAP isomer (Fig. 1), it should not be a surprise that Yb1 adopts a TSAP coordination geometry. The N₄-O₄ twist angle (α) in Yb1 is −26.8, typical of the values observed for other complexes that adopt the TSAP isomer (Table 1).^25,26 The reason why Yb1 adopts a TSAP coordination geometry may be found by considering how the ligand system is viewed. As presented in Chart 1 it is easiest to consider the complex as a modified DOTA-type structure; however, this ligand system is in fact bicyclic, consisting of 12- and 21-membered ring systems. As each ring shares two ethylene bridges, the system will have the lowest energy when the two rings have the same conformation, either δ or λ. Since the 21-membered ring incorporates two of the ligating amide pendant arms of the complex, the orientation of these two pendant arms (Δ or Λ) will be defined by the conformation of both macrocycles. The pendant arms in DOTA-type complexes bind cooperatively, so all the pendant arms adopt the same orientation as those that are part of the 21-membered macrocycle. This means that the pendant arms adopt the same helicity as the two macrocyclic systems, i.e. δ confers Δ and λ confers Λ, and this results in a TSAP coordination geometry.

The result of adopting this coordination geometry is that the O₄ plane is pushed away from the N₄ plane as required by the smaller N₄-O₄ torsion angle in the TSAP isomer compared with that of the SAP isomer. The 2.496 Å that separate these planes is characteristic of a TSAP isomer,^25,26 and although this increase in the N₄-O₄ distance has been shown to accelerate water exchange by pushing the water molecule away from the metal ion, it does not usually result in the water molecule being pushed off the complex completely. However, when this increase in N₄-O₄ distance is coupled with movement of the ytterbium ion towards the N₄ plane it results in a significant decrease in the O-Yb-O angle (β). Lukes and co-workers have suggested that if this O-Yb-O angle falls below 136° then steric and electrostatic replusion prevent a water molecule from gaining access to the metal’s inner coordination sphere.²⁹ So the distortions observed in the coordination sphere of Yb1 result in exclusion of water from the inner coordination sphere because the O-Yb-O is significantly smaller than that observed in similar complexes (Table 1).

The question still remains, why should this complex should adopt such a strained conformation? The answer can be found by looking at the dimensions of the complex with repect to those of its bridging unit. The bridging unit of Yb1 incorporates two of the corners of the 21-membered macrocycle and these two corners lie 6.10 Å apart. The six central atoms of the bridging unit adopt a co-planar arrangement and lie parallel to the N₄ and O₄ coordinating planes. The amide nitrogen atoms of DOTAM complexes lie over 8.5 Å apart, regardless of the coordination geometry or metal ion radius.^23–25 In consequence the bridging unit of Yb1 pulls the two amide nitrogen atoms of the 21-members ring together such that they lie over 1 Å closer together than is usually observed (Table 1). This has the effect of moving the coordinating oxygen atoms closer together over the lanthanide ion and reducing the O-Yb-O angle. However, there appears to be an imperative in the complex that the four coordinating amide oxygen atoms remain in plane, since each atoms lies on the mean plane (Figure 2 top). Indeed, the two independent pendant arms also move together to facilitate this. But perhaps more significantly in order to accommodate this co-planar arrangement of the amide oxygen atoms, the two amide nitrogens that are part of the bridging unit are levered upwards by the bridging group. This brings the bridging amide nitrogens above the mean plane of the four amide nitrogen atoms (Figure 2 top) and the non-bridging amide nitrogens below the mean plane. This distortion is only possible because of the flexibility of the NC-C-O chelating group. In other complexes this angle may vary substantially, even within the same complex it may rise as high as 38° or as low as 12°. In Yb1, for the independent pedant arms this torsion angle is in the middle of this range (Table 1), in contrast this torsion angle in the bridging unit is an unprecedented 5.9°. This represents an extremely strained chelate ring. The closing of this N-C-C-O torsion angle is found to have significant consequences as the ionic radius of the lanthanide increases, as described below.

There is no interaction between the ytterbium ion and the ether oxygen atoms of the bridging unit of Yb1, these Yb-O distances are in excess of 4.8 Å. However these ether oxygens are involved in hydrogen bonding interactions with the water molecules found in the crystal structure. Each complex molecule is associated with two water molecules of crystallisation, one on each side of the bridging unit. These water molecules form the so-called second hydration sphere of the complex.³⁰ These two water molecules are closely associated with the complex, each forming a hydrogen bond to one of the protons of the primary amide protons as well as with the ether oxygens. These hydrogen bonding interactions appear to be quite strong, with bond distances of just 2.013 Å and 1.926 Å for the O-O and O-N distances, respectively.

Ln8O₂-bridged-DOTAM Complexes in Solution

Solution State Dynamics of Yb8O₂-bridged-DOTAM

The ¹H NMR spectrum of Yb1 (Figure 3) shows 18 resolved resonances consistent with a complex having C₂-symmetry in solution as it has in the crystal structure. An initial assignment of the spectrum was performed on the basis of ¹H-¹H 2D COSY and EXSY spectra, with reference to the spectra of other related complexes.^13,15,31 A full description of the coupling in the COSY and EXSY spectra can be found in the Supplementary Information (S3–S6). In general, the most down-field shifted resonances of the macrocyclic ligand in DOTA-type complexes of ytterbium are the axial protons located on the carbon at the side of the macrocycle labeled here ax ^S (Figure 3). These protons exhibit characteristic coupling patterns with the other protons of the ethylene group on which they are located. In the COSY spectrum an intense cross peak is observed for the geminal coupling with the equatorial proton on the same carbon (eq^S). The two vicinal couplings have different intensities as a result of the Karplus relationship.³² Thus, a second weaker coupling is observed between the (ax^S) axial proton and the axial proton on the carbon at the corner (ax^C). The weakest coupling is between axial protons and the equatorial proton on the adjacent carbon at the corner, e.g. ax^S – eq^C. This coupling is often too weak to be observed in the COSY spectra of these paramagnetic complexes. Owing to the quality of the COSY spectrum acquired for Yb1 the two vicinal coupling cross peaks cannot be distinguished from noise and only geminal coupling are observed. Nonetheless, in concert with the EXSY data, enough information is present to allow an assignment to be made.

Figure 3.

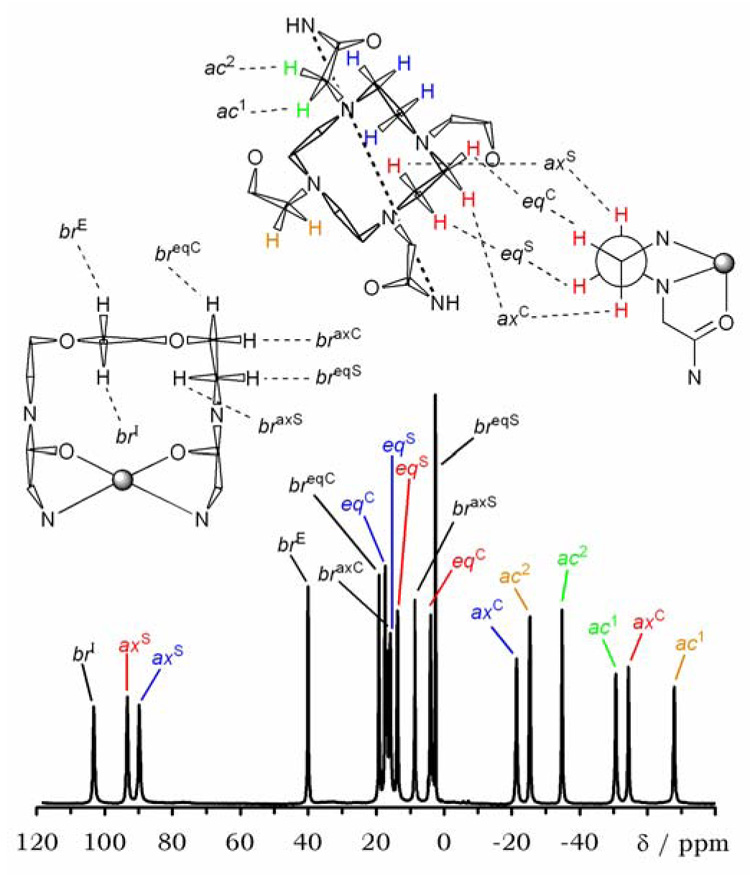
The ¹H NMR spectrum of Yb1 recorded in D₂O at 500 MHz with solvent suppression. The assignment of the spectrum is based upon the COSY, EXSY and shift analysis data. Axial and equatorial protons are designated ax and eq, respectively. The acetamide protons are designated ac and those on the bridging unit, br. The designation ‘C’ indicates that the proton is located on a carbon at the corner of a ring, the designation ‘S’ indicates that the proton is located on a carbon on the side of a ring. The protons on the central ethylene group of the bridging unit, which is anti-periplanar rather than gauche, are designated br ^I for the internal proton and br ^E for the external proton.

The protons of the macrocycle also exchange places with one another and these exchange processes may be followed by exchange spectroscopy (EXSY).^13,15,31,33 In DOTA, and its tetraamide derivatives, the two coordination isomers, SAP and TSAP, may interconvert by two processes: a reorientation of the pendant arms or a conformational ring flip of the macrocycle.^11,13 The effect of these exchange processes on the position of protons on the cyclen macrocycle is shown (Figure 4). It can be seen that arm rotation has the effect of moving a proton from one coordination isomer to the other, without altering the position of that proton on the ethylene group. A ring flip, on the other hand, has the effect of moving the proton from one coordiantion isomer to the other but also changes its position on the ethylene bridge; ax ^S exchanges with eq^C of the other coordination isomer and eq^S exhanges with ax^C of the other coordination isomer. When both ring flip and arm rotation exchange processes occur in a complex, two crosspeaks are observed for each resonance of the macrocyclic ring. Occasionally, a third peak may be observed arising from sequential ring flip and arm rotation and these motions combined interconvert the two enantiomers of the same coordination geometry. Using all this information it is possible to make the assignment shown in Figure 3.

Figure 4.

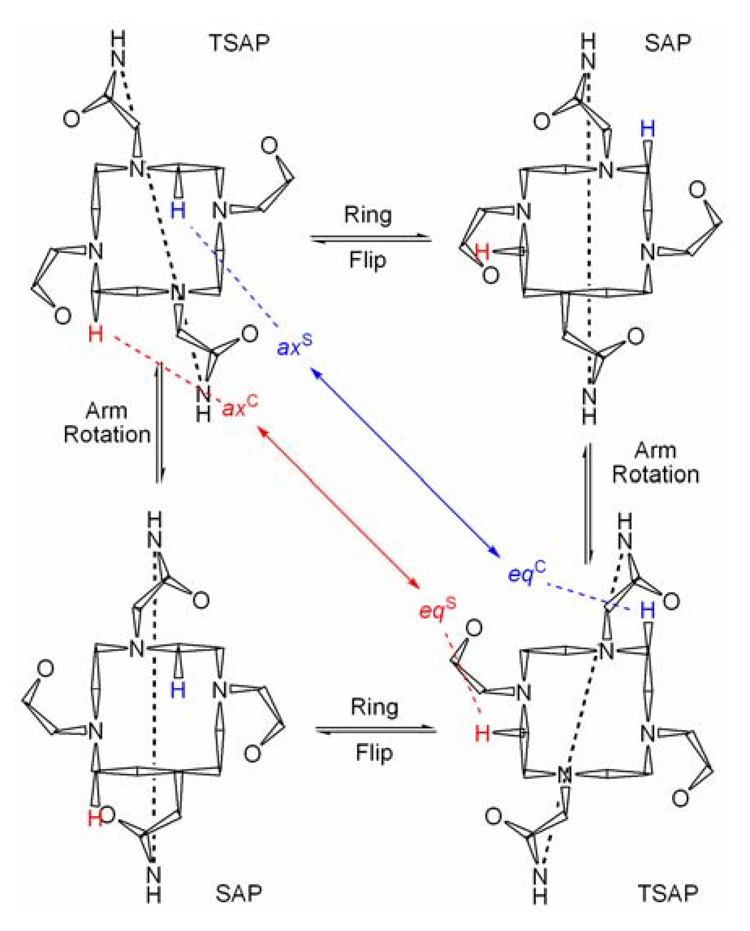
The effect of the possible exchange processes on the position of protons on the ethylene groups of cyclen in lanthanide complexes 8O₂-bridged-DOTAM.

The most shifted resonance in the spectrum of Yb1 is coupled to just one other resonance, with which it also exchanges. These two resonances correspond to the protons on the central ethylene group of the bridging unit (br ^I and br ^E). The only other protons in the complex which couple with just one other proton with which they also exchange are the acetamide protons α- to the nitrogen atoms of cyclen (ac ¹ and ac ²). These protons are easily identified on the basis of their exchange and coupling patterns, and because these protons experience a large up-field shift. The protons of the ethylene group on the side of the bridging unit undergo exchange only with their geminal partners and so these, weakly shifted, protons may be readily assigned. This leaves the eight resonances of the cyclen ring showing only one cross peak in the EXSY spectrum for each of these cyclen resonances. Comparing these EXSY cross peaks with the information provided by the COSY spectrum shows that this exchange motion is equivalent to a sequential ring flip and arm rotation. These motions convert the complex into its enantiomer and so the protons on one ethylene group exchange places with those of the adjacent ethylene group of the opposing enantiomer, i.e. ax ^S _δ ↔ eq^C_λ′, eq^S_δ ↔ ax^C_λ′ and so forth (ESI S6). In order to complete the assignment of the ¹H NMR spectrum of Yb1 an analyis of the ytterbium induced shifts was performed, comparing the observed shifts to those calculated from the crystal stucture. This analysis allowed the position of each ethylene group of cyclen and the acetamide protons to be determined. More significantly however, this analysis would also show that the structure observed in the crystal was in fact the same as that found in solution.

NMR Shift Analysis of Yb8O₂-bridged-DOTAM

Ytterbium is an extremely useful probe for analysing lanthanide induced shifts (LIS) because its pseudo-contact (or dipolar) shift contribution significantly dominates over its contact contribution. In complexes such as this that have low symmetry, the pseudo-contact shift (Δ) is made up of a sceond-order axial term and a rhombic term (Eqn 1):³⁴

$${\mathrm{\Delta }}^{pc}=D_1\frac{(3{\text{cos}}^2\theta -1)}{r^3}+D_2\frac{\text{sin}2\theta \text{cos}2\varphi }{r^3}$$ (1)

where (r, θ, ϕ) are the Cartesian coordinates of the ligand proton with the ytterbium ion at the origin and z-axis along the principal magnetic axis; D₁ and D₂ are constants for a given complex determined by the principal components of the molecular magnetic susceptibility tensor and defined by Eqn 2 and Eqn 3.

$$D_1={\chi }_{ZZ}-\frac{Tr(\chi )}{3}$$ (2)

$$D_2=({\chi }_{XX}-{\chi }_{YY})$$ (3)

In complexes with lower symmetry the pseudo-contact shift also contains contributions from the non-diagonal components of magnetic susceptibility tensor components: χ_xy, χ_xz and χ_yz. Thus the pseudo-contact shift is given by Eqn 4.³⁴

$${\mathrm{\Delta }}^{pc}=\frac{1}{2N}\left[\left({\chi }_{ZZ}-\frac{Tr(\chi )}{3}\right)\langle \frac{3z^2-r^2}{r^5}\rangle +({\chi }_{XX}-{\chi }_{YY})\langle \frac{3x^2-y^2}{r^5}\rangle \right]+\frac{1}{N}\left[{\chi }_{XY}\langle \frac{4xy}{r^5}\rangle +{\chi }_{XZ}\langle \frac{4xz}{r^5}\rangle +{\chi }_{YZ}\langle \frac{4yz}{r^5}\rangle \right]$$ (4)

This relationship means that the experimentally observed shifts can be compared with the shifts calculated for a given structure of the complex. First, the experimental pseudo-contact shifts (Δ^pc) where found by use of Eqn 5.

$${\mathrm{\Delta }}^{\text{pc}}={\mathrm{\delta }}^{\text{exp}}-{\mathrm{\Delta }}^{\text{dia}}$$ (5)

where δ^exp is the observed chemical shift of the proton and Δ^dia is the diamagnetic contribution to this shift. This diamagnetic contribution was estimated from the chemical shift of the diamagnetic lutetium complex. The ¹H NMR spectrum of Lu1 is relatively complex with several overlapping resonances, however, on the basis of the known deshielding effects of the heteroatoms of the ligand and with assistance from the EXSY spectrum (ESI S12), a reasonable estimate of the diamagnetic shift of each proton was obtained. Subtracting these values from the observed shift of the corresponding proton in the ytterbium complex afforded experimental values for Δ^pc.

The coordinates of all atoms in the crystal structure of Yb1 were transformed onto a framework that had the ytterbium ion as its origin, with the z-axis passing through the center of the cyclen nitrogen and oxygen amide planes. The coordination prism was oriented such that the x- and y-axes were parallel to the sides of the square of the nitrogen plane of the cyclen ring (ESI S12). From the Cartesian coordinates determined in this way the pseudo-contact shift of each proton could be calculated using Eqn 4. A least squares fitting procedure was performed in Microsoft Excel, minimizing the difference between the observed and calculated pseudo-contact shifts of the protons in Yb1. This procedure afforded an axial magnetic component D₁ (χ_zz −Tr(χ)/3) = 5785.4 ± 149.6 and a non-axial magnetic component D₂ (χ_xx − χ_yy) = −1484.6 ± 73.4, indicating that the primary magnetic component of the ligand field lies along the z-axis. The agreement factor ([Σ_i<Δ_exptl − Δ_cal>²/Δ² _exptl]^1/2) obtained for this procedure was 4.95%. The observed and calculated psuedo-contact shifts for each proton are collated in Table 3. Considering the close agreement between the two sets of values it seems reasonable to conclude that the structure of Yb1 in solution is very close to that observed in the crystal.

Table 3.

The experimental and calculated pseudo-contact shifts, Δ^pc, for all the protons in Yb1.

1H Assignment	Δpc / ppm
	Experimental	Calculated
Ethylene group of cyclen under bridged arms a
ax S	86.9	85.5 ± 1.7
eqS	12.9	11.9 ± 1.4
eqC	13.9	15.1 ± 1.4
ax C	−24.5	22.4 ± 1.5
Ethylene group of cyclen under the independent arms b
ax S	90.4	86.5 ± 2.3
eq S	10.8	16.6 ± 4.6
eq C	0.9	2.7 ± 1.1
ax C	−57.5	−55.5 ± 1.6
α-Acetamide protons on bridging unit c
ac 1	−54.5	−56.8 ± 2.1
ac 2	−38.6	−41.0 ± 1.9
α-Acetamide protons on independent arms d
ac 1	−71.7	−72.9 ± 1.9
ac 2	−29.1	−31.9 ± 2.1
Bridging Unit e
br axS	4.7	5.0 ± 1.0
br eqS	−1.3	−1.5 ± 1.1
br eqC	13.5	10.4 ± 3.3
br axC	15.3	14.8 ± 1.5
br I	99.3	99.5 ± 1.1
br E	36.1	36.6 ± 1‥4

^a)labeled blue in Figure 4

^b)labeled red in Figure 4

^c)labeled green in Figure 4

^d)labeled orange in Figure 4

^e)labeled black in Figure 4

Solution State Dynamics of Eu8O₂-bridged-DOTAM

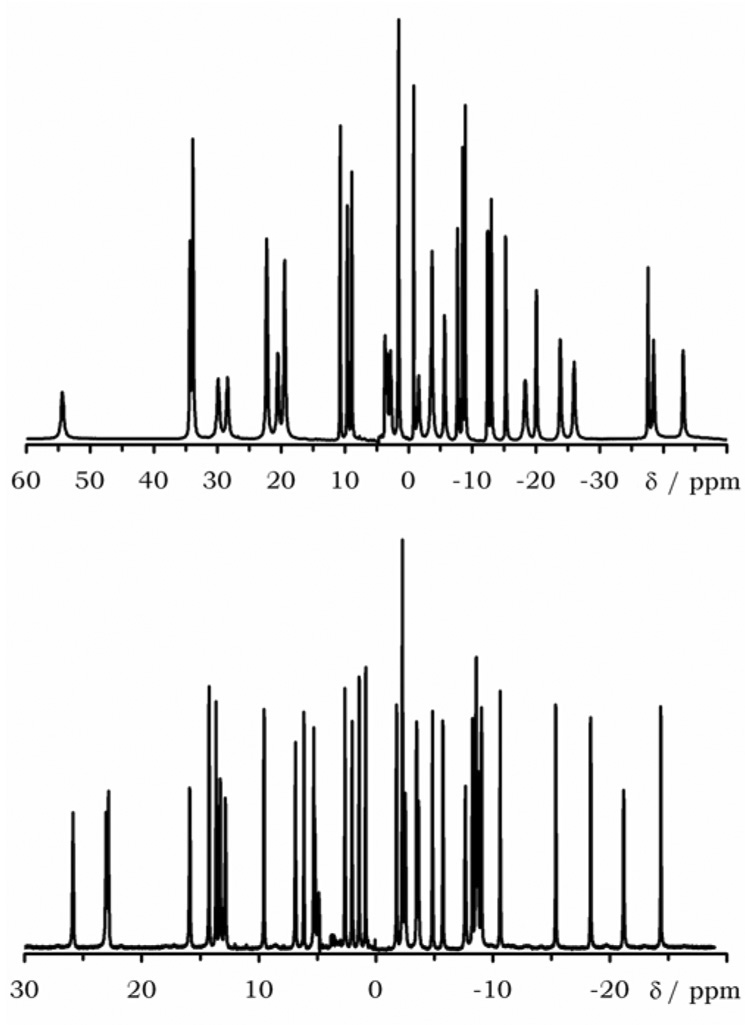
The NMR spectra of some other later lanthanide ions, holmium and erbium, also exhibit 18 resonances (data not shown), consistent with C₂-symmetry. However, in the NMR spectra acquired for earlier lanthanide ions, with larger ionic radii, such as europium or praseodymium, 36 resonances were observed (Figure 5).

Figure 5.

The ¹H NMR spectra of Pr1 (top) and Eu1 (bottom) recorded in D₂O at 500 MHz, with solvent suppresion.

There are essentially two possible explanations for this observation; either the complex undergoes a small conformational shift and loses all symmetry or a second coordination isomer is observed for the earlier lanthanide ions such as occurs with DOTAM (Figure 1). However, all 36 resonances in the spectra of both Pr1 and Eu1 are of equal intensity, suggesting that loss of symmetry is a more likely explanation. The COSY and EXSY spectra of Eu1, analyzed on the same basis as those of Yb1, allowed a partial assignment of the NMR spectrum (ESI). A full break down of the COSY and EXSY spectra are given in the supplementary information (S7–S11). From analysis of the COSY spectrum, it is possible to identify 28 resonances associated with seven ethylene groups. For three of these ethylene groups, the exchange was found only between protons on the same carbon. As in the case of Yb1, these ethylene groups correspond to the three ethylene groups of the bridging unit. The presence of three magnetically distinct ethylene groups in the bridging unit confirms that the symmetry of the complex has been lost by incorporating a larger metal ion. The remaining four ethylene groups therefore correpsond to the four magnetically inequivalent ethylene groups of the cyclen ring.

The reason for this sudden loss of symmetry is most likely the short length of the bridging unit. We have seen how in the ytterbium complex the bridging unit pulled the two coordinating amide groups closer together, levering the amide nitrogen out of plane and distorting the N-C-C-O torsion angle. Clearly, as the metal ion gets larger the distortion of the N-C-C-O torsion angle will increase until eventually it reaches 0° and there is no more give in the system. At this point the bridge is too short to reach across the complex if the 21-membered macrocycle adopts the [7,5,4,2,3] ring conformation shown in Figure 6 and observed in the crystal structure of Yb1.³⁵ The only way in which the bridge can span the complex is if the 21-membered macrocycle alters its confromation to make the bridging span longer. In practice this can be achieved by moving one of the corners towards the coordinating amide group and so effectively incorporating another atom in the bridging span. This would involve the 21-membered ring adopting the [6,6,4,2,3] conformation shown in Figure 6. It would also render the bridging unit, and the rest of the complex, completely asymmetric.³⁵

Figure 6.

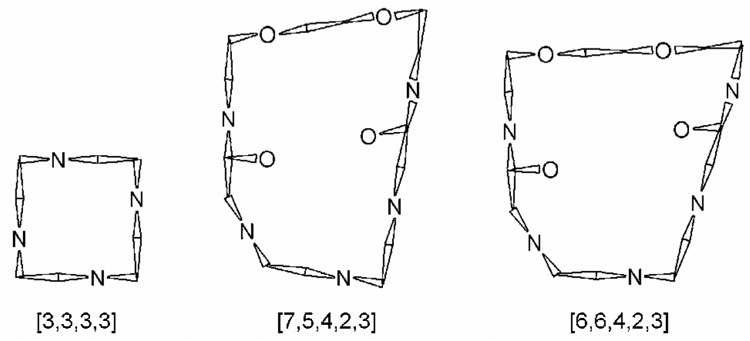
Representations of the two macrocyclic systems to be found in the 1. Cyclen adopts the classic [3,3,3,3] conformation (left), the 21-membered macrocycle (right) that incorporates half of the cyclen ring as well as the bridging group is more complex incorportaing five genuine corners.³⁵ However, it can be seen that both macrocycles adopt the same conformation, defining the orientation of the amide pendant arms.

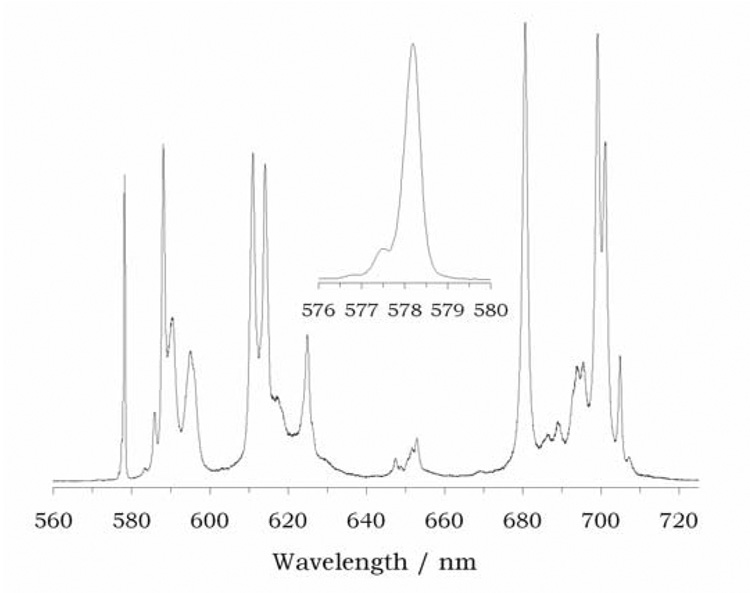
In common with the EXSY spectrum of Yb1, the EXSY spectrum of Eu1 (Figure 7) shows only a single crosspeaks for each of these cyclen resonances, consistent with exchange of two enantiomers. In this case all the protons of one ethylene group of cyclen exchange with those of an adjacent ethylene group. Comparing these exchanging pairs with the COSY spectrum reveals that the exchange process here is also one that corresponds to sequential ring flip and arm rotation. Since the conformation of the cyclen ring is found to influence the conformation of the bridging unit, and thus the orientation of the pendant arms, in the crystal structure of Yb1, it would be easy to conclude that ring flip and arm rotation must be a concerted process and that the SAP isomer is completely inaccessable. However, a high resolution emission spectrum of Eu1 reveals that two ΔJ = 0 bands are present around 578 nm (Figure 8). Since this emission band is non-degenerate a single line is observed for each coordination enviroment of europium present in solution. The more intense peak at 578.2 nm clearly arises from the TSAP isomer of Eu1 and confirms that this isomer is a single asymetric complex in solution. But a smaller peak is also observed at 577.4 nm, this observation prompted a reexamination of the NMR spectrum of Eu1.³⁶ Just visible in the baseline of the spectrum may be observed small peaks (ESI S13), and in particular resonances corresponding to 4 protons (ax ^S) may be observed between 40 and 50 ppm. The chemical shifts of these protons are consistent with presence of trace amounts of the SAP coordination isomer. Although this coordination geometry must be high in energy, because the conformations of the cyclen ring and the bridging unit must be opposed, its presence clearly indicates that ring flip and arm rotation remain independent motions in this complex. There is not a single concerted intramolecular motion. So, although the predominant species in soltuion is the TSAP isomer (Δ(δδδδ) and Λ(λλλλ)), the SAP isomer is accessable, although it is present in only trace amounts.

Figure 7.

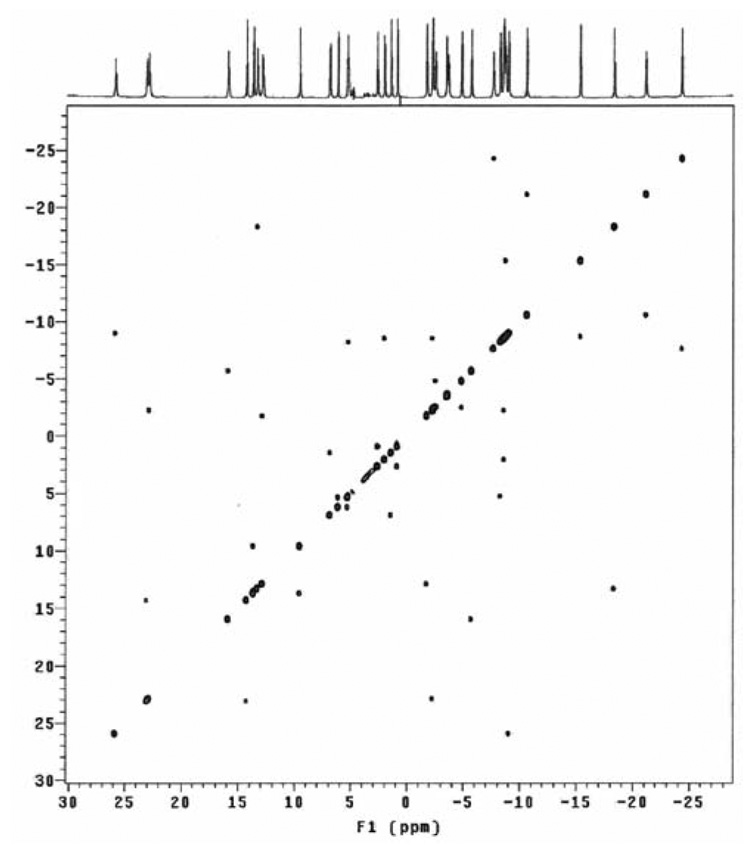
The ¹H EXSY spectrum of Eu1 recorded at 500 MHz and 298 K in D₂O with solvent suppression.

Figure 8.

The emission spectrum of Eu1 recorded at 0.05 nm resolution in water.

Hydration State and Relaxometry Studies

The absence of a coordinated water moelcule from the inner coordination sphere, as observed in the crystal structure of Yb1, would significantly reduce the utility of the complex as a PARACEST agent. Although, it may be possible to use the amide NH protons for this purpose.²³ Given the correlation between the observed and calculated shifts for the crystal structure of Yb1, it is reasonable to assume that the O-Yb-O angle does not alter significantly from the crystal to the solution state and that the ytterbium complex is also q = 0 in solution. This idea is supported by the fact that no CEST effect arising from a coordinated water molecule could be observed for the ytterbium, dysprosium or europium complexes. However, to confirm the absence of an inner coordination sphere water molecule in these complexes, independent q value determinations were performed for the dysprosium and europium complexes.

The q value of a dysprosium complex may be determined by measuring the chemical shift of the ¹⁷O NMR resonance of the solvent water as a function of the dysprosium complex concentration.³⁷ Inner sphere water molecules that exchange rapidly with the bulk solvent cause an up-field shift of the solvent resonance. The extent of this up-field shift is proportional to the number of inner sphere water molecules. So by measuring the difference between the ¹⁷O shift of water and water in a solution of the dysprosium complex at different concentration, a linear regression analysis may be performed to determine q. When this experiment was performed on Dy1 a q value of 0.03 was obtained (see ESI S14). Although this method assumes that the coordinated water molecules are in rapid exchange with the bulk solvent, a molecule in slow exchange would most likely have resulted in a CEST effect, so this possibility may be ruled out. It may therefore be concluded that the dysprosium complex is also absent any inner sphere water molecules.

The hydration state of the europium complex was measured using an adaptation of Horrocks’ method. The vibronic levels of OH oscillators overlap with those of the excited state (⁵D₀) of euporium better than those of OD oscillators. Horrocks and Sudnick exploited this difference and, by comparing the rate of luminescent decay in both H₂O and D₂O, were able to determine the hydration state of a europium ion.^38,39 Parker and co-workers proposed a modifcation to this method that would take into account other oscillators such as outer sphere oscillators and amide NH oscillators. They indicated that q could accurately be determined by using Eqn 6 where c is a correction factor for other oscillators.⁴⁰ The luminescent decay rate constants in H₂O and D₂O where determined for Eu1 (k_H2O = 1.27 s⁻¹, k_D2O = 0.698 s⁻¹). Subtracting a contribution of 0.075 for each of the 6 NH amide oscillators gives a value of q = 0.15, a value typical of the outer-sphere contribution in this type of complex.⁴⁰ Thus, it may be concluded that Eu1 is also without a water molecule in the inner hydration sphere.

$$q=1.2({\mathrm{k}}_{{\mathrm{H}}_2\mathrm{O}}-{\mathrm{k}}_{{\mathrm{D}}_2\mathrm{O}}-\mathrm{c})$$ (6)

In addition to these q value determinations the relaxivity of Gd1 was determined. The relaxivity, or the increase in longitudinal proton rate rate of water per unit gadolinium complex, is composed of an inner sphere and an outer sphere component. The inner sphere component is directly related to the number water molecules coordinated to the gadolinium ion and the rate at which they exchange with the bulk solvent. The relaxivity of Gd1 is 1.79 mM⁻¹s⁻¹ (25 °C and 20 MHz); in contrast, the relaxivity of GdDOTAM (q = 1) was reported as 2.5 mM⁻¹s⁻¹ (25 °C and 20 MHz).⁶ However, because the inner sphere water molecule of GdDOTAM is in relatively slow exchange with the bulk solvent,⁶ the inner sphere mechanism does not contribute significantly to the overall relaxivity of the complex. The 28 % decrease in relaxivity observed for Gd1 is therefore presumably the extent of the inner sphere contribution to relaxivity in GdDOTAM. However, second coordination sphere water molecules are known to contribute to relaxivity³⁰ and from the crystal structure of Yb1 (Fig 2) we know that there may be two second sphere water molecules closely associated with the complex. The contribution of any second sphere water molecules to the overall relaxivity of Gd1 is probably quite small; the M-H distance in the crystal are quite long (4.77 and 6.25 Å), so relaxation of these protons will be quite inefficient. Also, if these second sphere water molecules are present in the Gd complex their exchange kinetics are unlikely optimal. From these observations, one may conclude that all the lanthanide complexes of 1 lack an inner sphere water molecule.

Stability of Ln³⁺ complexes formed with 8O₂-bridged-DOTAM

The crystal structure of Yb1 shows that the lanthanide ions are complexed by the 8O₂-bridged-DOTAM ligand in a similar manner as other DOTA-type ligands. Although Yb1 is somewhat more distorted, the essential features, four co-planar cyclen nitrogen donor atoms below the metal ion and four co-planar amide oxygen donors above the metal ion, are identical. On this basis, the stability constants of this ligand with the trivalent lanthanide cations might be expected to resemble those of DOTAM. However, the protonation constants of the ligand deterimined in an ionic background of 1.0 M KCl so that direct comparisons can be made with DOTAM⁴¹ show that 8O₂-bridging DOTAM is somewhat less basic overall than DOTAM (Table 4). The most striking observation is that the first two protonation constants in both DOTAM and 8O₂-bridged-DOTAM are more than 3 orders of magnitude lower than those in DOTA. This reflects the fact the negatively charged acetate side-chains in DOTA providing better hydrogen bonding sites for the protonated macrocyclic nitrogens than do the neutral amide groups on DOTAM and 8O₂-bridged-DOTAM.⁶ Given that the total basicity of such ligands typically parallels the thermodynamic stability of complexes formed with lanthanides, it is not surprising that the LnL stability constants fall in the order, 8O₂-bridged-DOTAM < DOTAM ≪ DOTA. The somewhat greater disparity between the stability constants of the 8O₂-bridged-DOTAM system in comparison to DOTAM over that expected based upon ligand basicity alone likely reflects the conformational distortion of the Ln³⁺-8O₂-bridging-DOTAM complexes and particularly the cyclen ring which may be prevented from forming a perfect gauche conformation by the bridging unit in these complexes.

Table 4.

Protonation constants of 8O₂-bridged-DOTAM, DOTAM and DOTA and their stability constants with some lanthanide ions. The constants were determined at 25 °C in an ionic background (I) of 1.0 M KCl (in the case of DOTA I = 0.1 Me₄NCl). The standard deviations are given in parentheses.

Equilibrium Constant	1	DOTAMa	DOTAb
log K1H	8.44 (0.02)	9.08	12.60
log K2H	5.51 (0.03)	6.44	9.70
log K3H	–	–	4.50
log K4H	–	–	4.14
log K5H	–	–	2.32
log KCeL	4.85 (0.06)	11.93	23.4c
log KEuL	6.44 (0.08)	13.54	23.5c
log KYbL	9.58 (0.06)	–	25.0c
log KLuL	–	13.53	–

^aValues taken from reference ⁴¹

^bValues taken from reference ⁴²

^cValues taken from reference ⁴³

The LnDOTA⁻ complexes show a dramatic increase in stability near the center of the Ln³⁺ series (near Gd³⁺) that may reflect the optimal size match of the DOTA cavity with Ln³⁺ ion radius.⁴³ Only small increases in stability were noted for further deceases in ionic radius for those Ln³⁺ cations near the end of the series. Molecular mechanics calculations on DOTAM have shown that the ligand strain energy is minimum for the Sm³⁺ complex, suggesting that this would be the most stable complex with donor atoms-metal distances and angles that best meet the requirements of the Ln³⁺ ion.⁴⁴ Despite this indication, experimental data shows that Eu³⁺ forms the most stable complex but again, as the ionic radius of the lanthanide ion becomes smaller, no further increases were seen in the stability constants of DOTAM complexes.⁴¹

Each lanthanide investigated was found to form complexes that were weaker with 8O₂-bridged-DOTAM than were found for DOTAM (Table 4). Given the lower basicity of the ligand (∑_logKa = 13.95 vs 15.52 for DOTAM), this result is not altogether surprising. However, one would have predicted log K_LnL values to be in the range 11–12 simply based upon the ∑_logKa value for 8O₂-bridged-DOTAM alone, so the fact that the experimental values (Table 4) are considerably smaller that this predicted value indicates that ligand strain plays a significant role in these complexes. It is also interesting to note that Yb³⁺-8O₂-bridged-DOTAM is ~3 orders of magnitude more stable than Eu³⁺-8O₂-bridged-DOTAM so lanthanide ion size in this system plays a much bigger role than in the corresponding DOTAM or DOTA complexes. This is consistent with the observation that larger lanthanide ions cause enough distortion in the ligand framework upon complexation that the complex loses its symmetry. The effective size of the “coordination cage” of 8O₂-bridged-DOTAM must therefore be quite small, able to accommodate a heavy lanthanide ion but too small to easily accept lanthanide ions from early in the series.

Conclusions

Lanthanide complexes formed with the bridging ligand, 8O₂-bridged-DOTAM 1, are quite unusual in that the bridging unit renders the complex bicyclic in nature. The interconnectedness of the macrocyclic rings mean that the conformation of the cyclen ring and the orientation of the pendant arms (through the conformation of the bridging unit) are inherently connected and they must adopt the same helicity (δ or λ). As a result, the complex predominantly adopts the TSAP coordination geometry in which the helicity of the pendant arms is the same as that of the cyclen ring. In this way, the bridging unit, although achiral,^16,17 determines which coordination geometry is found. Exchange is observed between the two enantiomeric TSAP isomers, Δ(δδδδ) and Λ(λλλλ). This exchange is the result of sequential arm rotation and ring flip motions and does pass through a high energy SAP isomer. The lanthanide complexes of this ligand do not possess a water molecule in the inner coordination sphere because the ligand structure is strained causing excess steric encumbrance around the water coordination site. As the ionic radius of the lanthanide increases the stability of the complexes was found to decrease. This drop in stability parallels a loss of symmetry in the complexes of the earlier lanthanides. These two observations appeared to relate to the size of the bridging unit and the magnitude of the N-C-C-O torsion angle. Once this torsion angle reaches 0°, the bridging unit must elongate in order to span the complex and, to accomplish this, the conformation of the 21-membered macrocyclic ring that incorporates the bridging unit must move one corner of this ring closer to the coordinating amide group. This action seems to increase the distortion present in the complex, reducing its stability and removing any elements of symmetry. Owing to the absence of an inner sphere coordinated water molecule, these complexes will not be useful as PARACEST agents.

Experimental

General

All reagents and solvents were purchased from commercial sources and used as received unless otherwise stated. A JEOL Eclipse 270 NMR spectrometer was used to record ¹H and ¹³C NMR spectra at 270.17 MHz and 67.5 MHz, respectively. A Varian Inova 500 NMR spectrometer was used to record ¹H (including ¹H-¹H COSY, ¹H-¹H EXSY), ¹³C and ¹⁷O NMR spectra at 500, 125 and 67.5 MHz, respectively. Melting points were recorded on a Fisher/Johns melting point apparatus and are uncorrected. Luminescent lifetimes were measured on a Perkin Elmer LS-50B fluorimeter using the pHlemming software developed by Dr. A. Beeby of the University of Durham. Direct excitation of europium was employed at 396 nm and emission was monitored at 594 nm. The high resolution emission spectrum of Eu1 was recorded on an Edinburgh Instruments FS900 fluorimeter.

Synthesis

1,4,7,10-tetraazacyclododecane-1,4,7,10-tetraacetamide (DOTAM)⁴⁵ and 1,7-bis-benzyloxycarbonyl-1,4,7,10-tetraazacyclododecane (2)^19,20 were prepared by previously described methods.

1,7-Bis-benzyloxycarbonyl-1,4,7,10-tetraazacyclododecane-4,10-bis-acetamide (3)

The diprotected cyclen 2 (9.38 g, 21.3 mmol) and 2-bromoacetamide (6.17 g, 44.7 mmol) were dissolved in acetonitrile (250 mL). Potassium carbonate (11.76 g, 85.2 mmol) was added and the reaction stirred at 60 °C for 2 days. The reaction was filtered and the filter cake washed with hot acetonitrile. The solvents were removed in vacuo and the residue taken up into dichloromethane (120 mL) and washed with water (2 × 120 mL). The organic layer was dried (Na₂SO₄) and the solvents removed in vacuo. The solid residue was recrystallized from hot acetonitrile to afford the title compound as a colourless solid (8.10 g, 69%).

mp = 160–162 °C; ¹H NMR (270 MHz, CDCl₃) δ= 7.30 (10H, m, Ph), 5.87 (4H, s br, CONH₂), 5.10 (4H, s, PhCH ₂), 3.35 (8H, s br, ring NCH₂), 3.07 (4H, s br, NCH₂CO), 2.73 (8H, s br, ring NCH₂); ¹³C NMR (67.5 MHz, CDCl₃) δ = 174.0, (CONH₂), 157.1 (NCO₂), 136.4 (Ph), 128.9 (Ph), 128.7 (Ph), 128.4 (Ph), 67.6 (PhCH₂), 58.2 (NCH₂CO), 55.0 (ring NCH₂), 49.0 (ring NCH₂); ν_max / cm⁻¹: 3010 (NH), 1685 (C=O), 1518, 1417, 1212, 924, 757, 664; m/z (ESMS ESI+) 555 (100%, [M+H]⁺); Anal. Found C = 58.5%, H = 6.8%, N = 14.3%, C₂₈H₃₈N₆O₆ requires C = 58.7%, H = 7.0%, N = 14.7%.

1,4,7,10-Tetraazacyclododecane-1,7-bis-acetamide (4)

The dicarbamate 3 (8.0 g, 14.4 mmol) was dissolved in absolute ethanol (150 mL) and 10 % palladium on carbon (1.0 g) added. The reaction mixture was shaken on a Parr hydrogenator for 3 days under a hydrogen pressure of 50 psi. The reaction was filtered and the solvents removed in vacuo. The residue was dissolved in hot absolute ethanol (10 mL) and hot acetonitrile (200 mL) was added. The solution was allowed to cool to room temperature affording the title compound as a crystalline solid (4.0 g, 91%).

mp = 202–204 °C; ¹H NMR (270 MHz, CD₃OD) δ = 3.20 (4H, s, NCH₂CO), 2.73 (16H, m br, ring NCH₂); ¹³C NMR (67.5 MHz, CD₃OD) δ = 175.3 (C=O), 58.5 (NCH₂CO), 52.7 (ring NCH₂), 44.4 (ring NCH₂); ν_max / cm⁻¹: 3479 (NH), 3441 (NH), 3383 (NH), 3196 (NH), 3192 (NH₂), 2940, 2870, 2831, 1666 (C=O), 1526, 1437, 1348, 1289, 1107, 633; m/z (ESMS ESI+) 287 (100% [M+H]⁺).

N,N′-[2,2′-(ethane-1,2-diylbis(oxy))diethanamine]bis(2-chloroacetamide) (5)

2,2′(Ethylenedioxy)bis(ethylamine) (2.96 g, 20.0 mmol) was dissolved in dichloromethane (100 mL) and potassium carbonate (11.0 g, 79.6 mmol) added. The mixture was cooled to 0 °C and a solution of chloroacetylchloride (4.6 mL, 57.5 mmol) in dichloromethane (50 mL) was added drop-wise with stirring. The reaction was stirred at 0 °C for 3 hours. The reaction was then quenched with a solution of water (120 mL). The reaction was transferred to a separatory funnel and the two phases separated, the organic layer was the washed with a 5% citric acid solution (100 mL) and then water (120 mL). The organic phase was dried (Na₂SO₄) and the solvents removed under reduced pressure. The residue was recrystallized from ethyl acetate to afford the title compound as a colorless crystalline solid (5.06g, 84%).

mp = 88–90 °C; ¹H NMR (270 MHz, CDCl₃) δ = 8.23 (2H, br, NH), 4.02 (4H, s, COCH₂Cl), 3.60 (4H, s, OCH₂CH₂O), 3.57 (4H, t, ³ J _H-H = 6 Hz, OCH ₂CH₂N), 3.42 (4H, t, ³ J _H-H = 6 Hz, OCH₂CH ₂N); ¹³C NMR (67.5 MHz, CD₃OD) δ = 168.1 (C=O), 70.0 (OCH₂CH₂O), 69.0 (OCH₂CH₂N), 42.0 (COCH₂Cl), 39.5(OCH₂ CH₂N); m/z (ESMS ESI+) 302 (100% [M+H]⁺; ν_max / cm⁻¹: 3313 (NH), 3182 (NH), 3006 (NH), 2958, 2929, 2875, 1647 (C=O), 1551, 1456, 1414, 1281, 1142, 1099, 760; Anal. Found C = 39.9%, H = 6.0%, N = 9.3%, C₁₀H₁₈Cl₂N₂O₄ requires C = 39.9%, H = 6.0%, N = 9.3%.

7,10-dioxa-1,4,13,16,19,24-hexaaza-bicyclo[14.5.5]hexacosane-3,14-dione-19,24-bisacetamide, 8O₂-bridged DOTAM (1)

DO2AM 4 (1.19 g, 4.15 mmol) and the bis-chloroacetamide 5 (1.24 g, 4.10 mmol) were dissolved in acetonitrile (1.3 L) and potassium carbonate (8.0 g, 57.9 mmol) added. The reaction mixture was heated to 50 °C with stirring for 5 days. The reaction mixture was then filtered and the solvents removed from the filtrate in vacuo. The solid residue was recrystallized from ethanol and dried under vacuum to afford the title compound as colorless crystals (1.26g, 60%).

¹H NMR (270 MHz, CD₃OD) δ = 3.78 (4H, s, OCH₂CH₂O), 3.58 (4H, t, ³ J _H-H = 6 Hz, OCH ₂CH₂N), 3.43 (4H, t, ³ J _H-H = 6 Hz, OCH₂CH ₂N) 3.10 (8H, s br, NCH₂CO), 2.57–2.87 (16H, m br, ring NCH₂); ¹³C NMR (67.5 MHz, CD₃OD) δ = 175.6 (CONH₂), 171.6 (CONHCH₂), 70.6 (OCH₂CH₂O), 70.2 (OCH₂CH₂N), 59.7 (NCH₂CONH₂), 56.3 (NCH₂CONHCH₂), 51.8 (ring NCH₂), 51.6 (ring NCH₂), 38.5 (OCH₂ CH₂N); ν_max / cm⁻¹: 3401 (NH), 3257 (NH), 2944, 2838, 1678 (C=O), 1654 (C=O), 1529, 1458, 1431, 1350, 1296, 1111, 1082, 582; m/z (ESMS ESI+) 515 (100%, [M+H]⁺); Anal. Found C = 50.4%, H = 8.2%, N = 20.3%, C₂₂H₄₂N₈O₆ requires C = 50.4%, H = 8.5%, N = 20.6%.

General procedure for the synthesis of Ln1³⁺

The ligand 1 (100 mg, 195 µmol) and ytterbium nitrate (100 mg, 214 µmol) were dissolved in water (8 mL) and heated at 50 °C for 3 hours. The pH of the reaction was then raised to 8 by addition of a dilute sodium hydroxide solution. The pH was maintained above 8 by periodic addition of sodium hydroxide while heating for a further 18 h. The solvents were then removed by lyophilization and the solid residue taken up into water (1 mL) and centrifuged to remove residual ytterbium hydroxide. Lyophilization of the resulting clear solution afforded the complex as a colorless solid.

Nitrate, triflate and chloride salts were all prepared in an analogous manner. Samples for use in relaxivity, luminescence and ¹⁷O NMR experiments were prepared using a 20 % excess of ligand to exclude free lanthanide ion from the sample.

Crystal structure determination of Yb(8O₂-bridged-DOTAM)(H₂0)₂(NO₃)₃

The structure is presented in Figure 2. Crystals were grown from aqueous solution by slow evaporation at room temperature. A colorless plate, 0.170 × 0.456 × 0.569 mm, was selected: C₂₂H₄₆N₁₁O₁₇Yb, mass = 909.74, trigonal, P₃₁₂₁, a = 10.775(2), b = 10.775(2), c = 27.882(6) Å, α = 90.00°, β = 90.00°, γ = 120.00°, U = 2803.4(8) ų, Z = 3, D_χ = 1.517 gcm⁻³, λ(Mo-Kα) = 0.71073 Å, µ = 2.076 mm⁻¹, F(000) = 1383, T = ambient. The sample was studied on a Bruker CCD 1000. The data collection gave 4092 unique reflections. Refinement was performed using a full-matrix least squares method on F² using SHELXTL Version 5. GOF = 1.13. This procedure afforded R1 = 0.0263; wR2 = 0.0519 for all data.

Stability Determinations

pH-potentiometric titrations were carried out with a Thermo Orion expandable ion analyzer EA940 pH meter and a Thermo Orion semi-micro combination electrode 8103BN. A Metrohm DOSIMATE 665 autoburette (5 mL capacity) was used for the base additions. The electrode was calibrated using Borax (0.01 M, pH 9.180) and KH-phthalate (0.05 M, pH 4.005) buffers. The titrant, a carbonate-free KOH solution, was standardized with KH-phthalate solution, by pH-potentiometric titration. All titrations were performed in 1.0 M KCl solution to maintain ionic strength and samples were thermostated at 25.0 °C. Titrations were performed under an argon atmosphere to exclude CO₂. H⁺ ion concentrations were determined from the measured pH values using the method proposed by Irving et al. ⁴⁶

Stock solutions of CeCl₃, EuCl₃, and YbCl₃ were prepared from LnCl₃·6H₂O salts and the concentration of each LnCl₃ solution determined by complexometric titration using standardized EDTA solution and xylenol orange indicator. The concentration of a solution of 1 was determined by potentiometric pH titration in the presence and absence of excess CaCl₂. The protonation constants of the ligand were calculated from the titration data obtained at 2.5 mM concentration (10 mL) in the pH range 2–12 and are defined by Eqn 7:

$$K_i^H=\frac{[H_{i}L]}{[H_{i-\mathit{1}}L][H^{+}]}$$ (7)

Due to slow formation of Ln8O₂-bridged-DOTAM³⁺ complexes, the stability constants were determined using the “out-of-cell” technique described previously.³³ Sixteen separate samples containing equimolar amounts of 1 and LnCl₃ (2.5 mM) were prepared, in duplicate, at different pH values in the range 3–6. The samples were sealed under a blanket of N₂ gas to prevent entry of CO₂ and equilibrated at 45 °C in an incubation chamber for four weeks. The samples were then re-equilibrated at room temperature. The samples were then opened and the pH value of each sample measured. The protonation constants $(\text{log}{K}_i^H)$ and stability constants of the complexes (log K_ML) were evaluated from the potentiometric titration data using the program PSEQUAD.⁴⁷