Solvent Reaction Field Potential inside an Uncharged Globular Protein: A Bridge between Implicit and Explicit Solvent Models?

Abstract

The solvent reaction field potential of an uncharged protein immersed in Simple Point Charge/Extended (SPC/E) explicit solvent was computed over a series of molecular dynamics trajectories, intotal 1560 ns of simulation time. A finite, positive potential of 13 to 24 k_bTe_c⁻¹ (where T = 300K), dependent on the geometry of the solvent-accessible surface, was observed inside the biomolecule. The primary contribution to this potential arose from a layer of positive charge density 1.0 Å from the solute surface, on average 0.008 e_c/ų, which we found to be the product of a highly ordered first solvation shell. Significant second solvation shell effects, including additional layers of charge density and a slight decrease in the short-range solvent-solvent interaction strength, were also observed. The impact of these findings on implicit solvent models was assessed by running similar explicit-solvent simulations on the fully charged protein system. When the energy due to the solvent reaction field in the uncharged system is accounted for, correlation between per-atom electrostatic energies for the explicit solvent model and a simple implicit (Poisson) calculation is 0.97, and correlation between per-atom energies for the explicit solvent model and a previously published, optimized Poisson model is 0.99.

1 Introduction

The electrostatic properties of solvated biomolecules are a subject of intense computational [1–3] as well as experimental interest [4–7]. The polar nature of water molecules influences the structure of proteins, nucleic acids, and lipid membranes. The processes that shape such structures are in turn related to the solubilities of (biologically relevant) ions [8] and the propensity of acidic or basic biochemical groups to ionize in solution [9–18].

Among the various types of solvent models developed to study solvation phenomena, fully explicit and implicit models are the most popular. In explicit solvent models, atomic properties such as size, partial charges [19–21] and possibly higher-order electrostatic features [22, 23] are parameterized to reproduce macroscopic properties of the solvent such as heat capacity, bulk dielectric constant, vaporization enthalpy, and atomic radial distribution functions. In contrast, implicit solvent models assign no structure to the solvent. Instead, they are parameterized to reproduce solvation effects based on configuration of the solute and some arbitrary parameters such as a dielectric constant and a solute volume definition.

The ability to track individual water molecules, which may comprise 90% of the particles in an explicitly-solvated system [24], is a demonstration of the power of biomolecular simulations [25]. The expectations on computational models are indeed very high: for example, the specificity of biomolecular interactions depends greatly on microscopic, solvent-mediated effects [26–28]. Although many microscopic properties of the neat liquid, and of solute-solvent interactions, are difficult to assess experimentally, advances in quantum calculations [29–35] of water structure as well as experimental data on the properties of water in the liquid phase [36] and around biomolecules [26] will provide a basis for increasingly detailed explicit water models for robust treatment of water in many environments.

Despite their capacity to model many important features of water, the computational expense of explicit solvent models has driven the development of implicit solvent alternatives. Often based on numerical solutions of the Poisson-Boltzmann equation [37, 38], implicit solvent models have been used to study ligand binding [39], molecular recognition [40], large-scale conformational changes [41, 42], and protein association [43]. However, because implicit solvent models consider solute geometries as opposed to solvent particles, their ability to grow and incorporate newly discovered features of water is limited.

In the future, implicit solvent models will remain useful for sampling of large numbers of radically different conformations in problems such as molecular docking [44–46], protein folding [47], and protein design [48, 49]. For other applications, such as simulation of protein enzymatic mechanisms [50] or analysis of biomolecular interactions [51, 52], explicit solvent models will become increasingly preferred. At the same time, increases in computing power and MD/GRAvity-PipE [53] hardware-accelerated systems will enable investigators to calculate average explicit-solvent characteristics for particular conformations of molecular systems of all scales. In order to bring the advances in explicit solvent simulations to docking and protein structure prediction problems, implicit solvent models must be adapted to mimic explicit solvent effects [54, 55].

The Poisson-Boltzmann model’s inability to address ion correlation has received a great deal of discussion [56–59]. However, the underlying Poisson model of the primitive solvent has also been reported to suffer from an inability to describe important aspects of the nonlinear and nonlocal response of real solvent around molecules of varying charge density and geometry [38, 59–61]. In particular, Ashbaugh [62] observed a potential of 9 kcal/mol-e_c within large (> 5Å radius), uncharged spherical particles immersed in SPC water. Rajamani and co-workers observed similar effects with several other water models, pointing out how the water microstructure influences the solvation energetics [63].

Here, we show that a theoretical globular protein with only Lennard-Jones properties induces significant structure in SPC/E solvent [19, 64], creating a significant positive electrostatic potential within the protein and an oscillating potential that extends several Ångstroms into solution. Extending previous studies [62, 63], we note some dependence of this electrostatic potential on the irregular protein shape, quantify how this result arises from perturbation of water structure at the protein:solvent interface, and find that this result is helpful but not sufficient for reconciling Poisson and explicit solvent models for protein hydration.

2 Methods

2.1 Accumulation of the Water Density Profile

Structure 1f94 [65], the bucadin snake venom toxin, was selected from the Protein Data Bank [66] as model system for analyzing protein hydration computationally due to its high solubility, compact shape, and highly charged surface residues. To neutralize the overall charge, one of the surface residues, lysine 14, was mutated to phenylalanine. The protein was solvated in a rectilinear box of 5926 SPC/E waters (enough to enclose the protein by 14 Å in all directions) using the TLEAP module of AMBER9 [67].

The protein/solvent system was relaxed over 50 steps of steepest descent and 450 steps of conjugate gradient minimization using the SANDER module of AMBER9. The efficient PMEMD module of AMBER9 was used to generate all MD trajectories. Equilibration of the unconstrained protein structure was performed in the NPT ensemble for 100 ps at a 1 fs timestep and then for 2 ns at a 2 fs timestep. The AMBER ff99 force field [68, 69], a real-space cutoff of 8.0 Å on nonbonded interactions, periodic boundary conditions, and particle-mesh Ewald [70, 71] electrostatics were used throughout all simulations. All partial charges on the protein were initially set to their full values and adjusted to zero in subsequent stages of simulation and analysis (see below); partial charges on water molecules were always set to their full values.

A “belly mask” [67] was used to freeze the protein in its final, equilibrated conformation, from which two branches of simulation were begun. In one branch, partial charges on all protein atoms were set to zero (henceforth referred to as the simulation of the “uncharged” protein). In the other, all partial charges on the protein were retained (hereafter the simulation of the “charged” protein).

All of the following protocols were applied to both the charged and uncharged protein simulations. To equilibrate the box volume given any changes made to the protein, 100 ps of MD was carried out at a 2 fs timestep in the isobaric-isothermal (NPT) ensemble. The snapshot with a volume most closely corresponding to the average box volume over the final 50 ps of this new equilibration was used as the initial coordinates for all subsequent simulations, hereafter referred to as the “base conformation.” In the base conformations, the simulation boxes for the charged and uncharged proteins measured 61.310 × 56.013 × 54.489 Å and 61.465 × 56.155 × 54.627 Å, respectively. In both cases, the protein was separated from the simulation box faces by at least 10.6 Å of water in all directions.

To study the equilibrium density of water around the frozen conformation of either the charged or uncharged protein, hundreds of separate trajectories in the canonical (NVT) ensemble were initiated from the coordinates of the base conformation. Partial charges on all protein atoms were set to zero and protein atoms were frozen using a belly mask. Initial velocities on the water were reassigned from a Maxwell distribution at 300 K using different initial random seeds. Data collection began after 50 ps, a length of time well above the orientational autocorrelation time of SPC/E water [72], shown to be a few picoseconds at 300K. Coordinates from the trajectories were saved at 200 fs intervals during production runs, which lasted from 500 ps to 10 ns depending on the computing platform.

Up to 300 production runs were run simultaneously on independent Xeon processors with clock speeds ranging from 1.8 to 3.6GHz. These computing resources included desktop computers and various clusters at the San Diego Supercomputer Center. In most cases the simulations were run by “scavenging” time from otherwise unused systems. In this manner, roughly 9 processor-years were accumulated for the collective simulations.

Although our simulations were started with different random seeds and allowed to diverge for an amount of time much longer than the relaxation time of pure SPC/E water, we wanted to ensure that this simulation strategy produced independent trajectories for a protein in SPC/E water. Therefore, the statistical inefficiency [73] (SI) was computed for certain parameters of each system. The SI compares the variance of some parameter α over block averages from sub-sections of a large data set to the variance of α:

$$\text{SI}=\underset{n_b\to \infty }{lim}\left[\frac{n_b{\sigma }^2({\langle \alpha \rangle }_b)}{{\sigma }^2(\alpha )}\right]$$ (1)

In Eq. 1, n_b is the number of data points in a block and 〈 α 〉_b denotes a block average of an observable α. Small values of the statistical inefficiency imply that numerous portions of the data could all give similar results, indicating that sufficient data has been collected and that sub-sections of the data are uncorrelated.

Trajectories were analyzed by re-imaging all atoms back to the original box and accumulating density histograms for water oxygen and water hydrogen atoms, as well as other properties (see below). Each histogram consisted of 309 × 281 × 275 bins for the uncharged protein simulation or 307 × 281 × 273 bins for the charged protein simulation, all bins roughly 0.2 Å on a side (the bin dimensions were set so that each grid would precisely span the proper simulation box). With 1560 ns of data (7,800,000 frames) collected on the uncharged protein system, the bulk oxygen density observed was roughly 2080 counts/bin. This proved to be much more data than was truly necessary to obtain good statistics (see Sec. 3.5). Later, only 620 ns (3,100,000 frames) were collected on the charged protein system, as convergent values of all desired quantities could be obtained at this point.

2.2 Explicit Solvent Electrostatic Calculations Using Fast Fourier Transforms

Poisson’s equation (Eq. 2) for a homogeneous dielectric relates electrostatic potential of a system to its charge distribution, which in our case was computed from the density histograms.

$$-{\nabla }^2\mathrm{\Phi }(\mathbf{r})=\frac{\varrho (\mathbf{r})}{{\epsilon }_0}$$ (2)

We chose a Fast Fourier Transform (FFT) method for solving the electrostatic potential due to the manner in which the FFT method closely resembled the Particle-Mesh Ewald summation and periodic boundary conditions used in the molecular dynamics simulations. In the FFT method, the electrostatic potential is computed by solving Equation 3. In what follows, we denote forward Fourier transforms as

$$\widehat{g}(\mathbf{k})=\mathcal{F}[g(\mathbf{r})]$$

and inverse Fourier transforms as

$$\widehat{g}(\mathbf{r})={\mathcal{F}}^{-1}[\widehat{g}(\mathbf{k})].$$

For the Poisson equation above (2), the Fourier transform gives

$$\widehat{\mathrm{\Phi }}(\mathbf{r})={\mathcal{F}}^{-1}\left[\frac{\widehat{\varrho }(\mathbf{k})}{4{\pi }^2{\epsilon }_0{k}^2}\right]$$ (3)

Routines found in the FFTW3 package [74] were used for all FFT calculations.

2.3 Implicit Solvent Electrostatic Calculations Using the Finite Difference Multigrid Approach

For comparison with the FFT-based solution of the Poisson equation, one finite difference multigrid (FDMG) calculation was done using the PMG multigrid library [75–78] (http://www.fetk.org/) via the APBS software package [37] (http://apbs.sf.net/) to obtain the potential due to the solvent charge distribution around the uncharged protein. The charge density obtained from our simulations was padded on all sides to accommodate a 321 × 289 × 289 grid suitable for the multi-grid algorithm in APBS, but grid spacings were otherwise kept the same. The electrostatic potential at the boundary was assumed to be zero and the dielectric constant was set to 1 throughout.

Also for comparison purposes, APBS was used to assess the electrostatics of the charged protein in a inhomogeneous dielectric, as used in traditional implicit solvent calculations. As in our MD simulations, charges from the AMBER ff99 force field were used to define the solute charge distribution. A molecular surface definition [79] was use to define the solute, with a 1.4 Å solvent probe and solute atom radii given by Lennard-Jones σ parameters, also taken from the AMBER ff99 force field. The dielectric of the solute was set to 1.0 and the dielectric of the solvent was set to 76.0, corresponding to SPC/E water [80]. The APBS software package can compute boundary conditions for Poisson calculations based on coulombic potentials due to all charges in the solute or focus electrostatic calculations using previously computed electrostatic grids as the boundary condition, but periodic boundary conditions are not supported. To reconcile the boundary conditions for implicit solvent calculations, a cube of 5 × 5 × 5 images of the charged protein was prepared, each image spaced by the charged protein simulation box lengths. A coarse solution of Poisson’s equation was computed for the 5 × 5 × 5 super-system and used as the boundary condition for focused Poisson calculations to a fine grid resolution of 0.28 Å on the central protein image in the super-system. (This resolution was previously found to give convergent results for the electrostatic energy of individual atoms in Poisson calculations [81].) The electrostatic properties of the central protein image in the 5 × 5 × 5 super-system were found to be virtually identical to those of the central protein image in a 3 × 3 × 3 supercell (data not shown), indicating that the periodic system had been well-approximated in our implicit solvent calculations.

2.4 Additional Spatial Properties of the Explicit Solvent

To examine the local structure of the solvent, the local interaction energy between pairs of water molecules was computed for a two-dimensional grid, the axes of which represented distances of each water molecule’s oxygen atom from the protein van der Waals surface. Bins on this grid measured 0.05 Å on each side. Two water molecules whose oxygen atoms were within 4.0 Å of one another were defined as locally-interacting, and in such a case the sum of all real-space non-bonded interactions between the two molecules was added to the running total for the appropriate bins (noting symmetry in the histogram). Averages were obtained by keeping a count of the total number of interactions in each bin. This average interaction energy helps address the “hydrogen bonding” character of the water as well as other local interactions as a function of distance from the protein. This indicator was chosen over geometric considerations as the AMBER ff99 force field and SPC/E water model lack explicit hydrogen bonding potentials, instead relying on Lennard-Jones and charge interactions to model such effects.

As a measure of the orientation of individual water molecules around the protein, the dipole moment vector of each water molecule was arbitrarily located at the molecule’s center of coordinates, and the net dipole moment density (or polarization) μ (r) was accumulated on a grid corresponding to the charge density histograms. ζ (r), the direction of molecular dipole moment vectors relative to the protein surface normal, was computed for each water molecule at each frame of the simulation trajectory using Equation 4,

$$\zeta (\mathbf{r})=\frac{\mu (\mathbf{r})\cdot \mathbf{n}(\mathbf{r})}{|\mu (\mathbf{r})||\mathbf{n}(\mathbf{r})|}$$ (4)

where n (r) is the biomolecular surface normal vector computed by finding the nearest protein atom to each grid point. This quantity still left some ambiguity in the orientations of water molecules; for instance, ζ (r) = 0 could mean that, on average, water molecules at point r pointed one hydrogen toward the protein and pointed the other away, or it could mean that water molecules at r pointed both hydrogens parallel to the protein surface. To resolve this ambiguity, we also computed ξ (r) based on γ (r), the cross product of the O:H1 and O:H2 bonds in the SPC/E water molecule:

$$\xi (\mathbf{r})=\left|\frac{\gamma (\mathbf{r})\cdot \mathbf{n}(\mathbf{r})}{|\mu (\mathbf{r})||\mathbf{n}(\mathbf{r})|}\right|$$ (5)

The absolute value of the entire right hand side of Equation 5 is used because of the symmetry of the water molecule. A situation where ζ (r) = 0 and ξ (r) = 0 means that, on average, water molecules at point r point one hydrogen towards the protein and the other away, while ζ (r) = 0 and ξ (r) = 1 means that water molecules at point r tend to point both hydrogens parallel to the protein surface.

To compute integrated radial distribution functions of solvent properties with respect to the solute, we defined a series of surfaces consisting of all points (a) at a distance r from the van der Waals surface of exactly one atom of the biomolecule and (b) at a distance ≥ r from the van der Waals surface of all other atoms. To obtain the integrated radial distribution function 〈 f (r)〉 (r) for a three-dimensional scalar function f (r) such as charge density or magnitude of the net dipole moment (see above), values of f (r) were computed for each point on the surface so that an average and standard deviation could be obtained for a given distance r from the protein surface. Values of r from 0.0 to 10.0 Å were sampled at 0.1 Å intervals. Note that, in this work as well as many others, the surface corresponding to a value of r = 1.4Å is given the special name “the solvent-accessible surface.”

3 Results

3.1 Statistical Inefficiency of Simulation Trajectories

To perform long-timescale molecular dynamics on our atomistic systems, we calculated hundreds of separate trajectories in parallel, each starting with a different random seed. The “production phase” of each trajectory began 50ps after initiation. To ensure that our multi-trajectory approach provided de-correlated results, we performed statistical inefficiency [73] (SI) tests on the atomic and net charge densities as well as the magnitude of the net dipole moment density observed at any given point around the charged or uncharged proteins. S.I. tests were performed on the integrated radial distributions for oxygen, hydrogen, and charge, and net dipole moment density to ensure that both the position and orientation of water molecules were de-correlated across different trajectories. The results of these tests, summarized in Table 1, assure the validity of our multi-trajectory approach.

Table 1.

Maximum values of the statistical inefficiency (S.I.) for solvent observables around the protein in different charge states. 〈f〉 (r) denotes an average value of the function f at all points a distance r from the protein surface. The S.I. was computed for all values of r between 0.8 and 10.0 Å, and the maximum value is reported. For r < 0.8 Å, values of S.I. decreased for 〈ρ_Ox〉 (r) and 〈 ρ_Hd〉 (r), but increased for 〈μ〉 (r).

Function	Result for Uncharged Protein	Result for Charged Protein
〈 ρOx〉 (r)	0.02	0.03
〈 ρHd〉 (r)	0.04	0.04
〈μ〉 (r)	0.06	0.10

3.2 Solvent Reaction Field Potential in and around the Uncharged Protein

To examine the behavior of polar solvent around an uncharged biomolecule, hundreds of nanosecond-scale molecular dynamics simulations were carried out on a fixed conformation of the bucadin snake venom toxin (PDB ID 1f94) [65] immersed in 5926 SPC/E mobile water molecules [19]. Partial charges on all protein atoms were set to zero. More detailed descriptions of the protein and simulations are available in Section 2.1, Accumulation of Water Density. The density of water oxygen and hydrogen atoms was used to plot the charge density throughout the simulation box for computation of the electrostatic potential via the Fast Fourier Transform (FFT) method in a manner similar to Peter et al [82].

We define the solvent reaction field potential (SRF) most generally by Equation 6:

$$\text{SRF}={\mathrm{\Phi }}^{(\text{water})}(\mathbf{r})-{\mathrm{\Phi }}^{(\text{vaccum})}(\mathbf{r})$$ (6)

Here, Φ^(water) represents the electrostatic potential due to either explicit or implicit solvent around the protein, and Φ^(vacuum) represents electrostatic potential due to the protein in the same state of charge in vacuum. Because the SRF is derived from different solvent models throughout this work, different symbols and superscripts are used in each instance. ψ^(Q) and ψ^{(No Q)} describe the explicit solvent reaction field potential around the charged and uncharged proteins, respectively, while ϕ^(Q) and ϕ^{(No Q)} describe the implicit solvent reaction field potential around the charged and uncharged proteins (a principal result of this work is that, while ϕ^{(No Q)} is obviously zero everywhere, ψ^{(No Q)} is not).

The explicit solvent reaction field potential, ψ^{(No Q)}, obtained through FFT-based convolution of the explicit solvent charge density around the uncharged protein, is shown in Figure 1. The FFT-computed electrostatic potential was slightly negative (−1.0 k_bTe_c⁻¹) at the boundaries of the simulation box, and everywhere more than 10 Å from the solute, reflecting a propensity of solvent dipoles to point inwards at the protein (see Sec. 3.4). Our FFT-based solution of ψ^{(No Q)} was thus offset from an alternate solution computed by the finite-difference multigrid (FDMG) method [37], wherein the boundary electrostatic potential was set to zero (see Sec. 2). Otherwise, the correlation between the two solutions exceeded 99.5% and the magnitudes of the potentials were in close agreement.

Figure 1.

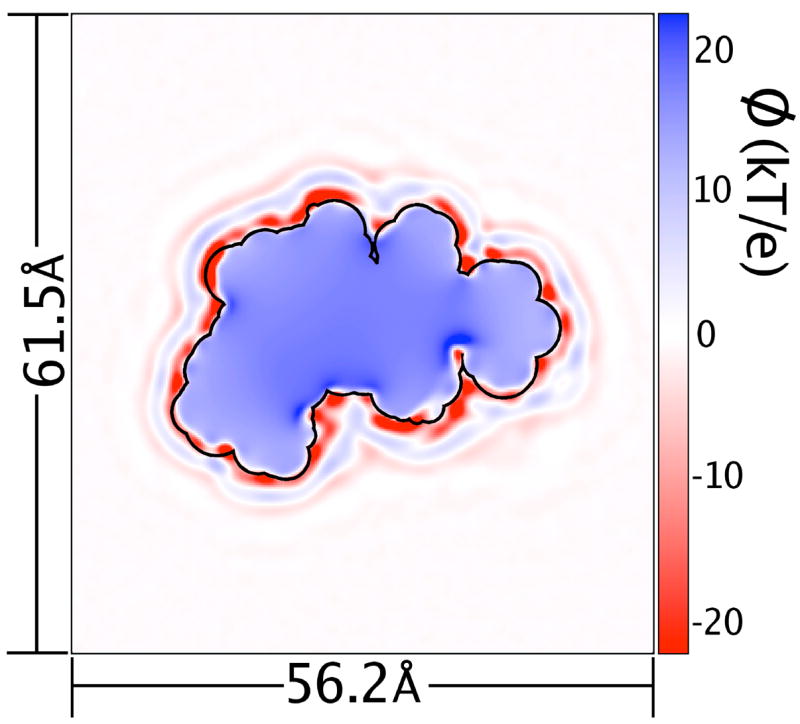
(Color online.) Solvent reaction field potential due to SPC/E explicit solvent charge density around the uncharged protein. This particular slice cuts through the centroid of the protein. Potential values as low as −70 k_bTe_c⁻¹ (T = 300K) are present, but the color scale has been adjusted for greater detail at more common values. As a guide, the protein’s solvent-accessible surface, measured with a 1.4 Å probe, is shown as a black outline.

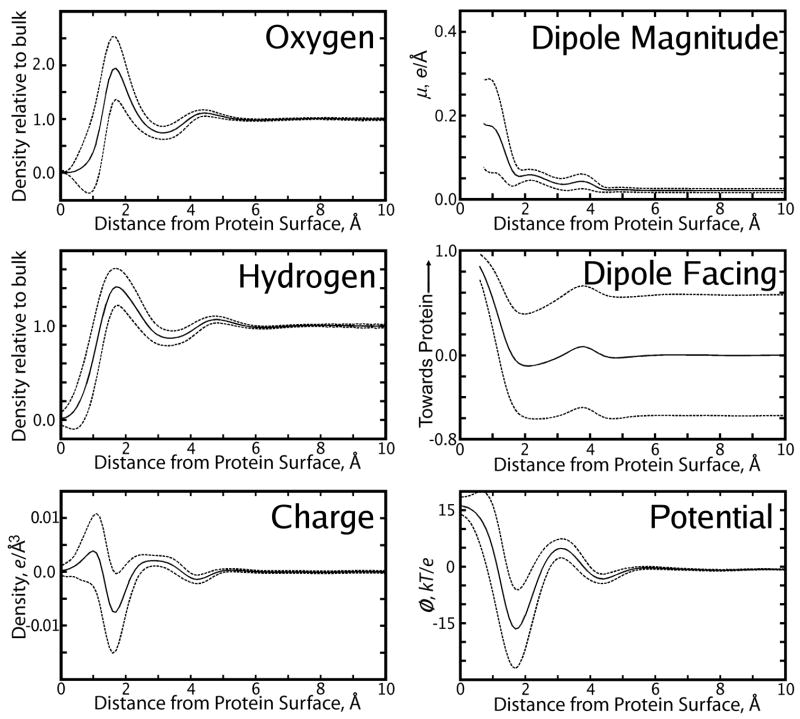
In accord with observations made by Ashbaugh [62] on solvated hard-sphere cavities, ψ^{(No Q)} was finite and positive inside the protein. The average value of ψ^{(No Q)} at the position of each protein atom was 16.4 k_bTe_c⁻¹ with RMS 1.7 k_bTe_c⁻¹, in good agreement with the value of 15 k_bTe_c⁻¹ observed in the limit of a large(>5 Å radius) spherical solute (1 k_bTe_c⁻¹ = 0.596 kcal/mol·e_c = 300K). Visual inspection of slices of the electrostatic potential such as Figure 1 indicates that the magnitudes of this potential were weakest (as low as 13 k_bTe_c⁻¹) in the core of the biomolecule and also in surface regions where the biomolecule shape created a convex solvent-accessible surface (SAS). Conversely, the potential was most positive (as high as 24 k_bTe_c⁻¹) just inside concave regions of the SAS. As can be seen in Figure 1, the electrostatic potential isocontours closely followed the SAS. Therefore, to simplify representation of this function, ψ^{(No Q)} was also mapped onto a function of distance from the protein’s biomolecular surface 〈ψ^{(No Q)}〉 (r), as shown in Figure 3. Details on the definition of this function are given in Sec. 2.4.

Figure 3.

Properties of the solvent (denoted by text inset in each panel) as a function of distance r from the uncharged protein van der-Waals surface (VDWS, x-axis). Solid lines show mean values of each property, dashed lines show the mean ± one standard deviation. In these plots, “0 Å” means that the center of a solvent atom is 0.0Å from the protein’s van-der Waals surface; an oxygen that comes within 1.0 Å of the VDWS of a protein nitrogen atom, for example, means that oxygen and nitrogen atoms are really 2.5Å apart.

3.3 Solvent Reaction Field Potential in and around the Charged Protein

A separate explicit-solvent MD trajectory was created for the charged form of the protein and used to create a similar charge density grid. As stated in Sec. 2.1, the protein was a computationally modeled mutant so that the fully charged form had no net charge, although it did contain six negatively charged aspartate and glutamate residues and six postively charged lysine and arginine residues. The solvent reaction field potential due to the explicit solvent charge density around the charged protein, ψ^(Q), was extremely rugged, as shown in Figure 2. At the locations of protein atoms, ψ^(Q) ranged from −155 k_bTe_c⁻¹ to 278 k_bTe_c⁻¹ with mean 18.9 k_bTe_c⁻¹ and standard deviation 49.5 k_bTe_c⁻¹. In the first solvation shell, ψ^(Q) exceeded −800 k_bTe_c⁻¹ and +400 k_bTe_c⁻¹. The details of ψ^(Q) were obviously highly dependent on charged groups in the protein, and a comparison of Figure 2 to Figure 1 suggested that a plot of 〈ψ^(Q)〉 (r) as a function of distance from the protein omitted much more detail about ψ^(Q) than 〈ψ^{(No Q)}〉 (r) omitted about ψ^{(No Q)}. Nonetheless, the average quantity 〈ψ^(Q)〉 (r) did closely parallel 〈ψ^{(No Q)}〉 (r), as shown in Figure 4.

Figure 2.

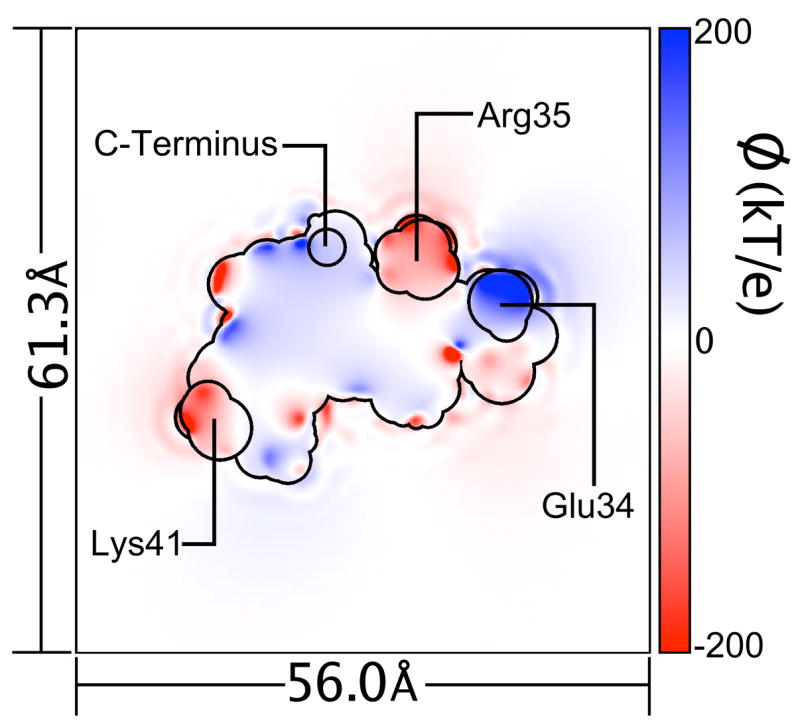
(Color online.) Solvent reaction field potential due to SPC/E explicit solvent charge density around the charged protein. The charge density due to the protein, though present in simulations with SPC/E water, was omitted during the calculation of this potential grid. As in Figure 1, the slice depicted cuts through the centroid of the protein. Potential values as low as −800 k_bTe_c⁻¹ and as high as +400k_bTe_c⁻¹ (T = 300K) are present, but the color scale has been adjusted for greater detail between these extremes. As a guide, the protein’s solvent-accessible surface, measured with a 1.4 Å probe, and the outlines of charged side-chain head groups and polypeptide chain termini are shown in a black outline.

Figure 4.

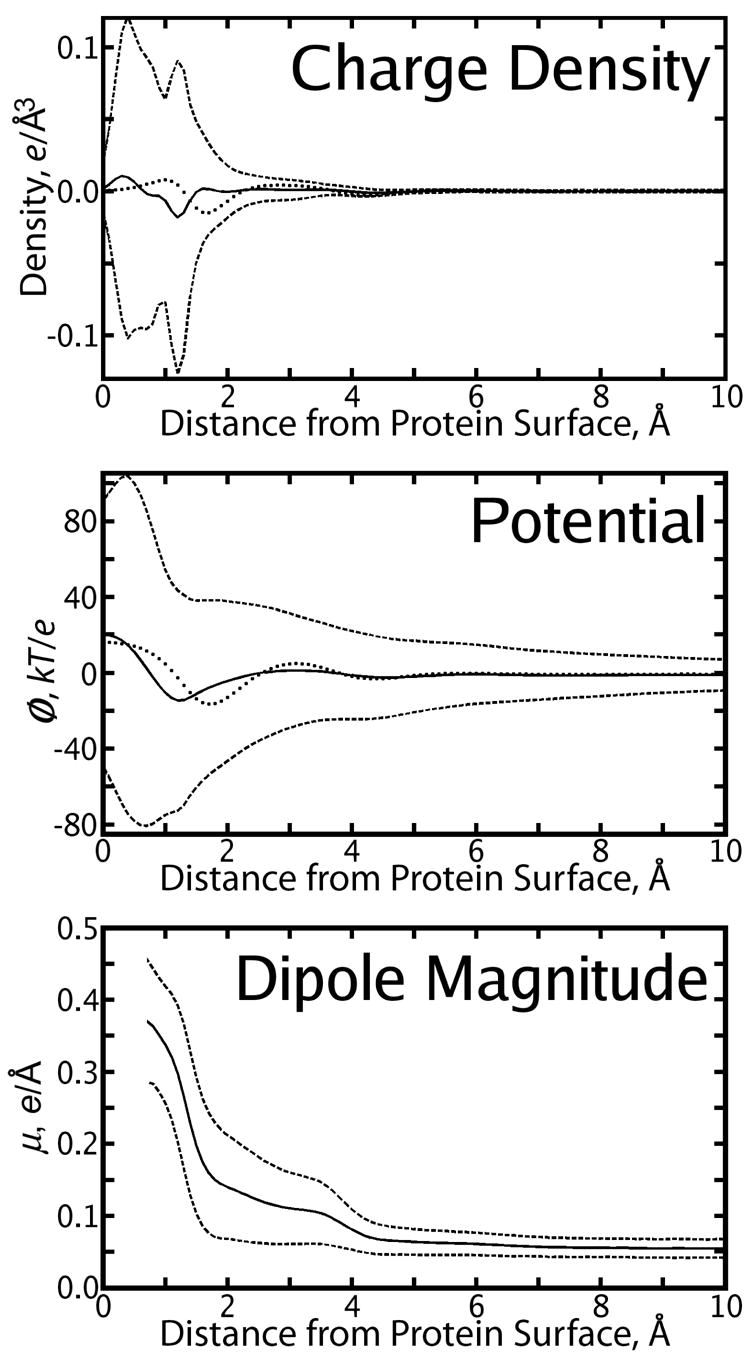
Properties of the solvent (denoted by text inset in each panel) as a function of the distance r from the charged protein van der-Waals surface (VDWS, x-axis). Solid lines show mean values of each property, dashed lines show the mean ± one standard deviation. In the top two panels, a dotted line is a guide to show the mean value of the corresponding property from simulations of the uncharged protein. See Figure 3 for an explanation of what it means for solvent atoms to be very close to the protein VDWS.

3.4 Solvent Structure around the Uncharged and Charged Proteins

If the ensemble-averaged orientation of water molecules were uniformly distributed at all points around the protein, then the solvent reaction field (SRF) would be nonzero only at gradients of solvent density. The significantly non-zero values of ψ^{(No Q)} inside the uncharged protein and highly rugged ψ^(Q) inside the charge protein therefore must have arisen from induced orientational preferences in the water near each protein’s surface.

To quantify the induced orientations of the water, the charge density ( ${\rho }_{\text{Q}}^{(\text{No Q})}$ and ${\rho }_{\text{Q}}^{(\text{Q})}$) and dipole moment density (μ^{(No Q)} and μ^(Q)) were tracked throughout the simulations. In the case of the uncharged protein, we also measured hydrogen and oxygen density, ${\rho }_{\text{Hd}}^{(\text{No Q})}$ and ${\rho }_{\text{Ox}}^{(\text{No Q})}$, and water molecular dipole orientation, ζ^{(No Q)}. All of the aforementioned three-dimensional functions were plotted as functions of distance from the solute van der Waals surface (VDWS) (see Sec. 2.4), as shown in Figures 3 and 4. As noted above, mapping these three-dimensional functions onto a function of only one parameter entails some loss of information. In the case of the uncharged protein, where isocontours of ψ^{(No Q)} (r) closely paralleled the protein surface (see Figure 1), the information loss was low¹. In the case of the charged protein, information loss was high because ψ^(Q) and related quantities did not follow the shape of the protein but also its charge composition (again, compare Figures 1 and 2). Nonetheless, the averages of these three-dimensional functions were plotted as functions of distance from the charged protein surface for comparison to results for the uncharged protein.

As shown in Figure 3 and in Table 2, a positive maximum in $\langle {\rho }_{\text{Q}}^{(\text{No Q})}\rangle (r)$ was generated near the uncharged protein surface by the penetration of water hydrogen atoms further toward the protein than water oxygen atoms. Further from the protein, the oxygen atoms of water molecules in the first solvation shell contributed to a highly negative charge density. Roughly the same behavior is seen in the case of the average $\langle {\rho }_{\text{Q}}^{(\text{Q})}\rangle (r)$ (see Figure 4), although its first two peaks occur closer to the protein surface than those of $\langle {\rho }_{\text{Q}}^{(\text{No Q})}\rangle (r)$.

Table 2.

Extrema of atom and charge density functions as seen in Figures 3 and 4. Locations of the extrema are given in A from the protein surface, maxima are given in units of bulk density for hydrogen and oxygen densities and in e_c Å⁻³ for charge densities. $\langle f_{\rho }^{(\text{Qstate})}\rangle (r)$ denotes an average of the X density at a distance r from the surface of the protein in charge state Qstate (e.g., “No Q” or “Q”).

Function	Location of First Maximum	Magnitude of First Maximum	Location of First Minimum	Magnitude of First Minimum	Location of Second Maximum	Magnitude of Second Maximum
$\langle {\rho }_{\text{Ox}}^{(\text{No Q})}\rangle (r)$	1.7	1.9	3.1	0.8	4.4	1.1
$\langle {\rho }_{\text{Ox}}^{(\text{Q})}\rangle (r)$	1.3	1.8	3.1	0.9	4.6	1.1
$\langle {\rho }_{\text{Hd}}^{(\text{No Q})}\rangle (r)$	1.8	1.4	3.3	0.9	4.8	1.1
$\langle {\rho }_{\text{Hd}}^{(\text{Q})}\rangle (r)$	1.5	1.5	3.1	0.9	5.0	1.0
$\langle {\rho }_{\text{Q}}^{(\text{No Q})}\rangle (r)$	1.0	0.008	1.7	−0.015	2.8	0.004
$\langle {\rho }_{\text{Q}}^{(\text{Q})}\rangle (r)$	0.3	0.011	1.2	−0.018	1.6	0.002

Although the averages $\langle {\rho }_{\text{Q}}^{(\text{No Q})}\rangle (r)$ and $\langle {\rho }_{\text{Q}}^{(\text{Q})}\rangle (r)$ do bear similarities, ${\rho }_{\text{Q}}^{(\text{No Q})}$ was smooth while ${\rho }_{\text{Q}}^{(\text{Q})}$ had many peaks. Extreme accumulation of solvent charge density was observed around the charged protein’s polar atoms (data not shown); in individual grid cells, charge densities as high as +5 e_c Å⁻³ and as low as −20 e_c Å⁻³ were recorded. To quantify the overall amount of charge represented by these features of ${\rho }_{\text{Q}}^{(\text{Q})}$, we defined a charge density peak by all points within a 1 Å cube centered on some extremum of the charge density which exceeded ±1e_c Å⁻³. Using this method, 31 positive and 74 negative charge density peaks were observed, the overall charges of which averaged +0.4 ± 0.1 and −0.6 ± 0.1 e_c, respectively. Such peaks in the solvent charge density were comparable in size and localization to atomic partial charges on the protein itself.

As shown in Figure 3, we also computed both the magnitude of the net dipole density μ (r), and ζ (r), its direction at some point r relative to the surface normal of the protein n (r) passing through r. The computation of μ (r) and ζ (r) are described in Sec. 2.4. Like the other features of the solvent around the uncharged protein, μ^{(No Q)} can be described as 〈μ^{(No Q)}〉 (r), a function of distance from the VDWS, without great loss of information, while 〈μ^(Q)〉 (r) does omit many features in μ^(Q). However, the two averages 〈μ^{(No Q)}〉 (r) and 〈μ^(Q)〉 (r) do have similar shapes and both show significant values extending roughly 4.5 Å from the protein surface. 〈μ^(Q)〉 (r) is roughly twice as large as 〈μ^{(No Q)}〉 (r).

To further probe the distributions of water molecules in the first solvation shell that most contributed to ψ^{(No Q)}, we computed the quantities ζ^{(No Q)} (see Eq. 4) and ξ^{(No Q)} (see Eq. 5). Results obtained from ζ^{(No Q)} contained ambiguities for values of ζ^{(No Q)} near zero: knowing that a water dipole moment vector pointed perpendicular to the protein surface normal vector and thus parallel to the protein surface could mean that the water was oriented with one O-H bond vector pointed toward the protein and one away, or that it was oriented with both O-H bond vectors pointed parallel to the protein surface. To resolve the ambiguities in ζ^{(No Q)}, we computed the quantity ξ^{(No Q)} (see Eq. 5). Among water molecules with center of mass between 1.5 and 1.9 Å from the uncharged protein VDWS with −0.1 <ζ^{(No Q)} < +0.1 (i.e., the water dipole was pointed parallel to the protein surface), there was a tendency for ξ^{(No Q)} to be large, meaning that the hydrogens of these water molecules were pointed parallel to the protein VDWS. Only 6% of these waters in the first solvation shell had a value of ξ^{(No Q)} ≤ 0.25, meaning that one of the water’s hydrogens was pointed towards the protein while the other was pointed away, and only 17% had a value of ξ^{(No Q)} ≤ 0.50. In contrast, 65% of the waters had a value of ξ^{(No Q)} ≥ 0.75; i.e., the majority of waters in the first solvation shell pointed their hydrogens parallel to the protein surface.

Although interactions between water molecules in the SPC/E model do not explicitly include hydrogen bonding, the strengths of Lennard-Jones and Coulomb interactions indicate structural features of the water. The average strength of short-range (≤ 4 Å) interactions was recorded as a function of the distance of each interacting water molecule from the charged or uncharged protein VDWS (see Sec. 2.4). As observed for spherical cavities [62], interactions between two waters near either protein are stronger than those between water molecules in solution (see Figures 5 and 6), but this effect was generally more pronounced in the case of the uncharged protein.

Figure 5.

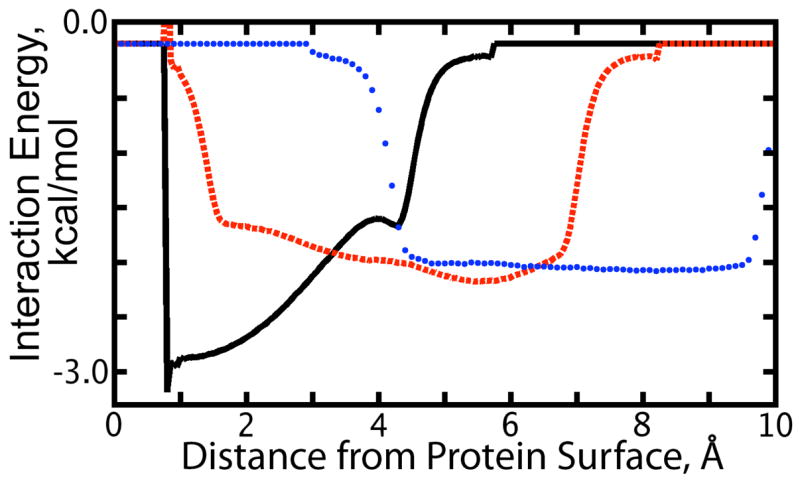
(Color online.) Average interaction energy of a water molecule located at 1.7 Å (black, solid line), 4.4 Å (red, dashed line), and 7.0 Å (blue, dotted line) from the surface of the uncharged protein with nearby water molecules at other distances from the protein van der-Waals surface as indicated by the x-axis. These graphs show the local interaction characteristics of the first and second solvation shells, and deep solution, respectively.

Figure 6.

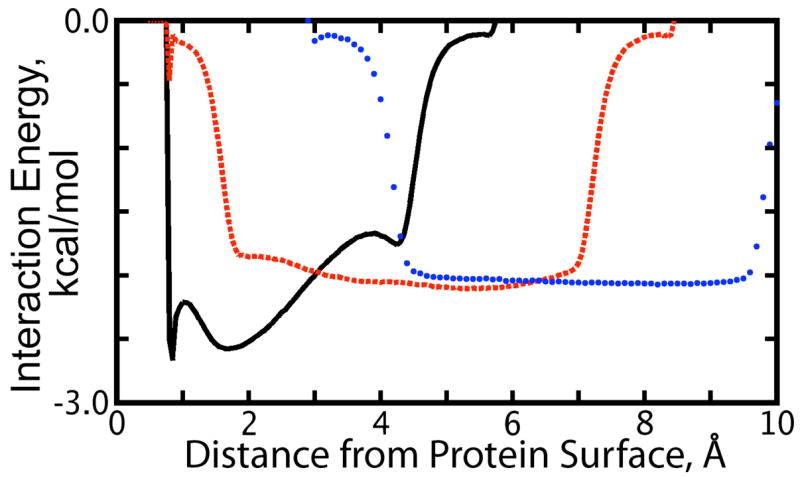
(Color online.) Average interation energy of a water molecule located 1.7 Å (black, solid line), 4.4 A (red, dashed line), and 7.0 Å (blue, dotted line) from the surface of the charged protein with nearby water molecules at other distances from the protein van der-Waals surface as indicated by the x-axis. These graphs correspond to those in Figure 5 describing water:water interaction energies around the uncharged protein.

3.5 Relating the Explicit Solvent Reaction Field Potential to Implicit Solvent Calculations

A major goal of this work was to test the agreement of the reaction field obtained with an implicit solvent model, ϕ^(Q), with that from the explicit solvent simulation, ψ^(Q). To do this, a Poisson calculation was tailored to reproduce ψ^(Q) as closely as possible but without optimizing the solute volume definition, as is often done in Poisson calculation parameterization (see Sec. 2.3 and the work of Swanson et al [54, 83]). For each method of computing φ^(SRF) (FFT of the explicit-solvent charge density or FDMG using implicit solvent with a pre-defined, low dielectric solute volume inside a high-dielectric solvent region), the electrostatic energy of an atom i in φ^(SRF) was calculated using

$$U_i=\frac{q_i}{2}\psi ({\mathbf{r}}_i)$$ (7)

for explicit solvent reaction fields, with variants $U_i^{(\text{Q})}$ and $U_i^{(\text{No Q})}$ for the charged and uncharged solute simulations, respectively. Likewise, for implicit solvent reaction fields, the electrostatic energy is defined as

$$G_i=\frac{q_i}{2}\varphi ({\mathbf{r}}_i)$$ (8)

with variants $G_i^{(\text{Q})}$ and $G_i^{(\text{No Q})}$ for the charged and uncharged solute simulations, respectively. Note that, by definition, $G_i^{(\text{No Q})}=0$ and $G_i^{(\text{Q})}$ is the contribution of atom i to the solvation energy of the solute.

Values of $G_i^{(\text{Q})}$ and $U_i^{(\text{Q})}$ are plotted against one another in Figure 7. Without modification, the Poisson model systematically over-stabilized positively charged atoms and de-stabilized negatively charged atoms by comparison to the SPC/E solvent, as shown in Table 3. Overall, the correlation between $G_i^{(\text{Q})}$ and $U_i^{(\text{Q})}$ was 0.90, but if computed only for positively or negatively charged atoms, this correlation was 0.92 or 0.96, respectively. Among all the atoms, the 30 largest outliers were determined by the absolute deviation from the line of best fit for implicit solvent energies on explicit solvent energies. All of these 30 atoms were solvent-exposed and highly charged; 21 were polar hydrogens and seven were carboxylate oxygen atoms (also included were the C-terminal carboxylate carbon atom and a nitrogen from the Arg34 guanidino group). In general, all atoms with charges larger than 0.3 and 20% of their surface area exposed to solvent showed deviations in excess of 5 kcal/mol between the Poisson and SPC/E solvent energies.

Figure 7.

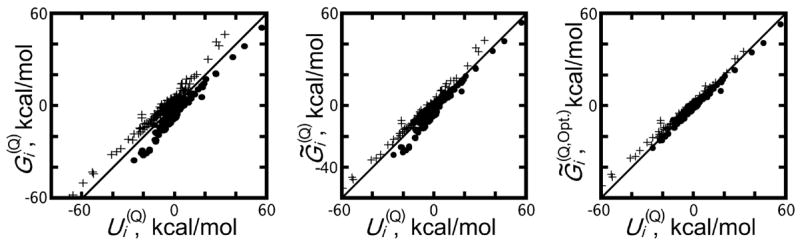
Comparison of protein atom electrostatic energies for the charged protein due to the solvent reaction field potential predicted by different implicit solvent models (y-axis) plotted against those generated by an explicit solvent model (x-axis). $U_i^{(\text{Q})}$ refers to per-atom energies in the explicit solvent reaction field, $G_i^{(\text{Q})}$ to per-atom energies in the implicit solvent reaction field, and $G_i^{(\text{Q},\text{Opt}\text{.})}$ to per-atoms energies in an implicit solvent reaction field obtained a solute volume definition optimized to fit the results of free-energy perturbation experiments. A ~ denotes implicit energies adjusted by the energy $U_i^{(\text{no Q})}$, the energy of atomic charges in the solvent reaction field potential created by the uncharged protein. Dots and crosses represent positively and negatively charged atoms, respectively. The black lines show y = x.

Table 3.

Comparison	Pearson Unsquared Correlation Coefficient			Regression Slope			Regression Intercept (kcal/mol)
VDWa (all | + | −)b	0.90	0.92	0.96	0.85	1.00	0.90	−0.3	−2.0	2.5
VDW ⊕a (all | + | −)	0.97	0.96	0.99	0.94	1.05	0.94	−0.2	−1.1	1.1
OPTa (all | + | −)	0.94	0.96	0.98	0.80	0.87	0.85	−0.1	−1.3	1.9
OPT ⊕a (all | + | −)	0.99	0.99	0.99	0.90	0.92	0.89	0.0	−0.3	0.5

^aImplicit solvent energies are defined by Eq. 8 in the text. “VDW” refers to solute definition by Lennard-Jones radii taken from the AMBER ff99 forcefield. “OPT” refers to solute definition by a set of optimized radii [54]. A molecular surface definition and 1.4 Å solvent probe were used for all implicit-solvent calculations.

^bComparisons were made between all atoms in the protein, as well as between positively or negatively charged atoms specifically. Results in table sub-cells are listed in this order.

^cA ⊕ symbol refers to implicit solvent energies corrected by adding the energy of each atomic partial charge in the solvent reaction field created by the uncharged protein in SPC/E solvent (see Eq. 10). Figure 7 shows three of these four sets of implicit solvent per-atom energies plotted against per-atom energies obtained with explicit SPC/E water.

Of all the quantities studied here, the energies of individual atoms in explicit were the most difficult to converge. Comparison of multiple 100ns segments of trajectories for either the charged or uncharged proteins revealed that, with just 100ns of simulation, values of both $U_i^{(\text{No Q})}$ and $U_i^{(\text{Q})}$ were converged to within 0.03 kcal/mol. The 1560ns and 620ns of MD collected for either charge state of the protein were more than sufficient to determine these values.

Electrostatic quantities (e.g. potentials, field, energies, and forces) calculated from implicit solvent models are most closely related to “charging” processes which relate free energies between the charged and uncharged forms of the solute [38, 55]. Based on this argument, the energy

$$\mathrm{\Delta }{U}_i=\frac{q_i}{2}\left({\psi }_i^{(\text{Q})}-{\psi }_i^{(\text{No Q})}\right)$$ (9)

calculated as a difference between the charged and uncharged explicit solvent simulations should give the best agreement with similar implicit solvent energies. This implies that a “correction” is needed to directly compare implicit solvent quantities such as per-atom energies and forces with explicit solvent results. Therefore, we define the quantity

$${\stackrel{\sim }{G}}_i=\frac{q_i}{2}\left({\varphi }_i^{(\text{Q})}+{\psi }_i^{(\text{No Q})}\right)$$ (10)

as an implicit solvent electrostatic energy which incorporates the electrostatic properties of the uncharged solute.

Correlations between ${\stackrel{\sim }{G}}_i^{(\text{Q})}$ and $U_i^{(\text{Q})}$ were superior to those between $G_i^{(\text{Q})}$ and $U_i^{(\text{Q})}$ for negatively charged, positively charged, and all atoms together, as shown in Table 3. The identities of various outliers remained largely the same, but the biases in electrostatic energy based on the sign of each atomic charge were reduced, and the overall slope of the implicit-explicit solvent energy comparison improved to nearly 1. Better overall correlation between per-atom energies was obtained using a set of optimized atomic radii [54] rather than Lennard-Jones σ values to define the molecular surface, as shown in Table 3 and Figure 7. Per-atom electrostatic energies obtained from this calculation are referred to as $G_i^{(\text{Q},\text{Opt}\text{.})}$. When the contributions from ψ^{(No Q)} are taken into account as before, the correlations and regression statistics between ${\stackrel{\sim }{G}}_i^{(\text{Q},\text{Opt}\text{.})}$ and $U_i^{(\text{Q})}$ improve to 0.99 overall and the biases in estimates of electrostatic energies for positively or negatively charged atoms are each reduced by 70%.

Investigators are tpyically interested in the total potential energy or total free energy of a system. With the data on per-atom energies, we can denote the sum $G^{(\text{SRF})}={\sum }_i{G}_i^{(\text{SRF})}$. U^{(No Q)}, the electrostatic energy of the fully charged protein in ψ^{(No Q)}, was a mere +0.3 kcal/mol (note that this quantity would be expected to be small, as the fully charged protein still carried a net charge of zero). Similarly, G^(Q) was −956.5 kcal/mol, G^(Q,Opt.) was −726.5 kcal/mol, and U^(Q) was −823.2 kcal/mol. G̃^(Q) and G̃^(Q,Opt.) can be obtained by adding the small contribution from U^{(No Q)} to G^(Q) and G^(Q,Opt.), respectively.

4 Discussion

4.1 Implications of the Positive Electrostatic Potential inside an Uncharged Solute

The solvent-induced positive electrostatic potential inside the uncharged protein is a known result for simple solute geometries [62], but the precise nature of this potential inside the complex solvent cavity created by a biomolecule has not been explored. The uncharged solute internal potential of 13 to 15 k_bTe_c⁻¹ qualitatively matches the effects previously observed for large hard-sphere cavities; however, at cusps and other concave features in the biomolecular surface, the potential is up to 80% greater. Thus, when uncharged solutes depart from spherical symmetry, the “baseline” solvent reaction field (termed ψ^{(No Q)} in the Results) becomes more complicated than a mere function of the distance from the biomolecular surface, but in ways that are, at least qualitatively, predictable.

While previous studies [62, 63] have shown that implicit and explicit solvent models converge for spherical charged solutes once the electrostatics of the equivalent uncharged sphere are considered, we wanted to test the convergence of implicit and explicit solvents for irregular solutes such as proteins. We found that ${\stackrel{\sim }{G}}_i^{(\text{Q})}$, the per-atom electrostatic energies obtained from an implicit solvent corrected with measure ments of the elecstrostatics an uncharged protein, are highly correlated with $U_i^{(\text{Q})}$, the energies of atoms in the solvent reaciton field potential created by SPC/E solvent around the corresponding fully charged protein. Even so, the sums of these energies, G̃^(Q) and U^(Q), respectively, do not agree. However, the difference between G^(Q) and the summed energies obtained from a Poisson model with slightly different radii, G^(Q,Opt.), is larger than the difference between U^(Q) and G^(Q). Because of the sensitivity of the overall energies obtained from Poisson calculations to the particular atomic radii used to define the solute, it is likely that G̃^(Q) and U^(Q) could be brought into better agreement by optimizing these radii [54, 83].

The results in 3 also suggest that the radii optimization made by Swanson and co-workers [54] using charging free energies of proteins in explicit solvent is critical for reconciling implicit solvent per-atom energies $G_i^{(\text{Q})}$ with explicit solvent energies $U_i^{(\text{Q})}$. However, this conjecture is difficult to quantify at the moment because Swanson et al. used a slightly different explicit solvent model.

In the case of this mutant bucadin protein, the magnitude of the total explicit solvent electrostatic energy for the uncharged solute is small (U^{(No Q)} = 0.3 kcal/mol) when compared to the corresponding electrostatic energy for the charged system (U^(Q) = −823.3 kcal/mol). However, the overall charge of this protein was neutralized in order to expedite simulations without the need for counterions in the solvent. Quantities like U^{(No Q)} could be a major component in free energy calculations, particularly when the species do carry a net charge. This effect has already been posited as a way to reconcile discrepancies in computed values of ion solvation [8, 56] and could have significant effects on the computed solvation energies of proteins [84]. In protein-protein [44, 85] or protein-ligand binding energy calculations [2, 52], where interfaces may create many cusps in the solvent-accessible surface, the contributions from the “baseline” electrostatic potential may be particularly pronounced. It is also likely that these effects influence amino acid pK_a values based on their relative solvent exposure and/or distance to the solute-solvent interface. An appropriate quantitative treatment of uncharged solute reaction field effects might offer one way to improve implicit solvent calculations of sidechain titration states, particularly for buried residues.

4.2 Solvent Structure around the Uncharged Protein

As expected, the microscopic solvent structure around even the uncharged protein is considerable. Unlike continuum models which assume a uniform distribution of solvent distributed strictly outside a probe-exclusion or other characteristic surface, the water oxygens form two high-density layers around the solute.

The first solvation shell, centered at 1.7 Å from the solute van der Waals surface, contributes to the highly negative charge density where water oxygen atoms reside, but also to the positive charge density closer to the solute as shown in Figure 3. Care must be taken, however, to describe the most significantly populated orientations of water contributing to the positive charge density observed close to the solute and between the oxygen density peaks. Dipole moments were located at the centroid of each water molecule during analysis, 0.39 Å from the water oxygen. The strong preferential orientation of significant dipoles as shown in the “Dipole Magnitude” and “Dipole Facing” frames of Figure 3 located 1.2 Å from the protein surface obviously arises from water molecules whose oxygens reside in the first solvation shell, ~1.6 Å from the protein surface. However, the close correspondence between the maxima and minima of the hydrogen and oxygen densities shown in Figure 3 suggests that this population, while potent for affecting the electrostatic potential, is fairly small. This was shown directly by our findings concerning ψ^{(No Q)}: on average, nearly two-thirds of the waters in the first solvation shell are oriented parallel to the protein surface, placing the dipole of such water molecules at the same distance from the surface as the oxygen atom and thereby not contributing to the solvent reaction field potential. The generally convex curvature of the protein surface would imply that the hydrogen density from such waters would be located at a slightly greater distance from the surface than the oxygen density, as is seen in Figure 3. Again as shown by our computations of ψ^{(No Q)}, there is a small population (6%) of waters in the first solvation shell which point their dipole moments parallel to the protein surface and point one hydrogen into the protein and the other out into solution, thus contributing to both positive charge density peaks seen in Figure 3. This population would contribute to a broadening of the first hydrogen density peak relative to the first oxygen density peak, again as observed in Figure 3. The strong interactions between waters in this first solvation shell seen in Figure 5 can be understood as a response to negation of favorable charge:charge interactions between water and protein atoms.

The second solvation shell around the uncharged solute is characterized by weaker local interactions with the first solvation shell than with waters deeper into solution (see Figure 5) and appears to act as an interface, approximately 4.4 Å from the protein surface, between the first solvation shell and bulk water.

4.3 Solvent Structure around the Charged Protein

Around the charged protein, solvent molecules become so localized as to appear as extensions of the solute rather than mobile solvent molecules. Such features are too complex to describe as functions of distance from the protein surface, and a detailed description of the solvent behavior is beyond the scope of this manuscript. However, the mean values of the solvent charge density and the solvent reaction field potential, as functions of distance from the protein surface, did bear similarity to the same quantities around the uncharged protein. These similarities between the two protein charge states offer explanation for our ability to resolve the energetic differences between implicit and explicit solvent models by using the solvent reaction field potential around the uncharged protein.

The differences between the water:water interaction energies around the protein in each charge state (see Sec. 3.4, Solvent Structure around the Uncharged / Charged Protein as well as Figures 5 and 6) may stem from the same source, the fact that the fully charged and flexible protein was equilibrated in the SPC/E water before fixing its conformation and removing the partial charges to do the simulations of the uncharged protein. This would explain the fact that interaction energetics for waters in the second solvation shell around the charged protein look more like those in bulk solution than do interaction energetics of waters in the second solvation shell around the uncharged protein. Because the uncharged protein system and its water bath were equilibrated at constant pressure, we can at least be assured that these differences are not the result of an abnormal system pressure (as observed in our studies, a 0.7% change in the system volume at 300K would correspond to change in pressure of roughly 180 atmospheres). Suddenly turning off the protein charges causes waters in the first solvation shell to lose electrostatic interactions with the protein and re-orient to interact more tightly with other waters in the first solvation shell, while the second solvation shell becomes a “buffer” between bulk solution and the newly restructured first solvation shell.

We also wish to note that an effect of these bound water molecules, to propagation of the charged protein’s electrostatic field as show in Figure 2, carries implications for biomolecular (e.g, protein-drug or protein-protein) interactions at both short and long length scales. Such effects are not included in the continuum solvent descriptions of most implicit solvent models and may be important for accurate modeling of these types of biomolecular interactions.

4.4 Consideration of a “Realistic” Solvent Model and Future Directions

Even explicit solvent representations have difficulty adequately representing the highly polar and tetrahedral hydrogen-bonding characteristics of water [29–35, 86]. In particular, restricting the negative charge on the water molecule to travel strictly with the Lennard-Jones site may create adverse effects at the water-protein interface in addition to the compromises that must be made to achieve certain properties of water under a biologically relevant set of conditions [86]. Price and Brooks [87] noted that three-point models, used in the vast majority of explicit-solvent molecular dynamics simulations, may be unable to achieve the dipole moment of water in solution (which has been observed experimentally to be as high as 2.9 D, or 0.60 e_c Å⁻¹ [36]) in conjunction with a realistic dielectric constant, density, and thermodynamic properties. Additional problems related to the dipole moment arise from the rigid nature of most water models, which in the present study permitted vastly accelerated sampling with a 4 fs timestep. The dipole moment of rigid water models is parameterized to meet an expected bulk value (typically ~2.3 D, which as stated above is likely an underestimate), but the dipole moment of water molecules at an air-water interface is thought to be closer to that of an isolated water molecule, 1.85 D or 0.38 e_c Å⁻¹ [88].

While a five-point water [20] model could represent water as a more realistic tetrahedron, this accuracy comes at a much greater computational expense and incurs the risk that the water model is inappropriate for the molecular mechanics force field describing the solute particles. Furthermore, although a larger dipole would seem quite feasible in the context of a five-point water model, the current parameterization schemes [21] merely target the same value as current three-point models. Another possible route towards more realistic models is the use of distributed, Gaussian charges rather than additional point charges [86], or even polarizable models [23, 89]. Any of these changes to the explicit solvent model could have a significant effect on the charge distribution and thus the solvent reaction field potential.

In conclusion, we have shown that the electrostatics of solvated proteins depend on the characteristics of the surrounding solvent, in addition to the biomolecular charge distribution that has traditionally been considered. These results suggest that a method to rapidly estimate such quantities based on geometric considerations is a promising short-term goal and of great potential benefit to future implicit-solvent calculations. The degree of solvent structure, particularly in the first solvation shell, presents a significant challenge for implicit solvent models applied to biomolecular association and folding problems. The microscopic sources and features of these effects prompt us to determine how different water models that appear equivalent in terms of macroscopic properties but differ considerably in microscopic structure may affect these results.