Atomistic insights into rhodopsin activation from a dynamic model

Abstract

Rhodopsin, the light sensitive receptor responsible for blue-green vision, serves as a prototypical G protein-coupled receptor (GPCR). Upon light absorption, it undergoes a series of conformational changes that lead to the active form, metarhodopsin II (META II), initiating a signaling cascade through binding to the G protein transducin (G_t). Here, we first develop a structural model of META II by applying experimental distance restraints to the structure of lumi-rhodopsin (LUMI), an earlier intermediate. The restraints are imposed by using a combination of biased molecular dynamics simulations and perturbations to an elastic network model. We characterize the motions of the transmembrane helices in the LUMI-to-META II transition, and the rearrangement of interhelical hydrogen bonds. We then simulate rhodopsin activation in a dynamic model to study the path leading from LUMI to our META II model for wild-type rhodopsin and a series of mutants. Those simulations show a strong correlation between the transition dynamics and the pharmacological phenotypes of the mutants. These results help identify the molecular mechanisms of activation in both wild type and mutant rhodopsin. While static models can provide insights into the mechanisms of ligand recognition and predict ligand affinity, a dynamic model of activation could be applicable to study the pharmacology of other GPCRs and their ligands, offering a key to predictions of basal activity and ligand efficacy.

Introduction

Rhodopsin is a light sensitive G protein-coupled receptor (GPCR) that is abundantly expressed in retinal rod cells.¹ It consists of a single polypeptide chain, known as opsin, that crosses the cell membrane with seven α-helical transmembrane domains (TMs). The photoreactive chromophore 11-cis retinal is covalently bound to the receptor via a Schiff-base linkage to Lys296. Absorption of light by rhodopsin leads to isomerization of the cis double bond of the chromophore to the trans form, initiating the cascade of events that ultimately result in receptor activation and signaling.² In the course of activation, rhodopsin populates a number of intermediate states with characteristic spectroscopic signatures. Early photointermediates are bathorhodopsin (BATHO), a blue-shifted intermediate (BSI), lumi-rhodopsin (LUMI), and metarhodopsin I (META I),¹ where LUMI is the first conformational state in which the retinal is found in the all-trans form. Subsequent photointermediates are characterized by the deprotonation of the Schiff-base linkage. High-affinity interactions with the G protein transducin (G_t) activate the signaling cascade. Metarhodopsin II (META II) is the first intermediate capable of initiating signalling.¹

Structurally, rhodopsin is the best-characterized GPCR and is considered the prototypical member of the superfamily. The first X-ray crystallographic structures of rhodopsin reflected the dark adapted ground state of the bovine receptor, captured in four different crystals, with resolutions of 2.8³, 2.8⁴, 2.65⁵, and 2.2Å⁶. Molecular dynamics (MD) simulations have been used extensively to study the dynamic properties of ground state rhodopsin in relation to the composition of the lipid bilayer^7–13. The isomerization of retinal from 11-cis to all-trans was also simulated to shed light on the structural changes that lead to the LUMI state ^14–18. Furthermore, since until recently direct 3D information was not available for any of the active states of rhodopsin, different computational approaches were exploited to build models of META II on the basis of the available experimental information and of proposed activation mechanisms.^{16,17,19–23}

The first experimental structure of an intermediate of the activation process was published by Schertler and coworkers, who reported a 2D electron crystallography structure of META I.²⁴ Solid-state ²H NMR was also recently applied to get insights into the structure of trans-retinal in META I^25,26.

3D crystallographic models of the early photointermediates BATHO (2.6 Å) and LUMI (2.8 Å) were published by Okada et al. ^27,28 On the basis of their structures, these authors suggested that the cis-trans isomerization of retinal affects the interhelical interactions of rhodopsin, that in turn initiates the process leading to activation.

Determining the structural properties of later intermediates in the rhodopsin photocycle is an ongoing effort. Recently, a low-resolution (4.15 Å) X-ray structure for a photoactivated deprotonated intermediate (PDI) of rhodopsin showing absorption maxima consistent with META II was published by Palczewski et al.²⁹. However, the structure did not confirm the significant conformational changes or rigid body movement of the TMs expected on the basis of many published biophysical measurements, including data from electron paramagnetic resonance spectroscopy (EPR) studies,^30–33 UV absorbance spectroscopy,³⁴ zinc cross-linking of histidines,³⁵ site-specific chemical labeling and fluorescence spectroscopy³⁶. The constraints of the crystal lattice and the low temperature at which the diffraction data for PDI were collected may have prevented larger-scale structural rearrangements in this structure.

In this work, we construct a model of the META II structure that incorporates both crystallographic and biophysical data. We start from the X-ray structure of LUMI²⁸ (pdb code: 2HPY) and apply, in a sequential manner, distance restraints derived from biophysical measurements. We then compare our META II model with the structures of the ground state rhodopsin, LUMI and PDI (pdb code: 2I37), and analyze the differences in hydrogen bond networks. Subsequently, we determine a path leading from LUMI to our model of META II by using MD simulations, thus generating a dynamic model for rhodopsin activation. We simulate the transition between the two states for the wild type receptor and various mutants that have altered activation. The correlation between the ratio of the predicted residence times of LUMI and META II and the experimental phenotype of the mutations provides pharmacological support for the model.

Results and Discussion

Structure of Activated Rhodopsin

A number of biophysical studies offer coarse information on the structural changes associated with the activation of rhodopsin (Table 1).^{30,32,33,37,38} The experimental probes are sensitive to two classes of structural changes. The first group includes the motion associated with the isomerization of retinal and the perturbations occurring in the binding pocket upon activation, while the second group includes the global movements of the TM helices.

Table 1.

Experimentally measured local and global movements associated with the transition from the ground state to the activated state of rhodopsin.

First set: Movements in the retinal binding pocket
	Measured distances
	Ground State (Å)	Activated State (Å)	Methods
S186 - C14,C15 of retinal	4–5	>6–7	Solid-state NMR38
Y178 - C14,C15 of retinal	10–11	4–5	Solid-state NMR38
W265 - C20 of retinal	3.9	>5.5	Solid-state NMR37
W265 - C19 of retinal	7	~5	Solid-state NMR37
Cζ3, Cη2 and Cε2 of W265 - Cα of G121	5.5–6.0	>6	Solid-state NMR37
Second set: Global movements of TMs
	Measured distances
	Ground State (Å)	Activated State (Å)	Methods
TM3–TM6
139–248	12–14	23–25	Site-directed spin-labeling30
139–251	12–14	23–25
139–249	15–20	15–20
139–252	15–20	23–25
TM1–TM8
65–316	9–13	9–13+1	Site-directed spin-labeling32–33
65– 319	8–11	8–11+1,
65–312	~10	~10+1,2
65–312	10–20	14–18
65–313	~12	12+1
65–315	10–15	10–15
65–306	8–9	8–9+1
TM1-TM7
65–310	7–14	11–15 (+4)
TM7-TM7
310–316	11–17	14

To build a model of rhodopsin in the META II state, we started from the LUMI x-ray structure and then drove it toward a putative META II structure by imposing distance restraints obtained from the two groups of experimental measurements. Restraints sensitive to global motion are most effective when applied to low resolution models with few degrees of freedom: they could also be satisfied by local deformations in all-atom models, especially when the number of available distance restraints is small. In contrast, local changes are more accurately described by using all-atom models.

Accordingly, the model was constructed in two steps. In the first step, we applied only the distance restraints derived from the first set of measurements, describing movements in the binding pocket by using biased MD simulations with an all-atom model. By doing so, we simulate the activation that starts at the binding pocket due to local rearrangements after retinal isomerization and propagates to the intracellular part by initiation of global helical movements.

In the ground state of rhodopsin, the protonated retinal forms an ion bridge with E113(3.28, Ballesteros and Weinstein residue indexing³⁹) in TM3. The isomerization of retinal in LUMI leads to the formation of META I. In the latter state the counterion of retinal may switch from E113(3.28) to E181, located in the second extracellular loop (EL2), as indicated by Raman spectroscopic studies of site-specific mutants of E181⁴⁰. According to this study, E181(EL2) was proposed to be protonated in the ground state and to transfer its acidic proton to E113(3.28) in the course of the activation process However, later results from Fourier-transform infrared (FTIR) spectroscopy demonstrated that E181(EL2) is deprotonated in the ground state and proposed that both E113(3.28) and E181(EL2) act as counterions of the protonated retinal in META I⁴¹. Recent results from ²H NMR data and MD simulations of the transformation leading from ground state rhodopsin to META I, conducted by explicitly simulating the proton transfer from E181 to E113(3.28) or by considering both residues as deprotonated, supported the FTIR spectroscopy data¹⁵. Taking into account these results, we treated E113 as protonated and the Schiff base of retinal as deprotonated, as it occurs in the transition from META I to META II..⁴² In addition, E134(3.50) of the (E)DRY motif was treated as protonated.⁴³

In this stage of the modeling, the β-ionone ring of retinal moved slightly toward the extracellular side of the receptor in the direction of TM4 and TM5. Consequently, the sidechains of F212(5.47), W265(6.48) and F261(6.44) underwent a conformational change and filled the created cavity. We did not detect a direct interaction between E181 and retinal. These local perturbations also caused a slight movement of the second extracellular loop (EL2) and the extracellular end of TM4. The comparison of the root mean square displacements (RMSDs) of the Ca atoms between LUMI and the model after the first step is shown in Figure 1a.

Figure 1.

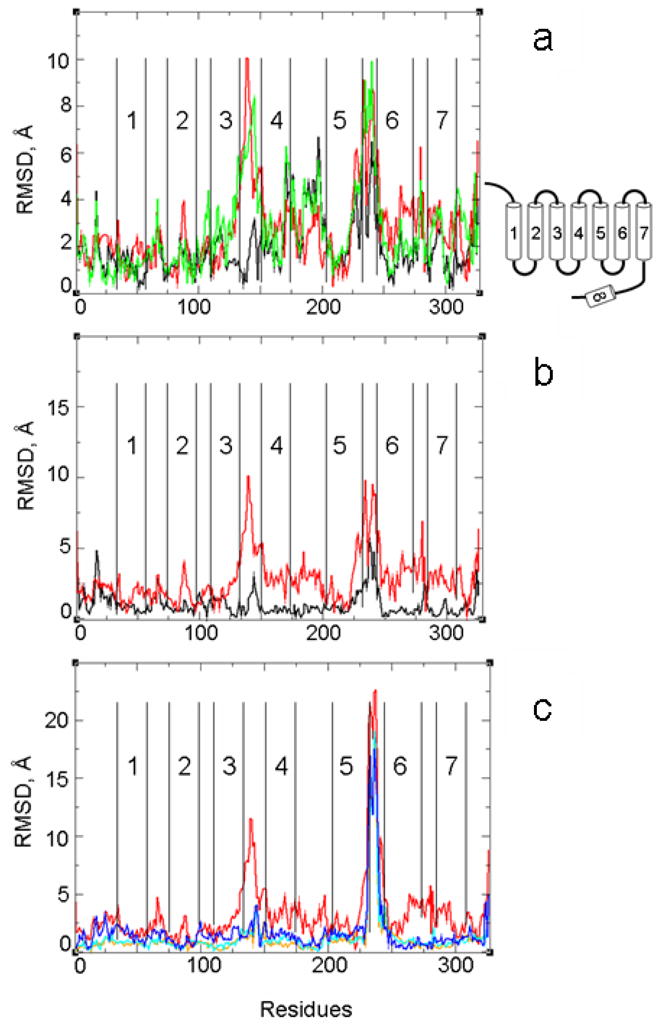
(a) Cα RMSD from the structure of LUMI for the initial all-atom model built based on the first (local) set of distance restraints (black), the coarse model obtained by applying the second (global) set of distance restraints (green), and the final all-atom model of META II (red). (b) Cα RMSD from the structure of LUMI for the PDI structure (black) and the META II model (red). (c) Cα RMSD from the ground state (PDB code: 1gzm) for BATHO (orange), LUMI (cyan), PDI (blue) and the META II model (red).

In the second step, we built an alpha-carbon elastic network model (ENM) of the rhodopsin structure resulting from the MD simulations. From this model, we computed the atomic displacements in response to mechanical forces arising from the second set of distance restraints, describing the global rearrangements of the TMs (see Methods). The smooth potential of the simplified ENM allows us to extrapolate helix movements from the experimentally measured pair-wise atomic distances without becoming trapped in local energy minima. The RMSD analysis in Figure 1a shows that in the second step the α-helices move relative to the starting model to satisfy the applied distance restraints, particularly at the intracellular ends of TM3, TM5, TM6, TM7 and helix 8 We detected significant displacements for the second and third intracellular loops (ILs) also (Figure 1a). These results are consistent with the high B-factor values detected in the crystal structure of LUMI for the intracellular ends of TM3 (135–139), TM5 (221–229) and TM6 (245–249) and for the ILs²⁸. The high mobility of these regions was also evident from unbiased prolonged MD simulations of the ground state of rhodopsin ^9,16,17,25 and from the analysis of the normal modes of an elastic network model¹⁹.

The displacement of the ENM in response to the applied restraints provided us with a simplified representation of the global conformational changes that accompany the activation process. However, the ENM model only includes the alpha-carbon atoms. To obtain an all-atom picture, we used biased MD to match the Cα atoms of the model obtained in the first step to the coordinates of the Cα atoms of the ENM. Comparison of our META II model with the PDI structure and the starting LUMI (Figure 1b) showed that the most significant differences occur in the loop regions, in helix 8, and at the intracellular ends of TM3, TM4, TM5, TM6 and TM7. The displacements of the intracellular loops (IL2 and IL3) from LUMI are seen in the PDI structure, and are more pronounced in our META II model. Figure 1c shows the RMSD of the Ca atoms from the ground state of rhodopsin (PDB code: 1GZM) for BATHO, LUMI, PDI and our META II model.

According to a PROCHECK⁴⁴ analysis, the stereochemical quality of our META II model is comparable to that of the LUMI X-ray structure²⁸, suggesting that the applied restrains did not induce large deviations from the typical values of φ, ψ, χ1 and χ2 angles. Ramachandran and χ1– χ2 plots are shown in Supporting Information (Figures S1 and S2).

In Figure 2, we compare the LUMI structure²⁸ and our final META II model at the large and local scale. At the large scale, we found significant motions of the transmembrane helices. The tilting angles between the helix axes of METAII and LUMI, calculated for each transmembrane helix using the TRAJELIX module⁴⁵ of the program SIMULAID,⁴⁶ are small for TM1 and TM2 (3° and 4.6°, respectively), and somewhat larger for TM3, TM4, TM5, TM6 and TM7 (7.16°, 7.74°, 6.2°, 8.4° and 11.3°, respectively). Comparing our METAII model with the structure of LUMI, we also detected small counterclockwise rotations around the axes of TM4, TM5 and TM6 of 5.43°, 10.93°, and 7°, respectively, when viewed from the cytoplasmic side. These data indicate outward/inward movements of the helices upon activation, coupled to small rotations of TM4, TM5 and TM6. We also noticed slight kinks in TM5 and TM2 of META II (Figure 2). The kink in TM5 occurs between H211(5.46) and F212(5.47) and is due to the absence of the backbone hydrogen bond between H211(5.46) and P215(5.50). The kink in TM2 occurs between G89(2.57) and F88(2.58), and is likely due to the presence of two consecutive glycines, G89(2.56) and G90(2.57). Locally, the movement of retinal toward the extracellular part of the receptor causes a rearrangement of the network of aromatic residues. In particular, we found that the χ₁ dihedral angle of W265(6.48) had changed from the g- to the t rotamer. We will show below that this change in rotamer state is closely coupled to the activation transition. The conformational flexibility of W265(6.48) was also evident in unbiased MD simulations of the rhodopsin ground state⁸ and in computational simulations of the retinal isomerization reaction^16,17,25.

Figure 2.

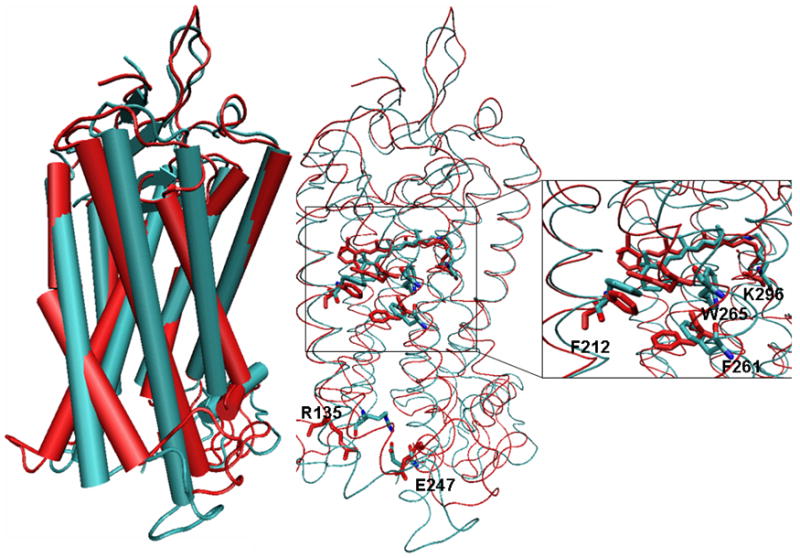
Superposition of the crystal structure of LUMI (cyan) and the META II model of rhodopsin (red) shown in cartoon representations (left) and Cα-trace (center). The right panel shows all-atom representations of the retinal, the covalently bound K296(7.43) and R135(3.50) of the D(E)RY motif with the partnering E247, and the aromatic residues F212(5.47), F261(6.44), and W265(6.48).

Hydrogen bonds are important contributors to the overall structural stability of a protein. This is particularly true for membrane proteins where tertiary hydrogen bonding between helices plays an important role in the low-dielectric membrane environment, somewhat analogous to hydrophobic interactions in water. To analyze how the network of hydrogen bonds changes in the different stages of the activation process, we computed the energy of each detectable hydrogen bond in the various crystal structures and in our META II model. 2D plots of the hydrogen bond network colored by energy are given as Supporting Information (Figure S3). The backbone hydrogen bonds remain stable for the intermediates, while appear to be weaker for PDI and our META II model. In particular, we observed weakening at the conserved motifs FX₂PX₇Y of TM5, FX₂CW(Y,F)XP of TM6 and X₃NPX₂Y of TM7 in proximity of the Pro kinks; however, the changes are small and could at least in part result from residual strain in the model caused by application of the restraints.

Significant differences were detected in the hydrogen bond network of the sidechains, which are critical for membrane proteins. On the basis of different experiments,^38,47–51 activation is thought to be associated with significant changes in the interhelical hydrogen bond network. The changes suggested by the experiments are reflected in our META II model. In particular, we noted the disruption of the following pairs of interactions: K296(7.43) and E113(3.28), N55(1.55) of the conserved motif GX₃N and D83(2.50) of the conserved motif N(S)LX₃Dx_7,8P, W126(3.41) and E122(3.37), R135(3.50) of the conserved motif D(E)RY and E247(IL3). The breakage of the latter salt bridge is caused by notable outward movements of the extracellular ends of TM3 and TM6 and results in a higher accessibility to R135(3.50) of the D(E)RY from the cytoplasmic side (Figure 2). The possibility of an interaction between this residue and the G protein has been suggested.⁵² In summary, our META II model captures the experimentally demonstrated changes in hydrogen bonding.

We also noted the breakage of the hydrogen bonds between Q64(1.59) and T320 of helix 8, W126(3.41) and H211(5.46), T243(IL3) and S240(IL3), and N55(1.55) and A299(7.46) in all photointermediates (Supporting Information, Figure S1). In addition, hydrogen bonds broke between S187(EL2) and E113(3.28), Y74(2.41) and E150(4.39), as well as W175(EL2) and S202(5.37) in both PDI and our META II model.

The movement of TM3, TM6, TM7 and helix 8 caused the disruption of the hydrogen bonds between T320 of helix 8 and H65(IL1), Q225(5.60) and Y136(3.51), N78(2.45) and T160(4.49), Y191(EL2) and Y268(6.51), Y43(1.38) and F293(7.40), N73(2.40) and Y306(7.53), as well as M183(EL2) and T289(7.36) in our META II model.

Compensating for the loss of these hydrogen bonds, we found that new hydrogen bonds were formed to stabilize the changed helical packing in the META II structure: N111(3.26) and P171(4.61), N111(3.26) and V173(4.63), S186(EL2) and T289(7.36), M288(7.35) and E181(EL2), 289(7.36) and E181(EL2), N302(7.49) and D83(2.50), Q312(helix 8) and N73(2.40), as well as T94(2.61) and E113(3.28).

The observed structural changes are possible factors in G-protein binding to the activated receptor. The increased flexibility resulting from weakening and breakage of several hydrogen bonds may cause the receptor to be more prone to interact with the G protein. At the same time, the formation of new hydrogen bonds especially in the intracellular loops may modify the surface to facilitate interactions with the G protein. The conformational perturbation of W265(6.48), a residue located in the binding pocket and implicated as a molecular switch,^24,37 could be an early event of the relaxation process leading to the activation cascade.

Dynamic Model of Rhodopsin Activation

To provide atomistic insights into the activation mechanism, we generated a dynamic model of rhodopsin activation. In nature, the conformational transition from LUMI to META II takes over 6 ms¹. Thus, to simulate it with a computer time suitable for a rapid analysis of the dynamics of rhodopsin activation, we performed biased MD simulations by driving the transition with mass-weighted RMSD restraints. A similar approach was recently taken to study the conversion of the cholecystokinin receptor 1 from the inactive to the active form⁵³. Although, different molecular compositions of lipid bilayers can substantially affect the properties of the membrane and consequently the dynamic behaviour of rhodopsin ^{7,9–11,17,54,55}, here we used the implicit GBSW solvation model^56,57 as implemented in CHARMM⁵⁸ in order to minimize the computer time necessary to simulate the transition. Since our simulations are driven with mass-weighted RMSD restraints and are short in time, we argue that the lack of explicit consideration of the membrane environment does not substantially affect our results.

The cis-trans isomerization of retinal, which is the first stage of activation, involves crossing a large energy barrier. To avoid this difficulty, we chose LUMI as a starting point of the simulations, where the isomerization of the chromophore has already occurred. We follow the transition by monitoring two characteristic coordinates: the χ₁ angle of W265 and the distance between R135 (3.50) of D(E)RY motif and E247 (i.e., the ionic bridge) as the most significant, experimentally demonstrated parameters to describe differences between inactive and active forms of rhodopsin and other GPCRs ^{24,30,37,49–51}.

In bovine rhodopsin the transition between LUMI and META I₄₈₀, i.e. the conventional META I which is in equilibrium with META II, appears to be unidirectional^{1 59}. Conversely, LUMI and META I have been shown to be in equilibrium in chicken rhodopsin.⁶⁰ Here, in light of the very small structural differences between LUMI and META I,²⁴ we treated the whole transition between LUMI and META II as an equilibrium reaction and simulated not only the forward but also the backward transitions for the wild type receptor and several mutants. Considering the two forms in equilibrium adds generality to our approach, since this study can be easily transferred to the analysis of the majority of GPCRs, for which equilibrium is known to exist. To mimic the conditions of the activation and inactivation processes, the forward transitions were carried out with protonated E113(3.28)⁴² and E134(3.49)⁴³, and deprotonated retinal Schiff base, while the protonation state was the opposite in the backward transitions.

Five trajectories each were generated for forward and backward transitions of wild type rhodopsin (Figure 3). Initial velocities were chosen from a Maxwell-Boltzmann distribution with different random seeds. The time evolution of all-atom RMSD, helix tilts and helix kinks of rhodopsin as well as that of several structural parameters of retinal are shown in the Supporting Information (Figures S4-7). The kink in TM2 was monitored following the N of G89(2.57) –C of F88(2.58) – CA of F88(2.58) – N of F88(2.58) dihedral angle. During the transition, the dihedral angle underwent a change of about 46°. The kink in TM5 was monitored following the N of H211(5.46) –CA of H211(5.46) – C of H211(5.46) – N of F212(5.46) dihedral angle. This dihedral angle underwent a change of about 30°. The dihedral angle about the C6-C7 bond of retinal did not change during the transition from LUMI to META II (Figure 7S, c), indicating that the β-ionone ring of retinal did not change conformation in the course of the simulation.

Figure 3.

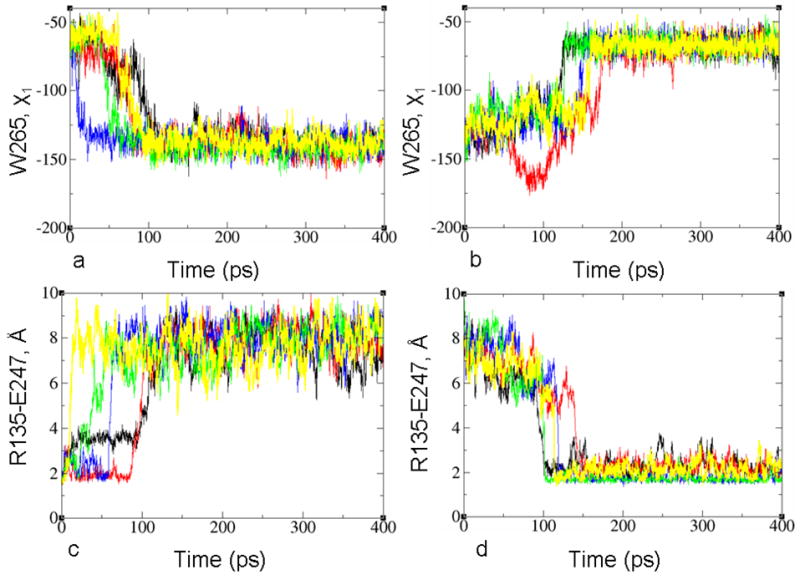
Forward (left) and backward (right) activation transitions of wild type rhodopsin calculated from five MD trajectories. The transition is monitored by using (a,b) the side-chain dihedral angle of χ₁ of W265(6.48), and (c,d) the distance between R135(3.50) of the D(E)RY motif and E247.

The changes of the χ₁ angle of W265 located around the retinal binding pocket tend to occur before the breakage of the salt bridge between R135 (3.50) and E247 in the intracellular part of rhodopsin in the forward transition. In particular, the χ₁ angle of W265 reached the final value in 66±16 ps, while the distance between R135 (3.50) and E247 reached the final value in 94±13 ps. The reverse sequence of events was found in the backward transition (i.e., the salt bridge formed first), with transition times of 116±9 ps for the salt bridge formation and 148±9 ps for the χ₁ angle of W265.

A number of rhodopsin mutants showed the ability to either favor or hamper the activation of the receptor. In the following, we explore possible correlations between the phenotypes of specific mutations and their effects on the transition times in our dynamic model. We performed simulations for five mutants that do not affect the folding of the receptor: T94I(2.61),⁶¹ A117F(3.32),⁶² G121V(3.36),⁶³ L125Y(3.40),⁶⁴ and M257Y(6.40)⁶⁵ (Figure 4). Among them, T94I(2.61), G121V(3.36), and M257Y(6.40) have been shown to favor activation of the receptor. They are localized in TM2, TM3 and TM6, respectively. In contrast, A117F(3.32) and L125Y(3.40) slow the activation transition and are localized in TM3. All substitutions have hydrophobic character with a larger van der Waals volume than the native residues. In our simulations, their biological properties seem to be linked to steric effects that selectively facilitate or hinder the forward or backward transitions.

Figure 4.

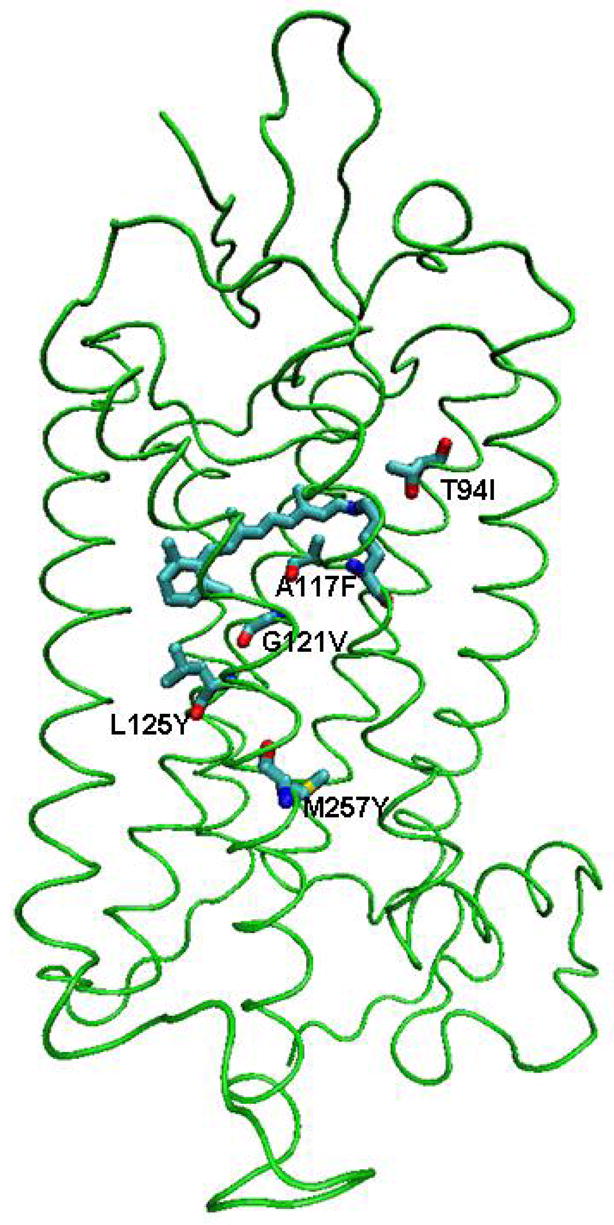
Mutations used to validate the dynamic model of receptor activation. The movement of retinal toward TM4 and TM5 is facilitated by T94I(2.61) and obstructed by A117F(3.32). The conformational change of the χ₁ angle of W265(6.48) is assisted by G121V(3.36), but is hindered by L125Y(3.40). M257Y(6.40) causes a steric interaction between TM6 and TM3 that helps the outward movement of TM6. In our dynamic model, the mutations that favor the activation of the receptor shift the reaction equilibrium toward META II, as deduced from the rough estimate K=t_b/t_f based on the waiting times (Table 2). Mutations that impair activation shift it toward the inactive state.³⁶–⁴⁰

To assess the effects of the mutations on the rate of conformational changes upon activation, we perform simulations in which we again drive the transition using mass-weighted RMSD restraints in CHARMM⁵⁸. In these biased simulations, we determine the “waiting time” as the time spent in the initial state before the conformational transition occurs. The absolute waiting times depend on the restraining procedure. Nevertheless, the relative waiting times can be used to compare the effects of the different mutations on the rate of the activation transitions.

By monitoring the two reaction coordinates based on five forward and backward trajectories, we found a clear correlation between predictions of our dynamic model and the phenotypes of the mutants. For the mutants that favor the activation of the receptor, the forward transitions are faster and the backward transitions are slower than those of the wild type, resulting in a shift of the apparent “reaction equilibrium” toward META II, while the opposite happens for the mutants that impair activation. In Table 2, we show the mean values of waiting times calculated from five trajectories, together with the standard error of the mean. The forward and backward transitions for wild type rhodopsin and mutants characterized on the basis of the distance between R135(3.50) of D(E)RY and E247 are shown on Figure 5. Corresponding curves for the χ₁ angle of W265 are given as Supporting Information (Figure S8).

Table 2.

Waiting times for the LUMI – META II transition for wild type rhodopsin and mutants. Waiting times t_f and t_b are for the completion of the forward and backward transitions, respectively. Means and standard errors were estimated from five simulations. As a rough approximation for the equilibrium population shift, we calculate the ratio of waiting times, K=t_b/t_f, which provides an estimate of the relative stability of the META II state over the LUMI state.

	Dihedral angle of the side chain of W265, (χ1)			Distance between R135 and E247
	tf (ps)	tb (ps)	K	tf (ps)	tb (ps)	K
T94I	38±6.5	142.6±32	3.8	38.6±10.7	128±14.9	3.3
G121V	56±9.8	231.2±13.1	4.1	63.5±7.3	196.5±28.9	3.1
M257Y	53±6.5	148.7±21.1	2.8	54.1±13.8	124.2±15.6	2.3
Wild type	65.9±16.1	147.6±9.4	2.2	94.1±12.5	115.6±8.5	1.2
A117F	140.4±22.3	127.7±27.6	0.9	152.1±19.5	84.3±15.0	0.6
L125Y	174.5±18.7	97.2±13.5	0.6	221.8±36.4	97.2±13.5	0.4

Figure 5.

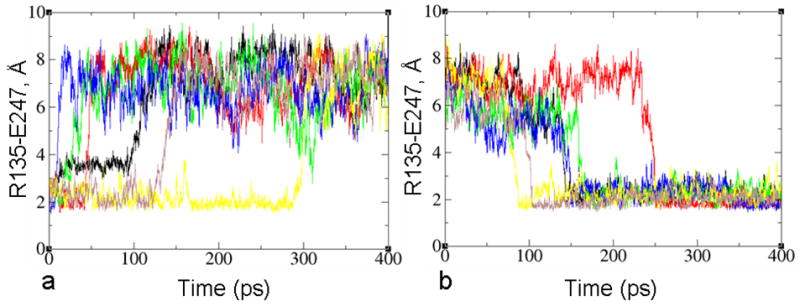
Representative forward (left) and backward (right) transitions for the activation of wild type rhodopsin (black) and mutants (G121V – red, M257Y – green, T94I - blue, L125Y – yellow and A117F - brown) chosen from five simulations with different Maxwell-Boltzmann initial velocities. The transition is monitored by following the distance between R135 of the D(E)RY motif and E247.

Following the analysis of the atomic trajectories, we hypothesize a possible mechanism underlying the phenotype of the mutants. The movement of retinal toward TM4 and TM5 seems to be facilitated by the T94I(2.61) mutant and obstructed by the A117F(3.32). The change of the χ₁ angle of W265(6.48) is assisted by the G121V(3.36) mutation, but hindered by the L125Y(3.40) mutation. Lastly, the M257Y(6.40) mutant causes a steric constraint between TM6 and TM3 that helps the outward movement of TM6.

This dynamic model may be relevant also for other GPCRs for which equilibrium exists between the inactive and active forms of the receptors. In particular, our analysis provides a tool for the prediction of mutations that cause enhanced levels of basal activity and a way to investigate the molecular mechanisms underlying the altered equilibrium between the inactive and active states of a receptor. These mutants, known as constitutively active, occur naturally and cause human disease.

Extending this dynamic analysis to GPCRs that bind ligands within their 7-TM bundle could provide a computational tool for the prediction of the pharmacological properties of ligands. Just as the approach here was able to distinguish between mutations that accelerate or decelerate activation, one may distinguish between inverse agonists, antagonist, partial agonists and full agonists. At least in the case of rhodopsin mutants, our model was able to perform the task, providing information not accessible by means of static experimental or computational models.

Conclusion

In the first part of the paper, applying experimentally based distance restraints to the structure of LUMI, we built a model of META II rhodopsin in two steps: first incorporating local experimental restraints in an all-atom model and then applying global restraints to a coarse model. We detected significant changes in interhelical hydrogen bonding that may be important for the interaction with the G protein, both by enhancing the overall flexibility associated with “induced-fit” rearrangements and by changing the character of the binding interface.

The structural model we obtained reflects the available experimental information, as compiled in Table 1. However, it is important to keep in mind that even this extensive set of local and global distance restraints does not guarantee a unique META II structure. We overcame this problem by using the coarse network model in conjunction with the more global experimental restraints. Additional restraints from future distance measurements will permit both a validation of the existing structural model and further improvements.

In the second part of the paper, we constructed a dynamic model of rhodopsin activation that describes the path leading from LUMI to our model of META II and vice versa. By providing atomistic insights into the molecular mechanisms of several mutations that affect activation of the receptor, the model shows a clear correlation between its dynamic properties and the pharmacological phenotype of the mutants. In particular, the mutations that facilitate activation of rhodopsin accelerate the transition to the active state and decelerate the backward transition, while the opposite happens for the mutants that hamper activation.

We emphasize, however, that the remarkable agreement of the dynamic model with the phenotype of the respective mutations may at least in part be fortuitous. The effects of amino acid mutations are often complex and not easily predictable. Here, the number of mutations considered was significant but by no means large.

While static models can provide insights into the mechanisms of ligand recognition and predict ligand affinity, dynamic models can be useful in studies of the activation mechanism of GPCRs and in computational predictions of pharmacology of mutant receptors and novel ligands. The accuracy and applicability of such dynamic models will be validated in the future, as new experimental structures become available for the inactive and active states of rhodopsin and other GPCRs.

Methods

Molecular Dynamics Simulations

MD simulations were performed with CHARMM⁵⁸ (version c33b2), employing the CHARMM27 force field^66,67. Simulations were carried out in implicit membrane using the GBSW^56,57 (Generalized Born with a simple switching) module of CHARMM. In this module, the membrane is approximated as a low-dielectric slab which reproduces the Poisson-Boltzmann electrostatic solvation energy profile across the membrane. Langevin simulations with a time step of 0.002 ps were performed at a temperature of 300 K. The charges for the protonated and deprotonated Schiff-base chromophore (retinal and Lys296) were obtained from a HF/6-31G** calculation in Gaussian.⁶⁸ The force field parameters for retinal were taken from the work of Saam and coworkers¹⁷.

We applied the HQBM module⁶⁹ of CHARMM first to force LUMI to satisfy experimentally derived distance restraints. In a second series of simulations, we forced the all-atom model toward the Cα scaffold of the ENM model obtained after imposing the global distance restraints. The lengths of the two simulations were 300 ps and 450 ps, respectively. In HQBM, a progress variable ρ was defined as the mean squared deviation between the current pair distances r_ij and the target distances $r_{ij}^0$, over all pairs (ij) in the restraint list:

$$\rho (t)=\frac{1}{N_{ij}}\sum _{(ij)}{(r_{ij}(t)-r_{ij}^0)}^2$$ (1)

A time-dependent bias potential E_HQBM was added to the total energy, which penalizes only fluctuations that increase ρ, that is:

$$E_{\text{HQBM}}=\{\begin{array}{cc}0& \rho (t)<{\rho }_0\\ \frac{\alpha }{2}{(\rho (t)-{\rho }_0)}^2& \rho (t)\ge {\rho }_0\end{array}$$ (2)

where ρ₀ is defined as ${\rho }_0=\underset{\tau <t}{min}\rho (t)$ and the stiffness of the potential is controlled by α, set to 0.6 kcal/mol/Å⁴.

Mass-weighted RMSD perturbation was performed as implemented in CHARMM⁵⁸, with a restraint energy in the form:

$$\text{E}={\mathrm{\sum }}_{\text{i}}{k_{\text{i}}}^{\ast }{[\text{RMSD}-{\mathrm{\Delta }}_{\text{i}}]}^2$$ (3)

where the RMSD is calculated with respect to the reference structure, k_i=800 kcal/mol/Ų is a force constant, and Δ_i is a target value for the relative distance to the reference structure. Five 400-ps simulations each for backward and forward transitions were performed using Maxwell-Boltzmann initial velocities. In the simulations, the van der Waals radii of the mutated non-hydrogen sidechain atoms (of M257Y, T94I, L125Y, A117F) were uniformly set to 1.4 Å. The structures of the rhodopsin mutants were constructed and minimized based on the wild type structures in the active and inactive states. The waiting time for the completion of the transitions in these driven simulations was taken as the time until the chosen reaction coordinate moved within a preset threshold of the final value. For the distance between R135 of D(E)RY and E247, the final values are 6.80 Å (1.82 Å) for the forward (backward) transition, with thresholds of 2 Å (1 Å), respectively; for the χ₁ angle of W265, the final values are −134.9° (−69°), with thresholds of 20° (10°). As a measure of the relative stabilities of the initial and final structures, we calculated the ratio of the waiting times in the forward and backward transitions.

Elastic Network Model and Calculation of Response Displacement

An elastic network model^70–72 was constructed based on a Gō-like model⁷³ in which the springs between alpha-carbon atoms were defined following three rules: (1) sequential carbons (i,i+1) were connected by “bond” springs with a force constant k_b, where k_b=378 kcal/(mol⁻¹ Å⁻²) is the bond spring constant of the Gō-like model, to capture the stiffness of bonded and local interactions relative to non-bonded interactions; (2) (i, i+2) and (i,i+3) carbon atoms (forming “angles” and “dihedrals,” respectively) were connected by springs of spring constant 0.3k_b; and (3) Cα pairs forming native contacts according to the Gō-like model were connected by harmonic springs whose spring constants were obtained from the second derivative at the minima of the respective pair potentials used in the Gō-like model. The average stiffness of these “non-bonded” springs was 0.02k_b.

As reference conformations, we used the structures obtained after the initial MD simulations (i.e., with local restraints imposed). For the resulting energy surface E(r), we calculated the Hessian matrix H such that E(r)≈ r^T·H·r/2 where r is the 3N-vector of atomic coordinates. We then calculated the response of the structure to the experimental distance restraints by applying external forces on the respective atom pairs in the direction of the pair distance vector. Within the Hessian approximation, the displacement induced by forces f_j acting on atoms j can be computed as

$$\mathrm{\Delta }{\text{r}}_{\text{i}}={\mathrm{\sum }}_{\text{k}}{\text{v}}_{\text{ik}}{{\lambda }_{\text{k}}}^{-1}{\mathrm{\sum }}_{\text{j}}{\text{v}}_{\text{jk}}{\text{f}}_{\text{j}}$$ (4)

where the sum extends over the non-zero eigenvalues of the Hessian matrix H. Δr_i is the displacement of atom i, v_ik and _k are the eigenvector and eigenvalue for atom i in the k-th normal mode, and f_j is the external force (3 kcal/mol/Ų) acting on atom j.⁷⁴ The magnitude of the force was chosen empirically to keep the helical structure of TMs. In the first step the distance restraints between TM1 and TM8, TM1 and TM7, and TM7 and TM7 were applied; this created space for the movement of TM6 and TM7 when the restraints between TM3 and TM6 were added in the second step.

Geometric Analysis of Transmembrane Helices

The TRAJELIX module⁴⁵ of the program SIMULAID⁴⁶ was used to calculate helix axes, angles of tilt between METAII and LUMI helix axes, and angles of helix rotation. The residue ranges of the helices were defined as follow: 34–63 (TM1), 71–99 (TM2), 107–139(TM3), 150–173(TM4), 201–229(TM5), 242–278(TM6), and 284–310(TM7). Changes in geometry were calculated for the first and last structures along the trajectory from LUMI to METAII.

Calculation of Hydrogen Bonding Energy

Hydrogen atoms were added to the crystal structures and energy minimized using CHARMM.⁵⁸ We classified a donor-hydrogen-acceptor interaction as a hydrogen bond if the hydrogen-acceptor distance was within 3 Å, and the hydrogen-donor-acceptor angle did not exceed 40°. The energy of the resulting hydrogen bonds was calculated using the DREIDING force field.⁷⁵