Dynamics of origination and extinction in the marine fossil record

Abstract

The discipline-wide effort to database the fossil record at the occurrence level has made it possible to estimate marine invertebrate extinction and origination rates with much greater accuracy. The new data show that two biotic mechanisms have hastened recoveries from mass extinctions and confined diversity to a relatively narrow range over the past 500 million years (Myr). First, a drop in diversity of any size correlates with low extinction rates immediately afterward, so much so that extinction would almost come to a halt if diversity dropped by 90%. Second, very high extinction rates are followed by equally high origination rates. The two relationships predict that the rebound from the current mass extinction will take at least 10 Myr, and perhaps 40 Myr if it rivals the Permo-Triassic catastrophe. Regardless, any large event will result in a dramatic ecological and taxonomic restructuring of the biosphere. The data also confirm that extinction and origination rates both declined through the Phanerozoic and that several extinctions in addition to the Permo-Triassic event were particularly severe. However, the trend may be driven by taxonomic biases and the rates vary in accord with a simple log normal distribution, so there is no sharp distinction between background and mass extinctions. Furthermore, the lack of any significant autocorrelation in the data is inconsistent with macroevolutionary theories of periodicity or self-organized criticality.

Decades of literature on large-scale taxonomic diversification and extinction patterns have hinged on compilations that record little more than first and last appearances of families or genera. Key examples include Sepkoski's compendia of marine families (1) and genera (2) and the Fossil Record 2 database of marine and continental families (3). Numerous patterns of widespread scientific and public interest have been identified on the basis of the older compilations, such as the identity of the five largest mass extinctions (4, 5), a gradual decline of extinction rates throughout the entire Phanerozoic (4), and possible cycles in extinction rates (6). A complete reevaluation of these hypotheses is now made possible by the maturation of the Paleobiology Database, a relational, web-based, and much more detailed resource created by and for the paleontological community (7).

Arguably, the most enduring and biologically important question these data can answer is whether global biodiversity is saturated (1, 8, 9). If so, then ecological interactions, such as competition and predation, must control rates of speciation and extinction (10–12). Speciation rates must be lower or extinction rates must be higher than they would be without these interactions. Diversity curves should increase logistically as they approach the saturation point (8) instead of exponentially (13). Increases in the diversity of major taxonomic groups should be balanced by decreases in the diversity of other groups (9). Most importantly, any recovery from a mass extinction, such as the current one, should eventually bring diversity back to the saturation point. Of course, the recovery will be rapid only in geological terms, the saturation point may change, and the extinction may fundamentally reorganize the global biota both taxonomically and ecologically, as seen in the wake of major perturbations, such as the end-Permian crisis (14).

Past predictions about recovery have been hampered by limited direct evidence for saturation in the fossil record. Sepkoski (1, 8, 9) did argue in detail that turnover rates have constrained the global diversity of all marine animals over the entire Phanerozoic. Some studies of particular taxonomic groups over specific parts of the Phanerozoic also suggested density-dependent dynamics (15–19). However, both earlier (20) and later (13) workers argued that Phanerozoic diversity was not constrained. Even though this view is very inconsistent with such well documented patterns as rapid rebounds from mass extinctions (14, 21, 22), a basic logistic model assuming a single equilibrium point (8) failed to explain in a simple way why diversity appeared to increase exponentially in the Cretaceous and Cenozoic, toward the end of the Phanerozoic (1). Instead, a model with multiple equilibria was invoked (1, 9).

More recently, evidence has accumulated that the late Phanerozoic radiation is actually a combined artifact of increased sampling intensity and a related effect called the Pull of the Recent (7, 23–25). Thus, the question of diversity equilibrium has been reopened. The strong statistical patterns reported here show that diversity does not increase exponentially without constraints and therefore make it possible to predict the rebound from the current mass extinction in strict quantitative terms. First, however, a series of other major hypotheses concerning mass extinctions and diversity dynamics need to be addressed.

Pulsed Turnover Rates.

Based on Sepkoski's classic family- and genus-level data (1, 2), it has been suggested that turnover comes in large pulses that coincide with interval boundaries (26, 27). If true, this result has the profound implication that even background turnover is largely forced either by perturbations, such as eruptions, sea level and climate changes, and bolide impacts (28), or by episodic ecological interactions, such as cascading extinctions (29). If turnover is not coupled with boundaries, an alternative hypothesis is that background extinction is effectively stochastic and results from the never ending process of competition over a fixed or slowly changing resource base, i.e., the Red Queen hypothesis (30).

The pulsed turnover hypothesis implies that per-million year (Myr) rates will correlate inversely with interval lengths because the assumption that turnover is continuous is violated (6). There is such a relationship for per-Myr extinction rates (Spearman rank-order correlation ρ = −0.409, P < 0.005). However, the same correlation does not exist in the unstandardized rates [ρ = −0.021, not significant (n.s.)] and is not significantly different from a distribution generated by bootstrapping (i.e., correlating raw rates with ratios of themselves to randomly drawn bin lengths). Thus, the relationship can be explained as resulting from random variation in the bin lengths because of random errors in the underlying time scale. The same pattern is seen with originations, i.e., first appearances of genera. Origination rates correlate negatively with bin length if they are standardized (ρ = −0.408, P = 0.005) but otherwise do not (ρ = 0.155, n.s.). These results, however, do not particularly endorse the Red Queen hypothesis because rates are still quite variable, as discussed below.

On balance, it is most parsimonious to infer that, although turnover may or may not be pulsed, interval boundaries do not coincide consistently with pulses, so continuous-time rates are more realistic than turnover proportions. These rates also have the advantage of removing the upper bound present in proportions, which can cause analytical artifacts. The continuous rates are not standardized for bin length in subsequent analyses because of the time scale's relative homogeneity and the suggestion that doing so would bias them. For the current dataset, this technical problem is most likely moot, because there is no trend through time in bin length (ρ = 0.168, n.s.), and the standard deviation of logged bin lengths is modest (0.348).

Phanerozoic Decline in Extinction Rates.

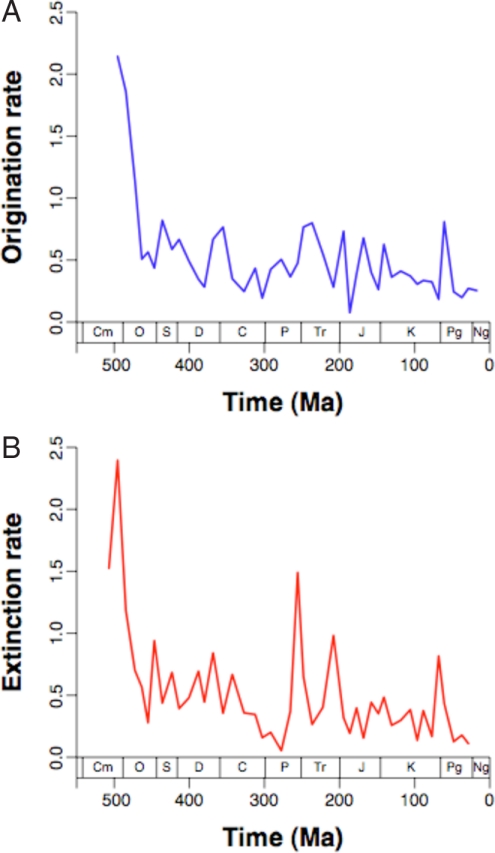
Again based largely on Sepkoski's data, it has long been believed that there has been a decline through the Phanerozoic in both extinction rates (4) and origination rates (31). These observed declines are robust to the choice of rate metrics (26). Indeed, the new data clearly support a decline in both kinds of rates (extinction vs. time: ρ = 0.547, P < 0.001; origination vs. time: ρ = 0.533, P < 0.001). The patterns are influenced by extremely high values at the beginning of the time series that represent the Cambrian and earliest Ordovician (Fig. 1). However, removing these points does not greatly weaken the trends (extinction: ρ = 0.446, P = 0.003; origination: ρ = 0.465, P = 0.002). It is noteworthy that the correlations still appear even though the earlier studies (4, 31, 32) used finer time scales and therefore had greater statistical power. They also did not correct for sampling biases that would favor finding such a pattern.

Fig. 1.

Per-interval instantaneous origination rates (A) and extinction rates (B) of marine invertebrate genera over the Phanerozoic. Data are binned into 48 intervals averaging 11.0 Myr in duration.

To quantify the steepness of the declines, it is appropriate to perform a linear regression after log-transforming the turnover rates (26, 33), which is necessary because they are skewed and bounded by zero. For extinction and origination after the earliest Ordovician, the respective regression slopes are 0.201% and 0.158% per Myr, and the intercepts at 0 Ma are 0.218 and 0.282. Sepkoski's data imply much steeper slopes and predict much lower extinction rates for the Neogene (34), which is expected because the data are influenced by the Pull of the Recent.

The drop in rates could be explained in at least four ways. First, a trend might be created by sampling biases or an increase through the Phanerozoic in the average durations of sampling bins (35). The former problem has been fully resolved by sampling standardization of the data and by the use of rate equations that are robust to edge effects such as the Pull of the Recent [see supporting information (SI) Text]. The latter problem has been resolved by careful lumping of stages to produce bins of approximately equal length, as mentioned above.

Second, the trends could reflect a handoff between major groups that had coupled logistic dynamics (1). Groups that were dominant early on might have had higher intrinsic turnover rates but lower carrying capacities, leading eventually to their replacement by slowly radiating competitors. Here, these groups would be the three “evolutionary faunas” (36). Evidence is lacking for dynamically distinct but interacting groups of taxa based on actual turnover rates in Sepkoski's own genus-level compendium (37), so the evolutionary fauna hypothesis is not relevant here and is most likely useful only to summarize coincidences between diversity trends (36) and onshore-offshore patterns (38).

Third, individual orders with high turnover rates might have randomly gone extinct by the mid-Paleozoic simply because of their volatile dynamics, leaving only the groups with low turnover rates (32). Neither this hypothesis nor the preceding one can be tested directly by using the new data without separating the major taxonomic groups, but at least the volatility model is supported by analyses of Sepkoski's data (32).

Finally, higher taxa such as families may tend to accumulate more species through time, reducing their chance of extinction (39). A similar argument holds for origination. Raup (40) provided estimated species totals for the Cenozoic and for each Paleozoic and Mesozoic period that can be compared with genus totals extracted from Sepkoski's compendium (2). Although the ratios are probably too low, because the species counts are two decades older, there is a striking increase from 2.6, 2.7, and 2.1 in the Cambrian, Ordovician, and Silurian, to 5.4 and 7.8 in the Cretaceous and Cenozoic, with all other periods falling in between. More detailed analyses are called for, but the difference is so large that it could easily explain the trend.

Big Five Mass Extinctions.

The apparent existence of five major peaks in extinction rates is another key finding in the literature on Phanerozoic marine diversity (4, 5). The Big Five theory is so widespread that it has given rise to the popular term “sixth extinction” in relation to the current crisis (41, 42). These peaks were first recognized because they rose beyond the parametric 95% confidence interval around a linear regression that described the Phanerozoic decline in extinction rates (4). The Big Five also appear to be present in a separate compilation of marine family-level data (13), and at least the Permo-Triassic and Triassic–Jurassic events register as well in data on continental organisms (13).

However, there were numerous problems with the original analysis, including failure to log the data (33) and the use of per-Myr but not per-taxon rates. Indeed, the original data (4) did not particularly support the existence of two mass extinctions now widely discussed, the late Devonian and end-Triassic (43). Although the five greatest proportional drops in diversity in Sepkoski's later genus-level data (2) do match the conventional Big Five extinctions, the late Devonian and end-Triassic drops apparently are driven more by origination deficits than by high extinction rates (ref. 44; however, in the new data, the latter decline is a legitimate mass extinction). Furthermore, the end-Ordovician peak in Sepkoski's family-level data has been called into question because its appearance depends on the rate metric being used (26).

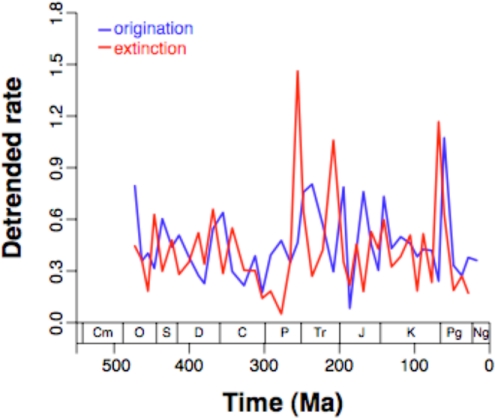
Finally, the very idea that the Big Five represent anything but the upper end of a continuous range of variation has been questioned almost from the start (5, 45). Although there are other good ways to test for outliers in rate distributions (45), it is sufficient to compare the rates with what is expected of the same number of observations drawn from a best-fit normal distribution. The rates first need to be detrended by taking residuals of the regression line that was earlier fit to the logged data. The detrended distributions (Fig. 2) are in fact indistinguishable from the log normal based either on a Kolmogorov–Smirnov test (extinction: D = 0.0888, n.s.; origination: D = 0.0883, n.s.) or a Shapiro–Wilk test (extinction: W = 0.9657, n.s.; origination: W = 0.9548, n.s.). Additionally, although extinction rates are much more variable than origination rates in Sepkoski's datasets (26), here the standard deviations of the detrended rates are very similar (extinction: 0.613; origination: 0.466) and the distributions are statistically indistinguishable (D = 0.2215, n.s.). Thus, not only are there no distinct classes of major origination or mass extinction events, but there is minimal evidence that extinction rates are more volatile than origination rates.

Fig. 2.

Origination rates (blue lines) and extinction rates (red lines) after being detrended by using exponential functions.

These results do not challenge the idea that true mass extinctions impose different rules of survivorship relating to factors such as geographic range size (46), because the rules could well vary with extinction intensity even if intensity per se is largely random. They also do not challenge the idea that we are in the midst of a mass extinction on par with all but a handful of such events over the last half billion years (47).

Furthermore, the data confirm that three of the Big Five extinctions (the Permo-Triassic, end-Triassic, and Cretaceous-Tertiary) are the three largest of the Phanerozoic, if only after detrending the rates (Fig. 2). These events stand out very clearly if the data are not log-transformed. Additionally, although the Paleozoic data show very little variability, one of the two largest events within the Paleozoic is indeed the end-Ordovician extinction. The other comes at the Devonian–Carboniferous boundary, immediately after the late Devonian event typically ranked in the Big Five. As mentioned, the late Devonian episode's importance already has been called into question (26, 43, 44). In summary, it is a matter of taste whether to speak of the Big Five, the Big Three, or just the Big One, but one way or another major mass extinctions are truly very rare.

Periodicity and Self-organized Criticality.

The hypothesis that mass extinctions show an ≈26-Myr cycle of periodicity (6) has arguably been the most debated hypothesis by paleontologists over the last quarter century. A host of potential mechanisms for periodicity have been offered, such as impacts driven by astrophysical factors (6) or the lag time needed either to accumulate species vulnerable to mass extinction (48) or to build networks of ecological interactions that can collapse if even slightly perturbed (29).

Qualitatively, it is hard to discern some of the extinction rate peaks that should fall in the periodic pattern (13). Quantitatively, extinction rates in the Fossil Record 2 family data (3) and Sepkoski's family and genus data (1, 2) are not correlated with themselves at any time lag (49), which is a necessary condition for periodicity to hold. That said, analyses of origination rates in all three datasets (49, 50) suggest short-term autocorrelation. However, the current dataset shows no autocorrelation in either kind of rate (Fig. S1), and a standard spectral analysis (Fig. S2) also suggests purely random variation through the time series (i.e., white noise).

The idea that mass extinctions may result from small perturbations of complex ecosystems (29) has been expanded to argue that food webs naturally evolve to a state of self-organized criticality that creates the extinction cascades, even in the absence of perturbations (51, 52). Criticality models make direct predictions about patterns of autocorrelation in time series (52, 53). However, results suggesting criticality in several major paleontological datasets (52) were quickly rebutted as statistical artifacts that resulted from interpolating turnover rates to create numerous evenly spaced intervals (54, 55). With the new data, the slope of the spectral density/frequency relationship is far from the value predicted by criticality; it is effectively zero (Fig. S2B). Thus, self-organized criticality can be dismissed as a plausible explanation of extinction rates.

Finally, it also has been suggested that diversity itself is cyclical with a period of ≈62 Myr, regardless of turnover rates (56). This pattern was again compromised by the use of Sepkoski's unstandardized data, and it had serious plausibility problems: Although extinction rates do not show long-range periodicity, most of the predicted peaks only appeared to be peaks because they were followed by the nominal Big Five extinctions (e.g., 4, 49). No distinct peaks were seen within the Cretaceous and Cenozoic (56) (Fig. S3), and there is also no evidence in the current dataset (25) for the predicted early Cambrian peak, or for a valley separating the supposed late Ordovician and Devonian peaks.

The current diversity curve does show a weak cycle after removing its U-shaped trend by taking residuals of a quadratic function fitted to the logged data (Fig. S3). However, the cycle has a period somewhat longer than 62 Myr (Fig. S1C), and the pattern is driven by clearly coincidental matches between two peaks and two valleys (Fig. S3). The spectral density data (Fig. S2C) also suggest periodicity. However, the steep falloff at medium frequencies is driven by these weak matches and consistent with either a power law or exponential function, so it is not evidence of self-organized criticality (55).

Equilibrial Dynamics

Density Dependence.

The lack of periodicity in turnover rates does not imply that these rates are random and therefore does not imply that the diversity curve evolves randomly. The reason is that at least three causal relationships might regulate diversity and turnover while not producing marked autocorrelation. First, origination rates may correlate negatively with preceding diversity levels (8, 11). An equilibrium will result, because high diversity will lead to an origination deficit, low diversity will lead to a burst of origination, and intermediate diversity will lead to a balance of origination and extinction. Second, diversity and subsequent extinction rates may correlate positively, producing an equilibrium for similar reasons (8, 11). Both relationships have been found in Sepkoski's family- and genus-level data (26, 57). Third, origination and extinction may be positively correlated (15, 17, 18, 20, 58). Such a correlation will greatly slow the net movement of the diversity curve and has been observed in Sepkoski's data (21, 22).

These hypotheses can be tested by computing simple correlations among the turnover rates (λ and μ) and diversity (N_s). There are no strong correlations in the raw data between either extinction or origination and diversity in the immediately preceding, current, or succeeding bins. However, the picture changes after detrending the turnover rates (Fig. 2) and diversity curve (Fig. S3); as it should, detrending markedly reduces the correlation between neighboring diversity values, with ρ = 0.769, P < 0.001 instead of ρ = 0.464, P = 0.002.

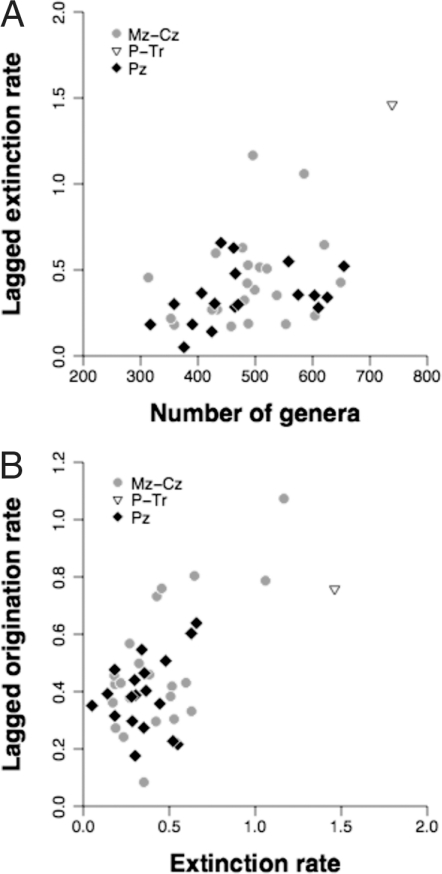
Now there is a correlation between past origination and current diversity (ρ = 0.327, P = 0.035). However, this weak relationship may be influenced by analytical biases (see SI Text), and there is no correlation between past extinction and diversity (ρ = −0.214, n.s.). Of more interest is a stronger match (Fig. 3A) between current diversity and immediately following extinction (ρ = 0.439, P = 0.004) but not origination (ρ = −0.039, n.s.). The diversity/extinction relationship is unlikely to result from a commonly encountered bias called regression to the mean (59). Concurrent diversity and extinction also correlate with the predicted positive sign, if not significantly (ρ = 0.243, n.s.), and likewise concurrent origination is not predictable (ρ = 0.223, n.s.). Finally, there is a match (Fig. 3B) between past extinction and future origination (ρ = 0.337, P = 0.029) but not the other way around (ρ = 0.016, n.s.), with independence of concurrent rates (ρ = 0.111, n.s.).

Fig. 3.

Key relationships between variables that govern marine invertebrate diversity dynamics on the Phanerozoic scale. Paleozoic points (black diamonds) and Meso-Cenozoic points (gray circles) show the same patterns in each case, and the values including the Permo-Triassic mass extinction (triangle) are consistent with the trends. (A) Correlation between diversity in one interval and extinction rates in the next interval. (B) Correlation between extinction rates in one interval and origination rates in the next.

The two strong relationships are crucial, because they are responsible for the suggested equilibrium: High diversity will be brought down by high extinction rates, and large extinctions will be compensated by high origination rates. After splitting the data at the Permo-Triassic boundary, sample sizes are too small to establish significance, but consistent patterns in both relationships are still seen (Fig. 3). Furthermore, the predicted relationships hold up after removing the outlying end-Permian extinction rate (diversity and future extinction: ρ = 0.396, one-tailed P = 0.006; extinction and future origination: ρ = 0.291, one-tailed P = 0.033).

Causal Model.

Obviously, origination rates cannot respond directly to a memory of extinction rates in the far past. Ghosts do not speak, so their empty niches must somehow beckon. The problem is how to reproduce such a process without making origination density-dependent, which cannot be accomplished in any way with conventional logistic models (8), simple lattice-based niche incumbency models (12), or percolation models in which all empty cells are filled immediately by origination (29).

The only way I have been able to predict all of the key relationships is with a cell model in which the number of cells is effectively infinite, underlying origination rates follow a random walk, new species can only fall in unoccupied neighboring cells, and underlying extinction rates are some joint function of white noise and the overall current number of species (see SI Text). Any other combination of factors seems to either create density dependence of origination rates or remove one or both of the two key correlations.

In plain English, this model depends on direct competition to regulate both speciation and extinction. The former process is basically niche incumbency (12) with limited rates of adaptation, local interactions, and no fixed number of niches, and the latter process is a routine logistic function (8). Competition is the opposite of the interdependency built into percolation and self-organization criticality models (29, 51, 53, 60). Meanwhile, the assumption of slowly changing origination rates is consistent with slow sorting of large clades that have distinctive turnover rates (32), whereas adding a high-frequency random component to extinction rates is consistent with evidence that the Permo-Triassic and Cretaceous-Tertiary mass extinctions involved unpredictable physical forcing mechanisms (14). The overall scenario may seem restrictively complex, but at least complexity maximizes testability. Perhaps a simpler theory can be found that predicts the correlations, but even this moderately rich one fails to cleanly predict the apparent nonlinearity of the origination rate response to mass extinction (Fig. 3B vs. Fig. S5B).

Previous Studies.

Put together, these results combine to make a plausible and straightforward scenario. First, a major drop in diversity for any reason will be followed by a significant recovery due to the near-absence of extinction. Extinction rates may continue to be low for a second 11.0-Myr interval after the immediate recovery. Second, if the drop was due to a large extinction pulse and not merely an unfavorable balance of origination and extinction, then speciation rates will increase dramatically.

Earlier researchers have argued for entirely different models. For example, autocorrelation in Sepkoski's origination rates (49); apparently greater variation in extinction than origination (50); and, most importantly, a lagged correlation between extinction and subsequent origination in Sepkoski's family- and genus-level data (21) have been used to construct a theory that diversity is slow to rebound from extinction because time is required to reconstruct ecological niches that might be filled.

There are numerous problems with Sepkoski's data that call these results into question: the lack of any sampling standardization, the unavoidable backwards smearing of extinction rates and forward smearing of origination events that results from using simple range data (22), and the oversplitting of the time scale into 106 intervals (as opposed to 48 in this study). Not surprisingly, the first two hypothesized patterns do not exist in the current dataset: Origination rates lack any significant autocorrelation and are not much less variable than extinction rates (Figs. S1 and S2).

An extinction-origination correlation is indeed present, but the pattern is different from expected under the hypothesis that niches need to be reconstructed. First, very high origination rates come immediately after what are clearly rapid mass extinctions (Fig. 3B), not a full temporal bin later (21). Second, only the largest extinctions seem to boost immediately subsequent origination. If Kirchner and Weil (21, 49, 50) are right that niches need to be reconstructed, then recoveries should be slower and not faster after a large extinction, because the relevant ecological interactions are more highly disrupted. Thus, if niches are relevant, then speciation in the wake of mass extinctions is most likely fostered by the lack of competition for existing niches instead of being delayed by the elimination of old niches that need to be reconstructed.

Meanwhile, some support for a diversity/extinction relationship has been found in Sepkoski's datasets (1, 57). However, these results did not involve lagging, and Sepkoski's genus-level data provide mixed support for density dependence in both kinds of rates instead of just extinction rates (57). The consistency of the diversity-extinction relationship through the Phanerozoic (Fig. 3A) also is at odds with earlier analyses suggesting fundamental changes across the Permo-Triassic in ecology (14, 61) and especially diversity dynamics (57). The latter study found correlations between changes in diversity and changes in rates. The motivation for differencing the rates was to avoid biases and autocorrelation (57), but the current dataset uses rates with low bias that lack autocorrelation (Figs. S1 and S2), so differencing is moot. Again, biases related to sampling, counting, and rate equations are likely to be a problem in all of the earlier studies.

Recovery Predictions.

The two major correlational relationships (Fig. 3) are well constrained over a realistic range of diversity and turnover levels, making it reasonable to offer specific predictions about the recovery from the mass extinction that is clearly underway (47, 62). First, however, the relationships need to be modeled as accurately as possible, which requires transforming the data appropriately and then fitting linear regression functions.

The detrended diversity curve (Fig. S3) falls in such a narrow range that it is normally distributed on either a linear, log, or square root scale according to a Shapiro–Wilk test. However, logging diversity data is intuitive because diversification is a multiplicative process. For the detrended extinction rates, the raw data are far too skewed to be normal (P < 0.001), and taking square roots does not really help (P = 0.030). However, logging does render them normal, and the parametric correlation r between log diversity and log future extinction (0.462) is much the same as the rank-order correlation ρ (0.439). Like extinction rates, origination rates are too skewed to be normal (P = 0.011). Technically, logging does normalize them (P = 0.090), but the square root transform does a slightly better job (P = 0.455).

For the data starting after the earliest Ordovician, the median extinction rate is 0.380, and the diversity:extinction regression line is so strong that it implies a near-zero rate when diversity is 1 (i.e., the intrinsic rate). For example, at diversity levels 50, 90, and 99% below the median, the predicted extinction rates are 0.133, 0.014, and 0.0005, respectively. Thus, there would be hardly any extinction if not for major environmental perturbations and the ecological interactions that generate density dependence. Of course, that does not mean the rates are entirely predictable; it simply means that if abundant data were to extend all the way down to a diversity level of 1, we would find that density dependence explained a large majority of the variance. Indeed, the residual variance of the actual regression (Fig. 3A) is substantial and, therefore, likely to be real.

The second step is to model origination as a function of past extinction. However, origination rates cannot be predicted solely from the contemporary extinction rates produced in the first step without producing pathological results, because the initially low extinction rates would imply low, not high, origination rates. Instead, the extinction rates put into the equation need to reflect the entire loss of diversity relative to the starting point. The solution is to add the log ratio of preextinction diversity to current diversity to the predicted rate.

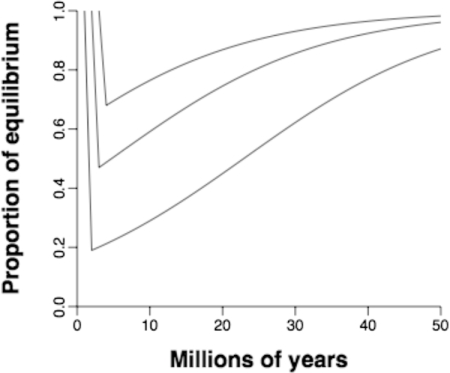
Put together, the two functions paint a grim picture (Fig. 4). A mass extinction on the scale of the Permo-Triassic event would probably leave diversity still 20% below its equilibrium level after ≈40 Myr, which is nearly as long as a typical geological period. Indeed, a comparable recovery from even the weakest modeled extinction is expected to take ≈10 Myr, and a 90% recovery would take ≈20 Myr. The worst-case scenario is not unthinkable for marine invertebrates: Any increase in global atmospheric CO₂ by >500 ppm would cause coral reef ecosystems to collapse (63), and, putting everything else aside, biotic homogenization through species introductions could cause up to a 58% mass extinction (64).

Fig. 4.

Predicted recoveries from mass extinctions modeled on the global Permo-Triassic and Cretaceous-Tertiary events (81% and 53% losses, respectively) and the early Pleistocene extinction in the Caribbean (32% loss) (67).

Origination rates do vary significantly from one 11.0-Myr bin to the next (Figs. 1A and 2A and Fig. S1A), so stochastically achieved high rates in a few bins could push diversity to its equilibrium much faster. Indeed, full recoveries seem to have taken place within the span of one bin after the end-Ordovician and Cretaceous-Tertiary mass extinctions (25). Nonetheless, a minimum 10-Myr recovery time is consistent with qualitative assessments of the pace of recovery in the geological record (14).

Discussion

The tests reported here show that diversity is constrained and provide direct evidence of the major mechanism. When diversity is high for any reason, extinction rates rise both in the same interval and the immediately following ones. When diversity is low because of a preceding major mass extinction, origination rates rise. Because the relationships are temporally offset, the direction of each causal relationship is clear. Extinction seems to be forced by some aspect of rising biodiversity, but the reverse is not true. Meanwhile, origination seems to be spurred by the emptying of many niches at once but origination bursts do not cause those niches to be emptied rapidly later on.

The only clearcut processes that could create such responses are ecological interactions, such as competition and predation, that affect the overall probability of speciation and extinction. Presumably, these interactions influence attributes of species, such as population size, population density, and geographic range size, that are not properties of individual organisms regardless of whether one wants to call them emergent or aggregate (65). Density dependence therefore may intensify differential reproduction of species based on traits that are likely to be heritable between species, again, regardless of whether one wishes to call this process species selection or sorting.

None of these results imply that density dependence is the sole governing mechanism of diversification. Quite the contrary, there is much variation left in both the diversity data and the turnover rates that might be explained by other factors, such as short-term perturbations [e.g., bolide impacts (28)] and longer-term changes in the environment [e.g., sea level (24, 34)]. The analyses also only pertain to genera common and widespread enough to be recovered in the fossil record, and the diversity of rare genera may be modulated by different mechanisms. Finally, a finer time scale might make it possible to demonstrate more complicated patterns, such as periodicity (6). However, the current number of data points should have been enough to demonstrate any biologically important patterns of this kind, and indeed it is sufficient to demonstrate the relationships leading to a dynamic equilibrium.

There are also dangers in misinterpreting the fact that diversity is regulated. On the one hand, the relevant correlations weaken considerably if the diversity data are not detrended. Thus, not only is the equilibrium dynamic, but the underlying equilibrium point evolves through time. On the other hand, the fact that a recovery in sheer taxonomic diversity will occur does not give cause for optimism about the current crisis. Any recovery will be unimaginably long on a human time scale and substantially protracted on a geological time scale. It also is clear that major mass extinctions in the past have led to enormous changes in taxonomic composition, trophic diversity, and body mass distributions that have effects for not merely tens of millions but hundreds of millions of years (2, 36, 46, 66–68). Finally, the numerous anthropogenic causes of today's mass extinction are deeply unrelated to the known causes of earlier ones, so we may never be able to predict much more about the next geological era beyond the general pace of recovery in numerical terms.

Materials and Methods

The data consist of genus counts for 48 intervals, averaging 11.0 Myr and ranging from the traditional Early Cambrian through the Neogene. These temporal bins sometimes correspond to marine stages, but often comprise sets of neighboring stages lumped to minimize variance in duration. The counts are derived from 281,491 occurrences of 18,541 genera within 42,627 fossil collections that have been sampling standardized by randomly drawing entire collections up to a quota of 15,800 specimens per bin. When the specimen count for an individual collection is not directly available, it is estimated from the occurrence count by examining rarefaction patterns for other collections in the same bin. Each collection's sampling probability is inversely weighted by its specimen count to avoid having a few large collections from a narrow range of environments and geographic areas dominate the analysis. Collections from entirely unlithified sediments are excluded. Details concerning the data and methods are reported in ref. 25.

A large number of equations have been proposed to quantify origination and extinction, using paleontological data (26, 27). Traditional measures consisted of simple first and last appearance counts that sometimes were divided by some form of a diversity count to create a proportion. Proportions are biologically meaningful if they describe a sudden turnover event, but a more realistic general approach is to view turnover as an exponential decay process (69) and, therefore, compute instantaneous rates that are equivalent to decay constants (23, 57, 66, 70).

The problem with all existing equations is that they were developed to handle traditional compilations that only record first and last appearances. Simple range data are subject to edge effects, such as the Signor–Lipps effect and Pull of the Recent, that create systematic smearing of rates backwards before a large extinction begins, smearing of rates forward after a burst of origination, and drops in extinction rates before a large sampling spike such as the Recent (23). For example, backwards smearing is clearly visible in family-level data on both marine and continental organisms (13), and the Pull of the Recent seems to amplify the downward trend in Sepkoski's genus-level extinction rates (23, 34).

Two new continuous rate equations (71) (Fig. S4) remove the edge effects by ignoring ranges and focusing instead on occurrence data that show which fossil taxa are actually sampled in which time intervals. These methods are only made possible by the existence of occurrence-based relational databases, and could not have been applied to the Phanerozoic marine record before the development of the Paleobiology Database (7).

The new rates depend on five fundamental counts: taxa sampled at all in a focal bin (N_s), taxa sampled in a bin but not immediately before or after (one-timers, or ¹t), taxa sampled immediately before and within the ith bin (two-timers, or ²t_i) or within and immediately after the ith bin (²t_i+1), taxa sampled in three consecutive bins (three-timers, or ³t), and taxa sampled before and after but not within a bin (part-timers, or ^Pt). The overall sampling probability P_s is just ³t/(³t + ^pt), where ³t and ^Pt are summed across the entire dataset.

The measures primarily used in this article are called three-timer rates (71). The three-timer extinction rate μ is log(²t_i/³t) + log(P_s), which expresses the exponential decay rate of a cohort crossing the base of a bin and continuing to its top, corrected for the fact that members of this cohort may be present but not sampled in the following (third) bin. The corresponding origination rate λ is log(²t_i+1/³t) + log(P_s). The same counts can be rearranged to compute a three-timer-based estimate of the extinction proportion, 1 − ³t/(P_s²t_i). Turnover rates for the first and last intervals in the time series cannot be computed because of the structure of these equations.

These expressions assume that sampling standardization has succeeded, so P_s is uniform across all intervals, and that P_s is not systematically correlated with μ or λ. It might be if high turnover makes it harder to sample taxa in a cohort that actually originated in the immediately preceding bin (for μ) or succeeding bin (for λ). However, it can be shown by simulation that this problem is not substantial over a reasonable range of turnover rates.

Nonetheless, P_s is never completely uniform. Therefore, it is better to use separately computed values for the relevant bins. To obtain μ one uses the sampling probability for the third bin (P_s,i+1), and to obtain λ one uses the probability for the first bin (P_s,i−1). The corrected formulas log(²t_i/³t) + log(P_s,i+1) and log(²t_i+1/³t) + log(P_s,i−1) are used throughout the main analyses. This correction decreases the volatility of the turnover rates. Volatility can be quantified by averaging changes in rates between bins, i.e., for extinction taking the mean of abs(log[μ_i+1/μ_i]). The volatility of extinction drops from 0.778 to 0.707 with the correction, and that of origination drops from 0.824 to 0.511. Likewise, N_s is systematically related to P_s,i, and the similar correction p_sN_s/P_s,i decreases the volatility of the diversity curve from 0.207 to 0.179.