The Role of Y94 in Proton and Hydride Transfers Catalyzed by Thymidylate Synthase

Abstract

Thymidylate synthase (TS) catalyzes the substitution of a carbon-bound proton in a uracil base by a methyl group to yield thymine in the de novo biosynthesis of this DNA base. The enzymatic mechanism involves making and breaking several covalent bonds. Traditionally, a conserved tyrosine (Y94 in E. coli, Y146 in L. casei, and Y135 in human) was assumed to serve as the general base catalyzing the proton abstraction. That assumption was examined here by comparing the nature of the proton abstraction using wild type (wt) E. coli TS (ecTS) and its Y94F mutant (with a two orders of magnitude reduced turnover rate). A subsequent hydride transfer was also studied using the wt and Y94F. The physical nature of both H-transfer steps was examined by determining intrinsic kinetic isotope effects (KIEs). Surprisingly, the findings did not suggest a direct role for Y94 in the proton abstraction step. The effect of this mutation on the subsequent hydride transfer was examined by a comparison of the temperature dependency of the intrinsic KIE on both the wt and the mutant. The intrinsic KIEs for Y94F at physiological temperatures were slightly smaller than for wt, but otherwise, were as temperature independent, suggesting a perfectly pre-organized reaction coordinate for both enzymes. At reduced temperature, however, the KIE for the mutant increased with decreasing temperature, indicating a poorly pre-organized reaction coordinate. Other kinetic and structural properties were also compared and the findings suggested that Y94 is part of a H-bond network that plays a critical role at a step between the proton and the hydride transfers, presumably the dissociation of H₄folate from the covalently bound intermediate. The possibility that no single residue serves as the general base in question, but rather, that the whole network of H-bonds at the active site catalyzes proton abstraction, is discussed.

Thymidylate synthase (TS) catalyzes the reductive methylation of 2’-deoxyuridylate (dUMP) with 5,10-methylene−5, 6, 7, 8-tetrahydrofolate (CH₂H₄folate), forming thymidine monophosphate (dTMP) and 7, 8-dihydrofolate (H₂folate) (1). TS activity is essential to living organisms since it catalyzes the de novo synthesis of one of the DNA building blocks. Consequently, TS is a common target in cancer chemotherapy, antibiotic drugs, and gene therapy (2, 3). The TS-catalyzed reaction has been elucidated in detail by a wide variety of kinetic, genetic, and structural methodologies (1, 4–6), which have shown that TS is a homo-dimer utilizing a half-of-the-sites-activity mechanism (7, 8). Steady state measurements indicated a bi-bi ordered mechanism with substrate (dUMP) binding before the CH₂H₄folate (4, 9). Kinetic and structural studies identified coherent protein motion that appear coupled to a hydride transfer step (10, 11), which is rate limiting for the wt TS.

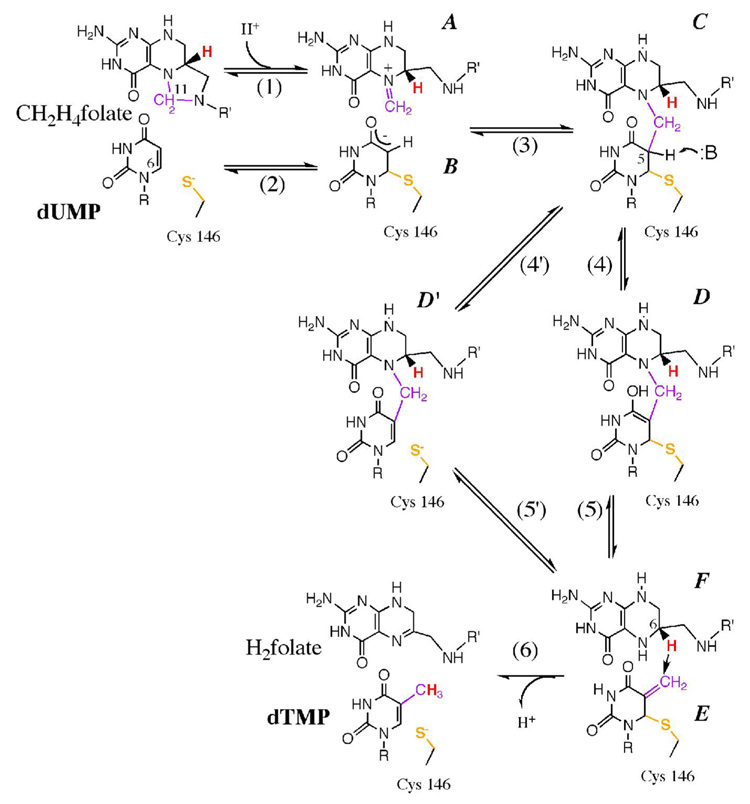
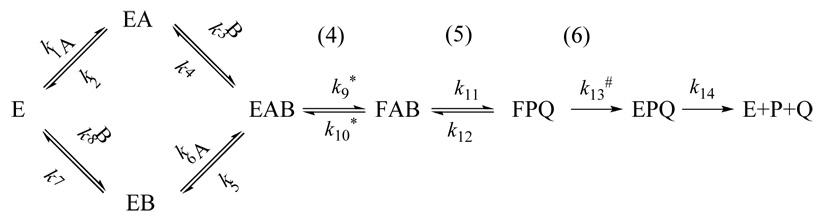
Scheme 1 illustrates the two main variations proposed for the chemical mechanisms along the complex cascade of TS catalysis. In the traditional proposed mechanism (1, 4), E58 assists in the formation of an iminium ion (A in scheme 1), which is is subjected to nucleophilic attack by the C5 enolate of the C146-activated dUMP (12) to form a ternary intermediate (C). A proton is then abstracted from C5 of dUMP to form the enol D (step 4) (4). This is followed by the release of H₄folate from the ternary complex (step 5, E1CB mechanism) (13) to generate the exocyclic methylene intermediate (E). Finally, the product dTMP is formed in step 6 by hydride transfer from (6S)-H₄folate to the exocyclic methylene of the enzyme-bound nucleotide via a 1,3-S_N2 mechanism. Several experimental studies indicate that this last step is the overall rate limiting step for both first order rate constant, k_cat, and second order rate constant, k_cat/K_M (depicted below as V/K) (10, 14, 15). Recently, QM/MM calculations (16) suggested an alternative path with lower activation energies. In the new path, the keto-enol tautomerization at C4 of dUMP plays a minor role while the labile C6-S-Cys bond plays a major role. The differences from the traditional mechanism are: (i) Steps 2 and 3 occur concertedly; (ii) The abstraction of the proton from the C5 of dUMP involves E2 elimination of C146 (step 4’), and (iii) The dissociation of CH₂H₄folate occurs via 1,3-S_N2 substitution with thiolate of C146 as the nucleophile and N5 of H₄folate as the leaving group (step 5’).

Scheme 1.

The proposed chemical mechanisms of the TS catalyzed reaction.

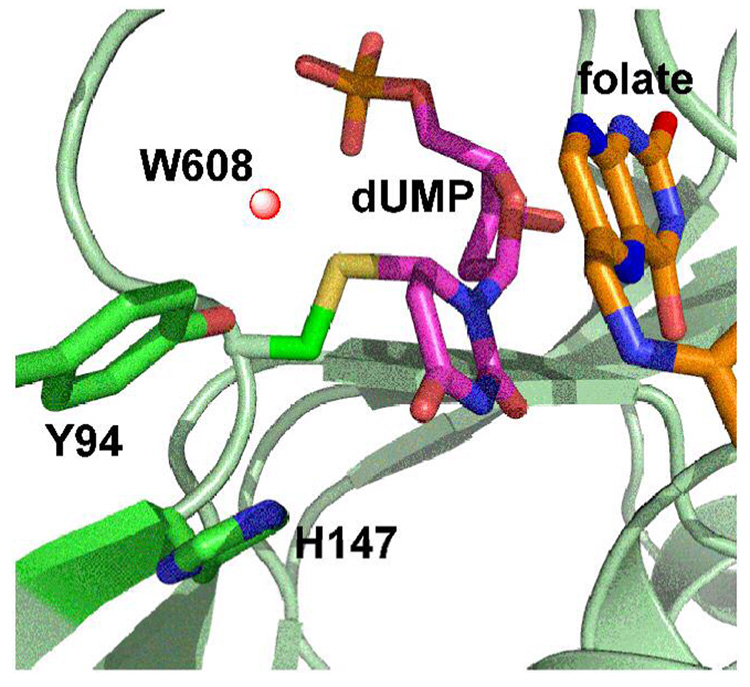
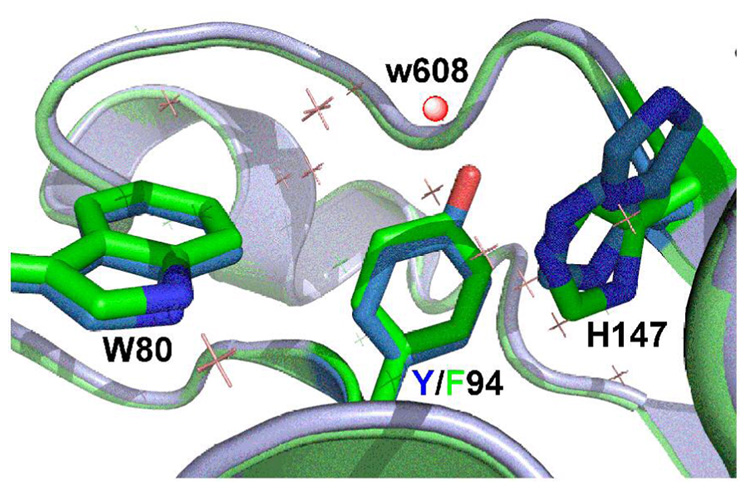
The proton abstraction from position 5 of the pyrimidine ring is crucial in the breakdown of the ternary intermediate and is the focus of this work. The general base in the active site has been proposed to be Y94 (see ref (4) and many cited therein). Figure 1 presents the crystal structure of the wt E. coli TS with covalently bound dUMP and non-covalently bound folate analogue at the active site (PDB # 2KCE). The water molecule (W608) is located 2.6 Å from the oxygen of Y94 and 3.6 Å from the C5 of dUMP, and was assumed to serve as the initial acceptor of the abstracted proton in step 5 (4, 13, 17–19). Hardy et al. (20) proposed that the general base in step 4 is N5 of the H₄folate through an “H-wire”, using water as conduit. Mutagenesis studies (19) demonstrated that several modifications of Y94 lead to loss of activity. This fact was interpreted as support of a mechanism in which Y94 assists in the proton abstraction. These issues are further examined in the current paper.

Figure 1.

Structure of wt E. coli TS covalently bound to dUMP (PDB code 2KCE) with Y94 and H147 highlighted in green, the water molecule closest to the Y94 (1.7 Å) and to C5 of the dUMP is highlighted as a red ball, the dUMP in magenta is covalently bound to C146, and the pterin ring is in orange.

Another interesting feature of the current work is that no isotope effects have been measured on the C5-H bond cleavage, which is not a rate limiting step for any measurable rate constant. Previous measurements monitored the ratio of ³H to ¹⁴C using [2-¹⁴C, 5-³H] dUMP as a substrate with a saturating CH₂H₄folate concentration and reported no KIE (unity) or even a slightly inverse KIE (4). The reason for the inverse KIEs is likely to be a fast and reversible exchange of the C5 proton through steps 1–4, prior to the irreversible and rate limiting hydride transfer in step 6. Furthermore, the high concentration of CH₂H₄folate, which binds after dUMP binds (4, 5), would mask a possible intrinsic KIE if the isotopic label is on the substrate (20–24). In the current work, the KIEs on this proton abstraction were studied as a function of the concentration of CH₂H₄folate in combination with the Northrop method (25–28). The observed KIEs versus the CH₂H₄folate concentration clearly indicated a kinetic mechanism with ordered substrate binding for the wt and less ordered binding for Y94F. A comparison of the intrinsic KIEs of the mutant and the wt served as a probe for the role of Y94 in this step.

Additionally, we investigated the effect of altering the hydrogen bond network at the active site by Y94F mutation and the nature of another chemical transformation remote from Y94, namely the hydride transfer (step 6 in scheme 1). The comparison of the temperature dependency of the intrinsic KIEs and activation parameters of Y94F with that of wt (10) indicated a minor effect of this mutation at physiological temperature, but a substantial distortion of the reaction’s pre-organization at reduced temperature. Together, the examination of the effect of Y94F on the proton abstraction (step 4 or 4’) and on the hydride transfer (step 6) indicated that a more likely role of Y94 is in the protonation of the N5 of H₄folate (the leaving group in step 5 or 5’), as discussed in detail below.

MATERIALS AND METHODS

Materials

[2-¹⁴C] dUMP (specific radioactivity 52 Ci/mol) and [5-³H] dUMP (specific radioactivity 13.6 Ci/mmol) were from Moravek Biochemicals. [²H] NaBH₄ (> 99.5% D) was from Cambridge Isotopes. [³H] NaBH₄ (15 Ci/mmol) was from American Radiolabeled Chemicals. Dihydrofolate (H₂folate) was synthesized following the procedure of Blakley (29). [2-³H] iPrOH was prepared by reduction of acetone with [³H] NaBH₄ (specific radioactivity of 15 Ci/mmol) as described in detail elsewhere (30). All other materials were purchased from Sigma.

Synthesis of [2- ¹⁴C, 5-D] dUMP (> 99.5% D)

[2- ¹⁴C, 5-D] dUMP was prepared by modifying the method of Wataya and Hayatsu (31–33) using L-cysteine in D₂O to catalyze H to D exchange at the C5 position of [2-¹⁴C] dUMP. The reaction was conducted by incubation of [2-¹⁴C] dUMP (~1mM and 52mCi/mmol) in a D₂O solution (> 99.9% D) containing 1 M of l-cysteine at 37°C and a pD of 8.8 for 7 days. The reaction was carried to completion as determined by ¹H NMR.

Synthesis of Isotopically C6 Labeled CH₂H₄folate for Measurement of KIE on Hydride Transfer

The synthesis of (R)-[6-³H] CH₂H₄folate was performed through a combination of two enzymatic reactions as described previously (30). Briefly, [2-³H]iPrOH was prepared by reduction of acetone with [³H]NaBH₄. NADP⁺ was reduced by [2-³H]iPrOH to (R) –[4-³H] NADPH by alcohol dehydrogenase from Thermoanaerobium brockii (tbADH). DHFR catalyzed the in situ conversion of H₂folate to (S)-[6-³H] H₄folate using (R) –[4-³H] NADPH and then the isotopically labeled H₄folate was converted to (R)-[6-³H] CH₂H₄folate upon quenching with formaldehyde. Similarly, the mixture of (R)-[6-³H] CH₂H₄folate and (R)-[6-²H]- CH₂H₄folate for the D/T KIE measurement was synthesized under same condition with the mixture of D- and T- labeled isopropanols. The radioactively labeled CH₂H₄folate was purified by reverse phase HPLC, lyophilized and stored at −80 °C prior to use.

Enzyme

Wild-type E. coli TS was prepared and purified according to the procedure of ref (34). Y94F was prepared and purified as described in detail elsewhere (6, 13, 19). The mutant was stored as ammonium sulfate pellets at −80 °C and prior to use, was dissolved and dialyzed against a mixture of 25 mM potassium phosphate, 10% ethylene glycol and 2 mM DTT. tbADH was purchased from Sigma.

Methods

Competitive and Intrinsic Primary Kinetic Isotope Effect (1 °KIE) for C5 Proton Abstraction

The 1° KIEs on proton abstraction from the 5 position of the dUMP were measured competitively. The reaction mixture contained 50 mM β-mercaptoethanol, 1 mM EDTA and 5 mM formaldehyde in 100 mM Tris buffer (pH 7.5). Prior to kinetic assay, 1.5 Mdpm [5-³H] dUMP, 0.5 Mdpm of [2-¹⁴C] dUMP and varied concentrations of CH₂H₄folate (2 µM to1000 µM) were added to the buffer mixture at 25 °C. The reaction was initiated by adding enzyme (wt or Y94F TS). Five aliquots of 100 µL were removed at different time points (t), quenched with 30 µM 5-fluoro-2’-deoxyuridine-5’-monophosphate (F-dUMP, a nM inhibitor of TS). Then, a concentrated solution of wt TS was added to the reaction mixture to a final concentration of 0.1 mM, followed by 10 more minutes of incubation to complete the reaction (t∞). Two t₀s (reaction mixture prior to adding enzyme and used as control) and three t∞s were obtained for each experiment and independent experiments were performed in triplicate. All the quenched samples were stored in dry ice before HPLC analysis. The method of RP HPLC separation and liquid scintillation counter (LSC) analysis of the ³H/¹⁴C ratio is described in detail elsewhere (30).

The competitive observed KIEs on the second order rate constant V/K were determined using the following equation (35):

$$\mathit{\text{KIE}}=\frac{\text{ln}(1-f)}{\text{ln}\left(1-f·\frac{R_t}{R_{\infty }}\right)}$$ [1]

where f is the fractional conversion to product dTMP (typically ranging from 20 to 80 %), R_t and R∞ are ratio of ³H/¹⁴C in products (water and dTMP) at each time point and time infinity. The fractional conversion f was calculated by:

$$f=\frac{[{}^{14}C]\mathit{\text{dTMP}}}{[{}^{14}C]\mathit{\text{dTMP}}+[{}^{14}C]\mathit{\text{dUMP}}}$$ [2]

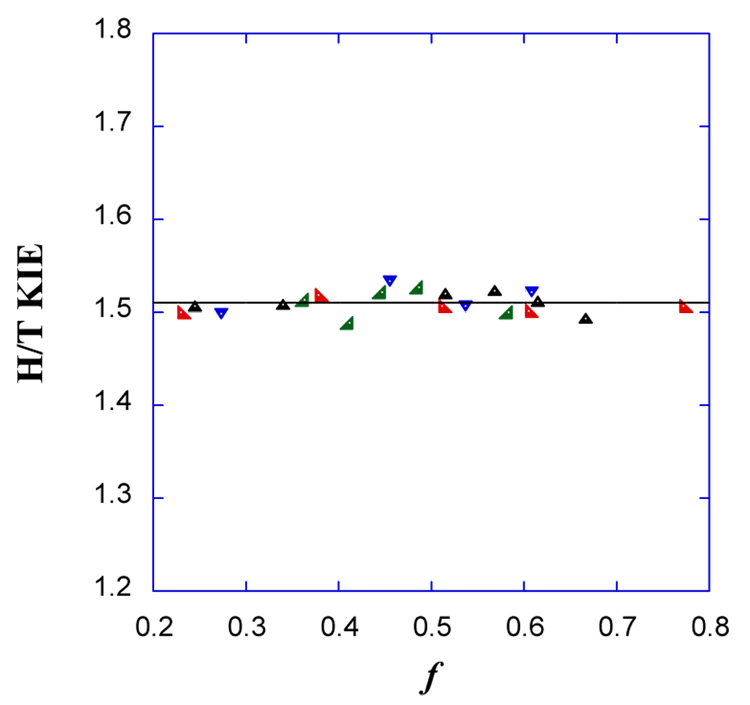
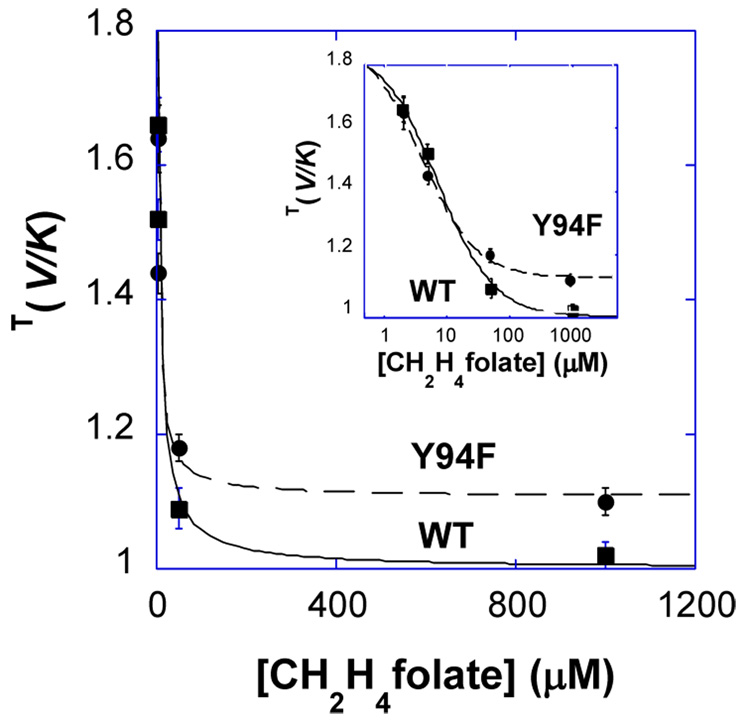
Figure 2 presents an example of measured H/T KIEs as function of f. Since the KIE on the proton abstraction has not been measured before, it is important to demonstrate that the KIE is reproducible in a series of independent experiments and that there is no upward or downward trends in the KIE as function of f.^* Figure 3 presents the observed H/T KIEs of the mutant and the wt as a function of CH₂H₄folate concentration. The analysis of the observed KIEs on the proton abstraction as function of CH₂H₄folate is presented under Results and Discussion.

Figure 2.

H/T KIEs as function of fractional conversion as measured for wt TS at 25 °C in 5 µM CH₂H₄folate. The different colors and shapes represent points measured in four independent experiments. The average value is 1.52 ± 0.03 and no upward or downward trend is observed within statistical error.

Figure 3.

H/T KIE for proton abstraction as a function of CH₂H₄folate concentration. Data with Y94F (circles) and with wt (squares) are compared. Solid and dashed lines are fits to Eq. 6 for the wt and the Y94F, respectively.

To determine the intrinsic KIE for this step, 5 µM CH₂H₄folate was used to measure the observed H/T and D/T KIEs. The observed D/T KIE was measured using the exact same conditions as that for the H/T KIE except the [2-¹⁴C] dUMP was replaced by [2-¹⁴C, 5-D] dUMP. So, the ¹⁴C now represents the D-transfer rather than H-transfer. Intrinsic KIEs are calculated from equation 3, (25–28):

$$\frac{{}^T(V/K)_{\mathit{\text{H obs}}}^{-1}-1}{{}^T(V/K)_{\mathit{\text{D obs}}}^{-1}-1}=\frac{k_T/k_H-1}{{\left(k_T/k_H\right)}^{1/3.34}-1}$$ [3]

where ^T(V/K)_{H, obs} and ^T(V/K)_{D, obs} are the observed competitive H/T and D/T KIEs; k_T/k_H represents the reciprocal of k_H/k_T (intrinsic H/T KIE). Although the intrinsic H/T KIE is the only unknown in this equation, it cannot be solved analytically. Therefore, a program has been developed to solve this equation numerically (now available free of charge at: http://cricket.chem.uiowa.edu/~kohen/tools.html). Since error propagations in this case cannot be conducted analytically from derivatization of Eq. 3, the intrinsic KIEs were analyzed by calculation the intrinsic KIEs from independent and random combinations of observed H/T and D/T KIEs (36). The Northrop method for a reversible step assumes ^TK_eq close to unity (25–27). We measured the ^DK_eq using the Cys activated dUMP as model compound for intermediate C in Scheme 1 (as described in the following item), and found it to be unity within experimental error. Additionally, the ^TK_eq for the proton abstraction can be estimated to be close to unity from fractionation factors for protons bound to similar carbons, and the fractionation factor in the product water molecule being unity since water is the reference system (37). Finally, since the reverse step in question involves the competition of tritium and protons from water, as discussed below, even a larger EIE should have little effect on the outcome of the Northrop method.

Equilibrium Isotope Effect (EIE) on activated dUMP

To assess the EIE (^DK_eq) on the proton abstraction on C5 of dUMP, we used a model in which C6 is activated by high concentration of Cys in solution. The activated complex was allowed to exchange with 50 % H₂O/D₂O. Specifically, 270 mM dUMP and 1 M of l-cysteine were incubated in 50 % H₂O/D₂O (mol/mol) at 37 °C and a pH of 8.8 for 5, 7, and 9 days. The progress of the exchange reaction was monitored by ¹H-NMR until completion (no further change in H content at C5). For an accurate NMR examination, the samples were lyophilized and redissolved in pure D₂O at a pD of 1.5 (the exchange reaction does not proceed at this pD). Then, the ratio between the hydrogen on C6 (unexchangeable) and the one on C5 was determined by ¹H-NMR. The hydrogen on C3’ was used as integration reference of unity and the H6/H5 ratio was determined in quintuplets. The H5/H6 values were 0.510 (±0.008) /1.010 (±0.007) indicating ^DK_eq = 0.99 (±0.02) for the proton exchange with water. ^*.

Competitive and Intrinsic Primary Kinetic Isotope Effect (1 °KIE) on Hydride Transfer from C6 (Step 6 in Scheme 1)

The competitive H/T and D/T KIEs for the hydride transfer from the 6 position of CH₂H₄folate with Y94F mutant were measured using the same conditions as with the wt TS (10). In short, the reaction mixture contains 1.5 Mdpm tritiated R- [6 - ³H] CH₂H₄folate for the H/T KIE or deuterated R-[6-²H] CH₂H₄folate for the D/T KIE, respectively, 0.5 Mdpm [2-¹⁴C] dUMP, 50 mM β-mercaptoethanol, 1 mM EDTA and 5 mM of formaldehyde in 100 mM Tris buffer with a pH of 7.5 (adjusted at each experimental temperature). About 30 % molar excess of dUMP was used in the reaction mixture in order to ensure 100 % conversion of tritiated CH₂H₄folate at time infinity (essential for R∞-see below). The reaction mixture was pre-incubated at the respective experimental temperatures and initiated by adding Y94F. At five different time points, 100 µL aliquots were removed and quenched with 30 µM F-dUMP. Concentrated wt TS was added to the reaction mixture to achieve 100% conversion (t∞). Two t₀s (used as quality control) and three t∞s were obtained for each experiment and independent experiments were performed in at least duplicate. The competitive observed KIEs were determined by Eq. 1 and the fractional conversion f was determined from equation 4 (30):

$$f=\frac{[{}^{14}C]\mathit{\text{dTMP}}}{\left(100-{\%}_{\text{excess}}\right)·([{}^{14}C]\mathit{\text{dTMP}}+[{}^{14}C]\mathit{\text{dUMP}})}$$ [4]

where % excess = [(total ¹⁴C) − ([2- ¹⁴C] dTMP)∞]/(total ¹⁴C).

The intrinsic H/T and D/T KIEs are calculated from Eq. 3 with the error propagation processed in that same as was for the aforementioned proton abstraction step. The analysis of these data is described in Result and Discussion, below.

Steady-State Kinetics

The initial velocities were measured under steady state conditions in a buffer mixture containing 50 mM DTT, 5 mM formaldehyde, 1 mM EDTA, and 100 mM Tris with a pH of 7.5 (adjusted at each experimental temperature). The reaction was monitored by following the increase of absorbance at 340 nm upon conversion of CH₂H₄folate to H₂folate (Δε_340nm = 6.4 mM⁻¹cm⁻¹) (14). The individual reaction mixture was pre-equilibrated at experimental temperatures and initiated by adding enzyme. Each measurement was conducted at least in duplicate and the data were analyzed as described in Results and Discussions.

RESULTS AND DISSCUSSION

Structural Comparison

A recent X-ray crystallography study (38) examined the Y94F mutant at 1.6 Å and 2.0 Å resolution (without and with ligands, respectively). An overlap of crystal structures of the wt and the mutant (Figure 4) indicates a perfect overlap, including electron density for defined water molecules (r.m.s.d. = 0.014 Å (38)). The obvious exception is the lack of the hydroxyl at residue 94 and the water molecule that is hydrogen bonded to the OH group in the wt. In the wt enzyme, Y94 is part of a H-bond network containing water molecules, H147, C146, and N5 of H₄folate. In Y94F, there is no electron density at the locations of the mutated hydroxyl and water 608. It is suggested that delocalized water molecules now occupy that space. It is also apparent that H147 in the wt has more than one conformation (from partial electron density), while Y94F only adopts a single conformation. This is the most substantial effect on the whole network of H-bonding at the active site.

Figure 4.

wt TS (blue - PDB ID # 2FTQ) and Y94F (green - PDB ID # 2FTN) with Y/F94, W80, and H147 presented as sticks. The water molecule closest to the Y94 (w608, 2.6 Å from its O) is highlighted as red ball and is missing in the mutant. All other water molecule are marked by crosses and practically overlap for the wt and the mutant. See also Figure 3 in ref (38). Note that the two-fold orientation of H147 is only apparent in the wt (blue), but not in Y94F (green).

Proton Abstraction

The substrate dUMP, labeled with tritium at C5, is commonly used to measure the enzyme’s activity (4). The use of tritium release from [5-³H]-dUMP to measure the reaction rate relies on the assumption that there is no effective (observed) KIE on that step. This assumption is substantiated by the fact that the proton abstraction is not rate limiting in the overall reaction (4, 10) and by the ordered nature of the wt TS reaction. The intrinsic KIE of step 5 in Scheme 1 has never been measured before (to the best of our knowledge). Previous experiments that monitored the ³H/¹⁴C ratio in the mixture of [5-³H] dUMP and [2-¹⁴C] dUMP (4, 24), reported KIEs close to unity. This is probably due to the ordered binding mechanism of the wt TS (1) that “masked” the KIE when the labeling was on the dUMP that binds first (21, 39, 40). The relationship between the observed KIE on the second order rate constant ^T(V/K) and the KIE after the formation of the ternary complex (^Tk₉ in Scheme 2) is described in equation 6 (21, 27, 41):

$${}^T\left(V/K\right)=\frac{{}^{T}k_9+C_f+C_r^T{K}_{\mathit{\text{eq}}}}{1+C_f+C_r}$$ [6]

where k_ns are the microscopic rate constants for the kinetic steps described in Scheme 2, C_r is the reverse commitment, which in the case of the current experiments is close to zero. ^{* T}K_eq is the equilibrium isotope effect on the proton abstraction, which is expected to be close to unity.

Scheme 2.

Binding scheme for a sequential mechanism. In this case, A represents dUMP and B represents CH₂H₄folate. The relevant steps from Scheme 1 are presented in parenthesis. Rate constants that are isotopically sensitive in the proton abstraction experiments (using labeled dUMP) are marked with * and the one that is isotopically sensitive in the hydride transfer experiments (using labeled CH₂H₄folate) is marked with #.

The forward commitment C_f is described by equation 7:

$$C_f=\frac{k_9}{k_5+\frac{k_2{k}_4}{k_2+k_3[B]}}$$ [7]

where [B] is the concentration of the second substrate (CH₂H₄folate in this case). As apparent from Eq 6 and Eq 7, the observed ^T(V/K) is dependent on the concentration of B and its observed value can change between two finite values (C_f changes from k₉/k₅ to k₉/(k₅+ k₄) as [B] changes from infinity to zero). In contrast to the random mechanism, the C_f in an ordered mechanism in which A binds first follows:

$$C_f=\frac{k_9}{k_4}+\frac{k_3[B]}{k_2{k}_4}$$ [8]

In this case, the observed ^T(V/K) is dependent on the concentration of B and its observed value can change from unity (no KIE) to a finite value (C_f changes from infinity to k₉/k₄ as [B] changes from infinity to zero (21)).

In the current study, the observed KIEs on the proton abstraction from C5 of dUMP were measured as a function of the CH₂H₄folate concentration to ascertain the kinetic mechanism for wt TS and Y94F. Figure 3 presents the observed KIEs as a function of CH₂H₄folate concentration. The observation that the observed H/T KIE for the wt approaches unity at high concentration of CH₂H₄folate (1.02 ± 0.02 at 1 mM CH₂H₄folate) while Y94F goes to an asymptote at a finite value (1.10 ± 0.02) indicates that the wt binding mechanism is strictly ordered (within experimental error and in agreement with previous studies (1)), but that of the mutant is more random (21). Also, the observed KIEs for the wt and Y94F are similar at zero [B] (1.86 ± 0.10 and 1.96 ± 0.15, respectively; Figure 3). This last observation, together with the intrinsic KIEs (see below), indicates a similar commitment on ^T(V/K) for the wt and the mutant.

To access the intrinsic KIE on the proton transfer step, we measured the D/T KIE at a low CH₂H₄folate concentration and then assessed the intrinsic KIE using the Northrop method (25– 27). A concentration of 5 µM CH₂H₄folate was used to assure sufficient conversion of radioactive labeled dUMP on one hand, and large observed KIE values (small relative error) due to a small commitment on the other hand. The intrinsic H/T KIE on the proton abstraction for the wt and Y94F are practically the same (3.25 ± 0.31 and 3.17 ± 0.22, respectively, Table 1).^*

Table 1.

Kinetic isotope effect of the wild-type and Y94F TS on proton abstraction at 25 °C.

KIE	Wild Type	Y94F
T(V/K)Ha	1.52 ± 0.03	1.44 ± 0.03
T(V/K)Da	1.17 ± 0.01	1.15 ± 0.01
H/T KIEint	3.2 ± 0.2	3.2 ± 0.3
D/T KIEint	1.41 ± 0.03	1.42 ± 0.04
H/D KIEint	2.2 ± 0.1	2.3 ± 0.2

^aAt 5 µM CH₂H₄folate.

Summary of the proton abstraction step

(step 4 or 4’ in Scheme 1): An intrinsic KIE of the C5 proton abstraction from dUMP is determined here for the first time. The intrinsic KIEs for both the mutant and the wt are similar (^Tk ≈3.2) suggesting that the effect of Y94 mutation on this transformation was too small to be detected. Apparently, while the Y94F mutation reduced the order of binding by increasing the rate of dUMP release from the ternary complex (k₅), it did not affect the actual proton transfer step. As apparent from Figure 3, the level of kinetic complexity that masks the intrinsic KIE (^Tk₉) on the second order rate constant ^T(V/K) at zero CH₂H₄fole appears to be small and similar for both wt and the mutant (C ≈0.45).^#

The relatively small intrinsic KIE is in accordance with a pre-activated C5-H bond and an asymmetric transition state for this transformation (35). QM/MM calculations (via collaboration with Moliner and co-workers) are underway to quantitatively examine this observation.

Hydride Transfer

The intrinsic KIEs on the hydride transfer step (step 6 in Scheme 1) were measured and compared with the wt using CH₂H₄folate labeled with H, D, or T at its R-C6 position as described in ref (10). Since in this part, only the hydride was isotopically labeled, all the other kinetic steps are not isotopically sensitive and the kinetic equations used are not different from those used for any other system with a single isotopically sensitive step. Figure 5 shows both the temperature dependence of the observed and intrinsic KIEs of the wt and Y94F. The analysis of the temperature dependence of intrinsic KIEs proceeded by exponential fitting of the data to the Arrhenius equation for KIEs:

$$k_L/k_T=A_L/A_T\exp \left[\left(E_T-E_L\right)/\mathrm{R}\mathrm{T}\right]$$ [9]

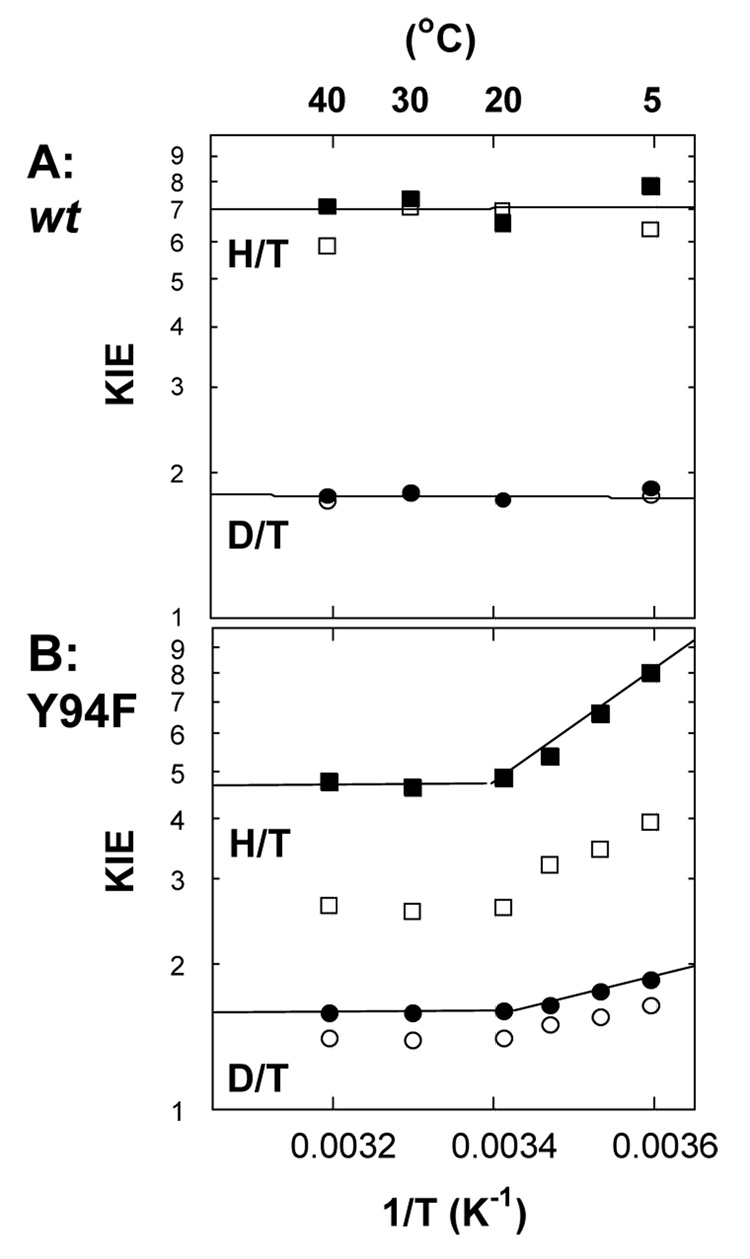
where k_L/k_T is L/T KIE with L representing the light isotopes, A_L/A_T is the isotope effect on preexponential factors, and E_T – E_L is the isotope effect on activation energy. The biphasic behavior of the intrinsic KIEs for the mutant (Figure 5B) suggested an intrinsic phase transition (42, 43) so the data were fitted at temperature ranges of 40 – 20 °C and 20 – 5 °C independently. Above 20 °C, the KIE was temperature independent (E_T -E_H = −0.03 ± 0.30 kcal/mol) and the ratio of the Arrhenius preexponential factors (Table 2) are well above the semiclassical values (44–46). At lower temperature range, the KIEs were temperature dependent and the KIE on the Arrhenius preexponential factors were inverse (A_H/A_T<1) and below the semi-classical limits (Table 2).

Figure 5.

Arrhenius plots of observed (empty structures) and intrinsic (filled structures) primary H/T KIEs (squares) and primary D/T KIEs (circles). The lines are the exponential fittings of the intrinsic KIEs to Eq. 5. A. wt. and B. Y94.

Table 2.

Rates and isotope effect on Arrhenius parameters of the wild-type and Y94F TS on hydride transfer^a.

	Wild typeb	Y94F		SC AL/ATc
	5 – 40 °C	5 – 20 °C	20 – 40 °C
AH/AT	6.9 ±1.0	0.0002 ±0.0001	4.5 ±0.5	0.5 –1.6
AD/AT	1.8 ±0.1	0.07 ±0.02	1.6 ±0.1	0.9 –1.2
ΔEaH-T	0.02 ±0.09	6.0 ±0.5	0.03 ±0.40
ΔEaD-T	0.01 ±0.02	1.8 ±0.2	0.06 ±0.12
Ea	4.0 ±0.3	6.2 ±0.3	3.1 ±0.1
ΔH‡	3.4 ±0.08	5.6 ±0.3	2.5 ±0.1
TΔS‡25°C	−13.7 ±0.7	−14.5 ±0.5	−17.6 ±0.7

^aAll energy units are kcal/mol.

^bFrom ref. (10).

^cSemi-classical limits of isotope effects on preexponential factor of Arrhenius equation.(35,45,46,53).

Whether the temperature dependence of the KIEs can be understood within the framework of tunneling correction to transition state theory (35, 45) depends on the assessment of the activation parameters on the reaction rate. To assess the activation parameters for the hydride transfer step at the high and low temperature ranges, it is necessary to extract the rates of that chemical step (k_hydride) at each temperature range. We used the method developed by Klinman and coworkers (47, 48):

$$k_{\mathit{\text{hydride}}}=\frac{k_{\mathit{\text{cat}}}\left({}^{D}k-1\right)}{{}^{D}k_{\mathit{\text{cat}}}-1}$$ [10]

where k_hydride is the unknown rate of the hydride transfer step; ^Dk is the intrinsic H/D KIE for this step at each temperature (see Figure 5B) and ^Dk_cat is the H/D KIE for k_cat using C6 labeled CH₂H₄folate. To assess the activation parameters for the two temperature regimes, k_cat was measured at 5, 20 and 40 °C, equation 10 was used to assess k_hydride (Table 3). The Arrhenius equation was used to calculate E_a for the physiological and the low temperature ranges (3.1 and 6.2 kcal/mol, respectively - Table 2).

Table 3.

Observed k_cat and ^Tk_cat used to assess the values of k_hydride at 5, 20, and 40 °C using Eq. 10^a.

wild typeb		Y94F
Temp. [°C]	kcat [s−1]	kcat [s−1]	Dkcat	khydride [s−1]
40	1.6	0.0067	2.24	0.0109
20	1.1	0.0055	2.36	0.0080
5	0.73	0.0023	4.20	0.0026

^aAll relative errors are under 2 % of the measured values and under 6 % of the calculated k_hydride.

^bFrom ref. (10).

The activation energy at the physiological temperature range, together with the temperature independent intrinsic KIEs suggested that, as with the wt, a Marcus-like model (46, 49–52) is needed to explain the findings for Y94F (10). In such a model, the rate for hydrogen tunneling arises from the combination of two terms: one is non-isotopically sensitive but determines most of the temperature dependence of the rates, and the other (depicted as the Franck-Condon term (49)) is isotopically sensitive and includes a tunneling contribution and classical fluctuations between donor and acceptor. The tunneling in such a model is dominated by the symmetry of the vibration levels (reorganization energy λ and driving force ΔG⁰, the referred to “rearrangement” term in Marcus theory) and by the fluctuations of the distance between donor and acceptor, referred to as “gating”) (49, 51). According to the Marcus-like model, lack of temperature dependence for both wt and Y94F at higher temperature range, indicates ideal prearrangement of the donor and acceptor prior to tunneling, which eliminates the effect of thermally activated “gating”. The comparison of Y94F to wt suggests that the hydride transfer for both proceeds with a similar “environmentally coupled tunneling” (50) at the physiological temperature range. However, at lower temperature, the increase of the Y94F activation energy relative to the wt (ΔE_{a Y94-wt} is about 2.8 kcal/mol) suggests a poorly pre-organized reaction coordinate and substantial need for “gating” (46, 49, 50).

Examination of the activation parameters in Table 2 results in an interesting observation: Most of the reduction in activity caused by the mutation appears to be on the entropy of activation (ΔTΔS^‡). The change in enthalpy of activation, ΔΔH^‡,was estimated to be 0.9 kcal/mol while -ΔTΔS‡ was about 3.9 kcal/mol at 25 °C. Similar results were also observed for mutants of dihydrofolate reductase (36), but it is not clear at this stage how general this phenomenon is. We hope that attracting the community’s attention to these observations will lead to more data collection addressing the effect of mutations on activation parameters, and maybe to a better rationalization of this phenomenon.

The relationship between the observed and intrinsic KIEs can be extracted from Eq. 6 (27, 46). At 20 °C, the observed H/T KIE on V/K of Y94F was measured to be 2.62 ± 0.01, while the intrinsic value is 4.86 ± 0.18, resulting in a commitment of 1.39 for the hydride transfer step. By contrast, the hydride transfer in the wt is commitment free (commitment close to zero) at room temperatures (10). The inflated commitment of the observed KIE on V/K for Y94F indicates that this hydride transfer step is no longer commitment free (rate limiting) and that a preceding step becomes rate limiting for this mutant.

Summary of the hydride transfer step

(step 6 in Scheme 1): The Y94F exhibits biphasic behavior, with temperature independent KIEs at physiological temperature and a steep temperature dependency under 20 °C (Figure 5). At physiological temperatures, the intrinsic KIEs were as temperature independent as the wt. This is in accordance with conservation of the internal dynamics and coupling of the environment to the hydride transfer step (46, 50), indicating only a minor role for the Y94 in step 6. At reduced temperature, the substantial temperature dependency of the KIEs with Y94F indicates a poorly pre-organized reaction coordinate and a need for thermal gating of the donor-acceptor distance (46, 50).

The phenomenon of intrinsic phase transition of this type has been previously reported for thermophilic enzymes (42, 43, 46) but not yet for a mesophilic enzyme. A possible explanation for the phase transition at 20 °C for Y94F (Figure 5) is that the removal of the “anchored” Tyr 94 hydroxyl and the lack of localization of the water molecule closest to C5 of dUMP (red ball in Figure 4) disrupts the H-bond network at the active site. This, in turn, may alter the structural and dynamic properties of that network (which serves as the acceptor for the C5 proton), leading to a poorly preorganized reaction coordinate and a longer effective donor-acceptor distance at reduced temperature (46, 50).

Kinetic analysis – Which step(s) is affected by the Y94F mutation?

Observations

1. Hydride transfer is rate limiting for both V/K and k_cat in wt (the commitments on both rate constants is close to zero). In contrast, for Y94F both k_cat and V/K for dUMP are masked (the observed KIEs are smaller than the intrinsic KIEs due to non-zero commitment). This indicates that the mutation affects a kinetic step that is part of both rate constants- e.g., the affected kinetic step is between the formation of the ternary complex and the first irreversible step. Specifically:

   1. For Y94F, the inflated commitment (relative to the wt) for the hydride transfer’s ^T(V/K) indicates that the step affected by mutation precedes the hydride transfer.

   2. For Y94F, there is a small difference in commitment for the second order rate constant ^T(V/K) of proton transfer, which indicates a small effect of mutation on the preceding steps, suggesting that most of the effect is after the proton abstraction.

2. The intrinsic KIEs for the proton transfer (using [5-³H]-dUMP) are the same for wt and Y94F. This result suggests that the mutation does not affect the proton abstraction step per sé.

3. The K_M for dUMP is not affected by mutation but the K_M for CH₂H₄folate is increased (19). This is in accordance with random binding for the mutant, which is proposed here based on the dependence of the observed KIEs for proton abstraction as function of CH₂H₄folate concentration.

4. Santi, D.V., Schultz P.G. and co-workers (19) examined relevant mutants (Y146 in L. casei TS) as catalysts for CH₂H₄folate-independent dehalogenation of [5-Br]-dUMP, a reaction which simulates early steps of the normal pathway up to and including enzyme-nucleotide covalent adduct formation. Many of these mutants had activity comparable to the wild-type enzyme, indicating that the effects of the mutations occur after the initial covalent adduct is formed.

Interpretation

The effect of the mutation on steps that precede the formation of the ternary complex and proton abstraction is small, and mostly reflects the reduced binding capacity of dUMP (larger k₅ in Scheme 2). Most of the effect is on a step(s) that take place between the two H-transfer steps, specifically steps 5 or 5’ in Scheme 1. Possible events that may occur along step 5 are deprotonation of the enolate in C4 and/or protonation of N5 of the H₄folate leaving group. Possible events that may occur along step 5’ are deprotonation of the thiol (if protonated during the elimination step 4’) and/or protonation of N5 of the H₄folate leaving group.

CONCLUSIONS

A new insight into the chemical mechanism of the thymidylate synthase catalyzed reaction is presented. Many studies have proposed that a conserved active site tyrosine (Y94 in ecTS) serves as a general base that enhances proton abstraction during the elimination of H₄folate (step 4 in Scheme 1; for review see ref (4)). The effect of the Y94F mutation on two distinct chemical steps has been examined. These steps were the proton abstraction step (step 4 in Scheme 1) and the hydride transfer step (step 6 in Scheme 1). The findings indicate that the proposed tyrosine (Y94, 3.6 Å from the proton donor) is not the main contributor to the proton abstraction step, but rather the whole network of H-bonds at the active site appears to serve as the general base. This conclusion is in accordance with the proposal of Hardy and coworkers (20) who used 5-deazatetrahydrofolate and concluded that N5 of H₄folate contributes to this general base. Additional candidates away from C5 are the imidazole and carboxylate side chains of H147 (5–6 Å) and E58 (~7 Å). Out of these we prefer the closer and more basic imidazole group. Future work will examine the H147V mutant and the wt TS from B. subtilis, which has a Val rather than His in that position. It is of course possible that no single functional group exclusively constitutes the general base, but all three contribute to the basicity of the initial proton acceptor (a water oxygen).

What accounts for the two order of magnitude decrease in Y94F activity relative to the wt TS? Taken together, the findings suggest that at physiological temperature the step most affected by the mutation occurs after the proton abstraction and prior to the hydride transfer. According to the mechanism illustrated in Scheme 1, these are likely to be step 5 or step 5’, specifically the protonation of N5 of H₄folate (in both paths) or the deprotonation of the enol in step 5. Additionally, the mutation weakens the binding and enhances the release of dUMP, which results in a random binding sequence (Scheme 2). QM/MM calculations comparing this mutant to the wt (16) are underway and may offer a molecular insight into the findings reported here.

1. Abbreviations and Textual footnotes

TS

thymidylate synthase

KIE

kinetic isotope effect

RP HPLC

Reverse Phase High Pressure Liquid Chromatography

LSC

Liquid Scintillation Counter

dUMP

5-FdUMP 5-fluoro- 2’-deoxyuridine-5’-monophosphate; 2’-deoxyuridine-5’-monophosphate

dTMP

2’-deoxythymidine-5’-monophosphate

CH₂H₄folate

N⁵, N¹⁰-methylene 5,6,7,8 tetrahydrofolate

H₂folate

7,8-dihydrofolate

H₄folate

5,6,7,8-tetrahydrofolate