Abstract
NMR spin relaxation retains a central role in the characterization of the fast internal motion of proteins and their complexes. Knowledge of the distribution and amplitude of the motion of amino acid side chains is critical for the interpretation of the so-called dynamical proxy for the residual conformational entropy of proteins, which can potentially significantly contribute to the entropy of protein function. A popular treatment of NMR relaxation phenomena in macromolecules dissolved in liquids is the so-called model-free approach of Lipari and Szabo. The robustness of the mode-free approach has recently been strongly criticized and the remarkable range and structural context of the internal motion of proteins, characterized by such NMR relaxation techniques, attributed to artifacts arising from the model-free treatment, particularly with respect to the symmetry of the underlying motion. We develop an objective quantification of both spatial and temporal asymmetry of motion and re-examine the foundation of the model-free treatment. Concerns regarding the robustness of the model-free approach to asymmetric motion appear to be generally unwarranted. The generalized order parameter is robustly recovered. The sensitivity of the model-free treatment to asymmetric motion is restricted to the effective correlation time, which is by definition a normalized quantity and not a true time constant and therefore of much less interest in this context. With renewed confidence in the model-free approach, we then examine the microscopic distribution of side chain motion in the complex between calcium-saturated calmodulin and the calmodulin-binding domain of the endothelial nitric oxide synthase. Deuterium relaxation is used to characterize the motion of methyl groups in the complex. A remarkable range of Lipari-Szabo model-free generalized order parameters are seen with little correlation with basic structural parameters such as the depth of burial. These results are contrasted with the homologous complex with the neuronal nitric oxide synthase calmodulin-binding domain, which has distinctly different thermodynamic origins for high affinity binding.
Keywords: Protein dynamics, conformational entropy, NMR relaxation, model-free, molecular recognition
Introduction
Over the past two decades NMR spectroscopy in the liquid state has emerged as a powerful probe of the internal dynamics of protein macromolecules.1 Its central position in the experimental characterization of amino acid side chain dynamics primarily arises from the establishment of methods to observe NMR relaxation phenomena in methyl groups.1 Deuterium relaxation, in particular, has proven particularly useful given the purity of relaxation mechanism and the availability of efficient isotopic enrichment schemes.2,3 Unfortunately, though the formal motional origins of NMR relaxation phenomena are clear, the relationship between what can be observed and the corresponding physical parameters underlying the motion is degenerate.1 Thus the question of what unique motional information can be extracted from NMR relaxation parameters dominated the early investigation of protein dynamics using NMR relaxation. A significant advance was the “model-free” (MF) treatment of Lipari and Szabo where, given a small number of reasonable assumptions, a particularly simple form of the spectral density function describing motion of the NMR probe could be employed with apparently high accuracy.4,5 The MF spectral density has been used in literally hundreds of studies of backbone motion 6, primarily via analysis of 15N relaxation, and in dozens of studies of side chain motion, primarily via analysis of carbon and deuterium relaxation in methyl groups.1 Recently this treatment has been challenged from several points of view by Freed and coworkers who reach the general conclusion that the model-free spectral density is inappropriate in many if not most cases and often results in counter-intuitive insights.7-11 In order to set the stage for analysis of deuterium relaxation data in calmodulin complexes, we re-examine the model-free approach with the issues raised by Freed and coworkers in mind.
In this work, we also examine the backbone and side chain motion in the complex between CaM and peptides corresponding to the calmodulin-binding domain of the endothelial nitric oxide synthase. A thermodynamic view of the dynamics seen in this and five other calmodulin complexes has revealed an provocative linear relationship between the total entropy of binding and the apparent change in conformational entropy of CaM derived from analysis of its dynamics.12 Here we explore the microscopic origins of the dynamical differences between this complex and that involving the neural isoform of NOS. The CaM-binding domains of nNOS and eNOS have a high degree of sequence conservation. Essentially identical binding affinities for CaM, and the enzymes they are derived from are functionally similar. However, the CaM:eNOSp complex formation is 25 kJ/mol more enthalpically-driven than that of CaM:nNOSp at 35 °C.12,13 We find that there are significant rearrangements of side chain order parameters and a change in the average dynamics (entropy) between the two CaM complexes despite the relatively high sequence similarity.
Experimental Methods
Samples
Human calmodulin was expressed and purified as previously described.14 For the 2H relaxation sample, Escherichia coli BL21(DES) cells were grown on minimal media containing 55% D2O and 45% H2O containing 15NH4Cl and D-glucose (U-13C6, 99%) as the sole nitrogen and carbon sources, respectively. For the backbone and side chain assignment sample, cells were grown on 100% H2O minimal media containing 15NH4Cl and unlabeled glucose. For the 15N relaxation sample, cells were grown on 100% H2O minimal media containing 15NH4Cl and unlabeled glucose.
A peptide corresponding to the calmodulin-binding domain of the endothelial nitric oxide synthase enzyme (RKKTFKEVANAVKISASLMG) was synthesized using solid phase methods and purified by reverse phase HPLC by Genscript. Peptide purity was determined by mass spectrophotometry. CaM:eNOSp complexes were formed by titration of ∼1 mM peptide in 20 μL aliquots into 250 μM CaM in buffer conditions 4 fold diluted with respect to those of the intact complex.15 The titrated sample was lyophilized and rehydrated with the appropriate volume of 92%:8% H2O:D2O. The CaM:eNOS stoichometery was 1:1.1. Final NMR sample conditions were 1 mM complex, 20 mM imidazole, pH 6.5, 100 mM KCl, 20 mM CaCl2 and 0.02% NaN3.
NMR Spectroscopy
All NMR data were collected at 35 °C on Varian Inova spectrometers operating at 1H Larmor frequencies of 600 and 500 MHz. Sequential assignments of the backbone 1H, 13Cα, 13Cβ, and 15N were obtained from gradient-enhanced CBCA(CO)NH and HNCACB spectra. 1613C and 1H resonances of the side chain methyl groups were assigned using C(CO)NH 17 and 3D-HCCH3-TOCSY 18 experiments. Stereospecific assignments for valine and leucine methyl groups were obtained using the trace 13C-glucose labeling strategy.19 Methionine methyl resonances were assigned using a two-dimensional HMBC experiment.20 NMR data were processed with Felix and assigned with Sparky.21
15N longitudinal (T1) and transverse (T2) relaxation time constants and the 15N nuclear Overhauser effects (NOE) were measured using experiments employing two-dimensional HSQC pulse sequences.22 Twelve time points ranging from 0.020 to 0.70 s (T1) and 7.8 to 124 ms (T2) were collected, three of which were duplicate. The RF field strength for 15N pulses was 6.6 kHz. A CPMG pulse spacing of 900 μs was employed for R2 measurements. Cross-peak intensities were used to quantify relaxation, and the uncertainties of these intensities were estimated either from duplicate measurements or the root-mean-square noise level of the spectrum base level. The relaxation parameters were measured at 11.7 T and 16.4 T. The dynamics of the side chain methyl groups in the protein complexes were investigated by measuring longitudinal (IzCzDz) and transverse (IzCzDy) relaxation rates of the 2H nucleus in 13CH2D isotopomers.3 The RF field strength for 2H hard pulses was 2.5 kHz and 1 kHz for spin locking. Contributions from relaxation mechanisms other than quadrupolar interactions were eliminated by correcting these rates for the decay of the IzCz coherence. A total of 11 time points (two of which were duplicate), ranging from 2.6 to 840 ms (IzCzDz), 0.9 to 26 ms (IzCzDy), and 8 to 220 ms (IzCz) were collected. 2H relaxation experiments were carried out at 11.7 T and 16.4 T.
Relaxation Data Analysis
Determination of dynamic parameters was accomplished by fitting the relaxation rates to the simple model free spectral density function4 with an in-house exhaustive grid search algorithm.23 The global rotational correlation time, τm, of 8.21 ns was first determined using 15N relaxation data of well-ordered residues assuming isotropic rotational diffusion. Residues were excluded if the NOE value was less than 0.65 or the T1T2 product exceeded one standard deviation from the mean.24 Subsequently, squared generalized order parameters and internal correlation times, τe, were fitted for all spectrally resolved residues. A chemical shift anisotropy tensor breadth of 170 ppm25 and an effective N-H bond distance of 1.04 Å ref. 26 were employed. Methyl squared generalized order parameters, , are reported after accounting for motion about the methyl symmetry axis, O2/0.111. A quadrupolar coupling constant of 167 kHz was used in the calculations.27 The reliability of determined model-free parameters was estimated with 150 Monte Carlo simulations.
Structural Property Calculations
Distance to a molecular surface were calculated with the GRASP program.28 To determine depth of burial, the solvent accessible protein surface was calculated by rolling a sphere of radius 1.4 Å over the van der Waals surface of the protein. Depth of burial was determined for individual sites by finding the shortest distance to this surface. Distances to the bound peptide were determined by calculating the molecular surface for the peptide and determining shortest distance to that surface. Electrostatic potential was determined using the Poisson-Boltzman solver in GRASP. Packing density was determined by subtraction of the van der Waals volume of the methyl group from the volume of the Vonoroi polyhedral. Packing density for surface exposed atoms (atoms without completed Vonoroi polyhedra) was determined by closing the polyhedra using a spherical surface 1 Å larger than that of the van der Waals surface of the atom. The solvent accessible surface area was determined using a rolling sphere with a radius of 1.4 Å.
Results
Theoretical Analysis
NMR relaxation observables are defined by linear combinations of spectral densities. In the case of the quadrupolar relaxation of deuterium, the Hamiltonian is a second-rank tensor that can be written in the laboratory frame as:
| (1) |
Where T2,m are the spherical tensors of rank 2 used to describe the spin components and F2,m(t) are employed to describe the time-dependent spatial fluctuations. The interaction constant CQ is defined as e2qQ / 4ћ where e is the elementary electronic charge, Q is the nuclear quadrupolar moment, q is the principle value of the electric gradient tensor, and I is the spin of the nucleus, which is equal to 1 for 2H. The standard density matrix formalism29,30 results in the expressions for deuterium relaxation parameters31 that are commonly measurable in protein systems.2,3 These include, for example, those to be used here:
| (2) |
The spectral density J(ω) is defined as the real Fourier transform of the autocorrelation function, C(t), which describes the time dependence of the interaction vector.
The MF treatment begins with the time dependence of the autocorrelation function. Two fundamental assumptions are made. The first is that the autocorrelation function can be factored into two components, one, Co(t), describing molecular reorientation and another describing internal motion within the molecular frame, CI(t) i.e.
| (3) |
This requires that macromolecular tumbling and internal motion not be correlated in microscopic detail. This is most often asserted by the separation of time scales though this is merely a sufficient but not necessary condition. The second critical assumption is that the internal correlation function can be approximated well by a simple exponential. The origin of this assumption is that if the motion is diffusive or jump-like without memory i.e. Markovian then the internal correlation function can be generally expressed as a weighted sum of exponentials:
| (4) |
It should be noted that even simple motions can lead to large numbers of terms contributing to the internal correlation function. This fact will become important shortly. The key step in the MF treatment is the approximation of the internal correlation function as a single exponential with a limiting value of O2, the square of the so-called generalized order parameter and the effective correlation time (τe) corresponding to its normalized integral i.e.
| (5) |
| (6) |
This leads to the MF definition of the internal correlation function:
| (7) |
Briefly, Lipari and Szabo pointed out that, in the limits of the integral defining the effective correlation time, the correlation function represented by Eq. 7 is exact. In this definition, there is no reference to the symmetry of the underlying motion. Freed and coworkers have repeatedly questioned the validity of the MF spectral density with the assertion that its utility is restricted to descriptions of axially symmetric motion only.7-10 This is incorrect as we will now show.
Validity of the MF treatment under highly asymmetric motion
The dynamics and NMR relaxation behavior of a model side chain were investigated using either a stochastic rotamer diffusion or rotamer jump model. With a small number of degrees of freedom, fully converged and fully sampled behavior could be established. A side chain with one to three torsional degrees of freedom was built with standard aliphatic carbon bond lengths (1.54 Å) and angles (104°). This is representative of side chain methyl/methylene dynamics of for example Ile and Met. Since bond lengths and angles are much stiffer than torsions, and so contribute little to the NMR dynamics, bond lengths and angles were considered to be fixed.
For the torsional diffusion model the motion occurred in a standard torsion 3-well cosine potential with minima at −60° (g), +60° (g+), and 180° (t) separated by a barrier height of Ub. An angular diffusion constant of 0.04 rad2/ps was used. This gives similar rotamer relaxation time/transition rates as those seen in molecular dynamics simulation. For the stochastic jump model, we define a transition probability per unit time, pij, i,j = 1,3 for jumping from rotamer i to rotamer j. The transition probabilities form a transition rate matrix Pij with ‘normalization’ conditions
| (8) |
and
| (9) |
The long time (equilibrium) population distribution ratio between two rotamers is
| (10) |
where fi is the fraction of the time the side chain is in the i'th rotamer, and f1+f2+f3 = 1. For meaningful stochastic simulations, the time step Δt must chosen such that all off diagonal Pij<<1. Using a time step of 1 ps, transition probabilities of the order of 0.01 give rotamer transition frequencies comparable to those seen in MD simulations of side chains with O2 of 0.1 to 0.8.
In a protein it is not unreasonable to expect that side chain dynamics can be greatly modified by local packing and H-bond interactions, and by longer range interactions. These can potentially affect both the rates motion and the equilibrium distribution of states of the side chains, and introduce considerable dynamic heterogeneity or asymmetry. By choosing appropriate values for the five independent values of pij so f1≠f2≠f3 we can model such asymmetric spatial motion and compare to more symmetric spatial motion (f1≈f2≈f3). We can also compare symmetric temporal motion (all transition rates of the same order of magnitude) with asymmetric temporal motion. For example, setting p13, p31, p23, and p32 to be an order of magnitude lower than p12, p21 transitions to/from rotamer 3 happen much more rarely than those between rotamers 1 and 2. Note however, that spatial asymmetry, as defined by the fi values, is controlled by the ratios pij/pji, so in the latter case, the long time occupancy of rotamer 3 may be chosen to be similar to rotamer 1, 2 occupancies or not, as desired. Thus the effect of the two types of motion asymmetry can be examined separately.
Spatial asymmetry is controlled through the values of fi. Choosing Pij such that f1 = f2 = f3 clearly produces symmetric motion where on the long time scale each rotamer is equally populated. As one or two rotamers become less populated than the third, the motion is less symmetric. However, going to the extreme case of f1 = f2 = 0, f3 = 1 results in symmetric motion again, indeed with maximal generalized order parameter, O = 1. Clearly some set of f1, f2, f3 values will produce maximally asymmetric motion, but to determine these values, we need an appropriate measure of asymmetry. This is now done in the context of the generalized order parameter.
Using either the diffusive or jump motion model a stochastic dynamics simulation is performed for several hundred times the longest time scale motion. This produces a time series for each bond vector. From a normalized C-C vector μ(t), the time correlation function4,5
| (11) |
is computed using fast Fourier transforms, where P2(x) = 3(x2-1)/2, and μ(τ+t).μ(τ) = cosθij, where θij is the angular movement of the bond vector between times ti = τ and tj = τ+t. From C(t), the squared generalized order parameter, O2, and relaxation time, τ, were obtained from the long time limit and decay constant by fitting to Eq. 7
Equation (7) is equivalent to the standard model used to reduce experimental NMR data, with the effect of molecular tumbling removed. If the simulation length is much greater than τ then O2 may be computed from the long time average of P2(μ(τ+t).μ(τ)) using32
| (12) |
where xi, yi, zi are the instantaneous Cartesian components of the bond vector at time ti and <> indicates the average over all configurations. Eq. (12) makes no assumption that the relaxation is single exponential, only that the total time of the simulation is much longer than the slowest relaxation time.
Using Eq. (12) for the g+, g-, t rotamer jump model, the analytical value of the order parameter O2, in the long time complete sampling limit may be obtained as
| (13) |
A is a constant (1-3/2sin2α)2 reflecting the fixed geometry for a bond angle α. We have also used the fact that torsion angles φ between these rotamers are all 120° so that cos(φ) = -0.5. fg-, fg+ and ft are the expected equilibrium probabilities of the three rotamers. These are obtained from the input transition probabilities as fg-/fg+= pg+g-/pg-g+ etc.
We now consider an appropriate definition of asymmetric motion for a side-chain undergoing torsional dynamics. Consider the motion of a bond vector undergoing torsional motion about an axis to which it makes a fixed angle α. For convenience we use a coordinate system with the axis aligned along the z-axis. The instantaneous components of the normalized bond vector μ are xi yi, and zi, and the average orientation of the bond vector is given by the normalized average vector
| (14) |
Note that <μ> need not coincide with the axis of rotation. Now if the motion about the axis is azimuthally symmetric then it can be shown that the generalized NMR order parameter may be obtained from
| (15) |
where cos θi = μi.<μ>, and now θi is the instantaneous angle the bond vector makes with its long time average position. This is in sharp distinction to the more general Eq. (11) which involves averages over the angle between two instantaneous positions after some elapsed time. This may be the source of apparent confusion in the literature. Conditions for azimuthal symmetry are that
| (16) |
So for example, equal occupancy of three or more equally spaced rotamers is azimuthally symmetric, and Eq. (15) gives the correct value for O. In contrast, equal occupancy of 2 equally spaced rotamers (φ=0, 180°) while bilaterally symmetric, is not azimuthally asymmetric. For this model with a bond angle α=104°, the correct value from Eqs. (12) or (13) is O2 = 0.834, while Eq. (15) gives = 0.169. We therefore take the difference between the correct and azimuthally symmetric expressions as the appropriate measure of the asymmetry of the motion with regard to NMR relaxation:
| (17) |
As far as we are aware, always underestimates the true value, so ΔO2 is positive. Physically, we can understand this as follows. The correct expression for the generalized order parameter involves an average over the time correlation of the vector with itself, and for short times this has contributions from small angular displacements θij, which contribute to larger values of O. Using the angle to the average vector underestimates the contribution of short time/small angles contributions to O. Consider the case of the 2 symmetric rotamers φ = 0, 180°. The bond will always have an angle of θI = α= 104° to the average direction, yet in the time correlation function, there will be samples with both θij=2α (the rotamer jumped during the time interval) and θij = 0° (the rotamer hasn't jumped yet).
For the g+, g-, t three rotamer jump model the rotamer population ratios fg-/ft and fg+/ft are the two free parameters that determine the spatial asymmetry of motion. A simple grid search from 0 to 1 determines the maximum asymmetry conditions to be given by ΔO2 = 0.398 at fg-/ft = 0 and fg+/ft = 0.6. The case fg-/ft = 0 and fg+/ft = 1 is close to maximally asymmetric, with ΔO2 = 0.374. A typical case described by this is an aliphatic side-chain with 3 possible rotamers in the unfolded state or in a peptide that has one rotamer quashed in the folded state. The loss of one rotamer produces a highly asymmetric spatial motion in regard to NMR relaxation.
Model sidechain dynamics
We first examined the effect of the number of accessible rotamers on the order parameter using the diffusion in a torsional potential well model.
Table 1 shows how the number of rotatable bonds prior to the methyl(ene) group affects the order parameter. With one bond and a modest barrier height of 1 kcal/mole the order parameter is O2 = 0.17. As the number of bonds is increased to two and then three, the order parameter drops drastically, more than five-fold per bond, as the number of accessible rotamers affecting the terminal C_C bond direction increases. This occurs even if the range of motion produced by a single torsion is quite restricted, and it is due to the 104° angle between successive axes of rotation. With just two rotatable bonds, assuming all 3 rotamers per bond are accessible O2 = 0.03, and the motion is effectively close to isotropic (or at least to free diffusion of the terminal C-C vector over a hemispherical cone). All the time correlation traces show the typical mono-exponential decay to a plateau value, subject to some noise due to the stochastic nature of the simulation. Importantly, O2 values are all close to the expected analytical values (Table 1). This type of behavior has also been seen experimentally on the polypeptide backbone in the free C-terminal residues of ubiquitin, for example.33 These results also serve to illustrate that even small motions can significantly reduce the generalized order parameter.
Table 1.
Robustness of the model-free spectral density
| Asymmetrye | ||||
|---|---|---|---|---|
| Dynamics | Model | Simulation | Exacta | Δ |
| Brownianb | 1-Torsionc | 0.17±0.01 | 0.170 | |
| Brownianb | 2-Torsionc | 0.030±0.005 | 0.0289 | |
| Brownianb | 3-Torsionc | 0.009±0.005 | 0.049 | |
| Jumpd | 1:1:1 | 0.17±0.01 | 0.170 | 0 |
| Jumpd | 1:3:9 | 0.41±0.01 | 0.425 | 0.184 |
| Jumpd | 1:0.6:0 | 0.41±0.01 | 0.416 | 0.398 |
| Jumpd | 1:1:0 | 0.36±0.01 | 0.377 | 0.374 |
From Eq. (13)
Diffusion in a three identical well cosine potential with 1 kcal/mol barriers.
Torsion refers to the number of rotatable bonds before the methyl.
Stochastic jump model. Ratios in the model column refer to the expected equilibrium g-, g+, t rotamer population ratios calculated from the jump probabilities.
Motional asymmetry is defined through Eq. (17), as the difference between calculated without and with assumption of azimuthal symmetry.
Next we examined the case of a single rotatable bond, with a varying barrier height, Vb. As expected, the generalized order parameter increases with increasing barrier height, as the number of rotamers sampled during the simulation drops (Figure 1). Interestingly the values increase somewhat discontinuously with barrier height, showing three clusters of values, around 0.17, 0.4 and 0.95. This reflects the stochastic nature of the simulation and the finite time of sampling. Of course in the infinite time limit, all three rotamers would be equally sampled, and O2 would always be ≈0.17. However, on a finite sampling time scale, chosen here to correspond to that probed by NMR relaxation, not all rotamers are sampled equally. Put another way, the probable number of rotamer transitions per sidechain occurring during the NMR time scale changes from ten or more at Ub < 3.5 kcal/mole (to populate say three rotamers), to about one at 3.5 < Ub < 10 kcal/mole (populating one or two rotamers) to less than one (populating one rotamer). We note that this discrete behavior may contribute to the trimodal or bimodal distributions of O2 often seen experimentally1 as well as the temperature dependence of each motional class34-36
Figure 1.
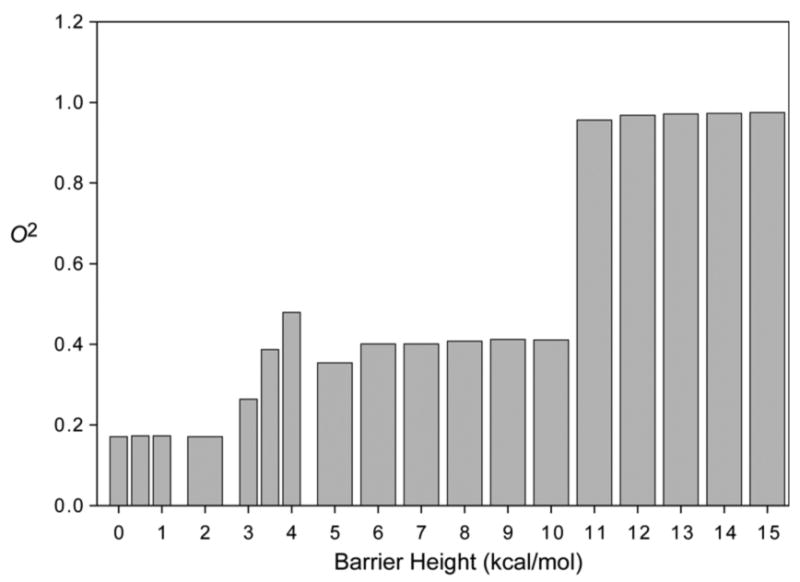
Effect of barrier height on the model-free squared generalized order parameter of a methyl group with one torsional degree of freedom. Motion modeled as diffusion in a three well cosine potential with minima at –60°, +60°, 180°, and varying barrier height.
In Figure 2 the diffusion in a well and discrete rotamer jump models are compared for the case of a single rotatable bond with 3 equally populated rotamers. The time correlation functions from the models show almost identical behavior: A mono-exponential decay to the expected value of O2 = 0.17. The different relaxation time constants merely reflect the details of the motion parameters chosen for the two models, not any fundamental difference. We note that the diffusion in a well model is somewhat more realistic, since it accounts for the fact that there is residual motion of the side chain within a single rotamer state. However, the contribution to the NMR order parameter from this residual motion can be overwhelmed by the rotamer transition contribution, so both models are comparable as regards calculating O2 for methyl bearing side chains.
Figure 2.
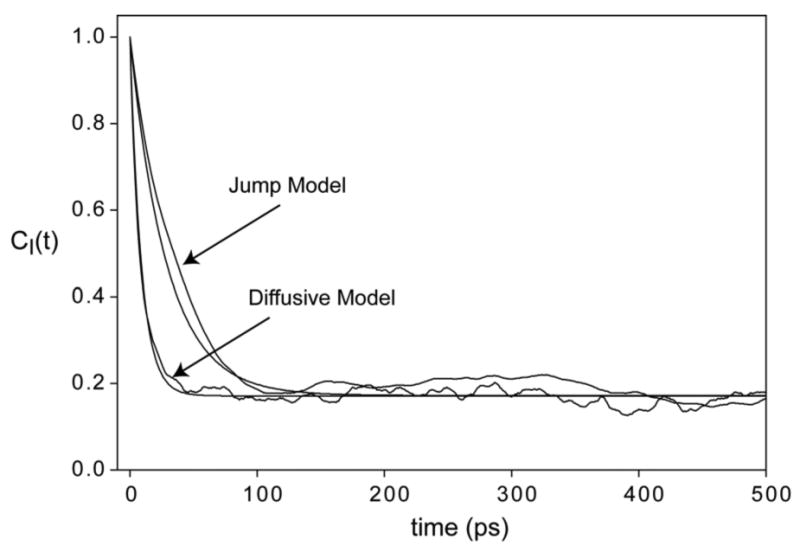
Time correlation functions for a methyl symmetry axis of a side chain. Motion was modeled as diffusion in a three well cosine potential with minima at –60°, +60°, 180°, and a barrier height of 1 kcal/mole and as a stochastic jump process between rotamers with angles –60°, +60° and 180°. All jump probabilities were 0.01/ps. Fits to Eqn. (3) are shown as smooth lines.
Finally, we considered the effect of asymmetric motion that has raised criticism from Freed and coworkers. For this we choose the jump model, since the discrete, discontinuous model, though a bit less realistic than the diffusion model, is for this very same reason more capable of asymmetry. We also restricted our attention to the single rotatable bond case, again because it can result in greater asymmetry. Motion around more than one bond quickly produces quite symmetric motion of the terminal C-C vector of interest, as Table 1 shows. Both these considerations mean than that this model is likely an upper limiting case of motional asymmetry. Figure 3 shows the time correlation functions for a single rotatable bond with no asymmetry (three equally populated rotamers), maximal spatial motion asymmetry (population ratios of 1:0.6:0), and a typical case of one suppressed rotamer (population ratios of 1:1:0). There is no qualitative difference between symmetric and maximally asymmetric motion. The time correlation functions are well described by a single exponential decay to a plateau value, and more importantly, the plateau O2 value is that expected from the analytical expression. In Figure 4 we consider a case with temporal asymmetry induced by a ten-fold range in rotamer jump rates. Here there is a significant deviation from the standard model, in that the time correlation function is not mono-exponential (Inset, Figure 4). However, the error is only in the attribution of the relaxation to a single time constant. The long time estimate of O2 is correct, and unaffected by the asymmetry. The important caveat to the latter is that the various time scales of the side chain motion are still within the time scale of the NMR experiment (and of course several-fold shorter than the simulation length in the modeling).
Figure 3.
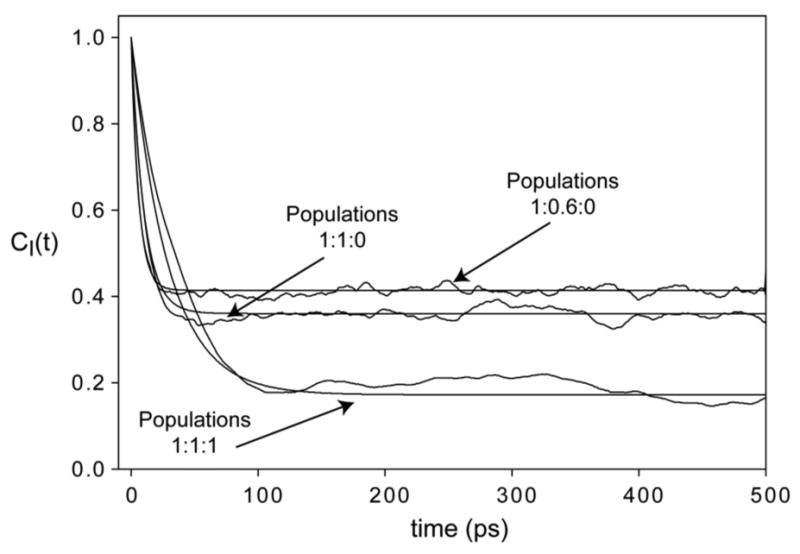
Impact of spatial asymmetry of motion. Time correlation functions for a methyl of a side chain. Motion was modeled as a stochastic jump process between rotamers with angles –60°, +60° and 180°. Pg-g+ =0.01/ps. Other jump probabilities were set to produce expected rotamer population ratios of 1:1:1, 1:1:0 and 1:0.6:0. Fits to Eqn. (3) are shown as smooth lines.
Figure 4.
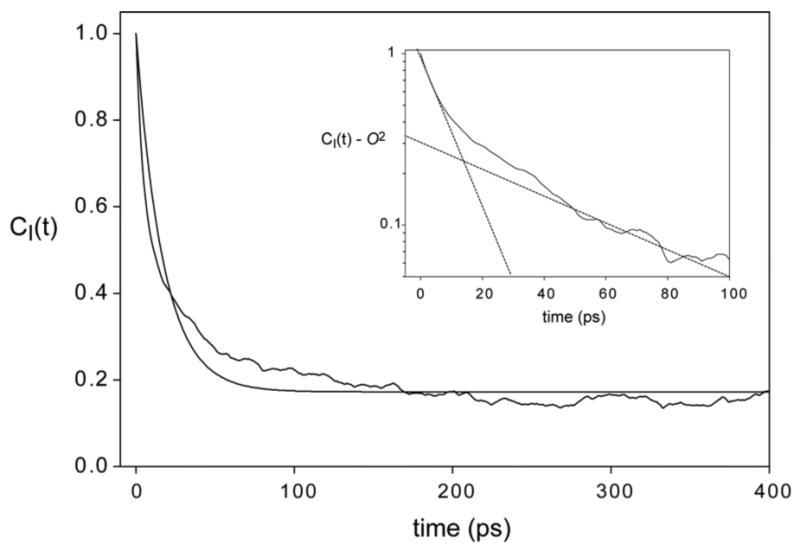
Impact of temporal asymmetry of motion. Time correlation functions for a methyl of a side chain. Motion was modeled as a stochastic jump process between rotamers with angles –60°, +60° and 180°. Jump probabilities were of the order of 0.01/ps for jumps between rotamers 1 and 2, and of the order of 0.001/ps for all jumps involving rotamer 3. Jump probabilities were set to produce expected rotamer population ratios of 1:1:1, O2 = 0.179. The smooth line is the fit to Eq. (3). Inset is an expansion of the semi-log plot (C(t) – O2) at early times, showing bi-exponential decay. Straight lines on the plot are to guide the eye only.
In summary, we have defined specific criteria for both spatial and temporal asymmetry of motion that would correspond to that of the methyl symmetry axis. Under conditions of maximal asymmetry, the MF spectral density is found to be generally robust when the basic assumptions of its derivation are met.
Backbone dynamics of CaM in the CaM:eNOSp complex
The above results provide renewed confidence in the model-free treatment and we now turn our focus to the dynamics of calcium-saturated calmodulin in complex with the calmodulin-binding domain of endothelial nitric oxide synthase (eNOS). The sequence of the peptide used to represent the eNOS CaM binding domain is: RKKTFKEVANAVKISASLMG and is termed eNOSp. Nitrogen-15 relaxation establishes the global molecular reorientation is isotropic and characterized by a time constant of 8.86 ns. Using the two-parameter Lipari-Szabo formalism and an isotropic diffusion tensor, the amide N-H bond vector squared generalized order parameters ( ) and effective internal correlation times (τe) were obtained for 134 of the 145 non-proline amide sites in CaM. No amide order parameters were determined for residues A1 and D2, the two proline residues (P43 and P66) and residues A15, Q41, E67, K77, E83, N97, G98, E104, V108, V121, and R126 due to resonance overlap. Twelve sites (K21, D22, G33, T34, R37, S38, I39, D95, H107, M109, D131 and D133) were found to have significant contributions from chemical exchange phenomena. These sites were fitted with an additional chemical exchange term ( Rex ). Determined Rex values ranged from 0.5 to 1.0 sec-1.
Amide parameters of indicate that the polypeptide backbone at this bond vector is homogeneously rigid with the exception of the linker regions and C and N termini. The distribution of backbone parameters can be described by Gaussian distribution (R2 = 0.97) centered at 0.960 ± 0.003 with a distribution width of 0.048 ± 0.003 (not shown). The average value for amide parameters for free CaM is 0.891 ± 0.086.ref. 37 The average difference in order parameters between free CaM and the CaM:eNOSp complexes indicates that the backbone becomes slightly more rigid (-0.027 ± 0.012) upon complex formation at the 80 amides measured in both states. The formation of the CaM:eNOSp complex results in a slight overall stiffening of the backbone.
Sidechain dynamics of CaM in the CaM:eNOSp complex
Model-free analysis of deuterium relaxation in methyl groups of CaM in the complex indicates effective correlation times between 10 and 80 ps and corresponding ranging from ∼0.1 to ∼0.9. Given that methyl jump rates are estimated to be on the order of 1-2 ps, the times scale separation between the three major motional modes – methyl rotation, methyl symmetry axis motion and global reorientation – is sufficient to ensure that they are uncorrelated. This validates the primary assumptions of the MF treatment in this case. Monte Carlo analysis based on the estimated precision of relaxation parameters derived from duplicates of primary data (3%) indicates an average precision for obtained parameters of 0.02. These data have been presented from a thermodynamic perspective.12 Here we provide a microscopic view of the motion within this complex and compare it to the highly homologous but thermodynamically distinct complex between CaM and the calmodulin-binding domain of the neuronal nitric oxide synthase (nNOS). The sequence of the peptide used to represent the CaM binding domain of nNOS is KRRAIGFKKLAEAVKFSAKLMGQ and is termed nNOSp.
The parameters of various CaM complexes have a striking tri-modal distribution.12 We have termed these groupings or classes the J-, α- and ω-classes, in accordance with the character of the motions underlying them.1 Of the six methyl-bearing common amino acids, most contribute to all three motional classes in the CaM complexes. In both the CaM:eNOSp and the CaM:nNOSp complexes, methionines do not contribute to the ω-class while alanine does not contribute to the α-class. Calmodulin is unusual in its high methionine content. The fact that methionines do not participate in the most rigid class is different from other characterized CaM:peptide complexes such as that corresponding to the calmodulin binding domain of the smooth muscle myosin light kinase (smMLCKp),37 the calmodulin kinase 1 (CaMK1p)38 and the calmodulin kinase kinase alpha (CaMKKαp).39 In those complexes, methionines are represented in all three classes of motion. This change perhaps reflects differences in the function of the protein that the CaM binding domain is derived from; all of these examples are from kinases whereas the domains being studied here are both derived from nitric oxide synthases. The fact that alanines do not participate in the intermediate class of motion is similar to the case for the CaM:smMLCKp complex and is consistent with the motional origins of the three classes i.e. the methyl group is rigidly attached to a relatively immobile scaffold.1
The binding of eNOSp to CaM results in a substantial loss of system entropy and an apparent reduction in conformational entropy of CaM as reflected in the over-all reduction of the motion of its methyl bearing sidechains.12 The dynamics of these sidechains of CaM in the complex with eNOSp are strikingly heterogeneously distributed (Figure 5). For the 44 sites measured in both free Ca2+-saturated CaM and CaM:eNOSp, CaM:eNOSp is on average more rigid (Δ = -0.076) with some sites such as Met 144ε, Met 109 ε, Ile 85γ2 and Met 72ε becoming more rigid by more than 0.2. The response to eNOSp binding is, however, a varied one. While the majority of sites become more motionally constrained, there are a half a dozen that become more dynamic upon formation of the complex such as Val 142γ1 and Ala 15β and Ile 52δ1. The average absolute difference is 0.103.
Figure 5.
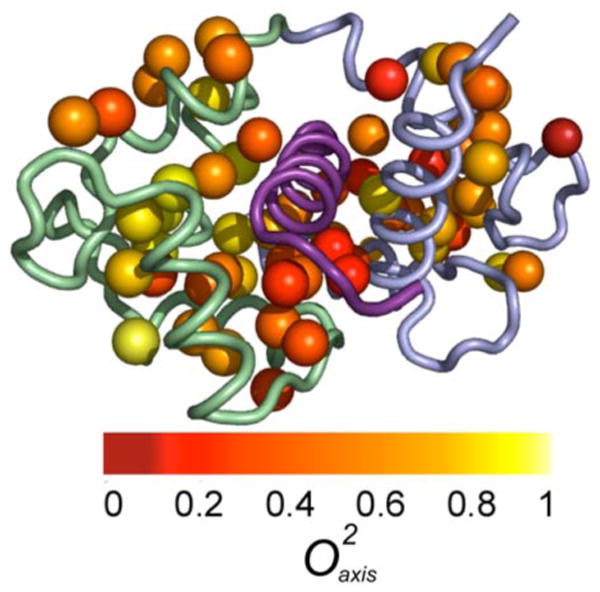
Distribution of NMR derived methyl side chain dynamics in the CaM:eNOSp complex. Methyl groups are represented by spheres and are color coded as to value. The bound peptide is shown in violet, the N-terminal domain in green and the C-terminal domain in blue. Based on the complex of the structure determined by Aoyagi et al (PDB ID 1NIW).44 Drawn with PyMol.45
An interesting issue is whether the local dynamic response to the binding of different target domains by calmodulin is the same. The average difference in values between the CaM:eNOSp and CaM:nNOSp complexes is, within experimental error, zero (-0.002 ± 0.018) for the 122 amides measured in both complexes. Overall, the measured amide dynamics emphasize the similarity of the response of the backbone between complexes i.e. largely a lack of response. There are 53 methyl sites for which values could be reliably determined in both the CaM:nNOSp and the CaM:eNOSp complexes. On average, the CaM:eNOSp complex is slightly ( = −0.026 ± 0.016) more rigid than the CaM:nNOSp complex. However, the average absolute difference is 0.08, reflecting large site-to-site variability in parameters between the two complexes (see Figure 6). Nevertheless, the parameters of most sites stay within the same class in the CaM:eNOSp and CaM:nNOSp complexes. For about a sixth of the sites measured this is not the case (Figure 6).
Figure 6.
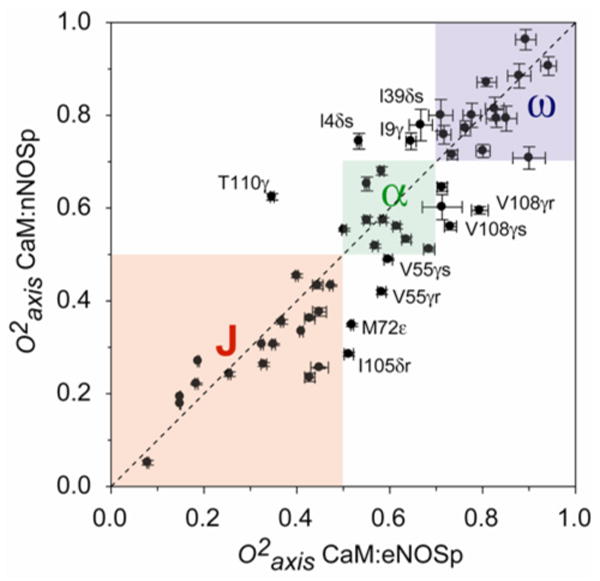
Correlation plot of methyl parameters for the CaM:eNOSp and CaM:nNOSp complexes. Boxes delineate the boundaries of motional class.12 A number of methyl groups change their motional class between the two complexes and are labeled.
The depth of burial, distance from the peptide, amount of solvent accessible surface area, electrostatic potential and packing were determined for each of the methyl groups in CaM in an effort to illuminate correlations of local dynamics and basic physical attributes of the protein complex. There is no correlation of dynamics with any of these physical correlates as exemplified by R2 of 0.1 or less (Table 2). This is in line with what is observed for a database of more than two dozen proteins, some in multiple functional states.1 For example, like other small proteins, there is no correlation in the CaM:eNOSp complex between depth of burial of a methyl group and its value. There are many exposed methyl groups that have highly restrained motions and many buried methyl groups that are mobile [e.g., Met 145ε = 0.40]. Generally, depth of burial is seems not to be a good predictor of measured methyl generalized order parameters.
Table 2.
Average values of structural correlates and their correlation with a
| Averages | Correlation | |
|---|---|---|
| CaM:eNOSp | R2 | |
| Depth of Burial (Å) | 2.42 ± 1.29 | 0.13 |
| Distance from Peptide (Å) | 5.56 ± 3.36 | 0.06 |
| Solvent Accessible Surface (Å2) | 10.7 ± 16.5 | 0.04 |
| Packing (Å3) | 24.3 ± 16.7 | 0.10 |
| Electrostatic potential (kT/e) | 19.0 ± 12.7 | 0.14 |
| 0.55 ± 0.22 |
Average values with standard deviation for several simple structural properties for the methyl groups of CaM. Difference represents the average pair-wise difference between the two properties.
R2 represents the correlation of at a site with the structural property at that site.
Discussion
The revolution in NMR relaxation studies in proteins has very much rested on the use of the model-free spectral density.4 Since its earliest applications to polypeptide systems,23 it has allowed detailed site-resolved insight into macromolecular motion.1,6 Freed and coworkers have argued that the MF treatment is an unwarranted over-simplification and can lead to quite misleading conclusions.7-11 They have proposed a more expansive treatment that is built upon the “slowly relaxing local structure” or SRLS approach, which was initially developed to handle the effects of strong coupling of motional modes of a solute within a “cage” of solvent.40 For macromolecules of significant size, structure and stability, this is a somewhat unusual view since a protein of 200 amino acids or so will tumble several orders of magnitude more slowly than and will suffer roughly 1012 collisions with solvent per second. The solvent shell (cage) will also have a lifetime two orders of magnitude less than time scale of macromolecular reorientation.41 In addition, most atoms of the protein are removed from contact with solvent. Finally, the time scales of internal motion that dominate NMR relaxation phenomena are generally an order of magnitude or more faster than the tumbling of the roughly 20 kDa CaM complexes. Thus, there appears to be little to motivate a detailed solvent coupling model for proteins of significant size in this particular context.
The SRLS model ostensibly takes into account “dynamical coupling between the global motion of the protein and the local motion of the dynamic probe” and this is manifested in the treatment by a rhombic coupling potential.7 The mathematical structure of the SRLS treatment in one asymptotic limit leads to the MF spectral density, but only in a formal sense. The physical underpinnings are quite different, which has led to much of the apparent antagonism between the two views. A potentially appealing feature of the SRLS model would be its claim that the asymmetric nature of internal motion can be reduced within the context of a rhombic model. Formally, the SRLS treatment seeks to reconstruct the spectral density describing internal motion as a linear combination of Lorentzian terms, each associated with its own time constant that is, in turn, associated with the modes of motion of the system.7 The orientational ordering is discriminated on the basis of a simple potential of mean force that is defined by fitted parameters. The model also allows for misalignment of reference frames. The SRLS model is significantly more complicated than the MF treatment and explicitly includes an energetic term. Though often described as an advantage by its proponents,7 the introduction of energetics in a purely dynamical description unavoidably confuses the issue.
The motivation for the use of the SRLS model seems to rest largely on the remarkable assertion that the “oversimplified spectral [MF] spectral density yields inaccurate best-fit parameters … with good statistics” and is termed forced-fitting.9 NMR relaxation is governed by relatively featureless spectral density functions. This was recognized early on as being problematic as it leads to locally rough but globally smooth refinement functions that are ill-structured for standard methods of regression.23 This feature is further exacerbated by the insensitive nature of the NMR experiment where the obtained primary relaxation parameters generally have a true precision (i.e. not fitted error) of a few percent, such as those reported here. Finally, in some contexts, NMR relaxation phenomena are also somewhat corrupted by small but ill-defined (i.e. variable) contributions. For example, 15N relaxation is potentially plagued by minor dipole-dipole contributions from non-bonded hydrogens and an uncertain variation in the nature of the chemical shift tensor that makes correction for chemical shift anisotropy incomplete.25 Though less of a problem for deuterium relaxation, where the quadrupolar interaction is clearly dominant and relatively uniform,42 it would seem unreasonable to claim that the primary relaxation parameters employed are accurate to better than 1-2%. In other words, it would appear that the criticisms attached to the model-free treatment regarding “forced fitting” might be more appropriately applied to the interpretation of the basic relaxation parameter that is being measured. Indeed, this is reflected in the precision of ∼3% estimated by Monte Carlo analysis for obtained parameters.
Given the limited precision and accuracy of NMR relaxation parameters (observables), one has to also question the ability to discriminate the various features of the SRLS model when the problem is often formally under-determined. Indeed, the lack of correspondence between MF parameters and SRLS parameters obtained from the same data sets has been attributed to difficulties associated with the former model while the instability would appear to arise from the difficulty in resolving the fitted parameters of the latter. Numerically, the SRLS model requires the distinction between exponentials in the correlation function (or, practically, the distinction of superimposed Lorentzians of nearly identical linewidths), a notoriously difficult numerical problem that is entirely avoided by the MF treatment. In a very real sense, the SRLS is effectively an over-fitting of the available data and seeks to discriminate critical model parameters using information that is simply not there. In contrast, the MF treatment recognizes that time scale separation is required to dissect the internal correlation function but that such time scale separation is not necessary to capture the basic character of the motion through its asymptotic limit, the squared generalized order parameter. Error in obtained model-free parameters due to deviation of the correlation function from a single exponential is primarily manifested in the effective correlation time, as illustrated above, which is of much less interest since it is more a normalization constant than a true time constant. We show here that the amplitude of motion, as measured by the generalized order parameter, of highly asymmetric motion, either in time scale or spatially, is completely well captured by the model free treatment. Thus the basic motivation for attempting the SRLS analysis in this context, that the generalized order parameter does not reliably represent the long time limit of the internal correlation function, is largely unfounded.
Underlying the dismissal of the model-free treatment is the claim that it cannot provide information regarding the detailed geometric nature (i.e. spatial symmetry) of the motion giving rise to relaxation.7-10 This is simply an expression of the degeneracy of the problem where many qualitatively distinct motions can give rise to the same generalized order parameter (see Table I, for example). But is the desired insight into the geometrical nature of the motion accessible? In the absence of distinctly different types of experimental data than is currently available, the answer, according to Figures 2-4 and Table 1, appears to be no. Mathematically this makes sense since terms of the general expansion of the spectral density arising from a specific motion cannot often be associated with specific “modes”. The physical picture of simple diffusion within a cone, which has an infinite number of eigenvalues of the transition operator (terms in the spectral density), is not maintained in the “rhombic” approximation. Thus, it would appear that the basic strategy of the model-free treatment, to obtain the fundamental features of autocorrelation function that can be reliably extracted, remains the preferred strategy, in the absence of significant time scale separation.
Side chain dynamics
The parameters in the CaM:smMLCKp complex have a striking tri-modal distribution.34 We have previously termed these groupings or classes the J-, α- and ω-classes, in accordance with the character of the motions underlying them.1 A similar distribution of methyl order parameters is seen in the CaM:eNOSp complex.12 Averaging of J-coupling provides conclusive evidence for rotamer interconversion on a sub-nanosecond time scale.35 The high parameter class corresponds to very restricted motion within a rotamer well while the intermediate parameter class involves more extensive motion within a single rotameric well and/or through connected torsion angles.1 As we show here, low parameters can arise through several mechanisms, none of which represent “unduly large excursions”,7 and seem completely consistent with both contemporary statistical thermodynamic and molecular dynamic simulations, such as those undertaken here and elsewhere43 for calmodulin complexes, and the general emerging view of protein cores as liquid-like. Indeed, Figure 1 suggests a particularly simple and physically reasonable origin for the clustering of motion into classes. As emphasized above, the distribution of rotamer states, though significantly influencing the value of the obtained parameters, does not lead to inaccurate values.
Of the six methyl-bearing amino acids, most contribute to all three motional classes. In both the CaM:eNOSp and the CaM:nNOSp complexes, methionines do not contribute to the ω-class while alanine does not contribute to the α-class. Calmodulin is unusual in its high methionine content. The fact that methionines do not participate in the most rigid class is different from other characterized CaM:peptide complexes such as those with smMLCKp,34 CaMK1p,38 and the CaMKKαp.39 In those complexes, methionines are represented in all three classes of motion. This change perhaps reflects differences in the function of the protein that the CaM binding domain is derived from; all of these examples are from kinases whereas the domains being studied here are both derived from nitric oxide synthases. The fact that alanines do not participate in the intermediate class of motion is similar to the case for the CaM:smMLCKp complex and is consistent with the motional origins of the three classes i.e. the methyl group is rigidly attached to a relatively immobile scaffold.1
As observed upon the formation of other CaM complexes, the binding of eNOSp results in a substantial loss of apparent conformational entropy. For the 44 sites measured in both free Ca2+-saturated CaM and CaM:eNOSp, CaM:eNOSp is on average more rigid (Δ = -0.076) with some sites such as Met 144ε, Met 109 ε, Ile 85γ2 and Met 72ε becoming more rigid by more than 0.2. The response to eNOSp binding is, however, a varied one. While the majority of sites become more motionally constrained, there are a half a dozen that become more dynamic upon formation of the complex such as Val 142γ1 and Ala 15β and Ile 52δ1. The average absolute difference is 0.103. The current approaches to interpreting these changes as a “dynamical proxy” for changes conformational entropy is model dependent.1 This is a major limitation and raises a number of important technical issues ranging from the influence of correlated motion, the applicability of the simple potentials that are generally employed and so on.1 Efforts to empirically correct for these issues are on-going. In the meantime, the qualitative implication is clear: proteins do have considerable residual conformational entropy and this entropy can contribute to biological function through the modulation of total system entropy.
Acknowledgments
Supported by NIH research grants DK 39806 (AJW) and GM 48130 (KAS). KKF is an NIH predoctoral trainee (GM 08275).
References and Notes
- 1.Igumenova TI, Frederick KK, Wand AJ. Chem Rev. 2006;106:1672. doi: 10.1021/cr040422h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Millet O, Muhandiram DR, Skrynnikov NR, Kay LE. J Am Chem Soc. 2002;124:6439. doi: 10.1021/ja012497y. [DOI] [PubMed] [Google Scholar]
- 3.Muhandiram DR, Yamazaki T, Sykes BD, Kay LE. J Am Chem Soc. 1995;117:11536. [Google Scholar]
- 4.Lipari G, Szabo A. J Am Chem Soc. 1982;104:4546. [Google Scholar]
- 5.Lipari G, Szabo A. J Am Chem Soc. 1982;104:4559. [Google Scholar]
- 6.Jarymowycz VA, Stone MJ. Chem Rev. 2006;106:1624. doi: 10.1021/cr040421p. [DOI] [PubMed] [Google Scholar]
- 7.Meirovitch E, Shapiro YE, Polimeno A, Freed JH. J Phys Chem B. 2007;111:12865. doi: 10.1021/jp072156s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Meirovitch E, Polimeno A, Freed JH. J Phys Chem B. 2006;110:20615. doi: 10.1021/jp061403+. [DOI] [PubMed] [Google Scholar]
- 9.Meirovitch E, Shapiro YE, Polimeno A, Freed JH. J Phys Chem A. 2006;110:8366. doi: 10.1021/jp056975t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Meirovitch E, Shapiro YE, Liang ZC, Freed JH. J Phys Chem B. 2003;107:9898. [Google Scholar]
- 11.Tugarinov V, Liang ZC, Shapiro YE, Freed JH, Meirovitch E. J Am Chem Soc. 2001;123:3055. doi: 10.1021/ja003803v. [DOI] [PubMed] [Google Scholar]
- 12.Frederick KK, Marlow MS, Valentine KG, Wand AJ. Nature. 2007;448:325. doi: 10.1038/nature05959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Brokx RD, Lopez MM, Vogel HJ, Makhatadze GI. J Biol Chem. 2001;276:14083. doi: 10.1074/jbc.M011026200. [DOI] [PubMed] [Google Scholar]
- 14.Urbauer JL, Short JH, Dow LK, Wand AJ. Biochemistry. 1995;34:8099. doi: 10.1021/bi00025a016. [DOI] [PubMed] [Google Scholar]
- 15.Seeholzer SH, Wand AJ. Biochemistry. 1989;28:4011. doi: 10.1021/bi00435a057. [DOI] [PubMed] [Google Scholar]
- 16.Muhandiram DR, Kay LE. J Magn Reson Ser B. 1994;103:203. [Google Scholar]
- 17.Montelione GT, Lyons BA, Emerson SD, Tashiro M. J Am Chem Soc. 1992;114:10974. [Google Scholar]
- 18.Uhrin D, Uhrinova S, Leadbeater C, Nairn J, Price NC, Barlow PN. J Magn Reson. 2000;142:288. doi: 10.1006/jmre.1999.1951. [DOI] [PubMed] [Google Scholar]
- 19.Neri D, Szyperski T, Otting G, Senn H, Wuthrich K. Biochemistry. 1989;28:7510. doi: 10.1021/bi00445a003. [DOI] [PubMed] [Google Scholar]
- 20.Bax A, Delaglio F, Grzesiek S, Vuister GW. J Biomol NMR. 1994;4:787. doi: 10.1007/BF00398409. [DOI] [PubMed] [Google Scholar]
- 21.Goddard T, Kneller D. SPARKY 3. University of California; San Francisco: 2004. [Google Scholar]
- 22.Farrow NA, Muhandiram R, Singer AU, Pascal SM, Kay CM, Gish G, Shoelson SE, Pawson T, Forman-Kay JD, Kay LE. Biochemistry. 1994;33:5984. doi: 10.1021/bi00185a040. [DOI] [PubMed] [Google Scholar]
- 23.Dellwo MJ, Wand AJ. J Am Chem Soc. 1989;111:4571. [Google Scholar]
- 24.Kneller JM, Lu M, Bracken C. J Am Chem Soc. 2002;124:1852. doi: 10.1021/ja017461k. [DOI] [PubMed] [Google Scholar]
- 25.Lee AL, Wand AJ. J Biomol NMR. 1999;13:101. doi: 10.1023/a:1008304220445. [DOI] [PubMed] [Google Scholar]
- 26.Ottiger M, Bax A. J Am Chem Soc. 1998;120:12334. [Google Scholar]
- 27.Mittermaier A, Kay LE. J Am Chem Soc. 1999;121:10608. [Google Scholar]
- 28.Nicholls A, Sharp KA, Honig B. Proteins. 1991;11:281. doi: 10.1002/prot.340110407. [DOI] [PubMed] [Google Scholar]
- 29.Abragam A. Principles of nuclear magnetism. Clarendon Press; Oxford: 1961. [Google Scholar]
- 30.Hoffman RA. Adv Magn Reson. 1970;4:88. [Google Scholar]
- 31.Jacobsen JP, Bildsoe HK, Schaumburg K. J Magn Reson. 1976;23:153. [Google Scholar]
- 32.Chatfield DC, Szabo A, Brooks BR. J Am Chem Soc. 1998;120:5301. [Google Scholar]
- 33.Schneider DM, Dellwo MJ, Wand AJ. Biochemistry. 1992;31:3645. doi: 10.1021/bi00129a013. [DOI] [PubMed] [Google Scholar]
- 34.Lee AL, Wand AJ. Nature. 2001;411:501. doi: 10.1038/35078119. [DOI] [PubMed] [Google Scholar]
- 35.Lee AL, Sharp KA, Kranz JK, Song XJ, Wand AJ. Biochemistry. 2002;41:13814. doi: 10.1021/bi026380d. [DOI] [PubMed] [Google Scholar]
- 36.Song XJ, Flynn PF, Sharp KA, Wand AJ. Biophys J. 2007;92:L43. doi: 10.1529/biophysj.106.102160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Lee AL, Kinnear SA, Wand AJ. Nat Struct Biol. 2000;7:72. doi: 10.1038/71280. [DOI] [PubMed] [Google Scholar]
- 38.Frederick KK, Kranz JK, Wand AJ. Biochemistry. 2006;45:9841. doi: 10.1021/bi060865a. [DOI] [PubMed] [Google Scholar]
- 39.Marlow MS, Wand AJ. Biochemistry. 2006;45:8732. doi: 10.1021/bi060420m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Polimeno A, Freed JH. J Phys Chem. 1995;99:10995. [Google Scholar]
- 41.Otting G, Liepinsh E, Wuthrich K. Science. Vol. 254. New York, N.Y: 1991. p. 974. [DOI] [PubMed] [Google Scholar]
- 42.Yang DW, Kay LE. J Magn Reson Ser B. 1996;110:213. [Google Scholar]
- 43.Prabhu NV, Lee AL, Wand AJ, Sharp KA. Biochemistry. 2003;42:562. doi: 10.1021/bi026544q. [DOI] [PubMed] [Google Scholar]
- 44.Aoyagi M, Arvai AS, Tainer JA, Getzoff ED. EMBO J. 2003;22:766. doi: 10.1093/emboj/cdg078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.DeLano WL. The PyMOL molecular graphics system. DeLano Scientific; San Carlos, CA, USA: 2002. [Google Scholar]


