Genomewide scan for real-word reading subphenotypes of dyslexia: Novel chromosome 13 locus and genetic complexity

Abstract

Dyslexia is a common learning disability exhibited as a delay in acquiring reading skills despite adequate intelligence and instruction. Reading single real words (real-word reading, RWR) is especially impaired in many dyslexics. We performed a genome scan, using variance-components (VC) linkage analysis and Bayesian Markov chain Monte Carlo (MCMC) joint segregation and linkage analysis, for three quantitative measures of RWR in 108 multigenerational families, with followup of the strongest signals with parametric LOD score analyses. We used single-word reading efficiency (SWE) to assess speed and accuracy of RWR, and word identification (WID) to assess accuracy alone. Adjusting SWE for WID provided a third measure of RWR efficiency.

All three methods of analysis identified a strong linkage signal for SWE on chromosome 13q. Based on multipoint analysis with 13 markers we obtained a MCMC intensity ratio of 53.2 (chromosome-wide p < 0.004), a VC LOD score of 2.29, and a parametric LOD score of 2.94, based on a quantitative-trait model from MCMC segregation analysis. A weaker signal for SWE on chromosome 2q occurred in the same location as a significant linkage peak seen previously in a scan for phonological decoding. MCMC oligogenic segregation analysis identified three models of transmission for WID, which could be assigned to two distinct linkage peaks on chromosomes 12 and 15. Taken together, these results indicate a locus for efficiency and accuracy of RWR on chromosome 13, and a complex model for inheritance of RWR accuracy with loci on chromosomes 12 and 15.

Introduction

Dyslexia is a specific reading disability that cannot be explained by low intelligence or inadequate instruction. Dyslexia has been estimated to occur in 5–10% of school-age children (Shaywitz et al., 1990), and is characterized by specific difficulties in spelling and word recognition (Raskind, 2001; Vellutino et al., 2004) as well as in reading fluency (Plomin, 2001). Although by adulthood many individuals have learned to compensate for the disorder (Raskind, 2001), reading impairment often persists (Pennington et al., 1990), with adverse social and economic consequences.

Dyslexia is thought to involve deficits in one or more reading-related cognitive processes (Berninger et al., 2001; Fisher and DeFries, 2002; Francks et al., 2002; Vellutino et al., 2004). One of these is phoneme awareness, or the ability to recognize and manipulate individual phonemes, the unit of spoken language that corresponds to letters in an alphabetic language. A second process is phonological decoding, or the conversion of printed words to spoken words, which is important in learning new words. A third process is lexical-level orthographic coding, or the recognition of an entire written word as a unit, which is required for rapid (fluent) reading. Finally, rapid access to a phonological name code during phonological decoding is also required for fluent reading, and is assessed through tests of rapid automatized naming of alphanumeric symbols (Berninger et al., 2001; Denckla and Rudel, 1976; Wolf et al., 1986; Wolf and Bowers, 1999). Deficits in these processes are all manifested in impairment of real-word reading (RWR), or word recognition, a major indicator of reading disability in children (Francks et al., 2002; Stanovich, 1988; Vellutino et al., 2004). RWR is an indicator of overall reading ability because it is a multicomponent process involving both lexical orthographic and sublexical phonological processes (Marlow et al., 2001). In some cases, dyslexic individuals can compensate for impairment in single-word reading with experience while still deficient in component phonological skills, but they generally do not reach normal reading ability (Fisher et al., 1999; Lefly and Pennington, 1991). Speed of word recognition as a measure of RWR may be a particularly meaningful measure: in languages such as German and Finnish, which have regular orthographies, low reading speed, rather than low reading accuracy, is a common persistent problem in dyslexia (Landerl, 2001; Leinonen et al., 2001).

A large body of evidence indicates that dyslexia, and specifically, RWR, has a genetic component (for reviews, see Fisher and DeFries, 2002; Francks et al., 2002; Raskind, 2001). Aggregation analysis shows patterns of correlation consistent with genetic models for several dyslexia-related measures including RWR (Hsu et al., 2002; Marlow et al., 2001; Raskind et al., 2000). Estimates of heritability of various measures of RWR are consistently high: 0.63 in a sib-pair sample (Marlow et al., 2001); 0.60 and 0.85 in two twin studies in children (Knopik et al., 2002; Gayán and Olson, 2003, respectively); and 0.45 in a recent study of adult male twins (Kremen et al., 2005). Segregation analyses of measures of RWR and other correlated component phenotypes further suggests a genetic basis, with evidence for a modest number of segregating loci (Chapman et al., 2004; Gilger et al., 1994; Grigorenko et al., 2003).

Evidence for a genetic basis to RWR is further supported by positive reports of linkage to specific genomic regions. While reports of linkage of RWR phenotypes to chromosomes 1p (Grigorenko et al., 2001) and 2p (Loo et al., 2004) have not yet been replicated, several other regions have shown reproducible evidence for linkage in more than one sample. Evidence for linkage for RWR has been reported for chromosomes 6p (DYX2, OMIM 600202, http://www.ncbi.nlm.nih.gov/omim) (Cardon et al., 1994; Cardon et al., 1995; Fisher et al., 1999; Grigorenko et al., 2003; Grigorenko et al., 1997; Grigorenko et al., 2000; Kaplan et al., 2002), 15q (locus DYX1, OMIM 127700) (Chapman et al., 2004; Grigorenko et al., 1997; Marino et al., 2004; Nopola-Hemmi et al., 2000; Smith et al., 1983), and 18p (DYX6, OMIM 606616) (Fisher et al., 2002; Marlow et al., 2003).

There is also evidence that the genetic basis of RWR is complex. As described above, heritability estimates vary, suggesting that environmental characteristics among samples may differ. Characteristics that appear to affect estimates of heritability include IQ (Knopik et al., 2002) and parental education levels (Kremen et al., 2005), with higher heritability associated with both higher IQ and parental education levels. Consistent with this, the highest published estimate of heritability is obtained from a sample representing a relatively affluent and well-educated population (Gayán and Olson, 2003). In addition, different measures of RWR have been used in different studies, complicating comparisons and interpretation of results. These include several different timed and untimed measures, as well as composite measures that incorporate scores from both types of RWR measures and also sometimes additional, correlated measures.

As for most complex traits, linkage analysis of RWR among studies has also shown inconsistencies. Positive reports of linkage in focused analyses of chromosome 6p have been reported for three samples: (1) initially, in a Colorado twin sample for a composite dyslexia phenotype based partly on RWR (Cardon et al., 1994; Cardon et al., 1995), as well as later for specific measures of timed and untimed word recognition (Gayán et al., 1999; Kaplan et al., 2002); (2) for an untimed RWR measure in a sample of British families (Fisher et al., 1999); and (3) for a composite RWR phenotype in another sample of families from the USA (Grigorenko et al., 2003). In contrast, we found no evidence for linkage of untimed RWR to 6p in our sample (Chapman et al., 2004). Also, two genome scans that used expanded data sets from the Colorado twin and British studies reported reduced evidence for linkage of RWR phenotypes to 6p (Fisher et al., 2002), and, instead, reported strong evidence in both samples for linkage of RWR phenotypes to a region on chromosome 18p. Although it appeared that this 18p locus affected specifically single-word reading, a multivariate linkage analysis (Marlow et al., 2003) suggested that this locus has an influence on multiple dyslexia-related phenotypes. Similar to the results for 6p, analysis of the 18p region using our sample failed to confirm linkage of untimed single-word reading (Chapman et al., 2004). Finally, there is similar variability among studies of RWR on chromosome 15q with four independent studies using a variety of RWR measures reporting significant or supportive evidence of linkage (Chapman et al., 2004; Grigorenko et al., 1997; Marino et al., 2004; Smith et al., 1983). The results for untimed word recognition in our sample of families support evidence of linkage to 15q (Chapman et al., 2004). In contrast, the genomewide scans on the two samples performed by Fisher and colleagues (Fisher et al., 2002), failed to provide evidence of linkage to chromosome 15q. Explanations include use of different measures for RWR as well as different sample ascertainment.

Additional support for the existence of loci contributing to RWR derives from molecular studies of genes in the chromosome 6p and 15q critical regions. A recent study of a 575-kb region on chromosome 6p22.2 identified SNPs with individual evidence of association in a case-control study, and for which a haplotype of two SNPs in the candidate gene KIAA0319 explained much of the association (Cope et al., 2005). One of the SNPs causes a missense mutation, Ala →Thr, and was also reported as being significantly associated with dyslexia in a second sample (Francks et al., 2004). Similarly, two reports provide evidence of linkage disequilibrium with dyslexia in the chromosome 15q region (Marino et al., 2004; Morris et al., 2000). A candidate gene, called DYX1C1 or EKN1, was recently identified and mapped to a position 2.2 cM proximal to the 15q linkage peak (Taipale et al., 2003), based on a translocation that co-segregated with dyslexia in one large family (Nopola-Hemmi et al., 2000). Two single-nucleotide polymorphisms (SNPs) in DYX1C1, –3G →A and 1249G →T, showed evidence for an association with dyslexia (Taipale et al., 2003), and one SNP (–3G →T in DYX1C1) showed evidence for association with a word recognition phenotype (Wigg et al., 2004). While it is doubtful that the SNPs identified for either gene are susceptibility alleles, the evidence for linkage disequilibrium provides additional support for the presence of genes involved in RWR in these two regions.

While these mapping and association studies provide considerable support for the general paradigm of a focus on narrow phenotypes, our ability to draw conclusions about genes involved in RWR from these studies remains limited for several reasons. First, a wide variety of related phenotypes have been studied, including timed and untimed as well as qualitative and quantitative measures of RWR (Chapman et al., 2004). Reproducibility, or lack thereof, may be affected by the specific measures used. Second, binary traits of affectation status based in part on RWR are often based on multiple component phenotypes, using a threshold criterion for affectedness (e.g., Grigorenko et al., 1997). Quantitative traits have included multivariate phenotypes (e.g., Marlow et al., 2003) and composite univariate phenotypes derived from several psychometric tests (e.g., Cardon et al., 1994), and the contribution of individual measures is not readily determined. Third, not all measures employed as phenotypes have been adjusted for IQ. Using an IQ-adjusted measure for sample ascertainment is expected to yield a superior sample for genetic studies of specific reading disability because it excludes potential probands whose reading ability is expected to be low (Olson et al., 1999). Fourth, mapping studies have used numerous methods of analysis and types and sizes of pedigrees ascertained (Fisher and DeFries, 2002), which may inadvertently affect which trait loci are most amenable to linkage detection in a given study.

Here, we report results of a genome scan focusing on two measures of RWR ability. We chose these related phenotypes for an in-depth analysis based partly on the encouraging results from a recent targeted linkage study (Chapman et al., 2004). We performed whole-genome screens using two different methods of analysis. After identifying initial regions of interest, we typed the families for additional markers and analyzed the augmented data with three different methods. The use of multiple methods of analysis on the same data should minimize the frequency of false positive and negative linkage signals that arise due to limitations or sensitivities of any one method. Our analyses reveal a new locus on chromosome 13 implicated in speed of word recognition. These analyses also provide suggestive support for linkage to several other regions, and demonstrate how the information from quantitative trait locus (QTL) models identified with oligogenic segregation analysis methods can be used to further our understanding of the genetic architecture, and consequently, to localize susceptibility genes.

Materials and Methods

Overview of strategy and rationale for analytical approaches

We performed whole-genome screens using two widely different methods of analysis for linkage: a variance components (VC) approach (Almasy and Blangero, 1998; Amos, 1994) and a Bayesian Markov chain Monte Carlo (MCMC) joint linkage and segregation analysis approach (Heath, 1997). We followed up on the strongest linkage analysis results with additional marker typing and analyses, including parametric LOD score analyses and simulation studies to estimate empirical p-values. For the LOD score analyses, we obtained the quantitative trait locus model parameters from segregation analyses.

We used three strategies to maximize the power of our study. First, our sample consists primarily of extended pedigrees, which offer better power to detect linkage and to localize genes than do nuclear families or sib pairs (Wijsman and Amos, 1997). Second, we treated the phenotypes under analysis as continuous rather than as dichotomous traits, which makes more efficient use of the available information (Graham et al., 1997; Wijsman and Amos, 1997). In the current study we focused on separate measures for timed and untimed RWR, each based on a single test instrument, and in addition, we analyzed a simple reading-rate measure constructed by adjustment of the timed measure for the untimed measure. Finally, we focused on single outcome measures for these initial linkage detection studies. Use of univariate outcomes has been successful in other studies of complex traits with similar complex correlated phenotypes, such as phenotypes associated with cardiovascular disease and simulated data sets where the underlying truth is known (Blangero, 1995; Wijsman and Amos, 1997). Also, use of univariate measures permits us to capitalize on both the full variety of available analytical approaches and the deep understanding of the statistical properties of the approaches and their sensitivities to violation of distributional assumptions. The alternative, use of a multivariate approach, restricts the analytical approach because of limited implementation and added distributional assumptions, and complicates interpretation because of lack of information about the statistical properties and effects of violation of distributional assumptions. Also, such methods have not to date provided strong empirical evidence that they provide substantial gains for linkage detection (Lin and Zou, 2004; Wijsman and Amos, 1997).

Study subjects

Recruitment of the sample used for this study has been described in detail elsewhere (Berninger et al., 2001; Raskind et al., 2000). In brief, families were ascertained through a school-age proband with low reading ability compared to his or her verbal IQ (VIQ), as assessed by ten index measures of reading (Berninger et al., 2001). Most probands were impaired on most or all of the index measures, though they were only required to be impaired on one. Probands were not excluded for comorbid ADHD, but were excluded for other medical, neurological or psychiatric conditions associated with learning disabilities. A total of 874 individuals comprising 108 pedigrees were included in each segregation analysis (SA). Of the 874 individuals, 720 had phenotype data: 108 probands, 170 additional children below age 18 years including 120 siblings of probands, and 442 adults over age 18 years, including 11 siblings of probands. Genotype data from a 10-cM STRP marker scan (see below) were available for a subset of this sample, Subset 1, consisting of 530 subjects in 51 pedigrees. These families were initially selected for genotyping because they appeared likely to be informative for a measure of memory for pseudowords (the nonword memory portion of the prepublication version of the Comprehensive Test of Phonological Processing; Wagner et al., 1999) (Wijsman et al., 2000). Subset 1 differs from that used previously (Chapman et al., 2004) because of removal of one family and eight individuals from a second family (Raskind et al., 2005). The remaining 57 families, Subset 2, were included in SA, but these families lacked genotype data.

Phenotypes

We assessed RWR efficiency with the prepublication version of the Single Word Efficiency (SWE) subtest of the Test of Word Reading Efficiency (TOWRE) (Torgesen et al., 1999), a test of the accuracy and speed of RWR (Berninger et al., 2001). Age-adjusted scores were calculated as z-scores compared to population norms scaled to have a mean of 0 and SD of 1. We assessed accuracy of RWR using the Word Identification (WID) subtest of the Woodcock Reading Mastery Test-Revised (WRMT-R) (Woodcock, 1987). Scores were normalized against grade-specific population norms scaled to have a mean of 100 and SD of 15, using the oldest normative group to normalize adult values. We constructed a third measure of RWR, SWE ~ WID, from these two test instruments by performing analyses of SWE in which WID was included as a covariate (see Statistical Analyses for discussion of covariate adjustment). Using 102 of the 108 pedigrees analyzed here, we had earlier estimated a correlation of 0.61 between SWE and WID in relatives of probands (Raskind et al., 2000), which suggests that the two measures do not have identical underlying architectures. Because SWE measures both rate and accuracy, and WID measures accuracy alone, our goal was to use the adjusted measure to try to isolate the speed component of RWR and therefore to identify with greater precision trait loci that affect ability to read quickly (Raskind et al., 2005).

Genotypes

DNA was extracted from peripheral blood leukocytes or from transformed cell lines as described elsewhere (Raskind et al., 1995). A 10-cM genomewide scan was performed by the NHLBI Mammalian Genotyping Service, Marshfield, WI, using screening set 10 (405 STRP markers, including 378 autosomal markers), on DNA from 428 participants in 51 families (Chapman et al., 2004). Pedigree structure was confirmed using RELPAIR 0.90 (Boehnke and Cox, 1997) using the full set of Marshfield screening set 10 markers. We removed three markers because of various errors. The set of markers used for the initial genomewide scans consisted of the 375 remaining autosomal markers from screening set 10, plus 13 additional markers on chromosomes 2p (D2S391, D2S337, D2S2368), 6p (D6S299, D6S276, D6S1629), 15q (D15S132, D15S143, D15S978, D15S117) and 18 (D18S1150, D18S453, D18S1107), which we typed in our laboratory (Chapman et al., 2004). Additional markers for follow-up (“follow-up markers”) on chromosomes 2q (D2S1326, D2S2241, D2S142), 11 (D11S987, D11S1314, D11S937), 12 (D12S85, D12S90, D12S326, D12S1708, D12S348) and 13 (D13S1304) were selected from the Marshfield map and were obtained from Research Genetics (Huntsville, AL), Applied Biosystems (Foster City, CA) or IDT (Coralville, IA). Families in Subset 2 were not typed for these additional markers, due to the lack of flanking markers for genotype verification.

In general, we used the Marshfield genetic maps for our analyses of the autosomes (http://research.marshfieldclinic.org/genetics). In three instances (Chapman et al., 2004; Raskind et al., 2005) we changed the map slightly to reflect map distances from the deCODE map (Kong et al., 2002) and our dataset. Marker positions were converted from a Kosambi map to a Haldane map for use in linkage analyses. All positions are reported here on the Haldane map.

Statistical analyses

General approach and strategy

We took several measures to ensure that our overall analysis was robust to potential pitfalls. We performed whole-genome analyses with both variance components (VC) and Bayesian Markov chain Monte Carlo (MCMC) analyses, using all markers per chromosome in multipoint analysis with a sex-averaged map. To guard against false positive signals resulting from map inaccuracy (Daw et al., 2000) we checked key signals with single-marker analyses and with multipoint analysis under sex-specific maps. We carried out segregation analysis employing both maximum-likelihood (ML) and Bayesian oligogenic MCMC approaches. ML-based SA produces point estimates of model parameters but can only incorporate one Mendelian locus, whereas the oligogenic MCMC approach produces posterior distributions of model parameters, which are less straightforward to interpret, but can incorporate multiple Mendelian loci. We performed parametric LOD score analyses, including additional follow-up markers, for selected regions, based on the genome scan results. Although this type of analysis requires a prespecified model of inheritance, trait model misspecification typically reduces evidence for linkage over use of a more accurate trait model, and thus is unlikely to give false positive evidence of linkage (Amos and de Andrade, 2001; Clerget-Darpoux et al., 1986; Greenberg et al., 1998; Ott, 1999).

Use of several diverse methods with complementary advantages allows us to combine their strengths and to minimize the number of false positive signals. Both the VC and Bayesian MCMC methods are well suited for analysis of complex traits (Almasy and Borecki, 1999; Amos, 1994; Heath et al., 1997; Shmulewitz and Heath, 2001). One advantage to the VC approach is that it does not require an explicit model of inheritance. Nevertheless, it can be sensitive to departures from the assumption of multivariate normality of the trait and IBD distribution (Allison et al., 1999; Blangero et al., 2000), such as those encountered under ascertainment of pedigrees for extreme trait values (Epstein, 2002; Glidden and Liang, 2002). Also, because VC analysis is based on pairwise relationships, it does not use the available mapping information as efficiently as does a parametric approach with a good trait model. Thus, the addition of parametric LOD score analysis was added to targeted regions because we expected that it may increase power. Bayesian MCMC oligogenic segregation linkage analysis enables simultaneous modeling and mapping of multiple diallelic QTLs and also does not require prespecified model parameters. In addition, unlike VC linkage analysis (Atwood and Heard-Costa, 2003) this MCMC approach provides relatively precise localization of QTLs (Daw et al., 1999). The two methods vary greatly in interpretability of linkage analysis results: the VC approach provides the commonly used LOD scores and p values based on asymptotic distributions, whereas the MCMC results must be interpreted under the less familiar Bayesian framework, although posterior parameter distributions are easily visualized (Wijsman and Yu, 2004), thus providing additional useful insights for interpretation of results.

Covariate adjustments

Models for analyses included adjustment for age in months, sex and verbal IQ (as measured by the Wechsler Intelligence Scale for Children—3rd Edition or by the Wechsler Adult Intelligence Scale—Revised; Wechsler, 1981; Wechsler, 1992) as covariates. Covariate adjustment was performed prior to ML segregation analyses and parametric LOD-score analyses by linear regression, and during VC linkage analyses and all Bayesian MCMC analyses.

The effect of age on the traits was modeled as piecewise linear, having a possibly different slope and intercept in children and adults, using models of the form:

$$y=\alpha +{\beta }_1·a+{\beta }_2·k+{\beta }_3·k·a+{\beta }_4·s+{\beta }_5·IQ+{\beta }_6·x,$$

where a is age in months, IQ is verbal IQ, and k and s are indicator variables for child status (less than 300 months) and male sex, respectively. In the current analysis, only the model for SWE ~ WID included a sixth coefficient, for WID, indicated by the variable x. A piecewise linear model for age is appropriate for developmental traits, where there are different age effects in children and adults. The models yielded residuals that were essentially normally distributed and showed no evidence for the presence of additional unmodeled age effects. The parameter values for the models are in Web Table A. The choice of age 25 years (300 months) as the knot is somewhat arbitrary, but conforms to the upper age (299 months) available for normalizing SWE scores on the TOWRE, and is therefore used to normalize the scores of adults. Also, because of the difference in the age distributions of the children and adults (Raskind et al., 2000) and the existence in the sample of very few individuals in the age range of 18–30 years, results on the coefficients in the regression analysis in this sample are insensitive to details of this choice of the knot.

Segregation analysis (SA) by maximum likelihood (ML)

Parameters for Mendelian inheritance of a single QTL were estimated using class D of the logistic regression models of Bonney (1986) as implemented in the REGC program in S.A.G.E. version 3.1 (S.A.G.E., 1997). The appropriateness of the model was tested by comparing the major-gene model to a model with an environmental component only, and by comparing models with fixed Mendelian transmission probabilities to those with arbitrary probabilities. No polygenic component was included in the analyses, because only the Mendelian component was used for parametric LOD score analysis (see below). We did not correct for ascertainment because we wished to compare directly models generated from ML and MCMC SA, and such correction is not currently available in the MCMC analysis package. However, for parametric LOD score analysis, the artificially high minor allele frequency expected from failure to correct for ascertainment will likely compensate for other types of model misspecification encountered when fitting a complex trait to a single-QTL model (Risch and Giuffra, 1992).

Linkage analysis using variance components (VC)

VC linkage analyses (Almasy and Blangero, 1998; Amos, 1994) were performed using SOLAR version 2.1 (http://www.sfbr.org/sfbr/public/software/solar/), with exact single-marker and multipoint IBD scores calculated using Merlin (Abecasis et al., 2002). Components of variance considered were additive and dominance variance attributable to a major gene (QTL) at the location considered, plus additive and dominance polygenic variance. Four models were fit at each marker locus: model M0-a (polygenic), in which the total major-gene variance was constrained to zero and the polygenic component has only additive variance; model M0-d (polygenic) in which the major-gene variance was constrained to zero and the polygenic component has both additive and dominance variance; model M1 (additive), in which both dominance variance components were constrained to zero; and M2 (dominant), with no constraint on any of the four variance components. All models contained a component for residual variance. LOD scores were calculated as log₁₀-likelihood ratios comparing either M1 to M0-a or M2 to M0-d. Log-likelihood ratios using M0 (a or d) as the restricted likelihood do not converge to simple χ² distributions, but rather to mixtures of distributions, with the LOD score for M1 converging to a 50:50 mixture distribution of a χ² distribution with 1 d.f. and a point mass at zero, and the LOD score for M2 to a more complicated distribution (Self and Liang, 1987). For the latter case we used the χ² distribution with the higher degrees of freedom, which is conservative, and used the associated p-value for interpretation of results. In a few cases we also computed empirical p-values by analyzing replicates in which single marker genotypes were simulated with MERLIN in the absence of linkage to the trait. For computational reasons, we generally limited such analyses to single-marker VC analysis, using 1000 such replicates. The exception was for chromosome 13 and SWE, as is described in more detail below.

MCMC joint linkage and SA

We used Loki version 2.4.5 (http://www.stat.washington.edu/thompson/Genepi/Loki.shtml) to perform joint oligogenic segregation and linkage analysis, as well as oligogenic SA in the absence of marker information. Loki estimates posterior distributions of model parameters using a Bayesian reversible-jump MCMC sampler (Heath, 1997), conditional on the data and prior distributions on several parameters (Wijsman, 2002). In this model, the number of QTLs is a random variable rather than a fixed quantity. Covariate adjustment was performed during the MCMC analysis, and details of the prior distributions and run conditions used were the same as described previously (Raskind et al., 2005), with initial linkage scans based on 200,000 MCMC iterations/chromosome, and runs of 400,000 iterations used for estimating genetic models associated with particular linkage signals. SA was generally based on 50,000 iterations.

Posterior distributions from the MCMC analyses were obtained for the number of QTLs; the parameters defining the mode of inheritance for QTLs; and, in linkage analyses, the locations of the QTLs. Specific parameters reported for each QTL accepted in the model during any given iteration include p_A, the frequency of allele A, and two “genotype effects” ε_AB = μ_AB − μ_AA and ε_BB = μ_BB − μ_AA, where μ_AA, μ_AB and μ_BB, are the means for genotypes AA, AB and BB, respectively. The allele labels A and B are arbitrary; we assigned allele A for each QTL such that the genotype BB effect was nonnegative. In some cases we also obtained the bivariate posterior distribution of ε_AB and ε_BB. The total genetic variance ( ${\sigma }_G^2$) was calculated from the model parameters for all QTLs, and this variance was subtracted from the overall trait variance after adjustment for covariates to obtain the residual trait variance for that model. We used the posterior mean of ${\sigma }_G^2$ summed over all QTLs from each iteration, as an estimate of the total genetic variance for a given phenotype: ${\sigma }_G^2=\frac{1}{I}{\displaystyle \sum _{i=1}^I}{\sigma }_{G_i}^2$, where ${\sigma }_{G_i}^2={\displaystyle \sum _{j=1}^k}{\sigma }_{g_{ij}}^2$ is the total genetic variation in iteration i, k is the number of QTLs in the model from iteration i, ${\sigma }_{g_{ij}}^2$ is the contribution of the jth QTL in iteration i, and I is the total number of iterations saved from the analysis (here, one-half of the total iterations performed after 1000 burn-in iterations). SA results are reported for τ_β values of 1, 256 and 1 for SWE, WID and SWE ~ WID, respectively, which maximized ${\sigma }_G^2$. These same values were also used for the linkage analyses. For linkage analyses, genotype effects were summarized for all QTLs with a location in a particular interval: anywhere on a chromosome, in a particular interval on a chromosome, or unlinked to any chromosomes.

Because the MCMC approach in Loki is based on a Bayesian framework, the strength of evidence for linkage in a particular data set and analysis cannot be expressed as a LOD score or as a p value. Instead, as described elsewhere (Raskind et al., 2005) we report the intensity ratio (IR), the ratio of the number of QTLs accepted in a particular region relative to the number expected if the distribution of QTLs were uniform across the genome, given the posterior mean of the total number of QTLs. The IR is conservative relative to the Bayes’ factors sometimes calculated from the posterior distributions of QTL location, if the posterior number of QTLs per iteration is greater than the prior mean number (Wijsman, 2002; Wijsman and Yu, 2004), and provides the ratio of the observed to expected number of times a particular location is accepted for a QTL in the linkage analysis, basing the expectation on the posterior mean number of QTLs. Another measure of signal intensity is the posterior probability of linkage (PPL) (Vieland, 1998), defined as the probability of linkage given the prior distributions and the data. The PPL to a chromosomal region is determined from MCMC output by calculating the proportion of MCMC iterations in which at least one QTL is accepted in the region.

Parametric LOD score analyses

Parametric LOD score analyses for small numbers of markers in key regions with positive evidence of linkage were carried out using FASTLINK (Cottingham et al., 1993). LOD scores were calculated based on genetic models for quantitative traits obtained from SA with both S.A.G.E. and Loki, using a maximum of three simultaneous markers because of computer memory constraints. Where the MCMC SA identified more than one prominent model of transmission, the model from the SA that was most similar to that associated with a linkage signal in the region was used. Covariate adjustments were performed using linear regression as described above, and the residuals were used as adjusted trait values. We also calculated heterogeneity LOD scores using HOMOG, but since the likelihood maximized under homogeneity, these results are not shown.

Additional analyses on chromosome 13

We carried out two additional analyses to further explore our strongest linkage result, which was for SWE on chromosome 13 (see Results). First, in addition to the 3-marker multipoint LOD scores obtained with exact computation, we estimated parametric LOD scores using simultaneously all 13 markers on chromosome 13 with an MCMC method implemented in the program LM_MARKERS from version 2.7 of the MORGAN suite of programs (http://www.stat.washington.edu/thompson/Genepi/MORGAN/Morgan.shtml). To the best of our knowledge, this is the only currently available program that provides parametric multipoint LOD score analysis for a quantitative trait model with many markers. Simulation studies (not shown) indicate that the approach used by LM_MARKERS slightly underestimates LOD scores in the presence of linkage. In this approach, sets of meiosis indicators consistent with observed data are sampled with a Gibbs sampler by MCMC and are used to calculate parametric LOD scores, given a particular genetic model for a diallelic QTL (George and Thompson, 2003; Thompson, 2003). The overall LOD score estimate is based on the mean of the likelihoods, computed for each iteration, over all iterations. Sequential imputation was used to generate 5000 initial sets of meiosis indicators (Kong et al., 1994), with the set yielding the greatest likelihood chosen as the starting configuration. Sampling was performed by scan, with equal probabilities of using a whole-meiosis and a whole-locus sampler (George and Thompson, 2003). Analyses were run over a long run of 200,000 MCMC iterations, following a 20,000-iteration burn-in period. The use of sex-specific maps did not substantially change the results obtained (data not shown).

The second analysis consisted of a simulation study to obtain empirical p-values under the null hypothesis of absence of linkage. With Merlin (for VC) or the program GENEDROP from the MORGAN package (for MCMC), we simulated marker data in the absence of linkage to the trait, using the empirical allele frequency distributions, missing data patterns, and meiotic maps as in the real-data analyses. Five hundred such simulated data sets were each analyzed with the same VC methods and the Bayesian MCMC oligogenic linkage analysis methods used on the real data, as described above, except that only 50,000 MCMC iterations were used for analysis. Computational demands limited this analysis to only evaluation of evidence of linkage of SWE to chromosome 13, and to analysis performed only for VC and Bayesian MCMC linkage analysis methods. The number of feasible replicates was similarly limited.

Quality control of genotype data

We checked the genotype data for Mendelian inconsistencies and highly unlikely genotypes, and resolved such potential genotype errors, as described previously (Chapman et al., 2004). Most individuals in the sample were well genotyped (Raskind et al., 2005), and thus we do not expect the results from statistical analyses to be highly sensitive to small changes in the estimated marker allele frequencies.

Results

Segregation analysis for real-word reading

Oligogenic SA indicated the presence of multiple QTLs affecting RWR, with distinct modes of transmission. From the MCMC SA we estimated the number of QTLs each accounting for at least 10% of the total variance of each trait, after adjustment for covariates: means of 1.6 for SWE, 2.1 for WID and 1.5 for SWE~WID. We investigated the mode of inheritance in greater detail using maximum-likelihood SA and analysis of posterior distributions of model parameters from MCMC SA.

Both ML and MCMC SA produced similar models for SWE (Table I). The parameter values differed primarily in that the estimate from ML had a slightly greater difference between the mean trait values of genotypes AB and BB than did the estimates from the MCMC model. From the MCMC analysis, the posterior bivariate distribution of genotype effects contained a single clear mode, as did the univariate distribution of p_A (data not shown).

Table I.

Models Obtained from Segregation Analyses for SWE, WID and SWE Adjusted for WID (SWE ~ WID)

Phenotype	Method	Model	pA	μAA	μAB	μBB	σ2
SWE	ML	RS	0.31	−1.77	−0.18	0.50	0.58
	MCMC	RL1	0.32	−1.70	−0.03	0.39	0.63
WID	ML	—	—	—	—	—	—
	MCMC	WL1	0.17	−26.4	4.8	−0.8	90.3
		WL2	0.85	−2.0	3.8	22.5	99.8
		WL3	0.36	−9.69	−0.29	3.54	100.2
SWE ~ WID	ML	RWS	0.08	−3.26	0.50	−0.07	0.49
	MCMC	RWL1	0.11	−2.31	0.34	−0.05	0.48
		RWL2	0.42	−0.65	0.05	0.27	0.47

p_A, frequency of minor allele A; μ_AA, μ_AB, μ_BB, mean trait values for genotypes AA, AB and BB, respectively; σ², environmental (residual) variance. The overall trait mean is zero in all phenotypes, which were adjusted for age (with different slopes for children and adults), sex and verbal IQ. A definite maximum-likelihood model could not be obtained for WID using ML.

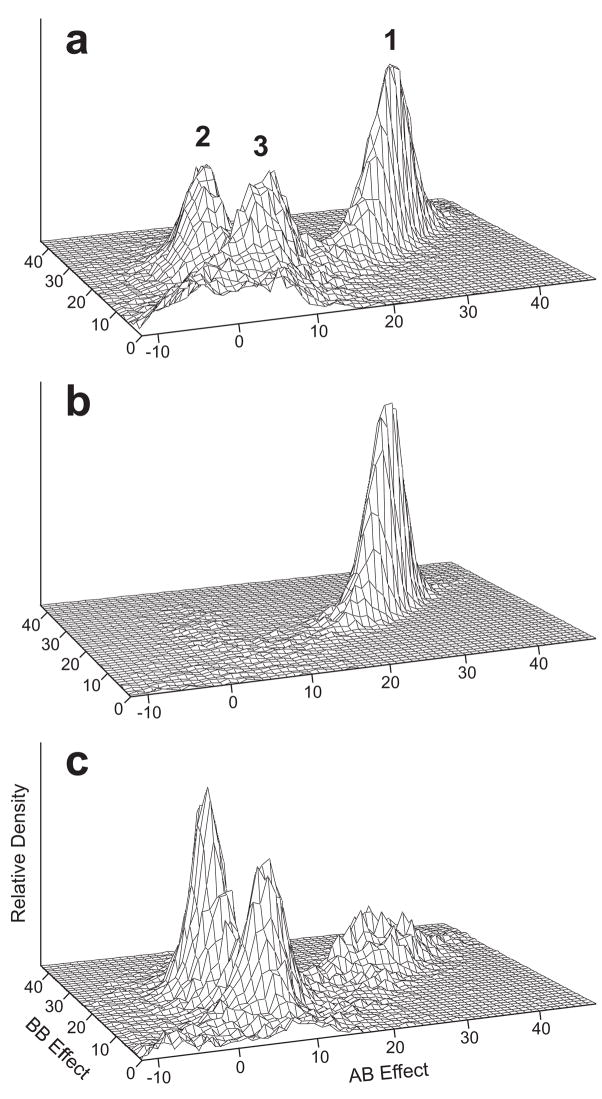
MCMC SA produced evidence for multiple QTLs for WID (Table I). The MCMC SA for WID produced a trimodal posterior distribution of genotype effects, representing three clearly different modes of transmission (Fig. 1a). The mode with the greatest posterior density corresponds to a slightly overdominant model with a heavily affected rare homozygote with mean trait value 2.8 SD below the overall trait mean (Fig. 1a, model 1 and Table I, model WL1). The three MCMC modes from the segregation analysis separated in linkage analyses to two different locations in the genome (Fig. 1b and Fig. 1c), as described further below. Unlike the MCMC results, the model parameters at convergence for ML analysis depended heavily on the starting values, and numerous models of similar likelihood were obtained, precluding identification of a single best model for WID.

Figure 1.

Plots of the posterior distribution of genotype effects for QTLs fitted in MCMC oligogenic model scans for WID adjusted for age, sex and verbal IQ. The relative posterior density (vertical axis) of QTLs accepted into the model over all MCMC iterations is plotted as a function of the effects of genotypes AB and BB relative to genotype AA (εAB and εBB, respectively). For clarity, allele A is always designated so that the εBB is at least zero, and the range of genotype effects is the same for all three panels. (a) All QTLs accepted in an MCMC segregation analysis. Numbers 1, 2, 3 correspond to the three genetic models WL1, WL2 and WL3 listed in Table I. The plateau of posterior density near the origin represents a background of QTLs of small effect. (b) QTLs placed between 38 and 48 cM in a joint MCMC segregation and linkage analysis of chromosome 15. (c) QTLs placed between 57 and 78 cM in an MCMC analysis of chromosome 12.

In the case of SWE ~ WID, both methods of analysis found a slightly overdominant transmission model with a rare and heavily affected minor homozygote (Table I). Analysis by ML estimated a considerably greater difference between the genotype AA and AB trait means (model RWS) than did analysis with the oligogenic MCMC approach (model RWL1). We found the existence of these models to be highly sensitive to the presence of three extreme scores for the adjusted phenotype, with values between −2.9 and −4.0, within the dataset of 108 families. However, a second mode in the posterior distribution from the MCMC analysis (model RWL2), with a larger minor allele frequency and much smaller differences in genotype means, was largely insensitive to changes in the three outlying trait values (data not shown), indicating that it was more appropriate for use in parametric linkage analyses.

Genomewide linkage scans

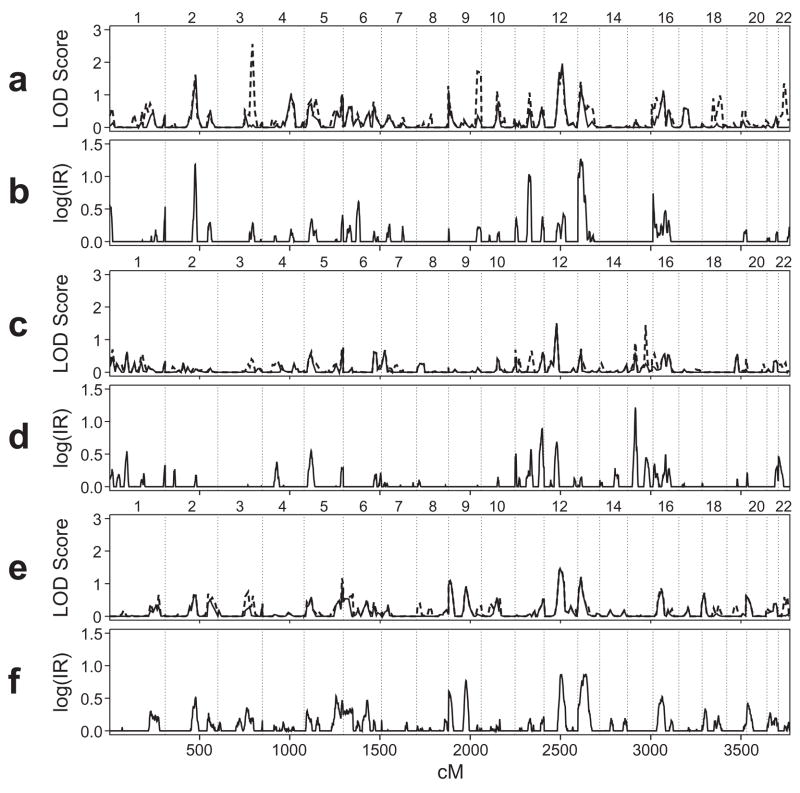
In the initial genomewide linkage scan for SWE, several regions provided evidence of linkage with VC and/or MCMC analysis (Fig. 2a-b). Except where noted we present VC results in the text for the dominance genetic variance model. Three regions gave consistent positive results with both methods: chromosome 2q (IR = 15.3 and VC-LOD = 1.62 at D2S1399; 169 cM); the pericentromeric region of chromosome 13 (IR = 22 and VC-LOD = 1.41 at ATA5A09; 23 cM); and more modest evidence on chromosome 11 (IR = 10.6 and VC-LOD = 1.07 at D11S2371; 83 cM). Each of these three regions is described in more detail below, particularly chromosome 13, which gave considerably stronger evidence for linkage with additional markers and followup analyses. The locations on 2q and 11 correspond to locations identified earlier in this sample with evidence of linkage for related measures of phonological decoding efficiency (Raskind et al., 2005). Chromosome 12q gave evidence for linkage in VC analysis with both additive and dominance models (VC-LOD = 1.8 at D12S1064; 105 cM), corresponding to a weak, bifurcated MCMC peak. Finally, two regions on chromosomes 3q (VC-LOD = 2.56 at D3S1763; 194 cM) and 9q (VC-LOD = 1.7 at D9S2157 and D9S1838; 161–181 cM) had moderately strong scores from VC analysis under a model that included dominance variance. These latter regions were not pursued further because of weak support from VC-LOD scores without dominance variance (Fig. 2a), and because MCMC single-marker analysis and parametric analysis based on models from the segregation analyses failed to support evidence for linkage to these two regions (results not shown).

Figure 2.

Whole-genome linkage scans for the phenotypes SWE (a, b), WID (c, d) and SWE adjusted for WID (e, f) using multipoint VC (top panel of each pair, VC-LOD) and MCMC (bottom panel, log(IR)) methods of analysis. VC-LOD scores with and without dominance variance are graphed with dashed and solid lines, respectively. Phenotypes were adjusted for age (with separate slopes for subjects above and below 25 years), sex and verbal IQ. Only MCMC IR values ≥1 (i.e., log(IR) ≥0) are shown, for consistency with the VC-LOD scores, which are bounded below at zero. Chromosome numbers are indicated above each pair of panels.

A somewhat different profile emerged from the initial scan for WID (Fig. 2c-d). Only two genomic regions, on chromosomes 12 and 15, provided relatively strong evidence for linkage from both VC and MCMC oligogenic analysis. Interestingly, the three modes of inheritance identified by MCMC SA in the absence of markers (Fig. 1a) corresponded precisely to models identified from two linkage signals on these two chromosomes. The QTLs mapping to the region on chromosome 15 with evidence of linkage represented Model WL1 (Table I) from the MCMC SA (Fig. 1a vs. Fig. 1b), while the QTLs mapping to chromosome 12 represented Models WL2 and WL3 (Table I) from the MCMC SA (Fig. 1a vs. Fig 1c). We previously characterized the chromosome 15 linkage signal (Chapman et al., 2004), associated with model WL1, here with IR = 16.4 at 43 cM and relatively weak support from the VC analysis. The second signal on chromosome 12 was associated with the other two QTL models (Fig. 1c), giving IR = 6 and VC-LOD = 1.5 at D12S297. Finally, modest evidence for linkage near the q-telomere of chromosome 11 was obtained with MCMC analysis (IR = 7.7 at 151 cM), but did not correspond to a sizeable VC signal.

The results from the genome scan for SWE adjusted for WID had partial overlap with the results obtained for SWE alone (Fig. 2e-f). In general, linkage signals obtained with this additional adjustment weakened signals obtained with SWE alone. Suggestive evidence for linkage with both VC and MCMC approaches persisted on chromosomes 12 (IR = 7.3 and VC-LOD = 1.47 at D12S1052; 92 cM) and 13 (IR = 7.5 and VC-LOD = 1.21 at ATA5A09, 45 cM). In contrast, the SWE peak on chromosome 2q (Fig. 2a-b) was markedly reduced by additional adjustment for WID (IR = 3.4 and VC-LOD = 0.65 at D2S1334, 158 cM).

Detailed linkage analyses

Four regions were investigated in more detail. These regions were selected (1) because they represented strong signals in the genome scans with consistent results across analysis methods, (2) because they represented signals that were observed across all three traits under investigation, and/or (3) because there was similar evidence of linkage to the same region for related measures (Raskind et al., 2005). In each region at least one additional marker was genotyped, and additional analyses were performed, including single-marker and parametric LOD score analyses.

Chromosome 13

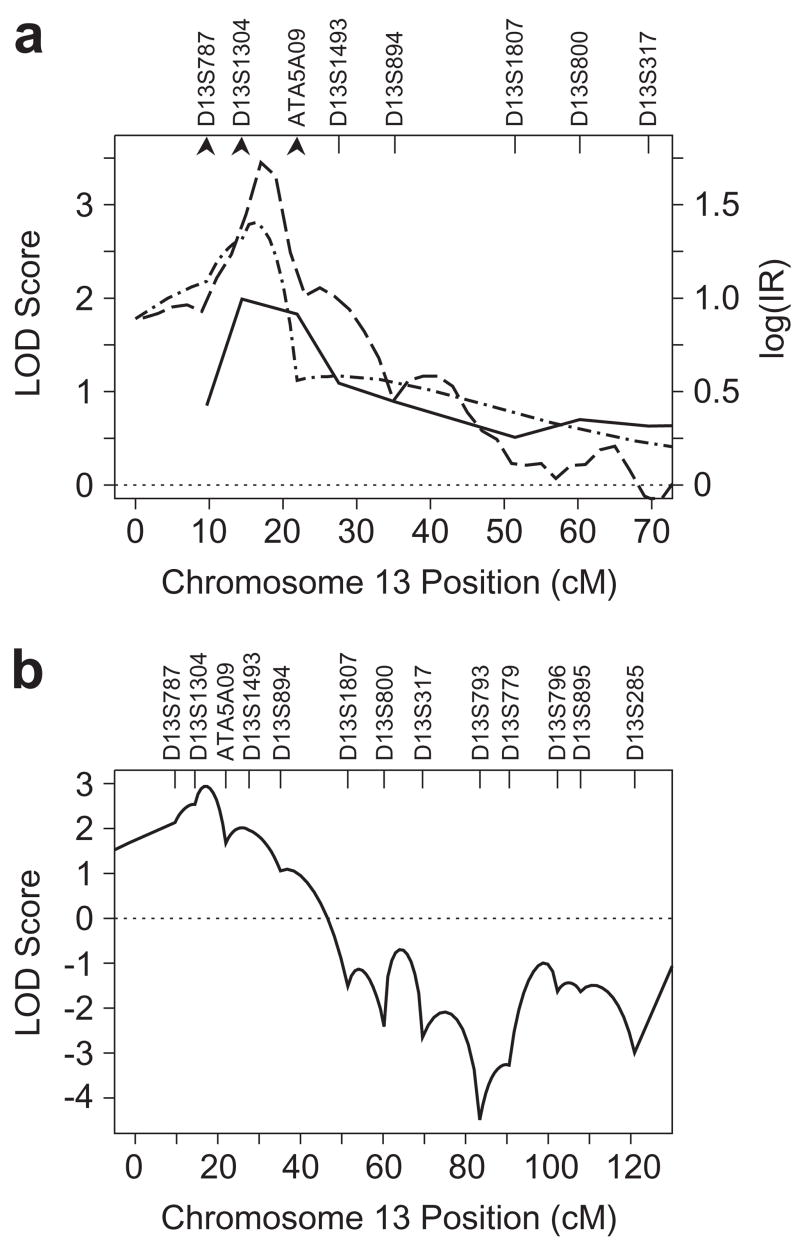
With the addition of a new marker and additional analyses, chromosome 13 provided significant evidence of linkage for SWE to the interval between D13S1304 and ATA5A09. The parameters for the QTLs identified in the pericentromeric region by MCMC oligogenic joint segregation and linkage analysis were virtually identical to model RL1, identified in oligogenic segregation analysis alone (results not shown). Genotypes for D13S1304 strengthened the evidence of linkage to the interval between D13S1304 and ATA5A09 (Fig. 3a). Strong evidence of linkage (maximum LOD = 2.94) was obtained with an MCMC-based parametric 13-marker LOD score analysis using on a quantitative trait model from the MCMC SA (Model RL1, Table I). The 13-marker LOD score maximized at 17.4 cM (Fig. 3b) and represented increases of 1.59 over the maximum single-marker parametric LOD score obtained with D13S1304 (Web Table B), and an increase of 0.13 over the maximum parametric LOD score obtained with the same trait model and exact computation with the three markers D13S787, D13S1304, and ATA5A09 that flank this region (Fig. 3a). All individual markers in the region gave results that were consistent with positive evidence for linkage for all three analysis approaches (Web Table B), and markers D13S1304 and ATA5A09 individually gave VC-LOD scores of 2.22 and 2.14, respectively. These results with single markers suggest that evidence of linkage is not explained by a single, influential marker. The posterior probability of linkage to chromosome 13 was estimated as 0.566 from the Bayesian MCMC analysis. Results from 500 marker data sets simulated in the absence of linkage to the trait locus support the strong evidence for linkage: these simulated marker data sets gave empirical chromosome-wide p-values of 0.004 and 0.04 for the observed multipoint maximum MCMC IR = 53.2 and VC-LOD_max = 1.99, respectively.

Figure 3.

Multipoint linkage analyses for SWE on chromosome 13. (a) Multipoint VC LOD scores (solid line), MCMC log IR (dashed line) and parametric LOD scores (alternating dashes and dots) are shown for the pericentromeric half of the chromosome. A dotted line marks the score expected in the absence of linkage (LOD score = 0, IR = 1). Four-point parametric LOD scores were calculated using segregation model RL1 (Table I) and the three markers indicated by arrowheads. (b) Multipoint MCMC parametric LOD scores for SWE, based on model RL1, and incorporating all available chromosome 13 markers.

The effect of adjusting SWE for WID was to reduce the peak strength the linkage signal on chromosome 13. Evidence of linkage for SWE ~ WID increased over the original genome scan with addition of D13S1304, but remained modest with a MCMC PPL of 0.298. Neither the multipoint VC-LOD nor parametric LOD scores exceeded 1.5, although the two-point VC-LOD was 1.64 at ATA5A09 (data not shown). The location of the maximum VC-LOD shifted to ATA5A09 at 22 cM, and the position of the LOD_max and maximum IR similarly moved to 32–33 cM on the map. Model parameters for this location from oligogenic joint linkage and segregation analysis were similar to model RWL2 obtained in the absence of linkage (results not shown).

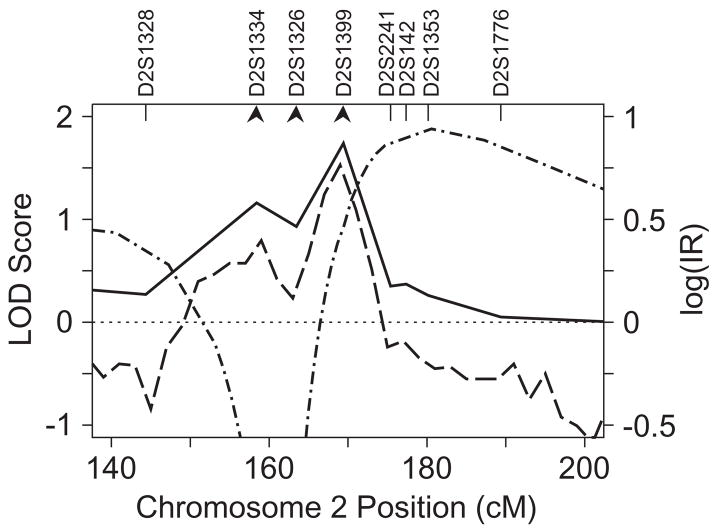
Chromosome 2q

Evidence of linkage to chromosome 2q was relatively unchanged with addition of three markers near D2S1399, the location of the highest linkage scores. There was only a slight enhancement of the multipoint VC-LOD score for SWE (VC-LOD = 1.74) (Fig. 4). The maximum parametric LOD score was slightly higher (LOD = 1.88), and was obtained for the three-marker combination D2S1334—D2S1326—D2S1399, using transmission model RS (Table I). The location of the maximum multipoint LOD score was about 11 cM distal to D2S1399. Single-marker LOD analyses supported evidence for linkage to this region, with positive LOD scores for all markers between D2S1334 and D2S142 (Web Table C), but the LOD scores generally maximized at recombination fractions in the range of 0.2–0.25. Since computation of heterogeneity LOD scores provided no evidence of heterogeneity, these results are most consistent with trait model misspecification.

Figure 4.

Multipoint linkage analyses for SWE on chromosome 2q. Multipoint VC LOD scores, MCMC log IR and parametric LOD scores are designated as in Fig. 3a. Four-point parametric LOD scores are shown using model RS (Table I) and the markers indicated by arrowheads.

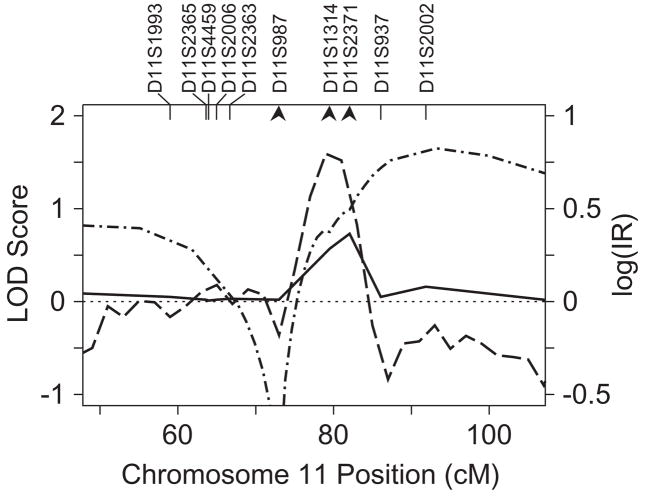
Chromosome 11

Typing of three additional markers in the region of chromosome 11 implicated for linkage here and previously (Raskind et al., 2005) also provided little change in the support for linkage (Fig. 5). Parametric LOD score analysis with markers D11S987, D11S1314 and D11S2371 provided additional suggestive evidence of linkage with LOD_max = 1.65 and LOD_max = 1.47 from models RL1 and RS, respectively, with the LOD score maximizing at 93 cM. This location was somewhat displaced from the MCMC and VC peaks at 79 and 82 cM, with maximum VC-LOD < 1, and IR = 6.2, respectively.

Figure 5.

Multipoint linkage analyses for SWE on chromosome 11. Multipoint VC LOD scores, MCMC log IR and parametric LOD scores are plotted as in Fig. 3a. Four-point parametric LOD scores using model RL1 and the three markers indicated by arrowheads.

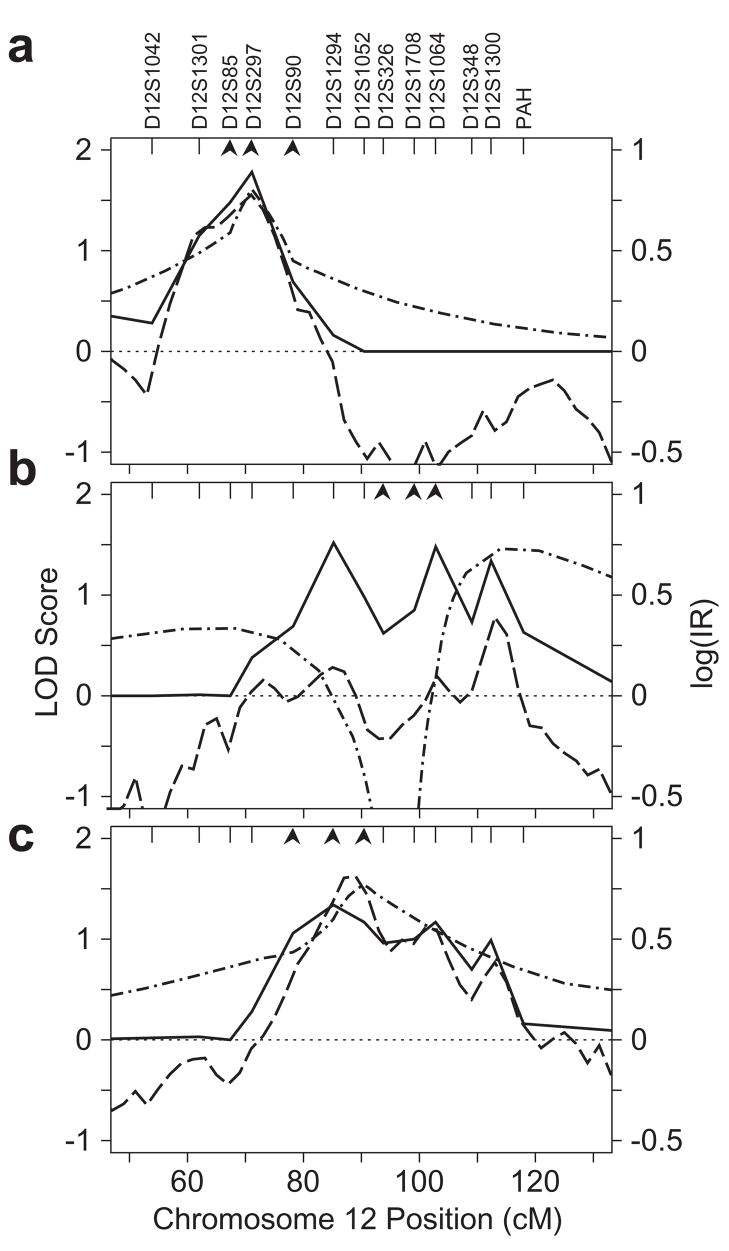
Chromosome 12

The most consistent evidence for linkage to chromosome 12 was obtained for WID. Multipoint analysis for WID, with additional markers, gave strong agreement among the three methods of analysis, with all approaches achieving a maximum score at marker D12S297 (71 cM) (Fig. 6a), and with little change in the location of the highest scores as new markers were included in the analysis. Additional investigation of the QTL models obtained with the Bayesian MCMC analysis approach revealed heterogeneity in the localization of the two models mapping to this region (Fig. 1c): QTLs with locations proximal to marker D12S85 (67 cM) primarily belonged to WL2, while QTLs with locations distal to D12S85 belonged predominantly to WL3 (data not shown). Because WL3 was the model best represented at the location with the maximum IR, we chose it for use in parametric 3-marker LOD score calculations. Signal strengths were all modest, with multipoint peak VC and 3-marker parametric LOD scores of 1.78 and 1.61, respectively, and an MCMC IR of 6.0.

Figure 6.

Multipoint linkage analyses for WID (a), SWE (b) and SWE ~ WID (c) on chromosome 12. Multipoint VC LOD scores, MCMC log IR and parametric LOD scores are plotted as in Fig. 3a. Four-point parametric LOD scores are shown using the marker combinations indicated by arrowheads in each panel. See text for explanation of choice of genetic models for WID.

Additional analyses of SWE and SWE~WID gave consistent evidence for linkage across more than 30 cM, with less focused localization than was obtained for WID. Several markers gave fairly strong evidence for linkage in single-marker analysis (Web Table D). Results were similar for SWE and SWE ~ WID, with D12S1064 (103 cM) in both cases providing the strongest evidence of linkage in single-marker analysis: VC-LOD = 2.19, IR = 29.1 and LOD_max = 2.56 for SWE, using the trait model on SA model RS; and VC-LOD = 1.34 for SWE ~ WID. Maximum multipoint linkage signals for these two phenotypes were broad and somewhat lower than the maximum single-marker LOD scores for the VC and Bayesian MCMC analyses. Three-marker parametric LOD scores gave LOD_max = 1.46 for SWE based on markers D12S326-D12S1708-D12S1064, and LOD_max = 1.54 for SWE ~ WID, based on model RWL2 and markers D12S90-D12S1294-D12S1052.

Discussion

We present here the results of genome scans for three related measures of real-word reading ability. Our scan for accuracy and speed of RWR (SWE) provided strong evidence for a locus on chromosome 13q12 with a parametric MCMC-based lod score of almost 3, and an empirical chromosome-wide p-value of 0.004 for results based on an oligogenic joint linkage and segregation analysis. In addition, we obtained support for a locus on chromosome 2 previously implicated using this dataset for phonemic decoding efficiency (Raskind et al., 2005). Results using our rate measure (SWE ~ WID) suggest that the locus on chromosome 13 affects primarily the rate of RWR. When we considered accuracy alone (WID), our strongest evidence for linkage was that previously identified on chromosome 15q (Chapman et al., 2004), although we also obtained weaker evidence here of linkage to chromosome 12. We were pleased to find consistency in the details of the QTL models identified by oligogenic segregation analysis alone, and the QTL models identified as part of the linkage analysis: even for the most complicated oligogenic trait model (that for WID), one of three QTL models identified in segregation analysis maps to chromosome 15, while the other two models map to a single interval on chromosome 12.

Our analyses revealed significant evidence for a novel locus for speed of word recognition on chromosome 13q. Evidence for linkage to 13q was still present when SWE was adjusted for WID, and no evidence was seen in this region using WID alone. Both of these results suggest that this locus is primarily associated with speed of word recognition. The absence of a prominent signal for WID on chromosome 13 may result from compensation for accuracy, but not rate, of word recognition in adults. In a subset of families from our dataset, when relative criteria (SWE compared to Verbal IQ) were used, affected adults were impaired in SWE but not WID (R. Abbott and V. W. Berninger, unpublished data). In contrast, their affected children (probands) were affected in both WID and SWE whether relative criteria or absolute criteria (at or below 1 SD below the population mean) were used. Consistent with this, in the current sample, the correlation between SWE and WID was 0.65 in the probands, but only 0.46 in the adults. These patterns suggest that a persisting subphenotype of dyslexia in adults is manifested through SWE rather than WID.

There is evidence from other studies for linkage to the proximal q arm of chromosome 13 for measures related to RWR. Although evidence for linkage of RWR phenotypes to this region has not been previously reported, significant evidence for linkage to a locus on 13q21 was reported for an IQ discrepancy measure of reading in a study focusing on specific language impairment (Bartlett et al., 2002). The measure used was WRMT-R Word Attack (WA) (Woodcock, 1987), which is a measure of accuracy of phonological decoding, and evidence for linkage was obtained with a parametric approach about 44 cM distal to the location of the LOD_max reported here for SWE. A speed-based measure of RWR was not used in the study by Bartlett et al. In addition, the values we obtained for the PPL of SWE to chromosome 13 are similar to the PPL of 0.53 reported by Bartlett et al., although care should be taken when comparing these PPL statistics, because they have different prior probability models and the sample sizes may not be large enough to completely overcome assumptions about prior distributions. Also, although the peak IR was considerably lower, the PPL for linkage of SWE ~ WID to chromosome 13 was still substantial. More work is needed to further evaluate the possibility that our results and those of Bartlett et al. may represent the same locus, especially in view of the difference in ascertainment of the two samples. Other reports of linkage to this region on 13q also have potential connections. Intriguingly, our maximum IR for SWE on chromosome 13 is located only about 5 cM proximal to a region implicated in linkage analysis of autism (Barrett et al., 1999), including measures of language acquisition in the parents of probands (Bradford et al., 2001).

Linkage peaks on chromosomes 2q and 11 in the present study overlapped locations implicated for measures of phonological decoding efficiency in analyses on the same sample of families (Raskind et al., 2005), but our results do not strongly support the existence of loci affecting word recognition on several other chromosomes with previous reports of linkage. Our linkage peak for SWE on chromosome 2q, at marker D2S1399, occurs at the same location as a significant finding for PDE, a measure of speed and accuracy of phonological decoding. Evidence for linkage to chromosome 2q persisted when PDE was adjusted for WA, suggesting that this locus acts primarily in speed of phonological decoding. Weak evidence for linkage to chromosome 11 in the case of SWE also occurs in the same region as suggestive linkage signals for both PDE and PDE adjusted for WA at marker D11S1314 (80 cM). The presence of a weak signal for SWE in the same locations as PDE supports this conclusion, and implies that this locus may affect word recognition as well as phonological decoding. Finally absence of strong support in our sample for loci affecting word recognition on chromosomes 1p, 2p, 6p or 18p in regions with previous reports of linkage is typical of complex traits and is not surprising, given the complex nature of dyslexia. Lack of confirmation should not be interpreted as exclusion of these other regions. Factors such as differences in the definition of the RWR phenotype may affect the results, as may ascertainment procedures used to obtain the families (Sillanpää and Auranen, 2004), and the well-known requirement for greater sample sizes in replication studies than in the original sample noted by Suarez et al. (1994).

Our analyses provide evidence for a genetically complex locus on chromosome 12. Both the current analysis of real word reading efficiency and a previous analysis of phonological decoding efficiency (Raskind et al., 2005) provided modest, but consistent, evidence of linkage to the same region with several methods of analysis. Evidence for linkage maximized over an interval of about 25 cM, depending on the specific phenotype and whether VC or oligogenic analysis was used. Two explanations may account for this variation in location. First, because of the assumption of a diallelic trait model, the MCMC approach may be more sensitive than the VC analysis to an underlying multiallelic trait model. The existence of two trait models for WID with the same location on chromosome 12 supports this interpretation since such multimodality has been observed in other situations where there is evidence for multiple alleles (Daw et al., 1999; Gagnon et al., 2003). Second, the assumption of an explicit trait model may mean that undetected data errors may more strongly influence the MCMC analysis. Results for two-point analysis compared to multipoint analysis are consistent with the interpretation that some aspect of model or data error may have influenced our results. Single-marker analyses, which are less sensitive to influences of both data and model error, identified D12S1064 as the marker with strongest evidence for linkage across all analysis approaches, and multipoint analysis based on a single QTL in the region gave the greatest displacement of estimated location.

The results presented here illustrate a particularly useful aspect of oligogenic segregation analysis. For all traits analyzed, the posterior distributions of QTL models obtained in oligogenic segregation analysis closely matched the equivalent distributions subsequently identified in linkage analyses. This gave particularly useful information for WID, since with a trimodal QTL model, no clear maximum-likelihood model was obtained via likelihood-based segregation analysis. In contrast, the MCMC oligogenic approach allowed investigation of the possibility of multiple modes of transmission and identified three such distinct modes for WID. These results suggest that failure to obtain a clear model from a SA assuming only one Mendelian locus may occur under a genetically heterogeneous trait. The MCMC oligogenic joint linkage and segregation analysis, on the other hand, was able to divide the modes of transmission between two specific locations in the genome, showing evidence for heterogeneity not only from segregation analysis, but also in the presence of linked markers. The SWE ~ WID phenotype further illustrates the advantages of an oligogenic modeling approach. This trait also gave different results for the two SA approaches, with two modes of transmission under the MCMC approach. The MCMC analysis provided additional information from which to choose parameters of a trait model for parametric LOD score analysis, giving positive evidence of linkage to chromosome 13q. Important insights regarding the genetic architecture of a trait can thus be obtained with oligogenic SA, and can be used making informed choices in design and analysis.

In summary, the results presented here provide evidence for linkage of a locus contributing to real-word reading efficiency on chromosome 13, and suggest that rate and accuracy measures for single-word reading have both shared and unique genetic determinants with each other and with other measures of phonological coding efficiency (Raskind et al., 2005). Although RWR incorporates phonological decoding to some extent, the present study indicates that some loci affecting RWR are unlikely to also govern phonological decoding. Specifically, in addition to the well-characterized DYX1 locus on chromosome 15, a rate and accuracy locus on chromosome 13 appears to contribute to RWR ability but not to phonological decoding. These studies highlight the complexity of dyslexia, and the need to focus on specific, well-defined measures of reading ability in genetic studies of this common trait.