Irregular and Semi-Regular Polyhedral Models for Rous Sarcoma Virus Cores

Abstract

Whereas many viruses have capsids of uniquely defined sizes that observe icosahedral symmetry, retrovirus capsids are highly polymorphic. Nevertheless, they may also be described as polyhedral foldings of a fullerene lattice on which the capsid protein (CA) is arrayed. Lacking the high order of symmetry that facilitates the reconstruction of icosahedral capsids from cryo-electron micrographs, the three-dimensional structures of individual retrovirus capsids may be determined by cryo-electron tomography, albeit at lower resolution. Here we describe computational and graphical methods to construct polyhedral models that match in size and shape, capsids of Rous sarcoma virus (RSV) observed within intact virions [8]. The capsids fall into several shape classes, including tubes, “lozenges”, and “coffins”. The extent to which a capsid departs from icosahedral symmetry reflects the irregularity of the distribution of pentamers, which are always 12 in number for a closed polyhedral capsid. The number of geometrically distinct polyhedra grows rapidly with increasing quotas of hexamers, and ranks in the millions for RSV capsids, which typically have 150 – 300 hexamers. Unlike the capsid proteins of icosahedral viruses that assume a minimal number of quasi-equivalent conformations equal to the triangulation number (T), retroviral CAs exhibit a near-continuum of quasi-equivalent conformations – a property that may be attributed to the flexible hinge linking the N- and C-terminal domains.

1. Introduction

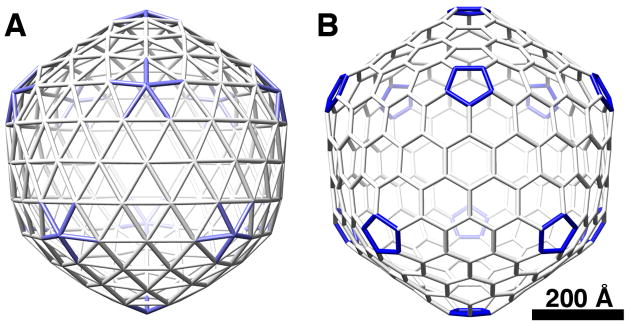
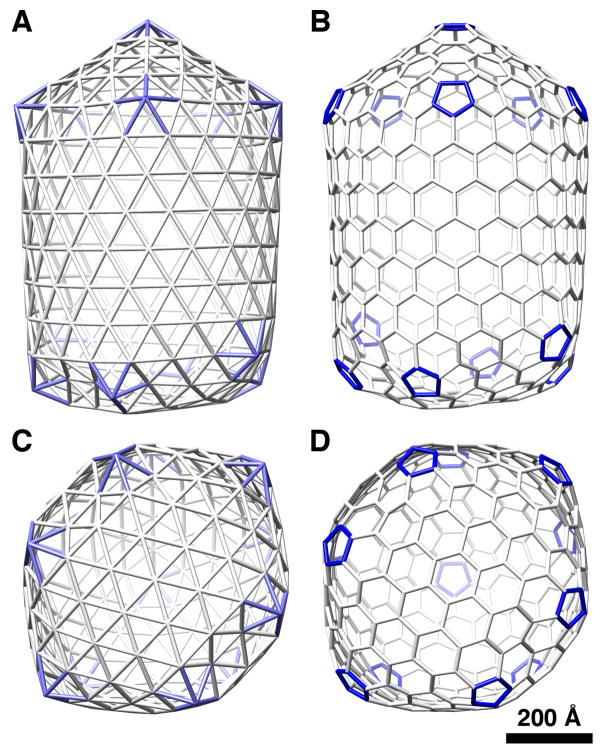
The ability of capsid proteins to assemble into closed hollow shells is a remarkable and still incompletely understood phenomenon. The best known architecture is icosahedral [12]. In the simplest case the shell is composed of 60 chemically and conformationally identical (equivalent) subunits. Larger capsids with more subunits are generated by tolerating small variations in subunit conformation and inter-subunit interactions (i.e. quasi-equivalence) [10]. With hexamer/pentamer clustering, a capsid has 12 pentamers and 10(T-1) hexamers where T is the triangulation number and reflects both the number of elementary triangles on an icosahedral facet and the number of distinct conformers. Continuous closure requires that T should comply with the selection rule T= (h² + h.k + k²) where h and k are non-negative integers. These structures may alternatively be considered as foldings of a planar hexagonal lattice of equilateral triangles or as honeycomb lattices of hexagons and pentagons (the latter is called a fullerene lattice). These are dual representations [11]. Fig. 1 shows the corresponding representations of a T=16 icosahedral polyhedron.

Figure 1.

Representations of a T=16 icosahedral polyhedron (A) by triangulation, i.e. as a deltagraph, and (B) as a fullerene with trivalent vertices and pentagonal (dark) and hexagonal faces.

Fullerene polyhedra have been studied quite extensively in carbon chemistry [25], and the short form “fullerene” has been adopted for all trivalent polyhedra with pentagonal and hexagonal faces. Here we will use the terms polyhedron and fullerene interchangeably, except in the case of triangular polyhedra or deltagraphs. Deltagraphs have triangular polygons and penta- or hexavalent vertices, and represent the dual graphs of fullerenes. The geometrical rules apply in the case of retroviral cores as it does for carbon fullerenes and other naturally occurring polyhedra.

Whereas most capsids observe icosahedral symmetry with a uniquely specified T-number, retroviral capsids are polymorphic; nor do they observe such a high order of symmetry. Human immunodeficiency virus (HIV) has predominantly conical capsids of varying sizes [3, 5, 6]. Tubular as well as roughly isometric capsids are encountered in other retroviruses [8, 43]. Ganser et al [20] proposed that the conical cores are fullerene cones, following a similar proposal for structures related to carbon nanotubes [37]. Tubular polymers with open or closed ends could be modeled from the same lattice [6, 22]. Although no detailed structure has yet been determined for any native retroviral capsid, a considerable body of evidence including electron microscopy (EM) analysis of in vitro CA assemblies (sheets and tubes) and low resolution images of virions support the hypothesis that the capsids are all foldings of the same basic lattice [19, 21, 27, 30–33]. In it, three CA subunits are arranged around each fullerene vertex, giving 6 CA subunits in each hexagonal face (Fig. 2) and – presumably - 5 in each pentagonal face. CA has two domains, the N and C-terminal domains (NTD and CTD), connected by a flexible linker [9]. Despite little sequence similarity, the domains’ folds are largely conserved among different retroviruses.

Figure 2.

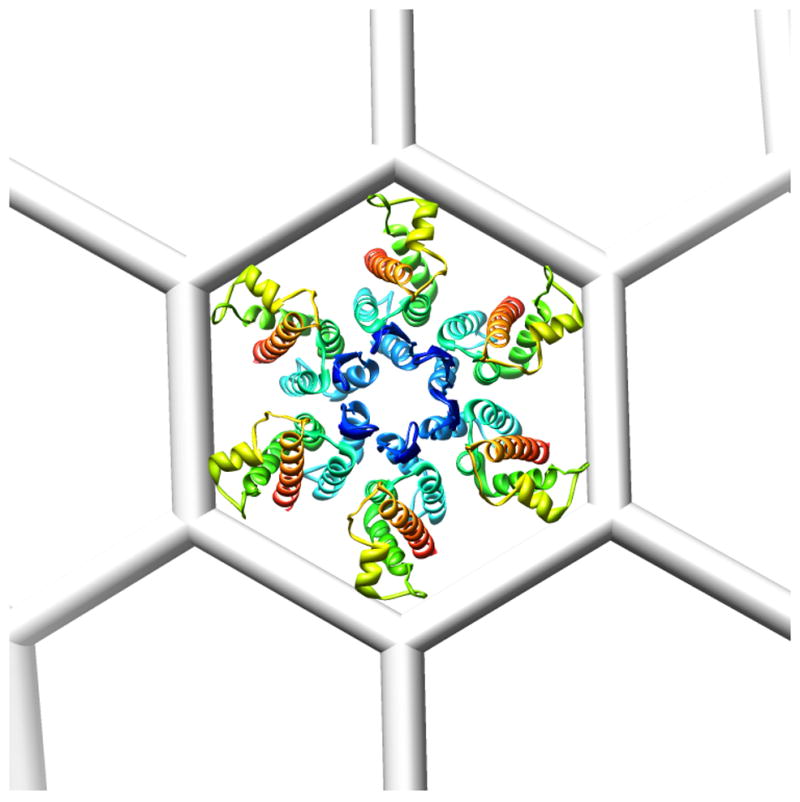
Placement of the N-terminal domain hexamer of murine leukemia virus (1U7K, [34] into a hexagon in a fullerene lattice, in an orientation based on a 2D crystal of RSV CA [32]. The inter-vertex links are 55 Å in length.

Cryo-electron tomographic (cryo-ET) reconstructions of virions provide a more informative point of reference than thin sections for modeling capsid structures [8]. Here we describe our approach to modeling and apply it to our data set of RSV virions to further explore their capsid geometry.

2. Materials and Methods

2.1. Tomography of RSV

Tomography was done and subvolumes with RSV particles extracted as described [8].

2.2. Constructing polyhedra

All computational work was done with programs written using the Bsoft package [23]. Visualizations were done with the UCSF Chimera package [36]. A model in Bsoft is defined as an object with a set of components and links between these components. In the context of the RSV cores, each component is a polyhedral vertex, and corresponds to 3 CA molecules. The file storage format for a model is either a Protein Data Bank (PDB) file, a Chimera Marker Model (CMM) file, or a Self-referencing Text Archiving and Retrieval (STAR) file.

2.3. Manual construction

A polyhedral network can be built by drawing a 2D network on paper, cutting it out in the desired shape, and folding it to close the seams. A small tool was written in Chimera [36], called the Triangle Net tool, which allows the user to go through these steps. First, a large 2D array of triangles is generated. Next, the unwanted vertices and triangles are deleted. The array is then folded into a cylinder, and the seams stitched up to close the polyhedron. Finally, the polyhedron is regularized as described below. The triangle net or deltagraph has vertices with 5 or 6 links to other vertices. Its dual graph is a polyhedron where the vertices and polygons have been interchanged, giving the fullerene type polyhedron with trivalent vertices, pentagons and hexagons. The difficulty with this approach is that there are only a few ways in which the seams close to give polyhedra without defects (i.e., closed polyhedra).

2.4. Cylindrical algorithm

Tubular polyhedra with open or closed ends can be built using a simple cylindrical algorithm. The ends can be defined as open, or capped by a hexagonal or pentagonal arrangement. A hexagonal cap is typically flat while a pentagonal cap forms a half-icosahedral shape on regularization.

2.5. Spiral algorithm

Polyhedra in general can be built from successive additions of polygons in spiral patterns [7, 16], and this spiral algorithm was implemented in the program bspiral. Not all sequences of polygons produce closed polyhedra, and these are eliminated as the spiral algorithm reaches a non-productive state and cannot continue to form a closed polyhedron.

The spiral algorithm produces a topological graph of the polyhedron, i.e., defining the links between vertices. The eigenvectors of the adjacency matrix corresponding to the second, third, and fourth largest eigenvalues were used to generate the initial Cartesian coordinates [16]. The set of eigenvalues was also used as a signature to identify identical polyhedra generated from different polygon sequences.

2.6. Polyhedron regularization

Whatever the technique for constructing an initial polyhedron, it invariably displays distortions from the desired result. The polyhedra were regularized in a manner similar to approaches used in molecular modeling, using an iterative method to minimize a cost or energy function:

$$\begin{array}{l}E=E_l+E_a+E_r+E_p\\ E_l=K_l\sum _{i,j}{(l_{ij}-l_0)}^2\\ E_a=K_a\sum _{i,j,k}{(cos{a}_{\mathit{ijk}}-cos{a}_0)}^2\\ E_r=K_r\sum _i{(d_{ic}-d_{0c})}^2\\ E_p=K_p\sum _i{d_{ip}}^2\end{array}$$

The different energy components are: E_l, link deviation; E_a, angular deviation; E_r, polygon regularity deviation; and E_p, polygon planarity deviation. The link deviation is a simple harmonic function of the difference between the link length and a reference link length, l₀. The reference angles used are the angles inscribing the type of polygon: a₀ = 108° for pentagons and a₀ = 120° for hexagons. The deviation from polygon regularity is defined as the difference between the distance of a vertex from the polygon center and a reference distance, d_0c. Similarly, the deviation from planarity is defined as the distance of a vertex to a plane fitted through the polygon vertices, d_ip. The contribution of each term in the energy function is determined by the energy constants, K_<x>.

For each vertex, a force vector is accumulated from the derivatives of the energy terms with respect to the coordinates for that vertex. All the coordinates are updated during each iteration by small shifts based on the force vectors. The number of iterations required is typically of the order of 10⁵.

The progress of regularization and the success of finding an acceptable minimum depend on an appropriate choice of the energy constants. Values that are too high result in very distorted polyhedra, while those that are too low produce very little change. In many cases polygon regularity and planarity cannot be satisfied simultaneously in a closed polyhedron, in which cases the regularity deviation term is usually omitted. In general, parameters can be found to regularize any polyhedron to an acceptable form.

3. Results and Discussion

3.1. Range of Polymorphic Variation in RSV Cores

Our data set comprises 95 virions determined by cryo-ET [8]. Of these, no two have capsids that are congruent, i.e. superimposably alike. The observed polymorphism led us to enquire as to the total number of geometrically distinct capsids that may be assembled from 1500 – 3000 copies of CA. In this survey, we distinguish between two forms: open-ended tubes and closed polyhedra. Tubes with both ends closed form a subset of the latter class, and tubes with one end closed may be accounted by referring to the two main classes.

3.2. Diversity of Open-ended Tubes

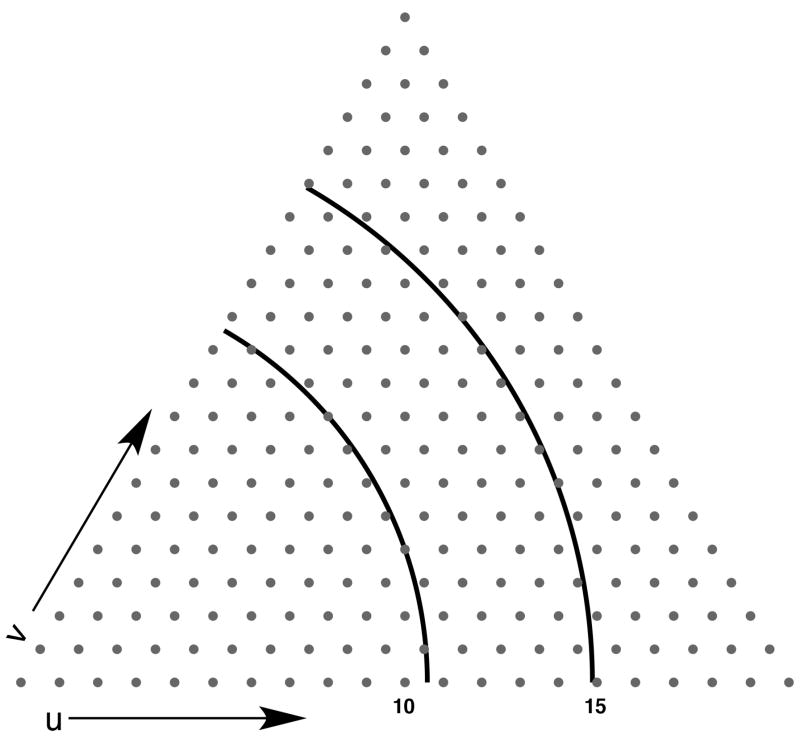
Tubular foldings of a hexagonal net have been studied in the context of “polyheads” of bacteriophage T4 (e.g. [38, 42]). Each tube may be described by a coordinate pair (u, v) on a hexagonal lattice (the Goldberg diagram), where u and v are non-negative integers and define the equatorial vector for a strip that, when cut out and folded into a cylinder, gives continuity of the lattice lines along the seam. The tube diameter is given by $\phi =\frac{l}{\pi }\sqrt{u^2+uv+v^2}$, where l is the lattice constant. In the case of RSV-CA tubes, l = 9.5 nm [32] and the observed minimum and maximum diameters of tubes in our data set were 320 Å and 450 Å, respectively. The number of distinct tubes in this diameter range is given by simply counting the lattice points in this sector (Fig. 3), which are approximately 40 for RSV tubes (not counting enantiomorphs –mirror symmetry related forms). This figure represents a maximum number and not all (u, v) pairs may be used. With T4 polyheads, only a subset of (u, v) coordinates in a given diameter range are observed, suggesting that assembly favors a certain intrinsic curvature [38].

Figure 3.

Every point in the Goldberg diagram, defined by the integer coordinates u and v, represents a distinct cylindrical tube. The points between the solid arcs correspond to tubes with observed diameters for RSV tubes open at one or both ends. Tubes with u > v (< v) have right-handed (left-handed) foldings.

3.3. Diversity of Closed Polyhedra

Whereas tubes could be assessed in a straightforward way in terms of triangulation geometry, polyhedra were more readily dealt with in the dual fullerene representation. Considerable effort has gone into investigating the geometry of fullerene shells in the context of carbon chemistry [7, 16]. Acknowledging the basic differences between C atoms and CA subunits, this work provides a platform for considering retroviral capsid geometry. Almost all fullerene polyhedra have the property that their constituent polygons may be unwrapped in a spiral pattern to yield a linear sequence [17]. (The smallest fullerene without this property has 380 vertices [29]). Thus a fullerene may be defined by a sequence of numbers, each referring to a polygon of the stated order, 5 for a pentagon and 6 for a hexagon. The smallest fullerene is the dodecahedron with 12 pentagons and 20 vertices, corresponding to the sequence 555555555555. Including two hexagons produces the next smallest fullerene with 24 vertices, encoded as 55555655655555.

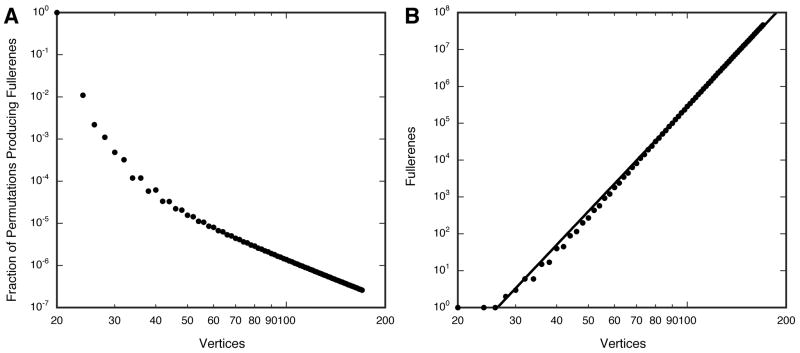
Just as polygons may be unwrapped in spiral fashion, so they may be constructed by reversing the process. An algorithm, called the spiral algorithm, has been devised for this purpose [17]. For a sequence of n polygons, 12 of which are pentagons and the remainder hexagons, the number of permutations is $\frac{n!}{12!(n-12)!}$. Application of the spiral algorithm shows that, for a given n, only a few of the permutations produce closed structures (Fig. 4A). For instance, a sequence starting with 12 pentagons followed by hexagons, e.g. 5555555555556666, will result in the construction of a dodecahedron from the 12 pentagons, leaving no vertices with less than 3 links available to add another polygon, rendering such a sequence unproductive. The trivial case of a sequence with fewer than 12 pentagons, e.g. 55555555, gives a partial dodecahedron, leaving some vertices with fewer than 3 links, and thus an open polyhedron. In addition, topologically identical structures can be generated with different sequences. These are eliminated using the eigenvalues derived from the adjacency matrix as a signature [16]. The numbers reported here are for unique structures.

Figure 4.

(A) The spiral algorithm was used to try every possible permutation of 12 pentagons for each given number of hexagons. The fraction of permutations that yields closed polyhedra decreases rapidly with increasing number of hexagons or (as shown) of vertices. (B) Notwithstanding, the number of possible closed fullerenes increases dramatically with increasing size (vertex number) in a combinatorial fashion. Fit: Fullerenes = 4.093 × 10⁻¹⁴ × vertices^9.416.

Even though the number of successful, i.e. closed, constructions drops to 1 in a million or less beyond a hundred vertices (Fig. 4A), the number of sequence permutations is so high that millions of fullerenes can be generated, increasing rapidly with the number of vertices (Fig. 4B). This diversity suggests that the total range of polymorphism that may be encountered among closed RSV capsids, which have 300 – 600 vertices (900 – 1800 CA molecules [8]), is very large.

Viewed in the light of these numbers, our failure to find two congruent capsids in a set of only 95 particles is unremarkable. However, it is by no means certain – indeed, we consider it unlikely – that all theoretically possible structures are, in fact, assembled. By using the cryo-tomograms to guide modeling of the 3D structures of bona fide intraviral capsids, we may begin to approach this issue.

3.4. Constructing Polyhedral Models

Many of the capsids appear to be closed shells. We cannot say with certainty that they are fully closed because the “missing wedge” effect of tomography [18] degrades resolution along the upper and lower surfaces. Nor is it unequivocal that these lattices are without local vacancies, because of limited resolution and residual noise. Nevertheless, we proceed on the basis of the assumption that the capsids are closed polyhedra, i.e., fullerenes.

We devised methods to construct polyhedra manually or using the cylindrical algorithm for tubular models. In our approach (see Methods and below), the constraint of closure is imposed by requiring that each vertex has exactly three links to neighboring vertices. Selection of polyhedra that best fit the cores was based on visual inspection. A few examples of the resulting models for different types of cores are shown in Figs. 5–7.

Figure 5.

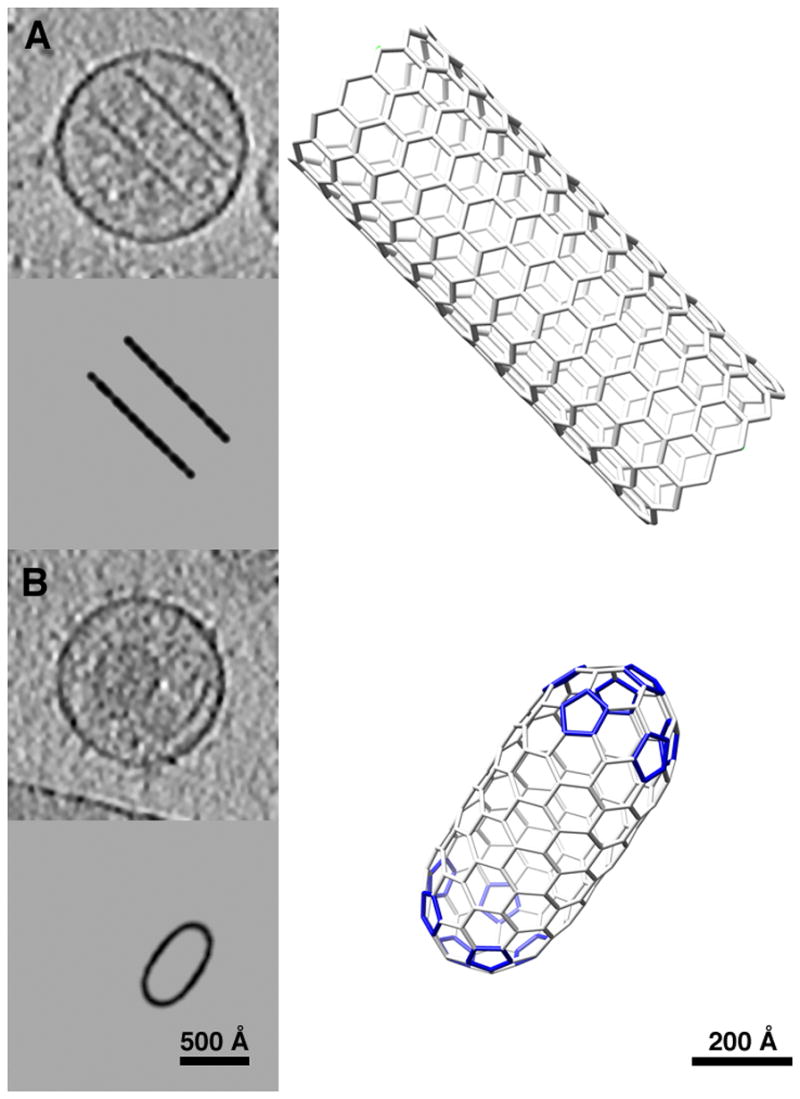
Polyhedral models similar to (A) open and (B) closed (“lozenge”) tubular cores observed in tomograms of RSV virions. In each panel a slice through the tomogram is shown in the upper left, with a corresponding slice through the modeled core beneath, and a 3D representation to the right.

Figure 7.

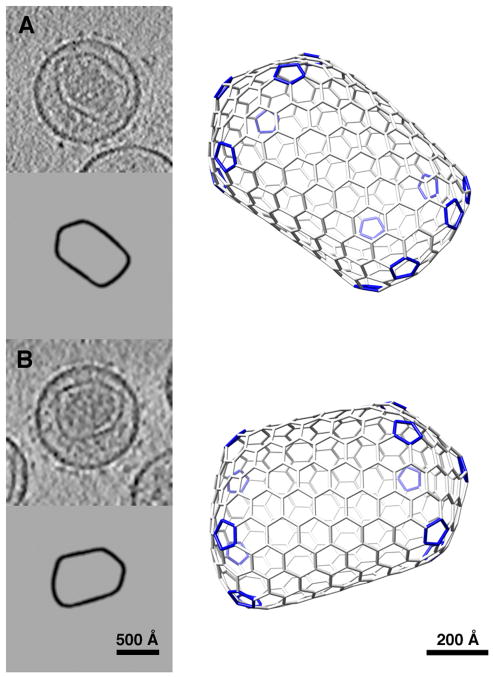
Polyhedral models similar to coffin-shaped cores observed in tomograms of RSV virions. In each panel a slice through the tomogram is shown in the upper left, with a corresponding slice through the modeled core beneath, and a 3D representation to the right. Each model has a sharp, icosahedron-like end, and a blunt end with pentagons arranged around the collar.

3.5. Tubes

Open-ended tubular cores were modeled with the cylindrical algorithm (Fig. 5A). This model corresponds to (u, v) = (13, 0), i.e. it has a set of zero-pitch lattice lines. Other solutions corresponding to all-helical lattice lines, i.e. with u ≠0 and v ≠0 (Fig. 3), but with a similar diameter are, in principle, applicable.

3.6. Lozenges

Several RSV cores have a tubular shape with rounded ends, which we call “lozenges” [8]. The simplest model is a tube with two icosahedral end-caps as generated by the cylindrical algorithm. In the example shown in Fig. 5B, which concerns a relatively small core, 720 Å long by 320 Å in diameter, the model fits well into the capsid density. The caps have a T=4 icosahedral arrangement and there are six hexagonal rows between the caps. This structure is similar to tubular cores observed and modeled for HIV [6] and MPMV [22]. Models were also generated with hexagonal caps, i.e., six pentagons around the collar with a hexagon in the center. These produce lozenges with either more rounded or flatter caps, depending on the diameter of the tubes. In many cases examined, such regular models did not fit well into the experimental densities, indicating that capsids with the form of regular fullerene lozenges are quite rare.

3.7. Coffins

Some RSV cores are somewhat elongated with one end pointed and the other end flat and have been dubbed “coffins” [8]. The sharp end resembles an icosahedral cap (Fig. 1) and this was used to guide our modeling. Fig. 6 shows the result of one such experiment in the form of dual graphs of a manually constructed polyhedron with a T=16 icosahedral cap at one end and a quasi-6-fold arrangement at the other end. Attempts to model the latter feature as an exactly six-fold base failed to yield a model without defects along the axial seam (defects being defined as vertices with fewer or more links than three). As the entirely manual approach turned out to be quite limited in scope, we developed methods to steer the cylindrical and spiral algorithm towards specific shapes.

Figure 6.

A coffin-like polyhedron represented both as a deltagraph (A,C) and as a fullerene (B,D). Both side views (A,B) and bottom views (C,D) are shown. The side views show the top cap that corresponds to five facets from the T=16 icosahedron shown in Fig 1. The bottom views show a quasi-hexagonal arrangement with six pentagons arranged around the bottom collar. Cf. Butan et al [8].

3.8. Other Irregular Polyhedra

To generate models that are similar in shape to coffins but less regular, we adapted the spiral algorithm, limiting the permutations of the polygon sequence to three regions: the cap, starting with a pentagon and only exploring pentagon positions around the collar; the body, consisting only of hexagons with some variation in their number; and the base, where the pentagons were mostly restricted to the collar. Even with these constraints, it was possible to generate hundreds of models. In some cases, the sharp angle of the core cap observed in a tomogram (such as in Fig. 7A) could not be reproduced accurately, suggesting the icosahedral design may not always apply to end-caps. The bases of the models typically are not flat (Fig. 7), indicating that it may be difficult to arrange the pentagons in a highly regular fashion.

3.9. Curvature in polyhedra

The RSV cores typically exhibit angular vertices that are well separated and are the most likely locations of pentagons (Figs. 5–7). This is consistent with the “isolated pentagon rule” for carbon fullerenes, where the separation of pentagons has been linked to stability [2]. These points of high curvature in the RSV cores represent the key locations where the lattice is folded to allow closure of the polyhedron.

3.10. Polymorphism and Conformational Variability

The precept that chemically identical subunits adopt different conformations in distinct locations in a capsid is widely applicable and of long standing [10]. Isometric icosahedral capsids require only a few variations in subunit conformation, the number being given by the triangulation number, T. The capsid contains 60 copies of each conformer. One generalization of the icosahedral design, as in bacteriophages T4 [1] and φ29 [40], involves extension along an axis of symmetry – the 5-fold axis in the case of T4, whereby the point group symmetry is reduced from 5-3-2 to 5-2. The number of quasi-equivalent conformations is given by T + Q where Q is the triangulation number of a facet in the elongated mid-section - e.g. T=13 [1] and Q=20 [14] for T4. For most viruses, the T-number is a uniquely defined and evolutionarily robust parameter, although there are exceptions such as hepatitis B virus which produces capsids of both T=3 and T=4 [39], and the bacteriophage P2/P4 system which produces capsids of T=4 and T=7 [13].

Retroviruses exhibit a much wider range of capsid polymorphism although it is still based on a fullerene lattice folded in ways that correspond to different, and generally less regular, insertion patterns of pentagons. The predominant type of core appears to vary among different retroviruses. The majority of HIV cores have the form of fullerene cones as proposed by Ganser et al. [20], and subsequently confirmed in tomographic studies [3, 5]. For other retroviruses, lozenge-like forms are envisaged for MPMV (Mason-Pfizer monkey virus) and rounder forms for MuLV (murine leukemia virus) - [22]. With RSV, cores with large, closed, irregular, quasi-isometric, polyhedral shells were inferred to be the form most likely to correlate with infectivity [8].

The two domains of CA are connected by a flexible linker and their folds are largely conserved in the absence of sequence homology outside of the MHR (major homology region). The structures of helical tubes [27] and two-dimensional crystals [19, 21, 30–33] of CA proteins established the pattern of NTD hexamers on a hexagonal lattice, connected to each other through CTD dimers. The closed polyhedral capsids also have 12 pentagons that are presumably occupied by NTD pentamers, although this configuration has yet to be confirmed in a solved structure. It is plausible that the extravagant polymorphism of retrovirus capsids reflects flexibility of the inter-domain linker that allows the hexamers to interface in many slightly different ways, resulting in a near-continuum of subunit conformations and capsid curvatures that vary, locally, from nearly planar to smoothly curving. Variations in the CTD dimer interface and/or warping of the oligomeric NTDs could also contribute to the curvature [21].

It appears likely that, with retroviruses, infectivity is not limited to virions with uniquely defined capsid structure. With RSV, closed polyhedral capsids tend to be well filled with ribonucleoprotein and are hypothesized to be viable cores of infectious virions [8], a property previously attributed to the conical capsids of HIV [15, 41]. These forms differ in the pattern in which pentamers are distributed over the polyhedral lattice. Although we are far from a detailed understanding of how assembly is regulated, we may speculate about some possible mechanisms. First, it has been posited that initiation is a determinant of the final capsid shape [5, 8]; moreover, initiation may involve the generation of one or more 5-fold sites from which the lattice grows out. Other factors that may influence its subsequent growth are: interaction with glycoprotein endodomains [8], and/or with the nucleocapsid, or simple steric balking when the growing capsid abuts against the inner surface of the envelope [5]. Another potential factor is the stepwise nature of processing of the Gag precursor. At one extreme, unprocessed or minimally processed Gag may be involved in initiation [8]. At the other extreme, co-assembly of mature CA subunits with incompletely processed subunits – e.g. subunits retaining SP, a 9 amino acid spacer peptide at the CA C-terminus [35] – may influence the outcome of assembly. CA-SP cleavage intermediates co-exist transiently with fully processed CA in maturing RSV virions [4]. Retention of SP1 in CA of HIV similarly affects the normal assembly of the capsid [24, 26]. There is precedent for such a morphogenic mechanism in the case of IBDV (infectious bursal disease virus), the assembly properties of whose VP2 capsid protein are modulated by the retention of a C-terminal peptide(s) from its precursor pVP2 [28].