Skip to main content
PMC home page
Molecular Biology of the Cell logoLink to Molecular Biology of the Cell
. 1998 Nov;9(11):3031–3040. doi: 10.1091/mbc.9.11.3031

A Polymer Model for the Structural Organization of Chromatin Loops and Minibands in Interphase Chromosomes

Joseph Ostashevsky 1
Editor: Joseph Gall1
PMCID: PMC25584  PMID: 9802894

Abstract

A quantitative model of interphase chromosome higher-order structure is presented based on the isochore model of the genome and results obtained in the field of copolymer research. G1 chromosomes are approximated in the model as multiblock copolymers of the 30-nm chromatin fiber, which alternately contain two types of 0.5- to 1-Mbp blocks (R and G minibands) differing in GC content and DNA-bound proteins. A G1 chromosome forms a single-chain string of loop clusters (micelles), with each loop ∼1–2 Mbp in size. The number of ∼20 loops per micelle was estimated from the dependence of geometrical versus genomic distances between two points on a G1 chromosome. The greater degree of chromatin extension in R versus G minibands and a difference in the replication time for these minibands (early S phase for R versus late S phase for G) are explained in this model as a result of the location of R minibands at micelle cores and G minibands at loop apices. The estimated number of micelles per nucleus is close to the observed number of replication clusters at the onset of S phase. A relationship between chromosomal and nuclear sizes for several types of higher eukaryotic cells (insects, plants, and mammals) is well described through the micelle structure of interphase chromosomes. For yeast cells, this relationship is described by a linear coil configuration of chromosomes.

INTRODUCTION

The higher-order structure of interphase chromosomes is still poorly understood. Many models in the literature include a loop structure as one of the high levels of packing of a chromatin fiber in the nucleus (for review see van Holde, 1989; Wolffe, 1995). Earlier studies have suggested that an average chromatin loop contains ∼50–100 kbp DNA (van Holde, 1989; Wolffe, 1995), whereas more recent studies suggest large loops of ∼1–3 Mbp, which may include 50- to 100-kbp loops (Razin and Gromova, 1995; Sachs et al., 1995; Yokota et al., 1995; Johnston et al., 1997).

On the scale of 1–3 Mbp, high-resolution mapping of replication bands in S phase (Drouin et al., 1990, 1994) is similar to a quasiperiodic pattern of G (for dark in Giemsa) and R (for reverse, light in Giemsa) minibands observed in prophase chromosomes (Bak et al., 1981; Yunis, 1981). G minibands are AT rich, late replicating, and gene poor, whereas R minibands are GC and gene rich and early replicating and contain a less compact chromatin than do G minibands (Holmquist, 1992; Craig and Bickmore, 1993; Yokota et al., 1997). Isochores, long DNA segments having a size range from 0.2 to 1.3 Mbp with an excess of one type of nucleotide (e.g., AT rich or GC rich), are found in the genome of higher eukaryotes (Bernardi, 1995).

An important feature of G1 phase chromosomes is that they behave approximately as ideal Gaussian chains, which obey random-walk statistics (van den Engh et al., 1992; Sachs et al., 1995; Yokota et al., 1995). This was concluded from the proportionality between the mean square geometrical distance between two points on the chromosome and their genomic distance, on the scale up to ∼1 Mbp. On a larger scale (up to 200 Mbp), this dependence has a much shallower slope than the initial one (Sachs et al., 1995; Yokota et al., 1995).

On the nuclear level, G1 chromosomes tend to occupy exclusive territories rather than overlapping extensively (Haaf and Schmid, 1991; Cremer et al., 1993; Zirbel et al., 1993; van Driel et al., 1995; Kurz et al., 1996; Ferreira et al., 1997; Zink et al., 1998). There is some contradiction between the random-walk behavior of chromatin and the discreteness of chromosomal domains: random coils do not have clear boundaries, and they are prone to overlap (de Gennes 1979; Grosberg and Khokhlov, 1994).

The size of a nucleus influences the compactness of individual chromosomes (Yokota et al., 1995, 1997; Sanchez et al., 1997). Compartmentalization of nuclear space is characteristic for chromosome functions (Spector, 1993; Strouboulis and Wolffe, 1996). In particular, DNA replication starts only in several hundred clusters per nucleus in early S phase (for review see Berezney et al., 1995a; Jackson and Cook, 1995).

Several polymer approaches to chromosomes exist in the literature (van den Engh et al., 1992; Hahnfeldt et al., 1993; Ostashevsky and Lange, 1994; Sikorav and Jannink, 1994; Duplantier et al., 1995; Sachs et al., 1995; Jannink et al., 1996; Ostashevsky, 1996, 1998; Houchmandzadeh et al., 1997; Liu and Sachs, 1997; Marko and Siggia, 1997a); however, only a few articles consider interphase chromosomes.

This study develops a model of the higher-order structure of interphase chromosomes that deals with the problems and takes into account the main facts mentioned above. In this model, based on the isochore model of the genome (Bernardi, 1995) and results obtained in the field of copolymer research (e.g., see Semenov et al., 1995, 1996), a G1 chromosome is approximated as a multiblock copolymer containing two types of blocks differing in GC content.

RESULTS AND DISCUSSION

The Model’s Background

The presented model of interphase chromosomes is based on the following assumptions.

1) A mammalian G1 chromosome can be approximated as a multiblock copolymer alternately containing two types of polymer blocks different in GC content (Figure 1). This assumption is supported by the observation that the DNA sequence of high eukaryotes is not random but is a mosaic of isochores, which are long DNA segments (0.2–1.3 Mbp) with an excess of one type of nucleotides (AT or GC) (Bernardi, 1995). Although five families of isochores can be defined in mammalian genomes, the division of polymer blocks in two classes, R (GC rich) and G (AT rich), as made in the presented model, can be considered as a first approximation. It is argued below that the R and G blocks in the model are related to the interphase and prophase R and G minibands, which are ∼1 Mbp in size (Bak et al., 1981; Yunis, 1981; Ronne et al., 1995); thus, the terms blocks and minibands will be used interchangeably in this article.

Figure 1.

Figure 1

Open in a new tab

A mammalian G1 chromosome is approximated as a multiblock copolymer containing two types of polymer blocks with different GC contents. Light and dark chromatin segments are R and G blocks, respectively.

2) A multiblock copolymer containing two alternately located types of blocks can form a single-chain string of loop clusters called micelles (Halperin, 1991). A micelle consists of a certain number of loops, the termini of which, formed by blocks of one type, are located in close proximity to each other (Figure 2). Micelle structures are well studied for diblock copolymers (polymer chains having only two blocks) and ionomers (polymer chains with charged groups at the ends) (e.g., see Semenov et al., 1995, 1996). Large multiblock copolymers form single-chain micelles, and small diblock copolymers form multichain micelles. Formation of loops and organization of them in micelles constitute an entropically unfavorable process, because the number of possible polymer conformations decreases, but it occurs in multiblock copolymers because of the energically favorable processes of repulsion between unlike monomer units and/or attraction between like monomer units (de Gennes 1979; Grosberg and Khokhlov, 1994). For a multiblock copolymer in aqueous solution, which contains two types of blocks with hydrophobic and hydrophilic groups, hydrophobic blocks form loop termini at the micelle cores, and hydrophilic blocks are located at loop apices.

Figure 2.

Figure 2

Open in a new tab

Schematic drawing of a micelle in a G1 chromosome. Dark and light chromatin blocks are G and R minibands, respectively. Segments drawn with free ends can be either chromosome ends or intermicelle links. The circle represents the micelle core (see inset), where loop termini are located. The dark dots at loop termini represent multiprotein complexes, e.g., replication complexes.

3) Incompatibility between GC- and AT-rich blocks can contribute to micelle formation. On average, R minibands are at least ∼3% richer in GC content than G minibands (Saitoh and Laemmli, 1994). Approximately 80% of the known genes are found in R minibands (Craig and Bickmore, 1993). This suggests that more histones are chemically modified, e.g., acetylated, in R than in G blocks, and more transcription complexes are bound to R than to G blocks. Because of the large size of the blocks (0.5–1 Mbp), even a small difference in interaction energy per monomer between unlike versus like monomers can lead to block separation: the blocks of one type form the loop termini, and the blocks of the other type are located at loop apices. Marko and Siggia (1997a) suggested that one can determine the parameters of the GC versus AT incompatibility by mixing bacterial DNA molecules that have very different GC contents.

Another contribution to stabilization of the chromosome micelle structure could come from multiprotein complexes, which participate in many chromosome functions at various stages of the cell cycle, e.g., transcription, replication, and chromosome condensation. Multiprotein complexes may associate differently with R and G blocks, as was suggested above for transcription complexes. For DNA replication, we assume that replication complexes are located in the micelle cores at the onset of S phase (see below).

4) The average loop size in interphase chromosomes in the model is assumed to be in the range of 1–2 Mbp. This is consistent with a loop containing two isochores or two replication minibands of size 0.5–1.0 Mbp, which seems to be reasonable (Bernardi, 1995; Simon and Cedar, 1996). The range of loop sizes for a large number of mammalian cell lines was estimated to be between 1.2 and 2.2 Mbp (Johnston et al., 1997). In the nuclei of early embryos of Drosophila, contacts between chromatin and the nuclear envelope have a frequency of one per 1–2 Mbp (Marshall et al., 1996). Because a loop contacts the nuclear envelope at its apex in the presented model, this leads to a 1- to 2-Mbp loop size.

Some Properties of Chromatin and Micelles

Individual loops in micelles behave as independent Gaussian coils. On the other hand, micelles are not interpenetrating (Semenov et al., 1995). Thus, the micelle structure of interphase chromosomes reconciles the contradiction mentioned in the INTRODUCTION between the discreetness of chromosomal territories and the random-walk behavior of chromatin.

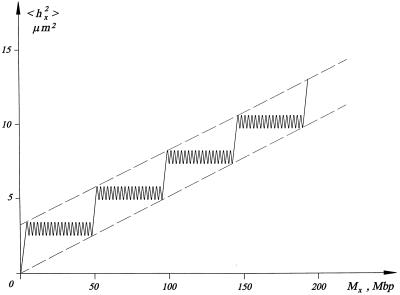
Random-walk behavior of chromatin was demonstrated (van den Engh et al., 1992; Sachs et al., 1995; Yokota et al., 1995, 1997) by the linear dependence of the mean square of the geometrical distance between two probes on the same chromosome, 〈hx2〉 (μm2), versus their genomic distance, Mx (Mbp):

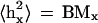graphic file with name M1.gif 1

where the coefficient B (μm2/Mbp) describes chromatin compactness. Equation 1 is valid on the scale up to ∼1 Mbp, no matter where two probes are located on the chromosome, and deviations from the linear dependence are observed for Mx > 1 Mbp. Equation 1 describes the behavior of ideal Gaussian chains, which particularly occurs in polymer melts or θ solvents (de Gennes 1979; Grosberg and Khokhlov, 1994). Although the conditions for chromosomes in nuclei might not be the same as in a melt or a θ solvent, here we consider ideal Gaussian chains as a first approximation, because the values of B have been obtained using this assumption (van den Engh et al., 1992; Sachs et al., 1995; Yokota et al., 1995, 1997).

It is known (e.g., see de Gennes, 1979) that 〈hx2〉 can also be represented as 〈hx2〉 = bLx, where b is the length of the Kuhn statistical segment, and Lx is the fiber contour length. These two quantities are interrelated through k, the mass of the Kuhn statistical segment, and Mx: b/k = Lx/Mx. Thus, B in Eq. 1 can be expressed as B = b2/k.

Because the 30-nm chromatin fiber has ∼0.2 kbp per nucleosome (van Holde, 1989; Wolffe, 1995), n, the number of nucleosomes per 10 nm of chromatin fiber contour length, can be estimated from the above expressions, as:

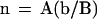graphic file with name M2.gif 2

where the coefficient A = 50 μm/Mbp (=10 nm/0.2 kbp).

It has been shown that values of B for chromatin in R minibands are ∼2.5-fold greater than those in G minibands, independent of fixation technique (Yokota et al., 1997). The fixation technique strongly affects the absolute values of BG and BR (values of B for G and R minibands, respectively), in parallel with nuclear size (Sachs et al., 1995; Yokota et al., 1995, 1997). For paraformaldehyde-fixed human fibroblast nuclei, nuclear size is not changed by fixation, and BG = 0.5 μm2/Mbp and BR = 1.3 μm2/Mbp (Yokota et al., 1997). We shall use these values and their average value B = 0.9 μm2/Mbp for the calculations below.

The larger value of BR relative to BG means that chromatin in R minibands is stretched in comparison with that in G minibands. In the accordion-like structure of the chromatin fiber (Woodcock et al., 1993; Horowitz et al., 1994; Woodcock and Horowitz, 1995), angles between links increase under stretching, which leads to an increase in the ratio of chromatin contour length to chromatin mass, L/M, which = b/k, and an increase in b/k leads to an increase in the values of B (see above).

Experimental data (Castro 1994; also see Marko and Siggia, 1997b) indicate that the Kuhn segment length b ∼ 60 nm. Substituting BG = 0.5 μm2/Mbp and BR = 1.3 μm2/Mbp, and b = 60 nm in Eq. 2, one obtains n = 6 and 2.3 nucleosomes per 10-nm contour length for G and R minibands, respectively. These values are consistent with experimental data for chromatin structure: n = 6–8 nucleosomes per 10 nm for a compact chromatin fiber and n = 1–2 nucleosomes per 10 nm for a stretched chromatin fiber (van Holde and Zlatanova, 1995, 1996; Woodcock and Horowitz, 1995).

It has been shown for micelles that the polymer blocks that form micelle cores are stretched (see e.g., Semenov et al., 1995, 1996), because a large block incompatibility favors an increase in micelle size, and this leads to stretching of polymer blocks in the micelle cores. Applied to R and G minibands in chromatin micelles, this suggests that R blocks, which are stretched, are located at loop termini, and G blocks, which are unstretched, are located at loop apices. This assignment of R and G minibands is consistent with their replication time patterns (see below).

Dependence of Mean-Square Geometrical Distance on Genomic Distance for G1 Phase Chromosomes

The dependence of mean-square geometrical distance, 〈hx2〉, on genomic distance, Mx, has been obtained on the 0.1–200 Mbp scale for three chromosomes (4, 5, and 19) in fixed human fibroblasts (Sachs et al., 1995; Yokota et al., 1995). These data can be summarized as having experimental points located between two parallel lines that have a shallow slope of ∼20-fold less than the slope of this dependence over a short range (<1 Mbp). The authors suggested a model of chromosome structure that includes ∼3-Mbp loops containing flexible chromatin that corresponds to a steep slope and a much less flexible nonchromatin backbone that corresponds to a shallow slope (also see Liu and Sachs, 1997). However, the measurements under separation of <1 Mbp, wherever one looks in the chromosome, never reveal a shallow slope (Yokota et al. 1995, 1997); this puts in doubt the existence of a rigid backbone.

The presented model suggests that intermicelle links and micelle tails contain the same material as micelle loops, the 30-nm chromatin fiber. The 〈hx2〉 versus Mx dependence following from this model is presented schematically in Figure 3. The net increase in 〈hx2〉 inside a micelle is zero, because the loop termini are located randomly and very close to each other in the micelle core. Thus, the 〈hx2〉 versus Mx dependence in the model is due to chromosome tails and intermicelle links.

Figure 3.

Figure 3

Open in a new tab

Schematic drawing of the dependence of 〈hx2〉, mean-square geometrical distance, vs. Mx, genomic distance between two points on a G1 chromosome. The 〈hx2〉 vs. Mx dependence is due to chromosome tails and intermicelle links, because the net increase in 〈hx2〉 inside a micelle is zero. Dashed lines represent the boundaries of the experimental points. The model predicts that their slope (Bapp) is f-fold shallower than the initial slope (see Eq. 6), where f is the average number of loops per micelle.

Let us consider the 〈hx2〉 versus Mx dependence quantitatively. Suppose a G1 chromosome of size Mo (megabase pairs) forms several micelles with an average loop size, Mf (megabase pairs), and an average number of loops per micelle, f. The number of micelles per chromosome, m, can be expressed as:

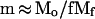graphic file with name M3.gif 3

As shown in Figure 3, straight lines for the boundaries of the experimental points can be defined as those connecting a telomere and the opposite tail base. Both lines have the same slope, Bapp, which can be defined as:

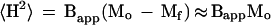graphic file with name M4.gif 4

On the other hand, the same mean-square distance can be expressed as caused by a chromosome tail and the m-1 intermicelle links:

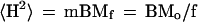graphic file with name M5.gif 5

Equating Eqs. 4 and 5, one obtains the expression for the average number of loops per micelle, f:

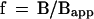graphic file with name M6.gif 6

The meaning of Eq. 6 is that because there is one linear intermicelle link per f loop, representation of micelle structure as a linear coil yields a slope = Bapp, which is f-fold shallower than that for the micelle. The estimate of f from Eq. 6 is independent of any parameter of the model and equals the ratio of two measurable values, which was found to be ∼20 (Sachs et al., 1995; Yokota et al., 1995). Thus, data for the geometrical versus genomic distances for human G1 fibroblasts (Sachs et al., 1995; Yokota et al., 1995) suggest that the average number of loops per micelle, f, is ∼20 in these cells.

The number of loops per micelle in G1 fibroblast chromosomes (f ∼ 20) is comparable with the number of loops per micelle for ionomers, which is 5–50 (Semenov et al., 1995, 1996). The value of f is limited by the maximal number of polymer chains that can be brought together in a micelle core (Semenov et al., 1996).

A crude estimate of flim, the maximal number of loops per micelle, is as follows. The number of loop termini confined in the micelle core is ≈f, the number of loops per micelle (exactly f + 1). Suppose Dc is the micelle core diameter, L is the loop terminus contour length, and h is the distance between the entrance and exit points of a loop terminus. The total volume occupied by chromatin fibers in the micelle core is ≈fd2L, where d is the chromatin fiber diameter (=30 nm). The average contour length, L, can be expressed as 〈h2〉/b (see above), where 〈h2〉, the mean-square average cord length in a sphere, = Dc2/2, and b is the Kuhn segment length (=60 nm). Equating the total volume occupied by loop termini to the micelle core volume = πDc3/6, one can estimate flim as:

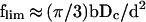graphic file with name M7.gif 7

It is argued below that chromatin replication starts at the micelle cores. Taking the diameter of replication “factories” (∼0.2–0.3 μm [Hozak et al., 1993; Tomilin et al., 1995]) as a range of Dc, Eq. 7 yields flim ∼ 10–20; this is comparable with the value of f estimated above.

The number of micelles per G1 nucleus, Nm, can be estimated as:

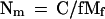graphic file with name M8.gif 8

where C is the G1 DNA content. Diploid human cells have C = 6.4 Gbp, and for f = 20 and Mf = 1–2 Mbp, Eq. 8 yields Nm = 160–320. This estimate is important for discussion of the relationship between micelle structure and DNA replication.

Micelle Structure and DNA Replication

In high eukaryotes, but not in yeast, chromosome structure plays an important role in replication initiation (Coverley and Laskey, 1994; Laskey and Madine, 1996; Gilbert, 1998). Let us show that the proposed model is consistent with data for early S phase replication in mammalian cells if we suggest that at the onset of S phase, chromatin replication is initiated at the loop termini in micelle cores. The following points support this suggestion.

1) If replication starts in the micelle cores, R blocks that form loop termini (see above) should replicate earlier than G blocks. This is consistent with the fact that R minibands replicate earlier than G minibands (for review see Drouin et al., 1994). Thus, in this model two features of R minibands, stretched chromatin and early replication, could be explained by their location in micelle cores.

2) In the model, chromatin fibers contact the nuclear membrane at loop apices. Thus, the observation that the nuclear periphery contains predominantly late-replicated G minibands (Ferreira et al., 1997) is consistent with the assignment of G minibands to loop apices.

3) If replication starts in the micelle cores at the beginning of S phase: a) the number of replication clusters per nucleus should be similar to the number of micelle cores (Nm) in G1 phase; b) the number of minifoci per cluster should be similar to the number of loop termini per core (f); and thus, c) the total number of minifoci per nucleus should be similar to the product fNm. At the onset of S phase, nuclei with C ∼ 6 Gbp (e.g., diploid human fibroblasts and V79 cells) have 100–300 replication clusters with ∼20 minifoci per cluster (Berezney et al., 1995a; Jackson and Cook, 1995); this is consistent with the estimates obtained above: Nm = 160–320 and f ∼ 20. Cell lines with C = 9–10 Gbp (e.g., mouse 3T3 and human HeLa) have 600–750 replication clusters with ∼10–12 minifoci per cluster (Jackson and Pombo, 1998), or a total number ∼6000–9000 minifoci per nucleus, which is consistent with fNm = C/Mf = 4500–10000 for these cells. These data suggest that f is ∼10–20 for various cells.

4) Replication-labeled clusters were observed through several cell cycles (Jackson and Pombo, 1998), and their number doubles in G2 versus G1 (Jackson and Pombo, 1998; Zink et al., 1998). The size of these labeled chromatid subdomains is ∼0.4–0.8 μm (Zink et al., 1998). This is comparable with our estimate of the size range of G and R minibands, i.e., 0.5–1.1 μm (=[BMf/2]1/2, see Eq. 1) for B = 0.5–1.3 μm2/Mbp (Yokota et al., 1997) and Mf = 1–2 Mbp.

Thus, the suggestion that replication clusters can be considered a fundamental aspect of the higher-order structure of the genome (Berezney et al., 1995b; Jackson and Pombo, 1998; Zink et al., 1998) can have micelle cores as its basis.

Relationship Between Size of Interphase Nucleus and Chromosome Compactness

One test of the model is that the chromosome size estimated with the model must not exceed the size (length and thickness) of the corresponding nucleus, and that the total chromosomal volume or area must not exceed the nuclear volume or area. To estimate the micelle diameter, a micelle can be represented as a star-branched polymer with branch size of Mf/2. Because chromatin in loops behaves as a Gaussian chain, and because the branch ends are close to each other in the micelle core, the mean-square micelle diameter, 〈Dm2〉, is equal to double the mean-square branch size:

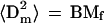graphic file with name M9.gif 9

where the average value B = (BG + BR)/2.

For human fibroblasts, replacing Mf = 1–2 Mbp and B = 0.9 μm2/Mbp in Eq. 9, one obtains 〈Dm2〉1/2 = 0.9–1.3 μm, which is close to the smallest nuclear thickness measured for cultured cells (=1.2 μm) observed for human AG1522 fibroblasts in monolayer (Raju et al., 1991). This suggests a two-dimensional (2-D) organization of micelles in a monolayer of flattened AG1522 cells.

The mean-square chromosome length, 〈H2〉, can be presented as the end-to-end distance for a random walk of m micelles, each of length (diameter) Dm. Replacing Dm and m from Eqs. 3 and 9, one obtains:

graphic file with name M10.gif 10

Equation 10 is the same as Eq. 5, where the expression for 〈H2〉 was obtained as a random walk of the intermicelle links. Thus, two approaches yield the same values of H. For human fibroblasts, replacing f = 20 and B = 0.9 μm2/Mbp in Eq. 10, one obtains 〈H2〉1/2 ∼ 4 μm for the largest (Mo = 263 Mbp) human chromosome. For a fibroblast in monolayer, this is much smaller than its nuclear dimensions (∼10–30 μm [Yokota et al., 1997]).

The 2-D chromosome territories have been measured for chromosomes 17 (=4.1 μm2; Mo = 92 Mbp) and the inactive X (=5.2 μm2; Mo = 164 Mbp), respectively, in human fibroblasts (Clemson et al., 1996). For a chromosome consisting of m micelles, the 2-D chromosome area, Ac, can be presented as a sum of micelle areas, = (π/4)Dm2m, which is only slightly different from the expression for 〈H2〉 (see Eq. 10). It follows from Eqs. 3 and 9 that Ac = (π/4)BMo/f. Thus, B can be estimated from Ac as:

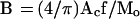graphic file with name M11.gif 11

For f = 20 and the above values of Ac, Eq. 11 yields B = 1.1 and 0.8 μm2/Mbp for chromosomes 17 and X, respectively. These values are close to the average value of B = 0.9 μm2/Mbp (Yokota et al., 1997).

Chromosome compactness seems to be adjusted to nuclear size (Yokota et al., 1995, 1997; Sanchez et al., 1997). We shall estimate B from nuclear cross-section areas and nuclear volumes. The test is whether the estimated values of B fall within the range of experimental values. We assume that the chromosomes fill all available space in the nucleus. This assumption is consistent with observations of constrained diffusional motion of chromosomes in the nucleus (Abney et al., 1997; Marshall et al., 1997).

For 2-D nuclei, the available nuclear area is αAn, where α is the occupancy factor, and An is the nuclear cross-section area. Because there is a large number (hundreds) of micelles in a nucleus (see above), the occupancy factor α for tightly packed micelles in a nucleus can be taken to be α ∼ π/4, as for squared circles. Equating the available nuclear area to the sum of micelle areas, = NmπDm2/4, and using Eqs. 8 and 9, one obtains an estimate for B from An:

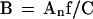graphic file with name M12.gif 12

Human HSF7 fibroblasts (C ∼ 6 Gbp) and HeLa cells (C ∼ 9 Gbp) form a monolayer of flattened cells, and their nuclei may be approximated as 2-D. Experimental values of their nuclear cross-section areas are An = 160, 240, and 400 μm2 for the paraformaldehyde-fixed HSF7 and MAA-fixed HeLa and HSF7 cells, respectively (Yokota et al., 1997). For f = 20, Eq. 12 yields B = 0.5–1.3 μm2/Mbp, which is close to the experimental values (Yokota et al., 1997).

For 3-D nuclei, the available nuclear volume is αVn, where Vn is the nuclear volume and α is the occupancy factor, which can be taken to be ∼π/6, as for cubed spheres. Equating the available nuclear volume to the sum of micelle volumes, Nmπ〈Dm2〉3/2/6, and using Eqs. 8 and 9, one obtains:

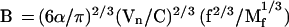graphic file with name M13.gif 13

Table 1 presents estimates of B from Eq. 13 for f = 10–20, Mf = 1–2 Mbp, and α = π/6. It follows from Table 1 that the whole range of estimated B, 0.2–1.5 μm2/Mbp, is consistent with the range of experimentally determined values (Yokota et al., 1997). The values of n, the number of nucleosomes per 10 nm of chromatin fiber contour length estimated from Eq. 2, range between 2 and 13, which seems to be reasonable (van Holde and Zlatanova, 1995, 1996; Woodcock et al., 1995).

Table 1.

Relationship between nuclear volume and coefficient B

Cells C (Gbp) Vn (μm3) C/Vn (Mbp/μm3) Ba (μm2/Mbp) nb nucleosomes (per 10 nm)
Series of 30 plants (Baetcke et al., 1967) 62 0.2–0.5 6–13
Lymphocyte 6.4 110c 58 0.2–0.5 6–12
AG1522 6.4 220d 29 0.4–0.8 4–8
Series of 18 mammalian cell lines (Sontag et al., 1990) 24 0.4–0.9 3–7
Drosophila 0.33 30e 11 0.7–1.5 2–4
S. cerevisiae 0.025 11f 2.2 0.6g 5
Open in a new tab
a

Calculated from Eq. 13 for f = 10–20, Mf = 1–2 Mbp, and α = π/6. 

b

Calculated from Eq. 2 for b = 60 nm. 

c

Volume of sphere of 6 μm diameter. 

d

Calculated from Vn = (4/π)SH, where S and H, the mean nuclear area and thickness, respectively, are taken from Table 1 in Raju et al., 1991. 

e

Calculated from volumes of polytene nucleus (Hochstrasser and Sedat, 1987) under the assumption that the nuclear volume doubles after each replication cycle. 

f

Calculated for an average nuclear diameter = 2.8 μm (Guacci et al., 1994). 

g

Calculated from Eq. 14 for a linear coil configuration of chromosomes. 

Equation 13 is not applicable to cells with very small chromosomes, such as the budding yeast Saccharomyces cerevisiae, because all or most of their chromosomes are smaller than Mf = 1–2 Mbp. We suggest that yeast chromosomes have a linear coil configuration. Because replication initiation in higher eukaryotes is suggested to begin in the micelle cores (see above), the lack of micelle structure in yeast chromosomes is consistent with the observation that higher and lower eukaryotes have different patterns of replication initiation (see review in Gilbert, 1998).

The expression for B for linear coil polymers (e.g., yeast chromosomes) can be obtained from Eq. 13 by replacing f with 1 and Mf with the average chromosome size Mo = C/N, where N is the number of chromosomes per nucleus (N = 32 for S. cerevisiae):

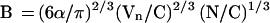graphic file with name M14.gif 14

Equation 14 yields B = 0.6 μm2/Mbp for S. cerevisiae, which is close to the estimated values of B obtained for the micelle structure of high eukaryote chromosomes (see Table 1). This is consistent with the observation that chromatin in interphase yeast cells has the same relationship between geometrical versus genomic distances as that in mammalian cells on the 1-Mbp scale (Guacci et al., 1994).

CONCLUSIONS

1) A G1 phase mammalian chromosome can be approximated as a multiblock copolymer containing two alternating types (R and G) of polymer blocks, which form a string of loop clusters (micelles), with each loop ∼1–2 Mbp in size. Application of the model to the experimental data (Sachs et al., 1995; Yokota et al., 1995) for the dependence of geometrical versus genomic distances between two points on the same chromosome yields an estimate of ∼20 loops per micelle.

2) The number of micelles per nucleus is close to the observed number of replication clusters at the onset of S phase, and the number of loops per micelle is close to the number of replication minisites per cluster. This is consistent with loop termini being sites of initiation of DNA replication at the onset of S phase.

3) R minibands form loop termini, whereas G minibands are located at loop apices. This conclusion follows from relating the chromatin fiber being stretched in R minibands (Yokota et al., 1997) to a known feature of micelles, that polymer blocks located in micelle cores are stretched. These locations of R and G minibands are consistent with their replication pattern; the former are replicated earlier than the latter.

4) The chromosome micelle structure describes the relationship between chromosomal and nuclear sizes for several types of higher-order eukaryotic cells (insects, plants, and mammals). For yeast cells, this relationship is described by a linear coil configuration of chromosomes.

ACKNOWLEDGMENTS

I am grateful to C.S. Lange for very helpful discussions and careful reading of the manuscript, A. Berens for drawing the figures, and the anonymous reviewers for their constructive suggestions.

Footnotes

Author’s E-mail address: ostasj23@hscbklyn.edu.

REFERENCES

  1. Abney JR, Cutler B, Fillbach ML, Axelrod D, Scalettar BA. Chromatin dynamics in interphase nuclei and its implications for nuclear structure. J Cell Biol. 1997;137:1459–1468. doi: 10.1083/jcb.137.7.1459. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Baetcke KP, Sparrow AH, Nauman CH, Schwemmer SS. The relationship of DNA content to nuclear and chromosome volumes and to radiosensitivity (LD50) Proc Natl Acad Sci USA. 1967;58:533–540. doi: 10.1073/pnas.58.2.533. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bak AL, Jorgensen AL, Zeuthen J. Chromosome banding and compaction. Hum Genet. 1981;57:199–202. doi: 10.1007/BF00282022. [DOI] [PubMed] [Google Scholar]
  4. Berezney R, Mortillaro M, Ma H, Wei X, Samarabandu J. The nuclear matrix: a structural millieu for genomic function. Int Rev Cytol. 1995a;162A:1–65. doi: 10.1016/s0074-7696(08)61228-0. [DOI] [PubMed] [Google Scholar]
  5. Berezney, R., Ma, H., Meng, C., Samarabandu, J., and Cheng, P.C. (1995b). Connecting genomic architecture and DNA replication in three dimensions. Zool. Stud. 1(suppl), 29–32.
  6. Bernardi G. The human genome: organization and evolutionary history. Annu Rev Genet. 1995;29:445–476. doi: 10.1146/annurev.ge.29.120195.002305. [DOI] [PubMed] [Google Scholar]
  7. Castro CA. Mechanisms of the Elasticity of Single Chromatin Fibers: The Effect of Histone H1. Ph.D. Thesis. University of Oregon; 1994. [Google Scholar]
  8. Clemson CM, McNeil JA, Willard HF, Lawrence JB. XIST RNA paints the inactive X chromosome at interphase: evidence for a novel RNA involved in nuclear/chromosome structure. J Cell Biol. 1996;132:259–275. doi: 10.1083/jcb.132.3.259. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Coverley D, Laskey RA. Regulation of eukaryotic DNA replication. Annu Rev Biochem. 1994;63:777–792. doi: 10.1146/annurev.bi.63.070194.003525. [DOI] [PubMed] [Google Scholar]
  10. Craig JM, Bickmore WA. Chromosome bands—flavours to savour. Bioessays. 1993;15:349–354. doi: 10.1002/bies.950150510. [DOI] [PubMed] [Google Scholar]
  11. Cremer T, et al. Role of chromosome territories in the functional compartmentalization of the cell nucleus. Cold Spring Harbor Symp Quant Biol. 1993;58:777–792. doi: 10.1101/sqb.1993.058.01.085. [DOI] [PubMed] [Google Scholar]
  12. de Gennes P-G. Scaling Concepts in Polymer Physics. Ithaca, NY: Cornell University Press; 1979. [Google Scholar]
  13. Drouin R, Holmquist GP, Richer CL. High-resolution replication bands compared with morphological G- and R-bands. Adv Hum Genet. 1994;22:47–115. doi: 10.1007/978-1-4757-9062-7_2. [DOI] [PubMed] [Google Scholar]
  14. Drouin R, Lemieux N, Richer CL. Analysis of DNA replication during S phase by means of dynamic chromosome banding at high resolution. Chromosoma. 1990;99:273–280. doi: 10.1007/BF01731703. [DOI] [PubMed] [Google Scholar]
  15. Duplantier B, Jannink G, Sikorav J-L. Anaphase chromatid motion: involvement of type II DNA topoisomerases. Biophys J. 1995;69:1596–1605. doi: 10.1016/S0006-3495(95)80032-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Ferreira J, Paolella G, Ramos C, Lamond AI. Spatial organization of large-scale chromatin domains in the nucleus: a magnified view of single chromosome territories. J Cell Biol. 1997;139:1597–1610. doi: 10.1083/jcb.139.7.1597. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Gilbert DM. Replication origins in yeast versus metazoa: separation of the haves and the haves not. Curr Opin Genet Dev. 1998;8:194–199. doi: 10.1016/s0959-437x(98)80141-x. [DOI] [PubMed] [Google Scholar]
  18. Grosberg AY, Khokhlov AR. Statistical Physics of Macromolecules. New York: AIP Press; 1994. [Google Scholar]
  19. Guacci V, Hogan E, Koshland D. Chromosome condensation and sister chromatid pairing in budding yeast. J Cell Biol. 1994;125:517–530. doi: 10.1083/jcb.125.3.517. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Haaf T, Schmid M. Chromosome topology in mammalian interphase nuclei. Exp Cell Res. 1991;192:325–332. doi: 10.1016/0014-4827(91)90048-y. [DOI] [PubMed] [Google Scholar]
  21. Hahnfeldt P, Hearst JE, Brenner DJ, Sachs RK, Hlatky LR. Polymer models for interphase chromosomes. Proc Natl Acad Sci USA. 1993;90:7854–7858. doi: 10.1073/pnas.90.16.7854. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Halperin A. On the collapse of multiblock copolymers. Macromol. 1991;24:1418–1419. [Google Scholar]
  23. Hochstrasser M, Sedat JW. Three-dimensional organization of Drosophila melanogaster interphase nuclei. I. Tissue-specific aspects of polytene nuclear architecture. J Cell Biol. 1987;104:1455–1470. doi: 10.1083/jcb.104.6.1455. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Holmquist GP. Chromosome bands, their chromatin flavors, and their functional features. Am J Hum Genet. 1992;51:17–37. [PMC free article] [PubMed] [Google Scholar]
  25. Horowitz RA, Agard DA, Sedat JW, Woodcock CL. The three-dimensional architecture of chromatin in situ: electron tomography reveals fibers composed of a continuously variable zig-zag nucleosome ribbon. J Cell Biol. 1994;125:1–10. doi: 10.1083/jcb.125.1.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Houchmandzadeh B, Marko JF, Chatenay D, Libchaber A. Elasticity and structure of eukaryote chromosomes studied by micromanipulation and micropipette aspiration. J Cell Biol. 1997;139:1–12. doi: 10.1083/jcb.139.1.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Hozak P, Hassan AB, Jackson DA, Cook PR. Visualization of replication factories attached to a nucleoskeleton. Cell. 1993;73:361–373. doi: 10.1016/0092-8674(93)90235-i. [DOI] [PubMed] [Google Scholar]
  28. Jackson DA, Cook PR. The structural basis of nuclear function. Int Rev Cytol. 1995;162A:125–149. doi: 10.1016/s0074-7696(08)61230-9. [DOI] [PubMed] [Google Scholar]
  29. Jackson DA, Pombo A. Replicon clusters are stable units of chromosome structure: evidence that nuclear organization contributes to the efficient activation and propagation of S phase in human cells. J Cell Biol. 1998;140:1285–1295. doi: 10.1083/jcb.140.6.1285. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Jannink G, Duplantier B, Sikorav J-L. Forces on chromosomal DNA during anaphase. Biophys J. 1996;71:451–465. doi: 10.1016/S0006-3495(96)79247-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Johnston PJ, Olive PL, Bryant PE. High-order chromatin structure-dependent repair of DNA double-strand breaks: modeling the elution of DNA from nucleoids. Radiat Res. 1997;148:561–567. [PubMed] [Google Scholar]
  32. Kurz A, Lampel S, Nikolenko JE, Bradl J, Benner A, Zirbel RM, Cremer T, Lichter P. Active and inactive genes localize preferentially in the periphery of chromosome territories. J Cell Biol. 1996;135:1195–1205. doi: 10.1083/jcb.135.5.1195. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Laskey R, Madine M. Role of nuclear structure in DNA replication. In: DePamphilis ML, editor. DNA Replication in Eukaryotic Cells. Cold Spring Harbor, NY: Cold Spring Harbor Laboratory Press; 1996. pp. 387–408. [Google Scholar]
  34. Liu B, Sachs RK. A two-backbone polymer model for interphase chromosome geometry. Bull Math Biol. 1997;59:325–337. doi: 10.1007/BF02462006. [DOI] [PubMed] [Google Scholar]
  35. Marko JF, Siggia ED. Polymer models of meiotic and mitotic chromosomes. Mol Biol Cell. 1997a;8:2217–2231. doi: 10.1091/mbc.8.11.2217. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Marko JF, Siggia ED. Driving proteins off DNA using applied tension. Biophys J. 1997b;73:2173–2178. doi: 10.1016/S0006-3495(97)78248-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Marshall WF, Dernburg AF, Harmon B, Agard DA, Sedat JW. Specific interactions of chromatin with the nuclear envelope: positional determination within the nucleus in Drosophila melanogaster. Mol Biol Cell. 1996;7:825–842. doi: 10.1091/mbc.7.5.825. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Marshall WF, Straight A, Marko JF, Swerdlow J, Dernburg A, Belmont A, Murray AW, Agard DA, Sedat JW. Interphase chromosomes undergo constrained diffusional motion in living cells. Curr Biol. 1997;7:930–939. doi: 10.1016/s0960-9822(06)00412-x. [DOI] [PubMed] [Google Scholar]
  39. Ostashevsky JY. Centromeric locations in karyotypes: a rule derived from the theory of branched polymers. J Theor Biol. 1996;181:293–298. doi: 10.1006/jtbi.1996.0131. [DOI] [PubMed] [Google Scholar]
  40. Ostashevsky JY. Gaussian-chain model for the formation of chromosome aberrations. Radiat Res. 1998;149:179–186. [PubMed] [Google Scholar]
  41. Ostashevsky JY, Lange CS. The 30 nm chromatin fiber as a flexible polymer. J Biomol Struct Dyn. 1994;11:813–820. doi: 10.1080/07391102.1994.10508034. [DOI] [PubMed] [Google Scholar]
  42. Raju MR, Eisen Y, Carpenter S, Inkret WC. Radiobiology of α particles. III. Cell inactivation by α-particle transversals of the cell nucleus. Radiat Res. 1991;128:204–209. [PubMed] [Google Scholar]
  43. Razin SV, Gromova II. The channels model of nuclear matrix structure. Bioessays. 1995;17:443–450. doi: 10.1002/bies.950170512. [DOI] [PubMed] [Google Scholar]
  44. Ronne M, Gyldenholm AO, Storm CO. Minibands and chromosome structure: a theory. Anticancer Res. 1995;15:249–254. [PubMed] [Google Scholar]
  45. Sachs RK, van den Engh G, Trask BJ, Yokota H, Hearst J. A random-walk/giant-loop model for interphase chromosomes. Proc Natl Acad Sci USA. 1995;92:2710–2714. doi: 10.1073/pnas.92.7.2710. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Saitoh Y, Laemmli UK. Metaphase chromosome structure: bands arise from a differential folding path of the highly AT-rich scaffold. Cell. 1994;76:609–622. doi: 10.1016/0092-8674(94)90502-9. [DOI] [PubMed] [Google Scholar]
  47. Sanchez JA, Karni RJ, Wangh LJ. Fluorescent in situ hybridization (FISH) analysis of the relationship between chromosome location and nuclear morphology in human neutrophils. Chromosoma. 1997;106:168–177. doi: 10.1007/s004120050236. [DOI] [PubMed] [Google Scholar]
  48. Semenov AN, Joanny J-F, Khokhlov AR. Associating polymers: equilibrium and linear viscoelasticity. Macromol. 1995;28:1066–1075. [Google Scholar]
  49. Semenov AN, Nyrkova IA, Khokhlov AR. Statistics and dynamic of ionomer systems. In: Schlick S, editor. Ionomers: Characterization, Theory and Applications. Boca Raton, FL: CRC Press; 1996. pp. 251–279. [Google Scholar]
  50. Sikorav J-L, Jannink G. Kinetics of chromosome condensation in the presence of topoisomerases: a phanton chain model. Biophys J. 1994;66:827–837. doi: 10.1016/s0006-3495(94)80859-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Simon I, Cedar H. Temporal order of DNA replication. In: DePamphilis ML, editor. DNA Replication in Eukaryotic Cells. Cold Spring Harbor, NY: Cold Spring Harbor Laboratory Press; 1996. pp. 387–408. [Google Scholar]
  52. Sontag W, Knedlitschek G, Weibezahn KF, Dertinger H. The DNA content of some mammalian cells measured by flow cytometry and its influence on radiation sensitivity. Int J Radiat Biol. 1990;57:1183–1193. doi: 10.1080/09553009014551281. [DOI] [PubMed] [Google Scholar]
  53. Spector D. Macromolecular domains within the cell nucleus. Annu Rev Cell Biol. 1993;9:265–315. doi: 10.1146/annurev.cb.09.110193.001405. [DOI] [PubMed] [Google Scholar]
  54. Strouboulis J, Wolffe AP. Functional compartmentalization of the nucleus. J Cell Sci. 1996;109:1991–2000. doi: 10.1242/jcs.109.8.1991. [DOI] [PubMed] [Google Scholar]
  55. Tomilin K, Solovjeva L, Krutilina R, Chamberland C, Hancock R, Vig B. Visualization of elementary DNA replication units in human nuclei corresponding in size to DNA loop domains. Chromosome Res. 1995;3:32–40. doi: 10.1007/BF00711159. [DOI] [PubMed] [Google Scholar]
  56. van den Engh G, Sachs R, Trask BJ. Estimating genomic distance from DNA sequence location in cell nuclei by a random walk model. Science. 1992;257:1410–1412. doi: 10.1126/science.1388286. [DOI] [PubMed] [Google Scholar]
  57. van Driel R, Wansink D, van Steensel B, Grande MA, Schul W, de Jong L. Nuclear domains and the nuclear matrix. Int Rev Cytol. 1995;162A:151–189. doi: 10.1016/s0074-7696(08)61231-0. [DOI] [PubMed] [Google Scholar]
  58. van Holde KE. Chromatin. New York: Springer-Verlag; 1989. [Google Scholar]
  59. van Holde KE, Zlatanova J. Chromatin higher order structure: chasing a mirage? J Biol Chem. 1995;270:8373–8376. doi: 10.1074/jbc.270.15.8373. [DOI] [PubMed] [Google Scholar]
  60. van Holde KE, Zlatanova J. What determines the folding of the chromatin fiber? Proc Natl Acad Sci USA. 1996;93:10548–10555. doi: 10.1073/pnas.93.20.10548. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Wolffe AP. Chromatin: Structure and Function. 2nd ed. London: Academic Press; 1995. [Google Scholar]
  62. Woodcock CL, Grigoryev SA, Horowitz RA, Whitaker N. A chromatin folding model that incorporates linker variability generates fiber resembling the native structures. Proc Natl Acad Sci USA. 1993;90:9021–9025. doi: 10.1073/pnas.90.19.9021. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Woodcock CL, Horowitz RA. Chromatin organization re-viewed. Trends Cell Biol. 1995;5:272–277. doi: 10.1016/s0962-8924(00)89038-8. [DOI] [PubMed] [Google Scholar]
  64. Yokota H, Singer MJ, van den Engh, Trask BJ. Regional differences in the compactness of chromatin in human G0/G1 interphase nuclei. Chromosome Res. 1997;5:157–166. doi: 10.1023/a:1018438729203. [DOI] [PubMed] [Google Scholar]
  65. Yokota H, van den Engh G, Hearst JE, Sachs RK, Trask BJ. Evidence for the organization of chromatin in megabase pair-size loops arranged along a random-walk path in the human G0/G1 interphase nucleus. J Cell Biol. 1995;130:1239–1249. doi: 10.1083/jcb.130.6.1239. [DOI] [PMC free article] [PubMed] [Google Scholar]
  66. Yunis JJ. Mid-prophase human chromosomes. The attainment of 2000 bands. Hum Genet. 1981;56:293–298. doi: 10.1007/BF00274682. [DOI] [PubMed] [Google Scholar]
  67. Zink D, Cremer T, Saffrich R, Fischer R, Trendelenburg MF, Ansorge W, Stelzer EHK. Structure and dynamics of human interphase chromosome territories in vivo. Hum Genet. 1998;102:241–251. doi: 10.1007/s004390050686. [DOI] [PubMed] [Google Scholar]
  68. Zirbel RM, Mathieu UR, Kurz A, Cremer T, Lichter P. Evidence for a nuclear compartment of transcription and splicing located at chromosome domain boundaries. Chromosome Res. 1993;1:93–106. doi: 10.1007/BF00710032. [DOI] [PubMed] [Google Scholar]

Articles from Molecular Biology of the Cell are provided here courtesy of American Society for Cell Biology

RESOURCES