Abstract
We developed an adaptive training algorithm, whereby an in vitro neocortical network learned to modulate its dynamics and achieve pre-determined activity states within tens of minutes through the application of patterned training stimuli using a multi-electrode array. A priori knowledge of functional connectivity was not necessary. Instead, effective training sequences were continuously discovered and refined based on real-time feedback of performance. The short-term neural dynamics in response to training became engraved in the network, requiring progressively fewer training stimuli to achieve successful behavior in a movement task. After 2 h of training, plasticity remained significantly greater than the baseline for 80 min (p-value <0.01). Interestingly, a given sequence of effective training stimuli did not induce significant plasticity (p-value = 0.82) or desired behavior, when replayed to the network and no longer contingent on feedback. Our results encourage an in vivo investigation of how targeted multi-site artificial stimulation of the brain, contingent on the activity of the body or even of the brain itself could treat neurological disorders by gradually shaping functional connectivity.
Introduction
A life’s experiences spur the brain to continuously rewire itself to best achieve behavioral goals. However, errors can occur when injury or a pathological condition causes aberrant neuronal activity, and often a disconnection arises between the activity of the brain and that of the body. Treating movement disorders using physical therapy has been shown to modify neuronal activity, and in different studies, neuronal activity has been shown to be modified by electrically stimulating neuronal tissue (see below). Thus theoretically, electrically induced neuronal plasticity could allow the brain to be rewired to achieve a more desired behavioral state. Here, we investigated how a neocortical network could learn to modulate its dynamics and achieve user-defined activity states through feedback training with electrical stimuli. Besides highlighting potential therapeutic roles for artificial stimulation of the brain, these experiments give insight into how the processes underlying learning and memory are expressed in and induced by network activity.
Electrical stimulation has been extensively used to artificially induce neuronal plasticity and to study learning and memory. For example, cellular plasticity has been observed in a variety of functions, including in synaptic efficacy (Bliss and Lømo 1973, Bi and Poo 2001, Markram et al 1997), intrinsic neuronal excitability (Daoudal and Debanne 2003, Zhang and Linden 2003), neuronal morphology (Uesaka et al 2007) and glial morphology (Fields 2005, Ishibashi et al 2006), action potential propagation (Bakkum et al 2008), and neurogenesis (Kempermann 2002). A much-needed progression in the field is to determine how cellular plasticity scales and integrates to influence neuronal network dynamics. In primate motor cortex, a neuron was repetitively stimulated 5 ms after recording the occurrence of an action potential in a different neuron using an electronic implant (Jackson et al 2006); after halting the stimulation, neural activity in pathways previously activated by the stimulated neuron was now also activated by the recorded neuron. Similar ‘pathway-specific’ plasticity (Jimbo et al 1999) and also a ‘region-specific’ variation in the flow of neuronal activity (Chao et al 2007) have been induced in in vitro networks. Thus electrical stimulation can sculpt the flow of neuronal information through a variety of mechanisms.
We hypothesize that spatio-temporally distributed electrical training stimuli contingent on neuronal or motor output could provide effective therapy for neurological disorders by either retraining or bypassing malfunctioning neuronal circuits. Many steps are required to reach this ambition, including quantifying the ability and limitations of electrical stimulation to induce functional or adaptive changes in neuronal activity. Here, using an extracellular multi-electrode array (MEA) to record and stimulate neural activity of neocortical networks in vitro, we refined a closed-loop adaptive training algorithm. An artificial embodiment, or animat (Meyer and Wilson 1991, De Marse et al 2001) controlled by the distributed activity of a cultured network, was trained to move in different user-defined directions by shaping the functional connectivity of the network. With our design to adaptively deliver training stimuli as a function of behavior, a priori knowledge of functional connectivity was not necessary. Instead, effective patterned training stimuli (PTS) were continuously selected by the hybrid (neural + computer) system, based on the embodiment’s real-time performance. The short-term neural dynamics in response to successful training stimuli became engraved in the network, requiring progressively fewer training stimuli applications to achieve correct behavior. Interestingly, a given training sequence did not induce plasticity, let alone desired motor output, when it was replayed to the network and no longer contingent on performance. These findings with living networks validate in vitro our previous electrical training results demonstrated in silico using a simulated network of 1000 integrate-and-fire neurons (Chao et al 2008). Results from our in vitro model encourage an in vivo investigation of how targeted electrical stimulation of the brain, contingent on the activity of the body or the brain itself, could treat aberrant neuronal activity.
Methods
Cell culture
We have developed techniques to maintain neuronal cultures with a bi-directional computer interface for many months. Briefly, cells from E18 rat cortices were dissociated and cultured at high density in DMEM containing 10% horse serum, sodium pyruvate, insulin and GlutaMax (Potter and DeMarse 2001, Wagenaar et al 2006b) on 59-electrode MEAs (30 μm diameter titanium nitride, arranged in a square grid with 200 μm spacing; Multichannel Systems), and allowed to grow between 3 and 5 weeks prior to experimentation. No activity-based selection criteria were used to choose cultures for these experiments. Data acquisition (using MEA60 and MCCard, Multichannel Systems), visualization, artifact suppression and spike detection were controlled using Meabench (Potter et al 2006). Stimuli were delivered with custom all-electrode stimulator circuits (Wagenaar and Potter 2004). Experiments lasting many hours were conducted using sealed-lid MEAs (US patent no. 6, 521, 451) inside an environmentally controlled incubator, allowing us to maintain very stable environmental conditions (Potter and DeMarse 2001).
Closed-loop electrical training system
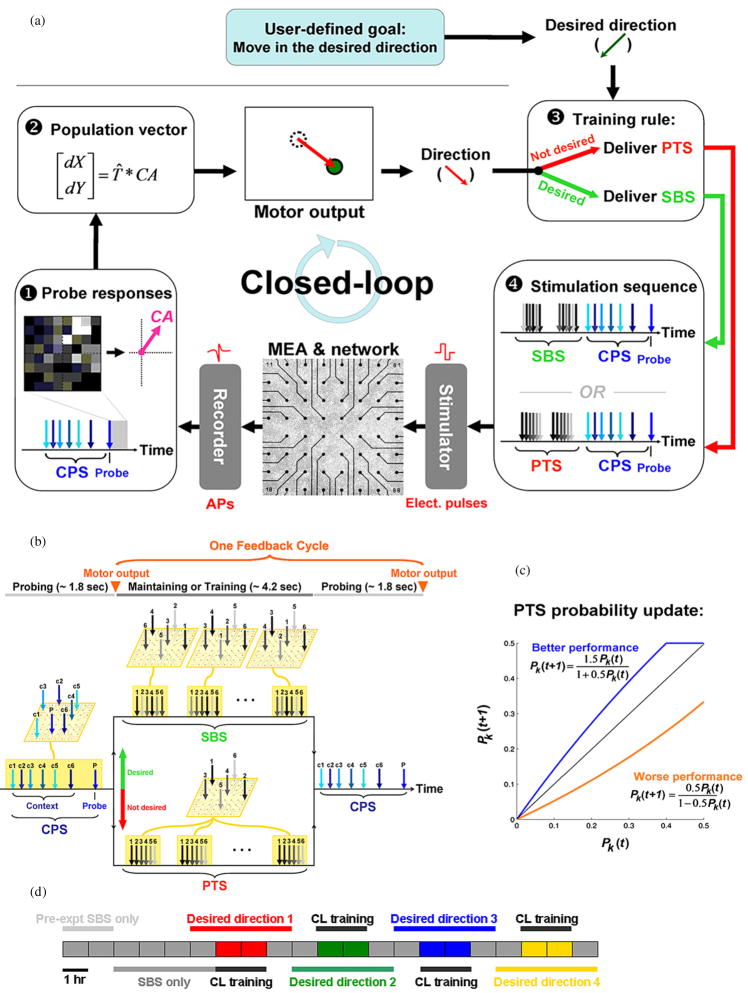
Closed-loop algorithms for embodied cultured networks comprise a feedback cycle from neuronal activity, to behavior of the embodiment, to assessment of performance by a computer, to electrical stimulation, to neural processing and back to recording of neural activity (Chao et al 2008). The animat in this work consisted of a simulated animal that could move in a two-dimensional plane, as controlled by the activity of the cultured network (see Motor Mapping, below). The goal was for the animat to learn to move in a pre-chosen direction, which was changed four times per experiment. The closed-loop system in the present work included (1) three different stimulation protocols for probing, directing and maintaining the network dynamics, (2) a motor mapping derived from a population coding that incorporated spatial information of network activity, and (3) a training algorithm that adaptively selected effective training stimuli (figure 1).
Figure 1.
Schematic of the closed-loop feedback, adaptive training and experiment protocol: see Methods for details. (a) ❶ A single probe electrode was repetitively stimulated every 6 s. After each stimulus, 100 ms of evoked responses were recorded to form the 2D center of activity (CA) vector. ❷ The CA was transformed (T̂) into incremental movement [dX, dY]. ❸ If the movement was within ± 30° of the user-defined desired direction, a shuffled background stimulation (SBS) was delivered. Otherwise, a patterned training stimulation (PTS) was repetitively delivered. ❹ Context-control probing sequences (CPS) were delivered after SBS or PTS, and ended with probe pulses. (b) One feedback cycle was 6 s long and consisted of a CPS preceded by either SBS or PTS. The 8 × 8 grids represent the electrode locations of an MEA; an example is given of how stimulation electrodes (arrows) of a given PTS were shuffled to create an SBS. (c) For unsuccessful movement, a PTS (PTSk) was selected from a pool of 100 possibilities. The probability of each PTS (Pk (t )) being chosen later (Pk (t + 1)) increased (blue) or decreased (red) depending on the success of the motor output. See equations (3) and (4). (d) An experiment lasted 21 h. It consisted of four 2 h training periods (closed-loop or open-loop) each with a different desired direction. SBS-only periods were added as a control before, between, and after training periods.
Three classes of stimulation protocols
We used three types of electrical stimulation for three different purposes, detailed below.
CPS. A constant context-control probing sequence was used to sample the network dynamics, to generate a command for the animat’s next motor output.
PTS. Patterned training stimuli were used to induce network plasticity when the performance was inadequate.
SBS. Shuffled background stimulation was used to stabilize accumulated plasticity.
Biphasic voltage-controlled rectangular pulses were used for all stimuli (positive phase first, ±300 mV, 400 μs per phase) (Wagenaar et al 2004). To map which electrodes were active (able to record and/or evoke action potentials) for each culture before an experiment, pulses were delivered in random order to the 59 usable electrodes (the 60th electrode is a large reference electrode) on the MEA for 30 min, one at a time, with random inter-stimulus intervals between 200 and 400 ms. The activity was always recorded from all the remaining electrodes.
Our stimulation system (Wagenaar et al 2004) allows real-time creation and delivery of arbitrary sequences of stimuli on any of the recording electrodes. By using the SALPA algorithm to subtract stimulation artifacts (Wagenaar et al 2002), action potentials beginning 2 ms after a stimulus could be detected. Stimulation voltages of ±300 mV were lower than those in our previous investigations of plasticity magnitude (Chao et al 2007) in order to better localize which neurons were activated (Chao et al 2008, Wagenaar et al 2004).
Context-control probing sequence (CPS)
A CPS consisted of a sequence of 6 ‘context-control’ stimulation pulses, followed by one ‘probe’ pulse, with inter-pulse intervals randomly chosen between 200 and 400 ms, and were 1.8 s long on average. Context refers to the state of neural activity when the probe is applied. The purpose of the context-control pulses was to quiet any ongoing bursting activity in the network (Wagenaar et al 2005), so that the response to the probe pulse was more reproducible. The 200–400 ms range was found to be the most effective at reducing variability in probe responses (Chao et al 2008). The six context electrodes were randomly selected from the set of active electrodes that evoked responses occurring mostly within 20 ms of the stimulation. Their short-latency responses were chosen so as not to overlap the response to the probe. The probe electrode, by contrast, was chosen from the set of active electrodes with clear, longer-latency polysynaptic responses, which ended within 100 ms in our experiments. A probe electrode that evokes polysynaptic activity at multiple electrodes is capable of revealing changes in network-level functional connectivity. Once the spatial (electrode locations) and temporal (inter-pulse intervals) structure of the 7-pulse CPS (ending with the probe pulse) was devised for a given experiment, it was fixed and used throughout the experiment to sample the network state once every 6 s (one feedback cycle, see figure 1(b)).
Action potentials evoked by the probe were recorded for the next 100 ms on all MEA electrodes. Probe responses served as a readout of the network’s current functional connectivity and were used to determine the next motor output (see the ‘Motor mapping’ section below). Because of the constancy of the CPS, any changes in probe responses during an experiment were due mainly to changes in network functional connectivity. Therefore, changes in probe responses, or the consequential motor outputs, directly reflected learning in the hybrid system.
Patterned training stimulation (PTS)
A PTS consisted of the repetitive delivery for ~4.2 s (6 s feedback cycle minus ~1.8 s CPS, giving on average ~12 repetitions per cycle) of a cluster of six stimulus pulses with an inter-cluster interval randomly chosen between 200 and 400 ms each time. For one cluster, the inter-pulse interval between two consecutive pulses was fixed at 10 ms, giving a cluster duration of 50 ms. We compiled a pool of 100 different PTSs, each characterized by its unique spatio-temporal sequence of six stimulation electrodes in a cluster; the electrode order was fixed for the repeated clusters in a given PTS. The six electrodes used in each PTS were randomly chosen from among the set of electrodes capable of evoking action potentials (repeated electrodes allowed; CPS electrodes excluded).
Paired stimulation of monosynaptically connected neurons evokes spike-timing-dependent plasticity (STDP), with greatest magnitude at intervals of 0–30 ms (Markram et al 1997, Bi and Poo 2001). At the network level, neurons at different electrodes can be connected through multiple neurons and pathways. Therefore, because PTSs with different electrode sequences can repetitively evoke different activation pathways with a variety of axonal and synaptic delays, we expected that they would alter the network functional connectivity toward different states, through a complex mixture of potentiation and depression from STDP mechanisms (Jimbo et al 1999).
Shuffled background stimulation (SBS)
Similar to PTS, an SBS consisted of the repetitive delivery of clusters of six stimuli with an inter-cluster interval randomly chosen between 200 and 400 ms each time, and with the inter-pulse interval of 10 ms within each cluster. When SBS was required, one of the 100 PTS clusters was randomly selected and delivered, but unlike PTS, where the sequence of six stimulation electrodes in each cluster was the same for all repetitions during one feedback cycle, the temporal order of the six stimulation electrodes was randomized for each cluster. The randomization maintained comparable overall stimulation rates and electrode distribution as the PTS, while removing the repeating spatio-temporal pattern of neuronal activation. We hypothesized that SBS, unlike PTS, would have an unbiased randomizing effect on changes in network functional connectivity (Chao et al 2005).
Motor mapping
Sequences of action potentials in probe responses were transformed into movements of the animat using a customized motor mapping. Population coding based on mean firing rates across a population of neurons is a candidate motor mapping found to occur in the motor cortex (Georgopoulos 1994), premotor cortex (Caminiti et al 1990), hippocampus (Wilson and McNaughton 1993) and other cortical areas: the firing rates of a group of broadly tuned neurons taken together provide an accurately tuned representation (e.g., to a preferred direction of arm movement). We used a related population coding, termed the center of activity (CA), which explicitly includes neuron (or recording electrode) location as a relevant variable (Chao et al 2005). Probe responses were mapped into incremental movement in the X–Y plane [dX, dY]:
| (1) |
where
| (2) |
Analogous to the center of mass, the center of activity (CA) is the vector summation of the number of action potentials recorded on each electrode k (i.e., the firing rate Fk) weighted by the spatial location of the electrode: [Xk, Yk] are the coordinates of electrode k relative to the reference point [RX, RY], which we set as the center of the MEA (figure 1(a)❶).
The inclusion of spatial information was found more reliable for quantifying network functional plasticity than using firing rates alone (Chao et al 2007). The CA was normalized by a transformation matrix, T̂, to remove any directional bias arising from different distributions of neurons in different MEA preparations (figure 1(a)❷): the transformation centered the distribution of CAs to [0, 0] to allow movement in all possible directions with equal magnitudes (offsets and scalings, respectively, in X and Y dimensions). The transformation matrix was fixed throughout any given 2 h closed-loop or open-loop trial (see below) and recalculated for each different trial.
Training algorithm
We designed an adaptive training algorithm in order to direct neuronal plasticity and gradually improve the animat’s performance at moving in a pre-specified direction.
When movement was successful (defined to be within ± 30° of the desired direction), no changes in network functional connectivity were desired. In this case, SBS, which contains no consistent structure of electrode stimulation order, was delivered until the beginning of the next CPS (figure 1(a), ❸ and ❹; detailed in figure 1(b)).
When movement was not successful, plasticity of probe responses was desired. In this case, a PTS randomly selected by the computer from the pool of 100 PTSs was applied in order to train the network. However, some PTSs may give desired neuronal plasticity while others may give the opposite or none. Therefore, we designed an adaptive algorithm that increased the likelihood of effective PTSs being selected, while decreasing the influence of maladaptive PTSs. Initially, each PTS had an equal probability of being chosen. If the current PTS (PTSk) improved the performance, then the probability of PTSk (Pk (t)) being chosen later (Pk (t + 1)) increased, and the probability of other PTSs (Pi (t + 1)) being chosen decreased (figure 1(c)):
| (3) |
Otherwise, if PTSk worsened the performance, then Pk(t + 1) decreased from Pk(t), and Pi(t + 1) for other PTSs increased:
| (4) |
With real-time adaptive selection of plasticity inducing stimuli, the dynamics of neuronal activity could be shaped toward the desired state. A maximum probability of 0.50 was set so that no one PTS was dominant. A minimum of 0.002 was set to ensure each PTS remained available in the future. This allowed the flexibility to adapt to ongoing changes in neuronal network dynamics. The lowered stimulation voltages (±300 mV) and the 6 s feedback cycle time were intended to induce plasticity incrementally to reach a desired performance while minimizing maladaptive plasticity.
Experimental design
SBS-only stimulation
At the beginning of an experiment and prior to each closed-loop training, CPS with probe stimuli were delivered, with only SBS (no PTS) in each feedback cycle for 6 h (figure 1(d)). This allowed 2 h for the network to habituate to the presence of electrical stimulation and another 4 h for measuring the baseline plasticity, which we call ‘drift’ (see figure 6(a), black triangles).
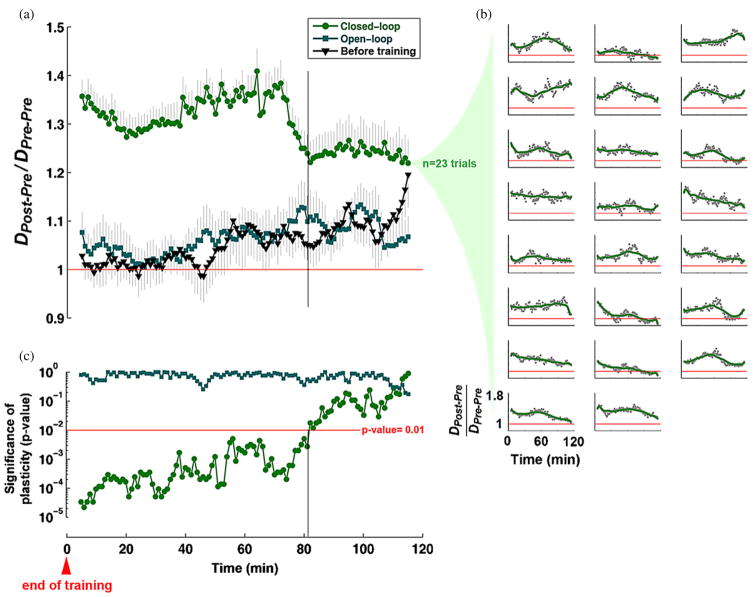
Figure 6.
Plasticity of neuronal activity induced by closed-loop training lasted on average for 80 min: plasticity induced by closed-loop training was significantly greater than intrinsic plasticity before training, for 80 min on average for all experiments, but not for replayed open-loop stimulation. (a) DPost–Pre/DPre–Pre (see the definition in Results) was calculated between CAs in consecutive 10 min periods after training (Post, see figure 5) stepped by 1 min and CAs in a 10 min reference period immediately before training (Pre). The mean and SEM of DPost–Pre/DPre–Pre across closed-loop and open-loop periods (n = 23 trials) was compared to DPost–Pre/DPre–Pre across SBS-only periods during the first 6 h of SBS-only stimulation. (Before training, n = 12 closed-loop and open-loop experiments.) (b) DPost–Pre/DPre–Pre across closed-loop periods for each trial. In each subplot, DPost–Pre/DPre–Pre of each 10min period is indicated as a gray dot, and the overall trend is shown by a smoothed time course (moving average with a 30-point span) of DPost–Pre/DPre–Pre (green curve). (c) Closed-loop training-induced plasticity was significantly greater than the baseline plasticity measured before training (black triangles in (a)) for 80 min. Adaptive plasticity in closed-loop experiments was significantly greater than intrinsic plasticity (drift) for 80 min (Wilcoxon rank sum test, α = 0.01).
Closed-loop experiments with different desired movement directions
One closed-loop experiment consisted of four 2 h training periods, each with a different desired direction, and 2 h SBS-only periods (with CPS) in between (figure 1(d)). After a training period, the stability of plasticity was measured during the 2 h SBS-only period. The transformation matrix for each training period, T̂, was calculated based on probe responses during the last 30 min in the preceding SBS-only period. Six closed-loop experiments were performed on five different cultures from three dissociations such that 23 training periods were analyzed (6 × 4 minus 1, where a technical error caused a loss of data). Two of the experiments were performed on one culture, with 13 days in between and different CPS and PTSs.
Open-loop stimulation experiments
To test if the improvement in performance was an artifact of the electronics or electrode chemistry arising from a particular stimulation sequence, the entire exact sequence of stimuli recorded from each closed-loop experiment was replayed to the same network about a day later. Since the previously used transformations might not successfully center the initial distribution of CAs if activity changed, the transformation matrices were recalculated as before. However, the particular transformation used does not affect the calculations of plasticity of motor output (figure 5) or of neuronal activity (figure 6). Moreover, transformation matrices between closed-loop and open-loop trials were found to not be significantly different (p-value = 0.34 Wilcoxon sign rank test, n = 23 trials * 2 offset dimensions; scaling transformations do not affect the movement direction).
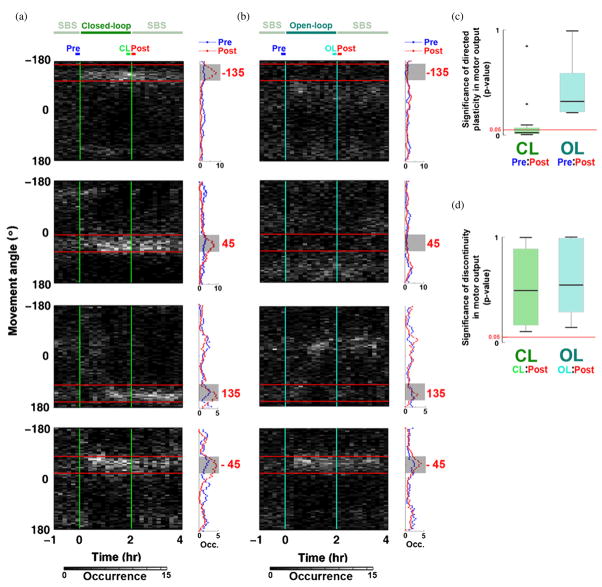
Figure 5.
Long-term plasticity of the movement direction. (a) Movement directions became concentrated within ±30° of the desired direction (red numbers and horizontal lines) during closed-loop training (CL) and persisted into the SBS-only periods. Data are from the same representative experiment as in figure 2. The distribution of movement angles was sampled every 10 min from 1 h before to 2 h after the closed-loop experiment (gray scale). The distributions of the occurrence of different movement angles during 10 min SBS-only periods immediately before (Pre) and immediately after (Post) closed-loop training are shown in the histograms (right). (b) Changes in the movement direction were seldom observed in the corresponding open-loop experiment (OL). (c) The distribution of movement angles in Pre periods was significantly different from that in Post periods for closed-loop training, suggesting directional plasticity occurred. It was not significant for replayed open-loop stimulation suggesting adaptive plasticity was not a stimulation artifact. The P-values of the difference in movement angle distributions for each of the 23 desired directions (two-sample Kolmogorov–Smirnov test, two tailed) are represented in box plots. Box edges indicate the first (lower) quartile and third (upper) quartiles, and the thicker line indicates the median. Outliers are indicated as black dots, and the largest and smallest non-outlier observations are indicated as tic marks (whiskers). The median p-value for closed-loop experiments (0.017) was below a significance level of 0.05. (d) The distribution of movement angles between the last 10 min in closed-loop (or open-loop trials; CL, OL) and that during the next 10 min of SBS-only (Post) were not significantly different, demonstrating that the directed plasticity was not an artifact of PTS history.
Results
Training contingent on motor output shifted neuronal activity towards the desired activity
We designed a closed-loop algorithm to use distributed electrical stimulation to train cultured networks to learn user-defined motor outputs: moving an animat in a pre-defined direction. The closed-loop training algorithm was tested in five cortical networks grown over MEAs. Array-wide action potentials evoked by repeating probe stimuli, delivered to a single fixed electrode, commanded motor output every 6 s. Spatio-temporally patterned electrical stimuli were delivered either repetitively (PTS) to induce directed plasticity, or randomly (SBS) to preserve current functional connectivity. The probability of selecting a specific PTS as a training signal, from a pool of 100 PTSs, was updated based on how its application influenced the network’s short-term activity dynamics during the following motor output (see Methods and figure 1(c)). Four goals were applied sequentially to a network, that is, the desired movement direction was changed by ±90° or 180° three times (see figure 2). Overall success was judged by the ability of the network to crystallize successful short-term changes into long-term adaptive plasticity and also by its ability to further adapt to new desired motor outputs. With training, the animat was able to head toward the pre-defined desired directions (one representative experiment is shown in figure 2(a)). The learning curves show that a greater proportion of movements were in the desired direction as training progressed (figure 2(c)). Since a correct movement meant applying SBS instead of PTS, fewer training stimuli were needed in time, suggesting the network learned by small increments the appropriate input/output function to produce successful animat behavior.
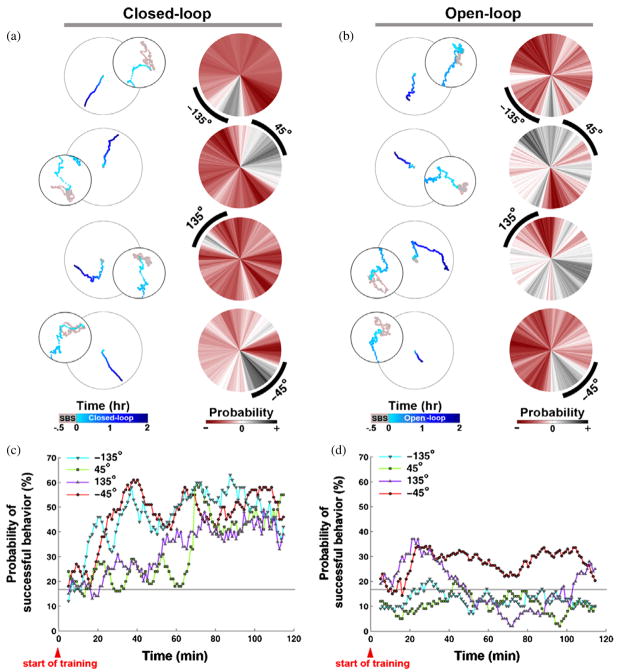
Figure 2.
Neuronal response to closed-loop and open-loop training. (a) Closed-loop training: animat movement trajectory (left column) and the change in the probability distribution of movement directions (right column) demonstrated the motor output adapted to the desired direction (black arcs). The desired directions of −135°, −45°, 135°, and 45° were set as goals in random order for 2 h periods (light to dark blue in time) interspersed by 2 h SBS-only periods (see Methods). A successful motor output was considered to be movement within ±30° of the desired direction. The smaller trajectory circle is a zoom-in of the beginning of the experiment and the 30 min SBS-only period (gray) is used to calculate the transformation, T̂. The probability distribution of movement directions during 10 min at the start of experiments was subtracted from that during the final 10 min, thus allowing negative values (red). (b) Open-loop training: the closed-loop stimulation sequence was recorded and replayed to the same network a day later. Movement trajectories (scaled to match the corresponding closed-loop experiment) changed but not necessarily toward the desired direction. The distribution of movement directions also changed but in a more distributed manner. Learning curves of (c) closed-loop and (d) open-loop examples shown in (a) and (b): a learning curve was defined as the probability of movement in the desired direction within a 10 min moving time window (time step = 1 min). The probability of the successful motor output increased in time when training was contingent on the motor output. A random movement would give a 16.67% chance (horizontal line) of movement within ± 30° of the desired direction (60°/360°).
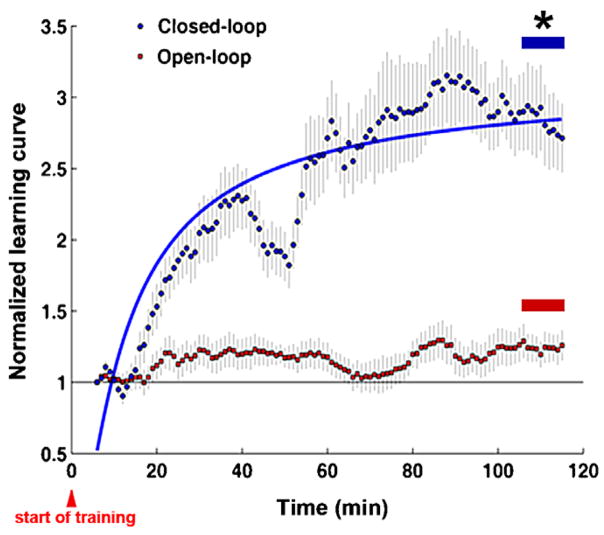
Learning curves for all experiments are shown in figure 3 and averaged in figure 4. The average normalized learning curve of all closed-loop experiments showed the success rate increased by a factor of 2.88 ± 0.08 (mean ± SEM; n = 23 trials, from six experiments) times after 2 h of training.
Figure 3.
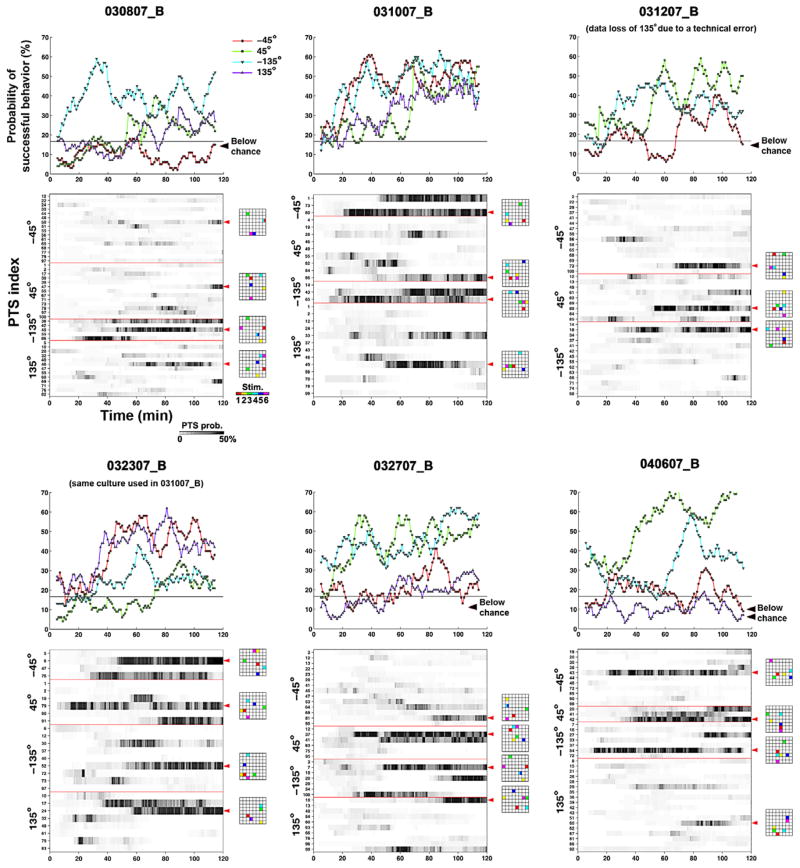
Learning curves for all closed-loop experiments: for each experiment, the learning curves (as in figure 2(c) and (d)) and the time courses of different PTS probabilities are shown. Various series of PTS were needed to induce appropriate neuronal plasticity and successful motor output. For clarity, the PTSs with lower probability were not plotted. Electrode locations and order (right) for the most frequent PTS indicated by red arrows are shown in 8 × 8 grids of electrode locations. In five out of 23 trials (21.7%), the learning curves were below the 16.67% chance in the last 10 min of training (black arrows).
Figure 4.
Average normalized learning curves of all closed-loop and open-loop experiments: to compare trends among different experiments, each learning curve was normalized by dividing the probability of a successful motor output when training began. The average normalized learning curve in the last 10 min of the closed loop experiments was 2.88 ± 0.08 (mean ± SEM) times higher than that at the start, which was significantly higher than 1.24 ± 0.03 for the open-loop experiments (p-value < 1 × 10−6, n = 23 trials from six experiments, Wilcoxon signed rank test). An exponential curve fit gives a time constant of 10.6 min and a learning curve asymptote of 3.13 (SSE = 2.95, R-square = 0.7814).
In five out of 23 trials (21.7%), the learning curves were below the 16.67% chance level (60°/360° chance of movement within ±30° of the desired direction) in the last 10 min of training (black arrows in figure 3). This suggests that a more optimal training algorithm could be created. For example, the randomly chosen set of 100 PTSs (from the billions possible) might not be diverse enough to produce plasticity in all directions. Moreover, an appropriate PTS may become inappropriate at a later time, and the 0.50 maximum criterion on the probability of selecting a PTS allows randomly applied inappropriate PTS to produce setbacks, which may contribute to the fluctuations in the learning curves.
The entire stimulation sequence delivered during a closed-loop experiment was recorded and replayed to the same network the next day as a control open-loop experiment. Unsuccessful behavior during the open-loop experiments would rule out the occurrence of artifactual changes in network responses arising from non-biological causes, such as electrochemistry or electronic noise, and ensure that neuronal plasticity was responsible for the observed learning during the closed-loop experiments. Replayed stimuli were no longer contingent on the performance of the animat, and consequently its movement failed to show directed, progressive change toward the desired directions (figures 2(b), (d), and 4). The average normalized learning curve of open-loop experiments was significantly lower than in closed-loop experiments (p-value < 1 × 10−6, n = 23 trials, Wilcoxon signed rank test) (figure 4). Changes in the movement direction were distributed across a wider range of angles than with closed-loop training (compare figures 2(b) and (a)). Therefore, successful learning reflected adaptive biological plasticity in the neuronal networks, and required closed-loop training in which stimuli were contingent on behavior.
Changes in motor output arose from neuronal plasticity, not an elastic dependence on stimulation history
The improved performance induced by closed-loop training could be due to enduring plastic changes in the neuronal network or, alternatively, due to a more transient elastic dependence on the recent stimulation history. An elastic change in responsiveness to stimuli was observed by Eytan et al in dissociated cortical cultures, where the sensitivity of neurons selectively adapted to stimulation at different very low frequencies, and this change in the sensitivity faded away within 15 min after stimulation was removed (Eytan et al 2003, Wagenaar et al 2006a). In order to characterize the durability of plasticity here, after 2 h of closed-loop training, we switched back to the SBS-only stimulation and quantified whether the learned movement was maintained, and if so, for how long.
By sampling the distribution of movement angles in 10 min time bins from 1 h before to 2 h after the closed-loop experiment, we found that (1) the movement angle gradually converged to the desired directions during closed-loop training, and (2) the learned directions were maintained after training during SBS-only stimulation: the learning reflected adaptive changes in the functional connectivity of the neuronal network. Results from the experiment depicted in figure 2 are shown in figure 5(a). The distribution of the 10 min SBS-only period immediately before (Pre) closed-loop training was significantly different from that immediately after (Post) closed-loop training (histograms on the right side of figure 5(a). Furthermore, this electrical training-induced plasticity led to desired motor outputs in 18 out of 23 trials (78.3%) (see figure 3), demonstrating that closed-loop training could successfully direct network plasticity (figure 5(a) histograms and figure 5(c)). Moreover, the distributions were not significantly different between the last 10 min of the training and the next 10 min of the SBS-only control (figure 5(d)), which indicates that the new distribution of motor outputs was preserved in the SBS-only period after PTS training was turned off. This also further demonstrated that the improved performance was due to network plasticity, not an elastic response to a particular PTS history or to non-biological causes.
In order to investigate the duration of training-induced plasticity, the mean distance (DPost–Pre) of CAs in consecutive 10 min periods after training (moved with 1 min time steps) (see Post, at the top of figure 5(a)) to the centroid of CAs in a 10 min reference period immediately before training (Pre), was calculated and compared to the mean distance (DPre–Pre) of CAs in Pre to their own centroid. The ratio of DPost–Pre to DPre–Pre was used to quantify the change in CAs from a Pre period to different Post periods (a ratio of 1 indicates no change) (Chao et al 2007). The mean and SEM of DPost–Pre/DPre–Pre across closed-loop and open-loop periods (n = 23 trials) was compared to that across equivalent periods of SBS-only stimulation conducted before training (n = 12 closed-loop and open-loop experiments, see Methods) (figure 6(a)). DPost–Pre/DPre–Pre across closed-loop periods for each trial is shown in figure 6(b). Closed-loop training-induced plasticity was significantly greater than baseline plasticity, or drift, measured before training (black triangles in figure 6(a)) for 80 min (Wilcoxon rank sum test, α = 0.01) (figure 6(c)). Replayed open-loop stimulation did not induce significant directed plasticity. That DPost–Pre/DPre–Pre was not significant 80 min after the end of closed-loop training indicates that CAs tended on average to relax back toward their previous distribution before training. This relaxation could be due to an active ‘re-habituation’ to the SBS-only stimulation. SBS, while less structured than PTS, still has a spatio-temporal structure and an ability to induce plasticity.
Interestingly, despite having an identical stimulation sequence, the PTSs in open-loop training did not cause desired behavior nor even noticeable plasticity. For replayed open-loop stimuli, the distribution of movements was less focused (figure 5(b); also see figure 2(b)), and no significant changes in motor output (figure 5(c)) or neuronal activity (figure 6) occurred for most of the experiments. Desired movement directions were found in four out of 23 open-loop trials (17.4%) during the last 10 min (see −45° trial in figure 2(b)), which was close to the 16.67% chance but significantly lower than the 78.3% success rate for closed-loop experiments. When contingent on neuronal activity, the set of PTSs was able to incrementally shift network dynamics until a significant adaptive functional change was easily detectable and persistent.
Training required different PTSs at different times
A neuronal network is continuously plastic, being modified by both stimulus-evoked and spontaneous activity. The same PTS may therefore have different effects at different points in time, and successful adaptation to a desired motor output would require application of PTSs in a certain sequence. This was observed, as shown in figures 3 and 7(b). A given PTS could induce appropriate plasticity initially, but continued application of the PTS could be maladaptive.
Figure 7.
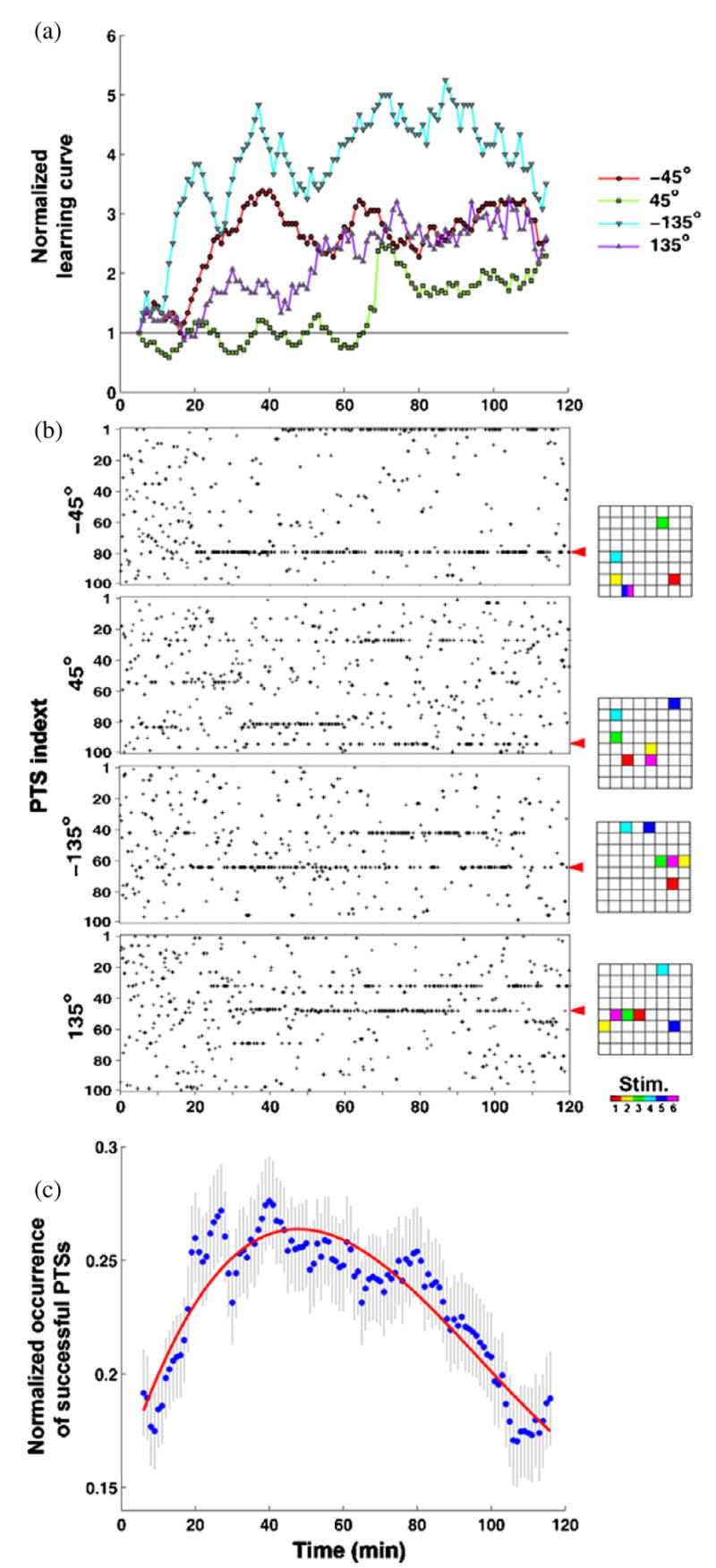
Training required different PTSs at different times. (a) A normalized version of the learning curve shown in figure 2(c). (b) PTSs delivered for different desired directions are shown as black pluses. The corresponding probability in time is shown in figure 3 (031007 B). Various different PTSs were needed to induce appropriate neuronal plasticity and successful motor output. Electrode locations and order (right) for the PTSs (indicated by red arrows) are shown in 8 × 8 grids of electrode locations. (c) Across the 23 trials, fewer PTSs were needed in time to maintain a successful motor output. The frequency of occurrence of a successful PTS was measured by a 10 min moving time bin with 1 min time step and normalized by its maximum value (set to 1). A successful PTS was defined as one that improved performance at least one time. The initial rise occurred while appropriate PTSs were searched. PTS occurrence decreased over the last hour (Spearman correlation of means (dots), one-tailed, rho = −0.89, p-value < 1 × 10−5, n = 231 successful PTSs in 23 trials), which indicates that the training stimuli that were successful in the first hour were less often or no longer required during the last hour to maintain an increased rate of correct motor outputs. A cubic polynomial (red) was fit to the data to better visualize the trend.
We also found that fewer PTSs were needed across a training period to maintain a successful motor output (figure 7(c)). The trend of the PTS-delivering frequency across all 23 trials was measured by counting successful PTSs in a 10-min moving time bin with 1-min time step and normalizing by its maximum value for that trial. We defined a successful PTS as one that improved the performance at least one time, and found that on average, the occurrence of successful PTSs decreased over the last hour (Spearman correlation of means, one-tailed, rho = −0.89, p-value <1 × 10−5, n = 231 successful PTSs in 23 trials). This suggests that the training stimuli that were successful in the first hour were less often or no longer required during the last hour to maintain an increased rate of correct motor outputs (see average closed-loop learning curve in figure 4).
Although the PTS selection algorithm increased the probability of occurrence of a PTS based on the success of short-term ‘elastic’ responses after the next probe stimuli, the elastic responses became consolidated as long-term adaptive changes in time. This is demonstrated by the stability of the distribution of movement directions into the SBS-only period following training (figure 5(d)), the learning curves (figure 4), maintenance of the plasticity of neuronal activity (figure 6) and progressively fewer PTSs being needed to maintain desired movement (figure 7(c)). At the start of training, the changes in the probe responses were indeed initially short-term elastic responses because they were not maintained, requiring reapplication of PTSs. The adaptation of the living networks’ responses to the probe pulse should not be confused with the adaptation, in the computer, of the probabilities of PTS selection to behavior. Recall that the CPS was kept constant throughout an experiment such that changes in the network’s responses to it were, by definition, via alterations in functional connectivity of the cortical network.
Discussion
This is to our knowledge the first successful demonstration, in vivo or in vitro, of goal-directed learning from patterned multi-electrode training stimulation. Our adaptive training algorithm builds upon previous static training protocols (DeMarse et al 2001, Bakkum et al 2004, Marom and Shahaf 2002, Ruaro et al 2005, Novellino et al 2007) by demonstrating that the same network can be re-trained to produce different behaviors. For reviews on the use of MEAs to study learning with electrical stimulation, see Morin et al (2005), Arsiero et al (2007). We hypothesize that directing plasticity using electrical stimuli contingent on the motor output is more efficient than blindly forcing plasticity, for example, via a large tetanic stimulation (Madhavan et al 2007, Jimbo et al 1999). Since neuronal activity is continuously plastic, each electrical stimulus and the ongoing spontaneous activity alter the network’s functional landscape, and routes toward successful behavior cannot be plotted in advance: learning is an ongoing and continuous process. Our closed-loop electrical training algorithm allowed the probabilities of the PTS pool to change, and ‘solutions’ to achieve desired motor outputs were explored by the hybrid (neural + computer) system in real time.
Improvement of stimulation protocols from the previous modeling study
In a preliminary study aimed at devising a successful training algorithm, we used a biologically inspired simulated network with simulated electrical stimuli as a test bed to quickly explore the effectiveness of various types of training algorithms. We successfully demonstrated that the network could be shaped to learn a goal animat behavior involving multiple sensory inputs and motor outputs, using a precursor of the current technique (Chao et al 2008). The stimuli (CPSs) used to encode different sensory inputs evoked neural responses used as motor outputs, and successful learning could be achieved only when these responses had little overlap. To begin testing whether living cultured networks could also exhibit goal-directed learning, we avoided overlapped responses by applying just one sensory input. That is, we delivered one CPS pattern to investigate whether the network could learn to control movement of an animat in a single pre-defined desired direction. Future studies will employ increasingly complex sensory inputs and tasks.
Even though many details of cellular biology and electrode physics were absent from the model network, the closed-loop training that proved successful for the animat controlled by a simulated network required only minor changes for the present study on living cortical networks. This suggests that the adaptive changes reported here were due to spike-timing dependent plasticity (STDP), which was the only long-term plasticity mechanism used in our simulated network (chao et al 2008). In the modeling study, random background stimulation (RBS), instead of SBS, was delivered when training was not required. RBS was delivered randomly at 60 electrodes, one at a time, with random inter-pulse intervals ranging from 200 to 400 ms. This stimulation was shown in a leaky integrate-and-fire model network to negate attractors in network synaptic weight distributions caused by spontaneous activity and also was shown to prevent network synaptic weights from drifting to such attractors after inducing plasticity with simulated electrical stimulation (Chao et al 2005). In the simulated neural network, this property allowed training-induced changes in the network activity to be stabilized (Chao et al 2008). Also, PTSs comprised of pairs of stimuli, instead of a sequence of six stimuli, were used for training. In preliminary experiments with living cultures, we found that CPS responses after two-electrode PTS were greater in number than those after a RBS distributed over all available electrodes (p-value < 1 × 10−6, n = 200 CPS responses after randomly-selected PTS and 200 CPS responses after randomly-selected RBS for three preliminary experiments, Wilcoxon rank sum test). We hypothesized that in order to keep the magnitude of the probe response consistent, the spatio-temporal distribution of training stimuli should also be consistent for different types of stimulation. Therefore, we increased the number of electrodes used in PTS and decreased the number used in RBS to an equal total of 6, and CPS responses after PTS and those after SBS became comparable (p-value = 0.62, n = 200 CPS responses after randomly-selected PTS and 200 CPS responses after randomly-selected RBS for 23 open-loop experiments, Wilcoxon rank sum test). By shuffling the PTS to produce SBS, we ensured that the total amount of stimulation delivered by either type of stimulation was equal, so any observed learning was a consequence of the subtle timing, not overall quantity, of inputs to the network. No longer random, RBS was renamed SBS. While the adaptive training using the new PTS/SBS implementation induced and maintained plasticity and successful movements, the SBS implementation may not be optimal considering its decreased randomness might slowly induce plasticity (interpreted as forgetting) more readily than would an all-electrode random background stimulation (see figure 6).
Potential treatment of neurological disorders
For neurological disorders, targeted distributed artificial stimulation of the brain contingent on the activity of the body or even of the brain itself could direct neuronal plasticity to bypass or accommodate aberrant neuronal activity. Initial candidate pathologies include those with (1) a focal neuronal source or related pathway at which to insert an MEA for electrical training and (2) a measurable physical manifestation from which to gather feedback on performance. As an example, to treat movement disorders such as those that occur after a stroke, electrical modification of motor areas could be guided by physical measurements of changes in muscle activity using electromyography. Directly measuring motor output negates the need for context and probe stimuli to sample neuronal activity, allowing training to be a continuous process. Ongoing afferent input to the artificially stimulated neurons from different brain areas would be expected to eliminate the need for SBS. Relinking the body and the brain with closed-loop stimulation systems could give existing brain mechanisms the potential to overcome neurological disorders.
Current therapeutic techniques used to treat neurological movement disorders attempt to relink neuronal activity to a goal movement via the use of directed mental attention or perceptible feedback signals of behavior, and a lot of practice. Physical therapy, including treadmill training and robotic-assisted or neuromuscular/functional electrical stimulation (NMES/FES)-induced limb movement, has been used to combine natural motion with proprioceptive feedback (Dobkin 2004, Sheffler and Chae 2007). This feedback reactivates existing motor circuits, eventually improving the control of paretic limbs. Further incorporating visual and aural cues, such as targets for foot steps or beats to maintain walking gaits, and also mental imagery of movement have been used to improve training by also priming motor circuits but in a top–down (cortical origin) manner (Morris 2000). Biofeedback therapy uses visual, aural, or tactile displays to improve performance by making underlying physiological or cognitive processes perceptible (Huang et al 2006). These examples all relink neuronal activity to a movement. Moreover, physical therapies have led to cortical plasticity. For example, improvement in hand movements, after constraint-induced movement therapy, was accompanied by an increased representational area in the motor cortex, observed by transcranial magnetic stimulation (Liepert et al 2000) and fMRI (Johansen-Berg et al 2002). However, while helpful, there are at least three shortcomings of these techniques. (1) Benefits are not guaranteed across individuals or different etiologies; (2) optimal therapeutic protocols have not been established; and (3) the relationship with neuronal plasticity is only indirectly inferred (Dobkin 2004, Huang et al 2006). Adaptive closed-loop distributed stimulation may improve therapeutic results by directly treating the abnormal neuronal circuits and related pathways themselves.
Electrical stimulation inside the brain has successfully managed pathological symptoms, but without relinking neuronal activity and behavior (more of a treatment rather than rehabilitation). Deep brain stimulation (DBS) has been used to treat severe cases of essential tremor, dystonia, and Parkinson’s disease (Kern and Kumar 2007), Tourette syndrome (Visser-Vandewalle 2007), clinical depression (Mayberg et al 2005), and epilepsy (Perlmutter and Mink 2006). However, its functional mechanisms are debated, and whether or not plasticity plays a key role in DBS therapy is unclear because the effects depend on continual stimulation. This can cause serious side effects including paresthesias, and attentional and learning impairments (Jahanshahi et al 2000). Other electrical methods to reduce epileptic seizures have been used, including repetitive vagus nerve stimulation (Schachter and Saper 1998) or electrical pulses at or near seizure foci applied prior to a predicted seizure onset (Martinerie et al 1998), but their consequences on neuronal plasticity are not known either. Therefore, designing an adaptive closed-loop algorithm to select appropriate training stimuli, contingent on neuronal or muscular output, could optimize the effect of a treatment while also avoiding extraneous side effects from excessive stimulation.
Possible improvements
The average closed-loop learning curve (figure 4) showed clear improvements in performance, but some trials showed no learning (figure 3). More optimal training algorithms likely exist, although successful performance may have continued to improve or become more permanent if training was not stopped after 2 h. Using a larger set of possible PTSs could improve success rates by inducing a greater range of plasticity; the tradeoff is a potentially longer duration of training to find an appropriate sequence of PTSs. Different spatio-temporally structured PTSs, e.g. using more or fewer stimulation electrodes and different temporal arrangements, could also produce different performance. Furthermore, the 0.50 maximum criterion on the probability of selecting a PTS allows randomly applied inappropriate PTS to produce setbacks, and the 0.002 minimum may keep unhelpful PTSs in the pool. Different optimization rules, such as evolving the PTS pool with a genetic algorithm, or introducing a PID controller to govern the duration of training could potentially improve performance. Future work includes further characterizing the abilities and limitations of distributed artificial stimuli to induce neuronal plasticity, optimizing training parameters and applying closed-loop algorithms to achieve multiple simultaneous desired motor outputs.
Acknowledgments
This work was supported by grants NS38628 from NIH/NINDS, EB000786 from NIH/NIBIB, and by the Whitaker Foundation, the NSF Center for Behavioral Neuroscience, and a NAKFI (National Academies/Keck Futures Initiative) Smart Prosthetics grant.
References
- Arsiero M, Lüscher HR, Giugliano M. Real-time closed-loop electrophysiology: towards new frontiers in in vitro investigations in the neurosciences. Arch Ital Biol. 2007;145:193–209. [PubMed] [Google Scholar]
- Bakkum DJ, Chao ZC, Potter SM. Long-term activity-dependent plasticity of action potential propagation in cortical networks. PLoS One. 2008;3:e2088. doi: 10.1371/journal.pone.0002088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bakkum DJ, Shkolnik AC, Ben-Ary G, Gamblen P, DeMarse TB, Potter SM. Removing Some ‘A’ from AI: Embodied Cultured Networks. In: Iida F, Pfeifer R, Steels L, Kuniyoshi Y, editors. Embodied Artificial Intelligence. Vol. 3139. New York: Springer; 2004. pp. 130–45. [Google Scholar]
- Bi G, Poo M. Synaptic modification by correlated activity: Hebb’s postulate revisited. Ann Rev Neurosci. 2001;24:139–66. doi: 10.1146/annurev.neuro.24.1.139. [DOI] [PubMed] [Google Scholar]
- Bliss TV, Lømo T. Long-lasting potentiation of synaptic transmission in the dentate area of the anaesthetized rabbit following stimulation of the perforant path. J Physiol (Lond) 1973;232:331–56. doi: 10.1113/jphysiol.1973.sp010273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caminiti R, Johnson PB, Burnod Y, Galli C, Ferraina S. Shift of preferred directions of premotor cortical cells with arm movements performed across the workspace. Exp Brain Res. 1990;83:228–32. doi: 10.1007/BF00232214. [DOI] [PubMed] [Google Scholar]
- Chao ZC, Bakkum DJ, Potter SM. Region-specific network plasticity in simulated and living cortical networks: comparison of the center of activity trajectory (CAT) with other statistics. J Neural Eng. 2007;4:1–15. doi: 10.1088/1741-2560/4/3/015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chao ZC, Bakkum DJ, Potter SM. Shaping embodied neural networks for adaptive goal-directed behavior. PLoS Comput Biol. 2008;4:e1000042. doi: 10.1371/journal.pcbi.1000042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chao ZC, Bakkum DJ, Wagenaar DA, Potter SM. Effects of random external background stimulation on network synaptic stability after tetanization: a modeling study. Neuroinformatics. 2005;3:263–80. doi: 10.1385/NI:3:3:263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daoudal G, Debanne D. Long-term plasticity of intrinsic excitability: learning rules and mechanisms. Learn Mem. 2003;10:456–65. doi: 10.1101/lm.64103. [DOI] [PubMed] [Google Scholar]
- DeMarse TB, Wagenaar DA, Blau AW, Potter SM. The neurally controlled animat: biological brains acting with simulated bodies. Auton Robots. 2001;11:305–10. doi: 10.1023/a:1012407611130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dobkin BH. Neurobiology of rehabilitation. Ann NY Acad Sci. 2004;1038:148–70. doi: 10.1196/annals.1315.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eytan D, Brenner N, Marom S. Selective adaptation in networks of cortical neurons. J Neurosci. 2003;23:9349–56. doi: 10.1523/JNEUROSCI.23-28-09349.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fields RD. Myelination: an overlooked mechanism of synaptic plasticity? Neuroscientist. 2005;11:528–31. doi: 10.1177/1073858405282304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Georgopoulos A. Selectionism and the Brain. San Diego, CA: Academic; 1994. Population activity in the control of movement; pp. 103–19. [DOI] [PubMed] [Google Scholar]
- Huang H, Wolf SL, He J. Recent developments in biofeedback for neuromotor rehabilitation. J Neuroeng Rehabil. 2006;3:11. doi: 10.1186/1743-0003-3-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishibashi T, Dakin KA, Stevens B, Lee PR, Kozlov SV, Stewart CL, Fields RD. Astrocytes promote myelination in response to electrical impulses. Neuron. 2006;49:823–32. doi: 10.1016/j.neuron.2006.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackson A, Mavoori J, Fetz EE. Long-term motor cortex plasticity induced by an electronic neural implant. Nature. 2006;444:56–60. doi: 10.1038/nature05226. [DOI] [PubMed] [Google Scholar]
- Jahanshahi M, et al. The impact of deep brain stimulation on executive function in Parkinson’s disease. Brain. 2000;123:1142–54. doi: 10.1093/brain/123.6.1142. [DOI] [PubMed] [Google Scholar]
- Jimbo Y, Tateno T, Robinson HPC. Simultaneous induction of pathway-specific potentiation and depression in networks of cortical neurons. Biophys J. 1999;76:670–8. doi: 10.1016/S0006-3495(99)77234-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johansen-Berg H, Dawes H, Guy C, Smith SM, Wade DT, Matthews PM. Correlation between motor improvements and altered fMRI activity after rehabilitative therapy. Brain. 2002;125:2731–42. doi: 10.1093/brain/awf282. [DOI] [PubMed] [Google Scholar]
- Kempermann G. Why new neurons? Possible functions for adult hippocampal neurogenesis. J Neurosci. 2002;22:635–8. doi: 10.1523/JNEUROSCI.22-03-00635.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kern DS, Kumar R. Deep brain stimulation. Neurologist. 2007;13:237–52. doi: 10.1097/NRL.0b013e3181492c48. [DOI] [PubMed] [Google Scholar]
- Liepert J, Bauder H, Wolfgang HR, Miltner WH, Taub E, Weiller C. Treatment-induced cortical reorganization after stroke in humans. Stroke. 2000;31:1210–6. doi: 10.1161/01.str.31.6.1210. [DOI] [PubMed] [Google Scholar]
- Madhavan R, Chao ZC, Potter SM. Plasticity of recurring spatiotemporal activity patterns in dissociated cortical networks. Phys Biol. 2007;4:181–93. doi: 10.1088/1478-3975/4/3/005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markram H, Lubke J, Frotscher M, Sakmann B. Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science. 1997;275:213–5. doi: 10.1126/science.275.5297.213. [DOI] [PubMed] [Google Scholar]
- Marom S, Shahaf G. Development, learning and memory in large random networks of cortical neurons: lessons beyond anatomy. Q Rev Biophys. 2002;35:63–87. doi: 10.1017/s0033583501003742. [DOI] [PubMed] [Google Scholar]
- Martinerie J, Adam C, Le Van Quyen M, Baulac M, Clemenceau S, Renault B, Varela FJ. Epileptic seizures can be anticipated by non-linear analysis. Nat Med. 1998;4:1173–6. doi: 10.1038/2667. [DOI] [PubMed] [Google Scholar]
- Mayberg HS, Lozano AM, Voon V, McNeely HE, Seminowicz D, Hamani C, Schwalb JM, Kennedy SH. Deep brain stimulation for treatment-resistant depression. Neuron. 2005;45:651–60. doi: 10.1016/j.neuron.2005.02.014. [DOI] [PubMed] [Google Scholar]
- Meyer JA, Wilson SW. Proc First International Conference on Simulation of Adaptive Behavior. Cambridge: MIT Press; 1991. From animals to animats. [Google Scholar]
- Morin FO, Takamura Y, Tamiya E. Investigating neuronal activity with planar microelectrode arrays: achievements and new perspectives. J Biosci Bioeng. 2005;100:131–43. doi: 10.1263/jbb.100.131. [DOI] [PubMed] [Google Scholar]
- Morris ME. Movement disorders in people with Parkinson disease: a model for physical therapy. Phys Ther. 2000;80:578–97. [PubMed] [Google Scholar]
- Novellino A, D’Angelo P, Cozzi L, Chiappalone M, Sanguineti V, Martinoia S. Connecting neurons to a mobile robot: an in vitro bidirectional neural interface. Comput Intell Neurosci. 2007:12725. doi: 10.1155/2007/12725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perlmutter JS, Mink JW. Deep brain stimulation. Annu Rev Neurosci. 2006;29:229–57. doi: 10.1146/annurev.neuro.29.051605.112824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Potter SM, DeMarse TB. A new approach to neural cell culture for long-term studies. J Neurosci Methods. 2001;110:17–24. doi: 10.1016/s0165-0270(01)00412-5. [DOI] [PubMed] [Google Scholar]
- Potter SM, Wagenaar DA, DeMarse TB. Closing the loop: stimulation feedback systems for embodied MEA cultures. In: Taketani M, Baudry M, editors. Advances in Network Electrophysiology Using Multi-Electrode Arrays. New York: Springer; Kluwer; 2006. pp. 215–42. [Google Scholar]
- Ruaro ME, Bonifazi P, Torre V. Toward the neurocomputer: image processing and pattern recognition with neuronal cultures. IEEE Trans Biomed Eng. 2005;52:371–83. doi: 10.1109/TBME.2004.842975. [DOI] [PubMed] [Google Scholar]
- Schachter SC, Saper CB. Vagus nerve stimulation. Epilepsia. 1998;39:677–86. doi: 10.1111/j.1528-1157.1998.tb01151.x. [DOI] [PubMed] [Google Scholar]
- Sheffler LR, Chae J. Neuromuscular electrical stimulation in neurorehabilitation. Muscle Nerve. 2007;35:562–90. doi: 10.1002/mus.20758. [DOI] [PubMed] [Google Scholar]
- Uesaka N, Hayano Y, Yamada A, Yamamoto N. Interplay between laminar specificity and activity-dependent mechanisms of thalamocortical axon branching. J Neurosci. 2007;27:5215–23. doi: 10.1523/JNEUROSCI.4685-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Visser-Vandewalle V. DBS in tourette syndrome: rationale, current status and future prospects. Acta Neurochir Suppl. 2007;97:215–22. doi: 10.1007/978-3-211-33081-4_24. [DOI] [PubMed] [Google Scholar]
- Wagenaar DA, Potter SM. Real-time multi-channel stimulus artifact suppression by local curve fitting. J Neurosci Methods. 2002;120:113–20. doi: 10.1016/s0165-0270(02)00149-8. [DOI] [PubMed] [Google Scholar]
- Wagenaar DA, Madhavan R, Pine J, Potter SM. Controlling bursting in cortical cultures with closed-loop multi-electrode stimulation. J Neurosci. 2005;25:680–8. doi: 10.1523/JNEUROSCI.4209-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagenaar DA, Pine J, Potter SM. Effective parameters for stimulation of dissociated cultures using multi-electrode arrays. J Neurosci Methods. 2004;138:27–37. doi: 10.1016/j.jneumeth.2004.03.005. [DOI] [PubMed] [Google Scholar]
- Wagenaar DA, Pine J, Potter SM. Searching for plasticity in dissociated cortical cultures on multi-electrode arrays. J Negative Results BioMed. 2006a;5:1–19. doi: 10.1186/1477-5751-5-16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagenaar DA, Pine J, Potter SM. An extremely rich repertoire of bursting patterns during the development of cortical cultures. BMC Neurosci. 2006b;7:11. doi: 10.1186/1471-2202-7-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagenaar DA, Potter SM. A versatile all-channel stimulator for electrode arrays, with real-time control. J Neural Eng. 2004;1:39–45. doi: 10.1088/1741-2560/1/1/006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson MA, McNaughton BL. Dynamics of the hippocampal ensemble code for space. Science. 1993;261:1055–8. doi: 10.1126/science.8351520. [DOI] [PubMed] [Google Scholar]
- Zhang W, Linden DJ. The other side of the engram: experience-driven changes in neuronal intrinsic excitability. Nat Rev Neurosci. 2003;4:885–900. doi: 10.1038/nrn1248. [DOI] [PubMed] [Google Scholar]