Do synergies decrease force variability? A study of single-finger and multi-finger force production

Abstract

We tested a hypothesis that force production by multi-finger groups leads to lower indices of force variability as compared to similar single-finger tasks. Three experiments were performed with quick force production, steady-state force production under visual feedback, and steady-state force production without visual feedback. In all experiments, a range of force levels was used computed as percentages of the maximal voluntary contraction force for each involved finger combination. Force standard deviation increased linearly with force magnitude across all three experiments and all finger combinations. There were modest differences between multi-finger and single-finger tasks in the indices of force variability, significant only in the tasks with steady-state force production under visual feedback. When fingers acted in groups, each finger showed significantly higher force variability as compared to its single-finger task and as compared to the multi-finger group as a whole. Fingers that were not instructed to produce force also showed close to linear relations between force standard deviation and force magnitude. For these fingers, indices of force variability were much higher as compared to those computed for the forces produced by instructed fingers. We interpret the findings within a feed-forward scheme of multi-finger control with two inputs only one of which is related to the explicit task. The total force variability reflects variability in only the task-related component, while variability of the finger forces is also due to variability of the component that is not related to the task. The findings tentatively suggest that total force variability originates at an upper level of the control hierarchy in accordance to the Weber-Fechner law rather than reflects a “neural noise” at the segmental level.

Introduction

The problem of control of multi-element, redundant systems has been addressed using the notion of synergies (Bernstein 1967; reviewed in Turvey 2007). In recent studies, synergies have been defined as neural organizations that ensure low variability of performance variables by co-variation across trials or across time samples in the space of elemental variables (Latash et al. 2002b, 2007; Latash 2008). Quantitative analysis within this approach has been developed within the framework of the uncontrolled manifold (UCM) hypothesis (Scholz and Schöner 1999). The UCM-hypothesis assumes that the controller organizes two subspaces in the space of elemental variables. One of these spaces (the UCM) corresponds to a fixed value of a potentially important performance variable, and the controller allows relatively large variability in that subspace. This component of variability has been addressed as good since it allows flexible ways of generating a desired value of the performance variable. The complementary (orthogonal) subspace corresponds to changes in that performance variable, and the controller tries to limit variability in that subspace (bad variability).

The view that synergies decrease variability of performance has been implicitly reflected in terms such as “error compensation” and “compensated variability” (Scholz et al. 2002; Latash et al. 2001, 2007) as well as in models based on action of feedback loops (Todorov and Jordan 2002: Latash et al. 2005). However, does a multi-effector synergy decrease variability of performance as compared to similar tasks performed by single effectors? Surprisingly, there is no clear answer to this basic question.

Imagine that a person is asked to produce a certain level of constant force with one finger and then with two fingers. A two-finger force-stabilizing synergy, commonly seen in such tasks (strong negative co-variation between the finger forces across trials, Latash et al. 2002a; Gorniak et al. 2007), leads to significantly higher values of good variability as compared to bad variability. So, does it lead to more accurate performance? Not necessarily, because, by definition, bad variability is the only component that affects variability of performance. So, a strong synergy may correspond to the same amount of bad variability plus much more good variability.

It is not easy to compare indices of force variability across different systems and tasks. One potential problem is in providing feedback for the subjects. The classical Weber-Fechner law of perception states that the ability of a person to distinguish between two sensory signals depends on their average magnitude (see Kunimoto et al. 2001; Johnson et al. 2002). So, if a person is given visual feedback and asked to produce force such that the cursor on the screen follows a target line, accuracy of performance and its variability will depend strongly on the visual resolution of the feedback signal, and this dependence may override any dependence on the number of effectors (fingers) that participate in the task and/or on co-variation of the effector’s outputs.

A subject may be asked to remember a certain value of force and to reproduce it with closed eyes or to continue producing a constant force after the visual feedback has been turned-off (e.g., Vaillancourt et al. 2002). In such experiments, the subject would probably rely on proprioceptive and tactile feedback and correct perceivable force deviations that, according to the Weber-Fechner law, might be expected to increase with force level leading to an increase in force variability. So, indices of force variability in any experiment that allows the subject to use feedback signals are likely to reflect the Weber-Fechner law - a perceptual component of the task - rather than the motor component such as co-variation of forces produced by the digits.

A person may be asked to produce a very fast action to a target (a very quick force pulse), an action that is too quick for any use of sensory feedback signals. This is indeed possible. However, such actions are associated with a lack of negative co-variation among finger forces, i.e. lack of force-stabilizing synergy (Goodman et al. 2005; Olafsdottir et al. 2005).

This looks like a catch. On the one hand, strong synergies are typically associated with relatively slow changes in the performance variable. However, such tasks offer the subjects plenty of time to use sensory signals to correct the performance variable. As a result, indices of variability of that variable are likely to reflect sensory processes governed by the Weber-Fechner law. On the other hand, very quick actions do not show force-stabilizing synergies.

There is one more confounding factor. Several studies have shown a nearly proportional increase in standard deviation of force with force magnitude that is rather similar to the Weber-Fechner law and may even be its consequence (Newell and Carlton 1988; Carlton et al. 1993; Slifkin and Newell 1999; Christou et al. 2002). Imagine that a person produces the total force of 40 N with one finger, and the standard deviation across a series of trials is 4 N. Now let us ask this person to perform this task with two fingers. Each finger is expected to produce less force, for simplicity assume that they share the force equally, 20 N each. If there is no co-variation and standard deviation of force is proportional to the force magnitude, each finger is expected to show a standard deviation of 2 N. Now recall that variance is standard deviation squared. This means that variance of the total force in the one-finger task will be 16 N². In the two-finger task, in the absence of co-variation, the variance of the total force will be the sum of the variances of individual finger forces: 4+4=8 N². The variance of the total force in the two-finger task dropped by 50% in the absence of a force-stabilizing synergy. Note that this predicted drop is substantially higher than reports from experimental studies (30% in Latash et al. 2001; and 15% in Sosnoff et al. 2005).

The lack of comprehensive data sets that would allow to disentangle the described knot of problems was the main driving force behind the three experiments reported in this paper. The same subjects performed force production tasks that allowed unrestricted visual feedback during steady-state force production, similar tasks without visual feedback but a possibility to use proprioceptive and tactile feedback to match a certain force level, and very quick force pulses to a visual target. In all three experiments, we used several target force levels presented as the same percentage values of the MVC of the involved finger groups (cf. Christou et al. 2002).

The following main hypotheses were explored:

• H1: Force standard deviation will increase linearly with force magnitude across all conditions corresponding to a constant coefficient of variation.

• H2: Multi-finger tasks will show lower variability of the total force as compared to single-finger tasks.

• H3: This dependence will be seen in the steady-state force production tasks but not in the quick force pulse production tasks.

• H4: Individual finger force variability will be higher in multi-finger force production tasks contributing to the larger good variability.

Methods

Subjects

Seven healthy volunteers (28.7 ± 8.7 years old, two males and five females) participated as subjects in the experiments. The weight of the subjects averaged 61.7 ± 7.5 kg, and their height was 1.70 ± 0.07 m. All the subjects were right-handed according to their preferred hand use for writing and eating. All subjects gave informed consent according to the procedures approved by the Office for Research Protection of the Penn State University.

Apparatus

The experimental setup is illustrated in Figure 1B. Four unidirectional piezoelectric force sensors (model 208C02; Piezotronic Inc.) with the diameter of 1.5 cm were used to measure the forces produced by each of the four fingers of the right hand. Each sensor was mounted on an aluminum post and covered with a cotton pad to increase friction and prevent the influence of finger skin temperature on the measurements. The sensors were placed within an aluminum frame (65 × 120 mm inner size) placed inside a groove made on a wooden board to ensure the stable position of the sensors. The sensors were medio-laterally distributed 30 mm apart within the frame. The position of the sensors within the frame could be adjusted in the forward-backward direction to fit the individual subject’s anatomy. Analog output signals from the sensors were processed by separate AC/DC conditioners (M482M66, Piezotronic Inc.) with the ± 1% error range over the typical epoch of recording of a constant signal. The force measured by each sensor was sampled at 1000 Hz, with the 12 bit resolution by a desktop IBM compatible computer. The sensors were calibrated 30 min before each testing.

Figure 1.

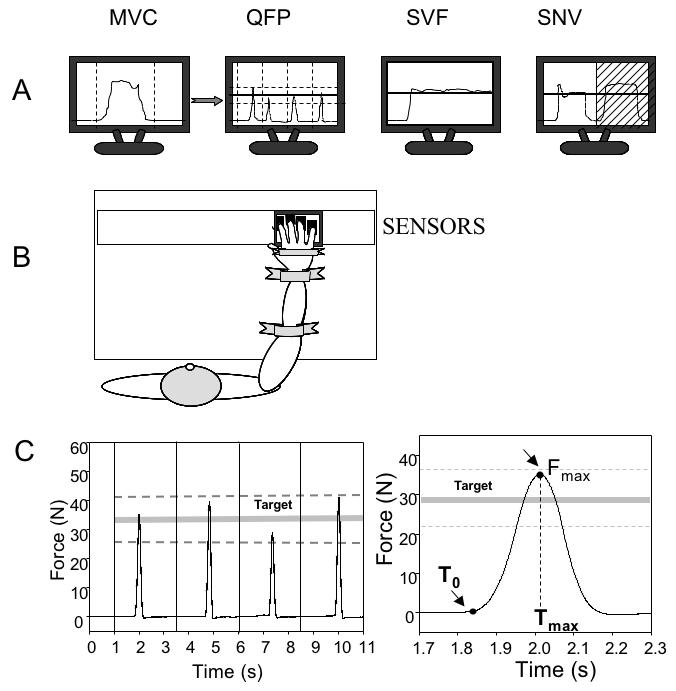
The experiment set-up and tasks. A: An illustration of the control trials (MVC) and three experiments (quick force pulse production, QFP; steady-state accurate force production with visual feedback, SVF; steady-state force production without visual feedback, SNV). B: An illustration of the subject’s position; C: An illustration of subject’s performance and force pulse analysis in experiment QFP.

During testing, the subject sat comfortably in a chair facing the testing table with his/her right upper arm at approximately 45° of abduction in the frontal plane and 45° of flexion in the sagittal plane, the elbow at approximately 45° of flexion (full extension corresponds to 0°). The wooden horizontal board supported the wrist and the forearm; two pairs of Velcro straps were used to prevent forearm or hand motion during the tests. A custom-fitted wooden piece was placed underneath the subject’s right palm to help maintain a constant configuration of the hand and fingers. A 17” LCD monitor was placed approximately 65 cm in front of the subject. It displayed both the task (a target total force) and the actual total force produced by the instructed finger(s).

Procedure

There were three experiments. Each of these involved the same set of control force production tasks (Figure 1A). The control tasks required the subjects to produce maximal pressing forces (maximal voluntary contraction, MVC) by each of the fingers of the right hand (I, index; M, middle; R, ring; L, little) and by three finger combinations (IM, IMR, and IMRL). During the MVC tests, a sound signal generated by the computer informed the subject to get ready. Then a trace showing the total force produced by the instructed finger(s) (master fingers) started to move across the screen. The subjects were asked to produce peak force within a 2-s time window shown on the screen and then to relax. The subjects were instructed to pay no attention to possible force generation by other, explicitly non-involved fingers, as long as the master finger(s) produced maximal force. There were no limits on involvement of the non-task fingers, but the subjects were not allowed to lift fingers off the sensors at any time. For each MVC task, two trials were performed with 30-s intervals between the trials, and the data for the trial with the highest force by the instructed finger(s) were used for setting further tasks and for data analysis.

The three accurate force production experiments involved quick force pulse production (QFP), steady-state force production with visual feedback (SVF), and reproduction of a steady-state force level without visual feedback (SNV). The three experiments were performed on different days to minimize effects of fatigue. In each experiment, five force levels were used as targets for each of the instructed fingers and finger combinations. The target forces were 5%, 10%, 20%, 40%, and 60% of the MVC measured for that particular finger combination. In the QFP and SVF experiments, seven conditions were used: I, M, R, L, IM, IMR, and IMRL. In the SNV experiment, only three conditions were used: I, M, and IM to limit the duration of that experiment.

In each test, the monitor showed the subject the initial (zero) force level and a force target presented as a straight horizontal line. The scale was adjusted for different force levels such that the target was always located at the same height of the screen. Hence, the gain of visual feedback differed across conditions. The total time of the signal progression across the screen was always 11 s. Both, the force levels and conditions (instructed finger(s)) were randomized. Subjects were given two practice trails before each new combination of force level and instructed finger(s).

Experiment-1: Quick force pulses, QFP

In this experiment, thin vertical lines divided the screen into four 2.5-s windows. Four force pulses were to be produced within each time interval. Two horizontal dotted blue lines showed the limits for trial acceptance (± 25% of the target force). Three out of four pulses had to have their peak force within the target zone. If more than one pulse was inaccurate, the trial was discarded and repeated immediately. For each condition, four trails were recorded containing not less than 12 acceptable force pulses.

Experiment-2: Steady-state force production with visual feedback, SVF

In this experiment, only the target line was presented, and the subjects were required to reach this line quickly by pressing with the instructed finger(s) and to maintain the target level of force as steady as possible until the end of the trial. One trial for each force level and instructed finger(s) was recorded.

Experiment-3: Reproduction of a steady-state contraction without visual feedback, SNV

In this experiment, the screen was divided into two halves by a vertical line; the subject could see the left part of the screen but not the right one. The instruction was: To reach the target force level quickly and to keep it for about 3 s. Then, the subject relaxed, waited until the cursor showing the total force moved into the right (invisible) half of the screen, and tried to press again to the same force level and to keep it steady until the end of the trial. The experimenter supervised each trial and rejected it if an obvious mistake was made during the second half of the trial, for example if the subject produced a force pulse to a certain level and then relaxed. For each force level and instructed finger(s), fourteen satisfactory trails were recorded.

Data Processing

Common Procedures

Data processing was performed off-line using Matlab-7 software. In the control MVC trials, the peak forces were measured at the time when the sum of the forces produced by the instructed finger(s) reached its peak. For multi-finger tasks in the main experiments, the total force was computed as the sum of the individual forces of the instructed fingers.

For every task and every force level, both average force (F) and its standard deviation (SD_F) across repetitive attempts were computed and expressed in percent of the MVC of the instructed finger(s). The non-instructed fingers produced forces in all tasks and all subjects - a phenomenon termed enslaving (Ohtsuki 1981; Li et al. 1998; Zatsiorsky et al. 2000). Forces produced by the enslaved fingers and their SD_F over the trials were also computed.

The relations between SD_F and F were analyzed using linear regression models: SD_F = a + k×F, where a and k are constants, fitted to the individual observations within each subject. Further, the regression coefficients (k) and amounts of variance (R²) accounted for by the linear regression models were analyzed.

Experiment-1: QFP

The following rejection criteria were applied to individual force pulses: (1) time to peak force over 300 ms; and (2) peak force value outside the 25% zone centered at the target force. Overall, 8% of the pulses were rejected based on these criteria. The start of the pulse was defined as the time (t₀) when the first force derivative, dF/dt reached 5% of its peak value in that particular pulse. The derivative was calculated using the 5-point window method. The time to peak force was calculated as the time from t₀ to the time when the force reached a peak value (Figure 1C).

Experiment-2: SVF

During the steady-state force production with visual feedback, average force value and its standard deviation were estimated using 6000 samples within the time interval from 4.5 s to 10.5 s from the trial initiation; all subjects in all trials showed steady-state force level within this time interval.

Experiment-3: SNV

During the steady-state force production without visual feedback, average force value was estimated over 400 consecutive samples within the time interval from 8 s to 8.4 s from the beginning of trail. The smaller time interval (as compared to Experiment-2) was selected to decrease effects of force trend. This particular time interval was selected as corresponding to the lowest force trend over all subjects and conditions as estimated by analysis of all the data. The mean force value in each trial was used to compute the mean F and SD_F across 14 trials by each subject and at each force level.

In this paper, for the sake of brevity, we do not present results of analyses within the framework of the uncontrolled manifold (UCM) hypothesis (Scholz and Schöner 1999; reviewed in Latash et al. 2007). These analyses quantify the co-variation of elemental variables (finger forces or finger modes, Danion et al. 2003) with respect to performance variables of the whole system such as, for example, the total force. Variance in the space of elemental variables is projected on two sub-spaces, one that corresponds to a constant value of the total force (the UCM) and its orthogonal complement corresponding to total force changes. Further, the amounts of variance within the two sub-spaces are compared. If the variance per dimension is larger along the UCM than in the orthogonal sub-space, a conclusion can be drawn that a multi-finger synergy stabilizes the total force across trials. We ran such analyses on the data sets and got results similar to those reported in earlier studies of steady-state and quick force pulse production (Goodman et al. 2005; Olafsdottir et al. 2005; Shim et al. 2005).

Statistical Analysis

Standard methods of parametric statistics were used. Analysis of variance (ANOVA) with and without repeated measures was applied to SD_F and regression coefficients k with factors selected from the following list: Finger-Combination (up to seven levels, I, M, R, L, IM, IMR, and IMRL), Task (two levels, single-finger and multi-finger), Force-Level (five levels, 5%, 10%, 20%, 40%, and 60%), Finger (four levels, I, M, R, and L), Finger-Role (single, group, and enslaved), and Experiment (QFP, SVF, and SNV). In particular, we used ANOVA to answer the following questions: Do single fingers differ from each other in their indices of force variability? Do single-finger tasks differ from multi-finger tasks in their indices of variability? Does finger variability depend on whether a finger acts alone, is an instructed finger within a group, or is a non-instructed (enslaved) finger? We also explored how answers to these questions might depend on force level within the studied range. Tukey’s honestly significant difference (HSD) tests and pair-wise comparisons were used to analyze significant effects.

Results

Experiment-1 (Quick force pulse, QFP)

When asked to produce a quick force pulse into a target window, different subjects showed times to peak force ranging from 148.2±0.65 ms to 204.3±2.12 ms (means ± standard error across force levels and finger combinations). The fastest times to peak force (averaged across subjects) were observed during force pulse production by the I and M fingers (177.6±3.7 and 178.8±3.75 ms), while the R and L finger tended to be slower (181.5±4.11 and 183.0±3.91ms). There were no significant differences in the pulse duration across the different fingers and finger combinations. The time to peak force averaged across different finger combinations showed a tendency to increase with force level, from 177.5±22.5 ms to 182.7±24.3 ms, but these differences were not statistically significant. The grand average time to peak force was 180.2±1.45 ms (across subjects).

An increase in the target force level was accompanied by a close to proportional increase in the standard deviation of the peak force (SD_F). This is illustrated in Figure 2 using averaged across the subjects data. Panel A shows the relations between peak force (F) and SD_F across a set of pulses for the four single-finger tasks with linear regression lines and equations. Panel B shows the data for the three multi-finger tasks. Panel C presents the same data for the forces produced by individual finger during the four-finger task (IMRL). Each of the regressions was statistically significant (p < 0.01) accounting for over 90% of the variance for each of the data sets. Note that in these and future panels, the data are presented in percent of the MVC force measured in the control trials for those particular fingers and finger combinations (see Methods). Note that the proportional changes in SD_F with F are equivalent to a constant value of the coefficient of variation; however, to simplify inferential statistical analysis, we will describe the results using SD_F and F data.

Figure 2.

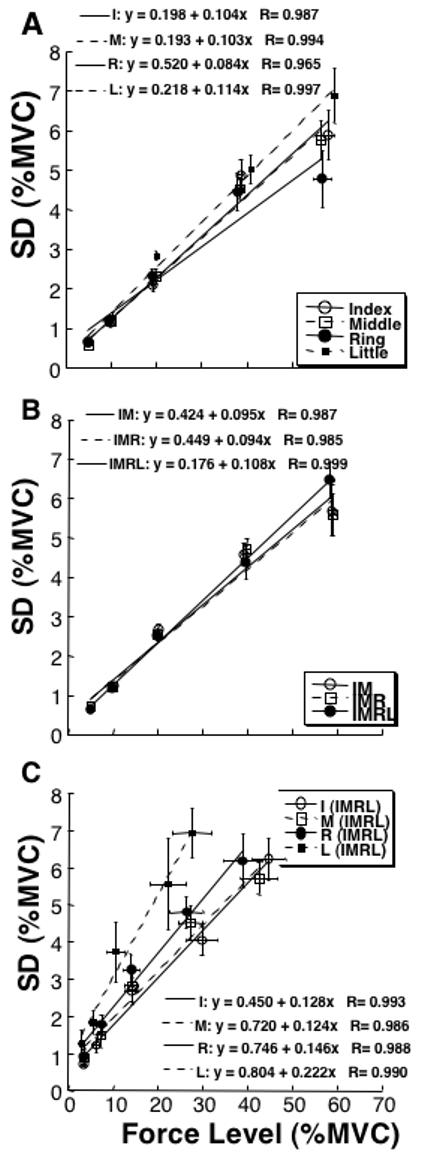
Experiment-1 (QFP). The dependence of force variability (standard deviation, SD in % of MVC) on force magnitude is shown for the data averaged across subjects for each of the five target force levels: 5, 10, 20, 40, and 60% of MVC. Linear regression lines and equations are presented with correlation coefficients. Error bars show standard errors. A: Single-finger tasks. B: Multi-finger tasks. C: The data for individual fingers participating in the four-finger task (IMRL). Each of the regressions was statistically significant (p < 0.01).

Increasing the number of fingers produced no change in the relation between F and SD_F. To explore this dependence, a two-way ANOVA with repeated measures was run on the SD_F indices (expressed in % of the MVC), with the factors Finger-Combination and Force-Level using Subjects as a random factor. There was a significant effect of Force-Level (F_[4,204]=329.15; p < 0.001) but not of Finger-Combination (F_{[6, 204]}=1.92; p > 0.1) and no significant interaction (p > 0.5). Tukey’s pair-wise comparisons confirmed significant differences between all pairs of the force levels (p<0.01).

Since the intercept of the linear regression model SD_F = a + kF (see Methods) was small (on average, a = 0.31± 0.097%), we used the regression coefficient k to further analyze the relations between SD_F and F. Coefficients k are dimensionless, they represent an average increase of SD_F (in % of MVC) per unit of force (also in % of the MVC). There were only small differences in the magnitude of the regression coefficient k across the tasks (within ±12% of the k-values, Figure 3A).

Figure 3.

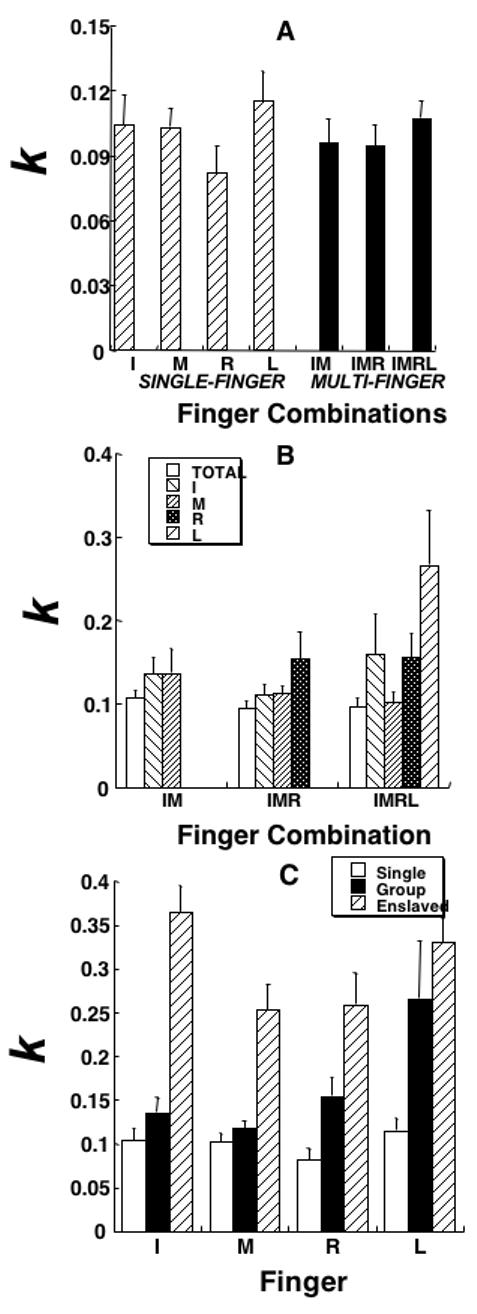
Experiment-1 (QFP). Regression coefficients (k, dimensionless) within the linear regression model computed across the different force levels for different tasks and fingers are shown averaged across subjects with standard error bars. A: The data for the total force in the seven tasks, four single-finger tasks (I, M, R, and L, striped bars) and three multi-finger tasks (IM, IMR, and IMRL, black bars). Note the lack of differences between the single-finger and multi-finger tasks. B: The data for the total force (white bars) and each of the fingers involved in multi-finger tasks. Note lower k for the total force as compared to the individual finger forces. C: The data for each finger in its own single-finger task (white bars), in multi-finger tasks, in which this finger was explicitly involved (hatched bars), and in tasks when this finger was not instructed (enslaved, black bars). I - index finger, M - middle finger, R - ring finger, L - little finger.

For multi-finger tasks, k values were computed for the regressions between the total force and its SD_F as well as between the forces produced by individual fingers and their corresponding SD_F. Individual finger forces showed substantially higher k values as compared to the total force (Figure 3B).

When SD_F indices were compared for individual fingers involved in single-finger and multi-finger tasks, higher SD_F indices were observed in the multi-finger tasks. Figure 2C shows an example for the IMRL task; note that the slopes of the regression lines are higher for each finger as compared to Figure 2A. Quantitative comparison of k for individual fingers involved in the single-finger and multi-finger tasks showed that in the multi-finger tasks k values were higher, on average, by 65.5%. This increase did not occur evenly across all fingers. For the I and M fingers, it was relatively small, 29.8% and 13.7%, respectively, while for the R and L fingers it was much larger, 88.6% and 129.7% respectively.

For statistical analysis, k values for each finger were averaged across all the multi-finger tasks, in which this finger was explicitly involved (IM, IMR, and IMRL for I and M; IMR and IMRL for R; and IMRL for L). Then, a two-way ANOVA was run Finger (four levels) × Task (two levels). The ANOVA showed main effects on both factors (F_{[1, 42]}=10.1; p < 0.01 for Task; F_{[3, 42]}=5.46; p < 0.01 for Finger), with a significant interaction (F_{[3, 83]}=2.72; p < 0.05). Tukey’s pair-wise comparisons confirmed higher values of k in multi-finger tasks as compared to single-finger tasks (p < 0.001); the L finger showed higher k as compared to each of the other three fingers (p < 0.01). The interaction reflected the significant differences between the M and L fingers in the effects of the Task factor (p < 0.05).

Fingers also produced forces in tasks where they were not instructed to produce force. For such non-task fingers, there was also a close to linear relation between SD_F and F. However, non-task fingers showed significantly higher variability across trials as compared to the instructed fingers. The regression coefficients of the SD_F(F) relations computed for each finger in its single-finger task, multi-finger tasks, and tasks in which that particular finger was not expected to generate force are shown in Figure 3C.

These data were analyzed with a two-way ANOVA with repeated measures with the factors Finger (four levels) and Finger-Role (three levels, single, group, and non-task). There were significant effects of Finger-Role (F_[2,66]=38.47; p<0.001) and Finger (F_[3,66]=3.71; p<0.05) without an interaction (F_[6,66]=1.50; p>0.1). Tukey’s pair-wise comparisons confirmed significantly higher k values for non-task fingers as compared to the same fingers instructed to act alone or in a group (p<0.001); the difference between the fingers involved in single-finger tasks and in multi-finger tasks was close to the level of significance (p<0.07).

Experiment-2 (Steady-state with visual feedback, SVF)

The subjects were very accurate in the production of the required force levels under visual feedback. Nevertheless, a strong dependence was seen between F and SD_F. This increase in SD_F with F is illustrated in Figure 4 using data averaged across subjects for each target force level. Figure 4 is organized similarly to Figure 2: Panel A shows the data for the four single-finger tasks, Panel B shows the data for the three multi-finger tasks, while Panel C shows the data for individual fingers that took part in the IMRL task. The linear regression models accounted, on average, for over 90% of the variance in the data; each of the regressions was statistically significant (p < 0.01).

Figure 4.

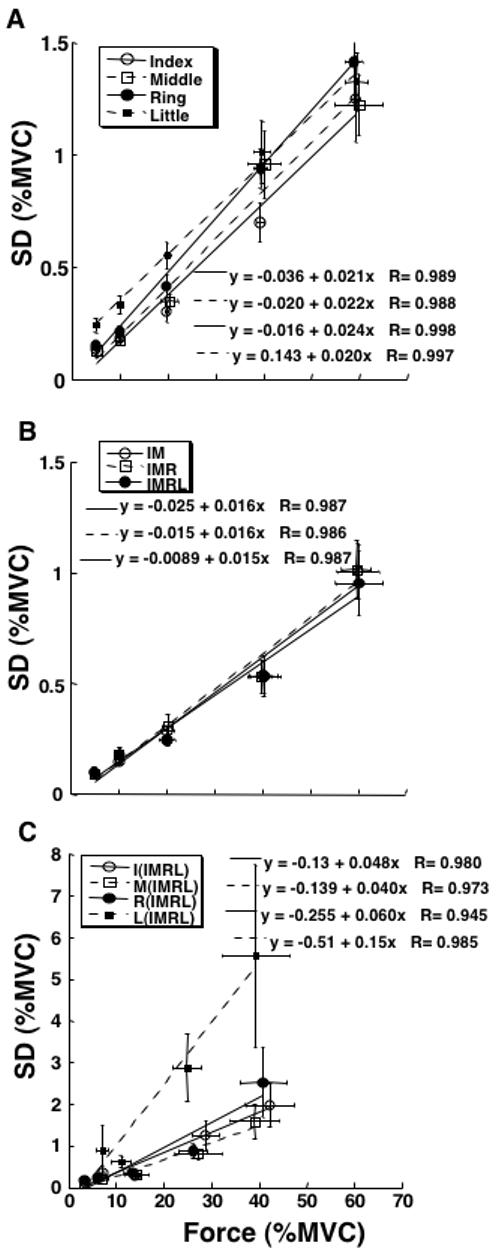
Experiment-2 (SVF). The dependence of force variability (standard deviation, SD in % of MVC) on force magnitude is shown for the data averaged across subjects for each of the five target force levels: 5, 10, 20, 40, and 60% of MVC. Linear regression lines and equations are presented with correlation coefficients. Error bars show standard errors. A: Single-finger tasks. B: Multi-finger tasks. C: The data for individual fingers participating in the four-finger task (IMRL). Each of the regressions was statistically significant (p < 0.01).

In this experiment, multi-finger tasks showed significantly lower variability indices (SD_F) as compared to the single-finger tasks. This was confirmed by a two-way ANOVA with repeated measures, Finger-Combination (seven levels) × Force-Level (five levels). It showed effects of both Finger-Combination (F_[6,204]=13.76; p < 0.001) and Force-Level (F_[5,204]=274.0; p < 0.001) without a significant interaction (p > 0.05). Tukey’s pair-wise comparisons found no significant difference in force variability indices among the three multi-finger tasks (p > 0.5) while SD_F in each of the single-finger tasks was higher as compared to each of the multi-finger tasks (p < 0.05). There were significant differences between each pair of the force levels (p < 0.001), except the 5%MVC and 10%MVC levels.

Similar to Figure 3A, Figure 5A shows regression coefficients (k) averaged across subjects for the seven tasks and five force levels. The multi-finger tasks showed significantly lower k values as compared to single-finger tasks, on average by about 26%. When k values were computed for the individual fingers, they were, on average, nearly three-fold higher when the fingers took part in multi-finger tasks as compared to the single-finger tasks. This result is illustrated in Figure 5B. The linear regression coefficients k for SD_F(F) for the I, M, and R fingers increased by 211%, 168%, and 257% respectively, while the highest increase (by about 580%) was seen for the L finger.

Figure 5.

Experiment-2 (SVF). Regression coefficients (k, dimensionless) within the linear regression model computed across the different force levels for different tasks and fingers are shown averaged across subjects with standard error bars. A: The data for the total force in the seven tasks, four single-finger tasks (I, M, R, and L, striped bars) and three multi-finger tasks (IM, IMR, and IMRL, black bars). Note the lower k for the multi-finger tasks. B: The data for the total force (white bars) and each of the fingers involved in multi-finger tasks. Note the much lower k for the total force as compared to the individual finger forces. C: The data for each finger in its own single-finger task (white bars), in multi-finger tasks, in which this finger was explicitly involved (hatched bars), and in tasks when this finger was not instructed (enslaved, black bars). Abbreviations are the same as in Figure 3.

For statistical analysis, k values were averaged for each finger across all the multi-finger tasks, in which this finger was involved (IM, IMR, and IMRL for I and M; IMR and IMRL for R, and IMRL for L). A two-way ANOVA with the factors Finger (four levels) and Task (Single- vs. Multi-) showed main effects on both Task (F_[3,42]=21.5; p < 0.001) and Finger (F_[1,42]=3.97; p < 0.05), with an interaction (F_[3,83]=3.98; p < 0.05). Tukey’s pair-wise comparisons confirmed significant differences between both I and M fingers as compared to the L finger (p < 0.05).

Figure 5C shows the regression coefficients k for each of the four fingers in their single-finger tasks, in multi-finger tasks (Group), and in tasks where they were not instructed to produce force (enslaved fingers). The lowest regression coefficients were observed in single-finger tasks. In multi-finger tasks, fingers showed, on average, three-fold higher k values. The largest k values were seen in fingers that were not required to produce force.

These observations were confirmed by a two-way ANOVA with repeated measures Fingers (four levels) × Finger-Role (single, group, and non-task). The ANOVA showed significant effects of Finger-Role (F_[2,66]=34.08; p < 0.001) and no effect of Finger (F_[3,66]=0.75; p > 0.5) without an interaction (p > 0.5).

Experiment-3 (Steady-state, no visual feedback, SNV)

Similar to the QFP and SVF experiments, in SNV an increase in the target force level led to a close to proportional increase in SD_F. This is illustrated in Figure 6 using data averaged across subjects for each target force level. Panel A shows data for the single-finger tasks (I- and M-fingers) and the two-finger task (IM). Panel B presents the same data for individual finger forces participating in the two-finger task. Compared to Figure 6A, the slopes of regression lines are visibly higher in panel B. Each of the regressions was statistically significant (p < 0.01).

Figure 6.

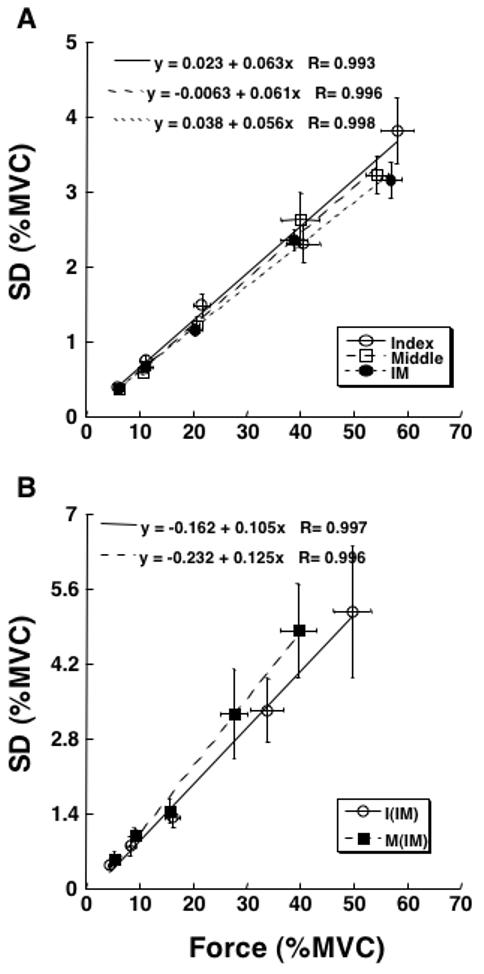
Experiment-3 (SNV). The dependence of force variability (standard deviation, SD in % of MVC) on force magnitude is shown for the data averaged across subjects for each of the five target force levels: 5, 10, 20, 40, and 60% of MVC. Linear regression lines and equations are presented with correlation coefficients. Error bars show standard errors. A: The data for the total force in the two single-finger tasks (I and M) and the two-finger task (IM). B: The data for individual fingers participating in the two-finger task (IM). Each of the regressions was statistically significant (p < 0.01).

A two-way ANOVA, Finger-Combination × Force-Level was run on SD_F indices (expressed in % of the MVC). The ANOVA showed a significant effect of Force-Level (F_[4,8]=136.66; p < 0.001) with no effect of Finger-Combination (F_[2,8]=1.59; p > 0.2) and no interaction (p > 0.5). Tukey’s pair-wise comparisons confirmed significant differences for each pair of target force levels (p<0.01), except 5%MVC and 10% MVC.

Figure 7 shows the regression coefficients (k) averaged across subjects for the single- and multi-finger tasks. It presents the data for the total force in the IM task, for the forces produced by individual fingers in their single-finger tasks and in the IM task, and also forces produced by the non-task finger in the single-finger tasks. Note the small differences in k between the two single-finger tasks and the IM task, higher k values for individual finger forces in the IM task, and much higher k values for the non-task finger forces. In particular, k for the I finger force was 1.68 higher in the IM task as compared to the I task, while for the M finger the increase was even high, by a factor of 1.96.

Figure 7.

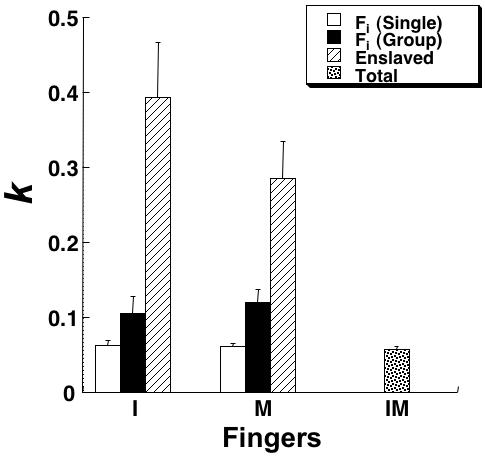
Experiment-3 (SNV). Regression coefficients (k, dimensionless) within the linear regression model computed across the different force levels for different tasks and fingers are shown averaged across subjects with standard error bars. The data for each finger in its own single-finger task (white bars), in the two-finger task (hatched bars), and in the task when the this finger was not instructed (enslaved, black bars). The last column (IM, dotted) shows the data for the total force in the IM task. Abbreviations are the same as in Figure 3.

These observations were confirmed by a two-way ANOVA with repeated measures, Fingers (2 levels) × Finger-Role (single, group, and non-task) was used to analyze the k values. The ANOVA showed a significant effect of Finger-Role (F_[2,36]=29.76; p < 0.001) and no effect of Finger (F_[1,36]=1.07; p > 0.3) without an interaction

Comparisons across the three experiments

There were both similarities and differences in the SD_F(F) dependences observed in the three experiments. In all experiments, SD_F increased nearly proportionally with F (compare Figures 2, 4, and 6). In all experiments, there were only minor differences in the indices of force variability across the single-finger tasks (see Figures 3A, 5A, and 7). In all three experiments, indices of finger force variability computed for the forces produced by individual fingers were significantly higher when the fingers took part in multi-finger tasks as compared to the same fingers acting in their single-finger tasks. To check whether this difference was similar across the three experiments, we run a two-way ANOVA on linear regression coefficients k, Experiment (three levels) × Task (Single- vs. Multi-). The ANOVA showed main effects of both Task (F_[1,113]=27.5; p < 0.001) and Experiment (F_[2,113]=63.87; p < 0.001) without an interaction (p=0.5). Tukey’s pair-wise comparisons confirmed significant differences across all three experiments (p < 0.01).

The three experiments showed significant differences in the magnitudes of SD_F. In particular, both SD_F and k were much smaller in the SVF experiment (on average, k across tasks was about 0.02), while in SNV experiment k was higher (about 0.06), and in the QFP experiment it tended to show the highest values (about 0.1). These observations were confirmed by a two-way ANOVA, Experiment (3 levels) × Finger-Combination (7 levels) on k values. The ANOVA showed a significant effect of Experiment (F_[2,110]=196.8; p < 0.001) but not of Finger-Combination (p > 0.4).

The differences between the single-finger and multi-finger tasks were also experiment-specific. In the QFP experiment, only minor differences were observed in the relative indices of variability across the seven tasks. On average, the difference in k between the single-finger and multi-finger tasks was about 2%. In the SNV experiment, the multi-finger task (IM) was slightly more accurate than the single-finger tasks (8% difference in k). Only in the SVF experiment, the multi-finger tasks were characterized by significantly lower variability indices compared to single-finger tasks (about 26% difference in k).

For statistical comparison, we used the data for the three tasks that were common across the three experiments, I, M, and IM. A two-way ANOVA, Experiment × Finger-Combination on k showed a significant effect of Experiment (F_[2,54]=94.3; p < 0.001), no effect of Finger-Combination (p>0.5), and no interaction (p > 0.9). Tukey’s pair-wise comparisons confirmed significant difference within each pair of the experiments (p < 0.01).

Discussion

Only one of the four main hypotheses (see the Introduction) received unambiguous support in the experiments. Namely, force standard deviation increased linearly with force magnitude across all three experiments and all finger combinations. Linear correlation coefficients were high (on average, over 0.95). These results support hypothesis H1 and are in line with earlier reports (reviewed in Newell and Carlton 1988; Carlton et al. 1993). Experimental support for the other three hypotheses related to differences between one-finger and multi-finger tasks has been less straightforward. Multi-finger tasks showed lower indices of variability as compared to single-finger tasks (hypothesis H2), but the differences were modest in magnitude (see panels A in Figures 3, 5, and 7). Such differences were significant only in the tasks with steady-state force production under visual feedback (Experiments 2), they were very small in a similar experiment without visual feedback (Experiment 3), and were absent in the quick force production task (Experiment 1). These differences among the three experiments are partly in line with hypothesis H3. When fingers acted in groups, each finger was significantly less accurate as compared to its single-finger task and as compared to the multi-finger group as a whole (in support of hypothesis H4). This effect differed across the fingers, it was smaller for the I and M fingers and larger for the L finger.

Relations between force and force variability in single-finger tasks

As in the cited earlier studies, all four fingers in their single-finger tasks showed a linear relation between the level of force and its standard deviation. Note that a few recent papers have reported substantial deviations of the SD_F(F) functions from a linear function (Slifkin and Newell, 1999, 2000; Moritz et al., 2005). In particular, quadratic relations between SD_F and F were reported by some authors (Slifkin and Newell, 1999, 2000), while others report S-shaped functions SD_F(F) (Christou et al. 2002). Note that in our experiments a relatively narrow 5-60% of MVC range of force tasks was used, while the studies reporting significant non-linearities in the SD_F(F) functions explored a wider range and reported these deviations at very low and very high forces.

We did not observe significant differences among the four fingers in the SD_F(F) functions. This result contrasts the report of a significant negative correlation between the degree of inter-digit individuation and force variability (Vaillancourt et al. 2002). The study of Vaillancourt and his colleagues was similar to our Experiment #3; it used a period of constant force production under visual feedback followed by a time period without visual feedback (the continuation paradigm). In our Experiments #1 and #2, all four fingers were tested including the most independent I finger and the least independent R finger (Li et al. 1998; Zatsiorsky et al. 2000). We did not observe significant differences in the SD_F(F) relations among the fingers. In Experiment #3, only the I and M fingers were tested; these fingers differ from each other in the indices of individuation (or enslaving, Zatsiorsky et al. 2000), although not by much. No differences in their SD_F(F) functions were seen either. The differences between the results of our study and that by Vaillancourt and colleagues (2002) suggest that, even if there are differences in the ability of individual fingers to produce accurate force levels, these differences are modest in magnitude and reveal themselves only under specific experimental conditions.

Across the three experiments of this study, the four fingers showed a common trend that can be summarized as: Feedback leads to lower variability, particularly visual feedback. In particular, the highest indices of variability were seen in Experiment #1 with quick force production that did not leave much time for feedback-based corrections. The lowest indices of variability were seen under continuous visual feedback on total force, while when the subjects were required to rely on proprioceptive feedback (Experiment #3), their indices of variability were in-between those observed in the other two experiments (cf. Vaillancourt et al. 2002). We will return to the issue of sensory feedback in one of the following subsections.

Variability in multi-effector systems

In the Introduction, we presented an example illustrating that the well-documented (and supported in our experiments) linear dependence of SD_F on F is expected to lead to lower indices of force variability in multi-effector tasks simply because of the sharing of the total force among the effectors. In addition, in steady-state tasks, one could expect predominance of negative co-variation among finger forces produced by individual fingers (Latash et al. 2002a; Shim et al. 2005). The negative co-variation is expected to lead to a further drop in total force variability. However, across all experiments, including Experiments #2 and #3 with steady-state force production, indices of variability showed similar scaling with force level between the single-finger and multi-finger tasks. Compared to the single-finger tasks, multi-finger tasks showed a relatively modest drop (by about 26%) in variability indices in Experiment #2, and no significant advantage in Experiment #3.

This observation resembles a recent report of similar indices of force variability in two-joint and one-joint contractions (Christou et al. 2003). With respect to the latter study note, however, that endpoint force vector defines moments of force in each joint of a multi-joint serial kinematic chain. Hence, adding a joint to such a task does not lead to an increase in the task redundancy unless changes in the multi-joint configuration are allowed. In our study, adding a finger turned a previously non-redundant task of force production by a single effector into a redundant task. However, the controller apparently failed to take advantage of the two mentioned possibilities to decrease force variability afforded by the redundant system.

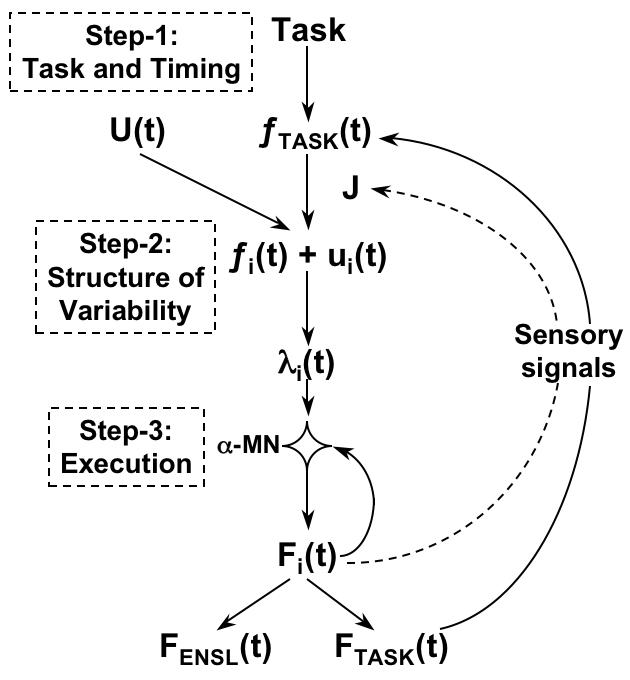
The expected beneficial effects of force sharing and negative force co-variation among the fingers were balanced nearly exactly by an increase in the variability of individual finger forces. This increase was significant in all three experiments. It is in line with the report of considerably higher total amount of variance in the space of individual finger forces per unit of force production when fingers act in a group as compared to their single-finger tasks (Goodman et al. 2005; also see Sosnoff et al. 2005). The two factors that were expected to benefit accuracy and the one that was expected to hurt it were in a nearly perfect balance independently of how many fingers were involved. To our opinion, the most logical interpretation of this finding is that accuracy of force production is set at a high level of the control hierarchy, before the task is shared among the explicitly involved fingers. Such control can be implemented, for example, using a feed-forward scheme suggested by Goodman and Latash (2006).

Despite the surprisingly small differences in the indices of force variability between single-finger and multi-finger tasks, these differences were significant in Experiment #2. This result suggests that feedback is indeed useful to decrease force variability, at least in some experimental conditions. However, feedback may be used not to coordinate output signals of individual elements (finger forces) as suggested in optimal control schemes (e.g., Todorov and Jordan 2002) and in a model based on action of central back-coupling loops (Latash et al. 2005). Rather it is used to define the input into the highest level of the hypothetical control hierarchy.

Such a hierarchy has been introduced in a scheme of feed-forward control of multi-finger sets (Goodman and Latash 2006; a similar account based on a different computational principle has been developed by Martin et al. 2004). Within this scheme, deviations from a planned time profile of the performance variable (total force in our experiments) are primarily defined at the level of input into the upper level of the hierarchy. When this signal is projected on a redundant set of elements, it is combined with another signal that is unrelated to the explicit task. After a transformation that takes into account the current Jacobian matrix (J, a matrix containing partial derivatives of the task variable with respect to each of the elemental variables), signals to elements are defined that may be viewed as the sum of two components, related and unrelated to the task. Within this scheme, variability of the total force reflects variability in only the task-related component, while variability of the finger forces may be much higher due to high variability of the other component.

This scheme differs from the earlier influential accounts on the relationships between motor output and its variability. In particular, Slifkin and Newell (1999, 2000) attributed the increase in force variability with force magnitude to recruitment of larger alpha-motoneurons during tasks that require higher levels of force output, thus reducing the precision of the total force output. Along somewhat different lines, Harris and Wolpert (1998; Jones, Hamilton, and Wolpert, 2002) attributed an increase in force variability to signal dependent noise in the synaptic input to motoneurons leading to variable signals to the muscles. Both these approaches assume that the source of variability is inherent to the processing of a control signal (that is assumed to be perfectly matching the task) by hierarchically lower neural structures. In contrast, our scheme suggests that the main source of force variability that defines the SD_F(F) relations is at a higher hierarchical level that projects onto the segmental apparatus.

The feed-forward control scheme has been corroborated by two recent studies (Zhang et al. 2008; Gorniak et al. 2008). The study by Zhang and her colleagues has suggested that increasing the seemingly irrelevant component of variability, u_i(t) may have an important functional role: It allows a redundant system of elements to perform secondary tasks without detrimental effects on the accuracy of performance of the primary task. For example, it may allow a person to open the door by pressing on it with the elbow of an arm while the hand of the same arm grasps a full mug of coffee without spilling the contents of the mug. The study of Gorniak and her colleagues has shown that multi-finger groups have no advantage as compared to single-finger groups in typical Fitts’ tasks, i.e., tasks that require actions “as quickly and as accurately as possible” to explicit targets.

Variability of unintended force

To our knowledge, this study is the first to quantify variability indices for the force produced by fingers that were not instructed to produce force (enslaved fingers). There were both similarities and differences in the relations between force and its variability in the enslaved fingers as compared to the master fingers. On the one hand, the SD_F(F) relations were close to linear within the observed range of forces for both master and enslaved fingers. This result is a natural consequence of the feed-forward scheme described in the previous sub-section. On the other hand, the enslaved fingers showed much higher indices of variability per unit of force production reflected in the significantly higher regression coefficients k within the linear models (SD_F = a + kF). This result underscores the approximate nature of the linear descriptions of finger interdependence (e.g., Zatsiorsky et al. 1998; Danion et al. 2003). It is more compatible with a recent study (Kim et al. 2008) that has shown that indices of finger interdependence may be range- and direction-dependent.

Obviously, not only the average magnitude of enslaving depends on a host of factors but its variability does as well. Note that higher variability of enslaved forces was seen in the “peripheral fingers”, I and L, which are more independent as compared to the M and R fingers (Zatsiorsky et al. 2000). The lowest variability indices were seen for the R finger - the least independent finger of the four (Li et al. 1998; Zatsiorsky et al. 2000). This finding, which seems to contradict an earlier report (Vaillancourt et al. 2002), may be related to a range effect: the I and L fingers produced very low forces when they were not involved explicitly, while the R finger produced substantially higher unintended forces. This interpretation fits well the reported non-linearity in the SD_F(F) relation such that an increase in force leads to a drop in the coefficient of variation of force (the ratio of SD_F to F) at low forces, up to 15% of MVC and, with further force increase, the coefficient of variation stays constant (Moritz et al. 2005).

Effects of sensory feedback and equilibrium-point control

According to the control scheme described earlier (also see Goodman and Latash 2006), sensory signals play a major role in defining force variability. Actually, at least three types of sensory-related effects on performance may be expected. First, sensory signals are always contributing to the overall presynaptic input to alpha-motoneurons and define excitatory input to the muscles given a value of the central control variable, λ(t) (Feldman 1986). Second, sensory signals are used within the suggested scheme to provide information on the effects of changes in individual finger forces on the total force change (the Jacobian). Third, these signals may be used to correct the task-related input into the upper level of the hierarchy. The first two loops are unlikely to distinguish among the three experiments of this study. The first one acts irrespectively of the task and explicit visual or somatosensory feedback on the total force. The Jacobian in all three experiments was the same and unchanged. In contrast, the third loop was likely to shape the dependence SD_F(F) in accordance with the Weber-Fechner law of perception mentioned in the Introduction. Effects of sensory signals on the task-related output of the highest hierarchical level do not have to be mediated by conscious perception but may represent an example of perception-action coupling in line with the Gibsonian ecological psychology (Gibson 1979). We have to admit however that our results might have been affected by the limited range of forces (5-60% of the MVC) explored in the experiments.

The equilibrium-point hypothesis of single-muscle control (reviewed in Feldman and Levin 1995) may be viewed as an example of how a large set of elements (motor units) can be united by a physiological mechanism (the tonic stretch reflex) to stabilize an important feature of performance - the equilibrium point characterized by values of muscle force and length. The main idea of this hypothesis has been generalized to the control of multi-effector systems using the notion of reference configuration as a control variable at a higher level of a control hierarchy involved in the production of natural, movements (Feldman and Levin 1995; Feldman et al. 2007; Pilon et al. 2007). Reference configuration defines, in the external space, a configuration, at which all the muscles would attain a minimal level of activity - a set of threshold values for muscle activation. If external conditions and/or anatomical constraints prevent a system from reaching its current reference configuration, muscles generate non-zero forces. In particular, fingertip forces on an external object emerge when a reference hand configuration corresponds to shorter flexor muscles as compared to the actual configuration. The general idea of control using reference configurations may be described as following a principle of minimal end-state action: The body tries to achieve an end-state, compatible with the external force field, where its muscles show minimal activation levels. This principle is a natural extension of the principle of minimal interaction (Gelfand and Tsetlin 1966).

The notion of reference configuration offers an attractive framework to analyze motor synergies. This framework assumes a hierarchical control system where, at each level of the hierarchy, the system is redundant, that is, it produces more output variables than the number of constraints specified by input variables. Other characteristics of action may be allowed to vary based on secondary considerations, possibly reflecting optimization of certain features of performance. Because the system is redundant, a reference configuration at a higher hierarchical level does not specify unambiguously all the reference configurations at a lower level. Emergence of particular lower-level reference trajectories may be based on a feedback mechanism or on a feed-forward mechanism. Hence, a hierarchy of control levels, where each level functions based on the equilibrium-point control principle, seems like a plausible control structure leading to motor synergies.

Limitations of the study

Our study has limitations (as most studies do) that might have affected some of our conclusions. First, we used a relatively small range of forces that might be expected to lead to the mostly linear relations between force and force variability indices; in particular, we did not study forces under 5% and above 60% (cf. Slifkin and Newell, 1999, 2000; Christou et al. 2002; Moritz et al., 2005). There were certain differences among the three experiments in both the number of trials and selection of time intervals for data analysis. These were due to practical considerations such as natural limits of the number of trials a subject may be expected to perform without fatigue and the fact that the total force followed the instructed level well during Experiment-2 while it could show significant trends in Experiment-3. We did not consider effects of learning assuming that out tasks were very simple (according to the subject’s reports) and the few practice trials could be viewed as sufficient for reaching a plateau of performance. In addition, the comparison of the visual to non-visual feedback conditions might have been confounded by an order effect (the visual feedback condition was always performed first).

Figure 8.