Abstract
Previous studies reporting the linear viscoelastic shear properties of the human vocal fold cover or mucosa have been based on torsional rheometry, with measurements limited to low audio frequencies, up to around 80 Hz. This paper describes the design and validation of a custom-built, controlled-strain, linear, simple-shear rheometer system capable of direct empirical measurements of viscoelastic shear properties at phonatory frequencies. A tissue specimen was subjected to simple shear between two parallel, rigid acrylic plates, with a linear motor creating a translational sinusoidal displacement of the specimen via the upper plate, and the lower plate transmitting the harmonic shear force resulting from the viscoelastic response of the specimen. The displacement of the specimen was measured by a linear variable differential transformer whereas the shear force was detected by a piezoelectric transducer. The frequency response characteristics of these system components were assessed by vibration experiments with accelerometers. Measurements of the viscoelastic shear moduli (G′ and G″) of a standard ANSI S2.21 polyurethane material and those of human vocal fold cover specimens were made, along with estimation of the system signal and noise levels. Preliminary results showed that the rheometer can provide valid and reliable rheometric data of vocal fold lamina propria specimens at frequencies of up to around 250 Hz, well into the phonatory range.
INTRODUCTION
Phonation is characterized by a flow-induced self-sustained oscillation of the vocal fold mucosa, involving primarily the vocal fold cover, or superficial layer of the lamina propria. The dynamics and energy transfer of vocal fold oscillation are dictated by the interactions between the aerodynamic stresses acting on the vocal fold surface and the mechanical response of the vocal fold tissue (Chan and Titze, 2006; Zhang et al., 2007). In particular, the viscoelastic shear properties of the vocal fold cover are critical, because the mucosal wave that propagates on the cover during oscillation is a shear wave (Chan and Titze, 1999; Gray et al., 1999). The viscoelasticity of the vocal fold cover under shear deformation contributes to the determination of the key parameters of phonation, such as the fundamental frequency, the amplitude of oscillation, and phonation threshold pressure (Chan and Titze, 2000, 2006; Titze, 2006; Zhang et al., 2007).
Many previous studies for measuring the viscoelastic shear properties of the vocal fold cover have used parallel-plate torsional rheometry at small-strain amplitudes (around 0.01 rad) and small gap sizes (around 0.2–0.3 mm) to quantify the elastic shear modulus (G′), viscous shear modulus (G″), dynamic viscosity (η′), and damping ratio (ζ) within the linear viscoelastic region of the tissue (e.g., Chan and Titze, 1999, 2000; Chan, 2004; Klemuk and Titze, 2004; Titze et al., 2004). The frequency range of viscoelastic measurement varied according to the rheometer used in the specific studies. Chan and Titze (1999) used a controlled-stress torsional rheometer (Bohlin CS-50) with a parallel-plate geometry to determine the linear viscoelastic shear properties of 15 excised human vocal fold mucosa (cover) specimens, across a frequency range of 0.01–15 Hz. Titze et al. (2004) used an improved controlled-stress torsional rheometer (Bohlin CVO-120), with higher resolutions and a more reliable controlled-stress mode. The system had a torque range of 0.0001–150 mN m and a resolution of 1 nN m, compared to the 0.001–10 mN m torque range and the 0.2 μN m resolution of the CS-50 model. Valid viscoelastic data were obtained at frequencies of up to 80 Hz, and when the gap size was decreased from 0.2 to 0.1 mm, the data could be valid for up to around 100 Hz.
Chan (2004) introduced the use of controlled-strain torsional rheometry, with a torsional shear strain applied to a tissue specimen and the shear stress response measured. Valid viscoelastic data of 17 canine vocal fold mucosa specimens were obtained at frequencies of up to around 50 Hz. Further measurements were made by Klemuk and Titze (2004) using the CVO-120 rheometer of Titze et al. (2004), but in controlled-strain mode. Phonosurgical biomaterials such as collagen (Zyderm), a thiolated hyaluronic acid (HA) hydrogel (HA-DTPH), and micronized alloderm (Cymetra) were tested at frequencies of up to around 80 Hz. The highest frequencies at which valid data were obtained were found to be around 40 Hz for HA-DTPH, and around 80 Hz for Zyderm and Cymetra (Klemuk and Titze, 2004).
The typical fundamental frequency (F0) range of speech is around 100–200 Hz for male and around 200–300 Hz for female. Although the frequencies of viscoelastic measurement had improved in previous studies, they were nonetheless still at the low end of the phonatory range (Chan, 2004; Klemuk and Titze, 2004; Titze et al., 2004). Viscoelastic characterization of vocal fold tissues should be done at phonatory frequencies in order that the rheometric data become directly applicable to phonation, without having to rely on extrapolations or theoretical predictions (Chan, 2001, 2004; Chan and Titze, 2000). This paper reports the design and validation of a custom-built, controlled-strain, linear, simple-shear rheometer system capable of direct empirical measurements of viscoelastic properties at frequencies in the phonatory range.
SIMPLE-SHEAR RHEOMETRY
First of all, it is of interest to review the physics of oscillatory shear rheometry as applied to simple-shear deformation according to the theory of linear viscoelasticity (Ferry, 1980), as opposed to torsional rheometry (Chan and Titze, 1999; Titze et al., 2004). Figure 1 shows the principle of linear, simple-shear rheometry, where a small-amplitude, translational sinusoidal displacement x is applied to a viscoelastic tissue or material specimen through a vibrating upper plate. The resulting shear force F due to the viscoelastic response of the specimen is transmitted to the lower plate, and can then be detected by a transducer. Consider the illustration in Fig. 1 as a single degree-of-freedom system, with lumped elements of mass, stiffness, and damping, the displacement of the upper plate x can be represented in complex notation as
| (1) |
where x0 is the amplitude of displacement, i is the imaginary number √−1, ω is the angular frequency, and t is time. The equation of motion for the system is
| (2) |
where m is mass, c is damping, k is stiffness of the system, and F* is the resulting shear force in complex notation. For linear, small-amplitude shear, once steady state is reached, the applied sinusoidal displacement would result in a harmonic shear force at the same frequency, with a phase shift of δ according to the theory of linear viscoelasticity (Chan and Titze, 1999) as follows:
| (3) |
where F0 is the amplitude of F*. For linear viscoelasticity, the phase shift δ will be independent of the displacement amplitude and the force amplitude (x0 and F0). Substituting x* and F* into the equation of motion yields
| (4) |
Figure 1.
The principle of simple-shear rheometry. A linear, simple-shear deformation is applied to a tissue or material specimen by the upper plate with a small-amplitude translational sinusoidal displacement x. A harmonic shear force F due to the viscoelastic response of the specimen is transmitted to the lower plate, separated from the upper plate by a gap size d. The contact area A between the specimen and the upper plate can be visualized from directly above through the transparent upper plate.
The complex frequency response of the system H(ω) can be defined as the displacement divided by the force as follows:
| (5) |
which results in the following expression from Eq. 4:
| (6) |
One could define the undamped resonant frequency and the damping ratio ; the frequency response is then given by
| (7) |
By considering the stiffness factor (1∕k) together with the force term F0, and by multiplying and dividing Eq. 7 by the complex conjugate of the denominator, a nondimensional expression can be derived for the complex system response H(ω) as follows:
| (8) |
where the magnitude response ∣H(ω)∣ and the phase response δ(ω) are given by
| (9) |
| (10) |
By definition, the damped resonant frequency ω0 is the frequency at which the magnitude of the frequency response ∣H(ω)∣ is maximum. It can also be deduced from Eq. 9 that ω0 is related to the undamped resonant frequency ωn by
| (11) |
| (12) |
In order to compute the viscoelastic shear properties of the specimen, shear strain and shear stress of the specimen can be defined based on the displacement and force given in Eqs. 1, 3. Shear strain can be defined as the displacement x divided by the distance between the plates, or the gap size d (Fig. 1) as follows:
| (13) |
whereas shear stress is defined as
| (14) |
where A is the area of the specimen experiencing the strain, as indicated by the area of contact between the specimen and the upper plate (Fig. 1). Hence,
| (15) |
| (16) |
where γ0 is the amplitude of γ* and τ0 is the amplitude of τ*. The corresponding linear constitutive equation relating shear stress to shear strain is
| (17) |
where G* is the complex shear modulus. By definition, G* is composed of a real part and an imaginary part as follows:
| (18) |
The real part G′ is the elastic shear modulus, and the imaginary part G″ is the viscous shear modulus. Hence, for the linear theory of viscoelasticity (Ferry, 1980), the constitutive equation can be expressed as
| (19) |
The elastic and viscous shear moduli G′ and G″ are related to the strain amplitude and the stress amplitude (γ0 and τ0), and the phase shift (δ). Based on Eqs. 15, 16, they are expressed in terms of the displacement amplitude and the force amplitude (x0 and F0) as follows:
| (20) |
| (21) |
The dynamic viscosity η′ is related to the viscous shear modulus G″, and the damping ratio (also called loss factor or damping factor) ζ is the ratio of the viscous to the elastic moduli as follows:
| (22) |
| (23) |
The amplitude of the displacement x0 can be detected by a displacement transducer at the upper plate, and the amplitude of the shear force response F0 of the specimen can be detected by a force transducer at the lower plate. The phase shift δ can be measured with a temporal analysis of the displacement and force signals, where it is shown as (δ∕ω) on the time axis. The area of contact between the specimen and the plates (A) can be estimated by analysis of scaled images taken from directly above the upper plate. With x0, F0, δ, and A determined, and given a known gap size d, the viscoelastic functions can be calculated from Eqs. 20, 21, 22, 23. The design of the rheometer to quantify these viscoelastic properties based on this principle is illustrated next.
METHOD
Design of the simple-shear rheometer
The EnduraTEC ElectroForce (ELF) 3200 mechanical testing system (Bose Corporation, ElectroForce Systems Group, Eden Prairie, MN) was chosen as a base system to provide several key design criteria that are critical to the development of a controlled-strain rheometer for the measurements of tissue viscoelasticity at high frequencies. First, the system is capable of prescribing a precise oscillatory deformation through a linear motor. The linear motor design is modified from that of Bose subwoofers, involving a lightweight permanent magnet suspending in a controlled electromagnetic field, producing translational, oscillatory motion of the permanent magnet upon alternations of the electromagnetic field. The design does not include any mechanical seals or bearings, but the moving permanent magnet is attached directly to an actuator and a fixture through which a specimen is mounted and deformed. As a result, frictional energy loss in the driving mechanism of the motor is minimized, enabling the motor to maintain the same sinusoidal displacement at various amplitudes over a wide range of frequency. This is facilitated by displacement feedback control, which monitors the actual displacement of the actuator real time through a linear variable differential transformer (LVDT), such that the target prescribed displacement is closely approximated. These features allow precise oscillatory shear deformation to be performed on specimens of varying stiffness both within and beyond the linear viscoelastic region, i.e., over a wide range of displacement amplitudes (up to around ±6.50 mm) covering both small-strain (linear) and large-strain (nonlinear) oscillations.
Second, it is crucial that the shear force resulting from the viscoelastic response of the specimen upon deformation is detected by a force transducer capable of accurate and reliable measurements over a wide range of frequency. This is especially challenging as the magnitude of the force response depends on the elastic modulus of the specimen, and is typically in the millinewton range or smaller for soft tissue specimens. Piezoelectric force transducers designed with quartz crystals generating an electrical potential proportional to an applied force have the natural advantage of detecting dynamic forces at high frequencies. The output impedance of such transducers must be low (<100 Ω) so as to minimize signal degradation and the output noise level, especially for the low magnitudes of force for our application.
Third, inertial effects due to the system and the specimen should be minimized, whereas the frequency of system resonance should be maximized, in order to minimize measurement errors and time-dependent artifacts caused by system inertia, sample inertia, and system resonance (Chan, 2004; Titze et al., 2004). The moving parts of the ELF 3200 system (shaft of the linear motor, the actuator, and the fixtures or plates in contact with the specimen) can be fabricated with lightweight acrylic material, leading to minimal inertial time delays and contributing to increase the system resonant frequency. The linear motor design enabling minimal friction in the moving parts over a wide range of frequency will contribute to the minimization of the system inertial effects during oscillation. Also, a piezoelectric force transducer with significant stiffness against deformation will also facilitate a higher system resonant frequency.
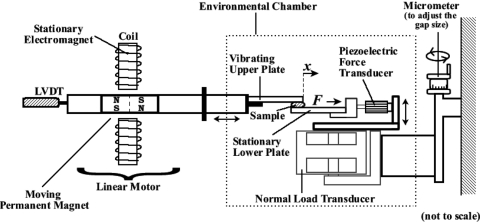
Taking into account these design criteria, a controlled-strain, simple-shear rheometer system was custom built based on the EnduraTEC ELF 3200 system (Fig. 2). As illustrated in Fig. 2, a tissue specimen is subjected to a linear, simple shear between two parallel, rectangular acrylic tissue plates according to the principle in Fig. 1. The upper plate is attached to the shaft of the linear motor through an actuator, applying a translational displacement x to the specimen at a specified magnitude and frequency. The linear motor is capable of a force range of ±225 N (peak amplitude), an acceleration of up to 100 G, a displacement range of ±6.50 mm, and a frequency range of 0.000 01–400 Hz. The motor is under displacement feedback control, with displacement of the upper plate detected by a lightweight LVDT (Schaevitz MHR 250; Measurement Specialties Inc., Hampton, VA) with minimal friction, in order to minimize system inertial errors. The shear force resulting from the viscoelastic response of the specimen to the applied strain is detected by a piezoelectric quartz force transducer (PCB Model 209C12; PCB Piezotronics, Depew, NY) rigidly attached to a stationary lower plate. The piezoelectric transducer has a force range of ±4.45 N, a force resolution of 90 μN, and a frequency range of 0.05 Hz–30 kHz. The output impedance of the transducer is very low (<100 Ω), which minimizes output signal distortion and noise. The stiffness of 3.5×108 N∕m is very high, which can minimize the system inertia. The discharge time constant of the piezoelectric quartz crystal is longer than 10 s, implying that DC signal drifting inherent in all piezoelectric transducers is not a significant source of error for dynamic measurements at 1–400 Hz.
Figure 2.
Schematic of the custom-built, controlled-strain, linear, simple-shear rheometer system. A LVDT displacement transducer (Schaevitz MHR 250) is attached to the shaft of the linear motor through an actuator, for estimation of shear strain of the specimen. The resulting shear force (F) at the lower plate is detected by a piezoelectric force transducer (PCB Model 209C12). A normal load transducer measures the compressive force between the specimen and the plates. A micrometer allows one to adjust the gap size (d) between the two plates to accommodate specimens of varying dimensions. Mechanical testing is performed in an environmental chamber at controlled temperature and humidity.
The lower plate in contact with the tissue specimen is capable of displacement in the vertical (perpendicular) direction for adjustment of the gap size through a micrometer. The nominal gap size is 1.0 mm, although it can be set to anywhere from 0 to around 5.0 mm. There is also a normal load transducer with a force range of ±2.45 N for detecting the compressive force between the specimen and the upper and lower plates. One purpose of the normal load transducer is to facilitate establishing a zero gap reference, when the normal force changes from zero to nonzero upon contact between the two tissue plates. The monitoring of normal load is also helpful for testing specimens of vastly different dimensions and volumes.
Rheometric measurements of viscoelastic properties are conducted in a transparent acrylic environmental chamber, where water at the base of the chamber is heated to a specified temperature (∼50 °C) to maintain the ambient air temperature in the chamber at around 37 °C, with a relative humidity of close to 100% in order to minimize tissue dehydration. A digital camera is mounted directly above the chamber and photos of the specimen mounted between the tissue plates are taken. Scaled images of the specimen in the chamber are later examined with an image analysis software (IMAGE J, National Institutes of Health, Bethesda, MD), in order to determine the area of contact (A) between the specimen and the upper plate (Fig. 1).
The rheometer is controlled by the WINTEST software (Bose Corporation, ElectroForce Systems Group, Eden Prairie, MN), which allows one to specify a displacement control signal to be applied to the linear motor, with specific target amplitude, frequency, and number of cycles prescribed and achieved through displacement feedback control. Data collection is performed on the displacement signal output of the LVDT and the force signal output of the piezoelectric force transducer, digitized at a rate of 8196 samples∕s. The digitized signals are processed by the WINTEST software after the experiments, for calculating x0, F0, and δ of the two signals.
For the viscoelastic measurements to truly reach into the phonatory range, it is critical to validate the rheometer by establishing its frequency response characteristics, as well as the reliability and validity of the measurements. Two key system components, i.e., the LVDT displacement transducer and the piezoelectric force transducer, were validated by an assessment of their frequency response over a frequency range of up to 400 Hz, as detailed below.
Frequency response of the displacement transducer (LVDT)
The Schaevitz MHR 250 LVDT for the detection of displacement of the actuator has a displacement range of ±6.35 mm, a sensitivity of 68 mV∕mm, and a nonlinearity (hysteresis) error of ±0.25%. It has a lightweight core with minimal friction that contributes to minimize system inertial errors. In order to assess the accuracy of displacement measurements of the LVDT as a function of frequency, an accelerometer (PCB Model 353B18; PCB Piezotronics, Depew, NY) was attached to the actuator of the ELF 3200 system. The procedure to establish the frequency response of the LVDT involved prescribing specific translational displacement amplitudes (0.1 and 0.05 mm) over a frequency range of 1–350 Hz. The target displacement was achieved by displacement feedback control, and was detected by the LVDT as the nominal displacement. The actual displacement of the actuator was derived from the acceleration measured by the accelerometer. The PCB 353B18 accelerometer has a range of 500 G and a sensitivity of 10.99 mV∕G at 100 Hz. The frequency response of the accelerometer was assessed by the manufacturer at 23 °C and at a relative humidity of 20%, over a frequency range of 10–10 000 Hz. A flat response with little deviation (<1%) was found between 10 and 3000 Hz.
The nominal displacement amplitude given by the output of the LVDT was compared to the actual displacement amplitude of the actuator estimated from the accelerometer output. For sinusoidal signals, the amplitude of displacement x0 is related to the amplitude of acceleration a0 as follows:
| (24) |
where f is frequency in Hz. The ratio of the nominal displacement amplitude to the actual displacement amplitude from Eq. 24 is an indication of the frequency response of the LVDT.
Frequency response of the piezoelectric force transducer
The PCB 209C12 piezoelectric force transducer has been calibrated by the manufacturer for sensitivity statically using standard weights (average sensitivity of 517.7 mV∕N) according to certified standards traceable to the National Institute of Standards and Technology (NIST) (ISO 9001, ISO 10012-1, ANSI∕NCSL Z540-1, and ISO 17025), but not for frequency response. Two separate procedures were conducted to assess the accuracy of the force measurements at low frequency, as well as the transducer response at higher frequencies. Figure 3 illustrates the setup for low-frequency calibration, where a semiconductor strain gauge (Sensotec Model 31; Honeywell International Inc., Columbus, OH) previously calibrated at 1.0 Hz was used to calibrate the force output of the transducer, i.e., gain of the PCB signal conditioning interface between the transducer and the WINTEST software. Strain gauges are generally used for the accurate measurements of static and low-frequency forces due to the inherent stability of DC signals generated by semiconductors. As shown in Fig. 3, the shaft of the piezoelectric force transducer was rigidly attached to the actuator of the ELF 3200 via an acrylic tissue clamp, whereas the body of the piezoelectric transducer was attached to the shaft of the Sensotec Model 31 strain gauge, rigidly fixed on the ELF 3200. The strain gauge has a force range of ±4.9 N, a nonlinearity (hysteresis) error of ±0.15%, and a frequency range of DC to 740 Hz. It was calibrated by the manufacturer at 1.0 Hz according to NIST traceable standards (ANSI∕NCSL Z540-1, ISO 9002 and ISO Guide 25). For calibration, translational sinusoidal deformation at 1.0 Hz was applied and the gain of the PCB signal conditioning interface was adjusted to match the piezoelectric transducer force output to that of the strain gauge. The linearity is verified by varying the amplitude of deformation. Results of the calibration showed that the force outputs of the two transducers were identical within a range of ±4.32 N, with error <±0.25% at 1.0 Hz.
Figure 3.
Schematic of the setup for low-frequency calibration of the piezoelectric force transducer. The shaft of the piezoelectric force transducer is attached to the actuator through a tissue clamp. The shaft of a rigidly fixed, calibrated strain gauge (Sensotec Model 31) is attached to the body of the piezoelectric force transducer. Under sinusoidal oscillation at 1.0 Hz, the gain of the piezoelectric force transducer is adjusted to achieve identical dynamic output voltages from both the piezoelectric transducer and the strain gauge.
The frequency response of the piezoelectric transducer was assessed over a frequency range of 25–400 Hz. The piezoelectric transducer and an accelerometer (PCB Model 353B18) were both attached to the actuator of the ELF 3200, as shown in Fig. 4. As noted above, the frequency response of the accelerometer used was flat over a wide range of frequency (10–3000 Hz). Three different levels of mass were attached to the shaft of the piezoelectric transducer, in order to vary the effective mass subjected to oscillation. They included a titanium tissue plate, an acrylic tissue plate, and no tissue plate (with the adapter only). In order to assess the frequency response of the piezoelectric transducer, varying sinusoidal displacement amplitudes were applied to the three conditions of masses, resulting in an acceleration amplitude of around ±5 G for each mass condition, over a frequency range of 25–400 Hz. At each frequency, the dynamic force output was measured by the piezoelectric transducer while the acceleration of the system was measured by the accelerometer. Based on Newton’s second law, the effective mass of vibration representing the total mass of all vibrating parts across different frequencies was obtained from dividing the dynamic force amplitude by the acceleration amplitude (F0∕a0).
Figure 4.
Schematic of the setup for establishing the frequency response of the piezoelectric force transducer. The body of the piezoelectric force transducer is attached to the actuator, and varying mass (acrylic tissue plate, titanium tissue plate, or no tissue plate) is attached to the shaft of the transducer through an adapter. An accelerometer (PCB Model 353B18) is also attached to the actuator simultaneously for the measurement of acceleration.
Estimation of system noise level
After establishing the accuracy and the frequency response of the LVDT displacement transducer and the piezoelectric force transducer, it was also important to determine the system signal-to-noise level, to reflect the functional frequency range within which measurements can be made with minimum errors. The system signal level was defined as the magnitude of the piezoelectric transducer force output resulting from the testing of specific specimens, whereas the system noise level was defined as the force output amplitude due to the electrical noise inherent in the system. The goal of this assessment was to compare the system noise level with the signal level, so as to determine the frequencies at which noise is or is not acceptable. For the measurement of system signal level, oscillatory shear deformation was conducted on an ANSI S2.21 standard polymer material and on seven human vocal fold cover specimens at frequencies of 1–300 Hz (see next two sections). For system noise, oscillatory shear deformation was conducted with no specimens mounted in the rheometer, under the exact same set of conditions as above.
Validation with a standard polymer material
The ANSI S2.21 standard material with known viscoelastic properties was used to validate the viscoelastic measurements of the rheometer system (American National Standards Institute, ANSI S2.21, 1998). This standard material was made for calibrating equipment that measures the dynamic mechanical properties of viscoelastic materials. The material is a polyurethane composed of polytetramethylene ether glycol (molecular weight 2000), 4,4′-diphenylmethane-diisocyanate, and a chain extender blend of 2,2-dimethyl-1,3-propanediol and 1,4-butanediol (ANSI, 1998). Three samples of the standard material were fabricated according to the standard procedure of ANSI S2.21, with the molar concentrations of the prepolymer and the chain extender reduced such that the shear modulus of the material is 1000 times lower (on the order of kPa rather than MPa) to be a closer match of the human vocal fold. The material samples were subjected to oscillatory shear in the rheometer, with a gap size of 1.0 mm, a displacement amplitude of 0.01 mm (1.0% strain), and over a frequency range of 1–300 Hz at 25 °C.
Measurements of human vocal fold specimens
Five human larynges were excised from cadavers, obtained from the Willed Body Program of our institution within 20 h postmortem. Laryngeal specimens were also obtained from two additional subjects who underwent total laryngectomy due to supraglottic or thyroid cancer that did not involve the true vocal folds. Table 1 shows some basic characteristics of the subjects. Most of the subjects were Caucasians, but race was not a factor in the tissue procurement procedure. All of the subjects were nonsmokers, with no history of laryngeal disease and pathology. Physical examination of the laryngeal specimens revealed that the true vocal folds of all subjects were normal. The tissue procurement protocol and the experimental protocol were approved by the Institutional Review Board of the University of Texas Southwestern Medical Center. The cadaveric larynges were acceptable since previous research showed that the viscoelastic shear properties of vocal fold tissues are not significantly altered after 24 h of postmortem storage in saline at room temperature (Chan and Titze, 2003). Vocal fold specimens were dissected from the larynges with instruments for phonomicrosurgery, similar to the procedure of Chan and Titze (1999). Briefly, an incision was first made on the superior surface of the vocal fold epithelium with a surgical blade (No. 11), so that the vocal fold cover (epithelium and the superficial layer of the lamina propria) could be separated from the vocal ligament (middle layer and deep layer of the lamina propria) through blunt dissection with a spatula similar to the Bouchayer spatula. This separation was facilitated by the natural plane of dissection between the superficial layer and the middle layer of the lamina propria. The vocal fold cover was then isolated from the larynx and kept in phosphate-buffered saline solution at a pH of 7.4 at room temperature prior to rheometric measurements. The volume of each vocal fold cover specimen was around 0.1–0.2 cm3, requiring the gap size (d) of the rheometer to be set to between 0.5 and 1.0 mm so that there was complete contact between the specimen and the tissue plates with an area of contact smaller than the overlapping area of the tissue plates. Two testing protocols were conducted with the rheometer. First, a strain sweep was performed, which involved oscillatory shear deformation of the vocal fold cover specimens over a range of displacement amplitude (0.004–1.0 mm) (corresponding to 0.4%–100% strain for a gap size of 1.0 mm), at a constant frequency of 100 Hz. This served to identify the linear viscoelastic region of the specimens, i.e., the range of strain amplitude within which small-amplitude, linear, simple-shear deformation is ensured (Chan and Titze, 1999). Next, a frequency sweep was performed, which involved oscillatory shear deformation of the vocal fold cover specimens at a small-strain amplitude (1.0% strain), over a frequency range of 1–300 Hz.
Table 1.
Human subjects characteristics.
| Subject | Age | Gender | Race | No. of hours postmortem1 |
|---|---|---|---|---|
| 1 | 53 | Female | African American | 3 |
| 2 | 58 | Female | Hispanic | 4 |
| 3 | 60 | Male | Caucasian | 9 |
| 4 | 64 | Male | Caucasian | 15 |
| 5 | 69 | Male | Caucasian | 20 |
| 6 | 79 | Male | Caucasian | 11 |
| 7 | 88 | Male | Caucasian | 10 |
The postmortem time was the time lapsed between a subject’s death and the rheometric experiments, except for subjects 1 and 2 who were total laryngectomy patients.
Viscoelastic data analysis
The WINTEST program of the rheometer system was used to examine and process the digitized displacement signal and force signal at each specific frequency obtained from any particular test. Figure 5 shows the typical sinusoidal signals obtained from the testing of (a) no specimen (for estimating the system noise level), (b) a sample of the ANSI S2.21 standard material, and (c) a human vocal fold cover specimen (79-year-old male). The gap size was 1.0 mm and the displacement amplitude was 0.01 mm for all three cases (i.e., 1.0% strain). A window of at least 20 cycles of the digitized displacement signal and force signal was chosen based on the actual displacement amplitude reaching the target prescribed amplitude (±5%), which usually occurred a few seconds after the onset of oscillation. The positive and negative peak amplitudes and their corresponding time points of each cycle were manually (visually) selected and recorded for both signals. The data points were then processed by MATLAB for calculating the displacement amplitude x0, the force amplitude F0, and the phase shift δ between the two signals. With the area of specimen (A) measured and the gap size d given, linear viscoelastic shear properties of the specimen can be calculated according to Eqs. 20, 21, 22, 23.
Figure 5.
(Color online) Typical sinusoidal waveforms of the displacement (x) and shear force (F) signals detected by the rheometer for the following: (a) no specimen, for the estimation of system noise level (frequency=25 Hz); (b) the ANSI S2.21 standard polymer material (frequency=150 Hz); and (c) a vocal fold cover specimen from the 79-year-old male (frequency=100 Hz). The displacement amplitude was 0.01 mm in all cases (dotted line=displacement; solid line=force).
The reliability of the manual procedure for the selection of peak amplitudes and their corresponding time points of the digitized sinusoidal displacement and force signals was examined. Two raters completed the analysis of the same signals of a sample of the ANSI S2.21 standard material independently, each of them for three trials. The intrarater reliability was determined as the percentage difference in the viscoelastic functions obtained from the three trials of analysis performed by the same rater, and the inter-rater reliability was determined as the percentage difference in the viscoelastic functions obtained from the two raters. Results showed that the average percentage differences in G′ and in G″ among the three trials completed by the same rater were 5.9571% (±4.2807%) and 6.0834% (±2.6233%), respectively. The average percentage differences in G′ and in G″ among the trials completed by the two raters were 1.8413% (±1.7544%) and 4.1445% (±4.0660%), respectively.
RESULTS AND DISCUSSION
Complex system response
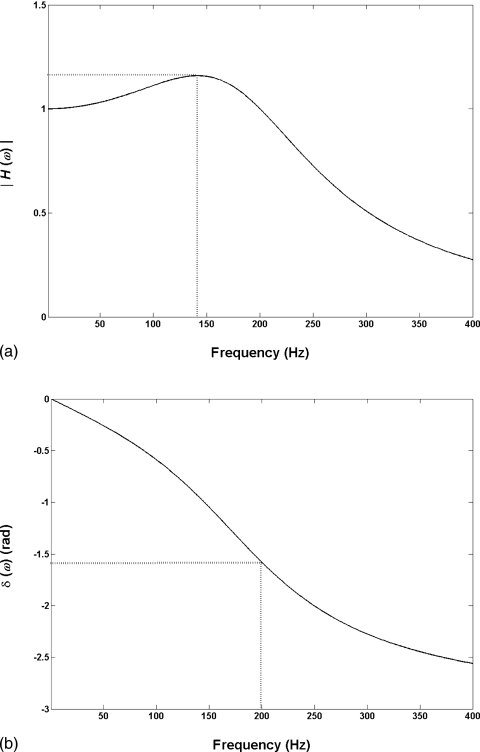
The complex frequency response, or displacement-force response of the rheometer system H(ω) can be summarized by the magnitude response ∣H(ω)∣ and the phase response δ(ω) as given by Eqs. 9, 10. The undamped resonant frequency ωn was given by , and the damping ratio . The effective mass m, stiffness k, and damping c of the system were determined from the setup for establishing the frequency response of the piezoelectric force transducer in Fig. 4. The effective mass m was computed from Newton’s second law as the force amplitude divided by the acceleration amplitude (F0∕a0), yielding an average of 0.000 645 5 kg. The effective stiffness k was determined as 1009.45 N∕m when the phase shift between displacement and force was small, in which case F0≈kx0. Hence, the undamped resonant frequency ωn was found to be 1250 rad∕s (or 199 Hz). Next, the effective damping of the system was c=0.802 512 N s∕m, as determined from F0≈cωx0 when the phase shift was close to π∕2. This resulted in a damping ratio of ζ=0.4971. With ωn and ζ identified, the magnitude response ∣H(ω)∣ and the phase response δ(ω) of the system can then be determined from Eqs. 9, 10.
Figure 6 shows the system response as a function of frequency. The damped resonant frequency ω0 was determined as the frequency at which the magnitude response ∣H(ω)∣ was maximum. Figure 6a shows the magnitude response, and it is clear that ∣H(ω)∣ reached a peak value of 1.1592 at ∼142 Hz (or 892 rad∕s) (as indicated by the dotted line), close to what is given by Eq. 12 (ω0=889 rad∕s or 141 Hz). Figure 6b shows the phase response. As expected, the phase δ(ω) became more negative with frequency. At the undamped resonant frequency of 199 Hz (dotted line), by definition the phase response δ should be at −π∕2 (or π∕2). It was found to be at −1.5714 rad, or close to −π∕2 (−90°).
Figure 6.
Complex frequency response of the linear rheometer system over a frequency range of 1–400 Hz: (a) magnitude response ∣H(ω)∣ (dimensionless), and (b) phase response δ(ω) in radians. In (a), the damped resonant frequency of the system is observed to be around 142 Hz, where ∣H(ω)∣ is maximum (dotted line). In (b), at the undamped resonant frequency (199 Hz), the phase is at around −π∕2 (dotted line).
Given the damped resonant frequency of the system at around 142 Hz, it is reasonable to expect that valid viscoelastic data could be obtained with the rheometer system at frequencies of up to around 280 Hz (i.e., twice the resonant frequency) (Titze et al., 2004). The data presented in the following sections on the frequency response characteristics of the displacement transducer and the force transducer, as well as the system noise level will verify whether meaningful data could indeed be obtained at such frequencies, well into the phonatory range.
Frequency response of the LVDT
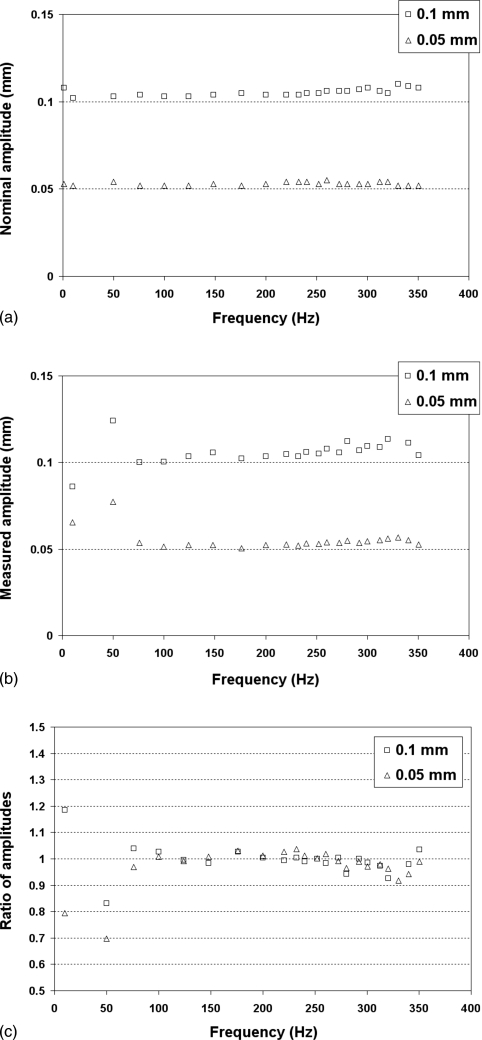
The frequency response of the LVDT displacement transducer was assessed by vibration studies with an accelerometer attached to the actuator. Target displacement amplitudes were prescribed for the linear motor, with the nominal displacement amplitude detected by the LVDT compared to the actual displacement amplitude derived from the acceleration of the actuator according to Eq. 24. Figure 7 shows the displacement amplitudes over a frequency range of 1–350 Hz, for the target displacements of 0.10 and 0.05 mm. Results showed that the nominal displacement amplitude measured by the LVDT [Fig. 7a] was steady and close to the prescribed target amplitudes across the entire frequency range, with lower than 10% error at all frequencies.
Figure 7.
(a) Nominal displacement amplitude of the LVDT as a function of frequency, with target amplitudes of 0.05 and 0.1 mm. (b) Measured displacement amplitude of the LVDT as estimated by the accelerometer as a function of frequency. (c) Ratio of the nominal displacement amplitude to the measured amplitude of the LVDT. This ratio indicates the frequency response of the LVDT, which is seen to be flat between around 75 and 275 Hz.
The actual displacement amplitude derived from the accelerometer [Fig. 7b] was as steady across most frequencies, except at low frequencies (50 Hz and below) where the magnitude of error in displacement ranged from 16% to 55%. This error was likely due to the inaccuracy of the peak-picking algorithm of the WINTEST software in selecting the peak amplitudes for low-frequency and low-magnitude acceleration signals, especially observed for the target amplitude of 0.05 mm. It should be noted that this error would not be incurred in the analysis of the displacement signal and the force signal for the viscoelastic measurement of specimens, because the selection of the signal peak amplitudes and their corresponding time points was performed manually, without the use of any peak-picking software algorithm. As stated in Sec. 3 the percentage errors in G′ and in G″ resulting from the manual peak selection procedure during viscoelastic data analysis were at or below 6%.
Figure 7c shows the ratio of the nominal displacement amplitude to the actual displacement amplitude as a function of frequency. This ratio was an indication of the frequency response of the LVDT, and it was found to be very close to unity at frequencies of 75–300 Hz (within 4% of 1.0, except for one data point at 280 Hz, which was 5.7% smaller than 1.0). Hence, it was determined that the LVDT displacement transducer is accurate within this frequency range. The ratio at low frequencies (at or below 50 Hz), however, was not as close to unity due to errors in the measurement of acceleration amplitudes, as described above. Since the LVDT demonstrated a steady output in the nominal displacement amplitude [Fig. 7a], the errors at low frequency may only reflect those of the accelerometer response. In order to confirm that the LVDT transducer is also accurate at frequencies below 50 Hz, further vibration experiments involving accelerometers with higher output magnitudes are warranted.
Frequency response of the piezoelectric force transducer
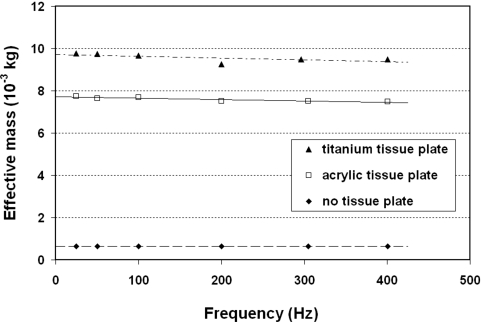
The frequency response of the piezoelectric force transducer was examined by applying an acceleration amplitude of around ±5 G to three levels of mass attached to the actuator of the ELF 3200 over a frequency range of 25–400 Hz, as shown in the setup in Fig. 4. The force amplitude was measured by the piezoelectric transducer and the acceleration amplitude was measured by the accelerometer, allowing for the calculation of the effective mass of vibration as an indication of the frequency response of the piezoelectric transducer.
Figure 8 shows the results of this assessment. As expected, it is clear that the effective mass of vibration was the highest for the titanium tissue plate condition, followed by the acrylic tissue plate condition, and the condition of no tissue plate (with only the adapter attached to the actuator of the ELF 3200). The average difference in effective mass across all frequencies between the titanium tissue plate condition and the no tissue plate condition was 8.9229 g, whereas the average difference between the acrylic tissue plate condition and the no tissue plate condition was 6.9542 g. These differences were within 2.4% of the actual physical mass of the two tissue plates (9.155 and 7.124 g, respectively), validating the current approach for the assessment of frequency response. It is clear that the effective mass did not vary significantly across all frequencies for all of the three levels of mass, suggesting that the frequency response of the piezoelectric transducer was flat and steady, up to a frequency of 400 Hz (Fig. 8).
Figure 8.
Frequency response of the piezoelectric force transducer as indicated by the effective mass of vibration over a frequency range of 25–400 Hz. Three levels of mass are shown corresponding to a titanium tissue plate, an acrylic tissue plate, and no tissue plate mounted to the adapter (Fig. 4). A flat frequency response can be seen for the piezoelectric transducer over the entire frequency range examined.
System noise level
The system noise level was measured as the piezoelectric transducer output force amplitude without the presence of a specimen, and was compared with the system signal level, which was the force amplitude for specific specimens, in order to determine the frequencies at which the system noise was at an acceptably low level. The system signal level was obtained with (1) three samples of the ANSI S2.21 standard polymer material and (2) seven human vocal fold cover specimens. Three trials of oscillatory shear deformation were performed without any specimen to determine the system noise at frequencies of 1–300 Hz. Figure 9a shows the force amplitude for the ANSI S2.21 standard material samples, in comparison with the system noise level as a function of frequency. The mean values and the standard deviations are shown for both, although the standard deviations of the noise trials were too small for the error bars to be visible (average SD=0.000 254 8 N as compared to an average noise of 0.001 849 N). The results showed that the system noise level was consistently lower than the signal level for the standard material, with the difference increasing with frequency. At phonatory frequencies (>100 Hz), the system noise was around two orders of magnitude below the signal level.
Figure 9.
(a) Comparisons of the sinusoidal force amplitude (system signal level) for the ANSI S2.21 standard polymer material (n=3) to the force amplitude without any specimen (system noise level from three trials) in the frequency range of 1–300 Hz (means±standard deviations). The system noise level remains much lower than the signal level across all frequencies. (b) Comparisons of the sinusoidal force amplitude (system signal level) for the human vocal fold cover (n=7) to the system noise level (from three trials) in the frequency range of 1–300 Hz (means±standard deviations). The system noise level remains about one standard deviation lower than the signal level at frequencies of up to around 275 Hz.
The system noise level was also consistently lower than the signal level for the average human vocal fold cover (n=7) across all frequencies [Fig. 9b]. The differences between the mean piezoelectric transducer output force amplitudes and the noise amplitudes were not as large as those in Fig. 9a, but the signal level remained around one standard deviation higher than the system noise level over the entire frequency range, except at 300 Hz where the difference was less than one standard deviation. The signal level at or above 275 Hz was highly variable, with large standard deviations that introduce uncertainties into the validity of the data. These findings suggested that the frequency range within which valid viscoelastic measurements of the human vocal fold cover can be made was up to around 250 Hz, with data collected at or above 275 Hz considered not as meaningful due to the overlap between the signal and the noise of the system.
Validation with ANSI S2.21 standard material
Figure 10 shows the elastic shear modulus G′ of three samples of the ANSI S2.21 standard polymer material, which is a viscoelastic standard for the calibration of equipment for viscoelastic characterization. The dependence of G′ on frequency was found to be consistent with that of published standards (American National Standards Institute, 1998). The target elastic shear modulus of the material was 3.0 kPa at 25 °C at around 170 Hz (dotted line in Fig. 10), and G′ obtained from the rheometer was found to be within 9% of the target modulus value. This indicated that the experimental error of measurements made with the rheometer was also likely within 9% of the measured values. This magnitude of error was similar to that of torsional rheometers (5%–10%) in previous studies (Chan and Titze, 1999; Chan, 2004; Titze et al., 2004).
Figure 10.
Elastic shear modulus (G′) of the three samples of the ANSI S2.21 standard polymer material as a function of frequency. The Dotted line represents the target elastic modulus of the standard material (3.0 kPa at 25 °C at around 170 Hz).
Viscoelasticity of the human vocal fold cover
The results of the strain sweep experiments of the human vocal fold cover are shown in Fig. 11, where the elastic and viscous shear moduli (G′ and G″) of three vocal fold cover specimens are plotted as a function of shear strain amplitude at a frequency of 100 Hz. For a linear stress-strain relationship, the elastic modulus of the specimen would be independent of the displacement amplitude and the force amplitude (x0 and F0) (Chan and Titze, 1999). It can be seen in Fig. 11 that G′ remained nearly constant in a small-strain, linear region of viscoelasticity, up to a strain amplitude of around 3%–7%, which varied slightly among the different specimens. This region of linear viscoelasticity was similar to that reported previously (5% in Chan and Titze, 1999). In order to ensure a linear, small-amplitude, simple-shear deformation, all frequency sweep experiments in the present study were performed at 1.0% strain.
Figure 11.
Elastic shear modulus (G′) and viscous shear modulus (G″) of three human vocal fold cover specimens as a function of shear strain (i.e., strain sweep; frequency=100 Hz). Based on the data of G′, the small-strain linear region of viscoelasticity can be identified with the strain amplitude up to around 3%–7%.
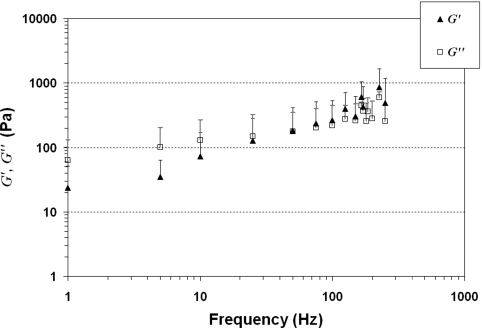
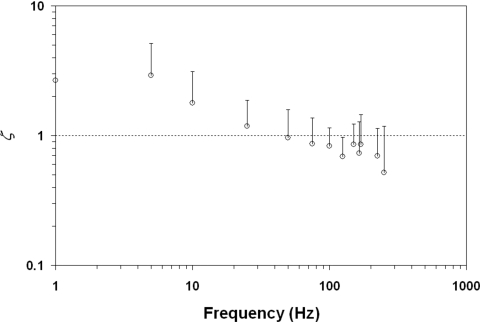
Figure 12 shows the elastic shear modulus (G′) and viscous shear modulus (G″) of the human vocal fold cover across the frequency range of 1–250 Hz, since this was identified as the functional range within which valid viscoelastic measurements can be made with the rheometer. The mean values of seven vocal fold cover specimens are shown, together with the standard deviations displayed as error bars (only upper error bars are shown for visual clarity on the plot). The average dynamic viscosity (η′) and damping ratio (ζ) of the specimens over the same frequency range are shown in Figs. 1314, respectively (once again with standard deviations as upper error bars). To characterize the empirical data with a parametric model (i.e., curve fitting), the dependence of G′, G″, and η′ on frequency f can be described by a power law as follows:
| (25) |
| (26) |
| (27) |
where p and q are the parameters (coefficients) of curve fitting. Some previous studies on the viscoelastic properties of vocal fold tissues and phonosurgical biomaterials have used the logarithmic equation (G′=a log f+b) to describe the empirical relationship between G′ and frequency (e.g., Klemuk and Titze, 2004). In the present study, however, the power law was found to be a superior model for parametrizing the current data, since it resulted in a much better fit for both G′ and G″. Average data for the seven vocal fold cover specimens were fitted to these equations by least-squares regressions. Results of the curve fitting are summarized in Table 2, with values of the parameters p and q given, as well as the coefficient of determination R2, as an estimate of the goodness of fit (Chan and Titze, 1999). It can be seen that the empirical data of G′, G″, and η′ were well described by the power law [Eqs. 25, 26, 27], with the values of R2>0.83.
Figure 12.
Elastic shear modulus (G′) and viscous shear modulus (G″) of the human vocal fold cover as a function of frequency. The means and standard deviations (upper error bars) of the seven specimens are shown.
Figure 13.
Dynamic viscosity (η′) of the human vocal fold cover as a function of frequency. The means and standard deviations (upper error bars) of the seven specimens are shown.
Figure 14.
Damping ratio (ζ) of the human vocal fold cover as a function of frequency. The means and standard deviations (upper error bars) of the seven specimens are shown.
Table 2.
Results of least-squares regressions for the parametric description of elastic shear modulus (G′), viscous shear modulus (G″), and dynamic viscosity (η′) of the human vocal fold cover according to Eqs. 25, 26, 27 (n=7). R2 is the coefficient of determination indicating the goodness of curve fitting.
| Viscoelastic function | p | q | R2 |
|---|---|---|---|
| G′ | 17.246 Pa.s | 0.6320 | 0.9493 |
| G″ | 58.448 Pa.s | 0.3243 | 0.8363 |
| η′ | 10.509 Pa.s2 | −0.7391 | 0.9934 |
The magnitudes of G′ and G″ at 10 Hz, as shown in Fig. 12, were in a similar range as those in previous studies of the human vocal fold cover (e.g., Chan and Titze, 1999). However, a striking finding from Fig. 12 was that unlike previous studies (Chan, 2004; Chan and Titze, 1999), where the elastic shear modulus G′ was consistently higher than the viscous shear modulus G″ at all frequencies of oscillation, G′ was observed to be lower than G″ at low frequencies, until a “cross over” point at which G′ and G″ seemed to converge and then crossed each other, at around 50 Hz. G′ did not become higher than G″ until it reached the frequency range above this crossover point. This is a very interesting finding, because such crossover behavior of the viscoelastic moduli has never been observed in previous studies of the human vocal fold cover (Chan and Titze, 1999). In rheology, such viscoelastic behavior is often observed for polymer melts and polymer solutions (Barnes et al., 1989; Ferry, 1980). In the frequency range below the crossover point, commonly called the terminal region, G′ was lower than G″, with the specimens demonstrating a liquidlike linear viscoelastic response dominated by their viscous properties. In the frequency range above the crossover point, commonly called the rubbery region or plateau region, G′ was higher than G″, indicating predominantly elastic properties in the specimens, characteristic of viscoelastic solids. For polymers, the transition of viscoelastic response between the terminal region and the rubbery region depends on the molecular weight, molecular weight distribution, and the extent of entanglement of the macromolecules (Barnes et al., 1989; Ferry, 1980). For the vocal fold lamina propria, it is likely that such factors also play a key role in determining the viscoelastic response, although it can be expected that the interactions among the fibrous and interstitial proteins in the extracellular matrix are much more complicated than those in synthetic polymers (Chan and Titze, 1999).
The dynamic viscosity η′ of the seven specimens decreased monotonically with frequency, indicating the behavior of shear thinning as observed previously (Fig. 13). The magnitude of η′ at 10 Hz was consistent with that in previous studies (Chan and Titze, 1999, 2000). Figure 14 shows that the damping ratio ζ of the seven specimens generally decreased with frequency, as opposed to being a relatively flat function in previous studies (Chan and Titze, 1999). An intriguing finding was that ζ was actually above 1.0 at low frequencies (<50 Hz), suggesting that the vocal fold cover was, on average, overdamped below 50 Hz due to the fact of G″ being higher than G′ in this terminal region. On the other hand, at higher frequencies in the rubbery (plateau) region (at or above 50 Hz), the damping ratio was always below 1.0, meaning that the vocal fold cover remained underdamped such that oscillation can be readily sustained during phonation. However, the mean value of ζ in the phonatory range (100–250 Hz) was 0.7383±0.1211, considerably higher than those reported before (0.1–0.5 at 10–15 Hz in Chan and Titze, 1999) as well as typical values used in computer models (around 0.1–0.2; Titze, 2006).
CONCLUSION
A controlled-strain, linear, simple-shear rheometer system was custom built based on the EnduraTEC ELF 3200 mechanical testing system. The rheometer was designed for direct experimental measurements of the linear viscoelastic shear properties of human vocal fold tissues at frequencies in the phonatory range (above 100 Hz). Vibration experiments were performed to examine the frequency response characteristics of key components of the system, including a LVDT displacement transducer and a piezoelectric force transducer. The system noise level was estimated as the piezoelectric transducer output force amplitude without the mounting of any specimens, and was compared to the signal level of a standard viscoelastic material (ANSI S2.21) and that of the human vocal fold cover. Our findings suggested that the rheometer is capable of valid and reliable measurements of the linear viscoelastic properties of the vocal fold lamina propria, including elastic shear modulus (G′), viscous shear modulus (G″), dynamic viscosity (η′), and damping ratio (ζ) at phonatory frequencies, up to around 250 Hz.
Despite the significance of these findings, the results of the current study should only be considered preliminary due to the small number of vocal fold lamina propria specimens examined. Further studies involving additional specimens are required to corroborate the present findings and conclusions. Viscoelastic shear properties of the vocal fold lamina propria should be examined in the phonatory frequency range with this rheometer, in order to explore important differences in tissue rheological properties due to age, gender, race, and pathology.
ACKNOWLEDGMENTS
This work was supported by the National Institute on Deafness and Other Communication Disorders, NIH Grant No. R01 DC006101. The authors wish to thank Min Fu and Bokkyu Lee for their assistance in rheological data collection and data analysis. Special thanks are extended to Alan McMullen, Kirk Biegler, and Troy Nickel of the ElectroForce Systems Group, Bose Corporation for their contributions to the design and validation of the rheometer.
References
- American National Standards Institute, Inc. (1998). “Method for preparation of a standard material for dynamic mechanical measurements,” ANSI S2.21-1998 (Acoustical Society of America, New York, NY: ). [Google Scholar]
- Barnes, H. A., Hutton, J. F., and Walters, K. (1989). An Introduction to Rheology (Elsevier, Amsterdam, The Netherlands: ). [Google Scholar]
- Chan, R. W. (2001). “Estimation of viscoelastic shear properties of vocal fold tissues based on time-temperature superposition,” J. Acoust. Soc. Am. 10.1121/1.1387094 110, 1548–1561. [DOI] [PubMed] [Google Scholar]
- Chan, R. W. (2004). “Measurements of vocal fold tissue viscoelasticity: Approaching the male phonatory frequency range,” J. Acoust. Soc. Am. 10.1121/1.1736272 115, 3161–3170. [DOI] [PubMed] [Google Scholar]
- Chan, R. W., and Titze, I. R. (1999). “Viscoelastic shear properties of human vocal fold mucosa: Measurement methodology and empirical results,” J. Acoust. Soc. Am. 10.1121/1.427947 106, 2008–2021. [DOI] [PubMed] [Google Scholar]
- Chan, R. W., and Titze, I. R. (2000). “Viscoelastic shear properties of human vocal fold mucosa: Theoretical characterization based on constitutive modeling,” J. Acoust. Soc. Am. 10.1121/1.428354 107, 565–580. [DOI] [PubMed] [Google Scholar]
- Chan, R. W., and Titze, I. R. (2003). “Effect of postmortem changes and freezing on the viscoelastic properties of vocal fold tissues,” Ann. Biomed. Eng. 10.1114/1.1561287 31, 482–491. [DOI] [PubMed] [Google Scholar]
- Chan, R. W., and Titze, I. R. (2006). “Dependence of phonation threshold pressure on vocal tract acoustics and vocal fold tissue mechanics,” J. Acoust. Soc. Am. 10.1121/1.2173516 119, 2351–2362. [DOI] [PubMed] [Google Scholar]
- Ferry, J. D. (1980). Viscoelastic Properties of Polymers, 3rd ed. (Wiley, New York, NY: ). [Google Scholar]
- Gray, S. D., Titze, I. R., Chan, R., and Hammond, T. H. (1999). “Vocal fold proteoglycans and their influence on biomechanics,” Laryngoscope 10.1097/00005537-199906000-00001 109, 845–854. [DOI] [PubMed] [Google Scholar]
- Klemuk, S. A., and Titze, I. R. (2004). “Viscoelastic properties of three vocal-fold injectable biomaterials at low audio frequencies,” Laryngoscope 114, 1597–1603. [DOI] [PubMed] [Google Scholar]
- Titze, I. R. (2006). The Myoelastic-Aerodynamic Theory of Phonation (National Center for Voice and Speech, Iowa City, IA: ). [Google Scholar]
- Titze, I. R., Klemuk, S. A., and Gray, S. (2004). “Methodology for rheological testing of engineered biomaterials at low audio frequencies,” J. Acoust. Soc. Am. 10.1121/1.1631941 115, 392–401. [DOI] [PubMed] [Google Scholar]
- Zhang, K., Siegmund, T., and Chan, R. W. (2007). “A two-layer composite model of the vocal fold lamina propria for fundamental frequency regulation,” J. Acoust. Soc. Am. 10.1121/1.2749460 122, 1090–1101. [DOI] [PubMed] [Google Scholar]