Abstract
Calix[4]arenes constrained to 1,3-alternate conformation and functionalized at the upper rim with four and two tert-butylnitroxides have been synthesized, and characterized by X-ray crystallography, magnetic resonance (EPR and 1H NMR) spectroscopy, and magnetic studies. The 1,3-alternate nitroxide tetraradical and diradical provide unique polyradical scaffolds for dissection of the through-bond and through-space intramolecular exchange couplings. In addition, detailed magnetic studies of the previously reported calix[4]arene nitroxide tetraradical, which possesses cone conformation in solution, reveal conformational dependence of exchange coupling. Through-bond coupling between the adjacent nitroxide radicals is mediated by the nitroxide-m-phenylene-CH2-m-phenylene-nitroxide coupling pathway, and through-space coupling is found between the diagonal nitroxide radicals at the conformationally-constrained N···N distance of 5–6 Å. Magnetic studies of the calix[4]arene polyradical scaffolds in frozen solutions show that the through-bond exchange coupling in the 1,3-alternate calix[4]arene tetraradical is antiferromagnetic, while that in cone calix[4]arene tetraradical is ferromagnetic. The through-space exchange couplings are antiferromagnetic in both cone and 1,3-alternate calix[4]arene tetraradical, as well as in the 1,3-alternate calix[4]arene diradical. The exchange coupling constants (|J/k|) are of the order of 1 Kelvin.
Introduction
The spin-spin interactions between unpaired electrons in organic diradicals and polyradicals are of critical importance in organic magnetism,1-3 molecular charge-transfer,4 and multiple spin labeling in structural biology.5 When unpaired electrons are in close proximity, the dominant interaction is likely to be exchange coupling, mediated through bonds and/or through space.1 In general, the exchange coupling is mediated more effectively through bonds, especially through cross-conjugated π-system, than through space.3,6-10 Such exchange coupling can be either ferromagnetic or antiferromagnetic, depending upon the topology and conformation of the coupling pathway connecting the radicals.1,8-12
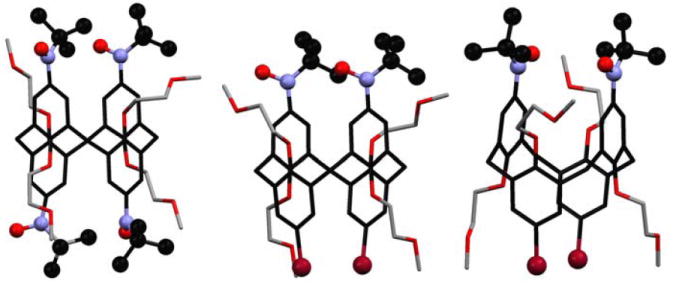
Stable polyradical scaffolds with constrained conformations may provide a new approach for controlling through-bond and through-space exchange couplings. The fixed conformations of 1,3-alternate and cone calix[4]arenes, that are functionalized at the upper rim with stable aryl-delocalized radicals, may be viewed as such scaffolds.13a,14 In these scaffolds, the through-bond exchange coupling between the adjacent radicals is mediated by the radical-m-phenylene-CH2-m-phenylene-radical coupling pathway, with distinct conformations in the 1,3-alternate and cone calix[4]arenes (Figure 1). In addition, the through-space exchange coupling at fixed radical-radical distances of approximately 5–6 Å, as found for the diagonal radicals, may be probed (Figure 1).
Figure 1.
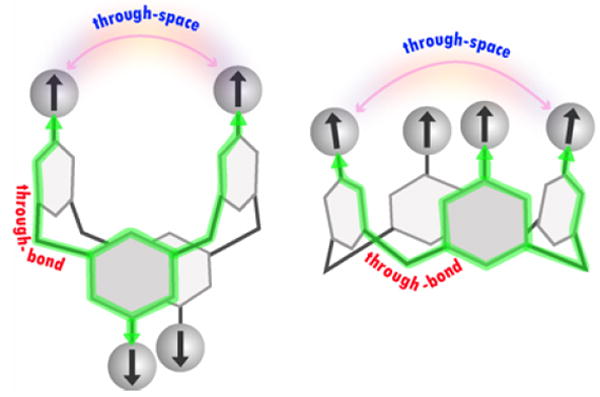
1,3-Alternate and cone calix[4]arene scaffolds, functionalized on the upper rims with radicals.
Recently, we reported synthesis, crystallography, and magnetic characterization of the cone calix[4]arene scaffold, nitroxide tetraradical 3 (Figure 2).13 In the solid state, this tetraradical adopts a pinched cone conformation, forming an intramolecular dimer with strong antiferromagnetic coupling (|J/k| = 200–300 K) between the two diagonal nitroxides. In solution, 3 was found to possess a 4-fold symmetric cone conformation but exchange coupling could only be estimated as 30 K > |J/k| ≫ 1.8 mK.13 Now we report the synthesis and studies of ambient stable nitroxide tetraradical 1 and diradical 2 in the fixed 1,3-alternate calix[4]arene conformations (Figure 2). Magnetic studies of 1 and 2, as well as magnetic studies of 3 in solution, are described. Both through-bond and through-space exchange couplings are determined, as well as their conformational dependence.
Figure 2.
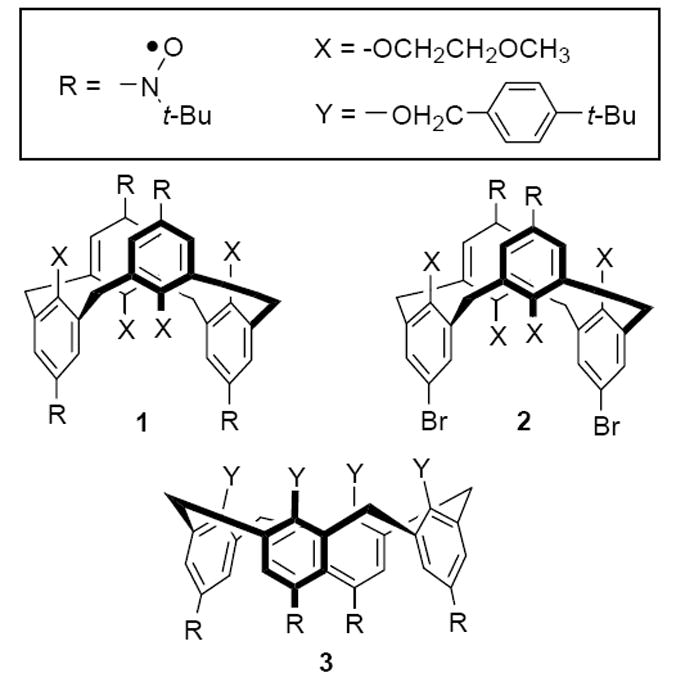
Nitroxide tetraradical 1 and diradical 2 with the constrained conformations of 1,3-alternate calix[4]arene, and nitroxide tetraradical 3 with the constrained conformation of cone calix[4]arene.
Results and Discussion
Synthesis
The synthesis starts from tetrabromocalix[4]arene 4, constrained in the 1,3-alternate conformation (Scheme 1 and Supporting Information).15 The Li/Br exchange on 4 with an excess amount of t-BuLi gives intermediate tetrakis(aryllithium), which is reacted with 2-methyl-2-nitrosopropane dimer, to provide tetrahydroxylamine 5. An analogous procedure, in which the t-BuLi is replaced with n-BuLi (2 equiv),16 gives dihydroxylamine 6.
Scheme 1.
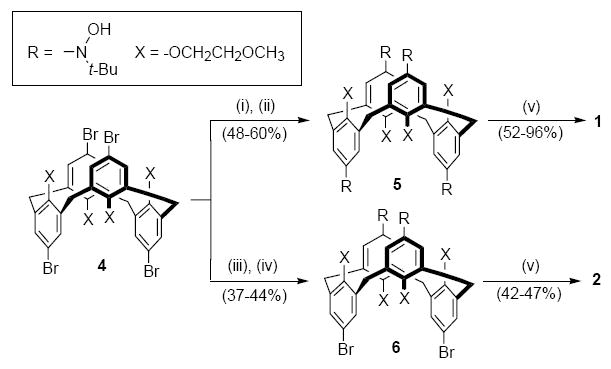
Synthesis of nitroxide tetraradical 1 and diradical 2
Conditions: (i) t-BuLi (8 equiv), THF, −78 °C for 2 h, then −20 °C for 15 min; (ii) [(CH3)3CNO]2 (2.1 equiv) in THF, −78 °C then slowly warm up to room temperature overnight; (iii) n-BuLi (2.2 equiv), THF; (iv) [(CH3)3CNO]2 (1.2 equiv); (v) Ag2O, CHCl3 or CH2Cl2.
The presence of the hydroxyl groups in 5 and 6 is confirmed by IR (e.g., νO-H ≈ 3230–3240 cm-1) and 1H NMR spectra (D2O-exchangable 4-proton or 2-proton singlet at 9.1–9.3 ppm). In the 1H NMR spectra, only one sharp singlet for tert-butyl group protons is observed for each compound. The other 1H resonances are relatively broadened at ambient temperature, due to the restricted rotations along the C(aromatic)-N bonds; the coalescence temperatures for aromatic protons suggest that the barrier for rotation is on the order of 15 kcal mol-1 (Table S1, Supporting Information). In the high temperature limit, 5 and 6 possess D2d (T > 325 K) and C2v (T > 306 K) point groups, respectively, on the 1H NMR (400 MHz) time scale.
Oxidation of 5 and 6 with freshly prepared silver oxide give the corresponding nitroxide tetraradical 1 and diradical 2 (Scheme 1).
Molecular structure of 1 and 2
Nitroxide tetraradical 1 crystallizes with one molecule per asymmetric unit, without inclusion of solvent. For diradical 2, two crystallographically unique molecules are found, with one quarter benzene molecule per formula unit (one half benzene molecule per asymmetric unit). The X-ray structure determinations of nitroxide tetraradical 1 and diradical 2 confirm 1,3-alternate conformation of the calix[4]arene macrocycle for both molecules (Figure 3, Table 1).
Figure 3.
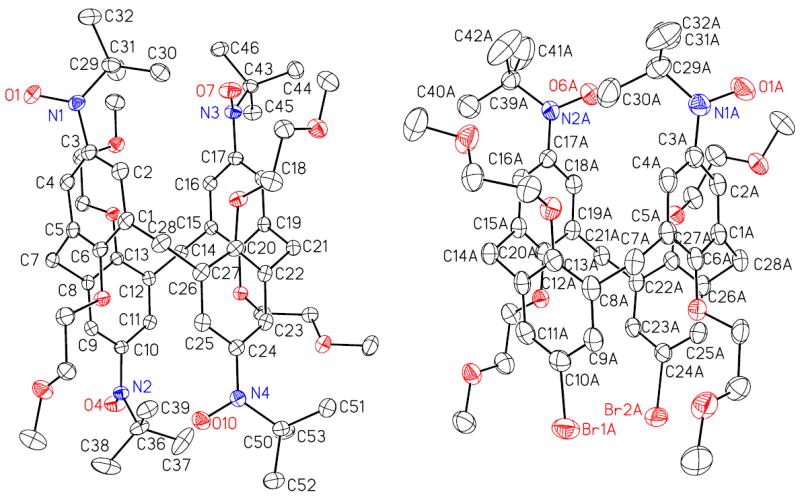
Molecular structure and conformation for nitroxide tetraradical 1 (left) and diradical 2 (right) with constrained conformations of 1,3-alternate calix[4]arene. Carbon, nitrogen, and oxygens atoms are depicted with thermal ellipsoids set at the 50% probability level. Only one of the two unique molecules of 2 and without the solvent of crystallization (benzene) is shown.
Table 1.
Summary of the X-ray crystallographic data.
| property | 1 | 2 (0.25•C6H6) |
| molecular formula | C56H80N4O12 | C49.50H63.50Br2N2O10 |
| formula weight | 1001.24 | 1006.34 |
| crystal/color | red block | red block |
| crystal system | monoclinic | triclinic |
| space group | P21/c | P-1 |
| a, Å | 14.920(4) | 14.698(5) |
| b, Å | 35.167(9) | 19.752(6) |
| c, Å | 10.593(3) | 20.370(7) |
| α, ° | 90 | 96.911(9) |
| β, ° | 100.379(7) | 110.227(9) |
| χ, ° | 90 | 111.428(9) |
| volume, Å3 | 5467(2) | 4955(3) |
| Z | 4 | 4 |
| Dcalcd/g cm-3 | 1.216 | 1.349 |
| reflns collected | 82665 | 66102 |
| unique reflns | 12675 (Rint = 0.0554) | 22927 (Rint = 0.0627) |
| data / restraints / parameters | 12675 / 0 / 665 | 22927 / 48 / 1206 |
| R1 (I > 2σ(I)) | 0.0461 | 0.0483 |
| wR2 (I > 2σ(I)) | 0.1141 | 0.1082 |
| GOF | 1.019 | 1.014 |
In tetraradical 1, the molecular structure is consistent with significant repulsion between the bulky tert-butyl nitroxide moieties. The N-C(ipso)-C(para) angles of <180° (e.g., N1-C3-C6 angle of 172°) and pyramidalized nitrogen atoms indicate outward bending of the nitroxide groups, with relatively long N1···N3 (5.78 Å) and N2···N4 (5.70 Å) distances between the diagonal nitroxide groups. Dihedral angles between nitroxide groups and benzene rings are significantly different for each of the four aryl nitroxide units; for each pair of the diagonal tert-butyl nitroxide moieties, the bulky tert-butyls occupy the significant part of the space between the nitroxide groups (Figure 4).
Figure 4.
Conformation of the tert-butyl nitroxide moieties (ball-and-stick) in crystalline nitroxide tetraradical 1 and diradical 2. For 2, two crystallographically unique molecules are shown; in one of the molecules, disorder in the ethylenoxymethyl chain and the tert-butyl group is omitted for clarity.
In diradical 2, the structures for the two crystallographically unique molecules show the two nitroxide groups in relatively closer proximity, with N···N distances 5.07 and 5.37 Å and nearly planar nitrogen atoms, compared to 1. In one of the unique molecules, the NO groups have antiparallel N-O bond axes (anti) and they are coplanar with the benzene rings within each aryl nitroxide moiety. In the other molecule, the NO groups have parallel N-O bond axes (syn) and they form torsional angles of ~40° with the benzene rings within each aryl nitroxide moiety.
For 1 and 2, the C(ipso)-C(CH2)-C(ipso) angles within calix[4]arene macrocycles are in the 110 – 113° range.17 The dihedral angles between the planes defined by the C(ipso)-C(CH2)-C(ipso) and the benzene rings are in the 59–73° range (Table S2, Supporting Information). In this geometry of 1,3-alternate conformation, the π-systems of the adjacent arylnitroxides are pointing away from each other. However, in a cone conformation, which is adopted by tetraradical 3 in solution, the dihedral angles between the C(ipso)-C(CH2)-C(ipso) and benzene ring planes are close to 90°, with the π-systems of the adjacent arylnitroxides pointing toward each other. Therefore, the through-space interactions between the adjacent arylnitroxide moieties in the 1,3-alternate conformation of 1 should be relatively small, compared to those in the cone conformation of 3.
Structure of 1 and 2 in solution
1H NMR spectra of tetraradical 1 and diradical 2 in chloroform-d at room temperature show resonances for those protons that are expected to possess relatively small spin densities, i.e., all protons except those of the aryl moieties of the arylnitroxides (Figure 5).1b,13a,18,19
Figure 5.
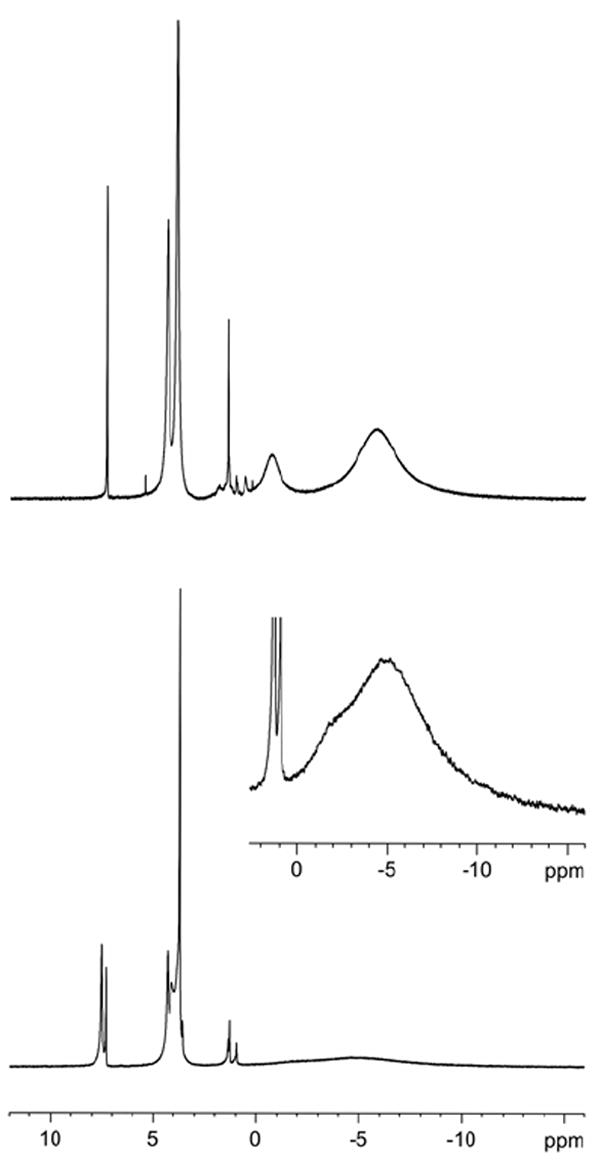
1H NMR (500 MHz, chloroform-d, LB = 1 Hz) spectra for nitroxide tetraradical 1 (top) and diradical 2 (bottom). Inset plot: LB = 10 Hz. The singlets at 7.26 ppm and ~1.5 ppm correspond to the residual non-deuterated chloroform and water peaks. The other sharp, relatively weak peaks are assigned to diamagnetic impurities.
Four broad resonances are observed for tetraradical 1, as expected for a structure with the D2d point group. The relatively less broadened 12-proton and 16-proton singlets at 4.34 and 3.84 ppm are assigned to the methyl (CH3) and dimethylene (CH2CH2) of the methoxyethyleneoxy (OCH2CH2OCH3) groups, respectively. The two most up-field shifted broad singlets, 8-proton at −0.8 ppm and 36-proton at −5.9 ppm, are assigned to the methylene groups of the macrocycle and the tert-butyl groups, respectively.
Four broad resonances with similar chemical shifts to those in 1 may be identified for diradical 2; specifically, two of those resonances appear in the −5 ppm region as a broad singlet with a shoulder, which may be assigned to the two tert-butyl groups and four methylene groups of the macrocycle.20 In addition, relatively narrow singlets at 7.47, 4.30, and 3.69 ppm are assigned to the aromatic, OCH3, and OCH2CH2O protons of the diamagnetic bromophenyl moieties of 2, respectively.
The significant up-field chemical shifts of several parts-per-million for the protons of tert-butyl groups and of methylene groups in tetraradical 1 and diradical 2, when compared to the corresponding hydroxylamines 5 and 6, indicate substantial negative spin densities at the hydrogen atoms in these groups. The negative sign of the spin density for the hydrogen atoms of the tert-butyl groups is consistent with the spin polarization through σ-bonds of the positive spin density at the nitrogen atom of the nitroxide, as found for N-tert-butylnitroxides.21 The negative sign for the hydrogen atoms of the methylene groups is compatible with both hyperconjugation and spin polarization of the negative spin density from the meta-carbon (meta-position with respect to the nitroxide) in the benzene ring.22 The near coincidence of resonances for the methyl (CH3) and dimethylene (CH2CH2) of the methoxyethyleneoxy (OCH2CH2OCH3) groups in 1 and 2, and in diamagnetic 5 and 6, suggests negligible spin densities at the hydrogen atoms of OCH2 fragment. Similar behavior was found in 3,5-dimethyl-4-methoxyphenyl-tert-butylnitroxide, in which a very small value of 1H-hyperfine splitting, aH = +0.0006 mT, for the methoxy hydrogens was ascribed to the twisting of the methoxy group out of conjugation with the benzene ring and the nitroxide.22,23 These 1H NMR spectral assignments confirm the structures of 1 and 2 in solution, and are in agreement with the reported spectra for the fixed cone calix[4]arene nitroxide tetraradical 3.13a
EPR spectrum of 1 in toluene at 295 K shows a well-resolved nonet (Figure 6). An excellent numerical spectrum fit to a single component, i.e., nitroxide tetraradical 1, is obtained, confirming high degree of radical purity (98+ %) of 1.24 The 14N hyperfine coupling with peak-to-peak splitting ΔHpp ≈ 0.319 mT = aN/4, i.e., aN = 1.28 mT, is identical to the value reported for 3,5-dimethyl-4-methoxyphenyl-tert-butylnitroxide.22,25 This result indicates exchange-coupled nitroxides with a coupling constant significantly greater than the 14N hyperfine coupling, |J/gμB| ≫ |aN|, i.e., |J/k| ≫ 1.8 mK. At 135 K, the EPR spectrum of 1 in toluene glass shows a single peak in the |Δms| = 1 region, with a somewhat broader spectral envelope, compared to the solution phase spectrum for the same sample (Figure 6). Furthermore, the |Δms| = 2 transition is barely detectable. These results suggest that tetraradical 1 possesses rather small zero-field splitting (|D/hc|) that is compatible with relatively high average symmetry for the disposition of nitroxide radicals.26,27
Figure 6.
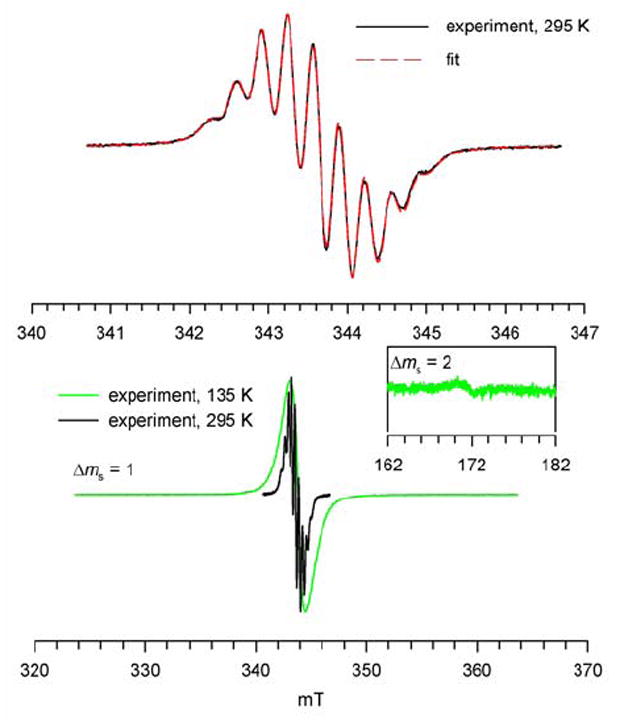
EPR (X-Band) spectra of 1 in toluene at 295 K and 135 K. Numerical fit (red dashed line) to the experimental spectrum at 295 K corresponds to a single nitroxide tetraradical species; correlation coefficient is 0.999 and the values for the variable parameters are: Lorentzian line width of 0.156 mT, g-shift of −0.045 mT (g-value = 2.0059), 14N-splitting of 0.319 mT for 4 nuclei, 1H-splitting of 0.048 mT for 8 nuclei.
EPR spectra of diradical 2 in solution (toluene, toluene/chloroform (4:1), acetonitrile, dichloromethane, and dichloromethane/methanol (4:1)) at ambient temperature show an intense broad peak, with discernable pentuplet spectral pattern; furthermore, additional sharp peaks, with relatively low intensity, are superimposed on the broad peak (Figure S6–S9, Supporting Information). The EPR spectra of 2 in dichloromethane/methanol (4:1) show pronounced sharpening at higher temperatures, with a clearly defined pentuplet at 320 K; upon decreasing the temperature, this peak is progressively broadened. For 1 mM solution of 2 in toluene at 295 K, the numerical spectrum fits are compatible with a mixture of diradical and monoradical (98:2). Because of the dynamic effects, the quality of these fits is rather low, especially compared to those for tetraradical 1;28 consequently, the 14N hyperfine coupling with peak-to-peak splitting ΔHpp ≈ 0.8 mT = aN/2, i.e., aN = 1.6 mT for 2, should be viewed as an approximate estimate. These results are in agreement with significant exchange coupling between nitroxide radicals (|J/gμB| ≫ |aN|).
In rigid matrices, the EPR spectra of 2 clearly show the presence of significant zero-field splitting, as indicated by the large spectral width of |Δms| = 1 region and relatively intense |Δms| = 2 transition. The |Δms| = 1 spectrum of 2 in toluene/chloroform glass at 140 K consists of four symmetrically disposed broad peaks, corresponding to the zero-field splitting parameters |D/hc| = 1.39×10−2 cm−1 and |E/hc| = 0 cm−1(Figure 7). Similar four-peak |Δms| = 1 spectra are obtained at low temperatures in 2-methyltetrahydrofuran, dichloromethane/methanol (4 : 1), and ethanol (Figures S10 and S11, Supporting Information); for the first two matrices, the two side peaks consist of five symmetrically disposed shoulders (pentuplet-like), corresponding to the 14N hyperfine coupling with spacings of (|Azz|/2)/hc ≈ 0.0013 cm-1 ((|Azz|/2)/gμB ≈ 1.4 mT). (The pentuplet in the |Δms| = 2 region possesses similar 1.4-mT line spacings.) It is usually assumed that the largest principal values of the magnetic dipole tensor and nuclear hyperfine tensor correspond to the direction of the z-axis connecting the nitroxide radicals and the direction of the nitrogen 2pπ-orbital, respectively.29 The observation of the relatively large value of |Azz|/2 in the |Δms| = 1 region suggests that these two directions are approximately coinciding; this may correspond to the limiting conformation of diradical 2, with the parallel N-O bond axes and the planar phenylnitroxide moieties. Spectral widths of the |Δms| = 1 regions, |2D/gμB| = 29 – 31 mT, are solvent dependent. Based upon a simple point-dipole approximation, |2D/gμB| = 29 – 31 mT corresponds to an effective distance of about 5.6 – 5.8 Å between the two magnetic dipoles.30 For 1 mM 2 in toluene/chloroform (4 : 1) with |2D/gμB| = 30 mT, the relative intensities of the |Δms| = 1 and |Δms| = 2 transitions are 5.06 × 10-4 at 9.4848 GHz, providing the interspin distance estimate of 5.73 Å.31 These distance measurements, which are comparable to the expected distance between the mid-points of the N-O bonds of the diagonal nitroxides in the 1,3-alternate conformation of 2, should be viewed as approximate estimates, as the spin density in 2 is delocalized and factors other than magnetic dipole-dipole interactions may contribute to the value of |2D|.
Figure 7.
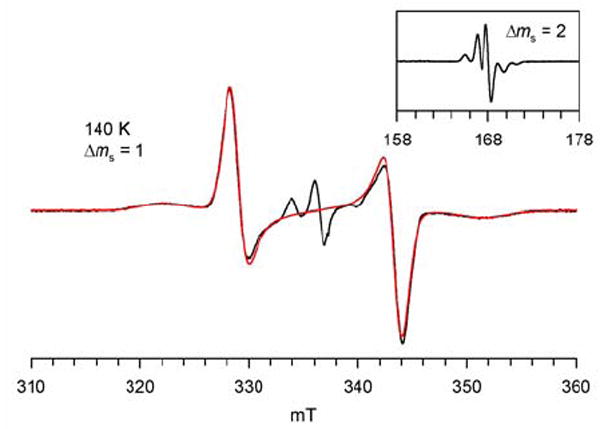
EPR (X-Band, 9.4424 GHz) spectrum of 0.6 mM nitroxide diradical 2 in toluene/chloroform (4 : 1) at 140 K. The spectral simulation of the |Δms| = 1 region is shown as red trace. The fitting parameters for the spectral simulation to the S = 1 state are: |D/hc| = 1.39 × 10−2 cm−1 (|D/gμB| = 14.9 mT), |E/hc| = 0 cm−1, gx = 2.0064, gy = 2.0064, gz = 2.0030, Gaussian line (Lx = 12 G, Ly = 20 G, Lz = 40 G). The center lines correspond to an S = ½ (monoradical) impurity.
The EPR spectra support structural assignments for 1 and 2, and provide the lower bound estimate for |J|, similar to that found for 3. Values of J are determined by magnetic studies of 1 – 3.
Magnetic studies of 1, 2, and 3 in solution
Magnetization (M) is measured as a function of magnetic field (H = 0–5×104 Oe and T = 1.8, 3, and 5 K) and temperature (T = 1.8–300 K at H = 30000, 5000, or 500 Oe). The M vs. H and M vs. T data are plotted as the M/Msat vs. H/T and the χT vs. T, respectively, where Msat is the magnetization at saturation and χ is the paramagnetic susceptibility.
For tetraradical 1 in tetrahydrofuran (THF), the value of χT is constant in the 40–150 K range (Figure 8). The downward turn in the χT vs. T plot at low temperature is consistent with antiferromagnetic exchange coupling, corresponding to a mean-field parameter, θ ≈ −2.3 K. The antiferromagnetic exchange coupling is most likely intramolecular, as the curvature and onset of the downward turn is not dependent on concentration of 1 (5 and 13 mM). The presence of antiferromagnetic exchange coupling is also indicated by the relatively slow saturation behavior for the M vs. H data; the M/Msat vs. H/T plots at T = 1.8–5 K have significantly different curvatures, that are much smaller than the curvature of the Brillouin curve for four independent spins S = ½.
Figure 8.
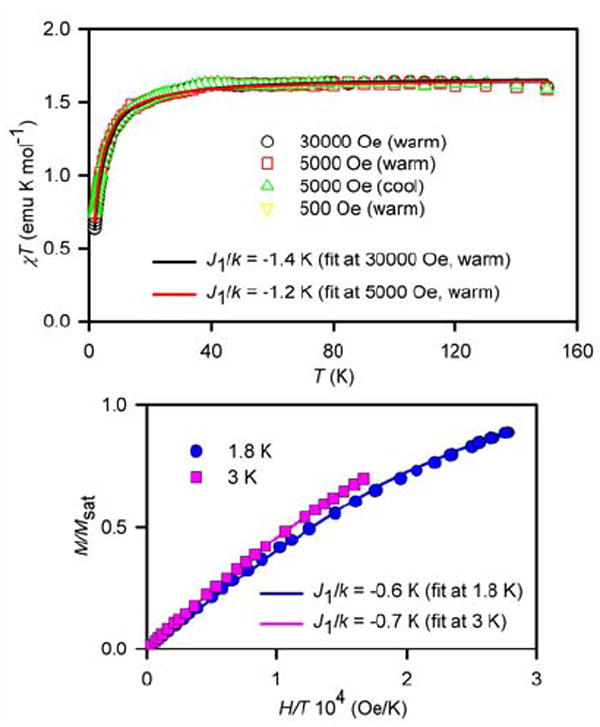
SQUID magnetometry for 5 mM 1 in THF with numerical fits to the tetraradical model (Figure 10, eq. 1 and 2). For the χT vs. T fits (top) and the M/Msat vs. H/T fits (bottom), the J2/k (diagonal coupling) is set to −1.1 K and −0.5 K, respectively. The variable parameters (parameter dependence and R2) are as follows: at 30000 Oe in the warming mode, J1/k = −1.4 K, w = 1.11 (0.32, 0.998); at 5000 Oe in the warming mode, J1/k = −1.2 K, w = 1.10 (0.30, 0.995); at 1.8 K, J1/k = −0.6 K, Msat = 0.76 μB (0.85, 0.999); at 3 K, J1/k = −0.7 K, Msat = 0.86 μB (0.97, 1.000).
Considering their structural similarity, magnetic studies of diradical 2 may provide additional insight into the nature of intramolecular antiferromagnetic exchange coupling in tetraradical 1. For 7 mM 2 in THF (Figure 9), the relatively small curvature of the downward turn in the χT vs. T plot at low temperature and the slightly different curvatures of the M/Msat vs. H/T plots in the T = 1.8–5 K range are readily corrected with a small mean-field parameter θ ≈ −0.5 K, accounting for weak antiferromagnetic exchange coupling between two spins S = ½. Similar weak antiferromagnetic coupling (θ ≈ −0.5 K) is observed for more concentrated, 15 and 24 mM, samples of 2 in THF (Figure S13 and S14, Supporting Information).
Figure 9.
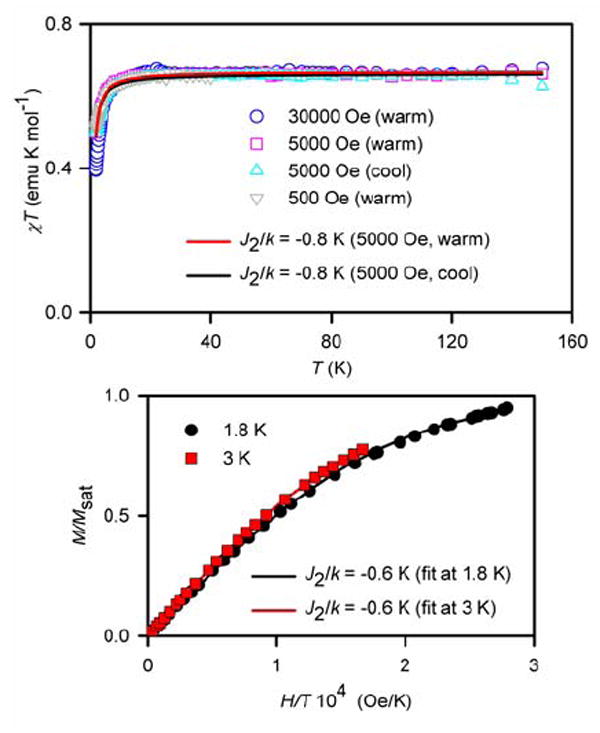
SQUID magnetometry for 7 mM 2 in THF with numerical fits to the diradical model (eq. 4 with J1/k = 0). For the χT vs. T fits (top) and the M/Msat vs. H/T fits (bottom), the variable parameters (parameter dependence and R2) are as follows: at 5000 Oe in the warming mode, J2/k = −0.8 K, w = 0.89 (0.25, 0.990); at 5000 Oe in the cooling mode, J2/k = −0.8 K, w = 0.88 (0.26, 0.982); at 1.8 K, J2/k = −0.6 K, Msat = 0.80 μB (0.62, 1.000); at 3 K, J2/k = −0.6 K, Msat = 0.82 μB (0.91, 1.000).
Magnetic data for 5 mM 1 in 2-MeTHF and ~5 mM 2 in chloroform/methanol (1:1) suggest significantly weaker antiferromagnetic exchange couplings, θ = −1.5 K and θ = −0.1 – (−0.2) K, respectively; for 2, the magnetic data are approaching the near perfect paramagnetic behavior of two independent spins S = ½ (Figure S16, Supporting Information).
These results indicate that exchange coupling in diradical 2 in THF is intramolecular and it is significantly weaker, compared to that in tetraradical 1 in THF. This suggests that the stronger antiferromagnetic exchange coupling in tetraradical 1 is mediated through bonds, with the coupling pathway consisting of nitroxide-m-phenylene-CH2-m-phenylene-nitroxide; in diradical 2, with the additional m-phenylene-CH2 unit in the coupling pathway, the through-bond exchange coupling should be negligible.32 This would imply that the weak antiferromagnetic exchange coupling for 2 in THF may be associated with the through-space exchange coupling between the diagonal nitroxides. Such through-space exchange coupling is likely to be antiferromagnetic and strongly dependent on the distance between the nitroxides (NO). Although the N···N distance in the 1,3-alternate conformation of 2 is fixed at 5–6 Å, rotation along the C(aryl)-N bonds may provide conformations with significantly different N···O and O···O distances that may lead to modulation of the through-space exchange coupling between the diagonal nitroxides. The evidence for such conformations is obtained from X-ray crystallography and EPR spectroscopy of 2. In particular, the nitroxide-nitroxide distances, as measured by the values of |2D| for 2, and the strength of the through-space antiferromagnetic exchange coupling are dependent on the solvent (matrix).
For tetraradical 1 and diradical 2, both temperature-dependence (χT vs. T) and field-dependence (M vs. H) of the experimental magnetic data are well fit by the tetraradical model and the diradical model, respectively. In these models, based upon the Heisenberg Hamiltonian (2JSn•Sn+1),33 tetraradical 1 may be viewed as a cluster of four S = ½ spins located at the vertices of a square (Figure 10, eq. 1 and 2); analogously, diradical 2 may be considered as a dimer of two diagonally positioned S = ½ spins (Figure 10, eq. 3 and 4). Each of the four identical pairwise exchange couplings (J1/k), along the sides of the square, corresponds primarily to the through-bond exchange coupling between the adjacent nitroxides, mediated by the nitroxide-m-phenylene-CH2-m-phenylene-nitroxide coupling pathway in 1. Each of the two diagonal exchange couplings (J2/k) in the square corresponds to the through-space exchange coupling between the diagonal nitroxides in 1 and 2. Another variable parameter is used to account for impurities and inaccuracies in the mass balance, i.e., “magnetization at saturation,” Msat (eq. 1 and 3, expressed in units of Bohr magnetons per nitroxide) and the mass factor, w (eq. 2 and 4). (For selected fits, the mean-field parameter, θ, could be used in place of J2/k.) N denotes number of moles of tetraradical (eq. 1 and 3). Equations 1 – 4 account for paramagnetic saturation.
Figure 10.
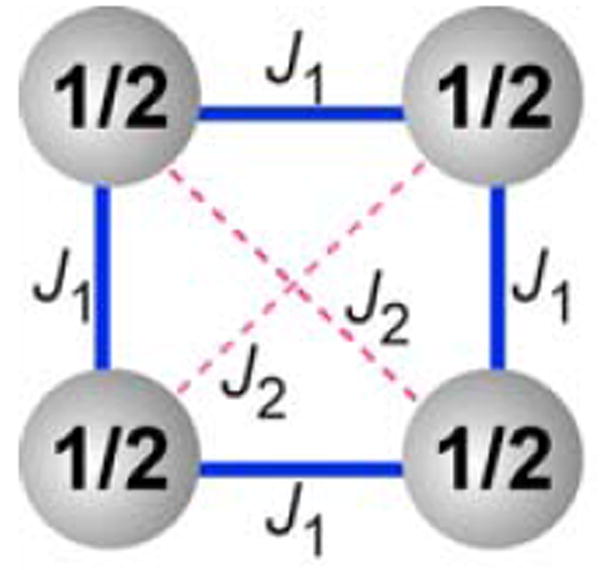
Cluster of spins S = ½ with pairwise exchange couplings J1 (through-bond) and J2 (through-space) as the tetraradical model for 1 and 3. The diradical model for 2 corresponds to a dimer of spins S = ½ with pairwise exchange coupling J2.
| (1) |
| (2) |
| (3) |
| (4) |
The two-parameter numerical fits of the χT vs. T and the M/Msat vs. H/T data for diradical 2 in THF, using the diradical model (eq. 3 and 4, with J1/k set to zero), give J2/k≈ −0.7 K for the through-space exchange coupling between the diagonal nitroxides (Figure 9, and Figure S15, Supporting Information).34
The numerical fits of 1 to the tetraradical model (Figure 10) would require three variable parameters: J1/k,J2/k, and w (or Msat). Because such three-parameter fits are typically overparametrized, the fits with two variable parameters for the χT vs. T data are considered. The two-parameter fits for tetraradical 1 in THF, which account only for the through-space exchange coupling (J2/k) as in diradical 2, give J2/k ≈ −2 K and unsatisfactory coefficient of determination (R2 = 0.96, eq. S2, Supporting Information). The quality of two-parameter fits is improved (R2 = 0.98) when the through-bond exchange coupling parameter is optimized (J1/k ≈ −1.5 K), with J2/k set to zero; however, R2 significantly improves, when J2/k is set to a small negative value rather than zero. For the χT vs. T data, the best fits (R2 = 0.998) give J1/k≈ −1.3 K with J2/k set to about −1 K. Analogous fits are obtained for the M/Msat vs. H/T data, with the smaller values of |J1/k| and |J2/k| (Figure 8 and Figure S12, Supporting Information).35 Therefore, it is concluded that the through-bond exchange couplings between the adjacent nitroxides and the through-space exchange couplings between the diagonal nitroxides in the 1,3-alternate calix[4]arene conformation of tetraradical 1 in THF are both antiferromagnetic, with J1/k ≈ J2/k ≈ −1 K. Similar through-bond antiferromagnetic exchange couplings, J1/k ≈ −0.9 K, but weaker through-space antiferromagnetic exchange couplings, J2/k ≈ −0.3 K, are obtained for 5 mM 1 in 2-MeTHF.36
The results of magnetic studies for ~20 mM tetraradical 3 in THF or 2-MeTHF (Figure 11 and Figure S18, and S19, Supporting Information) are qualitatively different, compared to those for 1 in THF or 2-MeTHF. Notably, the χT vs. T plot for 3 shows an upward turn at T < 40 K, consistent with the presence of ferromagnetic exchange coupling, most likely intramolecular. The ferromagnetic exchange coupling is also indicated by the relatively fast saturation behavior for the M vs. H data. The M/Msat vs. H/T plots at T = 1.8–5 K are bracketed by the Brillouin curves corresponding to S = 1 and S = 1/2, i.e., the curvatures of the experimental data are significantly greater, compared to the theoretically predicted paramagnetic behavior for four independent spins S = 1/2. In addition to this ferromagnetic exchange coupling, a weaker antiferromagnetic exchange coupling appears to be present; e.g., for 15 mM 3 in THF, an additional downward turn may be observed in the χT vs. T plot at T ≈ 2–3 K. The strength of antiferromagnetic exchange coupling in 3 is similar to that in diradical 2, and may be of a similar origin, i.e., due to the direct through-space exchange coupling between the diagonal nitroxides. In such a case, the magnetic data for 3 may be modeled by the cluster of four S = ½ spins positioned at the vertices of a square, as for tetraradical 1 (Figure 10).
Figure 11.
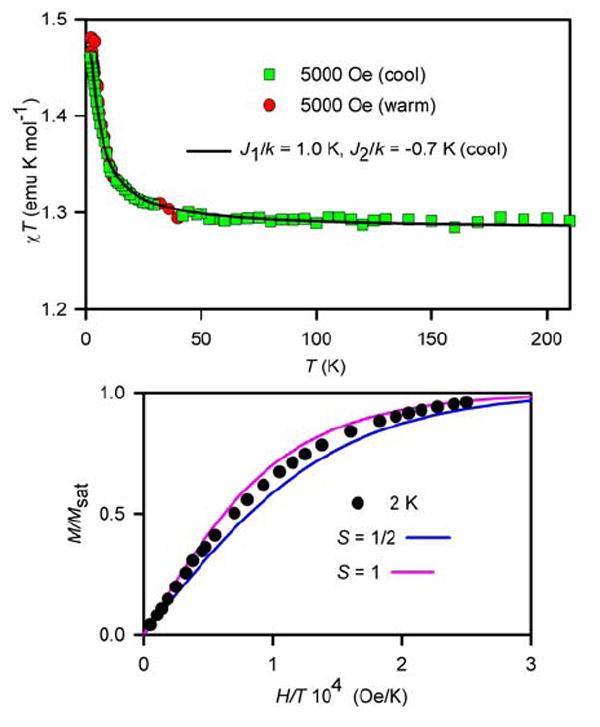
SQUID magnetometry for 20 mM 3 in 2-MeTHF with numerical fit to the tetraradical model (Figure 10, equation 2). For the χT vs. T plot (top), the variable parameters (parameter dependence) for the numerical fit to tetraradical model at 5000 Oe in the cooling mode are as follows: J1/k = 1.0 K (0.98), J2/k = −0.7 K (0.98), w = 0.85 (0.61); R2 = 0.996. For the M/Msat vs. H/T plot at T = 2 K (bottom), theoretical Brillouin curves for paramagnet with S = ½ and S = 1 are shown.
The χT vs. T data for 3 in 2-MeTHF (Figure 11) provide an excellent 3-parameter fit to the tetraradical model (eq. 2), to give J1/k = +1.0 K (ferromagnetic) for the through-bond exchange coupling between the adjacent nitroxides and J2/k = −0.7 K (antiferromagnetic) for the direct through-space coupling between the diagonal nitroxides. An alternative numerical fit with J1/k = +1.3 K is obtained, when the presence of the antiferromagnetic exchange coupling is modeled with a mean-field parameter θ = −0.7 K (Figure S17, Supporting Information). Similar numerical fits are obtained for 3 in THF, though the values of |J2/k| are relatively greater (Figure S18 and S19, Supporting Information).37,38
Magnetic studies of 1 and 2 in the solid state
The χT vs. T plots for solid tetraradical 1 (Figure 12) and diradical 2 (Figure S20, Supporting Information) are flat, except for a downward turn at low temperatures.
Figure 12.
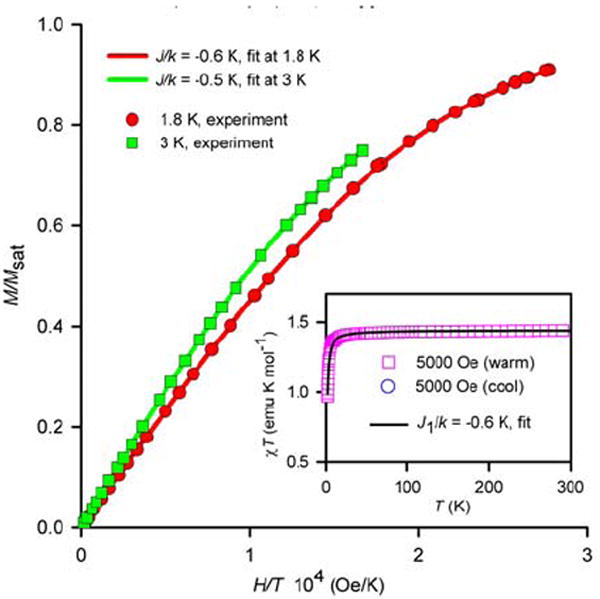
SQUID magnetometry for solid nitroxide tetraradical 1 with numerical fits to the tetraradical model, using J2/k = 0 (Figure 10, equations 1 and 2). The variable parameters (parameter dependence and R2) are as follows: at 1.8 K, J1/k = −0.6 K, Msat = 0.94 μB (0.75, 1.000); at 3 K, J1/k = −0.5 K, Msat = 0.95 μB (0.94, 1.000); at 5000 Oe in the warming mode, J1/k = −0.6 K, w = 0.96 (0.23, 0.993).
In the flat sections of the plots (20–300 K), the values of χT = 1.45 and χT = 0.70 emu K mol-1 are measured for solid 1 and 2, respectively. These values are in excellent agreement with the theoretical, spin-only χT = 1.50 and χT = 0.75 emu K mol-1 for tetraradicals and diradicals, with independent S = ½ radicals. Similarly, quantitative values of χT ≈ 1.3–1.5 and χT≈ 0.8 emu K mol-1 are obtained for 1 and 2 in chloroform at room temperature (295–300 K), respectively, using the 1H NMR-based Evans method.39 Within accuracy of the Evans method, these values are in good agreement with the values of χT for solid 1 and 2.
The downward turns of the χT vs. T plots at low temperature are consistent with overall antiferromagnetic exchange couplings between nitroxide radicals. The presence of anitferromagnetic exchange coupling is also indicated by the relatively slow saturation behavior for the M vs. H data at 1.8 K. In particular, the overall antiferromagnetic exchange coupling in 1 is significantly weaker in the solid state (θ ≈ −0.7 K), compared to that in THF solution (θ ≈ −2.3 K).
For a quantitative fit to the magnetic data for solid 1 and 2, both intramolecular and intermolecular exchange coupling would need to be considered. Such models may be suggested by the analysis of the crystal packing.
Crystal packing of 1 and 2
Crystal packing of both 1 and 2 may be described in terms of layers of calix[4]arene macrocycles in the approximate bc- or (100)-plane (Figure 13, Figures S1–S3, Supporting Information).
Figure 13.
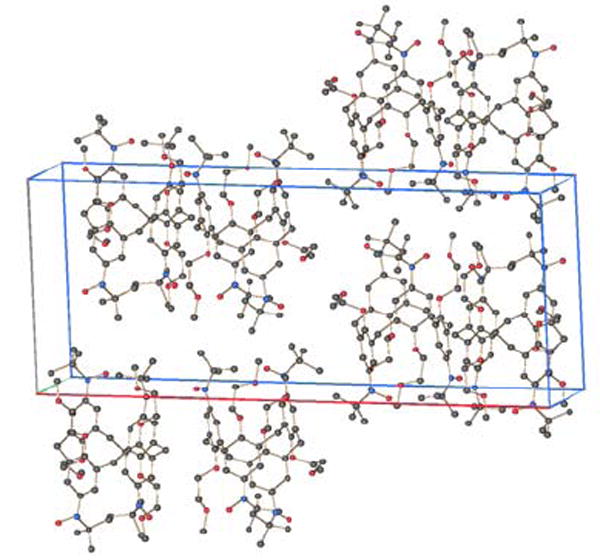
Crystal packing of nitroxide tetraradical 1. Hydrogen atoms are omitted for clarity.
For tetraradical 1, dimers of nitroxides, in which the two N2-O4 moieties form two short sides of parallelogram (N2-O4-N2-O4 torsion of 180°), with intermolecular O4···O4 distance of 4.60 Å, are found. Another intermolecular distance is the O1···N1 distance of 4.75 Å, which is found in a uniform one-dimensional zig-zag chain of nitroxides along the c-axis (N1-O1-N1-O1 torsion of 166 °). In addition, short intermolecular O···C distances (O1···C2 = 3.97 Å and O4···C11 = 3.58 Å) between the nitroxide groups and the corresponding ortho-carbon atoms of the benzene rings are found. For each O···C distance, the N-O bond axis and the 2pπ(C)-orbital axis (centered on carbon atom) are nearly orthogonal, with the N-O bond axis pointing approximately toward the nodal plane of the 2pπ(C)-orbital. As these intermolecular interactions are associated with relatively long distances and may contribute to either ferromagnetic or antiferromagnetic exchange coupling, their overall impact on magnetic data of solid 1 is probably small but not negligible. The χT vs. T and the M/Msat vs. H/T data for solid 1 may still be fit to the tetraradical model (Figure 10, equations 1 and 2) but the antiferromagnetic exchange coupling J1/k ≈ −0.6 K is much smaller compared to that in the analogous fits of the solution data with J2/k set to zero. However, in contrast to the samples of 1 in THF, the numerical fits for solid 1 could not be improved by the additional weak antiferromagnetic exchange couplings, such as J2/k < 0 or θ < 0, reflecting the impact of crystal packing on magnetic data.
For diradical 2, the shortest intermolecular contacts are associated with the rectangular dimers of nitroxides, which are formed between the two crystallographically unique molecules; the N2A···O6B and N2B···O6A distances of 4.96 and 4.98 Å are found, respectively (Figure S3, Supporting Information). Therefore, for one half of the nitroxide radicals, pairwise intermolecular antiferromagnetic exchange coupling in solid 2 is expected. This intermolecular exchange coupling may be described by the “diradical plus two monoradicals” model. In this model, the one half of the nitroxide radicals, forming dimers, corresponds to exchange-coupled “diradicals” and the other half of the nitroxide radicals are treated as independent S = ½ “monoradicals”. A comparable numerical fit for solid 2 is obtained using the diradical model, describing intramolecular exchange coupling only.
For 1 and 2, the magnetic data in the solid state, in conjunction with the analysis of crystals packing, are consistent with the magnetic data in solution. Nevertheless, the magnetic data for 1 and 2 in frozen solutions, devoid of detectable intermolecular exchange coupling, are far more informative.
Conformational dependence of exchange coupling in 1 – 3
The magnetic studies of 1, 2, and 3 in frozen THF (or 2-MeTHF) indicated that the through-bond exchange coupling between the adjacent nitroxides, mediated by the nitroxide-m-phenylene-CH2-m-phenylene-nitroxide coupling pathway, is antiferromagnetic in 1 (J1/k ≈ −1 K) and ferromagnetic in 3 (J1/k ≈ +1 K). In addition, the through-space exchange coupling between the diagonal nitroxides in 1, 2, and 3 is antiferromagnetic (J2/k ≈ −1 K).
For cross-conjugated m-phenylene-based diradicals, exchange coupling changes from ferromagnetic (J > 0) to antiferromagnetic (J < 0) when the radical moieties are twisted out of the plane of the m-phenylene with torsional angles of near 90 °.40-43 For diradicals, in which radical moieties are cross-conjugated through two m-phenylenes, i.e., through 3,3’-biphenylyne, antiferromagnetic exchange couplings are typically found;32b,44,45 however, there is no clear-cut evidence for the change of sign of J, upon severe twisting to the near 90 ° torsional angle along the C1-C1’ bond.9,46 For trimethylene diradicals (and the related tetraradicals) with constrained CCC-angles, Dougherty and coworkers developed the model explaining the preference for high-spin ground states (ferromagnetic exchange coupling).7,8,47-50
The antiferromagnetic and ferromagnetic through-bond exchange couplings in tetraradicals 1 and 3 indicate profound effect of torsions within the exchange pathway comprising of two m-phenylene groups and one methylene group. Although this magnetic behavior is not well understood, the relative orientations of π-systems, especially those of 2pπ-orbitals of the ipso-carbon atoms adjacent to the methylene group, are likely to play an important role. Based upon the experimental EPR spectra and the spin polarization mechanism within the π-system, the two carbon atoms, which correspond to the non-bonding MO nodal positions of the benzylic-like radicals, are expected to possess a substantial negative π-spin density.1,51 This electronic structure may be compared to simple diradicals such as 2,2’-bis(allyl)methane or trimethylene,52 though their detailed analyses concerning correlations between the torsional angles and the exchange coupling are not available.53,54 We propose the following analysis. In the 1,3-alternate calix[4]arene scaffold, the π-systems of the adjacent radicals are pointing away from each other, and in the cone, they are pointing toward each other. The relative orientations of the 2pπ-orbitals at ipso-positions in the 1,3-alternate and the cone calix[4]arene scaffolds are analogous to the approximate (70,70)- and (90,90)-conformations of bis(allyl)methane diradical (or trimethylene diradical), derived by the conrotatory and disrotatory motion from the (0,0)-conformation, respectively (Figure 14). We suggest that the closer balance between the through-space and through-bond interactions between the adjacent radicals is attained in the cone calix[4]arene scaffold, compared to its 1,3-alternate analogue. Therefore, the cone and 1,3-alternate calix[4]arene scaffolds favor through-bond ferromagnetic and antiferromagnetic exchange coupling, respectively.
Figure 14.
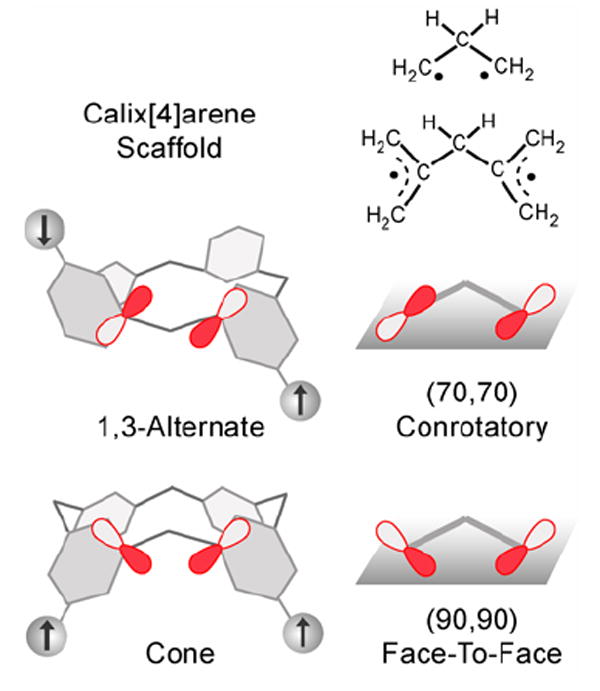
Relative orientations of the 2pπ-orbitals at the ipso-positions in the 1,3-alternate and cone calix[4]arene polyradical scaffolds, and the corresponding trimethylene and 2,2’-bis(allyl)methane diradicals.
Conclusion
Through-bond and through-space exchange coupling in the calix[4]arene scaffolds functionalized on the upper rim with nitroxide radicals were studied. The through-bond exchange coupling between the adjacent nitroxide radicals is controlled by the conformation of the nitroxide-m-phenylene-CH2-m-phenylene-nitroxide coupling pathway. In the 1,3-alternate calix[4]arene scaffold (tetraradical 1), the exchange coupling is antiferromagnetic (J1/k ≈ −1 K) and, in the cone calix[4]arene scaffold (tetraradical 3), the exchange coupling is ferromagnetic (J1/k ≈ +1 K). The through-space exchange coupling between the diagonal nitroxides at the N···N distance of 5–6 Å in the 1,3-alternate and cone calix[4]arene scaffolds (1, 2, and 3) is antiferromagnetic (J2/k < 0), with the matrix-dependent coupling strength (|J2/k| < −1 K).
Highly symmetric (D2d point group) and electron-rich 1,3-alternate calix[4]arene may serve as a scaffold for polyradicals with negligible net magnetic dipole-dipole coupling and, possibly, ionophoric properties. Control of both exchange coupling and magnetic dipole-dipole coupling, as well as their modulation by metal ions, are of importance for electronic relaxation processes, especially for the development of organic paramagnetic contrast agents.6
Experimental Section
Tetrahydroxylamine 5
t-BuLi in pentane (1.70 M, 0.80 mL, 1.31 mmol) was added to a solution of tetrabromocalix[4]arene 4 (0.152 g, 0.156 mmol) in THF (10 mL) at −78 °C. The resultant yellowish-orange solution was stirred at −78 °C for 2 h, and then allowed to attain −25 °C for 15 min. The color of the solution changed to a dark orange. Subsequently, the reaction mixture was cooled to −78 °C, and then a solution of 2-methyl-2-nitrosopropane dimer (65.4 mg, 0.375 mmol) in THF (3.5 mL) was added. The reaction mixture was allowed to attain room temperature overnight. The usual aqueous workup with ether, including drying over MgSO4, was followed by column chromatography (TLC grade silica, 14 – 20% ether in hexanes), to yield tetrahydroxylamine 5 (75.8 mg, 48%) as a white powder. From two other reactions done on 400-mg scale, 0.205 g (49%) and 0.248 g (60%) of tetrahydroxylamine 5 was obtained from 0.402 g and 0.401 g of tetrabromocalix[4]arene 4, respectively. M.p. 232–234 °C (under Ar, dec). 1H NMR (400 MHz, CDCl3): 9.277 (s, 4H, exch D2O), 7.369 (bs, 4H, ArH), 6.677 (bs, 4H, ArH), 3.911 (bs, s, 12H), 3.75 (bs, 4H), 3.540 (s, 12H, OMe), 3.47, 3.36 (bs 2H), bs, 8H), 1.152 (s, 36H, t-Bu). 13C NMR (100 MHz, CDCl3): 152.6, 142.1, 132.5, 131.8, 126.2, 124.7, 124.6, 72.4, 72.2, 59.7, 59.0, 26.1. IR (ZnSe, cm-1): 3225, 3090, 2931, 2875, 1592, 1454, 1386, 1359, 1210, 1125, 1063, 1030, 878. LR/HR FABMS (3-NBA matrix): m/z (ion type, % RA for m/z 500–1300, deviation for the formula) at 1005.6134 ([M + H]+, 100, 3.0 ppm for 12C561H8514N416O12), 1004.6084 ([M]+, 88, 0.2 ppm for 12C561H8414N416O12).
Dihydroxylamine 6
n-BuLi in hexane (2.14 M, 0.16 mL, 0.34 mmol) was added to a solution of tetrabromocalix[4]arene 4 (0.151 g, 0.155 mmol) in THF (10 mL) at −78 °C. The resultant bright orange solution was stirred at −78 °C for 2 h, and then allowed to attain −30 °C for 15 min. Subsequently, a dark orange solution was cooled to −78 °C, and then a solution of 2-methyl-2-nitrosopropane dimer (32.4 mg, 0.186 mmol) in THF (3 mL) was added. The reaction mixture was allowed to attain room temperature overnight. The green reaction mixture was subjected to a usual aqueous workup with ether, including drying over MgSO4, and then evaporated to dryness. Column chromatography (TLC grade silica, 14 – 17% ether in hexanes) gave dihydroxylamine 6 (57.6 mg, 37%) as white powder. M.p. 218–219 °C (under N2, dec). From another reaction on 400-mg scale, 0.183 g (44%) of dihydroxylamine 6 was obtained from 0.406 g of tetrabromocalix[4]arene 4. 1H NMR (400 MHz, CDCl3): 9.124 (s, 2H, exch D2O), 7.36 (bs, 2H), 7.260 (s, under the solvent peak, 4H), 6.79 (bs, 2H), 3.90, 3.87 (bm, m, 12H), 3.81 (m, 4H), 3.644 (s, 6H), 3.530 (s, 6H), 3.33–3.48 (bm, 8H), 1.177 (s, 18H). 13C NMR (125 MHz, CDCl3): 154.4, 152.6, 142.3, 135.5, 134.6, 133.2, 131.9, 114.9, 72.5, 72.4, 72.3, 72.0, 59.9, 59.4, 59.3, 58.9, 34.1, and 26.1. IR (ZnSe, cm-1): 3235, 3070, 2933, 2877, 1596, 1573, 1451, 1361, 1199, 1125, 1059, 1028, 850, 717. LR/HR FABMS (3-NBA matrix): m/z (ion type, % RA for m/z 700–1500, deviation for the formula) at 991.2975 ([M+4]+, 38, −7.0 ppm for 12C481H6414N216O1081Br2), 988.2939 ([M+2]+, 53, −3.3 ppm for 12C481H6414N216O1081Br79Br), 986.2918 ([M]+, 25, 1.0 ppm for 12C481H6414N216O1079Br2), 970.3 ([M−18]+, 100).
Nitroxide tetraradical 1
Freshly prepared silver oxide (0.285 g, 1.23 mmol) was added to a solution of tetrahydroxylamine 5 (0.124 g, 0.0199 mmol) in CHCl3 (6 mL). After stirring at room temperature in darkness for 9 h, the reaction mixture was filtered, and then the red filtrate was evaporated to dryness to obtain the nitroxide tetraradical 1 (0.119 g, 96 %) as a brick-red solid. Similar procedure, except for the increased amount of silver oxide (40 vs. 15 equiv), gave 0.193 g (96%) of 1 from 0.200 g of tetrahydroxylamine 5; this was the primary sample for magnetic and spectroscopic studies. Two other reactions were carried out with tetrahydroxylamine 5 (75.8 mg and 0.205 g) and silver oxide (40 equiv) in dichloromethane; the crudes obtained after filtration and drying, were further recrystallized from methanol, to yield 39.6 mg (52%) and 0.109 g (53%) of 1, respectively. 1H NMR spectra of the recrystallized samples showed a sharp singlet at ~3.6 ppm (1.5H, assigned to residual methanol) and a broad singlet at 7.1 ppm (0.14H). All yields are reported after correcting for the extraneous 1H NMR resonances (solvent of crystallization, stopcock grease, etc.). M.p. 169–171 °C (under Ar, dec). 1H NMR (500 MHz, CDCl3): 4.341 (bs, 12H), 3.842 (bs, 16H), −0.753 (bs, 8H), −5.881 (v. bs, 36H). IR (ZnSe, cm-1): 3078, 2978, 2930, 2878, 1576, 1458, 1347, 1203, 1123, 1050, 883. Evans method (4 measurements, CDCl3/CHCl3, 297–300 K), χT = 1.30–1.52 emu K mol-1 (3.6, 4.1, 4.0, 3.5 unpaired electrons).
Nitroxide diradical 2
Freshly prepared silver oxide (0.530 g, 2.286 mmol) was added to a solution of dihydroxylamine 6 (56.5 mg, 0.057 mmol) in CH2Cl2 (1.5 mL). After stirring at room temperature in darkness for 4 h, the reaction mixture was filtered, and then the red filtrate was evaporated to dryness to obtain a reddish-orange oil. Column purification with deactivated flash silica gel at 0 °C under nitrogen, followed by recrystallization from ether/heptane mixture gave diradical 2 (23.9 mg, 42%) as dark-red needles. From another reaction on 150-mg scale (using 20 equiv of silver oxide), 70.5 mg (47%) of diradical 2 was obtained from 0.150 g of dihydroxylamine 6. Yields are corrected for the residual solvents (ether and heptane) remaining after recrystallization. Magnetic and spectroscopic studies were carried using another sample of 2 (orange-red solid), which was prepared from dihydroxylamine 6 and silver oxide in chloroform. M.p. 151–153 °C (under Ar, dec). 1H NMR (500 MHz, CDCl3): 7.469 (s, 4H), 4.304, 4.084, ~3.9, 3.688 (s, bs, bs, s, 28–32H), −5.132 (v. bs(sh) 22–26H). IR (ZnSe, cm-1): 3077, 2929, 2875, 1574, 1451, 1364, 1195, 1124, 1054, 925, 858. Evans method (2 measurements, CDCl3/CHCl3, 298 and 300 K), χT ≈ 0.80, 0.78 emu K mol-1 (2.2, 2.1 unpaired electrons).
Acknowledgments
This research was supported by the National Science Foundation (CHE-0107241 and CHE-0414936), including the purchase of the Electron Paramagnetic Resonance (EPR) spectrometer (DMR-0216788). Part of this research was performed in facilities renovated with support from NIH (RR16544-01). We thank Drs. Kouichi Shiraishi and Hongxian Han, and Kausik Das, for help with the EPR spectroscopy and preparation of samples for SQUID magnetometry.
Footnotes
Supporting Information Available: general procedures and materials, additional experimental details (synthesis of 4, SQUID magnetometry data, EPR spectra), and X-ray crystallographic files in CIF format. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.(a) Iwamura H, Koga N. Acc Chem Res. 1993;26:346–351. [Google Scholar]; (b) Rajca A. Chem Rev. 1994;94:871–893. [Google Scholar]; (c) Lahti PM, editor. Magnetic Properties of Organic Materials. Marcel Dekker; New York: 1999. pp. 1–713. [Google Scholar]; (d) Itoh K, Kinoshita M, editors. Molecular Magnetism. Gordon and Breach; Kodansha: 2000. pp. 1–337. [Google Scholar]; (e) Rajca A. Chem Eur J. 2002;8:4834–4841. doi: 10.1002/1521-3765(20021104)8:21<4834::AID-CHEM4834>3.0.CO;2-E. [DOI] [PubMed] [Google Scholar]; (f) Rajca A. Adv Phys Org Chem. 2005;40:153–199. [Google Scholar]
- 2.(a) Rajca A, Wongsriratanakul J, Rajca S. Science. 2001;294:1503–1505. doi: 10.1126/science.1065477. [DOI] [PubMed] [Google Scholar]; (b) Rajca S, Rajca A, Wongsriratanakul J, Butler P, Choi S. J Am Chem Soc. 2004;126:6972–6986. doi: 10.1021/ja031548j. [DOI] [PubMed] [Google Scholar]; (c) Rajca A, Wongsriratanakul J, Rajca S. J Am Chem Soc. 2004;126:6608–6626. doi: 10.1021/ja031549b. [DOI] [PubMed] [Google Scholar]; (d) Rajca A, Wongsriratanakul J, Rajca S, Cerny RL. Chem Eur J. 2004;10:3144–3157. doi: 10.1002/chem.200306036. [DOI] [PubMed] [Google Scholar]; (e) Rajca A, Shiraishi K, Vale M, Han H, Rajca S. J Am Chem Soc. 2005;127:9014–9020. doi: 10.1021/ja052002v. [DOI] [PubMed] [Google Scholar]
- 3.Fukuzaki E, Nishide H. J Am Chem Soc. 2006;128:996–1001. doi: 10.1021/ja0569611. [DOI] [PubMed] [Google Scholar]
- 4.(a) Weiss EA, Ahrens MJ, Sinks LE, Gusev AV, Ratner MA, Wasielewski MR. J Am Chem Soc. 2004;126:5577–5584. doi: 10.1021/ja0398215. [DOI] [PubMed] [Google Scholar]; (b) Weiss EA, Wasielewski MR, Ratner MA. J Chem Phys. 2005;123:064504–1–8. doi: 10.1063/1.1995691. [DOI] [PubMed] [Google Scholar]; (c) Weiss EA, Tauber MJ, Kelley RF, Ahrens MJ, Ratner MA, Wasielewski MR. J Am Chem Soc. 2005;127:11842–11850. doi: 10.1021/ja052901j. [DOI] [PubMed] [Google Scholar]; (d) Chernick ET, Mi Q, Kelley RF, Weiss EA, Jones BA, Marks TJ, Ratner MA, Wasielewski MR. J Am Chem Soc. 2006;128:4356–4364. doi: 10.1021/ja0576435. [DOI] [PubMed] [Google Scholar]
- 5.(a) Hustedt EJ, Beth AH. Ann Rev Biophys Biomol Struct. 1999;28:129–153. doi: 10.1146/annurev.biophys.28.1.129. [DOI] [PubMed] [Google Scholar]; (b) Eaton SS, Eaton GR. Biol Magn Reson. 2000;19:1–27. [Google Scholar]; (c) Altenbach C, Oh K-J, Trabanino R, Hideg K, Hubbell W. Biochemistry. 2001;40:15471–15482. doi: 10.1021/bi011544w. [DOI] [PubMed] [Google Scholar]; (d) Hanson P, Millhauser G, Formaggio F, Crisma M, Toniolo C. J Am Chem Soc. 1996;118:7618–7625. [Google Scholar]
- 6.Spagnol G, Shiraishi K, Rajca S, Rajca A. Chem Comm. 2005:5047–5049. doi: 10.1039/b508094k. [DOI] [PubMed] [Google Scholar]
- 7.Dougherty DA. Acc Chem Res. 1991;24:88–94. [Google Scholar]
- 8.(a) Jacobs SJ, Shultz DA, Jain R, Novak J, Dougherty DA. J Am Chem Soc. 1993;115:1744–1753. [Google Scholar]; (b) Jacobs SJ, Dougherty DA. Angew Chem Int Ed. 1994;33:1104–1106. [Google Scholar]
- 9.Borden WT, Iwamura H, Berson JA. Acc Chem Res. 1994;27:109–116. [Google Scholar]
- 10.(a) Michon P, Rassat A. J Am Chem Soc. 1975;97:696–700. [Google Scholar]; (b) Metzner EK, Libertini LJ, Calvin M. J Am Chem Soc. 1977;99:4500–4502. [Google Scholar]; (c) Frank NL, Clérac R, Sutter J-P, Daro N, Kahn O, Coulon C, Green MT, Golhen S, Ouahab L. J Am Chem Soc. 2000;122:2053–2061. [Google Scholar]
- 11.Shultz DA, Fico RM, Jr, Bodnar SH, Kumar K, Vostrikova KE, Kampf JW, Boyle PD. J Am Chem Soc. 2003;125:11761–11771. doi: 10.1021/ja0367849. [DOI] [PubMed] [Google Scholar]
- 12.For an effect of heteroatoms on through-bond exchange coupling: West AP, Jr, Silvermann SK, Dougherty DA. J Am Chem Soc. 1997;119:1452–1463.Matsuda K, Yamagata T, Seta T, Iwamura H, Hori K. J Am Chem Soc. 1997;119:8058–8064.Berson JA. Acc Chem Res. 1997;30:238–244.Shultz DA, Bodnar SH, Lee H, Kampf JW, Incarvito CD, Rheingold AL. J Am Chem Soc. 2002;124:10054–10061. doi: 10.1021/ja020154+.
- 13.Rajca A, Pink M, Rojsajjakul T, Lu K, Wang H, Rajca S. J Am Chem Soc. 2003;125:8534–8538. doi: 10.1021/ja034115p. (b) Because of technical difficulties in measurements of magnetic susceptibility data for 3 in solution at low temperatures, wide range of values for the exchange coupling were obtained (30 K > |J/k| ≫ 1.8 mK).
- 14.Nitroxides and nitronyl nitroxides on the upper and lower rim of calix[4]arene: Ulrich G, Turek P, Ziessel R. Tetrahedron Lett. 1996;37:8755–8758.Wang Q, Li Y, Wu G. Chem Commun. 2002:1268–1269. doi: 10.1039/b201010k.Kröck L, Shivanyuk A, Goodin DB, Rebek J., Jr Chem Commun. 2004:272–273. doi: 10.1039/b311351e.
- 15.Verboom W, Datta S, Reinhoudt DN. J Org Chem. 1992;57:5394–5398. [Google Scholar]
- 16.Larsen M, Jørgensen M. J Org Chem. 1996;61:6651–6655. doi: 10.1021/jo9609440. [DOI] [PubMed] [Google Scholar]
- 17.C(CH2) and C(ipso) refer to the CC-bonded carbon atoms of the methylene group and benzene ring of the calix[4]arene scaffold. An example of the C(ipso)-C(CH2)-C(ipso) angle is C5-C7-C8 angle of 112.6° in 1.
- 18.La Mar GN, Horrocks WDeW Jr, Holm RH, editors. NMR of Paramagnetic Molecules. Academic; New York: 1973. [Google Scholar]
- 19.Sharp RR. Nucl Magn Reson. 2005;34:553–596. [Google Scholar]
- 20.Two types of protons (AB or AX spin system) are expected for the methylene groups of the macrocycle in diradical 2. An AB spin system is observed for the corresponding protons in dihydroxylamine 6 at T > 306 K.
- 21.(a) Rassat A, Ray P. Tetrahedron. 1973;29:2845–2848. [Google Scholar]; (b) Rajca A, Lu K, Rajca S, Ross CR., II Chem Commun. 1999:1249–1250. [Google Scholar]
- 22.Forrester AR, Hepburn SP, McConnachie G. J Chem Soc Perkin Trans I. 1974:2213–2219. [Google Scholar]
- 23.Hyperfine splitting of aH = +0.019 mT for the methoxy hydrogens in 4-methoxyphenyl-tert-butylnitroxide has been reported (ref 22).
- 24.The numerical fits with three components, tetraradical, triradical, and diradical, indicate 98+ % content of tetraradical. The three-component fit and the one-component fit have coincident values of hyperfine splittings for tetraradical and nearly identical sums of squared residuals (Figure S4, Supporting Information).
- 25.The agreement for the 1H hyperfine, which is not resolved in EPR spectrum of 1, is less satisfactory: aH = 0.019 mT vs. 0.024 mT in 1 and in 3,5-dimethyl-4-methoxyphenyl-tert-butylnitroxide, respectively.
- 26.Wertz JE, Bolton JR. Electron Spin Resonance. Chapter 10. Chapman and Hall; New York: 1986. pp. 223–257. [Google Scholar]
- 27.The small zero-field splitting in tetraradical 1 is in contrast to the spectral width of about 20 mT in tetraradical 3 in the cone conformation in solution (ref 13).
- 28.Polimeno A, Zerbetto M, Franco L, Maggini M, Corvaja C. J Am Chem Soc. 2006;128:4734–4741. doi: 10.1021/ja057414i. [DOI] [PubMed] [Google Scholar]
- 29.Griffith OH, Cornell DW, McConnell HM. J Chem Phys. 1965;43:2909–2910. (b) In particular, Azz = 3.2 mT was measured in di-tert-butylnitroxide radical. As the solution-phase 14N hyperfine splittings for aryl-alkyl nitroxide radicals, compared to the more localized alkyl-alkyl nitroxide radicals, are lowered by a typical factor of 0.8 – 0.9, the value of |Azz| ≈ 2.6 mT measured for aryl-alkyl nitroxide diradical 2 is reasonable.
- 30.(a) The following equation applies to distance, r (in Å), between two point-dipoles: r = (55600/|(2D/gμB)|)1/3, where |2D/gμB| and r are expressed in Gauss and Å, respectively. (b) For localized nitroxide diradical, in which the intramolecular distances between the midpoints of the N-O bonds were approximately 6.2 Å, |2D/gμB| ≈ 25 mT was measured: Rohde O, Van SP, Kester WR, Griffith OH. J Am Chem Soc. 1974;96:5311–5318.
- 31.Eaton SS, More KM, Sawant BM, Eaton GR. J Am Chem Soc. 1983;105:6560–6567. [Google Scholar]
- 32.(a) The presence of parallel exchange coupling pathways in diradical 2 may partially offset the decrease of the through-bond exchange coupling in 2, compared to tetraradical 1. Rajca A, Rajca S, Wongsriratanakul J. Chem Commun. 2000:1021–1022.
- 33.Belorizky E, Fries PH. J Chim Phys (Paris) 1993;90:1077–1100. [Google Scholar]
- 34.The singlet ground state for diradical 2 with J2/k = −0.7 K (the singlet-triplet gap of about 1 – 2 K) is consistent with the observation of thermally populated triplet state at 140 K in the EPR spectra of 2, as well as with the lower bound of exchange coupling, |J/gμB| ≫ |aN|, determined by the EPR spectroscopy.
- 35.Another model, which may be viewed as corresponding to a structure of tetraradical 1 with two distinct conformations of the diagonal pairs of nitroxides, was considered. One pair of the diagonal nitroxides was treated as a diradical with exchange coupling J2 (Figure 10) and the other pair was treated as two independent spins S = ½ (eq. S6a, Supporting Information). For two-parameter numerical fits of the χT vs. T data at 5000 Oe in the warming mode for 5 mM 1 (identical sample to that in Figure 8), the variable parameters (parameter dependence and R2) are as follows: J2/k = −5.2 K, w = 1.09 (0.38, 0.993). For analogous three-parameter fits, in which exchange couplings for both pairs of the diagonal nitroxides are optimized, similar results are obtained, i.e., one relatively large and one several times smaller value of |J/k| are found (eq. S4a with J1 ≠ J2, (Supporting Information). For such distinct conformations of the diagonal pairs of nitroxides, the structure of 1 would be significantly distorted from the D2d point group. However, the EPR spectra for 5 mM 1 in THF (identical sample to that in Figure 8, after magnetic measurements) show a single peak with the peak-to-peak width of 0.8 mT (8 G); thus, symmetry lowering is not detectable by EPR spectroscopy.
- 36.For 5 mM tetraradical 1 in 2-MeTHF, three-parameter fit has still acceptable values of parameter dependence of significantly less than one, e.g., values of parameter dependence are 0.87, 0.82, and 0.53 for J1/k, J2/k, and w, respectively (R2 = 0.998).
- 37.The M/Msat vs. H/T data for 3 could not be fit to the tetraradical model with ferromagnetic J1/k > 0, due to overparametrization.
- 38.The values of |J1/k| for through-bond ferromagnetic exchange coupling between the adjacent nitroxides in tetraradical 3 may be somewhat underestimated by the present model, due to the possible contribution from antiferromagnetic exchange coupling between the adjacent nitroxides. Such through-space contribution is possible, as the adjacent nitroxides are relatively close in space in 3 with cone conformation. We thank the reviewer for pointing out the possibility of significant antiferromagnetic through-space interactions between the adjacent nitroxides in the cone conformation.
- 39.(a) Evans DF. J Chem Soc. 1959:2003–2005. [Google Scholar]; (b) Live DH, Chan SI. Anal Chem. 1970;42:791–792. [Google Scholar]
- 40.Dvolaitzky M, Chiarelli R, Rassat A. Angew Chem Int Ed Engl. 1992;31:180–181. [Google Scholar]
- 41.Fang S, Lee M-S, Hrovat DA, Borden WA. J Am Chem Soc. 1995;117:6727–6731. [Google Scholar]
- 42.Rajca A, Rajca S. J Chem Soc Perkin Trans 2. 1998:1077–1082. [Google Scholar]
- 43.A “Karplus-Conroy-type” relationship for exchange coupling in trimethylenemethane-based bis(semiquinone) diradicals was proposed: ref 11.
- 44.Rajca A, Rajca S. J Am Chem Soc. 1996;118:8121–8126. [Google Scholar]
- 45.Sakane A, Kumada H, Karasawa S, Koga N, Iwamura H. Inorg Chem. 2000;39:2891–2896. doi: 10.1021/ic991205f. [DOI] [PubMed] [Google Scholar]
- 46.Rajca A, Utamapanya S, Smithhisler DJ. J Org Chem. 1993;5:5650–5652. [Google Scholar]
- 47.Goldberg AH, Dougherty DA. J Am Chem Soc. 1983;105:284–290. [Google Scholar]
- 48.(a) Hoffmann R. Acc Chem Res. 1970;4:1–6. [Google Scholar]; (b) Hay PJ, Thibeault JC, Hoffmann R. J Am Chem Soc. 1975;97:4884–4899. [Google Scholar]
- 49.(a) Buchwalter SL, Closs GL. J Am Chem Soc. 1975;97:3857–3858. [Google Scholar]; (b) Buchwalter SL, Closs GL. J Am Chem Soc. 1979;101:4688–4694. [Google Scholar]
- 50.Sherrill CD, Seidl ET, Schaefer HF., III J Phys Chem. 1992;96:3712–3716. [Google Scholar]
- 51.Hyperfine splitting of aH = 0.09 mT and aH = 0.18 mT for the meta and ortho hydrogens in 4-methoxyphenyl-tert-butylnitroxide in carbon tetrachloride has been reported (ref 22). As the positive sign of aH for the meta hydrogen was determined by 1H NMR spectroscopy, this implies the presence of negative π-spin density at the meta carbon.
- 52.We thank the reviewer for pointing out that bis(allyl)methane diradical would be a better model, compared to trimethylene diradical.
- 53.2,2’-Bis(allyl)methane diradical was apparently generated as an intermediate upon thermolysis of 1,3-dimethylenecyclopentane: Gajewski JJ, Salazar JDC. J Am Chem Soc. 1981;103:4145–4154.Gajewski JJ, Salazar JDC. J Am Chem Soc. 1981;103:4145–4154.
- 54.Calculations on trimethylene diradical: Yamaguchi Y, Osamura Y, Schaefer HF., III J Am Chem Soc. 1983;105:7506–7511.Skancke A, Hrovat DA, Borden WT. J Am Chem Soc. 1998;120:7079–7084.


