Multiscale modeling of nucleic acids: insights into DNA flexibility

Abstract

The elastic rod theory is used together with all-atom normal mode analysis in implicit solvent to characterize the mechanical flexibility of duplex DNA. The bending, twisting, stretching rigidities extracted from all-atom simulations (on linear duplexes from 60 to 150 base pairs in length and from 94 base-pair minicircles) are in reasonable agreement with experimental results. We focus on salt concentration and sequence effects on the overall flexibility. Bending persistence lengths are about 20% higher than most experimental estimates, but the transition from low-salt to high-salt behavior is reproduced well, as is the dependence of the stretching modulus on salt (which is opposite to that of bending). CTG and CGG trinucleotide repeats, responsible for several degenerative disorders, are found to be more flexible than random DNA, in agreement with several recent studies, whereas poly(dA).poly(dT) is the stiffest sequence we have encountered. The results suggest that current all-atom potentials, which were parameterized on small molecules and short oligonucleotides, also provide a useful description of duplex DNA at much longer length scales.

1 Introduction

Advances in biomolecular simulations have allowed the studies of larger and more interesting molecules while conserving an all-atom representation of the system. The implicit treatment of solvation effects -avoiding the inclusion of thousands of water molecules even for a modest-size biomolecule - has played an important role in this development and often provides an accurate treatment of the solvation effects.^1–3 In recent years the analytic generalized Born (GB) method has become increasingly popular over the more classical Poisson-Boltzmann approach due to its computational efficiency. Additionally, second derivatives of the solvation energy are easier to obtain for GB than for the Poisson-Boltzmann theory.⁴ Implicit models also have the advantage of allowing faster convergence in molecular dynamics simulations, hence, reducing the sampling time required; making them more affordable than explicit solvent simulations.⁵

In GB theory the electrostatic part of the solvation energy is given by:

$$\mathrm{\Delta }{G}_{el}\approx \mathrm{\Delta }GB=\frac{1}{2}\sum _{ij}\frac{q_i{q}_j}{f_{ij}^{GB}(r_{ij},R_i,R_j)}(1-\frac{e^{-\kappa f_{ij}^{GB}}}{{\epsilon }_w})$$ (1)

where r_{i j} is the distance between atom i and atom j, R_i and R_j are the effective Born radii of i and j, respectively. $f_{ij}^{GB}$ is usually defined as

$$f_{ij}^{GB}={(r_{ij}^2+R_i{R}_j\mathit{Exp}[-\frac{r_{ij}^2}{4R_i{R}_j}])}^{\frac{1}{2}}$$ (2)

although other alternatives have been investigated.^6–8 Finally, ε_w is a dielectric constant (≈ 80 in water at 300K) and κ is the Debye-Huckel screening parameter used to reproduce electrostatic screening of salt. More details about the generalized Born model can be found elsewhere.^{5, 9} Whereas generalized Born theory has been widely adopted for molecular dynamics simulations it has only recently been extended to normal mode analysis by Brown et. al.⁴ Normal mode analysis provides several advantages over classical molecular dynamics even though it approximates the global potential by a harmonic function.¹⁰ First, it provides a clearer representation of the collective motions of biomolecules through a few of the lowest energy vibrational modes; second, it makes the evaluation of entropy contributions and other thermodynamic properties straightforward, and, finally it is more affordable when long timescales (sampling times) are required. For example, in the case of a 60-bp duplex of DNA the relaxation times for the lowest energy modes are close to 20 ns with a viscosity of about 0.6 cp, and should presumably become larger for longer duplexes. The recent implementation of analytical second derivatives of the Born energy in the molecular mechanics program package Nucleic Acid Builder (NAB)¹¹ provides a new alternative to molecular dynamics in implicit solvent and was used to produce a picture of the vibrational motions for small nucleic acids.⁴ The same study can be extended to larger systems and may also be used to extract important information about the overall behavior of nucleic acids. These simulations have the advantages of allowing a sequence-dependent treatment as well as the study of salt concentration changes via a screening factor.

Here we examine the mechanical flexibility of DNA using comparisons to the elastic rod models for both linear and circular forms.^12–15 Such a technique not only allows the benchmark of the GB method itself, but also provides information about the intrinsic stiffness of a given DNA sequence. DNA binding to nucleosomes is probably related to flexibility, and degenerative disorders such as fragile x syndrome, myotonic dystrophy, and Huntington disease are believed to be the results of an increase in flexibility of some given nucleotide repeats.^16–18 There is, thus, considerable interest in fundamental, all atom-based approaches to estimating mechanical properties of DNA.

It is common practice, in both experimental and theoretical studies of nucleic acids, to compare results to a model where DNA is a homogeneous elastic rod, with bending, torsional and stretching rigidities as adjustable parameters. This analogy has been used in numerous studies to describe supercoiling of DNA^{19, 20} as well as DNA cyclization²¹. While such a representation can have obvious limitations for small sequences, it provides a useful picture for longer segments of DNA, focussing attention on general elastic properties, as opposed to a detailed analysis of the helical parameters of a given sequence. Since vibrational amplitudes are inversely proportional to frequencies, many of the long-range dynamical features of DNA are captured by its lowest energy vibrational modes. One can extract the rigidity constants governing the elasticity of the corresponding sequence by comparing the modes obtained from all-atom simulations to those coming from a continuum (elastic) model, where the characteristics of the rod (radius, length, mass …), are those of the optimized structure in the all-atom calculations. Such an approach was pioneered by Matsumoto and Gô, ¹⁵ who used a distance-dependent dielectric model with an all-atom force field and sequences as long as 36bp. The results were encouraging, but the rigidities reported were much higher than experimental and subsequent theoretical estimates. More recent extensions of this idea have relied on a knowledge-based force fields derived from the observed fluctuations at a local level in DNA duplexes.^12–14 Here, we extend these ideas to all-atom simulations using modern solvent models, including the effects of added salt, and to much longer oligonucleotides.

2 Methods

2.1 All-atom simulations

All simulations were carried out with the molecular mechanics program package NAB (nucleic acid builder) using the Cornell et al. (parm94) force field.²² We used the pairwise approach of Hawkins et a1^{23, 24} for the generalized Born model. The original model for salt effects in GB scaled the Debye-Huckel screening factor κ by a factor of 0.73, primarily to compensate for the lack of ion exclusion radius concept in the GB model. This could be important for short-range interactions but is less appropriate for long-range interactions of the type we are studying here where the asymptotic behavior of salt screening is more important. We thus did not scale κ for this study. The structures were minimized using a combination of conjugate gradients and Newton-Raphson minimization techniques to obtain an RMS gradient below 1 ×10⁻⁸ kcal/mol-Å. This level of convergence is necessary to avoid contamination from translational and rotational modes into true internal modes whose frequencies may be as low as 0.1 cm⁻¹. The xmin minimizer from the biomolecular simulation program package AMBER²⁵ was used to perform powerful but less costly Limited-memory Broyden-Fletcher-Goldfarb-Shanno (LBFGS) Truncated Newton Conjugate (TNC) minimizations. The diagonalization of the Hessian matrix was done using the ARPACK²⁶ routines in combination with a Cholesky decomposition and inversion of the Hessian matrix -therefore providing a better separation of the eigenvalues- to enhance convergence. Using the ARPACK routines reduces the cost of the diagonalization from a few days to a few minutes for a 200 base pair DNA fragment. This technique is most appropriate here since only a few normal modes are necessary (fewer than 200). Another advantage of using the ARPACK package is the ease and efficiency of distributing the calculation on several processors.

2.2 Linear DNA

This section is merely an overview of the elastic rod model that has been reviewed in several places.^{12, 15} The mechanical constants for a linear homogeneous rod are as follow:

$$\begin{array}{ccc}\mathit{Bending}\mathit{Rigidity}& \mathit{Stretching}\mathit{Rigidity}& \mathit{Twisting}\mathit{Rigidity}\\ A=\frac{M{(2\pi {\nu }_n)}^2}{L{P}_n^4}& C=\frac{I_M{(2L{\nu }_n)}^2}{n^2}& Y=\frac{ML{(2{\nu }_n)}^2}{n^2}\end{array}$$ (3)

where M is the total mass of the rod (molecule), I_M is the moment of inertia per unit length, L is the length of the rod (or helical axis in the present case), ν_n is the vibrational frequency associated to mode number n. The polynomial roots P_n satisfy the condition LP_n = 4.6941, 7.8548, 10.9955, 14.1372, 17.2788 (n=1,..5) for the differential equation defining the bending modes of an homogeneous rod.²⁷ Additionally, a, the (bending) persistence length, can be defined as

$$a=\frac{A}{K_{b}T}$$

In brief, we fit the all-atom vibrational frequencies to their analytical counterparts in order to evaluate the corresponding rigidities which are treated as adjustable parameters. Figs. 1 to 3 show all-atom normal modes that clearly exhibit bending, stretching and twisting behavior. The bending modes come in nearly-degenerate pairs in the all-atom calculation, corresponding to bending on the two directions perpendicular to the helix axis. The closer the degeneracy the less mixing there is with other internal modes. As an example, only the first three pairs of bending modes are considered in the 60bp case because for n > 4, there is more than 2–3% difference between the two frequencies. In the case of the stretching and twisting vibrational frequencies, discarding the contaminated modes is not as straightforward and one has to pay more attention to the eigenvectors. As the linear fragments get longer more modes can be included; roughly speaking, an additional mode can be included for each additional 30bps starting with 3 modes in the case of bending and stretching for 60bps (2 for twisting) to 6 modes for 150 bps (5 for twisting). The interactive essential dynamics plugin (IED),²⁸ an extension of the visualization package VMD, was used to identify the character of each normal mode.

Figure 1.

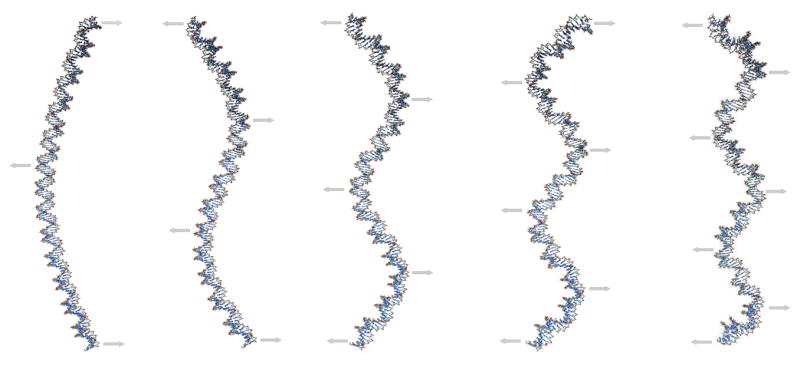
Low-frequency bending modes of a 150-bp linear segment of DNA. The arrows define the main motions associated with the corresponding vibration. There are nearly degenerate modes corresponding to each of these, but with displacements perpendicular to the plane of figure.

Figure 3.

Low-frequency twisting modes of a 150-bp linear segment of DNA. The arrows define the main motions associated with the corresponding vibration.

2.3 Circular DNA

As in the previous section, we present here a summary of the vibrational modes of circular elastic rod; details can be found elsewhere.^{13, 14, 29, 30} In the case of circular DNA there are three different types of motions: in-plane bending, out-of-plane bending, and torsion. The analytical solutions corresponding to these motions for a relaxed minicircle made from of a naturally straight elastic rod are as follow:

$${\omega }_n^{IP}={\left(\frac{n^2{(n^2-1)}^2}{R^2({(n^2-1)}^2+R^2(n^2+1))}\right)}^{1/2}$$ (4)

$${\omega }_n^{OP}={\left(\frac{n^2(\omega (n^2+R^2+2)+2(n^2-1)}{4R^2(n^2+R^2)}\pm \frac{n^2\sqrt{{(\omega (n^2+R^2+2)+2(n^2-1))}^2-8\omega (n^2-1)(n^2+R^2)}}{4R^2(n^2+R^2)}\right)}^{1/2}$$ (5)

where R is the radius of the circle, ω = C/A, and the frequencies are measured in units of (16A/πρr⁶)^1/2. When the circle is not torsionally relaxed these roots are no longer valid but one can add the excess twist and solve the dispersion equation directly.¹² In the present example the relaxed 94-bp minicircle will correspond to a linking number Lk=8 while for the overtwisted representation Lk=9. [In solution, the average twist for DNA is about 34.5° corresponding to 10.4 bp per helix turn; therefore, a relaxed 94-bp minicircle would have a linking number Lk=9. However, the force field used here²² is known to underestimate DNA twist by about 4°; this translates to an overall twist of roughly 30.5° and about 12bp per helix turn. Thus, the in silico linking number for the relaxed 94-bp minicircle is close to Lk=8; meaning that for Lk=9 the circle is overtwisted by about one turn of helix.]

There are two types of bending in this model, corresponding to deformations in and out of the plane of the minicircle. The in-plane bending motions come in pairs, in the two directions perpendicular to the axis of the circle. Similarly, the out-of-plane bending is also two-fold and approximately degenerate in the GB simulations; the corresponding motions are shown in Fig. 4. The twisting motions are shown in Fig. 5; the motion corresponding to n=0 is a free rotation around the torus with no flexural deformations, meaning that there is no deformation of the circle (the radius of the helix is conserved throughout the motion); this mode is discarded in the fitting process even though it appears in the GB simulations.

Figure 4.

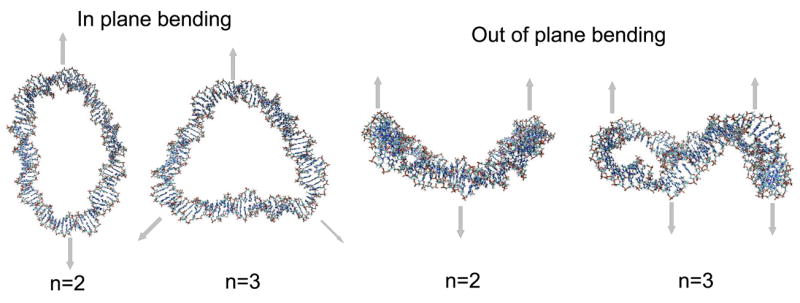
Low-frequency - in and out of plane bending - modes of circular DNA. The arrows define the main motions associated with the corresponding vibration. Bending motions corresponding to n=0 and n=1 do not exist in the analytical model,²⁹, ³⁰ so the first allowed bending comes for n=2.

Figure 5.

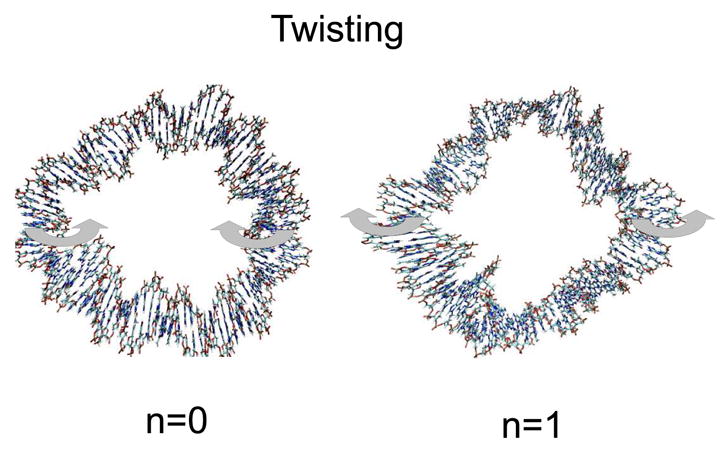
Low-frequency - torsional - modes of circular DNA. The arrows define the main motions associated with the corresponding vibration.

3 Results

3.1 Salt concentration dependence for linear DNA

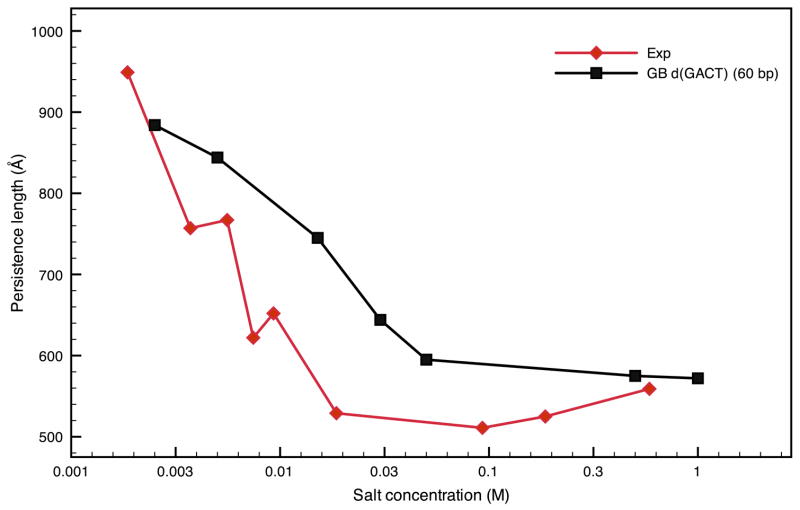
The method described in this work for extracting rigidities of DNA fragments has been primarily used for 60 bp-sequences, because such sequences offer an acceptable compromise between computational cost (especially for optimizing the structures) and being long enough to promote long-range bending motions. Longer sequences were also investigated in order to assess the dependence on sequence length. Here, we examine the sequence d(GTGACTGACTGACTG)_n, paired with its Watson-Crick complementary sequence in a B-form duplex. This sequence is referred to by its main nucleotide repeat GACT_n for the sake of succinctness, and has been the subject of previous computational studies.^{4, 31, 32} It appears to be a good choice to describe the behavior of DNA in general since it will be shown later to be of average rigidity. The salt dependence of the persistence lengths as well as the stretching rigidities are compared to experimental estimates^{33, 34} in Figs. 6 and 7 and in Table 1. The overall salt dependence of the persistence length (Fig. 6) is well reproduced by the GB results, although the transition from low-salt to high-salt behavior occurs at a higher concentration than is suggested by experiment, and the computed bending rigidities are somewhat too large. Both of these may be a result of the very simple dependence on salt given in Eq. 1, and more elaborate models have been proposed,^{35, 36} and will be examined in future studies.

Figure 6.

Comparison of the persistence lengths from experiment³³ and extracted from the elastic rod model for the d(GACT)₄ sequence as a function of salt concentration at 300K.

Figure 7.

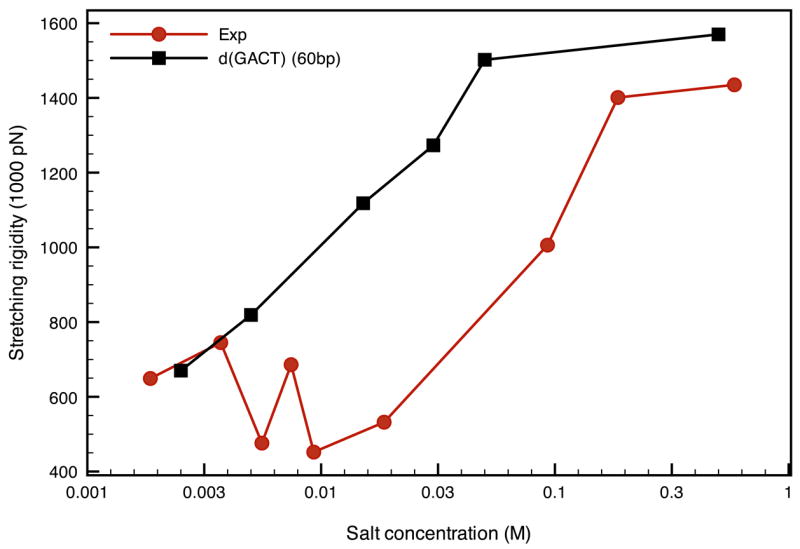
Comparison of the stretching moduli from experiment³³ and extracted from the elastic rod model for the d(GACT)₄ sequence as a function of salt concentration at 300K.

Table 1.

Lowest bending (B), stretching (S) and twisting (T) frequencies in cm⁻¹ for the sequence GACT_n, n = 4,6,8,10 with a salt concentration of 0.05M and T=300K.

Sequences	GACT4	GACT6	GACT8	GACT10
B1	0.114–0.116 (0.100)	0.053-0.053 (0.047)	0.030-0.030 (0.027)	0.019-0.019 (0.017)
B2	0.294–0.295 (0.275)	0.140–0.142 (0.130)	0.081-0.081(0.075)	0.052-0.052 (0.048)
B3	0.522–0.532 (0.539)	0.263–0.264 (0.254)	0.153–0.156 (0.147)	0.099–0.100 (0.094)
B4	—	0.408–0.413 (0.420)	0.246–0.247 (0.243)	0.159–0.163 (0.156)
B5	—	—	0.353–0.360 (0.363)	0.233–0.234 (0.233)
B6	—	—	—	0.317–0.323 (0.325)
S1	0.664 (0.619)	0.439 (0.406)	0.324 (0.307)	0.263 (0.248)
S2	1.289 (1.237)	0.852 (0.812)	0.646 (0.614)	0.526 (0.496)
S3	1.807 (1.856)	1.242 (1.218)	0.955 (0.921)	0.769 (0.744)
S4	—	1.577 (1.623)	1.232 (1.228)	1.010 (0.992)
S5	—	—	1.496 (1.535)	1.242 (1.240)
S6	—	—	—	1.446 (1.488)
T1	0.443 (0.413)	0.302 (0.276)	0.228 (0.206)	0.183 (0.164)
T2	0.811 (0.826)	0.589 (0.553)	0.442 (0.412)	0.358 (0.328)
T3	—	0.796 (0.829)	0.636(0.618)	0.522 (0.491)
T4	—	—	0.789 (0.824)	0.660 (0.655)
T5	—	—	—	0.781 (0.819)

The results are similar for stretching (Fig. 7), where the general trend is again well reproduced by the GB simulations. Note the opposite salt-dependence of the stretching and bending moduli: the bending persistence length increases with salt concentration whereas the stretching moduli decreases. This is not consistent with simple elasticity theory,³³ where both the bending and the twisting moduli are proportional to the Young’s modulus. Nevertheless, this property of simple elasticity theory clashes with both our results and conclusions from single molecule stretching studies. This could be one of the limitations of comparing DNA to an isotropic elastic rod where it is clear that effects other than purely macroscopic mechanisms are involved in the behavior of the persistence length and stretching rigidity. A possible explanation was that the decrease in the stretching modulus could be due to local melting of A.T rich regions,³³ but in our study this phenomenon occurs without any presence of melting.

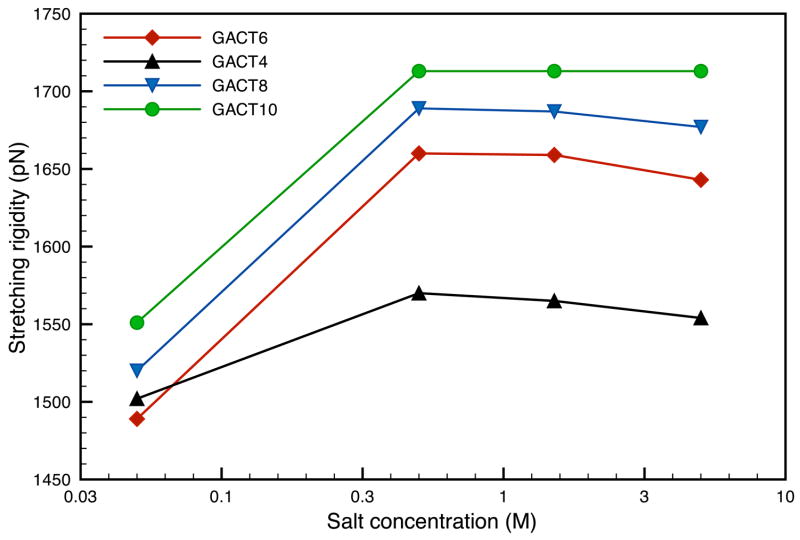
We also looked at longer sequences with up to 150 base pairs; the corresponding results are shown in Figs 8–10. The persistence length depends on the sequence length, and saturates at about 120bp; a possible explanation is the fact that for smaller sequences (less than 90bp), the calculated bending frequencies do not match the analytical frequencies as well as they do for larger sequences. This could mean that the elastic rod model is a more appropriate approximation for sequences longer than 100bp. A similar pattern was observed with comparable calculations by Matsumoto and Go, ¹⁵ though the persistence lengths reported there were much larger. This trend disappears for fragments longer than 100bp and the persistence lengths for the GACT sequence converge in the vicinity of 700 Å; a somewhat larger value than the 500–550 Å widely reported for random DNA. A similar behavior is observed with the stretching moduli (Figure 9) but to a lesser extent and the stretching rigidities quickly converge to a value of about 1700 pN, a value close to the 1500pN usually reported in the literature. In this case the stretching rigidities are close in value throughout the range of concentration investigated here.

Figure 8.

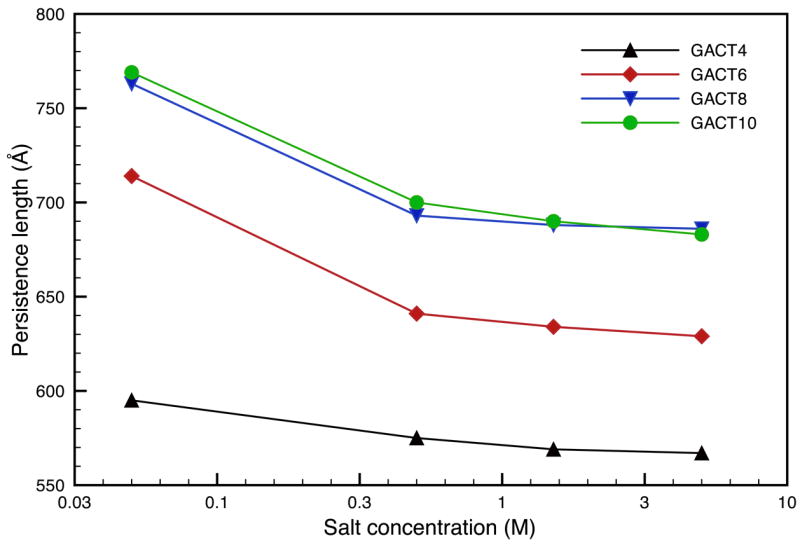
Comparison of the persistence lengths for various GACT repeat sequences as a function of salt concentration at 300K..

Figure 10.

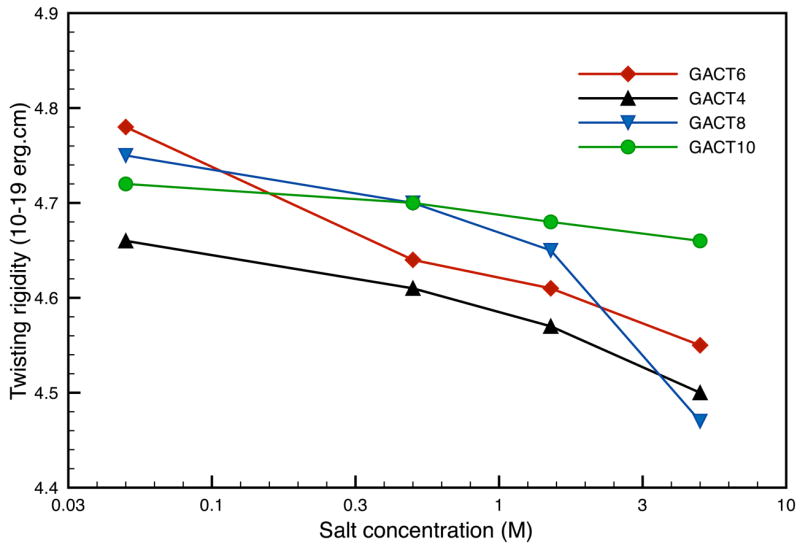
Comparison of the twisting moduli for various GACT repeat sequences as a function of salt concentration at 300K.

Figure 9.

Comparison of the stretching moduli for various GACT repeat sequences as a function of salt concentration at 300K.

The twisting motions were harder to identify and the quality of the fits to the elastic model is lower than for the bending and stretching modes. However, the average twisting modulus for the GACT sequence, 4.7 10⁻¹⁹erg.cm (Fig. 10), agrees well with the latest experimental estimates of 4.5 10⁻¹⁹erg.cm.^{37, 38} Note that the twisting rigidities depend less on sequence length than was the case for other mechanical constants. As noted above, the frequency fits get better as the sequence length increases, hence, indicating that DNA behaves more like an elastic rod for longer sequences. The macroscopic interactions take over the local phenomena more present in smaller sequences.

3.2 Sequence dependence of mechanical properties for linear DNA

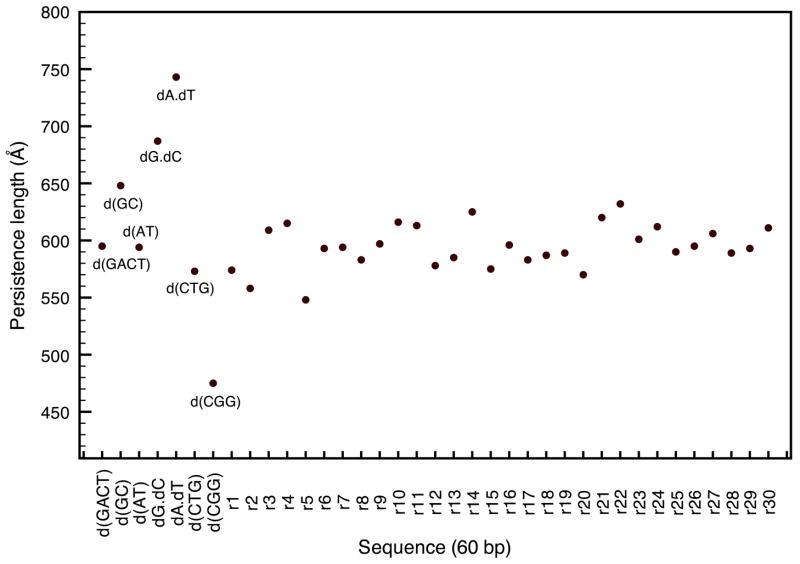
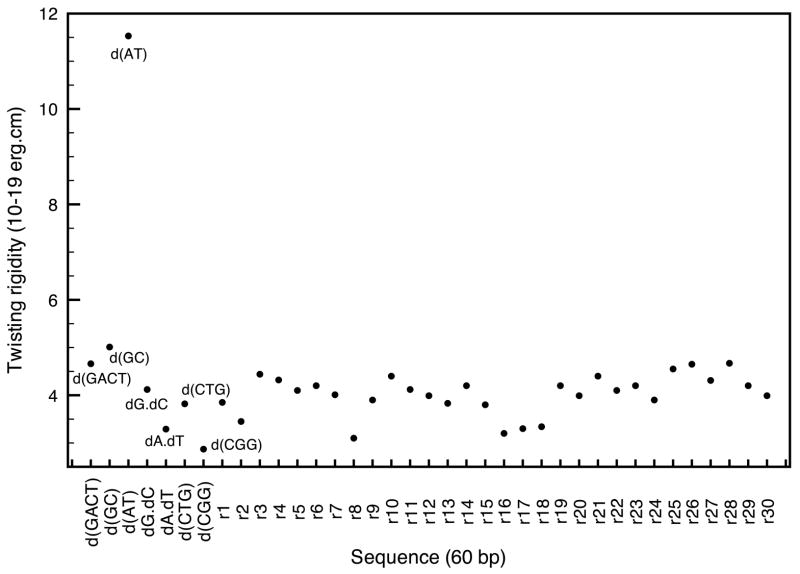
An area where mechanical properties of DNA are important is the interactions between nucleic acid and histone proteins in the nucleosome, and, for DNA packaging in general. Many degenerative diseases are believed to be caused by an increase of flexibility in DNA therefore preventing transcription. Several sequences have been linked to fragile x syndrome, myotonic dystrophy, and Huntington disease; and recent studies have shown an enhancement in the flexibility of DNA segments containing these triplet repeats.^16–18 One of the advantages of the microscopic method described here is its ability to take sequence effects into account and study the flexibility for different DNA sequences. Figure 11 shows the persistence lengths for various sequences that include the well-known CTG, CGG triplet repeats and other sequences. We also computed the persistence length of thirty randomly generated sequences of 60 bp each; the GC ratio chosen for the random sequences was assumed to be the average GC content in the human genome (42 percent).^{39, 40} The homopolymers poly(dA).poly(dT), poly(dG).poly(dC) (referred to as dA.dT and dG.dC) are the most rigid of the set while heteropolymers poly(dAT) and poly(dGC) offer more flexibility.^41–43 Similar conclusions are found in many experimental studies on nucleosome formations,^{44, 45} and both homopolymers are known to activate transcription due to their relative stiffness. The sequence - d(GACT)- used in the previous section was an appropriate choice as its persistence length is average.

Figure 11.

Comparison of the persistence lengths for various DNA sequences with a salt concentration of 0.05M and T=300K.

Among the most interesting repeats we looked at are CTG and CGG; both of them have been shown to exhibit a greater flexibility than random DNA with, in most studies, CTG being more flexible than CGG. In our results, CTG is located on the lower end of the persistence length spectrum, and CGG has a persistence length 25 percent smaller than average. The extreme flexibility of the CGG repeats was also tested by replacing the nine central base pairs of the homopolymer dA.dT by three CGG repeats, which enhanced its flexibility by 20–25 percent. The robustness of the method was also tested by comparing the persistence lengths of 90 (575 Å vs. 710 Å) and 120 (664 Å vs. 853 Å) base-pair segments of CGG repeats and GACT repeats in order confirm that the relative flexibility of the CGG repeat is still present for longer sequences and is not affected by the sequence-length dependence shown in the previous section.

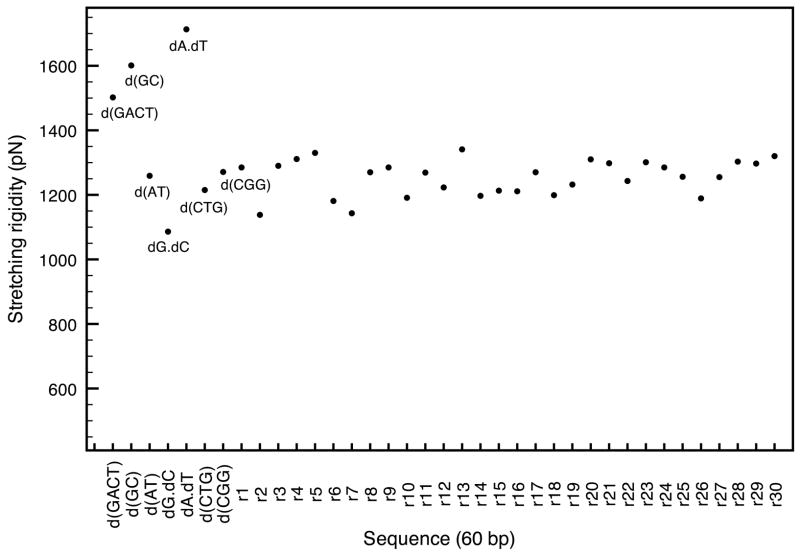
The results of this section also agree favorably with a study by Lankas et. al,⁴⁶ in that the four DNA oligomers, poly(dA).poly(dT), poly(dG).poly(dC), poly(dAT), poly(dGC), are found to have similar intrinsic flexibility in both studies, especially for the stretching rigidities; these can be found in table 2 and figure 12. In recent single-molecule studies, the melting transition happens for a lower stretching force in poly(dAT) (1259 pN) than for poly(dGC) (1601 pN),⁴⁷ which is consistent with the relative stretching rigidities in this work where poly(dAT) is much more flexible with respect to stretching than poly(dGC). As in the previous section, identifying the twisting modes is not as straightforward but the results are yet again within experimental estimates (Table 2 and figure 13). The average value for a random sequence is in the vicinity of 4.02 10⁻¹⁹erg.cm while the most flexible sequence so far (CGG) has a twisting modulus of 2.87 10⁻¹⁹erg.cm. In summary, it is clear that sequences including CGG and CTG triplet repeats are more flexible than random DNA. In both cases, at least two of their rigidity constants are smaller than that of random DNA. In contrast, stiffer repeats such as dA.dT and dG.dC have, in average, larger rigidity constants than random DNA.

Table 2.

Mechanical constants for various DNA sequences with a salt concentration of 0.05M and T=300K. The values reported in italics and bold correspond to stiffer and more flexible characteristics than random DNA, respectively

Sequences	Persistence Length (Å)	Stretching rigidity (pN)	Twisting rigidity (10−19erg.cm)
GACT	595	1502	4.66
poly d(AT)	594	1259	11.53
poly d(GC)	648	1601	5.01
poly d(A) . poly d(T)	743	1713	3.29
poly d(G) . poly d(C)	697	1086	4.12
CTG	573	1215	3.82
CGG	475	1271	2.87
Random	594	1251	4.02
Random min	548	1138	3.10
Random max	632	1341	4.67
Standard deviation	19	55	0.41

Figure 12.

Comparison of stretching moduli for various DNA sequences with a salt concentration of 0.05M and T=300K.

Figure 13.

Comparison of twisting moduli for various DNA sequences with a salt concentration of 0.05M and T=300K.

3.3 Circular DNA

In an influential study by Cloutier and Widom,⁴⁸ particular sequences of DNA were found to form DNA minicircles with expectations 400 fold higher than predicted. In this section we examine whether this increase in cyclization rate could be explained in part by the elastic properties of these sequences. We chose the 94bp sequence with the highest J value (TA94) (i.e. the sequence with the highest closure probability). This sequence increases nucleosome positioning by a few orders of magnitude compared to random DNA. The reason for this enhancement is not clear; sharp bending might be responsible for the increase in flexibility as it was pointed out in a study by Lankas et. al.⁴⁹

The bending motions that deform the circle within the plane of the molecule are twofold degenerate in the GB simulations and correspond to deformations along two perpendicular axis in the plane of the minicircle (Fig. 4 and table 3). Three pairs of in-plane bending motions were used in the fitting process. The frequencies corresponding to these motions are not exactly degenerate due to the fact that the mini-circle is not fully symmetrical in sequence. However, they are sufficiently close in value to consider them as equivalent in the model. The GB frequencies are in good agreement with the analytical model for both in-plane and out-of-plane bending motions for a relaxed and torsionally strained minicircle. However, the nearly-degenerate vibrational frequencies are not as close in energy in the case of the overtwisted circle, especially for larger values of n. Only two twisting modes were identified; corresponding to n = 1 and n = 2 in the analytical model (figure 5 and table 3). The rigidities extracted for both the relaxed and overtwisted circles are shown in Table 4. The bending persistence lengths are 571Å, 610 Å, and 628 Å for the relaxed, overtwisted, and linear configurations of TA94, respectively. Hence, even forcing DNA into a small circle seems to have only a mild effect on its intrinsic bending propensities. By contrast, the twisting rigidity for our linear model is much larger than that of random DNA (6.74 10⁻¹⁹erg.cm), whereas it is essentially the same as random DNA for both circular models (4.74 10⁻¹⁹erg.cm and 4.18 10⁻¹⁹erg.cm for the relaxed and overtwisted configuration, respectively).

Table 3.

Lowest in plane bending, out of plane bending, and twisting frequencies in cm⁻¹ for the 94-base-pair minicircle (TA94) with a salt concentration of 0.05M and T=300K.

	Relaxed minicircle			Overtwisted minicircle
Modes	GB frequencies		Analytical frequencies	GB frequencies		Analytical frequencies
IPB2	0.165	0.172	0.121	0.166	0.178	0.116
IPB3	0.394	0.452	0.366	0.443	0.471	0.377
IPB4	0.672	0.724	0.697	0.704	0.778	0.734
OP2	0.217	0.231	0.211	0.211	0.248	0.235
OP3	0.525	0.545	0.496	0.520	0.542	0.551
OP4	0.793	0.851	0.864	0.802	0.901	0.958
T1	0.663		0.529	0.654		0.556
T2	0.995		1.057	1.148		1.270

Table 4.

Mechanical constants extracted from the results presented in Table 3

	Relaxed minicircle	Overtwisted minicircle	Linear
Persistence length (Å)	571	610	628
Twisting rigidity (10−19erg.cm)	4.74	4.18	6.74

Based on the previous results, and considering the observed length dependence of the method, it appears that the sequence used in this section ranks within the most flexible sequences encountered (628 Å for TA94 vs. 732 Å for d(GACT), considered in this study to behave like random DNA). A comparison of the persistence lengths for several known sequences can be found in table 5. The conclusions of Cloutier and Widom⁴⁸ on the persistence length and twisting rigidity is in accord with our observations with our linear DNA model; the persistence length is found to be shorter than the one of random DNA, whereas the twisting rigidity is higher. Note that this is also true in the case of our circular DNA model, this is an encouraging sign that the force field and methods used in this work reproduce the different aspects of macromolecular motions of nucleic acids accurately. The high flexibility of this sequence could partly explain its large J value, though, it is clear that other factors such as kinks or extreme bending are also involved in the formation of nucleosomes. Further studies on DNA binding to nucleosome core proteins in in progress.

Table 5.

Mechanical constants for several 94bp sequences with a salt concentration of 0.05M and T=300K.

Sequences	Persistence Length (Å)	Stretching rigidity (pN)	twisting rigidity (10−19erg.cm)
dA.dT	862	1899	3.63
d(GACT)	732	1489	4.78
d(CGG)	570	1397	3.07
TA94	628	1385	6.85

4 Conclusions

Normal mode analysis in implicit solvent using the generalized Born model provides a powerful tool to describe collective molecular motions. The method developed in this paper allows a better understanding of how the flexibility of nucleic acids is affected by salt concentration and their lengths and sequences. The use of an all-atom force field allows us to both test the force field model itself (showing, for example, limitations in our current description of salt effects,) and to explore sequence dependences and to compare linear to circular structures. Our future plans include a systematic study of sequences that are found to bind (or not to bind) to nucleosomes, and which may provide new insights into DNA flexibility and its connections to transcription. Another extension under active investigation adds solvent frictional effects to the normal mode approximation, as so-called Langevin modes.⁵⁰ Such a method could potentially give an even more accurate picture of these molecular motions and direct knowledge of several important properties including relaxation times, rotational and translational diffusion constants. The initial results presented here suggest that many interesting features of duplex DNA, at a length scale of hundred of Angstroms, can be modeled reasonably well using force fields originally developed by comparisons to results for very short olignonucleotides. This provides a new window on ways to understand the behavior of DNA for much longer sequences.

Figure 2.

Low-frequency stretching modes of a 150-bp linear segment of DNA. The arrows define the main motions associated with the corresponding vibration.