A Combinatorial Approach to Detecting Gene-Gene and Gene-Environment Interactions in Family Studies

Abstract

Widespread multifactor interactions present a significant challenge in determining risk factors of complex diseases. Several combinatorial approaches, such as the multifactor dimensionality reduction (MDR) method, have emerged as a promising tool for better detecting gene-gene (G × G) and gene-environment (G × E) interactions. We recently developed a general combinatorial approach, namely the generalized multifactor dimensionality reduction (GMDR) method, which can entertain both qualitative and quantitative phenotypes and allows for both discrete and continuous covariates to detect G × G and G × E interactions in a sample of unrelated individuals. In this article, we report the development of an algorithm that can be used to study G × G and G × E interactions for family-based designs, called pedigree-based GMDR (PGMDR). Compared to the available method, our proposed method has several major improvements, including allowing for covariate adjustments and being applicable to arbitrary phenotypes, arbitrary pedigree structures, and arbitrary patterns of missing marker genotypes. Our Monte Carlo simulations provide evidence that the PGMDR method is superior in performance to identify epistatic loci compared to the MDR-pedigree disequilibrium test (PDT). Finally, we applied our proposed approach to a genetic data set on tobacco dependence and found a significant interaction between two taste receptor genes (i.e., TAS2R16 and TAS2R38) in affecting nicotine dependence.

Introduction

It is well recognized that joint actions or interactions of multiple genetic and environmental factors are an important biological basis for complex diseases and phenotype variation.^1–8 Ubiquitous interactions likely result in the effect of any single factor differing in magnitude and/or in direction, dependent on other genetic variations and environmental factors. This makes determining which genetic polymorphisms and/or environmental factors are associated with a disease of interest a difficult task. Traditional strategies attempt to investigate a single factor at a time and ascribe a phenotype to additive or combinatorial effects of these factors. These approaches fail to pinpoint determinants that have a weak marginal correlation between the levels of each individual factor and the phenotype. The interaction analysis methods established by extending single factor-based approaches are typically underpowered to detect high-order interactions because of problems including heavy computational burden (usually being computationally intractable), increased type I and II errors, and being less robust and potentially biased as a result of highly sparse data in a multifactorial model.^1,5 The determination of gene-gene (epistasis, G × G) and gene-environment (plastic reaction norms, G × E) interactions still presents one of the most daunting challenges in genetic epidemiology and new analytical approaches are needed.

Recently emerging combinatorial approaches such as the multifactor dimensionality reduction method (MDR),^9–11 the combinatorial partitioning method (CPM),¹² and the restricted partition method (RPM)¹³ are promising tools toward a better identification of interactions. To circumvent the limitations of the existing combinatorial methods (e.g., not allowing adjustment for covariates), we recently developed a comprehensive combinatorial approach for population-based studies of unrelated individuals, namely the generalized multifactor dimensionality reduction (GMDR) method that can entertain both qualitative and quantitative phenotypes, allow for both discrete and continuous covariates, and offer more flexibility for a population-based study design.¹⁴ However, these methods are applicable only to samples consisting of unrelated subjects or discordant sib-pairs. Because they are immune to bias and invalidity in the presence of population heterogeneity, family-based tests that are conditional on parental information are commonly used in human genetic studies. Over the past decades, a significant amount of clinical and genetic data has been collected on nuclear families and/or multigenerational pedigrees for linkage and family-based association analysis. Inability to handle family-based data has greatly limited the applicability of combinatorial approaches for detecting G × G and G × E interactions. Thus, the development of novel algorithms for detecting G × G and G × E interactions in family-based study designs is warranted.

Recently, Martin et al.¹⁵ proposed the MDR-pedigree disequilibrium test (PDT) method, which is applicable to family-based designs. However, like the original MDR, the MDR-PDT method does not permit adjustment for covariates such as ethnicity, sex, weight, and/or age and is applicable only to dichotomous phenotypes. To tackle these limitations, in this article we developed a pedigree-based generalized multifactor dimensionality reduction (PGMDR) method that represents an important extension of our previous GMDR method for designs that use samples of unrelated individuals. Compared to the MDR-PDT method,¹⁵ our proposed approach offers three major improvements: (1) allowing for covariate adjustment, (2) providing a unified framework for analyzing both continuous and dichotomous phenotypes, and (3) coherently handling different family types and sizes as well as patterns of missing data.

In the following sections, we begin by introducing a general statistic that is sensitive to only within-family association between genotypes at loci under consideration and a phenotype of interest. Next, we formulate the corresponding PGMDR method by integrating the genotypic-association statistic into the MDR framework. We conduct a series of simulations and analyze a real data set to demonstrate the use of the new method. Finally, we examine issues such as its relationship to MDR-PDT¹⁵ to gain a deeper insight into the method.

Material and Methods

Test Statistic

In sexual reproduction, haploid sex cells, also called gametes, are produced from diploid germline cells through a process involving meiosis. The fusion of two gametes, one egg from the female and one sperm from the male, known as syngamy or fertilization, gives rise to a zygote that potentially develops into a new organism. Each gamete united to form a zygote has a complementary gametid, termed nontransmitted gamete, which is produced from the meiotic division of the primary gametocyte but does not necessarily develop into a mature gamete (e.g., polar bodies that eventually disintegrate during meiosis) or participate in fertilization. We call the pseudo individual formed by the two nontransmitted gametes of a zygote the “pseudo nontransmitted sib.”

The genotype of the pseudo nontransmitted sib of a nonfounder at loci of interest, referred to as the nontransmitted genotype hereafter, can be determined or inferred based on the genotype information of the nonfounder and the other member(s) in the pedigree. (We assume here that the genotype of the nonfounder is always available. If genotype missing occurs in a nonfounder, we suggest a case-wise deletion of such a nonfounder or using a statistically imputed genotype based on the flanking markers or haplotypes.) Consider N pedigrees (or families), with n_i nonfounders in pedigree i. Let m_ij be the genotype of nonfounder j in pedigree i at the considered loci and ${\overline{m}}_{ij}$ be the corresponding nontransmitted genotype. When both parental genotypes are observed, we can easily determine ${\overline{m}}_{ij}$. For example, assuming that family i has parental genotypes AaBb and AaBB and two children, child 1 with AABb and child 2 with AaBB, then ${\overline{m}}_{i1}$ = aaBB and ${\overline{m}}_{i2}$ = AaBb. When parental genotype information is missing, we can sample one realization of the nontransmitted genotype from the conditional distribution given the minimal sufficient statistic for the null hypothesis through an algorithm that is modified from Rabinowitz and Laird¹⁶ and applicable to general pedigrees (see Appendix A). The exhaustive results of the algorithm for configurations of nuclear families are summarized in the three Appendix Tables. The nontransmitted genotype at a set of loci can be determined on the basis of locus by locus.

Let y_ij be the phenotype of individual j in pedigree i and t(y_ij) be some function of the phenotype, depending on possibly unknown parameters. Let g(m_ij) or $\mathbf{g}\left({\overline{m}}_{ij}\right)$ be a vector whose elements are coded for the corresponding marker genotypes. In what follows we will abbreviate g(m_ij) as g_ij, $\mathbf{g}\left({\overline{m}}_{ij}\right)$ as ${\overline{\mathbf{g}}}_{ij}$, and t(y_ij) as t_ij. To measure within-family association between genotype and phenotype, we define a general class of statistics as

$${\mathbf{s}}_{ij}=t_{ij}\ast ({\mathbf{g}}_{ij}-{\overline{\mathbf{g}}}_{ij})=t_{ij}\ast {\mathbf{g}}_{ij}+(-t_{ij})\ast {\overline{\mathbf{g}}}_{ij}.$$ (1)

When ${\mathbf{g}}_{ij}={\overline{\mathbf{g}}}_{ij}$, s_ij = 0, that is, when the transmitted and nontransmitted genotypes are the same, the individual is uninformative, and thus will be automatically excluded from the subsequent analysis. For each informative nonfounder, transmitted and nontransmitted genotypes contribute t_ij and −t_ij to the corresponding component in s_ij so that the nontransmitted genotype virtually provides a “pseudo-contrast.” Under the null hypothesis of no association between the genotype and phenotype under investigation, the transmission of either an observed genotype or its nontransmitted genotype is equally frequent and the expectation of the test statistic is 0.

For different purposes, we have diverse coding schemes for $\mathrm{g}(·)$, for example, the number of a given allele. To detect genotype-genotype and genotype-environment interactions, we use the genotype-coding scheme. We can also use different codings for t(y_ij). For example, letting t(y_ij) = 1 denote an affected subject and t(y_ij) = 0 an unaffected or phenotype-unknown subject, then only affected subjects contribute to the statistics. The validity of the statistic does not depend on the choice of genotype or phenotype coding, although the power does. Without loss of generality, in this article we use the score of generalized linear models¹⁷ or the score-like of quasilikelihood functions^18,19 for t(y_ij), which allows for covariate adjustment, is applicable to both continuous and categorical phenotypes, and is potentially more powerful.

The essential features of the test statistic are flexibility and generalization, while retaining validity (i.e., being unbiased under the null hypothesis). By decoupling phenotype coding from the evaluation of the conditional distribution of the nontransmitted genotype, the test statistic may be applied to arbitrary phenotypes, arbitrary pedigree structures, arbitrary patterns of missing information in the founders and even other settings not yet discussed in the literature, and also allows incorporating covariates. We are free to use any other association statistic that appears appropriate, regardless of phenotype distribution, genotype frequencies in the founder population, sampling design, and ascertainment process.

The Pedigree-Based GMDR Algorithm

The method proposed here uses the same data-reduction strategy (a constructive induction approach) as the MDR^9,10 and GMDR¹⁴ approaches. Specifically, the possible cells in a multifactor space are collapsed into two distinct groups according to their statistic values computed from Equation (1), effectively transforming the original representation of multiple attributes into that of a new two-level attribute, and thereby identifying from all potential combinations the specific combinations of factors that show the strongest dichotomous association with the phenotype of interest. The difference is that we consider here each nonfounder as an observed individual together with its nontransmitted control that are assumed to have opposite statistic values, instead of only the observed one in the unrelated-based GMDR method. Benefiting from a comprehensive statistic, the proposed method has the flexibility to incorporate an adjustment for covariates, can handle missing genotype data, and is applicable to arbitrary pedigree structures and phenotypes.

To identify and evaluate the best model, we propose using k-fold crossvalidation. Other choices are also possible within the same framework of data reduction, e.g., the best classification can be evaluated on the basis of a permutation p value as in the MDR-PDT.¹⁵ In brief, the data-reduction algorithm can be described as follows (see Figure S1 available online and Appendix B for further details). The informative nonfounders, each consisting of a transmitted genotype at loci of interest and its internal control, are randomly divided into k nearly equal subsets, and then the crossvalidation is repeated k times. Each time, one of the k subsets is used as the testing set and the remaining k−1 subsets are put together to form the training set. The training set is used to compute the average of the statistic values for all cells defined by a multidimensional space. Each nonempty multifactor cell is labeled as either “high risk” or “low risk” according to whether or not its average statistic value exceeds a preassigned threshold T (e.g., T = 0). High-risk and low-risk cells are pooled into separate groups, creating a dichotomous model that best captures the correlation between this set of classification factors and the phenotype. The averages of the statistic values in the high-risk and the low-risk groups can provide a measure of the classification precision: a larger difference between them represents a better classification. All potential combinations of the factors are evaluated sequentially for their ability to classify the statistic values in the training data, and the model that has maximum classification accuracy is chosen as the best from those with the same dimensionality. The independent testing set is used to estimate the prediction ability of the best model selected for each multifactor dimensionality. The results are averaged and the consistency of the model is computed across all k trials. Finally, among this set of best models, we select the model with maximum prediction accuracy and/or maximum crossvalidation consistency. We can use a sign test and/or a permutation test for prediction accuracy to assess the significance of an identified model.

Simulation Study

To demonstrate the validity and statistical power of the proposed approach, we performed extensive simulations in a variety of settings for both dichotomous and continuous phenotypes on the basis of 600 families. For simplicity of the exposition, we considered all functional and marker loci to be independent, diallelic, and at Hardy-Weinberg equilibrium. The functional loci were considered at two levels of allele frequencies, equifrequency and a minor allele frequency (MAF) of 0.25, and the marker loci (except for those coincident with the functional loci) had equifrequent alleles. Both phenotypes were simulated under the same digenic espistatic interaction models commonly used in recent simulation studies,^9,13,15 called the antidiagonal model (i.e., genotypes AAbb, AaBb, and aaBB are considered as a high-value group and the rest as a low-value group) and the checkerboard model (i.e., AABb, AaBB, Aabb, and aaBb versus the others), in which the marginal effects of each disease locus are very small or zero. These are models that on theoretical grounds would be most difficult to detect and for which there is some known biological basis or empirical evidence.^20–22 A total of 10 marker loci were simulated. To assess the type I error rates, the marker loci were simulated to be completely independent of the functional loci. To estimate power, the functional loci were specified as two of the marker loci.

Phenotypes were generated based on the following generalized linear model,

$$l\left({\mathrm{\mu }}_i\right)=\mathrm{\alpha }+x_i\mathrm{\beta }+z_i\mathrm{\gamma },$$ (2)

where μ_i is the expected phenotypic value of individual i, α is the intercept, β is the genetic effect, x_i is the indicator variable equal to 1 for the high-value group and 0 for the others, γ is the covariate effect, z_i is the observed covariate value, and l(μ_i) is an appropriate link function. For the continuous phenotype, we used the identity with a stochastic component assumed to have a normal distribution for the continuous phenotype, and for the dichotomous phenotype the logistic penetrance function. We assumed α = −5.29 and β = 1.09 for the dichotomous phenotype so that the high-risk genotypes have a penetrance of ∼0.015 and the others have a risk of ∼0.005 in the absence of a covariate. The covariate with γ = 1 was assumed to come from a normal distribution with mean 0 and variance 10; after adding the covariate, the relative risk is ∼1.70: the mean risk rates of the high-risk group and of the low-risk group are ∼0.124 and ∼0.073, respectively. The continuous phenotypes were generated at α = 0, β = 0.25, and normal deviations with mean 0 and variance 1. The covariate with γ = 1 was assumed to have a normal distribution with mean 0 and variance 1. We assumed that all covariate values were available for all study subjects.

If a sibling was affected for a dichotomous phenotype, or had a quantitative disease phenotypic value of 2.0 or more extreme (i.e., being in the ∼10% upper tail of the phenotype distribution varying with the genotype frequencies), we considered him/her as a proband. The families with a proband and a full-sib who also reached the phenotypic criterion for proband status were included in the study. Once a family met the conditions for enrollment, two additional family members (siblings and/or parents) were also included into the study, regardless of phenotype. A total of 600 families—200 families with both parents plus two siblings, 200 with one parent plus three siblings, and 200 with four siblings and no parent—were simulated according to the sampling scheme described above.

The nontransmitted genotypes were constructed with the proposed algorithm. The scores were computed with adjustment for the covariate and with no adjustment for the purpose of comparison. Then we used Equation (1) to build the test statistics for all siblings and applied them into the data-reduction algorithm with 10-fold crossvalidation to identify the best interaction model. An exhaustive computational search strategy was performed for all possible one- to five-locus models in our simulations. The average crossvalidation consistency and prediction accuracy, as well as the standard errors of the means (SEMs), were computed on the basis of 200 simulation replicates. To assess type I error rate and statistical power, we determined the p value for each simulated prediction accuracy based on its null distribution generated from permutation testing with 1000 replicates. To maintain the correlations structure of each family, we used the family as the permuting unit, i.e., randomly shuffled the transmitted set and the nontransmitted set in a whole family. Power and type I error rate were computed on the basis of 200 and 1000 simulations, respectively. For comparison, we also ran on the same simulated data sets an MDR-PDT analysis as implemented with a Beta version of the computer software provided by the authors.¹⁵

A Case Study of Nicotine Dependence

To illustrate the utility of the PGMDR method proposed above, we applied it to a real data set to investigate the role of two type 2 taste receptor genes in nicotine dependence (ND): taste receptor, type 2, member 16 (TAS2R16 [MIM 604867]) and taste receptor, type 2, member 38 (TAS2R38 [MIM 607751]). The subjects used in this study were the African-American (AA) participants who were part of the U.S. Mid-South Tobacco Family (MSTF) cohort, enrolled during 1999–2004 for linkage and/or family-based association studies. Proband smokers were required to be at least 21 years of age, to have smoked for at least the last 5 years, and to have consumed an average of 20 cigarettes per day for the last 12 months. All smoker probands selected for inclusion into the current study had a FTND²³ score of 4 or above and nonsmokers were defined as those who had smoked less than 100 cigarettes in their lifetime. Once a proband and a full-sib who was also nicotine dependent (for a majority of our families) were recruited, additional siblings and parents were included into the study whenever possible, regardless of smoking status. Participants included 1366 individuals from 402 AA families that ranged in size from 2 to 9 with an average size of 3.14 (±0.75; SD). Average age ± SD was 39.4 ± 14.4 years for the AA participants. Detailed demographic and clinical characteristics of this sample have been reported elsewhere.²⁴ All participants provided informed consents. The study protocol, forms, and procedures were approved by all participating Institutional Review Boards.

DNA was extracted from peripheral blood samples of each participant via a kit from QIAGEN (Valencia, CA). Three single-nucleotide polymorphisms (SNPs) in each of two genes, TAS2R16 and TAS2R38, were genotyped. Detailed information on the gene structures and SNPs is presented in Tables S3 and S4. For DNA extraction and genotyping information, please refer to one of our recent reports.²⁵

After examining genotyping quality and excluding possible genotyping errors, nontransmitted genotypes of nonfounders were derived based on the conditional distribution given the minimal sufficient statistic. Residual scores of nonfounders were computed under a null logistic model with gender and age as covariates for smoking status. Then, the PGMDR analysis was performed with the statistic computed as in Equation (1). An exhaustive search strategy and 10-fold crossvalidation were used for all possible locus combinations within each gene and between the two genes. The empirical p values of prediction accuracy were determined by permutation testing on the basis of 10,000 shuffles. The p values were also obtained via the sign test for prediction accuracy implemented in the MDR software.¹⁰

Results

Computer Simulations

All estimates of type I error rate determined by the permutation test were very close to the nominal level. For example, Figure 1 displays probability-probability (P-P) plots of significance level and type I error rate for a dichotomous phenotype (Figure 1A) and a quantitative phenotype (Figure 1B) under an antidiagonal model^20,21 with equifrequent functional alleles. The points on the plots fall on or near the reference line that goes through the origin and has unit slope, suggesting that the algorithm gives rise to a correct type I error rate for an arbitrarily specified significance level. The type I error rates at the 0.05 significance level were 0.052 and 0.049 for the dichotomous and quantitative phenotypes, respectively. Simulations for other scenarios also yielded similar P-P plots (data not shown). These results were in good agreement with theoretical expectation, verifying the validity of the proposed test procedure.

Figure 1.

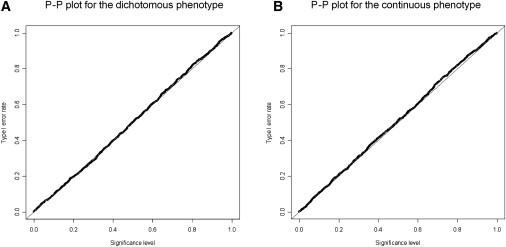
Probability-Probability Plot of Significance Level and Type I Error Rate

The horizontal axis represents significance level, a threshold value specified for permutation testing, whereas the vertical axis is type I error rate, the proportion of the permutations resulting in p values equal to and less than the threshold value in all permutations for a dichotomous phenotype (A) and a continuous phenotype (B). The reference line is the diagonal line with unit slope through the origin.

Table 1 presents the statistical power and wrongly positive rate (WPR, the rate that the false null hypothesis is rejected by wrong models) for a dichotomous trait under the simulation scenario of a checkerboard model^13,22 with an MAF of 0.25 from three methods: MDR-PDT, PGMDR without adjustment, and PGMDR with adjustment for the covariate. We could not make such a comparison for the quantitative trait because MDR-PDT is applicable only to dichotomous traits. Out of 200 simulations, at the 5% significance level PGMDR both with and without adjustment never declared a wrong model as the best model, whereas MDR-PDT did so four times. PGMDR with adjustment had the highest power, 7.5% and 30.0% higher than PGMDR without adjustment and MDR-PDT, respectively. Comparison of the PGMDR with the MDR-PDT demonstrated that the PGMDR is more powerful than the MDR-PDT. This might be due in part to loss of samples, because when parental genotypes are not completely available, the original MDR-PDT requires informative discordant sib-pairs with different marker genotypes, and/or the current MDR-PDT software is inappropriate for handling different types of pedigrees. It also possibly arises from the unequal contributions to the statistic from triads and discordant sib-ships in the MDR-PDT method.

Table 1.

Comparison of Power and Wrongly Positive Rate between MDR-PDT, PGMDR without Covariate Adjustment, and PGMDR with Covariate Adjustment

Method	Powera	WPRb
MDR-PDT	0.695	0.020
PGMDR without adjustment	0.920	0.000
PGMDR with adjustment	0.995	0.000

The results presented in this table were based on 200 simulations under a checkerboard model with MAF of 0.25 at both functional loci.

^aPower = the proportion of true models significant at 5% level in all simulations.

^bWPR (wrongly positive rate) = the proportion of wrong models significant at 5% level in all simulations.

Table 2 shows the prediction accuracy, crossvalidation consistency, and power of the best (2-locus) model identified by the PGMDR method with and without covariate adjustment under various simulation scenarios, for both dichotomous and quantitative traits. For detailed results of one- to five-locus models, please see Tables S1 and S2 for dichotomous and quantitative traits, respectively. Although both methods correctly identified the true model (i.e., the correct two-locus model always gave the maximum prediction accuracies and crossvalidation consistencies; see Tables S1 and S2), the inclusion of the covariate in PGMDR leads to a substantial increase in prediction accuracy, crossvalidation consistency, and power. The PGMDR with adjustment had, even in the case of a relative risk of ∼1.70, power of 96.5% or above in the four listed cases, 7.5%, 15%, 10.5%, and 8.5%, respectively, higher than the counterparts of the PGMDR without adjustment in the case of the dichotomous phenotype. The simulation results listed in Table 2 and Table S2 were similar for a quantitative trait, that is, PGMDR with adjustment had consistently higher prediction accuracy, crossvalidation consistency, and power as compared to the PGMDR without covariate adjustment. These results indicate the necessity for improved prediction ability and statistical power to consider the influence of covariate(s) when informative covariate(s) is (are) present.

Table 2.

Comparison of Prediction Accuracy, Crossvalidation Consistency, and Power between PGMDR with Covariate Adjustment and without Covariate Adjustment

Scenario	With Adjustment (Mean ± SEM)		Powera	Without Adjustment (Mean ± SEM)		Powera
	Prediction Accuracy	Crossvalidation Consistency		Prediction Accuracy	Crossvalidation Consistency
Checkerboard	Dichotomous
MAF = 0.25	0.581 ± 0.013	9.990 ± 0.100	0.995	0.546 ± 0.011	9.835 ± 0.769	0.920
MAF = 0.50	0.576 ± 0.017	9.900 ± 0.657	0.980	0.542 ± 0.014	9.715 ± 0.865	0.830
Checkerboard	Quantitative
MAF = 0.25	0.588 ± 0.011	10.000 ± 0.000	1.000	0.569 ± 0.010	9.995 ± 0.071	0.995
MAF = 0.50	0.585 ± 0.012	10.000 ± 0.000	1.000	0.566 ± 0.011	9.995 ± 0.071	1.000
Antidiagonal	Dichotomous
MAF = 0.25	0.575 ± 0.017	9.875 ± 0.634	0.975	0.544 ± 0.012	9.670 ± 1.003	0.870
MAF = 0.50	0.578 ± 0.019	9.905 ± 0.507	0.965	0.541 ± 0.014	9.655 ± 1.054	0.880
Antidiagonal	Quantitative
MAF = 0.25	0.573 ± 0.012	9.975 ± 0.354	0.995	0.558 ± 0.011	9.955 ± 0.322	0.995
MAF = 0.50	0.578 ± 0.019	9.905 ± 0.507	0.975	0.558 ± 0.014	9.960 ± 0.242	0.770

These results were under the identified best (2-locus) model for dichotomous and quantitative phenotypes.

^aPower = the rate of true positives in all simulations at 5% level.

Application to Nicotine-Dependence Data

Table 3 presents the best multilocus models for ND within each gene and across the two genes, along with the corresponding prediction accuracies, crossvalidations, and p values in African Americans (AAs). There were no significant models (all p values ≥ 0.120) within each of the genes studied, suggesting that the marginal contribution from either gene is not remarkable. When considering the two genes together, however, we identified a significant three-SNP interaction model (SNPs rs2233989 and rs846664 in TAS2R16 and SNP rs1726866 in TAS2R38) with prediction accuracy 0.556, crossvalidation consistency 9, and permutation p value 0.002, indicating an interactive role of TAS2R16 and TAS2R38 in the etiology of ND. Figure 2 provides a graphical representation of the interaction patterns of the identified model. The distribution of high-risk and low-risk cells differs across each single locus and can be captured only under a multidimensional model, which reveals the orchestral interplay of TAS2R16 and TAS2R38 in affecting ND.

Table 3.

Comparison of Best Multilocus Models, Prediction Accuracies, Crossvalidation Consistencies, and p Values Identified by PGMDR with Adjustment for Sex and Age within Each Gene and between the Two Genes for ND

Gene	No. of Loci	Best Model	Prediction Accuracy	Crossvalidation Consistency	p Value
TAS2R16	1	rs846664	0.520	9	0.181
	2	rs846664, rs2233989	0.526	8	0.120
TAS2R38	1	rs1726866	0.511	10	0.308
	2	rs1726866, rs713598	0.504	5	0.458
TAS2R16, TAS2R38	1	TAS2R16: rs846664	0.520	8	0.187
	2	TAS2R16: rs846664; TAS2R38: rs1726866	0.522	6	0.137
	3	TAS2R16: rs846664, rs2233989;	0.556	9	0.002
		TAS2R38: rs1726866
	4	TAS2R16: rs1204014, rs2233989;	0.533	8	0.103
		TAS2R38: rs10246939, rs1726866

Figure 2.

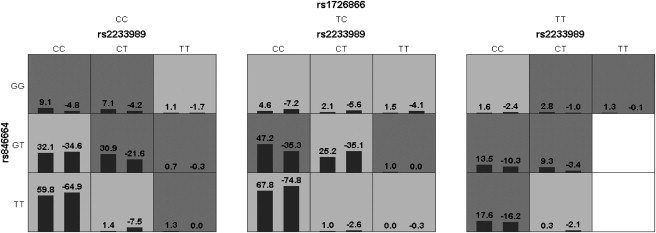
The Identified Best Model that Comprises rs2233989 and rs846664 in TAS2R16 and rs1726866 in TAS2R38

In each combinatorial cell, the left bar represents a positive score and the right bar is a negative score. High-risk cells are indicated by dark shading, low-risk cells by light shading, and empty cells by no shading.

The identified interaction model has a prediction accuracy of 0.556. Although it appears to be small, it is significant and biological meaningful because the prediction accuracy is calculated as $(\mathit{\text{True}}\mathit{\text{positives}}+\mathit{\text{True}}\mathit{\text{negatives}})/(\mathit{\text{True}}\mathit{\text{positives}}+\mathit{\text{False}}\mathit{\text{positives}}+\mathit{\text{True}}\mathit{\text{negatives}}+\mathit{\text{False}}\mathit{\text{negatives}})$ or its variants, where true positives and false positives are in the high-risk group those who exceed and those who do not exceed, respectively, the preassigned threshold that is used to define the high-risk and low-risk groups; false negatives and true negatives are those who exceed and those who do not exceed, respectively, the threshold in the low-risk group. Thus, the upper limit of prediction accuracy is determined by the contribution rate of the factors under consideration, for example, 100% contribution will result in a prediction accuracy of 100% whereas 0% contribution will yield a prediction accuracy of 50%. Considering the fact that smoking is a complex multifactor behavior and it is highly likely that many genes each with relatively small effect are involved, such prediction accuracy is biologically plausible.

Discussion

Identification of gene-gene and/or gene-environment joint actions is one of the most important and challenging topics in human genetics and genetic epidemiology. Our recently developed GMDR method¹⁴ represents a promising tool for detecting such joint actions for population-based samples of unrelated participants. In this article, we report the development of a pedigree-based GMDR algorithms that represents an important extension of our previous work for unrelated-person designs, because family-based designs that are robust against population stratification and allelic heterogeneity appear to be more popular in human genetics study. Although the name is the same for both types of genetic study designs, the algorithm underlying each approach are rather different. Our PGMDR is based on a conditioning algorithm for computing the distribution of nontransmitted genotypes given the minimum sufficient statistic under the null hypothesis for the sampling strategy and population structure in the founder population. Through such a conditioning, the proposed approach is valid, in the sense of resulting in correct type I error rates, regardless of patterns of population admixture and sampling plan, as supported by our simulation results.

Because the conditioning algorithm is broadly applicable, the PGMDR can be applied to virtually any scenario, including arbitrary pedigree structures and arbitrary patterns of missing marker allele information in the founders/parents. It can flexibly incorporate diverse pedigrees irrespective of structure, size, and missing data, and utilizes all available subjects in the data set of a study. For example, concordant sibs, unaffected offspring in a family, and subjects with missing genotypes, which are often encountered in real data sets but are not useful for the MDR-PDT and the original MDR, do inform our pedigree-based statistic. Without discarding any samples at hand, the proposed method is able to take full advantage of the whole data set and extract more genetic information. Our simulation comparisons between the PGMDR and the MDR-PDT algorithms and the ND data set demonstrate that our proposed algorithm is more powerful, likely benefiting from capitalizing on more of the data.

The proposed approach, in nature, represents a comprehensive statistical framework. Within this framework, we can use a broad category of test statistics that measure the covariance between the transmission of genotype and a function of the phenotype, such as the score-like statistics for quasilikelihood models, so that any kind of phenotype and multiallelic markers may be examined. In contrast to the MDR-PDT and the MDR methods that are restricted to the context of discordant sib-ships and dichotomous traits, the proposed approach is flexible enough to handle diverse phenotypes, categorical, censored, or continuous. The extension to multivariate phenotypes is also straightforward. Furthermore, one of the most important advantages of the proposed approach is that it allows adjustment for covariates so that it can increase predictive ability and statistical power by controlling confounding effects of covariates. Both the simulations and the application to the ND data set attest to the claim that our method can increase prediction accuracy and statistical power by inclusion of informative covariates.

Under this broad framework, available combinatory approaches can be thought of as special cases in various scenarios. The proposed method is an extension to family-based designs of our recent GMDR¹⁴ that itself is a generalization of the existing unrelated-person combinatorial approaches such as MDR, CPM, and RPM. By capitalizing on the “internal controls” extracted from family data, we construct a set of perfectly matched cases and controls and subsequently carry out the GMDR analysis based on the new data set. Thus, the original GMDR can be viewed as a special case without internal controls. An intuitive comparison among MDR, MDR-PDT, GMDR, and PGMDR is summarized in Figure 3.

Figure 3.

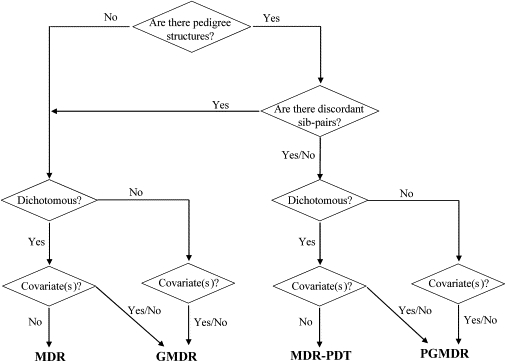
Schematic Representation of MDR, GMDR, MDR-PDT, and PGMDR

MDR and GMDR are applicable to analysis of unrelated samples or discordant sib-pairs that can be thought as case-control samples matched on the basis of family. GMDR is an extension of MDR, which can consider covariate(s) and flexibly handle a range of phenotypes that can be modeled by a generalized linear model or quasilikelihood function. Their counterparts in the context of pedigree-based design are MDR-PDT and PGMDR, respectively.

MDR-PDT¹⁵ may also be considered as a special case of the approach advocated here, although its PDT statistic is not uniformly equivalent to our general statistic. By defining t(y_ij) = 1 for affected and t(y_ij) = −1 for unaffected, our method has the same result as that of MDR-PDT for data consisting only of either family trios with an affected child or discordant sib-ships. When a pedigree is a mixture of these two kinds of data structures, nuclear families (both parents are observed in a family) and sib-ships (no parents are available), there will be a slight difference between the two methods because the two kinds of data contribute differently to the statistic in the MDR-PDT.¹⁵ In the MDR-PDT, the summary statistic is composed of two components, one for nuclear families in which each child contributes two shares (both transmitted and nontransmitted) to the statistic, and another for discordant sib-ships in which each child contributes one share (only the transmitted) to the statistic. For simplicity, we use a case of one locus to illustrate the difference between the two methods. Consider a pedigree containing a family with parents Aa and Aa, and two children, both AA and affected, and a discordant sib-pair (without parents), one aa and affected and the other AA and unaffected. The PDT statistics for this pedigree are D(AA) = 1 and D(aa) = −1, whereas our method gives S(AA) = 0 and S(aa) = 0. Thus, relative to the MDR-PDT method,¹⁵ in which the statistics are separately defined for triads and discordant sib-ships so that they unequally contribute to the overall statistic depending on family type and size, our method treats different family types coherently.

The proposed approach has a unified framework for coherently handling different family types. Under this concept, each nonfounder that informs the test statistic has a set of nontransmitted genotypes as a control. Unlike the MDR-PDT where there exists an intrinsic difficulty for permuting within larger extended pedigrees with general structures,¹⁵ a permutation test is always easy to perform for pedigrees with arbitrary structure and arbitrary size by randomly flipping the transmitted and nontransmitted genotype sets in a pedigree and thereby preserving in each permuted data set the possible nonindependence of transmissions across markers and across nonfounders.

The general statistical framework developed here also offers great flexibility in the use of different phenotype coding strategies. Although any phenotype-coding strategy is valid and results in correct type I error rates under the null hypothesis, some do provide more efficient and/or sensitive measures of association under the alternative and the choice of an appropriate coding strategy can substantially increase test power. Optimal choices for coding depend on the study design (e.g., only trios in which the offspring is affected versus a sample that also includes unaffected persons) and possibly unknown parameters (e.g., prevalence rate, relative risk, and allele frequency). We may obtain an approximately optimal coding based on prior knowledge of the disease. Power simulations may also provide guideline for the appropriate choice based on hypothetical scenarios in which the real parameters potentially fall, although it may be difficult to determine the real parameters exactly.

The illustrative example demonstrates that the proposed method can unveil cryptic interactions between the genes TAS2R16 and TAS2R38. Biologically, bitterness perception serves as a warning system that leads humans to reject substances that are potentially toxic.²⁶ Human taste receptors, including type 2 taste receptors (TAS2Rs), are expressed primarily in taste buds of gustatory papillae on the tongue surface and palate epithelia. Genetic studies point to diverse taste perception of bitter substances, as well as overall oral sensitivity, among individuals and between ethnic groups partly because of polymorphisms in taste receptor genes.²⁷ For example, several SNPs within the TAS2R genes, which encode TAS2R proteins, can characterize “tasters” and “nontasters.”²⁸ Polymorphisms in TAS2R genes are implicated in variations of orally related behaviors, including alcohol²⁹ and nicotine³⁰ consumption and dependence. Recently, we found that several polymorphisms in TAS2R genes are potentially implicated in ND ²⁵. Bitter taste receptor genes are heterogeneously expressed in taste receptor cells and TAS2Rs compete with each other for shared cellular resources, from biosynthesis to signaling and ultimately to turnover.³¹ This indicates that the significant statistical interaction detected in this study may represent a biological interaction between TAS2R genes. As illustrated in this study, the role of TAS2R genes in the etiology of ND is complex; further study is required to assess functional details.

Appendix A: Algorithm for Computation of the Conditional Distribution of Nontransmitted Genotypes

The key step involved in the proposed approach is the computation of the conditional distribution of nontransmitted genotypes given the minimal sufficient statistic under the null hypothesis for the phenotype distribution and the parental genotype distribution. When both parental genotypes are known, the observed phenotypes in all family members and the parental genotypes constitute the minimal sufficient statistic, and the conditional distribution of nontransmitted genotypes is straightforward. When parental genotype data are not completely available, however, the conditional distribution of the nontransmitted genotype of an offspring is not immediately obvious. In this appendix, we present an algorithm for computing the conditional distribution of nontransmitted genotypes given the minimal sufficient statistics. To some extent, this algorithm represents an extension of the approach proposed by Rabinowitz and Laird.¹⁶ The difference between the two is that we consider here the conditional distribution of nontransimitted genotypes rather than that of transmitted genotypes as is done in Rabinowitz and Laird.¹⁶ For each pedigree, the observed genotypes of nonfounders constitute the set of transmitted genotypes whereas their nontransmitted counterparts form a set of nontransmitted genotypes. Under the null hypothesis, each parent is equally likely to transmit either of her/his marker alleles and all these parental transmissions are considered to be independent. Thus, if we do not need to consider the compatibility of nontransmitted genotypes with the observed genotypes, a set of transmitted genotypes can be viewed as one of the plausible realizations of nontransmitted genotypes and the conditional distribution of transmitted genotypes derived by Rabinowitz and Laird's algorithm¹⁶ can also represent that of nontransmitted genotypes given the minimal sufficient statistic. Our algorithm is based on such a concept of equally frequent transmissions. Both the transmitted and nontransmitted sets are assumed to come from a hypothetical homogenous population.

While remaining the framework unaltered in the original algorithm,¹⁶ we define here all observed traits, typed marker alleles, and a plausible set of nontransmitted alleles in a pedigree as an outcome for the pedigree, instead of that consisting of all observed traits and typed marker alleles. Similar to that of Rabinowitz and Laird,¹⁶ the condition that characterizes the minimal sufficient statistic under the null hypothesis is that: if two different outcomes have the same value of the minimal sufficient statistic, then for any pattern of founders' genotypes, either the conditional probabilities of two outcomes given the pattern of founders' genotypes are both equal to zero, or the ratio of the conditional probabilities of the outcomes is invariant to the choice of the pattern of founders' genotypes. As pointed out by Rabinowitz and Laird,¹⁶ such a minimal sufficient statistic is not represented as a particular function of the data, but rather as a partition of the sample space.

The general steps involved in the algorithm for deriving the minimal sufficient statistic and computing the conditional distribution of nontransmitted genotypes in a pedigree (a nuclear family is a special case) can be summarized as follows.

(1) Find all the patterns of founder (parent in a nuclear family) marker genotypes that are compatible with the observed genotypes.

(2) For each of the patterns of compatible founder marker genotypes obtained in step (1), find the set of compatible patterns of nontransmitted genotypes in the pedigree. Find the subset of these compatible patterns that, together with the observed nonfounders' genotypes, have exactly the same compatible patterns of founders' genotypes as the observed nonfounders' genotypes.

(3) Find the subset of these compatible patterns found in step (2) that are compatible with all observed founder and nonfounder genotypes. Some of the nontransmitted genotypes may be fixed in this subset whereas the others may not. Below we call them fixed nontransmitted genotypes and nonfixed nontransmitted genotypes, respectively.

(4) For every pattern of compatible founder genotypes found in step (1) and for every pattern of nontransmitted genotypes in the subset found in step (3), compute the ratio of the geometrical mean of the conditional probability of the observed genotypes (pseudo nontransmitted genotypes) to that of the conditional probability of the nonfixed nontransmitted genotypes in the subset given the pattern of founders' genotypes.

(5) For some patterns of nontransmitted genotypes in the subset found in step (3), the ratios found in step (4) will be the same for all of the compatible patterns of founders' genotypes found in step (1).

(6) The conditional distribution is found by arbitrarily choosing any of the compatible patterns of founder genotypes found in step (1) and computing the conditional probabilities of the patterns of nontransmitted genotypes given the chosen pattern of founders' genotypes and given the set of patterns of nontransmitted genotypes described in step (5).

The exhaustive results for nuclear families are tabulated in Tables A1, A2, and A3. Without loss of generality, we consider only one marker locus, A. Throughout, A₁, A₂, …, represent generic marker alleles, and the configurations of the observed nonfounder genotypes in the form of sets, e.g., the notation {A₁A₂, A₁A₃} corresponds to a sibship of arbitrary size with at least one child carrying A₁A₂ and one child carrying A₁A₃, and no other genotypes. To help readers follow our presentation, we use an example to illustrate the steps involved in this algorithm. Consider a child configuration {A₁A₁} with a heterozygous parent A₁A₂. The compatible patterns of the parents are A₁A₂ × A₁A₁, A₁A₂ × A₁A₂, and A₁A₂ × A₁A₃ found in step (1). The patterns of nontransmitted genotypes, {A₁A₁}, {A₁A₂}, {A₁A₁, A₁A₂}, together with the observed set {A₁A₁}, have the compatible patterns of founders' genotypes A₁A₂ × A₁A₁, A₁A₂ × A₁A₂, and A₁A₂ × A₁A₃. Only the pattern of nontransmitted genotypes {A₁A₂} is found in step (3), i.e., they are fixed. Finally, we obtain a conditional distribution of the nontransimtted configuration {A₁A₂} with probability 1 as a result of the algorithm.

Table A1.

Conditional Distribution of Nontransmitted Genotypes when One Homozygous A₁A₁ Parent's Genotype and Children's Genotypes Are Available at Marker Locus A

Children's Genotype Configuration	Transmitted	Nontransmitted
{A1A1}	A1A1	A1A1
{A1A2}	A1A2	A1A2
{A1A1, A1A2}	A1A1	A1A2
	A1A2	A1A1
{A1A2, A1A3}	A1A2	A1A3
	A1A3	A1A2

A default implies a conditional probability of 1.

Table A2.

Conditional Contribution of Nontransmitted Genotypes when One Heterozygous A₁A₂ Parent's Genotype and Children's Genotypes Are Available at Marker Locus A

Children's Genotype Configuration	Transmitted	Nontransmitted
{A1A1}	A1A1	A1A2
{A1A2}	A1A2	A1A2
{A1A3}	A1A3	A2A3
{A1A1, A1A2}	A1A1	A1A2
	A1A2	random assignment of A1A1 and A1A2 that keeps the number of each proportional to that in the observed set
{A1A3, A2A3}	A1A3	A2A3
	A2A3	A1A3
{A1A1, A2A2} or	A1A1	A2A2
{A1A1, A1A2, A2A2}	A1A2	A1A2
	A2A2	A1A1
{A1A1, A1A3}, {A1A1, A2A3},	A1A1	A2A3
{A1A1, A1A2, A1A3},	A1A2	A1A3
{A1A1, A1A2, A2A3},	A1A3	A1A2
{A1A1, A1A3, A2A3} or	A2A3	A1A1
{A1A1, A1A2, A1A3, A2A3}
{A1A2, A1A3} or {A1A2, A1A3, A2A3}	A1A2	randomly assign A1A3 and A2A3 with probabilities 0.5 and 0.5, independently to each sib
	A1A3	A1A2
	A2A3	A1A2
{A1A3, A2A4},	A1A3	A2A4
{A1A3, A1A4},	A1A4	A2A3
{A1A3, A1A4, A2A3} or	A2A3	A1A4
{A1A3, A1A4, A2A3, A2A4}	A2A4	A1A3

Note: {A₁A₃, A₁A₄, A₂A₄}, {A₁A₃, A₂A₃, A₂A₄}, and {A₁A₄, A₂A₃, A₂A₄} are configurations equivalent to {A₁A₃, A₁A₄, A₂A₃} because A₁, A₂, A₃, and A₄ represent just generic alleles and are not limited to specific alleles.

Table A3.

Conditional Contribution of Nontransmitted Genotypes when Only Children's Genotypes Are Available at Marker Locus A

Children's Genotype Configuration	Transmitted	Nontransmitted
{A1A1}	A1A1	A1A1
{A1A2}	A1A2	A1A2
{A1A1, A1A2}	A1A1	A1A2
	A1A2	random assignment of A1A1 and A1A2 that keeps the number of each proportional to that in the observed set
{A1A1, A2A2} or	A1A1	A2A2
{A1A1, A1A2, A2A2}	A1A2	A1A2
	A2A2	A1A1
{A1A2, A1A3}	A1A2	A1A3
	A1A3	A1A2
{A1A3, A2A4}	A1A3	A2A4
	A2A4	A1A3
{A1A1, A2A3},	A1A1	A2A3
{A1A1, A1A2, A1A3},	A1A2	A1A3
{A1A1, A1A2, A2A3} or	A1A3	A1A2
{A1A1, A1A2, A1A3, A2A3}	A2A3	A1A1
{A1A2, A1A3, A2A3}	A1A2	randomly assign A1A2, A1A3, and A2A3 with probabilities 1/3, 1/3, and 1/3 independently to each sib
	A1A3	randomly assign A1A2, A1A3, and A2A3 with probabilities 1/3, 1/3, and 1/3 independently to each sib
	A2A3	randomly assign A1A2, A1A3, and A2A3 with probabilities 1/3, 1/3, and 1/3 independently to each sib
{A1A3, A1A4, A2A3} or	A1A3	A2A4
{A1A3, A1A4, A2A3, A2A4}	A1A4	A2A3
	A2A3	A1A4
	A2A4	A1A3

Appendix B: A Schematic Illustration of the Pedigree-Based GMDR Algorithm

We briefly use Figure S1 to illustrate the steps involved in conducting the pedigree-based GMDR method. Without loss of generality, we consider here a classic TDT design in which each family consists of an affected child and both parents. To focus on exposition of the data-reduction algorithm, we assume in Figure S1 no covariate and take t(y_ij) = 0.5 for affected children, although we can use any appropriate statistic instead of this, as deemed necessary. From Equation (1), all the transmitted genotypes in informative family triads constitute cases whereas the nontransmitted genotypes serve as artificial internal controls, thus constituting a balanced case-control sample. In Step 1, the pairs of the transmitted and nontransmitted genotypes are randomly split into some number of equal parts for crossvalidation; as an illustration, 10-fold crossvalidation is used in Figure S1. One subdivision is used as the testing set and the rest as the independent training set. Then, Steps 2 through 5 are run for the training set and Step 6 for the testing set. (To reduce the fluctuations resulting from chance divisions of the data, Steps 2 through 6 are repeated in turn for each possible crossvalidation and the results are averaged. The consistency of the model across crossvalidation training sets, i.e., how many times the same MDR model is identified in all the possible training sets, is also evaluated.) In Step 2, a set of n genetic and/or discrete environmental factors is selected from the list of all factors. In Step 3, the possible multifactor classes or cells defined by the n factors are represented in n-dimensional space. Then, the sum of statistic values is calculated within each multifactor cell. In Step 4, each multifactor cell in n-dimensional space is labeled as either “high risk” if the average of the statistic values meets or exceeds a preassigned threshold T (e.g., T = 0), “low risk” if the threshold is not exceeded, or “empty” otherwise. A model is formulated by pooling high-risk cells into one group and low-risk cells into another group. In Step 5, all potential combinations of n factors are evaluated sequentially for their ability to classify statistic values in the training data and the best n-factor model that yields minimum misclassification error is chosen. In Step 6, the independent testing set is used to estimate the prediction error of the best model selected from Step 5. Finally, among this set of best models, we pick the model that has minimum prediction error and/or maximum crossvalidation consistency. We can use a sign test and/or a permutation test for prediction accuracy to assess the significance of an identified model.

Supplemental Data

Supplemental Data include one figure and four tables and can be found with this article online at http://www.ajhg.org/.

Web Resources

The URLs for data presented herein are as follows:

• dbSNP, http://www.ncbi.nlm.nih.gov/SNP/

• Ensembl Human, http://www.ensembl.org/Homo_sapiens/

• Entrez Gene, http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?db=gene

• Epistasis.org, Computational Genetics Laboratory, http://www.epistasis.org/

• Epistasis Blog, http://compgen.blogspot.com/2006/05/mdr-applications.html

• MDR-PDT software, http://chgr.mc.vanderbilt.edu/ritchielab/MDRPDT.html

• Online Mendelian Inheritance in Man (OMIM), http://www.ncbi.nlm.nih.gov/Omim/

• PGMDR program, http://www.healthsystem.virginia.edu/internet/addiction-genomics