On the frequency of copy number variants

Abstract

Motivation: Estimating the frequency distribution of copy number variants (CNVs) is an important aspect of the effort to characterize this new type of genetic variation. Currently, most studies report a strong skew toward low-frequency CNVs. In this article, our goal is to investigate the frequencies of CNVs. We employ a two-step procedure for the CNV frequency estimation process. We use family information a posteriori to select only the most reliable CNV regions, i.e. those showing high rates of Mendelian transmission.

Results: Our results suggest that the current skew toward low-frequency CNVs may not be representative of the true frequency distribution, but may be due, among other reasons, to the non-negligible false negative rates that characterize CNV detection methods. Moreover, false positives are also likely, as low-frequency CNVs are hard to detect with small sample sizes and technologies that are not ideally suited for their detection. Without appropriate validation methods, such as incorporation of biologically relevant information (for example, in our case, the transmission of heritable CNVs from parents to offspring), it is difficult to assess the validity of specific CNVs, and even harder to obtain reliable frequency estimates.

Availability: Software implementing the methods described in this article is available for download at the following address: http://www.isites.harvard.edu/icb/icb.do?keyword=k36162

Contact: iionita@hsph.harvard.edu

Supplementary informantion: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Copy number variants (CNVs) represent a recently discovered class of genetic variation, defined as DNA segments of length at least 1 kb, that vary in copy number among individuals in a population. In contrast to the well-developed databases available for single nucleotide polymorphisms (SNPs), we are still in the early stages of discovering and characterizing CNVs. Over the past few years, various computational and experimental methods have been proposed for the discovery of CNVs in the human genome (Conrad et al., 2006; Hinds et al., 2006; Iafrate et al., 2004; Jakobsson et al., 2008; Korbel et al., 2007; McCarroll et al., 2005; Pinto et al., 2007; Redon et al., 2006; Sebat et al., 2004; Wang et al., 2007; Zogopoulos et al., 2007). Their applications to various types of data show that CNVs are pervasive in the human genome. The database of genomic variants (DGV) (http://projects.tcag.ca/variation/) provides useful information on the structural variation reported in these peer reviewed research studies. However, much work remains to be done; in particular, information on the frequency of CNVs is scarce. Many studies employing computational methods report that, overall, the frequencies of most CNVs are likely to be low [e.g. 95% of CNVs reported by Pinto et al. (2007) have frequencies of<2%]. Understanding the true frequency spectrum for CNVs is important in its own right, and also for various applications, such as the problem of detecting associations between these variants and complex phenotypes, such as diabetes, asthma, cancer. Current genome-wide association studies have very low power to detect associations with single rare variants.

In this article, our goal is to investigate the frequencies of CNVs. For CNV discovery and frequency estimation, we apply the following two-step procedure. In the first step, the discovery step, the locations of CNVs are detected using a stringent criterion, based on the presence of an apparent CNV segment in multiple individuals. An initial frequency estimate is also computed at this stage (as usually estimated from results of segmentation procedures). In the second step, the frequency update step, the frequencies of the CNV regions discovered at Step 1 are re-estimated using a less stringent criterion. The idea of this second step is to identify additional individuals with a true CNV segment which, due to a lower amplitude log₂ variation, are missed in Step 1. Of course, the caveat is that such a relaxed criterion will not only capture true CNV segments, but also false ‘CNV segments’. However, the availability of family information, in particular the ability to check the transmission of CNV segments from parents to offspring, allows us to focus only on the most reliable CNV regions, and report robust frequency estimates for these regions.

2 METHODS

2.1 CNV discovery and frequency estimation

2.1.1 Step 1—CNV Discovery

The first step in our procedure is to discover the locations of putative CNVs. We employed the circular binary segmentation (CBS) algorithm proposed by Olshen et al. (2004), and implemented in the R package ‘DNAcopy’ of the Bioconductor project. This algorithm analyzes one individual at a time and divides the data (i.e. log₂ intensity ratios) into segments such that probes belonging to the same segment come from the same common distribution. The algorithm tests for change points using a maximal t-statistic with P-value evaluated by a permutation procedure (Venkatraman and Olshen, 2007). The result of this procedure is a set of breakpoints, corresponding to the start/end points of CNV segments detected for an individual. (Note: As recommended in the documentation of the DNAcopy package, single point outliers are smoothed out before the segmentation procedure. After smoothing, the segmentation is run with change points that do not separate the two means by at least two SDs being removed.)

The ability of this approach to detect true CNVs is increased when data on many unrelated individuals are available and the frequency of CNVs is not small. Naturally, breakpoints occurring at the same location/marker across multiple, different individuals are good candidates for locations of CNVs. Our aim in this first step is to detect such regions.

The problem of discovering CNV regions from segmented data can be reformulated naturally in a graph theoretic framework. We construct a large graph G, defined by a set of vertices and a set of edges connecting various vertices. The vertices are represented by all the markers (on a chromosome, as each chromosome is analyzed separately) and the edges by the CNV segments identified by the CBS procedure; an edge is defined between two markers/vertices if there is a segment bounded by the two markers in any of the individuals in the dataset. Each vertex has a degree associated with it, namely the number of edges that leave that vertex. Note that an edge can occur multiple times, corresponding to the same segment being identified in multiple individuals. Vertices with many incident edges are ‘hotspots’ for breakpoints, and will have large degree. However, the majority of vertices will have degree 0, with the CNV regions appearing as islands of concentrated breakpoints interspersed among breakpoint-poor regions along the chromosome. To find these breakpoint-rich regions, a simple algorithm that traverses the graph (such as depth-first search — DFS; Cormen et al., 2001) and finds its connected components can be applied. As a result, the graph is decomposed into small connected components, corresponding to CNV regions (see Fig. 1 for an example of a component corresponding to a known CNV). In most cases, the CNV segments are small, with segments between close-by markers. However, isolated edges between markers far apart may also occur reflecting either a true or a spurious segment. Edges between markers far apart (i.e. edges uniting markers at least 20 markers apart) and which occur sporadically (i.e. only once) are removed from the graph prior to the DFS traversal. In our experience, the majority of breakpoints in common CNVs are focused on a few markers. This observation was also noticed in other studies (de Smith et al., 2007; Gilling et al., 2006).

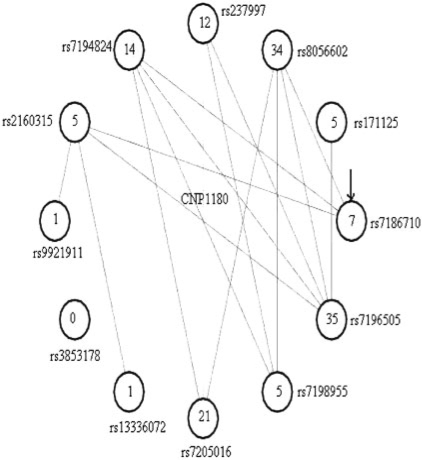
Fig. 1.

The graph corresponding to a CNV region (CNP1180—Redon et al., 2006). This graph has 12 vertices (consecutive markers in the genome, the start marker is rs7186710 and continues in a clock-wise direction) and edges between the vertices, some occuring multiple times. Each vertex has a degree, defined as the number of edges incident to the vertex (i.e. the number of segments that have that vertex as an extremity). The degree is shown inside the circle corresponding to the vertex/marker. Some of the vertices have very high degree (e.g. rs7196505 has degree 35), signifying multiple segments in different individuals that have that marker as an extremity. Note that all markers that sit physically in the region delimited by the connected component are automatically included in the CNV region, regardless of whether they are connected (by an edge) to the graph or not (e.g. marker rs3853178).

Then, we select as our candidate CNV regions all connected components in the graph that contain at least one marker with relatively high degree. (More precisely, a CNV region is defined as the region delimited by the markers in the corresponding connected component.) For our application (next section), we use 7 as the lower threshold for the degree at a marker. To justify this threshold, we assume that each marker is equally likely to be a breakpoint (this assumption may not be accurate, as markers in regions with lots of other markers are more likely to be breakpoints, than markers in less dense areas). Then the number of breakpoints (summed over all individuals in the sample) happening at one particular marker m1 can be approximated by a Poisson distribution, under the null hypothesis of breakpoints being randomly distributed over markers:

where λ=B/M, B is the total number of breakpoints, M is the total number of markers and k is the observed number of breakpoints at the marker under consideration. [We used k≥7 for all chromosomes, as the resulting P-value was always <10⁻⁷; the Bonferroni cutoff is 0.05/550;000≈10⁻⁷; for example, for chromosome 1, there are M=41566 markers and B=4872 breakpoints; then P(#breakpoints at marker m1≥7)=6.4×10⁻¹¹.]

At the end of this step, we acquired a set of candidate CNV regions. For each such CNV region, we obtain an estimated frequency (Freq1) from the individuals that have a segment overlapping the CNV region. In Step 2, we propose a procedure to update these frequencies.

2.1.2 Step 2—CNV frequency re-estimation

For each CNV region detected in Step 1, we propose a procedure to re-evaluate each individual's status with regard to having a CNV segment at that location. This step allows us to get an updated estimate of the frequency (Freq2) of the CNV region.

Our criterion for updating the status of an individual is defined as follows. Let c₁,…,c_l be the log₂ ratio values at the markers within the CNV, of length l, and x₁,…,x_N be the log₂ ratio values at the markers within a segment of length N, adjacent and to the left of the CNV. We assume the variances for the two sets of data are the same and then define the following t²-statistic for each individual:

Under the null hypothesis of equal means, t² follows an F-distribution with (1,N+l−2) degrees of freedom. The same t²-statistic is computed for the right side adjacent to the CNV. In our application, we used N=100. Then for each individual, we count the individual as having a CNV segment if the following conditions are met:

(1)

(2)

(3)

[In (1) the deviation, i.e. duplication or deletion, is in the same direction as in Step 1.] We note that this type of statistic is similar to the ones used in segmentation algorithms (Daruwala et al., 2004; Olshen et al., 2004), only the threshold is more liberal. Using this rule, we update the status of each individual and calculate the new frequency (Freq2).

It is important to note that the CNV regions that we find (after step 1) are likely to extend beyond the true underlying CNV regions, due to reasons such as noisy data and/or marker density on the array, and also due to our lumping together the various CNV segments from different individuals into a single CNV region. The effect of this imprecision of the extent of a CNV region is that, in step 2, those individuals that have a much smaller CNV segment may not be identified as having a segment using the criteria (1)–(3) above, and so even in step 2 there is the risk of false-negatives.

3 RESULTS

We applied this method to a dataset of 1170 individuals, part of the Childhood Asthma Management Program (CAMP) Genetics Ancillary Study (CAMP Research Group 1999). All individuals were genotyped at ∼550 000 SNPs (Illumina's HumanHap550 BeadChip, Illumina, San Diego, CA). logR intensity ratios (Peiffer et al., 2006) were computed for each SNP using Illumina's Bead Studio package. These individuals belong to 386 families (mostly trios), and the children have asthma.

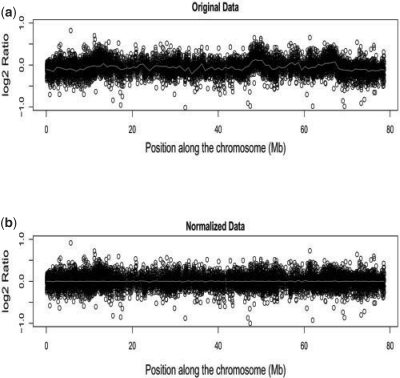
As in Marioni et al. (2007), we noticed the presence of a technical artifact in our dataset, i.e. wave-like patterns that can look as CNVs, as shown in Figure 2. Therefore, we first proceeded to remove these patterns from data by fitting a loess curve to the log₂ ratios on each sample/chromosome independently, as recommended by Marioni et al. (2007). After this normalization step, we employed our two-step procedure and detected a total of 839 putative copy number variable regions, together with frequency estimates (Freq1 and Freq2).

Fig. 2.

Wave-like patterns in the original logR intensity data for a single individual (a) are being removed (b). The red, solid curve is the loess fit to the data.

We used two independent measures to validate these CNV regions. First, we assessed the overlap between our CNV regions and those present in the DGV. We quantify the overlap between any two CNV regions using the Jaccard coefficient defined as the size of the intersection divided by the size of the union of the two regions. A second and perhaps more important validation measure is the significance of the familial clustering of a CNV region. For a CNV region, we define a measure of familial clustering as the proportion of CNV calls identified in an offspring that were also identified in either parent. We refer to this measure as the heritability of the CNV region, although it is more an attempt to measure consistency with Mendelian transmission. Note that since our CNV detection and frequency estimation methods are agnostic to the family relationship, the frequency estimates of CNV regions with high heritability are not biased.

We calculate the statistical significance of the clustering of CNV calls in families given the estimated frequency and under the null hypothesis of the CNV being not heritable (see Appendix). Note that while a low heritability for a CNV does not necessarily mean that the CNV is not real, a high heritability is strong evidence for the veracity of the CNV (especially since our CNV detection method does not take into account the family information).

The mean heritabilities for CNVs using the Steps 1 and 2 estimates were 0.35 and 0.47, respectively. These low heritability estimates can be due to various reasons, including false positive/negative results in the CNV discovery method, de novo CNVs, or a combination of these reasons. We, therefore decided to concentrate on the fraction of CNVs with higher heritability estimates, as these are the ones that we can make predictions about with higher confidence. We selected the 139 CNV regions with a heritability estimate in Step 2 above 0.70, and for these we show frequency estimates (Freq1 and Freq2) and also an approximate lower bound for the unknown true frequency (see Appendix). On average, for these 139 CNV regions, using the estimated frequencies in Step 1 we detected 7.8 CNV calls per individual, and using the updated frequencies in Step 2 we detected about 10.7 CNV calls per individual.

In Tables 1–4 (Supplementary Material), we show the detailed results. Notably, 82% of these 139 selected CNV regions had a non-zero overlap with a CNV in the DGV (h18.v3), in contrast to only 55% for all 839 CNV regions discovered at Step 1. Moreover, the familial clustering for 132 of them (95%) was also highly significant (P < 10⁻⁷).

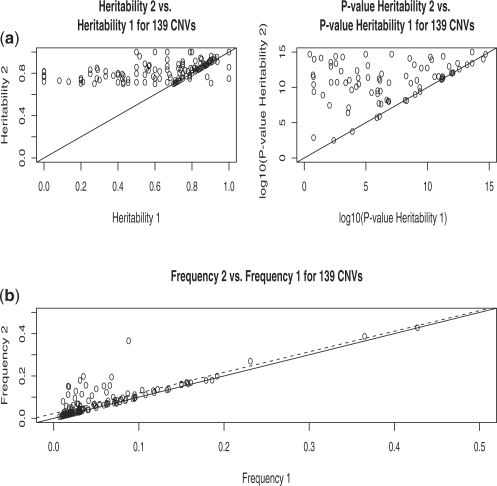
Figure 3 summarizes the tables in a graphical way. We show significant increases in frequency estimates obtained in Step 2 over those in Step 1. Supporting these frequency increases, we also show that the resulting increases in heritability in Step 2 compared with Step 1 are very significant.

Fig. 3.

Summary plot for 139 CNVs with high heritability after Step 2. Heritability Step 2 versus Heritability Step 1, together with their significance (a). Frequency Step 2 versus Frequency Step 1 (b). The solid line in all graphs is y=x. The broken line in (b) is the regression line.

For CNVs with high heritability and very significant familial clustering (such as the ones we selected), the frequency estimate in Step 2 has to be fairly good, as not many false positives/negatives can be added before the heritability estimates and/or their significance become low. It is in fact possible to calculate an approximate lower bound for the true unknown frequencies of these CNVs. This is important, as it constitutes additional support to the high increases in frequency for some of the CNVs (the CNVs with increases of over 50% in Freq2 versus Freq1 are marked with ⋆ in Tables 1–4 in Supplementary Material). For example, for the CNV starting at marker rs1065024 in Table 3, the frequency estimates are: Freq1=0.04, Freq2 =0.20 and the lower bound for the true frequency is 0.13. Similarly, for the CNV starting at marker rs7091141 in Table 1, the frequency estimates are: Freq1=0.06, Freq2=0.12 and the lower bound for the true frequency is 0.11.

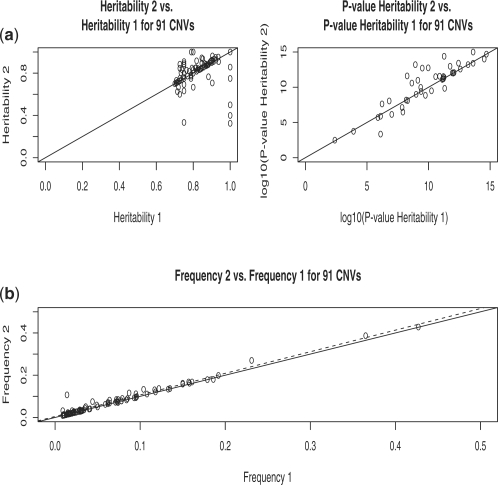
As an additional check that our second step is sensible and identifies true CNVs, we also asked how many of the CNV regions with high heritability in Step 1 (hence likely true CNVs) are present among the 139 CNV regions with high heritability in Step 2. Out of 91 CNVs with heritability above 0.70 in Step 1, 81 (89%) have heritability at least 0.70 in Step 2 as well. Hence, most CNVs with high heritability in Step 1 maintain high heritability in Step 2 as well. Moreover, the frequency increases in Step 2 over Step 1 for these CNVs are small, as expected (Fig. 4). The idea is that CNV regions that have high heritability in Step 1 are likely to be already well detected in Step 1, and hence Step 2 cannot add much improvement over Step 1. It is those CNVs, which in reality are highly heritable, but which have low estimated heritability in Step 1, due to false negative results, for which Step 2 can detect additional individuals with CNV segments, resulting in higher heritability estimates in Step 2. In Figure 5, we show an example of how Step 2 helps in identifying the parent that transmitted a CNV segment to both of its children, with one child identified in Step 1 as having a CNV segment. In fact, for this CNV, of estimated frequency 0.12, its heritability in Step 2 is 0.96, compared with only 0.52 in Step 1.

Fig. 4.

Summary plot for 91 CNVs with high heritability after Step 1. Heritability Step 2 versus Heritability Step 1, together with their significance (a). Frequency Step 2 versus Frequency Step 1 (b). The solid line in all graphs is y=x. The broken line in (b) is the regression line.

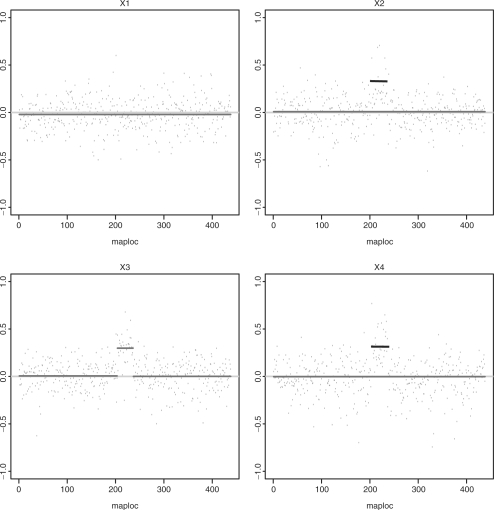
Fig. 5.

The figure depicts the log2 ratio data for a family with parents X1 and X2 and their children X3 and X4. The region depicted includes a CNV segment, estimated to run between positions 201 and 238 on the x-axis. Only one individual (X3) was detected in Step 1 to have an amplification in the region, as shown by the elevated red segment. After Step 2, both individuals X2 (parent) and X4 (child) were detected to also possibly harbor CNVs (shown as black segments).

To summarize, the high overlap with the DGV (82%), the highly significant P-values for familial clustering (95% of CNVs have P < 10⁻⁷), and the fact that 89% of the highly heritable CNVs in Step 1 have high heritability in Step 2, and similar Freq1 and Freq2 estimates, show that the increases in frequencies we observe from Step 1 to Step 2 are reasonable.

4 DISCUSSION

Estimating the frequency distribution of CNVs is an important issue for various reasons, not the least important of which is the ability to perform disease genome-wide association studies with these variants. The current skew toward low-frequency variants poses many obstacles to this important problem in human genetics, as current genome-wide association studies have low power to detect associations with single rare variants.

In this report, we investigated the frequencies of common CNVs. We employed a two-step procedure, whereby in the first step we used a stringent criterion to find the putative locations of CNVs, and in the second step we used a more liberal threshold to find additional individuals with CNV segments in these regions. We use family information a posteriori to draw our conclusions based only on the most reliable CNV regions. For common CNVs (i.e. frequency >1%), our results suggest that the low-frequencies reported thus far may be caused, in part, by stringent criteria, that cause individuals with true CNV segments to be missed. False positives among the low-frequency CNVs discovered so far are also likely, as true rare CNVs are hard to detect, and the low signal-to-noise ratio that characterizes many of the platforms used in the detection process makes their discovery process even harder and less reliable. Ideally, CNV regions should be validated using biologically relevant information, for example, the transmission of heritable CNVs from parents to offspring etc. In the absence of such information, it is difficult to assess the validity of specific CNVs, and even harder to obtain reliable frequency estimates.

Funding

NIH/NIMH (R01 MH59532); National Heart, Lung and Blood Institute, National Institutes of Health (U01 HL075419, U01 HL65899, P01 HL083069, R01 HL 086601, T32 HL07427 to CAMP Genetics Ancillary Study).

Conflict of Interest: none declared.

APPENDIX

CALCULATION of SIGNIFICANCE FOR HERITABILITY

For a CNV region, we estimate its heritability by the proportion of CNV segments identified in an offspring that were also identified in either parent. Note that since our CNV detection method does not make use of the family information, the heritability estimate is not biased. The definition depends on the estimated frequency of the CNV; in particular, a higher frequency estimate is by chance alone likely to produce a higher heritability. We calculate a significance value for the heritability estimate given the estimated frequency, as follows. Let N be the total number of offspring with a detected CNV segment, and let C be the number of those offspring that also have a parent with a CNV segment. Under the null hypothesis of the CNV being not heritable, C follows a binomial distribution with parameters n=N and P=1−(1−f)², where f is the estimated frequency, and 1−(1−f)² is the probability of observing at least one of the two parents with a CNV segment. This allows us to calculate a P-value.

LOWER BOUND CALCULATION

We calculate an approximate lower bound for the true frequency of a CNV, based on the observed heritability and estimated frequency in Step 2. A rough lower bound can be calculated as the product of the observed heritability and the estimated frequency (in other words, considering only the CNV segments in children that were determined to have been inherited from parents). However, this does not take into account the fact that randomly it is possible that both child and parent have a ‘CNV segment’ (an extreme example would be when everybody is wrongly determined to have a CNV, in which case the heritability is 1, the estimated frequency is 1; and the rough lower bound is also 1). Below we derive a lower bound that takes this possibility into account.

Let N_t be the true number of offspring with a CNV segment, and p_t be the true CNV frequency. We assume that our estimated frequency in Step 2 is p_o=x · p_t, and the corresponding number of offspring with CNV segment is N_o=x · N_t.

In the following, we are going to assume that in Step 2 we overestimate the true frequency, and calculate an upper bound for x≥1 (or equivalently a lower bound for the true frequency p_t). For simplicity, we also assume that we are able to detect all children with a true CNV segment and their parents. This assumption is only going to result in larger upper bounds for x, as for the same heritability, we are in fact saying that there are no false negatives, and the observed reduction in the value of the heritability from the maximum theoretical value of 1 could be due to the presence of more false positive findings.

The heritability can then be approximated by:

This leads to the following equation:

Since x · p_t ≥ 0, we get the following inequality:

This inequality is satisfied when x≤x₁ or when x≥x₂, where x₁ and x₂ are functions of the observed heritability h and the true, unknown p_t. x₂ turns out to be too big, and leads to non-significant P-values for the heritability estimate. Therefore the only useful bound is the upper bound x≤x₁, resulting in an upper bound for the observed frequency (p_o=x·p_t≤x₁·p_t).

It is then easy to find a lower bound on the true frequency, using the observed frequency (Freq2) and the heritability estimate h. The reasoning is as follows. If the observed frequency (Freq2) is larger than x₁·p_t (i.e. the upper bound for the observed frequency calculated based on the observed heritability estimate and an assumed true frequency p_t), then the true frequency has to be bigger than the specific value assumed for p_t in the calculation of x₁. Precisely, the lower bound for the true frequency that we obtain is: min p_t} over the following set: {observed heritability is h, calculated upper bound based on h and p_t≥Freq2.

JACCARD COEFFICIENT OF OVERLAP

The Jaccard coefficient used to quantify the overlap between a CNV region in our set and a CNV region in the DGVs is defined as follows. Let I₁ and I₂ be two intervals, i.e. two CNV regions. Then, we define the overlap as the size of the intersection divided by the size of the union of the two regions.

In particular, O=0 for no overlap and O=1 for complete overlap.

CAMP GENETICS ANCILLARY STUDY

CAMP is a multicenter North American clinical trial designed to investigate the long-term effects of inhaled anti-inflammatory medications in children with mild to moderate asthma. Details regarding sample collection, phenotype measurements, and primary outcome analysis have been previously reported (CAMP Research Group 2000). A diagnosis of asthma was based on methacholine hyperresponsiveness (provocative concentration of methacholine causing a 20% fall in FEV1 [PC20] ≤12.5 mg/ml) and one or more of the following criteria for at least 6 months in the year before recruitment:(1) asthma symptoms at least two times per week, (2) at least two uses per week of an inhaled bronchodilator and (3) use of daily asthma medication. The Institutional Review Board of the Brigham and Women's Hospital (Boston, MA, USA), as well as those of the other CAMP study centers, approved this study. Informed assent and consent were obtained from the study participants and their parents to collect DNA for genetic studies. DNA from peripheral blood samples was obtained from 983 participants and 1,517 parents. Of these, 422 complete nuclear families of self-reported white ancestry were genotyped using the Illumina Infinium 550K SNP array (Illumina, San Diego, CA).